Preprint
Article
Effect of a Long-Range Dislocation Pileup on the Atomic-Scale Hydrogen Diffusion near a Grain Boundary in Plastically Deformed BCC Iron
Altmetrics
Downloads
153
Views
111
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
09 July 2023
Posted:
10 July 2023
You are already at the latest version
Alerts
Abstract
The microstructure of oil pipeline steels is polycrystalline due to the presence of a complex grain boundary (GB) network in them. The performance of them when exposed to stresses in corrosive environments is largely dictated by the interplay between the hydrogen (H) diffusion, the dislocation slip, and their interactions with the GBs. However, the slip-GB interaction in the presence of H and the subsequent cracking along the GBs remains not fully understood up to date. It is challenging to simultaneously resolve the collective dislocation motions away from the GBs together with the H diffusion near the atomically structured GBs using single-scale techniques. To address this challenge, taking bcc iron as a model material, here we present a a concurrent atomistic-continuum (CAC) computational analysis of the interaction between dislocation slip and a H-charged GB. With the large number of dislocations-mediated plastic flow away from the GB together with the atomistic structure evolution at the GB being simultaneously retained, several main findings from our simulations are: (i) the large number of dislocation-mediated pileup-induced internal stress nearby the H-charged GB can be as high as 3GPa; (ii) the more dislocations accumulated nearby the GB, the slower H diffusion ahead of the slip-GB intersection; (iii) H atoms diffuse fast behind the pileup tip, get trapped within the GB, and diffuse slow ahead of the pileup tip; (iv) the local stresses nearby the pileup tip exhibits a strong heterogeneity along the dislocation line direction. This differs from the common wisdom in many existing 2D theories/models. The buildup of such a high local stress heterogeneity leads to inhomogeneous H diffusion within the GB plane. The CAC simulation-predicted local H diffusivity, Dpileup−tip, and local stresses, σ, nearby the GB are then correlated with each other and consolidated into a mechanics model by considering the dislocation pileup as an Eshelby inclusion. These findings will provide researchers with opportunities to: (a) characterize the coupled dynamics between plasticity, H diffusion, and crack initiation underlying the hydrogen-induced cracking (HIC); (b) develop mechanism-based constitutive rules to be used in diffusion-plasticity coupling models for understanding the interplay between mechanical and mass transport in materials at the continuum level; and (c) connect the atomistic deformation physics of polycrystalline materials with their overall performance in aqueous environments, which is currently difficult to achieve in laboratory experiments.
Keywords:
Subject: Engineering - Metallurgy and Metallurgical Engineering
1. Introduction
Compared to rail, trucks and tankers, oil pipeline remains as the most economical and efficient means for crude oil transportation in term of the routes flexibility and the transported quantities. As a mixture of solid, liquid and gaseous phases, crude oil contains sediments, water, salts, carbon monoxide, and acid gases such as . The presence of facilitates the H diffusion into pipeline steels, which interacts with material defects, such as dislocations and grain boundaries (GBs), resulting in a hydrogen-induced cracking (HIC) and then oil leakage. It was reported that more than 50% of the failure experienced in oil and gas production industry is caused by HIC in oil pipelines [1]. In order to combat with oil spills, a computational framework that can predict the onset of HIC in polycrystalline oil pipeline materials is needed. Up to date, such a predictive computational framework, however, has not been well established yet due to an intrinsic complexity associated with the coupling between dislocation plasticity and HIC, which occurs across a broad range of length scales. That is: (a) the H-enhanced localized plasticity (HELP) [2,3] spanning tens of micrometers when a large number (tens or hundreds) of dislocations are blocked by an atomically structured GB [4,5,6]; (b) the buildup of a high internal stress field ahead of such a microscale pileup not decaying to zero until several micrometers away from pileup tip [7,8]; and (c) the H-enhanced decohesion (HEDE) [9] of the GB at the atomic scale if such a long-range high internal stress cannot be fully relieved by a dislocation cross-slip, transmission, twinning, phase transformation, hydride formation, and so on [10,11,12]. Clearly, a mechanistic understanding of the fundamental mechanisms underlying HIC in plastically deformed polycrystalline materials necessitates computer simulations ranging from the atomistic up to the continuum level.
At the atomic scale, molecular dynamics (MD) has been one most powerful tool for studying H diffusion, dislocation motion, GB structure evolution, as well as their interaction with each other. Through tracking the motion of each atom in the simulation cell, MD retains the atomistic nature of materials. It is thus applicable to link GB and dislocation core structural details with the local H diffusivity, which play a key role in HIC but difficult to resolve in experiments. For example, MD simulations were performed to: (1) provide a direct evidence that H diffuses significantly slower around a screw dislocation core than it does in lattices away from the core [13]; (2) quantify the effects of dislocation types, GB and triple junction structures on the H diffusion barrier [14,15]; (3) discover a new mechanism responsible for the ductile-to-brittle transition in bcc iron referred as the H aggregation-suppressed dislocation emission from the crack tip [16]; (4) help explain the H-induced pop-in load reductions in the force-depth curves of a H-charged sample under indentation [17,18]; (5) identify the possible interstitial H sites at a given GB by dividing it into polyhedral packing units with the H segregation energies at these sites being calculated and then fed into the Rice-Wang thermodynamic theory of interfacial embrittlement [19]; (6) survey the possible nanoscale mechanisms responsible for HELP through quantifying the effects of H on edge dislocation mobility [20]; and (7) analyze the interactions between dislocation and the H-segregated GB [21]. Despite its great popularity, the results from MD simulations need to be understood cautiously because, due to the high computational cost, typical MD simulations employ only one single or a few dislocations very near a GB embedded in a simulation cell with a limited volume [21,22,23,24]. With such a nanoscale simulation cell, the dislocation density becomes unrealistically high. In addition, in many MD simulations, only equilibrium GBs (EGBs) composed of periodic structure units have been considered. As a consequence, the long-range structure heterogeneity of non-equilibrium GBs (NEGBs), especially the GBs charged with H, has been cut off. In such scenario, the forces induced by the interaction between periodic images of dislocations or NEGBs are non-negligible, which may have polluted the results [24,25]. As such, nanoscale MD simulations alone might not be sufficient if one relies on them to develop/calibrate the higher-scale constitutive rules for predicting how the H-charged polycrystalline materials behaves in engineering practices.
By contrast, with a capability of scaling up in length continuum models have been widely used in simulating the deformation behavior of polycrystalline materials exposed to complex environments. In the past several decades, a variety of such models have been developed for characterizing the coupling between plastic flow, H diffusion, and HIC. Here, for the first time, we categorize them into four types as follows.
Type-I: one-way coupling models without considering any underlying grain structures. This type of models follow a pioneering approach by Sofronis and co-workers [26,27,28]. In such models, the H diffusion is considered in conjunction with the material’s elasto-plastic deformation. A two-field boundary value problem is formulated. The displacement field and the H concentration are the two primal kinematic variables. As a first step of such approaches, the traditional elasto-plastic constitutive rules, such as the traditional J2 flow rules, are used in solving for the displacement, strain, and stress fields. Thereafter, H diffusion equation is solved to determine how H is distributed under those stresses and plastic strains. Numerically, this is usually realised via the standard finite element (FE) procedures in a readily available software, such as ABAQUS, through two steps: (a) computing the displacement, strain, stress, and a gradient of them by calling UMAT subroutines; and then (b) solving the H diffusion equation for the H distribution by calling UMATHT subroutines which impose the hydrostatic stress and plastic strains calculated from UMAT on the diffusion. Such models are believed to be "one-way coupling" because only the mechanical effect on H diffusion is considered while the H-induced material property degradation is not. Moreover, such models are always built upon four key assumptions: (i) the material microstructure complexity is smeared out; (ii) H in these models is considered to reside at either normal interstitial lattice sites (NILS) or trapping sites (GBs, dislocation cores, and so on). The H occupancies at NILS and those trapping sites are considered to be always in equilibrium according to Oriani’s theory [29]; (iii) there are no interactions/communications between those trapping sites; and (iv) they only take the reversible shallow traps into account, and thus can be used to estimate the plastic strain-induced concentration of H trapped at dislocations only. In these models, all the deep traps, such as GBs, are ignored and assumed to be filled with H, which obviously may not be the case in reality;
Type-II: two-way coupling models without considering any underlying grain structures. As an extension of the previous one-way coupling model, in this type of approaches, the effect of H on the material property is added through including the H-induced volume dilatation or flow stress reduction into the framework [30,31,32]. By accounting for the effect of H on the materials’ constitutive response, such models could capture the onset of plastic instability in a H-charged materials under deformation. The predictive capability of them is, however, still limited because, in addition to the same assumptions as that in Type-I models, these models further assumed that H always induces a flow stress reduction and a deformation localization. From the microscopic point of view, this assumption argues that the presence of H will only enhance the mobility of dislocations. According to the recent MD simulations [33], this, however, might not be the case. From the macroscopic point of view, this assumption implies that the presence of H will always cause a materials softening. It is inconsistent with the results from many experimental studies, where both the H-induced hardening [34,35] and H-induced softening [2,36,37,38,39,40] were observed;
Type-III: one-way coupling models for polycrystalline materials with the underlying grain structures being explicitly included. In these models, H transport and the elasto-plasticity are simulated through coupling diffusion with crystal plasticity finite element (CPFE) [41,42,43,44,45,46,47]. Particularly, the effects of hydrostatic stress and plastic strain on the H transport were considered when solving the diffusion equation, while the H-induced material property changes in CPFE were not included. Based on the same assumptions as that in [26,27,28], such approaches share similar limitations with Type-I models but gain in one aspect: H diffusion has been linked to the stress fields calculated from CPFE, rather than that from the standard J2 theory [48,49,50]. With the slip and the elasto-plastic anisotropy being accommodated, these models shed light on assessing the effects of material microstructure on the H diffusion, although only in a qualitative sense due to its ’one-way coupling’ nature and a neglect of the H diffusion along dislocations and GBs;
Type-IV: two-way coupling models with the underlying grain structures being explicitly retained [51,52,53,54,55,56]. If one desires to capture of all the salient features of HIC, a fully two-way coupling model is needed and should at least contain four components: (1) a model that can explicitly characterize the heterogeneous stresses/strains induced by the complex grain structures; (2) a diffusion model that is decorated with local stresses/strain for simulating the H occupancy equilibrium between NILS and trapping sites in materials under deformation; (3) a set of constitutive rules for describing the H-induced property degradation, such as the H-induced material softening/hardening [32,57], GB cohesive strength reduction [51,52,53], and so on; as well as (4) a set of constitutive parameters about the H diffusivity, such as the pipe diffusion along the dislocations and GBs. Nevertheless, to the best of our knowledge, such a fully two-way coupling model equipped with all of those four components does not exist yet. For instance, in a pioneering work by Rimoli and Ortiz [51] and a recent work by Pu et. al. [53], a CPFE model for polycrystals, a Fisher model for GB diffusion, as well as a cohesive zone model for intergranular fracture were all integrated together but with a consideration of neither pipe diffusion nor the H concentration dependence of the CPFE model parameters. As an expansion of [51], in [52], the effects of initial dislocation density and its evolution on HIC were added. Comparing with the traditional CPFE in [51], such a framework indeed gained more physics about how the dislocation slip reacts with the GBs in the presence of H, although with a neglect of the H diffusion along the GBs. By contrast, in a recent diffusion-stress coupled model [54], the GB diffusion under the effect of a normal cohesive traction was explicitly included, but the effects of H on the slip inside the grains were ignored. Obviously, existing two-way coupling models usually include only a few among those four components. Moreover, even with those four components being all equipped, Type-IV models will still require the constitutive rules, such as the H concentration-dependent CPFE model parameters, GB cohesive strength, the local stress-dependent GB diffusivity, and so on, to be carefully calibrated from either experiments or fine-scale simulations. This is non-trivial but is definitely necessary if one desires to achieve a high predictive capability.
Overall, neither continuum nor atomistic models alone can capture all the salient physics underlying the interplay between H diffusion, plastic flow, and the subsequent HIC. Multiscale models are needed to overcome many inherent difficulties in them. To meet this need, a concurrent atomistic-continuum (CAC) methoddeveloped in [58,59,60,61,62,63,64,65] is deployed here. The CAC method is built upon an atomistic field formulation [66]. The governing equations in this formulation are identical in form to that in continuum theories. Thus, continuum modeling techniques, such as FE, can be used to solve them. The utilization of FE in regions where materials deform cooperatively leads to a coarse-grained (CG) model [59,60,62,67]. The combination of CG and atomistic leads to a CAC model. The resulting CAC model was shown to be effective and efficient in predicting: (i) the heterogeneous stress field evolution in polycrystalline SiC with different chemical dopants on the GB [68] and (ii) the formation of a microscale dislocation pileup followed by a atomic-scale dislocation transmission [69], twinning, and phase transformations (PTs) [70,71]. In this paper, taking the plastically deformed bi-crystalline bcc iron sample as a model system, the reaction between a 0.2 m long dislocation slip and an atomically structured GB in the presence of H is simulated by CAC. With the interatomic potential being the only constitutive rule, at a fraction of the cost of full MD simulations, the coupled dynamics between the microscale dislocation slip, the long-range internal stress buildup, and the atomic-scale H diffusion at the GBs is characterized. In the rest of this paper, we first briefly introduce the methodology and the computer model set-up in Section 2. CAC simulations results are then presented in Section 3.1. Thereafter, we conclude this paper with a summary of the major findings and a discussion of future research in Section 4.
2. Computer Model Set-up
The CAC model for a bi-crystalline bcc iron sample containing a GB charged with H is shown in Figure 1. One main novelty of such a CAC model is to bridge several length scales relevant to HIC in one single model. In details, it explicitly accommodates the GB at an atomistic resolution while the lagging dislocations away from GB in a coarse-grained (CG) description using FEs. In this way, a majority of the atomistic degrees of freedom (DOF) are eliminated by assuming a collaborative deformation at the lattice-cell level in the CG domains, where the displacements of atoms will be constrained by the FE nodal displacements. Such a computational set-up is multiscale in nature and has two unique features: (i) it requires the interatomic potential as the only constitutive rule, such as the EAM potential for the Fe-Fe and Fe-H interactions [16] used in this work; and (ii) it can scale up to microns and even above but retains an atomistic resolution nearby the critical region (GB in this work) in the materials. A variety of defects, including screw/edge dislocations, twist/tilt GBs, and crystallographic orientation-dependent phase boundaries (PBs) can be constructed as desired. It should be noted that the H segregation from the far region into the GB is not simulated here. As such, a certain number of H atoms at a concentration of 0.5% are directly introduced into a region in the vicinity ( 4nm on both sides of the GB) of the atomically structured GB.
The lattice orientations are chosen to be , , and in the left grain, and , , and in the right grain, respectively. In this way, one of the slip planes, along which the dislocation pileup will be formed in the left grain, is along y direction and perpendicular to the GB plane. The crystalline grains in the domains 4nm away from the GB are discretized into coarse FEs. Each FE contains 512 atoms. These FEs are carefully configured (see details in [58,67]). They can slide with respect to each other for accommodating the dislocation slip along the FE boundaries. Such a CG description of dislocation was shown to be a first model of its kind that can capture the collective behavior of many µm-long dislocation lines without smearing out the atomic-level kink dynamics along each of them [67]. For the sample with a dimension of 95 nm×300 nm×85 nm, such a CAC model contains 381,000 FEs in the two grains and 5.9 million atoms on the GB, which is equivalent to 201 million atoms in a full MD model. In this way, the number of the computational degree of freedom of such a CAC model will be only 5% of that in full MD simulations. This in turn, provides us with opportunities on quantifying how a pileup containing a few to tens of dislocations may affect the atomic-level H diffusion at the GB.
A queue of dislocations with a uniform separation in between are initially introduced into middle plane of the left grain (see the location of one dislocation nearby the GB in the inset picture of Figure 1). As demonstrated in our previous work [58,59,60,61,62], because the CG domain in a CAC model can accommodate dislocations without smearing out their atomistic natures, the dislocations are built into the CG domain through displacing FE nodes according to the elasticity-based solution fof the displacement field around a screw dislocation. Different from traditional FE models in which the neighboring elements are connected by sharing the FE nodes, the FEs in CAC models across the slip plane are disconnected (see the zoom-in view of an inset picture in Figure 1). Thus, the displacement jump induced by a dislocation along the slip plane will be allowed. After dislocations are introduced into the model, the upper and bottom boundaries of the model is moved along but in an opposite direction to impose a shear on the sample. Thereafter the increase of each shear strain, the top and bottom ends of the sample are then fixed for a finite duration to equilibrate the dislocation configuration in the pileup. Since the H diffusion at the GB is concerned here, a temperature of 300K is imposed on the system and maintained as a constant. It should be noted that, although a phonon dynamics-based finite-temperature CG [67]) has been recently developed, the constant temperature in this work is realized through a velocity rescaling scheme (the FE nodal velocities in the CG domain and the velocities of the atoms in the GBs are scaled together towards a desired temperature) for simplicity. A time step of 0.001ps is deployed for the time integration in both the atomistic and CG domains.
3. Simulation Results
3.1. Dislocation pileup-induced internal stress nearby a H-charged GB
After the introduction of dislocations, the model is equilibrated under a constant shear with its top and bottom boundaries being fixed. Due to the large geometric mismatch between the two grains, the random GB under consideration here acts as a strong barrier to dislocation motion. As a consequence, the equilibration of the current model under a shear leads to the formation of a pileup. The separation between dislocations in this pileup is at several nanometers nearby the GB but gradually increases up to tens of nanometers in the region away from the GB. Not surprisingly, a progressive pileup leads to an obvious local stress concentration (Figure 2a,b), where the front and top views of an instantaneous shear stress () distribution are presented, respectively. Although the dislocation pileup is formed only under a very low applied shear, once formed, a stress magnitudes significantly higher than the applied shear can develop at its spearhead. To characterize the dislocation pileup-induced internal stress profile, the material domain ahead of the slip-interface intersection is divided into a series of finite-sized volume elements, each of which is in a dimension of 0.5nm × 0.5nm × 0.5nm. The stresses acting on each volume element can be then calculated and plotted as a function of its distance away from the pileup tip (Figure 2c). Similar to our previous results from 2D simulations, two main observations here are: (a) CAC successfully captures the local stress concentration at a level up to 3GPa when the number of the dislocations in the pileup, noted as n, increases from 5 to 15; (b) this local stress concentration does not decay to zero at a site 80nm away from the pileup tip when n = 15, and is expected to span an even longer range when n > 15.
The stress profiles in Figure 2c can be then fit into an equation resulting from the theory by Eshelby, Frank, and Nabarro [72]:
where K describes the intensity ahead of the slip-GB intersection, r is the distance away from the pileup tip at the GB; is introduced to accommodate an uncertainty of stress state at the reference point where the stress state was relatively low and uniform; is introduced to indicate the position where the maximum stress concentration occurs. A fitting of the CAC simulation data into Equation (1) leads to a quantification of the stress intensity factor, K, and its dependence on the number of the dislocations (see the fitted values of K in Table 1).
3.2. H atom diffusion nearby the slip-GB intersection
As mentioned before, CAC has a capability of quantifying how the long-range plastic flow affects the atomic-level H diffusion nearby the GB because: (i) the CG model for the material domain far away from the GB enables it to accommodate the long-range plastic flow mediated by a large number of dislocations; and (ii) the fully atomistic resolution at the GB enables us to explicitly track the motion of each H atom, from which the GB diffusivity can be extracted. As a demonstration of such a capability, Figure 3a,b present the trajectories of three H atoms in a domain nearby the slip-GB intersection when zero and 15 dislocations are piled up in the region far away from the GB, respectively. It should be noted that, for comparison purpose, the trajectories in both Figure 3a,b are recorded within a same duration. They are all projected on an initial atomistic configuration containing no dislocations nearby the slip-GB intersection. In this way, the H diffusion trajectories with respect to the same atomistic structure are clearly visible and displayed. Three main observations from Figure 3a,b are: (i) within a same time window, the H atom behind the pileup tip in the left grain diffuse a significantly longer distance when n = 15 that it does when n = 0 (see the left trajectories in Figure 3a,b); (ii) by contrast, the H atom ahead of the pileup tip in the right grain diffuse considerably less when n = 15 than it does when n = 0 (see the right trajectories in Figure 3a,b); and (iii) the H atom within the GB (see the middle trajectories in Figure 3a,b) does not diffuse much when comparing with the H atoms in left and right grains no matter n = 15 or n = 0. This is consistent with common wisdom of considering the GB as a deep trapping sites of H.
To determine the H diffusion coefficient at the slip-GB intersection when different number of dislocations participate in th pileup, we measure the mean square displacement (MSD) of those H atoms, calculate the H diffusion coefficient, and connect it with the pileup tip stress intensity factor at n = 0, 5, 10, and 15, respectively. In details, we calculate the MSD of the H atoms ahead of the pileup tip over a finite duration and then the diffusion coefficient, D, as below:
where N is the number of the H atoms ahead of the pileup tip, is the position of the ith H atoms at time t with respect to a reference position of at .
Figure 3c show the MSD curves resulting from such calculations within a duration of 100 ps. It is recalled that, when a particle (the H atoms here) is in a diffusive motion, its MSD will be linearly proportional to the diffusion coefficient. Using the MSD curves in Figure 3c, we measure the local H diffusion coefficient as the slope of each MSD curve. The extracted H diffusion coefficients are summarized as below. Clearly, the more dislocations piled up at the GB, the higher stress intensity and the lower H diffusion ahead of the pileup tip. One consequence of such a reduced diffusion of the H atoms ahead of the dislocation pileup can be a clustering of them. To confirm it, we choose several pairs of H atoms and monitor the relative distances between those two atoms in each pair. Results show that the separation between the two H atoms in each pair decreases upon the increase of the number of the dislocations in a pileup. Figure 3d,e present the typical trajectories of two H atoms in one pair nearby the GB when n = 0 and n = 15, respectively. It is seen that those two H atoms get significantly closer to each other when n = 15 than they do at n = 0.
3.3. H Diffusion Heterogeneity and Its Dependence on Local Stresses
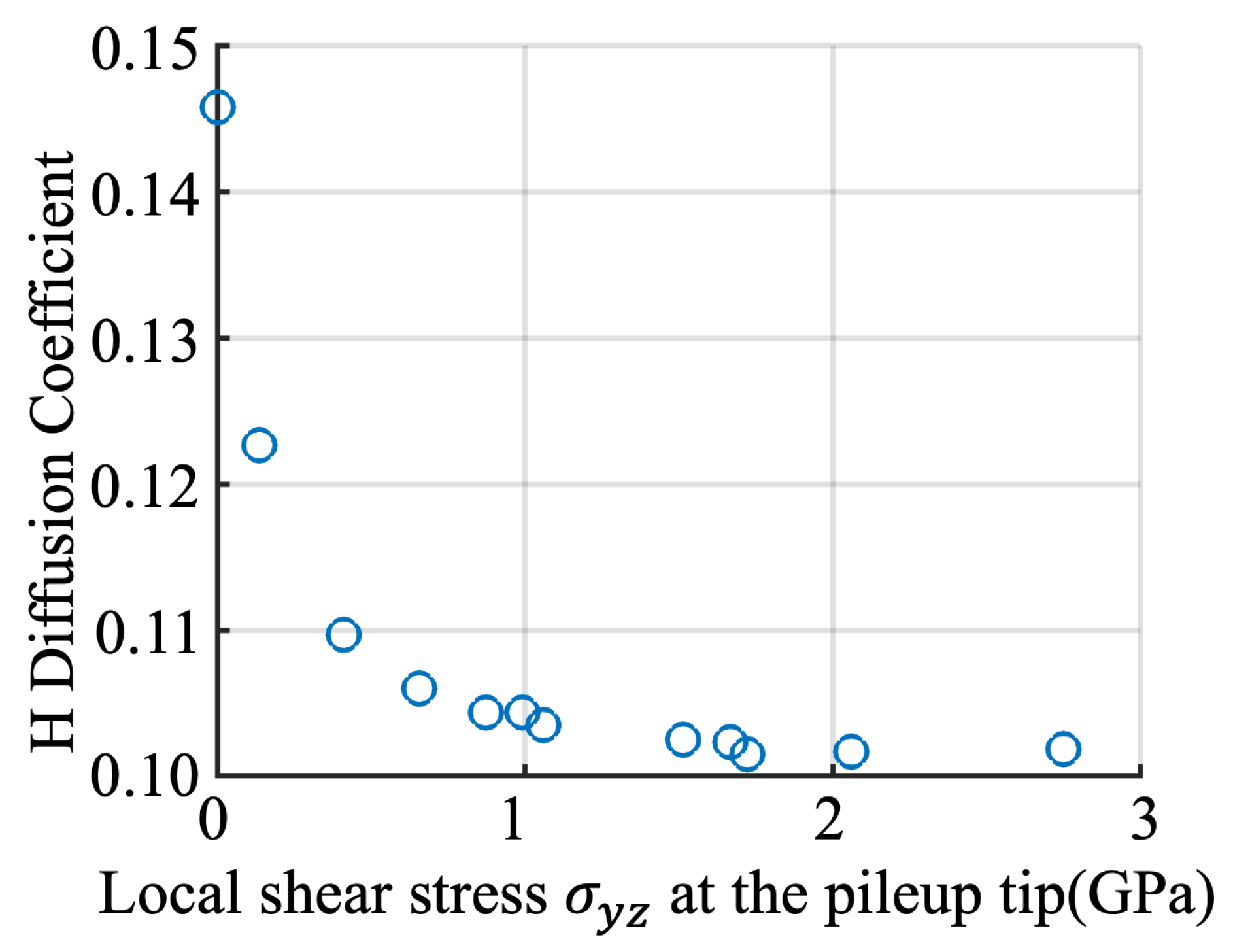
Different from many existing full MD or continuum models/theories [26,27,28] which either only considers very short dislocation segments or formulated in a plane-strain framework by assuming a homogeneity along the dislocation line, the present CAC model is fully three-dimensional and thus can be used to characterize the heterogeneity of the stresses/diffusivity along very long dislocation lines. As a preliminary demonstration, Figure 4a presents an in-plane view of an instantaneous local shear stress distribution resulting from CAC simulations of the pileup of fifteen 95 nm-long dislocations at an atomically structured GB. The H diffusion and stress heterogeneity along the dislocation line direction are then characterized through: (i) dividing the pileup tip material domain along the line direction into 9 bins, each of which is in a width of 10 nm; (ii) calculating the MSD of the H atoms in each bin as shown in Figure 4b and extracting the the slope of each of these MSD curves the local diffusion coefficient; (iii) fitting the stress profiles ahead of each of these 9 bins into Equation (1); and then (iv) correlating the obtained local diffusion coefficients, the local stress intensity factors, and the positions of those 9 bins with each other. The data resulting from the above four steps shows: (a) both the local diffusion coefficients and stress intensity factors can fluctuate more than 20% around the averaged value of them, although such a fluctuation might be suppressed/amplified if a larger/smaller bin width is deployed in the above step-1; (b) for all the 9 positions under consideration here, there exists a good correspondence between local stress intensity and local H diffusion coefficient, i.e., the higher stress intensity, the lower diffusion coefficient. This finding motivates us to develop a mechanics model as below for describing such a local stress-dependent diffusivity ahead of the pileup tip nearby the GB.
Similar to the Oriani theory [29], considering the material domain ahead of the pileup tip as H-trapping sites, the H diffusion coefficient within them can be expressed as
where is the H diffusion coefficient at NILS under zero stress, is the local stress, and T is the temperature. The ratio function of is used here to include the effects of on by considering the dislocation pileup as an Eshelby inclusion. It can be written as
where R is Boltzmann constant, T is the temperature, is the pileup tip trap density (the ratio between the number of the pileup tip trap sites and the total number of the trapping sites). is the H binding energy at the pileup tip. The H-binding energy at such trapping sites is assumed to follow the form of a Eshelby transforming energy dissipation [73,74,75]. If only the first-order interaction between H and trapping site is considered, can be expressed as , where is the hydrostatic stresses. Here, to include the effect of the shear stress into the consideration, is expanded as
with being the local strain associated with the finite-sized volume in a material domain with a dimension of ahead of the pileup tip, and are the local stresses and the stress (if there is any) in the far field, respectively. An insertion of Equation (5) into Equation (4), and then Equation (4) into Equation (3) leads to an expression of the pileup tip H diffusion coefficient as below
with being the shear components of the stresses ahead of the pileup tip and all other stress components being negligible in the current computational set-up.
Since , , and can be all directly measured from CAC simulations, a fitting of the CAC simulation-predicted at chosen sites (such as Position-5 in Figure 4a) ahead of the tip of a pileup containing different number of dislocations into Equation (6) will enable us to determine all the model parameters in Equation (6). An incorporation of such a CAC simulation data-informed mechanics model as shown in Equation (6) into the higher length scale models, such as the continuum level CPFE model, will be tested and reported in a separate work.
Figure 5.
CAC simulation-predicted local H diffusion coefficient and its dependence on the local stresses ahead of the tip of a pileup containing different number of dislocations. Here, only the correlation between the stress intensity and the H-diffusion at Position-5 as indicated in Figure 4a has been considered as an example.
Figure 5.
CAC simulation-predicted local H diffusion coefficient and its dependence on the local stresses ahead of the tip of a pileup containing different number of dislocations. Here, only the correlation between the stress intensity and the H-diffusion at Position-5 as indicated in Figure 4a has been considered as an example.
4. Summary and Discussion
To summarize, in this work, a multiscale computational analysis of the effects of a long-range dislocation pileup on the H diffusion nearby an atomically structured GB in a plastically deformed bi-crystalline bcc iron sample is performed. With the interatomic potential being the only constitutive relation, at a fraction of the cost of full MD, the present simulations go beyond not only nanoscale MD model by scaling up in length by accommodating tens of long dislocations using a novel CG description away from the GB , but also continuum models by retaining a fully atomistic resolution near the GB. Our several main findings are: (i) the local shear stress concentration induced by a pileup containing a large number of screw dislocations can be as high as 3GPa although it might be slightly relaxed by the atomic-level H diffusion nearby; (ii) the H diffusivity behind the pileup, at the pileup tip, and ahead of the pileup tip should be differentiated. It diffuses faster behind the pileup tip due to a pipe diffusion along the dislocations arriving at the GB, gets trapped at the pileup tip due to the presence of deep trapping sites within the GB, and diffuses slower ahead of the pileup tip due to a notable stress concentration there. The slow H diffusion ahead of the pileup tip implies a plasticity induced clustering of H atoms (PICH). This may be one important intermediate step during the process of HIC; (iii) both the local stresses and H diffusivity ahead of the pileup tip exhibit a strong heterogeneity along the dislocation line direction. And most importantly, the local stress-dependent GB diffusivity ahead of a pileup tip can fit into a model with its parameters being well calibrated from CAC simulations. This is one main outcome of this research because such a local stress-based model for the long-range pileup-affected GB diffusivity is usually considered in neither MD simulations at the atomic scale nor the continuum-level simulations at the macroscale.
In spite of the above interesting findings, the present CAC simulation results should be also taken with great caution due to its limitations in the following several aspects: (1) although our CG model was recently shown to be able to accommodate not only dislocations but also H diffusion along the dislocation [76], neither the H atoms carried by the dislocations away from the GB nor their segregation from the far region into the GB region is considered here. The reason is that such a H segregation or deposition process is significantly slower than the dislocation pileup. A capture of the dislocation pileup formation together with the H migration from the far region into the GB region necessitates a combination of CAC with the kinetic Monte Carlo (kMC), which is still under development and will be reported in the future; (2) the constant temperature of 300K is simply realized through scaling the velocities of the atoms near the GB together with the FE nodal velocities in the CG domain away from the GB, which may induce a mismatch of the phonon dynamics between the atomistic and the CG domain. The effect of such a phonon dynamics mismatch on the H diffusivity at the GB is unclear. It will be carefully quantified in our future work through implementing either the lattice dynamics-based FE shape function [77] or phonon density of states-based finite temperature algorithm in the CG domain [67]; (3) the observed clustering might result from the artifacts of the EAM potential deployed here. A confirmation of it requires the implementation of high-fidelity potentials, such as the machine learning (ML)-based potential [78], for describing the Fe-Fe, Fe-H, and H-H interactions at an accuracy comparable to that in quantum mechanical calculations. An implementation of the ML-based potential into CAC has been recently implemented in [79], and will be expanded for the problem under consideration in this work.
A further expansion of CAC along those three aspects and a connection of it with the previously reviewed two-way coupling continuum models will be attempted in the future. Such efforts may lead to a predictive multiscale computational platform that can be used to address the full complexity associated with the interaction between plasticity, diffusion, and failure in many engineering materials, such as oil pipeline steel, H-storage materials, and so on.
Author Contributions
Conceptualization, LX; methodology, YP, RJ, TP, and LX; software, YP, RJ, TP, XC, and SX; validation, AB and LX; formal analysis, NZ, SX, AB, and LX; investigation, YP, RJ, and TP; resources, AB and LX; data curation, YP, RJ, and LX; writing—original draft preparation, YP and LX; writing—review and editing, YP, RJ, TP, XC, NZ, SX, AB, and LX; visualization, YP, RJ and LX; supervision, LX; project administration, AB and LX; funding acquisition, NZ, AB and LX. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by U.S. National Science Foundation (CMMI-2322675 and CMMI-2328533 for LX; DMR-2316676 for NZ), U.S. Department of Transportation, Pipeline and Hazardous Materials Safety Administraion under Competitive Academic Agreement Program No. DTPH5614HCAP01 and 693JK31950003CAAP for AB.
Data Availability Statement
Data will be made available on reasonable request.
Acknowledgments
PT and LX also acknowledge the support of U.S. National Science Foundation and Oak Ridge National Laboratory through a NSF INTERNSHIP program under CMMI-1930093.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ossai, C. Advances in asset management techniques: an overview of corrosion mechanisms and mitigation strategies for oil and gas pipelines. International Scholarly Research Network 2012, p. 570143. [CrossRef]
- Beachem, C. A new model for hydrogen-assisted cracking (hydrogen embrittlement). Met. Trans. 1972, 3, 437–451. [CrossRef]
- Birnbaum, H.; Sofronis, P. Hydrogen-enhanced localized plasticity - a mechanism for hydrogen related fracture. Mater. Sci. & Eng. A 1994, 176, 191–202. [CrossRef]
- Ferreira, P.; Robertson, I.; Birnbaum, H. Hydrogen effects on the interaction between dislocations. Acta Materialia, 46. [CrossRef]
- Kacher, J.; Robertson, I. Quasi-four-dimensional analysis of dislocation interactions with grain boundaries in 304 stainless steel. Acta Materialia 2012, 60, 6657–6672. [CrossRef]
- Kacher, J.; Robertson, I. In situ and tomographic analysis of dislocation/grain boundary interactions in alpha-titanium. Philosophical Magazine 2014, 94, 814–829. [CrossRef]
- Guo, Y.; Collins, D.; Tarleton, E.; Hofmann, F.; Tischler, J.; Liu, W.; Xu, R.; Wilkinson, A.; Britton, T. Measurement of stress fields near a grain boundary exploring blocked arrays of dislocations in 3D. Acta Materialia 2015, 96, 229–236. [CrossRef]
- Andani, M.; Lakshmanan, A.; Sundararaghavan, V.; Allison, J.; Misra, A. Estimation of micro-Hall-Petch coefficients for prismatic slip system in Mg-4Al as a function of grain boundary parameters. Acta Materialia 2022, 226, 117613. [CrossRef]
- Lynch, S. Interpreting hydrogen-induced fracture surfaces in terms of deformation processes: A new approach. Scripta Materialia 2011, 65, 851–854. [CrossRef]
- Wang, L.; Yang, Y.; Eisenlohr, P.; Bieler, T.; Crimp, M.; Mason, D. Twin nucleation by slip transfer across grain boundaries in commercial purity titanium. Metallurgical and Materials Transactions A 2010, 41, 421. [CrossRef]
- Kacher, J.; Eftink, B.; Cui, B.; Robertson, I. Dislocations interactions with grain boundaries. Current Opinion in Solid State and Materials Science 2014, 18, 227–243.
- Robertson, I.M.; Sofronis, P.; Nagao, A.; Martin, M.; Wang, S.; Gross, D.; Nygren, K. Hydrogen embrittlement understood. Metallurgical and Materials Transactions A 2015, 46, 2323–2341. [CrossRef]
- Kimizuka, H.; Ogata, S. Slow diffusion of hydrogen at a screw dislocation core in α-iron. Physical Review B 2011, 84, 024116. [CrossRef]
- Sanchez, J.; Fullea, J.; Andrade, M.; De Andres, P. Ab initio molecular dynamics simulation of hydrogen diffusion in α-iron. Physical Review B 2010, 81, 132102.
- Zhou, X.Y.; Zhu, J.H.; Wu, H.H. Molecular dynamics studies of the grain-size dependent hydrogen diffusion coefficient of nanograined Fe. International Journal of Hydrogen Energy 2021, 46, 5842–5851. [CrossRef]
- Song, J.; Curtin, W. Atomic mechanism and prediction of hydrogen embrittlement in iron. Nature materials 2013, 12, 145–151. [CrossRef]
- Zhou, X.; Ouyang, B.; Curtin, W.; Song, J. Atomistic investigation of the influence of hydrogen on dislocation nucleation during nanoindentation in Ni and Pd. Acta Materialia 2016, 116, 364–369. [CrossRef]
- Yavas, D.; Phan, T.; Xiong, L.; Hebert, K.; Bastawros, A. Mechanical degradation due to vacancies produced by grain boundary corrosion of steel. Acta Materialia 2020, 200, 471–480. [CrossRef]
- Huang, S.; Chen, D.; Song, J.; McDowell, D.; Zhu, T. Hydrogen embrittlement of grain boundaries in nickel: an atomistic study. npj Computational Materials 2017, 3. [CrossRef]
- Song, J.; Curtin, W. Mechanisms of hydrogen-enhanced localized plasticity: an atomistic study using alpha-Fe as a model system. Acta Materialia 2014, 68, 61–69. [CrossRef]
- Chen, J.; Zhu, Y.; Huang, M.; Zhao, L.; Liang, S.; Li, Z. Study on hydrogen-affected interaction between dislocation and grain boundary by MD simulation. Computational Materials Science 2021, 196, 110562. [CrossRef]
- Jin, Z.; Gumbsch, P.; Albe, K.; Ma, E.; Lu, K.; Gleiter, H.; Hahn, H. Interactions between non-screw lattice dislocations and coherent twin boundaries in face-centered cubic metals. Acta Materialia 2008, 56, 1126–1135. [CrossRef]
- Chassagne, M.; Legros, M.; Rodney, D. Atomic-scale simulation of screw dislocation-coherent twin boundary interaction in Al, Au, Cu, and Ni. Acta Materialia 2011, 59, 1456–1463. [CrossRef]
- Wang, J. Atomistic simulations of dislocation pileup: grain boundaries interactions. Journal of Materials 2015, 67, 1515–1525. [CrossRef]
- Szajewski, B.; Curtin, W. Analysis of spurious image forces in atomistic simulations of dislocations. Model. Simul. Mater. Sci. and Eng. 2015, 23, 025008. [CrossRef]
- Sofronis, P.; McMeeking, R. Numerical analysis of hydrogen transport near a blunting crack tip. J. Mech. Phys. Solid 1989, 37, 317–350. [CrossRef]
- Liang, Y.; Sofronis, P. Micromechanics and numerical modeling of the hydrogen-particle-matrix interaction in nickel-base alloys. Model. Simul. Mater. Sci. Eng. 2003, 11, 523–551. [CrossRef]
- Novak, P.; Yuan, R.; Somerday, B.; Sofronis, P.; Ritchie, R. A statistical, physical-based, micro-mechanical model of hydrogen-induced intergranular fracture in steel. J. Mech. Phys. Solids 2010, 58, 206–226. [CrossRef]
- Oriani, R. The diffusion and trapping of hydrogen in steels. Acta Metallurgical 1970, 18, 147–157. [CrossRef]
- Sofronis, P.; Liang, Y.; Aravas, N. Hydrogen induced shear localization of the plastic flow in metals and alloys. Eur. J. Mech. A/Solids 2001, 20, 857–872. [CrossRef]
- Barrera, O.; Tarleton, E.; Tang, H.; Cocks, A. Modelling the coupling between hydrogen diffusion and the mechanical behaviour of metals. Computational Materials Science 2016, 122, 219–228. [CrossRef]
- Zirkle, T.; Costello, L.; McDowell, D. Crystal plasticity modeling of hydrogen and hydrogen-related defects in initial yield and plastic flow of single-crystal stainless steel 316L. Metallurgical and Materials Transactions A 2021, 52A, 3961–3977. [CrossRef]
- Song, J.; Curtin, W. Mechanisms of hydrogen-enhanced localized plasticity: an atomistic study using alpha-Fe as a model system. Acta Materialia 2014, 68, 61–69. [CrossRef]
- Asano, S.; Otsuka, R. The lattice hardening due to dissolved hydrogen in iron and steel. Scripta Materialia 1976, 10, 1015–1020. [CrossRef]
- Abraham, D.; Altstetter, C. The effect of hydrogen on the yield and flow stress of an austenitic stainless steel. Met. Trans. A 1995, 26, 2849–2858. [CrossRef]
- Matsui, H.; Kimura, H.; Moriya, S. The effect of hydrogen on the mechanical properties of high purity iron I. Softening and hardening of high purity iron by hydrogen charging during tensile deformation. Mat. Sci. Engng 1979, 40, 207–216. [CrossRef]
- Matsui, H.; Kimura, H.; Kimura, A. The effect of hydrogen on the mechanical properties of high purity iron III. The dependence of softening on specimen size and charging current density. Mat. Sci. Engng 1979, 40, 227–234. [CrossRef]
- Moriya, S.; Matsui, H.; Kimura, H. The effect of hydrogen on the mechanical properties of high purity iron II. Effect of quenched-in hydrogen below room temperature. Mat. Sci. Engng 1979, 40, 217–226. [CrossRef]
- Eastman, J.; Heubaum, N.; Matsumoto, T.; Birnbaum, H. The effect of hydrogen on the solid solution strengthening and softening of nickel. Acta Metall. 1982, 30, 1579–1586. [CrossRef]
- Meyers, S.; Baskes, M.; Birnbaum, H.; Corbett, J.; DeLeo, G.; Estreicher, S.; Haller, E.; Jena, P.; Johnson, N.; Kirchheim, R.; Pearton, S.; Stavola, M. Hydrogen interactions with defects in crystalline solids. Rev. Mod. Phys. 1992, 64, 559–617. [CrossRef]
- Ilin, D.; Saintier, N.; Olive, J.; Abgrall, R.; Aubert, I. Simulation of hydrogen diffusion affected by stress-strain heterogeneity in polycrystalline stainless steel. International Journal of Hydrogen Energy 2014, 39, 2418–2422. [CrossRef]
- Charles, Y.; Nguyen, H.; Gasperini, M. Comparison of hydrogen transport through pre-deformed synthetic polycrystals and homogeneous samples by finite element analysis. International Journal of Hydrogen Energy 2017, 42, 20336–20350. [CrossRef]
- Abdolvand, H. Progressive modelling and experimentation of hydrogen diffusion and precipitation in anisotropic polycrystals. International Journal of Plasticity 2019, 116, 39–61. [CrossRef]
- Arnaudov, N.; Kolyshkin, A.; Weihe, S. Micromechanical modeling of fatigue crack initiation in hydrogen atmosphere. Mechanics of Materials 2020, 149, 103557. [CrossRef]
- Hassan, U.; Govind, K.; Hartmaier, A. Micromechanical modelling of coupled crystal plasticity and hydrogen diffusion. Philos. Mag. 2019, 99, 92–115. [CrossRef]
- Hussein, A.; Krom, A.; Dey, P.; Sunnardianto, G.; Moultos, O.; Walters, C. The effect of hydrogen content and yield strength on the distribution of hydrogen in steel: a diffusion coupled micromechanical FEM study. Acta Mater. 2021, 209, 116799. [CrossRef]
- Tondro, A.; Taherijam, M.; Abdolvand, H. Diffusion and redistribution of hydrogen atoms in the vicinity of localized deformation zones. Mechanics of Materials 2023, 177, 104544. [CrossRef]
- Oh, C.; Kim, Y.; Yoon, K. Coupled analysis of hydrogen transport using ABAQUS. Journal of Solid Mechanics and Materials Engineering 2010, 4, 908–917. [CrossRef]
- Barrera, O.; Bombac, D.and Chen, Y.; Daff, T.; Galindo-Nava, E.; Gong, P.; Haley, D.; Horton, R.; Katzarov, I.; Kermode, J.; Liverani, C.; Stopher, M.; Sweeney, F. Understanding and mitigating hydrogen embrittlement of steels: a review of experimental, modelling and design progress from atomistic to continuum. Journal of Materials Science 2016, 53, 6251–6290. [CrossRef]
- Diaz, A.; Alegre, J.; Cuesta, I. Coupled hydrogen diffusion simulation using a heat transfer analogy. International Journal of Mechanical Sciences 2016, 115–116, 360–369. [CrossRef]
- Rimoli, J.; Ortiz, M. A three-dimensional multiscale model of intergranular hydrogen-assisted cracking. Philos. Mag. 2010, 90, 2939–2963. [CrossRef]
- Wu, Q.; Zikry, M. Prediction of diffusion assisted hydrogen embrittlement failure in high strength martensitic steels. J. Mech. Phys. Solids 2015, 85, 143–159. [CrossRef]
- Pu, C.; Gao, Y.; Wang, Y.; Sham, T. Diffusion-coupled cohesive interface simulations of stress corrosion intergranular cracking in polycrystalline materials. Acta Materialia 2017, 136, 21–31. [CrossRef]
- Benabou, L. Coupled stress-diffusion modelling of grain boundary seggregation and dynamic embrittlement in a copper alloy. Modelling Simul. Mater. Sci. Eng. 2019, 27, 045007. [CrossRef]
- Valverde-Gonzalez, A.; Martinez-Paneda, E.; Quintanas-Corominas, A.; Reinoso, J.; Paggi, M. Computational modelling of hydrogen assisted fracture in polycrystalline materials. International Journal of Hydrogen Energy 2022, 47, 32235–32251. [CrossRef]
- Chakraborty, A.; Lebensohn, R.; Capolungo, L. Coupled chemo-mechanical modeling of point-defect diffusion in a crystal plasticity fast Fourier transform framework. Journal of the Mechanics and Physics of Solids 2023, 173, 105190. [CrossRef]
- Kumar, A.; Mahajan, D. Hydrogen distribution in metallic polycrystals with deformation. J. Mech. Phys. Solids 2020, 135, 103776. [CrossRef]
- Xiong, L.; Tucker, G.; McDowell, D.; Chen, Y. Coarse grained atomistic simulations of dislocations. J. Mech. Phys. Solids 2011, 59, 160–177. [CrossRef]
- Xiong, L.; Deng, Q.; Tucker, G.; McDowell, D.; Chen, Y. A concurrent scheme for passing dislocations from atomistic to continuum domains. Acta Materialia 2012, 60, 899–913. [CrossRef]
- Xiong, L.; McDowell, D.; Chen, Y. Nucleation and growth of dislocation loops in Cu, Al, and Si by a concurrent atomistic-continuum method. Scripta Materialia 2012, 67, 633–636. [CrossRef]
- Xiong, L.; Ji, R.; Chen, X.; Xu, S.; McDowell, D.; Chen, Y. Coarse-grained elastodynamics of fast moving dislocations. Acta Materialia 2016, 104, 143–155. [CrossRef]
- Chen, H.; Xu, S.; Li, W.; Ji, R.; Phan, T.; Xiong, L. A spatial decomposition parallel algorithm for a concurrent atomistic-continuum simulator and its preliminary applications. Computational Materials Science 2018, 144, 1–10. [CrossRef]
- Xu, S.; Payne, T.; Chen, H.; Liu, Y.; Xiong, L.; Chen, Y.; McDowell, D. PyCAC: The concurrent atomistic-continuum simulation environment. Journal of Materials Research 2018, 33, 857–871. [CrossRef]
- Xu, S.; Xiong, L.; Chen, Y.; McDowell, D. Validation of the concurrent atomistic-continuum method on screw dislocation/stacking fault interactions. Crystals 2017, 7, 120. [CrossRef]
- Xiong, L.; Chen, Y. Multiscale modeling and simulation of single-crystal MgO through an atomistic field theory. International Journal of Solids and Structures 2009, 46, 1448–1455. [CrossRef]
- Chen, Y. Reformulation of microscopic balance equations for multiscale materials modeling. Journal of Chemical Physics 2009, 130, 134706. [CrossRef]
- Ji, R.; Phan, T.; Chen, Y.; McDowell, D.; Xiong, L. A finite-temperature coarse-grained atomistic approach for understanding the kink-controlled dynamics of micrometer-long dislocations in high-Peierls-barrier materials. MRS Communications 2022, pp. 1–9. [CrossRef]
- Xiong, L.; Chen, Y.; Lee, J. Modeling and simulation of boron-doped nanocrystalline silicon carbide thin film by a field theory. Journal of Nanoscience and Nanotechnology 2009, 9, 1034. [CrossRef]
- Su, Y.; Phan, T.; Xiong, L.; Kacher, J. Multiscale computational and experimental analysis of the slip-GB reactions: in-situ high-resolution electron backscattered diffraction and concurrent atomistic-continuum simulations. Scripta Materialia 2023, p. under review. [CrossRef]
- Peng, Y.; Ji, R.; Phan, T.; Capolungo, L.; Levitas, V.; Xiong, L. Effect of a micro-scale dislocation pileup on the atomic-scale multi-variant phase transformation and twinning. arXiv 2022, p. 2208.03592.
- Peng, Y.; Ji, R.; Phan, T.; Gao, W.; Levitas, V.; Xiong, L. An atomistic-to-microscale computational analysis of the dislocation pileup-induced local stresses near an interface in plastically deformed two-phase materials. Acta Materialia 2022, 226, 117663. [CrossRef]
- Eshelby, J.; Frank, F.; Nabarro, F. XLI. The equilibrium of linear arrays of dislocations. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1951, 42, 351–364. [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proceedings of the royal society of London. Series A. Mathematical and physical sciences 1957, 241, 376–396. [CrossRef]
- Eshelby, J.D. The elastic field outside an ellipsoidal inclusion. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 1959, 252, 561–569. [CrossRef]
- Vasoya, M.; Kondori, B.; Benzerga, A.A.; Needleman, A. Energy dissipation rate and kinetic relations for Eshelby transformations. Journal of the Mechanics and Physics of Solids 2020, 136, 103699. [CrossRef]
- Phan, T.; Peng, Y.; Gao, W.; Xiong, L. Coarse-grained atomistic characterization the properties of micrometer-long dislocations charged with hydrogen. Scripta Materialia 2023, p. under review.
- Chen, Y.; Diaz, A.; Xiong, L.; McDowell, D.; Chen, Y. Passing waves from atomistic to continuum. Journal of Computational Physics 2018, 354, 393–402. [CrossRef]
- Meng, F.; Du, J.P.; Shinzato, S.; Mori, H.; Yu, P.; Matsubara, K.; Ishikawa, N.; Ogata, S. General-purpose neural network interatomic potential for the alpha-iron and hydrogen binary system: Toward atomic-scale understanding of hydrogen embrittlement. Physical Review Materials 2021, 5, 113606. [CrossRef]
- Peng, Y. An atomistic-to-mesocale prediction of the complex reaction between the plastic flow and the interfaces in heterogeneous materials. Iowa State University Ph.D. Dissertation 2023.
Figure 1.
The CAC computer model for simulating the interaction between a H-charged GB and a queue of dislocations piling up at the GB in a bi-crystalline sample : (a) the CG description that can accommodate a large number of dislocations away from the GB and the atomistic resolution for the H-charged GB. Each element (gray) in the CG domain is a collection of atoms. The motion of each atom in CG is interpolated from the FE nodal displacements. The dislocation slip in the CG domain is allowed on the FE boundaries, which are aligned with the slip planes of bcc crystals under consideration here; (b) a zoom-in view of the atomically structured GB showing the lattice orientations of both grains. The coarse FEs in the domain away from the GB and the iron atoms on the GB are colored in grey. The H atoms are colored in red, the GB plane is indicated as blue. A finite number of dislocations are initially introduced into the CG model of the left grain along the slip plane (see one dislocation nearby the atomically structured GB in the zoom-in view).
Figure 1.
The CAC computer model for simulating the interaction between a H-charged GB and a queue of dislocations piling up at the GB in a bi-crystalline sample : (a) the CG description that can accommodate a large number of dislocations away from the GB and the atomistic resolution for the H-charged GB. Each element (gray) in the CG domain is a collection of atoms. The motion of each atom in CG is interpolated from the FE nodal displacements. The dislocation slip in the CG domain is allowed on the FE boundaries, which are aligned with the slip planes of bcc crystals under consideration here; (b) a zoom-in view of the atomically structured GB showing the lattice orientations of both grains. The coarse FEs in the domain away from the GB and the iron atoms on the GB are colored in grey. The H atoms are colored in red, the GB plane is indicated as blue. A finite number of dislocations are initially introduced into the CG model of the left grain along the slip plane (see one dislocation nearby the atomically structured GB in the zoom-in view).
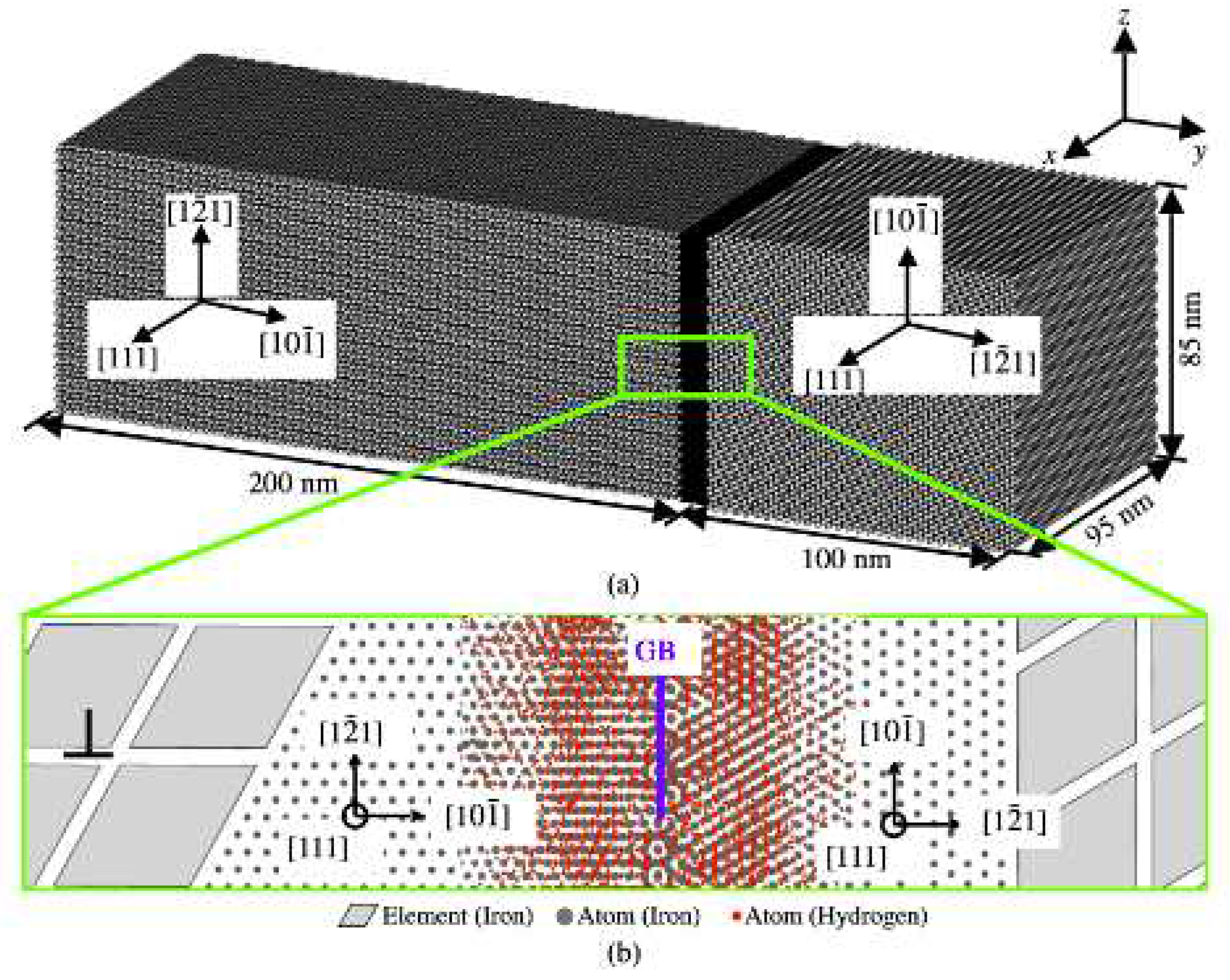
Figure 2.
The dislocation pileup-induced internal stress (): (a-b) front and top view of the shear stress contour when 15 dislocations are piled up at the GB; (c) the stress profiles ahead of the tip of a pileup containing 5-15 dislocations and their fits into Equation (1).
Figure 2.
The dislocation pileup-induced internal stress (): (a-b) front and top view of the shear stress contour when 15 dislocations are piled up at the GB; (c) the stress profiles ahead of the tip of a pileup containing 5-15 dislocations and their fits into Equation (1).
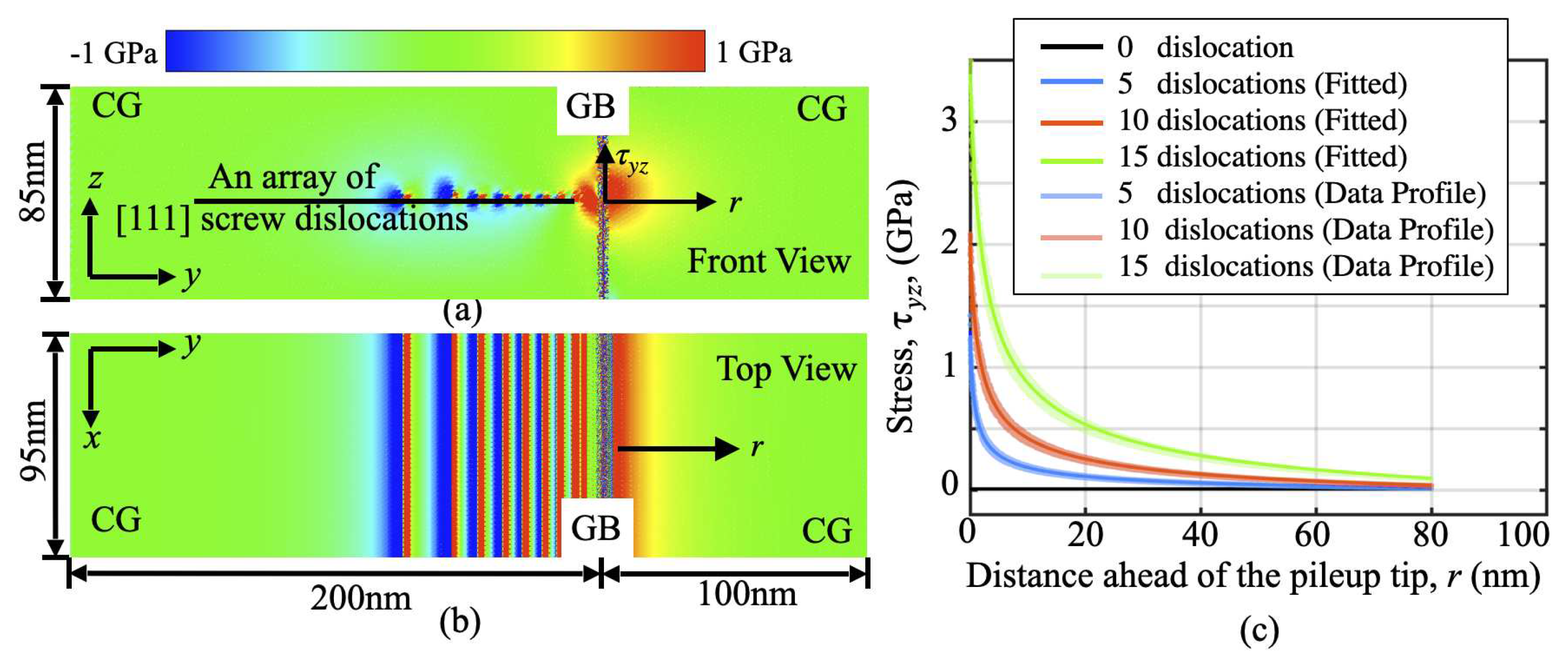
Figure 3.
Quantifying the effects of the dislocation pile up on the H diffusion by tracking the motion of the individual H atoms and projecting them on an un-deformed atomic configurations containing no dislocations nearby the GB: (a-b) the trajectories (red) of three H atoms (one in the left grain, the other in the right grain, and another within the GB) when n = 0 and n = 15, respectively (n is the number of the dislocations in a pileup); (c) the mean square displacement (MSD) of the H atoms and its dependence on the number of the dislocations in a pileup; (d-e) the trajectories of two H atoms in the left grain nearby the slip-GB intersection when different number of dislocations, i.e., n = 0 and n = 15, are piled up near the GB.
Figure 3.
Quantifying the effects of the dislocation pile up on the H diffusion by tracking the motion of the individual H atoms and projecting them on an un-deformed atomic configurations containing no dislocations nearby the GB: (a-b) the trajectories (red) of three H atoms (one in the left grain, the other in the right grain, and another within the GB) when n = 0 and n = 15, respectively (n is the number of the dislocations in a pileup); (c) the mean square displacement (MSD) of the H atoms and its dependence on the number of the dislocations in a pileup; (d-e) the trajectories of two H atoms in the left grain nearby the slip-GB intersection when different number of dislocations, i.e., n = 0 and n = 15, are piled up near the GB.
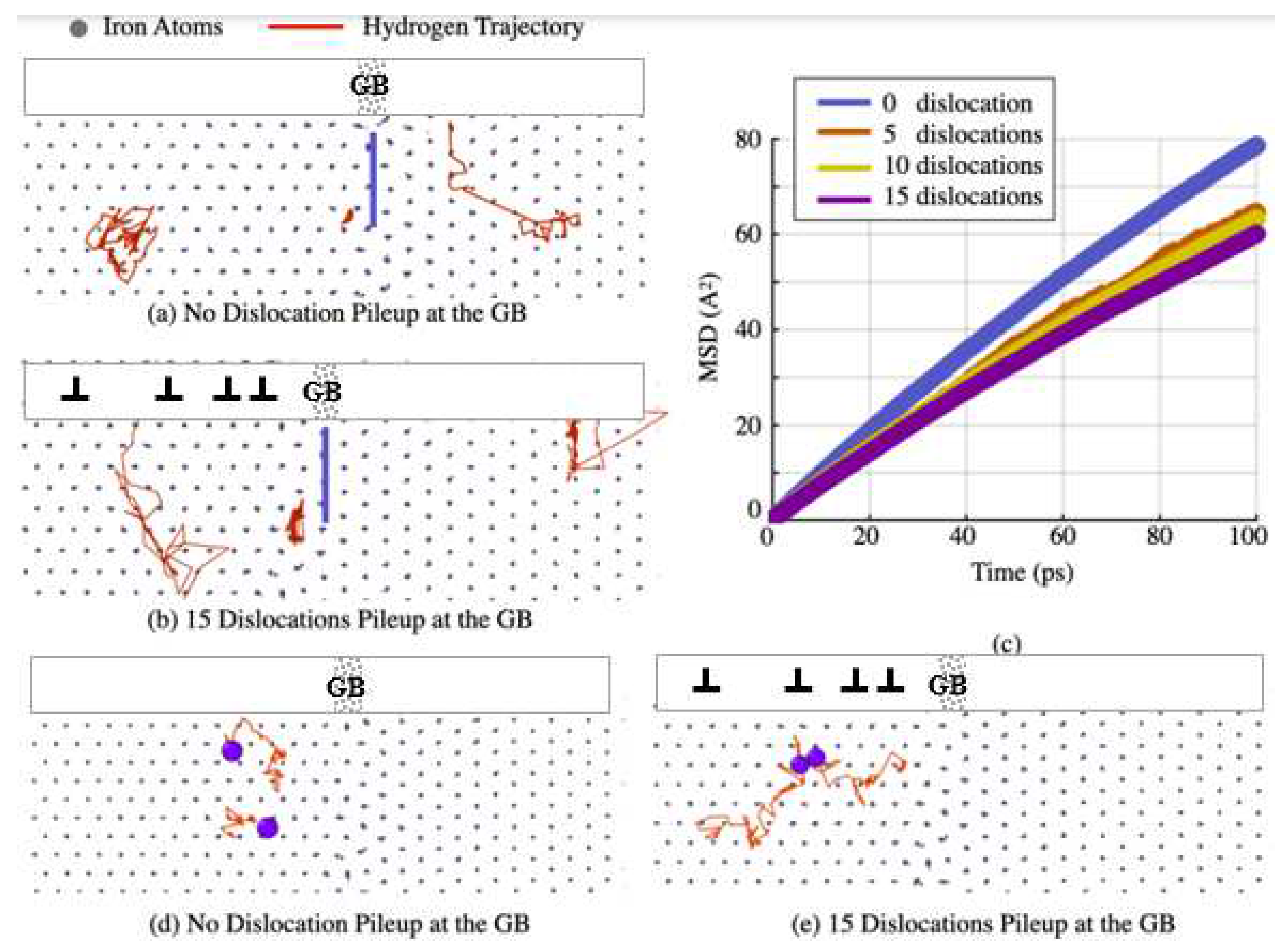
Figure 4.
Characterizing the H diffusion and local stress heterogeneity induced by the accumulation of a large number of long dislocations at a H-charged GB in CAC: (a) the distribution of the shear stress within the slip plane nearby a H-charged GB when tens of 95nm-long dislocations (n = 15, each dislocation carries a clearly visible shear stress field) are accumulated nearby; (b) the MSD of the H atoms at nine different locations in the GB along the dislocation line;
Figure 4.
Characterizing the H diffusion and local stress heterogeneity induced by the accumulation of a large number of long dislocations at a H-charged GB in CAC: (a) the distribution of the shear stress within the slip plane nearby a H-charged GB when tens of 95nm-long dislocations (n = 15, each dislocation carries a clearly visible shear stress field) are accumulated nearby; (b) the MSD of the H atoms at nine different locations in the GB along the dislocation line;
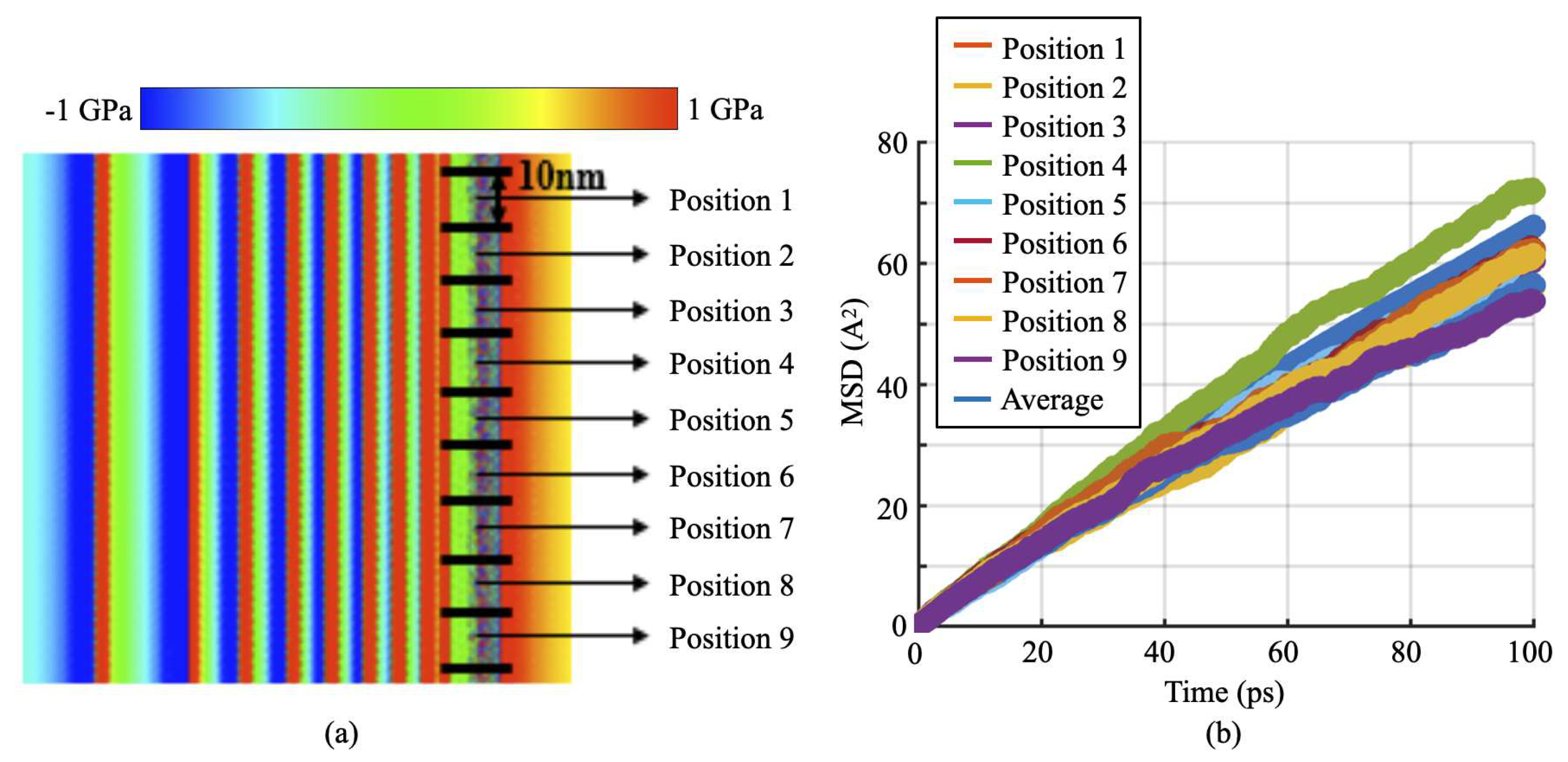
Table 1.
Stress intensity factors S and H diffusion coefficients D for n = 0, 5, 10, and 15.
| Number of Dislocations | 0 | 5 | 10 | 15 |
|---|---|---|---|---|
| Stress Intensity Factor K (GPa/m) | 0 | 0.82 | 1.98 | 4.12 |
| H Diffusion Coefficient | 0.146 | 0.110 | 0.104 | 0.102 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






