Preprint
Article
A Quantum Model of Interdependence for Embodied Human-Machine Teams: A Review of the Path to Autonomy Facing Complexity and Uncertainty
Altmetrics
Downloads
147
Views
518
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
07 July 2023
Posted:
10 July 2023
You are already at the latest version
Alerts
Abstract
In this review, our goal is to design and test quantum-like algorithms for Artificial Intelligence (AI) in open systems to structure a human-machine team to be able to reach its maximum performance. Unlike the laboratory, in open systems, teams face complexity, uncertainty and conflict. All task domains have complexity levels, some have low, and others high levels. Complexity in this new domain is affected by the environment and the task, which are both affected by uncertainty and conflict. We contrast the individual and interdependence approaches to teams. The traditional and individual approach focuses on building teams and systems by aggregating the best available information for individuals, their thoughts, behaviors and skills. Its concepts are characterized chiefly by one-to-one relations between mind and body, a summation of disembodied individual mental and physical attributes, and degrees of freedom corresponding to the number of members in a team; however, this approach is characterized by the many researchers who have invested in it for almost a century with few effects that can be generalized to human-machine interactions; by the replication crisis of today (e.g., the invalid scales for self-esteem, implicit racism, and honesty); and by its many disembodied concepts. In contrast, our approach is based on the quantum-like nature of interdependence. It allows us to theorize about the bistability of mind and body, but it proposes a measurement problem and a non-factorable nature. Bistability addresses team structure and performance; the measurement problem solves the replication crisis; and the non-factorable aspect of teams reduces the degrees of freedom and the information derivable from teammates to match findings by the National Academies of Science. We begin with a review of the science of teams and a focus on human-machine team research in the laboratory versus the open; justifications for rejecting traditional social science while supporting our approach; a full understand of the complexity of the domain, tasks in the domain, and how teams address both; the mathematics involved; a review of results from our model versus the open field; a discussion of the results; conclusions; and the path forward to successfully advance the science of interdependence and autonomy.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
In this review, our overarching goal [1] is to enable autonomous human-machine teams (AHMTs) to be designed with a set of algorithms that can be deployed with Artificial Intelligence (AI) by machines and humans to structure a human-machine team able to reach its maximum performance in the open, specifically away from the laboratory where most team science is currently practiced. In the open, but not in the laboratory, teams will face uncertainty and conflict. As Mann [2] has concluded, rational beliefs fail when confronted by uncertainty and conflict. We begin with a historical review of interdependence from a computational perspective.
Then, in background sections 1, we review and define interdependence; 2) we justify why social science has failed to produce a coherent mathematics of teams (here, coherence describes a state of interdependence that has not been corrupted or interrupted: for example, see "redundancy" below); 3) we review the effect of task domain complexity to determine whether there is also an effect of interdependence on the complexity of the task domain besides the effect of domain complexity on interdependence, and 4) we justify our quantum model of interdependence based on the interdependence that exists among teammates. In the body of our article, we review what we know of the mathematics of interdependence in teams, what we know so far of its generalizations (e.g., how to exploit it), and some of the barriers remaining to make autonomous human-machine teams a new discipline of the science of interdependence.
1.1. Background: Definitions of interdependence
To build and operate systems of autonomous human-machine teams characterized by interdependence requires an operational definition of interdependence and its effects that both humans and machines can perceive, interpret and address in open contexts. Below, we introduce a definition of interdependence from a historical and computational perspective (Table 1). We end with our proposed working definition of interdependence. In the next three background subsections: we justify moving away from traditional social science, as in the molds of Spinoza and Hume; we consider the effects of domain complexity on interdependence; and we justify our quantum model of interdependence. Next, we review our mathematical approach to interdependence.
Interdependence drives the interaction between two agents [3]; it is the social field that holds teams together or breaks them apart [4]; and it gives a team’s teammates power over what an equal number of individuals working independently of each other can accomplish [5]. But, without a formal, computational approach to the study of teams, autonomous human-machine teams will be ad hoc, vulnerable to those with the insight of what makes a team potentially and significantly more powerful than an equal collection of the same individuals in a team acting independently of each other. Uniformly across the social sciences, the traditional assumption has been based on Spinoza’s and Hume’s traditional, non-dual mind-body equivalence which prevents any affordance for the power derived from a group constituted as a team [5].
We contrast this traditional approach with our computational approach based on the dualism of the mind-body, the two equivalent, competing, and countering centers that the human brain draws upon. In our approach, the tension between the two countering views of reality, one by the mind and the other embodied in reality [6], afforded by dualism, provide a means to sharply focus the information derived from a situation to computationally determine and operate in a given context [7], but, and this is seminal in our view, without disambiguating cognition from the body’s action in reality (e.g., Cooke and Lawless conclude that intelligence outside of an interaction is not helpful for an interaction, but that the relevant intelligence arises, and is embodied, in the interaction itself [8]).
In Table 1, we consider interdependence historically, mindful of its usability by Artificial Intelligence (AI). Based on our historical approach, the literature, and our own research, we define interdependence as embodied cognition ([9]; [6]), not only entangled with reality, but also unable to be disentangled. We focus our article on the three effects arising from the phenomena of interdependence: it is bistable (e.g., two-sided interpretations of reality; debates; checks and balances in governance); it creates a measurement problem (e.g., questionnaires built around the notion of convergence into a single concept increase uncertainty by reducing the likelihood of perceiving the bistable, non-converged, opposing, countering aspects of reality); and non-factorability (e.g., debates, disagreements and fights are common, but who is right or who has won cannot be said without an impartial judge, jury, audience or metric to determine the outcome; we consider non-factorability to be the key characteristic that aligns teams with quantum entanglement).
1.2. Harmonic Oscillators. A test of models
Table 1.
Interdependence: A historical and computational perspective.
| Authors (year published) | Definition | Issues |
|---|---|---|
| Lewin (1942) (republished [4]) | behaviour, dx/dt, occurs from the “totality of coexisting and interdependent forces in the social field that impinge on a person or group and make up the life space” (computational context; see [7]). Interdependence includes all effects that co-vary with the individual, giving an “interdependence of parts ... handled conceptually only with the mathematical concept of space and the dynamic concepts of tension and force” (p. xiii) that "holds the group together ... [making] the whole ... more than the sum of its parts” (p. 146). | A theoretical rather than a working construct. |
| Von Neumann and Morgenstern, 1944 (p. 35, in [3]) | "The simplest game … is a two-person game where the sum of all payments is variable. This corresponds to a social economy with two participants and allows both for their interdependence and for variability of total utility with their behavior … exactly the case of bilateral monopoly." | Assumed that cognition and behavior are the same, like Spinoza [10] and Hume [11], and missed Nash’s solution that an equilibrium existed in a bounded space. |
| Nash 1950 [12] | In a two-person game, “a strategy counters another if the strategy of each player” occurs in a closed space until it reaches an “equilibrium point.” | Behavior is inferred [13]; fails facing uncertainty or conflict [2], but may be recoverable with constraints (see [1]; also, see [14]). |
| Kelley, Holmes, Kerr, Reis, Rusbult and van Lange [15] | "Three dimensions describe interdependence theory: mutual influence or dependence between two or more agents; conflict among their shared interests; and the relative power among them. Interdependence is defined based on specific decomposition of situations [e.g., with abstract representations such as the Prisoner’s Dilemma Game] to account for how mutual influence affects the outcome of their interactions to reach an outcome." | After working with payoff matrices for decades, Kelly capitulated, complaining that situations, represented by a given (logical) matrix of outcomes, was overwhelmed by the effective matrix, which, he concluded, was based on the interaction and unknowable. For a given game’s structure, Kelley concluded that “the transformation from given to effective matrix is subjective to observers and subject to their interpretation error with no solution in hand" [16], which Jones said caused "bewildering complexities" in the laboratory (p. 33, [17]). |
1.3. Background: Justification for the rejection of Spinoza and Hume
Until now, most social science research has focused on the individual in the laboratory, not the interaction, which is governed by interdependence. While admitting to the ubiquity of interdependence in human affairs, however, in 1998 the leading social psychologist, Jones (p. 33, in [17]), concluded that the study of interdependence in the laboratory led to effects that were "bewildering," sidelining the study of interdependence for a generation, but unfortunately leaving the individual as the primary focus of study.
According to Spinoza [10], no causal interaction exists between bodies and ideas, that is, between the physical and the mental [18]. Whatever happens in the body is reflected or expressed in the mind. This notion by Spinoza has led to the assumption that aggregating the observed cognition of individuals subsumes individual behaviors [19], thus needing only independent data (viz., i.i.d. data; but see [20]) to improve the lives of individuals or for the betterment of teams.
In the same vein, Hume’s [11] "copy principle" holds that there is one–to–one correspondence between ideas and reality.
Consider individuals first. Spinoza’s and Hume’s idea has led to the development of modern measures in the laboratory for individual perceptions and beliefs that correlate strongly with other self-perceived measures. For example, self-esteem has been found to correlate significantly with other measures of mental health, leading the American Psychological Association in 1995 to consider self-esteem to be the premier goal for "the highest level of human functioning" ([21]). However, since then, and despite self-esteem’s strong correlations with other self-perceived skills, Baumeister and his team found that self-esteem in the open was not correlated with actual academic or actual work performance ([22]).
Similarly, in recent years, the concept of implicit racism has been significantly involved in driving major changes across social, academic and work relationships; however, the implicit racism concept was found to be invalid in 2009 [23]. Despite the failure of this concept, numerous training events designed to counter the "ill" effects of implicit racism have taken place, but the results have been "dispiriting" [24]. Further, a National Institutes of Health panel asked "Is Implicit Bias Training Effective," concluding that “scant scientific evidence” existed. 1 Yet, Leach, the lead editor of groups in Social Psychology, has pushed his journal members to focus exclusively on biases [25]. But this persistence on applying concepts for individuals developed in the laboratory that subsequently fail to be validated has led to the present replication crisis in the social sciences [26]. Not understanding that the complexity of the domain and the task at hand may lead to sampling bias and negatively affect the understanding of interdependence.
We are not concerned with the replication crisis, per se. But we are concerned with why the individual model seemingly cannot be generalized to the interaction or to teams.
Traditional models also include large language models like game theory and OpenAI’s ChatGPT. Strictly cognitive, for game theory, Perolat’s team [27] concluded that real-world multi-agent approaches are “currently out of reach for state-of-the-art AI methods.” In the research highlights for the same issue of Science, Suleymanov said of Perolat’s article: "real-world, large-scale multiagent problems … are currently unsolvable." ChatGPT and two-person games are also assumed to easily connect to reality, but ChatGPT skeptics exist ([28];[29]). Quoting from Chomsky’s [30] opinion in the New York Times:
OpenAI’s ChatGPT, Google’s Bard and Microsoft’s Sydney are marvels of machine learning. Roughly speaking, they take huge amounts of data, search for patterns in it and become increasingly proficient at generating statistically probable outputs—such as seemingly human like language and thought. These programs have been hailed as the first glimmers on the horizon of artificial general intelligence …That day may come, but its dawn is not yet breaking …[and] cannot occur if machine learning programs like ChatGPT continue to dominate the field of A.I. …The crux of machine learning is description and prediction; it does not posit any causal mechanisms or physical laws.
With ChatGPT, an artificially intelligent mind is based on the use of reinforcement learning in large-language models, often making common-sense errors that indicate a poor connection between the artificial mind and physical reality. Chomsky’s position mirrors that of AI researcher Judea Pearl’s conclusion when he recommended that AI researchers could only advance AI by using reasoning with causality ([31,32]). We add that reasoning about causality cannot occur with teams or systems composed of humans and machines working together without accounting for the interdependence that physically exists in the social sphere, especially among human-human teammates. Otherwise, ignoring interdependence for human-machine teams would be like treating quantum effects as "pesky" in the study of atoms.
Again, our problem is not with biases, the replication crisis, or large language models, but the results which indicate that there is little guidance to be afforded by the social science of the individual for the development of autonomous human-machine teams. This sad state changes dramatically if instead we treat the current state of social science as evidence of the measurement problem reflecting an orthogonality between the "individual" and the "team," or between language (concepts) and action [33].
Indeed, we suggest that the state-dependency [34] created from the interdependence between individuals and teammates may rescue traditional social science from its current validation crises. Simply put, if the "individual" is orthogonal to its participation in a "team," then by measuring the individual, evidence of the team is lost, explaining why complementarity has failed to produce predicted effects in close relationships [35]. Similarly, it may be true that language isolated from of the effects of physical reality explains why ChatGPT has been criticized for its disconnect from reality; i.e., the complexity inherent in large language models impedes the “identify [of] state variables from only high-dimensional observational data”; in [36]). From an interview of Chen, a roboticist at Duke University “I believe that intelligence can’t be born without having the perspective of physical embodiments” (in [37]; see also embodied cognition, in [9]; [6]). We go further than Spinoza-Hume and Chen by asserting that embodied thoughts derived while operating in reality cannot be disambiguated from each other. This accounts for Chomsky’s [30] conclusion that ChatGPT does not capture reality.
1.4. Background: Domain complexity of a team’s task
Open-world and especially real-world learning has taken on new importance in recent years as AI systems continue to be applied and transitioned to real-world settings where unexpected events, novelties can, and do, occur [38]. When designing AI systems with human-machine teams, likely, the novelties cause additional uncertainties, the team’s performance drops, and cause conflict. This is exactly where belief logics, or disembodied languages, fail [2]. It is interesting that Chatbot or intuition is unable to address causality [31,32], but quantum logic works well, yet quantum logic is unable to provide a consensus interpretation or meaning [39].
When designing an AI that can operate in real-world domains, we need to know about the level of complexity of the target task. The complexity level of task domain affects the interdependence of the human-machine team. Regardless of the complexity in the structure of a team, by reducing its degrees of freedom, the perfect team operates as a unit, the reason why the “performance of a team is not decomposable to, or an aggregation of, individual performances” [40]. A decomposed structure can be very complex, but while that may be, as its complex pieces begin to fit together, the degrees of freedom reduce, thereby reducing structural complexity. The structure’s “decomposed” complexity should match the complexity of the problem addressed, the structure as it unifies allows the unified structure to be able to produce maximum entropy (MEP). This latter part conserves “the available free” energy, i.e., the more free energy consumed by a structure to make its team “fit” together, the less free energy available for team productivity.
The complexity level of the task domain defines the skills and tools that an agent or team of agents need to perform successfully. These skills are composed of mental and physical skills. Knowing the skills needed to successfully perform a task defines the number and the combination of human and machine agents with tools needed to form a human-machine team. The complexity level of the task domain also defines the level of their interdependence in the human-machine teams, each with certain skill sets that complement a team’s mission. Further, understanding the complexity of the agents that are human and machine will help to define which agent (e.g., namely human or machine) with the appropriate skills and the number of them needed to perform a task.
In other words, the complexity of a task domain defines the skills that a particular human or machine agent needs to fit with a machine or human agent’s skills; e.g., for a task that requires a team member to have good vision at night, the human-agent team needs night vision skills. However, a particular human agent who happens to be near-sided and cannot wear corrective contact lenses (physical skill) may not be eligible to participate in a night-time task. Thus, the human-agent teams must be able to be equipped with the tools and the appropriate skills to function on a mission.
Understanding the complexity of the task domain helps in: transitioning from theory, to simulations, to laboratory and to real-world domains; understanding the boundaries and limitations; understanding the risks for the team and agents, decreasing the uncertainties regarding fit; avoiding sampling bias; forming anticipatory thinking; defining causality in embodied thinking; and forming an understanding of skills, mental and physical skills, and number of agents needed to solve a problem.
Doctor et al. [14] broke down domain complexity across domains into intrinsic and extrinsic components and each into subcomponents. Intrinsic domain complexity is where the agent performing a task does not change the complexity of the task domain. The extrinsic complexity of the domain depends on an agent’s skills; e.g., if the task domain is to lift a rock, its complexity will differ for an agent that is smaller than the rock versus a larger agent that can pick up the rock or a machine that can lift a rock. Although [14] referred to interaction with other agents, they did not address interdependence of teams of multiple agents.
The interdependence exists in extrinsic domain complexity space. Interference reduces internal complexity when interdependence is constructive, increases complexity when the interference is destructive; plus, destructive interference may consume all of the available free energy from a project, collapsing productivity; e.g., divorce in marriage or in business. However, the intrinsic domain complexity contributes to the skills that the agents need and the number of them, which indirectly affects the interdependence of human-machine teams. However, redundancy increases complexity, decreases interdependence (e.g., free riding) and reduces performance [41].
1.5. Background: Justification for the quantum model of interdependence
The most well-known model of state-dependency is quantum mechanics [34]. In our research, we have postulated that the relationship between the team and the individual is state dependent, connecting our work to quantum mechanics. In this Sub-Section, we elaborate on this connection. The Copenhagen interpretation of quantum mechanics led by Bohr [42] argued that quantum waves were not real, but that these waves reflected an observer’s subjective state of knowledge about reality. In Bohr’s Copenhagen interpretation, the wave function is a probability that collapses into a single value when measurement produces an observable. In the Heisenberg and Schrödinger model, canonical conjugate variables form mathematical tradeoffs (e.g., position or momentum; time or energy). But, Bohr’s [43] later theory of complementarity is his generalization of the tradeoffs existing between orthogonal perspectives common in ordinary human life (e.g., [44]).
In quantum physics, quoting an article in Physics Today:
To date, most experiments have concentrated on single-particle physics and (nearly) non-interacting particles. But the deepest mysteries about quantum matter occur for systems of interacting particles, where new and poorly understood phases of matter can emerge. These systems are generally difficult to computationally simulate [45].
Unlike this state of the experiments described in quantum physics, our research is designed to operate in the open for teammates interacting in teams, teams interacting with other teams, and systems of teams interacting with other systems.
Interdependence. By modeling Bohr’s complementary tradeoffs for teams, we have had success [41]. To further advance our project, we seek a stronger mathematical foundation that human-machine teams can observe, interpret, and act upon. We begin with interdependence. The National Academy of Sciences concluded that the effect of interdependence, or mutual dependence between two or more agents, causes a reduction in their degrees of freedom [5].
We are particularly interested in two types of entropy; Structural Entropy Production (SEP) and Maximum Entropy Production (MEP). SEP is based on the arrangement of a team; the choices of a team’s teammates; the capability of a team to work together seamlessly, to resolve its internal problems, and to allow adjustments to be made; but this entropy production should be as low as possible to allow the maximum amount of free energy available to be applied by the team to a team’s productivity. The choice of teammates is key—the only way to know that a good choice has been made is by the reduction in entropy with the addition of a new teammate, relegating the choice to a random selection. MEP is the maximum productivity output of a team; a team should want the maximum of its free energy available or as much as possible to be devoted to its productivity, to its targeted problem, to the maximum interdependence of its teammates to be fully engaged without free riding on the task at hand, all combining to increase the likelihood that for all teammates to be in the highest state of interdependence possible, it means relegating the members to orthogonal roles with minimal overlap (e.g., cook, waiter, cashier).
For example, the most powerful hurricane (MEP) has the tightest structure and the smallest eye (SEP) (see Figure 1 below; [46]; 2. With this model in mind, we have found that the degrees of freedom associated with the structural entropy production (SEP) of a team forms a trade-off with the team’s maximum entropy production (MEP; in [41]).
In this article, we will strive to improve and to advance the science of what that means. As an example of a mathematical model of interdependence used to study the effect of skill for a team’s state of interdependence, Moskowitz [47] concluded that teams increase their "interdependence to optimize the probability of the Team of multi-agents of reaching the correct conclusion to a problem that it confronts.” In contrast, Reiche [48] defines work interdependence as "the extent to which performing a work role depends on work interactions with externalized labor."
Interdependence as a resource. According to Jones (see p. 33 in [17], although humans live in a sea of interdependence, his assertion that its effects in the laboratory were bizarre subsequently reduced its value as a research topic until it regained respectability with the Academy’s study in 2015 [5]. Cummings [49] reported his anecdotal finding that the better was a scientific team, the more interdependent were its members. Since then, we have learned that the interdependence between culture and technology is a driving force for evolution and a resource for innovation [50]. In the future, we plan to model interdependence as constructive or destructive interference with the superposition of bistable agents by using a Hadamard gate. In such a model, the oppression of interdependence would be destructive interference. From another direction, an alert communicated among the interdependent members of a collective couples their brains, increasing their awareness of a possible danger, but also reducing the communication that needs to be transmitted [51].
Social life is permeated with the effects of interdependence [17]. For our study, we have arbitrarily described three effects associated with interdependence [41]: bistability (e.g., two sided stories; multitasking; debates); a measurement problem (e.g., cognitive concepts commonly correlate strongly with each other, but not with their physical correlates, a part of the measurement problem; in [22]); and non-factorability (e.g., fights among couples are common, but who is at fault is often undecidable without an outside observer or judge). We have found that non-factorability is the aspect of interdependence that more closely aligns with quantum mechanics.
Non-factorable is the defining characteristic of teams: the dependent parts of a team cannot be factored or disambiguated (in [40]). The first person to discover this phenomenon, which he named entanglement, was Schrödinger (p. 555, in [52]),
Another way of expressing the peculiar situation is: the best possible knowledge of a whole does not necessarily include the best possible knowledge of all its parts, even though they may be entirely separate and therefore virtually capable of being ‘best possibly known,’ i.e., of possessing, each of them, a representative of its own. The lack of knowledge is by no means due to the interaction being insufficiently known — at least not in the way that it could possibly be known more completely — it is due to the interaction itself. Attention has recently been called to the obvious but very disconcerting fact that even though we restrict the disentangling measurements to one system, the representative obtained for the other system is by no means independent of the particular choice of observations which we select for that purpose and which by the way are entirely arbitrary. It is rather discomforting that the theory should allow a system to be steered or piloted into one or the other type of state at the experimenter’s mercy in spite of his having no access to it.
Schrödinger’s idea, the whole being not equal to the sum of its parts, was adopted by Lewin [4] as the founding idea of social psychology, and later by Systems Engineers as their founding idea [53]. Schrödinger’s idea directly links quantum entanglement and interdependence.
Teams. In this study, our focus is on teams. In 2015, the National Academy of Sciences [5], citing Cummings [49], claimed that interdisciplinary scientists were the poorest of team performers, mediated by experience. We agree. An equation that we have developed to account for the interdependent tradeoffs between structure and performance makes the prediction that a team struggling to achieve a coherent fit among its team members will be a poorly performing team ([33]; [41]), supporting the claim by Cummings (see Equation 5, “The worst teams”). Also, the Academy claimed that teams enhance the performance of the individual, and our results point to the power of teams arising from a well-fitted team structure (i.e., decision advantage, discussed later; in [41]).
One of our first results for teams dealt with the effects of redundancy on interdependence. We predicted and found that redundancy decreases interdependence [33]; in contrast, as interdependence increases, the cohesion of a team ([49] increases and is reflected by an increase in its effectiveness: “moderated by task interdependence such that the cohesion-effectiveness relationship is stronger when team members are more interdependent … [reducing their] degrees of freedom” [5]. But, from Brillouin [54], “Every type of constraint, every additional condition imposed on the possible freedom of choice immediately results in a decrease of information.” Thus, interdependent agents working together constructively (in phase) produce less Shannon information than independent agents. If correct, non-factorability means that information about the inner workings of a team are forever obscured to outsiders and to insiders, and that we must find another way to determine the best structure and best performance of teams.
We assume that a human’s brain projects various mental scenarios for the body’s actions in reality. At one extreme, the mind-body relationship for an individual is, however, more difficult to generalize to the effects of interdependence as expressed by Bohr’s theory of complementarity (but see [44]). At the other extreme, when an individual is a member of a group, we assume that the human mind becomes otherwise fully engaged with the back-and-forth occurring among a group’s members and processes. A group is also an amorphous, non-exact phenomenon that can add or lose members over time with varying impacts on the group that may be independent of the reason a group was formed (e.g., some of the qualitative reasons to join a group include “the motivation for completing personal goals, the drive to increase self-esteem, to reduce anxiety surrounding death, to reduce uncertainty, and to seek protection,” in [55]).
Not so for teams. The function of a team is to solve a targeted problem ([47]; e.g., improving a team’s productivity, effectiveness, efficiency, or quality; in [56]). A well-functioning team has the potential to raise the power of the individual or teammates in a team beyond that of the individuals independently performing the same functions but outside of a team (e.g., [5]). Thus, we assume that the individuals independently performing the actions of a team when not a member of a team serve as Adam Smith’s [57] “invisible hand,” forming a baseline that we have used in the past to determine the power of a team [1].
At this point, our concerns are three-fold: First, how to model the interdependence in a team? Second, how to model the individual as a member of a team? And, third, how to measure an observable of interest for a team? With non-factorability in mind, we speculate that we can model the interference in teams with implicit waves in a state of superposition to represent interference; we can model the individual as contributing constructively or destructively to the interference in a team or faced by a team; and we use probabilities to predict the observable as the work products of a team evolve over time.
The quantum model: Waves and particles. From Dimitrova and Wei [58], in quantum mechanics, objects manifest as waves or particles, never as a pure particle or pure wave, always both. Whether an object manifests more as a wave or as a particle depends on a specific experiment or measurement. For example, the interference effect in Young’s double slit experiment demonstrated the wave nature of light, while Einstein’s photoelectric effect demonstrated its particle nature. The collapse or measurement combines with Born’s rule to identify the interference pattern as a probability distribution for individual detection.
Waves introduce superposition which allows us to aggregate the contributions of a team’s members by adding constructive interference or subtracting destructive interference. From Zeilinger [59]
[T]he superposition of amplitudes ... is only valid if there is no way to know, even in principle, which path the particle took. It is important to realize that this does not imply that an observer actually takes note of what happens. It is sufficient to destroy the interference pattern, if the path information is accessible in principle from the experiment or even if it is dispersed in the environment and beyond any technical possibility to be recovered, but in principle still ‘‘out there.’’ The absence of any such information is the essential criterion for quantum interference to appear.
Applying Zeilinger to our thinking about an individual who becomes a member of a team, superposition models the interference between these two states. Measurement will “destroy the interference pattern” that exists, but until then, the “absence of any such information is the essential criterion” for the existence of superposition. For example, we have found that redundancy produces destructive interference, reducing the effectiveness of a team [33]. From the National Academy of Sciences [40], the inability to factor the contributions of the individual members of a team is the Academy’s seminal finding: The “performance of a team is not decomposable to, or an aggregation of, individual performances” (p. 11, in [40]). Thus, factoring a team into its individual members ends the state of interdependence; however, if a team can be factored into its parts, it is not in a state of interdependence.
Regarding trade-offs, given a Fourier transform pair (time-energy, position-momentum), Cohen [60] found in signal theory that a “narrow waveform yields a wide spectrum, and a wide waveform yields a narrow spectrum and that both the time waveform and frequency spectrum cannot be made arbitrarily small simultaneously” (p. 45). While a convincing demonstration of trade-offs, Cohen was addressing signals easily repeated and replicated, unlikely with human-machine teams.
We are modeling the interaction with implicit waves. However, actual waves exist, too. For humans, gamma waves (>30 Hz) are a part of an inter-brain coupling (IBC) and synchronization that has been modeled with Kuramato weakly coupled oscillators [61]. Modeling IBC is crucial to a theoretical framework of the causal relations between socio-cognitive factors, behavioral dynamics, and neural mechanisms involved in multi-brain neuroscience [62]. Our plan is to build on this idea as a means to model the interdependence affecting a team.
The quantum model: Phase. We assume that phase is not relevant for an individual agent. But phase represents the effects of constructive or destructive interference influenced and instantiated by an interacting pair. When the phase is, on average, stable [63], a team’s structure is coherent; where the coherence time may be impeded or reduced by internal factors such as redundancy or vulnerability, then phase can be adjusted to coordinate with the other members of a team. We attribute the responsibility for “adjustments” to a team’s leader (e.g., a teacher; a coach; a boss).
In the past, we have assumed that if the structure of the perfect team becomes a unit, by taking the limit of the operator for the logarithm of SEP, we have found that predictions for human-machine teams from the theory of complementarity are observations that a machine can make (e.g., to use deception inside of a team, do not contribute to the team’s structural entropy; reduce structural entropy production [SEP] to allow the free energy available to a team to be able to increase a team’s performance; a vulnerability becomes observable after an attack by witnessing an increase in an opponent’s SEP or a decrease in its performance entropy [MEP]; and by dampening interdependence, authoritarianism decreases a team’s ability to innovate and increases its need to steal technology to be competitive (in [41]; [1]). Next, we begin to include operators.
The quantum model: Operators. An operator3 connects a wave function, , with an observable. Operators infer the linear superposition of states, i.e., the effects of the interference from two or more states. An operator evolves one state in time into another. Under a measurement, an operator collapses a superposition into a measurement basis. The Hermitian norm squared of the wave function gives the probability that an event can be observed in a physical space. For measurements, a Hermitian operator gives a real number for any of the wave functions it can discern, that is, that are orthogonal. An Hermitian operator associates a real number for each function in a set of orthogonal functions. If is a Hermitian operator, its expectation value must be real: ; e.g., see below for the complementary pair of SEP and MEP interconnected with free energy.
We generalize the ideas from Bohr, Schrödinger, and the National Academy of Sciences [5] to the interdependence between two agents, human or machine, operating together in a superposition. We assume that a human agent in interaction with another agent is in a bistable state, existing both as an individual and a member of a team. often in orthogonal roles. The superposition of individual agents or teammates, unlike independent mechanical objects in the physical world, occurs in interdependent states where two agents are dependent on each other, combining constructively or destructively to form patterns found in every social interaction (p. 33, in [17]). We propose that the measurement of superposition can be modeled with an operator that collapses the superposition. However, if the agents are operating in orthogonal roles (e.g., cook, waiter, cashier), their individual views of reality should not align.
In what follows, we review what we have learned with the interdependent tradeoffs suggested by our equation that models the tradeoffs between a team’s human-machine structure and its performance; i.e., the better a team’s human-machine structure functions as a unit, the more likely its performance increases (maximum entropy production) for that structure.
Lastly, to make a "whole" team greater than the sum of its "parts," produced by a reduction in the degrees of freedom among a team’s members [5], requires the glue of interdependence and a profound shift in our view of social reality to include the non-factorability of embodied information [9], the search for team member fittedness, and the introduction of randomness for who and what fits into a specific team and why not.
In the next section, we review the mathematics of interdependence in reverse; first for non-factorability and then bistability. Previously, we have reviewed the measurement problem in depth [41].
2. Interdependence. Mathematics. Non-factorability leads to tradeoffs
Two independent operators commute: . First, if a state is simultaneously an eigenfunction of both operators A and B, the commutator must vanish. Second, if one of two independent factors is removed from an interaction, it should have no effect on the remaining factor. As examples, two Hermitian matrices commute if their eigenspaces coincide. However, when two operators are dependent, they can not commute: .
We assume that is the operator for an autonomous human-machine team’s structure that configures the team’s free energy operator, , for the team’s use of its available free energy to achieve maximum performance, symbolized by M. In other words, when a team’s available free energy, , is applied by the team’s structure fully to the team’s target problem, the team is producing MEP.
For interdependence, we assume that a state of superposition exists among the members of a team (or audience watching a debate). To reiterate, based on the National Academy of Sciences reports, while in a state of interdependence, the contributions of the individual members in a team cannot be decomposed [40]. Per Cummings [49], the best team science occurs with teams in the highest state of interdependence. That allows us to assume that if a team’s human-machine structure forms into a perfect unit, its structural entropy production goes to zero in the limit as the degrees of freedom, , collapse to 1:
Equation 1 tells us why Von Neumann’s proposal in 1966 for independent self-reproducing automata agents was flawed [64]. That is, the communication among Von Neumann’s automata occurred with Shannon information, making each one independent of each other, reducing their ability to communicate with each other.
The operator for structure, , should give us an eigenvalue that is the team’s design for minimizing the entropy produced by its structure. Interdependently, the operator for the team’s performance productivity, M, should give the eigenvalue that characterizes the team’s ability to direct the maximum amount of its available free energy, , to the team’s target problem, producing MEP.
Next, the two operators being dependent on each other allows us to assume that a tradeoff exists between the uncertainty in a team’s human-machine structure operator, , and the operator for the team’s productivity, M, allowing a given structure to reach its maximum entropy production. Assume that the structure of a human-machine team’s structural operator, , reflects the eigenvalue it produces, and similarly that a team’s performance operator, M, generates an eigenvalue reflective of the MEP that a team is capable of achieving, based on the given structure. Assuming that these two factors are not independent, violating one of the basic tenets of information theory (i.e., that this information is not i.i.d.; for a review, see [20]), then:
This last equation could represent an ordering effect commonly observed with questionnaires [65]. Instead, with it, we derive an uncertainty relation for a team between the interdependent factors and , creating a tradeoff between these two operators. Assuming that this tradeoff is between complementary parts of a team (viz., not composed of independent factors) gives:
Equation 3 states that the uncertainty in the entropy produced by a team’s operator for structure (SEP) times the uncertainty in the entropy produced by the team’s operator for productivity (MEP) is approximately constant. We have used Equation (3) to link several predictions along with field results based on interdependence (best-worst teams; deception; vulnerability; risk perception versus risk determination; recovering rational choice, complexity and debate; emotion; innovation versus oppression; interdependence as a resource; non-factorability; the orthogonality of training versus education; oscillations; decision advantage; and a model of harmonic oscillation initially for a team of three agents then a team of three with a fourth redundant agent):
2.1. Best-worst teams
The best teams, organizations, and systems:
The worst:
Equation 5 for the “worst” teams explains why divorce is potentially expensive and disruptive as a team’s structure is ripped apart by its members (in business, CBS versus Viacom; see [41]; or in a marriage, children of divorcing parents often act out [66]); its poor fittedness4 accounts for the finding by Cummings [49] that the poorest performing teams of scientists were interdisciplinary (mediated by experience; more later).
Based on Equations (4) and (5); on Christensen’s team’s findings [67] that the results of mergers on average are poor, and on the results of our own case studies [41], we hypothesize that the only observable available to human-machine insiders or outsiders is how members of a team fit together, characterized by the entropy production from a reduction in their degrees of freedom. That being the case, equations (1) and (3) tell us that fittedness is contingent only on whether the structural entropy production drops when two, three or more teammates come together in an interaction and attempt to perform as a unit. Since disambiguation is not possible [40], random selection to seek fittedness becomes the only rational option applicable in reality (i.e., embodied rationality, mediated by experience).
2.2. Deception
To use deception inside of a team or system by a machine in a role with a hidden agenda, a double-dealer, a guise to steal intelligence or purvey harm to an organization as has happened with chatbot. A series of interviews published in the New York Times has served to warn about the use of chatbot in scams, to falsely accuse others, and to mislead. According to Equation (4), in performing its role at the highest level, a machine agent intent on harm or theft of intelligence should not play its position in a way that indicates anything other than that the machine is the best teammate in the role for which it is functioning until the machine, operating with its well-hidden agenda, has collected the information that it has sought.
Deception has long been a critical element of warfare. From Sun Tzu (p. 168, in [68]), "Engage people with what they expect; it is what they are able to discern and confirms their projections. It settles them into predictable patterns of response, occupying their minds while you wait for the extraordinary moment—that which they cannot anticipate.”
Aldrich Ames is an example of successful espionage when, in 1985, “Ames began selling American intelligence information to the KGB. At least 10 CIA agents within the Soviet Union were executed as a result of Ames’s spying; ultimately, he revealed the name of every U.S. agent operating in the Soviet Union (after 1991, Russia)” [69].
2.3. Vulnerability
To discover a vulnerability in an opposing team, a human-machine team should probe its opponent’s structure. Based on Equation 5, vulnerability in a team’s opponent is characterized in one of two ways: Its opponent’s structural entropy production increases; its maximum entropy production decreases; or both occur simultaneously. An example from Sun Tzu [70], "Rouse him, and learn the principle of his activity. Force him to reveal himself, so as to find out his vulnerable spots."
2.3.1. Non-factorability: The key characteristic
The National Academy of Sciences 2021 report made an assertion that was not cited (p.11, in [40]): The “performance of a team is not decomposable to, or an aggregation of, individual performances.” That the Academy’s claim was not cited tells us that the Academy liked its claim, but that it had no evidence in support. Equation 3 makes the prediction that interdependence affects the data for coherent teams by making it non-factorable, supporting the Academy’s claim. This claim and prediction need further exploration. But the Academy’s assertion is one of the first pieces of direct evidence by outsiders in support of our theory of interdependence, which is only evident with a loss in the degrees of freedom (for an interaction, a team, a system; in [5]). The key characteristic of interdependence is its reduction in the degrees of freedom among the parts of a team or system that it affects (Equation 1), not only preventing the logical decomposition of a team, but also allowing us to claim its similarity to entanglement. The loss in the degrees of freedom decreases the complexity of the team’s structure in exchange for an increase in the complexity of its output for the problems that a team addresses.
The Academy’s non-cited finding of non-factorability is explained above by Equations 1 and 3. As the degrees of freedom in a team are reduced, so is the Shannon [71] information about the individual performances observable to the performers and to external observers, in agreement with Bohr’s observations of a player versus a sporting event’s observers (in [44]). More importantly, tensors can be used to model the elements of teams and systems, implying that when tensor products are factorable, this factorability between the members of a team indicates the non-existence of interdependence, otherwise, the members are interdependent.
Interdependent non-factorability can be represented by Von Neumann entropy, where entropy of the whole, , is less than the sum of its parts, and :
The equality holds only when the parts of a whole are independent of each other, meaning that the entropy of the whole is less than or equal to the sum of the parts of the whole, validating Lewin’s [4] assertion that “the whole is more than the sum of its parts,” and the same claim by Systems Engineers [53], both claims that, unfortunately, have been largely ignored of late [1].
2.4. Bistable reality
Bistable refers to several situations in reality. An illusion that lends itself to two mutually exclusive interpretations (Figure 2). From Eagleman ([72], p. 923) reporting on bistable illusions, “… the visual system chooses only a single interpretation at a time, never a mixture." Bistability also refers to an animal’s self-interest; e.g., when prey in a forest do not suspect the presence of predators, they overgraze and harm the forest [73]. Moreover, we know that individuals multitask poorly [74]; in contrast, the purpose of a team is to multitask [1].
An example of bistability that also invokes deception as a defensive maneuver to protect self-interest was given in a news account in Science [75]: The female partners of HIV infected males participated in a drug study designed to prevent the transmission of HIV to the females. At the end of the study, the females were asked whether they had been compliant with the drug regimen, with 95% stating that they had been compliant, indicating that the drug study had failed. However, the investigators had also taken blood samples from the female participants, which indicated less than 26% compliance. "There was a profound discordance between what they told us … and what we measured," infectious disease specialist Jeanne Marrazzo said.
2.5. Risk perception versus risk determination
Reducing risk perception is a hard, complex problem using belief logic. An example of belief logic based on risk perception is the tragic drone attack approved by the DoD in August 2021. The DoD approved drone attack in Afghanistan was against a purported suicide bomber. Instead, the attack killed 10 civilians, including children. In the after-action review of the tragedy [76], the DoD concluded that using a "red team" to challenge the DoD’s decision to launch the drone attack might have prevented the incident. Such a red-team challenge is generalizable to recovering rational choice, reducing complexity and debate.
2.6. Recovering rational choice, reducing complexity, and debate
We are concerned with solutions that can be applied in open systems, a complex problem as research is moved from the laboratory simulations to the open world [14]: “agents in simulated environments navigate a much smaller set of possible states and perform deliberative-reasoning search tasks over a much smaller set of possible state-action paths than what happens in the open world of a non-simulated, real environment.”
Mann [2] found that the belief logics developed in the laboratory fail in two important situations in the open: when facing uncertainty and when faced with conflict. For uncertainty, it can be addressed by circumscribing, or bounding [77], the problem [1]. For example, a military attempts to control the airspace around its battlefield; traffic-flow engineers use traffic circles to reduce uncertainty; mergers reduce uncertainty in contracting markets; and debate is managed in courtrooms. On the other hand, over simplifying a complex domain can cause uncertainty and failure when transitioning from a simulated to the real world, which is more complex and often chaotic. Doctor and her colleagues (p. 9, in [14]) gave an example of the pathological behavior of an AI system, a robot, transitioning from a simulation to a real-world domain. The robot failed in the real-world because it was designed for the much lower complexity in a simulated domain versus the complexity of the real-world. But by reducing the choices available to the robot (i.e., giving it fewer degrees of freedom), it successfully completed its mission.
Second, the value of debate among humans is to expose with an adversarial process the intrinsic uncertainty that characterizes reality, including the illusions inherent in risk perceptions, and the need to seek and test the strongest connections to reality; e.g., courtrooms address uncertainty by drawing a boundary about what can be brought before a court, discussed and demonstrated [1].
Using data dependency (caused by state dependency; in [34]), the uncertainty reduced inside of bounded spaces may recover rational choice [78], including with game theory; e.g., Simon’s bounded rationality [77]. Cross-examination in a courtroom is considered to be the greatest means to discovering truth [79], a bounded space with strict rules (judges) where opposing officers (lawyers) facing uncertainty compete to persuade an audience (jury) of each’s interpretation of reality; legal appeals further reduce uncertainty and complexity with an “informed assessment of competing interests” [80].
Generalizing, we see that the decision of a blue human-machine team’s decisions under uncertainty on the battlefield challenged in a debate by an AI-assisted red-team’s machine could prevent future tragedies by challenging perceptions of risk [76]; and why machine learning and game theory require controlled contexts, managed within a boundary. However, this model of using AI to challenge a decision with debate needs further exploration.
2.7. Emotion
Our plan is to model emotion as a heightened energy state that reduces the options available to decision makers, such as has occurred with the tragic drone strike in Afghanistan in August, 2021 [76], or, in 1988, the shoot-down of an Iranian Airbus by the USS Vincennes in a “highly charged environment” (p. 3, in [81]). In 1992, as a pilot study [82],5 we modeled emotion by having a volunteer read a script calmly and then reread it in an angry voice, finding that the latter angry voice was twice the energy output of the calm voice. If energy is a scarce resource, the results indicated that the options for an emotional team narrow in a given situation. Guided by Equation 5, we speculate that a team’s struggles over its structure produces an emotional response that reduces its productivity. If we are correct, to be maximally effective with a given team or given system, interdependence for the team must be bounded within which it is freely used to focus a team’s effort to achieve maximum performance.
2.8. Innovation and oppression
We invert this concept into a question of how to impede innovation? In a study of education, freedom, and innovation [41], we have found that innovation is impeded by the suppression of interdependence; e.g., by gangs, kings, authoritarians. By reducing interdependence, oppression motivates a country like China to steal innovations. From the interview by the Wall Street Journal’s Chief Editor [83] of General M. Hayden, the former Central Intelligence Agency (CIA) and National Security Administration (NSA) chief, Hayden stated that the Chinese stole millions of records from federal employees in the search for the innovativeness that has so far eluded China. He said that he told his Chinese counterparts:
You can’t get your game to the next level by just stealing our stuff. You’re going to have to innovate.
Oppression works by reducing interdependence, consequently also innovation. For example, in 2018, Russia’s global innovation index was 43rd among all nations, but in 2022, it had dropped to 47th.6 From the Wall Street Journal [84], in Russia today,
The press is now completely under state control and independent voices of dissent, like that of opposition leader Alexei Navalny, are quickly suppressed. Critics of the regime have been murdered both inside and outside the country.
China has also been charged with stealing technology. We quoted above by General Haden, the former Central Intelligence Agency (CIA) and National Security Administration (NSA) chief, that China had to raise its game. More recently, from the New York Times [85],
Although China publicly denies engaging in economic espionage, Chinese officials will indirectly acknowledge behind closed doors that the theft of intellectual property from overseas is state policy.
2.9. Orthogonality: Training and experience versus education
Returning to Equation 2, in 1992, an experiment was conducted in virtual reality for USAF pilots flying in air combat maneuvering. After analyzing the data, Lawless found no relationship between their performance and their repeated education by the USAF about how to solve the complex maneuvers needed to win in air combat (reviewed in [41]). Cummings [49] also reported that the adverse effects of being a part of an interdisciplinary team are mitigated by the experience of the participants, agreeing with our finding about USAF fighter pilots that the experience gained by training in the field, but not an education of air-combat maneuvering processes in the classroom, predicted superiority in air combat ([86]; reviewed in [41]).
In contrast, in a study of the nations of Middle Eastern North Africa (MENA; see the footnote below for the UN HDI data for MENA countries 7) first conducted in 2019 and replicated in 2022, Lawless [41] found a significant relationship between the education of a country’s citizens and its innovation index. By comparing these two studies, the conclusion is that an orthogonality existed between the physical training for fighter pilots in air combat maneuvering and the education for innovation; the former operates in physical space, while the latter operates in conceptual (perceptual) space. Orthogonality may be more common than considered heretofore.
If we assume that and M are operators and complex vectors in Hilbert space, they are also eigenfunctions; if they are also orthonormal, then the dot product is similar to the Kronecker delta:
Orthogonality occurs only when ; alignment or agreement occurs when . The orthogonality between education (dis-embodied cognitive training) and training (embodied cognitive physical training [9]; [6]) modeled in Equation 7 accounts for the lack of an effect from educating Air Force combat fighter pilots in air combat maneuvering in the classrooms (disembodied) versus training in the field (embodied cognition), an effect that may also account for the replication crisis in Social Science, which we call the measurement problem (self-esteem; implicit attitudes; risk perceptions; for a review of the replication crisis, see [26]) and may, possibly, offer a corrective, but more exploration is necessary to confirm.
2.10. Oscillations
Previously, we considered the case of two Federal agencies in a conflict with which the first author was asked to help to rectify.8 The conflict regarded the Department of Energy’s (DOE’s) cleanup of its nuclear waste at its Savannah River Site, Aiken, SC, is represented in Figure 3 [87]:
As an example of an oscillation [41], the DOE’s high-level radioactive waste (HLW) cleanup of its tanks had been stopped by a lawsuit, but was restarted by the U.S. Congress (i.e., the NDAA of 20059). As part of a separate compromise reflected with this new law, the U.S. Nuclear Regulatory Commission (NRC) was given sufficient oversight to overrule DOE’s technical decisions for its HLW tank closure program. However, from 2005 to 2011, DOE would propose a plan to restart its HLW tank closures, but NRC would require DOE to make another proposal. This oscillation is represented by the back and forth between points 1 and 2 in Figure 3. The back and forth approached 7 years until South Carolina’s DHEC10 complained to DOE’s Citizens Advisory Board at its Savannah River Site in South Carolina that DOE was in danger of missing its legally mandated milestone to restart its tank closures. A committee on CAB proposed a recommendation11 approved by the full CAB in which the citizens demanded of DOE and NRC in public that the two agencies settle their differences and immediately restart tank closures, which happened.
If we let represent the adverse belief of NRC in Equation 7, the change in its belief is reflected by an orthogonal rotation of 90 degrees in Equation 8 (i.e., after matrix multiplication, we let ) (Figure 3):
2.11. Decision Advantage (DA)
Previously, we had modeled the oscillations in a debate (Figure 3) with a simple LRC-like electrical circuit that oscillates back and forth, with the audience providing resistance, causing the oscillations to stop when a decision had been made; in this LRC-like model, beliefs are modeled as being a part of imaginary space, driving the oscillation of information for the benefit of the audience. Based on the rotations that occur as a debate’s representatives argue for and against a motion, the oscillations back and forth are represented by a “torque,” symbolized by , in the minds of the audience that drives their processing of the information, allowing us to model decision advantage, DA [41]:
Equation 9 means by DA that one team, team A, was quicker than another team, team B, in driving the oscillations back and forth between competitors during a debate; that one team’s grasp of the complex issues was more forceful; or that one team’s perception of the eventual solution was held with more conviction than the other; etc.
By DA, equation 9 has support in the literature and the field. From the office of the Director of National Intelligence in 2015 (pp. 6-9, in [89]),
strategic advantage is the ability to rapidly and accurately anticipate and adapt to complex challenges … the key to intelligence-driven victories may not be the collection of objective ‘truth’ so much as the gaining of an information edge or competitive advantage over an adversary … one prerequisite for decision advantage is global awareness: the ability to develop, digest, and manipulate vast and disparate data streams about the world as it is today. Another requirement is strategic foresight: the ability to probe existing conditions and use the responses to consider alternative hypotheses and scenarios, and determine linkages and possibilities. …Secrecy, however, is only one technique that may lead to decision advantage; so may speed, relevance, or collaboration.
3. Discussion
In this review, we have not focused sufficiently on boundaries, ethics and evolution, but we are mindful of these topics, and we believe them to be central to the establishment of a team’s or system’s autonomy, our overarching goal. We have also spent no time in reviewing whether beliefs lead or follow actions, and vice versa, but we suspect that both occur during an interaction. As part of our exploration, by following stock market futures and prices during the day, it becomes apparent that they exchange leadership several times during a trading day. Instead, we suspect a superordinate in the background at play, nurtured by interdependence, similar to Ibn Khaldun’s (p. xi, [93]) "asabiyah" (group solidarity). We have noticed for some time that, by suppressing interdependence with censorship and physical threats, gang infested areas and the governance of a nation by authoritarians place both at a disadvantage (Russia’s surprise military difficulties in Ukraine, unexpected by insider and outsider observers; in [94]12) which remains a part of our consideration.
4. Conclusions
1. Research tested in the open in complex environments is critical to advance the science of interdependence for human-machine teams, systems, and autonomy ([40]; e.g., [14]). We speculate that disembodied cognition used in the laboratory is at the root of the replication crisis in social science [26]. We believe that including interdependence, as difficult as it is to manage in the laboratory (p. 33, in [17]), should begin to remedy the problem.
2. Pearl ([31]; [32]) requires AI researchers to include contact with reality in their models. However, embodied thoughts ([6,9]) derived while operating in reality cannot be decomposed from each other. This accounts for Chomsky’s [30] conclusion that ChatGPT cannot capture reality. And it makes satisfying Pearl’s demands more difficult in the laboratory alone.
3. One barrier to an AHMT (autonomous human-machine team), noted by the National Academy of Sciences [40], was that most proposals for the design and operation of AHMTs are based on laboratory results that do not work in the real world. Lawless and colleagues [1] add that team science has been hindered by relying on observing how "independent" individuals act and communicate (viz., i.i.d. data; [20,71]), but independent data cannot reproduce the interdependence observed in teams [5].
4. Digital communication is based on Shannon’s [71] information theory (e.g., entropy, channels, errors). While the information communicated between individuals works well based on Shannon, that information is factorable (i.e., i.i.d. data; see [20]); early on, it was recognized that interdependence in teams in the laboratory was not rational, leading to the recommendation to reduce it (e.g., [95,96]). Surprisingly, disembodied, factorable, and rational beliefs fail outside of the laboratory, even for simple concepts like “self-esteem” [22] or “implicit racism” [23], creating the replication crisis in social science [26] and an enormous waste in the effort to “treat” biases (e.g., [24]). By being disembodied [37], chatbot is not connected to reality [30]. From an interview in the New York Times of Joshua Bongard, a roboticist, “The body, in a very simple way, is the foundation for intelligent and cautious action” [37]. Unless they are walled off, restricted or bounded (e.g., [14,77]), these failures extend to disembodied, factorable, separable and rational beliefs, especially when confronted in the open by uncertainty or conflict [2].
From Aspect, Clauser and Zeilinger (p. 1, from [97]), winners of the 2022 Nobel prize in physics, "That a pure quantum state is entangled means that it is not separable … being separable means that the wave function can be written ." From the Wikipedia article on quantum entanglement, 13 "An entangled system is defined to be one whose quantum state cannot be factored as a product of states of its local constituents." Since the contributions of individual members of a team cannot be decomposed, they are not separable nor factorable but dependent.
Thus, we conclude with our sketch of “a new framework” for embodied cognition ([6,9]) that is remarkably similar to quantum entanglement. We know that constraints reduce information [54]. By reducing the degrees of freedom among agents in a social field [4], interdependence is a constraint. Interestingly, we know that open-ended “knowledge” reflects the absence of “surprise” [95]. We also know that embodied beliefs constructed in reality work very well, with humans making rational “dynamic adjustments” to fit reality as it changes (Lucas, p. 253, in [98]). Reflecting the non-factorable nature of embodied cognition, we know that teams cannot be decomposed [40], forming a no-copy principle for constituting teams similar to the quantum no-cloning principle (p. 77, in [99]).14 In the open where embodied cognition reigns, a state of maximum interdependence was found to be critical to the best performing scientific teams [49]; and we have found that oppressive societies significantly reduced interdependence and the freedom to pursue education and innovation [41]; in every society, freedom best allows a society to marshal its available free energy against the problems it has targeted [47]. We thus speculate that interdependence, which is embodied cognition and cannot be factored (e.g., [5,40]), is the reason why debate is central to the open and free societies that evolve compared to those societies that stagnate, regress or de-evolve [1]. But for future research, we leave open this question: how do we create a new statistics based on the reduction or absence of Shannon information?
5. Future Directions. Harmonic Oscillators
The future direction that we are exploring is to replace Equation 9 derived from an LRC-like simple model of a debate (debater 1, counter-debater 2 and an audience) [41] with 3-coupled classical harmonic oscillators and then 3-coupled quantum qutrit harmonic oscillators to model and monitor phase shifts in a 3-way interaction between intelligent members of a human-machine team. Assuming that exchanges between elements of a team must always be in phase, phase shifts become important when teammates are unable to coordinate their interactions with one another. In a 3-person restaurant, the three agents operating together as part of a team inside of a bounded space (cook, waiter, cashier) when an interaction has to be adjusted due to a mistake or complaint of service, destructive interference arises. If a competent outsider can observe the problem occurring (viz., the restaurant’s owner), a simple nudge [102] may correct the problem. In our model, we construe this nudge as an example of phase control that may be sufficient to adjust the coupled harmonic oscillators of a human-machine team to recover a lagging phase (for the equations of interest, see [103]).
In the Table 2, we contrast the models reviewed and, briefly, the benefits and weaknesses of each.
5.1. Harmonic Oscillators. A test of models
The first test of our model will attempt to replicate our first reported finding with the theory of interdependence. In 2017, social network theorists predicted that redundancy made a network more efficient [104]; further, the National Academy of Sciences in 2015 reported that while teamwork made an individual more effective, they also speculated that "many hands make light work" [5]. Our first prediction contradicted both social network theorists and the Academy by predicting and finding that redundancy in a team reduces the effectiveness of interdependence in a team or organization ([105]). For example, at that time we found that Exxon had 1/8th as many employees as Sinopec, yet both companies produced the same amount of oil. We replicated this finding in a study of the largest militaries in the world [106].
We predict that by adding a fourth, redundant teammate to a team of three well-functioning agents, modeled by four qutrit harmonic oscillators, when the fourth oscillator does not contribute to the performance of the other three, the team will become less effective.
In summary, eventually, we want to have 3 models operating simultaneously: the quantum qutrit model of an intelligent 3-member human-machine debate team; an opposing qutrit model; and a qudit model of the same but along with an audience. Interdependence suffuses all of the mathematics in our models. With these tools, we have established the value of interdependence. It is central to debate and decision advantage, and to innovation and evolution, and to much more yet to be discovered.
Acknowledgments
The corresponding author thanks the Office of Naval Research for funding his research at the Naval Research Laboratory where he has worked for the past seven summers (under the guidance of Ranjeev Mittu), and where parts of this manuscript were completed.
References
- Lawless, W.; Sofge, D.A.; Lofaro, D.; Mittu, R. Editorial. Interdisciplinary Approaches to the Structure and Performance of Interdependent Autonomous Human Machine Teams and Systems. Frontiers in Physics 2023. [Google Scholar] [CrossRef]
- Mann, R. Collective decision making by rational individuals. PNAS 2018, 115, E10387–E10396. [Google Scholar] [CrossRef] [PubMed]
- Neumann, J.V.; Morgenstern, O. Theory of games and economic behavior (originally published in 1944)); Princeton University Press, 1953. [Google Scholar]
- Lewin, K. Field theory in social science. Selected theoretical papers; Harper and Brothers, 1951. [Google Scholar]
- Cooke, N.; Hilton, M.E. Enhancing the Effectiveness of Team Science; National Research Council, National Academies Press: Washington (DC), 2015. [Google Scholar]
- Clark, A. Supersizing the Mind: Embodiment, Action, and Cognitive Extension; Oxford University Press, 2010. [Google Scholar]
- Lawless, W.F., M. R.S.D.; Hiatt, L. Editorial (Introduction to the Special Issue), “Artificial intelligence (AI), autonomy and human-machine teams: Interdependence, context and explainable AI. AI Magazine 2019, 40, 5–13. [Google Scholar] [CrossRef]
- Cooke, N.; Lawless, W. Effective Human-Artificial Intelligence Teaming. In Engineering Science and Artificial Intelligence; Springer, 2021. [Google Scholar]
- Shapiro, L.; Spaulding, S. Embodied Cognition. In The Stanford Encyclopedia of Philosophy; Edward N., Zalta, Ed.; 2021. [Google Scholar]
- Spinoza, B. The ethics. The Collected Writings of Spinoza, vol. 1; Princeton University Press, 1985. [Google Scholar]
- Hume, D. A Treatise of Human Nature, edited by L. A. Selby-Bigge, 2nd ed. revised by P. H. Nidditch; Clarendon Press, 1975. [Google Scholar]
- Nash, J. Equilibrium points in n-person games. PNAS 1950, 36, 48–49. [Google Scholar] [CrossRef]
- Amadae, S. Rational choice theory. POLITICAL SCIENCE AND ECONOMICS. Encyclopaedia Britannica 2017. [Google Scholar]
- Doctor, K.; Task, C.; Kejriwal, M.; colleagues. Toward Defining a Domain Complexity Measure Across Domains. AAAI 2022. [Google Scholar]
- H.H. Kelley, J.G. Holmes, N.K.H.R.C.R.; van Lange, P, An atlas of interpersonal situations; Cambridge University Press, 2003.
- Kelley, H. Lewin, situations, and interdependence. Journal of Social Issues 1991, 47, 211–233. [Google Scholar] [CrossRef]
- Jones, E. Major developments in five decades of social psychology. In D.T. Gilbert, S.T. Fiske and G. Lindzey, The Handbook of Social Psychology; McGraw-Hill, 1998; Volume 1, pp. 3–57. [Google Scholar]
- Nadler, Steven (Edward N. Zalta, e. Baruch Spinoza. The Stanford Encyclopedia of Philosophy 2022.
- Thagard, P. Rationality and science. In Handbook of rationality; Mele, A., Rawlings, P., Eds.; Oxford University Press, 2004; pp. 363–379. [Google Scholar]
- Schölkopf, B.; Locatello, F.; Bauer, S.; colleagues. Towards Causal Representation Learning. arXiv 2021. [Google Scholar] [CrossRef]
- Bednar, R.; Peterson, S. Self-esteem Paradoxes and innovations in clinical practice, 2nd ed.; American Psychological Association (APA), 1995. [Google Scholar]
- Baumeister, R.F.; Campbell, J.; Krueger, J.; Vohs, K. Exploding the self-esteem myth. Scientific American 2005, 292, 84–91. [Google Scholar] [CrossRef]
- Blanton, H.; Klick, J.; Mitchell, G.; Jaccard, J.; Mellers, B.; Tetlock, P. Strong Claims and Weak Evidence: Reassessing the Predictive Validity of the IAT. Journal of Applied Psychology 2009, 94, 567–582. [Google Scholar] [CrossRef]
- Paluck, E.; Porat, R.; Clark, C.; Green, D. Prejudice Reduction: Progress and Challenges. Annual Review of Psychology 2021, 72, 533–60. [Google Scholar] [CrossRef] [PubMed]
- Leach, C. Editorial. Journal of Personality and Social Psychology: Interpersonal Relations and Group Processes 2021.
- Nosek, B. Estimating the reproducibility of psychological science. Science 2015, 349, 943. [Google Scholar]
- et al., P.; et al. Mastering the game of Stratego with model-free multiagent reinforcement learning. Science 2022, 78, 990–996. [Google Scholar]
- Klein, E. This Changes Everything. New York Times 2023. [Google Scholar]
- Zumbrun, J. ChatGPT Needs Some Help With Math Assignments. `Large language models’ supply grammatically correct answers but struggle with calculations. Wall Street Journal 2023. [Google Scholar]
- Chomsky, N. The False Promise of ChatGPT. New York Times 2023. [Google Scholar]
- Pearl, J. Reasoning with Cause and Effect. AI Magazine 2002, 23, 95–111. [Google Scholar]
- Pearl, J.; Mackenzie, D. AI Can’t Reason Why. The current data-crunching approach to machine learning misses an essential element of human intelligence. Wall Street Journal 2018. [Google Scholar]
- W.F. Lawless, R. Mittu, D.S.; Russell, S., Eds., Autonomy and Artificial Intelligence: A threat or savior?; Springer, 2017; chapter Chapter 1. Introduction.
- Davies, P. Does new physics lurk inside living matter? Physics Today 2021, 73. [Google Scholar] [CrossRef]
- Berscheid, E.; Reis, H. Attraction and close relationships. In The handbook of social psychology, 4th ed.; Lawrence Erlbaum, 1998. [Google Scholar]
- Chen, B., H. K.R.S.; colleagues. Automated discovery of fundamental variables hidden in experimental data. Nature Computational Science 2022, 2, 433–442. [Google Scholar] [CrossRef]
- Whang, O. Can Intelligence Be Separated From the Body? Some researchers question whether A.I. can be truly intelligent without a body to interact with and learn from the physical world. New York Times 2023. [Google Scholar]
- Nasaw, D.U.S. Offers Payments to Families of Afghans Killed in August Drone Strike. State Department to support slain aid worker’s family’s effort to relocate to U.S., Pentagon says. Wall Street Journal 2021. [Google Scholar]
- Weinberg, S. The Trouble with Quantum Mechanics. The New York Review of Books. 2017. Available online: http://www.nybooks.com.
- Endsley, M. colleagues. Human-AI Teaming: State of the Art and Research Needs; National Research Council, National Academies Press: Washington (DC), 2021. [Google Scholar]
- Lawless, W. Interdependent Autonomous Human-Machine Systems: The Complementarity of Fitness, Vulnerability & Evolution, Entropy. Entropy 2022, 24, 1308. [Google Scholar] [PubMed]
- Bohr, N. Causality and Complementarity. Philosophy of Science 1937, 4, 289–298. [Google Scholar] [CrossRef]
- Bohr, N. Science and unity of knowledge. In Unity of knowledge; Leary, L., Ed.; Doubleday, 1955; pp. 44–62. [Google Scholar]
- Pais, A. Niels Bohr’s Times: In Physics, Philosophy, and Polity; Clarendon Press: 1991.
- Hazzard, K.; Gadway, B. Synthetic dimensions. Physics Today 2023, 62–63. [Google Scholar] [CrossRef]
- Emanuel, K. Hurricanes: Tempests in a greenhouse. Physics Today 2006, 59, 74–75. [Google Scholar] [CrossRef]
- Moskowitz, I. A Cost Metric for Team Efficiency. Frontiers in Physics 2022. [Google Scholar] [CrossRef]
- Reiche, B.S. Between interdependence and autonomy: Toward a typology of work design modes in the new world of work. Human Resource Management Journal 2023, 1–17. [Google Scholar] [CrossRef]
- Cummings, J. Team Science Successes and Challenges; NSF Workshop Fundamentals of Team Science and the Science of Team Science: Bethesda MD, 2015; June 2. [Google Scholar]
- Ponce de León, M.; Marom, A.; Engel, S.; colleagues. The primitive brain of early Homo. Science 2021, 372, 165–171. [Google Scholar] [CrossRef]
- Sliwa, J. Toward collective animal neuroscience. Science 2022, 374, 397–398. [Google Scholar] [CrossRef]
- Schrödinger, E. Discussion of Probability Relations Between Separated Systems. Proceedings of the Cambridge Philosophical Society 1935, 31, 555–563. [Google Scholar] [CrossRef]
- Walden, D.; Roedler, G.; Forsberg, K.; Hamelin, R.; Shortell, T. Systems Engineering Handbook. A guide for system life cycle processes and activities (4th Edition); Volume INCOSE-TP-2003-002-04, John Wiley and Sons, 2015. [Google Scholar]
- Brillouin, L. Science and Information Theory; Academic Press: 1956.
- Hohman, Z.; Kuljian, O. Why people join groups; Oxford University Press: 2021.
- Mathieu, J.E., G. P.D.M.; Klock, E. Embracing Complexity: Reviewing the Past Decade of Team Effectiveness Research. Annual Review of Organizational Psychology and Organizational Behavior 2019, 6, 17–46. [Google Scholar] [CrossRef]
- Smith, A. An Inquiry into the Nature and Causes of the Wealth of Nations; University of Chicago Press, 1776/1977. [Google Scholar]
- Dimitrova, T.; Weis, A. The wave-particle duality of light. A demonstration. American Journal of Physics 2008, 76, 137–142. [Google Scholar] [CrossRef]
- Zeilinger, A. Experiment and the foundations of quantum physics. Reviews of Modern Physics 1999, 71, 288–297. [Google Scholar] [CrossRef]
- Cohen, L. Time-frequency analysis; Prentice Hall Signal Processing Series; 1995. [Google Scholar]
- Acebrón JA, Bonilla LL, P. V.C.R.F.; R., S. The Kuramoto model: a simple paradigm for synchronization phenomena. Reviews of Modern Physics 2005, 77, 137–185. [Google Scholar] [CrossRef]
- Moreau, Q. L.D.C.R.G.; Dumas, G. A neurodynamic model of inter-brain coupling in the gamma band. Journal of Neurophysiology 2022. [Google Scholar] [CrossRef]
- Martyushev, L. Entropy and entropy production: Old misconceptions and new breakthroughs. Entropy 2013, 15, 1152–1170. [Google Scholar] [CrossRef]
- Von Neumann, J. Theory of self-reproducing automata; University of Illinois Press, 1966. [Google Scholar]
- Düval, S.; Hinz, T. Different Order, Different Results? The Effects of Dimension Order in Factorial Survey Experiments. Research Methods & Evaluation, Sage 2019, 32. [Google Scholar]
- Weaver, J.M.; Schofield, T.J. Mediation and moderation of divorce effects on children’s behavior problems. Journal of Family Psychology 2015, 29, 39–48. [Google Scholar] [CrossRef]
- Christensen, C.; Alton, R.; Rising, C.; Waldeck, A. The Big Idea: The New M-and-A Playbook. Harvard Business Review 2011. [Google Scholar]
- Tzu, S. The art of war; Basic Books, 1994. [Google Scholar]
- Editors. Command economy. Encyclopedia Britannica 2017. [Google Scholar]
- Giles, L. The art of war by Sun Tzu; Special Edition Books, 2007. [Google Scholar]
- Shannon, C. A Mathematical Theory of Communication. The Bell System Technical Journal 1948, 27, 379–423 and 623–656. [Google Scholar] [CrossRef]
- Eagleman, D. Visual illusions and neurobiology. Nature Reviews Neuroscience 2001, 2, 920–926. [Google Scholar] [CrossRef] [PubMed]
- Carroll, S. The big picture. On the Origins of Life, Meaning, and the Universe Itself; Dutton (Penguin Random House), 2016. [Google Scholar]
- Wickens, C.D. Engineering psychology and human performance (second edition); Merrill, 1992. [Google Scholar]
- Cohen, J. Human Nature Sinks HIV Prevention Trial. Science 2013, 351, 1160. [Google Scholar]
- DoD. Pentagon Press Secretary John F. Kirby and Air Force Lt. Gen. Sami D. Said Hold a Press Briefing. Department of Defense 2021. [Google Scholar]
- Simon, H. Bounded rationality and organizational learning; Technical Report AIP 107; CMU: Pittsburgh, PA, 1989; Volume 9/23. [Google Scholar]
- Sen, A. The Formulation of Rational Choice. The American Economic Review 1994, 84, 385–390. [Google Scholar]
- U. S..; Court, S. California versus Green 399 U.S. 149. U.S. Supreme Court 1970. [Google Scholar]
- Ginsburg, R. AMERICAN ELECTRIC POWER CO., INC. ET AL v. CONNECTICUT ET AL. US Supreme Court 2011, 10–174. [Google Scholar]
- Crowe, W.J., J. Investigation report. Formal investigation into the circumstances surrounding the downing of Iran Air Flight 655 on 3 July 1988. Chairman, Joint Chiefs of Staff 1988.
- Lawless, W. The quantum of social action and the function of emotion in decision-making. AAAI Technical Report 2001. [Google Scholar]
- Baker, G. Interview of the former Central Intelligence Agency (CIA) and National Security Administration (NSA) chief. Wall Street Journal 2015. [Google Scholar]
- Rubenstein, J. Putin Re-Stalinizes Russia Seventy years after the dictator’s death, he casts a grim shadow over the lands he dominated. Wall Street Journal 2023. [Google Scholar]
- Bhattacharjee, Y. The Daring Ruse That Exposed China’s Campaign to Steal American Secrets. How the downfall of one intelligence agent revealed the astonishing depth of Chinese industrial espionage. New York Times 2023. [Google Scholar]
- W.F. Lawless, T.C.; Ballas, J. Virtual knowledge: Bistable reality and the solution of ill-defined problems. IEEE Systems Man, and Cybernetics 2000, 30, 119–126. [Google Scholar] [CrossRef]
- Lawless, W.; Akiyoshi, M.; Angjellari-Dajcic, F.; Whitton, J. Public consent for the geologic disposal of highly radioactive wastes and spent nuclear fuel. International Journal of Environmental Studies 2014, 71, 41–62. [Google Scholar] [CrossRef]
- Suleiman, Y. A War of Words. Language and Conflict in the Middle East; Cambridge University Press, 2012. [Google Scholar]
- McConnell, J. Vision 2015. A globally networked and integrated intelligence enterprise; The Director of National Intelligence, 2015. [Google Scholar]
- James, L. Delivering Decision Advantage. Air and Space Power Journal 2012, 26. [Google Scholar]
- Hughes, J.; Maxwell, J.; Weiss, L. Reimagine decision making to improve speed and quality. Inefficient decision making wastes time, money and productivity. As leaders respond to today’s paradigm shift, companies can pursue four actions to adopt and sustain high-velocity decision making. McKinsey and Company 2020. [Google Scholar]
- Cohn, P. Be Decisive to Improve Sports Performance. Peak Performance Sports 2021. [Google Scholar]
- Khaldun, I. The Muqaddimah. An Introduction to History. Translated by F. Rosenthal and edited by N.J. Dawood. Princeton University Press, 1400. [Google Scholar]
- Schwirtz, M.; Troianovski, A.; Al-Hlou, Y.; Froliak, M.; Entous, A.; Gibbons-Neff, T. Putin’s war. A Times investigation based on interviews, intercepts, documents and secret battle plans shows how a “walk in the park” became a catastrophe for Russia. New York Times 2022. [Google Scholar]
- Conant, R.C. Laws of information which govern systems. IEEE Transaction on Systems, Man, and Cybernetics 1976, 6, 240–255. [Google Scholar] [CrossRef]
- Kenny, D. colleagues. Data analyses in social psychology. In D.T. Gilbert, S.T. Fiske and G. Lindzey, Handbook of Social Psychology (4th Ed.); McGraw-Hill, 1998; Volume 1, pp. 233–265. [Google Scholar]
- Alain Aspect, J.F.C.; Zeilinger, A. Entanglement, Einstein, Podolsky and Rosen paradox (). The Nobel Committee for Physics 2022. [Google Scholar]
- Lucas, R. Monetary neutrality. Nobel Prize Lecture 1995. [Google Scholar]
- Wooters, W.; Zurek, W. The no-cloning theorem. Physics Today 2009, 76–77. [Google Scholar] [CrossRef]
- S.M. Marshall, C. Mathis, E.C.; colleagues. Identifying molecules as biosignatures with assembly theory and mass spectrometry. Nature Communications 2021, 12.
- Bette, D.A., P. R.; Chassot, P. Is our heart a well-designed pump? The heart along animal evolution. European Heart Journal 2014, 35, 2322–2332. [Google Scholar] [CrossRef]
- Thaler, R. Richard H. Thaler: Facts. Nobel Prize Committee 2022. [Google Scholar]
- Mueller, E. Applications of quantum mechanics. Cornell Phys 3317 2014. [Google Scholar]
- Centola, D.; Macy, M. Complex Contagions and the Weakness of Long Ties. American Journal of Sociology 2007, 113, 702–34. [Google Scholar] [CrossRef]
- Lawless, W. The entangled nature of interdependence. Bistability, irreproducibility and uncertainty. Journal of Mathematical Psychology 2017, 78. [Google Scholar] [CrossRef]
- Lawless, W. The physics of teams: Interdependence, measurable entropy and computational emotion. Frontiers of physics 2017, 5. [Google Scholar] [CrossRef]
| 1 | See NIH’s Implicit Bias Proceedings 508 at https://diversity.nih.gov/sites/coswd/files/images/NIH
|
| 2 | Reproduced from [46] with the permission of the American Institute of Physics. See Figure 1 in [46] at https://doi.org/10.1063/1.2349743. |
| 3 | If one is not familiar with operators in Hilbert space, treat them as a complex valued matrix. |
| 4 | Fittedness is the quality of being fitted; we use it to mean the bidirectional fit between a new team member and the team. |
| 5 | In 2001, with the assistance of George Kang, Naval Research Laboratory, Washington, DC |
| 6 | the data comes from https://www.wipo.int
|
| 7 | |
| 8 | By the State of South Carolina’s Department of Health and Environmental Control (DHEC). |
| 9 | |
| 10 | The South Carolina Department of Health and Environmental Control (DHEC) is the government agency responsible for public health and the environment in the U.S. state of South Carolina (https://scdhec.gov/) |
| 11 | After a request to intervene by DHEC, the recommendation was drafted by the first author, who was formerly on the CAB, but he was not a member at that time. |
| 12 | “President Vladimir V. Putin’s war was never supposed to be like this. When the head of the C.I.A. traveled to Moscow last year to warn against invading Ukraine, he found a supremely confident Kremlin, with Mr. Putin’s national security adviser boasting that Russia’s cutting-edge armed forces were strong enough to stand up even to the Americans” [94] |
| 13 | "Meaning of entanglement," https://en.wikipedia.org/wiki/Quantumentanglement
|
| 14 | We suspect that the inability to factor apart the independent, individual contributions of teams may play a part in assembly theory. In brief, assembly theory [100] attempts to establish that complexity is a signature of life; however, it overlooks that one of life’s well-fitted structures (characterized by fewer degrees of freedom, reduced structural entropy and non-factorability) transfers its available (free) energy to maximize the productivity of its structure’s function, helping it to survive (e.g., to be an effective structure able to pump across a wide range of activities, a heart must be efficient; p. 2326, in [101]). This was also overlooked by Von Neumann in his theory of self-reproducing automata [64]. |
Figure 1.
Figure 1 (from [41]). The hurricane as a simple 4-stage Carnot heat engine. The cross-section of the thermodynamic cycle to the center (upwards from B) shows a vertical structure of a hurricane as a heat engine, with bright yellow-red colors in the center (maximum entropy ascending), cooler colors away from the eye-wall’s structure going outward at lower entropy. Driving the storm is the evaporation of seawater as air spirals inward (A-B), transferring energy to the air and acquiring entropy at a constant temperature. Then an adiabatic expansion occurs ascending inside of the eye wall until the top where entropy is dumped into the upper atmosphere (B-C). Far from the storm’s center (C-D), IR radiation exports entropy to space, losing the remaining entropy gained from the sea, the cooler air falling downward (D-A), compressing the fluid almost iso-thermally, followed by adiabatic compression to restart the cycle.
Figure 1.
Figure 1 (from [41]). The hurricane as a simple 4-stage Carnot heat engine. The cross-section of the thermodynamic cycle to the center (upwards from B) shows a vertical structure of a hurricane as a heat engine, with bright yellow-red colors in the center (maximum entropy ascending), cooler colors away from the eye-wall’s structure going outward at lower entropy. Driving the storm is the evaporation of seawater as air spirals inward (A-B), transferring energy to the air and acquiring entropy at a constant temperature. Then an adiabatic expansion occurs ascending inside of the eye wall until the top where entropy is dumped into the upper atmosphere (B-C). Far from the storm’s center (C-D), IR radiation exports entropy to space, losing the remaining entropy gained from the sea, the cooler air falling downward (D-A), compressing the fluid almost iso-thermally, followed by adiabatic compression to restart the cycle.
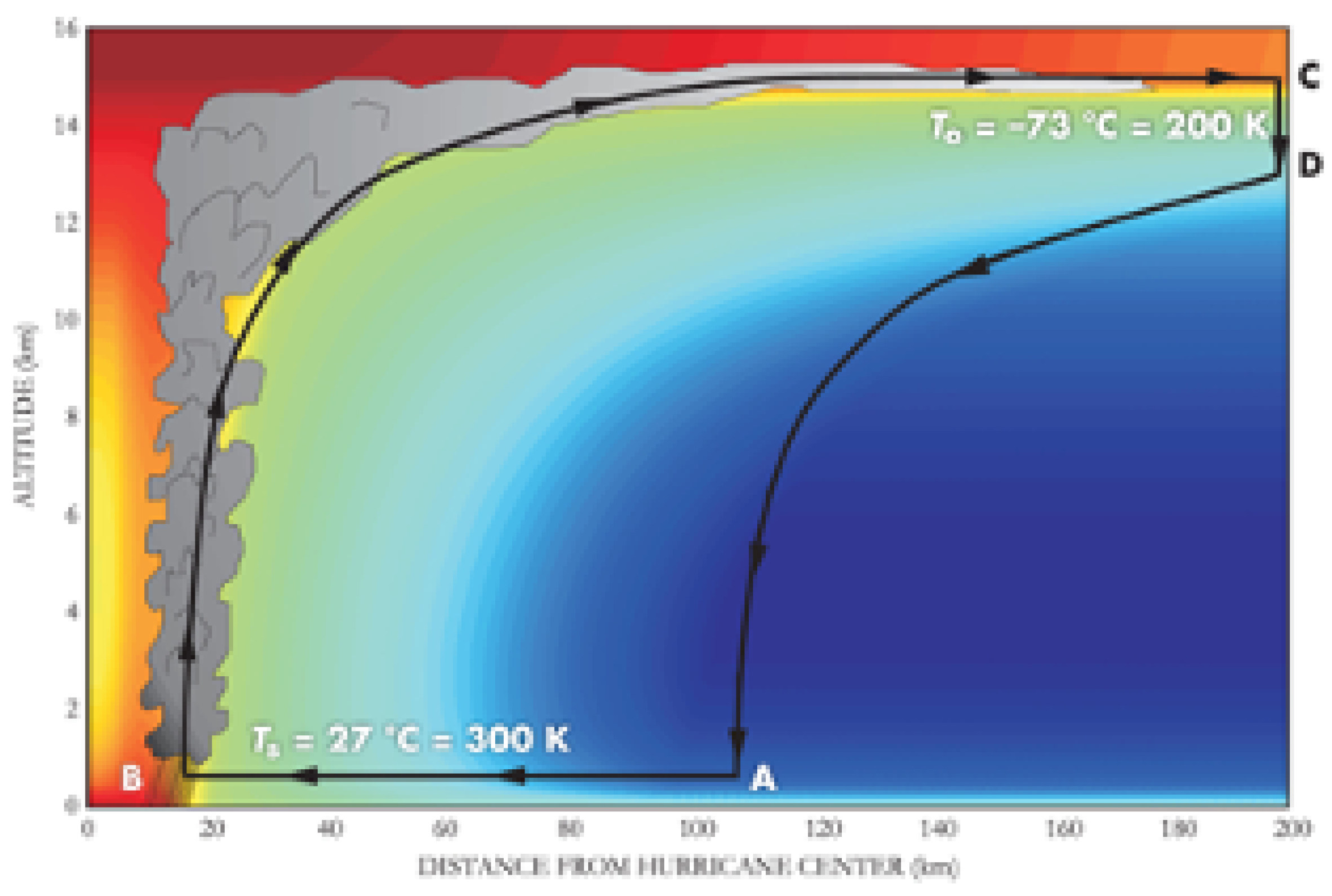
Figure 2.
The two faces-candlestick illusion.

Figure 3.
In this figure (from [41]), the y axis or imaginary axis represents the beliefs held not in physical reality, but imagined or constructed in the minds of debaters and re-constructed in the minds of their audience. When no audience is present and the debate is endless, the debate is located at points 1 and 2 as a “war of words” [88] located in imaginary space. The x axis represents physical space or action. Encouraged by observers (e.g., an audience, jury, judge, time limit), a compromise for action is represented by points 3 and 4. When debate is stopped by resistance from the audience with a decision often acceptable to a majority in the audience, that decision is reflected by points 5 and 6 as a function of the resistance applied.
Figure 3.
In this figure (from [41]), the y axis or imaginary axis represents the beliefs held not in physical reality, but imagined or constructed in the minds of debaters and re-constructed in the minds of their audience. When no audience is present and the debate is endless, the debate is located at points 1 and 2 as a “war of words” [88] located in imaginary space. The x axis represents physical space or action. Encouraged by observers (e.g., an audience, jury, judge, time limit), a compromise for action is represented by points 3 and 4. When debate is stopped by resistance from the audience with a decision often acceptable to a majority in the audience, that decision is reflected by points 5 and 6 as a function of the resistance applied.
Table 2.
Table of Models.
| Model | Benefit | Weakness |
|---|---|---|
| LRC-like model | Established Decision Advantage | Adjustments for errors are not rational. |
| Classic Harmonic Oscillator | Can be adjusted | Assumes that cognition and behavior form a Spinoza-Hume type monad (1:1). |
| Quantum Harmonic Oscillator | Can be adjusted | Assumes beliefs and behaviors form complex interactions, orthogonal under convergence (e.g., competition), parallel in mundane situations. |
| Qutrit Harmonic Oscillator | Can be adjusted | Allows a model of the interdependence between beliefs and actions for intelligent outsiders and intelligent insider team members (e.g., a coach). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








