Applications of Machine Learning in Subsurface Reservoir Simulation—A Review—Part I

Preprint

Review

Applications of Machine Learning in Subsurface Reservoir Simulation—A Review—Part I

Altmetrics

Downloads

609

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 July 2023

Posted:

11 July 2023

You are already at the latest version

Alerts

Abstract

In recent years, Machine Learning (ML) has become a buzzword in the petroleum industry with numerous applications which guide engineers in better decision-making. The most powerful tool that most production development decisions rely on is reservoir simulation with applications in numerous modeling procedures, such as individual simulation runs, history matching and production forecast and optimization. However, all these applications lead to considerable computational time and computer resources associated costs, rendering reservoir simulators as not fast and robust enough, thus introducing the need for more time-efficient and smart tools, like ML models which are able to adapt and provide fast and competent results that mimic the simulator’s performance within an acceptable error margin. The first part of the present study (Part I) offers a detailed review of ML techniques in the petroleum industry, specifically in subsurface reservoir simulation, for the cases of individual simulation runs and history matching, whereas the ML-based Production Forecast Optimization applications will be presented in Part II. This review can assist engineers as a complete source for applied ML techniques since, with the generation of large-scale data in everyday activities, ML is becoming a necessity for future and more efficient applications.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

The discovery of oil and gas reserves and their exploitation to provide access to affordable energy, meet the world’s energy demand and maximize profit is the main objective of the petroleum industry and its applications. Subsurface reservoir simulation is currently the most essential tool available to reservoir engineers for achieving those goals. It is crucial for the deep understanding and detailed analysis of a reservoir’s behavior as a whole, as well as for designing and optimizing recovery processes. Simulation is utilized in all essential planning stages, for reservoir development and management purposes, to make the exploitation of underground hydrocarbon reservoirs as efficient as possible.

Reservoir simulation is developed by combining principles from physics, mathematics, reservoir engineering, geoscience and computer programming for modeling the hydrocarbon reservoir performance under various operating strategies, according to each reservoir’s respective characteristics and production conditions. The reservoir simulator’s output, typically comprised of the spatial and temporal distribution of pressure and phase saturation, is introduced to the simulation models of the following physical components in the hydrocarbon production chain, including those to produce fluids at surface (wellbore) and process the reservoir fluids (surface facilities), thus allowing for the complete modeling system down to the sales point [1,2]. Reservoir simulations are the mathematical tools built to accurately predict all the physical fluid flow phenomena inside the reservoir with a reasonable error margin, thus acting as a ‘’digital twin’’ of the physical system.

Simulators estimate the reservoir’s performance by solving the differential and algebraic equations derived from the integration of mass, momentum and energy conservation together with thermodynamic equilibrium, which describe the multiphase fluid flow in porous media. By using numerical methods, typically finite volumes, these equations can be solved throughout the entire reservoir model for variables with space- and time-dependent characteristics, such as pressure, temperature, fluid saturation, etc., which are representative of the performance of a reservoir [2]. For this task, the reservoir is divided into many cells (grid blocks), or otherwise into a large number of space and time sections, where each cell is modelled individually (Figure 1). The simulation method assumes that each reservoir cell behaves like a tank with uniform pressure, temperature and composition of the individual phases for each specific time. During the fluid flow, each cell communicates with all neighboring cells to exchange mass and energy. Subsurface reservoir models can be highly complex, exhibiting high inhomogeneity, a vast variance of the petrophysical properties, such as porosity and permeability, and peculiar shapes capturing the structure and stratigraphy of the real reservoir.

Typically, the simulation of the thermodynamic behavior of fluids in reservoirs is handled by means of black oil or compositional fluid models. Black oil models are widely used to express simple phase behavior phenomena, especially for low to medium-volatility oils [3], providing a simple and sufficiently precise approach. These models utilize the black oil assumption based on which the fluid, at any point along the flow inside the reservoir to the surface facilities, is considered as a binary composition fluid consisting of the stock tank oil and the surface gas. Consequently, at any given pressure, the stock tank oil is saturated with a quantity of tank gas that induces its swelling and if a further quantity of gas is present, it coexists with the oil as a free gas phase. The volume change of water with pressure can also be considered whereas any phase-related changes are ignored since water is assumed not to interact with hydrocarbons in such a way. Those phase behavior phenomena are quantified using PVT properties that are only functions of pressure and temperature, hence ignoring the influence of the exact fluid composition [4].

When complex phase behavior phenomena take place, such as in the case of CO₂ injection into a reservoir for Enhanced Oil Recovery (EOR) purposes, the black oil assumption is no longer valid. Thus, fully compositional simulations need to be utilized to monitor in detail the fluid composition’s changes at each block and at each time step [5]. In compositional reservoir simulation, phase behavior calculations needed for each grid block of the reservoir are conducted by running stability and flash calculations based on an Equation of State (EoS) model. Stability provides the number of fluid phases present in the cell (typically oil gas, or both) whereas flash calculations provide the amount and composition of all phases in equilibrium. Those computations normally account for a significant part of the total CPU time and, as a result, compositional simulations need high-performance systems with great computing power to be executed successfully [6,7]. Depending on the number of components used to describe the fluids, there is a very high demand for computational power due to the complexity and the iterative nature of the phase behavior problem solution process. Phase stability and phase split computations often consume more than 50% of the simulation’s total CPU time, as both problems need to be solved repeatedly for each discretization block, at each iteration of the non-linear solver and for each time step [7]. The reservoir model configuration is completed by adding the reservoir-rock interaction, typically in the form of relative permeability and capillary pressure curves, as well as information on the producing/injecting wells, their perforations and their operating schedule.

Once the reservoir model has been set up, the most fundamental and, at the same time, computationally expensive applications of compositional simulation are reservoir adaptation, known as History Matching (HM), and Production Forecast and Optimization (PFO) of future reservoir performance. HM is the most important step preceding the calculations for the optimization of reservoir performance. It is the process of calibrating the uncertain properties and parameters of a reservoir model (such as petrophysics), based on a trial-and-error procedure until the production and pressure values predicted by the field’s dynamic model match the historically recorded ones. Therefore, HM is an optimization problem since the Objective Function (OF) that must be minimized accounts for the difference between the data derived from the simulator and the measurements obtained from the field. Once completed, the reservoir model can be considered reliable enough to be used to perform any desired engineering and economic calculations, predictions, and production optimization [8].

Prediction of reservoir performance under various production scenarios and its optimization is the next most crucial application of reservoir simulation since production management and techno/economic planning are highly dependent on it. The primary use of reservoir performance prediction is focused on estimating the oil recovery under various production schemes, designing the wells’ configuration based on those strategies, and conducting economic analysis for the future development of a field so that strategic decisions and economic evaluations are properly justified [9].

Although the above two applications are considered the core of reservoir engineering, they suffer from extremely large computational expenses due to the iterative nature of the calculations needed for their proper execution. They can be very cumbersome for very extensive and detailed reservoir models since the increasing number of grid blocks, the variant distribution of the reservoir parameters and the complexity of the wells operation schedule increase the time required for the calculations of a conventional non-linear solver [8]. Therefore, speeding up these applications is of great importance and each one must be considered as a separate subject for optimization.

Reservoir simulators have been modernized to anticipate the current needs of large data management by incorporating recent developments in High-Performance Computing (HPC), including the use of multi-threading, multi-core, multi-computer grids and cloud computing [10]. However, the continuous growth of the models’ size, resolution and physics complexity renders simulators as not fast and robust enough, thus introducing the need for more time-efficient and smart computational tools, like proxy models which are able to adapt and provide fast and competent results that mimic the real reservoir performance within an acceptable error margin.

Proxy reservoir models, also known as Surrogate Reservoir Models (SRMs), behave as the ‘’digital twin’’ of a conventional reservoir simulator, in the sense that they aim to mimic its results identifying and modeling the underlying complex relationships between various input variables and the desired outcome (i.e., pressure and saturation), in a very small fraction of the time that would otherwise be required. Proxy modeling can be broadly classified into four categories, based on their development approach, namely statistics-based models, Reduced Physics Models (RFMs), Reduced Order Models (ROMs), and Artificial Intelligence (AI)-based models, like Machine Learning (ML). Statistics-based models (e.g., response surfaces) provide a function that approximates the response of a full numeric simulator by capturing the input-output relationship of a sample of input parameters [11]. RFMs aim at simplifying the physics of a process, in this case the fluid flow process inside the reservoir, by applying several hypotheses, while ROMs are used to decrease a primary system’s dimensionality by ignoring insignificant parameters while, at the same time, keeping the dominant features and physics over a defined space [11,12]. In the present review, the ML-based models will be considered in detail thanks to their ability to identify trends and patterns between input variables and the desired outcome and of handling multi-dimensional and multi-variety data.

1.2. Machine Learning in Reservoir Simulation

Learning from data has been a rich topic of research in many engineering disciplines since the volume of data increased invariably and human cognition is no longer able to decipher that information and find patterns within that data [13]. In the latest years, data-driven ML techniques have gained major support and have been applied successfully to assist field development plans. They allow the development of models that represent physical problems without the demand to mathematically express first principle laws. Typically, they constitute of a function or a differential equation that estimates the output of the conventional full-scale reservoir simulation models [14,15,16] producing approximate and partially imprecise results to give fast, robust, and low-cost solutions in return, by sacrificing some accuracy for the gain of agility and acceleration [16].

ML provides an automated approach to the development of numerical models that learn to recognize patterns from observed data and facilitate the decision-making process with minimal human interference. The most common types of ML are Supervised Learning (SL), Unsupervised Learning (UL), and Reinforcement Learning (RL), as presented in Figure 2. SL models aim in identifying the underlying relationship between the observed data (inputs) and the corresponding observed outcome (output) and build a mathematical model to express their relationship. This way, when new input data arrives, the model is able to provide predictions of the output as efficiently as possible. They are used to solve classification and regression problems depending on whether the required output is a discrete variable (i.e., a class number) or a continuous one. UL is used when the observed data is unlabeled (i.e., there is no corresponding output) and the main purpose is to identify hidden patterns only between the given input data. Such models are mostly used for the purpose of data clustering, which is a method for data partitioning into groups based on similarities with each other. RL is a method, lying in the system control context, that is based on generating models, known as agents, which predict the appropriate actions, based on the observed data, to reward desired outcomes and/or punish undesired ones. As in UL, the observed data is unlabeled and, thus, the RL algorithm must instead try to firstly explore its environment and then determine the output which maximizes a reward through a trial and error process [17].

SL models can be used for classification and regression problems. In cases where the output is a continuous numerical value, the problem can be solved using regression algorithms, whereas if the output is a qualitative/discrete label, the problem is handled with classification models. Classification assigns a given observation to a number of discrete categories, called labels or classes, and is mostly used for pattern recognition and class predictions [17]. In their elementary form, binary classification problems assign classes to the input data, such as yes/no, 0/1, etc., although multiclass problems can be handled as well. During their training, classifiers learn each class’s decision boundary using ML algorithms that try to minimize the misclassification error [18]. Typical examples of regression modeling are models predicting fluid properties given field measurements. Similarly, classifiers can be used to identify whether a fluid is in its vapor, liquid or supercritical state based on its composition and prevailing conditions.

An ML model development is completed in three main steps. The first step is data gathering into a sufficiently large dataset, which is of utmost importance since the quantity of data directly affects the accuracy of the model. This dataset, called the training dataset, will be later used for the model’s training process. The second step is data preparation, or else data pre-processing, such as dimensionality reduction, outliers and missing data detection, etc. This step is crucial since the model’s prediction precision depends also on the data quality, along with quantity. Finally, the last step is the model’s training, using the training dataset, which consists of the input variables as well as the desired output (for SL). The latter is represented by a class number for the classification and by a numeric value for the regression model. It must be noted that both regression and classification models should be assessed based on their ability to predict and classify, respectively, a blind dataset (i.e., previously “unseen” data) that has not been incorporated in the original training dataset. That way, a model’s generalization capability can be evaluated and optimized to avoid creating overtrained models, which, although they provide very good results for a specific training dataset, they provide poor accuracy for a new “unseen” one (overfitting) [19,20].

In the subsurface reservoir simulation context, as shown in Figure 3, conventional simulators are utilized to offline generate large ensembles of data, for various operating conditions, which are then used to train an ML model. It is crucial to note that, unlike most ML applications, the derived data is usually obtained by a computational process (i.e., the offline simulation runs) rather than some experimental procedure, hence it is noiseless. After the model has been trained using the noiseless calculated data, it acts as the reservoir’s ‘’digital twin’’ which can now provide fast and accurate predictions about the reservoir’s past, ongoing and future performance that a classic industry simulator would need an extensively large amount of time to perform. That way, the model can be used to solve multiple problems and successfully assist the decision-making process more quickly.

Τhe era of ML as a fitting technique emerged back in the early ‘90s by researchers who fully introduced the concept of ML, more specifically Artificial Neural Networks (ANNs), like Freeman and Skapura [21], Fauset [22], and Veelenturf [23]. Nevertheless, since then, numerous attempts have been made towards the application of ML in the oil gas industry for the development of smart AI systems as an alternative to conventional reservoir simulation calculations. The number of offered ML-based solutions to engineering problems has significantly increased, as evidenced by the successful implementation of several methods for a variety of petroleum engineering problems, such as exploration [24,25], drilling operations [26,27], PVT behavior [28], reservoir management and field development planning [29], facilities monitoring and inspections [30], and, a recent one that is chatbots [31], which guide engineers through the process of archive digging, suggest solutions to problems, etc.

This review discusses the approaches of ML-based reservoir simulations to provide a wide perspective on the state-of-the-art methods currently in use for the purposes of individual simulation runs and HM. It must be noted that the ML methods for PFO applications will be reviewed in the second part (Part II) of the present review series due to the excessively large number of approaches that have been proposed on this subject.

The main goal of the first category that is based on individual simulation runs is to build ML models that reduce the overall simulation runtime by rapidly determining cell-specific parameters. Proxy models predicting directly the prevailing pressure and saturation, thus replacing the non-linear solver, as well as predicting the prevailing k-values to boost the complex and iterative phase behavior calculations are typical examples. Subsequently, the rapidly responding proxies can be introduced to any desired HM or PFO calculation, thus, accelerating those tasks by orders of magnitude. The second category of HM, as a computationally expensive process, can benefit largely from the generation of proxy models that aim to optimally calibrate the uncertain parameters to achieve a good match between calculated and observed production data.

In this paper, the ML methods for subsurface reservoir simulation reviewed are categorized based on the context of the problem under investigation and the ultimate purpose of each reviewed method. Section 2 describes generic proxy methods, like predicting the k-values, which can be utilized to speed up any desired reservoir simulation application whereas Section 3 reviews methods that directly serve the HM. Section 4 concludes the present review.

2. Machine Learning Strategies for Individual Simulation Runs

Reservoir simulation software packages are continuously modernized based on the current needs for large data management and despite the availability of ever-growing computer power. However, simulations are still not fast and robust enough, in the context that they entail high computational costs, introducing the need for more time-efficient smart tools that can adapt and provide fast and competent predictions which mimic the real reservoir performance within an acceptable error margin. In this section, ML is employed as the suitable means to accelerate individual simulation runs that can assist any desired HM or production related calculations by using two approaches.

Firstly, fast proxy models (or else SRMs) of the reservoir simulator have been proposed which can be implemented to answer a wide range of engineering questions in a fraction of the time that it would otherwise be required. Secondly, ML has been utilized to accelerate specific CPU time-intense sub-problems while maintaining the rigorous differential equation-solving method. The most pronounced application in this category is the handling of the phase equilibrium problem in its black oil or compositional form which needs to be solved numerous times during the course of the reservoir simulation run.

SRMs using ML and pattern recognition methods to fully replace the non-linear solver were firstly proposed by Mohaghegh and his associates who developed SRMs that could fully reproduce the traditional black oil or compositional reservoir simulation results (i.e., high-fidelity models) on a cell basis without sacrificing the physics or the order of the system under investigation, as is the case of RFM and ROM methods respectively. What they did instead is that they built grid-based and well-based proxy models. Grid-based models usually provide pressure and saturation predictions for the fluid phases at the grid level based on information from the surrounding grid blocks rather than the whole reservoir. This way, the very weak dependency of the state of a cell on the ones far away from it is ignored while allowing at the same time the disengagement of the cell state. Well-based models are developed similarly to predict well-related parameters, such as gas, oil and/or water production rates, Bottom Hole Pressures (BHPs), etc.

The second category is based on predicting rapidly and accurately the fluid properties, both for compositional and black oil models. As already mentioned in Section 1, compositional models are developed to monitor the fluid composition’s changes at each grid block and at each time step. Therefore, the phase behavior calculations needed for each grid block are conducted by running stability and flash calculations, processes that normally take a significant part of the total CPU time. The most burdensome fluid parameter involved in those calculations is the equilibrium coefficients, known as k-values. Their estimation is based on complicated numerical calculations, utilizing EoS-based fluid thermodynamic models, which require a large number of iterations to converge, while simultaneously they need to be performed for all grid blocks at each timestep and each iteration of the non-linear solver. Thus, it is made clear, that a regression-based ML model that is capable of directly predicting the necessary k-values and replacing the conventional iterative approach can significantly accelerate any simulation process [19].

Apart from predicting the k-values, another efficient way to reduce the overall computational cost is to recast the phase stability problem to a classification one, using classification ML methods, with two labels corresponding to stable/unstable fluid mixtures, or single/two-phase flow. Note that it is the stability problem that gives the ‘’green light’’ for a phase split calculation to be executed since stability tests are always run and invoke phase split only when instability is detected. In this kind of classification problem, the input comprises of fluid composition, pressure and temperature values for the classifier to reach a solution (stable or unstable mixture) based on the phase boundaries of the p-T phase diagrams. That way, the trained classifier can replace the traditional, iterative stability algorithm and substantially accelerate flow simulations with its direct non-iterative predictions [32].

For the case of black oil simulations, the grid blocks are assumed to contain three primary fluid phases (oil, gas, water). The PVT properties needed to account for the compressibility of each phase (oil, gas and water formation volume factors-B_o, B_g and B_w respectively), the solution of gas to reservoir oil (Gas to Oil Ratio—GOR) and saturation conditions (bubble and dew point pressure) which are usually readily available from experimental procedures and are introduced into the simulator to perform the desired calculations. If experimental values are not available, empirical correlations are used to predict the fluids’ PVT properties utilizing field data (API, gas specific gravity and GOR). However, these correlations are not always accurate since they only perform well for the range of compositions and conditions against which they were generated, thus exhibiting poor behavior outside these bounds. As a result, to speed up and improve the accuracy of the simulation process, ML-based models have been developed, predicting those crucial parameters [33].

2.1. Machine Learning Methods for Surrogate Models

The first attempt to develop a fast proxy of a subsurface reservoir simulator was accomplished by Mohaghegh and his associates, who run numerous studies and set up SRM methodologies by utilizing intelligent system techniques to approximate the simulation process of huge complex oil fields which would otherwise require an extremely large amount of CPU time. SRMs can mimic the behavior of a full reservoir model with precision, can be used in many applications (i.e., PFO and HM), and, in some cases, they can fully replace numerical simulators or work with them in a coupled way. This group developed many workflows, usually using ANNs, in which they propose the detailed development of such models, such as fracture propagation inverse problems to identify the potential hydraulic fracture designs [34], uncertainty analysis [35,36,37,38,39], prediction of dynamic reservoir properties [40], waterflooding operations [41], CO₂ EOR and storage projects [42,43], etc. Results show that the SRMs are capable of efficiently mimicking the simulator’s predictions with fewer runs, compared to the conventional reservoir simulator that needs an excessive amount of simulations, especially for complex fields.

Dahaghi et al. [44] proposed a similar methodology to obtain cumulative production predictions, this time for a complex fractured shale gas reservoir. They used ML and data mining methods to create a single well shale SRM model to deal with direct (e.g., production prediction), as well as inverse problems (e.g., HM). According to the authors, the model was characterized as of great efficiency and it successfully mimicked the conventional simulator with great accuracy and speed. The proposed model can be utilized for HM, uncertainty quantification and real-time production optimization. Memon et al. [45] tried a similar method by building a well-based Radial Basis Function Neural Network (RBFNN) SRM based on black oil simulation results for an initially under-saturated reservoir to predict the flowing BHP. The model’s input parameters consisted of a spatiotemporal dataset (e.g., porosity, permeability, initial oil and water saturation and oil rate). The proposed model was very efficient in comparison to conventional simulators and it can be used for many production optimization purposes by generating hundreds of accurate runs, in a fraction of time that would otherwise be needed. Amini et al. [11,46] generated a SRM using ANNs to approximate the CO₂ and pressure distributions for a CO₂ sequestration process in a depleted reservoir. The authors run several scenarios using a conventional simulator to create a database of static (porosity, permeability, grid block coordinates, etc.) and dynamic (phase saturation, CO₂ mole fraction in the different phases, injection rate, BHPs, etc.) data for training. The model exhibited great grid block accuracy in predicting reservoir pressures and CO₂ allocation within seconds.

2.2. Machine Learning Methods for Handling the Stability and Phase Split Problems

For the case of compositional simulations, several ML methods have been developed, aiming at reducing the excessively long time required for solving stability and flash calculations. In the first case, the phase stability problem is expressed as a classification one to determine the number of phases for any given composition and pressure and temperature values. For flash calculations, ML applications are oriented toward predicting the k-values needed for those calculations in a more robust, efficient and rapid way.

The phase stability-targeted methodology was firstly proposed by Gaganis et al. [47] who used Support Vector Machines (SVMs) to generate a discriminating function that emulates/replicates the phase boundary. This discriminating function is set to zero at the boundary, positively signed (+1) inside the phase envelope and negatively signed (-1) outside that. The authors obtained the dataset to train the classifier by running regular stability tests for various uniformly drawn random combinations of composition (selected to run over the whole compositional space) and pressure and temperature values. The training data needed were obtained in an automated offline way based on sample runs. The classifier was trained using labels of stable/unstable mixtures obtained by running regular stability tests, using composition and pressure and temperature values. That way, they obtained fast stability predictions which are the same as those obtained by the conventional minimum Tangent Plane Distance (TPD) ones since the classifier provides correct answers for both classes based on the sign of the predicted discriminating function. Later, Gaganis et al. [7,48] expanded their research and answered both phase stability and phase split problems by combining SVMs for classification and ANNs for regression, respectively, in a single prediction system. A single-layer ANN to predict the k-values is used only if the classifier predicts an unstable mixture. To further accelerate calculations, reduced variables were used to shrink the output. This way the number of outputs to be predicted was at least equal to three and definitely less than that of mixture components. The ANN-predicted reduced variables are then back-transformed to regular k-values. The results demonstrated that the proposed methodology is very efficient, with respect to the accuracy and the computational cost reduction and its applicability can be expanded reservoir simulation to any kind of fluid flow simulation that demand numerous phase behavior calculations. After that, Gaganis [49] proposed an even more efficient treatment of the stability problem by means of two custom discriminating functions, d_A and d_B, each single-sided correct. If d_A is positive, the sample is definitely stable. If d_B is positive, the sample point is definitely unstable. No concrete answer can be obtained if either of the two is negative. However, as d_A and d_B are built so that the ambiguous space, called “the grey area” (where none discriminating function is positive) is as narrow as possible, the need to run a conventional stability test is hugely reduced. Furthermore, kernel functions are utilized to allow for simple curved, non-linear discriminating functions which can be evaluated rapidly. The method is greedy in that d_A and d_B can replace the lion’s share of the required stability calculations in a simulation run. Conventional, iterative calculations are only needed for points lying within the grey area.

Kashinath et al. [50] moved in the same direction as Gaganis et al. [7,48], treated the stability problem as a binary classification one and tailored it to CO₂ flooding simulations. They developed two SVMs, one to determine whether the fluid under study is in the supercritical phase and a second one to predict the number of unstable phases when in the subcritical region. If the second classifier predicts an unstable phase, an ANN model was used to predict the prevailing k-values. Therefore, the authors divided the problem into three categories, 1) supercritical phase determination, since this entails a large calculation burden by using EoS, 2) sub-critical phase stability, and 3) the phase-split problem. By applying this method, the authors utilized a negative flash algorithm to create a phase diagram that differentiates the subcritical and supercritical areas to determine the fluid properties of the latter. The anticipated composition phase diagrams are then used to generate a training data set for the ML models. SVMs are employed to build two classifiers by utilizing composition and pressure inputs, where the first classifier determines if conditions are met for the supercritical region, and the second identifies the number of stable phases in the sub-critical region. Finally, the phase-split problem is handled by predicting k-values for sets of pressure and composition data using an ANN. The results showed that the models can effectively cut down the overall CPU time required for compositional reservoir simulations, causing a very limited decline in accuracy. Schmitz et al. [51] developed a classification method using ANN models to extend the previous approach and solve the multiphase phase stability problem. The authors examined two classification models, a feed-forward and a probabilistic ANN. The training set for the models’ training was collected for pressure and temperature ranges corresponding to liquid–liquid, vapor–liquid–liquid, vapor–liquid and homogenous liquid and vapor so that the trained models can distinguish these five regions. The results showed that the proposed models could predict the equilibrium state with high precision. Gaganis et al. developed a similar technique to solve rapidly the multiphase stability problem using SVMs [52]. Wang et al. [53] developed two ANN models to treat the stability (ANN-STAB) and phase split (ANN-SPLIT) problems, in a process similar to that of Kashinath et al. For the ANN-STAB model to learn if a given mixture at given conditions is stable or unstable, the authors generated two auxiliary models, one for predicting the upper saturation curve and one for the lower. That way, they could compare the prevailing pressure with the mixture’s saturation one to determine if the mixture lies inside or outside the two combined saturation pressure curves. If the ANN-STAB model indicates instability, the ANN-SPLIT model is called to predict the mole fractions and k-values, which are utilized as initial values in conventional phase split calculations. The results showed that the proposed models provide initial estimates of high accuracy, while they also achieve significantly shorter computational time.

Apart from the simple ANN models that have been reviewed so far, there are several proposed approaches based on Deep Learning (DL) methods. DL is a subset of the ML family widely used in cases of extremely large reservoir fields. Roughly speaking, ANNs are considered DL networks if they consist of more than three layers, including the input, hidden and output ones. Unlike regular ANNs, DL ANNs can digest unstructured data in its raw form, like text and images, and they can automatically determine the set of variables that can distinguish the desired output for regression, classification and clustering tasks. By observing patterns in the data, a DL model can cluster inputs appropriately, by discovering hidden patterns without the need for the user’s intervention. Most DL ANNs are feed-forward meaning that the information is transferred from the input to the output. Back-propagation is used to calculate and attribute the error associated with each neuron to adjust and fit the algorithm appropriately.

Li et al. [54] developed a DL ANN to accelerate binary component (methane/ethane) flash calculations and compared that model against three classic methods (Successive Substitution-SS, Newton’s and sparse grids method). The input consisted of critical pressure, critical temperature and acentric factor for both mixture components, as well as temperature and pressure values and the output consisted of the mole fraction of the first component in the liquid and vapor phase. The proposed DL model was found to be significantly more efficient and faster than the SS, Newton’s and sparse grids methods.

In another study, Li et al. [55] developed a single DL ANN to approximate multicomponent stability test and phase split calculations using results obtained from a conventional iterative NVT flash calculator (specified moles, volume and temperature) as a training dataset. To achieve an integrated stability and phase split DL ANN, the authors used a training dataset that incorporated compositional properties (critical pressure and temperature, acentric factor, etc.), overall mole fractions, overall molar concentration and temperature as input and the number of phases and mole fraction of vapor and liquid components as output. Therefore, by using a single trained DL ANN, they were able to solve simultaneously the phase stability and phase split problems in a way that the phase state can be identified without an additional stability test. The proposed model can successfully estimate the different phase states in the subcritical region of a given mixture and can make significantly faster predictions, as compared with the conventional NVT flash calculator.

For the case of very low permeability, unconventional reservoirs, flash calculations are coupled with substantial capillary pressure effects (very narrow pore throat, thus large capillary pressure on the vapor-liquid phase interface) and they tend to be extremely computationally burdensome, as well as unstable. In that case, conventional compositional simulations can become a difficult task. Wang et al. [56] worked in the DL field and developed two multi-layered stochastically trained ANN models to predict the phase behavior of hydrocarbon mixtures in such unconventional reservoirs. The first ANN is used to classify the phase state of the system (stable/unstable) and the second, if the first leads to an unstable mixture, to predict the k-values and the capillary pressure. The training dataset for the ANN models was generated from a standalone flash calculator and consisted of composition, pressure and temperature values, as well as pore radius data, all normalized to [0,1] scale before entering the networks. It was shown that the models were very efficient and, subsequently, the predicted k-values were used as initial estimates in a conventional reservoir simulator, whose speed was significantly increased. In addition, Zhang et al. [57] developed a DL ANN, similar to the one of Li et al. [55], to predict phase states and phase compositions for hydrocarbon multicomponent mixtures in complex reservoirs with large capillary effects. The authors generated the training dataset using the results of an NVT flash calculator which is developed based on the diffuse interface theory with a thermodynamically stable evolution algorithm for a wide range of reservoir conditions. They also used the same input parameters as in their previous study (Li et al. [55]), however, they modified the output in a way that almost half of the parameters were replaced by a coefficient ϕ (mole fraction of vapor phase), aiming at securing the material balance. The only parameters remaining are the mole fractions of the vapor components. This is considered by the authors to significantly improve the model’s training, particularly for highly complex fluids with many components. In addition, the model’s hyperparameters are adjusted to optimize its architecture and, hence, its efficiency. Results show that the model can provide precise predictions with the authors claiming that the proposed workflow can be utilized for various mixtures, substantially accelerating flash calculations.

Zhang et al. [58] were the first to develop a self-adaptive DL ANN to predict the number of phases present in multicomponent mixtures and their equilibrium thermodynamic properties (component mole fractions in each phase) under various reservoir conditions. As in their previous studies (Li et al. [55], Zhang et al. [57]) the authors used the results of an NVT flash calculator to generate the model’s training dataset which consisted of the fluid’s composition, overall molar concentration and temperature values as input and the total number of phases at equilibrium and component mole fractions in each phase as output. The authors also used the critical properties of each component of the fluid under investigation as additional input to generalize the model’s capability. The authors developed a two-network structure to accelerate flash calculations for any number of components a user might select each time a new run is performed. The first network transforms the input of various numbers of components of the mixture under investigation into a unified space before the second network is put in motion. “Ghost components” of zero concentration are introduced to complete the input vector in the case of components which do not naturally appear in the mixture under study so as to honor the fixed input vector size. The above proposed network structure makes the model self-adaptive when a different number of components (i.e., different model dimensionality) is considered. The results showed that the proposed model is capable of producing accurate predictions, while also reducing the computational burden that is usually imposed by the conventional methods.

Reservoir systems such as gas condensates or systems where reinjection operations take place are characterized by extremely time-consuming reservoir simulations due to the complex phase behavior phenomena taking place, especially in dry gas reinjection plans where gas recycling takes place inside the reservoir and, thus, the reservoir composition is constantly updated. Samnioti et al. [19] employed an ML approach using ANNs to accelerate those complex calculations by supplying the k-values at each time step and at each pair of prevailing pressure-temperature conditions to solve the flash problem at a fraction of the time needed by conventional iterative methods. The ANN was trained using an ensemble of pressure, temperature and composition data as input and k-values as the output, all obtained by running offline conventional reservoir simulations on a simplistic reservoir model (sugarbox). Although this process sounds straightforward, the reservoir composition displays large variability in the case of gas reinjection, thus imposing the need for a more extended compositional space compared to the typically used fixed composition one. To handle that, they proposed training the ANN with an extensive dataset obtained from the simulation of various gas recycling schemes, covering any possible composition changes that might occur inside the reservoir. As a result, the computational expenses of the flash calculations were reduced by more than one order of magnitude, compared to the conventional iterative ones. Recently, Anastasiadou et al. [32] moved in a similar way by trying to solve the phase stability problem, this time for an acid gas reinjection system where the required phase behavior calculations are more complex and time-consuming since they need to be repeated for an even broader compositional space to cover for the acid components (H₂S and CO₂) and the hydrocarbon contaminants that are being reinjected into the reservoir. The authors proposed three classification ML approaches, ANNs, Decision Trees (DTs) and SVMs to solve the phase stability problem, which is crucial in acid gas reinjection designs, at a fraction of the time needed by conventional iterative methods. A large ensemble of training data was obtained by offline running the stability problem using a conventional method and the dataset was then introduced to the classifiers. As a result, the recommended methodology was shown to be able to adapt to all types of acid gas flow simulations.

In cases where complicated systems are under investigation (i.e., CO₂-EOR), the iterative algorithm in conventional reservoir simulators may fail to converge since there are cases where the flash and the nonlinear solver cannot agree over which phase (gas or liquid) is present when a stability test labels the fluid as stable. For that reason, Sheth et al. [59] used stability test results and developed two ANN models, one classifier and one regressor, to accelerate EOR simulations, such as dry gas and CO₂ re-injection by predicting the fluid’s critical temperature. Hence, the authors’ main goal was to devise an efficient way to accurately predict that crucial value so as to determine the fluid phase state, hence the correct viscosity and relative permeability values to utilize, thus preventing any problems that may arise when simulating the phase behavior of complex fluids. They run several simulation scenarios and generated a relatively small compositional training dataset using a linear mixing rule between the injected and the in-situ fluid compositions, consisting of the final composition, pressures and temperatures as input and the corresponding critical temperatures as output. The first model (classifier) is used to identify if a sequence of iterations will diverge and the second model (regressor) is used to predict the critical temperature for those iterations. The results showed that the proposed model presents critical temperature values comparable with the ones obtained from conventional simulators, while also significantly reducing the computational burden.

2.3. Machine Learning Methods for Predicting Black Oil PVT Properties

Correct reservoir fluid PVT properties, such as saturation pressures, volumetric factors and solubility, are crucial for all kinds of black oil reservoir calculations (material balance, oil production forecast, etc.), where a relatively small error can lead to a considerable error regarding the development of the reservoir model, future operations, etc., which can subsequently lead to inferior prediction performance. Although there are readily available empirical correlations for the determination of those properties [60], they are usually not accurate enough, imposing the need for ML model development instead.

The most important volumetric parameter of dry gases and condensates is the gas compressibility factor (Z-factor), a property needed for B_g estimations, since it is responsible for flow and volumetric calculations, between reservoir and surface conditions. Most of the time, the Z-factor can be easily determined using empirical correlations fitted on the classic Standing-Katz (S-K) chart. These correlations are not always accurate enough or even valid as they have been generated based on specific pressure and temperature conditions and can sometimes produce poor results when used outside of the predetermined range. Additionally, low accuracy estimates can be obtained when ‘’unusual’’ compositions are considered as is the case with acid or polar components.

Various recent studies have appeared making use of ML methods to predict the Z-factor from the S-K chart. Moghadassi et al. [61] developed ANN models to predict the Z-factor for pure gases using reduced temperature and pressure as input, thus replacing the hand-fitted models by Beggs & Brill [62] and Dranchuk & Abou-Kassem (DAK) [63]. The authors used various training back-propagation algorithms for comparison reasons, namely Scaled Conjugate Gradient (SCG), Levenberg–Marquardt (LM) and Resilient Back Propagation (RBP), with the LM providing the best results. Similarly, Kamyab et al. [64] build an ANN for the estimation of the Z-factor of natural gas by utilizing a training data set directly digitized from the S-K chart. The results showed that the trained ANN required less computational effort, was more precise than the iterative DAK algorithm, and can be used for the whole pressure and temperature range of the S-K chart. Moving in a slightly different direction, Sanjari and Lay [65] built an ANN to calculate the Z-factor which, however, was trained against experimental Z-factor values rather than ones extracted from the S-K chart. The efficiency and the accuracy of the proposed ANN was compared to the most well-known empirical correlations and to the Peng & Robinson EoS. The results showed that the model is more accurate compared to the other methods. Furthermore, Irene et al. [66] and Al-Anazi et al. [67] developed an ANN model to estimate the Z-factor using PVT data points extracted from the available literature. The authors performed quantitative and qualitative evaluations to examine the models’ efficiency and overall accuracy and the results showed that the developed models were compatible with experimental data upon which they weren’t trained, thereby verifying generalization capability, and, that the models are more accurate compared to the results of numerous EoS and correlations.

Mohamadi et al. [68] developed a similar approach using experimental PVT data sets of gas condensates, but this time the authors developed three ML models, namely an ANN, a Fuzzy Interface System (FIS) and an Adaptive Neuro-Fuzzy Inference System (ANFIS). The trained models were shown to perform considerably better than the available empirical correlations, with the ANN outperforming the other models. Two more research groups, Fayazi et al. [69] and Kamari [70] built SVMs to predict the Z-factor of rich gases by training their model with experimental data corresponding to a plurality of compositions, including sour gases. The former approach utilized Least Square Support Vector Machines (LSSVMs) together with the Coupled Simulated Annealing (CSA) optimization algorithm and the Z-factor was predicted as a function of gas composition, Molecular Weight (MW) of the heavy components, and pressure and temperature values. The LSSVM method [71] is an advancement of the SVM one, in the sense that the solution can be more easily found using a set of linear equations instead of convex quadratic programming problems associated with the classic SVMs. The results of both groups showed that the ML models were more efficient and precise than the empirical correlations. Chamkalani et al. [72] used the Particle Swarm Optimization (PSO) [73] and Genetic Algorithms (GA) to perform an optimization process for the weights and biases of an ANN by minimizing the network’s error function against data derived from the S-K chart, in a sense of avoiding getting trapped in some local minimum. The developed model presented high efficiency and precision, as compared to empirical correlations, but, when optimization methods were used, the performance was enhanced significantly, with the PSO-ANN outperforming all of the other models, both from the accuracy and computational time point of view.

Although the above methods are considered quite an improvement for the Z-factor calculation, almost all of them are suitable only for limited pressure ranges. Some of them exhibit an oscillating behavior that is attributed to the fact that the models are driven by the available data, thus leading to unrealistic derivatives of Z-factor which in turn cannot be mapped to normal fluid compressibility values. Gaganis et al. [74] developed a hybrid ML model using the Kernel Ridge Regression (KRR) method, and more specifically the truncated regularized KRR algorithm [75], together with a linear-quadratic interpolation method to predict the Z-factor, vanquishing the disadvantages of the above techniques. The model is generated using a data set digitized from the S-K chart. The results presented smooth, in a sense of Z-factor derivative continuity, and physically solid predictions of the Z-factor, while also achieving great accuracy. The novelty of this approach is that it can be straightforwardly used to determine the Z-factor for hydrocarbon mixtures of any composition, even when impurities are present, and at any possible pressure and temperature reservoir conditions. The model can be considered as an excellent tool for estimating gas density in many reservoir simulation applications to reduce the computational time required, such as the estimation of reserves, fluid flow inside the reservoir and the wellbore, the surface pipeline system and processing equipment, etc. The proposed methodology is, however, only applicable for compositions similar to those the S-K chart was created for, and it might present significant errors when used for mixtures with significant amounts of non-hydrocarbon and/or polar compounds.

Apart from natural gases, many hydrocarbon reservoirs around the world contain a considerable amount of acid components, that is usually a mixture of light hydrocarbons, H₂S and CO₂, known as sour gases. Engineers should be able to obtain accurate thermodynamic information on those gases to successfully conduct techno-economical evaluations and make predictions about future production. Furthermore, due to the economically unattractive sulphur market price, and the increasingly strict air emission standards and regulatory authorities, many oil and gas operators are in search of environment-friendly and cost-effective methods for dealing with that kind of gases, such as acid gas re-injection for EOR or sequestration purposes, where extensive thermodynamic knowledge of the associated fluids and their interactions is needed [76]. Considering the above, Kamari et al. [77] developed an LSSVM model, coupled with the CSA optimization method, to predict the Z-factor of natural and sour gasses, as well as of pure acid substances. Due to the shortage of experimental studies on sour gases, the authors used pseudoreduced pressure and temperature values from the literature as input to the model and performed a comparative study with several empirical correlations and EoS models to validate the performance of their proposed approach. The results showed that their model is significantly more reliable and efficient, as compared to the available correlations and EoS for estimating the compressibility factor of sour and natural gases.

Saturation pressure (bubble/dew point pressure) is another important parameter for accurate black oil reservoir simulations. Saturation pressure is an extremely important fluid property in reservoir simulation since it marks the distinction between single and multiphase state, thus providing a phase stability indication. Two kinds of methods for estimating the saturation point pressure can be identified. The first is through experimental procedures using laboratory samples (e.g., Constant Volume Depletion-CVD), which are highly expensive and time-consuming. The second method concerns the use of empirical correlations or an iterative procedure based on an EoS. Although an EoS is effective for classic hydrocarbon systems without many impurities, fitting it to efficiently predict the phase behavior of complicated systems (e.g., volatile oils, gas condensates, oils with too many impurities, etc.) is not a trivial task. Furthermore, most of the correlations existing in the literature and appearing in commercial software, although very accurate for the range of parameters they were tuned against, they exhibit poor performance outside these bounds.

Researchers have tried to devise fast and efficient ways to predict those values using ML-based methods. Seifi et al. [78], developed a feed-forward multilayer ANN model, trained with fluid properties (e.g., composition) to predict reliable initial values for the saturation pressure of given mixtures that would decrease the total time required by the iterative calculations. Gharbi et al. [79] built ANN models to directly predict saturation pressure and B_o using real field crude oil data (i.e., GOR, gas and oil specific gravity and temperature). Similar models were developed by Al-Marhoun et al. [80] and Moghadam et al. [81], although each research group utilized different real field input parameters. Their results showed that the proposed approach presents a significantly higher accuracy, as compared to Al-Marhoun’s previous correlations [82,83], developed also for the same crudes. As a general conclusion, all the above ANN models provide quality predictions, significantly improving the accuracy of the most commonly used, hand-developed correlations (e.g., Standing, Vasquez and Beggs, Al-Marhoun, etc.) [84].

Rather than ANNs, Farasat et al. [85] developed an SVM model to predict the saturation pressure using reservoir temperature, hydrocarbon and impurity compositions, and MW and specific gravity of the heavy fraction. El-Sebakhy et al. [86] developed SVMs to predict saturation pressures and B_o using PVT data obtained from the literature, such as reservoir temperature, oil and gas gravity and solution GOR. The results of both studies demonstrated that the proposed models are significantly more precise than most well-known correlations.

For gas condensate reservoirs the accurate prediction and constant monitoring of dew point pressure is very important for many engineering calculations, especially for the prediction of future production and for the design of operations where liquid condensation should be avoided. Numerous ML methods have been proposed to predict the dew point pressure such as the one by Akbari et al. [87] and Nowroozi et al. [88] who developed ANN and ANFIS models, respectively, to predict the dew point pressure of gas condensate systems using compositional and thermodynamic parameters. Similarly, Keydani et al. [89] generated a conventional back-propagation ANN to estimate the dew point of lean retrograde gas condensates using experimentally obtained PVT data (e.g., reservoir temperature, moles fractions of volatile and intermediate gases, etc.). Gonzales et al. [90] used an ANN model to estimate the dew point in retrograde gas reservoirs using experimental CVD data (gas composition, MW, specific gravity of the heavy fraction, reservoir temperature). Their results showed that the proposed model was more efficient than straight run or mildly tuned Peng-Robinson EoS models, as well as other empirical correlations. Similarly, Majidi et al. [91] developed an ANN model to estimate the dew point pressure in gas condensate reservoirs using a set of experimental data, such as compositional analysis up to C₇₊ and concentration of impurities (N₂, CO₂, H₂S), reservoir temperature and C₇₊ specific gravity and MW. The results showed that the proposed approach is more efficient than all existing methods thanks to the enhanced, more informative input. Furthermore, the proposed model can predict the physical trend of the dew point pressure-temperature curve among the cricondenbar and cricondentherm on the phase envelope.

The continuous improvement and the emerge of new, high-end ML technologies has led researchers to utilize them in the fluid properties domain as well. Rabiei et al. [92] developed a Multi-Layer Perceptron (MLP)—GA model to estimate the dew point pressure using reservoir temperature, mole percentage of gas components and heavy fractions properties, whereas Ahmadi et al. [93] developed a coupled ANN-PSO model to estimate the dew point for gas condensate reservoirs using compositional and thermodynamic parameters. Ahmadi et al. [94] devised a LSSVM approach, as developed by Suykens et al. [71], coupled with a GA to determine the dew point pressure in condensate gas reservoirs. For comparison reasons, a classic feed-forward ANN has also been developed and, according to the results, the proposed LSSVM model exhibited superior performance. Arabloo et al. [95] developed LSSVMs to estimate the dew point pressure for gas retrograde reservoirs, coupled with the CSA optimization algorithm for the model’s hyperparameters. The authors used the same experimental data as Majidi et al. [91] to form the model’s input, thus arriving to a new approach which is more efficient than all existing methods. Furthermore, the LSSVM-CSA model can predict the physical trend of the dew point pressure against temperature for a constant composition fluid, to form a part of the phase envelope.

Along a similar line, Ikpeka et al. [96] built ML models, namely MLPs, SVMs and DTs (Gradient Boost Method-GBM and XGB), to predict the dew point pressure for gas condensates using fluid composition, specific gravity, MW of the heavier component and compressibility factor as input. A classic multiple linear regression model was developed to compare the efficiency of the proposed models. The SVM model outperformed the other models, however, for large complicated data more support vectors are utilized for the same accuracy level, thus, resulting in extended computational time. Zhong et al. [97] developed an SVM model, utilizing a mixture of kernel functions, coupled with a PSO algorithm to predict dew point pressure. The authors used real compositional and thermodynamic data as input, same to those by Majidi et al. [91] and Arabloo et al. [95] and they arrived to a more efficient model than all of the well-known empirical correlations, with enhanced generalization ability.

3. Machine Learning Strategies for History Matching

Quantifying and addressing the uncertainties of oil fields is always in the spotlight as reliable predictions must be made to support any management and financial decisions. Typically, the uncertainty of a field is addressed by the HM process where uncertain reservoir parameters are calibrated according to the mismatch of the reservoir model calculated versus observed field data.

In the process of HM, the reservoir model is set up to reproduce the past production history of the field by assigning the well schedule to the modeled wells. Subsequently, static and/or dynamic reservoir parameters are adjusted (e.g., permeability and porosity distributions, etc.) until the cumulative production, or the production of individual wells, along with the field pressure (or BHP) predicted by the dynamic model match the corresponding values which were recorded at the field. The adjustment is done by selecting combinations of uncertain parameters that are perturbated to achieve a good match. Alternatively, if the uncertain parameters are not known beforehand, a Sensitivity Analysis (SA) is run, in which each potential parameter is manually perturbated one-at-a-time to determine the ones that exhibit the largest impact on the HM process. The approach is presented in Figure 4. Thus, as a trial-and-error procedure, which requires a separate simulation run per trial, it is computationally expensive since it is usually conducted manually and its evaluation is based on the experience of the engineer and, thus, it is prone to human bias and error. The already extremely large amount of simulation runs tend to get bigger as the reservoir model size and complexity expands, usually with the continuously incoming data that contains new information.

There are many methods focusing on the optimization of the HM process and, most important, the mitigation of its ill-posedness and the reduction of the total time required to achieve the desired match, i.e., the minimization of the mismatch error. The most common optimization methods used are, among others, gradient-based, stochastic and probabilistic algorithms. Gradient-based algorithms use the direction of derivatives, or else gradients, to find the optimum value (i.e., minimum) of the error function. These algorithms are widely used since they are quite effective in converging to a local minimum in a reasonable number of iterations. Nonetheless, they can manifest several complications when complex problems with an extensive number of parameters are concerned, as is the case of HM. On the other hand, stochastic optimization, gradient tree algorithms, like GA, can examine the parameters’ space more efficiently, however, they need many more function evaluations, thus higher computational time compared to gradient-based ones. Probabilistic algorithms, like the Bayesian inference statistical technique, are algorithms whose behavior is partially controlled by random events and their probability distribution. These algorithms usually need fewer function evaluations, however, they may not eventually achieve convergence, or if they do, an incorrect result may be obtained [98].

The above problems can be addressed to a great extent using ML methods, or a combination of them with the aforementioned algorithms to achieve a more efficient HM [99,100]. There are two ways to configure the output of an ML model for HM purposes, as depicted in Figure 5. The first approach, known as the indirect one, defines the difference between the real and the predicted production data as the model’s output, usually in the form of a sum of squared differences. In that case, the HM problem utilizes ML-based models, usually ANNs, to learn the underlying relationship between the input (static uncertain variables) and output variables. An optimization procedure must be followed to minimize the error function, which is essentially the output of the model, based on tunable input parameters. Thus, the HM process is significantly accelerated since the error function is now obtained from the cheap to evaluate ANN rather than by the simulator itself. The second category of HM models, known as the direct one, utilizes the same input variables as in the first category and some property that needs to be matched as the output, usually production or pressure data. Once the model is trained, it can provide predictions about the field’s production and/or pressure values by interpolating between a limited number of simulation runs, producing thus a huge amount of realizations.

3.1. Machine Learning Methods for Indirect History Matching

Following the indirect HM approach, Costa et al. [101] and Zangl et al. [102] developed an ANN model to speed up the HM process. The input data sets were generated using the Box Behnken (BB) and Latin Hypercube (LH) sampling techniques, and an experimental design process, respectively. After the ML models were successfully trained and validated using a new blind dataset i.e., new unseen data that was not included in the original training set, the GA was implemented to run an optimization procedure by adjusting the input parameters until the output of the model is minimized, i.e., the error between the real and calculated production data. The results showed that the total CPU time was remarkably reduced and proved that an integrated ANN and GA approach can be successfully used to address field uncertainties and optimize operational strategies. Rodriguez et al. [103] set up a similar method for multiscale HM combined with a singular value decomposition method to reduce the number of parameters used to train the ANN model. That way, the authors achieved to mitigate the highly ill-posedness of the inverse HM process and decreased the total number of simulation runs while also reducing the total CPU time by over 75%. Esmaili and Mohaghegh [104] developed a simple but novel framework for history matching the gas production of a shale reservoir model using an ensemble of ANNs. The authors developed a model that is accustomed to any field parameter (production history, geomechanical and geochemical properties, etc.), along with any hydraulic fracture parameters. The results showed that this approach is faster than a numerical simulator as it offers an acceptable accuracy and it can make use of all available data, in comparison to conventional simulators that are very selective in the type parameters they use for HM.

Beyond the classic back-propagation ANN models, many other regression models have been shown to achieve good results in the HM problem. Silva et al. [105,106,107] extended the research area and examined several models, such as RBFNNs, Generalized Regression Neural Networks (GRNNs), Fuzzy Systems with Subtractive Clustering (FSSC) and ANFIS, to optimize the automatic HM. Their main goal was to validate the results of various models with the ones obtained from the simulator, regarding the changes in the OF. After the models were trained, the GA was used to perform a global optimization procedure, i.e., adjust the input parameters until the desired outcome is reached. Finally, a further refining procedure is performed to the most optimal results of the GA using the Hooke and Jeeves pattern search method [108]. Results showed that the models demonstrated high accuracy, with the most efficient networks being the ANFIS and the GRNN, in terms of the total number of simulations required and the total CPU time reduction.

3.2. Machine Learning Methods for Direct History Matching

In this section, various ML methods used for HM purposes are reviewed in detail. Most authors tend to use ANNs since, most of the time, they are easy to develop and they provide fast and reliable results. However, other methods have also been proposed, including Bayesian ML models, classic ML models, such as DTs, SVMs, etc., DL models and models based on the RL technique.

3.2.1. History Matching Based on ANN Models

Shahkarami et al. [109] and Sampaio et al. [110] followed the second (direct) approach and built ANN models to deal with uncertainty reduction and the acceleration of the HM process. The authors’ main purpose was to speed up HM while at the same time maintaining the high accuracy of the conventional approach. More specifically. Sampaio et al. trained the ANN using several uncertain reservoir parameters (porosity, permeability and rock compressibility) as input and the water production rates and BHPs at each time step as output. They parametrized the output in the [-1,1] interval to generate a more efficient model that could predict the water production curve through a specific time interval. The results showed that the production rates were history matched with good accuracy and the number of simulations needed was greatly reduced, demonstrating that ANNs can be competent tools for the HM procedure.

Cullick et al. [111] developed two assisted HM approaches. In their first approach, they used a conventional reservoir simulator together with a stochastic optimization algorithm to globally optimize the misfit function (simulated vs field measurements) by varying several arbitrarily selected reservoir parameters. To reduce the large number of iterations, and, thus, the required simulation time due to the high dimensionality of the search space, an experimental design procedure was used to identify the parameter sensitivities and build combinations that maximize the information gained while also minimizing the number of iterations. In their second more robust approach, they built an ANN model to reduce the number of simulations required by the first model and to perform sensitivity evaluations since the derivative for any output value with respect to any input parameter can be easily calculated by differentiating the ML model’s functional form. The ANN was trained with a small set of simulation data containing several static parameters (permeability and rock pore-volume modifiers, fault transmissibility factors, etc.) as the input and oil production and water injection rates as the output, to generate solutions of parameter sets that produce a good match. Finally, Lechner et al. [112] developed an ANN to perform HM using a limited number of simulation run results. Firstly, the authors perturbated the reservoir parameters exhibiting the highest impact on the matching process (permeability multiplier, gas cap size, etc.) and went through several experimental design steps to obtain sets of parameter combinations. Subsequently, these combinations were used to run a limited number of conventional simulations, the results of which were used to train the ANN. That way, the trained model could interpolate between the limited simulation scenarios, producing a huge amount of realizations for a smaller amount of runs. As a final step, the trained ANN was used in conjunction with a Monte Carlo simulation to generate probability distributions of the input parameters, showing that the permeability multiplier exhibits greatest impact on the results. The results were of good quality, verifying that ANNs are capable of producing accurate predictions.

HM is strongly related to decision-making and affects both production and economic evaluations. Therefore, oil and gas operators rely on risk analysis to determine the innate setbacks of the HM process which may include data uncertainty, inability to map spatiotemporal variabilities of a dataset and an erroneous judgment on the impact of crucial parameters. To anticipate that, Reis L. C. [113] developed multiple reservoir models, rather than just one, by setting filters that represent various accuracy tolerance criteria of the OF to select the models for risk analysis. Subsequently, the authors created filtered ANNs, trained with a set of uncertain static parameters, such as rock compressibility, net/gross ratio and fault transmissibilities, and their associated production predictions (cumulative oil production), constrained with several dynamic parameters. The purpose was to improve the quality of the results by incorporating trustworthy dynamic data that can efficiently constrain the model and improve the reliability of the results. When the trained proxies make predictions, they are evaluated based on the tolerance range set. The main idea in that study was that a more flexible anticipation of the HM minimum can be justified when the existence of field measurement errors is suspected. Most important, the decision will be made based on many solutions exhibiting sufficiently low matching error rather than the supposed global minimum one, which may not necessarily be the right one. The results showed that the ANN was expensive enough regarding the number of simulations that were required, however, good quality results were achieved, in terms of uncertainty reduction, accuracy and speed. Mohmad et al. [114] focused on the risk analysis area by developing a simple ANN to match a highly complex faulted reservoir with dual-string wells, creating a more efficient model that minimizes the risk uncertainty related to production and management plans. Their results showcased that this approach is much more competent, as far as the calculation time is concerned when compared to conventional simulators.

The approaches discussed so far are based on the same core paradigm: the ML models are trained using uncertain reservoir parameters as input to predict the pressures and/or production rates, followed by an optimization step to match the historical data. Ramgulam et al. [115] worked in an inverse direction by generating a back-propagation ANN to directly predict the uncertain parameters which optimize the HM process, achieving high quality in less computational time. The authors selected the differences between predicted and actual production values as inputs and trained the ANN to predict representative reservoir parameters. That way, they were able to train a network architecture that would yield optimum outputs, which can be further used as an efficient starting point for the simulator to improve the history matching procedure in significantly fewer runs.

3.2.2. History Matching Based on Bayesian ML Models

In a different context, Bayesian learning, in combination with ML methods, has also been widely used. This method considers history matching from a probabilistic point of view since a more potent solution can be endorsed, allowing the evaluation and uncertainty reduction of reservoir properties in an explicit statistical way. Based on this method, the parameters are described by their prior probabilities (i.e., initial knowledge). By sampling a number of instances out of those probabilities and running corresponding simulation runs, the quality of the predictions can be evaluated using a likelihood function that is an assessment of to what extent the initial parameter values (as obtained from their prior distributions) generate a reservoir model which fits the field data (i.e., to what extent the real and simulated data vary). Subsequently, the instances that best fit the data are appointed with higher probabilities. The initial knowledge of the field’s behavior is then updated using Bayes rule to obtain the posterior probability based on new observations [116].

For complex inverse problems like HM, the posterior probability cannot be calculated since an analytical expression doesn’t exist due to the extremely high number of unknown parameters [117]. To solve this problem, adaptive sampling techniques can be applied to collect samples from the posterior distribution. Based on this, Maschio et al. [117] developed ANN models to solve the HM problem by applying the Bayesian inference statistical technique with a Markov Chain Monte Carlo (MCMC) sampling algorithm (Metropolis–Hastings [118]), which would otherwise be restricted due to the high computational cost of the algorithm since it requires a large number of samples to converge, thus a large number of simulations. The authors proposed an iterative process in which each sampling step is followed with the training of an ANN, which in the first training step is fed with points from the prior distribution as inputs. Then, the Metropolis–Hastings algorithm is used to generate a chain comprising of the likelihood, which is determined by the ANN’s misfit output. A number of uniformly distributed points are selected from the chain and are imported into the simulator to calculate the new target data for the next ANN training. Those steps are repeated until a stopping criterion is achieved. The model’s outputs are then used to create a cumulative probability curve of the resulting OF values, from which a number of equally spaced percentiles among two selected extreme values (e.g., P10 and P90) is selected. The models that correspond to those percentiles are again imported into the reservoir simulator and its output is considered the final result. The sequential ANN training process was shown to lead to accurate and fast results.

Chai et al. [119] moved in the same direction and developed a similar workflow for quantifying the uncertainties and simplifying the HM of a fractured shale reservoir. Their results present a significant reduction in computational time and, at the same time, the model’s accuracy is successfully maintained. Furthermore, Eltahan et al. [120] developed a similar approach using a Bayesian-inference method for assisted HM, extended to appraise the possibility of a huff-n-puff EOR process by using the final solution to execute probabilistic forecasts. The difference here is that a proxy-based acceptance-rejection criterion is implemented, instead of the MCMC algorithm, that incorporates an RBFNN which acts as a sampler to quantify the uncertainty of several parameters by approximating the relationship between them and the posterior distribution. If the estimated posterior of a specific model is accepted, only then the complex and time-consuming reservoir simulation is run. For a given model to be accepted, the estimated posterior should be equal to or greater than the estimated posterior of the best model. Then, the new results are used to train the next proxy to improve its quality. The authors noted that although the MCMC algorithm is more precise for the posterior sampling than the method applied here, the results showed that the RBFNN model is much more effective in discovering the correct solutions. Finally, Christie et al. [116] developed a Bayesian technique by using a GA in combination with ANN models that could generate models to quantify uncertainties and perform an HM process faster. The ANN is used to decrease the time needed for the determination of regions in the parameter input space where a good match can be achieved. The workflow consists of firstly sampling a number of uncertain parameter sets, with a uniform distribution. Those data are used to train the ANN, which is used to guide the sampling process within the context of a stochastic search algorithm like the GA, by incorporating a bias to regions with a satisfactory match. That way, the ANN is performing all the expensive calculations faster, and, therefore, a large number of models that perform good history matches can be generated. When those models are used in conjunction with the Bayesian method, the uncertainty of the unknown parameters can be addressed quicker, in two orders of magnitude fewer simulations than would otherwise be required.

Although ML and data mining methods have been shown to produce accurate results, as compared with conventional reservoir simulators, those approaches have been questioned as the affiliated computational cost can sometimes be great since these methods usually demand large data sets for training and validation purposes [8]. To handle this question, Shams et al. [121] tried several ML-based and data mining methods for HM purposes, namely thin plate splines, RBFNNs, kriging, and ANNs, proving that the last two are more efficient than the first ones.

3.2.3. History Matching Based on ML Models other than ANNs

Apart from the widely used ANNs, many more ML techniques can help solve the inverse HM problem. Brantson et al. [122] tried several ML techniques to match tight gas reservoirs, namely Multivariate Adaptive Regression Splines (MARS) [123], Stochastic Gradient Boosting (SGB) algorithm, which entails growing DTs using a training set that is split to form new trees that boost the predictions [124] and single-pass GRNNs. The results were compared with the ones of a Random Forest (RF) model. Although the GRNN model presented the best match during the training process, it failed to do the same for the testing sets. The authors attributed this behavior to, as quoted, ‘’the ability of the GRNN model to exhibit extreme wiggles of individual signals [125], which are defined at inflection points where there should not be any inflection. Hence, these wiggles can be rampant and severe that each sudden change in data values of the predictions happens such that these changes almost appear to exhibit a step-like phenomenon’’. Overall, the computation time was reduced and, comparatively and in terms of each model’s predictive performance, the MARS and SGB models presented a predominantly better efficiency over the GRNN one since they were successfully tested against blind data, achieving very good predictions.

Moving away from the comfort zone of the most popular ML methods, Al Thuwaini et al. [126] tried to improve the HM speed by introducing a new two-step approach. Firstly, they clustered reservoir regions with similar petrophysical characteristics, thus reducing the number of values of each parameter from one per grid block to one per grouped region. The clustering was run using a Self Organizing Map (SOM), which is a unique type of self-learning (unsupervised) ANN that reduces data dimensions and generates a low-dimensional, discretized depiction (map) of a dataset’s original input space [127]. The authors identified the parameters that mostly affect the matching process and defined reservoir regions, where a single parameter multiplier per region could be applied to boost the match. Secondly, the identified regions were exported to the simulator to perform three sensitivity runs for each region by applying the parameter initial, uppermost and lowermost limit values. The obtained error (difference between calculated and real target values) from the runs was used to highlight the impact of each parameter adjustment. Then, the parameter value with the highest error was discarded, while keeping the remaining two as the new uppermost and lowermost limits, setting up a new run by incorporating a third mean parameter value between the remaining two, in a way that resembles the bisection method [128]. This process is continued until the desired error margin is reached, leading to a greatly reduced search area. The advantage of this method is that it is automated and user-friendly since the user must only define the number of grouped regions. The results showed that the computational time of the proposed workflow, hence the total number of simulations required to perform a successful history matching, was significantly reduced.

Gradient-based optimization methods often suffer from severe issues when estimating the OF gradient due to the numerical noise, resulting from the allowed solver tolerance criteria. To handle that problem, Guo et al. [129] developed a Support Vector Regression (SVR) model in conjunction with a Distributed Gauss-Newton (DGN) optimization algorithm to produce precise and discontinuity-free OF gradients that are not very susceptible to a simulator’s numerical noise, thus enhancing the performance of the matching. The authors trained the model using reservoir parameters as input with the help of the pluri-Principal Component Analysis (pluri-PCA) method, which was utilized to produce the partial derivatives of several parameters and create a sensitivity matrix used by the DGN algorithm to generate new search points for a new simulation run. The results are fed back to the proxy to improve its accuracy and the procedure is repeated until the optimization process converges. As the numerical noise level increases, the SVR-DGN performance is very good while it also maintains fast convergence rates, reducing the calculation time burden that would otherwise be imposed by the simulator when tighter convergence criteria are set.

3.2.4. History Matching Based on Deep Learning Methods

As mentioned in Section 2, DL is a subset of the ML family widely used in cases of extremely large reservoir fields with hundreds of uncertain parameters and can digest unstructured data in its raw form and automatically determine the set of variables that can distinguish the desired output for regression, classification and clustering tasks.

Another category of ML models, that of Recurrent Neural Networks (RNNs), although they do not necessarily belong strictly to the DL family, they are only considered in that form in the current review since the RNN-based methods available in the literature for the solution of the HM problem lie within the DL context. RNNs are known to perform well at modeling sequential data to make predictions by using the so-called sequential memory, which is a mechanism to recognize patterns in time. Just like other networks, RNNs have the same basic architecture and parameter structure but the big difference is that they have a feedback loop mechanism that acts as a highway to allow information to flow back to the input before proceeding to the output, in contrary to the feed-forward ANNs where information flows only towards one direction [130]. As a result, RNNs can be used to provide a full data series (e.g., well production over time) rather than a single output value.

Ma et al. [131] developed an RNN model with a gated recurrent unit to match a large-scale reservoir by approximating the relationship between a vector input containing geological information, to which a parameterization method is imposed to reduce the dimensionality, and an output corresponding to the production data. The output is transformed using a log-based normalization method to improve the memorization mechanism of the model. The model is then integrated into a Multimodal Estimation Distribution Algorithm (MEDA) for HM. In a consecutive study, Ma et al. [132] introduced well-control variables, in addition to the geological parameters of the previous study, as inputs to the model to impose further accuracy improvements.

Other types of DL ANNs include the Convolutional Neural Network (CNN) and the Generative Adversarial Network (GAN), both used mostly for image analysis and pattern recognition applications. The former is a supervised subtype of DL networks, consisting of a large number of convolutional layers (known as convolutional filters) that are able to reduce the high dimensionality of images, without losing too much important information. These types of networks are usually used for image recognition purposes [133]. The latter are also a subtype of DL networks, however, they belong to the UL family. In GANs, two ANNs compete each other to become more precise in their predictions by identifying patterns in the input dataset. More specifically, GANs ‘’play’’ a zero-sum game between a generator model (first ANN) that generates fake new examples and a discriminator model (second ANN) that tries to distinguish between the real or fake examples. These models are trained together until the discriminator is deceived so many times, meaning the generator is starting to create conceivable examples [134]. Ma et al. [135] developed a CNN in conjunction with an Ensemble Smoother (ES) algorithm [136] to perform a HM process and make predictions about production rates from reservoir parameters with high dimensionality. The authors included a GAN in their study, which, when compared to the CNN, generated predictions with higher resolution.

3.2.5. History Matching ML Methods Using Dimensionality Reduction Techniques

Focusing on the dimensionality of uncertain parameters in complex reservoir models, which need to be fixed during HM, several methods have been proposed, both in the DL and the classic ML context. To this end, Honorio et al. [137] integrated the Pluri-PCA method with a novel ML one, called Piecewise Reconstruction from a Dictionary (PRaD), to simulate HM for a highly channelized reservoir. This method has been designed to learn prior geological data and is used to reconstruct the model, after the Pluri-PCA method is utilized, by incorporating lost information that helps to create a more realistic final model. Although all parameter reduction methods, such as PCA, can successfully help a proxy model’s training, the reconstructed model can several times be crooked, something that can cause problems, especially in cases of HM a highly complex reservoir model where its critical features should remain intact. The authors used the PRaD method to learn geological data and store in a ‘’dictionary’’ all generated geological models. Then, the Pluri-PCA method is used to reduce the number of cell-based parameters of the models and transform the facies of the model to Gaussian PCA coefficients, as efficiently as possible without losing too much information that would otherwise be useful. The PCA coefficients are then adjusted through HM and a pluri-Gaussian rock-type-rule is enforced for the reconstruction of the complex facies model from the adjusted coefficients. Finally, the PRaD method is employed, and, having previously stored all useful geological information, it efficiently reduces the interval between the reconstructed and the trained model.

Alguliyev et al. [138] developed a convolutional Variational AutoEncoder (VAE) network (a special case of learning model trained to reproduce input images in the output layer) [139] which is integrated into an ES algorithm to perform HM. This network consists of an encoder, which aims to encode input features into short vectors and a decoder which reproduces the output features back from the encoding vector. The results showed that the model is very effective within an acceptable error margin. Canchumuni et al. [140] developed a DL-based parameterization technique for HM facies models with ensemble methods, which advances the accuracy of the results by integrating multiple models. Sets of prior facies realizations are used to train the DL network, which determines the most important characteristics of the facies images to parameterize the models, updated to account for the dynamic history data using an ES multiple data assimilation method. After the HM, the DL model is utilized to reconstruct the facies models. Jo et al. [141] developed several CNNs in an ensemble mode (Convolutional AutoEncoder-CAE, CNN and Convolutional Denoising AutoEncoder-CDAE) that sample posterior reservoir models for fluvial channel reservoirs for HM. Since the dimensionality of the reservoir data was very big to determine a relationship between prior models and their corresponding simulated production data, the authors used the CAE to generate low-dimensional latent features from prior models. Next, the relationship between those low-dimensional features (input) and their corresponding production (output) is determined using CNNs. Finally, the output of the CNN is used by the CDAE to enhance the geological connectivity of the posterior models. The results showed that this ensemble model surpasses the efficiency of other methods, while also maintaining a low computational cost of sampling posterior models.

Another ML framework using CNN along with the PCA parameterization method was developed by Liu et al. [142] for HM purposes. This novel low-dimensional CNN–PCA model is trained as an explicit transformation function that can pre-treat PCA realizations to quickly produce models coherent with the original reference model. The method uses a series of metrics from a pre-trained CNN model to determine numerous correlations, allowing the conservation of the complex geological features that exist in the original reference model. The results showed that the CNN–PCA method achieved satisfactory HM and uncertainty reduction for existing wells, as well as reasonable predictions for new wells. Finally, Jo et al. [143] developed GAN models to match a deepwater lobe system, trained by applying rule-based models to explore the latent reservoir space, since that way the multidimensional data that are used are converted into latent random vectors. The models produced are integrated with a simulator to generate production values and then an Ensemble Kalman Filter (EnKF) updates the latent vectors by minimizing the error obtained when comparing the calculated production values with the real ones. The EnKF is a probabilistic algorithm that utilizes ensembles of realizations, updated using a variance-minimizing strategy, to describe any uncertainties in the model. It needs fewer function evaluations but, as it is a probabilistic method, it may not converge [98]. The results showed that GAN-EnKF outperforms the EnKF alone, as far as the accuracy of prediction, the preservation of geological features, and the computational efficiency for updating the ensemble are concerned. The GAN-EnKF method can be easily utilized for various reservoir types since no constraints are required depending on data types or geological structures.

3.2.6. History Matching Based on Reinforcement Learning Methods

Apart from DL methods in the conventional supervised/unsupervised learning framework, the application of RL has also been investigated [17,144]. The framework in RL is pretty similar to that of unsupervised forward modeling, in the sense that there is an input corresponding to the current state of the system to be controlled, which runs through the ANN model to produce an output for which the target label is not known beforehand. The model, called the policy network, transforms inputs (states) into outputs (actions) and it is trained to learn a policy by directly interacting with the environment of interest so that it maximizes a reward in the operating environment [98]. Li and Misra [145] developed such a strategy by expressing the HM problem as a Markov Decision Process (MDP). They tried to reduce the manual effort and bias imposed by the process and to automatically examine the parameter space by using a fast-marching simulator as the environment for the RL method, where a DL ANN agent is set to communicate with. A discrete Deep Q Network (DQN) and continuous Deep Deterministic Policy Gradients (DDPGs) are used as the learning agents, with the latter displaying a greater accuracy than the former since the continuous processes allow the DDPG technique to examine a higher number of states at each iteration of the learning phase. The results showed that both approaches achieved good accuracy. It was also shown that the DDPG approach surpasses the performance of the DQN, as far as the RMS error is concerned. However, even if the authors presented a highly innovative method, their research is relatively narrow since it is restricted to a simple model that contains a small number of parameters.

As of the time of this paper, Alolayan et al. [98] are the only authors that have employed a stochastic way with an RL method to identify multiple solutions to the HM problem. They described the model as an MDP and implemented an integrated system where an RL model (Proximal Policy Optimization, PPO, in which the agent uses two DL ANNs) can connect with a simulator to discover numerous solutions for much more complex reservoir models with numerous parameters. This is achieved by a parallel learning capability in which multiple coexisting learning environments can be put in motion, allowing the model to learn synchronously from all of them. A reservoir simulator with synthetic data was used to generate production rates, considered historical ones, and the uncertain parameter that must be adjusted to achieve a good match. To generate initial values for the algorithm, the previous model was discarded and the parameter values for each cell were slightly modified by adding random noise. The reservoir simulator was used as the learning environment where the agent is used to learn how to take actions that will eventually lead to minimizing the OF, obtaining a new state of the environment at each learning time-step that encloses all the uncertain parameters that must be adjusted, as well as a reward that measures how good the action taken by the agent is. The reward is directly determined by the OF, which gives positive values for good actions that reduce it and negative values for actions that increase it. This process will eventually designate higher rewards to actions that correspond to higher reductions in the OF, forcing thus the agent to take actions that accelerate the convergence. Finally, as the agent attempts to maximize the rewards, it will adjust the uncertain parameters that reduce the OF and will discover a solution to the HM problem.

4. Conclusions

This paper presents an extensive review of all Machine Learning (ML) models developed for subsurface reservoir simulations and highlights the different applications and challenges concerning individual reservoir simulation runs and History Matching. Since reservoir simulations are typically run using conventional simulators which are extremely costly in terms of computational time, ML models are capable of simplifying those complicated procedures and providing fast subsurface evaluations within an acceptable error margin.

As it is showcased by the reviewed research papers, the most appropriate choice of ML model can be a difficult task since the model that is developed must be able to perform efficiently based on the needs of the specific problem under study. Therefore, it is considered wiser to first understand deeply the problem under investigation from the reservoir engineer’s point of view to efficiently decide the right course of action.

ML models coupled with dimensionality reduction techniques have been shown to lead to very accurate prediction results, while also maintaining a smaller computational cost when compared to simpler ML models which take into account a fully dimensional database. It must be noted that the biggest contribution of these techniques is towards complex reservoir systems where the number of parameters can be extremely high, while also presenting large distribution variations from one field location to the other. In those cases, the dimensionality reduction can significantly reduce the time that would otherwise be required since the prediction calculations are executed much faster.

For the ML strategies concerning individual simulation runs, two approaches have dominated the research area. The first entails proxy models (or else Surrogate Reservoir Models) which can be implemented to answer a wide range of engineering questions in a fraction of the time that it would otherwise be required. The second ML approach aims at accelerating specific CPU time-intense sub-problems, such as handling the phase equilibrium problem in its black oil or compositional form. For the case of compositional simulations, several ML methods have been developed, aiming at reducing the excessively long time required for solving stability and flash calculations. The phase stability problem is expressed as a classification one to determine the number of phases for any given composition and pressure and temperature values whereas flash calculations are performed using regression models to predict the k-values needed in a more robust, and efficient way. For the case of black oil simulations where the grid blocks are assumed to contain only oil, gas and water fluid phases, ML methods have been proposed to predict the necessary PVT properties that are needed to account for the compressibility of each phase and of the solution of gas to reservoir oil (such as the Z-factor and saturation pressures). Although those crucial properties are usually available from experimental procedures or empirical correlations using field data, in cases where experimental values are not available or empirical correlations cannot be utilized since they only perform well for the conditions they were created for, ML methods are used to overcome these problems and speed up and improve the accuracy of black oil simulations.

Concerning the History Matching process, many ML methods have been developed to mitigate the ill-posedness phenomenon and reduce the time required to achieve a good match. Many of them utilize simple Artificial Neural Network (ANN) models, usually combined with stochastic or probabilistic algorithms for optimization reasons, while others use more complicated methods, such as Self Organizing Maps, Deep Learning (DL) methods, etc., or more novel ones such as Reinforcement Learning (RL). However, although DL models can improve the HM process in terms of computational performance, they are most commonly implemented to match large-scale reservoirs where the need to deal with accelerated calculations is much more intense due to the hundreds of millions of reservoir grid blocks.

Concluding, although ML methods have been shown to significantly assist and accelerate subsurface reservoir simulations by providing fast and accurate results, there is still much progress to be made. Improvement of the different model’s capability to generalize, obtaining reliable conclusions from sparse data and introducing physical laws and technical constraints to the models training are just few future trends for more accurate and realistic predictions.

Author Contributions

Conceptualization, A.S. and V.G.; methodology, A.S. and V.G.; investigation, A.S.; writing—original draft preparation, A.S.; writing—review and editing, V.G.; visualization, A.S.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table A1. Table of abbreviations.

Abbreviation	Meaning
ML	Machine Learning
EOR	Enhanced Oil Recovery
EoS	Equation of State
HM	History Matching
PFO	Production Forecast and Optimization
OF	Objective Function
HPC	High-Performance Computing
SRM	Surrogate Reservoir Model
RFM	Reduced Physics Model
ROM	Reduced Order Model
AI	Artificial Intelligence
SL	Supervised Learning
UL	Unsupervised Learning
RL	Reinforcement Learning
ANN	Artificial Neural Network
BHP	Bottom Hole Pressure
B_o	oil formation volume factor
B_g	gas formation volume factor
GOR	Gas to Oil Ratio
RBFNN	Radial Basis Function Neural Network
SVM	Support Vector Machine
TPD	Tangent Plane Distance
DL	Deep Learning
SS	Successive Substitution
DT	Decision Tree
Z-factor	gas compressibility factor
S-K	Standing-Katz
SCG	Scaled Conjugate Gradient
LM	Levenberg–Marquardt
RBP	Resilient Back Propagation
FIS	Fuzzy Interface System
ANFIS	Adaptive Neuro-Fuzzy Inference System
LSSVM	Least Square Support Vector Machines
CSA	Coupled Simulated Annealing
MW	Molecular Weight
PSO	Particle Swarm Optimization
GA	Genetic Algorithm
KRR	Kernel Ridge Regression
CVD	Constant Volume Depletion
MLP	Multi-Layer Perceptron
GBM	Gradient Boost Method
SA	Sensitivity Analysis
BB	Box Behnken
LH	Latin Hypercube
GRNN	Generalized Regression Neural Network
FSSC	Fuzzy Systems with Subtractive Clustering
MCMC	Markov Chain Monte Carlo
MARS	Multivariate Adaptive Regression Splines
SGB	Stochastic Gradient Boosting
RF	Random Forest
SOM	Self Organizing Map
SVR	Support Vector Regression
DGN	Distributed Gauss-Newton
PCA	Principal Component Analysis
RNN	Recurrent Neural Network
MEDA	Multimodal Estimation Distribution Algorithm
CNN	Convolutional Neural Network
GAN	Generative Adversarial Network
ES	Ensemble Smoother
PRaD	Piecewise Reconstruction from a Dictionary
VAE	Variational AutoEncoder
CAE	Convolutional AutoEncoder
CDAE	Convolutional Denoising AutoEncoder
EnKF	Ensemble Kalman Filter
MDP	Markov Decision Process
DQN	Deep Q Network
DDPG	Deep Deterministic Policy Gradient
PPO	Proximal Policy Optimization

References

Alenezi, F.; Mohaghegh, S.A. Data-Driven Smart Proxy Model for a Comprehensive Reservoir Simulation. In Proceedings of the 4th Saudi International Conference on Information Technology (Big Data Analysis) (KACSTIT), Riyadh, Saudi Arabia, 6-9 November 2016; pp. 1–6. [Google Scholar]
Ghassemzadeh, S. A Novel Approach to Reservoir Simulation Using Supervised Learning, Ph.D. dissertation, University of Adelaide, Australian School of Petroleum and Energy Resources, Faculty of Engineering, Computer & Mathematical Sciences, Australia, November 2020.
Danesh, A. PVT and Phase Behavior of Petroleum Reservoir Fluids; Elsevier: Amsterdam, The Netherlands, 1998; ISBN 9780444821966. [Google Scholar]
Gaganis, V.; Marinakis, D.; Samnioti, A. A soft computing method for rapid phase behavior calculations in fluid flow simulations. Journal of Petroleum Science and Engineering 2021, 205, 108796. [Google Scholar] [CrossRef]
Voskov, D.V.; Tchelepi, H. Comparison of nonlinear formulations for two-phase multi-component EoS based simulation. Journal of Petroleum Science and Engineering 2012, 82–83, 101–111. [Google Scholar] [CrossRef]
Wang, P.; Stenby, E.H. Compositional simulation of reservoir performance by a reduced thermodynamic model. Computers & Chemical Engineering 1994, 18, 2–75. [Google Scholar]
Gaganis, V.; Varotsis, N. Machine Learning Methods to Speed up Compositional Reservoir Simulation. In Proceedings of the EAGE Annual Conference & Exhibition incorporating SPE Europe, SPE 154505. Copenhagen, Denmark, 4–7 June 2012. [Google Scholar]
Jaber, A.K.; Al-Jawad, S.N.; Alhuraishawy, A.K. A review of proxy modeling applications in numerical reservoir simulation. Arabian Journal of Geosciences 2019, 12. [Google Scholar] [CrossRef]
Aminian, K. Modeling and simulation for CBM production. In Coal Bed Methane: Theory and Applications, 2nd ed; Elsevier: Amsterdam, The Netherlands, 2020; ISBN 9780128159972. [Google Scholar]
Shan, J. High performance cloud computing on multicore computers. PhD dissertation, New Jersey Institute of Technology, USA. 31 May 2018. [Google Scholar]
Amini, S.; Mohaghegh, S. Application of Machine Learning and Artificial Intelligence in Proxy Modeling for Fluid Flow in Porous Media. Fluids 2019, 4. [Google Scholar] [CrossRef]
Bahrami, P.; Moghaddam, F.S.; James, L.A. A Review of Proxy Modeling Highlighting Applications for Reservoir Engineering. Energies 2022, 15. [Google Scholar] [CrossRef]
Sircar, A.; Yadav, K.; Rayavarapu, K.; Bist, N.; Oza, H. Application of machine learning and artificial intelligence in oil and gas industry. Petroleum Research, 2021, 6, 379–391. [Google Scholar] [CrossRef]
Bao, A.; Gildin, E.; Zalavadia, H. Development Of Proxy Models for Reservoir Simulation by Sparsity Promoting Methods and Machine Learning Techniques. In Proceedings of the 16th European Conference on the Mathematics of Oil Recovery, Barcelona, Spain, 3-6 September 2018. [Google Scholar]
Denney, D. Pros and cons of applying a proxy model as a substitute for full reservoir simulations. Journal of Petroleum Technology 2010, 62, 41–42. [Google Scholar] [CrossRef]
Ibrahim, D. An overview of soft computing. In Proceeding of the 12th International Conference on Application of Fuzzy Systems and Soft Computing, ICAFS, Vienna, Austria., 29-30 August 2016. [Google Scholar]
Bishop, C.M. Pattern Recognition and Machine Learning. Springer: New York, 650 NY, USA, 2006; ISBN-10: 0241973376.
Nocedal, J.; Wright, S. Numerical Optimization, 2nd ed.; Mikosch, T.V., Robinson, S.M., Resnick, S.I., Eds.; Springer: New York, 650 NY, USA, 2006. [Google Scholar]
Samnioti, A.; Anastasiadou, V.; Gaganis, V. Application of Machine Learning to Accelerate Gas Condensate Reservoir Simulation. Clean Technol. 2022, 4, 153–173. [Google Scholar] [CrossRef]
James. G.; Witten, D., Hastie, T., Tibshirani, R. An Introduction to Statistical Learning: with Applications in R, Eds.; Springer: New York, 650 NY, USA, 2013; ISBN 978-1-4614-7139-4. [Google Scholar]
Freeman, J.A.; Skapura, D.M. Neural Networks: Algorithms, Applications, and Programming Techniques. Addison-Wesley: Boston, Massachusetts, USA, 1991. ISBN 0201513765.
Fausett, L. Fundamentals of Neural Network: Architectures, Algorithms, and Applications. Prentice-Hall international editions, Hoboken, 1994.
Veelenturf, L.P.J. Analysis and Applications of Artificial Neural Networks, 1st ed; Prentice-Hall international editions, Hoboken, 1995.
Kumar, A. A Machine Learning Application for Field Planning. In Proceedings of the Offshore Technology Conference, OTC-29224-MS. Houston, Texas, 6-9 May 2019. [Google Scholar]
Zhang, D.; Chen, Y.; Meng, J. Synthetic well logs generation via Recurrent Neural Networks. Petroleum Exploration and Development 2018, 45, 629–639. [Google Scholar] [CrossRef]
Castiñeira, D.; Toronyi, R.; Saleri, N. Machine Learning and Natural Language Processing for Automated Analysis of Drilling and Completion Data. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 23-26 April 2018; SPE-192280-MS.
Bhandari, J.; Abbassi, R.; Garaniya, V.; Khan, F. Risk analysis of deepwater drilling operations using Bayesian network. Journal of Loss Prevention in the Process Industries 2015, 38, 11–23. [Google Scholar] [CrossRef]
Varotsis, N.; Gaganis, V.; Nighswander, J.; Guieze, P. A Novel Non-Iterative Method for the Prediction of the PVT Behavior of Reservoir Fluids. In Proceedings of the SPE Annual Technical Conference and Exhibition, SPE-56745-MS. Houston, Texas, 3-6 October 1999. [Google Scholar]
Avansi, G, D. Use of Proxy Models in the Selection of Production Strategy and Economic Evaluation of Petroleum Fields. In Proceeding of the SPE Annual Technical Conference and Exhibition, New Orleans, Louisiana, 4-, SPE-129512-STU.
Aljameel, S.S.; Alomari, D.M.; Alismail, S.; Khawaher, F.; Alkhudhair, A.A.; Aljubran, F.; Alzannan, R.M. An Anomaly Detection Model for Oil and Gas Pipelines Using Machine Learning. Computation 2022, 10, 138. [Google Scholar] [CrossRef]
Jacobs, T. The Oil and Gas Chat Bots Are Coming. J. Pet. Technol. 2019, 71, 34–36; [Google Scholar] [CrossRef]
Anastasiadou, V.; Samnioti, A.; Kanakaki, R.; Gaganis, V. Acid gas re-injection system design using machine learning. Clean Technol. 2022, 4, 1001–1019. [Google Scholar] [CrossRef]
Navrátil, J.; King, A.; Rios, J. Kollias, G.; Torrado, R.; Codas, A. Accelerating Physics-Based Simulations Using End-to-End Neural Network Proxies: An Application in Oil Reservoir Modeling. Front. Big Data 2019, 2. [Google Scholar] [CrossRef] [PubMed]
Mohaghegh, S.; Popa, A.; Ameri, S. Intelligent systems can design optimum fracturing jobs. In Proceedings of the SPE Eastern Regional Conference and Exhibition, SPE-57433-MS., 21-22 October 1999. [Google Scholar]
Mohaghegh, S.D.; Hafez, H.; Gaskari, R.; Haajizadeh, M.; Kenawy, M. Uncertainty analysis of a giant oil field in the middle east using surrogate reservoir model. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference; 2006. [Google Scholar]
Mohaghegh, S.D. Quantifying uncertainties associated with reservoir simulation studies using surrogate reservoir models. In Proceedings of the SPE Annual Technical Conference and Exhibition, SPE-102492-MS. San Antonio, Texas, USA, 24-27 September 2006. [Google Scholar]
Mohaghegh, S.D.; Modavi, A.; Hafez, H.H.; Haajizadeh, M.; Kenawy, M.; Guruswamy, S. Development of Surrogate Reservoir Models (SRM) for Fast-Track Analysis of Complex Reservoirs. In Proceedings of the Intelligent Energy Conference and Exhibition, SPE-99667-MS. Amsterdam, The Netherlands, 11-13 April 2006. [Google Scholar]
Kalantari-Dahaghi, A.; Esmaili, S.; Mohaghegh, S.D. Fast Track Analysis of Shale Numerical Models. In Proceedings of the SPE Canadian Unconventional Resources Conference, SPE-162699-MS. Calgary, Alberta, Canada, 30 October-1 November 2012. [Google Scholar]
Mohaghegh, S.D. Reservoir simulation and modeling based on artificial intelligence and data mining (AI&DM). Journal of Natural Gas Science and Engineering 2011, 3, 697–705. [Google Scholar]
Alenezi, F.; Mohaghegh, S. A data-driven smart proxy model for a comprehensive reservoir simulation. In Proceedings of the 4th Saudi International Conference on Information Technology (Big Data Analysis) (KACSTIT), Riyadh, Saudi Arabia, 6-9 November 2016. [Google Scholar]
Alenezi, F.; Mohaghegh, S. Developing a Smart Proxy for the SACROC Water-Flooding Numerical Reservoir Simulation Model. In Proceedings of the SPE Western Regional Meeting, SPE-185691-MS. Bakersfield, California, 23-27 April 2017. [Google Scholar]
Shahkarami, A.; Mohaghegh, S.D.; Gholami, V.; Haghighat, A.; Moreno, D. Modeling pressure and saturation distribution in a CO₂ storage project using a Surrogate Reservoir Model (SRM). Greenhouse Gases: Science and Technology 2014, 4, 289–315. [Google Scholar] [CrossRef]
Shahkarami, A.; Mohaghegh, S. Applications of smart proxies for subsurface modeling. Pet. Explor. Dev. 2020, 47, 400–412. [Google Scholar] [CrossRef]
Dahaghi, A.K.; Mohaghegh, S. Numerical simulation and multiple realizations for sensitivity study of shale gas reservoirs. In Proceedings of the SPE Production and Operations Symposium; 2011. [Google Scholar]
Memon, P.Q.; Yong, S.P.; Pao, W.; Sean, P.J. Surrogate reservoir modeling-prediction of bottom-hole flowing pressure using radial basis neural network. In Proceedings of the Science and Information Conference (SAI); 2014. [Google Scholar]
Amini, S.; Mohaghegh, S.D.; Gaskari, R.; Bromhal, G. Uncertainty analysis of a CO₂ sequestration project using surrogate reservoir modeling technique. In Proceedings of the SPE Western Regional Meeting, SPE-153843-MS. Bakersfield, California, USA, 21-23 March 2012. [Google Scholar]
Gaganis, V.; Varotsis, N. Non-iterative phase stability calculations for process simulation using discriminating functions. Fluid Phase Equilibria 2012, 314, 69–77. [Google Scholar] [CrossRef]
Gaganis, V.; Varotsis, N. An integrated approach for rapid phase behavior calculations in compositional modeling. J. Petrol. Sci. Eng. 2014, 118, 74–87. [Google Scholar] [CrossRef]
Gaganis, V. Rapid phase stability calculations in fluid flow simulation using simple discriminating functions. Comput. Chem. Eng. 2018, 108, 112–127. [Google Scholar] [CrossRef]
Kashinath, A.; Szulczewski, L.M.; Dogru, H.A. A fast algorithm for calculating isothermal phase behavior using machine learning. Fluid Phase Equilibria 2018, 465, 73–82. [Google Scholar] [CrossRef]
Schmitz, J.E.; Zemp, R.J.; Mendes, M.J. Artificial neural networks for the solution of the phase stability problem. Fluid Phase Equilibria 2016, 245, 83–87. [Google Scholar] [CrossRef]
Gaganis, V. , Varotsis N. In Rapid multiphase stability calculations in process simulation. In Proceedings of the 27th European Symposium on Applied Thermodynamics, Eindhoven, Netherlands, July 2014. [Google Scholar]
Wang, K.; Luo, J.; Yizheng, W.; Wu, K.; Li, J.; Chen, Z. Artificial neural network assisted two-phase flash calculations in isothermal and thermal compositional simulations. Fluid Phase Equilibria 2019, 486, 59–79. [Google Scholar] [CrossRef]
Li, Y.; Zhang, T.; Sun, S.; Gao, X. Accelerating flash calculation through deep learning methods. Journal of Computational Physics 2019, 394, 153–165. [Google Scholar] [CrossRef]
Li, Y.; Zhang, T.; Sun, S. Acceleration of the NVT Flash Calculation for Multicomponent Mixtures Using Deep Neural Network Models. Industrial & Engineering Chemistry Research 2019, 58, 12312–12322. [Google Scholar]
Wang, S.; Sobecki, N.; Ding, D.; Zhu, L.; Wu, Y.S. Accelerating and stabilizing the vapor-liquid equilibrium (VLE) calculation in compositional simulation of unconventional reservoirs using deep learning-based flash calculation. Fuel 2019, 253, 209–219. [Google Scholar] [CrossRef]
Zhang, T.; Li, Y.; Sun, S.; Bai, H. Accelerating flash calculations in unconventional reservoirs considering capillary pressure using an optimized deep learning algorithm. Journal of Petroleum Science and Engineering 2020, 195, 107886. [Google Scholar] [CrossRef]
Zhang, T.; Li, Y.; Li, Y.; Sun, S.; Gao, X. A self-adaptive deep learning algorithm for accelerating multi-component flash calculation. Computer Methods in Applied Mechanics and Engineering 2020, 369(1), 113207. [Google Scholar] [CrossRef]
Sheth, S.; Heidari, M.R.; Neylon, K.; Bennett, J.; McKee, F. Acceleration of thermodynamic computations in fluid flow applications. Computational Geosciences 2022, 26, 1–11. [Google Scholar] [CrossRef]
Ahmed, T. Equations of State and PVT Analysis; Gulf Publishing Company: Houston, TX, USA, 2007; ISBN 978-1-933762-03-6. [Google Scholar]
Moghadassi, A.R.; Parvizian, F.; Hosseini, S.M.; Fazlali, A.R. A new approach for estimation of PVT properties of pure gases based on artificial neural network model. Braz. J. Chem. Eng. 2009, 26. [Google Scholar] [CrossRef]
Beggs, D.H.; Brill, J.P. A Study of Two-Phase Flow in Inclined Pipes. J Pet Technol 1973, 25, 607–617; [Google Scholar] [CrossRef]
Dranchuk, P.M.; Abou-Kassem, H. Calculation of Z Factors For Natural Gases Using Equations of State. J Can Pet Technol 1975, 14, PETSOC-75-03–03. [Google Scholar] [CrossRef]
Kamyab, M.; Sampaio, J.H.B.; Qanbari, F.; Eustes, A.W. Using artificial neural networks to estimate the z-factor for natural hydrocarbon gases. Journal of Petroleum Science and Engineering 2010, 73, 248–257. [Google Scholar] [CrossRef]
Sanjari, E.; Lay, E.N. Estimation of natural gas compressibility factors using artificial neural network approach. Journal of Natural Gas Science and Engineering 2012, 9, 220–226. [Google Scholar] [CrossRef]
Irene, A.I.; Sunday, I.S.; Orodu, O.D. Forecasting Gas Compressibility Factor Using Artificial Neural Network Tool for Niger-Delta Gas Reservoir. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, SPE-184382-MS. Lagos, Nigeria, 2-4 August 2016. [Google Scholar]
Al-Anazi, B.D.; Pazuki, G.R.; Nikookar, M.; Al-Anazi, A.F. The Prediction of the Compressibility Factor of Sour and Natural Gas by an Artificial Neural Network System. Petroleum Science and Technology 2011, 29, 325–336. [Google Scholar] [CrossRef]
Mohamadi-Baghmolaei, M.; Azin, R.; Osfouri, S.; Mohamadi-Baghmolaei, R.; Zarei, Z. Prediction of gas compressibility factor using intelligent models. Nat. Gas Ind. B 2015, 2, 283–294. [Google Scholar] [CrossRef]
Fayazi, A.; Arabloo, M.; Mohammadi, A.H. Efficient estimation of natural gas compressibility factor using a rigorous method. J. Nat. Gas Sci. Eng. 2014, 16, 8–17. [Google Scholar] [CrossRef]
Kamari, A.; Hemmati-Sarapardeh, A.; Mirabbasi, S.-M.; Nikookar, M.; Mohammadi, A.H. Prediction of sour gas compressibility factor using an intelligent approach. Fuel Process. Technol. 2013, 116, 209–216. [Google Scholar] [CrossRef]
Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Processing Letters 1999, 9, 293–300. [Google Scholar] [CrossRef]
Chamkalani, A.; Maesoumi, A.; Sameni, A. An intelligent approach for optimal prediction of gas deviation factor using particle swarm optimization and genetic algorithm. Journal of Natural Gas Science and Engineering 2013, 14, 132–143. [Google Scholar] [CrossRef]
Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, 1942-1948. 1995. [Google Scholar]
Gaganis, V.; Homouz, D.; Maalouf, M.; Khoury, N.; Polycrhonopoulou, K. An Efficient Method to Predict Compressibility Factor of Natural Gas Streams. Energies 2019, 12, 2577. [Google Scholar] [CrossRef]
Maalouf, M.; Homouz, D. Kernel ridge regression using truncated newton method. Knowledge-Based Systems 2014, 71, 339–344. [Google Scholar] [CrossRef]
Samnioti, A.; Kanakaki, E.M.; Koffa, E.; Dimitrellou, I.; Tomos, C.; Kiomourtzi, P.; Gaganis, V.; Stamataki, S. Wellbore and Reservoir Thermodynamic Appraisal in Acid Gas Injection for EOR Operations. Energies 2023, 16. [Google Scholar] [CrossRef]
Kamari, A.; Hemmati-Sarapardeh, A.; Mirabbasi, S.M.; Nikookar, M.; Mohammadi, A.H. Prediction of sour gas compressibility factor using an intelligent approach. Fuel Processing Technology 2013, 116, 209–216. [Google Scholar] [CrossRef]
Seifi, M.; Abedi, J. An Efficient and Robust Saturation Pressure Calculation Algorithm for Petroleum Reservoir Fluids Using a Neural Network. Petroleum Science and Technology 2012, 30. [Google Scholar] [CrossRef]
Gharbi, R.B.C.; Elsharkawy, A.M. Neural Network Model for Estimating the PVT Properties of Middle East Crude Oils. SPE Res Eval & Eng 1999, 2, 255–265; [Google Scholar]
Al-Marhoun, M.A.; Osman, E.A. Using Artificial Neural Networks to Develop New PVT Correlations for Saudi Crude Oils. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, SPE-78592-MS. Abu Dhabi, United Arab Emirates, 13-16 October 2002. [Google Scholar]
Moghadam, J.N.; Salahshoor, K.; Kharrat, R. Introducing a new method for predicting PVT properties of Iranian crude oils by applying artificial neural networks. Petroleum Science and Technology 2011, 29, 1066–1079. [Google Scholar] [CrossRef]
Al-Marhoun, M. PVT correlations for Middle East crude oils. Journal of Petroleum Technology 1988, 40, 650–666. [Google Scholar] [CrossRef]
Al-Marhoun, M. New correlations for formation volume factors of oil and gas mixtures. Journal of Canadian Petroleum Technology 1992, 31. [Google Scholar] [CrossRef]
Ahmed, T.H. Reservoir engineering handbook, 4th ed.; Gulf Professional Publishing: Oxford, UK, 2010; ISBN 978-1-85617-803-7. [Google Scholar]
Farasat, A.; Shokrollahi, A.; Arabloo, M.; Gharagheizi, F.; Mohammadi, A.H. Toward an intelligent approach for determination of saturation pressure of crude oil. Fuel Processing Technology 2013, 115, 201–214. [Google Scholar] [CrossRef]
El-Sebakhy, E.A.; Sheltami, T.; Al-Bokhitan, S.Y.; Shaaban, Y.; Raharja, P.D.; Khaeruzzaman, Y. Support vector machines framework for predicting the PVT properties of crude-oil systems. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, SPE-105698-MS. Manama, Bahrain, 11-14 March 2007. [Google Scholar]
Akbari, M.K.; Farahani, F.J, Abdy, Y. Dewpoint Pressure Estimation of Gas Condensate Reservoirs, Using Artificial Neural Network (ANN). In Proceedings of the EUROPEC/EAGE Conference and Exhibition, SPE-107032-MS. London, UK, 11-14 June 2007.
Nowroozi, S.; Ranjbar, M.; Hashemipour, H.; Schaffie, M. Development of a neural fuzzy system for advanced prediction of dew point pressure in gas condensate reservoirs. Fuel Processing Technology 2009, 90, 452–457. [Google Scholar] [CrossRef]
Kaydani, H.; Hagizadeh, A.; Mohebbi, A. A Dew Point Pressure Model for Gas Condensate Reservoirs Based on an Artificial Neural Network. Petroleum Science and Technology 2013, 31. [Google Scholar] [CrossRef]
González, A.; Barrufet, M.A.; Startzman, R. Improved neural-network model predicts dewpoint pressure of retrograde gases. J Pet Sci Eng 2003, 37, 183–194. [Google Scholar] [CrossRef]
Majidi, S.M.; Shokrollahi, A.; Arabloo, M.; Mahdikhani-Soleymanloo, R.; Masihi, M. Evolving an accurate model based on machine learning approach for prediction of dew-point pressure in gas condensate reservoirs. Chemical Engineering Research and Design 2014, 92, 891–902. [Google Scholar] [CrossRef]
Rabiei, A.; Sayyad, H.; Riazi, M.; Hashemi, A. Determination of dew point pressure in gas condensate reservoirs based on a hybrid neural genetic algorithm. Fluid Phase Equilibria 2015, 387, 38–49. [Google Scholar] [CrossRef]
Ahmadi, M.A.; Ebadi, M.; Yazdanpanah, A. Robust intelligent tool for estimating dew point pressure in retrograded condensate gas reservoirs: Application of particle swarm optimization. Journal of Petroleum Science and Engineering 2014, 123, 7–19. [Google Scholar] [CrossRef]
Ahmadi, M.A.; Ebadi, M. Evolving smart approach for determination dew point pressure through condensate gas reservoirs. Fuel 2014, 117, 1074–1084. [Google Scholar] [CrossRef]
Arabloo, M.; Shokrollahi, A.; Gharagheizi, F.; Mohammadi, A.H. Toward a predictive model for estimating dew point pressure in gas condensate systems. Fuel Processing Technology 2013, 116, 317–324. [Google Scholar] [CrossRef]
Ikpeka, P.; Ugwu, J.; Russell, P.; Pillai, G. Performance evaluation of machine learning algorithms in predicting dew point pressure of gas condensate reservoirs. SN Applied Sciences 2020, 2, 2124. [Google Scholar] [CrossRef]
Zhong, Z.; Liu, S.; Kazemi, M.; Carr, T.R. Dew point pressure prediction based on mixed-kernels-function support vector machine in gas-condensate reservoir. Fuel 2018, 232, 600–609. [Google Scholar] [CrossRef]
Alolayan, O.S.; Alomar, A.O.; Williams, J.R. Parallel Automatic History Matching Algorithm Using Reinforcement Learning. Energies 2023, 16(2), 860. [Google Scholar] [CrossRef]
Bishop, C.M. Neural Networks for Pattern Recognition. Oxford University Press, USA. ISBN-10: 9780198538646.
Aggarwal, C.C. Neural Networks and Deep Learning: A Textbook. Springer: Cham, Switzerland, 2018. ISBN 978-3-319-94463-0.
Costa, L.A.N.; Maschio, C.; Schiozer, D.J. Study of te influence of training data set in artificial neural network applied to the history matching process. In Proceedings of the Rio Oil & Gas Expo and Conference, January 2010. [Google Scholar]
Zangl, G.; Giovannoli, M.; Stundner, M. Application of Artificial intelligence in gas storage management. In Proceedings of the SPE Europec/EAGE Annual Conference and Exhibition, SPE-100133-MS. Vienna, Austria, 12-15 June 2006. [Google Scholar]
Rodriguez, A.A.; Klie, H.; Wheeler, M.F.; Banchs, R.E. Assessing multiple resolution scales in history matching with metamodels. In Proceedings of the SPE Reservoir Simulation Symposium, SPE-105824-MS. Houston, TX, USA, 26-28 February 2007. [Google Scholar]
Esmaili, S.; Mohaghegh, S.D. Full field reservoir modeling of shale assets using advanced data-driven analytics. 2016.
Silva, P.C.; Maschio, C.; Schiozer, D.J. Applications of the soft computing in the automated history matching. In Proceedings of the Petroleum Society’s 7th Canadian International Petroleum Conference (57th Annual Technical Meeting), Calgary, Alberta, Canada, 13-15 June 2006. [Google Scholar]
Silva, P.C.; Maschio, C.; Schiozer, D.J. Application of neural network and global optimization in history matching. J Can Pet Technol 2008, 47, 11. [Google Scholar] [CrossRef]
Silva, P.C.; Maschio, C.; Schiozer, D.J. Use of Neuro-Simulation techniques as proxies to reservoir simulator: Application in production history matching. Journal of Petroleum Science and Engineering 2007, 57, 273–280. [Google Scholar] [CrossRef]
Gottfried, B.S.; Weisman, J. Introduction to Optimization Theory, 1st ed; Prentice Hall, Englewood Cliffs, NJ, 1973; ISBN-10: 0134914724.
Shahkarami, A.; Mohaghegh, S. D.; Gholami, V.; Haghighat, S. A. Artificial Intelligence (AI) Assisted History Matching. In Proceedings of the SPE Western North American and Rocky Mountain Joint Meeting, 17-18 April 2014, SPE-169507-MS.
Sampaio, T.P.; Ferreira Filho, V.J.M.; de Sa Neto, A. An Application of Feed Forward Neural Network as Nonlinear Proxies for the Use During the History Matching Phase. In Proceedings of the Latin American and Caribbean Petroleum Engineering Conference, SPE-122148-MS. Cartagena de Indias, Colombia, 30-31 May 2009. [Google Scholar]
Cullick, A.S. Improved and more-rapid history matching with a nonlinear proxy and global optimization. In Proceedings of the SPE Annual Technical Conference and Exhibition, SPE-101933-MS. San Antonio, Texas, USA, 24-27 September 2006. [Google Scholar]
Lechner, J.P.; Zangl, G. Treating Uncertainties in Reservoir Performance Prediction with Neural Networks. In Proceedings of the SPE Europec/EAGE Annual Conference, SPE-94357-MS. Madrid, Spain, 13-16 June 2005. [Google Scholar]
Reis, L.C. Risk analysis with history matching using experimental design or artificial neural networks. In Proceedings of the SPE Europec/EAGE Annual Conference and Exhibition, SPE-100255-MS. Vienna, Austria, 12-15 June 2006. [Google Scholar]
Mohmad, N.I.; Mandal, D.; Amat, H.; Sabzabadi, A.; Masoudi, R. History Matching of Production Performance for Highly Faulted, Multi Layered, Clastic Oil Reservoirs using Artificial Intelligence and Data Analytics: A Novel Approach. In Proceddings of the SPE Asia Pacific Oil & Gas Conference and Exhibition, Virtual, 17-19 November 2020, SPE-202460-MS.
Ramgulam, A.; Ertekin, T.; Flemings, P.B. Utilization of Artificial Neural Networks in the Optimization of History Matching. In Proceedings of the Latin American & Caribbean Petroleum Engineering Conference, SPE-107468-MS. Buenos Aires, Argentina, 15-18 April 2007. [Google Scholar]
Christie, M.; Demyanov, V.; Erbas, D. Uncertainty quantification for porous media flows. Journal of Computational Physics 2006, 217, 143–158. [Google Scholar] [CrossRef]
Maschio, C.; Schiozer, D.J. Bayesian history matching using artificial neural network and Markov Chain Monte Carlo. Journal of Petroleum Science and Engineering 2014, 123, 62–71. [Google Scholar] [CrossRef]
Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
Chai, Z. , Yan, B., Killough, J.E; Wang, Y. An efficient method for fractured shale reservoir history matching: The embedded discrete fracture multi-continuum approach. Journal of Petroleum Science and Engineering 2018, 160, 170–181. [Google Scholar] [CrossRef]
Eltahan, E.; Ganjdanesh, R.; Yu, W.; Sepehrnoori, K.; Drozd, H.; Ambrose, R. Assisted history matching using Bayesian inference: Application to multi-well simulation of a huff-n-puff pilot test in the Permian Basin. In Proceddings of the Unconventional Resources Technology Conference, Austin, Texas, USA, 20-22 July 2020.
Shams, M.; El-Banbi, A.; Sayyouh, H. A Comparative Study of Proxy Modeling Techniques in Assisted History Matching. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, April 2017. [Google Scholar]
Brantson, E.T; Ju, B.; Omisore, B.O.; Wu, D.; Selase, A.E.; Liu, N. Development of machine learning predictive models for history matching tight gas carbonate reservoir production profiles. J. Geophys. Eng 2018, 15, 2235–2251. [Google Scholar] [CrossRef]
Gao, C.C.; Gao, H.H. Evaluating early-time Eagle Ford well performance using Multivariate Adaptive Regression Splines (MARS). In Proceedings of the SPE Annual Technical Conference and Exhibition, SPE-166462-MS. New Orleans, Louisiana, USA, 30 September-2 October 2013. [Google Scholar]
Friedman, J.H. Stochastic gradient boosting Comput. Stat. Data Anal. 2002, 38, 367–78. [Google Scholar] [CrossRef]
Bauer, M. General regression neural network—a neural network for technical use. Master’s Thesis, University of Wisconsin, Madison, USA, 1995. [Google Scholar]
Al-Thuwaini, J.S.; Zangl, G.; Phelps, R. Innovative Approach to Assist History Matching Using Artificial Intelligence. In Proceedings of the Intelligent Energy Conference and Exhibition, SPE-99882-MS. Amsterdam, The Netherlands, 11-13 April 2006. [Google Scholar]
Simplilearn, AL and machine learning. What are self-organizing maps. Beginner’s guide to Kohonen map. Available online: https://www.simplilearn.com/self-organizing-kohonen-maps-article (accessed on 10 March 2023).
Dharavath, A. Bisection Method. Available online: https://protonstalk.com/polynomials/bisection-method/ (accessed on 10 March 2023).
Guo, Z.; Chen, C.; Gao, G.; Vink, J. Applying Support Vector Regression to Reduce the Effect of Numerical Noise and Enhance the Performance of History Matching. In Proceeding of the SPE Annual Technical Conference and Exhibition, SPE-187430-MS. San Antonio, Texas, USA, 9-11 October 2017. [Google Scholar]
Rui Liu; Siddharth Misra. Machine Learning Assisted Recovery of Subsurface Energy: A Review. Authorea 2021.
Ma, X.; Zhang, K.; Zhao, H.; Zhang, L.; Wang, J.; Zhang, H.; Liu, P.; Yan, X.; Yang, Y. A vector-to-sequence based multilayer recurrent network surrogate model for history matching of large-scale reservoir. Journal of Petroleum Science and Engineering 2022, 214, 110548. [Google Scholar] [CrossRef]
Ma, X.; Zhang, K.; Zhang, J.; Wang, Y.; Zhang, L.; Liu, P.; Yang, Y.; Wang, J. A novel hybrid recurrent convolutional network for surrogate modeling of history matching and uncertainty quantification. Journal of Petroleum Science and Engineering 2022, 210, 110109. [Google Scholar] [CrossRef]
MathWorks, Convolutional neural network. What Is a Convolutional Neural Network? Available online: https://www.mathworks.com/discovery/convolutional-neural-network-matlab.html (accessed on 22 March 2023).
Brownlee, J. A Gentle Introduction to Generative Adversarial Networks (GANs). Available online: https://machinelearningmastery.com/what-are-generative-adversarial-networks-gans/ (accessed on 22 March 2023).
Ma, X.; Zhang, K.; Wang, J.; Yao, C.; Yang, Y.; Sun, H.; Yao, J. An Efficient Spatial-Temporal Convolution Recurrent Neural Network Surrogate Model for History Matching. SPE J. 2022, 27, 1160–1175. [Google Scholar] [CrossRef]
Evensen, G.; Raanes, P.N.; Stordal, A.S.; Hove, J. Efficient Implementation of an Iterative Ensemble Smoother for Data Assimilation and Reservoir History Matching. Frontiers in Applied Mathematics and Statistics 2019, 5. [Google Scholar] [CrossRef]
Honorio, J.; Chen, C.; Gao, G; Du, K.; Jaakkola, T. Integration of PCA with a Novel Machine Learning Method for Reparameterization and Assisted History Matching Geologically Complex Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, SPE-175038-MS. Houston, TX, USA, 28-30 September 2015.
Alguliyev, R.; Aliguliyev, R.; Imamverdiyev, Y.; Sukhostat, L. History matching of petroleum reservoirs using deep neural networks. Intelligent Systems with Applications 2022, 16, 200128. [Google Scholar] [CrossRef]
Kana, M. Variational Autoencoders (VAEs) for dummies — Step by step tutorial. Available online: https://towardsdatascience.com/variational-autoencoders-vaes-for-dummies-step-by-step-tutorial-69e6d1c9d8e9v (accessed on 2 April 2023).
Canchumuni, S.A.; Emerick, A.A.; Pacheco, M.A. Integration of Ensemble Data Assimilation and Deep Learning for History Matching Facies Models. In Proceedings of the OTC Brazil, OTC-28015-MS. Rio de Janeiro, Brazil, 24-26 October 2017. [Google Scholar]
Jo, S.; Jeong, H.; Min, B.; Park, C.; Kim, Y.; Kwon, S.; Sun, A. Efficient deep-learning-based history matching for fluvial channel reservoirs. Journal of Petroleum Science and Engineering 2022, 208, 109247. [Google Scholar] [CrossRef]
Liu, Y.; Sun, W.; Durlofsky, L.J. A Deep-Learning-Based Geological Parameterization for History Matching Complex Models. Mathematical Geosciences 2019, 51, 725–766. [Google Scholar] [CrossRef]
Jo, H.; Pan, W.; Santos, J.E.; Jung, H.; Pyrcz, M.J. Machine learning assisted history matching for a deepwater lobe system. Journal of Petroleum Science and Engineering 2021, 207, 109086. [Google Scholar] [CrossRef]
Sutton, R.; Barto, A. Reinforcement Learning: An Introduction; 2nd ed; Bradford Books: Denver, CO, USA, 2018; ISBN 0262039249. [Google Scholar]
Li, H.; Misra, S. Reinforcement learning based automated history matching for improved hydrocarbon production forecast. Applied Energy 2021, 284, 116311. [Google Scholar] [CrossRef]

Figure 1. Reservoir model with millions of grid blocks.

Figure 2. Selection process for a machine learning technique.

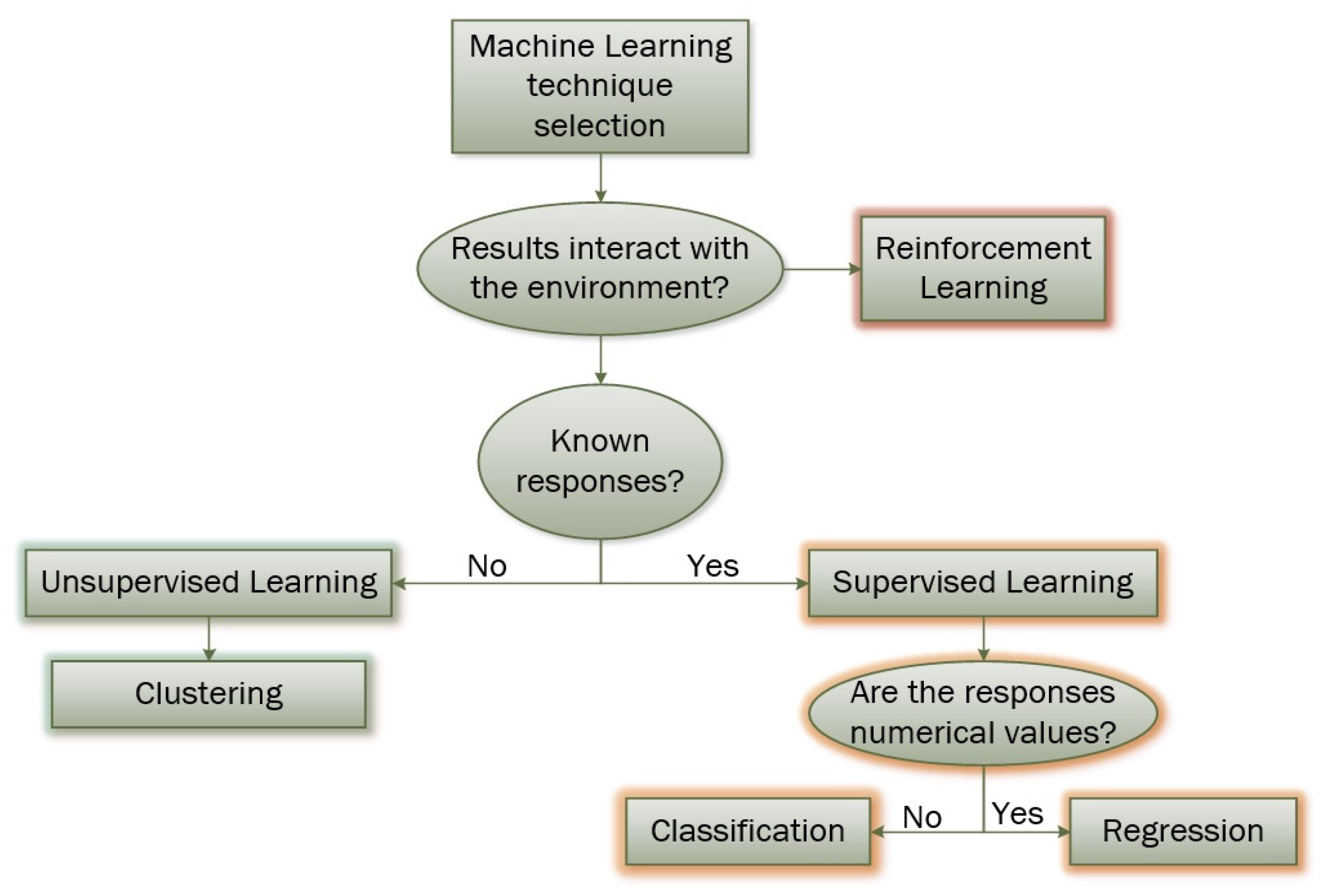
Figure 3. The process of machine learning approach for reservoir simulation applications.

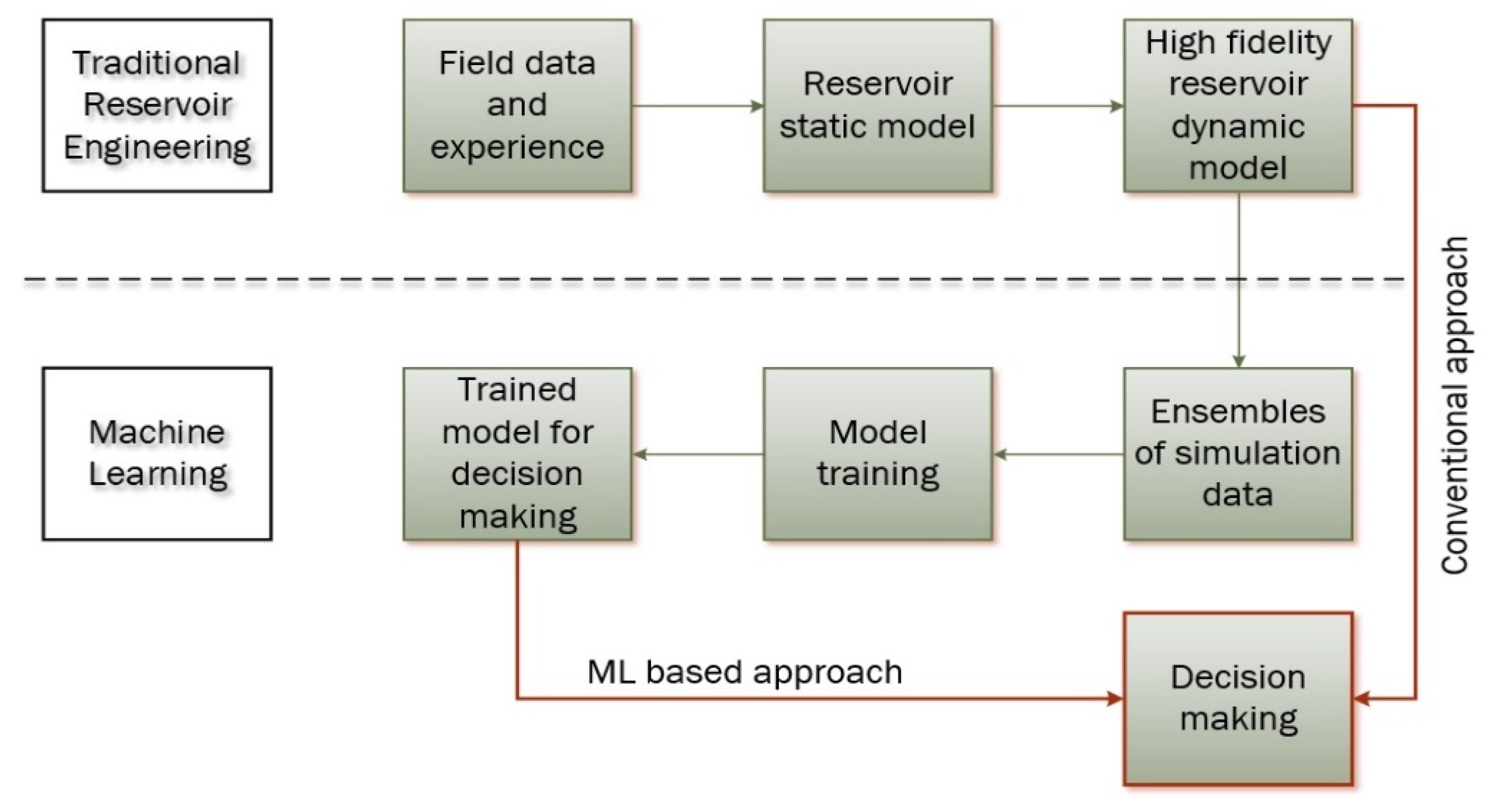
Figure 4. History matching procedure.

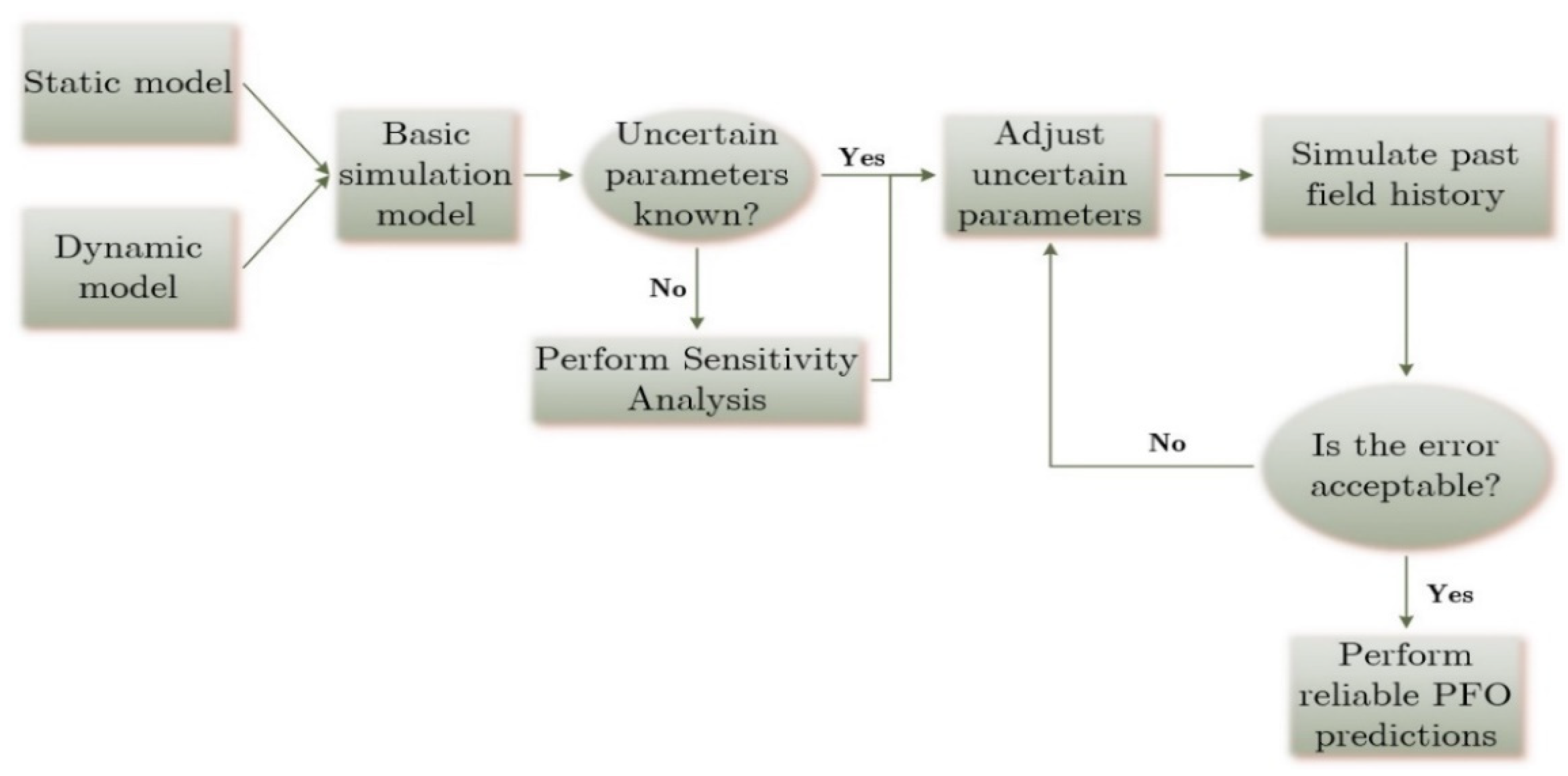
Figure 5. Direct and Indirect history matching.

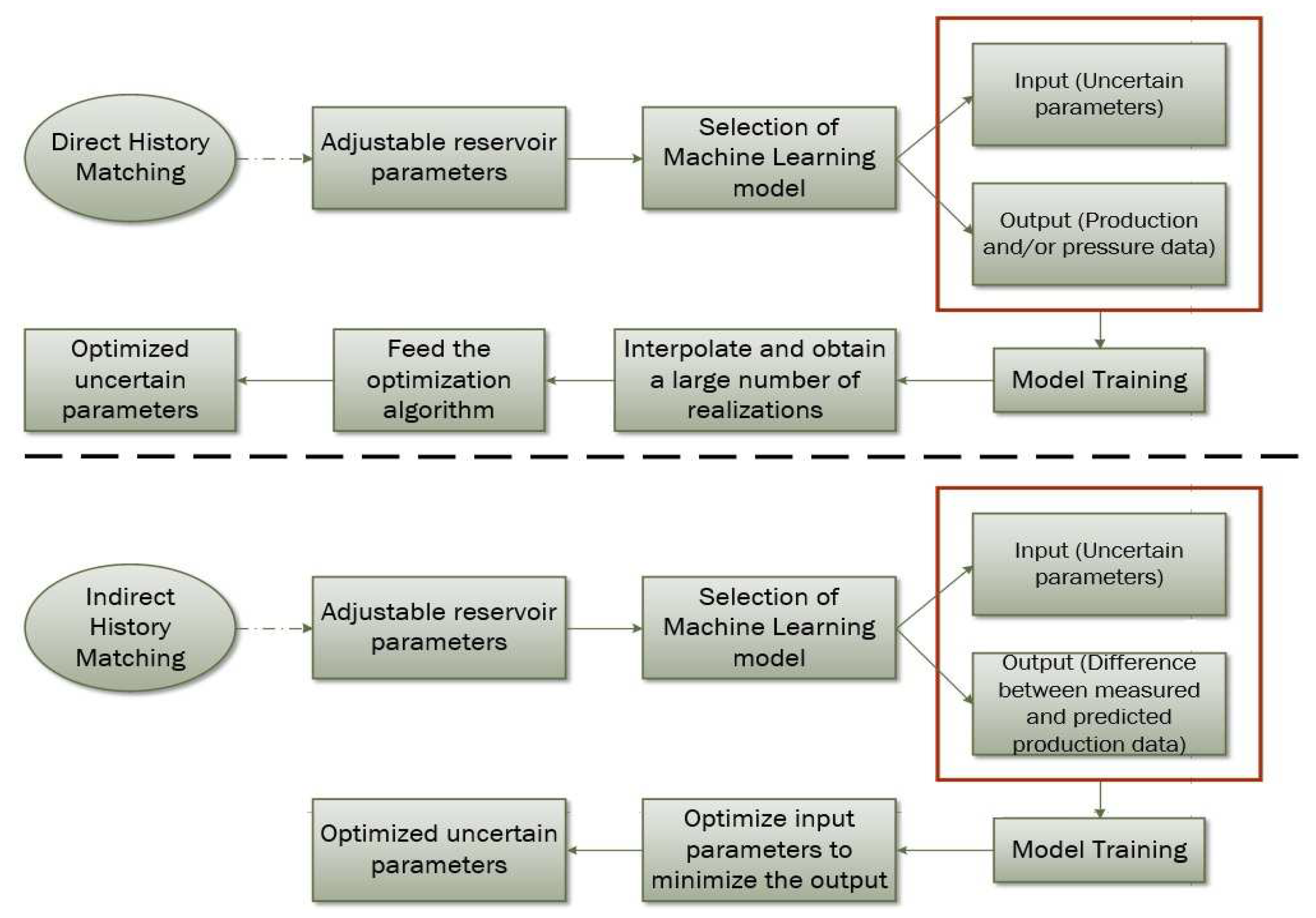
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Applications of Machine Learning in Subsurface Reservoir Simulation—A Review—Part I

Abstract

1. Introduction

1.2. Machine Learning in Reservoir Simulation

2. Machine Learning Strategies for Individual Simulation Runs

2.1. Machine Learning Methods for Surrogate Models

2.2. Machine Learning Methods for Handling the Stability and Phase Split Problems

2.3. Machine Learning Methods for Predicting Black Oil PVT Properties

3. Machine Learning Strategies for History Matching

3.1. Machine Learning Methods for Indirect History Matching

3.2. Machine Learning Methods for Direct History Matching

3.2.1. History Matching Based on ANN Models

3.2.2. History Matching Based on Bayesian ML Models

3.2.3. History Matching Based on ML Models other than ANNs

3.2.4. History Matching Based on Deep Learning Methods

3.2.5. History Matching ML Methods Using Dimensionality Reduction Techniques

3.2.6. History Matching Based on Reinforcement Learning Methods

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Appendix A

References

MDPI Initiatives

Important Links

Subscribe