Preprint
Article
Nearshore Observations and Modeling: Synergy for Coastal Flooding Prediction
Altmetrics
Downloads
164
Views
31
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.mp4 (27.04MB )
This version is not peer-reviewed
Submitted:
10 July 2023
Posted:
11 July 2023
You are already at the latest version
Alerts
Abstract
Coastal inundation is recently requiring a significant attention worldwide. The increasing frequency and intensity of extreme events (sea storms, tsunami waves) are highly stressing the coastal envi-ronments, e.g. endangering a large number of residential areas, ecosystems, tourist facilities, and also leading to potential environmental risks. Predicting such events and the generated coastal flooding is thus of paramount importance and can be reached by exploiting the potential of different tools, like remote sensors and numerical modeling. To this aim, a combination is possible between marine radars and wave-resolving propagation models. While instruments like X-band radars are able at precisely reconstructing both wave field and bathymetry within a coastal area that is some kilometers offshore, wave-resolving Boussinesq-type models can reproduce the wave propagation in the nearshore and the consequent coastal flooding. The present work illustrates the reconstruc-tion of coastal data (wave field and seabed depth) conducted using radar signals and a specifically suited data processing, named “Local Method”, and the use of such coastal data to run numerical simulations of wave propagation (using the FUNWAVE-TVD solver) aimed at reproducing coastal inundation over different scenarios. Such scenarios are built using two different European beaches, i.e. Senigallia (Italy) and Oostende (Belgium), and three different directional spreading values, to evaluate the performances in case of either long- or short-crested waves. The overall validation of the methodology, in terms of maximum inundation, shows good performances, especially in case of short-crested wind waves. Furthermore, the application on the Oostende beach demonstrates that the present methodology might work only using open-access tools, i.e. an easy investigation of the coastal inundation and a potential low-cost integration into early warning systems.
Keywords:
Subject: Engineering - Marine Engineering
1. Introduction
Coastal inundation is one of the most relevant threats for communities all over the world. Although usually triggered by extreme events, the flooding of coastal areas is related to a series of diverse forcing actions; not only severe water waves like those occurring during sea storms or induced by tropical cyclones, but also storm surge, tidal oscillations, and additional contributions associated with low-frequency waves (e.g., infragravity waves) [1]. Furthermore, global warming is very likely to lead to an increased frequency and intensity of extreme events, and is already inducing a non-negligible sea-level rise [2]. Although the objectives of Paris Agreement, focused on global climate mitigation policy, will be achieved in the near and far future, many of the world coasts would potentially experience extreme events of unprecedented intensity [3].
The above actions have thus the potential of combining each other, giving rise to a phenomenon known as “compound flooding”, which leads to an impact on the coastal region, and potentially on the nearby urban environment, that is larger than the sum of the impacts induced by the single events [4]. More relevant effects can be reached in estuarine coastal areas, where additional combination with river-induced forcings (e.g., flood peaks) is possible.
The flooding of coastal areas may ultimately lead to dramatic effects on both population, infrastructures, and structures [5,6], with potential drawbacks also related to seawater intrusion at both superficial (estuarine areas) and groundwater (coastal aquifers) levels [7].
Field observations are of paramount importance for safeguarding the coastal areas that are more prone to inundation phenomena. To this aim, remote sensors, like cameras or marine radars, are a common solution. These systems, indeed, represent a valid alternative to the in-situ systems (e.g., wave rider buoy), since they permit observing a site under test in a non-invasive way and can be also used during severe weather and sea conditions [8]. However, these remote sensors require a bit of practice, but the technology selected to conduct the experiment and the algorithms for the analysis of the collected data are nowadays robust and mature enough to guarantee a reliable characterization of the local coastal area, in terms of bathymetry, shoreline motion, location of submerged bars, etc. [9,10,11,12,13].
On the other hand, the use of suitable remote instrumentation is not always possible, due to either economic issues (installation and maintenance of the equipment might be costly) or topographic/geographic difficulties (lack of a suitable area to reach a sufficient height over the sea level), among others. In such contexts, a low-cost solution is the novel short range K-band marine radar, which is able at reconstructing the sea surface current and estimating direction of the dominant waves in very nearshore area [14].
In addition to the observations carried out using remote sensors, a straightforward method is required to evaluate the coastal inundation. Specifically, an approach is based on the modeling chain, which allows one to exploit both the skills of numerical models and the field observations. This allows one to save a significant amount of time and money, through a synergic approach. Recent examples related to the coastal region refers to the use of data gathered in open databases (e.g. Copernicus) or collected by remote sensors (e.g., X-band radar), which are then used as boundary or initial conditions for a numerical model, which operates over a relatively small domain (order of some km2) and aims at propagating the waves within a reduced nearshore region [15,16,17]. Simplified depth-averaged models, like those based on Boussinesq-type equations or Nonlinear Shallow Water Equations (NSWE hereafter), can be employed with the final purpose of obtaining reliable information on potential inundation, at a reduced computational cost [18,19,20,21].
Hence, use of X-band marine radars combined to the nearshore modeling of the wave propagation results in a cheap approach for the analysis of future coastal inundation, as the radar allows one to reconstruct both offshore bathymetry and estimate the characteristic sea state parameters (between some hundred meters and 3 km from the coast), while a shallow water model provides the wave propagation over and the consequent shoreline motion exploiting the offshore radar-derived data and available or reconstructed nearshore bathymetries [22,23].
The approach could potentially be integrated within early warning systems. As an example, if a large number of simulations is run using a parametric approach (e.g., varying the spectral wave characteristics), an alert matrix could be built and a “safe area” could be identified, which is related to the coastal inundation that can derive from the wave characteristics recorded offshore by the installed X-band radar.
The present work describes the potential of the synergic use of X-band radar and shallow-water modeling in the prediction of coastal inundation. Different wave characteristics are tested (significant height, peak period, main direction, spreading), and two different configurations are exploited. One is related to Senigallia coast (Marche Region, Italy), where bathymetric data are available thanks to recent bathymetric campaigns. The other configuration is Oostende (Belgium), chosen with the aim to test open-access databases and show the reliability of the presented approach in a very low-cost framework.
2. Materials and Methods
The main goal of the present work is to demonstrate and corroborate the combined use of numerical modeling and remote sensors, like X-band radars, to properly face the coastal inundation issue. To this purpose, we here use a methodology, sketched in Figure 1, that can be successfully applied in a real-world environment. The initial step (STEP 1) consists of recording the incoming wave field with the X-band radar as a specific data sequence. The wave field is here simulated through baseline numerical simulations, referred to as large-scale tests hereinafter. Afterwards, a specific algorithm is used to reconstruct the bathymetry and the wave field from the data sequence up to about (3-5) m depth, since the algorithm does not work properly in the nearshore zone (STEP 2). Such information is then used to produce boundary and initial conditions for the following inundation modeling (STEP 3). The final phase consists of smaller scale numerical modeling (small-scale tests) with bathymetry and wave input coming from the previous step, with the final purpose of evaluating the inundated coastal area (STEP 4). The final output is here validated using both baseline (large-scale) simulations and inundation (small-scale) simulations, to ensure the suitability of the proposed approach.
2.1. The methodology
The above-described methodology, based on a modeling-chain approach, have already been proposed in several works (e.g., [17,24,25,26]). Specifically, the specific use of an X-band algorithm combined to the numerical modeling of coastal inundation has been recently described [23], although it demonstrated the applicability of the methodology to the case of long-crested waves with negligible spreading traveling within a known environment. To complement the analysis conducted in [23], the present work will illustrate: a) the potential of the present approach to the case of wave spectra characterized by non-zero spreading; b) the applicability of the methodology to unknown environments, through use of open access datasets, i.e. only exploiting freely available data.
The numerical modeling has been conducted through use of FUNWAVE-TVD, a nearshore phase-resolving Boussinesq-type model, which exploits the Total Variation Diminishing approach [27]. It is suitable for the description of shallow-to-intermediate water flows, and is here applied for both baseline/large-scale (STEP 1) and inundation/small-scale (STEP 4) modeling (Figure 1).
The numerical water elevations coming from the baseline simulations have been used to produce X-band radar images, then used for the reconstruction of both bathymetry and wave characteristics (STEP 2, see [22,23] for the details). In particular, the X-band radar images have been obtained implementing a simulator, extensively described in [28,29], which takes into account the modulation effects (shadowing and tilt modulation) affecting the radar echoes, which depend on the generated sea model and radar antenna geometry.
Accordingly, the radar image is not a direct representation of the wave elevation profile, rather a distortion version of it. Therefore, in order to obtain the information about the sea state parameters as well as the bathymetry field, the radar data sequence is elaborated by means of a dedicated algorithm, named “Local method” and commonly adopted in coastal area [22,23,30]. This method involves a spatial partitioning of the radar images into partially overlapping sub-areas, since the hypothesis of the spatial homogeneity is not satisfied in scenarios under investigation [30,31,32]. Specifically, this task is treated as a linear inverse problem and it is based on the knowledge of the fundamental laws which rule the dynamics of the sea gravity waves, whose dispersive behavior obeys the linear dispersion relationship [23].
Therefore, the main steps of the inversion procedure applied to each sub area are summarized below:
- 3D Fast Fourier Transform (FFT) is employed to convert a sub-area of a radar image sequence from space-time to wavenumber-frequencies coordinates;
- estimation of the bathymetry value from the radar spectrum;
- a band-pass filter is applied to account for the dispersion relation describing the gravity sea waves;
- the Modulation Transfer Function (MTF) is applied to the radar spectrum, as it allows compensating the spectral distortion introduced by the modulation effects and passing from the radar spectrum to the sea spectrum.
Finally, from the reconstruction of bathymetry and wave characteristics, initial and boundary conditions have been extracted (STEP 3) for the inundation modeling.
2.2. The investigated sites
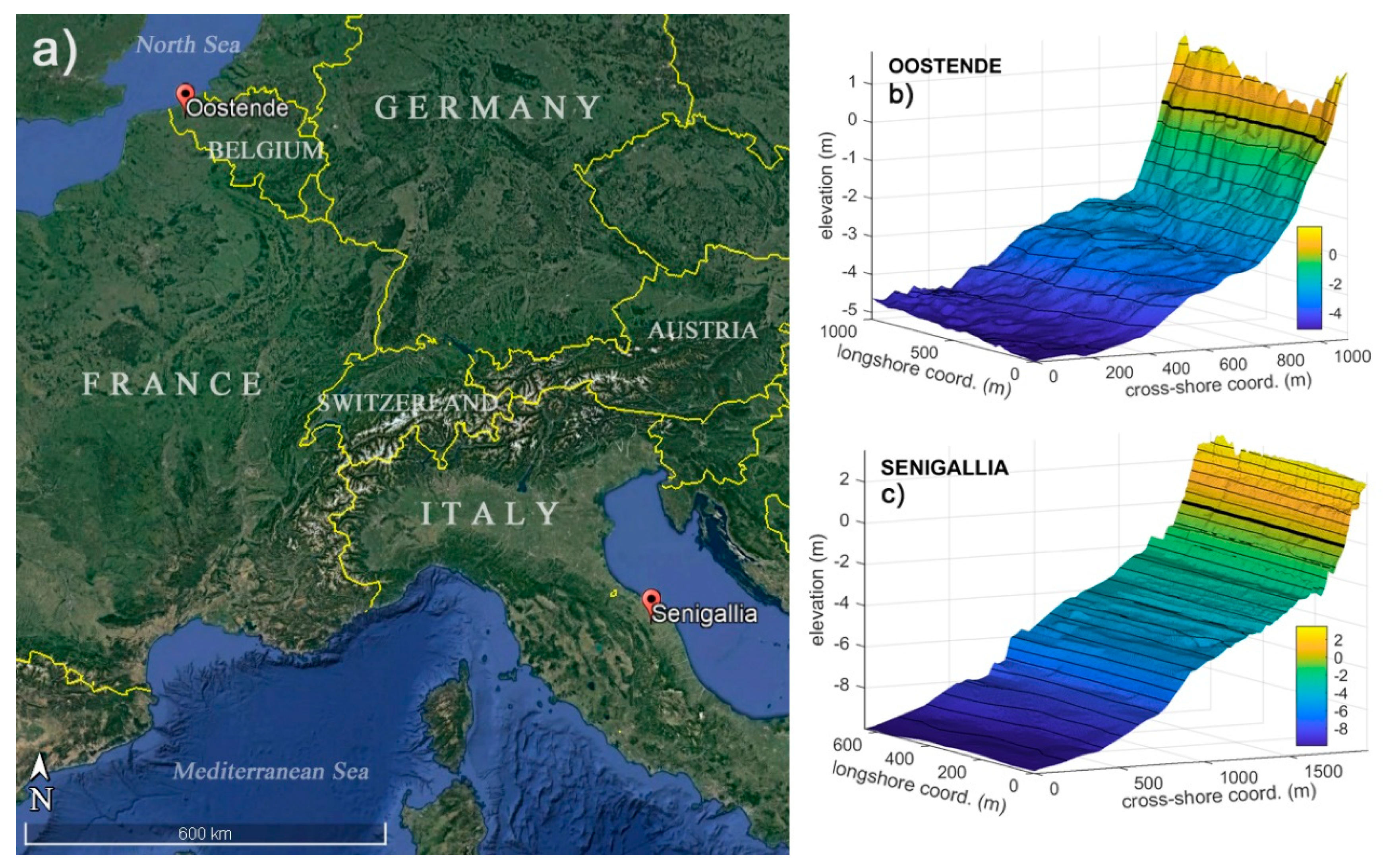
Two different geographical sites have been selected for the present study, each of them tested with different wave conditions. The first location is the South coast of Senigallia, a tourist town located along the Eastern Italian coast and characterized by the Misa River, a little water course flowing within the historical town and debouching into the Adriatic Sea. The choice has been motivated by the following reasons: the bathymetric data made available by the municipality of Senigallia, the existence of a monitoring system, continuously providing several hydrodynamic parameters, like offshore wave characteristics, and to the dataset collected during a field campaign conducted in January 2014 at the estuary of the Misa River [1,33,34].
The second location is Oostende, a coastal city located in the province of West Flanders in the Flemish Region of Belgium, typified by a sandy and overlooking the North Sea. Compared to Senigallia, Oostende is characterized by a completely different environment, in terms of wave climate, tidal forcing, and data availability. The data used for the numerical simulations have been extracted from open access services: Copernicus Marine Service (CMEMS)1 for wave characteristics, and the European Marine Observation and Data Network (EMODnet)2 for the bathymetry.
Figure 2.
a) Location of the two coastal sites (adapted from Google Earth). b-c) Bathymetries for the two sites. Contours at 0.5 m intervals are traced with thin black lines. The 0 m contour is given with a thick black line. A different vertical scale is used.
Figure 2.
a) Location of the two coastal sites (adapted from Google Earth). b-c) Bathymetries for the two sites. Contours at 0.5 m intervals are traced with thin black lines. The 0 m contour is given with a thick black line. A different vertical scale is used.
2.3. Tested conditions
To better understand the performance of the methodology at the chosen locations, one wave condition has been used at each location for the baseline/large-scale simulations, i.e. a single triplet (hoff, Hs, Tp), where hoff is the offshore depth in still water condition, Hs is the significant wave height and Tp the peak period of a JONSWAP spectrum, defined as an input spectral condition in FUNWAVE-TVD [27]. In addition, three different directional spreading parameters have been used at each location (e.g., see [35]). All tested conditions have been characterized by a main wave direction perpendicular to the shore. Table 1 summarizes all the main input characteristics at the offshore boundary used for the baseline simulations.
Using the numerical results found from the baseline simulations, the “Local method” is applied to reconstruct both wave climate and bathymetry from the original boundary depth up to depths h > 3 m. Reconstruction at shallower depths has been discarded due to the unsuitability of radar-driven methods in correspondence of significantly shallow depths (i.e. h < 3 m). The reconstructed wave parameters have been consequently used for the small-scale inundation modeling (see Section 2.1), with wave generation at depths of about h = 5 m for Senigallia and h = 3.5 m for Oostende.
3. Results
3.1. Baseline (large scale) modeling
The different configurations described in Table 1 have been tested as baseline conditions and employed in large-scale simulations. The purpose of this modeling was twofold: (a) to obtain a first baseline estimate of coastal inundation from a large-scale approach, and (b) to extract a bundle of 200 snapshots of the propagating wave field at an interval of 1 s, to be later provided as input for the reconstruction method (see Subsection 3.2). Examples of wave fields modelled over the Senigallia bathymetry in the baseline simulations, for two different wave spreading parameters, are provided in Figure 3.
3.2. Local method reconstruction
This section presents the results obtained from the elaboration of the radar data sequence by means of the “Local method” (see Section 2.1). The numerical baseline data have been used for the reconstruction of both bathymetry and wave characteristics. Specifically, each considered dataset consists of 200 individual (synthetic) snapshots of wave surface, simulating the same number of radar images, with a time interval (see Section 3.1) and the extent of the pixel in the Cartesian grid is equal to 2 m. It is worth noting that the radar images were simulated by considering the antenna located at and , with an elevation .
Figure 4 shows an example of both synthetic sea-wave image obtained by means of the FUNWAVE-TVD (left panel) and amplitude of the corresponding radar image (right panel) at the same time instant (t = 100 s) for the Oostende case with a directional spreading .
In order to estimate the local sea-state parameters and bathymetry, the “Local method” is applied to each radar data sequence. In particular, a sub-area size equal to (250 × 250) m2 is adopted for all considered radar sequences.
.
Firstly, the local procedure provided the bathymetry reconstructions, here shown using a pixel spacing of 10 m for all of the considered wave types. The reliability of the bathymetric reconstruction using the above-mentioned strategy has been widely demonstrated [22,31], thus the statistics analysis obtained from the comparison with the ground-truth is reported in Table 2 for all wave types, in terms of Root Mean Square Error (RMSE) and correlation coefficient square (R2).
To estimate the wave characteristics from the radar data, compensation of the modulation effect introduced by the radar imaging is required. Specifically, after application of the band pass filter, the MTF is applied to the filtered radar spectrum to obtain the desired sea wave spectrum at each sub-area. For more details, the reader can refer to the article in [21].
An example of reconstructed bathymetry and spatial map of the reconstructed significant wave height for the Oostende case with a directional spreading are reported in Figure 5 and Figure 6, respectively. Results of comparable accuracy are obtained with the other tested configurations. The mean values of some wave parameters (significant height Hs, peak period Tp, peak length Lp, main direction ) at different bathymetric lines and referring to all of the considered spreading values, are reported in Table 3.
3.3. Setup of inundation (small scale) simulations and comparison with large-scale modeling
The data reconstructed using the “Local method” (Table 3) have been used for the initialization of FUNWAVE-TVD for small-scale inundation modeling.
The boundary conditions for the small-scale simulations have been generated starting from the wave characteristics Hs, Tp and reconstructed at h = 5 m and 3.5 m for Senigallia and Oostende, respectively, and have been applied as JONSWAP spectral waves at the same depths. The bathymetries used to simulate the small-scale inundation are, however, the same as for the large-scale baseline simulations, with an increased spatial resolution of .
The envelope of the shoreline oscillations obtained during the coastal inundation modeling (at small scale) is then compared to the envelope obtained from the baseline simulations (at large scale). Figure 8 compares small-scale and large-scale envelopes for the two investigated sites, as a function of the wave spreading. A quantitative comparison of small-scale and large-scale inundation coordinates is also given in Figure 9 along with some error statistics. It can be observed that the small-scale modeling (input depth of 3.5 to 5 m) yields slightly smaller inundation levels than the corresponding large-scale modeling at all wave spreading levels. The largest differences are observed with a directionally narrow wave state (), with discrepancies as large as 20-25 m for Senigallia (yellow lines in Figure 8a) and 10-15 m for Oostende (yellow lines in Figure 8b). On the other hand, waves with a larger spreading () yield much more comparable inundations.
The goodness-of-fit between large- and small-scale inundations can be also inferred from Figure 9. Although with some biases, especially in Senigallia for which inter-scale differences are the highest, small- and large-scale simulated inundations are always in good correspondence, as indicated by consistently high values of the coefficient of correlation P (0.94 to 1). This suggests that FUNWAVE-TVD, in the context of the approach here presented, can be applied to recreate wave dynamics at different scales quite reasonably, although not in absolute value. A better performance at Oostende is also highlighted by a smaller RMSE, which does not exceed 8 m.
4. Discussion and conclusions
The present work illustrates the application of field observations and numerical modeling for the investigation of the wave-driven flooding in coastal areas. The illustrated methodology, already tested in previous studies running a NSWE solver over a simplified bathymetry and using zero-spreading/long-crested waves [22,23], is here tested running a Boussinesq-type, open-source solver over two different bathymetries and using non-zero-spreading/short crested waves. This allowed us to inspect the performance of the method in modeling more realistic scenarios.
The application of the methodology to such new scenarios shows that fairly good results are obtained when the maximum flooding obtained through baseline (large-scale) simulations are compared to the maximum flooding of (small-scale) inundation simulations. In particular, in case of short-crested wind waves, i.e. characterized by a relatively high spreading (), the comparison is extremely good, while long-crested waves (especially with small spreading ) provide worse comparisons, the inundation simulations underestimating the wave runup and the flooded beach.
Such discrepancy may be due to the different momentum or radiation stress that characterizes long-crested and short-crested waves. Specifically, the larger is the wave spreading (i.e. the shorter is the wave crest), the smaller is the radiation stress evaluated along the main wave propagation direction in deep waters [36]. This means that long-crested waves ( in our case) are characterized by a higher radiation stress, which means that the waves are characterized by a significant momentum in the large-scale simulations, which is not taken into account in the small-scale, being the boundary condition simply assigned in terms of water surface elevation. Such issue is more evident where the boundary depth is larger, i.e. in the case of Senigallia where h = 5 m.
On the other hand, the use of an open-access approach, in terms of numerical solver (FUNWAVE-TVD), wave field (Copernicus Marine Service) and bathymetry (EMODnet) ensures a suitable application of the methodology to all the analyzed configurations, with good values of all statistical parameters used to evaluate goodness of the maximum inundation prediction, i.e. RMSE not exceeding 8 m and determination coefficient larger than 0.84.
A suitable application should be thus based on: i) a preliminary and thorough calibration of the used tools (radar-driven reconstructions and numerical model); ii) a precautionary application of the boundary conditions, adopting a zero- or almost-zero-spreading (independently of the actual length of the wave crests), in order to get larger/precautionary inundation values; iii) an offshore boundary of the numerical domain located at a relatively small depth, to avoid inaccuracies of the model predictions due to the neglect of the wave momentum.
In conclusion, the present methodology could be thus applied to coastal communities with the aim to properly predict the maximum inundation induced by wind and swell waves, either in case of data availability from the local authorities (as in the case of Senigallia) or when data are missing but can be retrieved for free through reliable web services (case of Oostende). Furthermore, such methodology, especially in view of the scenarios analyzed in the present work, might be potentially implemented into warning systems aimed at alerting the coastal communities about potential coastal flooding (e.g., [26]).
Further analyses are however required to better inspect the role of more complex environments, characterized by, e.g., nearby estuaries, particular morphologies like embayments or gulfs.
Supplementary Materials
The supplementary video shows the wave propagation in the small-scale simulation of Senigallia with wave spreading .
Author Contributions
Conceptualization, Matteo Postacchini and Giovanni Ludeno; Data curation, Lorenzo Melito and Giovanni Ludeno; Investigation, Lorenzo Melito and Giovanni Ludeno; Methodology, Matteo Postacchini and Giovanni Ludeno; Supervision, Matteo Postacchini; Validation, Lorenzo Melito; Visualization, Lorenzo Melito and Giovanni Ludeno; Writing – original draft, Matteo Postacchini, Lorenzo Melito and Giovanni Ludeno; Writing – review & editing, Matteo Postacchini, Lorenzo Melito and Giovanni Ludeno.
Funding
This research was partially funded by European Commission under the project SMART4ENV (Grant Number 101079251). The financial support from the PRIN 2017 program, funded by the Italian Ministry of Education, Universities and Research (Grant Number 20172B7MY9) is also acknowledged.
Data Availability Statement
In this section, please provide details regarding where data supporting reported results can be found, including links to publicly archived datasets analyzed or generated during the study. Please refer to suggested Data Availability Statements in section “MDPI Research Data Policies” at https://www.mdpi.com/ethics. If the study did not report any data, you might add “Not applicable” here.
Acknowledgments
The authors would like to thank the municipality of Senigallia for sharing the bathymetric survey.
Conflicts of Interest
The authors declare no conflict of interest.
References
- L. Melito, M. Postacchini, A. Sheremet, J. Calantoni, G. Zitti, G. Darvini, P. Penna, M. Brocchini, Hydrodynamics at a microtidal inlet: Analysis of propagation of the main wave components, Estuar. Coast. Shelf Sci. 235 (2020). [CrossRef]
- Intergovernmental Panel on Climate Change., IPCC’s Sixth Assessment Report, 2021.
- C. Tebaldi, R. Ranasinghe, M. Vousdoukas, D.J. Rasmussen, B. Vega-Westhoff, E. Kirezci, R.E. Kopp, R. Sriver, L. Mentaschi, Extreme sea levels at different global warming levels, Nat. Clim. Chang. 11 (2021). [CrossRef]
- M.I. Vousdoukas, L. Mentaschi, J. Hinkel, P.J. Ward, I. Mongelli, J.C. Ciscar, L. Feyen, Economic motivation for raising coastal flood defenses in Europe, Nat. Commun. 11 (2020). [CrossRef]
- H.D. Niemeyer, C. Berkenbrink, A. Ritzmann, H. Knaack, A. Wurpts, R. Kaiser, Evaluation of coastal protection strategies in respect of climate change impacts, in: Kuste, 2014.
- A.I. Olbert, J. Comer, S. Nash, M. Hartnett, High-resolution multi-scale modelling of coastal flooding due to tides, storm surges and rivers inflows. A Cork City example, Coast. Eng. 121 (2017). [CrossRef]
- M. Mastrocicco, G. Busico, N. Colombani, M. Vigliotti, D. Ruberti, Modelling actual and future seawater intrusion in the variconi coastal wetland (Italy) due to climate and landscape changes, Water (Switzerland). 11 (2019). [CrossRef]
- S.P. Neill, M.R. Hashemi, In Situ and Remote Methods for Resource Characterization, in: Fundam. Ocean Renew. Energy, 2018. [CrossRef]
- R. Archetti, Quantifying the evolution of a beach protected by low crested structures using video monitoring, J. Coast. Res. 25 (2009). [CrossRef]
- J. Rutten, S.M. De Jong, G. Ruessink, Accuracy of Nearshore Bathymetry Inverted from X-Band Radar and Optical Video Data, IEEE Trans. Geosci. Remote Sens. 55 (2017). [CrossRef]
- L. Parlagreco, L. Melito, S. Devoti, E. Perugini, L. Soldini, G. Zitti, M. Brocchini, Monitoring for coastal resilience: Preliminary data from five italian sandy beaches, Sensors (Switzerland). (2019). [CrossRef]
- W. Huang, X. Liu, E.W. Gill, Ocean wind and wave measurements using X-band marine radar: A comprehensive review, Remote Sens. 9 (2017). [CrossRef]
- Serafino, F. Bergamasco, G. Ludeno, F. Ardhuin, P. Sutherland, M. Sclavo, F. Barbariol, Stereo imaging and X-band radar wave data fusion: An assessment, Ocean Eng. 152 (2018). [CrossRef]
- G. Ludeno, I. Catapano, F. Soldovieri, G. Gennarelli, Retrieval of Sea Surface Currents and Directional Wave Spectra by 24 GHz FMCW MIMO Radar, IEEE Trans. Geosci. Remote Sens. 61 (2023). [CrossRef]
- E. Casella, A. Rovere, A. Pedroncini, L. Mucerino, M. Casella, L.A. Cusati, M. Vacchi, M. Ferrari, M. Firpo, Study of wave runup using numerical models and low-altitude aerial photogrammetry: A tool for coastal management, Estuar. Coast. Shelf Sci. 149 (2014). [CrossRef]
- E. Armenio, F. De Serio, M. Mossa, A.F. Petrillo, Coastline evolution based on statistical analysis and modeling, Nat. Hazards Earth Syst. Sci. 19 (2019). [CrossRef]
- M. Postacchini, F. Lalli, F. Memmola, A. Bruschi, D. Bellafiore, I. Lisi, G. Zitti, M. Brocchini, A model chain approach for coastal inundation: Application to the bay of Alghero, Estuar. Coast. Shelf Sci. 219 (2019). [CrossRef]
- C. Favaretto, L. Martinelli, P. Ruol, Coastal flooding hazard due to overflow using a level II method: Application to the Venetian littoral, Water (Switzerland). 11 (2019). [CrossRef]
- C. Lo Re, G. Manno, G. Ciraolo, Tsunami propagation and flooding in Sicilian Coastal areas by means of a weakly dispersive boussinesq model, Water (Switzerland). 12 (2020). [CrossRef]
- R. Briganti, A. Torres-Freyermuth, T.E. Baldock, M. Brocchini, N. Dodd, T.-J. Hsu, Z. Jiang, Y. Kim, J.C. Pintado-Patiño, M. Postacchini, Advances in numerical modelling of swash zone dynamics, Coast. Eng. 115 (2016). [CrossRef]
- A.R. Grilli, G. Westcott, S.T. Grilli, M.L. Spaulding, F. Shi, J.T. Kirby, Assessing coastal hazard from extreme storms with a phase resolving wave model: Case study of Narragansett, RI, USA, Coast. Eng. 160 (2020). [CrossRef]
- G. Ludeno, M. Postacchini, A. Natale, M. Brocchini, C. Lugni, F. Soldovieri, F. Serafino, Normalized Scalar Product Approach for Nearshore Bathymetric Estimation from X-Band Radar Images: An Assessment Based on Simulated and Measured Data, IEEE J. Ocean. Eng. 43 (2018). [CrossRef]
- M. Postacchini, G. Ludeno, Combining numerical simulations and normalized scalar product strategy: A new tool for predicting beach inundation, J. Mar. Sci. Eng. 7 (2019). [CrossRef]
- D. Bellafiore, L. Zaggia, R. Broglia, C. Ferrarin, F. Barbariol, S. Zaghi, G. Lorenzetti, G. Manfè, F. De Pascalis, A. Benetazzo, Modeling ship-induced waves in shallow water systems: The Venice experiment, Ocean Eng. 155 (2018) 227–239. [CrossRef]
- A.G. Samaras, T. V. Karambas, Modelling the impact of climate change on coastal flooding: Implications for coastal structures design, J. Mar. Sci. Eng. 9 (2021). [CrossRef]
- L. Melito, F. Lalli, M. Postacchini, M. Brocchini, A Semi-Empirical Approach for Tsunami Inundation : An Application to the Coasts of South Italy, (2022). [CrossRef]
- F. Shi, J.T. Kirby, J.C. Harris, J.D. Geiman, S.T. Grilli, A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation, Ocean Model. (2012). 2012. [CrossRef]
- J.C.N. Borge, G. Rodríquez Rodríguez, K. Hessner, P.I. González, Inversion of marine radar images for surface wave analysis, J. Atmos. Ocean. Technol. 21 (2004). [CrossRef]
- G. Ludeno, F. Serafino, Estimation of the significant wave height from marine radar images without external reference, J. Mar. Sci. Eng. 7 (2019). [CrossRef]
- P.S. Bell, J.C. Osler, Mapping bathymetry using X-band marine radar data recorded from a moving vessel, Ocean Dyn. 61 (2011). [CrossRef]
- G. Ludeno, S. Flampouris, C. Lugni, F. Soldovieri, F. Serafino, A novel approach based on marine radar data analysis for high-resolution bathymetry map generation, IEEE Geosci. Remote Sens. Lett. 11 (2014). [CrossRef]
- G. Ludeno, C. Brandini, C. Lugni, D. Arturi, A. Natale, F. Soldovieri, B. Gozzini, F. Serafino, Remocean system for the detection of the reflected waves from the costa concordia ship wreck, IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 7 (2014). [CrossRef]
- Perugini, P. Penna, L. Parlagreco, M. Brocchini, A comprehensive study of the river plume in a microtidal setting, Estuar. Coast. Shelf Sci. 275 (2022) 107995. [CrossRef]
- M. Postacchini, A.J. Manning, J. Calantoni, J.P. Smith, M. Brocchini, A storm driven turbidity maximum in a microtidal estuary, Estuar. Coast. Shelf Sci. (2023) 108350. [CrossRef]
- J. liang Gao, H. zhou Chen, L. li Mei, Z. Liu, Q. Liu, Statistical Analyses of Wave Height Distribution for Multidirectional Irregular Waves over A Sloping Bottom, China Ocean Eng. 35 (2021). [CrossRef]
- J.A. Battjes, Radiation Stresses in Short-Crested Waves, J. Mar. Res. 30 (1972).
Figure 1.
Sketch of the applied methodology.
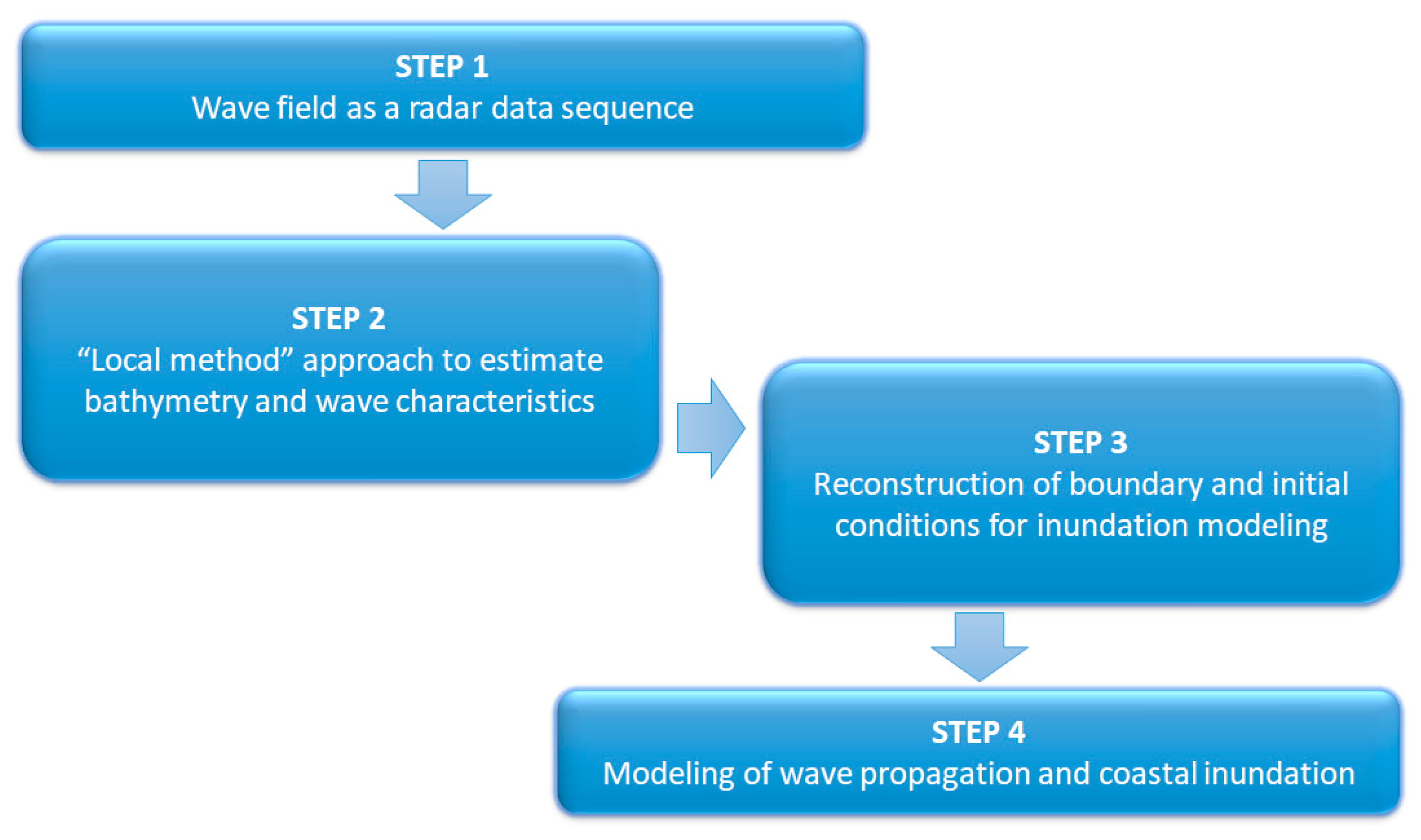
Figure 3.
Numerical propagation of short waves over the Senigallia bathymetry (lower color map) in the baseline (large-scale) FUNWAVE simulations, for different wave spreading parameters: σ = 10 (middle color map) and σ = 30 (upper color map).
Figure 3.
Numerical propagation of short waves over the Senigallia bathymetry (lower color map) in the baseline (large-scale) FUNWAVE simulations, for different wave spreading parameters: σ = 10 (middle color map) and σ = 30 (upper color map).
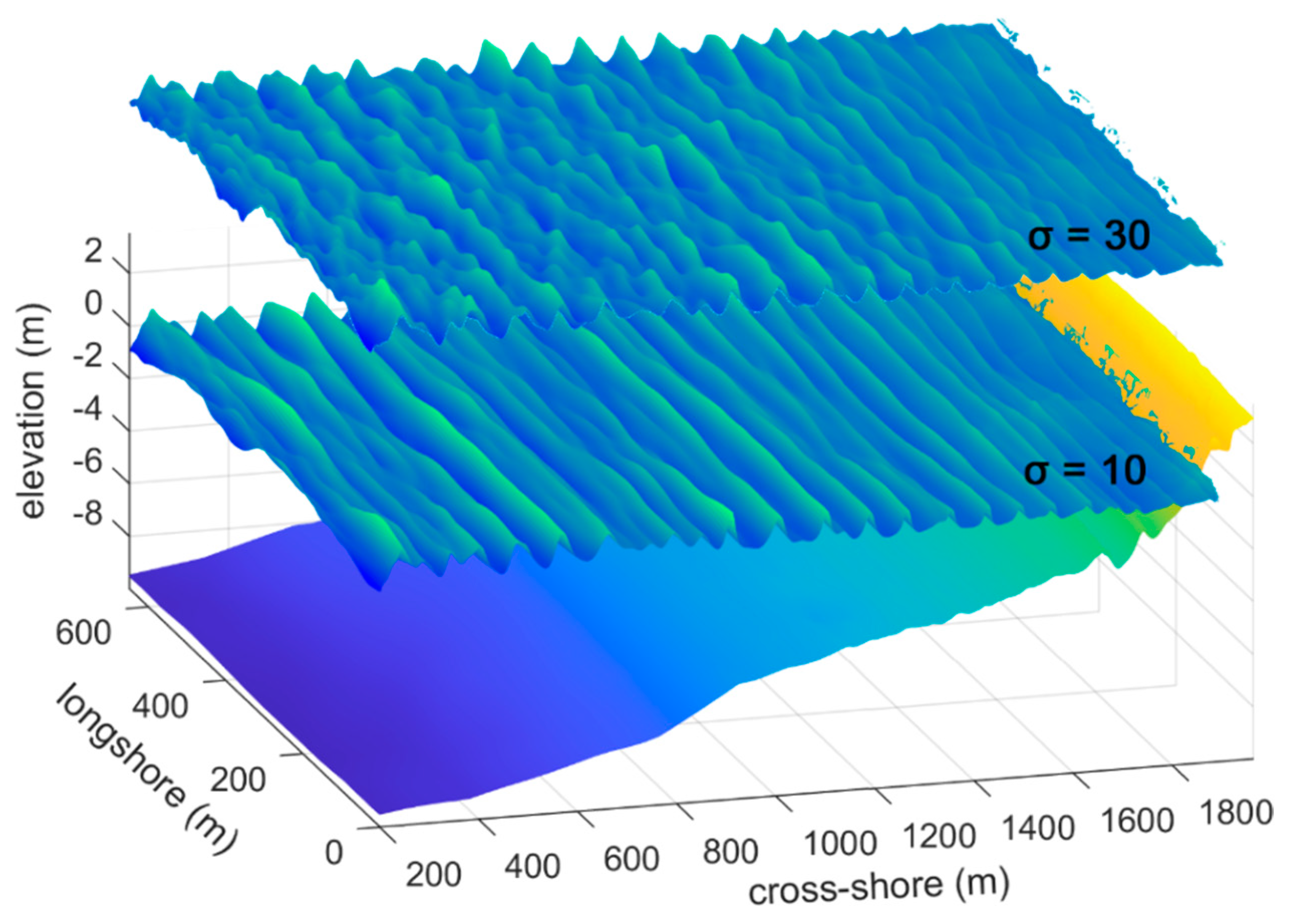
Figure 4.
Synthetic sea-wave image obtained using FUNWAVE-TVD (left panel) and simulated radar image (right panel) for the Oostende case with a directional spreading
Figure 4.
Synthetic sea-wave image obtained using FUNWAVE-TVD (left panel) and simulated radar image (right panel) for the Oostende case with a directional spreading
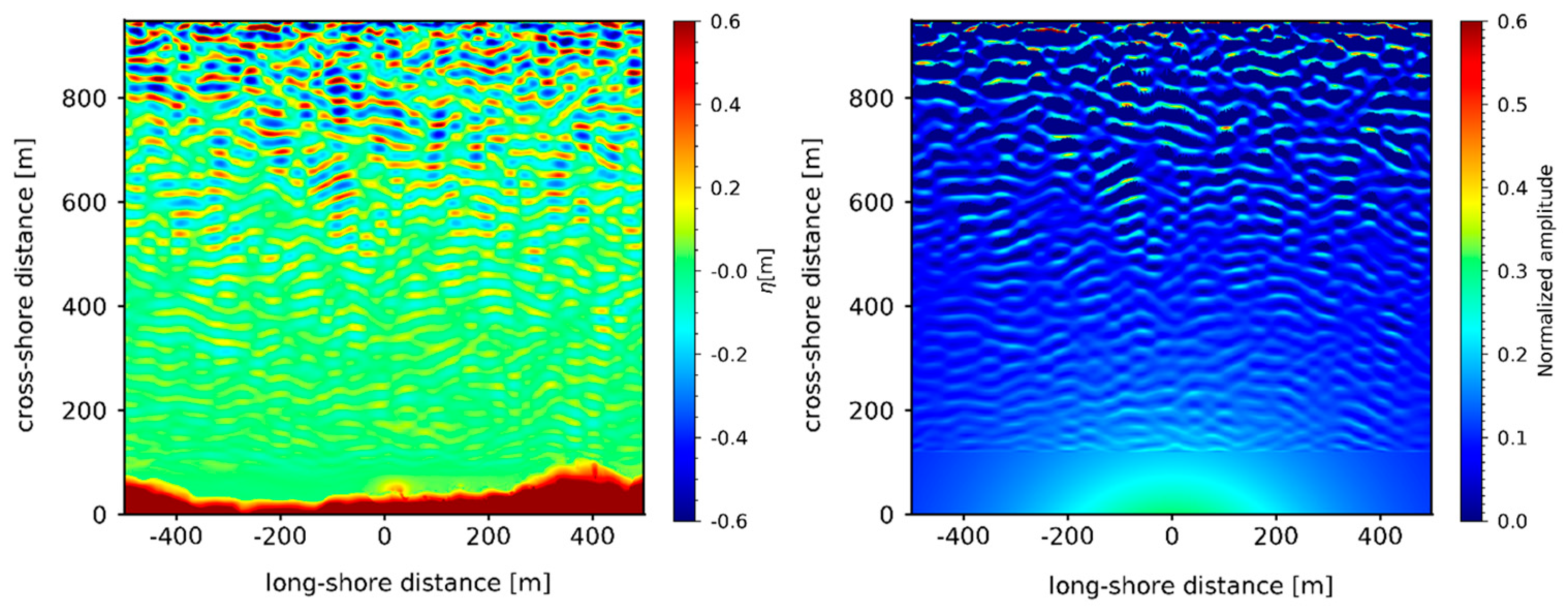
Figure 5.
Comparison between (left panel) ground-truth and (right panel) reconstructed bathymetry for Oostende case, with spreading .
Figure 5.
Comparison between (left panel) ground-truth and (right panel) reconstructed bathymetry for Oostende case, with spreading .
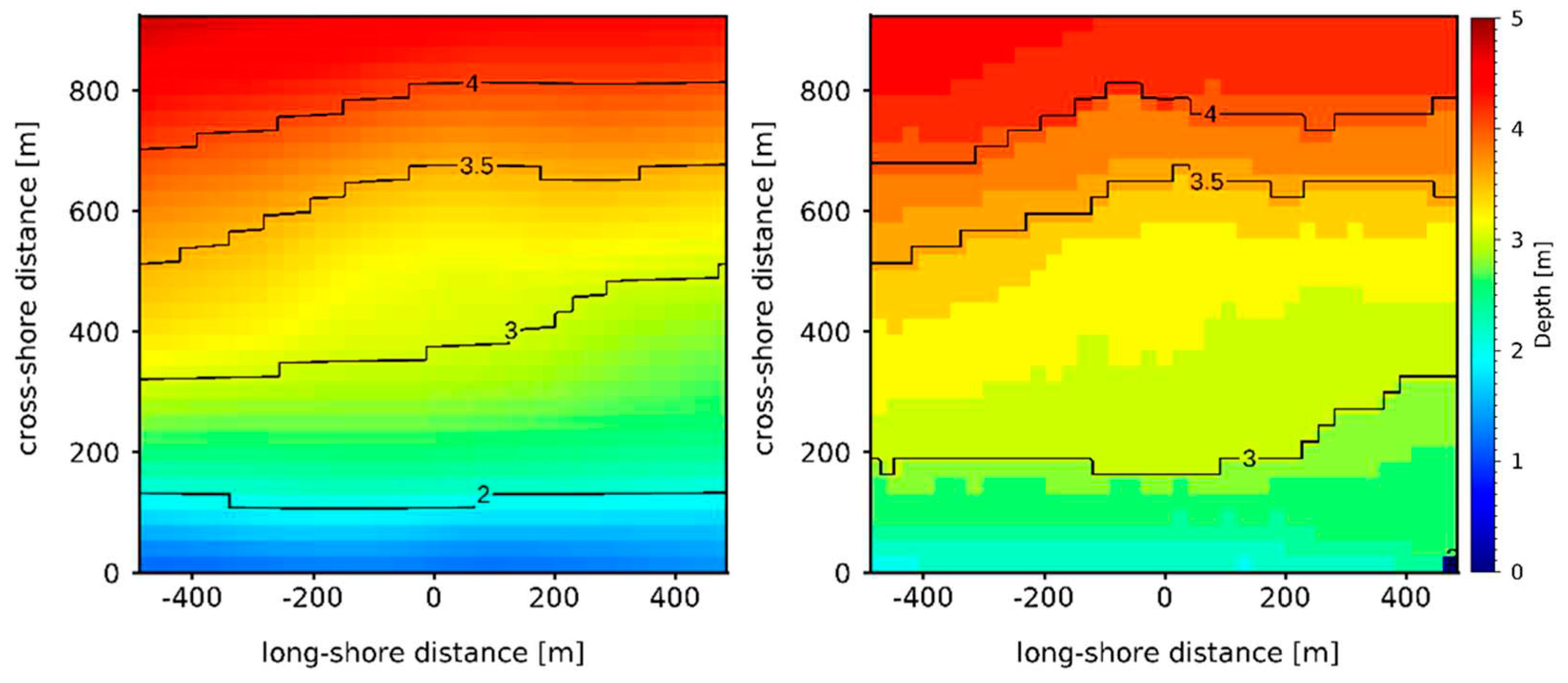
Figure 6.
Comparison between (left panel) ground-truth and (right panel) reconstructed spatial map of significant wave height for Oostende case, with spreading .
Figure 6.
Comparison between (left panel) ground-truth and (right panel) reconstructed spatial map of significant wave height for Oostende case, with spreading .

Figure 8.
Large-scale (thick lines) and small-scale (dotted lines) inundations modelled at a) Senigallia and b) Oostende, for different wave spreading parameters (: yellow; : red; : blue).
Figure 8.
Large-scale (thick lines) and small-scale (dotted lines) inundations modelled at a) Senigallia and b) Oostende, for different wave spreading parameters (: yellow; : red; : blue).
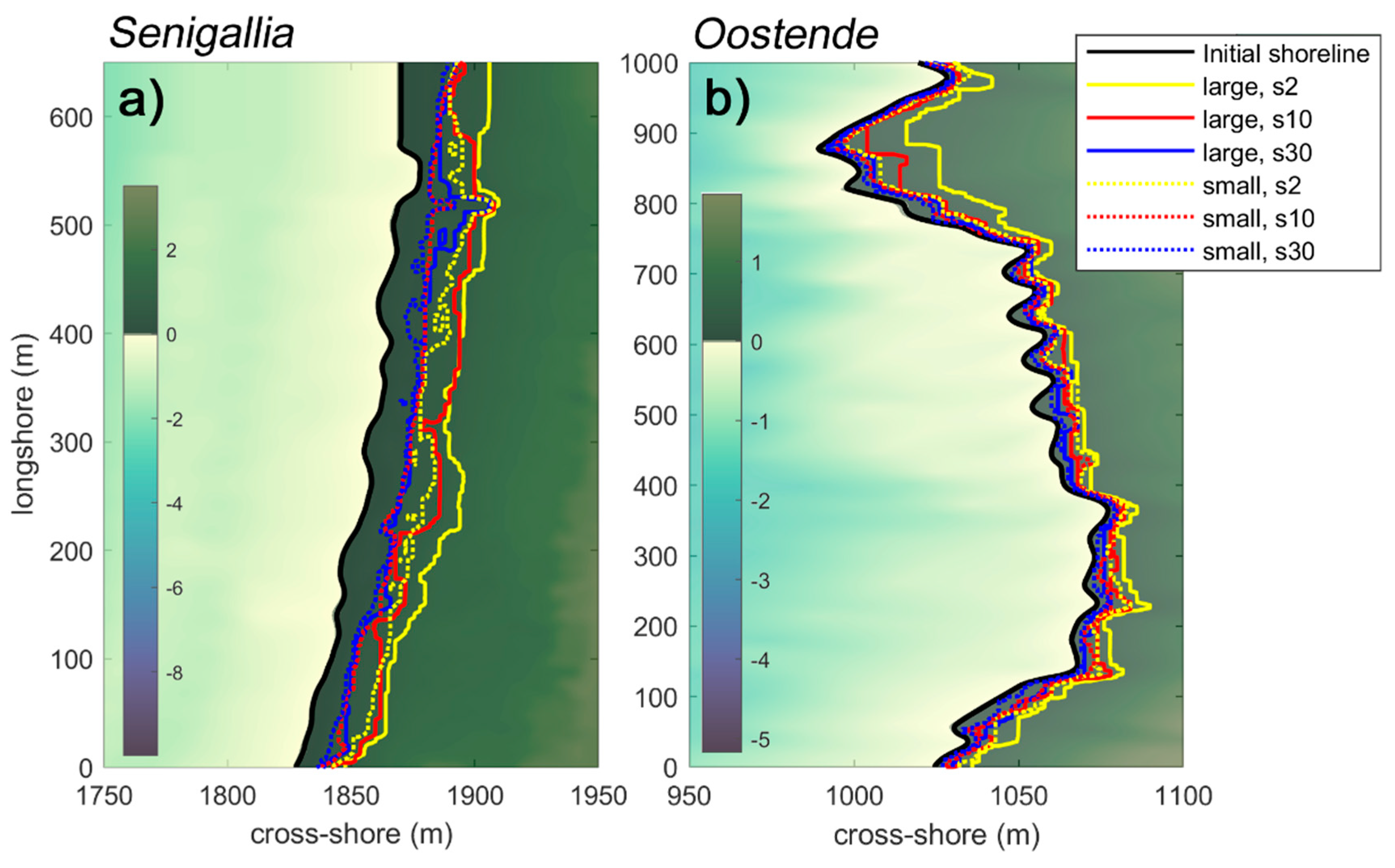
Figure 9.
Comparison of cross-shore coordinates of small-scale vs large-scale inundation for (a-c) Senigallia and (d-f) Oostende, as a function of the wave spreading parameter. Classical error statistics (correlation coefficient P, RMSE, and coefficient of determination R2) are given for each case.
Figure 9.
Comparison of cross-shore coordinates of small-scale vs large-scale inundation for (a-c) Senigallia and (d-f) Oostende, as a function of the wave spreading parameter. Classical error statistics (correlation coefficient P, RMSE, and coefficient of determination R2) are given for each case.
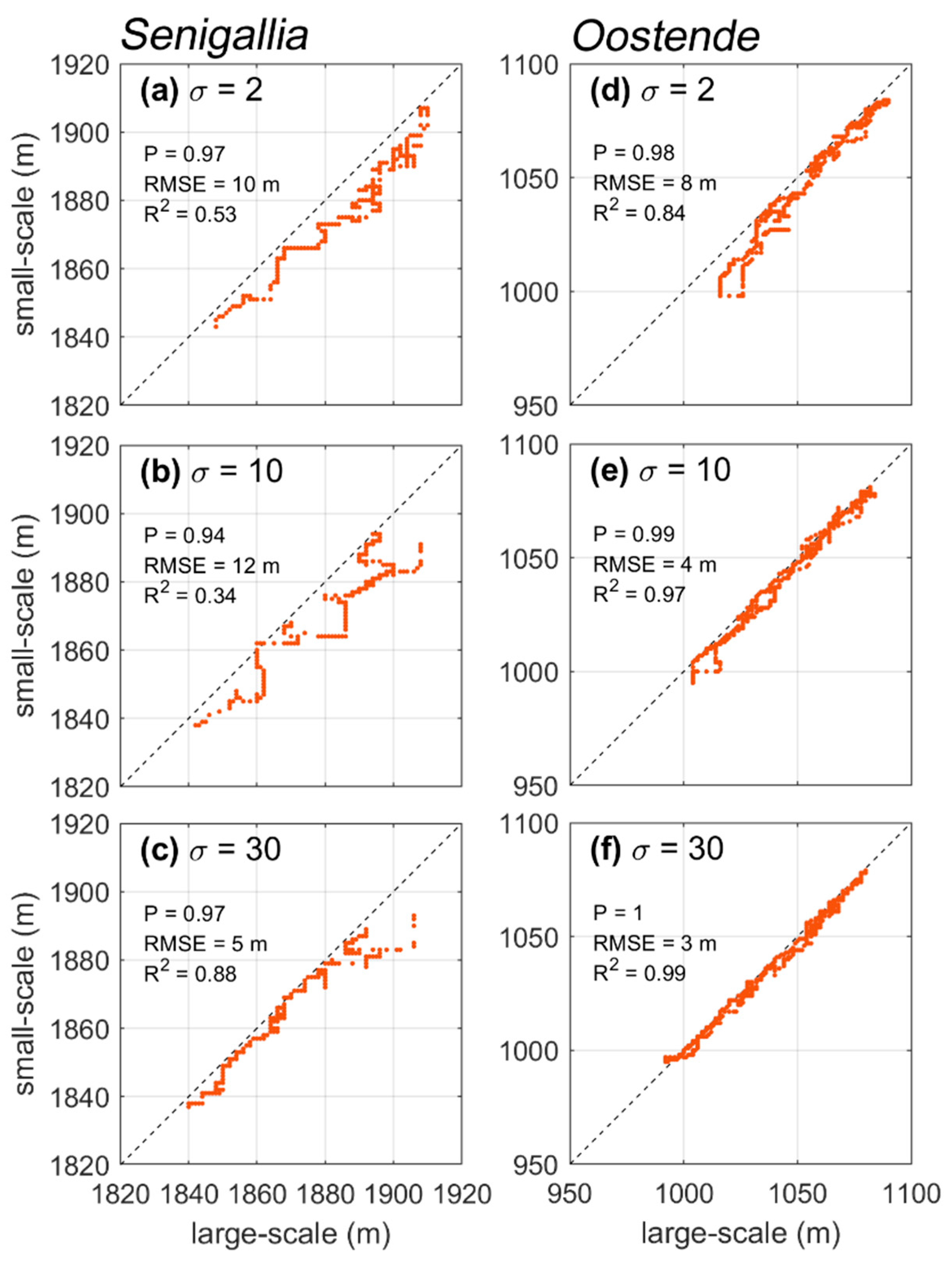
Table 1.
Main wave characteristics at the offshore boundary.
| Location |
hoff [m] |
Hs [m] |
Tp [s] |
[deg] |
|---|---|---|---|---|
| Senigallia | 10 | 1.8 | 13 | 2, 10, 30 |
| Oostende | 5 | 1.7 | 5.8 | 2, 10, 30 |
Table 2.
Statistics analysis of the bathymetric reconstruction.
| Senigallia | Oostende | |||
|---|---|---|---|---|
|
[deg] |
R2 [m] |
RMSE [m] |
R2 [m] |
RMSE [m] |
| 0.97 | 1.01 | 0.94 | 0.28 | |
| 0.97 | 0.86 | 0.94 | 0.34 | |
| 0.98 | 0.77 | 0.95 | 0.36 | |
Table 3.
Mean wave parameters (significant height Hs, peak period Tp, peak length Lp, main direction ) at different isobaths as a function of spreading. The wave conditions reconstructed at a depth h = 5 m for Senigallia and h = 3.5 m for Oostende are used to initialize the small-scale simulations.
Table 3.
Mean wave parameters (significant height Hs, peak period Tp, peak length Lp, main direction ) at different isobaths as a function of spreading. The wave conditions reconstructed at a depth h = 5 m for Senigallia and h = 3.5 m for Oostende are used to initialize the small-scale simulations.
| Senigallia | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wave parameters | |||||||||||||
| [deg] | |||||||||||||
|
Depth h [m] |
3 | 0.45 | 0.46 | 0.44 | 62 | 62.5 | 62 | 0 | 0 | 0 | 12 | 12 | 10.5 |
| 4 | 0.67 | 0.67 | 0.63 | 62 | 62.5 | 62 | 0 | 0 | 0 | 12 | 11 | 10.5 | |
| 5 | 0.75 | 0.79 | 0.72 | 65 | 74.7 | 73 | 0 | 0 | 0 | 11.5 | 10 | 10.5 | |
| 6 | 0.77 | 0.75 | 0.70 | 83 | 83 | 83 | 0 | 0 | 0 | 10.5 | 11 | 10.5 | |
| 7 | 0.85 | 0.77 | 0.75 | 83 | 83 | 83 | 0 | 0 | 0 | 11 | 11.5 | 10.5 | |
| 8 | 0.8 | 0.75 | 0.70 | 83 | 83 | 83 | 0 | 0 | 0 | 11 | 11 | 10.5 | |
| Oostende | |||||||||||||
| Wave parameters | |||||||||||||
| [deg] | |||||||||||||
|
Depth h [m] |
3 | 0.22 | 0.22 | 0.20 | 36 | 35.6 | 34.6 | 0 | 0 | 0 | 6.7 | 6.3 | 6.27 |
| 3.5 | 0.35 | 0.35 | 0.35 | 36 | 35.6 | 35 | 0 | 0 | 0 | 6.4 | 6.25 | 6.13 | |
| 4 | 0.48 | 0.50 | 0.47 | 36 | 35.6 | 35.7 | 0 | 0 | 0 | 6.2 | 6.1 | 5.8 | |
| 1 | |
| 2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








