Thermodynamics is the most general qualitative theory for description of complex systems, dealing with simple mathematics in an elegant way. The Fist Law of thermodynamics recognizes the energy conservation $dU=\sum y_{k}d{X}_k$, where $X_k$ are the system extensive variables, while $y_k={\partial }_{X_k}U$ are the conjugated intensive parameters. The Zeroth Law of thermodynamics reflects transitivity of thermodynamic equilibrium and introduces temperature $T$ accordingly as a unique intensive parameter, which becomes uniform in the entire system at equilibrium. Its conjugated extensive variable is the entropy $S$, being thermodynamically linked to temperature via the relation $T={\partial }_{S}U$. Entropy is ruled by the Second Law of thermodynamics, which governs the direction of spontaneous processes in Nature. The Third Law specifies temperature positively. Because thermodynamics is a macroscopic theory, the underlying microscopic dynamics is hidden from the observer. It is not lost, however, and the entire missing mechanical information builds up the entropy $S$ and temperature $T$, which are not present in mechanics. Since the internal energy is a homogeneous function of first degree from the extensive variables, it equals to $U=\sum y_k{X}_k$ according to the Euler theorem. Substituting this expression in the First Law of thermodynamics yields the important Gibbs-Duhem equation $\sum x_{k}d{y}_k=0$, which relates the intensive parameters $y_k$ via the intensive molar quantities $x_k=X_k/N$, where $N$ is the number of particles in the system. These fundamental laws are the summit of thermodynamics, and the entire subject is application of the basic principles to solve particular problems. It was recently applied in socio-econophysics [1], which is nowadays known as Thermodynamics 2.0 [2].

Let us try to apply the thermodynamic approach to society. Because all underlying microscopic processes respect the energy conservation, it seems reasonable that this will be the case in the society as well, where the social internal energy $U$ preserves. There is no doubt in the presence of social entropy $S$, because the society is even more complex than the simple molecular systems [3]. Due to the well-known relation of entropy to information, one can sense the social entropy level in different countries via the Press Freedom Index of the mass media, for instance. From this perspective, it is obvious that the historical evolution of human society follows a permanent increase of the global social entropy. Therefore, the usual striving for liberty is simply a manifestation of the Second Law. Considering the social entropy $S$ as dimensionless freedom, the social temperature $T={\partial }_{S}U$ is the energy gain by unit liberalization. Temperature of living species is related to temperament [4]. Economy is the second important element of the society, which is characterized by the dimensionless economic volume $V$. The conjugated intensive parameter $p={-\partial }_{V}U$ is the price pressure, which shows the relative energy cost for the economic growth. Finally, a minimalistic model requires number of people $N$ with conjugated intensive quantity $\mu ={\partial }_{N}U$. The latter is exploitation, which is measuring the contribution of a person to the increase of the social energy. Thus, following thermodynamics the social energy $U=TS-pV+\mu N$ obeys the First Law $dU=TdS-pdV+\mu dN$. The exploitation $\mu =u+pv-Ts=h-Ts$ balances the social contribution $h$ and the social reward $Ts$. Obviously, people generate either social energy $u$ or economy $v$, and for this reason their contribution to the society equals to the molar social enthalpy $h=u+pv$. The exploitation obeys the Gibbs-Duhem equation $d\mu =vdp-sdT$, which shows that ${{(\partial }_p\mu )}_T=v$ and ${{(\partial }_T\mu )}_p=-s$. Therefore, the exploitation increases with inflation ${{(\partial }_p\mu )}_T>0$ but decreases with the social temperature rise ${{(\partial }_T\mu )}_p<0$. Naturally, people migrate to lower exploitation. For instance, $h$ is huge in the USA, which is evident from the highest economic standard, but obviously the reward $Ts$ compensate enough the enthalpy to facilitate essential inflow of immigrants from countries with higher $\mu$.

The thermodynamics definition of a natural society requires an equation of state which relates the thermodynamic parameters. The universal van der Waals equation of state, which obeys the Theorem of corresponding states, has been proven to be a very successful one, describing various important phenomena,

Here the minimal volume $v_0=1/3$ refers to the personal belongings. The van der Waals Equation (1) predicts a critical point at $T=p=v=1$. Above the critical temperature $T>1$ the system cannot separate of two phases in equilibrium. Thus, supercritical fluids correspond to the Marx communist society, which cannot split into two classes. Below the critical temperature the capitalist society consists of two phases [5]. The condensed phase $A$ is poor because it does not own much economy per person. It is the Marx proletariat, whose molar volume depends primarily on the social temperature because the pressure $p$ is negligible in Equation (1) at $v_A<1$. The dilute phase B resembles the Marx bourgeoisie, which owns the economy. If $v_B\gg 1$ the phase B is almost ideal gas obeying the Clapeyron-Mendeleev law $p_B{v}_B=8T/3$. Thus, the molar price of economy is a measure for the social temperature. The thermodynamic equilibrium between the two phases requires the same temperature, pressure, and exploitation. The latter balance is introduced in the van der Waals theory via the Maxwell construction.

According to the FRED data [6] the share of the Total Net Worth held by the bottom 50% in the USA is 2.5% in 2022. Employing the parameter $v_B/v_A=97.5/2.5=39$ in the van der Waals theory leads straightforward to $v_A=0.432$, $v_B=16.86$, $T=0.599$ and $p_A=p_B=0.086$. Therefore, the contemporary temperature of the US society is 40% below the critical one. Because the Customer Price Index was $CPI=293$ in 2022 [6] it follows that $CPI=3400p_B$.

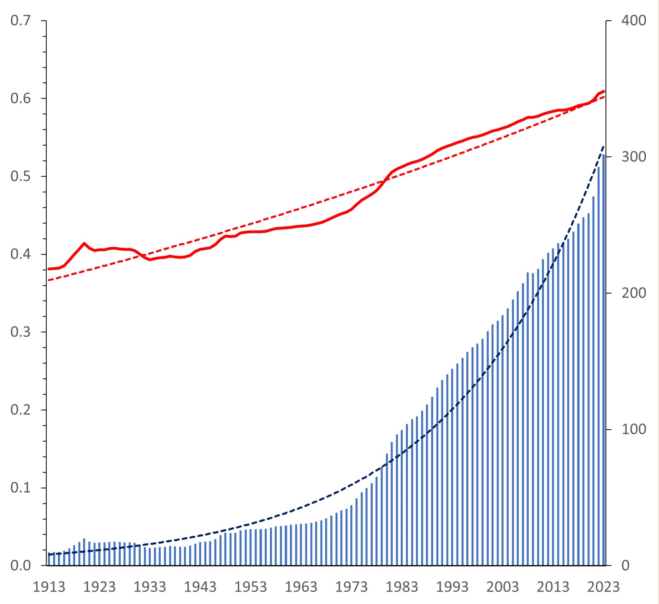
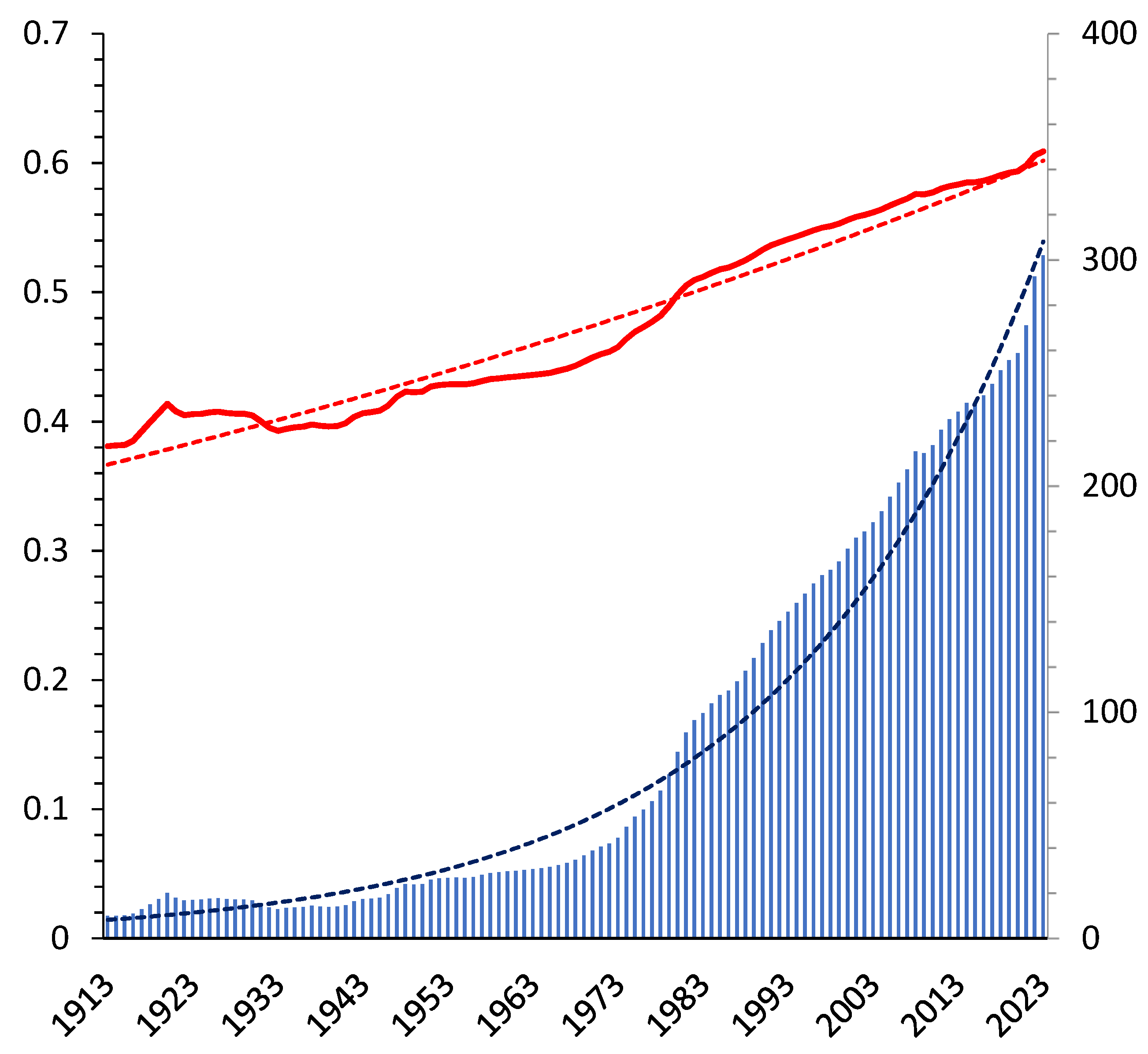
As is seen from Figure 1, the Customer Price Index increases historically almost exponentially in time with an average rate of inflation 3.3%.

This fit evidently shows that the triple point of the US society was the American Civil War (1861-1865), which marked the onset of the US capitalism in the middle of the 19^th century. Substituting Equation (2) in $p_B=CPI/3400$ yields the trend of the price pressure

As is seen, if the inflation persists at the same level in the future, Marx communism is expected to come in the USA at the end of the 21^st century. The critical $CPI$ value will be 3400.

One can employ Equation (3) in the van der Waals theory to determine the trend of the social temperature as well. An alternative way is to use the Gibbs-Duhem equation $d\mu =vdp-sdT$, coupled with the equivalence of exploitation, pressure and temperature in the two phases, to obtain the Clapeyron equation where $∆s$ and $∆v$ are the positive jumps in social entropy and economic volume from condensed to dilute pleases. Equation (4) is very important, since it states that inflation is always accompanied by an increase of the social temperature. Integrating the well-known thermodynamic relation ${(\partial u/\partial v)}_T=T{(\partial p/\partial T)}_v-p=3/v^2$ yields the positive energy jump $∆u=3∆v/v_A{v}_B$ for the van de Waals gas. The social entropy jump can be related to other jumps via the standard thermodynamic expressions for the latent heat $T∆s=∆h=∆u+p∆v$, which is equivalent to $∆\mu =0$ and the Maxwell construction. Substituting here the energy jump yields

In the derivation of the last expression, we employed an original approximation ${v_{A}v}_B=T/p_B$, which holds up to the critical point, where $T=p_B=v_A=v_B=1$. Introducing Equation (5) in Equation (4) and integrating the result yields the Clausius-Clapeyron equation for the van der Waals gas

This equation provides the dependence of the price pressure $p_B=T\mathrm{e}\mathrm{x}\mathrm{p}\left[3\right(1-1/T\left)\right]$ from the social temperature. The inverse dependence $T=3/W_0\left[3\exp (3){/p}_B\right]$ goes via the principal branch of the Lambert W function. It is used in combination with $p_B=CPI/3400$ to reconstruct the historical evolution of the social temperature in the USA as plotted in Fig. 1. Using the fit from Equation (3), the temperature evolves accordingly as $T=3/W_0\left[3\mathrm{e}\mathrm{x}\mathrm{p}\left(72.17-0.033t\right)\right]$.

Another useful approximation is to consider the B phase in the ideal gas limit, where $v_B=8T/3p_B\gg 1$. In this case $v_A=T/p_B{v}_B=3/8\approx v_0$ and $∆u=8$. The latter constant energy difference represents wealth, which is typical for the B phase only. Therefore, $u_B=8+c_{v}T$ and $u_A=c_{v}T$, where $c_v$ is the molar heat capacity at constant volume. Since people live on the Earth surface in pairs, they possess 6 degrees of freedom. Hence, $c_v=(6/2)(8/3)=8$ and the kinetic energy $c_{v}T$ becomes equal to the potential wealth $c_v$ at the critical temperature. The molar social entropy of the ideal gas reads where the heat capacity at constant pressure is given by the Mayer law $c_p=c_v+8/3$. The first constant term $c_v$ represents here the wealth entropy. Altogether, the exploitation, being the molar Gibbs potential $\mu =u+pv-Ts$, acquires the form

Naturally, inflation leads to an increase in the exploitation of capitalists due to investments at constant social temperature. The first term accounts for the passive wealth exploitation. Introducing the social pressure from Equation (6) in Equation (8), the Gibbs potential for the condensed phase acquires the following form, which depends solely on temperature,

Equation (9) shows remarkably that the positive exploitation in capitalism becomes negative in communism. The corresponding entropy of the A phase $s_A=c_v+c_v\ln T$ increases logarithmically with temperature and the entropy difference $∆s$ coincides with Equation (5) in the ideal gas limit. Since $v_A$ is constants, a single worker does not work, $d{u}_A=Td{s}_A$. On the other hand, because the wealth $∆u$ is constant, it follows $d{u}_A=d{u}_B=Td{s}_B-p_{B}d{v}_B$. Thus, the work done by a capitalist is due to the heat exchanged between the two phases, $d{w}_B=-p_{B}d{v}_B=-Td∆s$. Substituting here $∆s=8/3+8/T$ for the ideal gas yields

Obviously, $v_B=V_B/N_B$ shrinks in time, which is due to quicker increase of the number of capitalists $N_B$ than the economic growth. Using Equation (6) one can relate the inflation to the work:

As is seen, the positive operation of capitalism generates compulsory inflation, but this effect declines slightly with the temperature increase. At present 75% of the work produces inflation, which will drop to 50% at the critical point. Employing Equation (3) the economic power $d{w}_B/dt=0.033c_v/(1+3/T)$ will increase from 4.4% to 6.6%, accordingly. The traditionally used economic indicators are calculated per capita. The internal energy per capita reads $u=c_v(T+{\theta }_B)$, where ${\theta }_B=N_B/N$ is the molar fraction of capitalists. As mentioned above, ${\theta }_B$ increases much quicker than temperature, which can explain the observed robust economic growth. Indeed, adopting the Pareto distribution ${\theta }_B=1/v_B^n$, where $n>1$ is a parameter [7], the energy per capita will be $u=c_v\{T+\mathrm{e}\mathrm{x}\mathrm{p}[3n(1-1/T)\left]\right\}$. Thus, capitalism will accelerate dramatically [8] near its end.

The last expression in Equation (10) is very important, showing that $s_A$ is the real potential driving the economy. Thus, the source for economic expansion is proletariat liberation. On the other hand, paraphrasing Marx the latter is the gravedigger of capitalism, because it is due to the social temperature increase. As was mentioned in the beginning, the driving force of the social evolution is, in general, the Second Law of thermodynamics. Assuming constant entropy production $d{s}_A/dt>0$, the social temperature must grow exponentially where numerical constants are obtained by fitting the experimental temperature in Figure 1. Hence, the entropy $s_A$ increases by 4% annually, which is a reasonable constant economic power [8]. The temperature from Equation (12) leads via Equation (11) to inflation $d\ln p_B/dt=0.005(1+3/T)$, which depends on temperature. It decreases from 3% at present to 2% at the critical point. Surprisingly, the latter corresponds to the healthy level of inflation sought by the central banks. Because of the declining inflation, the onset of communism in the USA will be postponed from the previous prediction via the constant inflation rate model in Equation (3), but in any case, it will come no later than a century from now.

At the critical point, the first order proletariat/bourgeoisie phase transition, which is driving capitalism, changes to the second order one, because $∆s=∆v=0$. Therefore, in contrast to the previous social revolutions, the transformation from capitalism to communism will not be accompanied by latent social heat. It will happen without any entropic jump as the Marx evolutionary viewpoint was, not revolutionary as proposed by Lenin. The van der Waals theory also predicts the critical exponents of the proletariat/bourgeoisie phase transition: $\alpha =0$, $\beta =1/2$, $\gamma =1$ and $\delta =3$. They describe the convergence of the two antagonistic classes near the critical point. Additionally, the interfacial tension $\sigma =c_v(1-T)$ between the two social phases can play an essential role for the spatial and temporal distributions like countries, for instance. Finally, a more advanced multi-component social model can consider various social groups with different Gibbs potentials. The dynamics of people exchange among the social components can be described as chemical transformations. So, politicians are original surfactants, trying to reduce the social interfacial tension, who are almost insoluble in all bulk social phases.