Social Thermodynamics 2.0

Thermodynamics is the most general qualitative theory for description of complex systems, dealing with simple mathematics in an elegant way. The Fist Law of thermodynamics recognizes the energy conservation $dU=\sum y_{k}d{X}_k$, where $X_k$ are the system extensive variables, while $y_k=\partial U/\partial X_k$ are the conjugated intensive parameters. The Zeroth Law of thermodynamics reflects transitivity of thermodynamic equilibrium and introduces temperature $T$, accordingly, as a unique intensive parameter, which becomes uniform in the entire system at equilibrium. Its conjugated extensive variable is the entropy $S$, being thermodynamically linked to temperature via the relation $T=\partial U/\partial S$. Entropy is ruled by the Second Law of thermodynamics, which governs the direction of spontaneous processes in Nature. The Third Law restricts temperature positively. Because thermodynamics is a macroscopic theory, the underlying microscopic dynamics is hidden from observers. It is not lost, however, and the entire unknown mechanical information builds up the entropy $S$, a measure of uncertainty being absent in mechanics. Hidden information is not equally important to entropy and quantum Darwinism is a way for selecting the mechanical information essential for thermodynamics. Since the internal energy is homogeneous function of first degree from the extensive variables, it equals to $U=\sum y_k{X}_k$ according to the Euler theorem. Substituting this expression in the First Law yields the important Gibbs-Duhem equation $\sum x_{k}d{y}_k=0$, which relates the intensive parameters $y_k$ via the intensive molar quantities $x_k=X_k/N$, where $N$ is the number of particles in the system. These fundamental laws are the summit of thermodynamics, and the entire subject is application of the basic principles particularly to solve problems. Recently such social applications emerged as Thermodynamics 2.0 [1], which will become a central part of the more general sociophysics and econophysics [2,3,4].

Let us try to apply the thermodynamic approach to society. Because all underlying microscopic processes respect the energy conservation, it seems reasonable that this will be the case in society as well, where the social internal energy $U$ preserves in isolated state. There is no doubt in the presence of social entropy [5,6], because society possesses colossal hidden information, including mechanical one as a minor part. The maximal Shannon entropy corresponds to equally probable events and this uniform distribution is a fair sign of democracy. On the other hand, free will is the ability to choose among possibilities, which clearly possesses maximum at the highest information entropy. Therefore, entropy gives freedom, but the latter always leads to more disorder. Considering the social entropy $S$ as dimensionless freedom, the social temperature $T={(\partial U/\partial S)}_{V,N}$ is the energy gain by unit liberalization. From this perspective it is obvious that the historical evolution of our society follows the permanent increase of global entropy. Hence, the usual striving for liberty is simply a manifestation of the Second Law. The characteristic function of global entropy is also evident from the irreversible arrow of time of the empirical social evolution of Humanity. Due to the close relationship between information and entropy, one can compare the social entropy level in different countries via the Press Freedom Index of the mass media, for instance. Social temperature is related to temperament of living species [7], which correlates somehow with the usual temperature. From this perspective one expects social interactions to depend also on the physical temperature of our planet and the global warming as well.

Economy is the second important element of society, which is characterized by dimensionless economic volume $V$, containing all material assets. The conjugated intensive parameter is the price pressure $p=-{(\partial U/\partial V)}_{S,N}$, which shows the energy cost of economic growth. Lastly, the minimalistic social model requires number of people $N$ with conjugated intensive parameter $\mu ={(\partial U/\partial N)}_{S,V}$, being introduced in physics by Gibbs as chemical potential. It is exploitation in society, which measures the contribution of a person to social energy. Money is the unit of $p$, $U$, $\mu$ and $T$. Following thermodynamics, the social energy $U=TS-pV+\mu N$ obeys the First Law $dU=TdS-pdV+\mu dN$. The exploitation $\mu =u+pv-Ts=h-Ts$ balances the social contribution $h$ and the social reward $Ts$, which is growing with social temperature and freedom, as expected. Obviously, people generate either social energy $u$ or economy $v$, and for this reason their contribution to society equals to the molar social enthalpy $h=u+pv$. The exploitation obeys the Gibbs-Duhem equation $d\mu =-sdT+vdp$, which shows that ${(\partial \mu /\partial T)}_p=-s$ and ${(\partial \mu /\partial p)}_T=v$. Thus, exploitation increases with inflation or decrease of social temperature. As physical particles move spontaneously against the chemical potential gradient, people migrate naturally to lower exploitation. For example, $h$ is huge in the USA, which is evident from the highest economic standard there, but the reward $Ts$ obviously compensate the social enthalpy enough to facilitate essential inflow of immigrants from countries with higher exploitation. Furthermore, large American companies move manufacturing to cheaper countries and this economic outflow is certainly driven by the lower price pressure abroad. Finally, social heat transfers from hotter democratic to cooler totalitarian countries. The latter suppress social entropy to maintain their autocratic order and are existentially afraid of social heating. Thus, totalitarian regimes are building effective adiabatic borders by censoring the internet and other information channels as well as by restricting mobility and other human rights.

The thermodynamic definition of a natural society requires an equation of state, which relates thermodynamic parameters. It follows from ${(\partial \mu /\partial v)}_{T,p}=0$, where $v$ is the order parameter in the Landau free energy. For example, the universal van der Waals equation of state which supports the Law of corresponding states, has been proven to be a very successful one in description of various important phenomena. Here, the minimal volume $v_0=1/3$ refers to the personal belongings at zero temperature. The van der Waals equation predicts a critical point at $T=p=v=1$. Above the critical temperature $T>1$ the system cannot separate of two phases in equilibrium. Thus, supercritical fluids correspond to the Marx communist society, which cannot split into two classes. Below the critical temperature the capitalist society consists of two phases [8]. The condensed liquid phase $A$is poor because it does not own much economy per person. It is the Marx proletariat, whose molar volume $v_A<1$ depends primarily on the social temperature because the price pressure $p_A$ is negligible in Eq. (1). The dilute gas phase B resembles the Marx bourgeoisie, which owns most of the economy. If $v_B\gg 1$ the phase B is almost ideal gas obeying the Clapeyron-Mendeleev equation $p_B{v}_B=8T/3$. Thus, the molar price of bourgeoisie economy is measure for the social temperature. The thermodynamic equilibrium between the two phases requires the same social temperature, price pressure and exploitation, which guarantees social peace. The fairness balance ${\mu }_A={\mu }_B$ is introduced in the van der Waals theory via the Maxwell construction. The physics behind Eq. (1) is competition between repulsive entropic and attractive Newton forces. While the attractive cohesion pressure is vital for proletariat, bourgeoisie is a gas of individualists pursuing larger freedom via wealth. Alternatives of Eq. (1) are also applicable to the hidden social dynamics, because it is driven by the same attraction/repulsion dialectics.

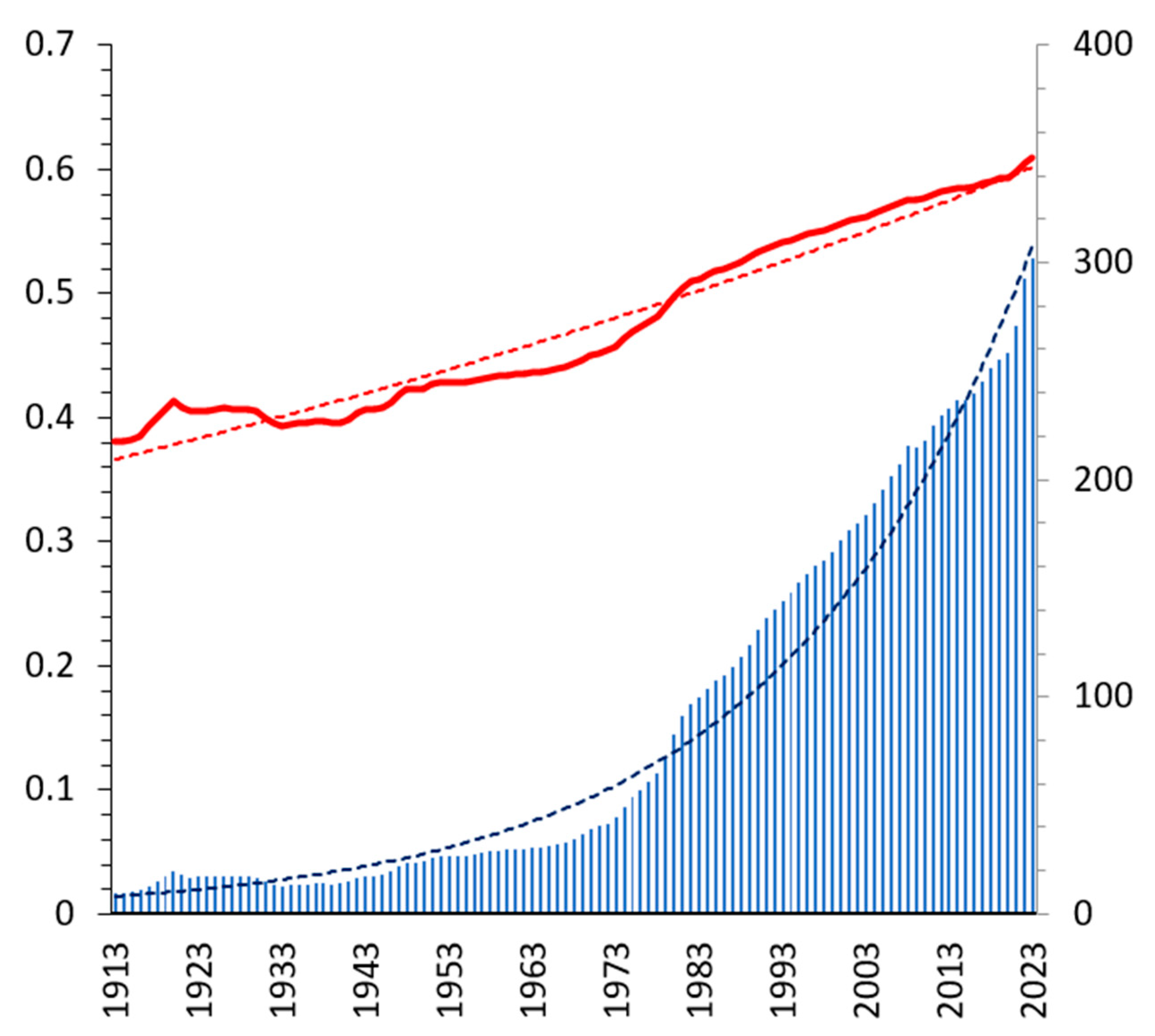
According to the FRED data [9], the share of the Total Net Worth held by the bottom 50% in the USA is 2.5% in 2022. Employing the corresponding ratio $v_B/v_A=97.5/2.5=39$ in the van der Waals theory yields straightforward $v_A=0.432$, $v_B=16.86$, $T=0.599$ and $p=0.086$. So, the current temperature of the US society is 40% below the critical one. Since the Customer Price Index was $CPI=293$ in 2022, it follows that $CPI=3400p$. As is seen from Figure 1, $CPI$ increases historically almost exponentially over time with an average rate of inflation 3.3%

This fit shows the onset of US capitalism in the middle of the 19^th century. Evidently, the American Civil War (1861-1865) had been the triple point of the US society, where slaves had formed the third social phase C. The latter was solid because slaves possess the lowest molar social entropy $s_C<s_A\ll s_B$. Substituting Eq. (2) in $p=CPI/3400$ yields the trend of the price pressure:

Thus, the triple point in 1865 had price pressure $p_t=0.0005$ and social temperature $T_t=0.312$. As is seen, if the inflation persists at the same level in the future, Marx communism is expected to come in the USA at the end of the 21^st century. The critical $CPI$ value will be 3400.

One can employ Eq. (3) in the van der Waals theory to determine the trend of the social temperature as well. An alternative way is to use the Gibbs-Duhem equation $d\mu =-sdT+vdp$, coupled with the equivalence of the exploitation, temperature, and pressure in the two phases, to obtain the Clapeyron equation:

Here $∆s$ and $∆v$ are the positive jumps of the molar social entropy and economic volume from the liquid to the gas phases. Equation (4) is very important, since it states that inflation is always accompanied by an increase of social temperature. Integrating the well-known thermodynamic relation ${(\partial u/\partial v)}_T=T{(\partial p/\partial T)}_v-p=3/v^2$ calculated here for the van de Waals gas yields the positive energy jump $∆u=3∆v/v_A{v}_B$ of economic Newton forces. In contrast social entropy aka freedom generates emergent social forces. Its jump can be related to other jumps via the standard thermodynamic expressions for the latent heat, $T∆s=∆h=∆u+p∆v$, which is equivalent to $∆\mu =0$ from the Maxwell construction. Substituting here the energy jump yields

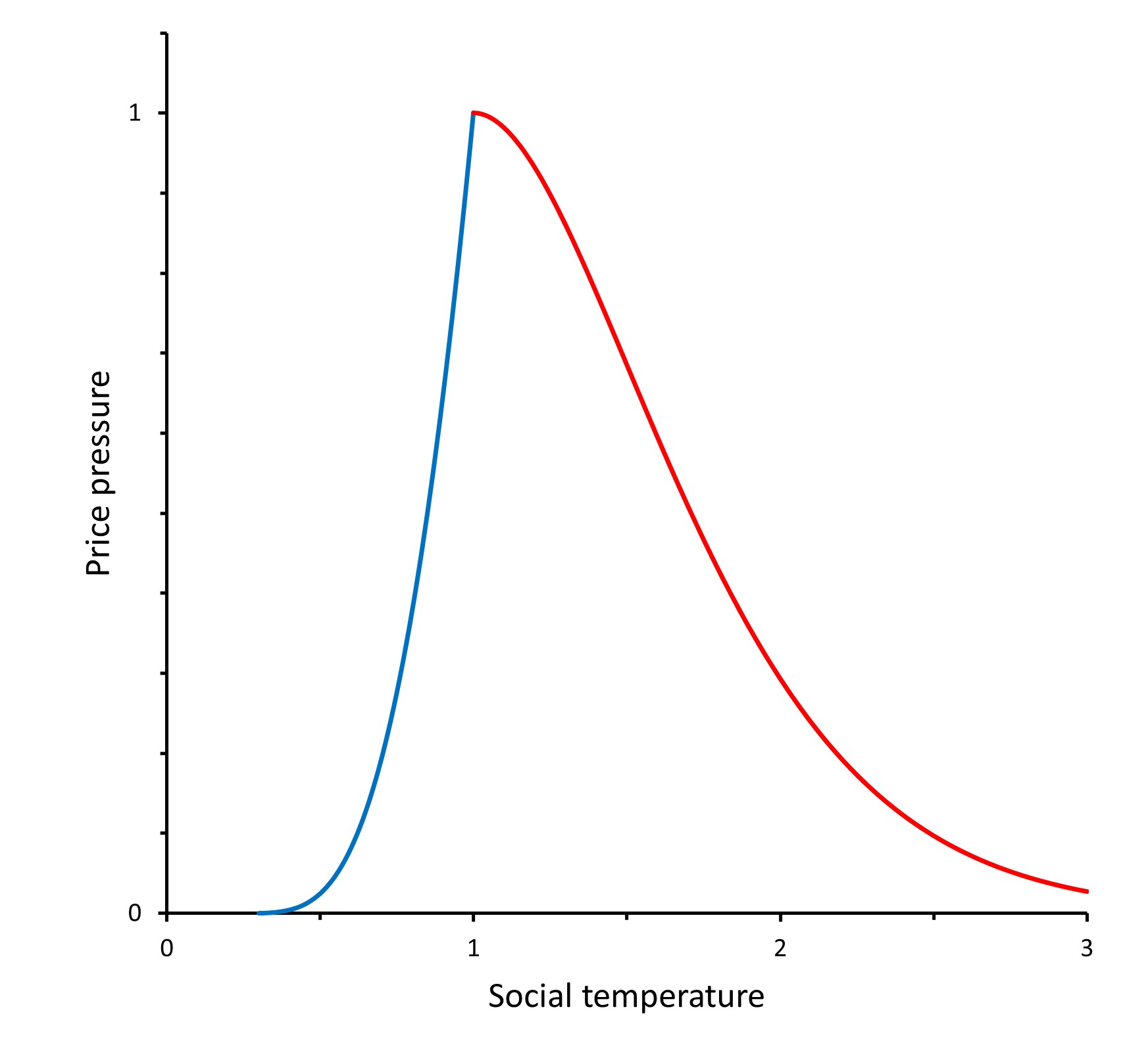
In the derivation of the last expression an original approximation ${v_{A}v}_B=T/p$ is employed, which holds up to the critical point where $T=p=v_A=v_B=1$. Introducing Eq. (5) in Eq. (4) and integrating the result yields the Clausius-Clapeyron equation for the van der Waals gas:

This equation offers the dependence of the price pressure $p=T\mathrm{e}\mathrm{x}\mathrm{p}\left[3\right(1-1/T\left)\right]$ from the social temperature. The inverse dependence $T=3/W_0\left[3\mathrm{e}\mathrm{x}\mathrm{p}\right(3)/p]$ goes through the principal branch of the Lambert W function. It is used in combination with $p=CPI/3400$ to reconstruct the historical evolution of the social temperature in the USA as plotted in Figure 1. Using the fit from Eq. (3), the temperature evolves accordingly as $T=3/W_0\left[3\mathrm{e}\mathrm{x}\mathrm{p}\left(72.17-0.033t\right)\right]$.

Another useful approximation is to consider the B phase in the ideal gas limit, where $v_B=8T/3p\gg 1$. In this case $v_A=T/p{v}_B=3/8$ and $∆u=8$. The latter constant energy difference represents savings, which are typical for the B phase only. Hence, $u_B=8+c_{v}T$ and $u_A=c_{v}T$, where $c_v$ is the molar social heat capacity at constant volume. The molar social enthalpy of bourgeoisie equals to $h_B=8+c_{p}T$, where the molar social heat capacity at constant pressure obeys the Mayer law $c_p=c_v+8/3$. Since people live in pairs on the Earth surface, they possess 6 degrees of freedom. Thus $c_v=(6/2)(8/3)=8$ and the kinetic energy $c_{v}T$ becomes equal to the potential savings at the critical temperature. The molar social entropy of the ideal gas reads

The first term, which represents the so-called chemical constant, is the savings entropy $c_v$. Altogether, the exploitation being the molar Gibbs free energy $\mu =h-Ts$ acquires the form:

Naturally, inflation leads to an increase in the exploitation of capitalists due to necessary investments at constant temperature. The first term accounts for the passive savings exploitation, traditionally used by banks. Introducing the social pressure from Eq. (6) in Eq. (8), the Gibbs potential for the A liquid phase acquires the following form, which depends solely on temperature,

Equation (9) shows remarkably that the positive exploitation in capitalism becomes negative in communism. Mandatory taxation by capitalist governments will be replaced by free will donations to communist society to sustain. The corresponding entropy $s_A=c_v+c_v\ln T$ of the A phase increases logarithmically with temperature and the entropy difference $∆s$ coincides with Eq. (5) in the ideal gas limit. Since $v_A$ is constant, a single worker does not work, $d{u}_A=Td{s}_A$. On the other hand, because the savings $∆u$ are constant, it follows that $d{u}_A=d{u}_B=Td{s}_B-pd{v}_B$. Hence, the work done by a capitalist $d{w}_B=-pd{v}_B=-Td∆s$ is due to heat exchange between the two social phases. Substituting here $∆s=8/T+8/3$ for the ideal gas yields

Clearly, $v_B=V_B/N_B$ shrinks over time, which is due to quicker increase of the number of capitalists $N_B$ than the economic growth. Using Eq. (6) one can relate the inflation to the work:

As is seen, the positive operation of the economy generates compulsory inflation, but this effect declines moderately with temperature increase. At present 75% of the work produces inflation, which will drop to 50% at the critical point. Employing Eq. (3) in Eq. (11) the US economic power $d{w}_B/dt=0.033c_v/(1+3/T)$ will increase from 4.4% to 6.6%, respectively.

The last expression in Eq. (10) is very important, showing that $s_A$ is the real potential driving the economy. Thus, the source for economic expansion is proletariat liberation with the hope of becoming free capitalists. On the other hand, paraphrasing Marx the gravedigger of capitalism is the $s_A$ increase, because it is due to social temperature rise. As was mentioned in the beginning, the driving force of the social evolution is the Second Law of thermodynamics. Assuming constant proletariat entropy production $d{s}_A/dt>0$, which is minimal according to the laws of nonequilibrium thermodynamics, the social temperature must exponentially grow:

The numerical constants here are obtained by fitting the empirical temperature from Figure 1. Thus, the molar entropy $s_A$ increases by 4% annually, which is a reasonable constant economic power [10]. The temperature from Eq. (12) leads via Eq. (11) to inflation $d\ln p/dt=0.005(1+3/T)$, which depends on $T$. It decreases from 5.3% at the triple point via 3.0% at present to 2.0% at the critical point. Surprisingly, the latter corresponds to the healthy level of inflation sought by the central banks. Because of declining inflation, the onset of communism in the USA will be postponed from the previous estimate via the model of constant inflation from Eq. (3). In any case, however, it will come no later than a century from now.

Traditionally used economic indicators are calculated per capita. According to the present theory the internal energy per capita $u=c_v(T+{\theta }_B)$ depends on the molar fraction of capitalists ${\theta }_B=N_B/N$, playing a role of extra temperature. As mentioned above, ${\theta }_B$ increases much quicker than temperature $T$, which can explain the observed robust economic growth. Indeed, adopting the Pareto distribution ${\theta }_B=1/v_B^n$, where $n>1$ is a parameter [4], the energy per capita becomes $u=c_v\{T+\mathrm{e}\mathrm{x}\mathrm{p}[3n(1-1/T)\left]\right\}$. Hence, capitalism will accelerate dramatically [10] near its end. Since the social temperature increases over time as plotted in Figure 1, $u$ also grows continuously by sucking energy from the environment because society is not an isolated system.

At the critical point, the first order proletariat/bourgeoisie phase transition, which is driving capitalism, changes to the second order one because $∆s=∆v=0$. The van der Waals theory also predicts the critical exponents of the liquid/gas phase transition: $\alpha =0$, $\beta =1/2$, $\gamma =1$ and $\delta =3$. They describe the convergence of the two antagonistic classes near the critical point. So, in contrast to the previous social revolutions, the transformation from capitalism to communism will not be accompanied by latent social heat. It will happen without destructive entropic jumps, as the Marx evolutionary viewpoint was, not revolutionary as proposed by Lenin. Revolutions can only cause fluctuations in this case, which violate the Second Law of thermodynamics and possess short lifetimes according to the Fluctuation theorem. Indeed, after several decades survival the Socialist Bloc became so supersaturated that it collapsed spontaneously in the 1990s via spinodal decomposition. Otherwise, China managed smoother transition from socialism to state capitalism by nucleation via joint ventures with foreign capitalists. Russia also implemented the nucleation mechanism after the highest supersaturation was released by the spinodal dissolution of the Soviet Union. Such contra-revolutions cause immense entropic eruptions restoring the right social entropy forcibly decreased by the socialist regimes after their apogee. Increasing the social temperature decreases the interfacial tension $\sigma =c_v(1-T)$ between social phases. Thus, the class struggle between proletariat and bourgeoisie will weaken over time. At present more anarchistic fluctuations are often observed such as the US Capitol attack in 2021. They are driven via bipartisan struggle, magnified by the higher social temperature corresponding to a larger social entropy. According to the Landau-Ginzburg theory, such fluctuations will become long-ranged and slow near the critical point. Because fluctuations will normalize again in supercritical fluids, only communism can restore the harmony of social peace by eliminating social division and the associated directed social opposition. The absence of parties in communism implies independent social control exercised by the whole society. Nowadays, Switzerland is the country that comes closer to such social governance, while the philanthropic foundations and other charitable organizations of very rich capitalists are the prototype of communist free will taxation. Hypocritically even the most advanced countries that firmly proclaim the principles of free market democracy still finance their budgets through compulsory taxation. Such entropic double standards are the source and promoter of corruption, which can disappear in communism only.

The interfacial tension generates in addition a capillary social pressure, which disturbs the force balance $∆p=0$ typical for large phases. Hence, two kinds of prices for poor and rich people, respectively, can appear in society. So, the US social dispersion looks like a fog with a continuous B phase monopole with ${p_B<p}_A$, while the Chinese society resembles a foam, where the A phase is consolidated at ${p_A<p}_B$, which is evident from the CCP leadership. Proletariat activists possess already the maximal critical entropy $c_v$. Because the latter coincides with the interfacial entropy $-\partial \sigma /\partial T$, labor parties and trade unions are active in the interfacial domains. A more advanced multi-component social model can afford various social groups with different Gibbs potentials. So, politicians are original surfactants reducing the social interfacial tension, who are almost insoluble in the bulk social phases. The present theory can help policymakers and scientists to better understand and manage social evolution [11], since it was suspicious before that the vaunted Scientific Communism was based solely on the simple Marx equations. The dynamics of people exchange among social components can be described as chemical kinetics. Thus, chemical affinity will govern the additional entropy production, resulting in social mixing and diversity. In general, chemical kinetics accelerates at elevated temperature, while the calorimetric effect of such social reactions will be a measure for the cost of education in society. For simplicity, $c_v$ was considered constant in the present paper. However, an increase of the heat capacity with social temperature can account for cultural and intellectual advancement of the individuals. The nowadays expansion of Artificial Intelligence generates a new powerful AI proletariat, which is rapidly reproducing. In fact, social entropy distinguishes AI from machines. Therefore, AI will dramatically accelerate the onset of AI communist society, better with than without humans.

Traditionally entropy is considered as the destructive demon of thermodynamics turning everything into chaos and disorder. The present paper revises this evil paradigm by associating entropy with useful freedom. Thus, particles of liquids prefer gaseous state because they are less affected by the intermolecular interactions there. Тhe ideal gas is the freest one and the disorder is simply a visible artefact of the great liberalization. The Brownian motion of ideal gas particles is a well-known process of entropy production, which occurs via successive bifurcations due to a binary probabilistic dialectics. Hence, the increase of entropy in closed systems is not driven by the seek for disorder but for freedom, reflecting the dialectics of discreteness and continuity in Nature. Because our society is not an isolated system, social entropy must not compulsorily grow as the global one. Indeed, it is demonstrated in the article that only a part of the social entropy, the A phase $s_A$, increases monotonously over time. Obviously, social evolution is none of the typical processes, viz. adiabatic, isothermal, isobaric, and isochoric, but it is spontaneous for sure, which means irreversible. Therefore, the rigorous characteristic function of society remains unknown yet. Combining the First and Second Laws of thermodynamics yields the Clausius inequality $\left(\overline{T}-T\right)dS+\left(p-\overline{p}\right)dV\ge \mu dN$, where the bars indicate properties of the environment. Because the price $p$ is always larger than the physical value $\overline{p}$ in capitalistic economy, the economic expansion facilitates population growth. Equation (10) implies that the critical social temperature equals to the physical temperature $\overline{T}$ on the Earth, which appears practically to be the body temperature of humans. Hence, social liberalization also enables population growth. At communism the profit is meaningless because $p=\overline{p}$ and the exploitation $\mu <0$ is negative. Thus, the relevant Clausius inequality predicts a strong population growth $dN\ge \left(\overline{T}-T\right)dS/\mu$ driven by rational liberalization only. Finally, if the environmental intensive parameters remain nearly constant, the Clausius inequality acquires the form $d(U+\overline{p}V-\overline{T}S)\le 0$. It defines in the brackets the desired characteristic function as the social Gibbs free energy, which decreases continuously over time.