Prerpints.org logo
Preprint
Article

Theoretical Interpretation of pH and Salinity Effect on Oil in Water Emulsion Stability Based on Interfacial Chemistry and Implications for Produced Water Demulsification

Altmetrics

Downloads

157

Views

45

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

10 July 2023

Posted:

12 July 2023

You are already at the latest version

Alerts
Abstract
The petroleum industry produces thousands of barrels of oilfield waters from the initial stage driven by primary production mechanisms to the tertiary stage. These produced waters contain measurable amounts of oil in water emulsions, the exact amounts being determined by the chemistry of the crude oil. To meet strict environmental regulations governing the disposal of such produced waters, demulsification to regulatory permissible levels is required. Within the electric double layer theory, coupled with the analytical solutions to the Poisson Boltzmann Equation, continuum electrostatics approaches can be used to describe the static and electrokinetic properties of such emulsion systems. Therefore, theoretical understanding of the stability of oil in water emulsions within such fundamental concepts provides reliable approaches to demulsification. In this paper, we have used theoretical approaches, based on zeta potential and surface charge density models to determine the stability of oil in water emulsions for different crude oil samples. Accordingly, we have used literature based data on the chemistry of the crude oils, and have ranked the order of emulsion stability based on criterial established by zeta potential plots for the oil. Our theoretical calculations show that where the isoelectric points of crude oil samples are closer to each other, the degree of ionization plots versus pH indicate close tends for salinities at varying pH of oilfield waters. Based on the chemistry of crude oil samples, the most efficient and cost-effective means of demulsification is by reducing produced water pH to values closer to the average point of zero charge pH values
Keywords: 
Subject: Environmental and Earth Sciences  -   Waste Management and Disposal

1. Introduction

Conventional source of crude oil has fuelled sustained global economic growth since its discovery in Pennsylvania, in 1859 [1]. Accordingly, the exponential growth in global demand for several decades has caused imminent decline in conventional deposits [2,3,4,5]. To sustain the vulnerable global supply chain, the development of unconventional oil resources consisting of heavy crude oil has for decades, been considered a technically and economically viable option [6,7]. While crude oil production has sustained global economic growth, it production comes with measurable environmental footprints in several aspect including the pollution of both surface and underground water bodies due to the imminent irresponsible disposal of oilfield produced water waters [8,9,10]. Consequently, produced water cleanup before disposal is endorsed in the EPA Act, [11,12] and elsewhere [13,14].
An emulsion is a thermodynamically unstable[15,16,17] dispersion of one liquid phase in another continuous liquid phase that can arise through a mechanically induced processes, such as shear mixing/homogenization of the dispersed phase [18]. Therefore, considering the mechanically induced multiphase flow of oil, water and gas phases in the production tubing, the formation of oil in water and water in oil emulsions is possible [19], as is possible in transportation pipeline[20,21]. Such emulsions are stabilized by different processes [22], notable among them being the electrostatic stabilization processes [23,24,25,26].
Heavy oil deposits have high concentrations of heteroatom components in the form of high molecular weight asphaltenes [27] and organosulfur components [28]. Asphaltenes have OH and carboxyl [29] and amine groups [30] that render them amphoteric in nature, being able to develop electrostatic charges with varying pH, due to the existence of an imminent point of zero charge pH [31]. Therefore, there is the potential for stabilization of oil in water emulsion due to the electrostatic repulsion between dispersed oil phases that can be measured based on zeta potential measurement technique [32]. Under such conditions, the number density of basic and acidic ionisable components of crude oils (Heteroatom components) will control the surface charge density at a given pH and so will the emulsion droplet sizes, implying pH and droplet size distribution are critical to determining coalescence potential and emulsion stability [33,34,36,36]. Moreover, Mehta and Kaur [37], believe that from thermodynamic approach, the stability or instability of the emulsion is related to emulsion droplet size which depends on surface tension/surface charge density of drops [38]. Recently, Bonto et al. (2019) [39] proposed a new surface complexation model of the oil-water interface, where the importance of basic and acidic groups of crude oils were emphasized. Their model integrates the chemistry of crude oils by assuming surface sites being linearly dependent on the total acid number (TAN) and total basic number (TBN). In the literature, Nenningsland et al. (2010) [40] have researched the effect of the basic molecules components of crude oil on the water-oil interface, reporting changes in the IFT due to protonation below pH 5. However, the decrease was less than at high pH favorable for the dissociation of the carboxylic acids group, implying a lower surface affinity of the basic group than the naphthenic acid (OH) fraction[40,41]. Ameri et al., (2018) [42] have also demonstrated the effect of salinity on oil-brine interfacial tension and its consequences on asphaltene stability, with the most recent experimental demonstration of salinity effect of asphaltene precipitation being carried out by [43]. Recently, a new model of zeta potential of asphaltene was presented that integrates the effect of the number density of basic acidic and OH groups of asphaltenes [44]. The fundamental tenet of the model is that that the ionisable (in aqueous solution) carboxylic and hydroxyl groups present on the asphaltene molecule lead to their charging. For the case systems with added salt, there was a quantitative match of predicted results with experimental results. In all the aspects of asphaltenes studied above, the degree of ionization of the basic and acidic functional groups will play a major role on zeta potential, surface charge density and emulsion stability. All the mention physicochemical properties will be further controlled by salinity and pH. However, to date, no literature has been specifically devoted to the effect of salinity and pH on the extent of ionization of acidic and basic functional groups of asphaltene, which controls asphaltene-brine interfacial chemistry. Moreover, the presence of these acidic and basic groups on asphaltenes has been demonstrated spectroscopically [42]. The theoretical relationship between the degree of ionization of a surface ionisable group and the scaled surface potential exists in the literature [45], and the surface potential due to the ionized group can be theoretically linked to the pH of the aqueous phase, suing the Nernst equation [46]. Recently, Bonto at al. (2019) [39] published a study report that contains data on the surface concentrations of acidic and basic groups of asphaltenes from different crude oils. Herein, we exploit the above theoretical developments to study the effect of oilfield brine salinity and pH on the degree of ionization of the acidic and acidic functional groups of asphaltenes. We also used the fundamental relationship between surface charge density and surface potential within the electric double layer theory to derive the differential capacitance. We further developed sound theoretical models based on interfacial chemistry, utilizing concepts of the electric double layer and surface complexation models. Based on our theoretical models and that of zeta potential dependence on pH, surface charge density and differential capacitance, we have discussed emulsion stability trends of different crude oils based on the composition of heteroatomic groups. We have also used surface specific data of ionisable carboxyl group of a crude oil sample to calculate what we call in this paper as intrinsic/bare surface charge density and have compared it with the effective surface charge density. Finally, we have discussed the implications for produced oilfield water emulsion destabilization for oilfield wastewater treatments.

2. Backgrounds

In the literature, different models of asphaltenes have been proposed [47,48,49,50]. In all cases of published literature, asphaltenes have been acknowledged to be among heteroatoms consisting of several fused benzene rings with polar functional groups [51], with minor concentrations of trace metals [52,53]. However, the dominant roles of the polar functional groups, namely acidic [54] and basic ones [42] have been revealed by spectroscopic studies, while the basic nature of asphaltenes in general has been experimentally justified by[55]. Figure 1 shows model asphaltenes containing acidic and basic nitrogen groups in addition to resin and naphthenic acid components of crude oil [56].
Naphthenic acids (NAs) generally refers to a family of cycloaliphatic carboxylic acids found in crude oils with an empirical formula of CnH2n+zO2 n being the number of carbon and z is zero or negative even integer presenting the hydrogen deficiency (unsaturated degree) of the acid [57]. Consequently, the amphoteric nature of the OH group of asphaltene and naphthenic acid and that associated with the nitrogen basic group of asphaltene implies deprotonation and protonation of OH and nitrogen groups respectively at pH conditions characteristic of oilfield produced waters. Therefore, the Polar and acidic groups of asphaltenes play a more vital role, regarding interfacial activity and solubility [58]. At high and low pH, the acidic and basic groups have been shown to be increasingly charged [59] and since these surface charges will reflect the degree of functional groups ionizations, salinity, temperature and surface charge density, we will devote the next section to the integration of published theoretical concepts in the literature to the development of a multi-parameter dependent equation that will link the degree of ionization to the relevant physicochemical parameters of interest. Accordingly, the following sections will also consider the fundamental concepts of surface charge and zeta potential which are intimately linked to interfacial properties of the oil in water emulsion.

3. Study Background Theoretical Foundations

3.1. Degree of Ionization

Ionization of surface functional groups is the principal cause of surface complexation in colloidal systems and metal ion coordination to them [60] as well as adsorption phenomena, and the extent to which a surface functional group will ionize in its aqueous environment is the degree of ionization[45,61]. Generally, oil in water emulsions contain presumably oil particles dispersed in a continuous wastewater phase [62] with particle size distribution that obey known statistical distribution functions [63]. Therefore, the surface of oil bubble/particles will contain ionisable acidic and polar groups with densities that can be described by the following equations [64]:
N S − C O O H = 0.602 ∗ 10 6 T A N 1000 a o i l M W K O H
N S − N H = 0.602 ∗ 10 6 T B N 1000 a o i l M W K O H
In Eq. (1) and Eq. (2), N S − C O O H is the number density of acidic functional groups on crude oil surface [m-2], N S − N H is the number density of basic functional groups [m-2], and a o i l is the specific surface area of oil[m2g-1], T A N and T B N are total acid and total base numbers respectively and M W K O H is the molecular weight of potassium hydroxide used in the determination.
The following figure shows a typical bubble/particle size distribution of oil in water emulsion [65]
From Figure 2, an emulsion with a narrow bubble size distribution that shows a predominant frequency can be used to obtain an idea about the relative importance of the surface function group in emulsion stability. Thus, the following equation can be written for the total number sites of acidic and basic groups on crude oil for oil in water emulsion:
N S − T C O O H = π 4 π R p r e d 3 3 0.602 ∗ 10 6 T A N 1000 a o i l M W K O H
N S − T N H = π 4 π R p r e d 3 3 0.602 ∗ 10 6 T B N 1000 a o i l M W K O H
In Eq. (3) and Eq. (4), R p r e d 3 is the radius of the most frequently encountered bubble.
Asphaltenes generally occur in nature as a mixture of molecules of different architecture, characterized by the presence of a polycyclic aromatic core, aliphatic side groups, and frequently different types of heteroatoms [66].The heteroatoms may constitute different functional groups that are continually being elucidated through methods such as FT-ICR MS [67]. In general, the main heteroatom functional groups are S: thiophene, sulfidic, sulfoxide; N: pyrrolic, pyridine, quinoline; and O: hydroxyl, carbonyl, carboxyl [68].
Considering an amphoteric oil surface with pH dependent ionisable acidic and basic groups [69] and following Nagy & Kónya, 2007 [70] the following ionization reactions for acidic and basic groups of crude oil can be written:
≡ C O O H → ≡ C O O − 1 + H +
K C O O − 1 i n t = ≡ C O O − 1 H + ≡ C O O H e x p F ψ 0 / R T
≡ N H + H + → ≡ N H 2 +
K N H 2 + i n t = ≡ N H 2 + H + ≡ N H H + e x p F ψ 0 / R T
In Eq. (5) through Eq. (8), ≡ C O O H is crude oil surface acidic functional group, ≡ C O O − 1 is the deprotonated surface basic group, H + is hydrogen ion, ≡ N H is the surface basic group, F is Faraday constant[F/m], ψ 0 is the surface potential due to surface charge, R is the universal gas constant[J/K), T is the thermodynamic temperature, K C O O − 1 i n t is the intrinsic ionization constant for reaction 5, and K N H 2 + i n t is the intrinsic ionization constant for reaction 7.
In this paper, we have considered the carboxyl group as the predominant ionisable group in crude oil due to its presence in naphthenic acid, resins and asphaltenes as has been acknowledged elsewhere in relationship to their effect on interfacial tension[71,72] , in relationship to produced water [73], and in connection to acidity of crude oil acidity [74].
At a given pH and salinity of produced wastewater, the degree of ionization of surface acidic and basic groups, which is the fraction that is ionized is given as [75]:
α = 0.5 − 1 1 + 10 z p H − p K 2.7 z y s
In Eq. (9), α is the degree of ionization of ionisable groups [-], p H is the negative logarithm to base 10 of the hydrogen ion concentration of produced water [-], p K is the logarithm to base 10 of the ionization constant of surface ionisable group, z is the charge; negative for acidic site and positive for basic site, and y s is the scaled potential defined as [76]:
y s = e ψ 0 T k B
In which, ψ 0 is surface potential [V], k B is Boltzmann constant and e is electronic charge.
Therefore, the total ionized acidic and basic sites can be obtained from Eq. (3) and E. (4) as:
N S − T C O O H − i o n = α π 4 π R p r e d 3 3 π 4 π R p r e d 3 3 0.602 ∗ 10 6 T A N 1000 a o i l M W K O H
N S − T N H − i o n = α π 4 π R p r e d 3 3 π 4 π R p r e d 3 3 0.602 ∗ 10 6 T B N 1000 a o i l M W K O H

3.2. Electric Double Layer Development in Oil in Water Emulsion Systems

Equation (11) and Eq. (12) imply an interfacial charge at the oil-water interface. The free energy of the electric double layer is negative [77], so it develops spontaneously, where surface ionization of ionisable groups on a colloidal particle cause surface adsorption of counter ions from solution.
The Surface Complexation Model in geochemistry is a general concept considering the interfacial equilibrium caused by specific reactions of bulk species with active surface groups [78]. In oil in water emulsion systems, oil is in contact with produced wastewater (brine) and the implication for pH and salinity dependent surface charge density given by Eq. (11) is that the adsorption of solution ions onto variably charged and dispersed crude oil particles will be thermodynamically feasible, resulting in surface complexation reactions. Therefore, there will be ionic interactions at the oil-water interface [79]. Assuming a predominantly sodium chloride brine for oil field waters [80] the following describe the corresponding surface complexation reactions:
≡ C O O − 1 + N a + → ≡ C O O − 1 N a +
K N a + a b s ≡ ≡ C O O − 1 N a + ≡ C O O − 1 N a +
≡ N H 2 + + C l − → ≡ N H 2 + C l −
K C l − a b s ≡ N H 2 + C l − ≡ N H 2 + C l −
In Eq. (21) through Eq. (24), K N a + a b s and K C l − a b s are adsorption constants for sodium and chloride ions respectively [81], N a + is sodium ion, C l − chloride ion, C O O − 1 N a + and N H 2 + C l − are concentrations of the respective surface species [mol2m-2].
The surface charge density (charge per surface area) is linked to the surface concentrations of corresponding ionic species (amount adsorbed at the interface per surface area). Assuming an acidic and basic species dominated oil-water interface with a predominantly sodium chloride brine, the surface charge density is given as: [82]:
σ = F Γ ≡ N H 2 + + Γ ≡ N H 2 + C l + − ≡ C O O − 1 N a + − Γ ≡ C O O − 1
In Eq. (17a), σ is surface charge density [Cm2], F is Faraday constant [Cmol1], ≡ N H 2 + a surface protonated species [m-2], ≡ N H 2 + C l + and ≡ C O O − 1 N a + are surface complexes [m-2] and ≡ C O O − 1 is s surface deprotonated species.
For acidic group dominated crude oil-brine interface, Eq. (17a) reduces to the following:
σ = F Γ ≡ N H 2 + C l + − ≡ C O O − 1 N a + − Γ ≡ C O O − 1
Therefore, to account for the effect of salinity on surface charge density due to surface complexation reactions, models of surface charge density exist in the thermodynamic literature[83,84,85]. In this regard, if the distribution of ionic charge in solution is described by the Poisson-Boltzmann equation (PB), then the surface charge density satisfies the Grahame equation as (Behrens & Grier, 2001) [84]:
σ ψ 0 = 2 ε r ε 0 Κ β e s i n h β e 2 ψ 0
In Eq. (18), σ is the surface charge density [Cm-2], ε r is the relative permittivity of aqueous phase [-], ϵ 0 is the permittivity of space [Fm-1], and Κ is the inverse of the Debye screening length [m-1],
Equation (18) gives the effective surface charge density due to surface complexation effect resulting from electrolytes in solution.
Consequently, the concentration of surface species responsible for bear surface charge density due solely to the pH dependent ionization of acid and basic groups can be given by the following equations:
N S − C O O H − i o n = α 0.602 ∗ 10 6 T A N 1000 a o i l M W K O H
N S − N H − i o n = α 0.602 ∗ 10 6 T B N 1000 a o i l M W K O H
Substitution of the expression for ionization degree gives:
N S − C O O H − i o n = 0.5 − 1 1 + 10 z p H − p K 2.7 z y s 0.602 ∗ 10 6 T A N 1000 a o i l M W K O H
N S − N H − i o n = 0.5 − 1 1 + 10 z p H − p K 2.7 z y s 0.602 ∗ 10 6 T B N 1000 a o i l M W K O H
In Eq. (21) and Eq. (21), N S − C O O H − i o n and N S − N H − i o n are the surface concentrations of ionised acidic and basic groups respectively at a given pH of brine/produced oilfield water. Accordingly, the bear surface charge density due to acidic and basic sites can be written as:
N S − C O O H − i o n = e 0.5 − 1 1 + 10 z p H − p K 2.7 z y s 0.602 ∗ 10 6 T A N 1000 a o i l M W K O H
N S − N H − i o n = e 0.5 − 1 1 + 10 z p H − p K 2.7 z y s 0.602 ∗ 10 6 T B N 1000 a o i l M W K O H
In which e is the electronic charge[C]
Equation (22a) and Eq. (22b) highlight the critical role that the chemistry of crude oil plays due to the ionization of surface acidic and basic groups, given the TAN and TBN which are global characterization parameters for crude oils. The relationship of these equations to interfacial e

3.3. Zeta Potential Model (define zeta potential)

In the electric double layer structure, the zeta potential is the potential at the shear plane [86], and it can be obtained electrokinetically. Thus, using measurement of zeta potential versus pH, and determining the pH at which the value is zero gives the point of zero charge pH of the solid. Behrens and Grier (2001), developed the following model for calculating the zeta potential due to surface charge density [84].
ζ = k T e l n − σ e Γ + σ + l n 10 e / k B T p K − p H − σ C
In Eq. (23), ζ is the zeta potential [V], Γ is the surface concentration [m-1] C is the differential capacitance [Fm-1], p K is logarithm to base 10 of the dissociation constant of surface acidic group, Γ is the surface concentration of acidic group [m-1], k B IS Boltzmann constant [JK-1]
The capacity of the electric double layer to store energy is related to the differential capacitance, and it is given by the free energy stored in the system after charging. On a per unit area basis, the energy density can be calculated by the reversible work of charging [87].The differential capacitance is defined as the derivative of the surface charge density with respect to the surface potential difference. It is given as [88]:
C = d σ ψ 0 d ψ 0
In which ψ 0 is the surface potential [V].
Bsed on Eq. (18), the result of Eq. (24) can be written in another form as [89,90]:
C = d σ ψ 0 d ψ 0 = 2 c z 2 F 2 ϵ r ϵ 0 / R T 0.5 c o s h z F ψ 0 2 R T
In Eq. (25), c is the concentration [molm-3], z is the ion valence, ϵ r is the relative permittivity [-], ϵ 0 is the permittivity of free space [Fm-1],R is the universal gas constant [JK-1], T is the absolute temperature, and F is Faraday constant [Cmol-1

4. Relevance of Theoretical Models to Oil Water Interfacial Chemistry and Emulsion Stability

The detailed background and theoretical developments of Section 3 can be exploited for further interpretation of the electrostatics of the oil-water interface in oil in water emulsion systems. The following sections will be devoted to that.

4.1. Salinity and pH Depended Surface Charge Density

To obtain a theoretical plot of effective surface charge density at the oil-water interface for oil in water emulsions systems, three fundamental parameters are required. They are the point of zero charge pH of an oil surface, the number density of ionic species in brine in contact with the oil phase and the pH of brine. The number density, n [m-3], in Eq. (15) is calculated as:
n = I N A
Where I is the ionic strength [90] [M] and N A is Avogadro’s number [M-1]
I = 0.5 ∑ 1 n c i z 2
In this Eq. (27), ∑ 1 n c i is the concentration of a species i [M], and z is the charge on the ionic species.
A model of surface potential based on the Gouy-Chapman model [91] exists in the literature, but we will use the surface potential variation with aqueous pH as given by the Nernst equation as [92]:
ψ 0 = 2.303 k B T e p H p z c − p H
In Eq. (13), p H p z c is point of zero charge pH of crude oil surface [-] and p H is the negative logarithm to base 10 of the hydrogen ion concentration.
Hence the differential capacitance equation becomes:
C = d σ ψ 0 d ψ 0 = 2 c z 2 F 2 ϵ r ϵ 0 / R T 0.5 c o s h z F 2 R T 2.303 k B T e p H p z c − p H
The Debye length is salinity dependent. Hence, the surface charge density equation (Eq.18) becomes:
σ ψ 0 = 2 ε ε 0 Κ β e s i n h β e 2 2.303 k B T e p H p z c − p H
Equation (30) gives the effective surface charge density due to surface complexation effect resulting from electrolytes in solution.

4.2. pH Depended Degree of Ionization of Surface Ionisable Groups on Oil

Equation 9 and Eq. (10) together with data on the pK of the surface ionisable group provide the theoretical basis for calculating the pH dependence of the degree of ionization at the oil-water interface. The relationship between surface charge density and surface potential is given as [93]:
e ψ 0 k B T = σ 2 π ϵ n k B T
In which n is the number density of ions in solution [m-3].
From Eq. (10), the dimensionless potential gives:
y s = e ψ 0 k B T = σ 2 π ϵ n k B T
Thus, the degree of ionization equation (Eq.9) can be written as:
α = 0.5 − 1 1 + 10 z p H − p K 2.7 z σ 2 π ϵ n k B T
Based on Eq. (24), the degree of ionization at a given and salinity determined by the number density n (Eq. 30) of electrolyte and temperature can be calculated.
The following table shows the pK of acid base components of crude oil

5. Methodologies

5.1. Theoretical Calculations

To theoretically interpretation pH and Salinity Effect on oil in water emulsion stability based on Interfacial Chemistry and the implications for produced water demulsification, theoretical calculations based on Eq. (26), Eq. (27), Eq. (29), Eq. (30) and Eq. (33) will be required together with relevant data from literature sources. In this regard the research work of Bonto et al. (2019) [39] contains data on the isoelectric points of different crude oils. Table 1 sums up the required data.
Assuming a salinity range of 12 to 180 parts per thousand [94] for produced oilfield waters, the following table is valid using Eq. (26) and Eq. (27).
Column 5 of Table 2 contains permittivity data extracted from the graph of Gavish and (2016) [95]. Additional data regarding the pKa value for the dissociation of acidic group were taken from Bonto et al. (2019) [39] research work. The following table gives the details.
Based on data from Table 1, Table 2 and Table 3, and application of Eq. (26), Eq. (27), Eq. (29), Eq. (30) and Eq. (30), plots for typical pH range (4.7-7.5) [96] of produced oilfield water have been generated and the results will be discussed in the following sections. The values of physical constants used in the calculations were [97]: electronic charge (1.6*10-19 C) Avogadro’s number (6.02*10-23 mol-1), Boltzmann constant (1.38*10-23 JK-1), Faraday’s constant (96485 Cmol-1) and permittivity of vacuum (8.85*10-12 Fm-1 [98]. The number density of carboxyl group of Moutray oil was taken from the research work of [99]. Calculations were based on a temperature of 294 K, to reflect that of produced oilfield water in the ambient environment.

5. Results and Discussion

5.1. Degree of Ionization of carboxyl Acidic Group of Oils

The pH dependent ionization degree of carboxyl group is similar to that of pH dependent dissociation of acidic components of crude oil [73]. Figure shows a plot of the ionization degree of the acidic group of crude oils versus pH at a temperature 294 K. The isoelectric point (IEP) and the point of zero charge (PZC) reflect the response of a surface to an electrolyte [100,101]. Following protonation and deprotonation reactions, due to amphoteric behavior, positive or negative charges can be generated on the surface. Due to the presence of acidic and basic sites on surfaces, positive and negative charge may coexist. The isoelectric point is the value of pH at which the Electrokinetic potential is equal to zero and, therefore, the pH at which colloidal particle remains stationary in an electrical field. Under normal circumstances, the isoelectric point is expected to differ from the point of zero charge pH at the particle surface, except for pristine surfaces with no specific ion adsorption [101,103]. In the present study, the point of zero charge at the surface is taken as equal to the isoelectric point in the absence of specific adsorption on that surface. Elsewhere, the pH dependence of the effective pKa has been reported [103]. In our study, we assume constant pKa values for the different crude oil samples. Therefore, in line with the role of the pKa in surface charge regulation [104] and its relationship to the point of zero charge pH Eq. (33) was used for the calculation of the degree of ionization of the carboxyl group of crude oils in line with its dominance. Table 1 shows the isoelectric points of the crude oils. From the table, it is clear that the isoelectric points of the oil samples are closer, and that justifies the appearance of the curves. Most importantly, the figure shows that for all the salinities considered, the degree of ionization increases with pH and salinity as reported elsewhere [105]. Moreover, considering the pH range of produced oilfield waters used in this study, the isoelectric point/point of zero charge are below the pH range which means the development of negative surface charge for all the oils [107]. Generally, salinity has a positive effect on surface charge density and this reflects the trend of ionization degree with salinity as found in Figure 3.
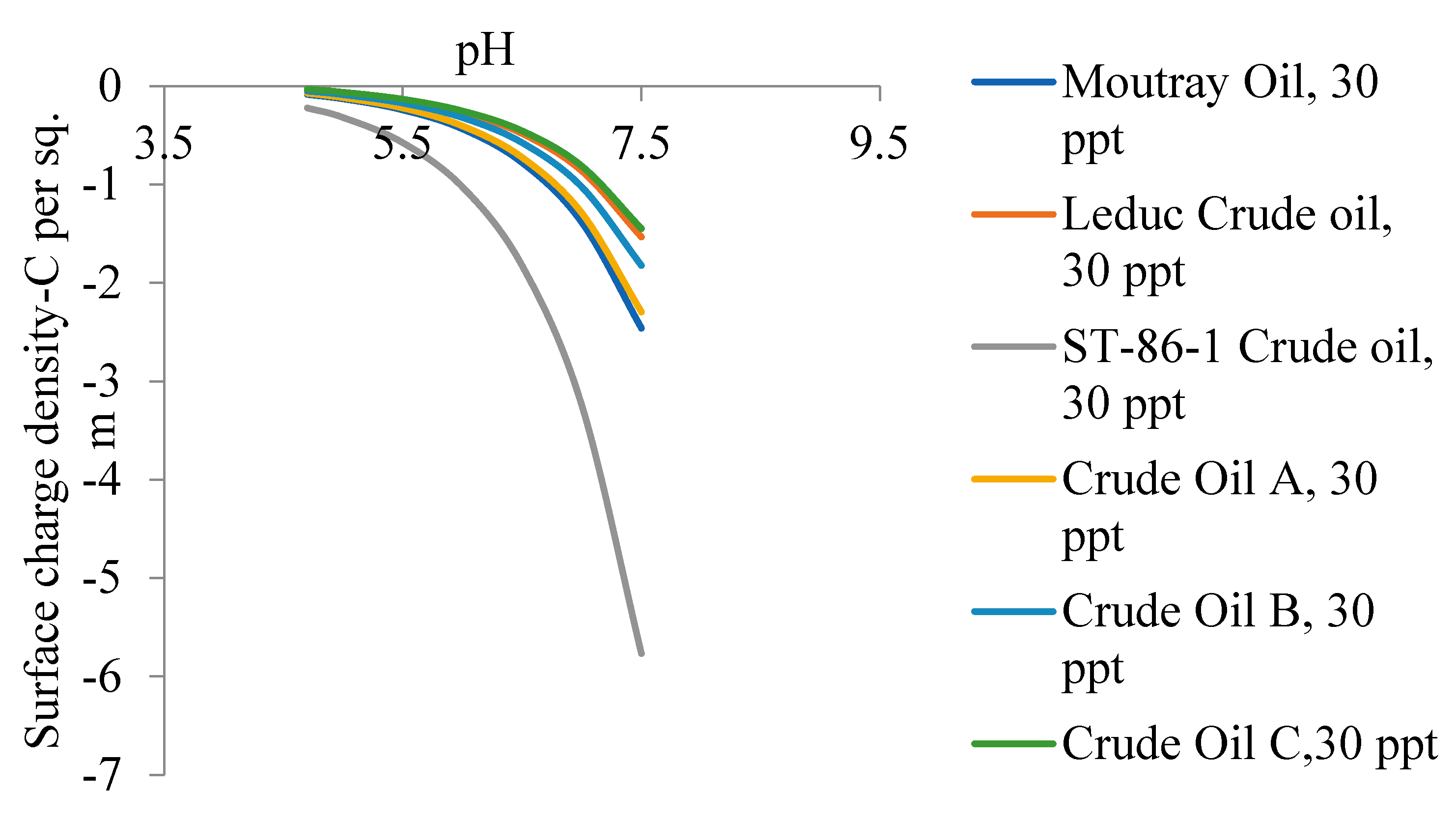
In addition to the most recent work of Bonto at al. (2019) [39], Moutray Crude oil was studied in relationship to the effect of brine on its recovery by water flooding [108]. Therefore, we have been motivated by these two cited references to single out Moutray Crude oil for showing the effect of pH on surface charge density as a function of salinity. Accordingly, Figure 4 shows the plots. The figure shows that as pH increases, surface charge density on the droplets of Moutray Crude oil in oil in water emulsion systems will increase. Moreover, salinity has a positive effect on surface charge density, implying increasing salinity increases surface charge density [84,108,109]. From Table 1, Crude Oil A has the lowest isoelectric point after Moutray Oil, with the potential to develop surface charge over a wider range of pH. Figure 3 shows plots of surface charge density versus pH for Crude Oil A as a function of salinity, for different salinities where higher salinities show higher surface charge density. Figure 6 shows plots of surface charge density versus pH for the 6 oil samples for salinity equal to 30 ppt. The figure shows that Crude Oil ST-86-1 has the highest surface charge density for the salinity considered followed by Moutray Crude Oil while Crude Oil C has the lowest surface charge density.
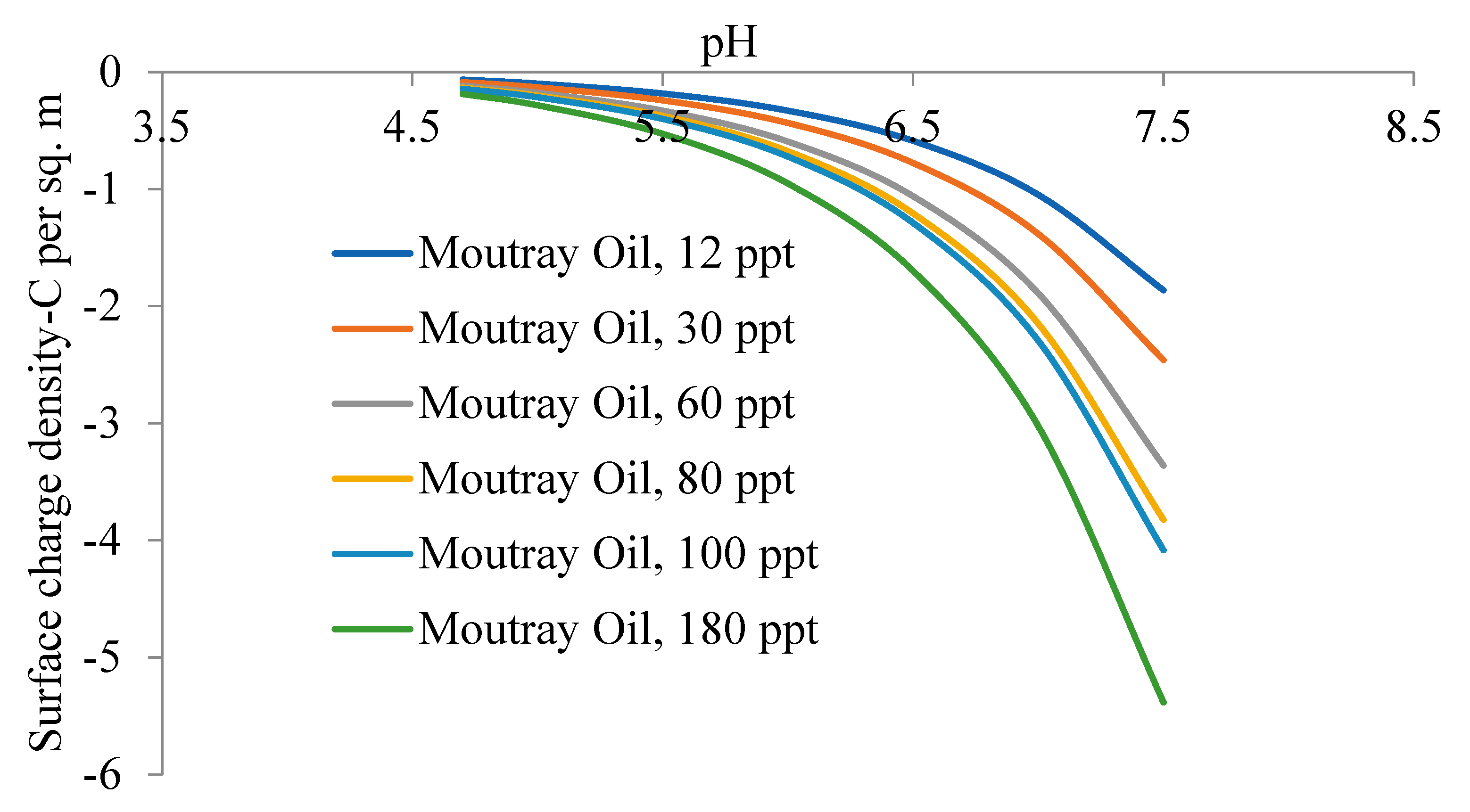
Preprints 79121 g004
Figure 4. Surface charge density of Moutray Oil versus pH as a function of salinity.
Figure 4. Surface charge density of Moutray Oil versus pH as a function of salinity.
Preprints 79121 g004
Preprints 79121 g005
Figure 5. Surface charge density of Crude Oil A versus pH as a function of salinity.
Figure 5. Surface charge density of Crude Oil A versus pH as a function of salinity.
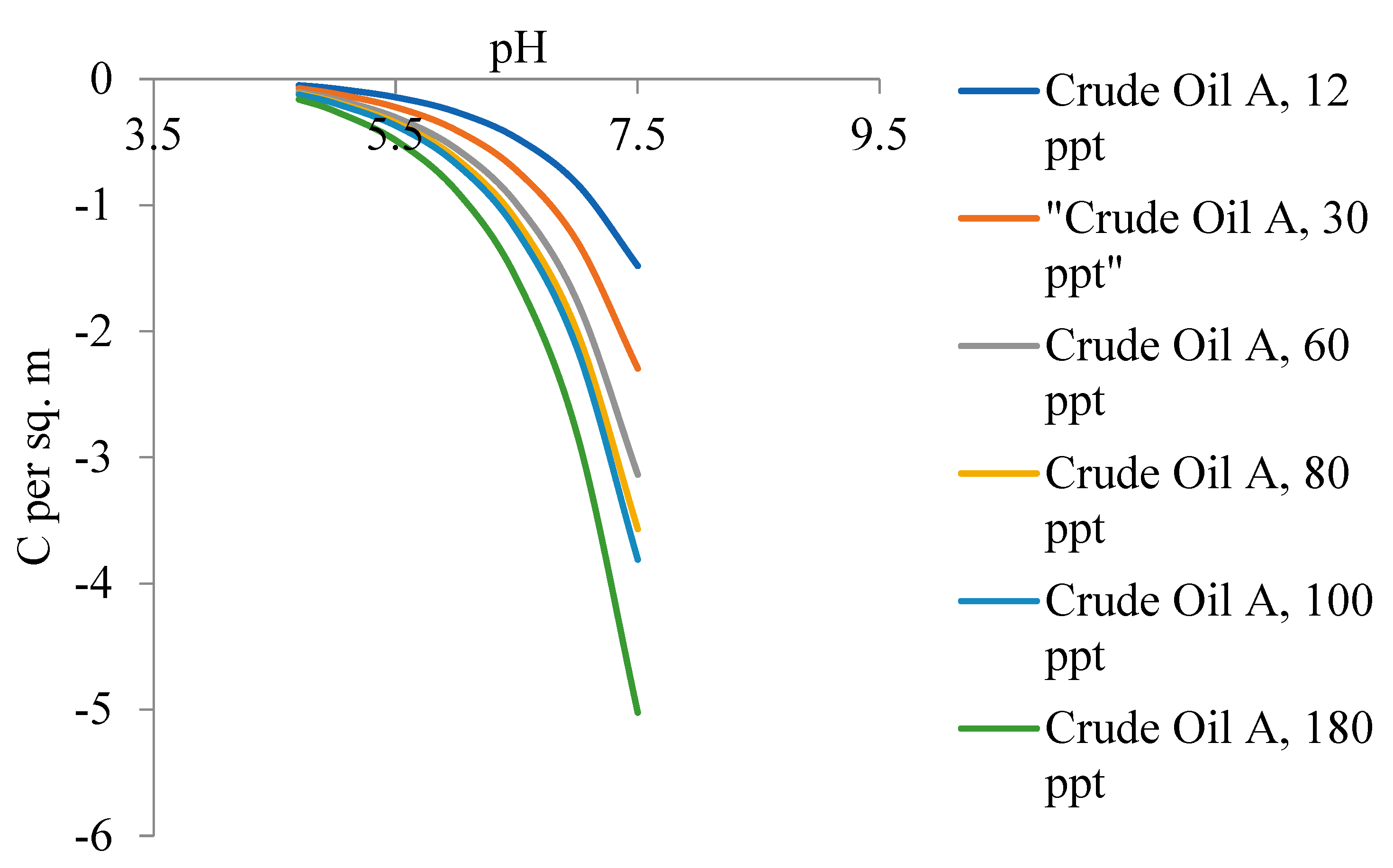
Preprints 79121 g005
Preprints 79121 g006
Figure 6. Surface charge density of 6 Crude Oil samples versus pH for salinity equal to 30 ppt.
Figure 6. Surface charge density of 6 Crude Oil samples versus pH for salinity equal to 30 ppt.
Preprints 79121 g006

5.2. Zeta Potential of Crude Oils Samples

The zeta potential of oil droplets depends on the oil chemical composition, on water pH and salinity and on the presence of surfactants [110].
Figure 7 through Figure 9 show plots of zeta potential versus pH for Crude Oils A, B and C respectively. The plots show a monotonous decrease in zeta potential with pH, where higher salinity corresponds to lower zeta potential for all the oil samples. Therefore, trends revealed by these figures are those reported in connection with low salinity water flooding oil recovery schemes [112] and in connection with the improving oil recovery through the clay state change during low salinity water flooding in sandstones [112]. Figure 10 shows comparison of zeta potential versus pH as a function of salinity for Crude Oil samples ST-86-1, B, and C for salinities 12 ppt. and 100 ppt. Trends revealed by Figure 7 through Figure 9 are also consistent with those revealed the findings of Kataya et. al.(2022) [113], who studied the effect of brine salinity, cation type, pH, and produced sand on seta potential measurements. The plots show that for all the salinities considered, Crude oil sample ST-86-1 has the highest zeta potential versus pH followed by Crude Oil sample B, with Crude Oil sample C being the sample with the lowest zeta potential.
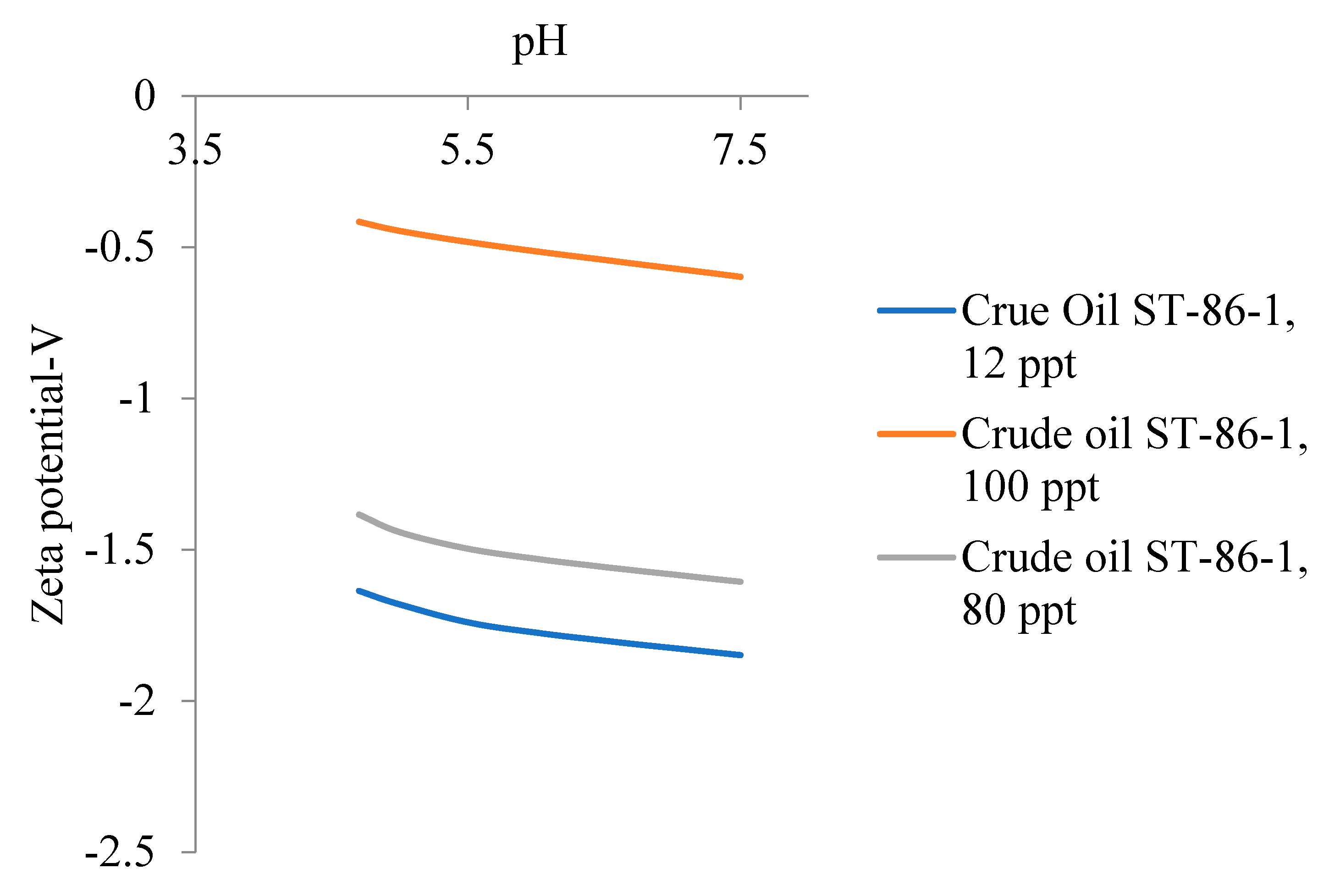
Preprints 79121 g007
Figure 7. Zeta potential versus pH for Crude Oil A.
Figure 7. Zeta potential versus pH for Crude Oil A.
Preprints 79121 g007
Preprints 79121 g008
Figure 8. Zeta potential versus pH for Crude Oil B.
Figure 8. Zeta potential versus pH for Crude Oil B.
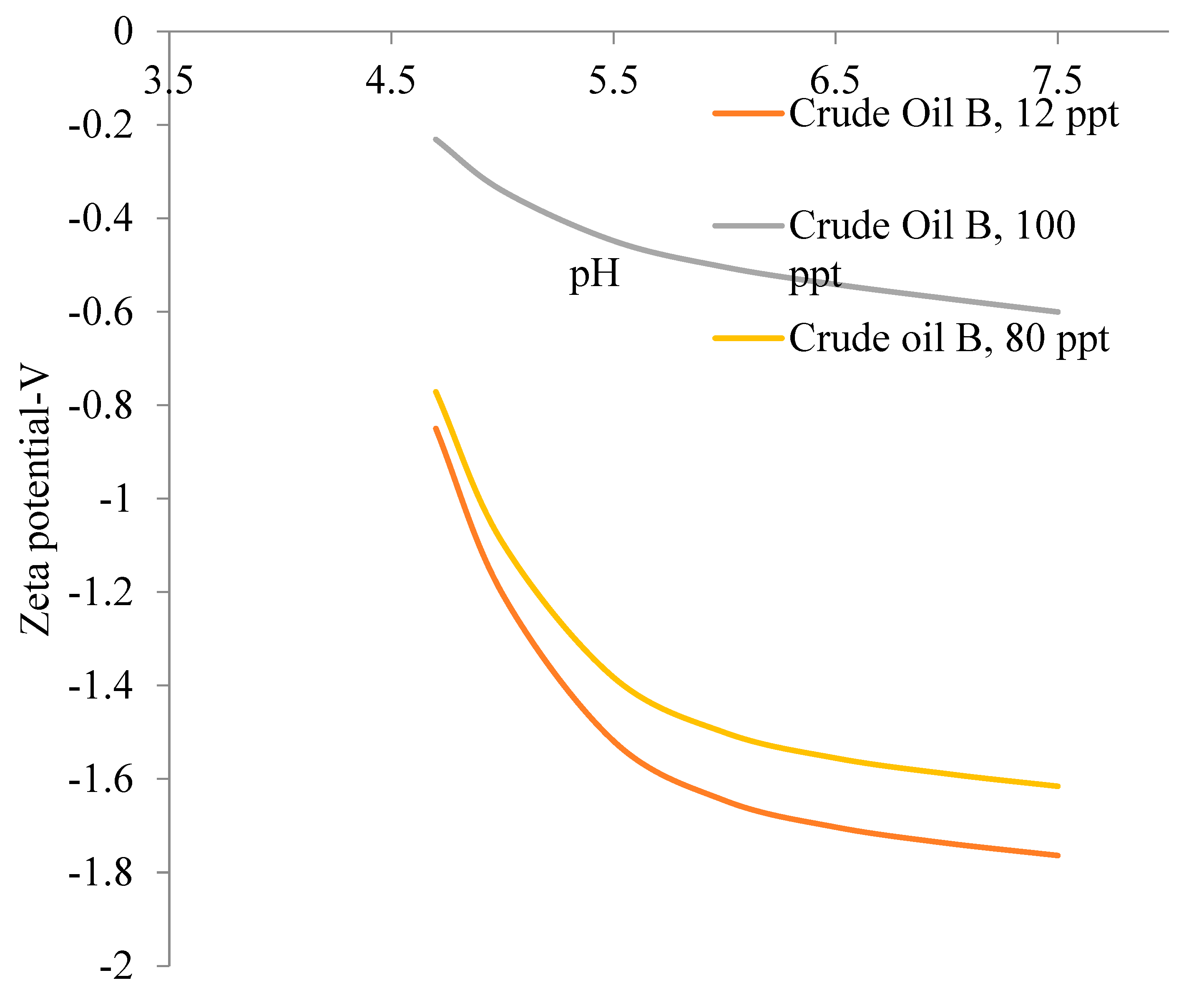
Preprints 79121 g008
Preprints 79121 g009
Figure 9. Zeta potential versus pH for Crude Oil C.
Figure 9. Zeta potential versus pH for Crude Oil C.
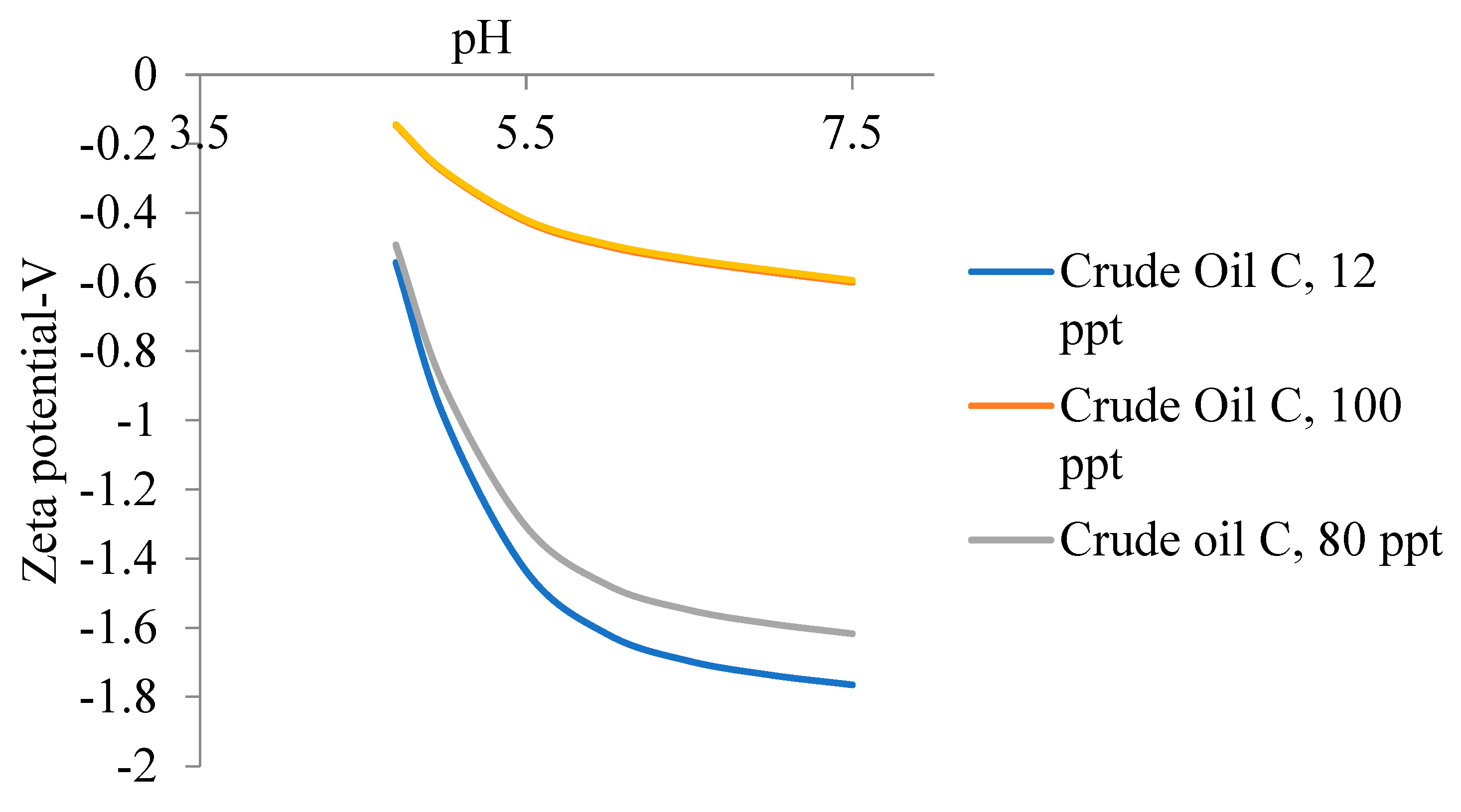
Preprints 79121 g009
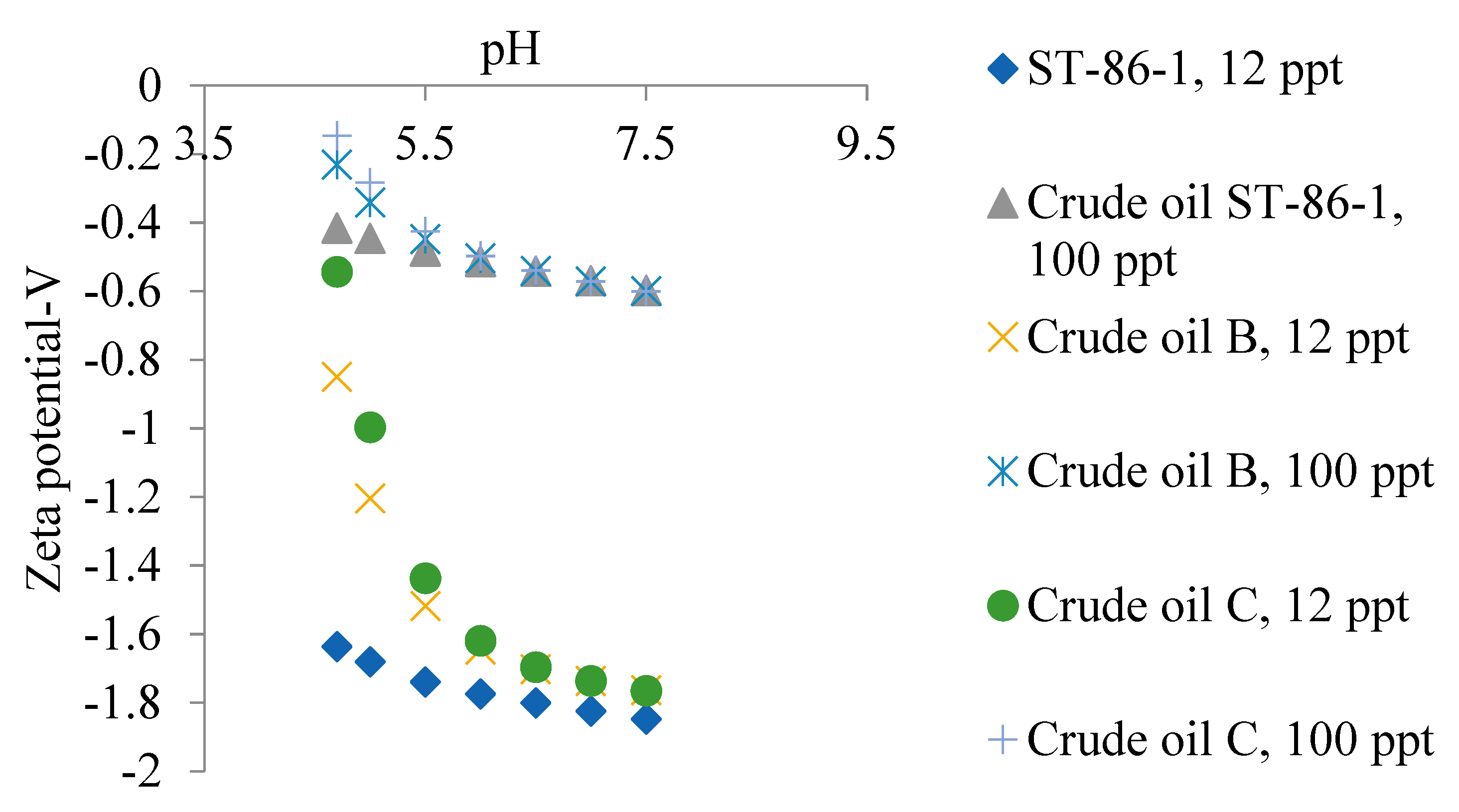
Preprints 79121 g010
Figure 10. Zeta potential versus pH for Crude Oil A.
Figure 10. Zeta potential versus pH for Crude Oil A.
Preprints 79121 g010

5.3. Emulsion Stability of Oil in Water Emulsion for Different Crude Oil Samples

In line with the direct correlation between surface charge density and zeta potential and those between salinity and these interfacial parameters in colloidal systems [108,114,115,116] the eminent difference among the crude samples as seen in the figures discussed so far imply different degrees of stability of oil in water emulsions systems involving these crude oil. Moreover, surface forces involving disjoining pressure are directly linked to double layer repulsion stabilization of colloidal systems, where zeta potential and surface potential have direct correlations [117,118]. Based on Figure 6, where surface charge densities of the six crude oils have been plotted for a 30 ppt salinity of produced oilfield water, sample ST-86-1 will show the highest double layer electrostatic repulsive contribution to colloidal stabilization due to the direct positive correlation between surface charge density and surface potential [119]. Accordingly, by modelling oil droplets in oil in water emulsion as a spherical, the order of decreasing emulsion stability will be: ST-86-1>Moutray Oil> Crude Oil A> Crude Oil B> Leduc Oil > Crude Oil C. Accordingly, trend revealed by this electrostatic stabilization reflects zeta potential as seen in Figure 10 for two different salinities involving three of the oil samples, where Sample ST-86-1 shows the highest zeta potential, followed by Sample C, with Sample B having the least zeta potential for the salinities considered.

5.4. Implications for Produced Oilfield Water Demulsification with Different Demulsifiers

In the oil and gas industries operators face limits to the permissible oil content in produced water before it can be discharged back into the environment, and limits are typically set by national authorities based on both instantaneous and average discharge limits. Federal regulations normally set the daily maximum limit at 42 mg/L average and 50 mg/L for the marine environment. Considering the offshore environment, the daily maximum limit is 48 mg/L average and 72 mg/L for an instantaneous discharge. These stringent environmental regulations require treatment of produced oilfield water to remove enough oil to meet these thresholds discharge in to the environments [120]. Therefore, produced water must be treated, using emulsifiers which are molecules enhancing the separation of oil from water, often at a reduced concentration by lowering the interfacial shear viscosity to extend the interfacial mobility and destabilizing emulsions [121]. Consequently, the amount of demulsifier required will depend on the extent of emulsion stability. Typically, the amount of demulsifier applied is between ten and one hundred parts per million (ppm) in total production, which can be higher in tertiary oil recovery. There are three basic methods for demulsification: physical, chemical and biological [122], and the effectiveness is based on the ability in reducing the emulsion stability to produce two distinct phases [123]. Generally, water soluble demulsifiers are used employed to destabilize oil in water emulsions. To destabilize the emulsion, the oil droplets must flocculate and eventually coalesce. Under such conditions, experimental results based on analysis of Variance (ANOVA) show that the dosage of demulsifier, temperature, and sedimentation times was the key variables [124].
It is obvious that at higher temperatures, the Bjerrum length scale, which is the fundamental length scale at which thermal energy becomes comparable to electrostatic energy, will be relatively higher [125]. This trend will be augmented, given the generally high salinity range of produced oilfield waters and the consequence reduction in the dielectric permittivity [126]. The implication is that for produced oilfield waters, electrostatic equalize thermal energy at relatively shorter distance in the emulsion system.
Chemical demulsification consists in adding chemicals called demulsifiers to accelerate the coalescence of the dispersed phase of the emulsion [127]. Such chemicals are designed to neutralize the effect of surfactants (surface ionisable groups) that naturally stabilized the emulsion, and displace them from the interfacial films that stabilize emulsion droplets leading to enhance demulsfication. Therefore, effective chemical demulsification requires circumspection in the selection of demulsifiers for a given emulsion systems. The effectiveness of surfactants must not be hindered by electrostatic repulsion. Given the relatively wider range over which electrostatic stabilization will occur; such surfactants must be able to diffuse over a wider range without electrostatic interaction effects. Consequently, for oil in water emulsion system characteristic of oilfield produced waters, water soluble non-ionic ethoxylated surfactants with a wider range of pH and salinity stability are potential demulsifiers. Therefore, under room temperature demulsification of produced oilfield water waters, higher salinity waters will experience less effective demulsification where diffusion mechanism control the transport of surfactants between interfaces. On the part of zeta potential effect, higher salinities mean lower values and lower emulsion stability, which requires lower concentration of surfactants. Therefore, trends of zeta potential as found in Figure 5 to Figure 7 will reflect the effectiveness of demulsification.
However, while non-ionic surfactants are potential demulsifiers, to eliminate electrostatic repulsive effects of potential surfactants, the point of zero charge pH/isoelectric point of oil droplets in oil in water emulsions are a perfect guide in selecting demulsifiers. For the oil samples studied in this paper, the point of zero charge pH values are averagely below the average pH of produced oilfield waters, 6.00-6.78 [128]. Consequently, from Table 1, the droplets of oil samples will develop negative surface charge densities and the selection of water soluble cationic surfactants is other options [129]. Under such options, trends revealed by Figure 8 with regard to zeta potential will determine the effectiveness of demulsification for the oils (SR-86-1, B, and C), where the positive correlation between zeta potential and surface charge density means oils with higher zeta potentials will experience higher electrostatic attraction between surfactant molecules. Moreover, under such conditions, the electrostatic repulsion between positively charge surfactant species will enhance the surface activity of adsorbed surfactants leading to enhanced demulsification [130].

5.5. Effect of Interfacial Energy on Demulsification

A fundamental property of liquid−liquid systems/interfaces governing their behavior is the interfacial tension, which is defined as the excess energy per unit area at a fluid−fluid interface or the work done required to create unit interface [131], arising from unbalanced cohesive forces between molecules in the two bulk phases [132]. Systems with higher interfacial energy drive a reduction in the interfacial are and colloidal systems with high interfacial tensions tend to coalesce more readily
In the literature, the interfacial electrical potential difference, which has a positive correlation with the surface charge density and zeta potential, has been experimentally found to decrease the interfacial tension in a manner consistent with Poisson−Boltzmann theory inspired from Frenkel and Verwey−Overbeek [133], implying lower interfacial tension for oils with higher zeta potential. Studies have demonstrated that a smaller particle size and more uniform distribution could improve emulsion stability [134]. The implication for interfacial tension reduction related to surface potential is that oil droplet sizes will reflect trend in zeta potential of oil samples (See Section 5.2), where oil samples with higher zeta potential will have the lowest radii [135] due to the ease with which an interface can be formed in the colloidal systems. Therefore, the surface excess or coverage of diffusing demulsifiers will be greater, leading to efficient demulsification.

6. Conclusions

Considering the mechanical and hydrodynamic shearing effects inherent in crude oil production from the reservoir to oilfield surface facilities, the formation of oil in water emulsion is inevitable. To meet stringent environmental regulations governing the disposal of produced waters, demulsification of such waters is essential. To efficiently carry out demulsification, the type of emulsion, and the chemistry of crude oil and produced water must be properly understood. The chemical and physical behavior of such emulsion systems can be described by fundamental principles enshrined in the electric double layer theory and the analytical continuum electrostatics potential [136] obtained from the approximate solution to the Poisson-Boltzmann equation. In this paper, we have used the theoretical foundations underlying the electrostatics of emulsion systems to study oil in water emulsions of six different oilfield produced waters with closer values of electrokinetic properties at room temperature. The following sum up our conclusions.
  • Calculated trends in Surface charge densities obtained in this study conform to those found in the colloids literature, where there is a positive correlation with increasing salinity,
  • Calculated trends in zeta potential obtained in this study conform to those found in the colloids literature, where there is a negative correlation with increasing salinity,
  • The closeness of the isoelectric points of the oil samples studied in this paper causes a slight distinction between the degrees of ionization of the oils at a given pH for the range of produced oilfield water salinity,
  • The zeta potential is the most significant determinant for emulsion stability. Based on our theoretical calculations, oil sample ST-86-1, has the most stabilized emulsion systems under room temperature conditions, and it will require a more intensive chemical demulsification procedures,
  • Given the acidic nature of the isoelectric points of the oil samples, and the near neutral pH of produced oilfield waters, decreasing pH to approximately 4 will constitute a near zero surface charge/zeta potential, which is a cheap and efficient means of coalescence and coagulation leading to efficient demulsification.

Author Contributions

Conceptualization, M. A. and A. M..; methodology, M. A. and A. M.; writing—original draft preparation, M.A.; Calculations, M.A.; graph plotting, M.A.; supervision, A.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research has received no external funding.

Data Availability Statement

Not Applicable.

Acknowledgments

We wish to acknowledge the immense role played by Cape Breton University Library Document Delivery Section for the timely supply of relevant literature. Moreover, data processing and plotting would not have been easy without the use of up-to-date computer resources in the library.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. ACS. "Development of the Pennsylvania Oil Industry," 2009. [Online]. Available online: https://www.acs.org/education/whatischemistry/landmarks/pennsylvaniaoilindustry.html#:~:text=On%20this%20site%20Edwin%20Drake,to%20be%20burned%20in%20lanterns.
  2. A. Brandt, "Oil substitution and the decline in conventional oil," 2023. [Online]. Available online: https://eao.stanford.edu/research-project/oil-substitution-decline-conventional-oil.
  3. Bentley, R. Global oil & gas depletion: an overview. Energy Policy 2002, 30, 189–205. [Google Scholar] [CrossRef]
  4. Höök, M.; Davidsson, S.; Johansson, S.; Tang, X. Decline and depletion rates of oil production: a comprehensive investigation. Philos. Trans. R. Soc. London. Ser. A: Math. Phys. Eng. Sci. 2014, 372. [Google Scholar] [CrossRef] [PubMed]
  5. R. Weyler, "The decline of oil has already begun," 2020. [Online]. Available online: https://www.greenpeace.org/international/story/29458/peak-oil-decline-coronavirus-economy/.
  6. Stratas-Advisors, "Heavy Crude Oil Supply Outlook Quarterly Q2 2019," 2019. [Online]. Available online: https://stratasadvisors.com/Insights/2019/061719-Upstream-Heavy-Crude-Outlook-Quarterly-Q2#:~:text=Global%20Heavy%20Crude%20Oil%20production%20Overview&text=Global%20heavy%20oil%20supply%20is,HSFO)%20yield%20in%20the%20world.
  7. L. Paszkiewicz, "EXTRA HEAVY OILS IN THE WORLD ENERGY SUPPLY," 2012. [Online]. Available online: http://www.oilproduction.net/files/extra-heavy-oils-in-the-world-energy-supply.pdf.
  8. Hedar, Y. ; Budiyono Pollution Impact and Alternative Treatment for Produced Water. E3S Web Conf. 2018, 31, 03004. [Google Scholar] [CrossRef]
  9. Konkel, L. Salting the Earth: The Environmental Impact of Oil and Gas Wastewater Spills. Environ. Heal. Perspect. 2016, 124, A230–A235. [Google Scholar] [CrossRef]
  10. Shaikh, S.S.; Abu-Dieyeh, M.H.; Al Naemi, F.A.; Ahmed, T.; Al-Ghouti, M.A. Environmental impact of utilization of “produced water” from oil and gas operations in turfgrass systems. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef] [PubMed]
  11. EPA, "Detailed Study of the Centralized Waste Treatment Point Source Category for Facilities Managing Oil and Gas Extraction Wastes EPA-821-R-18-004," 2018. [Online]. Available: (2018) Detailed Study of the Centralized Waste Treatment Point Source Category for Facilities Managing Oil and Gas Extraction Wastes EPA-821-R-18-004.
  12. EPA, "Summary of Input on Oil and Gas Extraction Wastewater Management Practices Under the Clean Water Act," EPA, Washington, 2020.
  13. J. Pichte, "Oil and Gas Production Wastewater: Soil Contamination and Pollution Prevention," Soil Pollution Prevention and Remediation, pp. 1–14, 2016. [CrossRef]
  14. Jiang, W.; Lin, L.; Xu, X.; Wang, H.; Xu, P. Analysis of Regulatory Framework for Produced Water Management and Reuse in Major Oil- and Gas-Producing Regions in the United States. Water 2022, 14, 2162. [Google Scholar] [CrossRef]
  15. Maphosa, Y.; Jideani, V.A. Factors Affecting the Stability of Emulsions Stabilised by Biopolymers, in Science and Technology Behind Nanoemulsions, IntechOpen, 2018, pp. 65–81. [CrossRef]
  16. F. Ishii and T. Nii, "Chapter 22 - Lipid emulsions and lipid vesicles prepared from various phospholipids as drug carriers," in Colloid and Interface Science in Pharmaceutical Research and Development, 2014, pp. 469–501. [CrossRef]
  17. C. Costa, B. C. Costa, B. Medronho, A. Filipe, I. Mira, B. Lindman, H. Edlund and M. Norgren, "Emulsion Formation and Stabilization by Biomolecules: The Leading Role of Cellulose," Polymers (Basel). 2019, vol. 11, no. 10, pp. 1–18, 2019. [CrossRef]
  18. Håkansson, A. Emulsion Formation by Homogenization: Current Understanding and Future Perspectives. Annu. Rev. Food Sci. Technol. 2019, 10, 239–258. [Google Scholar] [CrossRef]
  19. Abdulredha, M.M.; Hussain, S.A.; Abdullah, L.C. Overview on petroleum emulsions, formation, influence and demulsification treatment techniques. Arab. Jounal Chem. 2020, 13, 3403–3428. [Google Scholar] [CrossRef]
  20. Ahmed, N.S.; Nassar, A.M.; Zaki, N.N.; Gharieb, H.K. Formation of fluid heavy oil-in-water emulsions for pipeline transportation. Fuel 1999, 78, 593–600. [Google Scholar] [CrossRef]
  21. S. S. Dol, "The Effect of Flow-Induced Oil-Water Emulsions on Pressure Drop," Journal of Theoretical and Applied Mechanics, vol. 2, pp. 73–78, 2019.
  22. Fajun, Z.; Zhexi, T.; Zhongqi, Y.; Hongzhi, S.; Yanping, W.; Yufei, Z. Research status and analysis of stabilization mechanisms and demulsification methods of heavy oil emulsions. Energy Sci. Eng. 2020, 8, 4158–4177. [Google Scholar] [CrossRef]
  23. Sams, G.W.; Zaouk, M. Emulsion Resolution in Electrostatic Processes. Energy Fuels 1999, 14, 31–37. [Google Scholar] [CrossRef]
  24. Cerbelaud, M.; Aimable, A.; Videcoq, A. Role of Electrostatic Interactions in Oil-in-Water Emulsions Stabilized by Heteroaggregation: An Experimental and Simulation Study. Langmuir 2018, 34, 15795–15803. [Google Scholar] [CrossRef]
  25. Tian, Y.; Zhou, J.; He, C.; He, L.; Li, X.; Sui, H. The Formation, Stabilization and Separation of Oil–Water Emulsions: A Review. Processes 2022, 10, 1–34. [Google Scholar] [CrossRef]
  26. Leunissen, M.E.; Van Blaaderen, A.; Hollingsworth, A.D.; Sullivan, M.T.; Chaikin, P. M. Electrostatics at the oil–water interface, stability, and order in emulsions and colloids. Proc. Natl. Acad. Sci. USA 2007, 104, 2585–2590. [Google Scholar] [CrossRef]
  27. Ghanavati, M.; Shojaei, M.-J.; S.A., A.R. Effects of Asphaltene Content and Temperature on Viscosity of Iranian Heavy Crude Oil: Experimental and Modeling Study. Energy Fuels 2013, 27, 7217–7232. [Google Scholar] [CrossRef]
  28. Shi, Q.; Wu, J. Review on Sulfur Compounds in Petroleum and Its Products: State-of-the-Art and Perspectives. Energy Fuels 2021, 35, 14445–14461. [Google Scholar] [CrossRef]
  29. Das, S.; Thundat, T.; Mitra, S.K. Analytical model for zeta potential of asphaltene. Fuel 2013, 108, 543–549. [Google Scholar] [CrossRef]
  30. Acevedo, S.; Castillo, J. Asphaltenes: Aggregates in Terms of A1 and A2 or Island and Archipielago Structures. ACS Omega 2023, 8, 4453–4471. [Google Scholar] [CrossRef]
  31. Salmón-Vega, S.; Herrera-Urbina, R.; Lira-Galeana, C.; Valdez, M.A. The Effect of Ionic Surfactants on the Electrokinetic Behavior of Asphaltene from a Maya Mexican Oil. Pet. Sci. Technol. 2012, 30, 986–992. [Google Scholar] [CrossRef]
  32. Li1, Y.; Xiang, D. Stability of oil-in-water emulsions performed by ultrasound power or high-pressure homogenization. PLoS ONE 2019, 14, 1–14. [Google Scholar]
  33. Bera, B.; Khazal, R.; Schroën, K. Coalescence dynamics in oil-in-water emulsions at elevated temperatures. Sci. Rep. 2021, 11, 1–10. [Google Scholar] [CrossRef]
  34. Macritchie, F. Barrier to Coalescence in Stabilized Emulsions. Nature 1967, 215, 1159–1160. [Google Scholar] [CrossRef]
  35. Huang, B.; Nan, X.; Fu, C.; Liu, W.; Guo, W.; Wang, S.; Zhang, L. Probing the Coalescence Mechanism of Oil Droplets in Fluids Produced by Oil Wells and the Microscopic Interaction between Molecules in Oil Films. Energies 2022, 15, 4274. [Google Scholar] [CrossRef]
  36. Zhang, Z.; Song, J.; Lin, Y.-J.; Wang, X.; Biswal, S.L. Comparing the Coalescence Rate of Water-in-Oil Emulsions Stabilized with Asphaltenes and Asphaltene-like Molecules. Langmuir 2020, 36, 7894–7900. [Google Scholar] [CrossRef]
  37. Mehta, S.; Kaur, G. Microemulsions: Thermodynamic and Dynamic Properties. Thermodynamics 2011, 381–406. [Google Scholar] [CrossRef]
  38. Zore, A.; Geng, P.; Van De Mark, M.R. Equilibrium and Dynamic Surface Tension Behavior in Colloidal Unimolecular Polymers (CUP). Polymers 2022, 14, 2302. [Google Scholar] [CrossRef]
  39. Bonto, M.; Eftekhari, A.A.; Nick, H.M. An overview of the oil-brine interfacial behavior and a new surface complexation model. Sci. Rep. 2019, 9, 1–16. [Google Scholar] [CrossRef]
  40. Nenningsland, A.L.; Simon, S.; Sjöblom, J. Surface Properties of Basic Components Extracted from Petroleum Crude Oil. Energy Fuels 2010, 24, 6501–6505. [Google Scholar] [CrossRef]
  41. Bertheussen, A.; Simon, S.; Sjöblom, J. Equilibrium partitioning of naphtenic acids and bases and their consequences on interfacial properties. Colloids Surf. A-Physicochem. Eng. Asp. 2017, 529, 45–56. [Google Scholar] [CrossRef]
  42. Ameri, A.; Esmaeilzadeh, F.; Mowla, D. Effect of Brine on Asphaltene Precipitation at High Pressures in Oil Reservoirs. Pet. Chem. 2018, 58, 1076–1084. [Google Scholar] [CrossRef]
  43. R. Mokhtari, A. R. Mokhtari, A. Hosseini, M. Fatemi, S. I. Andersen and S. Ayatollahi, "Asphaltene destabilization in the presence of an aqueous phase: The effects of salinity, ion type, and contact time(2022," Journal of Petroleum Science and Engineering, vol. 208, pp. 1–11, 2008.
  44. Das, S.; Thundat, T.; Mitra, S.K. Analytical model for zeta potential of asphaltene. Fuel 2013, 108, 543–549. [Google Scholar] [CrossRef]
  45. Biesheuvel, P. Electrostatic free energy of interacting ionizable double layers. J. Colloid Interface Sci. 2004, 275, 514–522. [Google Scholar] [CrossRef]
  46. J. W. P. Chan and L. R. White, "Regulation of surface potential at amphoteric surfaces during particle–particle interaction," Journal of the Chemical Society, Faraday Transactions 1: Physical Chemistry in Condensed Phases, vol. 71, pp. Chan, D., et al. "Regulation of surface potential at amphoteric surfaces during particle–particle interaction. (1975): 1046-1057., 1975.
  47. Mullins, O.C.; Sabbah, H.; Eyssautier, J.; Pomerantz, A.E.; Barré, L.; Andrews, A.B.; Ruiz-Morales, Y.; Mostowfi, F.; McFarlane, R.; Goual, L.; et al. Advances in Asphaltene Science and the Yen–Mullins Model. Energy Fuels 2012, 26, 3986–4003. [Google Scholar] [CrossRef]
  48. Dolomatov, M.Y.; Shutkova, S.A.; Bakhtizin, R.Z.; Dolomatova, M.M.; Latypov, K.F.; Gilmanshina, K.A.; Badretdinov, B.R. Structure of Asphaltene Molecules and Nanoclusters Based on Them. Pet. Chem. 2020, 60, 16–21. [Google Scholar] [CrossRef]
  49. Alshareef, A.H. Asphaltenes: Definition, Properties, and Reactions of Model Compounds. Energy Fuels 2022, 34, 16–30. [Google Scholar] [CrossRef]
  50. Gharbi, K.; Benamara, C.; Benyounes, K.; Kelland, M.A. Toward Separation and Characterization of Asphaltene Acid and Base Fractions. Energy Fuels 2021, 35, 14610–14617. [Google Scholar] [CrossRef]
  51. Zheng, F.; Shi, Q.; Vallverdu, G.S.; Giusti, P.; Bouyssiere, B. Fractionation and Characterization of Petroleum Asphaltene: Focus on Metalopetroleomics. Processes 2020, 8, 1504. [Google Scholar] [CrossRef]
  52. Pillay, A.E.; Bassioni, G.; Stephen, S.; Kühn, F.E. Depth Profiling (ICP-MS) Study of Trace Metal ‘Grains’ in Solid Asphaltenes. J. Am. Soc. Mass Spectrom. 2011, 22, 1403–1408. [Google Scholar] [CrossRef]
  53. Erdman, J.G.; Harju, P.H. Capacity of Petroleum Asphaltenes to Complex Heavy Metals. J. Chem. Eng. Data 1963, 8, 252–258. [Google Scholar] [CrossRef]
  54. Thorn, K.A.; Cox, L.G. Probing the Carbonyl Functionality of a Petroleum Resin and Asphaltene through Oximation and Schiff Base Formation in Conjunction with N-15 NMR. PLoS ONE 2015, 1–25. [Google Scholar] [CrossRef]
  55. Hosseinpour, N.; Khodadadi, A.A.; Bahramian, A.; Mortazavi, Y. Asphaltene Adsorption onto Acidic/Basic Metal Oxide Nanoparticles toward in Situ Upgrading of Reservoir Oils by Nanotechnology. Langmuir 2013, 29, 14135–14146. [Google Scholar] [CrossRef]
  56. Langevin, D.; Poteau, S.; Hénaut, I.; Argillier, J.F. Crude Oil Emulsion Properties and Their Application to Heavy Oil Transportation. Oil Gas Sci. Technol. – Rev. d’IFP Energies Nouv. 2004, 59, 511–521. [Google Scholar] [CrossRef]
  57. Yang, C.; Zhang, G.; Serhan, M.; Koivu, G.; Yang, Z.; Hollebone, B.; Lambert, P.; Brown, C.E. Characterization of naphthenic acids in crude oils and refined petroleum products. Fuel 2019, 255, 1–10. [Google Scholar] [CrossRef]
  58. Nordgård, E.L.; Sjöblom, J. Model Compounds for Asphaltenes and C80 Isoprenoid Tetraacids. Part I: Synthesis and Interfacial Activities. J. Dispers. Sci. Technol. 2008, 29, 1114–1122. [Google Scholar] [CrossRef]
  59. J. Sjöblom, S. Simon and Z. Xu, "Model molecules mimicking asphaltenes," Advances in Colloid and Interface Science, vol. 218, pp. 1–16, 2015.
  60. Bolintineanu, D.S.; Lane, J.M.D.; Grest, G.S. Effects of Functional Groups and Ionization on the Structure of Alkanethiol-Coated Gold Nanoparticles. Langmuir 2014, 30, 11075–11085. [Google Scholar] [CrossRef]
  61. Porus, M.; Labbez, C.; Maroni, P.; Borkovec, M. Adsorption of monovalent and divalent cations on planar water-silica interfaces studied by optical reflectivity and Monte Carlo simulations. J. Chem. Phys. 2011, 135, 064701. [Google Scholar] [CrossRef]
  62. Murray, B.S.; Dickinson, E.; Wang, Y. Bubble stability in the presence of oil-in-water emulsion droplets: Influence of surface shear versus dilatational rheology. Food Hydrocoll. 2009, 23, 1198–1208. [Google Scholar] [CrossRef]
  63. Lien, T.R.; Phillips1, C.R. Determination of Particle Size Distribution of Oil-in-Water Emulsions by Electronic Counting. Environ. Sci. Technol. 1974, 8, 558–561. [Google Scholar] [CrossRef]
  64. Eftekhari, A.A.; Thomsen, K.; Stenby, E.H.; Nick, H.M. Thermodynamic analysis of chalk-brine-oil interactions. Energy Fuels 2017, 31, 11773–11782. [Google Scholar] [CrossRef]
  65. Jang, W.; Nikolov, A.; Wasan, D.T.; Chen, K.; Campbell, B. Prediction of the Bubble Size Distribution during Aeration of Food Products. Ind. Eng. Chem. Res. 2005, 44, 1296–1308. [Google Scholar] [CrossRef]
  66. Adams, J.J. Asphaltene Adsorption, a Literature Review. Energy Fuels 2014, 28, 2831–2856. [Google Scholar] [CrossRef]
  67. Ok, S.; Mal, T.K. NMR Spectroscopy Analysis of Asphaltenes. Energy Fuels 2019, 33, 10391–10414. [Google Scholar] [CrossRef]
  68. Ok, S.; Mahmoodinia, M.; Rajasekaran, N.; Sabti, M.A.; Lervik, A.; van Erp, T.S.; Cabriolu, R. Molecular Structure and Solubility Determination of Asphaltenes. Energy Fuels 2019, 33, 8259–8270. [Google Scholar] [CrossRef]
  69. Bonto, M.; Eftekhari, A.A.; Nick, H.M. An overview of the oil-brine interfacial behavior and a new surface complexation model. Sci. Rep. 2019, 9, 1–16. [Google Scholar] [CrossRef] [PubMed]
  70. Nagy, l.M.; Kónya, J. Study of pH-dependent charges of soils by surface acid–base properties. J. Colloid Interface Sci. 2007, 305, 94–100. [Google Scholar] [CrossRef] [PubMed]
  71. Andersen, S.I.; Chandra, M.S.; Chen, J.; Zeng, B.Y.; Zou, F.; Mapolelo, M.; Abdallah, W.; Buiting, J.J. Detection and Impact of Carboxylic Acids at the Crude Oil–Water Interface. Energy Fuels 2016, 30, 4475–4485. [Google Scholar] [CrossRef]
  72. Miadonye, A.; Irwin, D.J.G.; Amadu, M. Effect of Polar Hydrocarbon Contents on Oil–Water Interfacial Tension and Implications for Recent Observations in Smart Water Flooding Oil Recovery Schemes. ACS Omega 2023, 8, 9086–9100. [Google Scholar] [CrossRef]
  73. Intertek, "Quantification of Naphthenic Acids in Produced Water," Worley, 2021.
  74. N. S. b. Shafiee, "CARBOXYLIC ACID COMPOSITION AND ACIDITY IN CRUDE OILS AND BITUMENS," 2014. [Online]. Available: https://theses.ncl.ac.uk/jspui/bitstream/10443/2763/1/Binti%20Shafiee%2C%20N%202014.pdf.
  75. Virga, E.; Spruijt, E.; de Vos, W.M.; Biesheuvel, P.M. Wettability of Amphoteric Surfaces: The Effect of pH and Ionic Strength on Surface Ionization and Wetting. Langmuir 2018, 34, 15174–15180. [Google Scholar] [CrossRef]
  76. Saboorian-Jooybari, H.; Chen, Z. Calculation of re-defined electrical double layer thickness in symmetricalelectrolyte solutions. Results Phys. 2019, 15, 1–13. [Google Scholar] [CrossRef]
  77. Chan, D.Y.; Mitchell, D. The free energy of an electrical double layer. J. Colloid Interface Sci. 1983, 95, 193–197. [Google Scholar] [CrossRef]
  78. Kallay, N.; Kovačević, D.; Žalac, S. Chapter 6 - Thermodynamics of the solid/liquid interface - its application to adsorption and colloid stability. Interface Sci. Technol. 2006, 11, 133–170. [Google Scholar]
  79. Tetteh, J.T.; Barimah, R.; Korsah, P.K. Ionic Interactions at the Crude Oil–Brine–Rock Interfaces Using Different Surface Complexation Models and DLVO Theory: Application to Carbonate Wettability. ACS Omega 2022, 7, 7199–7212. [Google Scholar] [CrossRef] [PubMed]
  80. Hanor, J.S. Origin and Migration of Subsurface Sedimentary Brines. SEPM 1987, 21. [Google Scholar]
  81. Milonjić, S.K. Determination of surface ionization and complexation constants at colloidal silica/electrolyte interface. Colloids Surfaces 1987, 23, 301–312. [Google Scholar] [CrossRef]
  82. Kallay, N.; Kovačević, D.; Žalac, S. Chapter 6 - Thermodynamics of the solid/liquid interface - its application to adsorption and colloid stability. Interface Sci. Technol. 2006, 133–170. [Google Scholar]
  83. Driver, H.; Elliott, H.; Linder, P. Application of the Gouy—Chapman equation in metal speciation modelling. Chem. Speciat. Bioavailab. 1991, 3, 61–62. [Google Scholar] [CrossRef]
  84. S. H. Behrens and D. G. Grier, J. S. H. Behrens and D. G. Grier, J. Chem. Phys., 115, pp. 6716–6721, 2001.
  85. Saboorian-Jooybari, H.; Chen, Z. Calculation of re-defined electrical double layer thickness in symmetricalelectrolyte solutions. Results Phys. 2019, 15, 1–13. [Google Scholar] [CrossRef]
  86. P. Bajpai, "Chapter 10 - Papermaking Chemistry," in Biermann's Handbook of Pulp and Paper (Third Edition), 2, 2018, pp. 207–236.
  87. Qing, L.; Zhao, S.; Wang, Z.-G. Surface Charge Density in Electrical Double Layer Capacitors with. J. Phys. Chem. B 2021, 125, 625–636. [Google Scholar] [CrossRef]
  88. D. K. Schroder, Semiconductor material and device characterization, John Wiley & Sons, 2015.
  89. R. M. Torresi, "Double layer capacitance," 2023. [Online]. Available: https://edisciplinas.usp.br/pluginfile.php/4283018/mod_resource/content/1/Double_layer.pdf.
  90. K. Divan, "IMPROVED SEPARATION AND DETECTION OF INORGANIC IONS BY CAPILLARY ELECTROPHORESIS," in Progress in Ion Exchange-Advances and Applications, Elsevier, 1977, pp. 176–186.
  91. R. J. Hunter, Foundations of Colloid Science, 1, Oxford University Press: Oxford, 1989.
  92. Bowden, J.; Posner, A.; Quirk, J. Ionic adsorption on variable charge mineral surfaces. Teoretical-charge development and, titration curves. Aust. J. Soil Res. 1997, 15, 121–136. [Google Scholar]
  93. Atkinson, R.J.; Posner, A.M.; Quirk, J.P. Adsorption of potential-determining ions at the ferric oxide-aqueous electrolyte interface. J. Phys. Chem. 1967, 71, 550–558. [Google Scholar] [CrossRef]
  94. R. W. Roach, R. S. R. W. Roach, R. S. Can and C. L. Howard, "An Assessment of Produced Water Impacts at Two Sites in the Galveston Bay System," 2023. [Online]. Available online: https://www.tceq.texas.gov/assets/public/comm_exec/pubs/gbnep/gbnep-23/gbnep_23_133-152.pdf.
  95. N. Gavish and K. Promislow, "Dependence of the dielectric constant of electrolyte solutions on," Phy Chem, pp. 1–14, 2016.
  96. G. Thyne and P. Brady, "Evaluation of Formation Water Chemistry: Bakken Shale," SAND2015-9055J, 2015.
  97. S. P. Clark Jr., Handbook of Physical Constants, vol. 97, Geological Society of America, 1966.
  98. T. J. Ahrens, Global Earth Physics: A Handbook of Physical Constants (AGU Reference Shelf), OH: Published by American Geophysical Union, 1995.
  99. Buckley, J.S.; Takamura, K.; Morrow, N.R. Infuence of electrical surface charges on the wetting properties of crude oils. SPE Reserv. Eng. 1989, 4, 332–340. [Google Scholar] [CrossRef]
  100. S. C. Moldoveanu and V. David, "Chapter 5 - Properties of Analytes and Matrices Determining HPLC Selection," 189-230, 2017.
  101. A. Adamson and A. Gast, "Physical Chemistry of Surfaces, John Wiley and Sons, 1997, 1997.
  102. Menéndez, J.A.; Illán-Gómez, M.; Leon, C.A.L.Y.; Radovic, L. On the difference between the isoelectric point. Carbon 1995, 33, 165–1659. [Google Scholar] [CrossRef]
  103. Holmes-Farley, S.R.; Reame, R.H.; McCarthy, T.J. Acid-Base Behavior of Carboxylic Acid Groups Covalently Attached at the Surface of Polyethylene: The Usefulness of Contact Angle in Following the Ionization of Surface Functionality. Langmuir 1985, 1, 725–740. [Google Scholar] [CrossRef]
  104. Lunkad, R.; Murmiliuk, A.; Tošner, Z.; Štěpánek, M.; Košovan, P. Role of pKA in Charge Regulation and Conformation of Various Peptide Sequences. Polymers 2021, 13, 1–21. [Google Scholar] [CrossRef] [PubMed]
  105. Delhorme, M.; Labbez, C.; Caillet, C.; Thomas, F. Acid-Base Properties of 2:1 Clays. I. Modeling the Role of Electrostatics. Langmuir 2010, 26, 9240–9249. [Google Scholar] [CrossRef]
  106. M. Kosmulski, "The pH dependent surface charging and points of zero charge. IX. Update," Advances in Colloid and Interface Science, vol. 296, 2021.
  107. Yildiz, H.O.; Morrow, N.R. Effect of brine composition on recovery of Moutray crude oil by waterflooding. J. Pet. Sci. Eng. 1996, 14, 159–168. [Google Scholar] [CrossRef]
  108. Sugimoto, T.; Adachi, Y.; Kobayashi, M. Heteroaggregation rate coefficients between oppositely charged particles in a mixing flow: Effect of surface charge density and salt concentration. Colloids Surf. A: Physicochem. Eng. Asp. 2022, 632, 1–8. [Google Scholar] [CrossRef]
  109. Stenberg, S.; Forsman, J. Overcharging and Free Energy Barriers for Equally Charged Surfaces Immersed in Salt Solutions. Langmuir 2021, 37, 14360–14368. [Google Scholar] [CrossRef]
  110. Chakibi, H.; Hénaut, A.S.I.; Langevin, D.; Argillier, J.-F. Role of Bubble–Drop Interactions and Salt Addition in Flotation Performance. Energy & Fuels 2018, 4049–4056. [Google Scholar]
  111. Jackson, M.D.; Al-Mahrouqi, D.; Vinogradov, J. Zeta potential in oil-water-carbonate systems and its impact on oil recovery during controlled salinity water-flooding. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
  112. Ma, Q.; Li, H.; Li, Y. The Study to Improve Oil Recovery through the Clay State Change during Low Salinity Water Flooding in Sandstones. ACS Omega 2020, 5, 29816–29829. [Google Scholar] [CrossRef] [PubMed]
  113. Kataya, A.; Khamehchi, E.; Bijani, M. The impact of salinity, alkalinity and nanoparticle concentration on zeta-potential of sand minerals and their implication on sand production. Energy Geosci. 2022, 3, 314–322. [Google Scholar] [CrossRef]
  114. D. A. Haydon, "A Study of the Relation Between Electrokinetic Potential and Surface Charge Density," in Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1960.
  115. Ge, Z.; Wang, Y. Estimation of Nanodiamond Surface Charge Density from Zeta Potential and Molecular Dynamics Simulations. J. Phys. Chem. B 2017, 121, 3394–3402. [Google Scholar] [CrossRef] [PubMed]
  116. Ohshima, H. Approximate expressions for the surface charge density/surface potential relationship and double-layer potential distribution for a spherical or cylindrical colloidal particle based on the modified Poisson-Boltzmann equation. Colloid Polym. Sci. 2018, 296, 647–652. [Google Scholar] [CrossRef]
  117. S. Mohapatra, S. Ranjan, N. Dasgupta, R. K. Mishra and S. Thomas, Characterization and Biology of Nanomaterials for Drug Delivery, Elsevier, 2019.
  118. Brown, M.A.; Abbas, Z.; Kleibert, A.; Green, R.G.; Goel, A.; May, S.; Squires, T.M. Determination of Surface Potential and Electrical Double-Layer Structure at the Aqueous. Phys. Rev. X 2016, X, 1–12. [Google Scholar]
  119. Ohshima, H. Surface Charge Density/Surface Potential Relationship for a Spherical Colloidal Particle in a Salt-Free Medium. J. Colloid Interface Sci. 2002, 247, 18–23. [Google Scholar] [CrossRef]
  120. E. DeCola, A. E. DeCola, A. Hall, M. Popovich and H. P. Dahlslett, "Assessment of Demulsification and Separation Technologies for Use in Offshore Oil Recovery Operations," Bureau of Safety and Environmental Enforcement, Plymouth, 2018.
  121. Alao, K.T.; Alara, O.R.; Abdurahman, N.H. Trending approaches on demulsification of crude oil in the petroleum industry. Appl. Petrochem. Res. 2021, 11, 281–293. [Google Scholar] [CrossRef]
  122. Yonguep, E.; Kapiamba, K.F.; Kabamba, K.J.; Chowdhury, M. Formation, stabilization and chemical demulsification of crude oil-in-water emulsions: A review. Pet. Res. 2022, 7, 459–472. [Google Scholar] [CrossRef]
  123. Zolfaghari, R.; Fakhrul-Razi, L.; Abdullah, A.; Elnashaie SSEH, P.A. Demulsifcation techniques of water-in-oil and oil-in-water emulsions in petroleum industry. Sep. Purif. Technol. 2016, 170, 377–407. [Google Scholar] [CrossRef]
  124. Lv, P.; Liu, Y.; Zhang, Y.; Sun, L.; Meng, X.; Meng, X.; Zou, J. Optimization of non-ionic surfactants for removing emulsified oil from gas condensate oil–water emulsion in N oilfield. J. Pet. Explor. Prod. Technol. 2020, 10, 3025–3030. [Google Scholar] [CrossRef]
  125. Moritz, R.; Zardalidis, G.; Butt, H.-J.; Wagner, M.; Müllen, K.; George, F. Ion Size Approaching the Bjerrum Length in Solvents of Low Polarity by Dendritic Encapsulation. Macromolecules 2014, 47, 191–196. [Google Scholar] [CrossRef]
  126. Seal, S.; Doblhoff-Dier, K.; Meyer, J. Dielectric Decrement for Aqueous NaCl Solutions: Effect of Ionic Charge Scaling in Nonpolarizable Water Force Fields. J. Phys. Chem. B 2019, 123, 9912–9921. [Google Scholar] [CrossRef] [PubMed]
  127. S. M. Abed, N. H. Abdurahman, R. M. Yunus, H. A. Abdulbari and S. Akbari, "Oil emulsions and the different recent demulsification techniques in the petroleum industry - A review," in 1st ProSES Symposium, 2019.
  128. Miadonye, A.; Amadu, M. How pH induced surface charge modification explains the effect of petrophysical and hydrological factors on recovery trends of water drive gas reservoirs. J. Nat. Gas Sci. Eng. 2022, 98, 1–10. [Google Scholar] [CrossRef]
  129. Kobayashi, J.; Hinoue, T.; Watarai, H. Study of Adsorption of Water-Soluble Porphyrin at Glass–Solution Interface in the Presence of Cationic Surfactant Admicelles by Means of Total Internal Reflection Spectroscopy. Bull. Chem. Soc. Jpn. 1990, 71. [Google Scholar] [CrossRef]
  130. Vatanparast, H.; Shahabi, F.; Bahramian, A.; Javadi, A.; Miller, R. The Role of Electrostatic Repulsion on Increasing Surface Activity of Anionic Surfactants in the Presence of Hydrophilic Silica Nanoparticles. Sci Rep. 2018, 8, 8–1. [Google Scholar] [CrossRef] [PubMed]
  131. Andersson, M.P.; Bennetzen, M.V.; Klamt, A.; Stipp, S.S. First-Principles Prediction of Liquid/Liquid Interfacial Tension. J. Chem. Theory Comput. 2014, 10, 3401–3408. [Google Scholar] [CrossRef]
  132. Chen, Y.; Narayan, S.; Dutcher, C.S. Phase-Dependent Surfactant Transport on the Microscale: Interfacial Tension and Droplet Coalescence. Langmuir 2020, 36, 14904–14923. [Google Scholar] [CrossRef]
  133. Vis, M.; Peters, V.F.; Blokhuis, E.M.; Lekkerkerker, H.N.; Erné, B.H.; Tromp, R.H. Effects of Electric Charge on the Interfacial Tension between Coexisting Aqueous Mixtures of Polyelectrolyte and Neutral Polymer. Macromolecules 2015, 48, 7335–7345. [Google Scholar] [CrossRef]
  134. Zha, F.; Dong, S.; Rao, J.; Chen, B. Pea protein isolate-gum Arabic Maillard conjugates improves physical and oxidative stability of oil-in-water emulsions. Food Chem. 2019, 285, 130–138. [Google Scholar] [CrossRef]
  135. Meegoda, J.N.; Aluthgun Hewage, S.; Batagoda, J.H. Stability of Nanobubbles. Environ. Eng. Sci. 2018, 35. [Google Scholar] [CrossRef]
  136. Schaefer, M.; Karplus, M. A Comprehensive Analytical Treatment of Continuum Electrostatics. J. Phys. Chem. 1996, 100, 1578–1599. [Google Scholar] [CrossRef]
Preprints 79121 g001
Figure 1. Examples of molecular structure. a) asphaltene (adapted from proposition for 510C residue of Venezuelan crude, INTEVEP SA Tech. Rept., 1992); b) resin (Athabasca Tarsand bitumen); c) naphthenic acid [56].
Figure 1. Examples of molecular structure. a) asphaltene (adapted from proposition for 510C residue of Venezuelan crude, INTEVEP SA Tech. Rept., 1992); b) resin (Athabasca Tarsand bitumen); c) naphthenic acid [56].
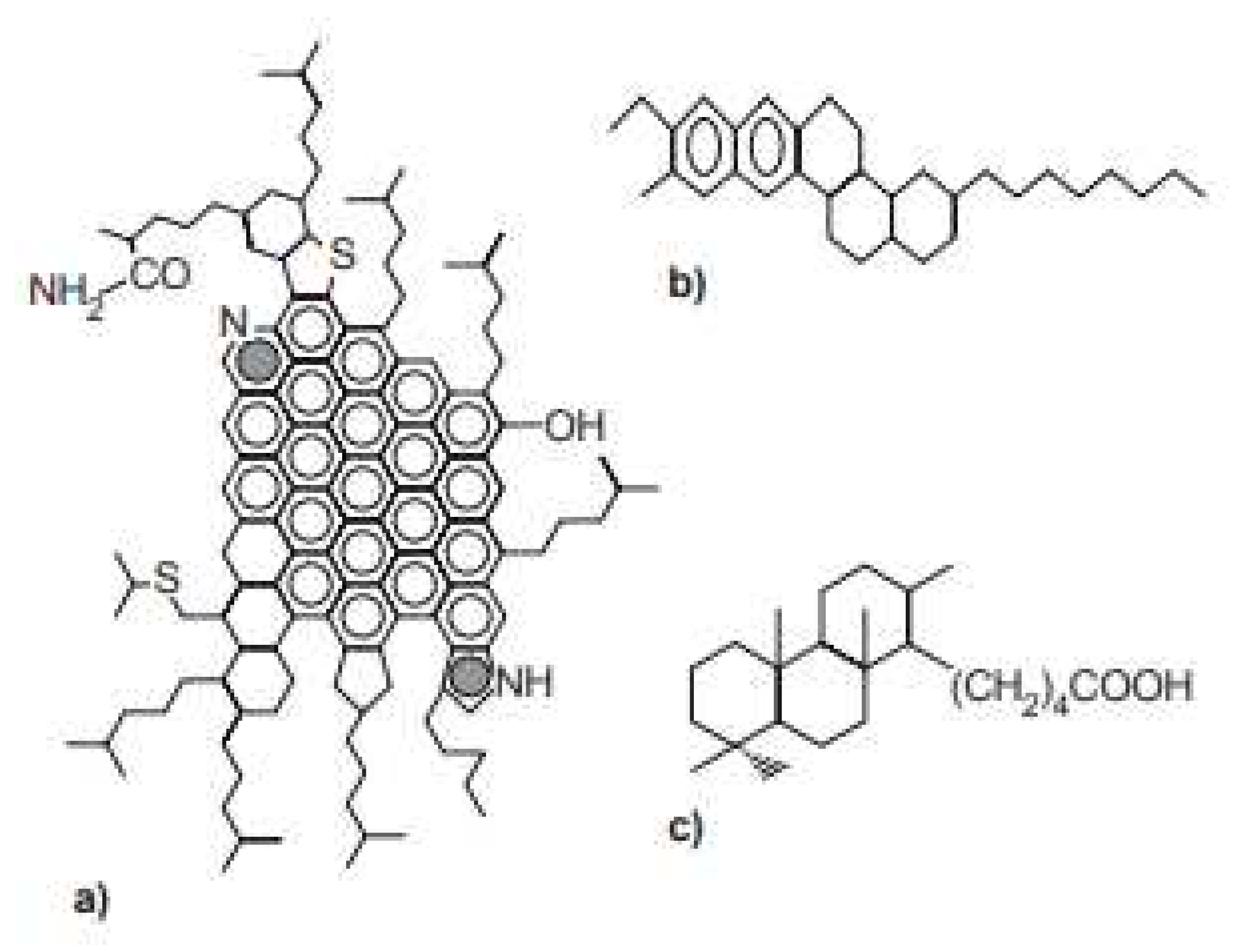
Preprints 79121 g001
Preprints 79121 g002
Figure 2. Bubble size distribution frequency (Jang et al., 2005) [65].
Figure 2. Bubble size distribution frequency (Jang et al., 2005) [65].
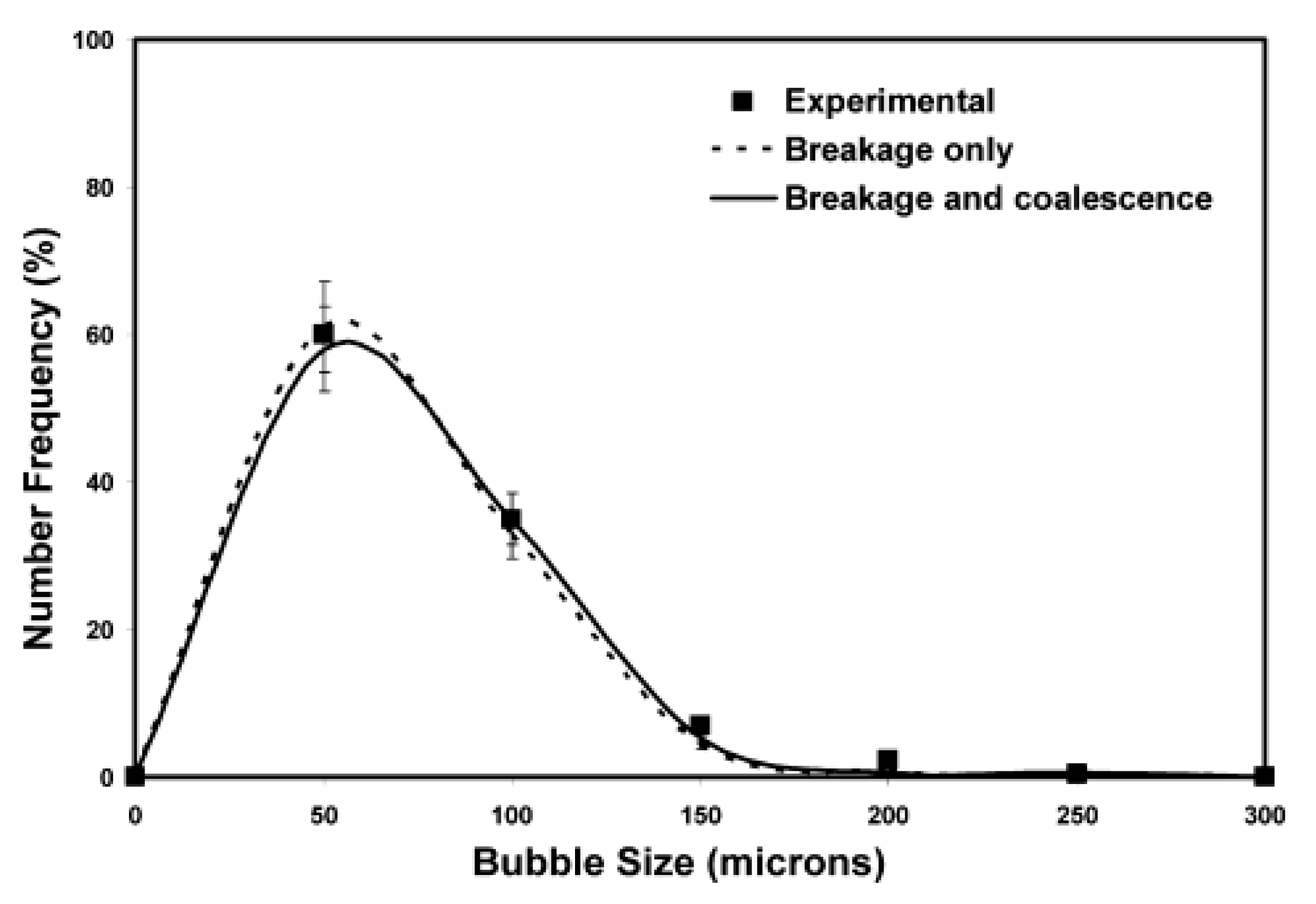
Preprints 79121 g002
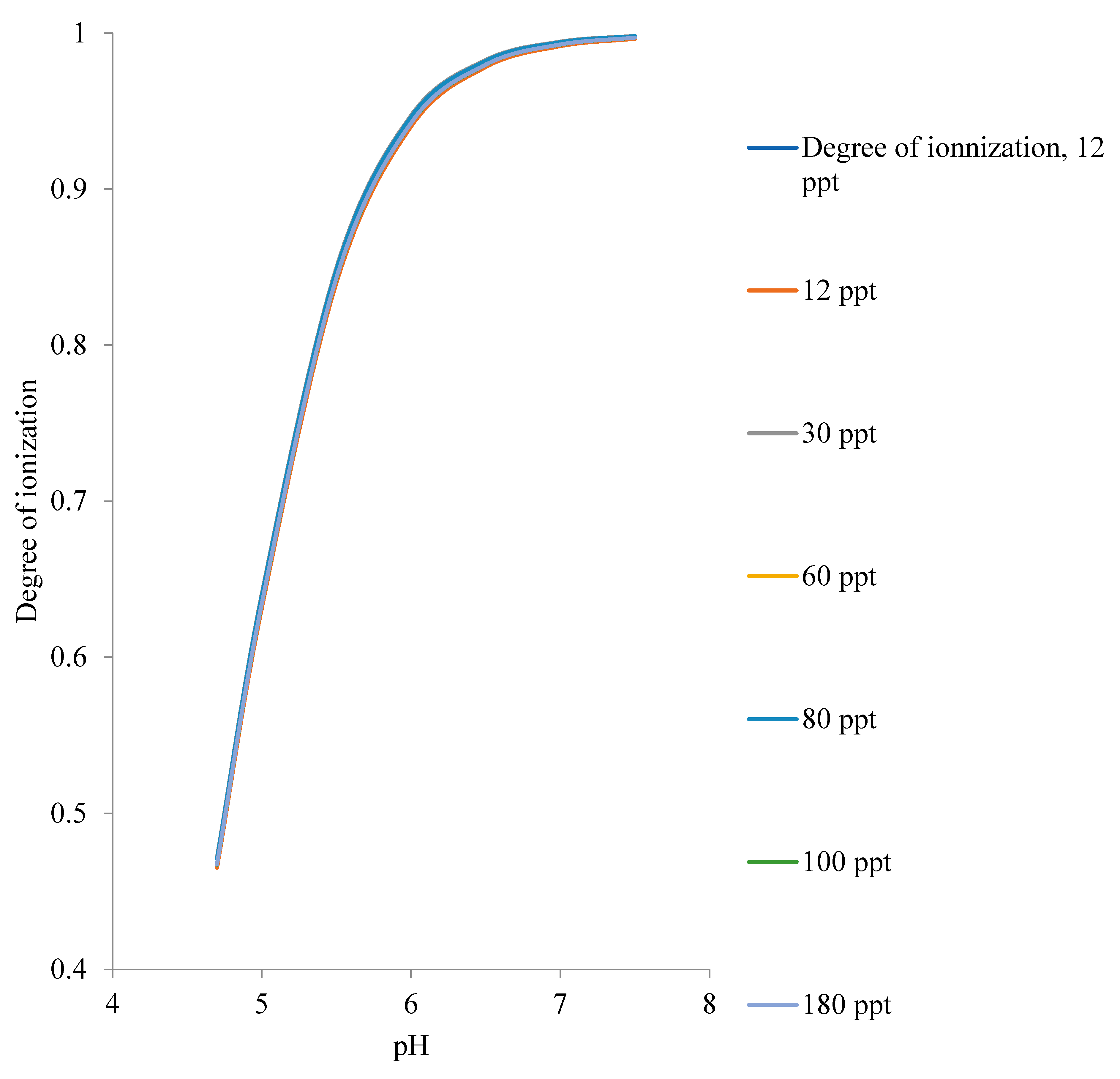
Preprints 79121 g003
Figure 3. Degree of ionization of acidic group of crude oils versus pH at 294 K.
Figure 3. Degree of ionization of acidic group of crude oils versus pH at 294 K.
Preprints 79121 g003
Table 1. Isoelectric points of different crude oils (Bonto et al., (2019) [39].
Table 1. Isoelectric points of different crude oils (Bonto et al., (2019) [39].
Crude Oil Isoelectric point
Moutray Crude 3.80
Leduc Crude 4.35
ST-86—1 Crude 3.20
Crude Oil A 4.00
Crude Oil B 4.20
Crude Oil C 4.40
Table 2. Salinity, permittivity and number density of a sodium chloride dominated oilfield produced brine.
Table 2. Salinity, permittivity and number density of a sodium chloride dominated oilfield produced brine.
Sodium chloride dominated salinity[ppt] Molar concentration of ions [M] Ionic strength [M] Number density[m3] Permittivity [Fm-1]
12 0.21 0.205339 1.27721 78.00
30 0.51 0.513347 3.19302 75.00
60 1.03 1.026694 6.38604 70.00
80 1.37 1.368925 8.51472 68.00
100 1.71 1.711157 1.06434 62.00
180 3.08 3.080082 1.91581 60.00
Table 3. pKa values for dissociation of acidic groups on 3 crude oil (Bonto et al. (2019) [39].
Table 3. pKa values for dissociation of acidic groups on 3 crude oil (Bonto et al. (2019) [39].
≡ C O O H → ≡ C O O − 1 + H + Crude oil A Crude oil B Crude oil C
-4.75 -4.62 -4.65 -4.8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated