Detecting Pseudo Manipulated Citations in Scientific Literature through Perturbations of the Citation Graph

Ensuring the integrity of scientific literature is essential for advancing knowledge and research. However, the credibility and trustworthiness of scholarly publications are compromised by manipulated citations. Traditional methods, such as manual inspection and basic statistical analyses, have limitations in detecting intricate patterns and subtle manipulations of citations. In recent years, network-based approaches have emerged as promising techniques for identifying and understanding citation manipulation. This study introduces a novel method to identify potential citation manipulation in academic papers using perturbations of a deep embedding model. The key idea is to reconstruct meaningful connections represented by citations within a network by exploring slightly longer alternative paths. These indirect pathways enable the recovery of original and reliable citations while estimating their trustworthiness. The investigation takes a comprehensive approach to link prediction, leveraging the consistent behavior of prominent connections when exposed to network perturbations. Through numerical experiments, the method demonstrates a high capability to identify reliable citations as the core of the analyzed data and to raise suspicions about unreliable references that may have been manipulated.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

The integrity and dependability of scientific literature are essential for the advancement of knowledge and the advancement of research. From this standpoint, the manifestation of manipulated citations presents a significant obstacle to the credibility and trustworthiness of scholarly publications. Manipulated citations involve intentional actions by authors to artificially enhance the quantity or influence of their papers by including non-necessary or irrelevant citations. This practice undermines scholarly discussions’ accuracy, impartiality, and scientific validity. Despite researchers recognizing the unequal value of citations and their attempts to assign varying weights based on different types, most studies have primarily focused on differentiating and assigning weights to a specific citation type. In fact, as demonstrated by Prabha [1], more than two-thirds of the references in a paper are deemed unnecessary, providing further evidence of the existence of dubious citations. Citation manipulation aimed at increasing researchers’ citation counts can furthermore occur when editors or peer reviewers of a manuscript request the inclusion of unnecessary and unrelated references, a practice known as "coercive citation."

Numerous surveys have assessed different elements related to manipulating reference lists. In this connection, [2,3,4] can be reminded within others. Most authors acknowledge that such citations are anomalous compared to typical or regular references.

While traditional methods like manual inspection and basic statistical analyses have been employed, they have limitations in capturing intricate patterns and subtle manipulations. In recent years, network-based approaches have emerged as promising techniques for identifying and comprehending citation manipulation. Due to the intricate nature of graph data, characterized by irregular structures and relational dependencies, conventional anomaly detection techniques struggle to address this issue effectively. In contrast to traditional detection methods, anomaly detection methods that leverage graph learning have the capability to simultaneously preserve both the node attributes and network structures throughout the learning process. This provides a more suitable approach for tackling the complexities associated with graph data. By leveraging the structure and connections within the citation network, network-based approaches can unveil hidden relationships and abnormalities that indicate potential citation manipulation. These methods go beyond individual papers and examine the broader network dynamics, allowing for a more comprehensive understanding of the manipulation patterns. Research of this kind is presented in papers [5,6,7,8,9].

The article [10] can be highlighted. The paper introduces a new approach called GLAD (Graph Learning for Anomaly Detection), which is a deep graph learning model designed specifically for identifying anomalies in citation networks. GLAD integrates semantic text mining into the process of network representation learning by incorporating both node attributes (related to the content of the papers) and link attributes (capturing the citation relationships) using graph neural networks. This combined approach enhances the ability to detect and classify anomalous citations within the network.

In this research, a novel method is presented to identify possible manipulation of citations in academic papers. The central concept suggests that citations, which indicate meaningful connections between different types of research, can be reconstructed within a network by following slightly longer alternative paths. As a result, these indirect pathways can be effectively employed to recover the original, authentic citations while also estimating their reliability.

We approach our investigation from a general perspective of link prediction, utilizing a natural suggestion based on the stable behavior of prominent connections when exposed to network perturbations. In simpler terms, we propose that the specified relationships are expected to endure more effectively amidst distortions that entail the removal of a subset of connections, followed by their reconstruction using a link prediction method. Our study encompasses a broad view of link prediction, drawing logical inferences from the consistent behavior of significant connections in the network when subjected to perturbations. To summarize, we suggest that the identified relationships are more likely to persist through distortions that involve selectively omitting connections and subsequently reconstructing them using a link prediction technique.

In the current paper, we use link prediction in a graph based on an embedding technique involving predicting the presence or absence of edges (connections) between nodes in a graph.

Graph embedding methods transform nodes and edges into vectors or embeddings that encode important information about the graph’s structure and semantics. The basic idea behind graph embedding is to map each node or edge in the graph to a continuous vector representation in a relatively lower-dimensional space. This depiction captures the relational information between nodes and can be used to infer potential links or relationships that are missing in the original graph. By learning meaningful embeddings, link prediction algorithms can estimate the likelihood or similarity of a potential edge between two nodes based on the proximity or similarity of their embeddings.

Here we use the Node2Vec approach. Node2Vec is a widely used algorithm that learns continuous representations of nodes by capturing the neighborhood structure of the graph. It explores the notion of "node neighborhoods" by defining a random walk strategy to sample node sequences from the graph. These sequences are then used to train a skip-gram model, similar to word2vec, to learn node embeddings. Once the embeddings are learned, link prediction can be performed by measuring the similarity between the embeddings of two nodes.

The remainder of the paper is organized as follows. Section 2 provides an overview of the mathematical preliminaries that are relevant to the study. In Section 3, the proposed model for identifying citation manipulation is presented. Section 4 presents the experimental study conducted to evaluate the effectiveness of the proposed model. Finally, Section 5 concludes the paper by summarizing the main findings and discussing their implications.

2. Mathematical preliminaries

2.1. Word2Vec

Numerous traditional methods in the field of text mining are linked to vector representations, such as the bag-of-words approach, which treats texts as vectors of term occurrences. However, these techniques have a known limitation: they disregard the sequencing of words and the relationships between them, leading to a loss of semantic information. To address these limitations, deep learning embedding systems offer novel strategies. They provide real-valued vector representations for words, where words with similar meanings are represented by vectors that are close in proximity. Word embedding, encompassing a range of language modeling techniques, plays a crucial role in natural language processing. It represents words from a given vocabulary in high-dimensional vector spaces, effectively preserving the underlying semantic and syntactic information. As a result, word embedding proves invaluable for enhancing performance across various natural language processing tasks.

Word2Vec [11] is a popular algorithm for learning word embeddings. The algorithm is based on a shallow, two-layer neural network and employs the Continuous Bag-of-Words (CBOW) or Skip-gram architecture.

2.2. Note2Vec

As was mentioned earlier, the Note2vec algorithm is designed to generate vector representations for nodes in a graph. The algorithm achieves its objective by simulating random walks on the graph, letting it generate low-dimensional representations for nodes. It optimizes a neighborhood-preserving objective using a skip-gram model. To strike a balance between exploration and exploitation during the random walks, Note2vec employs two hyperparameters: (p) "return" and (q) "inout". These hyperparameters control the probabilities associated with the random walk, determining whether it stays close to previous nodes, explores outward, or explores inward. So, the hyperparameters "return" and "inout" in Node2vec play a crucial role in shaping the behavior of the random walks conducted during the algorithm’s learning process. Adjusting the "return" hyperparameter can control the likelihood of revisiting previous nodes during the random walk. This influences the algorithm’s exploration of local neighborhoods and its ability to capture the structural properties of the graph. Similarly, the "inout" hyperparameter allows for governing the decision-making process of the random walk, determining the probabilities of exploring outward or inward at each step. This empowers control of exploring global information versus exploiting local neighborhood information.

Specifically, the probabilities 1/p and 1/q are used to calculate the likelihood of exploring outward or inward, respectively.

In the mentioned study, a perturbation analysis is conducted on the BlogCatalog network to explore the impact of imperfect information regarding the network’s edge structure. The study examines two specific scenarios where the accuracy of the network’s edge information is compromised. In the first scenario, the network’s performance is evaluated by considering the fraction of missing edges concerning the entire network. The missing edges are randomly selected, ensuring the number of connected components within the network remains constant. The study measures the decrease in the Macro-F1 score as the fraction of missing edges increases. The findings indicate that the decline in the Macro-F1 score follows a roughly linear trend, suggesting a certain level of robustness to missing edges. Furthermore, the slope of the linear decrease indicates a slight decrease in performance, indicating that the network can tolerate some level of missing edges without significant degradation in performance.

3. Approach

This section presents the proposed approach. As previously mentioned, the assumption is that manipulated or fraudulent citations may exhibit anomalies within a citation network. These anomalies are expected to make the manipulated citations vulnerable to appropriate perturbations within the network, causing them to be unstable or detectable. The hypothesis is based on the idea that manipulated citations, intentionally added to inflate the impact or credibility of certain publications, may not conform to the natural patterns and structures of the citation network. Therefore, when subjected to network perturbations, such as removing specific nodes or edges, the manipulated citations are more likely to exhibit inconsistencies or inconsistencies that distinguish them from genuine citations. By investigating the stability of citations under perturbations and analyzing the deviations from expected patterns, it is possible potentially identify anomalous citations that may indicate manipulation or fraudulent behavior within the citation network. Based on the pairwise similarities, a ranking can be established for potential links. Nodes with higher similarity scores are considered more likely to have a connection. The top-ranked pairs of nodes can be predicted as potential new or missing links in the network.

The perturbations of the considered citation network are similar to some extent to those mentioned earlier ones involved in the perturbation analysis of the model consisting of artificial changes or modifications to the network structure. In the context of the citation network, they consist of randomly removing citations. These perturbations simulate different scenarios or conditions to evaluate the robustness, stability, or integrity of the citation network and individual links.

Perturbations can reveal vulnerabilities or weaknesses in a network, making it more likely for anomalies or manipulated elements to exhibit abnormal behavior or stand out from the genuine components.

In the next step, a link prediction using embeddings is performed. Once an embedding is obtained, the similarity or proximity between pairs of nodes can be measured by means of various similarity metrics, such as cosine similarity, Euclidean distance, or graph-based measures like mutual neighbors or the Jaccard coefficient. We propose including two additional parameters: a similarity measure (S) and a threshold value (Tr). The similarity measure quantifies the similarity between pairs of nodes, while the threshold value determines the cutoff point for determining whether pairs are considered "connected" or not. Specifically, if the similarity score between two nodes exceeds the threshold (Tr), they are deemed as connected, whereas pairs with a similarity score below the threshold are considered disconnected.

We would like to emphasize that the studied citation graph is considered not-directed. This scenario focuses on the connectivity between papers rather than the specific direction of citation that allows to analyze and understand the overall structure and patterns of the network. Disregarding edge direction in the citation graph enables a more holistic view of the network, capturing the relationships and interdependencies between papers regardless of whether one paper is citing another or being cited.

Algorithm 1. The proposed procedure’s pseudocode.

Input parameters:

✓

Graph_C-A graph of papers citations.

✓

p and q – “return” and "inout" parameters of Node2vec.

✓

Nwalk- a number of random walks in a model generation.

✓

Lwalk-a length of a random walk.

✓

d- a dimension of the Word2vec embedding in Node2vec.

✓

N_iter-a number of perturbations.

✓

Fr- a fraction of nodes randomly omitted in each iteration.

✓

S -a similarity measure.

✓

Tr - a similarity threshold.

Procedure:

Load the dataset Graph_C
Initialize an array Result of zeros with light equaling the number of edges in Graph_C
For iter = 1: N_iter do:

3.1

Create a temporal dataset Graph_T by removing the Fr fraction of edges in Graph_C without replacement.

3.2

Create an embedding of Graph_T:

W(Graph_T) = Node2vec(Graph_C, Nwalk ,p, q, d)

3.3

Calculate for all pairs of nodes the similarity values between all nodes.

3.4

Compose a set ED_R of the edges reconstructed using the procedure

Link_prediction(Graph_T , W(Graph_T), S, Tr)

3.5

For edge in ED_R do:

Result(edge)= Result(edge)+1
Summarize by sorting of Result in ascending order.

Procedure Link_prediction(Graph_T, W(Graph_T), S, Tr)

A procedure is designed to predict the presence of an edge between two nodes.

Input parameters:

✓

Graph_T -A graph of papers citations.

✓

W(Graph_T)- An embedding of Graph_T.

✓

S -a similarity measure.

✓

Tr - a similarity threshold.
Procedure

✓

If the similarity score S(n₁, n₂) is greater than 1-Tr, the procedure returns 1, indicating that there could potentially be an edge between n₁ and n₂.

✓

Otherwise, if the similarity score is less than or equal to 1 - Tr, the procedure returns 0, indicating that there is likely no edge between n₁ and n₂.

4. Experiments

4.1. Cora dataset

The Cora dataset (https://relational.fit.cvut.cz/dataset/CORA) is a well-known and extensively used dataset in the fields of machine learning and natural language processing, specifically for studying citation networks. The dataset consists of a collection of scientific research papers primarily from the computer science domain covering various subfields, including machine learning, artificial intelligence, databases, and information retrieval. Each paper in the dataset is represented by a bag-of-words feature vector, which indicates the presence or absence of specific words within the document. In addition to the textual data, the Cora dataset provides information about citation links between the documents to establish connections among the papers, allowing us to study citation patterns and investigate techniques for citation network analysis.

The Cora dataset contains 2,708 scientific publications categorized into seven classes. With a total of 5,429 links, the dataset’s citation network captures the connections between these publications. Each publication is additionally represented by a binary word vector consisting of 0s and 1s, indicating the presence or absence of words from a dictionary. This dictionary comprises 1,433 different words.

Figure 1. Partial visualization of the CORA dataset.

In order to investigate the structure of the dataset, a set of numerical experiments was performed involving various Fr values (30, 40, and 50) and Tr values (0.05, 0.1, and 0.2) across 100 iterations. It is worth mentioning that the use of such small thresholds does not yield conclusive evidence for the existence of the required connecting edges. Just like in statistical hypothesis testing, when the similarity falls below these critical values, it signifies the rejection of the hypothesis that such edges are present. However, it does not offer substantial evidence to confirm the presence of a connecting edge. Therefore, connections that collapse below these thresholds are deemed questionable and suggest possible manipulation.

Experiments are performed with a specified set of parameters.

✓: p=1.
✓: q=1.
✓: Nwalk = 200.
✓: Lwalk = 30.
✓: d= 64.
✓: N_iter = 100.
✓: Fr – 30/40/50 %.
✓: S – the cosine similarity.
✓: Tr – 0.05 / 0.1 / 0.2.

Recall that cosine similarity is a metric used to measure the similarity between two vectors in a vector space. It calculates the cosine of the angle between the vectors, providing a value that indicates their degree of similarity. The range of cosine similarity is from -1 to 1, where a value of 1 indicates identical vectors, 0 indicates no similarity, and -1 indicates entirely different vectors. To compute cosine similarity, the dot product of the two vectors is divided by the product of their magnitudes or norms. This normalization ensures that the similarity measure is independent of the vectors’ lengths and only depends on their directions. The concept of cosine similarity finds applications in various fields, such as natural language processing, information retrieval, and data mining. It allows quantifying the similarity between vectors or documents based on their relative orientations in a multi-dimensional space.

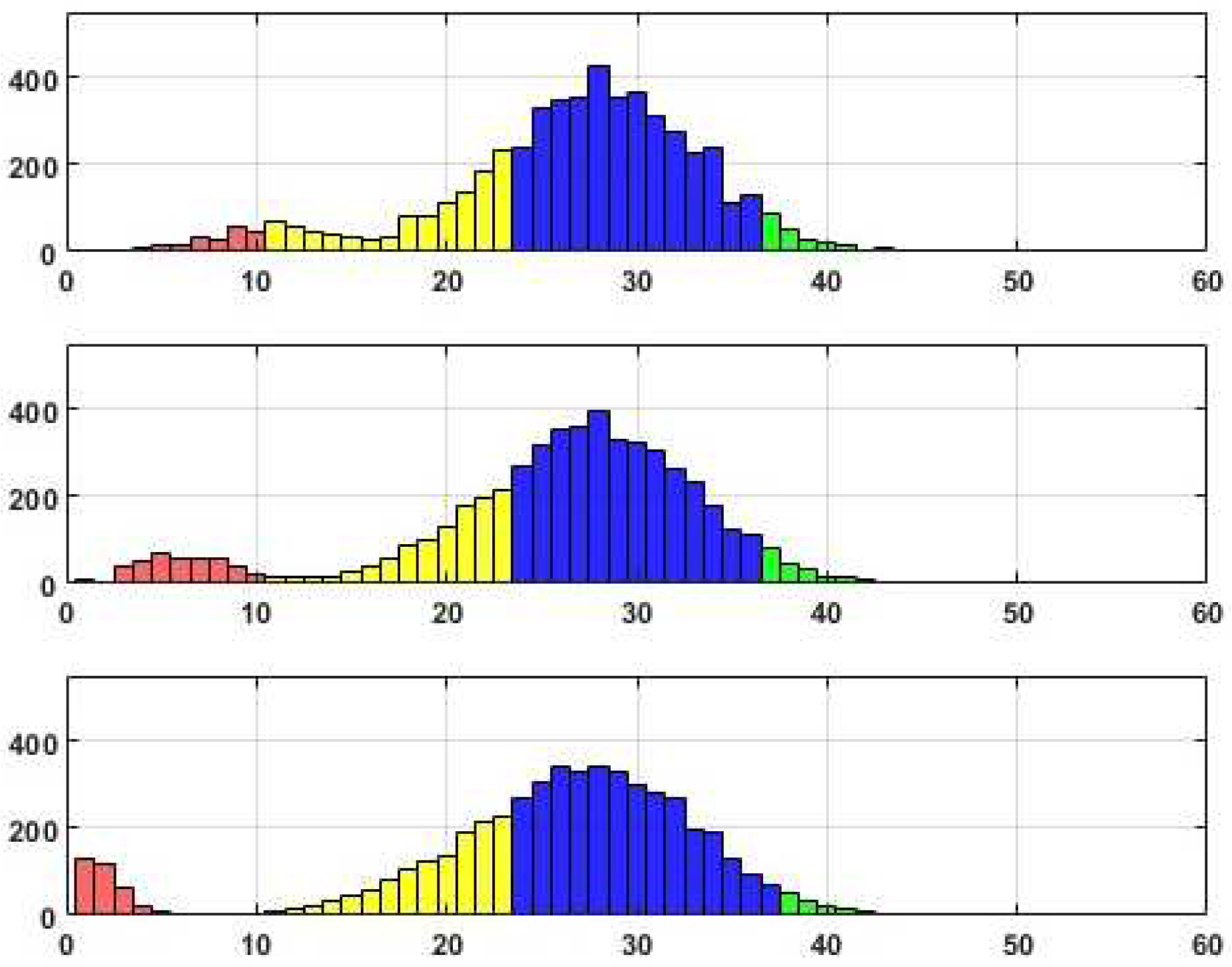
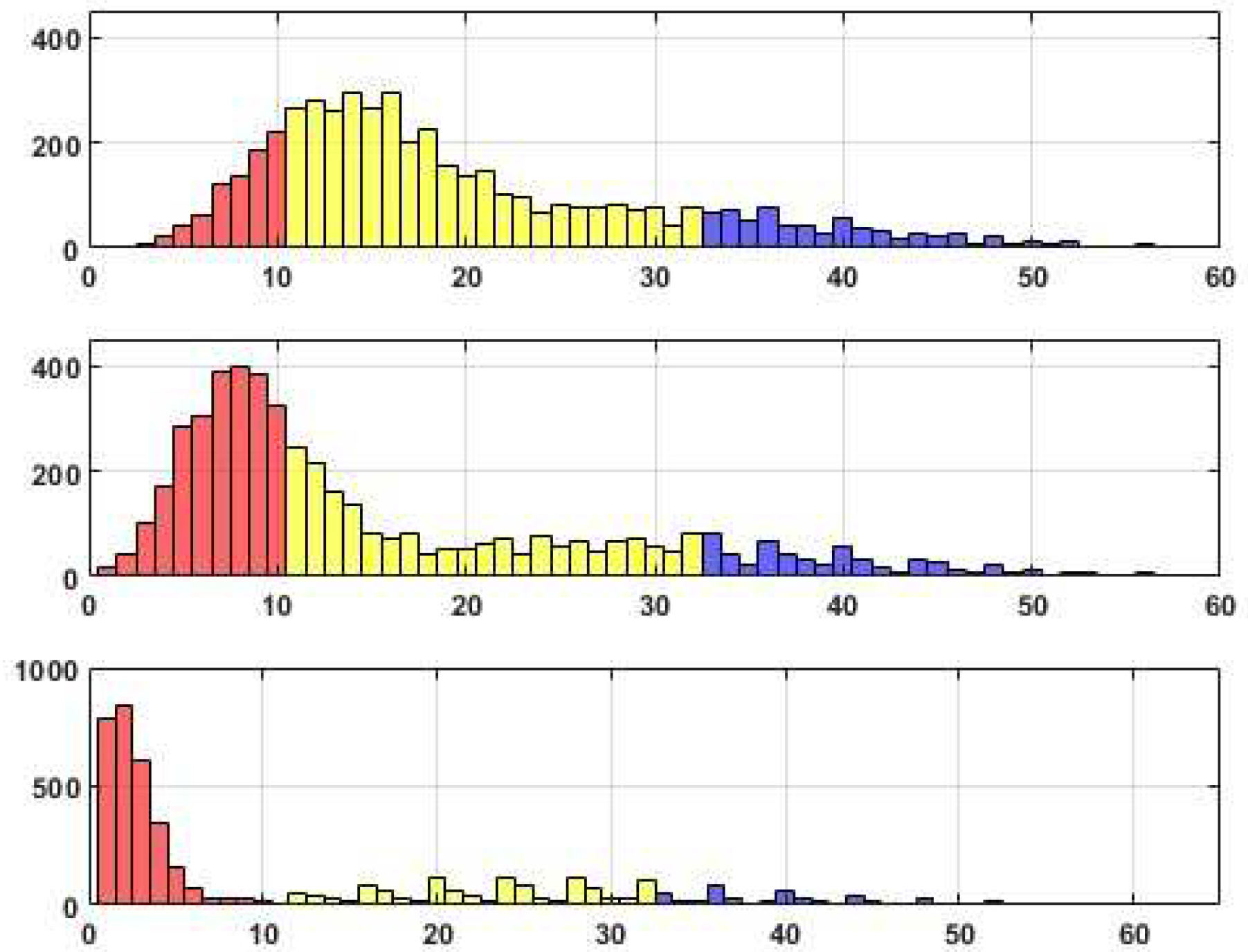
We have prepared three sets of histograms to illustrate the distributions of the scores obtained during the experiments. Each set includes three histograms, so the upper histogram represents the scores achieved with a threshold of Tr=0.05, the middle histogram corresponds to Tr=0.1, and the last histogram represents Tr=0.2. In the visual depiction, the section in red corresponds to upper bound 10. The next interval’s upper bound, highlighted in yellow, is at half the maximum Reconstructed edges. The subsequent intervals, marked in blue and green, represent the upper bounds of the intervals based on the maximum number minus 10 and the maximum number of reconstructed edges, respectively. Figure 3, Figure 4 and Figure 5 display histograms that illustrate the distributions of edges within these categories. Accompanying tables provide additional detailed information regarding the edges’ allocation across the categories.

Figure 2. Distributions of edge recovering for the CORA dataset for Fr=30%.

Table 1. Distributions of edge recovering for the CORA dataset for Fr=30%.

	Frequencies			Mean	Median
0.04	0.22	0.72	0.02	26.57	28.00
0.08	0.21	0.69	0.02	25.79	27.00
0.07	0.24	0.66	0.03	24.96	27.00

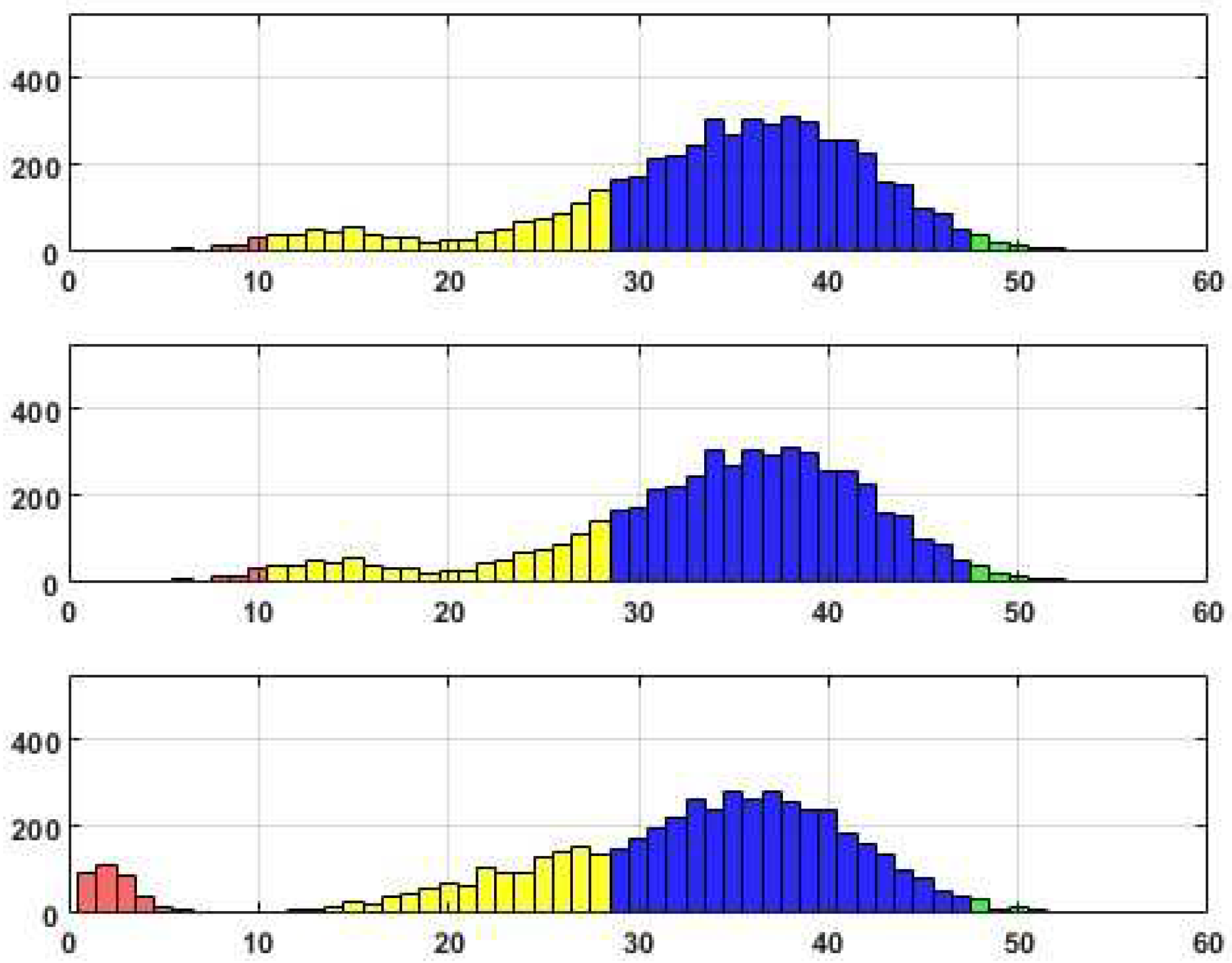
Figure 3. Distributions of edge recovering for the CORA dataset for Fr=40%.

Table 2. Distributions of edge recovering for the CORA dataset for Fr=40%.

	Frequencies			Mean	Median
0.01	0.19	0.77	0.02	33.96	35.00
0.01	0.19	0.77	0.02	33.96	35.00
0.07	0.23	0.68	0.01	30.86	33.00

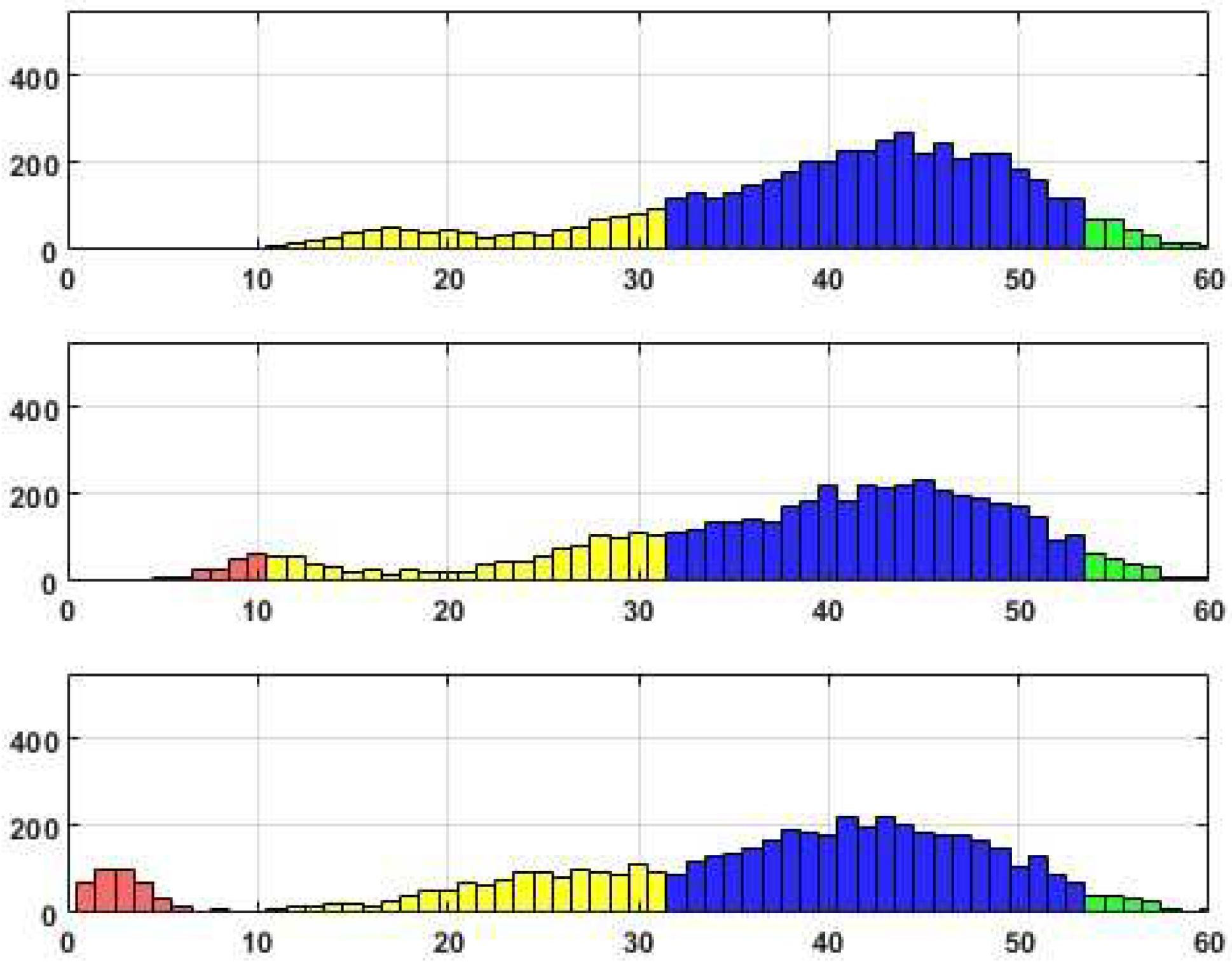
Figure 4. Distributions of edge recovering for the CORA dataset for Fr=50%.

Table 3. Distributions of edge recovering for the CORA dataset for Fr=50%.

	Frequencies			Mean	Median
0.00	0.18	0.77	0.05	40.04	42.00
0.04	0.21	0.71	0.04	37.98	40.00
0.08	0.24	0.66	0.03	35.24	38.00

Upon analyzing the histograms and tables obtained for various Fr values, a noticeable similarity between them becomes apparent. This finding suggests the presence of a consistent underlying structure within the dataset that remains resilient to permutations. It is worth noting that approximately 20% of the total edges (citations) fail to withstand the distortion procedure adequately. These edges, which exhibit high sensitivity to data transformation, do not align with the stable inner structure of the core system. Consequently, the corresponding citations may be considered suspicious and potentially manipulated.

Alternatively, it is worth noting that a distinct set of edges exhibits consistent behavior when subjected to perturbations, resulting in their high probability of being accurately reconstructed. These connections, in fact, constitute a stable core within the data, comprising a substantial number of critical edges that encompass these connections.

The tables provided below showcase 15 distinct sets of specific edges that consistently emerge across various parameter combinations, demonstrating the behavior discussed earlier. It is important to note that there is a significant overlap or intersection between these sets, indicating a strong association among the identified edges. Furthermore, the following table presents the top 15 highly reconstructed edges for all removed fractions (30%, 40%, and 50%) and all similarity thresholds, along with their corresponding average counts. The edges that successfully reconstructed each iteration are visually highlighted in red.

Table 4. The top 15 highly reconstructed edges.

Edge	30			40			50			Average Count
	0.05	0.1	0.2	0.05	0.1	0.2	0.05	0.1	0.2	30	40	50
(116553, 116545)	√	√	√	√	√	√	X	X	X	46.3	49.6	51.6
(559804, 73162)	√	√	√	√	√	√	√	X	X	44.3	50.6	53.6
(17476, 6385)	√	√	√	√	√	√	√	√	√	44	55	62
(96335, 3243)	√	√	√	√	√	√	√	√	√	44	53	55.6
(582343, 4660)	√	√	√	√	√	√	√	√	√	44	50	56
(6639, 22431)	√	√	√	√	√	√	√	√	√	43.3	53	60.3
(78511, 78557)	√	√	√	√	√	√	√	√	√	43.3	50	58.6
(1104379, 13885)	√	√	√	√	√	X	√	X	X	42.6	50	52.6
(39126, 31483)	√	√	√	√	√	√	√	√	√	42.6	51.3	56
(10177, 27606)	√	√	√	√	√	√	√	√	√	42.3	53	58
(1129683, 608326)	√	√	√	X	X	X	X	X	X	42.3	45.3	49.6
(38829, 1116397)	√	√	√	X	X	X	X	X	X	40.3	44.6	38.6
(1107567, 12165)	√	√	√	√	√	√	√	√	√	42.3	57	60
(287787, 634975)	√	√	√	√	√	√	X	X	X	42	50.3	50.6
(643221, 644448)	√	√	√	√	√	√	√	√	X	42	49.3	54.3

The following table presents obtainable papers’ titles. Please take note that due to the incompleteness of the CORA dataset, certain ID’s do not have corresponding names available. These cases are represented as "--" in the information provided below.

Table 5. The titles of the top 15 highly reconstructed edges.

Edge	Name of ID 1	Name of ID 2
(116553, 116545)	A survey of intron research in genetics.	Duplication of coding segments in genetic programming.
(559804, 73162)	On the testability of causal models with latent and instrumental variables.	Causal diagrams for experimental research.
(17476, 6385)	Markov games as a framework for multi-agent reinforcement learning.	Multi-agent reinforcement learning: independent vs.
(96335, 3243)	Geometry in learning.	A system for induction of oblique decision trees.
(582343, 4660)	Transferring and retraining learned information filters.	Context-sensitive learning methods for text categorization.
(6639, 22431)	Stochastic Inductive Logic Programming.	An investigation of noise-tolerant relational concept learning algorithms.
(78511, 78557)	Genetic Algorithms and Very Fast Reannealing: A Comparison.	Application of statistical mechanics methodology to term-structure bond-pricing models.
(1104379, 13885)	--	Learning controllers for industrial robots.
(39126, 31483)	Toward optimal feature selection.	Induction of selective bayesian classifiers.
(10177, 27606)	Learning in the presence of malicious errors.	Statistical queries and faulty PAC oracles.
(1129683, 608326)	--	A sampling-based heuristic for tree search.
(38829, 1116397)	From Design Experiences to Generic Mechanisms: Model-Based Learning in Analogical Design.	--
(1107567, 12165)	--	Slonim. The power of team exploration: Two robots can learn unlabeled directed graphs.
(287787, 634975)	A User-Friendly Workbench for Order-Based Genetic Algorithm Research,	Reducing disruption of superior building blocks in genetic algorithms.
(643221, 644448)	Minorization conditions and convergence rates for Markov chain Monte Carlo.	G.O. and Sahu, S.K. (1997) Adaptive Markov chain Monte Carlo through regeneration.

4.2. Pubmed-Diabetes dataset

The term "Pubmed-Diabetes dataset" commonly refers to a compilation of scientific articles concerning diabetes that can be found in the PubMed database. PubMed is an extensive online resource managed by the National Center for Biotechnology Information (NCBI) and the U.S. National Library of Medicine, housing various biomedical literature, including research papers, reviews, and scholarly publications. In our research, we utilized the dgl.data.PubmedGraphDataset() function from the Deep Graph Library (DGL) to retrieve and load the Pubmed-Diabetes dataset. This function is a component of the Deep Graph Library (DGL) that facilitates the retrieval and loading of the Pubmed-Diabetes dataset consisting of scientific articles focusing on diabetes, which are sourced from the PubMed database. Designed specifically for this dataset, the function enables researchers to conveniently access and analyze the interconnected information present within these articles

During our analysis, we randomly chose a subset of 5201 edges from the dataset. Interestingly, we observed that among these selected edges, 4867 edges were connected. This discovery offers valuable insights into the interconnectedness within the chosen portion of the PubMed-Diabetes dataset, representing a random sample accounting for 10% of the original dataset. An analysis of such a sample dataset can be conducted similarly to the analysis performed on the CORA dataset.

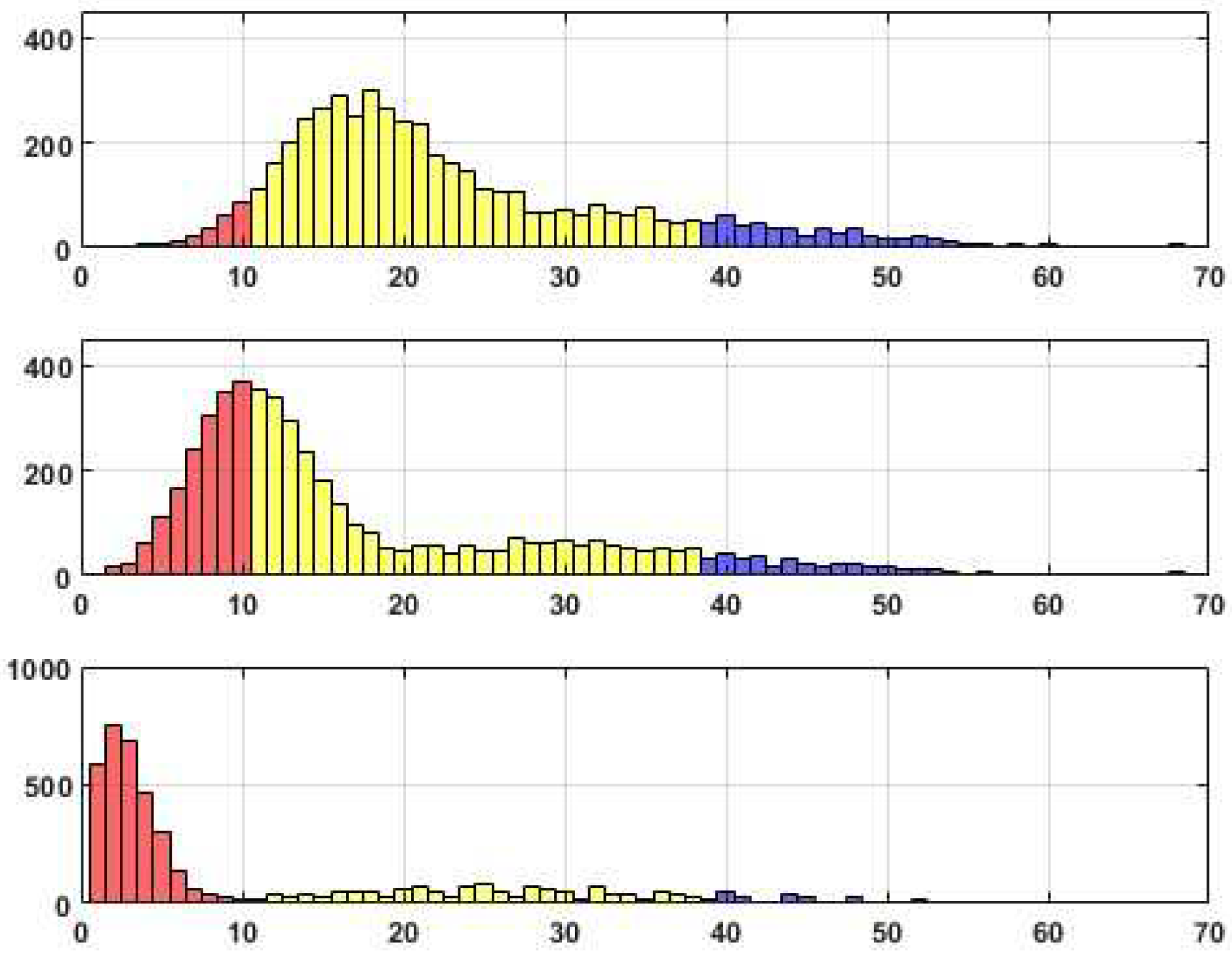
In line with previous discussions, histograms in Figure 6, Figure 7 and Figure 8 showcase the distributions of edges across these specific categories. Corresponding tables provide detailed supplementary information regarding the allocation of edges within each category.

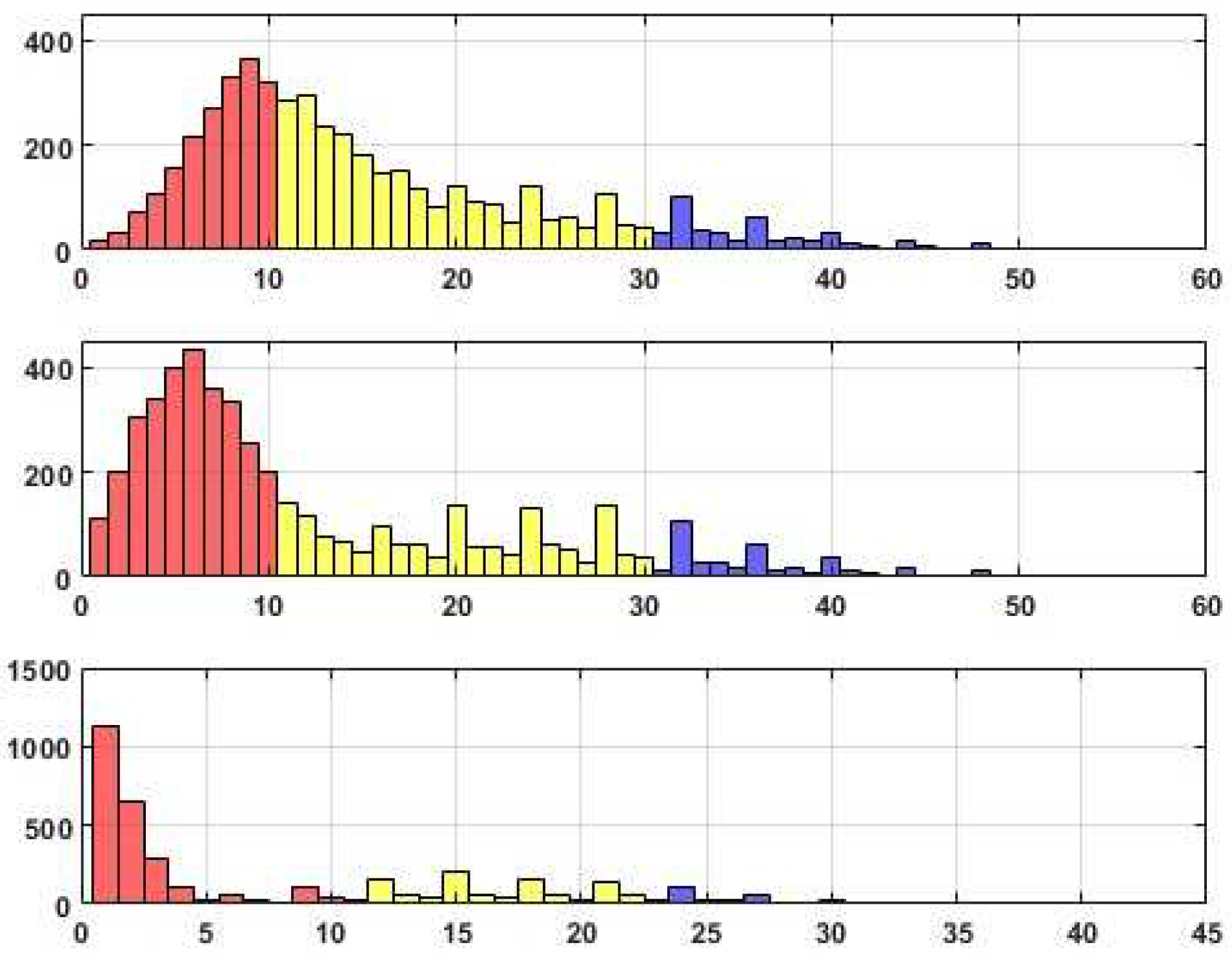
Figure 6. Distributions of edge recovering for the PubMed dataset for Fr=30%.

Table 6. Distributions of edge recovering for the PubMed dataset for Fr=30%.

	Frequencies		Mean	Median
0.39	0.52	0.09	15.26	12.00
0.61	0.31	0.08	12.36	8.00
0.64	0.26	0.09	6.57	2.00

Figure 7. Distributions of edge recovering for the PubMed dataset for Fr=40%.

Table 7. Distributions of edge recovering for the PubMed dataset for Fr=40%.

	Frequencies		Mean	Median
0.17	0.69	0.14	19.56	16.00
0.49	0.39	0.11	15.45	11.00
0.65	0.26	0.09	10.42	3.00

Figure 8. Distributions of edge recovering for the PubMed dataset for Fr=50%.

Table 8. Distributions of edge recovering for the PubMed dataset for Fr=50%.

	Frequencies		Mean	Median
0.05	0.84	0.11	23.17	20.00
0.34	0.58	0.08	17.72	13.00
0.67	0.27	0.06	11.22	4.00

The observed sensitivity of the dataset to the considered perturbations highlights the need for careful parameter selection. Notably, the results indicate that the dataset is exceptionally responsive when the similarity threshold (Tr) is set to 0.05. This setting consistently produces suitable outcomes for Fr values of 0.3 or 0.4, indicating a robust relationship between the selected threshold and the desired results. However, when Fr is increased to 0.5, the optimal choice for the similarity threshold becomes slightly more nuanced. In this case, both Tr values of 0.05 and 0.1 provide favorable results, suggesting a broader range of acceptable thresholds. Nevertheless, it is essential to note that despite achieving desirable outcomes, the expected core associated with the reconstructed edges appears to be of inferior quality compared to other cases. This finding implies that the reliability and relevance of the reconstructed edges within this particular subset may be questionable and should be treated with caution.

It is important to note that the results discussed so far are based on analyzing a subset of the dataset, representing only 10% of the entire collection. This limited sample size may have implications for the generalizability and reliability of the findings. Therefore, it is crucial to interpret the results within the context of this subset and exercise caution when drawing broader conclusions about the entire dataset.

The obtained results corroborate the previous findings concerning the CORA dataset. Specifically, a consistent pattern emerges where around one-third (or possibly slightly more, considering the lower fraction of the first category) of the edges demonstrate instability and lack relevance. This consistency between the results obtained for both datasets suggests a common underlying characteristic regarding the reliability of the edges. It indicates that a significant portion of the connections within citation datasets may be less trustworthy or subject to potential manipulation.

5. Conclusions

To sum up, analyzing the CORA and Pubmed-Diabetes datasets using the proposed methodology has yielded valuable insights into citation interconnectivity and its sensitivity to perturbations. It is necessary to acknowledge that these findings are based on a subset representing only 10% of the complete Pubmed-Diabetes dataset. Despite the distinct internal structures of the datasets, the results obtained from the numerical experiments exhibit meaningful comparability. This comparability suggests the presence of a potential general inclination within the mutual citation structure, indicating shared characteristics that transcend specific dataset variations. To further explore this phenomenon, we intend to utilize multiple deep-learning models on the respective datasets. This approach can facilitate a more comprehensive examination of the underlying patterns and dynamics within citation networks on a broader scale.

By conducting these forthcoming investigations, we anticipate gaining deeper insights into the general citation interconnectivity, enabling more nuanced interpretations and analyses across diverse domains. Leveraging multiple deep-learning models will uncover additional valuable insights and uncover potential commonalities in citation structures, thereby advancing the field of research in this area.

Author Contributions

Dr. Ranata Avros, Dr. Dvora Toledano Kitai, and Prof. Zeev Volkovich collaborated on model creation, design, and the writing and organization of the paper. Mr. Saar Keshet and Mr. Evgeny Vexler were responsible for designing and conducting the experimental study.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

Chandra G. Prabha. Some aspects of citation behavior: A pilot study in business administration. Journal of the American Society for Information Science 1983, 34(3), 202–206. [CrossRef]
D. B., Gutierrez-Ford, C.; Peddada, S. Perceptions of Ethical Problems with Scientific Journal Peer Review: An Exploratory Study. Science and Engineering Ethics 2008, 14(3), 305-310. https://doi.org/10.1007/s11948-008-9059-4. [CrossRef]
Wilhite, A.; Fong, E. Coercive citation in academic publishing. Science 2012, 335(6068), 542-543. https://doi.org/10.1126/science.1212540. [CrossRef]
Wren, J.D.; Georgescu, C. Detecting anomalous referencing patterns. In PubMed papers suggestive of author-centric reference list manipulation. Scientometrics 2022, 127, 5753-5771. [CrossRef]
M. Dong: B. Zheng; N. Quoc Viet Hung; H. Su; G. Li. Multiple rumor source detection with graph convolutional networks. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, 569–578, Beijing, China, November 3 - 7, 2019. [CrossRef]
Y.-J. Lu ; C.-T. Li. Gcan. Graph-aware co-attention networks for explainable fake news detection on social media. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, 505–514, Virtual conference July 5 - 10, 2020. [CrossRef]
T. Bian; X. Xiao; T. Xu; P. Zhao; W. Huang; Y. Rong; J. Huang. Rumor detection on social media with bi-directional graph convolutional networks. In Proceedings of the AAAI Conference on Artificial Intelligence, 34(1), 549–556, New York, NY, USA, February 7–12, 2020. [CrossRef]
Li; Z. Qin; R. Liu; Y. Yang; D. Li. Spam review detection with graph convolutional networks. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, 2703–2711, Beijing, China, November 3 - 7, 2019. [CrossRef]
S. Yu; F. Xia; Y. Sun; T. Tang; X. Yan; I. Lee. Detecting outlier patterns with query-based artificially generated searching conditions. IEEE Transactions on Computational Social Systems 2020, 8(1), 134–147. [CrossRef]
J. Liu; F. Xia; X. Feng; J. Ren; H. Liu. Deep Graph Learning for Anomalous Citation Detection. IEEE Transactions on Neural Networks and Learning Systems 2022, 33(6), 2543-2557. https://doi.org/10.1109/TNNLS.2022.3145092. [CrossRef]
Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representa-tions in Vector Space. In Proceedings of the 1st International Conference on Learning Representations, ICLR 2013, Scottsdale, AZ, USA, 2–4 May 2013. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer