Prerpints.org logo
Preprint
Article

Rotational Curves of the Milky Way and Andromeda in light of Vacuum Polarization around Eicheon

Altmetrics

Downloads

156

Views

24

Comments

1

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 July 2023

Posted:

16 August 2023

You are already at the latest version

Alerts
Abstract
Eicheon properties are discussed. It is shown that the eicheon surface allows setting a boundary condition for the vacuum polarization and obtaining a solution describing the dark matter tail in the Milky Way. That is, the dark matter in the Milky Way is explained as the F-type of vacuum polarization, which could be treated as dark radiation. The model presented is spherically symmetric, but a surface density of a baryonic galaxy disk is taken into account approximately by smearing the disk over a sphere. This allows the reproduction of the large distance shape of the Milky Way rotational curve. Andromeda's rotational curves are also discussed.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

Observation of the stellar orbits around the center of the Milky Way [1,2], detecting the gravitational waves from the black hole/black hole and black hole/neutron star coalescence (e.g., see the catalog [3] for an overview), radio-astronomy observation of the “black hole shadows” in the centers of galaxies [4,5] are widely considered as the direct evidence of an extremely compact astrophysical object (ECO) existence with a radius of an order of the Schwarzschild one. The observable properties of such an object are well-described by an exact Schwarzschild (or, more precisely, Kerr) solution of the general relativity (GR) equations [6,7]. A principal question is whether the Schwarzschild solution interprets reality quite adequately. Indeed, there are a lot of theoretical attempts to describe ECO whose properties approach those of an ordinary GR black hole sufficiently far from the event horizon (so-called horizonless “exotic compact objects” [8]). Some of them are based on the modified theories of gravity1. Recently, ECOs without a horizon have been discussed intensively (e.g., [12,13,14,15]). A zoo of exotic ECO, such as bosonic stars [16], gravastars [17], and other exotic stars [18,19], was proposed and theoretically explored. Also, the approaches based on constructing the nonsingular black-hole metrics in the spacetimes of different dimensions were proposed (e.g., see [20,21]).
The question about the nature of ECO is also related to the need for dark matter (DM) to explain the galactic rotational curves [22,23,24]. In particular, the first observation of the DM density around the stellar-mass ECO appears [25]. It was conjectured that the primordial black holes could be considered the candidates to DM [26].
Besides, there is a plethora of DM candidates [27]. However, could we advance without extraordinary physics but only by taking a vacuum polarization into account correctly [28]? Conventional answer is “No” in the frame of the renormalization technique of quantum field theory on a curved background [29,30]. Still, this approach demands covariance of the mean value of the energy-momentum tensor over the vacuum state [29]. This demand has no solid foundation because it is known that there is no vacuum state invariant relative to the general transformation of coordinates. On the contrary, an argument was put forward that the preferred conformally-unimodular metric (CUM) could describe a vacuum polarization and resolve the DM problem [28,31]. In this metric, a black hole as an object having a horizon is absent. Its disappearance results from the coordinate transformation relating the Schwarzschild-type metric to CUM, which selects some shell over the horizon and draws it into a node. As a result, a point mass without a horizon arises in a CUM. It is an idealized picture. In reality, one must know the equation of the state of a substance forming such ECO (named “eicheon” [32]).
Here, aiming at understanding the eicheon nature, we will use an approximation of the constant energy density and a trial “equation of state” relating the maximal pressure and the energy density. In our approach, we construct eicheon, and, after determining its properties, describe an eicheon surrounded by “dark radiation” to explain the rotational curves of the Milky Way and Andromeda (M31). “Dark radiation” is one of two kinds of vacuum polarization considered in [28], namely the polarization of F-type. Finally, to be closer to observations, we introduce a baryonic matter into the model by smearing the galactic disks of the Milky Way and M31.

2. What is “eicheon”?

Eicheon is a horizon-free object which appears instead of a black hole in CUM. As an idealized structure, eicheon represents a solution of a gravitational field of a point mass in CUM. In the metric of a Schwarzschild type, it looks like a massive shell situated over the Schwarzschild radius. In the real world, where there is no infinite density and pressure, the eicheon could be modeled in the Schwarzschild-type metric by a layer of finite width over the horizon, as it is shown in Figure 1. In CUM, it looks like a solid ball [32,33]. A constant density model is convenient for understanding the main features of the eicheon.
CUM for a spherically symmetric space-time is written as
d s 2 = a 2 ( d η 2 − γ ˜ i j d x i d x j ) = e 2 α d η 2 − e − 2 λ ( d x ) 2 − ( e 4 λ − e − 2 λ ) ( x d x ) 2 / r 2 ,
where r = | x | , a = exp α , and λ are the functions of η , r . The matrix γ ˜ i j with the unit determinant is expressed through λ ( η , r ) . The interval (1) could be also rewritten in the spherical coordinates:
x = r sin θ cos ϕ , y = r sin θ sin ϕ , z = r cos θ
resulting in
d s 2 = e 2 α d η 2 − d r 2 e 4 λ − e − 2 λ r 2 d θ 2 + sin 2 θ d ϕ 2 .
However, let us discuss eicheon properties in the Schwarzschild-type metric, which is more convenient for a reader
d s 2 = B ( R ) d t 2 − A ( R ) d R 2 − R 2 d Ω .
In this metric, the Volkov-Tolman-Oppenheimer (TOV) equation for a layer R ∈ { R i , R f } reads as:
p ′ ( R ) = − 3 4 π M p 2 R 2 M ( R ) ρ ( R ) 1 + 4 π R 3 p ( R ) M ( R ) 1 + p ( R ) ρ ( R ) 1 − 3 M ( R ) 2 π M p 2 R − 1 ,
where the function
M ( R ) = 4 π ∫ R i R ρ ( R ′ ) R ′ 2 d R ′
and the reduced Planck mass M p = 3 4 π G = 1.065 × 10 − 8 k g . We will model a layer of constant density ρ so that M ( R ) is reduced to
M ( R ) = 4 π 3 ρ R 3 − R i 3 .
It is convenient to measure distances in units of the Schwarzschild radius r g = 3 M 2 π M p 2 , and density and pressure in the units of M p 2 r g − 2 . In these units, it follows from (7) and M = M ( R f ) that
ρ = 1 2 ( R f 3 − R i 3 ) .
The TOV equation (5) is reduced to
p ′ = ( p + ρ ) 3 p R 3 + ρ R 3 − R i 3 R 2 ρ R 3 − R i 3 − R
and has to be solved with the boundary condition p ( R f ) = p R i 3 + 1 2 ρ 3 = 0 , where the second equality follows from (8). Let us simplify the problem further and assume that R i = 1 in the Schwarzschild radius units. Even in this case, there is no analytical solution of the equation (9), but the most interesting quantity is a maximal pressure p m a x = p ( 1 ) , which could be approximated by the expression
p m a x ≈ ρ 6 − 1 3 + 11 36 6 ρ − 35 864 6 ρ 3 / 2
as is shown in Figure 2.
If one supplements Eq. (10) by the “equation of state”, which connects the maximal pressure with the density, then it is possible to determine the pressure and density. For instance, the “equation of state” corresponding to a degenerate relativistic fermion gas
p m a x = ρ / 3
gives no solution because of Eqs. (10) and (11) are incompatible.
The equation of state of the nonrelativistic degenerate Fermi gas is written in physical units as [34]
p ˜ m a x = 1 5 3 π 2 m N 4 2 / 3 ρ ˜ 5 / 3 ,
where m N is a particle mass, and the tilde denotes that the quantity is expressed in the physical units. When ρ is large, one could use only the first term in Eq. (10), and its equating to the pressure from (12) gives the following expression
M p r g − 1 ρ ˜ 6 = 3 2 / 3 π 4 / 3 5 1 m N 4 2 / 3 ρ ˜ 5 / 3 ,
allowing us to find the physical density
ρ ˜ = 5 3 6 / 7 2 3 / 7 m N 16 / 7 M p 18 / 7 3 π 2 / 7 M 6 / 7 ,
which decreases with an increase of mass M of the eicheon. Dimensionless density is found by dividing (14) by M p 2 r g − 2 and reads
ρ = 3 7 5 6 / 7 M 8 / 7 m N 16 / 7 2 11 / 7 π 16 / 7 M p 24 / 7 .
It grows with the increase of M , so that approximation p m a x ≈ ρ / 6 becomes justified at some mass according to (10). Respectively, the width of the eicheon shell decreases: Δ R = 1 + 1 2 ρ 3 − 1 ≈ 1 6 ρ and becomes very thin at large M . Certainly, we measure the relative width in units of r g . For instance, if one takes the eicheon mass equal to the Sun mass M = M ⊙ = 1.989 × 10 30 k g and m N equals the neutron mass, then the dimensional density ρ ˜ = 2.4 × 10 19 k g / m 3 , while the dimensionless ρ equals 0.66 . This eicheon has a rather thick skin Δ R ≈ 0.33 and, in the principle can be distinguished from a conventional black hole. One more example is the eicheon of a large mass 40 × 10 9 M ⊙ . In this case, the physical density is much lower and we could consider the “equation of state” for a cold hydrogen plasma, where the pressure is created by a degenerate electron gas, and the dimensional density satisfies
M p r g − 1 ρ ˜ 6 = 3 2 / 3 π 4 / 3 5 1 m e 4 2 / 3 ρ ˜ m e m N 5 / 3 ,
so that
ρ ˜ = 5 3 6 / 7 2 3 / 7 m e 6 / 7 m N 10 / 7 M p 18 / 7 3 π 2 / 7 M 6 / 7 .
The dimensionless density is given by
ρ = 3 7 5 6 / 7 M 8 / 7 m e 6 / 7 m N 10 / 7 2 11 / 7 π 16 / 7 M p 24 / 7 .
Numerically, these values are ρ ˜ = 3.1 × 10 7 k g / m 3 , ρ = 1.4 × 10 9 . The eicheon skin is very thin Δ R ∼ 1 6 ρ ∼ 10 − 10 . Such eicheon is indistinguishable from a conventional black hole. At the same time, it is rather “mellow” by virtue of (17). Certainly, there is no paradox here because Δ R is measured in the units of r g , which is large in the case considered. Finally, we can estimate eicheon in the center of the Milky Way using the formulas (16), (17), (18). For M = 4.154 × 10 6 M ⊙ , they give ρ ≈ 3.8 × 10 4 , Δ R ∼ 10 − 6 and ρ ˜ ≈ 8.2 × 10 10 k g / m 3 that is greater than the white dwarf mean density ρ ˜ ≈ 4 × 10 8 k g / m 3 [35]. The eicheons of any mass exist because the inner R i and outer R f radii (see Figure 1b ) exceed the Schwarzschild radius, and Buchdahl’s bound [36] M < 4 R / 9 G is not eligible.
To consider eicheon in CUM (3), one could set t = η , R = R ( r ) and compare the metrics (3) and (4) to obtain:
B ( R ) = e 2 α ,
R 2 = r 2 e − 2 λ + 2 α ,
A ( R ) d R d r 2 = e 4 λ + 2 α .
Using (19), (20) in (21) to exclude λ and α yields
d r d R = R 2 r 2 A 1 / 2 B 3 / 2 .
In the region filled by matter, A ( R ) and B ( R ) obey [37]
d d R R A = 1 − 6 ρ R 2 , 1 B d B d R = − 2 p + ρ d p d R .
For the model of a constant density ρ ( R ) = c o n s t , the equation () can be integrated explicitly
A = R R − 1 − 2 ρ R 3 − R f 3 .
B = 1 − 1 R f ρ 2 ( p ( R ) + ρ ) 2 ≈ 1 − 1 R f ,
where the pressure is neglected compared to the energy density in the last equality of (25). According to (22), the eicheon radius is
r f = 3 ∫ 1 R f A 1 / 2 B 3 / 2 R 2 d R 3 ≈ 3 11 3 ρ 1 / 6 2 5 / 6 + 43 2 5 / 6 3 5 / 2 11 2 / 3 ρ 5 / 6 ,
where a small “thickness” of the eicheon surface R f − 1 is assumed, and R f is expressed as R f = 1 + 1 2 ρ 3 . For a supermassive eicheon, using (18) and first term of (26) results
r f ≈ 3 11 / 21 5 7 11 3 2 23 / 21 π 8 / 21 M 8 m e 6 m N 10 M p 24 42 ,
i.e., in CUM, the eicheon radius in the units of r g increases when the eicheon mass m rises.

3. Vacuum polarization around of eicheon

Considering the vacuum polarization for an arbitrary curved space-time background is a highly complex problem. Instead, one could consider the scalar perturbations of CUM:
d s 2 = ( 1 + Φ ( η , x ) ) 2 d η 2 − 1 + 1 3 ∑ m = 1 3 ∂ m 2 F ( η , x ) δ i j − ∂ i ∂ j F ( η , x ) d x i d x j
and calculate a spatially nonuniform energy density and pressure arising due to vacuum polarization in the eikonal approximation [28].
As was shown [28], the energy density and pressure of vacuum polarization corresponding to the F-type of metric perturbations (28) have the radiation equation of state δ p F = 1 3 δ ρ F . That gives a possibility to use a hypothetical “dark radiation” in some heuristic nonlinear models, such as the TOV equation. For a radiation substance alone, a singular solution of the TOV equation exists that is devoid of physical meaning [37]. However, the situation changes cardinally in CUM in the presence of the nonsingular eicheon. This gives a possibility to set a boundary condition for a radiation fluid at r = 0 and obtain a nonsingular solution, including the dark radiation. In the Schwarzschild type metric (4), the boundary condition is set at the radial coordinate of an inner shell R = R i , which corresponds to the point r = 0 in CUM (see Figure 1) .
The system of equations (see Appendix A ) in the metric (4), implies three substances: the eicheon of the constant density ρ 1 , the dark radiation density ρ 2 , and the density ρ 3 of baryonic matter of the galactic disk and bulge:
p 1 ′ = − 3 ( p 1 + ρ 1 ) M + 4 π R 3 p 1 + ρ 2 3 2 R 2 π R − 3 M , M ′ = 4 π R 2 ( ρ 1 + ρ 2 ) , ρ 2 ′ = − 6 ρ 2 M + 4 π R 3 p 1 + ρ 2 3 R 2 π R − 3 M , R i < R < R f , ρ 2 ′ = − 6 ρ 2 M + 4 π R 3 ρ 2 3 R 2 π R − 3 M , M ′ = 4 π R 2 ( ρ 2 + ρ 3 ) , R > R f .
where the baryonic matter ρ 3 is considered as some external matter density. According to (29), there are two equations for the pressure and "dark radiation" density inside the eicheon and a single equation for “dark radiation” density outside the eicheon.
As is shown in the upper panel of Figure 3, the eicheon without galactic disk and bulge contributes at a small distance, and the dark radiation contributes at large distances. The density of dark radiation depends on the eicheon structure, which was considered in the previous section. It is convenient to introduce a universal quantity of a dark radiation density for the Milky Way at the radius of a photon sphere R = 3 / 2 , which almost does not depend on eicheon structure, namely ρ 2 * ≡ ρ 2 ( 3 / 2 ) = 9.3 × 10 − 32 = 2.1 × 10 − 25 k g / m 3 . Moreover, it remains a single parameter because the eicheon mass in the dimensionless units equals M = 2 π / 3 . Thus, a DM tail is reproduced by virtue of the universal equations
ρ 2 ′ = − 3 ρ 2 M + 4 π R 3 ρ 2 3 π R R − 3 M 2 π , M ′ ( R ) = 4 π R 2 ρ 2 , M ( 3 / 2 ) = 2 π / 3 , ρ 2 ( 3 / 2 ) = ρ 2 * , R > 3 / 2 .
That is a spherically symmetric model where the amount of dark radiation is adjusted to fit the observations. The rotation velocity is calculated according to [28]
v r o t = R 2 B d B d R = − R p 2 + ρ 2 d p 2 d R = 1 2 − R ρ 2 d ρ 2 d R ,
where the last equality of (31) says that the dark radiation ρ 2 serves a “reference fluid” because satisfies continuity equation (23) rewritten in the form of
d ρ 2 d R + 2 B d B d R ρ 2 = 0 .
To consider the baryonic matter, one could smear a baryonic galactic disk on a sphere and view the resulting mass density as some external non-dynamical density in the TOV equations for the eicheon and dark radiation. This external density creates an additional gravitational potential.
Let us consider the surface density of matter in a galactic disk:
℘ = M D 2 π R D 2 e − R / R D ,
and write the mass d M corresponding to the radial distance d R
d M = M D R D 2 e − R / R D R d R = M D R D 2 R e − R / R D R 2 d R .
According to (34), the smeared 3-dimensional density has the form:
ρ 3 = M D 4 π R D 2 R e − R / R D .
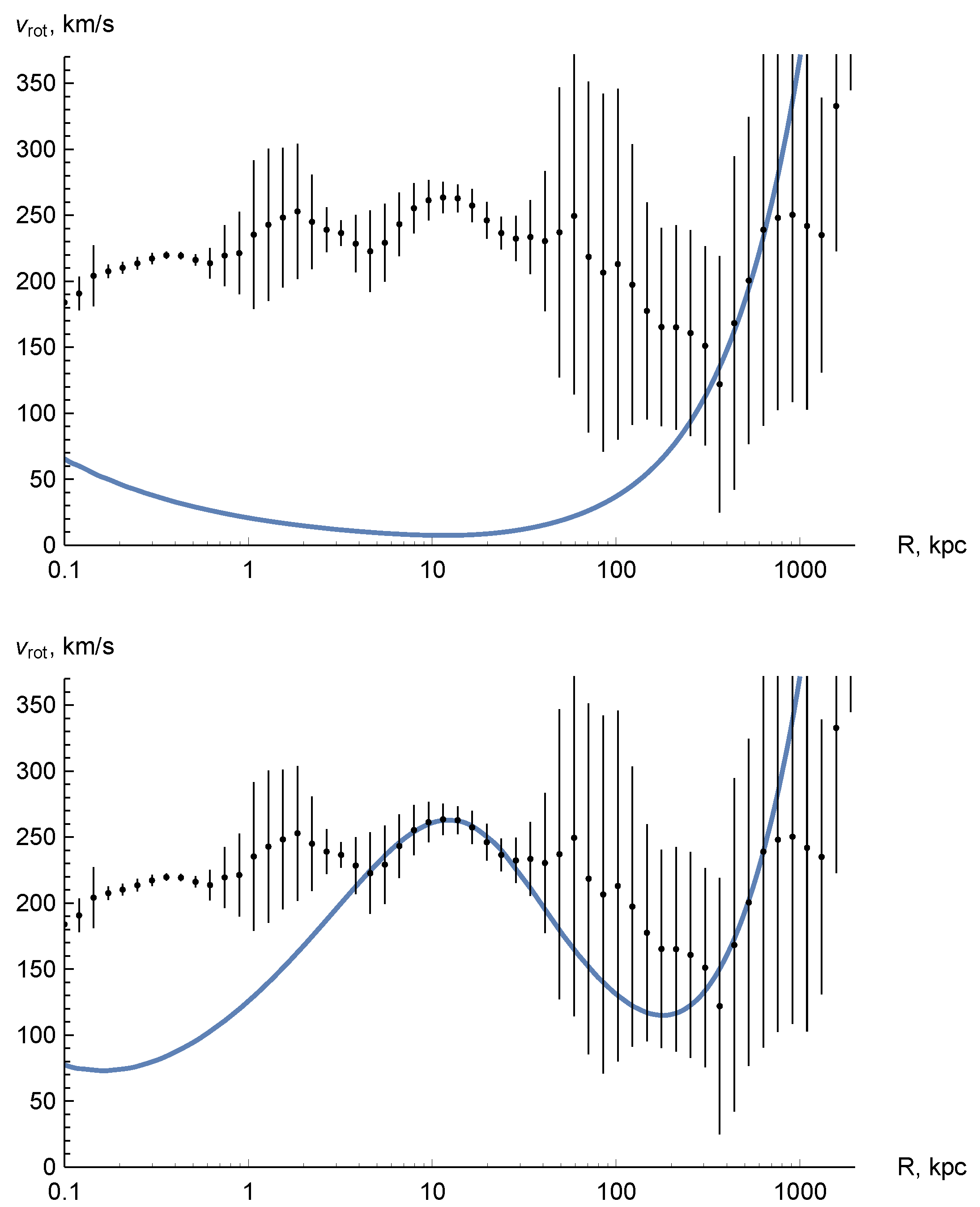
The result of the calculations for the Milky Way rotational curve is shown in the lower panel of Figure 3. As one can see, the simple model with smeared disk describes the baryonic matter roughly, but the observed rotational curve has a more complicated structure.

4. Andromeda

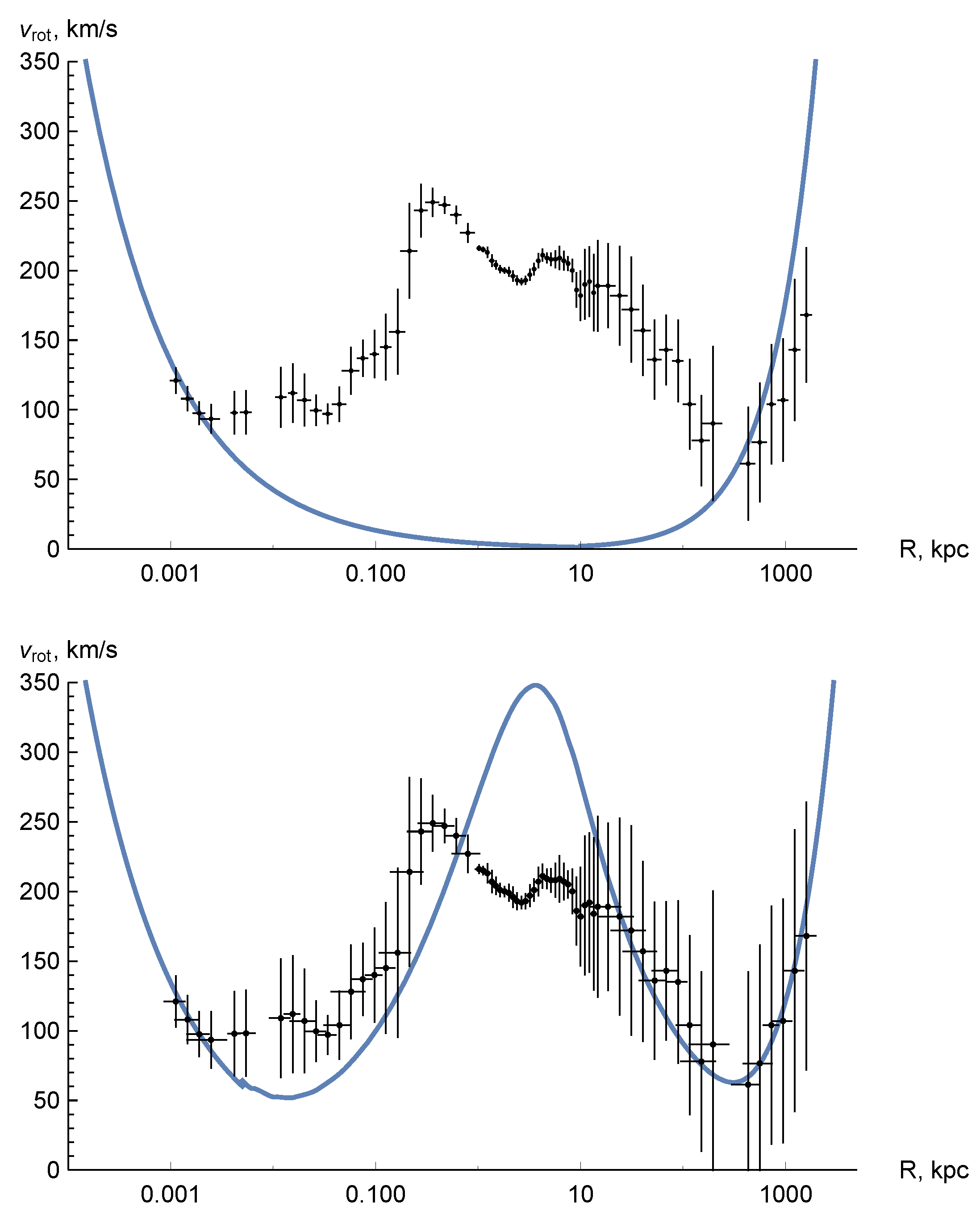
Andromeda galaxy (M31) is nearest to the Milky Way and is situated at a distance ∼ 800 k p c . For M31, there are no small distances data ∼ 0.01 k p c , allowing us to identify a compact object in the center explicitly. Indeed, the situation is more complicated because cluster B023-G078 of M31 hosts one more black hole ∼ 10 5 M ⊙ [38,39]. For the correct description, we need to apply a solution with two eicheons. This problem seems complicated, and we leave it for the future, considering only one central eicheon with the mass 10 8 M ⊙ [38,39]. We again used (33) for a disk surface density distribution and smeared it over a sphere.
The results of modeling are shown in Figure 4. The dimensionless parameter equaled the dark radiation density in the units of M p 2 r g − 2 at a photon sphere radius is ρ 2 ( 3 / 2 ) = 6.2 × 10 − 28 = 2.3 × 10 − 24 k g / m 3 . This value is greater than that for the Milky Way, i.e. these suggest the greater mass of central eicheon and the greater dark radiation density at a radius of the eicheon photon sphere. After introducing the baryonic matter as in the previous section, we have the curve shown in a lower panel of Figure 4.

5. Discussion and conclusion

We have shown that the F-type vacuum polarization could explain DM, which mimics a sort of “dark radiation.” Namely the presence of ECO, or eicheon, in the center of the galaxy provides a nonsingular solution for dark radiation. The eicheon resembles a black hole for an external observer but has no horizon. Our model is spherically symmetric. However, the appropriate approximation of the distribution of baryonic matter in a galaxy by the disk smearing over a sphere allows for obtaining the qualitative agreement of the rotational curves with the observed ones.
Still, possibly, in the spreading of a galactic disk, we overestimated a baryonic matter. Usually, it is supposed that DM begins to play a role from a few k p c , but according to the above consideration, the contribution of dark radiation becomes considerable only at tens k p c . For M31, we are not able to obtain an amount of DM needed in the region of 10 − 100 k p c . We conjecture that, if there is not only a central eicheon in the galaxy but a number of eicheons, one could glue dark radiation tails to every eicheons and create a needed amount.
Let us remind the principles of calculation. We have considered the vacuum polarization of F-type in CUM (28) and find that it has a radiation-like equation of state. Then, we solve the TOV equation for incompressible fluid and dark radiation and obtain a nonsingular solution. To consider the baryonic matter, we smear a galactic disk and use the resulting density as some external density. Interestingly, each galaxy’s dark radiation tail can be described by a single parameter: density of dark radiation at the radius of a photon sphere of the eicheon. The numerical value of this density for the Milky Way is 2.1 × 10 − 25 k g / m 3 , and for Andromeda it is 2.3 × 10 − 24 k g / m 3 .
These values could be compared with the spatially uniform residual energy density of vacuum fluctuations, which remain after compensation of its main part by the constant in the Friedman equation [41]. It is of the order of critical density ∼ × 10 − 26 k g / m 3 . Certainly, we use the amount of the dark radiation at a photon radius of the eicheon R = 3 / 2 r g . Still, this amount rapidly decreases at R > 3 / 2 r g and increases at R < 3 / 2 r g . In this light, it is interesting to obtain a general picture of matter structure formation in the universe by the solution of the system of the equations for the perturbations of the metric and the matter, including vacuum polarisation of both types [28].

Appendix A. TOV equation for a mixture of ordinary and dark fluids

Each of the fluids obeys the equation of the hydro-static equilibrium [37]:
B ′ B = − 2 p 1 ′ ρ 1 + p 1 ,
whereas the equations for gravitational field give [37]
R A ′ = 1 − 8 π G ρ R 2 ,
− 1 + R 2 A − A ′ A + B ′ B + 1 A = − 4 π G ( ρ − p ) R 2 ,
where p = p 1 + p 2 , and ρ = ρ 1 + ρ 2 . Solution of the equation (A2) is written formally as
A = 1 1 − 2 G M / R ,
where M is given by (6) Expressing B ′ / B from (A1), A, A ′ from (A4), () and substituting them into (A2) gives
p 1 ′ = − ( p 1 + ρ 1 ) G M + 4 π R 3 p R ( R − 2 G M ) .
The analogous equation holds for the second fluid.

References

  1. Gillessen, S.; Eisenhauer, F.; Trippe, S.; others. Monitoring stellar orbits around the Massive Black Hole in the Galactic Center. Astrophys. J. 2009, 692, 1075–1109. [Google Scholar] [CrossRef]
  2. Nampalliwar, S.; Kumar, S.; Jusufi, K.; Wu, Q.; Jamil, M.; Salucci, P. Modeling the Sgr A* Black Hole Immersed in a Dark Matter Spike. Astrophys. J. 2021, 916, 116. [Google Scholar] [CrossRef]
  3. Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.; Adya, V.; Affeldt, C.; Agarwal, D. others. GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run, 2021. C: GWTC-3; arXiv:gr-qc/2111.03606.
  4. Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; others. First M87 event horizon telescope results. VI. The shadow and mass of the central black hole. Astrophys. J. Lett. 2019, 875, L6. [Google Scholar]
  5. Johnson, M.D.; Narayan, R.; Psaltis, D.; Blackburn, L.; Kovalev, Y.Y.; Gwinn, C.R.; Zhao, G.Y.; Bower, G.C.; Moran, J.M.; Kino, M.; others. The Scattering and Intrinsic Structure of Sagittarius A* at Radio Wavelengths. Astrophys. J. 2018, 865, 104. [Google Scholar] [CrossRef]
  6. Landau, L.D.; Lifshitz, E. The Classical Theory of Fields; Vol. 2, Butterworth-Heinemann: Oxford, 1975. [Google Scholar]
  7. Chandrasekhar, S. The mathematical theory of black holes; Oxford University Press: New York, USA, 1983. [Google Scholar]
  8. Cardoso, V.; Pani, P. Testing the nature of dark compact objects: a status report. Liv. Rev. Rel. 2019, 22, 1–104. [Google Scholar] [CrossRef]
  9. Berti, E.; Barausse, E.; Cardoso, V.; Gualtieri, L.; Pani, P.; Sperhake, U.; Stein, L.C.; Wex, N.; Yagi, K.; Baker, T.; others. Testing general relativity with present and future astrophysical observations. Class. Quant. Grav. 2015, 32, 243001. [Google Scholar]
  10. Yagi, K.; Stein, L.C. Black hole based tests of general relativity. Class. Quant. Grav. 2016, 33, 054001. [Google Scholar] [CrossRef]
  11. Logunov, A.A.; Mestvirishvili, M.A. On the possibility of gravitational collapse in the relativistic theory of gravity. Theor. Math. Phys. 1997, 112, 1056–1067. [Google Scholar] [CrossRef]
  12. Barceló, C.; Liberati, S.; Sonego, S.; Visser, M. Fate of gravitational collapse in semiclassical gravity. Phys. Rev. D 2008, 77, 044032. [Google Scholar] [CrossRef]
  13. Chapline, G. Emergent Space-Time. In Beyond Peaceful Coexistence: The Emergence of Space, Time and Quantum; Licata, I., Ed.; Imperial College Press: London, the UK, 2016; pp. 419–432. [Google Scholar]
  14. Carballo-Rubio, R.; Di Filippo, F.; Stefano Liberati, S.; Visser, M. A connection between regular black holes and horizonless ultracompact stars, 2022. 2022; arXiv:gr-qc/2211.05817. [Google Scholar]
  15. Carballo-Rubio, R.; Filippo, F.D.; Liberati, S.; Visser, M. Singularity-free gravitational collapse: From regular black holes to horizonless objects, 2023. F: gravitational collapse, 2023; arXiv:gr-qc/2302.00028. [Google Scholar]
  16. Schunck, F.E.; Mielke, E.W. General relativistic boson stars. Class. Quant. Grav. 2003, 20, R301. [Google Scholar] [CrossRef]
  17. Ray, S.; Sengupta, R.; Nimesh, H. Gravastar: An alternative to black hole. Int. J. Mod. Phys. D 2020, 29, 2030004. [Google Scholar] [CrossRef]
  18. Urbano, A.; Veermäe, H. On gravitational echoes from ultracompact exotic stars. JCAP 2019, 2019, 011. [Google Scholar] [CrossRef]
  19. Singh, K.N.; Ali, A.; Rahaman, F.; Nasri, S. Compact stars with exotic matter. Phys. Dark Universe 2020, 29, 100575. [Google Scholar] [CrossRef]
  20. Hayward, S.A. Formation and evaporation of nonsingular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [PubMed]
  21. Frolov, V.P. Notes on nonsingular models of black holes. Phys. Rev. D 2016, 94, 104056. [Google Scholar] [CrossRef]
  22. Sofue, Y. Rotation Curve and Mass Distribution in the Galactic Center – From Black Hole to Entire Galaxy. Publ. Astron. Soc. Jpn. 2013, 65, 118. [Google Scholar] [CrossRef]
  23. Baes, M.; Buyle, P.; Hau, G.K.; Dejonghe, H. Observational evidence for a connection between supermassive black holes and dark matter haloes. MNRAS 2003, 341, L44–L48. [Google Scholar] [CrossRef]
  24. Dai, D.C.; Starkman, G.; Stojkovic, D. Milky Way and M31 rotation curves: ΛCDM versus MOND. Phys. Rev. D 2022, 105. [Google Scholar] [CrossRef]
  25. Chan, M.H.; Lee, C.M. Indirect evidence for dark matter density spikes around stellar-mass black holes. Astrophys. J. Lett. 2023, 943, L11. [Google Scholar] [CrossRef]
  26. Carr, B.; Kühnel, F. Primordial black holes as dark matter: recent developments. Ann. Rev. Nucl. Part. Sci. 2020, 70, 355–394. [Google Scholar] [CrossRef]
  27. Bertone, G.; Tait, T.M. A new era in the search for dark matter. Nature 2018, 562, 51–56. [Google Scholar] [CrossRef]
  28. Cherkas, S.L.; Kalashnikov, V.L. Vacuum Polarization Instead of Dark Matter in a Galaxy. Universe 2022, 8, 456. [Google Scholar] [CrossRef]
  29. Birrell, N.D.; Davis, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, England, 1982. [Google Scholar]
  30. Brunetti, R.; Fredenhagen, K. Quantum Field Theory on Curved Backgrounds. In Quantum Field Theory on Curved Spacetimes: Concepts and Mathematical Foundations; Bär, C.; Fredenhagen, K., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2009; pp. 129–155. [CrossRef]
  31. Cherkas, S.L.; Kalashnikov, V.L. Æther as an Inevitable Consequence of Quantum Gravity. Universe 2022, 8, 626. [Google Scholar] [CrossRef]
  32. Cherkas, S.L.; Kalashnikov, V.L. Eicheons instead of Black holes. Phys. Scr. 2020, 95, 085009. [Google Scholar] [CrossRef]
  33. Cherkas, S.L.; Kalashnikov, V.L. Structure of the compact astrophysical objects in the conformally-unimodular metric. J. Belarusian State Univ. Physics 2020, 3, 97–111. [Google Scholar] [CrossRef]
  34. Landau, L.D.; Lifshitz, E. Statistical Physics; Butterworth-Heinemann: Oxford, United Kingdom, 1980. [Google Scholar]
  35. Weidemann, V. White dwarfs. Ann. Rev. Astron. Astrophys. 1968, 6, 351–372. [Google Scholar] [CrossRef]
  36. Buchdahl, H.A. General Relativistic Fluid Spheres. Phys. Rev. 1959, 116, 1027–1034. [Google Scholar] [CrossRef]
  37. Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley & Sons: New York, 1972. [Google Scholar]
  38. Kormendy, J.; Bender, R. The Double Nucleus and Central Black Hole of M31. Astrophys. J. 1999, 522, 772–792. [Google Scholar] [CrossRef]
  39. Bender, R.; Kormendy, J.; Bower, G. ; others. HSTSTIS Spectroscopy of the Triple Nucleus of M31: Two Nested Disks in Keplerian Rotation around a Supermassive Black Hole. Astrophys. J. 2005, 631, 280–300. [Google Scholar] [CrossRef]
  40. Sofue, Y. Dark halos of M 31 and the Milky Way. Publ. Astron. Soc. Japan 2015, 67, 75. [Google Scholar] [CrossRef]
  41. Haridasu, B.S.; Cherkas, S.L.; Kalashnikov, V.L. A reference level of the Universe vacuum energy density and the astrophysical data. Fortschr. Phys. 2020, 68, 2000047–1912. [Google Scholar] [CrossRef]
1
For the comprehensive reviews, see [9,10], and one may add an additional alternative approach based on the relativistic theory of gravity with a massive graviton [11].
Preprints 80872 g001
Figure 1. (a) Nonsingular eicheon surrounded by dark radiation in CUM (3) has a nonsingular core. (b) In the Schwarzschild type metric (4), this core looks like a hollow sphere. Vacuum polarization around an eicheon is shown as the gradient of a density.
Figure 1. (a) Nonsingular eicheon surrounded by dark radiation in CUM (3) has a nonsingular core. (b) In the Schwarzschild type metric (4), this core looks like a hollow sphere. Vacuum polarization around an eicheon is shown as the gradient of a density.
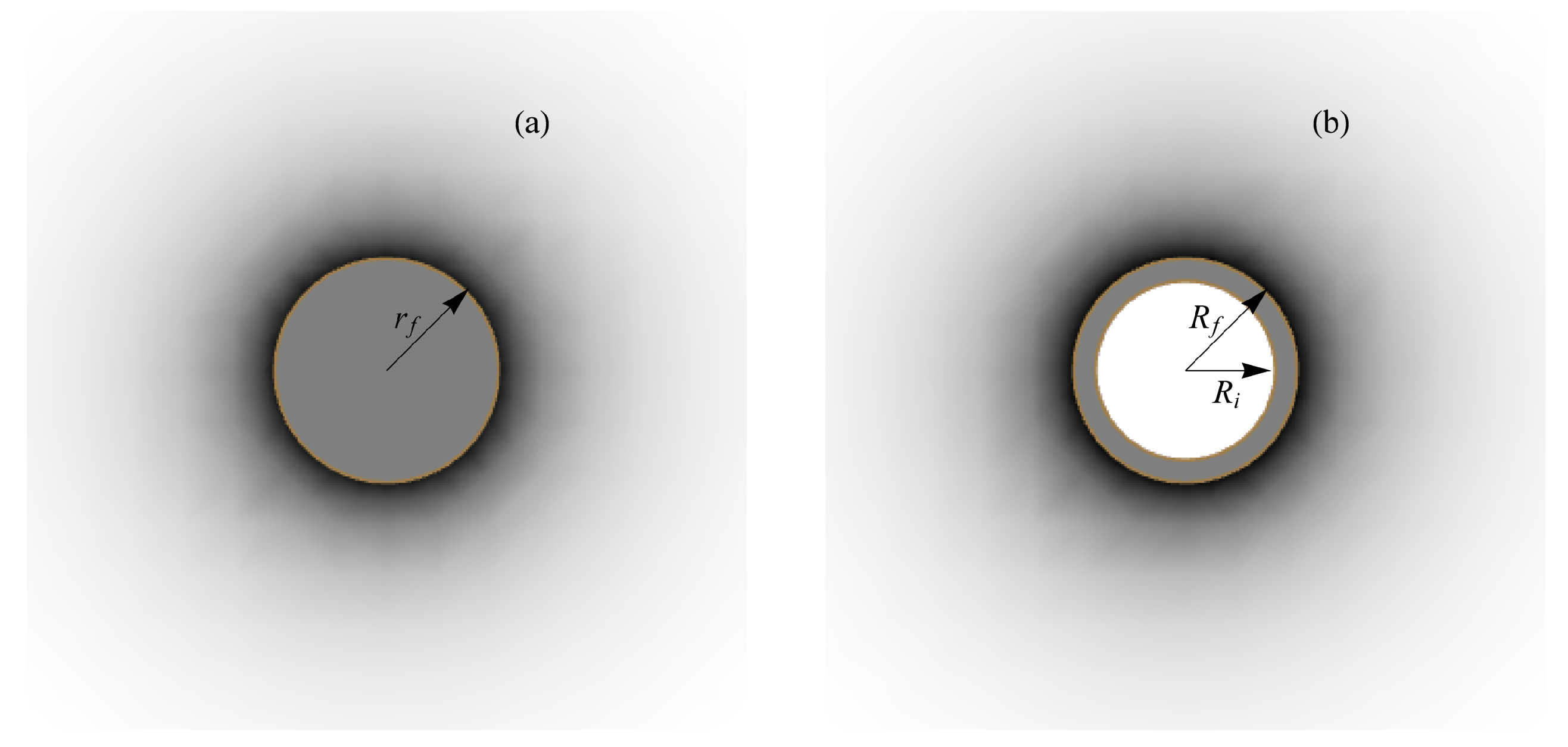
Preprints 80872 g001
Preprints 80872 g002
Figure 2. Pressure p m a x in the center of eicheon (see Figure 1 (a) ) in CUM, coinciding with the pressure p ( R i ) in the metric (4) (see Figure 1 (b) ). Blue and brown curves correspond to the numerical integration of the equation (9) and approximation (10), respectively.
Figure 2. Pressure p m a x in the center of eicheon (see Figure 1 (a) ) in CUM, coinciding with the pressure p ( R i ) in the metric (4) (see Figure 1 (b) ). Blue and brown curves correspond to the numerical integration of the equation (9) and approximation (10), respectively.
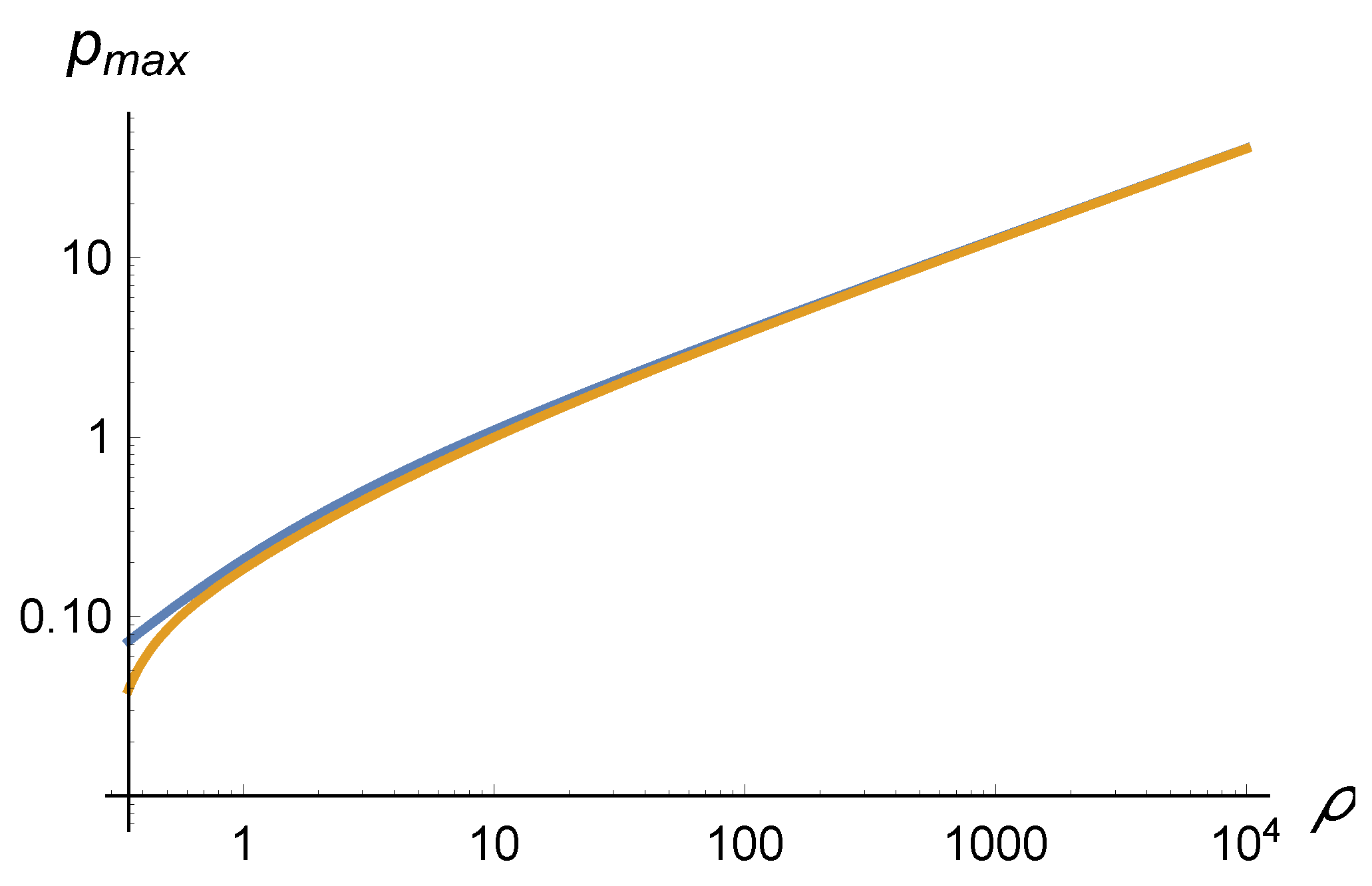
Preprints 80872 g002
Preprints 80872 g003
Figure 3. (Upper panel). The calculated rotational curve of the Milky Way from Ref. [28], which includes contributions of the eicheon and dark radiation. (Lower panel) Rotational curve taking into account the baryonic matter by (33)-(35). The result of observations with the error bars are taken from Ref. [22].
Figure 3. (Upper panel). The calculated rotational curve of the Milky Way from Ref. [28], which includes contributions of the eicheon and dark radiation. (Lower panel) Rotational curve taking into account the baryonic matter by (33)-(35). The result of observations with the error bars are taken from Ref. [22].
Preprints 80872 g003
Preprints 80872 g004
Figure 4. (Upper panel). Andromeda rotational curve, which includes contributions of the eicheon and dark radiation only. (Lower panel) Rotational curve taking into account the baryonic matter by (33)-(35). The result of observations with the deviations bars are taken from Ref. [40].
Figure 4. (Upper panel). Andromeda rotational curve, which includes contributions of the eicheon and dark radiation only. (Lower panel) Rotational curve taking into account the baryonic matter by (33)-(35). The result of observations with the deviations bars are taken from Ref. [40].
Preprints 80872 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated