Prerpints.org logo
Preprint
Review

Structural and Shape Optimization in Aerodynamic Airfoil Performance: A Literature Review

Altmetrics

Downloads

529

Views

198

Comments

0

Submitted:

03 July 2023

Posted:

12 July 2023

You are already at the latest version

Alerts
Abstract
An airfoil is the geometric shape of a cross-section of a wing. When it is exposed to the flow of a fluid over its surface, it generates both lift and drag forces through a pressure distribution. Designing an efficient airfoil for aerodynamic applications is a complex challenge in the field of aerodynamic engineering, with the aim of achieving an optimal lift-to-drag ratio. The success of airfoil design hinges on the effective reduction of drag force under specific conditions, while simultaneously attaining the desired lift without encountering significant flow separation, such as boundary layer shedding. Furthermore, the design must adhere to lifting force limitations and meet structural requirements. In the field of airfoil design and optimization, literature review articles provide a valuable resource by offering an overview of the latest advancements in specific areas. These areas encompass a wide range of topics including the design and testing of adaptive geometry wings, such as morphing wing technology as well as the application of shape optimization techniques to enhance airfoil performance. Our goal is to provide researchers with an in-depth review of relevant articles published to date, examining the applied approaches utilized to tackle the complex problem of airfoil design and explore the methodology employed to address it, from a broad perspective on the topic.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

Nomenclature

P = pressure
τω = shear force
FL = lift force
FD = drag force
ρ = density
V = velocity
g = gravity force
u = spatial velocity field
μ = viscosity

1. Introduction

Modern mathematical models for aerodynamic shape design rely on the application of partial differential, integral, and algebraic equations which often require the utilization of computational fluid dynamics (CFD) techniques. Approaches to airfoil design can be classified into two main groups: (a) the direct problem, which involves analyzing the fluid dynamics for a given geometric shape, and (b) the inverse problem, which aims to find a specific airfoil geometry that is compatible with the desired fluid behavior while satisfying predetermined boundary conditions.
The first approach can be convenient for leveraging the expertise and previous experience of the designer, as well as for verifying shapes obtained from other methods. However, depending on factors such as the materials involved in the design, the range of working conditions, the number of tests required, and the precision needed for data extraction, this approach can become expensive in terms of the number of experiments that need to be conducted.
The second approach holds the potential for enhancing the comprehension of the physics and cause-effect relationships inherent in airfoil design. However, its implementation requires a high-performance computing system to obtain results within a reasonable computational time, and may also involve efforts in modeling and mathematical formulation. In practice, a combination of both approaches may be used to better understand and design airfoils for specific working conditions [2]. Once the aforementioned approach is established, a numerical method is commonly employed, taking into account aspects such as: (a) The accurate determination of the physical aspects of the problem, that include whether the flow is compressible or incompressible, viscous or inviscid, subsonic or transonic, among others [1]; (b) The generation of the airfoil geometry, which is often achieved using curve parameterization methods [14] and (c) The discretization and mesh generation methods for numerical resolution, which are essential for obtaining accurate results [6,13].
When operating conditions are stable and specific design considerations are taken into account, the aforementioned approaches can be applied. Furthermore, when a specific optimal airfoil is required for a particular operating condition, the airfoil design can be formulated as an optimization problem. In this context, optimization algorithms have found extensive use in pure aerodynamic design [6]. Various techniques have been developed using this approach, ranging from single objective function optimization [12] to optimization with multiple (and sometimes conflicting) objective functions, incorporating multiple constraints that need to be simultaneously optimized [10]. The latter approach enables the designer to obtain an optimal solution that is well-suited to the specific required operating conditions.
When the operating conditions undergo dynamic changes or exhibit instability, the complexity of airfoil design significantly increases. This gives rise to at least two paradigms: (1) multiple operating conditions geometry, and (2) multi-structural and multiple geometries. The former aims to design an airfoil geometry that considers multiple operating conditions. This can be achieved when the operating conditions are similar or change smoothly. However, in cases where the operating conditions changes abruptly, it becomes necessary to adapt the geometry to the new conditions as effectively as possible [23]. This may involve the use of adaptive methods or even multiple geometries, where the geometry consists of several structural components depending on the circumstances. It is worth noting that new techniques can be combined with existing ones, such as machine learning approaches for adapting geometries to operating conditions or dynamic mode decomposition for extracting models from experimental data [56,57].

2. Problem Definition

2.1. Forces Acting on an Airfoil

A fluid at rest exerts only normal pressure forces on the surface of a body. However, when the fluid is in motion it exerts tangential shear forces due to the non-slip condition caused by viscous effects inside the boundary layer. The sum of the pressure components and the shear forces in the direction normal to the flow is called lift force and tends to move the body in that direction [31]. The sum of the pressure and shear components in the direction of the flow is known as the drag force and acts in the opposite direction to the displacement of the object (Figure 1).
The pressure and shear forces acting on a differential area dA on the surface are PdA and τ w d A , respectively. The differential drag and lift forces acting on dA in two-dimensional flow are:
d F D = − P d A c o s θ + τ w d A s e n θ ,
d F L = − P d A s i n θ − τ w d A c o s θ ,
where θ is the angle between the outer normal of dA and the direction of positive flow.
The total drag and lift forces acting on the body are determined by integrating equations (1) and (2) over the entire surface of the body:
F D = ∫ A d F D = ∫ A ( − P c o s θ + τ w s i n θ ) d A ,
F L = ∫ A d F L = ∫ A ( − P s i n θ + τ w c o s θ ) d A .
The drag and lift forces are influenced by various factors, such as the density ρ of the fluid, the upstream velocity V, the size, shape and orientation of the body, among other things. However, instead of dealing with these forces it is more convenient to work with dimensionless parameters that represent the drag and lift characteristics of the body. These parameters are the drag coefficient C D and the lift coefficient C L , which are defined as:
C D = F D 1 2 ρ V 2 A ,
C L = F L 1 2 ρ V 2 A .

2.2. Problem Approach

In the field of aerodynamics, there are two approaches to tackle the problem of airfoil shape design and optimization: the analysis (direct problem) and the design (inverse problem).
Direct problem: In the case of analysis or direct problem, the geometry of the airfoil is known, and the primary task is to characterize the fluid around its surface (Figure 2) and determine the forces acting on it ( F D and F L )
Inverse problem: In the case of design or inverse problem, the objective is to predict the geometry of an airfoil that satisfies the governing equations for the flowfield and the desired boundary conditions. Depending on the prescribed features of the flowfield, design methodologies can be grouped into two general categories:
  • 1- Surface flow design: Given certain flow parameters (pressure, Mach number, etc.) on the surface of the object (in region A), the objective is to find the shape of the object that will generate these desired surface conditions, without considering the rest of the flowfield (Figure 2).
  • 2- Flowfield design: Given certain flowfield features (shock-free flow, minimal entropy generation, etc.) at every point of the flowfield (in B, C, etc), the objective is to determine the shape that will satisfy these constraints locally (Figure 2).

2.3. Mathematical Modeling

The motion of a fluid is described mathematically by the Navier-Stokes equations, which are a set of coupled time-dependent nonlinear equations. These equations represent the principles of conservation of mass and conservation of momentum for Newtonian fluids and supplemented with conservation of energy. The general Navier-Stokes equations can be expressed in vector form as follows:
ρ D u D t = ρ g − ▿ p + μ ▿ 2 u + 1 3 μ ▿ ▿ · u ,
where μ is the coefficient of viscosity.
In the case of incompressible homogeneous flow ( ρ = ρ 0 = constant), the complete set of Navier-Stokes equations reduces to:
ρ 0 D u D t = − g r a d p + μ ▿ 2 u ,
d i v u = 0 .
The Reynolds number is a key parameter in fluid mechanics that describes the behavior of a fluid. It quantifies the relationship between density, viscosity, velocity and characteristic dimensions of a flow in a dimensionless expression. In high Reynolds number applications, where inertial forces prevail over viscous forces, an inviscid flow analysis, which ignores the effect of viscosity on flow is suitable. The Navier-Stokes equations, which account for viscous effects, simplify to the Euler equations in such scenarios:
ρ D u D t = − g r a d p + ρ b ,
d i v u = 0 ,
were b is the body force per unit mass.
An inviscid analysis provides a quick estimate of the primary forces acting on the body. Then by modifying the shape of the object to maximize lift forces and minimize drag forces, a viscous analysis can be performed to include the effects of viscosity and turbulence.
When employing CFD for turbulent flow modeling, the Reynolds-Averaged Navier-Stokes (RANS) method is is widely utilized. The RANS equations are derived through the technique known as Reynolds decomposition which is a mathematical technique employed to separate the expected value of a quantity from its fluctuations. In this case, the RANS equations use a solution that is split into a time-independent mean flow velocity and time-varying fluctuations about the mean:
u ( x , t ) = u ¯ ( x ) + u ′ ( x , t ) ,
were x is the position vector.

3. Methodology

In this work We have analyzed scientific publications from 1987 to 2022, related to aerodynamic shape design and optimization. We carefully selected articles specifically focused on the design and optimization of wing profiles, categorizing them based on the various approaches employed to address the problem. Specifically, our analysis focuses on three main approaches: (a) the structural approach, which emphasizes the mechanical and geometric characteristics of the shapes analyzed as well as the properties of the materials used; (b) the numerical approach and discretization criterion, which analyzes the different numerical approaches used to characterize the behavior of the fluid; and (c) the approach to shape optimization process and the various optimization methods employed in the process.

3.1. Structural Approach

In this section, we organize the papers based on their focus on the structural characteristics of the airfoil. This classification takes into account whether the airfoil is designed as a single or multi-element body as well as whether it is intended to be rigid or flexible. In conventional aircraft wings, airfoils are designed to be optimal for a specific flight condition. However, when analyzing flight conditions for different regimes such as takeoff, landing, or cruise flight, researchers often investigate multi-element geometries with components such as flaps or slats [3,4,19] (Figure 3a) In recent years, the analysis of flexible geometries has gained significant interest among researchers. This innovative design concept aims to enhance aerodynamic and energy efficiency during flight by actively adjusting the shape of the wing in real-time. In an article published by Terrence A. Weisshaar [49] the author highlights that the term "morphing aircraft" has come to be associated with exotic smart materials, which is too restrictive. Morphing objectives include efficient, multipoint adaptability achieved by state change, including geometric reconfiguration (Figure 3b).
According to a work by S. La et al. [47] wing morphing can be classified into three categories: in-plane morphing, airfoil morphing and out-of-plane morphing (Figure 4). In this work we are going to focus only on the airfoil morphing concept that means changes in the shape (camber rate and camber thickness) in a two dimension problem (Figure 4b) Some papers address only the aerodynamic study of an airfoil shape modifications, leaving the problem of design and manufacturing to other researchers [22] Other works investigate the mechanisms, focusing on the nature of the design, the features of the materials, the implementation and testing methodologies as well as the effects of morphing in flight.
Table 1 provides a comparison between conventional airfoils with moving elements and morphing airfoils with morphing mechanisms in terms of their features.

3.1.1. Paper Review

A summary of the papers analyzed is presented below:
Effective directional control of an airplane demands adjustments to the angle of attack of the wings. However, at high angles of attack, the torque required to operate the mobile control surface increases significantly, limiting the functionality of these systems. One solution is to add a separate rigid element (tab) to the mobile control surface to improve its capabilities (Figure 5a). However, this approach creates a gap between the control surface and the tab, which can disrupt the surrounding flow. To address this issue, Yu-Tai Lee et al. [8] developed a concept that uses a single element geometry made of flexible material (such as shape memory alloy) that utilizes electrical power to manipulate the control surface, eliminating the need for hydraulics and the gap between the flap and the tab. (Figure 5b).
Orthotropic materials display unique mechanical properties in different directions, making them ideal for developing innovative structures with intriguing possibilities. These materials have properties that vary along the orthogonal axes that define their section or volume. The concept of orthotropy serves as the foundation for developing composite materials. Paolo Bettini et al.[7] have developed complex composite cellular structures that are capable of undergoing large displacements and withstanding limited stress on their components. Numerical simulations are used to investigate and compare the advantages of using orthotropic materials, with the results being compared to those obtained from metallic prototypes (Figure 6).
Yokozeki et al. [15] developed a morphing airfoil with variable geometry by utilizing corrugated structures and wire tension actuation, which was tested in a wind tunnel. The flexible seamless flap was actuated by a wire system in the leading part of the body, using C-shaped circular sections and vertically straight sections for the corrugated structure with uniform curves. The wire was attached to the trailing edge region and passed through the corrugated structure near the lower wing surface, with the other end connected to a servomotor mounted inside the wing. (Figure 7).
Roelof Vos et al. [9] have developed a warp-controlled wing twisting prototype based on the concept of controlled wing twisting. By introducing variable torsion through rotating ribs around a fixed aluminum rod, they were able to create a lightweight and robust structure without relying on extremely powerful actuators. The wing itself is made of carbon fiber skin. This study demonstrated that active wing twist can effectively control the rolling motion of an aircraft, maximizing the lift-drag ratio under various flight conditions. While the weight of the wings is lighter compared to those with hinged morphing mechanisms made of aluminum or steel, the weight of the skin and driving mechanisms in the whole morphing structure is still too heavy for a compliant wing aircraft.
In a study by Hongda Li et al. [17], an innovative structural solution was developed for an adaptive variable camber compatible wing. The proposed solution features a skin that can change thickness and a trailing edge transformation mechanism designed based on a new type of artificial muscles (Figure 8). Although artificial muscles, particularly Pneumatic Artificial Muscles (PAMs), are not new in aerospace applications, they have been studied extensively for use in driving flaps or morphing mechanisms.
As mentioned in the previous paragraph, the weight of the skin is a significant contributor to the overall weight of morphing wing structures. Consequently, the development of a lightweight, flexible skin is a key challenge in creating successful morphing wings. In a study by Maurizio Arena et al. [25], an innovative structural concept was developed and tested on a two-bay trailing edge segment consisting of three articulated finger-like ribs and a multi-box arrangement covered by an elastomer-based morphing skin. The primary objective of this study was to understand and evaluate how the morphing skin could affect the dynamic response of the adaptive structural system. (Figure 9).
Topology optimization is a mathematical method that optimizes material layout within a specific design space to maximize system performance for a given set of loads, boundary conditions, and constraints. In a study by Pedro Gomes et al. [26], a strategy for density-based topology optimization of fluid-structure interaction problems is proposed to address some of the shortcomings associated with non-stiffness-based designs. The objective of this study is to improve the passive aerodynamic shape adaptation of highly compliant airfoils at multiple operating points. The authors found that better results were obtained using topology optimization in addition to shape optimization because the optimized material layout allowed the airfoil to better adapt to the different fluid loads at different speeds.
In the study conducted by S. A. Meguid et al. [45] the authors provide a comprehensive review of the underlying technologies related to shape morphing wing concepts and describes the design, analysis, prototyping, and flight testing of a novel morphing wing system for small unmanned aerial vehicles (UAVs). The wing system was designed to be lightweight and flexible, using a camber-adjustable airfoil shape and a flexible-rib system (Figure 10) driven by servomotor-actuated mechanisms. The designed prototype was manufactured and tested in compliance with aircraft design standards. The success of the project, including flight testing of the flexible rib assembly, is summarized in the paper.
Q. Chanzy et al. in [46] describes the process of designing, testing, and optimizing a novel set of morphing wings for a 15kg maximum take-off weight Unmanned Aerial Vehicle (Figure 11). A comparator set of conventional wings was used throughout the study to assess the advantages of adopting the morphing technology. Recent advancements in morphing wing technologies have been driven by the use of composite materials that offer precise control over the stiffness properties and shape changes of the wings. In this study, a careful combination of fiber and foam structural elements was used to control the wing shape changes. The wings have an open slot at the trailing edge, allowing the upper and lower trailing edge surfaces to slide over each other and change their camber. The results demonstrate that the morphing wings provide a controllable aircraft while reducing drag by 40% compared to wings with conventional ailerons in a deflected position.
In an article presented by U. Fasel et al. [48] the authors discuss the potential of combining continuous carbon fiber composite additive manufacturing and morphing mechanisms to improve the flight performance of aerospace structures. The high design freedom of the manufacturing process allows for tailored fiber placement, fully exploiting the anisotropy and strength of the composite material. Morphing mechanisms, which use the elastic properties of the material to achieve shape changes, are prohibitively expensive to manufacture with conventional processes due to their complex internal topologies. The article presents a proof of concept of the combination of these two technologies, where a complete composite primary- and morphing structure of a fixed-wing drone (Figure 12)is additively manufactured and successfully flight-tested.
In the papers we have reviewed thus far, the designs have primarily been either structure-based or material-based to achieve desired shape changes. However, some works have taken a combined approach, incorporating both the structural characteristics and material properties into their designs. Some examples involve using material properties to morph specific parts of the section, while employing distinctive structural elements to morph other areas. Additionally, some works utilize smart materials as actuators within an internally structured design, based on a topology optimization approach. This is the case of the work developed by Yaqing Zhang et. al. [50] The paper describes the design of a variable camber morphing wing using compliant mechanisms and hyperelastic structure topology optimization (Figure 13). A laminated leading-edge skin is designed to fit the curvature changing phenomenon of the leading edge during deformation. A morphing wing demonstrator was manufactured to testify its deformation capability. The proposed design can realize larger deflection of leading and trailing edges, leading to improved aerodynamic performance and sufficient strength to resist aerodynamic and structural loadings.
Another example of a hybrid design can be found in the research conducted by B. K. S. Woods et al. [51] The paper presents a new airfoil morphing structure called the Fishbone Active Camber (FishBAC) that uses compliant mechanisms to create significant and continuous changes in airfoil camber and section aerodynamic properties (Figure 14). The structure consists of a chordwise bending beam spine with stringers branching off to connect it to a pre-tensioned Elastomeric Matrix Composite (EMC) skin surface. Actuators mounted in the D-spar induce bending moments on the spine through tendons, similar to natural musculature systems. The paper focuses on a trailing edge morph configuration, where the compliant spine connects a rigid leading edge D-spar to a solid trailing edge strip. A prototype device is built to explore various aspects of manufacturing this concept and to prove the large deflection capability of the FishBAC.
There are other papers that are also worth commenting on:
The article published by H. L. Şahin et al. [52] discusses the integration of multiple scientific disciplines in the design and analysis of morphing wings. It presents a new scissor-structural mechanism (SSM) for the trailing edge of morphing wings. Using a novel kinematic synthesis concept, the SSM achieves minimal design error in tracking the airfoil camber.
In [53] A. V. Ivchenko et al. discusses two proposed design solutions for creating an adaptive compliant aircraft wing frame using a reconfigurable honeycomb core with hidden topological surfaces. The first solution involves lever actuators integrated into the honeycomb structure, while the second solution utilizes mechatronic nodes as actuators. The research also explores the potential of smart materials and artificial muscles.
The potential of combining structural material and fluid pressure to create a morphing structure with integrated shape-change and stiffness functions, is shown in the work presented by S. Vasista et al. [54] by utilizing a cellular arrangement, distributed actuation and precise control. The moving isosurface threshold topology optimization method was used to design the cell shapes.
We will now refer to some recently published review articles related to this topic:
The first article, authored by S. Ameduri et al. [23], provides a review of the progress made in morphing research within the European Project "AIRGREEN2" in the Clean-Sky 2 GRA platform. This paper provides an overview of the scientific achievements in morphing research by three Italian research organizations: the Italian Aerospace Research Centre, the University of Naples "Federico II," and the Politecnico of Milano. The development plans followed by each organization are discussed, highlighting their roles and accomplishments. Examples of their projects include the development of wind tunnel models, variable chamber trailing edges, adaptive wing systems, and high-lift generation architectures. The paper also outlines the specific contributions of each organization in various European-level projects. The ongoing activities and upcoming milestones, such as flight tests and critical design reviews, are described. The overall goal of the project is to realize adaptive winglet, wingtip, and control systems for enhanced performance in climb, cruise, and landing.
Another article presented by J. Sun et al. [55] discusses the advantages of morphing technologies for aircraft and reviews recent developments in the application of smart materials and structures in morphing aircraft. Traditional aircraft are optimized for only one or two flight conditions, not for the entire flight envelope, while morphing aircraft can adapt their shape to optimize performance across a wide range of conditions. The use of "smart" materials and structures, which offer benefits such as high energy density, ease of control, variable stiffness, and strain tolerance, provides new possibilities for designing morphing aircraft. The article focuses on four categories of applications: actuators, sensors, controllers, and structures.
Finally we quote the article, presented by Tuba Majid et al. [28] provides an overview of the current state-of-the-art in camber morphing mechanisms in the context of design and implementation. It highlights the importance of thoroughly investigating morphing mechanisms and their design principles and methodologies from the implementation and test flight aspects. The article categorizes the camber morphing mechanisms into three categories based on their design features and synthesis methodology: structure-based, material-based, and hybrid. The review provides researchers with choices of materials, actuators, and design methodologies for the implementation of morphing mechanisms with practical aspects of flight performance and applications. However, a majority of these works primarily focuses on structural integrity and aerodynamic performance, lacking comprehensive data on aerodynamic benefits in different flight conditions, energy requirements, morphing control, weight, and fatigue failure.

3.1.2. Numerical Approach and Discretization Criterion

In this section, we will primarily concentrate on the numerical approach utilized to analyze and characterize the fluid’s behavior, along with its parameterization.
In aerodynamics, the flow regime is often described in terms of Mach number. The flow is subsonic when Mach < 1, transonic when Mach ≅ 1, supersonic when Mach > 1 and hipersonic when Mach > > 1 [31]. We will focus only in subsonic and transonic regimes.
In the subsonic regime, which is the primary focus of airfoil performance analysis, compressibility effects are generally negligible. Under these conditions, the fluid density can be assumed to be constant, and the flow is considered incompressible. However, as the Mach number exceeds a critical value at certain points on the airfoil surface, the flow velocity surpasses the speed of sound, leading to the formation of shock waves. These shock waves typically form perpendicular to the flow direction and cause the velocity to drop below the speed of sound, transitioning the flow back to the subsonic regime. During typical cruising conditions in the transonic regime, the presence of shock waves becomes a significant contributor to drag. Therefore, from a numerical perspective, a non-viscous flow solver capable of calculating the drag induced by weak shock waves is an appropriate tool for simulating the fluid’s physical behavior, as long as there is no extensive flow separation.
As it was described in section 2.3, the Navier-Stokes equations represent a set of coupled, time-dependent, and nonlinear equations. Analytically solving these equations is often impractical or impossible in many cases. Therefore, numerical analysis becomes necessary to obtain an approximate solution. The Reynolds-averaged Navier-Stokes (RANS) equations provide a reduced representation of the general Navier-Stokes equations. These equations separate the steady-state solution from the time-varying fluctuations within the system. The derivation of the RANS equations employs a mathematical technique called Reynolds decomposition, which separates the expected value of a quantity from its fluctuations. In the context of RANS equations, the solution is divided into a time-independent mean flow velocity and time-varying fluctuations about the mean: u ( x , t ) = u ¯ ( x ) + u ′ ( x , t ) , were x is the position vector. Following the development of RANS equations, Boussinesq introduced the concept of eddy viscosity, which allows for modeling the momentum transfer caused by turbulent eddies. This concept simplifies the Reynolds stress tensor into a more manageable form [32]. This is in analogy with how the momentum transfer caused by the molecular motion in a gas can be described by a molecular viscosity.
In 1987, Mark Drela and Michael B. Giles [1] introduced and validated a viscous-inviscous analysis method called ISES (Implicit Sequential Euler Solver). This method proved to be well-suited for analyzing transonic and low Reynolds number airfoils. They opted for the ISES method over Navier-Stokes analysis, citing the latter’s computational inefficiency for routine design work and lack of proven superiority in terms of accuracy compared to faster zone approaches. The ISES code provides a rapid and dependable solution for addressing strong viscous-inviscid interactions commonly encountered in transonic and low Reynolds number airfoil flows. The presented results demonstrate the capability of the ISES code to accurately predict transitioning separation bubbles and their associated performance losses, as well as the rapid degradation of airfoil performance at decreasing Reynolds numbers.
The aerospace industry heavily relies on computational fluid dynamics (CFD) tools for designing and analyzing flying vehicles, leveraging the exponential growth of computing capabilities. Over time, significant expertise has been gained in using the Reynolds-averaged Navier-Stokes (RANS) equations and coupled integral boundary layer (IBL) methods to predict the flow fields and design trends of aerospace vehicles with attached flow. However, the accuracy of these simulation tools diminishes when analyzing regions with flow separation, such as multi-element configurations, which poses challenges in modeling the phenomenon precisely. In a comprehensive survey conducted by Christopher L. Rumsey et al. [33], various CFD methods applied to high-lift multi-element computations are examined. The study highlights the crucial need for aircraft designers to have reliable CFD tools capable of accurately predicting the effects resulting from small configuration changes under high-lift conditions, emphasizing the importance of employing both IBL and RANS methods. This conclusion underscores the significance of advancing CFD techniques to enhance the understanding and optimization of complex aerodynamic phenomena in aerospace design.
The design of high-lift systems holds significant importance in aerodynamics, directly impacting the performance of takeoff and landing. However, this design process is complex due to various factors and constraints that must be considered by designers. Evaluating multiple candidate configurations is essential during the initial design phase before finalizing the optimal design. Low-fidelity tools, such as potential flow theory, are commonly employed in the conceptual phase due to their cost-effectiveness and ability to analyze numerous configurations. Nonetheless, relying solely on low-fidelity tools can lead to unexpected outcomes when transitioning to high-fidelity computational fluid dynamics (CFD) analysis in subsequent phases. Hence, it is crucial to enhance the accuracy of low-fidelity tools to avoid surprises when designs undergo CFD assessment. Addressing this concern, Partha Mondal et al. [19] developed a discrete-vortex-method (DVM)-based model for evaluating functions within a genetic algorithm (GA)-based flapposition-optimization strategy. DVM is renowned for effectively capturing camber effects and lifting surface interference, making it a suitable approach for optimizing high-lift systems. By integrating DVM into the optimization process, the study aims to enhance the fidelity of low-fidelity tools and expand their applicability in high-lift system optimization.
Mesh generation is a fundamental step in the field of computational fluid dynamics and shape optimization techniques, particularly when dealing with search spaces that involve vastly different geometries. Two common types of meshing schemes are unstructured and structured. Unstructured meshing allows for fast variation of element size but lacks flexibility in handling domains with complex geometries. On the other hand, structured meshing can handle any geometry but may produce low-quality meshes and distorted finite elements for irregular contours. To address these challenges, D. López et al. [6] propose a structured meshing procedure that creates subdomains to generate high-quality structured meshes in critical flow regions around aerodynamic sections. They demonstrate the effectiveness of this procedure by applying it to a straightforward shape optimization problem in fluid dynamics. The method involves dividing the mesh domain into blocks that vary according to the airfoil’s geometry. This approach ensures the generation of quality structured meshes for any geometry within the search space.
An alternative approach to address the meshing challenge in shape optimization with highly varied geometries is to employ mesh deformation techniques, particularly when working with gradient-based search methods where geometry changes are gradual. S. Jajobsson et al. [34] introduced a method in their paper that utilizes an interpolant of boundary node displacements to extrapolate these displacements throughout the entire mesh domain, enabling deformation of both structured and unstructured meshes in 2D or 3D. The proposed method demonstrates its effectiveness by achieving deformed meshes with qualities comparable to the initial mesh in numerical examples. Furthermore, it offers the advantage of low computational cost and minimal memory requirements, making it suitable for situations that involve repeated deformations of the flow domain. By utilizing this approach, the mesh can be adapted and deformed to accommodate varying geometries efficiently and effectively in shape optimization processes.
When discussing aircraft design, the parameterization of geometry plays a key role. According to Daniel P. Raymer [37], this design process can be divided into three phases: conceptual design, preliminary design, and detailed design. Wenbin Song et al. [36] conducted a study on parameterization methods for airfoil shape optimization within a CAD-based design optimization framework. In their research, different parameterization methods were explored. The NACA airfoils, for instance, are defined by a series of y-coordinates at specified chord locations. Non-uniform Rational B-splines (NURBS) utilize control points to define the curvature of airfoils. B-splines and Bezier curves have been widely employed to fit airfoil shapes using interpolation techniques. Another parameterization method mentioned is PARSEC, developed by Sobieczky [35], which uses geometric parameters such as leading edge radius, thickness-to-chord ratio, and maximum thickness to define the airfoil shape.
Scientists and engineers employ computer simulations to examine the relationships between input parameters and model outputs. However, conducting comprehensive parameter studies can be challenging or even impractical when simulations are computationally expensive and models have numerous inputs. In such cases, engineers seek ways to reduce the dimensionality of the input parameter space to enable more feasible studies. One promising approach to address this challenge is the use of active subspaces, which are a set of emerging dimension reduction tools. These tools help identify the most significant directions within the parameter space. By uncovering the active subspace, engineers can focus their analysis on the most influential factors, effectively reducing the dimensionality of the problem. In the book "Active Subspaces: Emerging Ideas for Dimension Reduction in Parameter Studies" by P. Constantine [38], various techniques for discovering a model’s active subspace are discussed. The author also proposes methods for leveraging this reduced dimensionality to facilitate parameter studies that would otherwise be impractical or unfeasible. By utilizing active subspaces, engineers can gain valuable insights into the underlying structure of the parameter space, enabling them to streamline and optimize their simulations. This approach opens up new possibilities for efficient parameter studies and enhances the understanding of complex systems.
In their research paper, Zachary J. Grey et al. [39] delve into the investigation of two commonly employed shape parameterizations: a) parametric sections (PARSEC) [35] and b) class-shape transformation (CST) [40]. Their primary focus is on estimating the active subspaces associated with airfoil performance metrics, specifically lift and drag. These metrics are computed using computational fluid dynamics considering various airfoil parameters. The study demonstrates the consistency of design-oriented insights derived from active subspaces across the two parameterizations. This consistency highlights the robustness and reliability of active subspaces as a dimension reduction technique. By reducing the dimensionality of the problem, active subspaces enable the use of simple visualization tools that provide valuable insights into the lift/drag Pareto front in multiobjective optimization for airfoil design.
Haipeng Li et al. [5] present a very interesting paper that explores the application of an exergy-based method in aerodynamic designs. They investigate the impact of exergy on both two-dimensional airfoils and various three-dimensional wing planforms. To achieve the desired shapes of airfoils and wings, the researchers couple a numerical code with an exergy analysis, a shape-shifting algorithm, and an optimization code. The concept of exergy is rooted in the second law of thermodynamics, which states that exergy is not conserved during real processes. Instead, it is consumed to meet system objectives and some is irreversibly destroyed. The destruction of exergy corresponds to the generation of entropy. By minimizing entropy generation, one can better utilize exergy. Consequently, entropy generation minimization (EGM) methods have proven valuable in many thermodynamic optimization problems. In this paper, the authors combine entropy generation minimization with a RANS-based numerical flow solver, a shape-shifting algorithm, and an optimizer, resulting in a novel design methodology. This integrated approach enables the creation of optimized designs that maximize exergy utilization and minimize entropy generation..

3.1.3. Shape Optimization Approach

Optimization techniques have emerged as indispensable tools in the overall process of numerical analysis aimed at aerodynamic shape design. Due to the vast amount of literature available on this subject and limited space constraints, we can only highlight a few notable articles in this section that specifically focus on shape optimization processes. It is important to acknowledge that the mentioned papers represent only a fraction of the extensive body of literature on shape optimization. Nonetheless, they serve as valuable references for those seeking to explore this topic further.
In the past, optimization algorithms were primarily employed to minimize the difference between calculated and specified surface flow data, but this approach was not directly linked to optimizing the aerodynamic shape. In contrast, modern aerodynamic optimization methods integrate conventional analysis techniques with optimization algorithms, enabling iterative modifications to the geometry with the goal of minimizing a specific "cost" function, such as drag or the deviation from desired surface pressure distributions. While these aerodynamic optimization methods offer significant advantages, it is important to acknowledge that they can incur a high computational cost. The iterative nature of the optimization process, combined with the complexity of the underlying flow simulations, often demands substantial computational resources and time. By addressing the computational cost associated with aerodynamic optimization, researchers strive to make these methods more viable for real-world applications, enabling engineers to design more efficient and high-performance aerospace systems.
In 1992, G. S. Dulikravich conducted a study on Aerodynamic Shape Design [2], which highlighted the potential of sensitivity analysis formulations as a promising approach for evaluation and optimization under off-design conditions. However, it was noted that sensitivity analysis can be computationally expensive, requiring a large number of analysis runs. To address this challenge, the concept of single cycle optimization was introduced and welcomed. This approach allows for a stable iterative algorithm, where an optimizer is applied to each updated configuration even before the flowfield has fully converged to the new geometry. This early integration of optimization within the iterative process shows promise in reducing computational expenses. Through a comparative analysis of optimization-based approaches, it was concluded that more economical methods can be achieved with gradient-based algorithms. These algorithms leverage the gradient information of the cost function to guide the optimization process efficiently. The availability of a wide variety of gradient-based optimization algorithms provides flexibility in choosing the most suitable one for a given problem. Additionally, it is worth noting that remarkable results were obtained using an evolution-type algorithm, which demonstrated reduced sensitivity to local minima. This alternative approach offers a different perspective by exploring the search space in a more comprehensive manner, potentially avoiding convergence to suboptimal solutions.
The Genetic Algorithm (GA) [58], as an evolutionary computing technique, has gained significant popularity among researchers due to its effectiveness in finding global optima for complex functions. However, its computational time requirements pose a challenge in aerodynamic optimization problems that involve the use of computational fluid dynamics for fitness function computation. To address this limitation, researchers have explored various approaches to improve the optimum design and enhance the convergence rate of the optimization process, with a particular focus on proper population dispersion methods. Among the different dispersion methods, those incorporating mutation adaptation have proven to be particularly powerful. In a paper by M. Ebrahimi et al. [44], an efficient method for scattering GA individuals in the design space is proposed to accelerate airfoil shape optimization. This method leverages the variation of the mutation rate for each gene of the chromosomes, guided by feedback from the current population. The proposed method introduces diversity into the population, allowing for a more thorough exploration of the design space.
In the optimization process involving genetic algorithms, fitness evaluations play a crucial role, particularly in shape optimization analyses of multi-element airfoils where viscous turbulent effects dominate the gap region of the control surfaces. To effectively utilize evolutionary algorithms, the integration of a mesh regeneration process into the design optimization cycle becomes necessary, as significant shape changes need to be incorporated. In their paper, Yu-Tai Lee et al. [8] addressed this challenge by presenting a novel approach that combines a computational fluid dynamics process with a GA-based optimization procedure to evaluate the fitness function during the design/optimization iterations. This integration was considered essential due to the presence of strong viscous and turbulent effects in the gap region between the stabilizer and flap, particularly at large flap angles. By employing a multi-element unstructured Reynolds-Averaged Navier-Stokes (RANS) framework within the CFD process, the researchers were able to accurately capture and analyze the intricate flow phenomena associated with the multi-element airfoil configuration. The GA-based optimization procedure then utilized the insights gained from the CFD simulations to iteratively refine the airfoil shape and enhance its performance.
In a study related to the aforementioned topic, Ernesto Benini et al. [10] presented a comprehensive approach for the design of multicomponent airfoils consisting of slat, main, and flap components. Their research focused on employing a multi-objective genetic algorithm in conjunction with an Euler/boundary-layer flow solver to drive the design procedure.
As discussed earlier in section 3.1.1, the accurate prediction of the behavior of high-lift multicomponent airfoil devices using numerical simulation poses a significant challenge for designers. The flow characteristics in these cases are complex, and transition phenomena occur within each aerodynamic element. To tackle these complexities, a multiobjective design approach for high-lift multicomponent airfoils becomes an attractive option for the optimization process. This approach allows designers to consider multiple conditions and requirements simultaneously, leading to more comprehensive and robust designs. In particular, direct multi-objective optimization proves to be valuable when dealing with conflicting requirements that need to be satisfied concurrently. By employing this method, designers can explore trade-offs between various objectives and identify design solutions that achieve a balance between competing criteria. D. Quagliarella et al. [4] have contributed to this field by developing a multi-point design optimization method specifically designed for transonic and high-lift airfoil configurations. Their approach incorporates a multiobjective genetic algorithm that is coupled with two distinct flow field solvers. This integration enables the system to consider both transonic and high-lift requirements simultaneously through multiobjective optimization. By leveraging the strengths of this methodology, designers can explore a broader design space and identify optimal solutions that satisfy diverse performance criteria. The development of a multi-point design optimization method tailored to transonic and high-lift airfoil configurations is a significant advancement in the field.
In many design processes, especially in the context of shape optimization, understanding the underlying relationship between design variables and output variables can be a challenging task. In such cases, surrogate models provide a valuable tool to statistically relate input data to output data, enabling the approximation of complex, higher-order models in a simplified manner. Alfredo Arias-Montaño et al. [12] presented a noteworthy study that applied a surrogate-based multiobjective evolutionary optimization approach to optimize airfoil aerodynamic design. The researchers employed multiple surrogate models, operating in parallel, with the objective of leveraging their respective strengths when tackling a computationally expensive multi-objective optimization problem. The team was able to create efficient approximations of the underlying aerodynamic models, reducing the computational burden associated with repeated evaluations.
Particle Swarm Optimization (PSO) [59], although part of the emerging methods within evolutionary computation, differs from the previous ones in that each particle or individual in the swarm has memory and is capable of remembering the best position in the search space it has visited. Swarm algorithms have emerged as a powerful class of optimization methods capable of addressing both single and multi-objective optimization problems, with or without constraints. Unlike conventional evolutionary methods, swarm algorithms simulate social behavior, where each individual in a swarm adjusts its flight based on personal flight experience and the collective experience of its companions. The success of this strategy hinges on the effective exchange of information between individuals. In a paper presented by T. Ray and H. M. Tsai [43], a swarm algorithm is applied to airfoil design optimization studies. The algorithm is grounded in a sociobehavioral model, providing designers with the desired flexibility to tackle various forms of the airfoil shape optimization problem, whether it involves constraints or not, and encompasses both single and multi-objective optimization. The study highlights that while the socialist behavior exhibited by the swarm algorithm may lead to an increased number of costly evaluations, it also offers the potential for further exploration and makes it a valuable tool for challenging airfoil design optimization problems.
While optimization methods based on evolutionary algorithms offer great potential, it is worth noting that for shape optimization processes involving small changes in the final geometry, simpler methods can often sufficient and even prove to be more robust than other optimization approaches. A noteworthy conclusion supporting this viewpoint is presented in the work by Matthias Schramm et al. [42]. In their study, the researchers highlight that in scenarios where the modifications to the geometry are relatively minor, gradient-based optimization using the method of steepest descent can yield satisfactory results. This approach involves iteratively adjusting the design variables in the direction of the steepest descent, aiming to locate the minimum of the objective function. The advantage of the steepest descent method lies in its simplicity and computational efficiency compared to more complex optimization techniques.

4. Results

In this section, we provide a concise summary of the analysis conducted within each of the three categories discussed in the previous section. The purpose is to offer a condensed overview of the key findings and insights derived from our exploration in each specific area.

4.1. Structural Approach

The conventional design of aircraft wings often involves complex configurations with multiple structural components to accommodate the aircraft to different operating regimes. However, a new approach known as morphing wings has gained increasing interest among researchers in recent decades. This advancement it is being possible due to significant progress in material technology and modern optimization techniques. Moreover, the concept of morphing wings go beyond shape adaptation alone and encompass the integration of advanced control systems. These systems, such as feedback control and adaptive control algorithms, actively regulate and optimize wing shape based on real-time input data. By dynamically adjusting the wing’s shape to match various flight conditions, aircraft can improve their aerodynamic performance, optimize the lift-to-drag ratio, and achieve greater fuel efficiency. This, in turn, leads to a reduction in carbon emissions and contributes to a more environmentally sustainable aviation industry.
It is worth noting that while the morphing wing concept encompasses the entire three-dimensional wing structure, most of the papers selected in this review primarily concentrate on analyzing the behavior of the wing section (airfoil) as a two dimensions problem in order to have a better understanding of the implications of shape changes on flight conditions in real-time. Furthermore, it is worth mentioning that upon reviewing the existing literature, it becomes apparent that the majority of studies have primarily concentrated on analyzing the transformation mechanisms within the low Reynolds number regime, which is appropriate for Micro Air Vehicles (MAVs) or small Unmanned Aerial Vehicles (UAVs). Additionally, it is important to highlight that the prototypes developed thus far have primarily undergone testing at Mach numbers below or equal to 0.3. This limited range of data hinders the ability to evaluate the performance of these models at high speeds and make meaningful comparisons. Further investigation is needed to determine its effectiveness in more realistic flight conditions.
Current research on morphing wings lacks sufficient data on the specific aerodynamic benefits of integrating morphing capabilities across different flight conditions, such as take-off, landing, and cruise. To gain a comprehensive understanding, further investigation is required to thoroughly analyze the specific advantages, energy requirements, control mechanisms, weight considerations, and fatigue-related aspects associated with the manufacturing of morphing wings. By addressing these areas, the aviation industry can fully exploit the potential of morphing wing technology to enhance aircraft performance and promote sustainability.

4.2. Numerical and Discretization Approach

The fundamental mathematical concepts of fluid mechanics have always served as the foundation for discretizing numerical models used in optimizing aerodynamic shapes, and they continue to do so today. The Navier-Stokes equations, along with their simplified cases or modified versions such as RANS, have long been known for their mathematical complexity, posing challenges in formulation. However, with the exponential growth of computing capabilities in recent years, there has been a shift towards design methods rather than purely analysis-based approaches.
The advancement in computing power has enabled the application of design methods, which rely on iterative processes to generate and search for optimal geometries that satisfy design conditions. These design methods would not be possible without the utilization of modern optimization techniques. These techniques play a crucial role in guiding the iterative search for an optimal geometry by efficiently exploring the vast design space.
Nevertheless, it is important to note that the analysis-based approach still has a significant following in the field of aerodynamic optimization. Many researchers and practitioners continue to employ analysis methods to gain insights into the underlying physics and behavior of fluid flow. Analysis-based approaches provide valuable understanding and can complement the design methods by validating the performance of optimized geometries or providing guidance for further improvements.
In summary, the elementary mathematical concepts of fluid mechanics remain essential in the numerical modeling of aerodynamic optimization. The growth in computing capabilities has facilitated the adoption of design methods, supported by modern optimization techniques, for generating optimal geometries. However, the analysis-based approach still holds value and attracts a substantial number of practitioners. The combination of both analysis and design approaches contributes to advancing our understanding and achieving optimal aerodynamic shapes.

4.3. Optimization Technics

This section serves to reaffirm the significance of Evolutionary Computing [58] in the aerospace industry such as Evolution Strategies, Genetic Algorithms, Evolutionary Programming, etc. All these are based on the principles of evolution and adaptation of species proposed by Darwin in 1859. On the other hand, Particle Swarm Optimization, although belonging to the emerging methods of evolutionary computation, differs from the previous techniques by employing principles based on social or socio-cognitive-intelligent behaviors observed in nature.
These techniques have proven to be highly efficient due to their remarkable ability addressing multi-objective problems and locate global optima. It is crucial to emphasize that the computational costs, which were previously considered limiting factors, are now significantly mitigated in modern applications. Thanks to the progress in computing power and algorithmic optimizations, the computational expense is no longer a major concern in contemporary aerospace design and optimization endeavors.
While optimization methods based on evolutionary algorithms hold significant potential, it is important to recognize that simpler approaches can often be equally effective and more robust for shape optimization processes involving small changes in the final geometry. In situations where the modifications to the geometry are relatively minor, gradient-based optimization methods, specifically the method of steepest descent, can provide satisfactory results thanks to its ability to utilize the local gradient information to iteratively update the design variables towards the optimal solution. This method is particularly well-suited for scenarios where the search space is not excessively complex and the optimization problem is not highly nonlinear. Additionally, gradient-based optimization methods are computationally efficient, making them a practical choice for problems with limited computational resources.
It is important to note that our work primarily focuses on the design and analysis of airfoils in a two-dimensional context. While 2D analysis allows for early-stage predictions of phenomena such as flutter that impact the overall wing structure, it is important to acknowledge that this review work does not cover analyses involving the twist effect or comprehensive assessments of wing-level performance.
In future studies, exploring the broader implications of wing design, including the effects of flutter and incorporating the twist effect, would provide valuable insights. Understanding these additional factors can contribute to a more comprehensive understanding of the aerodynamic behavior of complete wing structures and facilitate more accurate optimization in practical applications.

5. Discusion and Remarks

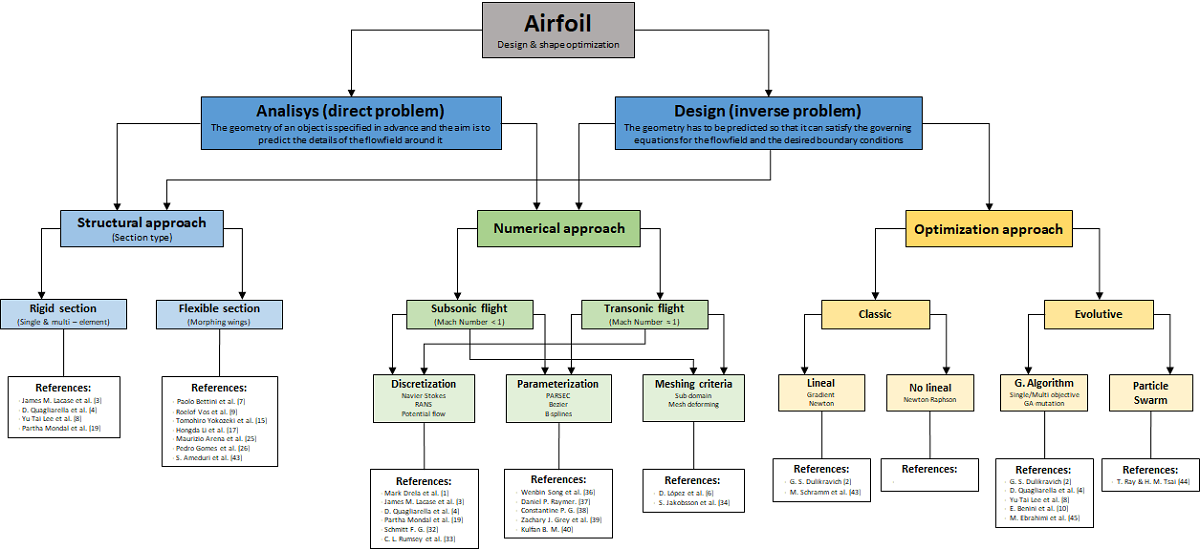
We are going to present a graphic taxonomic scheme that summarizes the structure and processes involved in the optimization of aerodynamic shapes. We believe that using this taxonomic scheme provides an interesting and visually intuitive representation of the evolution of approaches and treatments for aerodynamic shape optimization over the past four decades (Figure 15).
This diagram serves as a valuable tool for stimulating discussions and identifying potential areas of research and development. Through our analysis, we have identified some specific areas that we believe deserve particular attention:
a) The first area of focus centers around harnessing the useful work potential of a given amount of energy, which is necessary for operating the system. This methodology involves establishing a connection between the concepts of exergy and entropy within the system, allowing for a more comprehensive understanding of energy utilization.
b) Another promising area is the utilization of machine learning as a powerful tool for discovering parametric functions that can generate a wide range of optimal geometries. By leveraging known shapes that exhibit optimal lift-drag ratios under specific operating conditions, machine learning techniques can assist in identifying parametric functions that lead to enhanced performance across various flight conditions.
c) The majority of the analyzed works that explore the concept of morphing wings have primarily focused on evaluating the structural integrity and aerodynamic performance of the designs. However, these works often lack sufficient data regarding the specific aerodynamic advantages resulting from the implementation of morphing wings in various flight conditions, including takeoff, cruise, and landing. Additionally, there is a lack of information regarding the resources required to facilitate the transformation of the wing structure. Given the importance of the aforementioned aspects, future work should aim to focus on these areas.

Acknowledgments

Authors acknowledge the partial support given by FEEI-CONACYT-PROCIENCIA and PRONII.

Conflicts of Interest

The authors declare no conflict of interest

References

  1. Mark Drela; Michael B. Giles. Viscous-Inviscid Analysis of Transonic and Low Reynolds Number Airfoils. In AIAA, 1987 10th, pages 1347–1355. [CrossRef]
  2. George, S. Dulikravich. Aerodynamics Shape Design and Optimization; Status and Trends. In Journal of Aircraft, 1992 6th, pages 1020–1026. [CrossRef]
  3. James, M. Lacasse; Oktay Baysal. Shape Optimization of Single and Two-Element Airfoils on Multiblock Grids. In 5th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, 1994 ; AIAA, pages 01–09.
  4. D. Quagliarella; A. Vicini. Viscous single and multicomponent airfoil design with genetic algorithm. In Finite Elements in Analysis and Design, 2001 37th, pages 365–380. [CrossRef]
  5. Haipeng Li; Jason Stewart ; Richard S. Figliola. Exergy based design methodology for airfoil shape optimization and wing analysis. In International Congress of the Aeronautical Sciences, 2006 25th, pages 01–11.
  6. D. López; C. Angulo; L. Macareno. An improved meshing method for shape optimization of aerodynamic profiles using genetic algorithms. In International Jourmnal for Numerical Methods in Fluids, 2008 56th, pages 1383–1389. [CrossRef]
  7. Paolo Bettini; Alessandro Airoldi; Giuseppe Sala; Luca Di Landro; Massimo Ruzzene; Alessandro Spadoni. Composite chiral structures for morphing airfoils: Numerical analyses and development of a manufacturing process. In Composites; Part B, 2010 41th, pages 133–147. [CrossRef]
  8. Yu-Tai Lee; Vineet Ahuja; Ashvin Hosangadi; Michael Ebert. Composite chiral structures for morphing airfoils: Shape Optimization of a Multi-Element Foil Using an Evolutionary Algorithm. In Journal of Fluids Engineering, 2010 132th, pages 01–117.
  9. Roelof Vos; Zafer Gürdal; Mostafa Abdalla. Mechanism for Warp-Controlled Twist of a Morphing Wing. In Journal of Aircraft, 2010 47th, pages 450–457.
  10. Ernesto Benini; Rita Ponza; Andrea Massaro. High-Lift Multi-Element Airfoil Shape and Setting Optimization Using Multi-Objective Evolutionary Algorithms. In Journal of Aircraft, 2011 48th, pages 683–696. [CrossRef]
  11. Juan Carlos Gomez; Ephrahim Garcia. Morphing unmanned aerial vehicles. In Smart Materials and Structures, 2011 20th, pages 01–16.
  12. Alfredo Arias-Montaño; Carlos A. Coello Coello; Efrén Mezura-Montes. Multi-Objective Airfoil Shape Optimization Using a Multiple-Surrogate Approach. In WCCI 2012 IEEE World Congress on Computational Intelligence, pages. [CrossRef]
  13. Charles, A. Mader; Joaquim R. R. A. Martins. Stability-Constrained Aerodynamic Shape Optimization of Flying Wings. In Journal of Aircraft, 2013 53rd, AIAA/ASME/ASCE/AHS/ASC, pages 01–19. [CrossRef]
  14. G. Pierluigi Della Vecchia; Elia Daniele; Egidio D’Amato. An airfoil shape optimization technique coupling PARSEC parameterization and evolutionary algorithm. In Aerospace Science and Technology, 2014 32nd, pages 103–110. [CrossRef]
  15. Tomohiro Yokozeki; Aya Sugiura. Development and Wind Tunnel Test of Variable Camber Morphing Wing. In AIAA, 2014 22nd, AIAA/ASME/AHS, pages 01–08. [CrossRef]
  16. Oranit Traisak; Teetut Dolwichai; Jiraphon Srisertpol; Chalothorn Thumthae. Study of airfoil shape optimization by using the evolutionary method. In Advances in Engineering Research, 2016 90th, AIAA/ASME/AHS, pages 109–113.
  17. Hongda Li; Haisong Ang. Preliminary airfoil design of an innovative adaptive variable camber compliant wing. In JVE INTERNATIONAL LTD. Journal of Vibroengineering, 2016 18th, pages 1861–1873. [CrossRef]
  18. G. Zhenghon; W. Chao. Aerodynamic shape design methods for aircraft:status and trends. In Acta Aerodynamica Sinica, 2017 35th, pages 516–528.
  19. Partha Mondal; Anup V. Kanale; N. Balakrishnan; Nikhil V. Shende; Rohan Pradeep Wadnerkar. Optimization of Flap Position Using a Modified Discrete-Vortex Method. In AIAA, 2017 34th, pages 01–11. [CrossRef]
  20. Ruxandra Mihaela Botez; Andreea Koreanschi; Oliviu Sugar Gabor; Youssef Mebarki; Mahmoud Mamou; Yvan Tondji; Francesco Amoroso; M. Rosario Pecora; Leonardo Lecce; Gianluca Amendola; Ignazio Dimino; Antonio Concilio. Numerical and Experimental Testing of a Morphing Upper Surface Wing Equipped with Conventional and Morphing Ailerons. In AIAA, 2017 57th, pages.
  21. Zachary, J. Grey; Paul G. Constantine. Active Subspaces of Airfoil Shape Parameterizations. In AIAA, 2018 58th, pages 2003–2017. [CrossRef]
  22. Pratik Meghani. A 2D Aerodynamic Study on Morphing of the NACA 2412 Aerofoil. In Research and Education in Aircraft Design Conference, 2018 13th, pages 56–65. [CrossRef]
  23. S. Ameduri; A. Concilio; I. Dimino; R. Pecora; S. Ricci. Airgreen 2 - Clean Sky 2 Programe: Adaptative Wing Technology Maturation, Challenges and Perspectives. In ASME, 2018, pages 01–10.
  24. Wei Chen; Kevin Chiu; Mark D. Fuge. Airfoil Design Parameterization and Optimization using Bézier Generative Adversarial Networks. In AIAA Scitech, 2019, pages 01–30. [CrossRef]
  25. Maurizio Arena; Christof Nagel; Rosario Pecora; Oliver Schorsch; Antonio Concilio; Ignazio Dimino. Static and Dynamic Performance of a Morphing Trailing Edge Concept with High-Damping Elastomeric Skin. In Aerospace, 2019, pages 01–22. [CrossRef]
  26. Pedro Gomes; Rafael Palacios. Aerodynamic-driven topology optimization of compliant airfoils. In Structural and Multidisciplinary Optimization, 2020, pages 2117–2130. [CrossRef]
  27. Yuanjing Wang; Binbin Lv; Pengxuan Lei; Wenkui Shi; Yu Yan. Study on Flow Mechanism of a Morphing Supercritical Airfoil. In Hindawi-Shock and Vibration, 2021, pages 01–11. [CrossRef]
  28. Tuba Majid; Bruce W. Jo. Status and Challenges on Design and Implementation of Camber Morphing Mechanisms. In Hindawi-International Journal of Aerospace Engineering, 2021, pages 01–14. [CrossRef]
  29. Aditya Joshi; Avnish Surendra Rai. Twist Morphing: A Simulation Approach to Compare Twist Morphed Wing and Flap Configuration. In International Journal for Research in Applied Science and Engineering Technology (IJRASET), 2021, 9th, pages 353–359.
  30. Alexandre Chorin; Jerrold E. Marsden. A Mathematical Introduction to Fluid Mechanics, 3rd ed., Springer-Verlag Publishing Company, Inc., 1221 Avenue of the Americas, New York, N.Y., United States, 2014, pp. 001–169.
  31. Yunes, A. Cengel; John M. Cimbala. Fluid Mechanics. Fundamentals and Aplications. In 3rd ed., The McGraw-Hill Companies, Inc., 175 Fifth Avenue, New York, N.Y., United States, 2000, pp. 001–983.
  32. Schmitt, F.G. About Boussinesq’s turbulent viscosity hypothesis: historical remarks and a direct evaluation of its validity. In Comptes Rendus Mécanique, 2007, 335, pages 617–627. [CrossRef]
  33. Christopher, L. Christopher L. Rumsey; Susan X. Ying. Prediction of high lift: review of present CFD capability. In Progress in Aerospace Sciences, 2002, 38th, pages 145–180. [CrossRef]
  34. S. Jakobsson; O. Amoignon. Mesh deformation using radial basis functions for gradient-based aerodynamic shape optimization. In Computers Fluids, 2007, 36th, pages 1119–1136. [CrossRef]
  35. Helmut Sobieczky. Parametric Airfoils and Wings. In Notes on Numerical Fluid Mechanics, 1998, 68th, pages 71–88. [CrossRef]
  36. Wenbin Song; Andrew J. Keane. A Study of Shape Parameterization Methods for Airfoil Optimisation. In AIAA, 2004, 10th, pages 01–08.
  37. Raymer, D.P. Aircraft Design: A Conceptual Approach,Fifth ed., AIAA Educational Series, Inc., 1801 alexander Bell Drive, Suite 500, Reston, VA 2019-4344., United States, 1999, pp. 001–910.
  38. Constantine, P. G. Active Subspaces: Emerging Ideas for Dimension Reduction in Parameter Studies, 3rd ed., Soc. for Industrial and Applied Mathematics, 3600 University City Science Center Philadelphia, PA, United States, 2015, pp. 001–110.
  39. Zachary, J. Grey; Paul G. Constantine. Active Subspaces of Airfoil Shape Parameterizations. In AIAA, 2018, N0.5, pages 2003–2017. [CrossRef]
  40. Kulfan, B. M. Universal Parametric Geometry Representation Method. In Journal of Aircraft, 2008, Vol. 45, pages 2142–158.
  41. Gerhard Venter. Review of Optimization Techniques. In Encyclopedia of Aerospace Engineering, 2010, ResearchGate, pages 01–12.
  42. M. Schramm; B. Stoevesandt; J. Peinke. Simulation and Optimization of an Airfoil with Leading Edge Slat. In Journal of Physics: Conference Series, 2016, ResearchGate, pages 01–08. [CrossRef]
  43. T. Ray; H. M. Tsai. Swarm Algorithm for Single- and Multiobjective Airfoil Design Optimization. In AIAA, 2004, Vol. 42, N0. 2, ResearchGate, pages 366–373. [CrossRef]
  44. M. Ebrahimimi; A. R. jahangirian. Airfoil Shape Optimization with Adaptive Mutation Genetic Algorithm. In Journal of Aerospace Science and Technology, 2017, Vol. 11, N0. 1, ResearchGate, pages 47–59.
  45. S. A. Meguid; Yu Su; Yue Wand. Airfoil Complete morphing wing design using flexible-rib system. In International Journal of Mechanics and Materials in Design, 2017, Vol. 13, N0. 1, ResearchGate, pages 159–171.
  46. Q. Chanzy; A. Keane. Analysis and experimental validation of morphing UAV wings. In The Aeronautical Journal, 2018, Vol. 122, N0. 1249, ResearchGate, pages 390–408. [CrossRef]
  47. La, S.; Joe, W.Y.; Akbar, M.; Alsaidi, B. Surveys on Skin Design for Morphing Wing Aircraft: Status and Challenges. In AIAA aerospace sciences meeting, p. 0315, Kissimmee, FL, USA. 2018; pp. 01–02. [CrossRef]
  48. U. Fasel; D. Keidel; L. Baumann; G. Cavolina; M. Eichenhofer; P. Ermanni. Composite additive manufacturing of morphing aerospace structures. In Manufacturing Letters, 2020, Vol. 23, pages 01–11. [CrossRef]
  49. T. A. Weisshaar. Morphing aircraft systems: historical perspectives and future challenges. In Journal of Aircraft, 2013, Vol. 50, No. 2, pages 337–353. [CrossRef]
  50. Y. Zhang; W. Ge; Z. Zhang; X. Mo; Y. Zhang. Design of compliant mechanism-based variable camber morphing wing with nonlinear large deformation. In International Journal of Advanced Robotic Systems, 2019, Vol. 16, No. 6, pages 01–19. [CrossRef]
  51. B. K. S. Woods; M. I. Friswell. Preliminary investigation of a fishbone active camber concept. In Smart Materials, Adaptive Structures and Intelligent Systems, 2012, pages 555–563. [CrossRef]
  52. H. L. Şahin; Y. Yaman. Synthesis, analysis, and design of a novel mechanism for the trailing edge of a morphing wing. In Aerospace, 2018, Vol. 5, No. 4, pages 01–20.
  53. A. V. Ivchenko; N. Sharonov; R. Ziatdinov. New conceptual design of the adaptive compliant aircraft wing frame. In Engineering Science and Technology, an International Journal, 2019, Vol. 22, No. 5, pages 1149–1154. [CrossRef]
  54. S. Vasista; L. Tong. Topology-optimized design and testing of a pressure-driven morphing-aerofoil trailing-edge structure. In AIAA Journal, 2013, Vol. 51, No. 8, pages 1898–1907. [CrossRef]
  55. Sun, J.; Guan, Q.; Liu, Y.; Leng, J. Morphing aircraft based on smart materials and structures a state-of-the-art review. In Journal of Intelligent Material Systems and Structures, 2016, Vol. 27, No. 17, pages 2289–2312. [CrossRef]
  56. Jichao Li; Xiaosong Du; Joaquim R.R.A. Martins. Machine learning in aerodynamic shape optimization. In Progress in Aerospace Sciences, 2022, Vol.134, pages 01–50. [CrossRef]
  57. N. Fonzi; S. L. Brunton; U. Fasel. Data-driven nonlinear aeroelastic models of morphing wings for control. In Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2020, Vol. 476, Issue. 2239, pages 01–23. [CrossRef]
  58. A. E. Eiben; J. E. Smith. Introduction to Evolutionary Computing, 1st ed., Springer-Verlag Berlin Heidelberg GmbH: 1221 Avenue of the Americas, New York, N.Y., United States, 2003, pp. 001–306.
  59. N. Fonzi; S. L. Brunton; U. Fasel. Particle Swarm Optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, IEEE Service Center, 1995, pages 4104–4109.
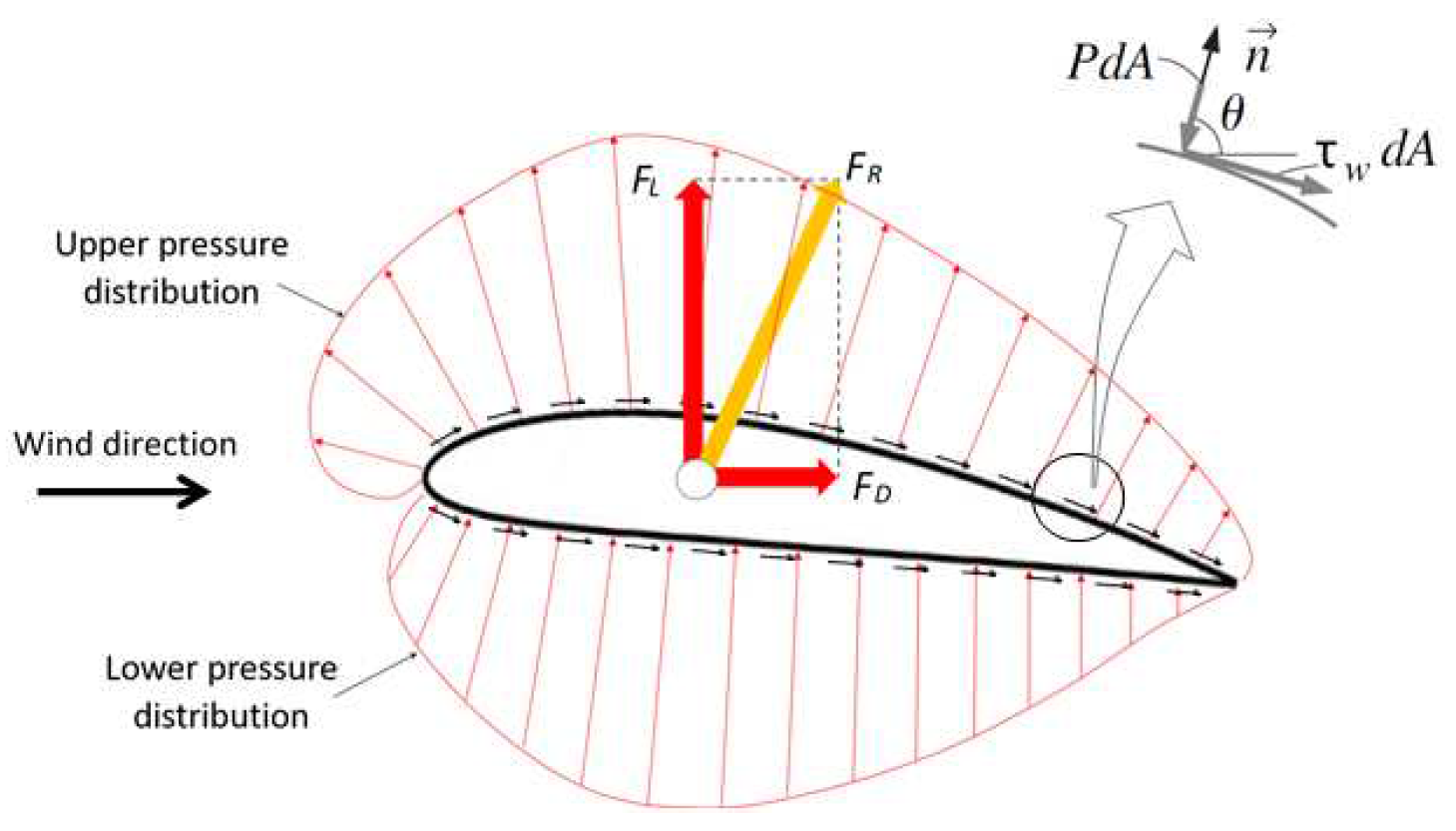
Preprints 78466 g001
Figure 1. Airfoil pressure and forces distribution.
Figure 1. Airfoil pressure and forces distribution.
Preprints 78466 g001
Preprints 78466 g002
Figure 2. Airfoil flow distribution.
Figure 2. Airfoil flow distribution.
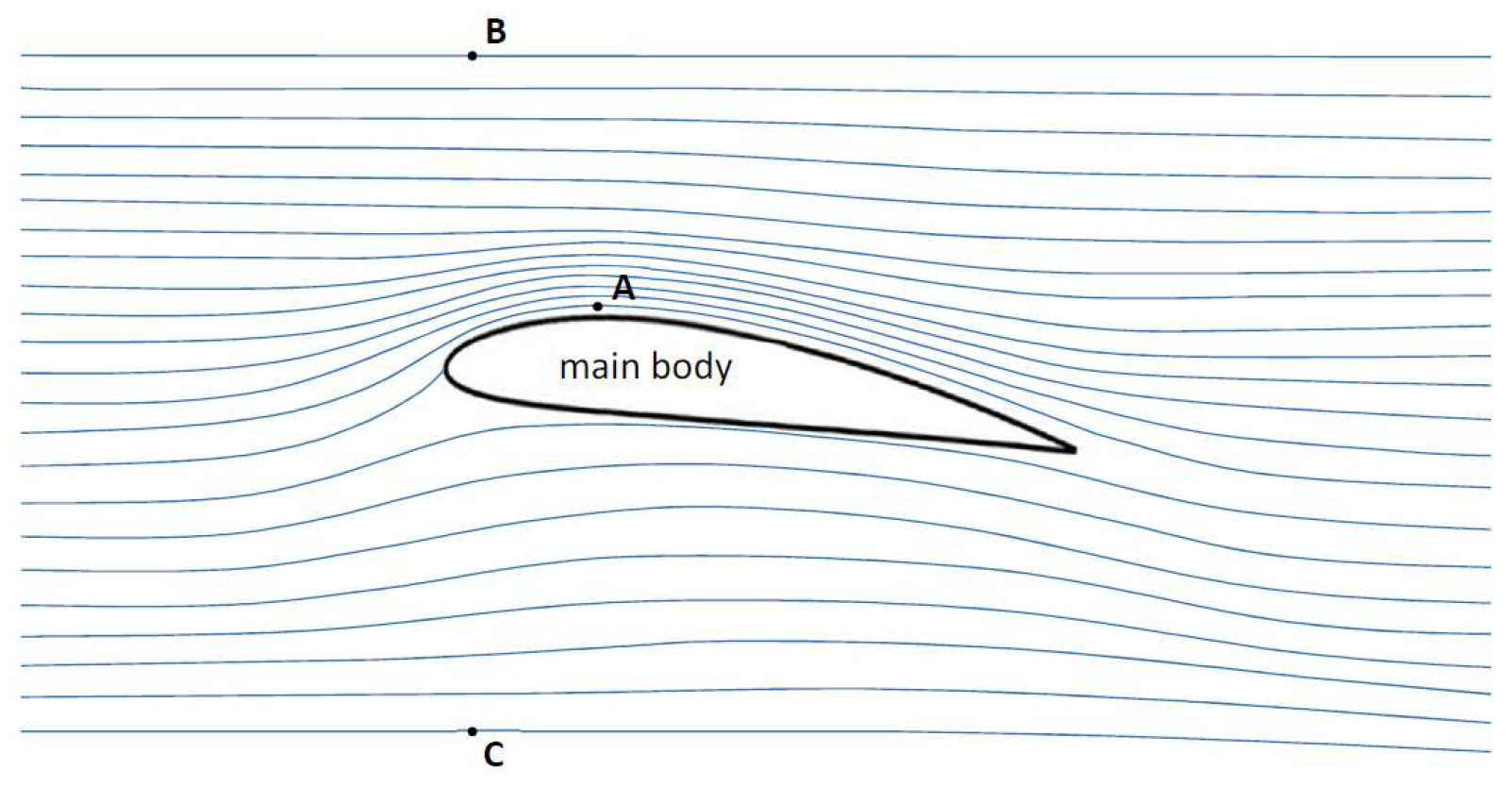
Preprints 78466 g002
Preprints 78466 g003
Figure 3. Airfoil structure: (a) Rigid multi-element body; (b) flexible morphing body
Figure 3. Airfoil structure: (a) Rigid multi-element body; (b) flexible morphing body
Preprints 78466 g003
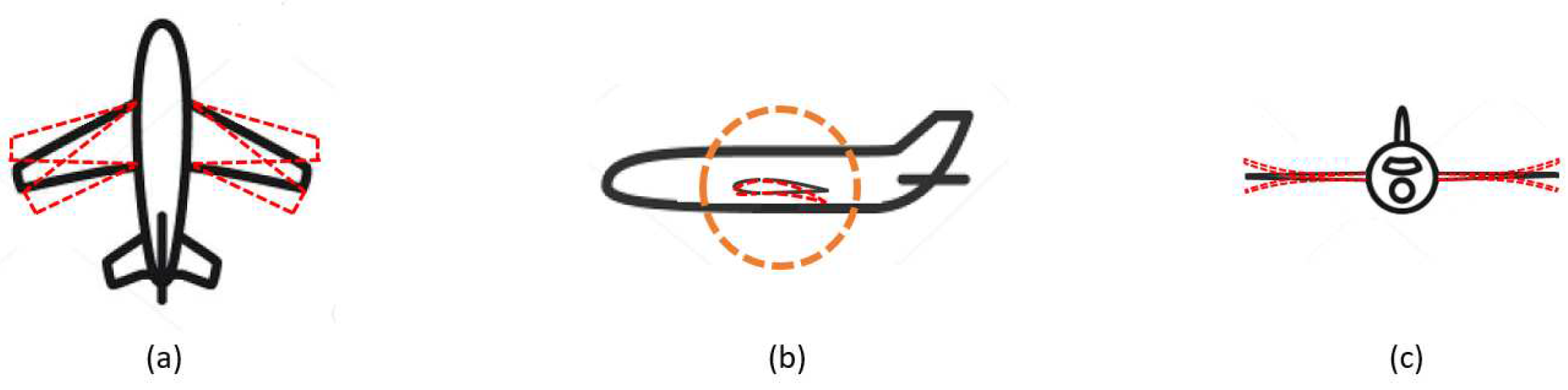
Preprints 78466 g004
Figure 4. Types of morphism: (a) In-plane morphing; (b) airfoil morphing; (c) out-of-plane morphing
Figure 4. Types of morphism: (a) In-plane morphing; (b) airfoil morphing; (c) out-of-plane morphing
Preprints 78466 g004
Preprints 78466 g005
Figure 5. (a) Foil with rigid multi-elements body; (b) Foil with SMA wires system. Extracted from [8].
Figure 5. (a) Foil with rigid multi-elements body; (b) Foil with SMA wires system. Extracted from [8].
Preprints 78466 g005
Preprints 78466 g006
Figure 6. Composite chiral core structure airfoil. Extracted from [7].
Figure 6. Composite chiral core structure airfoil. Extracted from [7].
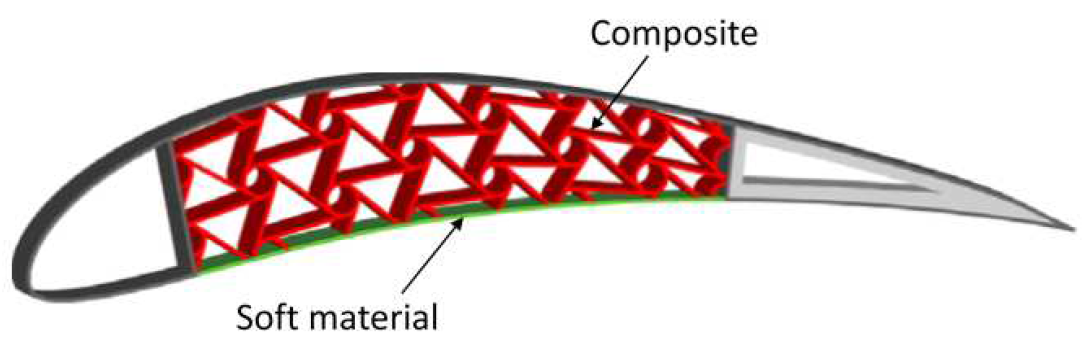
Preprints 78466 g006
Preprints 78466 g007
Figure 7. Corrugated trailing edge airfoil. Extracted from [15].
Figure 7. Corrugated trailing edge airfoil. Extracted from [15].
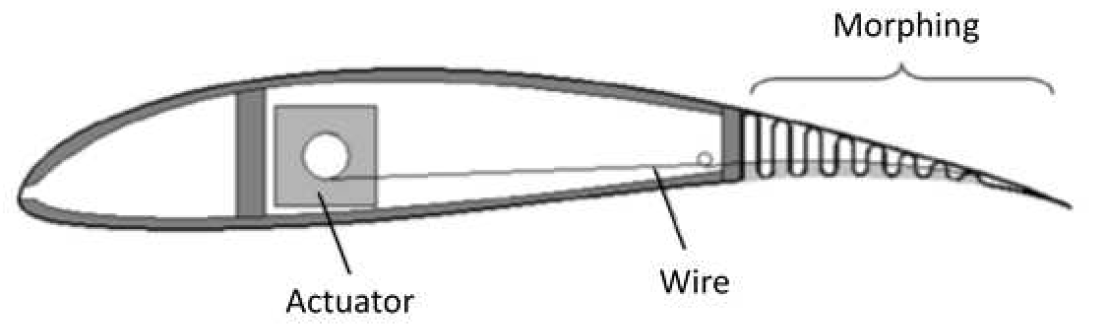
Preprints 78466 g007
Preprints 78466 g008
Figure 8. Adaptive variable camber compliant wing. Extracted from [17].
Figure 8. Adaptive variable camber compliant wing. Extracted from [17].
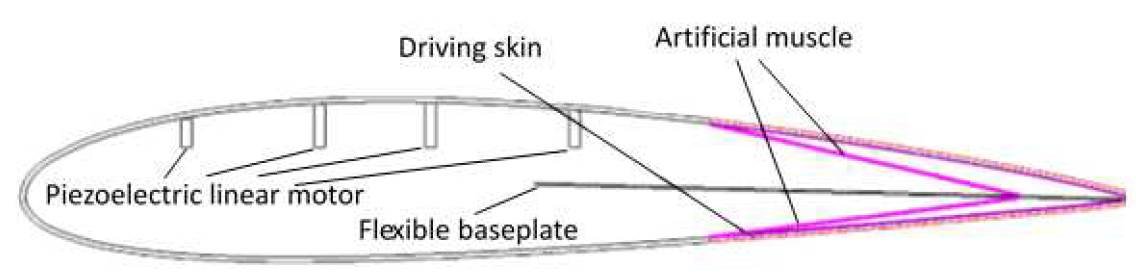
Preprints 78466 g008
Preprints 78466 g009
Figure 9. Compliant morphing rib with flexible skin. Extracted from [25].
Figure 9. Compliant morphing rib with flexible skin. Extracted from [25].
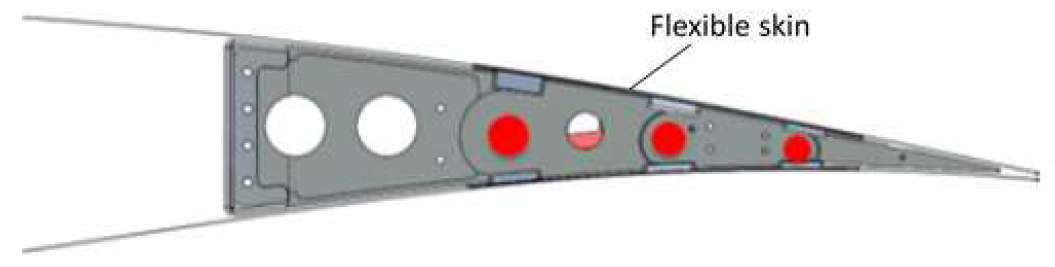
Preprints 78466 g009
Preprints 78466 g010
Figure 10. Flexible rib airfoil. Extracted from [45].
Figure 10. Flexible rib airfoil. Extracted from [45].
Preprints 78466 g010
Preprints 78466 g011
Figure 11. Glass-fibre-clad polystyrene foam airfoil with actuator mechanism. Extracted from [46].
Figure 11. Glass-fibre-clad polystyrene foam airfoil with actuator mechanism. Extracted from [46].
Preprints 78466 g011
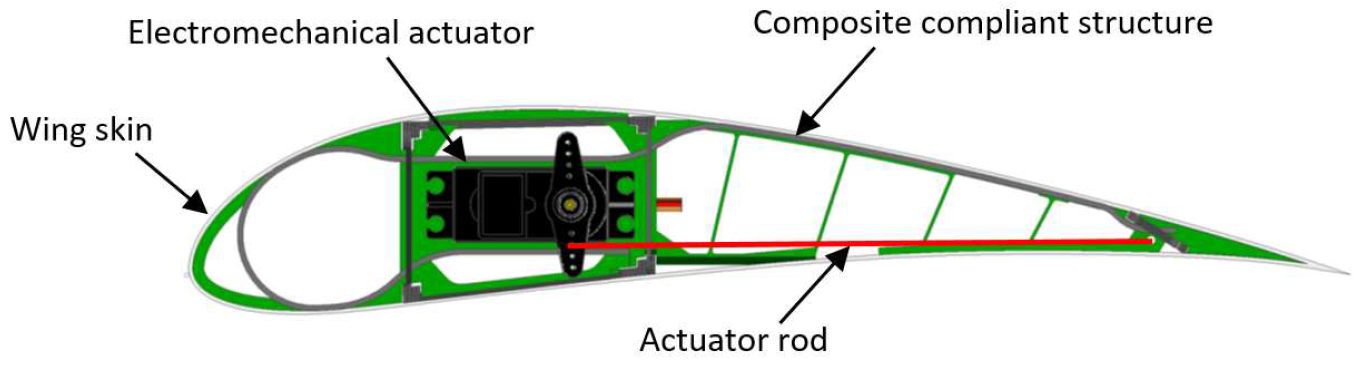
Preprints 78466 g012
Figure 12. Carbon fibre composite structure morphing airfoil. Extracted from [48].
Figure 12. Carbon fibre composite structure morphing airfoil. Extracted from [48].
Preprints 78466 g012
Preprints 78466 g013
Figure 13. Hybrid concept morphing airfoil. Extracted from [50].
Figure 13. Hybrid concept morphing airfoil. Extracted from [50].
Preprints 78466 g013
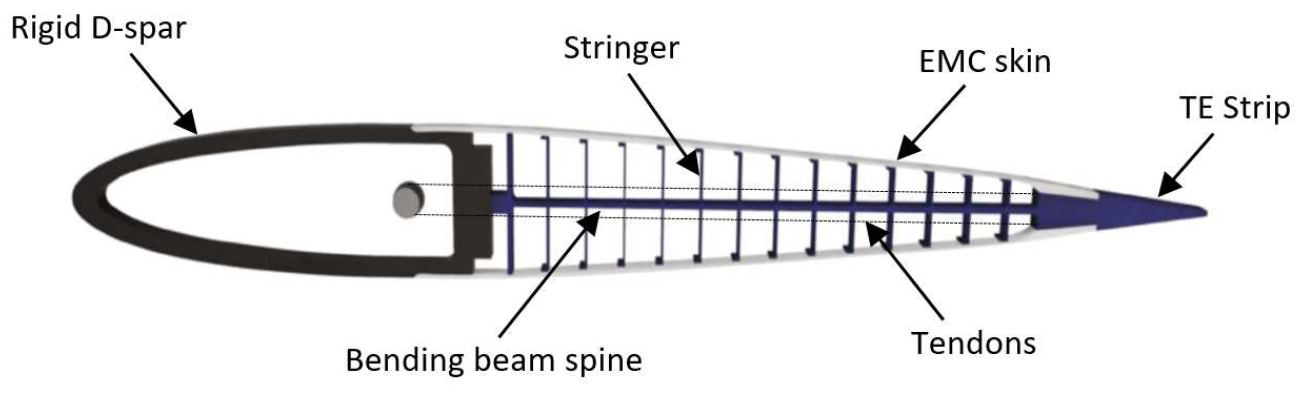
Preprints 78466 g014
Figure 14. Fishbone active camber morphing airfoil. Extracted from [51].
Figure 14. Fishbone active camber morphing airfoil. Extracted from [51].
Preprints 78466 g014
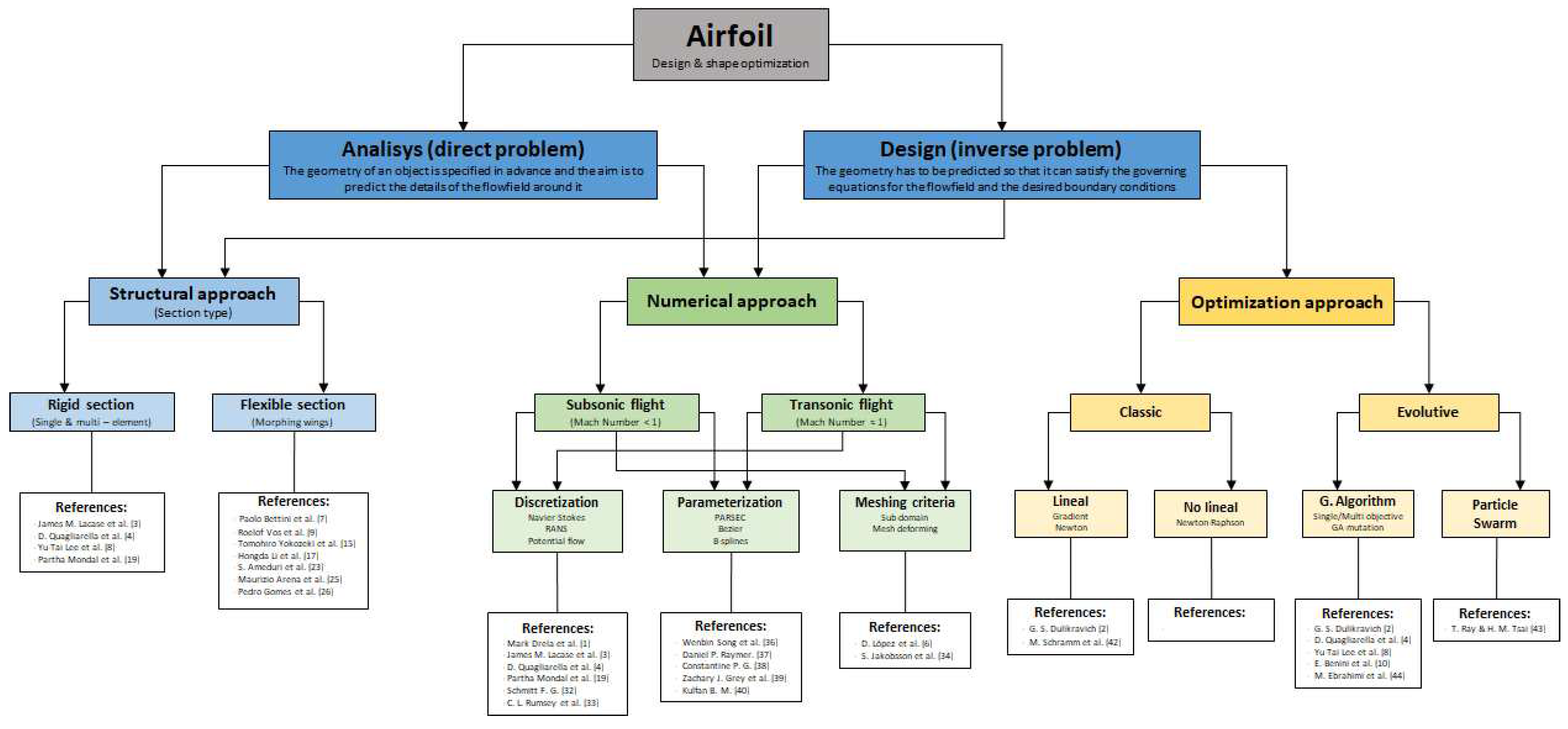
Preprints 78466 g015
Figure 15. Airfoil design and shape optimization graphic taxonomic scheme.
Figure 15. Airfoil design and shape optimization graphic taxonomic scheme.
Preprints 78466 g015
Table 1. This table summarizes features of both concepts, conventional airfoil and morphing airfoil.
Table 1. This table summarizes features of both concepts, conventional airfoil and morphing airfoil.
Features Conventional airfoil Morphing airfoil
Structure Consists of multiple components Single, flexible structure
Shape adjustment Range limited to movable control surfaces (e.g., flaps, slats) Active and wide range of adjustment of the entire shape in real time
Design focus Mechanical and geometric characteristics of movable control surfaces Structural, material, and hybrid approaches for morphing mechanisms
Control Actuated by separate control mechanisms Actuators and control systems for shape changes
Functionality Designed for specific flight conditions Adaptable to different flight conditions
Performance Optimized for specific configurations Optimized for various conditions, improving lift/drag ratio
Efficiency May have lower energy and aerodynamic efficiency Enhanced energy, aerodynamic efficiency and fuel consumption
Complexity More complex design and control systems Advanced design and reduced assembly complexities
Flow disruption Potential flow disruptions between components Smooth airflow and reduced disturbances
Structural weight Potentially higher due to additional components Potentially lighter due to simplified structure
Aplications Conventional aircraft with fixed wing shapes and movable control surfaces Future potential for advanced aircraft designs with adaptive, morphing wing shapes for improved performance and efficiency in various flight conditions
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated