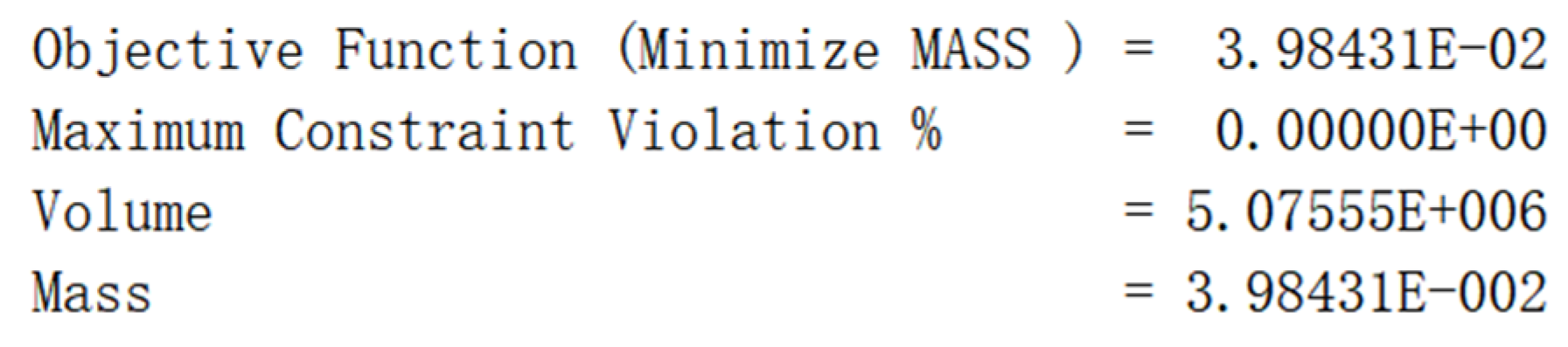0. Preface
Formula SAE is a university level student design competition aimed at designing and manufacturing small high-performance racing car, attracting numerous college students from around the world to participate every year. So far, hundreds of schools have participated in the competition [
1,
2,
3].
The participants focus on developing simple, lightweight, and easy to operate open chassis vehicle while ensuring compliance with SAE rules. To achieve this goal, various teams have conducted in-depth research on the design of racing frames, with the goal of improving racing performance. Currently, research on racing frame design includes the following aspects: (1) reducing racing car resistance. VAIDYA S et al. conducted aerodynamic analysis and design on SAE racing cars using fluid dynamics to reduce air resistance [
4]. (2) Adopting new materials. GUIC et al. studied the application of lightweight, high stiffness, and high-strength materials such as carbon fiber and resin in racing, resulting in high power and safety performance during the race [
5]. (3) Structural design of racing car frame. Yu Haiyan et al. designed a carbon fiber monocoque body with a total weight of 24.3kg, which reduces the mass by 34% compared to the truss type body. At the same time, by matching the laying direction, laying sequence, and laying quantity reasonably, the body achieves higher mechanical properties [
6]. (4) Lightweight design of the frame. Hu Li et al. used finite element method to lightweight design the truss frame of a college student racing car, reducing the mass while ensuring that the strength and stiffness still meet the design requirements [
7]. Kong Deying et al. used finite element analysis software to perform topology design and size optimization on the frame while meeting the constraints of vehicle vibration frequency, strength, stiffness, etc., achieving good lightweight effects [
8]. In recent years, a lot of universities have done some research on frame optimization, among which the first racing car of Taiyuan University of Science and Technology has carried out local topology optimization and size optimization on the frame, improving the frame performance and reducing the frame mass [
9]. However, under local optimization, only the structure of the front part is improved. There are many pipe fittings in the rear compartment and the specific direction of pipe fittings needs to be obtained, so topology optimization of the rear compartment is also particularly important; In addition, when optimizing the size of the frame, all variables were introduced and the influence weights of each variable were ignored, which would consume calculation time and the calculation accuracy would not meet the expected results.
In summary, due to the important role of optimizing the racing frame in improving the performance of racing cars, more research is currently focused on frame optimization. The optimization of the racing frame includes two aspects: structural optimization and dimensional optimization. In terms of structural optimization, the topology optimization method is usually used to find the optimal material distribution under the given structural design domain, applied load, fixed boundary and constraint conditions of the frame, so as to optimize its performance indicators. It is a very effective conceptual design method [
10,
11,
12]. The topology optimization model with maximum stiffness [
13] is adopted, so that the frame can obtain the topology with the best load transmission path, and the calculation efficiency is high.
Among them, the homogenization method is a typical topology optimization method, which decomposes the heterogeneous boundary value problem into a cell (micro) problem and a structure problem (macro), applies boundary conditions on the cell to solve its influence function control equation, and the results are accurate for one-dimensional structures, but low for two-dimensional structures [
14], and in the solution module, the method is only used for homogeneous isotropic materials.
There is another topological method for continuum structures - variable density method. With the unit density in the design space as the design variable, the initial discrete value topology optimization problem is established as an optimization problem based on continuous design variables. It allows for the addition of effective materials to the structure while removing inefficient materials, resulting in the optimal structure [
15]. By using the isotropic penalty microstructure model (SIMP) method, the penalty factor p is introduced to increase the cost of intermediate density elements and reduce the number of intermediate density elements, so as to make the density of elements as close as possible to 0 or 1 [
16], which highlights the overall structure of the vehicle frame. More importantly, in the solving module, the variable density method has a wider applicability.
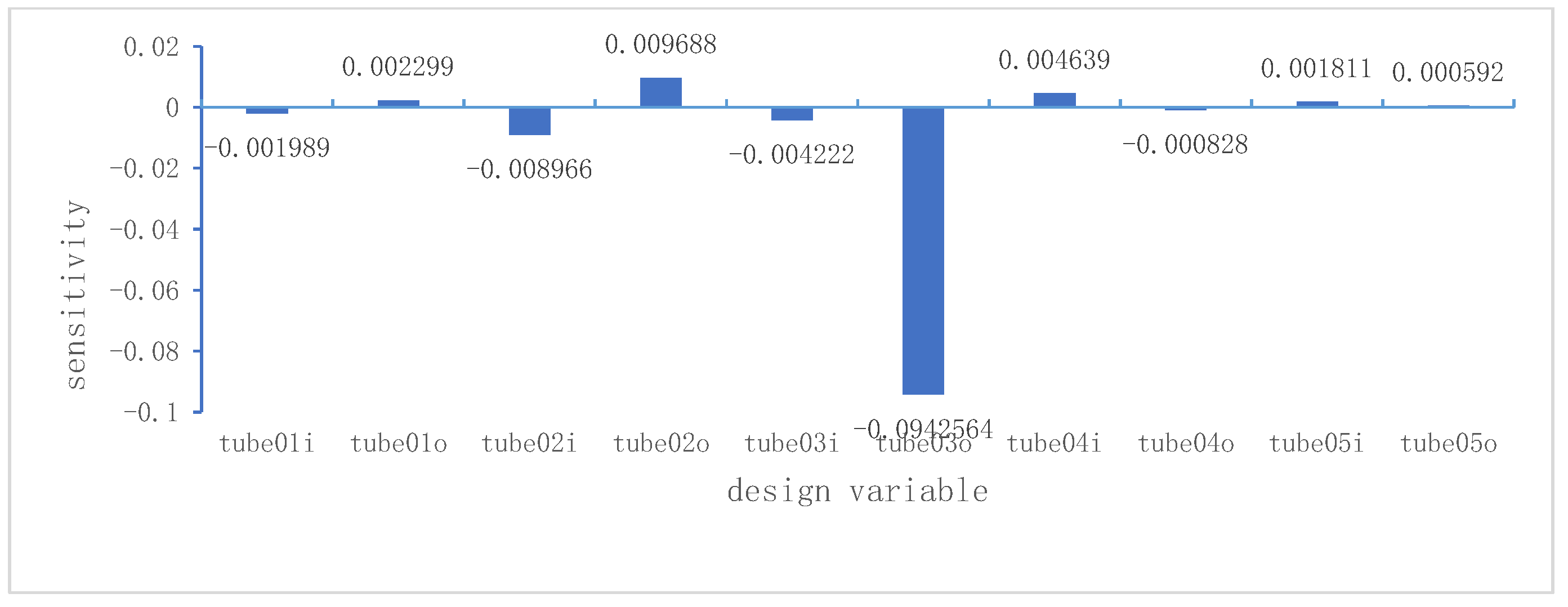
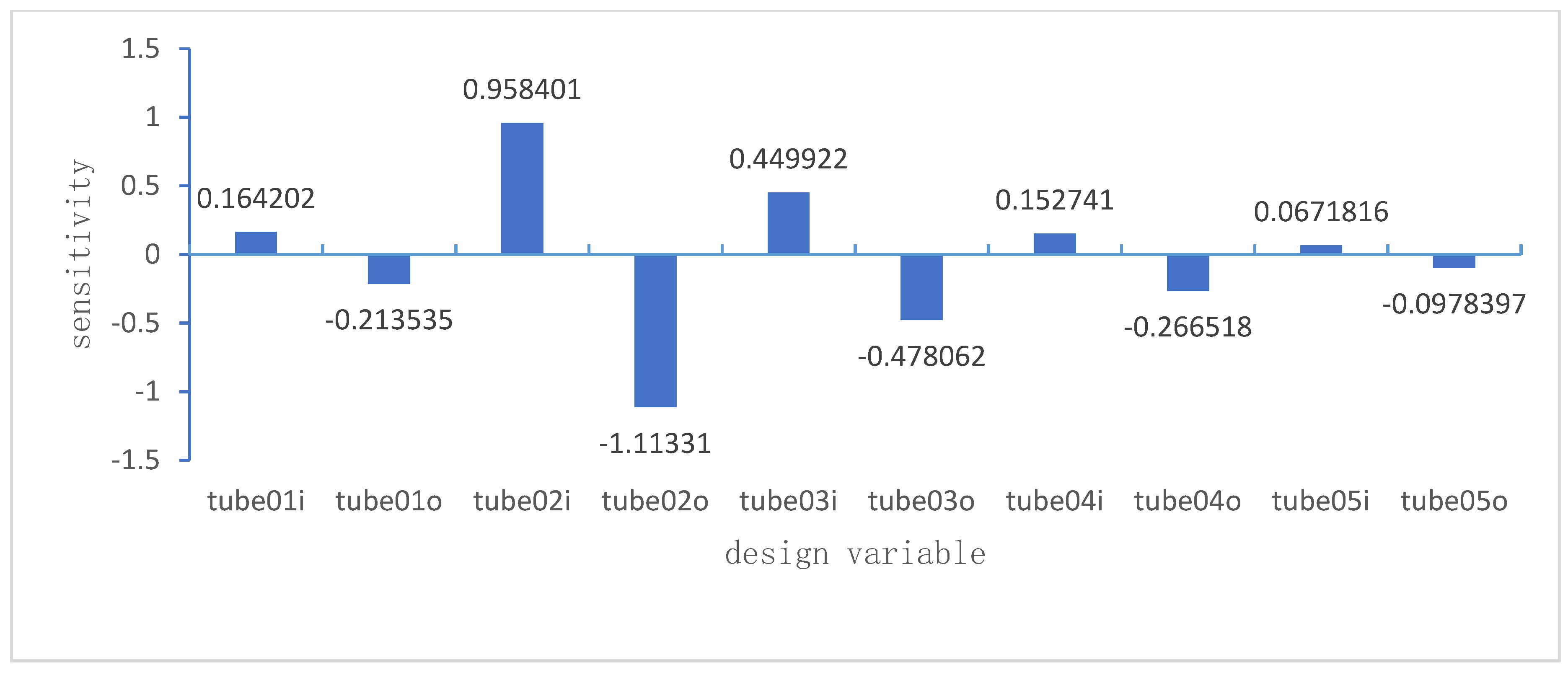
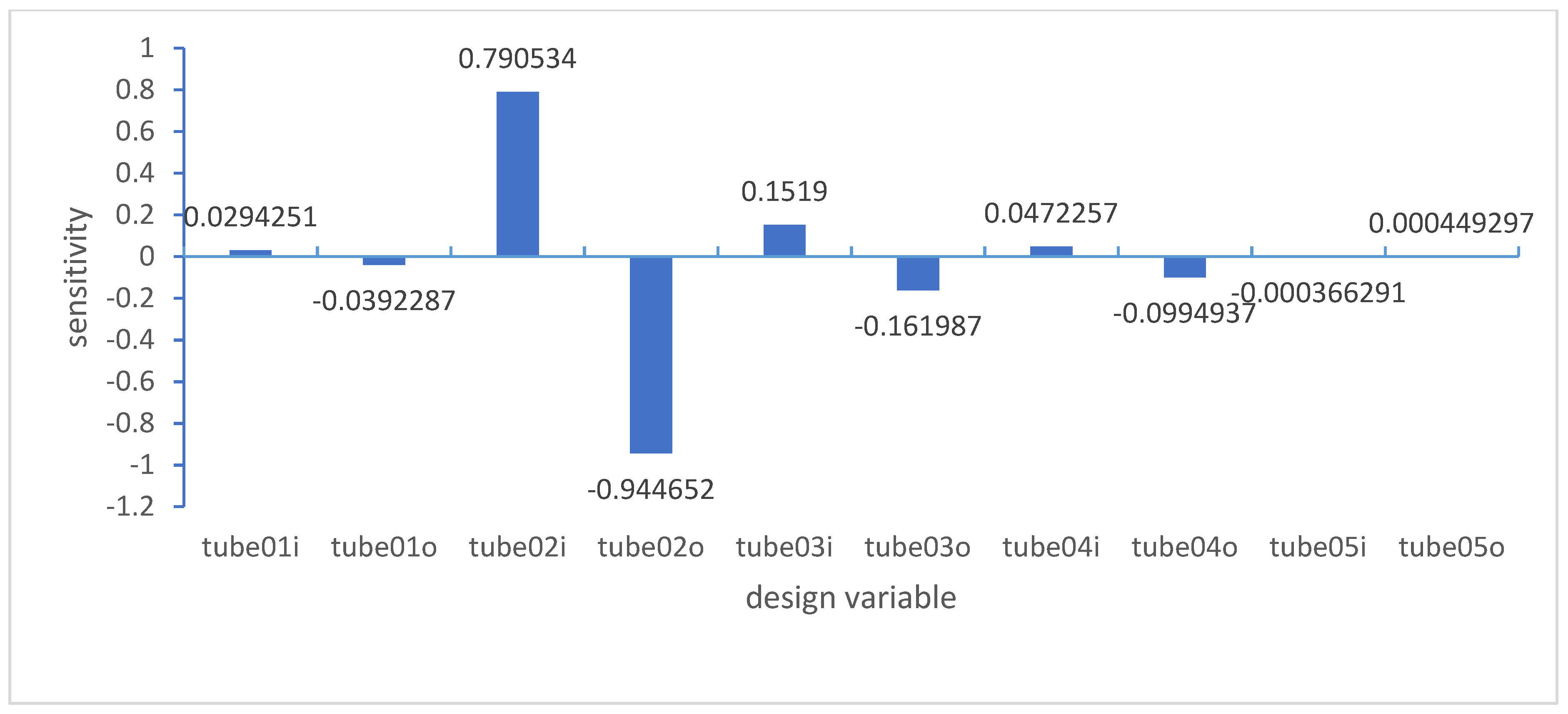
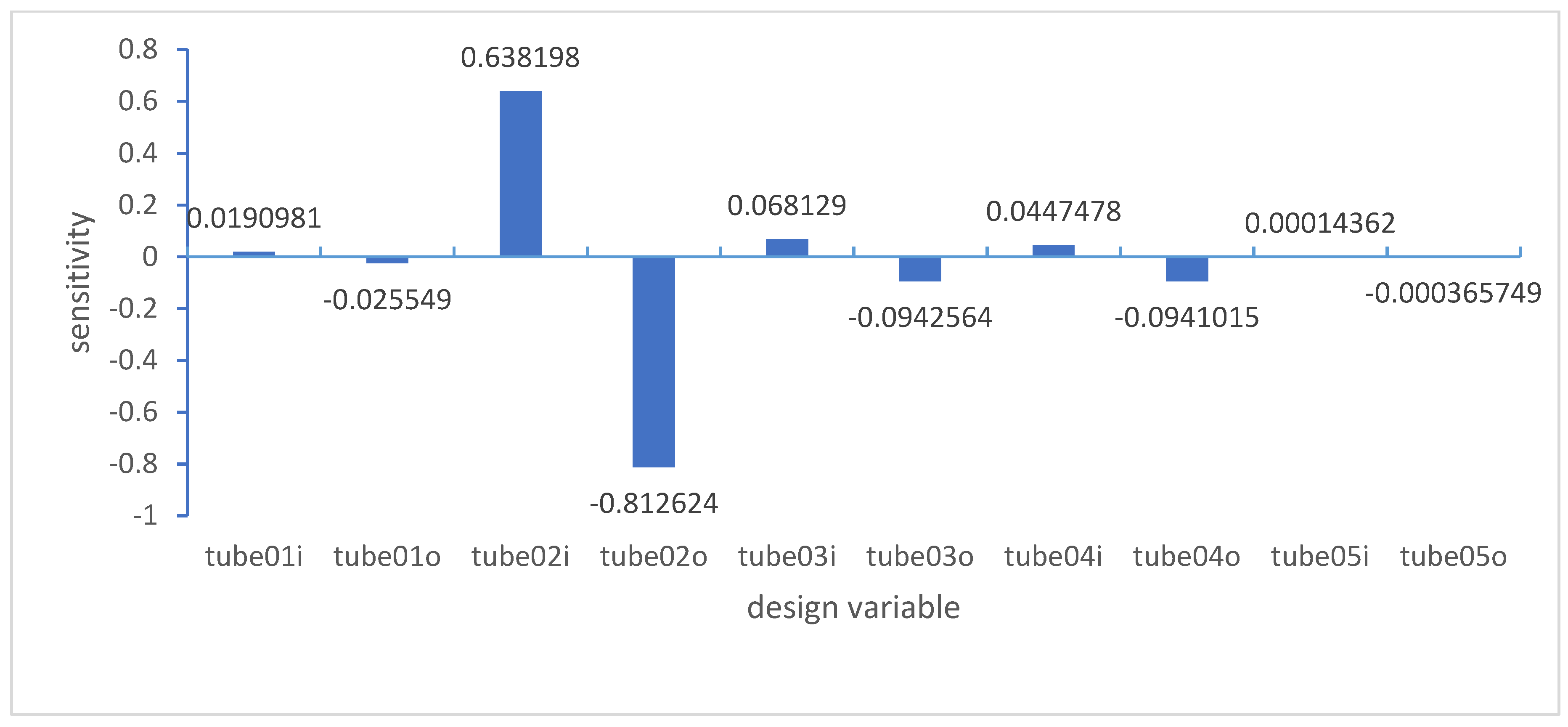
In terms of size optimization, the main issue is the large number of design variables. When optimizing dimensions, sensitivity analysis is added to select variables with larger influencing factors from numerous variables, and optimization design is carried out on these variables to improve the efficiency and effectiveness of size optimization.
Design sensitivity is the partial derivative of the design response to the optimization variable. From the perspective of calculation, the numerical methods of sensitivity analysis mainly include the following: finite difference method, direct differential method and adjoint variable method [
17]. The concept of difference method is simple, but the computational complexity is high; The direct differentiation method is used for sensitivity gradient calculation, and the numerical sensitivity of the final result to any introduced parameter increment must be verified. The accuracy is high, but it is suitable for the problem of less design variables [
18]. Due to the large number of vehicle frame fittings, there are many variables, and this method is not applicable; For optimization problems with fewer constraints and more design variables, the adjoint variable method considers the introduction of adjoint variables when calculating sensitivity, calculates the partial derivative of design response to design variables, improves the variables with greater sensitivity, and is more efficient for optimization design problems with more design variables.
Based on the above analysis, in order to improve the calculation accuracy, this paper conducts global optimization of the frame based on the variable density method, and retains the materials at the locations with high element density, so as to obtain the direction of the pipe fittings. In addition, the adjoint variable method is applied to perform sensitivity analysis on the frame, and the influencing factors of each variable are obtained based on the results. Based on the variables with greater influence, the size of the frame is optimized to make the design more accurate and achieve lightweight effect.
1. Frame Model Design and Structural Analysis
The frame is the "keel" of a racing car, providing positioning points for the transmission, steering, and suspension systems. Frame design is a key technology that plays an important role in automotive design. The high-performance frame of a racing car means that it requires high torsional stiffness, as it directly affects the turning performance of the car [
19]. Therefore, the design of the frame must fully consider the assembly of each assembly and the lightweight of the frame itself, and ensure that the frame can be in good condition under various working conditions, ensuring that the racing car can successfully complete the race task. Taking into account factors such as design difficulty, repair difficulty, and manufacturing cost, this article selects the frame structure as a spatial truss structure, and the material selection is 4130 steel.
1.1. Determine the geometric modeling of the frame
(1) Input the coordinates of suspension hard points in CATIA V5 part design to create a suspension line diagram.
(2) Determine the specific parameters of the main ring, front ring, and front partition.
(3) Connect the bottom of the front partition, the bottom of the front ring, and the bottom of the main ring with lines in sequence.
(4) Determine the main ring slant support and the upper and lower slant support support structure of the main ring.
(5) Use the cockpit opening detection board and the cockpit internal cross-sectional detection board to check whether the front cabin and cockpit of the frame meet the requirements of the competition rules.
1.2. Establishing a finite element model
1.2.1. Finite element theory
(1) The structure is discretized, transforming the ductile continuous medium into a relatively limited number of simple basic elements, which generate a combination based on node connections, and the load is also transmitted based on this node. In the whole process of discretization, different types and numbers of elements can be selected. The types and numbers of elements have a direct impact on the accuracy and stability of the numerical value of the finite element analysis solid model.
(2) After the construction of discretization, in order to better reflect the displacement, stress and strain of the element with the node displacement, the displacement function formula can be used to describe,
In the equation:
refers to the displacement column vector of a point in the element;
refers to the shape function matrix of the element;
refers to the node displacement column vector of an element.
According to the geometric equation in elasticity, the element strain correlation indicated by the element node displacement column vector is deduced:
In the equation:
refers to the strain column vector at any point in the element;
refers to the strain matrix of the element.
Based on the principle of virtual work, the relationship between node load and node displacement of the function on the element was created, and the bending stiffness equation of the element was derived:
where the [K] refers to the stiffness matrix of the element and {R} refers to the load column vector of the overall structure.
(3) Solve as a whole, synthesize all bending stiffness equations, and obtain the equilibrium equations for all constructions, namely:
where the {δ} Refers to all constructed node displacement space column vector.
1.2.2. Establishment process
This article conducts simulation analysis and optimization design in the Hypermesh environment. Import the geometric modeling in CATIA V5, and create the finite element analysis model. The steps are as follows:
① Establish materials. The frame is made of 4130 steel, namely 30CrMo, with an elastic modulus of 2.0510 MPa, Poisson’s ratio of 0.33, density of 7.8510 g/cm3, and allowable stress of about 390 MPa.
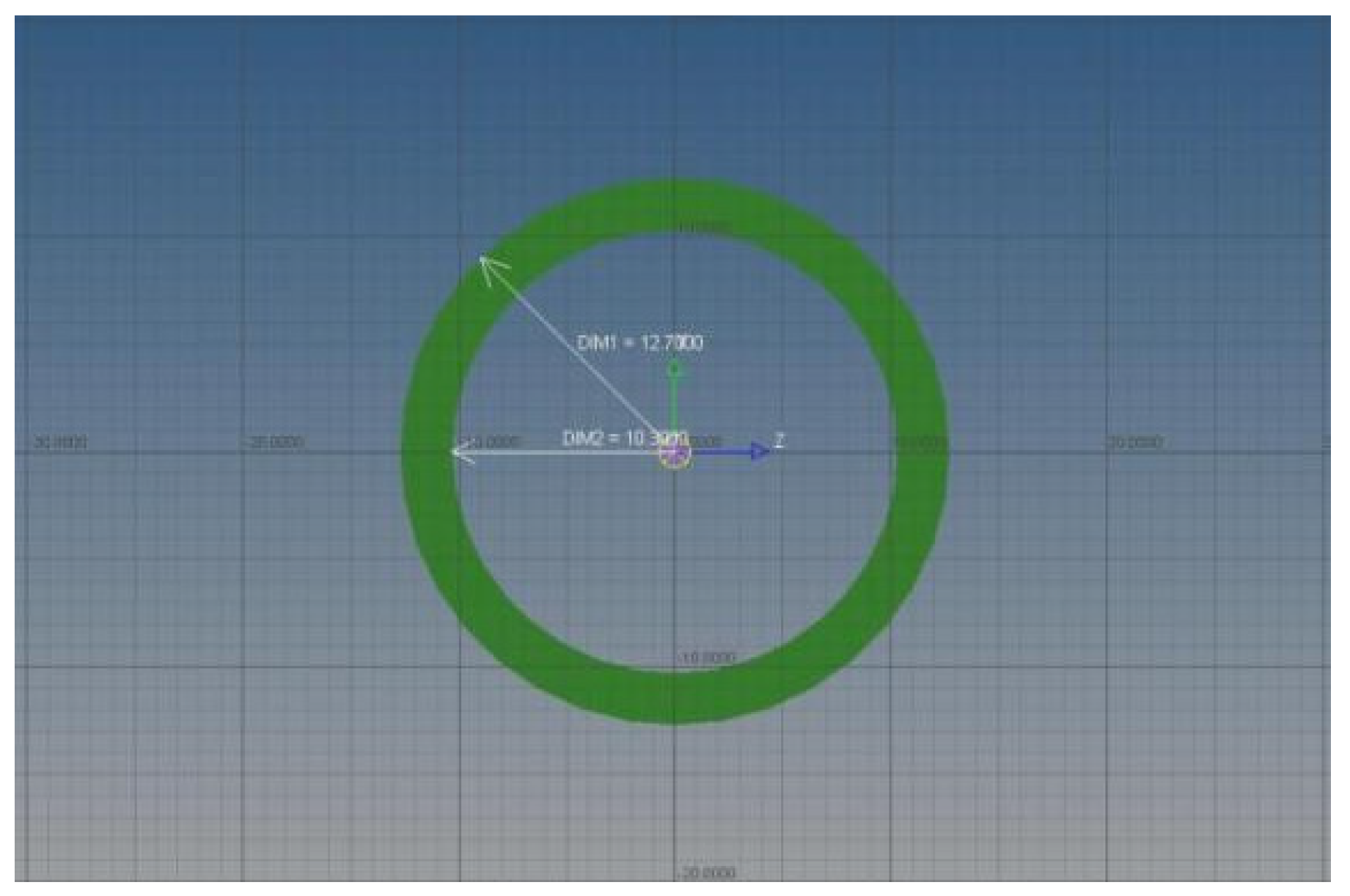
② Unit selection. Create a beam unit using Hyperbeam, as shown in Figure 1. The outer diameter of the pipes is uniformly 25.4 mm, and the outer diameter of individual pipes is 20 mm. According to the rules of the competition frame design section, four different wall thicknesses of steel pipes are established, namely 20 mm (outer diameter) * 1.2 mm (wall thickness), 25.4 mm * 2.4 mm, 25.4 mm * 1.65 mm, and 25.4 mm * 1.25 mm.
Figure 1.
Cross section of frame beam unit.
Figure 1.
Cross section of frame beam unit.
③ Establish attributes. Establish four attributes with the same name as the previously established four beam elements (for easy matching), and note that they correspond one by one with the Beam section.
④ Grid division. Divide the pipe fittings into grids and set the grid size to 10 mm for efficient calculation.
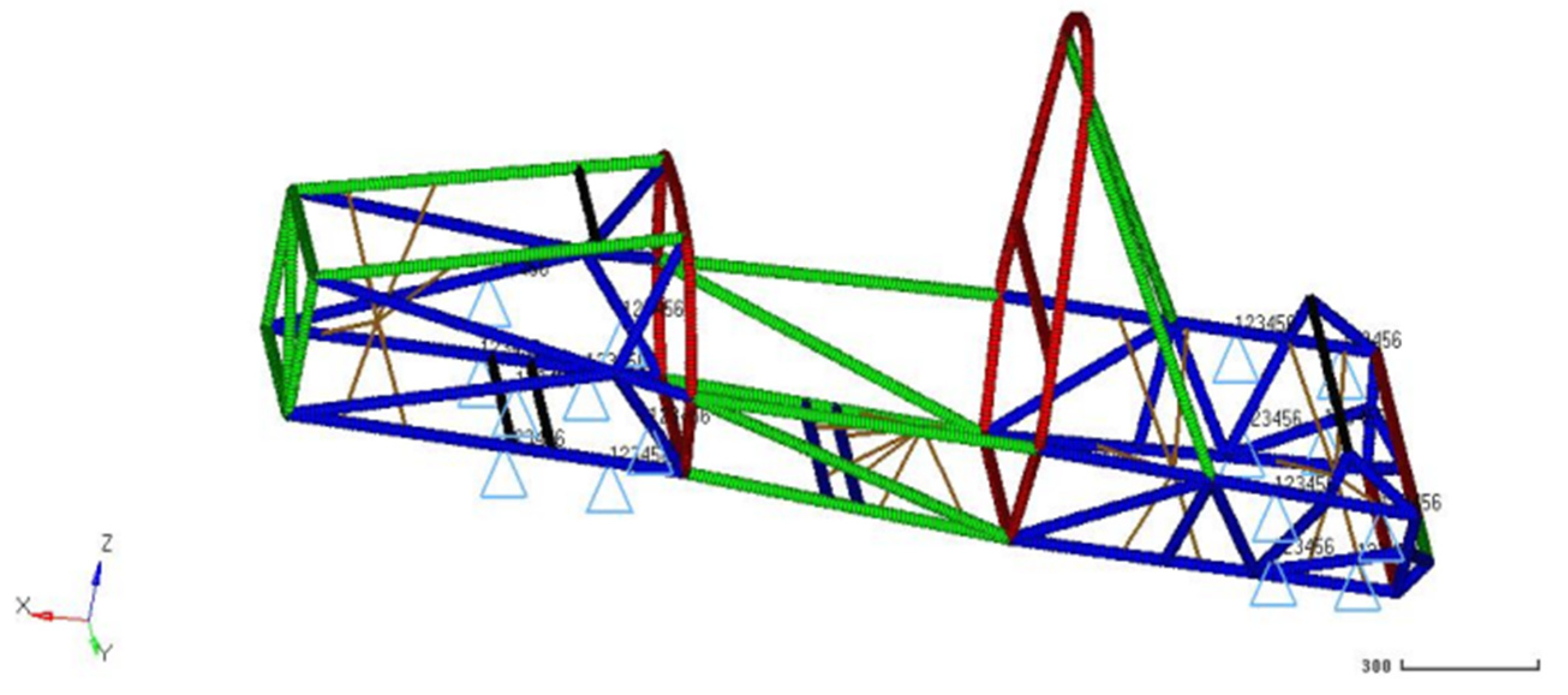
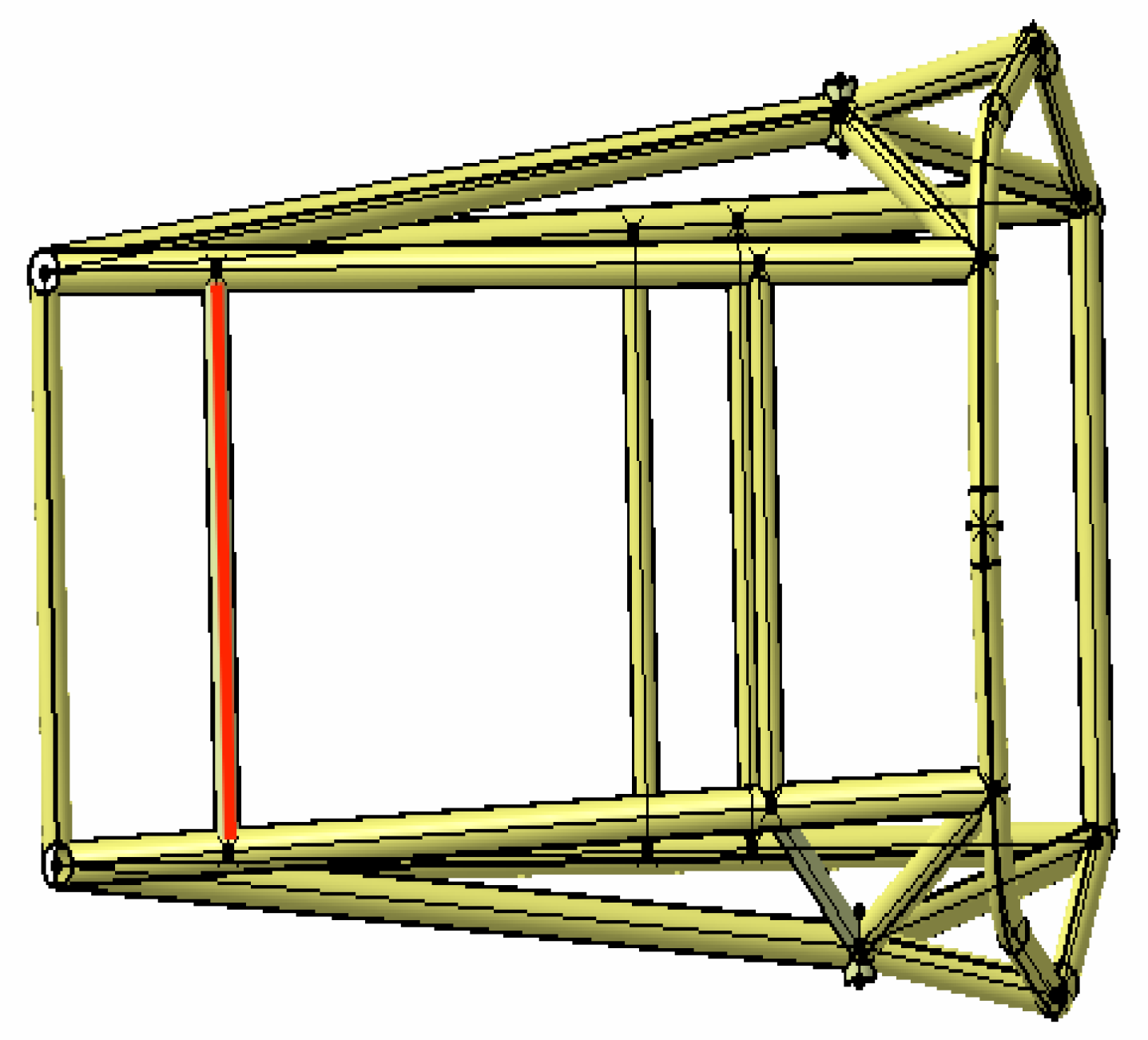
The established finite element model of the vehicle frame is shown in Figure 2.
Figure 2.
Finite Element Model of Vehicle Frame.
Figure 2.
Finite Element Model of Vehicle Frame.
1.3. Working condition analysis
1.3.1. Bending conditions
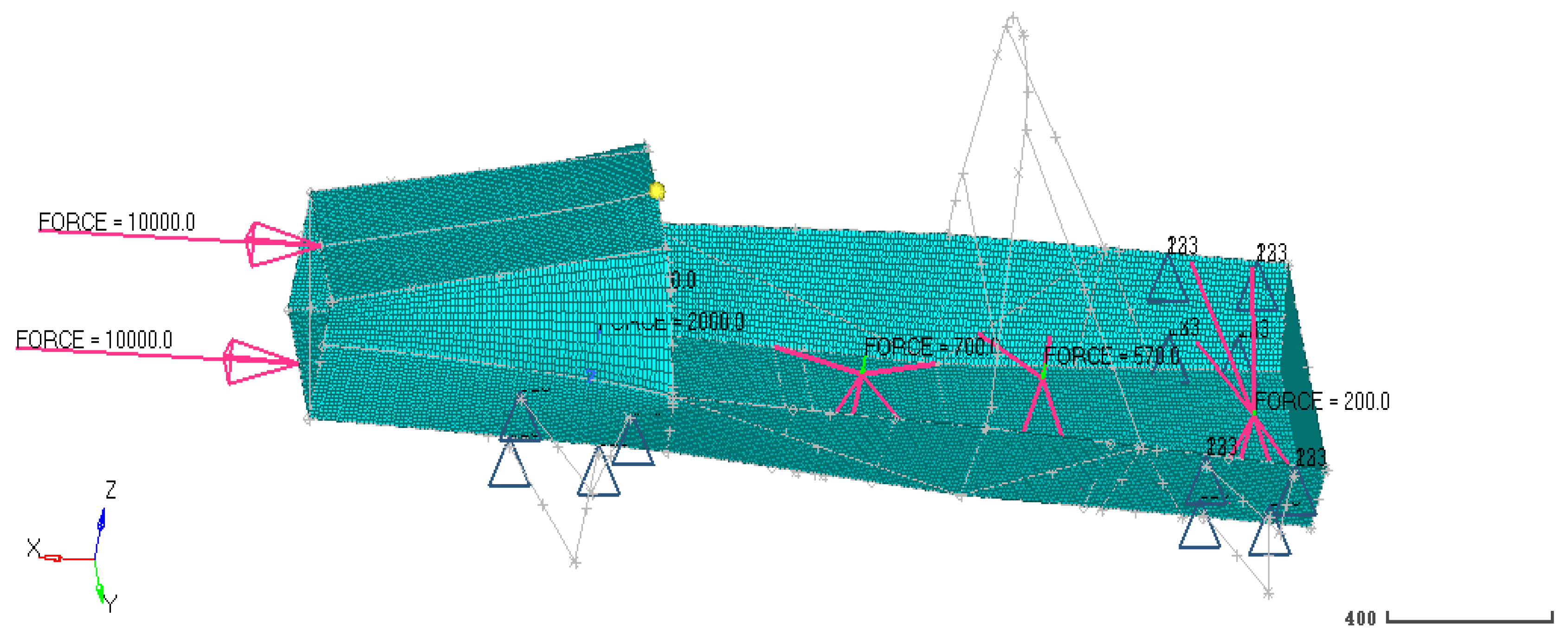
The bending condition is to analyze the strength and stiffness of a racing car when all four wheels land simultaneously under full load, mainly simulating the stress distribution and deformation of a racing car driving at a uniform speed on a good road surface. Establish constraint conditions, with a frame weight of approximately 45kg, and represent the vehicle weight by applying a gravity field. Set the gravity acceleration to 9.8N/kg, and input N3 to -1, indicating that the gravity field is loaded in the negative direction of the z-axis. Due to the relatively high speed under bending conditions, the dynamic load coefficient is taken as 2.0. Constrain the left and right front suspensions dof3, and constrain the left and right rear suspensions dof1, dof2, and dof3. Among them, dof1, dof2, and dof3 represent linear degrees of freedom along the x, y, and z axes, while dof4, dof5, and dof6 represent angular degrees of freedom around the x, y, and z axes.
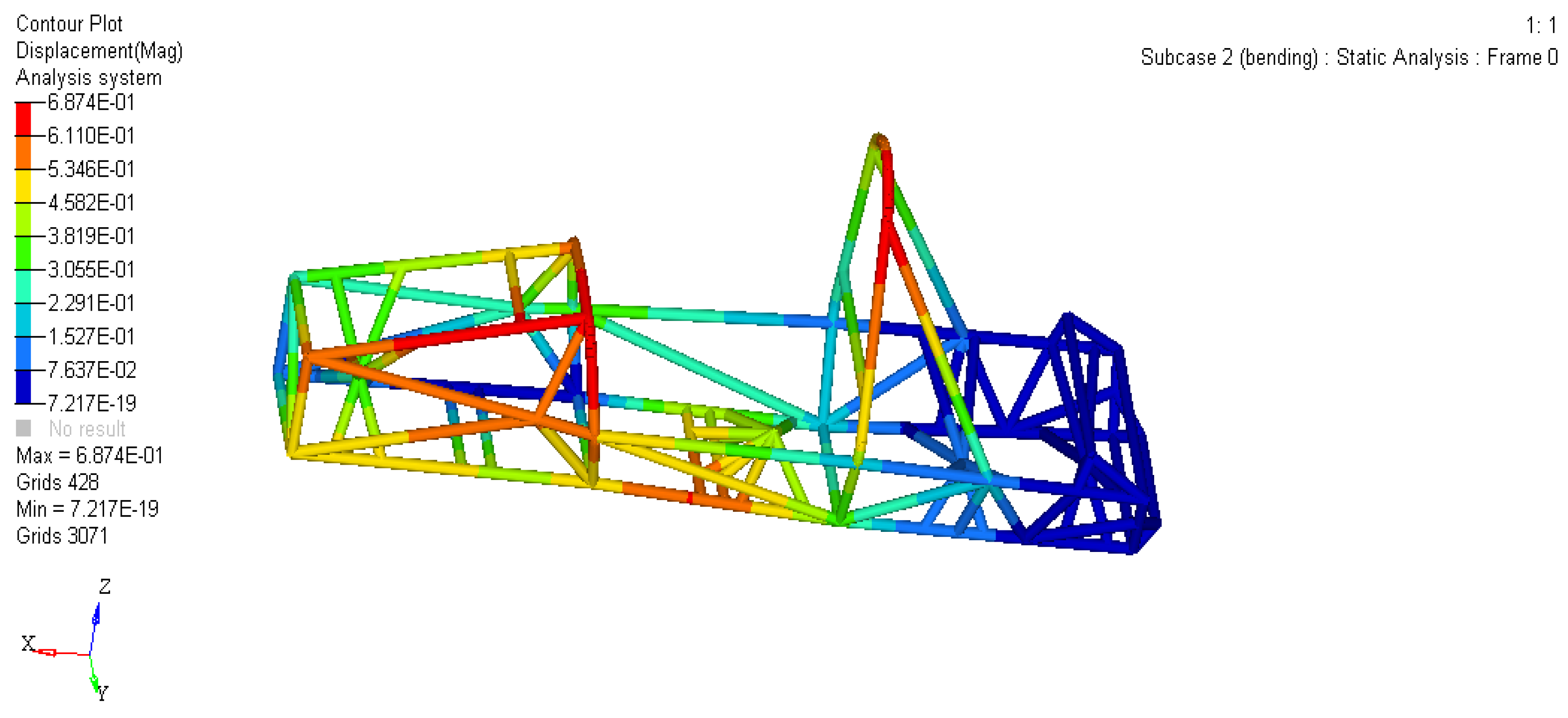
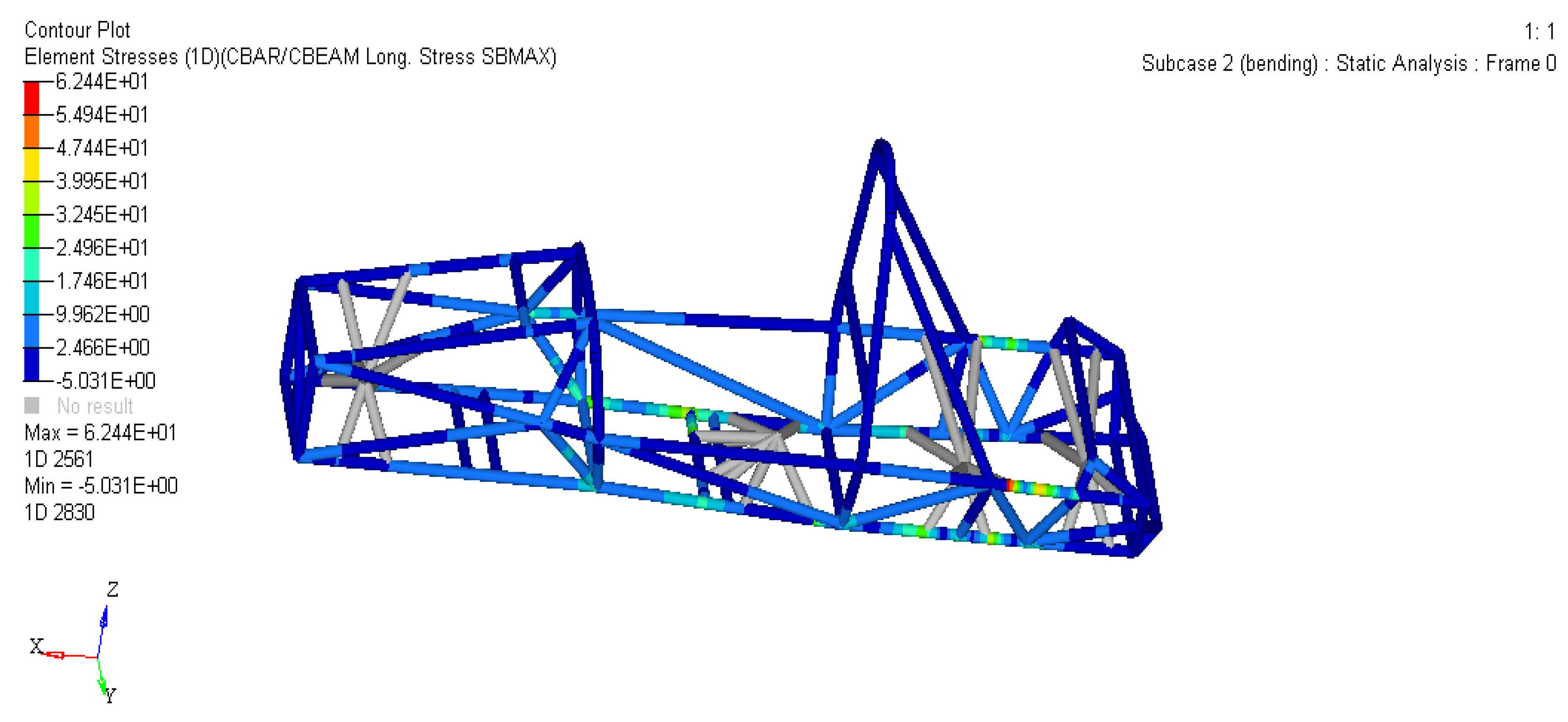
As shown in Figures 4 and 5, the maximum strain of the frame is 0.6874 mm, which appears at the connection of the front ring slant support, the front ring, and the main ring and the main ring slant support (i.e. the red area); The maximum stress of the frame is 62.44 MPa, which occurs not far from the connection point between the main ring slant support and the upper main ring slant support support rod.
Figure 4.
Displacement cloud diagram of the frame under bending conditions.
Figure 4.
Displacement cloud diagram of the frame under bending conditions.
Figure 5.
Stress cloud diagram of the frame under bending conditions.
Figure 5.
Stress cloud diagram of the frame under bending conditions.
1.3.2. Emergency braking conditions
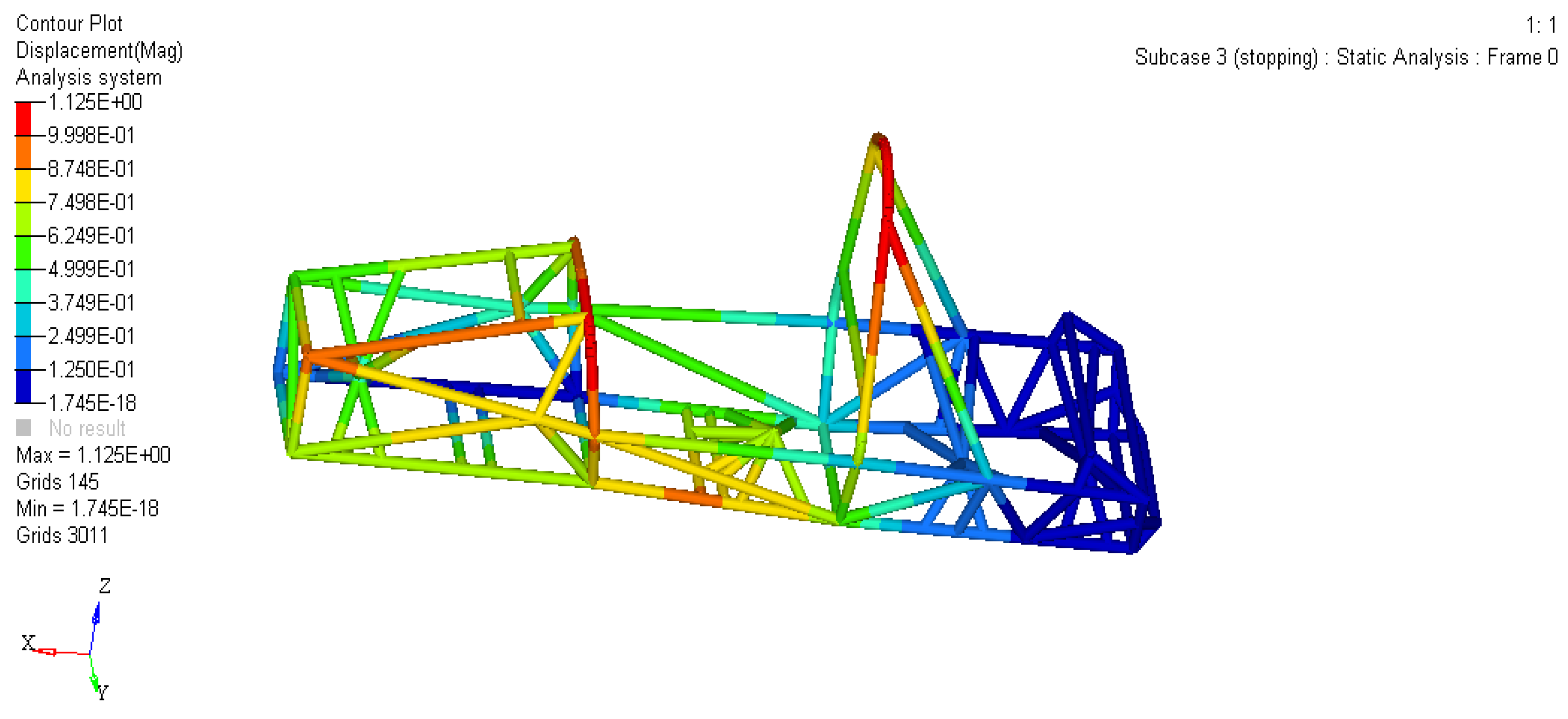
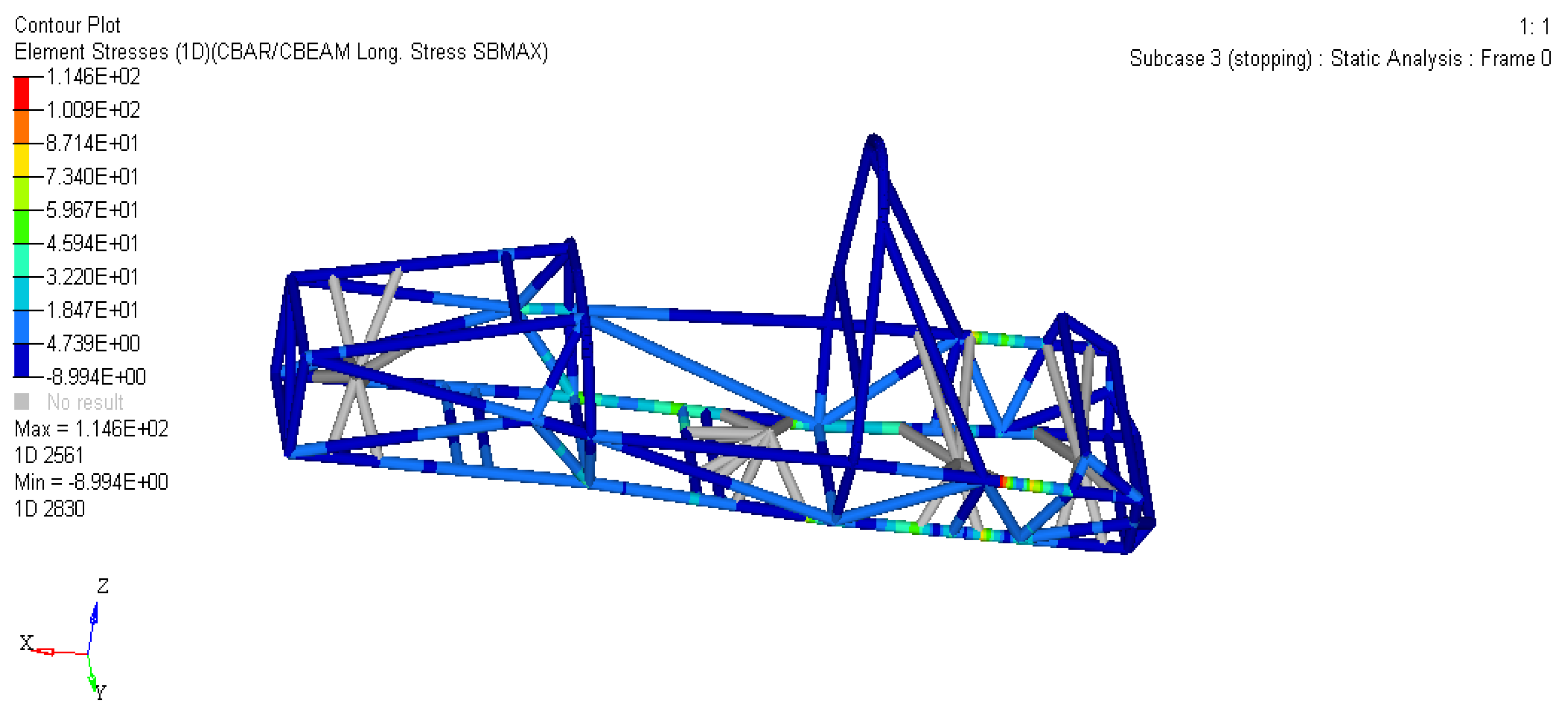
When a racing car brakes, the frame not only bears the same static load as the bending condition, but also receives the longitudinal inertia force generated by the braking force at the contact point between the tire and the ground. Here, the dynamic load coefficient is taken as 2.0, and the braking deceleration is 1.4 g. The constraint conditions are the same as those of the full load bending condition.
As shown in Figures 6 and 7, the maximum deviation of the frame is 1.125 mm, which occurs at the connection between the front ring and the front ring support point, as well as at the connection between the main ring and the main ring support point. The maximum pressure of the frame is 114.6 MPa, which is not far from the connection between the main ring slant support and the upper main ring slant support.
Figure 6.
Displacement Cloud Map of the Frame under Braking Conditions.
Figure 6.
Displacement Cloud Map of the Frame under Braking Conditions.
Figure 7.
Stress cloud diagram of the frame under braking conditions.
Figure 7.
Stress cloud diagram of the frame under braking conditions.
1.3.3. High speed turning conditions
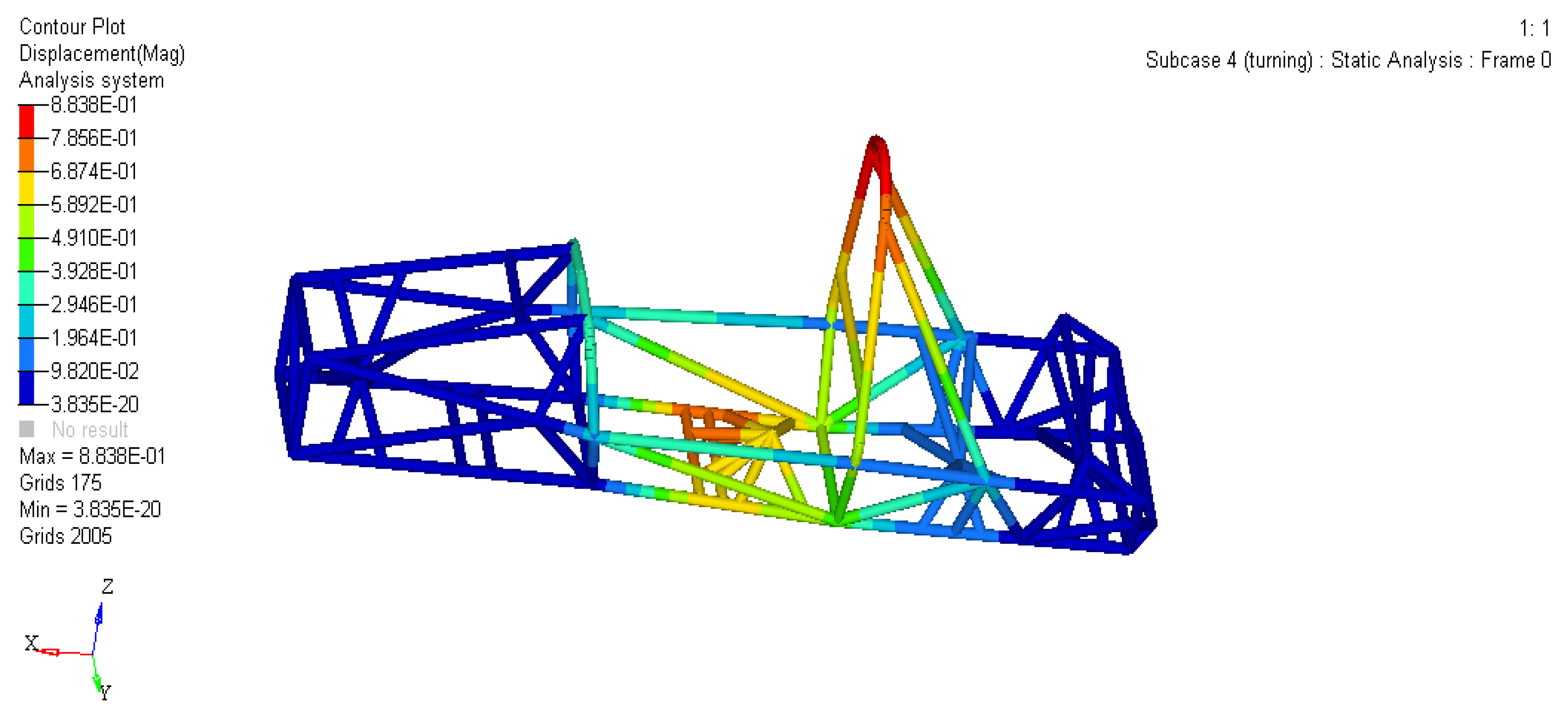
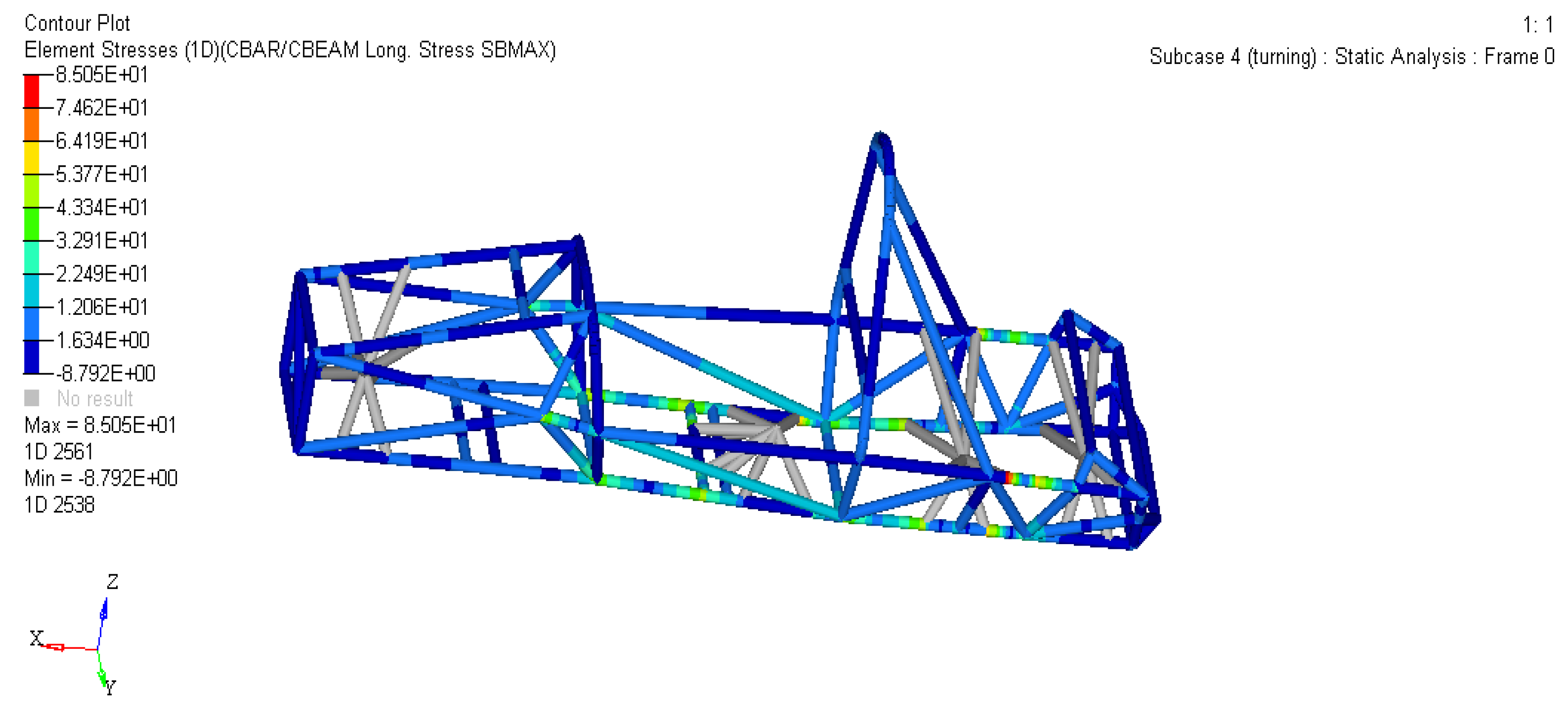
When a racing car enters a corner, the frame not only bears the same static load as the bending condition, but also undergoes lateral inertia force under the action of centrifugal force. The magnitude of this inertia force depends on the vehicle speed, turning radius, and road angle, etc. This condition corresponds to an eight figure surround test. Taking a left turn as an example, the dynamic load coefficient is 1.5 and the centripetal acceleration is about 1g. Constrain the left front suspension equivalent points dof1 and dof3, constrain the right front suspension equivalent points dof2 and dof3, and constrain the left and right rear suspension equivalent points dof3.
As shown in Figures 8 and 9, the maximum offset of the frame is 0.8838 mm, which occurs at or above the connection point between the main ring slant support and the main ring. The maximum pressure of the frame is 85.05 MPa, near the lower end of the main ring slant support.
Figure 8.
Displacement Cloud Map of the Frame under Turning Conditions.
Figure 8.
Displacement Cloud Map of the Frame under Turning Conditions.
Figure 9.
Stress cloud diagram of the frame under turning conditions.
Figure 9.
Stress cloud diagram of the frame under turning conditions.
1.4. Analysis of Frame Structure Stiffness
The static stiffness of the frame mainly includes bending stiffness and torsional stiffness, which have a significant impact on the strength, vibration, noise, and fatigue characteristics of the frame. Generally speaking, the greater the stiffness of the frame, the greater its strength. For FSC racing frames, their strength is usually guaranteed by rules, but their stiffness varies greatly. Therefore, it is necessary to analyze the stiffness of the frame, especially the torsional stiffness.
1.4.1. Bending stiffness analysis
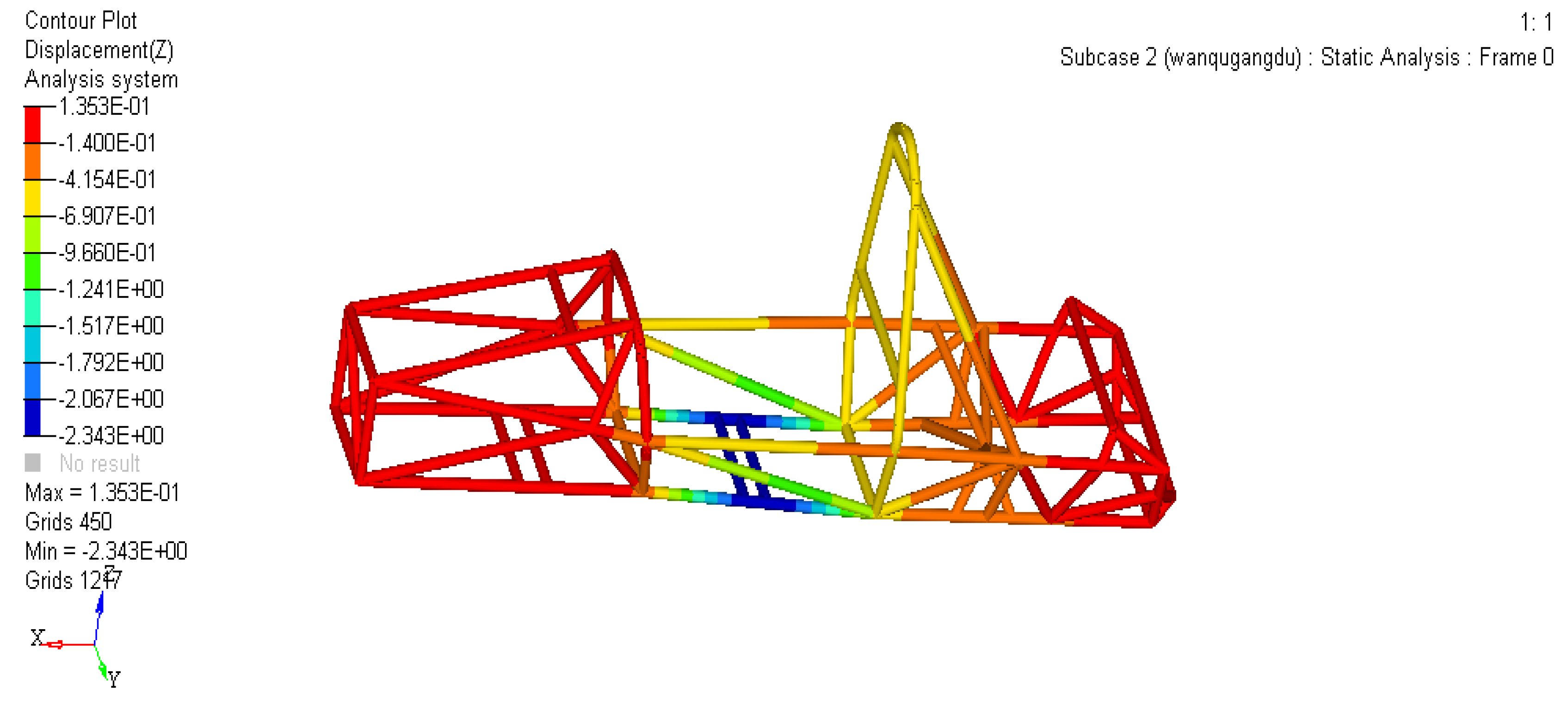
On the basis of the finite element model of the frame bending condition, remove the driver’s mass and retain the motor’s mass. At the middle of the longitudinal beams on both sides of the cockpit bottom, a concentrated force F=1000 N of equal magnitude and in the same direction (negative direction of the Z-axis) is applied, and the constraint conditions and other settings are the same as the bending condition.
The solution result is shown in Figure 10, with a deflection value of 0.1353 mm in the vertical direction; Calculate the bending stiffness EI=F/Z=7390 N/mm according to the formula (where F represents the bending load, Z represents the larger deflection value of the frame in the vertical direction, and EI represents the bending stiffness).
Figure 10.
Displacement variables of the frame in the z-axis direction.
Figure 10.
Displacement variables of the frame in the z-axis direction.
1.4.2. Torsional stiffness analysis
Constrain the left rear suspension dof1 and dof3, constrain the right rear suspension dof1, dof2, and dof3, and release all dofs from the left and right front suspensions. Apply a pair of equal and opposite concentrated forces F (left Z, right Z) to the equivalent points of the left and right front suspensions, where F=1000N.
The solution results in a significant deviation of 3.502 mm; Subsequently, the torsion angle between the two equivalent points of the front suspension was measured, and the result was 0.333 ° with a spacing of 490.008 mm. According to the formula K=T/ θ Calculate the torsional stiffness of the frame, with a value of 1471.5 N · m/°, where K represents the torsional stiffness, T θ After reviewing foreign design materials, it was found that the torsional stiffness range of the racing car is basically within the range of 1000-4000 Nm/° [
21], indicating that the torsional stiffness design of the frame is reasonable.
1.5. Modal Analysis
1.5.1. Modal Analysis Theory
Modal analysis is the process of obtaining the modal vibration characteristics of a modal construction system, with each mode including its inherent damping coefficient, modal frequency, modal shape, and other key parameters. The process of obtaining these basic parameters is called modal analysis. Based on modal analysis, on the one hand, the degree of influence between the supported component and the supporting component can be evaluated; On the other hand, as an evaluation indicator of dynamic characteristics, its modal frequency and mode shape can serve as a reference for dynamic changes. Therefore, conducting modal analysis on the frame is particularly important [
22].
1.5.2. Calculation process of frame mode
(1) Establish a finite element model of the structure
(2) Set solution methods and control parameters
(3) Create and edit a load collector, create a working load step, and set incentives at the same time
(4) Extracting Modal Results
(5) As shown in
Table 1, calculate the lower order modal frequencies and modal shapes of the frame based on the calculation. Among them, the frequency before the first mode is lower than 1Hz, which belongs to six degrees of freedom rigid mode in free mode analysis. Therefore, considering extracting the first order from the mode greater than 1Hz, the lowest first order frequency obtained is about 36Hz, while the general road excitation is around 20Hz, thus avoiding the natural frequency of the frame and preventing resonance.
3. Conclusions
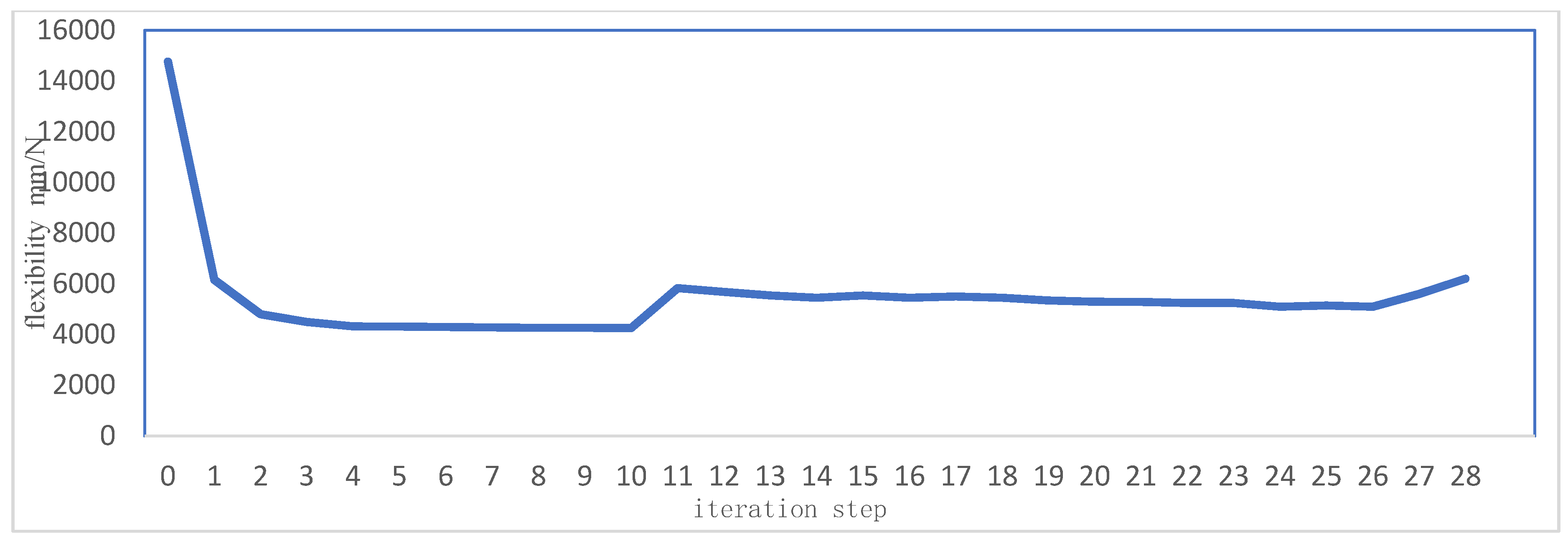
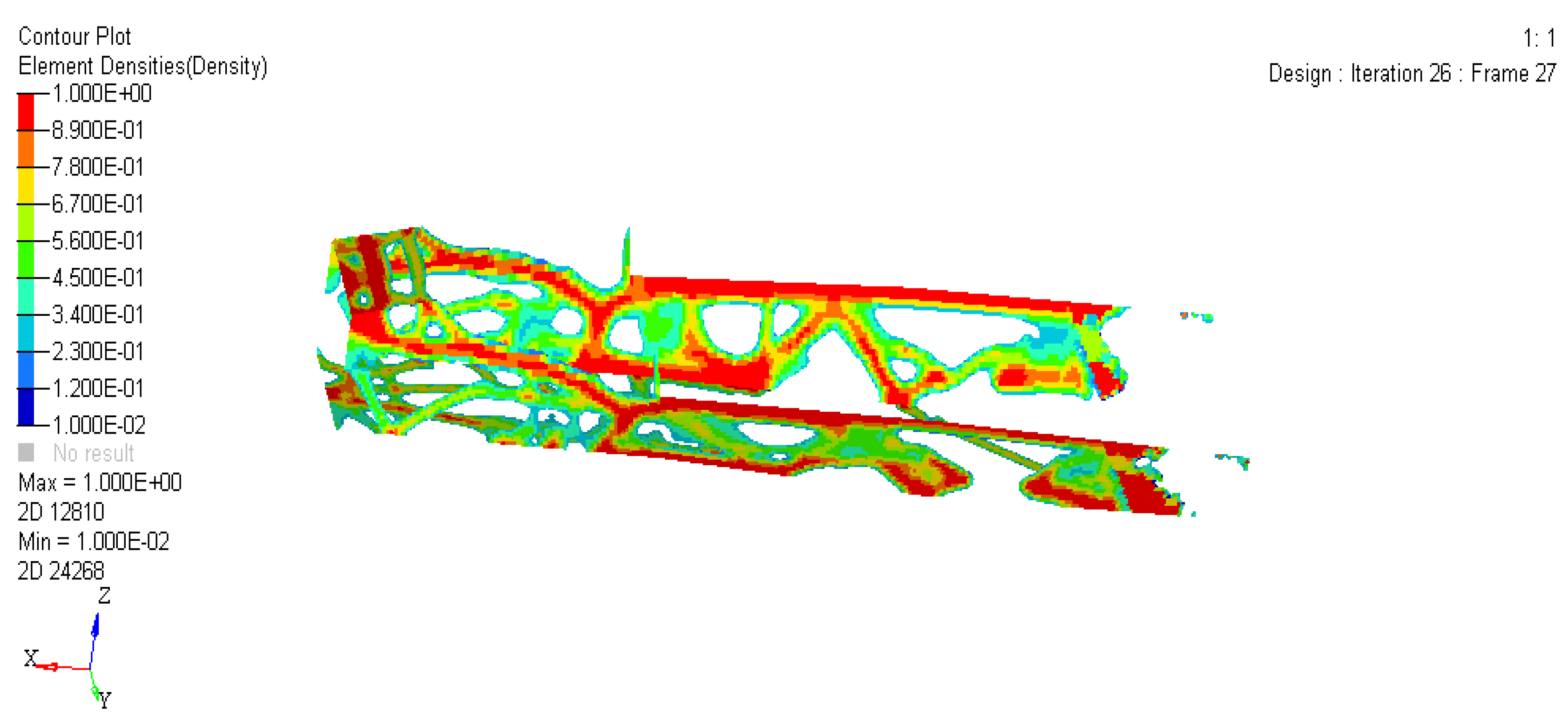
In this paper, according to the rules of the competition, the three-dimensional geometric modeling of the frame is preliminarily established by CATIA V520 software. According to the force characteristics of the frame under braking, bending and turning conditions, the offset and stress distribution information of the frame under various conditions are obtained by using Hyperworks software, and the bending stiffness and torsional stiffness are measured, and the free mode analysis of the frame is carried out.
Then, the global topology optimization based on variable density method is proposed, and the distribution of materials is obtained from the analysis results. Then, the sensitivity analysis based on the adjoint variable method is proposed, and the influence factors of design variables are obtained. The size of the frame is optimized according to the weight, which reduces the weight of the frame. From this, the final version of the frame is designed. Finally, the performance of the existing frame is compared with the data of the original frame, and the conclusion that the performance of the frame is better than the original frame is reached, Thus achieving lightweight design.