Prerpints.org logo
Preprint
Article

Analysis and Implementation of a Frequency Synthesis Based on Dual Phase-Locked Loops in Cs Beam Clock

Altmetrics

Downloads

143

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 July 2023

Posted:

13 July 2023

You are already at the latest version

Alerts
Abstract
The frequency synthesizer is a critical component in Cs beam clock technology. In this paper, we present a demonstration of a direct microwave frequency-synthesis chain for a cesium-beam atomic clock, which utilizes frequency multiplication and a dual-phase-locked loop mode. A detailed analysis of the frequency-synthesis chain is conducted, and a mathematical model is established. The phase settling time and system stability are simulated, measured, and verified. The experimental results for the phase settling time align with the simulation outcomes. The phase settling time can be adjusted within the range of 644.5 µs to 1.5 ms, and the absolute phase noise values are -63.7 dBc/Hz, -75.7 dBc/Hz, -107.1 dBc/Hz, and -122.5 dBc/Hz at 1 Hz, 10 Hz, 1 kHz, and 10 kHz offset frequencies, respectively. Additionally, the Ramsey fringes are detected, and the Allan deviations of the 10 MHz output from the cesium-beam atomic clock are measured to be 2.99×10−12 at 1s and 8.02×10−14 at 10,000 s.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Atomic clocks stabilize the frequency of an oscillator with high-frequency stability by aligning it to an atomic transition line[1,2,3,4]. Due to their exceptional frequency stability, atomic clocks are increasingly vital in various applications, including synchronization, precise timekeeping, information infrastructures, and fundamental physics research[5,6,7,8,9,10]. Cesium-beam clocks are widely used in these fields because of their advantages, such as good long-term frequency stability, compact structure, low power consumption, and ease of operation[11,12,13,14]. The frequency-synthesis chain, a crucial component of cesium-beam clocks, generates a highly pure microwave signal at 9.192 631 770 GHz to induce atomic magnetic resonance in a cesium-beam tube (CBT). The quality of the microwave signal directly influences the performance of the cesium-beam clock[15,16].
In recent decades, extensive research has been conducted to improve the frequency synthesis techniques used in cesium-beam clocks, focusing on enhancing stability, accuracy, and reliability. One research area has aimed at improving the stability and accuracy of the frequency synthesis process by exploring techniques to reduce phase noise, spurious signals, and other sources of frequency instability[17,18,19,20]. Strategies include the use of noise reduction techniques, such as phase-locked loops (PLLs) and digital signal processing algorithms, to enhance the precision and stability of the generated frequencies[21,22]. Additionally, efforts have been made to enhance the long-term stability of cesium-beam clocks[14,23]. This involves studying the aging characteristics of frequency synthesis components and developing compensation methods to mitigate the effects of aging on frequency accuracy over extended periods. The Allan deviation, which measures the stability of an atomic clock, is particularly sensitive to the noise present in the local oscillator (LO) signal[24,25,26].
Richard K. Karlquist, Leonard S. Cutler, and Robin P. Giffard observed that for slow modified modulation signals, adjustments in frequency and amplitude steps are necessary to accurately investigate the central and adjacent lobes of the principal Ramsey lines. Achieving optimal time utilization of the measurement requires accurate settling of the microwave signal phase within 1.5 ms. Once the frequency and amplitude are settled, the individual steps only take an additional 3 ms to complete, maximizing time utilization[15,16]. Currently, no literature analyzing the phase settling time of the frequency-synthesis chain has been found.
This paper presents the development of a microwave frequency-synthesis chain, based on frequency multiplication and dual-phase-locked loop circuits, that converts a 10 MHz reference clock to a 9.192 631 770 GHz output for a cesium-beam atomic clock. The phase settling time of the microwave frequency-synthesis chain is evaluated through theoretical analysis and simulation of the dual-PLL system. The phase settling time can be reduced by appropriately adjusting the gain of the PLL. By continuously adjusting the loop filter gain of the PLL, the measured phase settling times range between 644.5 us and 1.5 ms. Optimizing the system parameters allows for improved frequency stability.

2. Schematic and Experimental Setup og the Frequency-Synthesis Chain

Figure 1 presents the block diagram of the frequency-synthesis chain, which utilizes a dual-PLL circuit. The primary purpose is to function as a dual-loop jitter cleaner (dual-loop mode) when a reference clock with accurate frequency is employed to generate an output clock with ultra-low jitter. The dual-loop mode helps maintain a high phase-detector frequency and loop bandwidth in the clock generation PLL, especially when the greatest common divisor of the reference clock frequency and the output clock frequency is small. This approach prevents a low phase-detector frequency and minimizes the output phase noise of the clock.
In Figure 1, a 20× frequency multiplier is used to multiply the 10 MHz reference clock to 200 MHz. Then, the 200 MHz clock is phase-detected with the clock output from the 200 MHz Oven-controlled crystal oscillators (OCXO) in the first phase detector (PD1) at a frequency of 200 MHz. The output signal from the 200 MHz OCXO drives a frequency comb generator to produce harmonics of 200 MHz. In the second PLL (PLL2), the 46th harmonic of 200 MHz is selected by a narrow-band bandpass filter, and then the 9.2 GHz is mixed in the second phase detector (PD2) with another 9.192 GHz produced by the dielectric resonant oscillator (DRO). By a direct digital synthesis (DDS) module, a 7.368 MHz signal is generated. Then, the 7.368 MHz and the 9.192 GHz are compared in PD2. When the two PLLs are both phase-locked, a precise frequency at 9.192 631 770 GHz is ready. Considering the frequency precision error of 10 MHz reference, the final output signal will have a certain frequency deviation.
Figure 2 illustrates a more detailed architecture diagram of the frequency-synthesis chain, consisting of four main parts. Part (1) involves a 10 MHz OCXO source with ultralow phase noise. In Part (2), a 200 MHz clock from the 20× frequency multiplier is filtered and amplified before being compared with the 200 MHz OCXO output clock in PD1. The phase error signal generated by PD1 is filtered and then fed back to the proportional–integral controller to drive the 200 MHz OCXO. The signal from the 200 MHz OCXO output is split into two paths using a coupler. In the first path, the output clock is amplified with a low-noise amplifier, filtered, and sent to PLL2 as the reference clock. In the other path, the 200 MHz clock is amplified, filtered, and used to drive a comb generator. The 46th harmonic of the comb generator’s output is band-pass filtered, amplified with a microwave amplifier in part (3), and then sent to the mixer in part (4). In PLL1, a splitter is used to generate two 200 MHz signals, with one of them serving as the sampling rate of the direct digital synthesis (DDS, AD9854) to generate a 7.368 230 MHz clock[27]. In part (4), the 9.2 GHz microwave generated by the comb generator is mixed with the 9.192 GHz microwave generated from the DRO, and the resultant signal is passed through a power splitter. This process generates a 7.368 230 MHz clock. The two 7.368 230 MHz clocks are compared with each other to produce a phase error signal[28,29]. The phase error signal is then low-pass filtered, conditioned by the PID2, and used to drive the DRO[23]. When the frequency-synthesis chain is in a phase-locked state, the 9.192 GHz microwave is directed to an amplitude control module to excite atomic transitions in the CBT.
The phase noise of the output in the loop bandwidth of a PLL is primarily caused by the input reference clock, following the deterioration according to the 20 × log N rule. Outside of this bandwidth, the phase noise performance is mainly determined by the internal voltage-controlled oscillator (VCO) of the PLL. In Figure 2, PLL1 employs a narrow-loop bandwidth of 150 Hz to preserve the frequency accuracy of the reference signal while suppressing noise from higher offset frequencies. The 200 MHz OCXO has an output power of approximately +10 dBm, a tuning sensitivity of around 50 Hz/V, and a voltage tuning range of 0V to 8V. Similarly, the DRO operates at an output power of approximately +15 dBm, a tuning sensitivity of about 2.2 MHz/V, and a voltage tuning range of 0V to 9V. It is important to note that all input and output signals are matched to 50 Ω impedance.
Given the limitations in frequency accuracy of the 10 MHz reference clock, it is essential for the final microwave signal to be precisely adjustable within a range of approximately ±1 kHz, with a high frequency resolution of less than 0.1 Hz. To achieve this level of precision, the DDS module assumes a critical role within the frequency synthesis chain. In this structure, the DDS module is integrated to generate a 7.368 MHz clock with a remarkable frequency resolution of up to 0.7 µHz[23,28]. Accurate frequency matching holds significant importance in the design of highly stable atomic clocks[30,31].

3. Theoretical Analysis and Simulation of the Frequency-Synthesis Chain

3.1. Analysis of the model for the PLLs

From control theory, the PLL phase-transfer function H(s) can be defined, which establishes a relationship between the input reference clock and the output of the PLL. Figure 3 depicts a simplified configuration based on the architecture of the frequency-synthesis chain shown in Figure 2. In an analog PLL circuit, the mixer primarily functions as a phase detector.
In PLL1, as illustrated in Figure 3, the 10 MHz reference clock undergoes direct multiplication by a factor of M 1 to obtain a 200 MHz clock through the use of two cascaded frequency multipliers. The resulting clock is then compared with the 200 MHz clock generated from the 200 MHz OCXO in PD1. Thus, the phase argument of the 200 MHz clock Θ m 1 ( s ) is given by
Θ m 1 ( s ) = M 1 Θ i ( s ) ,
where Θ i ( s ) represents the phase argument of the 10 MHz reference clock. U e 1 ( s ) is defined as the phase error signal generated by PD1. In the complex frequency domain, U e 1 ( s ) can be expressed as:
U e 1 ( s ) = k d 1 Θ e 1 ( s ) = k d 1 ( Θ o 1 ( s ) − Θ m 1 ( s ) ) ,
where k d 1 denotes the detector gain of PLL1. Θ e 1 represents the phase argument of the error signal generated by PD1, while Θ o 1 ( s ) is the phase argument of the 200 MHz OCXO output. Equation (2) presents a linearized model of PD1.
The output from the 200 MHz OCXO is divided into two paths by a coupler. The main path is utilized directly, while the other path is amplified, low-pass filtered, and further divided into two additional paths. One of these paths serves as the sampling rate of the DDS, while the other is fed back to PD1. In Figure 3, the transfer function of the first loop filter is defined as F 1 ( s ) . Hence, the error signal of the filter can be expressed as
U f 1 ( s ) = F 1 ( s ) U e 1 ( s ) ,
where U f 1 ( s ) represents the error signal from the first low-pass filter (LPF1) in PLL1, which is employed to tune the 200 MHz OCXO. In the complex frequency domain, the output signal from the 200 MHz OCXO is proportional to the control signal and can be given as
Θ o 1 ( s ) = k o 1 s U f 1 ( s ) ,
where k o 1 represents the gain of the 200 MHz OCXO. When the phase error signal generated by PD1 is sufficiently small, the output signal from the mixer can be approximated by its argument. The transfer function G 1 ( s ) is defined as the first loop gain in Figure 3. Based on Eqs. (2)–(4), G 1 ( s ) can be expressed as
G 1 ( s ) = Θ o 1 ( s ) Θ e 1 ( s ) = k d 1 k o 1 F 1 ( s ) s ,
Furthermore, H 1 ( s ) in Figure 3 relates the input 10 MHz reference clock to the 200 MHz OCXO output. H 1 ( s ) can be expressed as
H 1 ( s ) = Θ o 1 ( s ) Θ i 1 ( s ) = Θ o 1 ( s ) Θ e 1 ( s ) / M 1 = k d 1 k o 1 M 1 F 1 ( s ) s + k d 1 k o 1 F 1 ( s ) ,
Equations (5) and (6) represent the mathematical model of PLL1. Assuming PLL1 is phase-locked in the time domain, the 200 MHz output signal u o 1 can be expressed as
u o 1 ( t ) = a 1 c o s ( ω 1 t + θ o 1 ) ,
where a 1 represents the amplitude argument of the signal, and ω 1 and θ o 1 are the radian frequency and initial phase of the 200 MHz OCXO output, respectively.
Figure 3 illustrates the utilization of the 200 MHz clock to drive a comb generator, generating harmonics of 200 MHz. We denote the order of these harmonics as M 3 , and the M 3 order of the 200 MHz harmonic as u m 3 ( t ) . Simultaneously, another 200 MHz clock serves as a sampling clock for the DDS (AD9854) to produce a 7.378 23 MHz clock. We denote the division factor of the DDS module as M 2 , and the signal derived from the DDS module as u m 2 ( t ) . The calculations for these two signals are as follows
u m 2 ( t ) = a m 2 c o s 1 M 2 ω 1 t + 1 M 2 θ o 1
u m 3 ( t ) = a m 3 c o s ( M 3 ω 1 t + M 3 θ o 1 ) ,
where a m 2 and a m 3 represent the amplitude arguments of the respective signals.
In PLL2, the center frequency of the dielectric resonant oscillator (DRO) is denoted as ω m 2 , and u 0 ( t ) represents the output signal of the DRO. For our design, the center frequency ω m 2 is approximately 9.192 GHz. In the time domain, u 0 ( t ) is given by the equation
u 0 ( t ) = a 0 c o s ( ω 2 t + θ 0 ) ,
where a 0 represents the amplitude and θ 0 is the initial phase of the DRO. The signal ω 2 is mixed with the 9.2 GHz signal from the comb generator to generate a clock at 7.368 MHz. This 7.368 MHz clock is then compared with the 7.378 MHz signal generated from the DDS. We define the output signal generated by the mixer as u p ( t )
u p ( t ) = a 0 a m 3 2 c o s ( ω 2 + M 3 ω 1 ) t + ( φ 0 + M 3 θ o 1 ) + a 0 a m 3 2 c o s ( ω 2 − M 3 ω 1 ) t + ( φ 0 − M 3 θ o 1 ) ,
Equation (11) describes u p ( t ) as having two parts. The first part is a higher-frequency signal, which is eliminated by a low-pass filter (LPF). The latter part represents a 7.368 MHz signal, which is compared with the 7.378 MHz signal from the DDS in PD2. The phase argument of the error signal generated by PD2 is denoted as θ e 2 ( s ) . In the complex frequency domain, based on Eqs. (7)-(11), the phase error signal θ e 2 ( s ) of PD2 can be expressed as
θ e 2 ( s ) = θ 0 ( s ) − M + a 0 a m 3 2 c o s ( ω 2 − M 3 ω 1 ) t + ( φ 0 − M 3 θ o 1 ) ,
where θ 0 ( s ) represents the phase argument of the DRO output. The transfer function G 2 ( s ) is defined as the loop gain of PLL2 shown in Figure 3. Thus, the phase argument of the DRO output Θ 0 ( s ) can be expressed as
Θ o ( s ) = k o 2 s U f 2 ( s ) = k o 2 s F 2 ( s ) k d 2 Θ e 2 ( s ) = k o 2 s F 2 ( s ) k d 2 Θ o ( s ) − M 3 + 1 M 2 Θ o 1 ( s ) ,
In Equation (13), k d 2 represents the detector gain of the DRO, k o 2 is the DRO gain, and F 2 ( s ) is the transfer function of the second loop filter in PLL2. Consequently, the phase-closed loop transfer function F 2 ( s ) of PLL2 can be derived as
H 2 ( s ) = Θ o ( s ) Θ o 1 ( s ) ,
Based on the aforementioned analysis, the phase-closed loop transfer function of the microwave frequency-synthesis chain H ( s ) can be expressed as
H ( s ) = H 1 ( s ) H 2 ( s ) = k d 1 k d 2 k o 1 k o 2 M 1 M 2 M 3 F 1 ( s ) F 2 ( s ) + k d 1 k d 2 k o 1 k o 2 M 1 F 1 ( s ) F 2 ( s ) M 2 s 2 + M 2 k d 1 k o 1 F 1 ( s ) + k d 2 k o 2 F 2 ( s ) s + M 2 k d 1 k d 2 k o 1 k o 2 F 1 ( s ) F 2 ( s ) ,
In Figure 4, an active loop filter is utilized, with a transfer function gain of k p ( 1 / T i + 1 ) , where k p and T i represent the gain and integration time of the loop filter, respectively. In this paper, a first-order passive LPF is employed, and its transfer function can be expressed as L ( s ) = 1 / ( τ s + 1 ) , where τ denotes the time delay of the LPF. For our design, only the proportional gain is utilized in the proportional-integral (PI) regulator, as shown in Figure 2. Consequently, k p ( 1 / T i + 1 ) can be simplified to k p . Additionally, the transfer function mode of an active loop filter can be expressed as F ( s ) = k p / ( τ s + 1 ) . Therefore, we have
F 1 ( s ) = k p 1 / ( τ 1 s + 1 ) ,
F 2 ( s ) = k p 2 / ( τ 2 s + 1 ) ,

3.2. Simulation results

3.2.1. Transient analysis

The PLL ensures the phase alignment of the output clock with the reference clock. Although the phase of the reference clock can experience instantaneous distortion, the PLL requires a certain amount of time to adjust its phase. Thus, the phase settling time plays a crucial role in evaluating the frequency-synthesis chain[32].Simulations of H ( s ) using Eq. (15) were conducted based on the theory presented in Section 2. The parameter values used are as follows: M 1 = 20, M 2 = 200/7.368230, M 3 = 46, k d 1 = 1 V/rad, k d 2 = 1 V/rad, k o 1 = 90 Hz/V, and k o 1 = 2.2 MHz/V. Since the frequency-synthesis chain consists of two PLLs, the parameters k p and τ can be adjusted for both PLLs.
Assuming that the parameters k p 2 and τ 2 are fixed simplifies the calculation of the modulation signal gain applied in the frequency-synthesis chain. The given parameter values were substituted into Eq. (15), and the step responses of the system are depicted in Figure 5. Figure 5(a) illustrates the settling times of the phase step response for various values of k p 1 (ranging from 2 to 4 in steps of 2/3), while τ 1 remains fixed at 2 × 10 − 4 s. The settling times obtained are 1.52 ms, 1.07 ms, 822 µs, and 674 µs,respectively. For comparison, Figure 5(b) demonstrates the effect of varying τ 1 (ranging from 2 × 10 − 4 s to 8 × 10 − 4 s) while k p 1 remains fixed at 2.
The simulation results indicate that increasing k p 1 leads to a decrease in the settling time of the signal. Conversely, keeping k p 1 constant and increasing τ 1 results in an increase in both overshoot and settling time of the signal. Therefore, reducing τ 1 not only shortens the transient response duration but also suppresses phase fluctuations. However, reducing τ 1 widens the bandwidth of the active loop filter, which introduces more noise. Hence, for practical design purposes, the loop filter gain k p 1 should be appropriately increased while τ 1 is appropriately decreased.
Figure 6 demonstrates that varying parameter k p 2 has minimal effect on the settling time. Thus, the settling time of the frequency-synthesis chain is primarily determined by PLL1.

3.2.2. Stability analysis

The impact of the loop filtering parameters of PLL1 on the transient characteristics and system stability is evident from the analysis in Section 3. Bode plots illustrating the frequency domain with the application of an external modulation signal are presented in Figure 7.
Figure 7(a) indicates that, when the τ 1 parameter is fixed, increasing the loop filter gain k p 1 leads to an increase in gain margin, phase margin, and stability. Conversely, Figure 7(b) demonstrates that, when the k p 1 parameter is fixed, an increase in τ 1 results in a decrease in gain margin, phase margin, and stability. System stability is maintained when the modulation frequency is below 150 Hz (equivalent to 150 × 2 π rad/s), as the phase deviation between the stepping signal and the reference clock remains close to zero. However, when the modulation frequency exceeds 150 Hz, the phase gain starts to decrease. As the modulation frequency increases, the phase gain decays rapidly, leading to reduced system stability. Based on the simulation results, the following guidelines for setting parameters k p 1 and τ 1 are recommended:
( 1 ) Moderately increasing k p 1 optimizes settling time.
( 2 ) Parameter τ 1 should be adjusted in combination with parameter k o 1 . Appropriate reduction of parameter τ 1 enhances settling time and effectively suppresses overshoot.

4. Experimental Results and Verification

4.1. Settling time measurement

In Section 2.2, the configuration of the phase-setting measurement was simplified to a functional block, as depicted in Figure 8. A dual-channel arbitrary function generator (AFG; Tektronix AFG3022B) was employed as the phase shifter, as shown in Figure 4. Figure 8 illustrates that the arbitrary waveform generator (AWG) utilizes the 10 MHz OCXO as a reference to generate two identical 10 MHz signals, which are then used to drive the two frequency synthesizers (FSs) for generating two cesium atomic resonant frequencies at 9.192 631 770 GHz. One of the FSs proposed in this paper is denoted as FSA, while the other is a commercial microwave signal synthesizer (FSB; SMB100A, Rohde & Schwarz).
The 10 MHz signal generated by the AWG can be phase-modulated to simulate the phase step function, allowing the FSs to experience a phase step by utilizing the phase shift produced by the AWG. Phase modulation is applied to FSA to generate the phase step, while maintaining a fixed phase in FSB. Since the two 9.192 GHz signals are simultaneously phase-locked to the same 10 MHz reference clock, their phases are precisely synchronized. The two signals are compared in a mixer (Mini-circuits, ZMX-10G+), and the resulting phase error signal is recorded using a digital storage oscilloscope. In accordance with the mixer principle described in Section 3.1, the higher-frequency output from the mixer is eliminated due to the bandwidth limitation of the oscilloscope, while the lower-frequency component is retained. When the phase step signal is applied to FSA, the mixer output signal is recorded, and the settling time of the step response is measured to assess the phase-tracking and phase-settling ability.
When the phase shift signal is applied to the 10 MHz reference clock of FSA, the phase response affecting the frequency of 9.192 631 770 GHz is multiplied by 919.2. Consequently, the minimum phase shift of the AWG is 0.01 ∘ , resulting in an approximate 9.192 ∘ phase shift at 9.192 631 770 GHz. The remarkable property of the DDS in an FS, as per the DDS principle, is the agility of the phase shift. Therefore, in comparison to the phase shift time, the phase-settling time is insignificantly short and can be disregarded.
When FSA and FSB are simultaneously phase-locked to the same 10 MHz reference clock, as depicted in Figure 8, the output signal from the mixer becomes a direct current (DC) signal. We adjust the phase of FSA until the DC signal reaches its maximum negative value. The phase step is applied within the range of π , resulting in an approximate phase shift of 0.2 ∘ applied to the 10 MHz reference. The measured values are compared with the simulation results under the same conditions, as shown in Figure 9. The dotted lines represent the simulation results, while the solid lines depict the results obtained using the configuration described in Figure 8.
Figure 9 illustrates the phase step response for various values of the loop filter gain F 1 ( s ) . As the F 1 ( s ) parameter increases from 2 to 4 in steps of 2/3, the measured settling times are 1.5 ms, 1.064 ms, 825.5 µs, and 644.5 µs, respectively. The measured results align with the simulated results, providing evidence that the theoretical calculation for the transfer function of the synthesis and the experimental setup for measuring the phase step response are accurate and reasonable.

4.2. Phase noise measurement

Figure 10 presents the absolute phase noise measurements for a frequency synthesis chain consisting of a 10 MHz reference clock, 200 MHz OCXO, and DRO. The phase noise measurements were conducted using the R&S FSWP26. The 10 MHz reference clock is sourced from an OXCO. As discussed in Section 3, PLL1 and PLL2 were set with bandwidths of 150 Hz and 300 kHz, respectively. Figure 10(a) illustrates the absolute phase noises of the 10 MHz reference clock, which are measured at -123.8 dBc/Hz, -137.5 dBc/Hz, -158.5 dBc/Hz, and -165.5 dBc/Hz at 1 Hz, 10 Hz, 1 kHz, and 10 kHz offset frequencies, respectively. The output clock of the 200 MHz OCXO in its free-running state was measured at a power level of approximately +26 dBm, using a signal passed through a directional coupler and amplifier. The absolute phase noises at 1 Hz, 10 Hz, 1 kHz, and 10 kHz offsets were recorded as -56.5 dBc/Hz, -93.2 dBc/Hz, -145.3 dBc/Hz, and -163.6 dBc/Hz, respectively (see Figure 10(c)). While PLL1 is locked, the absolute phase noises of the 200 MHz OCXO signal are observed to be -97.5 dBc/Hz, -110.1 dBc/Hz, -145.0 dBc/Hz, and -163.8 dBc/Hz at 1 Hz, 10 Hz, 1 kHz, and 10 kHz offset frequencies, respectively (see Figure 10(b)). Comparing Figure 10(c) and Figure 10(b), it is evident that the phase noise performance exhibits an improvement of approximately 40 dB around the 1 Hz offset frequency at a carrier frequency of 200 MHz. In PLL1, a narrow-loop bandwidth of around 150 Hz is employed to suppress higher offset frequency phase noise while ensuring low phase-noise performance for PLL2. As a result, PLL2 can operate with a moderate loop bandwidth of 300 kHz.
The selection of the loop bandwidth for PLL2 aims to leverage the superior high-offset frequency phase-noise characteristics of the DRO and the favorable low-offset frequency phase noise of the 200 MHz OCXO. Figure 10(d) illustrates the phase noises at 9.192 GHz when the frequency synthesis chain is locked, which are measured as -63.7 dBc/Hz, -75.7 dBc/Hz, -107.1 dBc/Hz, and -122.5 dBc/Hz at 1 Hz, 10 Hz, 1 kHz, and 10 kHz offset frequencies, respectively. When the DRO operates in a free-running state, as depicted in Figure 10(e), the phase noises are recorded as -66.2 dBc/Hz and -88.3 dBc/Hz at 1 kHz and 10 kHz offsets, respectively. Notably, it can be observed from Figure 10(e) that the phase noises at 1 Hz and 10 Hz offsets and a carrier frequency of 9.192 GHz are only 0.8 dB and 2.5 dB worse than the 20 logN rule derived from the 10 MHz reference clock. Consequently, the frequency synthesis chain demonstrates favorable phase noise performance at low offset frequencies below 150 Hz.
In Figure 10(d), the phase noise plot exhibits two inflection points around the offset frequencies corresponding to the two loop bandwidths. By appropriately increasing the loop bandwidths of both PLLs, a significant improvement in the phase noise performance can be achieved for offset frequencies lower than the bandwidths. However, a higher loop bandwidth results in more accumulated noise. Therefore, both loop bandwidths in the frequency-synthesis chain should be selected appropriately.

4.3. Frequency Stability measurement

The 9.2 GHz microwave signal was directed to the Ramsey cavity, where its resonant frequency was precisely tuned to match the clock frequency. Consequently, the separated oscillatory fields were successfully employed for hyperfine transition excitation in cesium. The interaction between the atomic beam and the microwave magnetic fields took place within the vacuum-sealed CBT, as illustrated in Figure 11(a). By scanning the microwave frequency emitted by the actual microwave source (Figure 11(b)), the Ramsey fringes were detected, as shown in Figure 11(c), thereby validating the design strategy of generating highly pure microwaves.
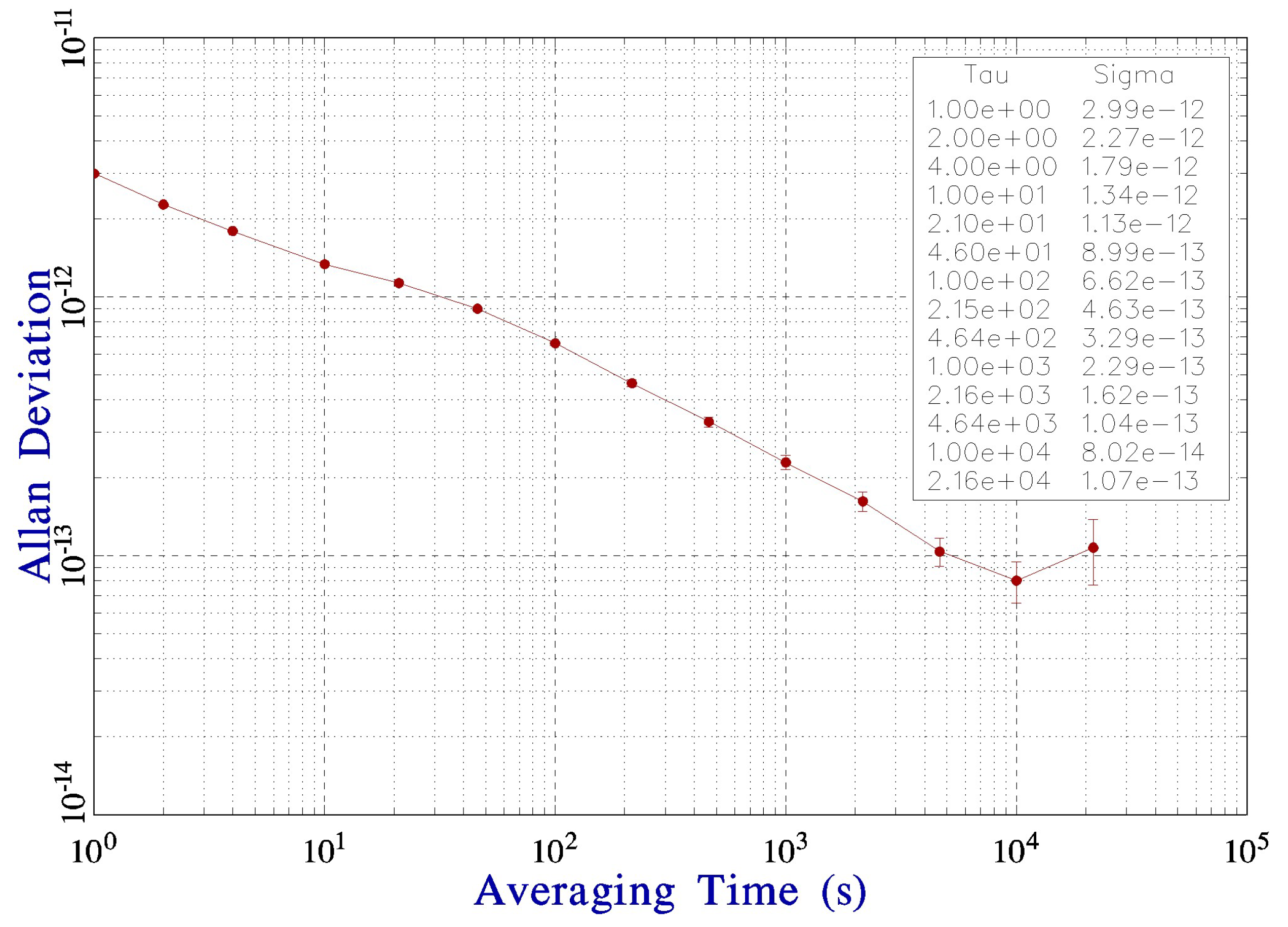
To characterize the long-term frequency stability, it is important to measure the Allan deviation of the device. We applied the frequency-synthesis chain to the cesium-beam atomic clock. In other words, the Allan deviation of 10 MHz output from the cesium-beam atomic clock was measured here. Figure 12 shows the Allan deviation over a period of 5 hours, measured by 3120A (Microsemi) at room temperature. It can be seen that the Allan deviations are 2.99 × 10 − 12 at 1s and 8.02 × 10 − 14 at 10,000 s.

5. Conclusions

We constructed a high-performance microwave frequency synthesis chain using a dual-loop PLL architecture in the context of a cesium-beam atomic clock application. This architecture provides excellent phase noise performance and a suitable setup time. PLL1 is driven by an external 10 MHz reference clock, generating a precise and low-jitter 200 MHz frequency signal that acts as the reference driver clock for PLL2. We achieve ultra-low phase noise by allowing the OCXO to dominate the phase noise at low offsets, while the phase noise of the DRO remains dominant at high offsets. The absolute phase noise levels at 9.192 631 770 GHz were measured at -63.7, -75.7, -107.1, and -122.5 dBc/Hz at 1 Hz, 10 Hz, 1 kHz, and 10 kHz offset frequencies, respectively. Additionally, we established a mathematical model and conducted an analysis of the loop theory. Notably, we conducted a theoretical analysis of the phase settling time, which was then verified through simulations and found to be consistent with the actual measurements. The settling times can be adjusted within the range of 674 us to 1.52 ms. We validated the design strategy for generating highly pure microwaves by detecting the Ramsey fringes. Finally, we measured the Allan deviations of the 10 MHz output from the cesium-beam atomic clock, which yielded values of 2.99 × 10 − 12 at 1s and 8.02 × 10 − 14 at 10,000 s. Our research findings hold practical relevance for similar scenarios.

Author Contributions

Conceptualization, D.H. and F.S.; methodology, D.H.; software, G.G. and D.H.; validation, G.G., C.L. and K.L.; formal analysis, G.G.; investigation, D.H. and G.G.; resources, F.S. and C.L.; data curation, G.G., C.L.; writing—original draft preparation, G.G.; writing—review and editing, F.S. and H.D.; visualization, G.G. and D.H.; supervision, D.H., F.S. and S.Z.; project administration, F.S.; funding acquisition, F.S. and S.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China grant number 62271109, the Equipment Advance Research Field Foundation grant numbers 315067207 and 315067206, and the Fundamental Research Funds for the Central Universities of China grant number ZYGX2021J019.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gill, P. Raising the standards. Science 2001, 294, 1666–1668. [Google Scholar] [CrossRef] [PubMed]
  2. Mohr, P.J.; Newell, D.B.; Taylor, B.N.; Tiesinga, E. Data and analysis for the CODATA 2017 special fundamental constants adjustment. Metrologia 2018, 55, 125–146. [Google Scholar] [CrossRef]
  3. Lodewyck, J. On a definition of the SI second with a set of optical clock transitions. Metrologia 2019, 56, 055009. [Google Scholar] [CrossRef]
  4. Li, C.; Sun, F.; Liu, J.; Li, X.; Ma, J.; Guo, G.; Hou, D.; Zhang, S. Non 0–0 states magnetically insensitive transitions in alkali species. Physica Scripta 2020, 95, 045402. [Google Scholar] [CrossRef]
  5. Hafele, J.C.; Keating, R.E. Around-the-world atomic clocks: Observed relativistic time gains. Science 1972, 177, 168–170. [Google Scholar] [CrossRef]
  6. McGrew, W.; Zhang, X.; Fasano, R.; Schäffer, S.; Beloy, K.; Nicolodi, D.; Brown, R.; Hinkley, N.; Milani, G.; Schioppo, M.; et al. Atomic clock performance enabling geodesy below the centimetre level. Nature 2018, 564, 87–90. [Google Scholar] [CrossRef]
  7. Gao, Q.; Zhou, M.; Han, C.; Li, S.; Zhang, S.; Yao, Y.; Li, B.; Qiao, H.; Ai, D.; Lou, G.; et al. Systematic evaluation of a 171Yb optical clock by synchronous comparison between two lattice systems. Scientific Reports 2018, 8, 8022. [Google Scholar] [CrossRef]
  8. Oelker, E.; Hutson, R.; Kennedy, C.; Sonderhouse, L.; Bothwell, T.; Goban, A.; Kedar, D.; Sanner, C.; Robinson, J.; Marti, G.; et al. Demonstration of 4.8× 10- 17 stability at 1 s for two independent optical clocks. Nature Photonics 2019, 13, 714–719. [Google Scholar] [CrossRef]
  9. Brewer, S.M.; Chen, J.S.; Hankin, A.M.; Clements, E.R.; Chou, C.w.; Wineland, D.J.; Hume, D.B.; Leibrandt, D.R. Al+ 27 quantum-logic clock with a systematic uncertainty below 10- 18. Physical review letters 2019, 123, 033201. [Google Scholar] [CrossRef]
  10. Bothwell, T.; Kedar, D.; Oelker, E.; Robinson, J.M.; Bromley, S.L.; Tew, W.L.; Ye, J.; Kennedy, C.J. JILA SrI optical lattice clock with uncertainty of. Metrologia 2019, 56, 065004. [Google Scholar] [CrossRef]
  11. Świerad, D.; Häfner, S.; Vogt, S.; Venon, B.; Holleville, D.; Bize, S.; Kulosa, A.; Bode, S.; Singh, Y.; Bongs, K.; et al. Ultra-stable clock laser system development towards space applications. Scientific Reports 2016, 6, 33973. [Google Scholar] [CrossRef] [PubMed]
  12. Antypas, D.; Tretiak, O.; Garcon, A.; Ozeri, R.; Perez, G.; Budker, D. Scalar dark matter in the radio-frequency band: atomic-spectroscopy search results. Physical Review Letters 2019, 123, 141102. [Google Scholar] [CrossRef]
  13. Sanner, C.; Huntemann, N.; Lange, R.; Tamm, C.; Peik, E.; Safronova, M.S.; Porsev, S.G. Optical clock comparison for Lorentz symmetry testing. Nature 2019, 567, 204–208. [Google Scholar] [CrossRef] [PubMed]
  14. Kazda, M.; Gerginov, V.; Lipphardt, B.; Weyers, S. Microwave Synthesis for the PTB Cesium Fountain Clocks. IEEE Transactions on Instrumentation and Measurement 2019, 69, 3711–3718. [Google Scholar] [CrossRef]
  15. Karlquist, R.K. A new RF architecture for cesium frequency standards. In Proceedings of the Proceedings of the 1992 IEEE Frequency Control Symposium. IEEE; 1992; pp. 134–142. [Google Scholar]
  16. Cutler, L.S.; Giffard, R.P. Architecture and algorithms for new cesium beam frequency standard electronics. In Proceedings of the Proceedings of the 1992 IEEE Frequency Control Symposium. IEEE; 1992; pp. 127–133. [Google Scholar]
  17. Francois, B.; Calosso, C.; Danet, J.; Boudot, R. A low phase noise microwave frequency synthesis for a high-performance cesium vapor cell atomic clock. Review of Scientific Instruments 2014, 85, 094709. [Google Scholar] [CrossRef]
  18. François, B.; Calosso, C.; Abdel Hafiz, M.; Micalizio, S.; Boudot, R. Simple-design ultra-low phase noise microwave frequency synthesizers for high-performing Cs and Rb vapor-cell atomic clocks. Review of Scientific Instruments 2015, 86, 094707. [Google Scholar] [CrossRef]
  19. Audoin, C. A limit to the frequency stability of passive frequency standards due to an intermodulation effect. IEEE Trans. Instrum Meas. 1991, 40, 121–125. [Google Scholar] [CrossRef]
  20. Ju, B.; Yun, P.; Hao, Q.; Nie, S.; Liu, G. A low phase and amplitude noise microwave source for vapor cell atomic clocks. Review of Scientific Instruments 2022, 93. [Google Scholar] [CrossRef]
  21. Danet, J.M.; Lours, M.; Guérandel, S.; De Clercq, E. Dick effect in a pulsed atomic clock using coherent population trapping. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 2014, 61, 567–574. [Google Scholar] [CrossRef]
  22. Li, W.B.; Hao, Q.; Du, Y.B.; Huang, S.Q.; Yun, P.; Lu, Z.H. Demonstration of a sub-sampling phase lock loop based microwave source for reducing dick effect in atomic clocks. Chinese Physics Letters 2019, 36, 070601. [Google Scholar] [CrossRef]
  23. Petrov, A.; Davydov, V. Digital frequency synthesizer for 133 Cs-vapor atomic clock. Journal of Communications Technology and Electronics 2017, 62, 289–293. [Google Scholar] [CrossRef]
  24. Boudot, R.; Guérandel, S.; De Clercq, E. Simple-design low-noise NLTL-based frequency synthesizers for a CPT Cs clock. IEEE Transactions on Instrumentation and Measurement 2009, 58, 3659–3665. [Google Scholar] [CrossRef]
  25. Vanier, J. Atomic clocks based on coherent population trapping: a review. Applied Physics B 2005, 81, 421–442. [Google Scholar] [CrossRef]
  26. Santarelli, G.; Audoin, C.; Makdissi, A.; Laurent, P.; Dick, G.J.; Clairon, A. Frequency stability degradation of an oscillator slaved to a periodically interrogated atomic resonator. IEEE transactions on ultrasonics, ferroelectrics, and frequency control 1998, 45, 887–894. [Google Scholar] [CrossRef] [PubMed]
  27. Du, Y.; Li, W.; Ge, Y.; Li, H.; Deng, K.; Lu, Z. Note: A high-frequency signal generator based on direct digital synthesizer and field-programmable gate array. Review of Scientific Instruments 2017, 88, 096103. [Google Scholar] [CrossRef]
  28. Liu, K.; Tian, S.; Guo, G.; Xiao, Y. Precisely synchronous and cascadable multi-channel arbitrary waveform generator. Review of Scientific Instruments 2017, 88, 035110. [Google Scholar] [CrossRef]
  29. Didier, A.; Millo, J.; Grop, S.; Dubois, B.; Bigler, E.; Rubiola, E.; Lacroûte, C.; Kersalé, Y. Ultra-low phase noise all-optical microwave generation setup based on commercial devices. Applied Optics 2015, 54, 3682–3686. [Google Scholar] [CrossRef]
  30. Dick, G.J. Local oscillator induced instabilities in trapped ion frequency standards. In Proceedings of the 19th Annual Precise Time and Time Interval Systems and Applications Meeting; 1989; pp. 133–147. [Google Scholar]
  31. Nelson, C.W.; Hati, A.; Nava, J.; Howe, D.A. Phase noise suppression in frequency comb generators. In Proceedings of the 2010 IEEE International Frequency Control Symposium; IEEE, 2010; pp. 440–442. [Google Scholar]
  32. Bin, L. A decision-feedback phase-tracking receiver for continuous phase modulation. IEEE transactions on communications 1997, 45, 396–399. [Google Scholar] [CrossRef]
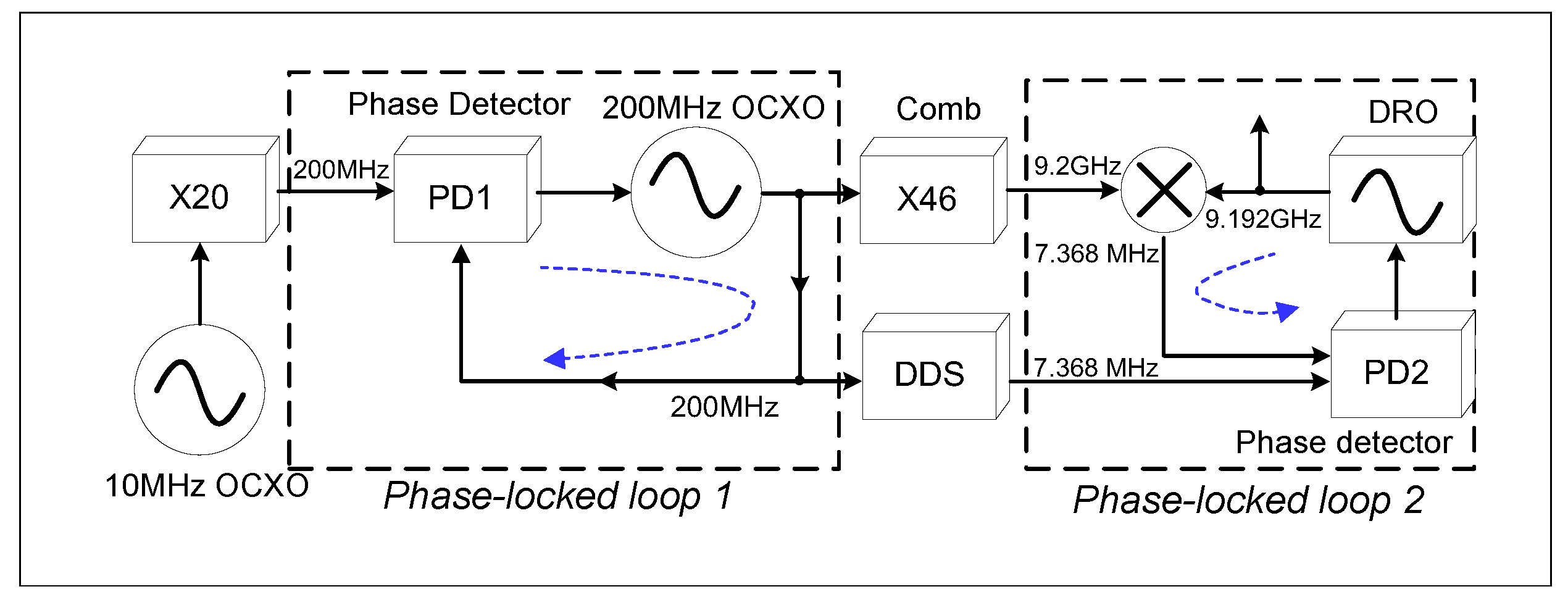
Preprints 79257 g001
Figure 1. Basic architecture of the frequency-synthesis chain.
Figure 1. Basic architecture of the frequency-synthesis chain.
Preprints 79257 g001
Preprints 79257 g002
Figure 2. The experimental setup of the frequency-synthesis chain. Part (1): 10 MHz OCXO. Part (2): the First PLL, including 20× frequency multiplier. Part (3): 200 MHz to 9.2 GHz. Part (4): the Second PLL, including the DRO. AMP, amplifier; ATT, attenuator; PD, phase detector; PID, proportional–integral–derivative controller; LPF, low-pass filter; BPF; band-pass filter.
Figure 2. The experimental setup of the frequency-synthesis chain. Part (1): 10 MHz OCXO. Part (2): the First PLL, including 20× frequency multiplier. Part (3): 200 MHz to 9.2 GHz. Part (4): the Second PLL, including the DRO. AMP, amplifier; ATT, attenuator; PD, phase detector; PID, proportional–integral–derivative controller; LPF, low-pass filter; BPF; band-pass filter.
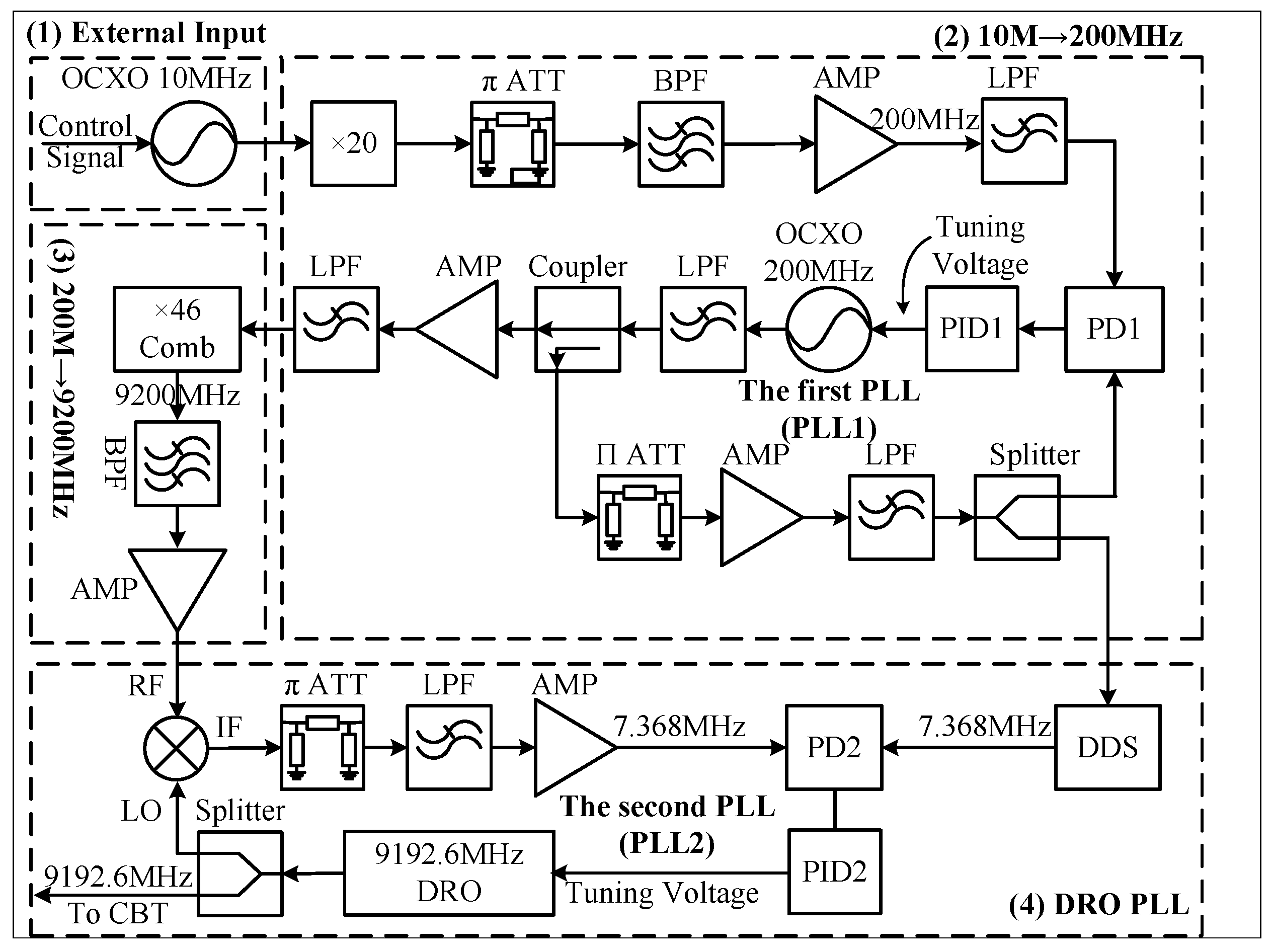
Preprints 79257 g002
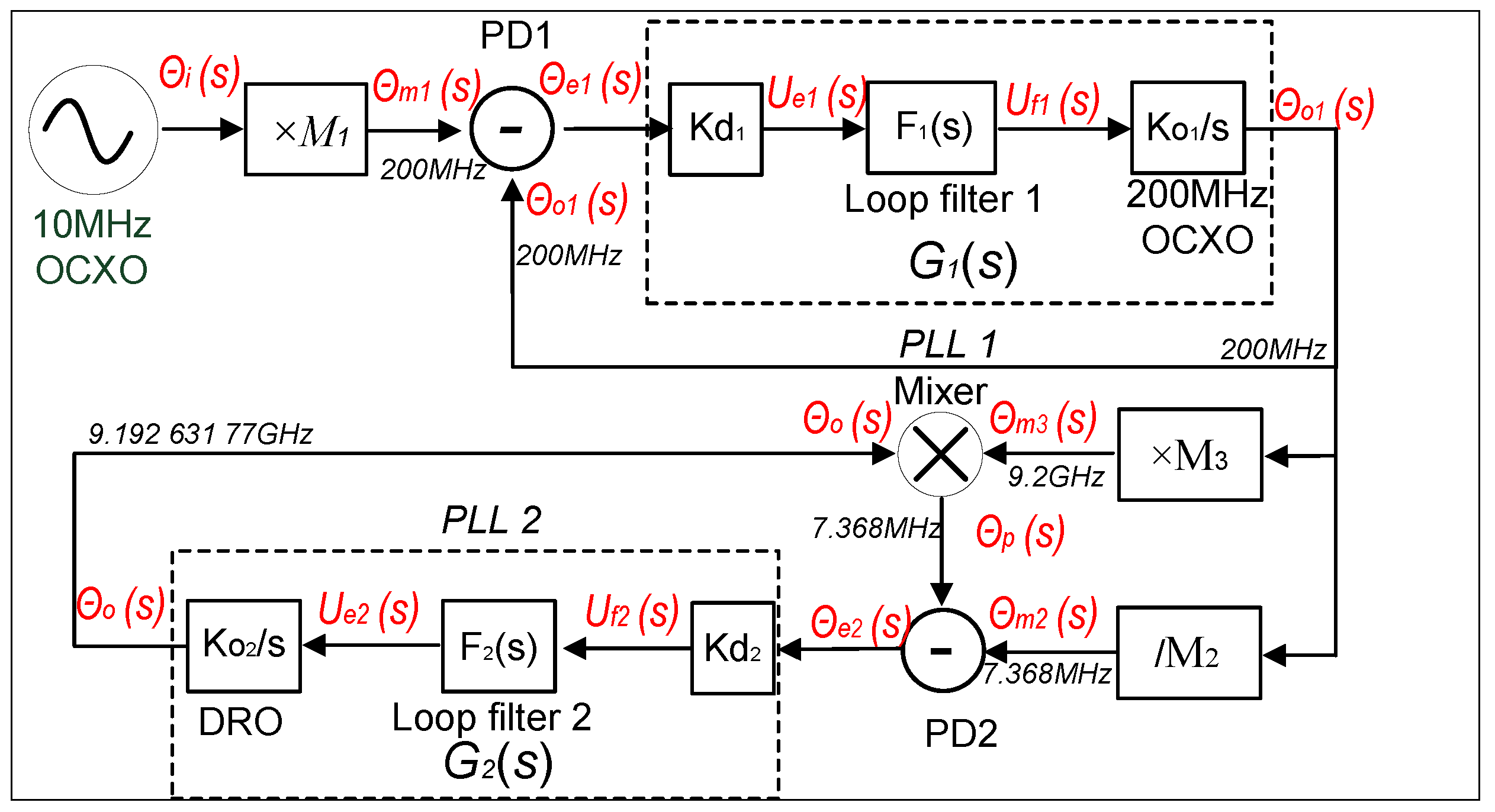
Preprints 79257 g003
Figure 3. Simplified configuration of the frequency-synthesis chain.
Figure 3. Simplified configuration of the frequency-synthesis chain.
Preprints 79257 g003
Preprints 79257 g004
Figure 4. Functional block diagram of the active loop filter PLL.
Figure 4. Functional block diagram of the active loop filter PLL.
Preprints 79257 g004
Preprints 79257 g005
Figure 5. Simulation results showing the phase step response. (a) Parameter τ 1 was fixed, while parameter k p 1 was varied. (b) Parameter k p 1 was fixed, while parameter τ 1 was varied.
Figure 5. Simulation results showing the phase step response. (a) Parameter τ 1 was fixed, while parameter k p 1 was varied. (b) Parameter k p 1 was fixed, while parameter τ 1 was varied.
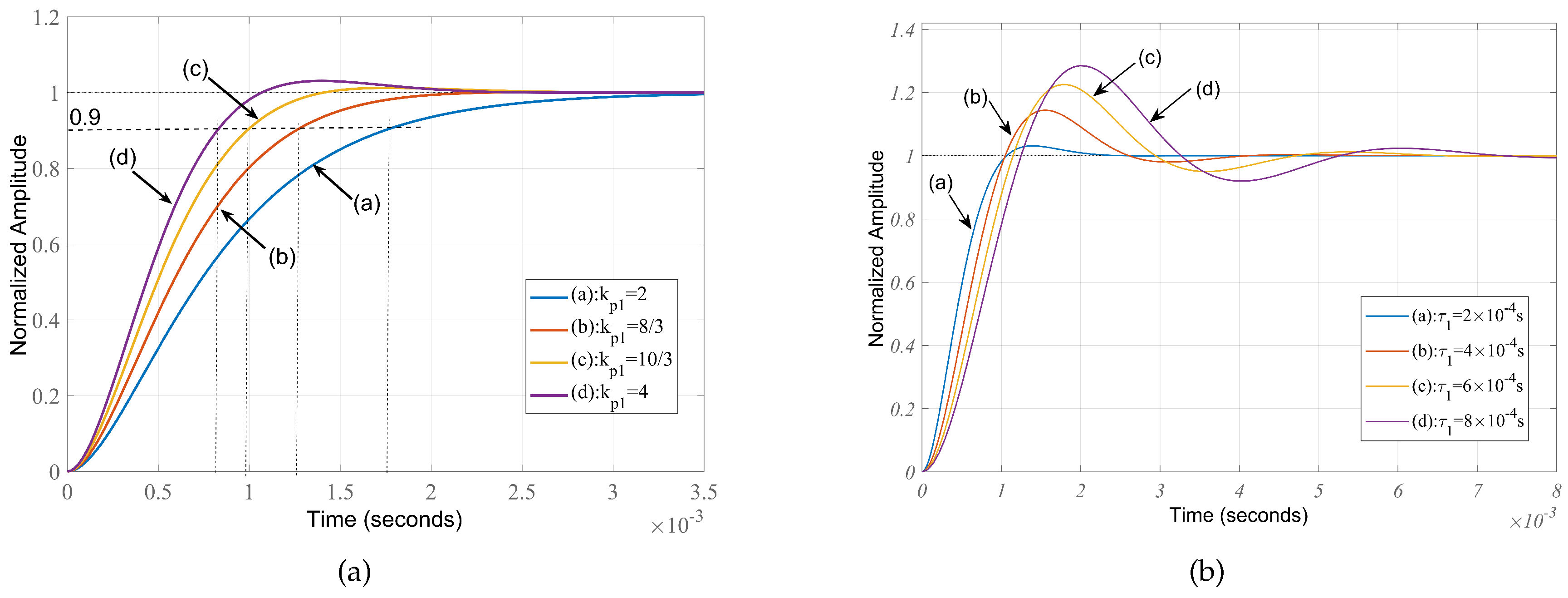
Preprints 79257 g005
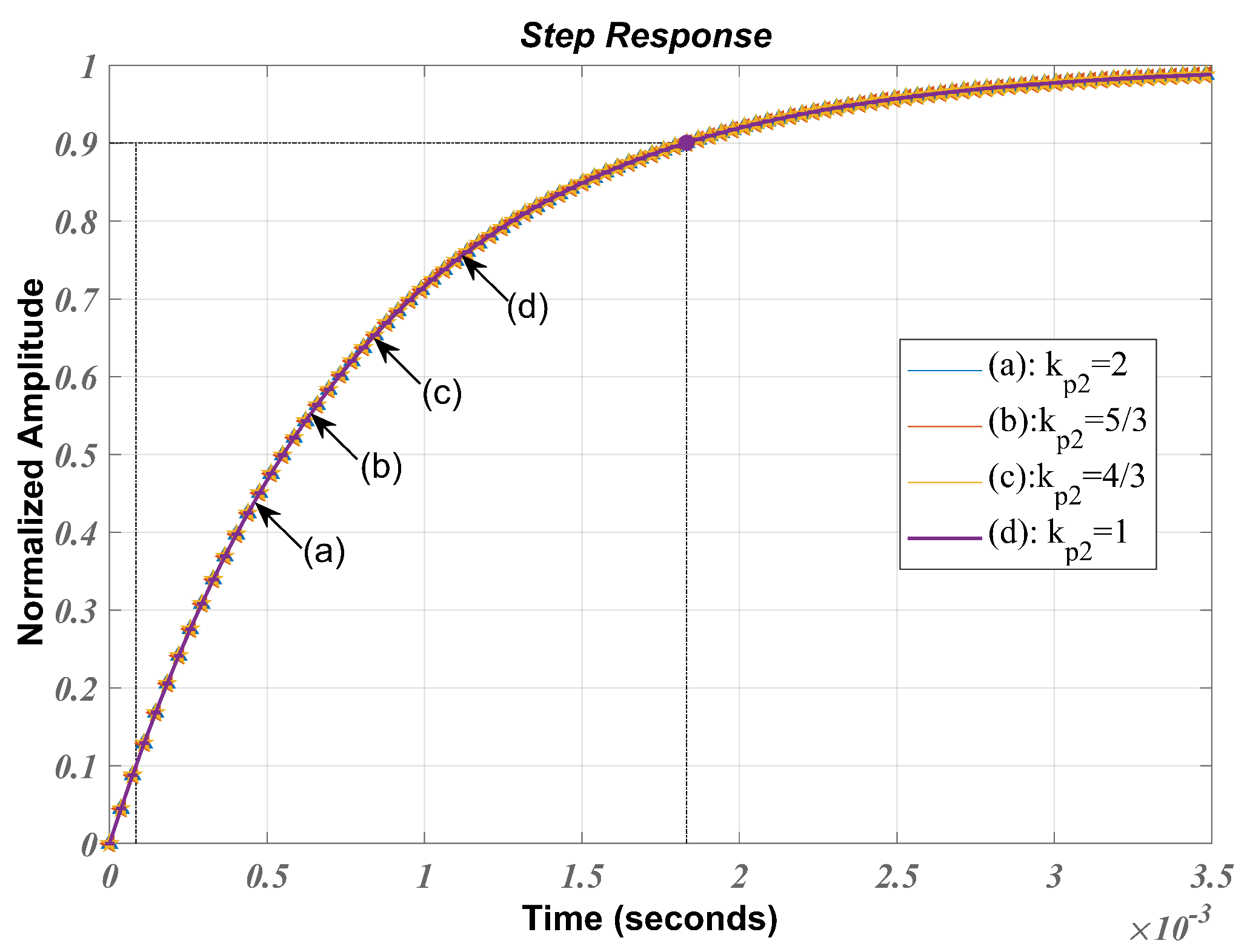
Preprints 79257 g006
Figure 6. Simulation results showing the phase step response. Parameter τ 2 was fixed, and parameter k p 2 was varied.
Figure 6. Simulation results showing the phase step response. Parameter τ 2 was fixed, and parameter k p 2 was varied.
Preprints 79257 g006
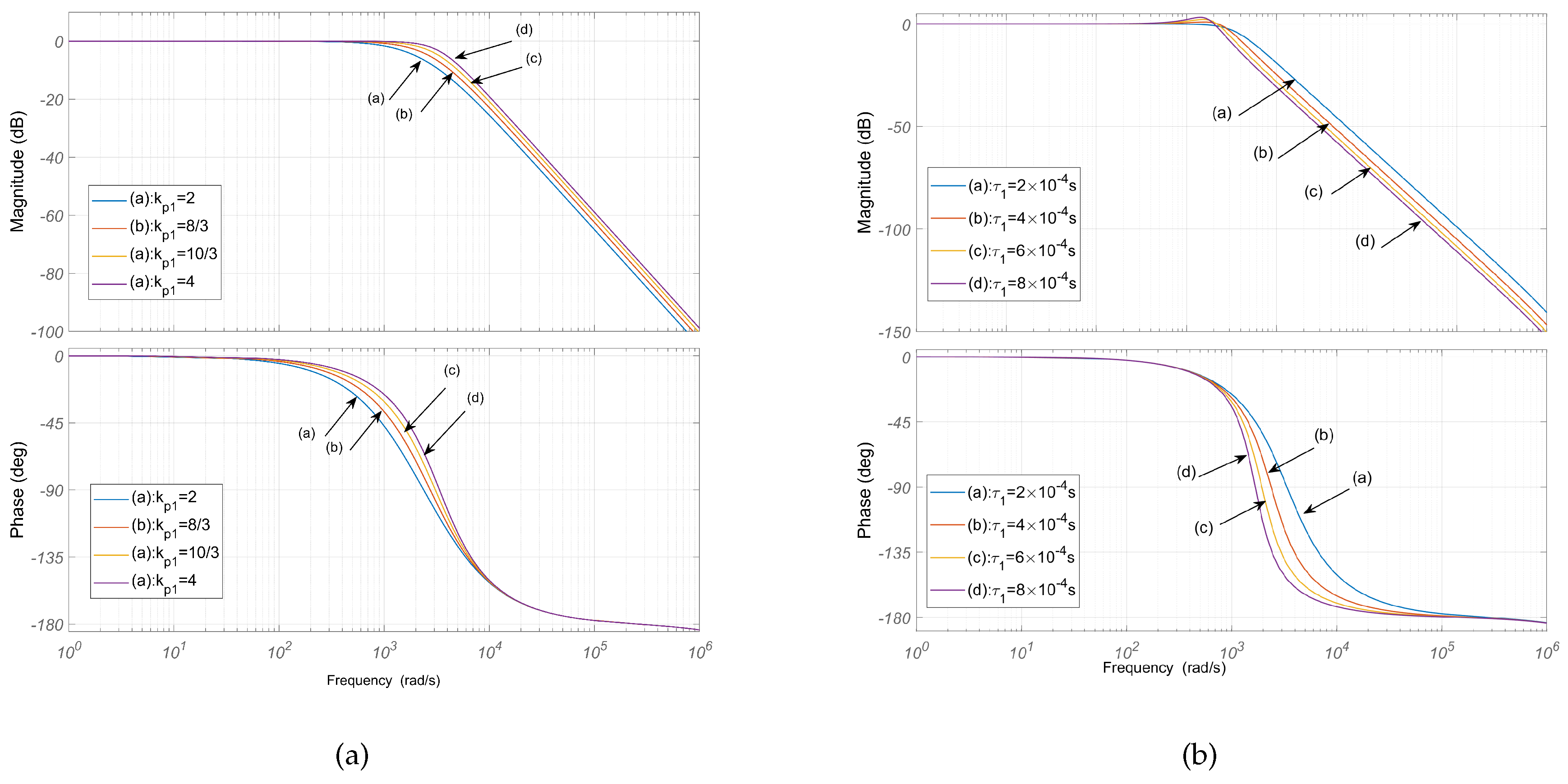
Preprints 79257 g007
Figure 7. Bode diagrams: (a) τ 1 = 2 × 10 − 4 s and k p 1 from 2 to 4 and (b) k p 1 = 4 and τ 1 from 2 × 10 − 4 s to 4 × 10 − 4 s.
Figure 7. Bode diagrams: (a) τ 1 = 2 × 10 − 4 s and k p 1 from 2 to 4 and (b) k p 1 = 4 and τ 1 from 2 × 10 − 4 s to 4 × 10 − 4 s.
Preprints 79257 g007
Preprints 79257 g008
Figure 8. Simplified configuration for measuring the phase-settling ability.
Figure 8. Simplified configuration for measuring the phase-settling ability.
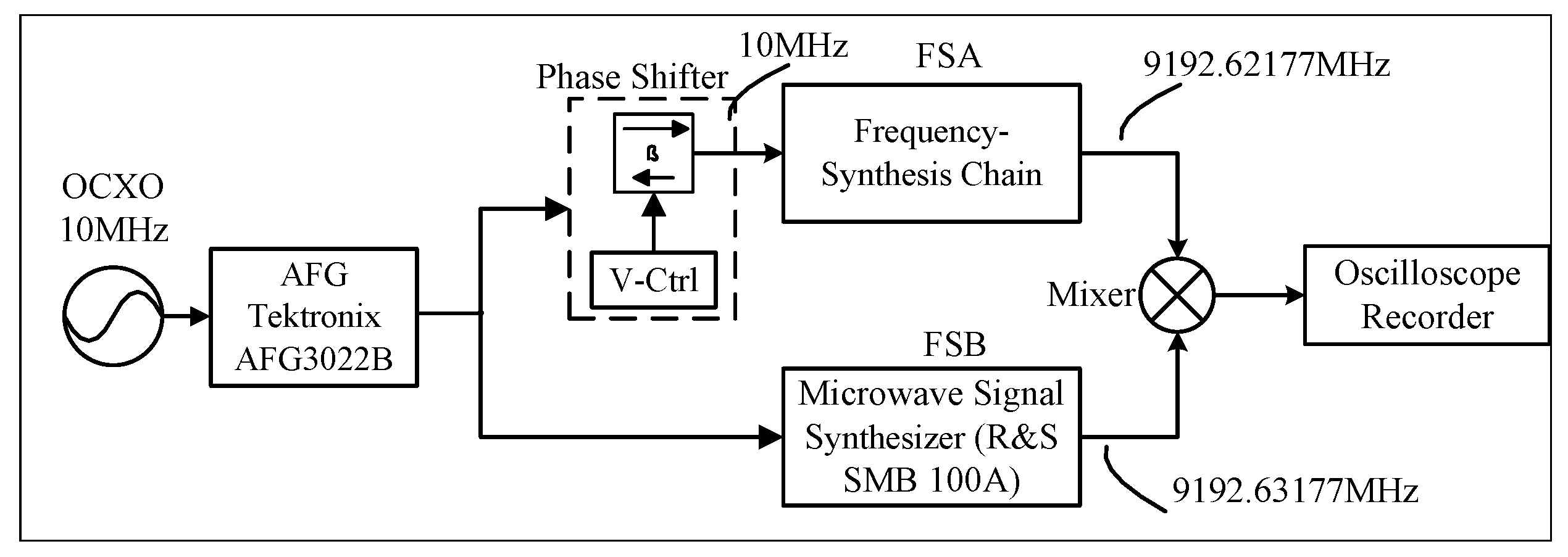
Preprints 79257 g008
Preprints 79257 g009
Figure 9. Phase step response. Dotted lines are the theoretical simulation results and the solid lines are the actual measurements.
Figure 9. Phase step response. Dotted lines are the theoretical simulation results and the solid lines are the actual measurements.
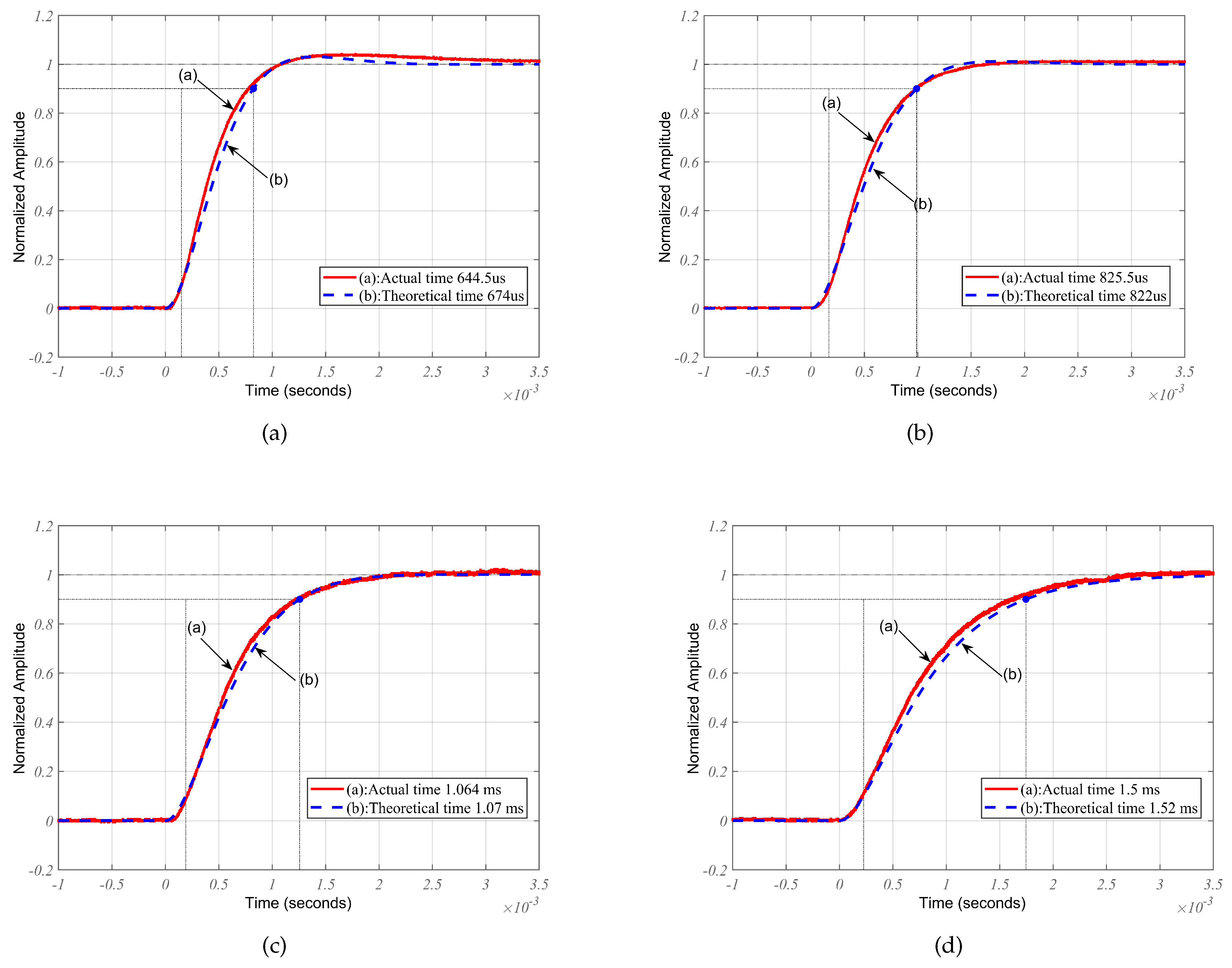
Preprints 79257 g009
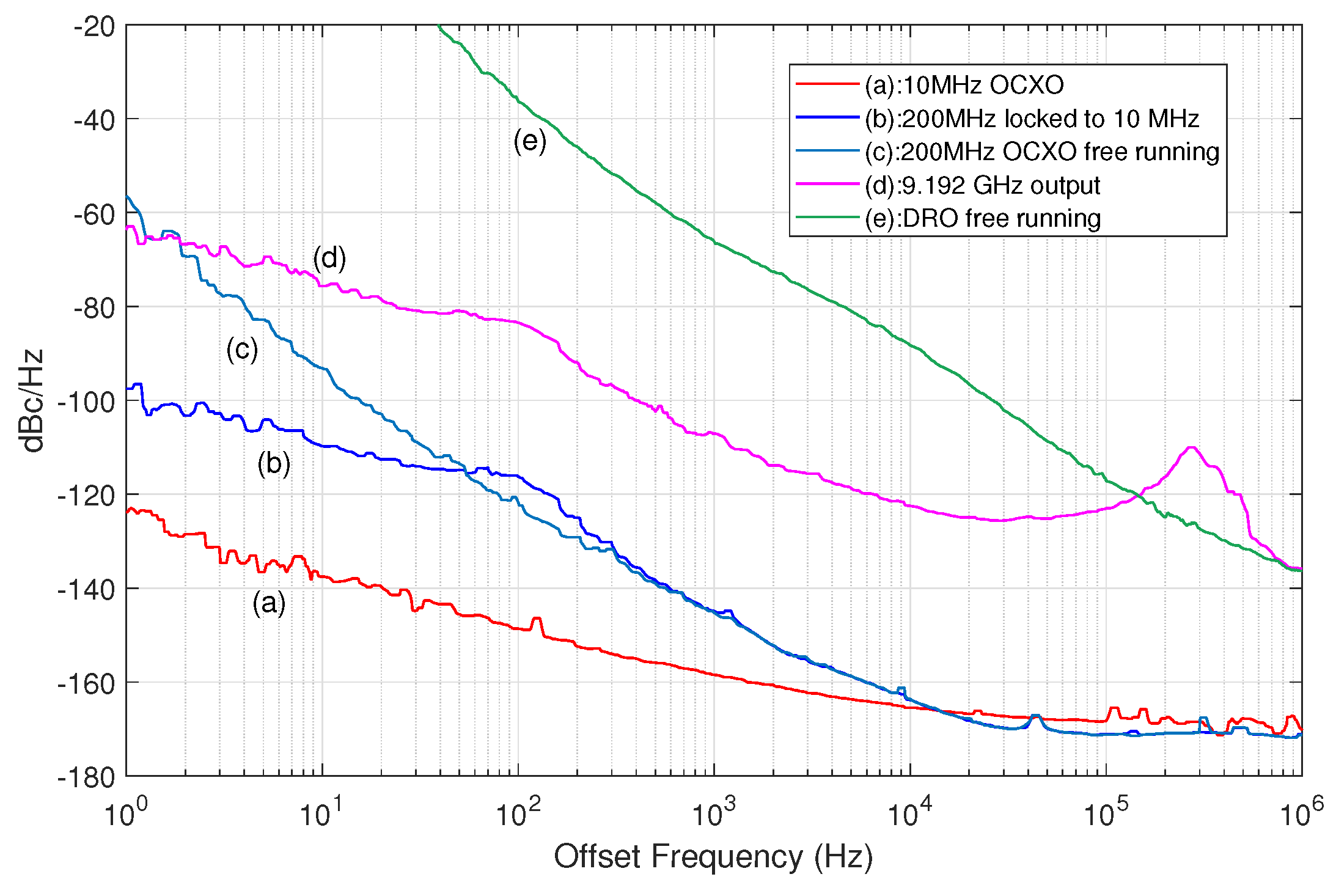
Preprints 79257 g010
Figure 10. Absolute phase noise plots. (a) 10 MHz OCXO, (b) 200 MHz phase-locked to 10 MHz, (c) 200 MHz OCXO free running, (d) 9.192 GHz phase-locked to 10 MHz, (e) free-running DRO.
Figure 10. Absolute phase noise plots. (a) 10 MHz OCXO, (b) 200 MHz phase-locked to 10 MHz, (c) 200 MHz OCXO free running, (d) 9.192 GHz phase-locked to 10 MHz, (e) free-running DRO.
Preprints 79257 g010
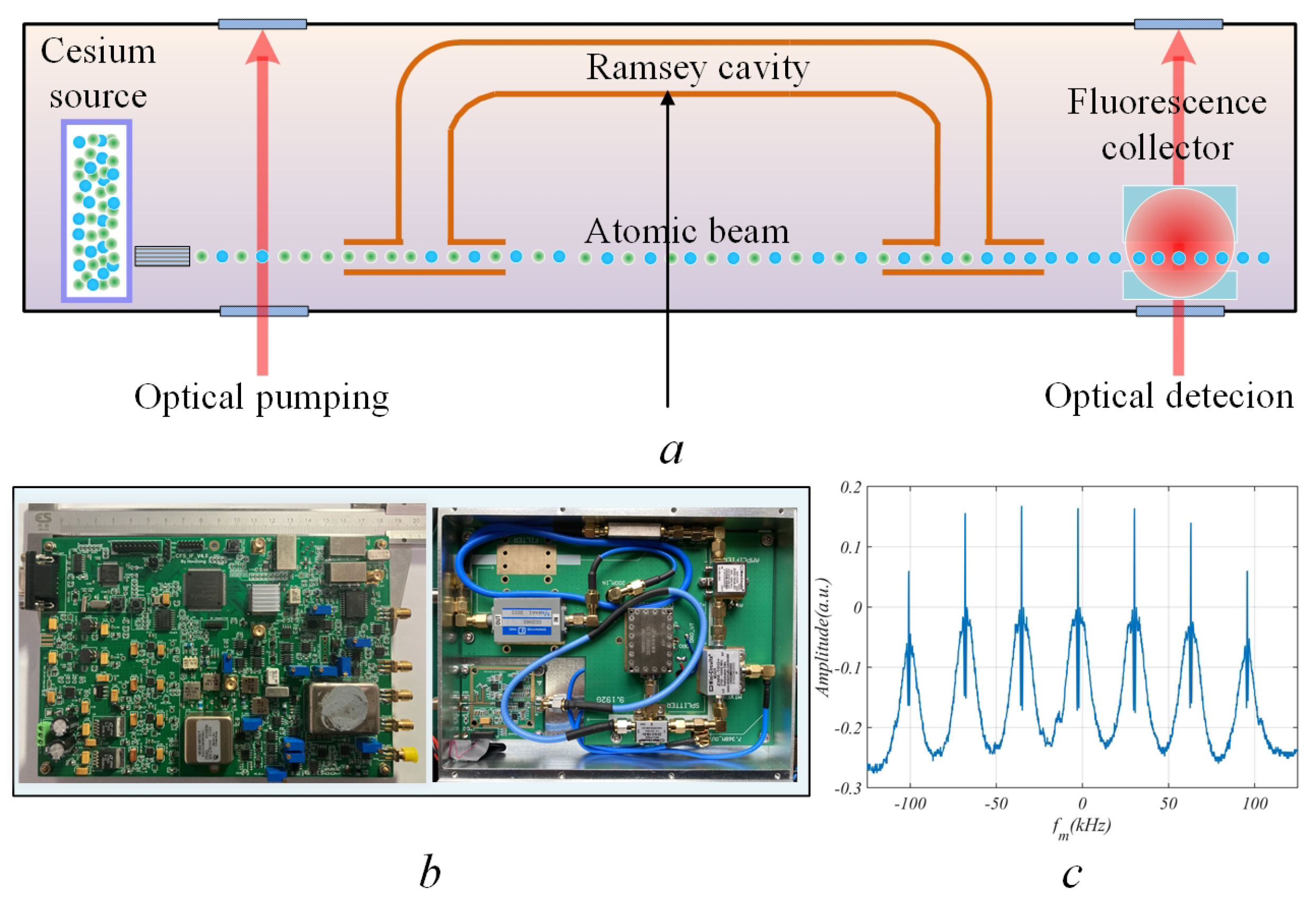
Preprints 79257 g011
Figure 11. Ramsey fringes measurement. (a) Vacuum-sealed CBT. (b) Physical structure of the frequency-synthesis chain. (c) Ramsey fringes detected.
Figure 11. Ramsey fringes measurement. (a) Vacuum-sealed CBT. (b) Physical structure of the frequency-synthesis chain. (c) Ramsey fringes detected.
Preprints 79257 g011
Preprints 79257 g012
Figure 12. Allan deviation of the cesium-beam atomic clock using our frequency-synthesizer.
Figure 12. Allan deviation of the cesium-beam atomic clock using our frequency-synthesizer.
Preprints 79257 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated