Prerpints.org logo
Preprint
Article

Modelling Precipitation Intensity Impacting Vehicles in Motion

Altmetrics

Downloads

131

Views

57

Comments

0

This version is not peer-reviewed

Submitted:

11 July 2023

Posted:

13 July 2023

You are already at the latest version

Alerts
Abstract
With advances in the development of autonomous vehicles (AVs), more attention has been paid to the effects caused by adverse weather conditions on them. It is well known that the performance of self-driving vehicles is reduced when they are exposed to stressors that impair visibility or generate water or snow accumulation on sensor surfaces. This paper proposes a model to quantify weather precipitation, such as rain and snow, perceived by moving vehicles based on outdoor data. The modelling covers a wide range of parameters, such as varying wind direction and realistic particle size distributions. The model allows the calculation of precipitation intensity on inclined surfaces of different orientations and on a circular driving path. The modelling results were partially validated against direct measurements carried out by a test vehicle. The model outputs showed strong correlation with the experimental data for both rain and snow. Mitigation strategies for heavy precipitation on vehicles can be developed and correlations between precipitation rate and accumulation level can be traced using the presented analytical model. Dimensional Analysis of the problem has highlighted the critical parameters that can help the design of future experiments. The obtained results highlight the importance of the angle of the sensing surface on the perceived precipitation level. The proposed model is used to analyze optimal orientations for minimization of the precipitation flux, which can help to determine the positioning of sensors on the surface of autonomous vehicles.
Keywords: 
Subject: Engineering  -   Automotive Engineering

1. Introduction

The Society of Automotive Engineers (SAE) defines different levels of automation for road vehicles, ranging from absence of control systems to self-driving capability. As much as the advancements in the field of autonomous vehicles (AVs) are at a developed stage, weather factors make complete autonomy in realistic situations unfeasible. The AVs’ perception systems are based on a class of embedded sensors called Advanced Driver Assistance System (ADAS). This group of devices includes technologies like RADAR, LiDAR, ultrasonic, cameras, and global navigation satellite systems (GNSS) [1]. Recognition of the surroundings by ADAS is compromised once the vehicle is exposed to conditions such as precipitation, fog, and lightning. For this reason, car manufacturers advise against full vehicle autonomy without driver supervision under adverse weather conditions. Concerns about road safety has increased with the expected growth in the number of AVs with the maximum level of autonomy available on the market [2]. Reports have been produced in an effort to monitor the cause of road accidents involving AVs [3,4].
In addition to driver safety and comfort, the interest behind the development of efficient ADAS is the creation of intelligent road management systems. For this, new technologies have been studied to improve the performance of sensors in conditions like those encountered on roads. Van Brummelen et al [5] provide a review on perception systems for AVs while Vargas et al (2021) focus on their vulnerability to weather stressors. Also, Hnewa and Radha [6] describe emerging object recognition algorithms under rainy conditions using CNNs (Convolutional Neural Networks). Regarding data collection, Dey et al [7] have addressed the potential of intelligent transport systems (ITS) such as vehicle-based sensors and the creation of public databases in mitigating the impact of adverse weather on road management. To use moving cars as rain gauges, Rabiei et al [8] designed a system that uses the windshield wipers to estimate rainfall intensity. Drobot et al [9] have adapted commercial vehicles for monitoring road conditions during and after episodes of heavy precipitation. Moreover, innovative compact weather stations have been developed using unmanned aerial vehicles (UAVs). Among the wide range of applications that they provide, the studies of the atmospheric boundary layer profile and air quality monitoring can be mentioned [10]. Road management is still a minority in studies involving UAVs, but low cost multicopters have been used to collect wind information using acceleration data [11,12]. This concept has gained strength with the development of climate measurement-oriented drones by Meteomatics [13]. It is therefore possible to imagine intelligent systems for mitigation of weather impacts on AVs that combine data collected in real time by embedded sensors and weather information recorded by static referential such as compact meteorological stations or UAVs.
The WoW (Weather on Wheels) project is part of a Canada Research Chair program in Adaptive Aerodynamics at Ontario Tech University and the Automotive Centre of Excellence (ACE) to seek solutions to the problems previously mentioned [14]. To accomplish this objective, the project follows a framework composed of three steps. First, full-scale measurements and numerical (CFD) simulations to derive statistically significant critical weather conditions are conducted. A method involving Principal Component Analysis (PCA) and unsupervised Machine Learning has been developed to classify weather data obtained with the test vehicle of the project [15]. Next, weather conditions considered as strategic are simulated in the ACE climatic wind tunnel at Ontario Tech University. Finally, adaptive control techniques are proposed to improve their aerodynamics, safety, and sensor functionality. Pao et al (2023) have conducted simultaneous disdrometer measurements using an instrumented test vehicle and a meteorological tower to quantify perceived precipitation from the vehicle’s perspective with a primary focus on 0° and 90° orientations. The results represent an important milestone for the development of a more robust model that accounts for dynamical parameters such as wind influence and aerodynamic upwash. The present paper proposes a theoretical approach to the same problem using a previously obtained database without simultaneous data, but which aims to cover a wider range of scenarios.
The development of effective weather mitigation systems depends on the analysis of climate conditions from the vehicle’s perspective. The action to be taken by the AV must rely on the optimization of a metric recorded by the on-board system. For this, a model to quantify the perceived precipitation rate during motion must be built. In this paper, the issue of rainfall perceived by a moving vehicle is interrogated to determine a parameter that can be used as a cost function to be minimized. Real weather conditions measured in southern Ontario are incorporated into simulations to calculate the precipitation rate over surfaces with various orientations. A data-driven method which uses unsupervised machine learning is used to select the strategic parameters [15]. Also, the critical variables of the problem are identified through Dimensional Analysis to explain the physics of the phenomenon and help prepare for future field measurement campaigns.

2. Precipitation Flux Model

To mitigate effects of heavy precipitation on the operation of autonomous vehicle sensors, an action strategy must be defined based on a metric recorded in real time. An analogy between this problem and the issue of running or walking in the rain so as not to get wet can be made. Literature provides different methods for establishing the optimal speed to reduce the volume of water encountered by moving objects in linear trajectories. Stern [16], for example, states that it is necessary to minimize the number of drop hits along the body’s path. He presents a method that calculates the number of drops swept by projections of a moving surface with a given orientation. De Angelis [17] also follows the thread of reducing the number of drop impacts. Despite the correct premise, he makes oversimplifying hypotheses that lead to the mistaken conclusion that it is always better to run than to walk in the rain so as not to get wet. Holden [18], in turn, introduces the concept of rain flux. He proposes the minimization of the total mass of water encountered by an object in motion, but he assumes only vertical rainfall for simplification purposes. Bailey [19] calculates the total volume of water in contact with the surface of a body using a similar method. He states that the amount of water depends only on its specific mass, the relative speed of the droplets, the surface area, and the exposure time. He defines the best strategy for different cases, according to the direction of motion and wind. Ehrmann and Blachowicz [20] describe a derivation of this method for generalized application. By approximating the shape of the human body as a cylinder, they present a model that finds the optimal speed for different tested parameters. Finally, Bocci [21] formulates the problem using equations from electromagnetism to calculate the rain flux on a moving surface. This methodology provides an approach that covers a wide range of cases. However, some adaptations need to be made since the problem addressed in the present paper deals with particle flux. In addition, experimental methods for recording rain data are not covered.
For educational purposes, the perceived rain methods mentioned so far consider only pre-established trajectories for the moving objects, which is not always the case in real applications. Constant precipitation rate is also assumed. Moreover, since the goal is to minimize the amount of water on the body in motion, many of them state that the best strategy is to move as fast as possible. The reason for this is that the exposure time is reduced. Increasing the speed means reducing the time in the rain. Addressing the case of AVs, this approach is not suitable due to external factors that influence travel time and the fact that the intensity of rain or snow varies over time. To mitigate the effects of intense precipitation on vehicles in real time, another parameter that the integration of the water mass on its surface should be considered.

2.1. Model Description

The method described in this paper for evaluating the precipitation perceived by the test vehicle is based on the approach of Bocci [21]. However, instead of reducing the total amount of water encountered by the car, the method defines the instantaneous rain flux Φ , in k g / s , as the cost function to be minimized. This flux can be expressed as the following integral over a closed surface A:
Φ = − ∮ j · d A
where j is the particle density vector defined as:
j = ρ V ( D ) N d v
where ρ is the specific mass of water, in k g / m 3 , and v is the resulting velocity vector between the droplets and the surface. The particle concentration number N d , in m − 3 , and the droplets volume V ( D ) in m 3 , can be obtained experimentally through size distributions. Following, since there is no field source and the flux over the surface S of a sensor is considered, Equation 1 defined on the interval [ 0 , ∞ [ can be written as:
Φ = − ∫ S j · d S
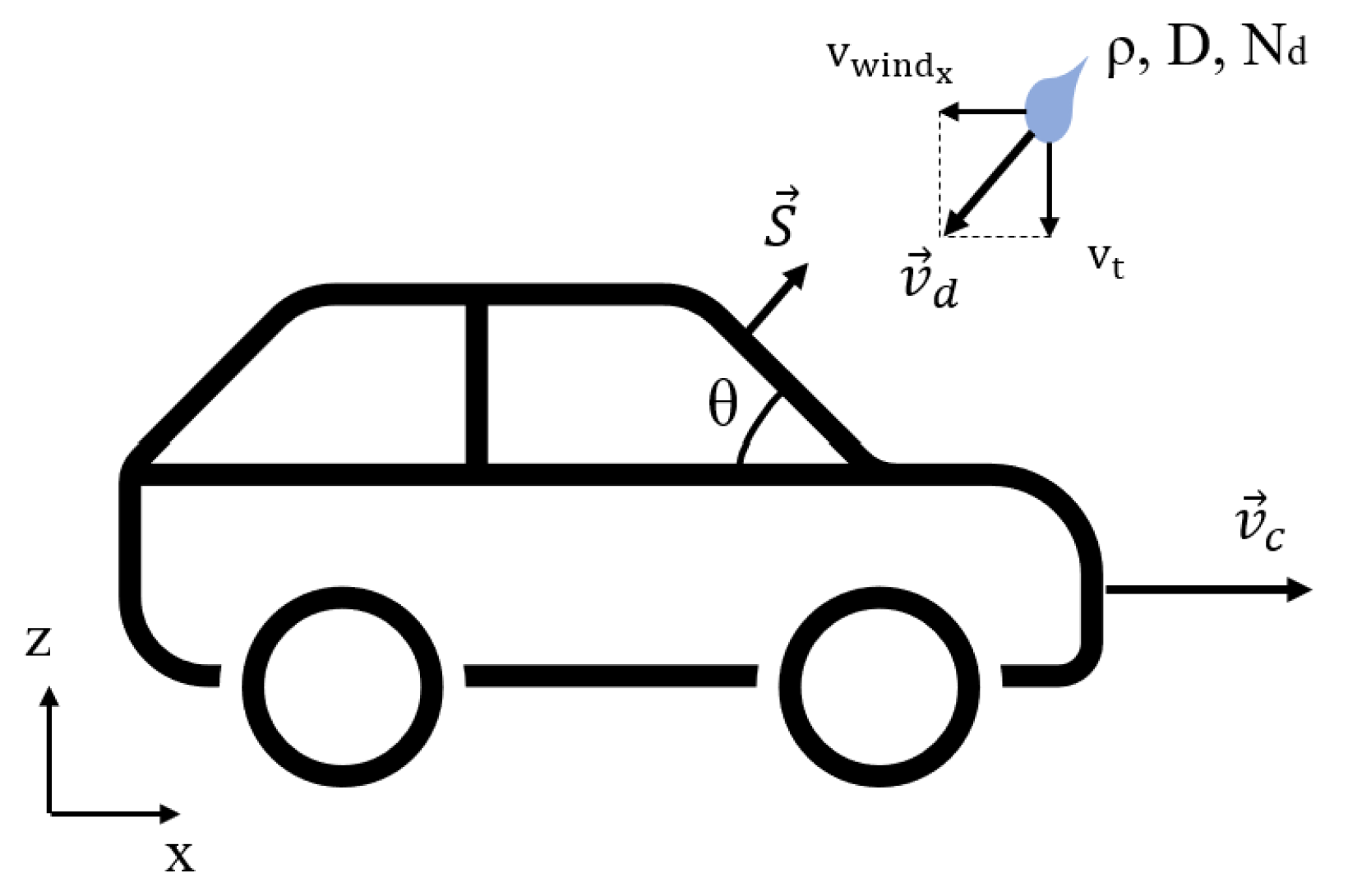
The flux equation shows that the amount of rainfall crossing the sensor surface is equivalent to the projection of the rain density over the normal surface vector. This means that only the component of j that falls perpendicularly toward the sensor is relevant for flux calculation. Therefore, crosswind is not considered in the equation since the inner product between the y direction and the sensor surface vector is zero. By considering only its front surface, the problem of a vehicle moving in the rain can be represented in two dimensions as shown in Figure 1.
The velocity of the vehicle and the droplet are represented by v c and v d , respectively. The latter can be decomposed as the sum of the terminal velocity v t and the wind speed v w i n d . Given all the problem parameters, the equation for rain flux over the rectangular, flat sensor surface can be written as:
Φ = − ρ N d V ( D ) v · S
where v is the resulting velocity magnitude normal to the sensor plane:
v = ( v c − v w i n d x , v t )
As the goal of this paper is to quantify the rain flux over moving objects under realistic conditions, a generalist approach is needed. Because of this, the simulations carried out in this work were designed to cover cases dealing with various surface orientations, nonlinear trajectories, and changing wind direction. Therefore, for a broad understanding of the problem, Dimensional Analysis is applied to identify the critical parameters to be investigated.

2.2. Dimensional Analysis

The Buckingham Π theorem defines how equations describing physical phenomena can be written as relations between dimensionless groups comprising the physical parameters involved [22,23]. This method has been widely used in experimental studies over the years, especially in the field of fluid mechanics as it provides an analytical approach to reduce the dimensionality of functions describing physical systems [24,25]. To that end, thanks to the increase of computational power, the Buckingham theorem has been integrated into data-driven methods in recent studies [26].
When it comes to the subject of rain flux on a moving object, the formulation of the problem made previously is important for the identification of the variables. Therefore, by analyzing the Equation 4 for a surface with given orientation θ , one concludes that it is a function of the following variables:
Φ = f ( v , ρ , N d , S , D )
Through Dimensional Analysis, f can be written in the form of G, a new function involving the dimensionless numbers:
Π 1 = Φ ρ D 2 | | v | |
Π 2 = S D 2
Π 3 = D 3 N d
Φ ρ D 2 | | v | | = G S D 2 , D 3 N d
The composition of the groups has a physical interpretation, as Π 1 is related to the amount of rain mass encountered, Π 2 is associated with the exposed surface area, and Π 3 represents the climatic condition in the surroundings of the object. This type of analysis shows that, to evaluate the precipitation perceived by the vehicle, it is necessary to access the mean particle size as well as their average velocity, in addition to collecting wind data such as speed and direction. This is important for the definition of the sensors to be employed in the measurement campaigns.
Besides, one important conclusion is that contrary to what many articles claim, the speed of the object does not define the flux of rain over it. The resulting velocity between the body and the drops is the crucial factor, since assuming an object in motion is analogous to imagining it as a static referential exposed to wind passing over it. Given that the dimensions of the sensor surface S are known and its orientation depends on the object’s geometry, the critical parameters for the analysis of the problem, which are considered in the simulations, are the surrounding weather conditions, expressed by D and N d . The specific mass of the water ρ can be estimated. The parameter to be simulated, therefore, is the resulting velocity between the surface and the precipitation v . Implicitly this vector contains the information about the speed of the vehicle, its trajectory, and the angle that is formed between the surface vector and the wind at each time step.

3. Model Validation

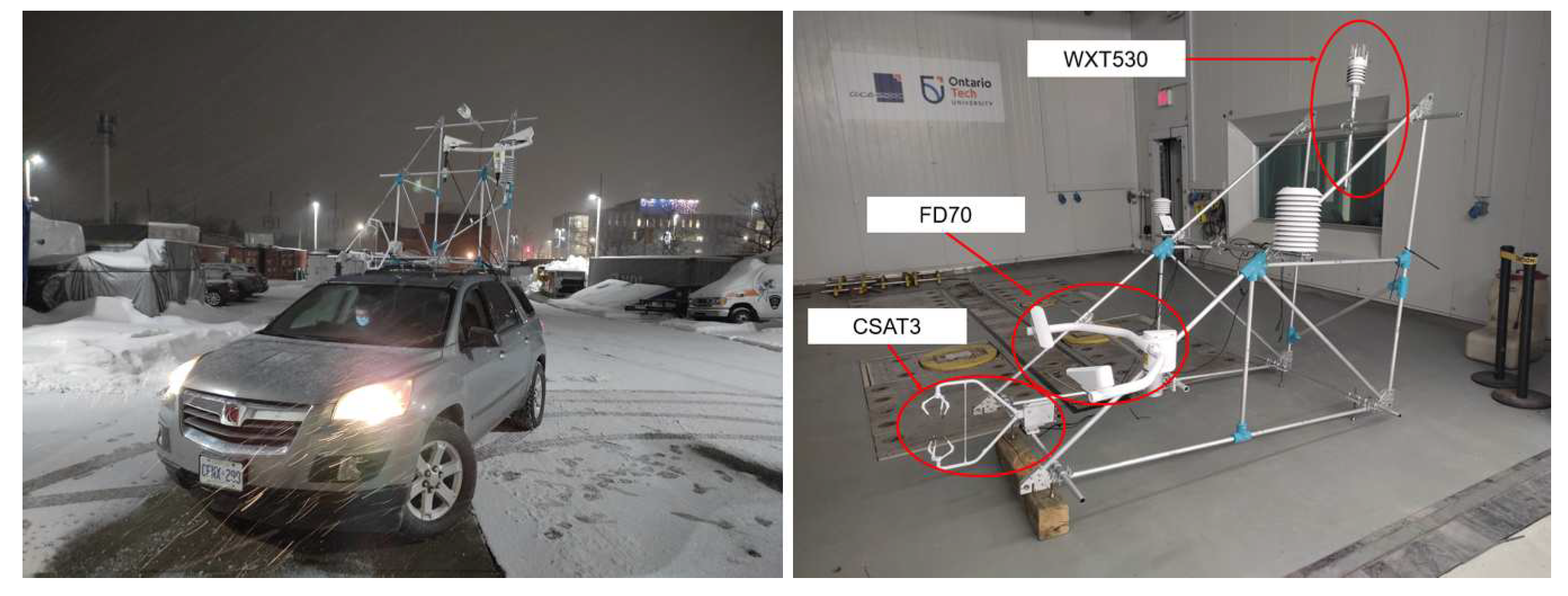
To validate the proposed rain flux model, outputs from the Equation 4 fed with experimental data are compared with direct rainfall rate readings. Data is recorded using a road vehicle adapted with sensors able to measure weather information such as temperature, relative humidity, and particle size and velocity distributions. The test vehicle was developed by ACE’s technical team and measurements were carried out at the Canadian Technical Center McLaughlin Advanced Technology Track (CTC MATT) located at GM’s assembly plant at Oshawa, Ontario. In this section, the experimental apparatus used in the measurement campaigns is described along with the processing of the sensors’ data. Then, the comparison between the results obtained with the theoretical model and the direct measurements coming from the sensors is presented.

3.1. Experimental Setup

The vehicle is equipped with a Vaisala FD70 optical disdrometer that provides 60-seconds histograms of particle size and velocity. Wind data are sampled at 5 H z using a Campbell CSAT3 3D sonic anemometer. Data is recorded in three orthogonal directions that are adjusted to match the coordinate system of the simulations. A Vaisala WXT530 weather station is used to measure temperature and relative humidity every 5 seconds. The equipment is installed on a rack above the car specially built for the measurements as shown in Figure 2. More details about the experimental setup are described by Carvalho and Hangan [15].

3.2. Data Processing

Optical disdrometers allow the quantification of the level of precipitation in different ways. Frasson et al [27], for example, estimate rainfall rate from outdoor measurements by summing the volume of the drops. Based on this approach, the total volume of precipitation found in the experimental samples is calculated as:
V ( D ) = ∑ j = 1 t ∑ i = 1 k N i , j 4 π 3 D b i , j 2 3
where N is the count number of each size bin of mean diameter D b . As the equation shows, it is common practice in disdrometer data processing to approximate the droplets volume by considering them as spheres. Parameters like k, the total number of size bins, depend on the disdrometer model. The count number N is used for the calculation of the concentration number N d [28] for each size distribution.
N d = 1 | | v n | | S Δ t ∑ i = 1 k N i
The magnitude of droplets net velocity v n can be obtained from the weighted average of the droplets speed distributions.
| | v n | | = ∑ i = 1 k N i v d i ∑ i = 1 k N i

3.3. Validation Results

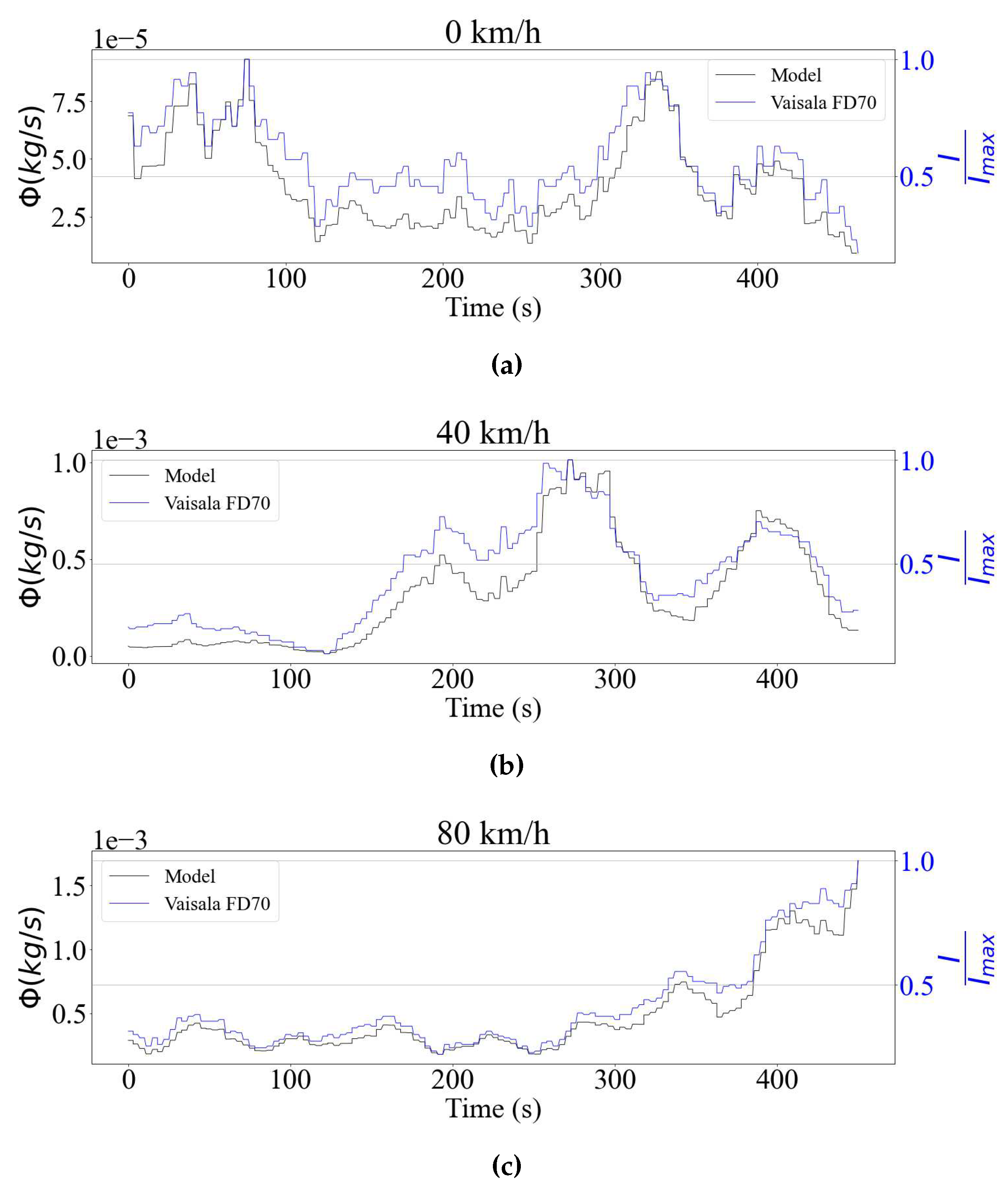
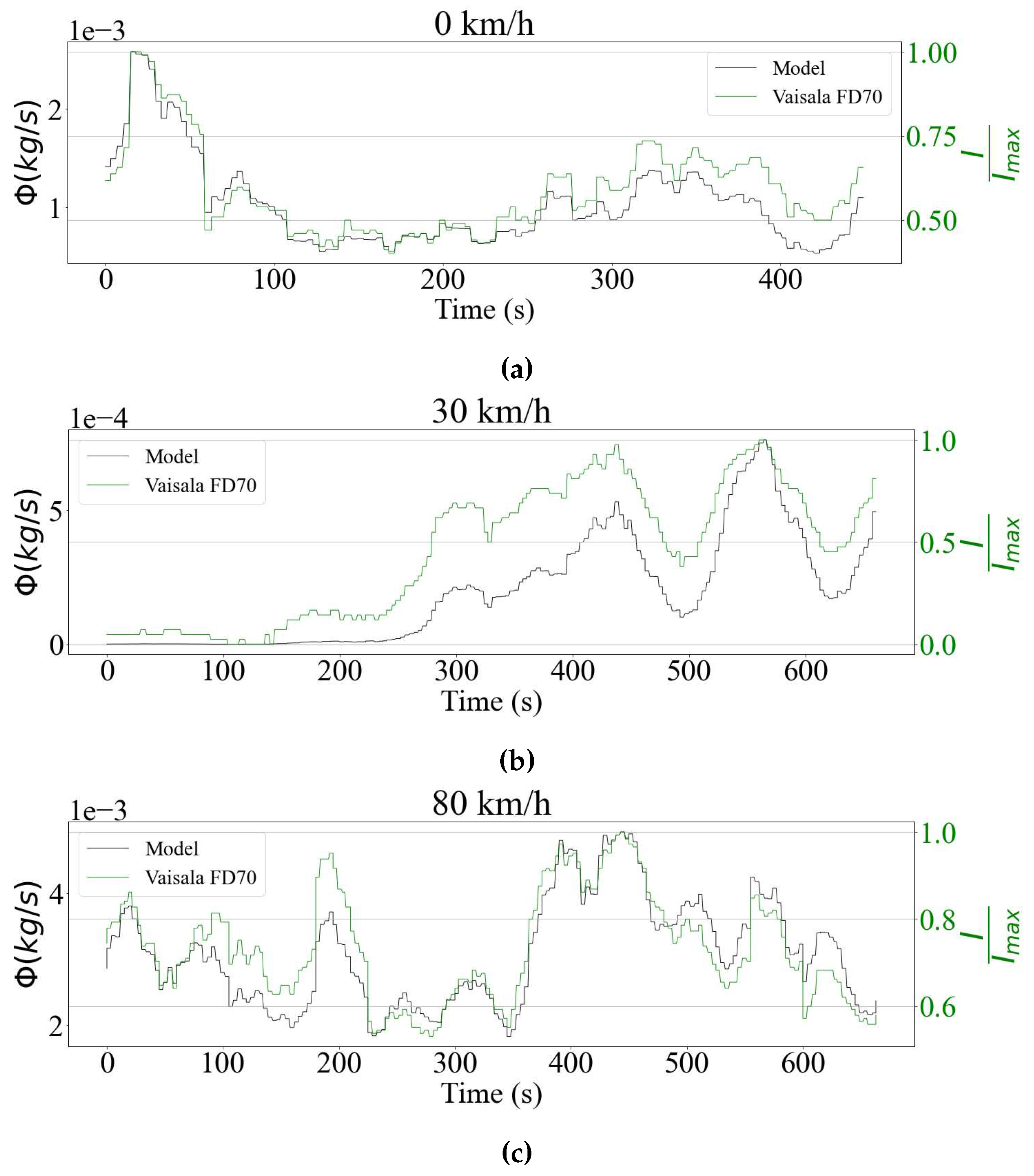
Data collected under snow and rain respectively on March 7 and 23, 2022 on the GM (General Motors) Canada McLaughlin Advanced Technology Track (MATT) track were used for validation. This specific data set relies on 1-second droplet size distributions (DSD) readings from the FD70 disdrometer with its sensing surface in horizontal position. The measurements are made over a period of 8 minutes, and three cases are considered regarding the driving speed. First, the car is stationary during data collection, similar to a standard meteorological tower. Then, the measurements are carried out while the test vehicle travels along the track at 40 k m / h and 80 k m / h .
The disdrometer provides direct precipitation intensity outputs in m m / h . Being an optical sensor, the FD70 processes the drop size distributions internally in order to generate these signals. The model validation process therefore seeks to verify if the rain flux equation gets signals that are comparable to those measured by the sensor. The results are shown in Figure 3 for rain data in Figure 4 for snowfall. For all tested cases, the time signals show strong correlation indicating that the model performs well for both stationary and moving vehicles. This shows agreement with what is predicted by flux theory, where the only component that matters is the normal to the analyzed surface. For the case of the horizontal sensing plane, this component is the droplet drop velocity, which does not depend on the driving speed.
To quantify the performance of the model in comparison to the sensor measurements, a correlation study between the signals was performed. Table 1 shows the values of the Pearson coefficients [29]. As was seen in the time series, the signals show strong correlation, especially in the case of rainfall, where the coefficients are always greater than 0.90 . As expected, the model has a lower performance when it comes to snow. Snow particles are more susceptible to aerodynamic forces, and have a variety of morphologies that depend on the surrounding weather conditions [30]. While these aspects are not taken into consideration in the present study, it is important to investigate in detail their impact to make the model more accurate.
Despite the similarity of the trends, a calibration experiment of the disdrometer should be done to compare precipitation mass values. The analysis of the validation results was limited to the computation of the correlation coefficient since the processing chain developed by the manufacturer is unknown. In the case of snow precipitation, this process is more complex since mass and density estimation models as a function of particle diameter must be considered to determine accumulation levels [31]. Nevertheless, the results are considered satisfactory for simulation purposes while future experimental campaigns are prepared.

4. Evaluation of Perceived Precipitation

The comparison between the magnitude of the values obtained by the model and by the sensor validates the rain flux calculation method through Equation 4. Scenarios that are more complex can then be tested. Simulations are performed considering a body moving along a circular path with a perimeter of 3.6 km, the same as the test track where the experiments were carried out. The rain flux is calculated on three surfaces with different orientations. Parameters such as the concentration number N d and total droplet volume V were estimated from the field measurements campaign mentioned previously using a machine learning-based method described by Carvalho and Hangan [15]. Wind speed v w i n d in three directions comes from anemometer measurements. The sensing surface has the same dimensions as the FD70 disdrometer.

4.1. Simulation Parameters

The works cited in the introduction to the Section 2 simulate different cases of objects moving along a linear path under rain. Since the goal of these papers is to define optimal traveling speeds, the difference between the simulation cases basically consists of the wind direction. The previously studied configurations are limited to situations where the object is moving towards or in the same direction as the precipitation, as well as vertical rain. Here, to cover a wide range of cases in the same simulation, the resulting vector v was modeled as a function of the components v c , the vehicle speed, and v d , the droplets velocity vector. The object’s trajectory was designed to be circular, in the x y plane. This choice was made as a compromise between the real trajectory of the road vehicle, which is an oval test circuit, and the simplicity of the analytical equation of a circle.
Spherical coordinates x = ( r , ϕ , θ ) are used to model the rain flux along the object’s motion. First, the angular position ϕ ( t ) is defined as being linearly varied over time:
ϕ ( t ) = ϕ 0 + d ϕ d t t
The object displacement vector r ( t ) , which describes the position of the vehicle as a function of time in terms of angle ϕ is:
r ( t ) = r cos ( ϕ ) i ^ + r sin ( ϕ ) j ^
Consequently, the velocity vector v c , which has the direction of the vehicle’s displacement along the trajectory, is obtained by the derivative of Equation 15:
v c ( t ) = r d ϕ d t − sin ( ϕ ) i ^ + cos ( ϕ ) j ^
The particle velocity v d is the sum of the wind speed components and the droplet terminal velocity. Regarding the droplets terminal velocity v t , the model obtained experimentally by Atlas et al [32] for vertical precipitation is adopted. The three-dimension vector is therefore:
v t ( D ) = ( 0 , 0 , − 9.65 + 10.3 e − 0.6 D )
Since the precipitation conditions used in the simulation do not vary, the terminal velocity of the droplets would also be constant. To create a time-varying aspect to the terminal velocity, the assumption that the vertical component of the wind is embedded in the value generated by the model is made. With v d being the sum of the wind vector v w i n d and the droplets terminal velocity v c , the rain flux Φ can be found by projecting the resultant vector formed with the vehicle vector v c onto the direction normal to the sensing surface as shown by Equation 4.

4.2. Setting Realistic Parameters for Simulation

The proposed theoretical rain flux model opens the door for various applications concerning AV safety. Numerical simulations that allow the quantification of perceived precipitation on moving objects can help the development of mitigation solutions for the operation of ADAS sensors. In addition, Reinforcement Learning (RL) techniques can be applied to train an agent to minimize the impact of weather stressors by considering the rain flux equation as a cost function.
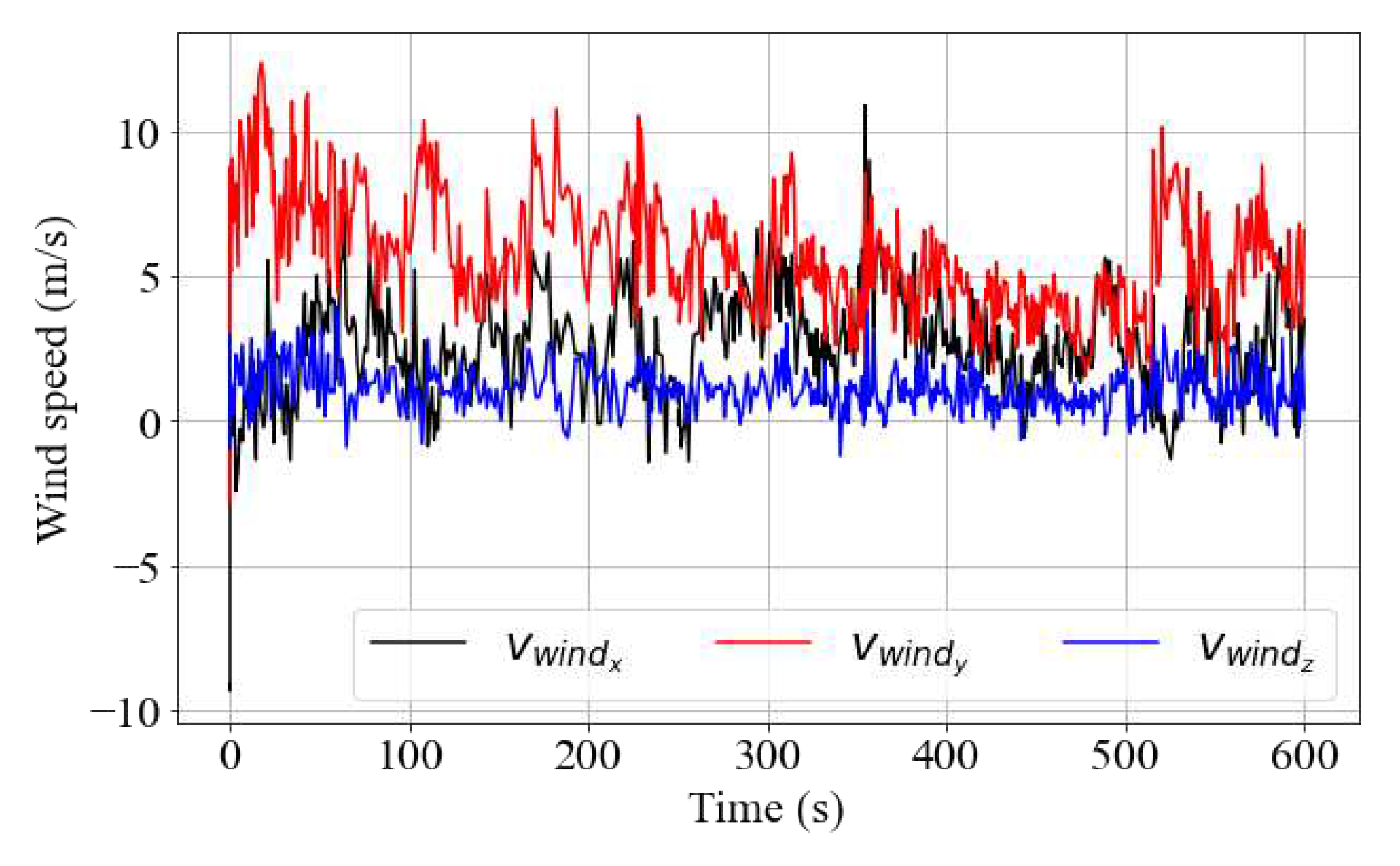
To generate realistic results, simulations were performed based on weather conditions measured by the test vehicle at GM’s MATT facilities on March 23, 2022. Since the goal is to compute the rain flux on surfaces with different orientations, it was decided to use real wind data from the CSAT3 sonic anemometer in the simulations. Thus, the wind is expected to play a determining role in the flux value, unlike the validation tests where the analyzed surface was oriented horizontally. The time series of the vector v w i n d components can be seen in Figure 5. The anemometer data was recorded with the car stopped over a period of 10 minutes. Wind data can also be generated synthetically using periodic functions as described in the Appendix A. By combining the real wind data with the terminal velocity model from the Equation 17, the velocity vector of the drops can be generated.
The next step is to implement the concentration number N d in the simulation loop and to set the total droplet volume V ( D ) . To match the duration of the wind signals, it is assumed that precipitation conditions remain constant throughout the test. To do so, realistic values of N d and V ( D ) are computed from measured droplet size distributions from the experimental campaign. A data-driven method is employed to establish strategic parameters for the simulation [15]. The process consists of fitting normalized DSDs with a theoretical model that combines the exponential distribution of Marshall and Palmer [33] with a Gaussian therm. Then, a data matrix containing the parameters of the fitted functions is created and Principal Component Analysis (PCA) is employed to reduce its dimensionality. Finally, a K-means model is used to define clusters that contain elements with similar features. Statistical analysis of the formed clusters allows the identification of average parameters that represent recurrent local types of precipitation, including drizzle, freezing rain and snowfall.
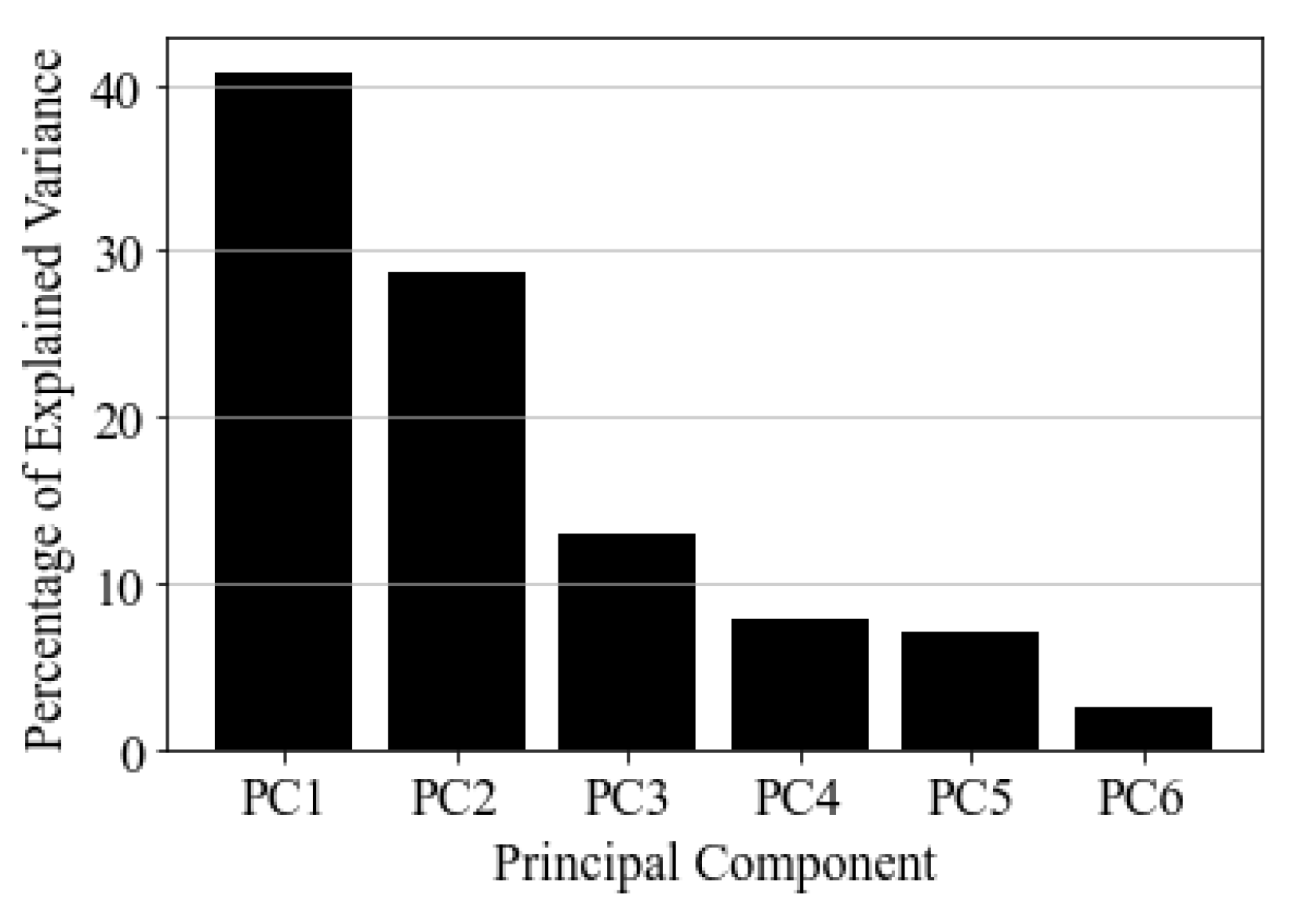
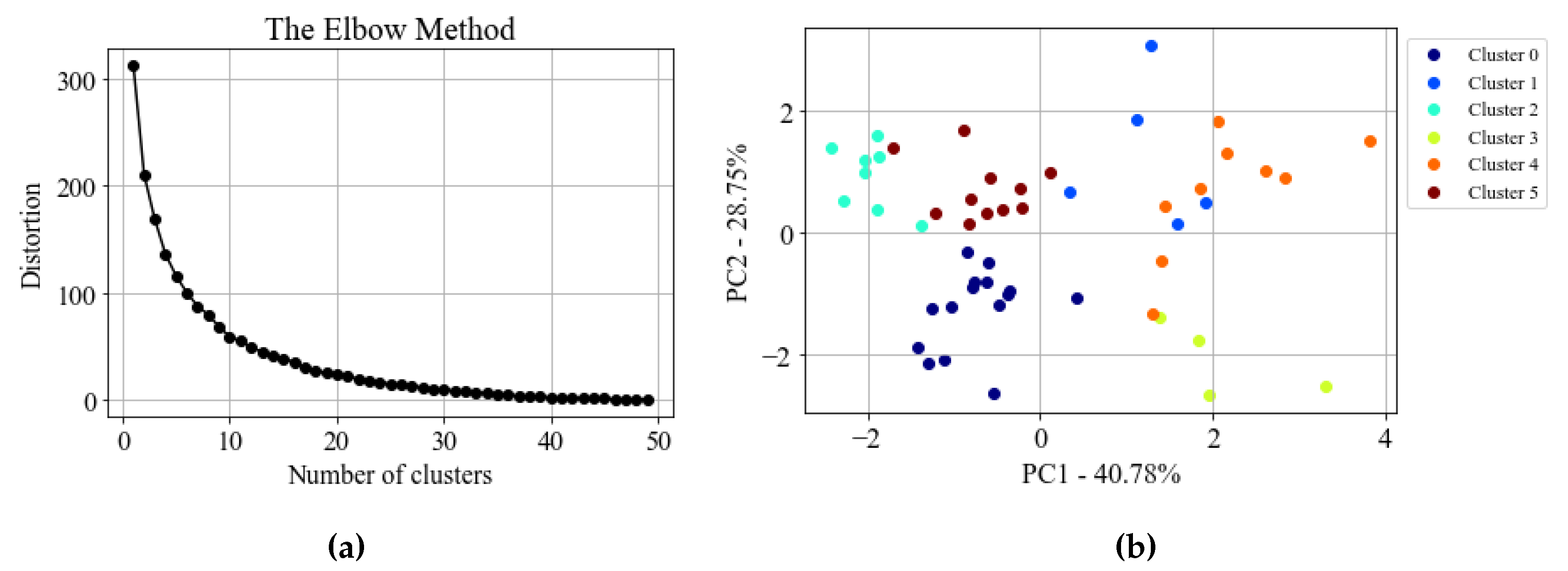
This method was applied to the entire rainfall data set that was formed throughout the project duration. Figure 6 shows the distribution of variance among the Principal Components of the data. PCA shows that more than 80% of the total variance is retained when considering the first three modes. To define the number of clusters for the K-means model, the elbow method was used. The curve in the Figure 7a shows that the variance within clusters starts to converge when the number of groups is approximately six. Figure 7b features the 2D scatter of the datapoints with their respective cluster.
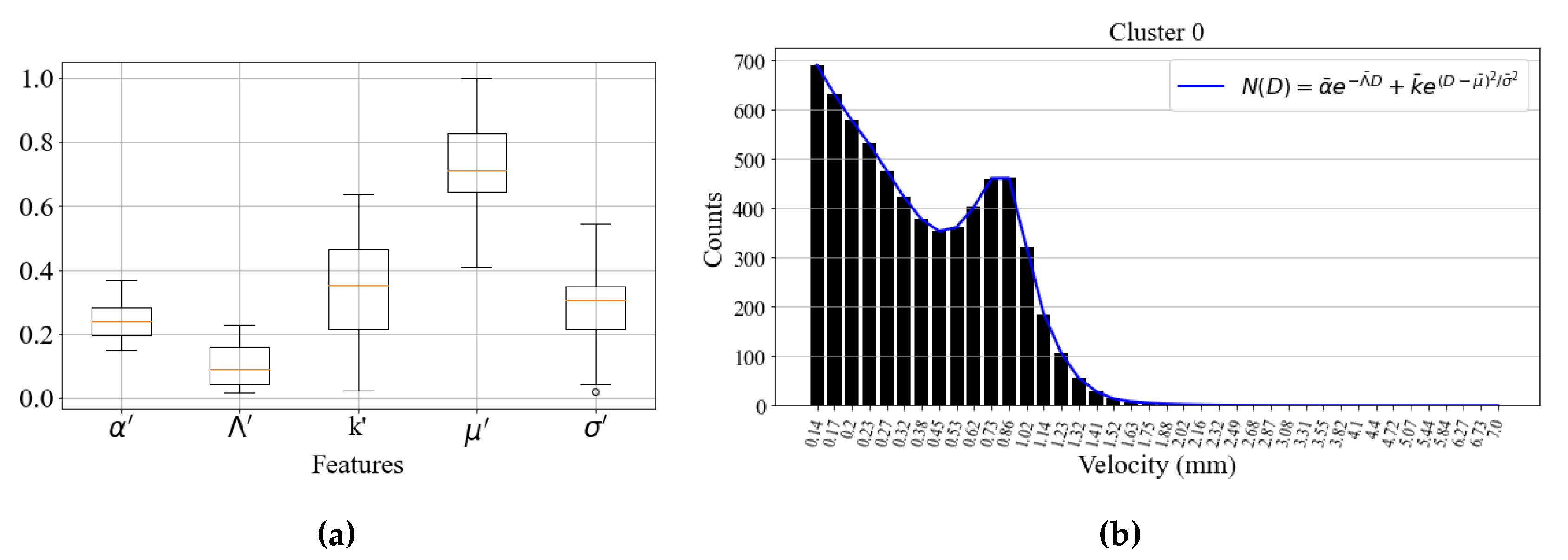
Since it contains the most samples, corresponding to 28.85% of total points, cluster 0 was chosen as the reference for setting the simulation parameters. By analyzing the parameter values of the theoretical model among its samples, it was possible to reconstruct a DSD that summarizes the characteristics of the cluster. It is important to mention that the generated distribution is normalized, so it is necessary to use an experimental sample to scale it. The criterion for the selection of this sample was the precipitation rate at the time of measurement. The sample of cluster 0 collected with the highest precipitation intensity value was chosen. Figure 8 shows the boxplot of the DSD model parameters of cluster 0 and the result of the reconstructed distribution. The operations described in Section 3.2 apply for the processing of the synthetic DSD to compute parameters such as the concentration number N d and the total droplet volume V ( D ) .

5. Simulation Results

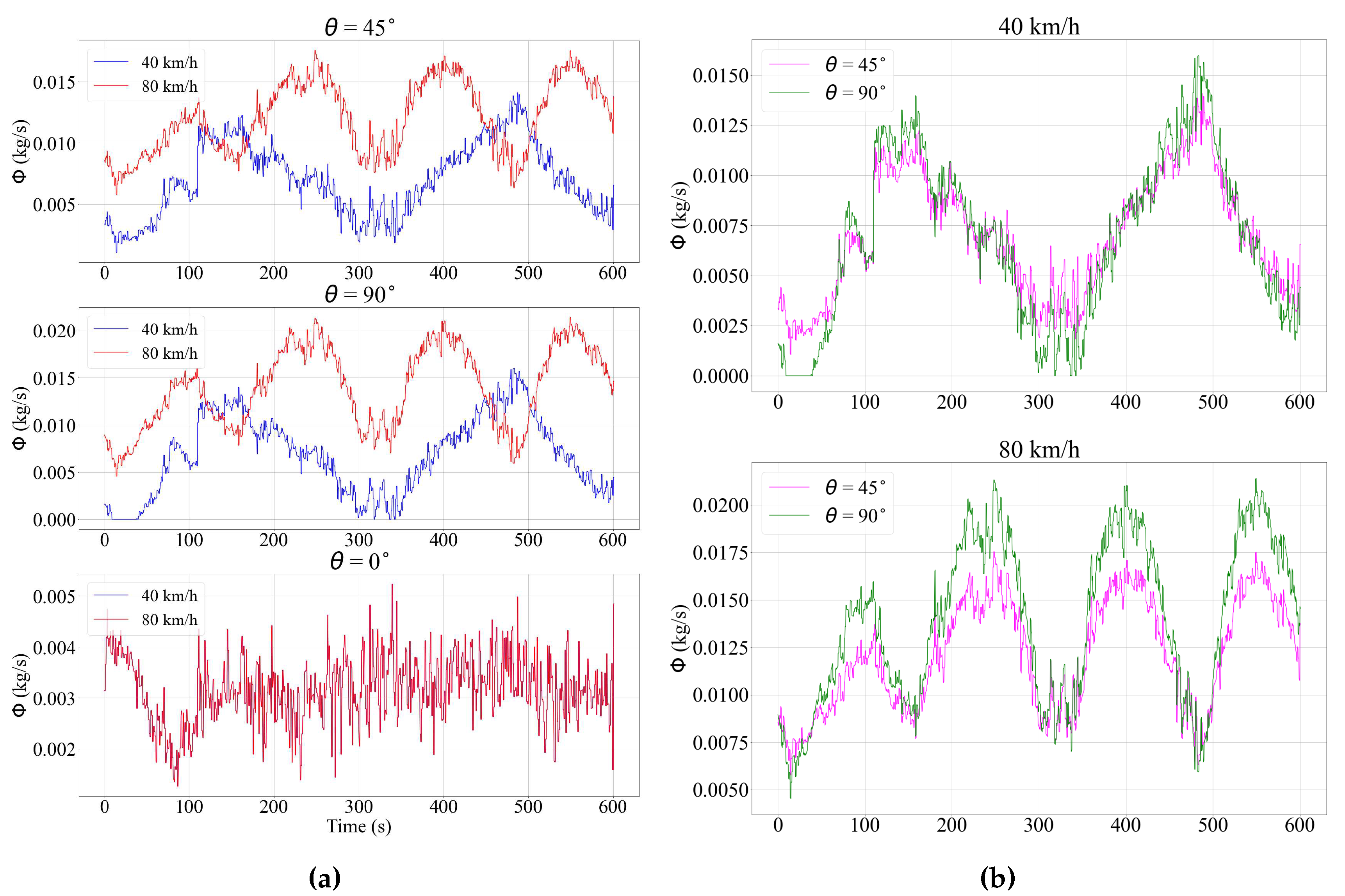
The described weather parameters were set to the same time scale and the simulations were launched for the circular trajectory mentioned at the beginning of the section in counterclockwise direction. The rain flux on three surfaces was computed for each time step of the simulation loop in order to generate individual time series for each orientation. The values of θ defined by the spherical system of coordinates used in the calculations were 90°, 45°, and 0°.
The simulation results for driving speeds of 40 and 80 k m / h , which were the same as those used in the data collection on the MATT track are shown in Figure 9. The flux values are compared for surfaces with the same orientation, but at different driving speeds (Figure 9), and test cases where the driving speeds are the same, but the angles vary (Figure 9). The first noticeable aspect of the time series is their periodicity as the surfaces alternate moments where they are directly exposed to wind and when they are shielded from it. This is due to the projection of the resultant vector v onto the vector normal to the surface S. When the vehicle travels upwind, the dot product between the vectors reaches higher absolute value, while traveling downwind generates lower flux. Consequently, the bell-shaped curves are wider at 40 k m / h as it takes longer to complete a full lap. On the other hand, the magnitude of the flux is larger when the driving speed is higher, which can be explained by the fact that the object sweeps more particles along the path. This can also be seen in Figure 9, where the flow at 90°becomes higher compared to the 45°angle when the surfaces are moving at 80 k m / h . The velocity vector of the vehicle determines the direction in which the precipitation projection will reach its maximum value.
For the horizontal surface, the flux values are the same for the two tested cases since only the drop velocity component normal to the surface is relevant to the model. In real life, the aerodynamics of the vehicle would influence the flux dynamics. Therefore, to make the model more accurate, data-driven methods are being developed to reduce the error arising from the air turbulence around the vehicle surface. Experimental campaigns are being prepared using meteorological towers as static referential in combination with the test vehicle to predict the level of precipitation experienced by the latter along complex trajectories.
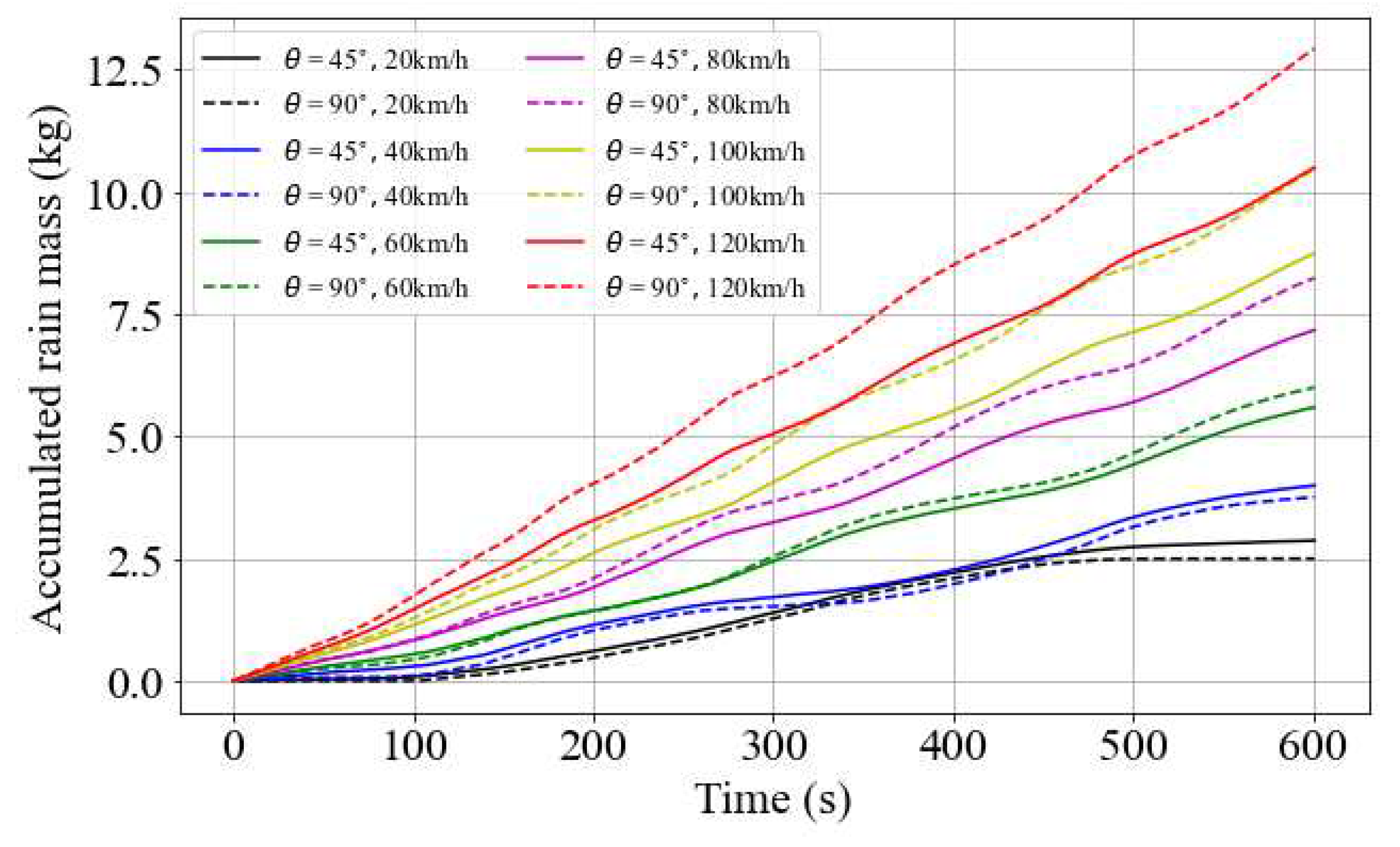
The fluxes over surfaces with different orientations behave in complex ways as they depend on variables that are susceptible to abrupt changes over time. Therefore, other driving speeds were tested under the same weather conditions and the flux over the surfaces where θ = 45 and 90 was integrated over time. The goal is to identify possible optimal driving speeds for minimizing the mass of encountered precipitation. Figure 10 shows the results of the simulation for velocities ranging from 20 to 120 k m / h . The accumulated rain mass shows that, when the exposure duration is imposed, the task of finding the optimal speed is not straightforward. As an example, driving at 40 k m / h proves to be more efficient than driving at 20 k m / h for a duration of between 350 and 450 seconds. In addition, the optimal orientation angle also depends on the driving speed. While the 90°angle shows lower flux values at low velocities, the same is not true for driving speeds above 40 k m / h . In the case at 120 k m / h , the rain mass over the vertical surface is 20% higher than over the plane at 45°. This issue is pertinent for the placement of sensors on AVs, especially when they are meant to operate at high speed, such as on highways.
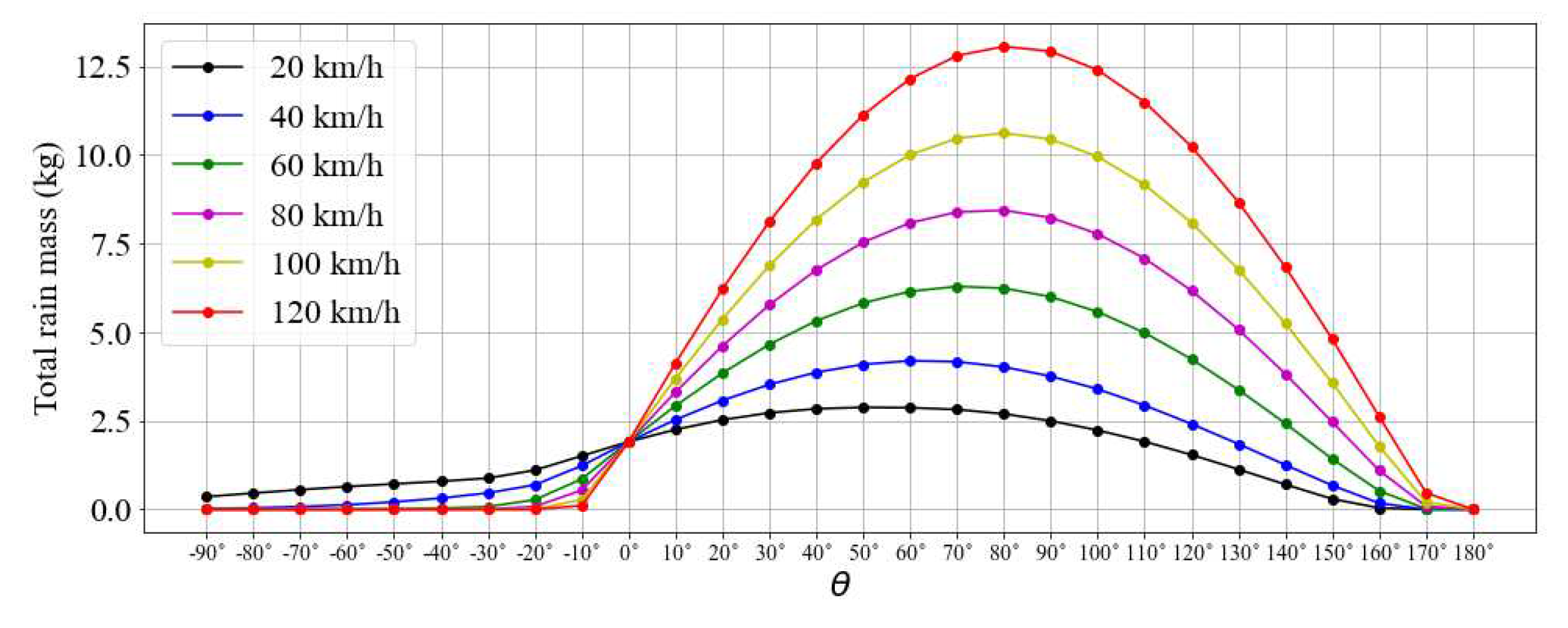
The results presented so far indicate that the optimal speed for traveling through rain must be evaluated instantaneously according to the weather conditions faced. The resultant vector between the vehicle displacement and the rain velocity dictates the value of the flux. In view of the complexity of the problem, Figure 11 aims to synthesize the various simulated scenarios showing maximum values of precipitation mass encountered for different surface orientations and driving speeds after 600 seconds. As can be seen, for all cases tested the model generates continuous curves that intersect at θ = 0 and 180. As discussed earlier, since the model does not account for the aerodynamics of the object, the flux value over horizontal surfaces does not change as a function of the driving speed. The curves also show that the flux is always lower over the rear. As driving speed increases, flux decreases over surfaces with more negative slope. The maximum points do not occur at the same angle, and they tend to approach 90°as the velocity increases. Finally, surfaces with normal vectors that point to the ground ( θ > 90 ) can offer effective solutions to minimize the level of precipitation over surface mounted sensors as they show reduced values of total rain mass that tend to zero as the angle increases.

6. Conclusion

In this paper, a model to quantify the level of weather precipitation perceived by moving vehicles is proposed. An analytical equation that predicts precipitation intensity over moving surfaces under rain or snow can serve as the foundation for data-driven methods to mitigate negative effects of weather stressors on the operation of autonomous vehicles. As prospects, the model can provide a physical background to prediction models for road safety management purposes. Also, the equation can serve as a cost function to be minimized by an agent exposed to weather precipitation conditions. Possible actions such as the adjustment of the traveling speed, trajectory and the location of sensors on strategic surfaces can be considered.
Up to this point, the issue of moving in the rain has been addressed to set optimal traveling speeds for linear paths under constant precipitation rate. Despite being consistent in their proposals, the created methodologies so far use oversimplifying hypotheses that cannot be considered in AV-oriented applications. Differently from previous studies, the present simulations target more realistic parameters regarding weather conditions and non-linear trajectories. Also, Dimensional Analysis was used to identify critical parameters of the problem. The non-dimensional groups found assisted in the design of the simulations as well as future experiments.
The rain flux model is based on electromagnetism equations but adapted to the issue of particles flow. It was conceived in such a way as to integrate data that can be obtained experimentally. The experimental apparatus used for the measurements as well as the processing chain of the sensor data is described in the paper. Partial validation tests have been done comparing direct measurements of precipitation rate with values coming from the model. The results present a strong correlation between theoretical and experimental values, showing that the model performs well for both rain and snow scenarios. Calibration experiments of the optical sensors that will be used in future campaigns are foreseen. Due to the orientation of the sensor during the experimental campaign, the comparison could only be done for the case where the surface is horizontal. Simulations based on real wind data highlighted the dependency of rain flux on wind direction while the integration of the results shows that the definition of the optimal travel speed depends on the projection of the resultant vector between vehicle and particle speeds over the sensing surface. However, it is known that aerodynamic forces can influence the flux value. Therefore, the model needs further development to account for this factor.
As a perspective for future experimental campaigns, simultaneous measurements will be conducted between the vehicle equipped with multiple disdrometers with different orientations and a meteorological tower. The goal is to analyze data from static referential combined with data collected in real time by the car. In addition, the future tests will aim to evaluate the influence of vehicle aerodynamics on the rain flux calculation. With this, it is expected that layers of complexity can be incorporated into the model presented in this present paper. With more accurate results, data-driven prediction methods using meteorological stations can be envisioned to be part of an intelligent road management system aimed at the safety of drivers.

Author Contributions

Conceptualization, M.C. and H.H.; methodology, M.C.; software, M.C.; validation, M.C.; formal analysis, M.C. and H.H.; investigation, M.C.; resources, H.H.; data curation, M.C. and H.H.; writing—original draft preparation, M.C.; writing—review and editing, H.H.; visualization, M.C.; supervision, H.H.; project administration, H.H.; funding acquisition, H.H.. All authors have read and agreed to the published version of the manuscript.

Funding

This research is part of a Canada Research Chair Tier 1 Program in Adaptive Aerodynamics and funded by Canada Foundation for Innovation.

Data Availability Statement

Due to privacy and ethical concerns, neither the data nor the source of the data can be made available.

Acknowledgments

This work is carried out as part of a Canada Research Chair Tier 1 program in Adaptive Aerodynamics which seeks to propose solutions to improve the operation of autonomous vehicle sensors under adverse weather conditions. The instrumentation of the road vehicle by the ACE team as well as insights into the use of the Vaisala WXT530 weather station by Dr. Ismail Gultepe are also acknowledged.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

If anemometer data is not available, the wind speed vector can be generated synthetically. To simulate the wind direction and velocity, a vector in three dimensions can be created. Its direction is defined by two angles, ϕ w in the x y plane, and θ w regarding the z axis, which form the unit vector:
w ^ = cos ϕ w , sin ϕ w , cos θ w | w |
Then, the magnitude of the speed follows a sinusoidal function of type:
v w ( t ) = v w 0 + k w sin ( f w t )
where k w is the amplitude of velocity variation and f w is the frequency of oscillation. The wind speed vector therefore has the form v w ( t ) w ^ .

References

  1. Vargas, J.; Alsweiss, S.; Toker, O.; Razdan, R.; Santos, J. An Overview of Autonomous Vehicles Sensors and Their Vulnerability to Weather Conditions. Sensors 2021, 21, 5397. Number: 16 Publisher: Multidisciplinary Digital Publishing Institute. [CrossRef]
  2. Favarò, F.M.; Nader, N.; Eurich, S.O.; Tripp, M.; Varadaraju, N. Examining accident reports involving autonomous vehicles in California. PLOS ONE 2017, 12, e0184952. Publisher: Public Library of Science. [CrossRef]
  3. Dixit, V.V.; Chand, S.; Nair, D.J. Autonomous Vehicles: Disengagements, Accidents and Reaction Times. PLOS ONE 2016, 11, e0168054. Publisher: Public Library of Science. [CrossRef]
  4. Szénási, S.; Kertész, G.; Felde, I.; Nádai, L. Statistical accident analysis supporting the control of autonomous vehicles. Journal of Computational Methods in Sciences and Engineering 2021, 21, 85–97. Publisher: IOS Press. [CrossRef]
  5. Van Brummelen, J.; O’Brien, M.; Gruyer, D.; Najjaran, H. Autonomous vehicle perception: The technology of today and tomorrow. Transportation Research Part C: Emerging Technologies 2018, 89, 384–406. [CrossRef]
  6. Hnewa, M.; Radha, H. Object Detection Under Rainy Conditions for Autonomous Vehicles: A Review of State-of-the-Art and Emerging Techniques. IEEE Signal Processing Magazine 2021, 38, 53–67. Conference Name: IEEE Signal Processing Magazine. [CrossRef]
  7. Dey, K.C.; Mishra, A.; Chowdhury, M. Potential of Intelligent Transportation Systems in Mitigating Adverse Weather Impacts on Road Mobility: A Review. IEEE Transactions on Intelligent Transportation Systems 2015, 16, 1107–1119. Conference Name: IEEE Transactions on Intelligent Transportation Systems. [CrossRef]
  8. Rabiei, E.; Haberlandt, U.; Sester, M.; Fitzner, D. Rainfall estimation using moving cars as rain gauges – laboratory experiments. Hydrology and Earth System Sciences 2013, 17, 4701–4712. Publisher: Copernicus GmbH. [CrossRef]
  9. Drobot, S.; Chapman, M.; Schuler, E.; Wiener, G.; Mahoney, W.; Pisano, P.; McKeever, B. Improving Road Weather Hazard Products with Vehicle Probe Data: Vehicle Data Translator Quality-Checking Procedures. Transportation Research Record: Journal of the Transportation Research Board 2010, 2169, 128–140. [CrossRef]
  10. Sziroczak, D.; Rohacs, D.; Rohacs, J. Review of using small UAV based meteorological measurements for road weather management. Progress in Aerospace Sciences 2022, 134, 100859. [CrossRef]
  11. Neumann, P.P.; Bartholmai, M. Real-time wind estimation on a micro unmanned aerial vehicle using its inertial measurement unit. Sensors and Actuators A: Physical 2015, 235, 300–310. [CrossRef]
  12. Palomaki, R.T.; Rose, N.T.; Bossche, M.v.d.; Sherman, T.J.; Wekker, S.F.J.D. Wind Estimation in the Lower Atmosphere Using Multirotor Aircraft. Journal of Atmospheric and Oceanic Technology 2017, 34, 1183–1191. Publisher: American Meteorological Society Section: Journal of Atmospheric and Oceanic Technology. [CrossRef]
  13. Chilson, P.B.; Bell, T.M.; Brewster, K.A.; Britto Hupsel de Azevedo, G.; Carr, F.H.; Carson, K.; Doyle, W.; Fiebrich, C.A.; Greene, B.R.; Grimsley, J.L.; et al. Moving towards a Network of Autonomous UAS Atmospheric Profiling Stations for Observations in the Earth’s Lower Atmosphere: The 3D Mesonet Concept. Sensors 2019, 19, 2720. Number: 12 Publisher: Multidisciplinary Digital Publishing Institute. [CrossRef]
  14. Hangan, H.; Agelin-Chaab, M.; Gultepe, I.; Elfstrom, G.; Komar, J. Weather aerodynamic adaptation for autonomous vehicles: a tentative framework. Transactions of the Canadian Society for Mechanical Engineering 2022. Publisher: NRC Research Press. [CrossRef]
  15. Carvalho, M.; Hangan, H. Machine Learning Method for Road Vehicle Collected Data Analysis. Journal of Applied Meteorology and Climatology 2023, 62, 755–768. Publisher: American Meteorological Society Section: Journal of Applied Meteorology and Climatology. [CrossRef]
  16. Stern, S.A. An optimal speed for traversing a constant rain. American Journal of Physics 1983, 51, 815–818. [CrossRef]
  17. Angelis, A.D. Is it really worth running in the rain? European Journal of Physics 1987, 8, 201–202. Publisher: IOP Publishing. [CrossRef]
  18. Holden, J.J.; Belcher, S.E.; Horvath, A.; Pytharoulis, I. Raindrops keep falling on my head. Weather 1995, 50, 367–370. [CrossRef]
  19. Bailey, H. On Running in the Rain. The College Mathematics Journal 2002, 33, 88–92. [CrossRef]
  20. Ehrmann, A.; Blachowicz, T. Walking or running in the rain—a simple derivation of a general solution. European Journal of Physics 2011, 32, 355–361. Publisher: IOP Publishing. [CrossRef]
  21. Bocci, F. Whether or not to run in the rain. European Journal of Physics 2012, 33, 1321–1332. Publisher: IOP Publishing. [CrossRef]
  22. Bertrand, J. Sur l’homogeneite dans les formules de physique. Cahiers de recherche de l’Academie de Sciences 1878, 86, 916–920.
  23. Rayleigh, L. VIII. On the question of the stability of the flow of fluids. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1892, 34, 59–70. Publisher: Taylor & Francis _eprint: . [CrossRef]
  24. Evans, J.H. Dimensional Analysis and the Buckingham Pi Theorem. American Journal of Physics 1972, 40, 1815–1822. [CrossRef]
  25. Curtis, W.D.; Logan, J.D.; Parker, W.A. Dimensional analysis and the pi theorem. Linear Algebra and its Applications 1982, 47, 117–126. [CrossRef]
  26. Bakarji, J.; Callaham, J.; Brunton, S.L.; Kutz, J.N. Dimensionally consistent learning with Buckingham Pi. Nature Computational Science 2022, 2, 834–844. Number: 12 Publisher: Nature Publishing Group. [CrossRef]
  27. Frasson, R.P.d.M.; da Cunha, L.K.; Krajewski, W.F. Assessment of the Thies optical disdrometer performance. Atmospheric Research 2011, 101, 237–255. [CrossRef]
  28. Acharya, R. Chapter 7 - Tropospheric impairments: Measurements and mitigation. In Satellite Signal Propagation, Impairments and Mitigation; Acharya, R., Ed.; Academic Press, 2017; pp. 195–245. [CrossRef]
  29. Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Cohen, I.; Huang, Y.; Chen, J.; Benesty, J., Eds.; Springer Topics in Signal Processing, Springer: Berlin, Heidelberg, 2009; pp. 1–4. [CrossRef]
  30. Kikuchi, K.; Kameda, T.; Higuchi, K.; Yamashita, A. A global classification of snow crystals, ice crystals, and solid precipitation based on observations from middle latitudes to polar regions. Atmospheric Research 2013, 132-133, 460–472. [CrossRef]
  31. Ghaderpour, E.; Dadkhah, H.; Dabiri, H.; Bozzano, F.; Scarascia Mugnozza, G.; Mazzanti, P. Precipitation Time Series Analysis and Forecasting for Italian Regions. Engineering Proceedings 2023, 39, 23. Number: 1 Publisher: Multidisciplinary Digital Publishing Institute. [CrossRef]
  32. Atlas, D.; Srivastava, R.C.; Sekhon, R.S. Doppler radar characteristics of precipitation at vertical incidence. Reviews of Geophysics 1973, 11, 1–35. _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1029/RG011i001p00001. [CrossRef]
  33. Marshall J., S. The distribution of raindrops with size. J. Meteor. 1948, 5, 165–166.
Preprints 79232 g001
Figure 1. 2D representation of a moving vehicle in the rain with sensing surface S oriented at θ degrees.
Figure 1. 2D representation of a moving vehicle in the rain with sensing surface S oriented at θ degrees.
Preprints 79232 g001
Preprints 79232 g002
Figure 2. The WoW vehicle used for field measurements [15].
Figure 2. The WoW vehicle used for field measurements [15].
Preprints 79232 g002
Preprints 79232 g003
Figure 3. Comparison between scaled readings of rain precipitation intensity, represented as I, from Vaisala FD70 disdrometer and theoretical flux model on horizontal surface for different driving speeds.
Figure 3. Comparison between scaled readings of rain precipitation intensity, represented as I, from Vaisala FD70 disdrometer and theoretical flux model on horizontal surface for different driving speeds.
Preprints 79232 g003
Preprints 79232 g004
Figure 4. Comparison between scaled readings of snow precipitation intensity (I) from Vaisala FD70 disdrometer and theoretical flux model on horizontal surface for different driving speeds.
Figure 4. Comparison between scaled readings of snow precipitation intensity (I) from Vaisala FD70 disdrometer and theoretical flux model on horizontal surface for different driving speeds.
Preprints 79232 g004
Preprints 79232 g005
Figure 5. Wind speed components recorded with CSAT3 sonic anemometer.
Figure 5. Wind speed components recorded with CSAT3 sonic anemometer.
Preprints 79232 g005
Preprints 79232 g006
Figure 6. Variance of Principal Components. The chart shows that approximately 70% of total variance is contained in the two first PCs.
Figure 6. Variance of Principal Components. The chart shows that approximately 70% of total variance is contained in the two first PCs.
Preprints 79232 g006
Preprints 79232 g007
Figure 7. (a): Elbow curve used to choose the number of K-means clusters. The distortion is obtained by the sum of the squared distances between the points and their centroid within the clusters. (b): 2D scatter of datapoints with the indication of their respective cluster.
Figure 7. (a): Elbow curve used to choose the number of K-means clusters. The distortion is obtained by the sum of the squared distances between the points and their centroid within the clusters. (b): 2D scatter of datapoints with the indication of their respective cluster.
Preprints 79232 g007
Preprints 79232 g008
Figure 8. (a): Boxplot of the model parameters contained in cluster 0. (b): Synthetic 60-seconds DSD generated from the average model parameters of cluster 0. The blue curve shows the theoretical model used to build the distribution.
Figure 8. (a): Boxplot of the model parameters contained in cluster 0. (b): Synthetic 60-seconds DSD generated from the average model parameters of cluster 0. The blue curve shows the theoretical model used to build the distribution.
Preprints 79232 g008
Preprints 79232 g009
Figure 9. Results of simulation using real wind data. Figure 9: For the same surface orientation, the rain flux is compared at the driving speed, 40 and 80 k m / h . Figure 9: For the same driving speed, values of rain flux are compared at different angles.
Figure 9. Results of simulation using real wind data. Figure 9: For the same surface orientation, the rain flux is compared at the driving speed, 40 and 80 k m / h . Figure 9: For the same driving speed, values of rain flux are compared at different angles.
Preprints 79232 g009
Preprints 79232 g010
Figure 10. Integral of flux over time for different driving speeds and surface angles.
Figure 10. Integral of flux over time for different driving speeds and surface angles.
Preprints 79232 g010
Preprints 79232 g011
Figure 11. Total rain mass encountered as function of the surface orientation.
Figure 11. Total rain mass encountered as function of the surface orientation.
Preprints 79232 g011
Table 1. Pearson correlation coefficients between model results and FD70 measurements.
Table 1. Pearson correlation coefficients between model results and FD70 measurements.
Rain Snow
0 km/h 40 km/h 80 km/h 0 km/h 30 km/h 80 km/h
0.95155 0.95422 0.99241 0.93424 0.91836 0.88894
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Modelling Precipitation Intensity Impacting Vehicles in Motion

Mateus Carvalho

et al.

,

2023

The Effect of Rainfall and Illumination on Automotive Sensors Detection Performance

Hexuan Li

et al.

,

2023

Optimizing Lane Departure Warning System Towards AI-Centered Autonomous Vehicles

Siwoo Jeong

et al.

,

2024

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated