Prerpints.org logo
Preprint
Article

Skeletal Space Structure Systems: Select Areas of Opportunity to Achieve Sustainability in Construction

Altmetrics

Downloads

79

Views

17

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 July 2023

Posted:

13 July 2023

You are already at the latest version

Alerts
Abstract
This paper examines some of the largely neglected areas of opportunity to utilize skeletal space structure systems in support of modular, industrialized, economical, sustainable and digital future of the construction industry. In this context, the feasibility of future use of skeletal space structures is studied for a few classes of engineering structures, namely, residential apartment buildings, and offshore platforms, along with their suitability for reconstruction, renovation, modernization and retrofit of damaged buildings and urban areas of cultural heritage significance. Finally, the particulars of lean project management of space structures are discussed with emphasis on engineering and economic factors, production management, environmental aspects, quality management, and reliability, maintainability and sustainability considerations. This article concludes that skeletal space structures can fulfil many of the essential construction requirements of modern societies, especially those facing environmental challenges, all while allowing for design flexibility and mass customization.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Skeletal Space Structure Systems

Skeletal space structure systems are modular, kit-of-parts ready [1], solutions comprised of a combination of spatial frames and trusses that may be arranged in various formations, such as double and triple layer grids, braced barrel vaults, and braced domes. Initial advancements in theory and practice of skeletal space structures have been well documented by Makowski [2,3,4]. These systems are lightweight, suitable for fast and easy fabrication/erection/dissembling, and scalable to promote economic mass production and industrialization. Originally, skeletal space structure systems were used predominantly as roof structures -particularly where large spans with load distribution in both perpendicular directions was desired- to satisfy the basic demands for fast and economical reconstruction and redevelopment after World War II. Later, due to changing construction demands, and with the advent of new materials [5] (e.g., wood dome, Figure 1c), construction techniques [6] (e.g., free-form botanic garden, Figure 1a), and computational engineering approaches [1] (free-form roof modules; Figure 1b), many architectural and engineering practitioners concentrated on creating innovative and geometrically custom space structural forms for attractive and free-form monumental buildings [7]. As such, in addition to the customary usage of modular space structures for mass production, the skeletal space structure systems can be utilized to design custom structures in terms of shape, geometry and characteristics. These established applications demonstrate that skeletal space structure systems are prime candidates for mass customization [8] with design flexibility to tackle a variety of societal demands.
Today, with the sudden incline in costs of construction [9], localized shortage of skilled labour [10], limitations in energy reserves, and concerns over climate change [11], the construction industry requires fast, economical, energy efficient, low-Carbon, and preferably locally sources solutions, particularly through industrialization, modularization, and mass customization strategies. To this end, in this paper, the potentialities of skeletal space structure systems in largely disregarded and vast areas of suitable applications are examined. In this context, the feasibility of future large-scale use of skeletal space structures has been studied for a few classes of engineering structures, namely, bridges, residential buildings, and offshore platforms, along with their applications in rehabilitation, renovation, modernization, and reconstruction of existing facilities, including cultural heritage buildings. It will be shown here that by prioritizing safety, functionality, performance, durability, maintainability, sustainability, cost-effectiveness, ease of construction, and construction quality in conjunction with aesthetics, skeletal space structures may be employed to meet many of the fundamental needs of contemporary societies, experiencing environmental issues, without sacrificing design flexibility and customization.

2. Select Areas of Opportunity Using Skeletal Spatial Structure Systems

Many innovative free-form space grids have been built that have proven their virtually unlimited capabilities for creating fascinating structures of unique character (see Figure 1a,b). Here, three new and overlooked areas of application of space grids are discussed, for which the structural forms are modular in nature. This modularization not only offers the benefits of prefabricated mass production and customization for efficient erection and dissembling, but also provides suitable bases to form repeating patterns in the corresponding structural stiffness matrices. Hence, by devising suitable numerical approaches, their analysis procedures become extremely easy and numerically stable (see Maalek [12,13] for more details).
The three new areas of application discussed in this manuscript are: (i) low to medium rise steel space frame buildings; (ii) Offshore steel jackets, including offshore wind turbine supports; and (iii) reconstruction of geometrically significant heritage dome structures. The application of spatial grids in bridge decks of composite double-layer steel grids and reinforced concrete are discussed in a separate manuscript. Each application area is discussed and its structural performance is compared to a common construction type as basis/benchmark for comparison. Moreover, the considerations and important discussions pertaining to factors, such as sustainability, management, production, inspection, health monitoring, architectural significance and aesthetics are provided. A summary of the applications and presented analysis and discussions are given in Table 1.
Table 1. Summary of Experiments, Analysis and Discussions.
Table 1. Summary of Experiments, Analysis and Discussions.
Considered Application Areas Type of Analysis Benchmark for Comparison Further Considerations and Discussions
Low to medium rise buildings
  • Single span with one and three storey
  • Seismic non-linear analysis
  • Material consumption
  • Moment frame
  • Braced-frame
  • Architectural design
  • Structural and seismic response
  • Mass production economics
  • Inspection, health monitoring and safety
  • Sustainability and resilience
  • Three and five storey
Offshore jacket structure
  • Static and dynamic non-linear analysis
  • Material consumption
 Completed project in the Persian Gulf
  • Structural behaviour
  • Economy of design and construction
  • Fatigue analysis
  • Sustainability
Reconstruction of cultural heritage dome structures Seismic Behaviour Analysis
  • Bam earthquake
  • Reconstruction for the damaged city by earthquake
  • Feasibility of reconstruction and retrofit
  • Economic considerations
  • Reliability under severe earthquakes
  • Seismic buckling
  • Local failure
  • Sustainability

2.1. Low to Medium Rise Apartment Buildings

The considerable rigidity and the low weight of double layer space grids exhibit high potentialities for their use as residential, administrative, educational and commercial buildings and hospitals. Such buildings are normally constructed by steel moment frames, braced frames or reinforced concrete frames with or without shear walls. In the proposed space grid system, the floors are considered to be double layer grids in composite action with reinforced concrete topping and the walls are partially or fully made of double layer grids, tailored for mass production and geometric and size customization. High redundancies of such systems leading to their high reliability against progressive collapse, their relatively extremely light weight and controllable ductility are key factors that make them distinguishable from many other customary types of building construction. Only perimeter walls are needed and up to the normal sizes of such buildings, floors can be designed such that no internal or intermediate columns are required. Openings in walls and floors can be, hence, provided with no difficulties. A variety of suitable claddings and methods of insulation are available, which can be utilized. These provide invaluable freedom of design and functionality for architects, along with support for low-energy and passive housing. To begin with, schematic views of a simple single-storey and an analogues three-storey building composed of double layer grid floors and perimeter walls are shown in Figure 2a,b, respectively.

2.1.1. Single-Storey Building: Benchmark Experiment Setup

First, some of the basic characteristics of such systems are investigated through simple examples with an emphasis on their seismic behaviour. Consider a 7.6 by 7.6 by 3.5 m single storey space structure as shown in Figure 2a. The roof grid layers have been chosen to be 500mm apart and the centre to centre distance of the grid layers of walls is 300 mm. Using an elastic design approach (e.g., [14]), we have designed a space grid consisting of modular pyramidal units as well as two types of moment frame structures, one with an internal column and one without any internal columns, as reference benchmark design. Obviously, for larger spans, the omission of internal columns in the moment frame system (the reference benchmark) may not be feasible.

2.1.2. Single-Storey Building: Seismic Behaviour Compared to Benchmark

The result of a push over analysis for the space frame system with the imposition of certain limitations on the slenderness ratios for certain members at the corners (vertical and diagonal members) resulted not only in 37% less structural steel weight, but also 2.5 times higher ultimate strength compared with the moment frame. In fact, preventing buckling is crucial in achieving a balanced system with high resistance and rigidity as well as an acceptable ductility. Furthermore, we limited the slenderness ratios for all the floor members to 90, all the vertical wall members to 60 and the diagonal wall members to 50. This structure responded without a sign of failure during a nonlinear dynamic analysis under simultaneous application of the time history of three translational components of the earthquake recorded at Altadena (from United States Geological Survey) with the Peak Ground Acceleration magnified to the gravitational acceleration (i.e., 1.0g) as shown in Figure 3a–c. The lateral load-lateral displacement relationships resulting from a push over analysis (Figure 3d) reveals that a desirable ductility can be achieved in design by preventing failure through member buckling and brittle fracture of connection bolts and other modes of failure.
In Figure 3, the results presented by thicker and thinner lines correspond to the compression member behaviour based on FEMA 365 [15].

2.1.3. Three-Storey Building: Seismic Behaviour Compared to Benchmark

As another example, we consider a three-storey apartment building with double layer composite grids as floors and double layered grids provided partially to act as both the load bearing walls and the lateral load resistant system (Figure 2b). The overall plan dimensions of the system have been taken as 22 m by 11 m. To compare the above with corresponding moment and braced framed models, the usual practice of the design of such buildings with internal columns was used. Hence, our moment resisting frame model had 4 internal columns that limits architectural freedom.
A spatial braced frame with “X” bracings was also designed with the same positions of columns. Longitudinal bracings were positioned along the perimeter walls, but transverse bracings were located within the plan area to avoid obstructing the entrance. Usual design practice based on the Iranian Codes (MPORG 2009 and NBR 2008) was followed. In the case of space grid system, the structural weight (and hence the steel material consumption) was found to be about half (50%) of the moment frame and 60% of the braced frame sample structures. Figure 4a,b show the dominant first and seventh modes of vibration of the space grid building. The first and second modes contributed significantly in the horizontal x and y directions, but the seventh mode, dominant in the vertical z direction, only contributed as much as 35%. To capture at least 90% of the equivalent mass contribution, up to 100 modes were needed to be taken into consideration in a response spectrum analysis.

2.1.4. Regular Building with Composite Double-Layer Grid Floor

In another study, a rather regular building was considered. The building was composed of composite 1x1 m2 square on square double layer grid floors which is well suited to mass production, in composite action with a rather thin reinforced concrete two way slab. The building plan was a square of 27 m in dimension and included a 7x7 m2 central core usually used to accommodate lifts and their surrounding stairways. All the double layer grids were 50 cm in depth and the gross storey height was taken as 3.5 m. As far as the gravitational and lateral load bearing structural system was concerned, three different configurations were employed for the purpose of comparison with each other and with the widely used traditional concentrically braced moment frame dual system considered here as a benchmark. The three configurations had been chosen as follows:
  • The lateral load bearing elements were concentrated around the position of the central core,
  • The lateral load bearing elements were placed at the four corners of the building in the form of four corner angles, in the plan view and
  • The lateral load bearing elements were considered as a combination of (1) and (2) above.
Preliminary investigations shown in Figure 5 revealed that the type (3) above, which consisted of the lateral load bearing elements at both the core and the four corners, was more efficient in terms of the structural weight, stiffness and force distribution.
Figure 5c shows the square on square double layer space grid structure for a typical floor. The topping concrete has not been shown for clarity. Figure 5a,d show the plan and perspective views of the space grid structure type (3) mentioned above, respectively. Plan and perspective views of a traditional (or common) type of structure widely used for such buildings (i.e., a dual system composed of moment frames combined with concentric bracings with an analogous form) are shown in Figure 5b,e. Composite castellated beam and slab system has been used as the floor structure. It is to be noted that the thickness of the concrete topping is higher in this system due to one-way action of the concrete top slab, while in the case of the double layer composite flooring, the slab acts in two-way. Another matter of utmost significance is the use of intermediate columns in the braced frame system that limits the architectural freedom that can easily be granted with the use of the double layer grid system that can cover large spans without internal columns. This is an immense advantage, particularly in the parking areas and where a relatively large spans are needed without intermediate columns. The floor system is of the type The intended configurations have been generated easily by Formian software [16], which is a versatile tool for generating topological and geometrical information of spatial structural configurations and the finite element meshes.
In the analysis model of the spatial grid construction, truss elements have been used to represent spatial grid members and thin shell/plate elements to stand for the reinforced concrete topping. The design of the sample buildings have been carried out to meet the requirements of [14,17] Figure 5f shows the first mode shape of the space grid structure resulted from the generalized eigenvalue analysis of the structural stiffness and mass matrices. Figure 5g shows the contour of dead load vertical displacement for a typical composite double layer grid floor. Quantitatively, the weights of the designed sample structures are given in the 3-D bar chart of Figure 5h. It can be seen that the weight of the type (3) space grid structure is the least of all the other systems investigated here and in all the cases, the space grid system is considerably lighter than the analogous conventional braced moment frame system. It is interesting to note that in the spatial grid systems, the weight of the structure reduces from type (1) towards the type (3) lateral load bearing system configurations; while this is not so in the braced moment frame structures for which even slight increase in the weight is noticeable in the type (3) configuration compared to others. In brief, the structural weight of the type (3) configuration (both the weight of steel shown in the figure as well as the weight of the concrete slab) is about half that of the corresponding braced moment frame. Technically, the space grid system is a safer structure due to its considerable better behaviour against progressive collapse. Further studies focusing on the nonlinear static (push over) and dynamic behaviour and the seismic response of the proposed double layer spatial structural system for buildings have already been reported in [18]. An investigation has revealed the potentialities of increasing the system ductility (and hence, the seismic behaviour factor) by utilizing the joint flexibility [19] and energy dissipation capabilities introduced in the joints of the lateral load bearing double layer walls [20]. Qualitatively, the omission of intermediate columns provides an unmeasurable advantage for the architectural designers. Environmentally, making use of the proposed system instead of the common framed and braced frame steel structures results in much less destruction of the environment in exploring steel and raw materials for cement and concrete and at the same time, much more savings in energy consumed for the production of significantly more additional steel, cement and aggregates are made. Reduced energy consumption apparently helps in reducing the related pollution.

2.1.5. General Construction and Functionality Considerations

Other than some of the important considerations provided in section 2.1.3, additional practical construction considerations of the proposed building system in terms of architectural design, mass production economics, inspection and safety, and sustainability are discussed in the following
  • Architectural design: Consider the two types of structures compared above, namely, one with space grid floorings with some partial double layer grid walls, only at a few panels and the other, braced moment frame dual system with internal columns. It is clear that the space grid structure with no internal columns provide the designer with significant flexibility in their architectural design, particularly in parking areas, conference rooms and interior partitioning and design. Passages for electrical, piping and ventilation works can be accommodated without concerns about clashes with structural members, such as beams and columns, enhancing functionality. In terms of absolute available plan area, the commonly used framed buildings usually contain 250 to 300 mm thick perimeter walls. Here, the proposed system with partial double layer grid walls provides nearly the same net plan area as the moment frame system with internal columns and slightly larger net available area compared with the braced frame model discussed above. However, the framed and braced frame samples studied here are truly far behind the proposed system in terms of functionality due to their span limitation that makes the existence of intermediate columns unavoidable.
  • Mass production economics: Such systems are most effective when mass fabricated within well-organized and lean industrialized production lines, followed by effective on-site management. This requires an initial investment for the construction of the manufacturing plant. Hence, the cost of a building constructed by this system should also include its part from initial investment in addition to the cost of materials, manufacturing, transportation and erection as well as the costs of serviceability, maintenance and possible demolition and recycling. Investigations need also be carried out to calculate the man-hour per meter of apartment buildings of the type discussed here in different parts of the world. A factory mainly designed for the housing industry should be designed for a predefined service life and production capacity. Particularly, in locations at risk of earthquake with shortage of skilled labour (e.g., for welding), a number of space grid manufacturing plants may be designed and constructed (based on the demand) to begin mass-production and mass-customization of fast, safe, economic, functional, reliable and aesthetically pleasing houses, schools, hospitals, administrative and other buildings to meet the ever-increasing demand of modern societies with the long-term satisfaction of the customer (human-centric) in mind.
  • Inspection, health monitoring and safety: Every part of the main structure can be easily accessible for inspection and maintenance. The space between the double layer grids can be used for the passage of piping and future inspection and maintenance as described for the decking system. As such, due to the existence of adequate space between elements, the system is a viable candidate for intelligent and/or smart structural systems. Fire resistance is an issue of concern; however, tests of Du Chateau [21] on large span double layer roof structures had shown good fire resistance. In fact, due to pronounced resistance of the highly indeterminate and redundant space structural systems, local failure can rarely lead to progressive collapse and the structure is usually capable of providing an alternative load path to withstand fire for a relatively considerable time. Desirable seismic performance as a result of their light weight and redundancy has been achieved and demonstrated in by [18,20]. Finally, a variety of soil structure interaction issues are to be further clarified. Advanced researches need further be conducted aiming at achieving resilient structures through desirable proportioning of strength, stiffness, ductility, damping and energy dissipation capability of such structures in the framework of the performance-based design philosophy.
  • Sustainability: Using the proposed system, all the aforementioned versatilities were made possible using only less than half of the structural materials used to construct the moment frame or braced moment frame systems, which also required obstructing and impeding internal columns. This reduction in weight reduces both the embodied energy and embodied Carbon for construction, which will be even further noticed in mass-production and customization settings. Due to the flexibility in design, particularly to add openings and windows around the structure with minimal obstructing structural members (such as load-bearing walls, columns and beams), natural lighting can be designed to be provided at any place as desired. This in turn increases the average daylight factor (ADF [22]) considerably, supporting low-energy and passive housing, particularly in mass-production settings. The structure can be designed to be dismountable for re-use or recycling.

2.2. Offshore Structures

For several decades, offshore structures have been designed and built with the use of welded tubular members. Valuable experiences have been gained during the design, installation and operation of such platforms. As many other engineering evolutions, alongside admirable achievements, some drawbacks still persist as a consequence of the intrinsic nature of welded tubular structures under the action of variable amplitude fatigue loading caused by influential actions; a problem that has resulted in the need for costly continuous permanent monitoring and inspection of the underwater structure joints. all the grown defects may not be timely recognized. The fatigue monitoring Gauges developed by the Fatigue Monitoring Bureau at UMIST helped a great deal in monitoring critical points and hot spots remotely at positions where the gauges have been installed (Fatigue Monitoring Bureau, 1989 onwards, commercially in confidence). Hence, Locating and installation of such gauges should be such that no critical point is missed. In other words, by all means, all the grown defects may not be timely recognized. Obviously, the tubular structures currently employed for the construction of offshore platforms as every other structure behave three dimensionally in nature as braced space frames. However, a clear distinction should be made here between those structures referred to as skeletal space trusses and the usual tubular structures. At this stage we concentrate on the jacket type of platforms for use on rather shallow sea beds. During these several decades, the behaviour of such tubular jackets has been an active area of research [23].
Thanks to the intrinsic advantages of space grid structures, such as excellent performance in preventing progressive collapse, the authors have been investigating the potential usage of double layer skeletal spatial structures with suitable connections for offshore platforms. The work can be equally extended to the offshore platforms for wind turbines persuading the use of this type of renewable energy technology [23,24].

2.2.1. Preliminary Studies: Offshore Double-Layer Spatial Grid Jacket

The initial step is to carry out an initial overall feasibility study of such proposed alternative structures from the conceptual design point of view as well as the fabrication and erection and hence, here, the emphasis has been made on the overall system behaviour. Accordingly, rather simple configurations have been studied. Figure 6a shows a simplified double layer grid to represent a deck of such a structure. In Figure 6b, a typical Jacket type structure, formed as an assembly of typical modules of the constituent double layer grids, is shown. For this jacket type structure on a shallow sea bed the foundation could be constructed with the use of steel piles, precast concrete caissons at corners, strip foundation with reinforcement at corners, and so on. Variables considered in the initial parametric studies were the widths at the top and bottom, the height, the thickness (distance between two grid layers) and the density (the number of sub-divisions).
An existing offshore platform in the Persian Gulf has been used together with its design documents to act as an acceptable benchmark with the following data: water depth (normal operational condition): 47.2 to 49.2 m; water depth in extreme tidal condition: 47.2 to 50.1 m. Furthermore, the Effects of buoyancy were studied at two extreme cases:
  • Sealed members and solid nodes; and
  • Submerged condition.
Results of an automated design and redesign loop based on the normal engineering calculations/judgment revealed that the proposed space truss jacket had 25% less weight compared with the benchmark existing project. Furthermore, considerable steel material saving was possible by using double and triple layer grids in place of the traditional flooring to save the material consumption of the deck by 50% of the traditional one. At the same time, the displacement of the space grid jacket had been reduced considerably under the design current and wind loading indicating higher rigidity of the spatial grid platform.

2.2.2. Real-World Study: Off-Shore Platform in the Persian Gulf

In a more refined study, another existing offshore platform constructed in the Persian Gulf in 1991 was employed as the benchmark structure. The platform is mainly constructed to accommodate the technical personnel together with some heavy equipment. It has been installed on the sea-bed at the depth of 60 meters. The jacket is symmetric and regular. The decks are supported on 4 batter piers/piles at the four corners with the slope of 1 to 10. The width of the jacket at the top working point is 12.2 m. The platform has a boat landing, two bumpers, 24 inch fire pipe lines and other common facilities and equipment. Some noteworthy geometrical characteristics are given in Table 2.
Table 3. Noteworthy levels with respect to the mean free sea water level (TWI, 2013).
Table 3. Noteworthy levels with respect to the mean free sea water level (TWI, 2013).
Working point: (+) 6.50 m
Pile connecting to Leg: (+) 4.93 m
Level-1: horizontal bracing (+) 4.00 m
Level-2: horizontal bracing (-) 11.00 m
Level-3: horizontal bracing (-) 27.00 m
Level-4: horizontal bracing (-) 44.00 m
Mud-Mat (-) 60.00 m
Cellar Deck: (+) 10.10 m
Lower Deck: (+) 14.80 m
Upper Deck: (+) 18.60 m
Roof Deck: (+) 22.40 m
Helideck: (+) 25.40 m
According to the design documents, the weight of the structures of the decks and the deck to pier structure is 215 tons and the weight of the jacket piers/piles above the sea-bed is 426 tons. The sum of the design live loads on all the decks are 752 tons and the total weight of flooring corrugated plates, railings, etc. are 117 tons. Other related weights such as the weights of boat landing and bumpers have also been taken into account.
Utilizing Formian [25], four different structural configurations were generated with different geometrical forms, density, and etcetera. A consistent approach was adopted to ensure reliability of designs to make a meaningful comparison possible. API Design Criteria and Procedures [26,27] have been followed considering load cases, loading conditions and combinations taking available regional data and design guidelines into consideration; including Dead Loads, Live Loads, Environmental Loads, Construction Loads, Static and dynamic Wave Loads, accounting for Marine growth thickness and roughness, Wind Loads, Current, Hydrodynamic and Earthquake Loads, Fabrication, Handling, Launching and installation forces, and so on.
For the purpose of all the static and dynamic analyses, SAP 2000, Version 14 [28] was used together with its steel design module. The requirements of API [26,27], AISC [14] and Code of Practice for the design of Space Structures [17] were simultaneously met. The seismic analysis included push over, response spectrum as well as the time history analyses based on the results of seismic risk analysis carried out for the region (i.e., recommended Peak Ground Acceleration and Design Response Spectrum). The time history analyses were carried out under excitation of seven different recorded actual earthquake time histories that had taken place around the region (PEER data base [29]) from which the average response values were used in design.
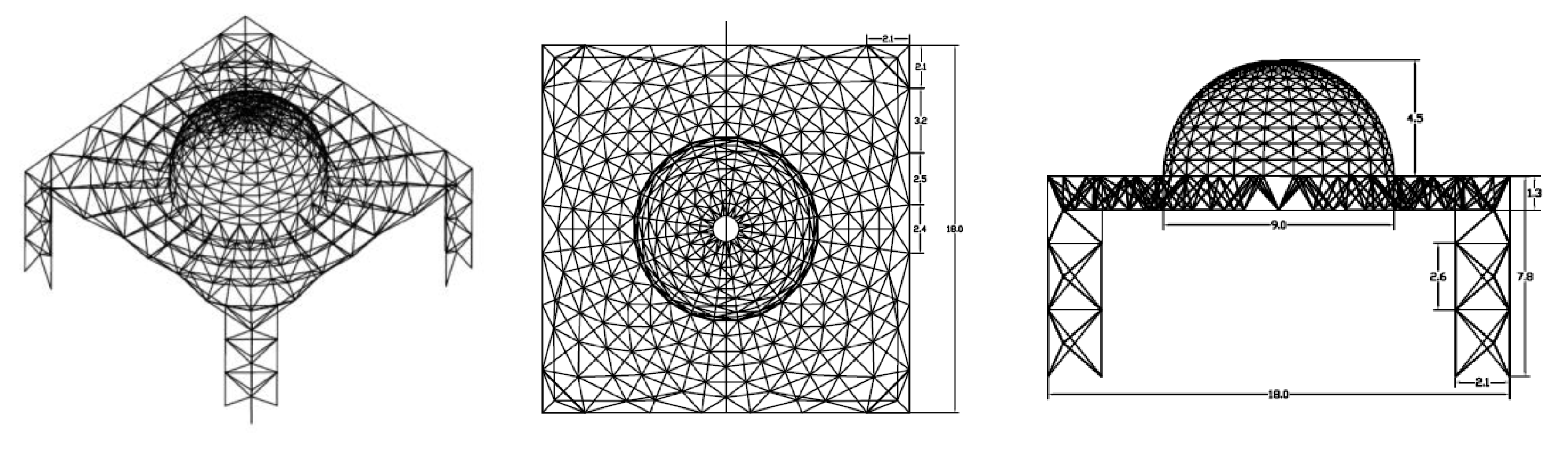
Figure 7 shows the preferred configuration for the platform under consideration resulting from the above comparative investigation. A number of free vibration mode shapes with significant modal participation are shown in Figure 7.
The results reveals that the maximum lateral displacement of the designed double layer grid spatial offshore structure, composed of the jacket and the superstructures undergoes lateral displacements at its top deck levels very close to those corresponding to the existing tubular benchmark offshore structure under the action of wind, wave, current and earthquake loads, demonstrating that the spatial grid structure has been so designed to have rather identical rigidity (stiffness) with the existing benchmark platform; however, the weight of steel material used in the spatial grid system is considerably lower than its traditional counterpart, as demonstrated in Table 3 below.
Table 3. Weights of jackets, superstructure and total structural weights (in tonnes) of the proposed spatial grid in comparison with the existing tubular offshore structure along with the percentage of material saving to be gained by employing the proposed system.
Table 3. Weights of jackets, superstructure and total structural weights (in tonnes) of the proposed spatial grid in comparison with the existing tubular offshore structure along with the percentage of material saving to be gained by employing the proposed system.
Type Existing Benchmark Tubular Platform Double Layer Grid Spatial Offshore Structure Percentage Reduction
Weight of the jacket (substructure) 426 249 41.5%
Weight of the superstructure (decks) 215 45 79.1%
Total weight of jacket and superstructure 641 294 54.1%

2.2.3. General Construction and Functionality Considerations

General derivations from experimental results along with further avenues for exploration for the spatial grid jacket offshore system suggest less material consumption, lighter weight and lighter handling equipment, ease of fabrication and erection, less damage to the environment, possibility of industrialized production and prefabrication resulting in less time, lower cost and a higher quality management standard, controllable stiffness and ductility in accordance with the desired performance and achievable higher level of reliability. Additional important considerations in terms of fatigue, future research paths, and sustainability are discussed in the following.
  • Fatigue: Given that the displacement is reduced by a factor of 8 compared to the traditional tubular structure, this may suggest improvement in the fatigue behaviour of the parts of the system that are experiencing variable amplitude loads under displacement control. In case if one achieves a considerably longer fatigue life of a suitable type of well-detailed friction grip bolted connections for such space structures, this old problem of the fatigue fracture of welded tubular joints may also be resolved. Furthermore, such space structures due to high redundancies are not as vulnerable as tubular ones to local fatigue failure.
  • Future research paths: An area of concern is related to the amount of pressure induced by the stream flow and wave on rather dense skeletal space structures both on the front face as well as on the leeward side. Another important domain of investigation is the seismic effects of this structure with considerably higher rigidity in the context of soil structure interaction for different soil conditions. Further works are needed on the dynamic and seismic behaviour, detailed specifications for the design, fabrication and erection, construction management issues, more sophisticated forms, lifting analysis, the feasibility of usage with required modifications for deeper platforms and last but not least, the fatigue behaviour of joints, especially under low temperature, and also the effects of corrosion fatigue.
  • Sustainability: One clear benefit of employing this system is the considerable reduction in weight of construction material, which will directly reduce the embodied energy and Carbon of the project. Due to the bolted joints, instead of the welded tubular members, this system can also be easily deconstructed for reuse/repurposing, or recycling, contributing to the circular economy. The higher possible fatigue life, increases the service life of the structure, and enhance sustainability. Finally, the 8-fold reduction in displacement of the structure under dynamic loading suggests that this type of system can work well with wind turbines for offshore renewable energy production. This includes the possibility of utilization of the gridded spatial structure jacket system as the foundation (base) of offshore wind turbines in transitional water depths (e.g., around 25-50 m) [30,31] as a substitution for current tubular jacket systems (e.g., Beatrice offshore wind farm off the coast of Scotland). Three sample designs for the base of wind towers using offshore spatial structures is provided in Figure 8.

2.3. Reconstruction and Preservation of Heritage Buildings

Consider the topic of rehabilitation and reconstruction of aging and ancient cities with geometrically custom, free-form or smooth components (e.g., hemispherical domes). One such example is provided in Figure 9, where medieval urban dome-shaped developments of this type are prevalent, especially in the central Iranian desert (Kavir). Such old cities exist, house a considerable number of residents, and in many cases must be further preserved due to their cultural and historical significance (e.g., supported by the UNESCO world heritage centre [32]). Given the established ability of spatial structure grids to foster the creation of custom free-form geometries (see Figure 1a,b), they may be employed for fast, and large-scale reconstruction of ancient cities and urban developments [33], particularly after natural disasters.

2.3.1. Proposed Spatial Structure System for Geometry-Preserving Reconstruction

The process of design and reconstruction of these custom shapes (in the case of Figure 7, hemispheres) using spatial structures requires two main frameworks to:
  • generate the geometric digital twin of the existing facilities (Figure 10a); and
  • use this geometry to generate modular spatial structural systems, specifically designed to address the serviceability needs (Figure 10b).
The former, automatic generation of geometric digital twins, using optical metrology (such as laser scanners, and photogrammetry) has been extensively investigated in the work of [33,34,35,36,37]. For instance, in the case of hemispherical domes, one can automatically select two convergent images from a network of overlapping images, taken from these types of hemispherical domes, to reconstruct the domes with millimetre-level accuracy [33]. In other cases, advanced image and point cloud processing methods can be employed (e.g., unsupervised learning strategies) to generate the 3D as-built model as depicted in Figure 8a. In the case shown in Figure 8a, a photogrammetry-based 3D reconstruction is carried out to generate dense 3D point clouds from images taken using drones. The point cloud is then fed to the robust sphere detection of [38] (Figure 10a-middle), where a final building information model (BIM) can then be generated.
For the latter case, Figure 10b shows the three stages required for the design optimization of the individual objects:
  • Spatial structure discretization of model: where each BIM element is decomposed into a set of single, double, triple (and so on) layer spatial structures. For instance, the case shown in Figure 10b-left shows a Formex representation [16,25] of one possible type of single layer space grid discretization solution. It is possible to automated this part using visual geometric programming from the generated BIM.
  • Design standard inputs: where the necessary load combinations as well as method of design (e.g., load resistance factored design (LRFD) [14,39]) are utilized as inputs to the design optimization strategy. Depending on the region and municipality, different standards exist, such as ASCE [40] for the US, DIN for Germany, or National Building Code (NBC) for Canada. For instance, the example shown in Figure 8b-middle demonstrates the loads as a result of live, dead, wind, and snow, acting upon a hemispherical dome using the Canadian NBC.
  • Design optimization for sustainability: finally, the aforementioned steps are utilized as input to an iterative (and in many cases heuristic) optimization process to find the best combination to minimize the weight of the structure. This optimization for weight directly minimizes both embodied energy and Carbon. Other design and sustainability considerations, such as ADF [22], cost, and etcetera, may be added to form a multi-objective optimization problem [41]. These optimization problems can be solved using heuristic methods, such as genetic algorithm artificial intelligence (AI) optimization to find the pareto optimality [42]. In the example shown in Figure 10b-right, the optimal shape and size of each element of a one-way Schwedler dome for weight minimization was determined using a genetic algorithm framework.

2.3.2. Spatial Structure Reconstruction of Domes: Seismic Response Analysis

A rather comprehensive research studies on the seismic behaviour of spatial dome structures [43] had proved excellent potentialities of braced dome spatial structures to withstand severe earthquakes, if properly designed and constructed to meet the requirements of the Iranian Code of Practice for Spatial Structures [17].
Figure 11a Shows a sample double-layer lamella dome structure. A number of mode shapes corresponding to larger modal participation in a horizontal and the vertical directions are shown in Figure 11b,c, respectively. In a modal analysis of such space domes, a considerable number of modes of vibration contribute to the dynamic response of the structure and need be taken into account in performing a modal analysis.
In addition to the response spectrum analysis, an extensive number of linear and nonlinear time history analyses were carried out to investigate the influences of a variety of important parameters on the seismic response of the dome structures under consideration. The parametric studies included the investigation of the effects of material properties, member slenderness ratios, member imperfections, joint flexibility, rise to span ratios, damping ratios and density (size of modules). The nonlinear analyses, account for nonlinear material behaviour as well as the geometrical nonlinearity. Possible modes of instability such as member buckling, nodal instability (including nodal torsional instability), coupled member and node buckling, local group instability, snap through buckling, instability around circumferential parallels, line instability along a part of a meridional line and general overall instability. Furthermore, accuracy achieved through different nonlinear dynamic analysis procedures were compared. In this study, two analysis programs were used: early versions of NISA [44], and ANSYS [45]. Eleven recorded time history of ground motion were used in two cases: (i) single horizontal component, and (ii) three translational components of ground motion in orthogonal directions acting together.

2.3.3. Spatial Structure Reconstruction of Domes: Nonlinear Dynamic Response

In this particular sample analysis, members were modelled to account for member buckling. An initial imperfection (maximum initial lateral deflection or out of straightness of a member) equal to 1/500th of the member length was assumed for each truss member. In such domes, usual practice was to emphasize on their nonlinear geometric behaviour; however, [13,46] revealed the importance of the nonlinear material behaviour as essential as the geometric nonlinearity that should be considered simultaneously with local and overall buckling on the static and dynamic response of such domes, to achieve a realistic prediction of their response. Hence, here, both geometric and material nonlinearities were included in the analysis. Distributed mass was defined for structural members, while the masses corresponding to claddings, mechanical and electrical facilities, and snow loads were assumed to be lumped at structural nodes appropriately.
The nonlinear dynamic analysis of the dome also included single and triple component excitations. El Centro ground motion was applied scaled with different scale factors such that PGA values were scaled to 0.10g, 0.25g, 0.35g 0.50g and 0.75g. Some representative results are given in Figure 12.
Figure 12a corresponds to the time history of the dynamic response of a member located at the uppermost outer layer ring when the PGA has been scaled to 0.35g and demonstrates the large discrepancies between the analysis results under the application of the three and the single component excitations on the unsafe side. When the same form of acceleration time history is scaled to 0.75g, a shift of the mean value of the response of the member can be noticed in both diagrams pertaining to the single and triple component excitations (Figure 12b). However, in the case of three component excitation, a sudden unloading of the member has occurred, which is indicative of the member buckling. Now under single component excitation, a sudden decrease of resistance to a residual strength (post buckling strength) can be noticed. Although this phenomenon occurred for a limited number of members under the PGA of 0.75g, it did not lead to overall instability. Apparently the high degree of indeterminacy of the structure had led to redistribution of the load path and provided a satisfactory resistance against progressive collapse. Reducing the slenderness ratios for those few members that had acted as member No. 64 prevented such shift of the mean value of vibrating stress and the structure behaved safely under s maximum PGA of the exciting earthquake scaled up to gravitational acceleration.
The Nonlinear vs. Linear response showed reasonably acceptable ratio of the maximum linear to maximum nonlinear response and controllable ductility by selecting appropriate slenderness ratios for different members just sufficient to prevent buckling under the action of the expected earthquake and its corresponding expected behaviour in a performance based design. The ratio of linear to nonlinear response increases as the PGA increases and the nonlinearity of behaviour extends.
Due to the particulars of the sample dome, even under the maximum PGA applied, the seismic effects did not cause overall failure. The difference between the results of single and three component excitations were found to be numerically considerable. As far as the dynamic behaviour is concerned, different responses are observed particularly with increasing PGA and the dominance of the nonlinear response. It can be seen from Figure 12c,d that under a PGA of 0.75g at the onset of overall nonlinear behaviour, sudden unloading occurs in some members for which the oscillation takes place above and below a shifted mean value of stress. The analysis under the single component excitation has not been capable of tracing this effect thoroughly, due to the neglect of the contributions of the other two components (in particular, the vertical component). The effect of three component excitation became more pronounced in the nonlinear analysis and as the acceleration scale factor increased from 0.35g to 0.75g. The percentage differences between the stresses calculated from the nonlinear analysis were less than those resulting from the linear analysis, due to the redistribution of forces within the highly indeterminate structure in the nonlinear range of behaviour. The differences between the results of single and triple component excitations became more significant as the ratio of span to crown height increased and the effects of the vertical component became more prominent for shallower domes; while as this ratio decreased, the influence of horizontal components became more pronounced. Regarding that the braced domes exhibit dominant 3-dimentional behaviour and usually have considerable span dimensions, it is expected that a three component excitation be a natural choice for the study of the seismic response of such structures. With the ever-increasing advances in computational facilities, it is reasonable to include the three component excitation in design practice which gives rise to a more realistic result with no significant additional computational efforts/costs. The error in disregarding the transverse and the vertical components for the dome analysed here was in an order that does not justify the use of single horizontal component excitation for the study of the seismic behaviour of such a dome. Hence, appropriate recommendations are needed to be provided in relevant codes of practice applicable to Space Structures, particularly under near field effects. Such recommendations have already been included in the Iranian Code of Practice for Space Structures [17]. Effects of imperfection were found to be considerable: however by limiting the initial imperfection of members to an achievable practical value of 1/1000th of the member lengths, such effects can be ignored [47].
In connection with the application of spatial braced dome structures in reconstruction of seismically damaged heritage buildings, a typical bazaar and a typical mosque [48], both existing in the city of Tabriz, were employed for the demonstration of the notion. Such buildings have been built centuries ago by available materials (i.e., masonry) and although the engineers at the time were aware of the importance of forms such as arches and domes in masonry structures, their efforts would not lead to the construction of buildings capable of resisting severe earthquakes as observed in the city of Bam in 2003 and many places around the world during decades. Figure 13 shows a graphical representation of such spatial grid structure composed of braced dome supported by double layer grid roof structure and grid piers at corners. In a very likely probability of destruction of such a masonry building under a severe earthquake event, it is desirable to reconstruct the building preserving the form and entity of the building as a historical and cultural heritage. In the case of a large seismic event leading to vast destruction of such buildings, such as the disastrous total destruction of the fascinating, astonishing and stunning human memorial work of art, architecture, engineering and town planning: the historical heritage Arg-e Bam The use of such space grid structures that can be constructed easily and quickly to preserve form and identity of the damaged buildings while ensuring excellent seismic behaviour to withstand future earthquakes, will definitely be a right, practical and economic solution. The current efforts to reconstruct the Arg by means of traditional heavy masonry materials to regain its as much identity as possible has been slow, impractical, uneconomical, and a never ending effort to reconstruct some possible parts of the Arg again prone to earthquake damage under a possible future earthquake event.
A series of response spectrum analyses with a combination of 100% of one component with 35% of the other two components of ground motion acting in three perpendicular directions as well as a considerable number of nonlinear time history analyses have proven that such structures, if designed according to a reliable code of practice (e.g., [17]) to prevent overall buckling and local failure, will not fail under the severe earthquakes up to Maximum Considered Earthquakes [48]. These structures are safe, reliable, cost effective and speedy and preserve the functionality of the original building in harmony with the built environment. Even cladding by means of newly developed lightweight materials can be so chosen and installed to give virtually the same appearance as the original structure before experiencing seismic damage. The importance of this topic is not limited to Iran and a few other countries. Most of the earthquake prone countries in southern Europe having a large number of masonry domes and arches may also get benefit from the ideas proposed here.

Conclusions

The ideas exemplified above can be extended with virtually no limitations. They have also been applied to temporary and permanent transmission towers [49], and by many researchers to shelters, temporary housing for post disaster situations [50], deployable, expandable and demountable systems [51,52], cooling towers [53] and many more cases. The joy of experimentation of building creative free form structures exhibiting unique characters will continue to expand as a part of the historical challenge of human being to overcome nature’s obstacles and to symbolize the man’s capabilities at a particular place and at a particular time. These are certainly valuable advancements to be encouraged. The authors see no contradiction between these efforts and those reminded here. They only wish to see more from the engineering community in making the most of limited available resources. In this context, the authors are hoping that they have given their message here, and have demonstrated clearly that modular skeletal space structures have yet plenty of usage and advantages to offer in order to meet the needs of contemporary societies combining economy and environmental aspects to build sustainable and resilient structures with a look to the future.

Author Contributions

Conceptualization, S.M. and R.M.; methodology, S.M. and R.M.; software, S.M. and R.M.; validation, R.M., B.M. and S.M.; formal analysis, S.M.; investigation, S.M., B.M. and R.M.; resources, S.M.; data curation, S.M.; writing—original draft preparation, S.M.; writing—review and editing, R.M. and B.M.; visualization, S.M. and R.M.; supervision, S.M.; project administration, S.M.; funding acquisition, S.M. and R.M. All authors have read and agreed to the published version of the manuscript.

Funding

The author wishes to acknowledge the support provided by the KIT Publication Fund of the Karlsruhe Institute of Technology together with the budget of the department of Digital Engineering and Construction at the Karlsruhe Institute of Technology in supplying the APC. This research received no additional external funding.

Data Availability Statement

Research data can be requested from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Brütting, J.; Senatore, G.; Fivet, C. Design and Fabrication of a Reusable Kit of Parts for Diverse Structures. Autom. Constr. 2021, 125. [Google Scholar] [CrossRef]
  2. Parke, G.A.R.; Behnejad, S.A. Z S Makowski: A Pioneer of Space Structures. Int. J. Sp. Struct. 2015, 30. [Google Scholar] [CrossRef]
  3. Behnejad, S.A.; Parke, G.A.R. Half a Century with the Space Structures Research Centre of the University of Surrey. Int. J. Sp. Struct. 2014, 29. [Google Scholar] [CrossRef]
  4. Makowski, Z.S. NEW TRENDS IN SPATIAL STRUCTURES. J. Int. Assoc. Shell Spat. Struct. 1986, 27–1. [Google Scholar]
  5. Villegas, L.; Morán, R.; García, J.J. Combined Culm-Slat Guadua Bamboo Trusses. Eng. Struct. 2019, 184. [Google Scholar] [CrossRef]
  6. Allen, E.; Zalewski, W. Form and Forces: Designing Efficient, Expressive Structures; Wiley, 2009; ISBN 978-1-118-17425-8.
  7. Schober, H. Transparent Shells: Form, Topology, Structure; 2015.
  8. Da Silveira, G.; Borenstein, D.; Fogliatto, F.S. Mass Customization: Literature Review and Research Directions. Int. J. Prod. Econ. 2001, 72, 1–13. [Google Scholar] [CrossRef]
  9. CBRE Research U.S. Construction Cost Trends: Rising Prices for Labor and Materials Pressuring Construction Costs; 2022.
  10. Moazzami, M.; Maalek, R.; Senanayake, S.; Ruwanpura, J. Adoption and Implementation of BIM in Canadian Construction Projects: Benefits, Challenges, and Limitations. In Proceedings of the Construction Research Congress 2020: Computer Applications - Selected Papers from the Construction Research Congress 2020; 2020.
  11. United Nations Environment Programme Global Status Report for Buildings and Construction: : Towards a Zero-emission, Efficient and Resilient Buildings and Construction Sector; Nairobi, 2022. T.
  12. Maalek, S. A Formex Formulation for Substructure Analysis of Open Web Grids. Int. J. Sp. Struct. 1989, 4. [Google Scholar] [CrossRef]
  13. Maalek, S. Structural Assessment and Quality Control Procedures for the Homa Aircraft Hangar No. 3. Int. J. Sp. Struct. 1999, 14. [Google Scholar] [CrossRef]
  14. AISC AISC 360-22 Specification for Structural Steel Buildings. Am. Inst. Steel Constr. 2022.
  15. ASCE Federal Emergency Management Agency, FEMA-356 Prestandard and Commentary for the Seismic Rehabilitation of Building. Rehabilitation 2000.
  16. Nooshin, H. Formex Approach. J. Int. Assoc. Shell Spat. Struct. 1988, 29–1. [Google Scholar]
  17. Maalek, S.; Nooshin, H.; Dianat, N.; Abedi, K.; Heristchian, M.; Chenaghlou, M.R. Code of Practice for Skeletal Steel Space Structures; Publicatio.; Management and Planning Organization of Iran: Tehran, Iran, 2011. [Google Scholar]
  18. Moradi, S. An Application of a Proposed Structural System Composed of Skeletal Space Structures, University of Tehran, 2015.
  19. Ahmadizadeh, M.; Maalek, S. An Investigation of the Effects of Socket Joint Flexibility in Space Structures. J. Constr. Steel Res. 2014, 102. [Google Scholar] [CrossRef]
  20. Dargahi, M. Seismic Behaviour of Space Grid Building Structures with Socket Joints, University of Tehran, 2019.
  21. Tarczewski, R.; Motro, R. The Beauty of Technical Thought in Architecture - The Lifework of Stéphane Du Chateau. Int. J. Sp. Struct. 2015, 30. [Google Scholar] [CrossRef]
  22. Alshaibani, K. Average Daylight Factor for the ISO/CIE Standard General Sky. Light. Res. Technol. 2016, 48. [Google Scholar] [CrossRef]
  23. Maalek, S.; Heidary-Torkamani, H.; Pirooz, M.D.; Naeeini, S.T.O. Numerical Investigation of Cyclic Performance of Frames Equipped with Tube-in-Tube Buckling Restrained Braces. Steel Compos. Struct. 2019, 30. [Google Scholar] [CrossRef]
  24. Heidary-Torkamani, H.; Maalek, S. Conceptual Numerical Investigation of All-Steel Tube-in-Tube Buckling Restrained Braces. J. Constr. Steel Res. 2017, 139. [Google Scholar] [CrossRef]
  25. Nooshin, H.; Disney, P. Formex Configuration Processing II. Int. J. Sp. Struct. 2001, 16. [Google Scholar] [CrossRef]
  26. API Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms — Working Stress Design. Api Recomm. Pract. 2007, 24-WSD.
  27. Younan, A.H.; Puskar, F.J. API RP2EQ - Seismic Design Procedures & Criteria for Offshore Structures. In Proceedings of the Proceedings of the Annual Offshore Technology Conference; 2010; Vol. 4. [CrossRef]
  28. Computers & Structures Inc Sap 2000. Sap 2000 2019.
  29. Berkeley University PEER Ground Motion Database - PEER Center.
  30. Bailey, H.; Brookes, K.L.; Thompson, P.M. Assessing Environmental Impacts of Offshore Wind Farms: Lessons Learned and Recommendations for the Future. Aquat. Biosyst. 2014, 10. [Google Scholar] [CrossRef]
  31. Bhattacharya, S.; Lombardi, D.; Amani, S.; Aleem, M.; Prakhya, G.; Adhikari, S.; Aliyu, A.; Alexander, N.; Wang, Y.; Cui, L.; et al. Physical Modelling of Offshore Wind Turbine Foundations for Trl (Technology Readiness Level) Studies. J. Mar. Sci. Eng. 2021, 9. [Google Scholar] [CrossRef]
  32. Masjed-e Jāmé of Isfahan Available online:. Available online: https://whc.unesco.org/en/list/1397/ (accessed on 29 August 2021).
  33. Maalek, R.; Maalek, S. Automatic Recognition and Digital Documentation of Cultural Heritage Hemispherical Domes Using Images. J. Comput. Cult. Herit. 2023, 16, 1–21. [Google Scholar] [CrossRef]
  34. Maalek, R.; Lichti, D.D.; Maalek, S. Towards Automatic Digital Documentation and Progress Reporting of Mechanical Construction Pipes Using Smartphones. Autom. Constr. 2021, 127, 103735. [Google Scholar] [CrossRef]
  35. Maalek, R.; Lichti, D.D.; Ruwanpura, J.Y. Automatic Recognition of Common Structural Elements from Point Clouds for Automated Progress Monitoring and Dimensional Quality Control in Reinforced Concrete Construction. Remote Sens. 2019, 11. [Google Scholar] [CrossRef]
  36. Maalek, R.; Lichti, D.D.; Walker, R.; Bhavnani, A.; Ruwanpura, J.Y. Extraction of Pipes and Flanges from Point Clouds for Automated Verification of Pre-Fabricated Modules in Oil and Gas Refinery Projects. Autom. Constr. 2019, 103, 150–167. [Google Scholar] [CrossRef]
  37. Maalek, R.; Lichti, D.D. Robust Detection of Non-Overlapping Ellipses from Points with Applications to Circular Target Extraction in Images and Cylinder Detection in Point Clouds. ISPRS J. Photogramm. Remote Sens. 2021, 176, 83–108. [Google Scholar] [CrossRef]
  38. Maalek, R.; Lichti, D.D. Correcting the Eccentricity Error of Projected Spherical Objects in Perspective Cameras. Remote Sens. 2021, 13, 3269. [Google Scholar] [CrossRef]
  39. Lin, S.H.; Yu, W.W.; Galambos, T. V. ASCE LRFD Method for Stainless Steel Structures. In Proceedings of the International Specialty Conference on Cold-Formed Steel Structures; 1990.
  40. Structural Wood Design – ASD/LRFD, 2nd Ed; 2017.
  41. Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms Kalyanmoy; 2001; Vol. 16.
  42. Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6. [Google Scholar] [CrossRef]
  43. Maalek, S. Shear Testing of Butt Joints. J. Test. Eval. 2014, 42. [Google Scholar] [CrossRef]
  44. Harle, S. Analysis and Design of Earthquake Resistant Multi-Storied Braced R.C.C. Building Using NISA Software. Int. J. Eng. Sci. Res. Technol. 2014, 3. [Google Scholar]
  45. Ansys Inc. Corp. Philanthr. Rep. 2023, 38. [CrossRef]
  46. Saka, M.P.; Ulker, M. Optimum Design of Geometrically Nonlinear Space Trusses. Comput. Struct. 1992, 42. [Google Scholar] [CrossRef]
  47. Maalek, S.; Akbari, R.; Maheri, M.R. The Effect of Higher Modes on the Regularity of Single-Column-Bent Highway Viaducts. Bridg. Struct. 2009, 5. [Google Scholar] [CrossRef]
  48. Maalek, S.; Seyedardakani, S.M. Reconstruction of Seismically Damaged Urban Areas of Historical Significance Utilizing Earthquake Resistant Space Grid Structures. In Proceedings of the 8th International Congress of Civil Engineering, Shiraz, Iran; 2009. [Google Scholar]
  49. Dong, S.; Zhao, Y.; Xing, D. Application and Development of Modern Long-Span Space Structures in China. Front. Struct. Civ. Eng. 2012, 6. [Google Scholar] [CrossRef]
  50. Dev, K.N.; Das, A.K. Design of Bamboo Shelter Kit for Post-Disaster Temporary Shelter Response. In Proceedings of the Smart Innovation, Systems and Technologies; 2021; Vol. 221. [CrossRef]
  51. Krishnan, S.; Liao, Y. Geometric Design of Deployable Spatial Structures Made of Three-Dimensional Angulated Members. J. Archit. Eng. 2020, 26. [Google Scholar] [CrossRef]
  52. Chai, T.J.; Tan, C.S. A Review on Planer Scissor Mechanisms for Spatial Deployable Structures. Int. J. Psychosoc. Rehabil. 2020, 24. [Google Scholar]
  53. Ke, S.T.; Ge, Y.J.; Zhao, L.; Tamura, Y. A New Methodology for Analysis of Equivalent Static Wind Loads on Super-Large Cooling Towers. J. Wind Eng. Ind. Aerodyn. 2012, 111. [Google Scholar] [CrossRef]
Preprints 79189 g001
Figure 1. Examples of skeletal space structure systems: (a) Free-form botanic garden (China); (b) Free-form roof structure (Germany); and (c) Geodesic dome (Denmark).
Figure 1. Examples of skeletal space structure systems: (a) Free-form botanic garden (China); (b) Free-form roof structure (Germany); and (c) Geodesic dome (Denmark).
Preprints 79189 g001
Preprints 79189 g002
Figure 2. 3D model of the proposed simple double layer grid spatial structure residential building: (a) single-storey; (b) multi-storey (three storey).
Figure 2. 3D model of the proposed simple double layer grid spatial structure residential building: (a) single-storey; (b) multi-storey (three storey).
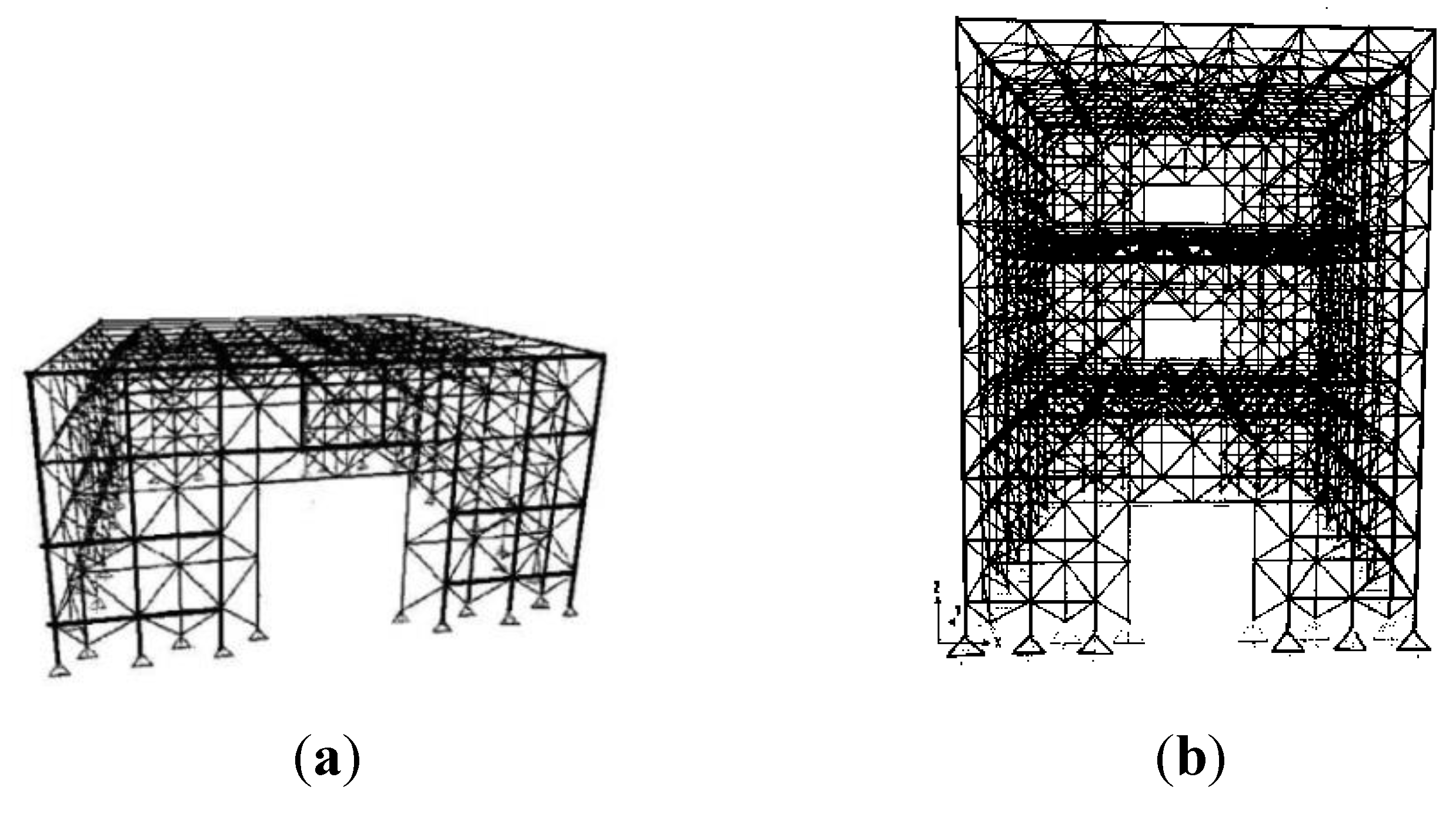
Preprints 79189 g002
Preprints 79189 g003
Figure 3. Results of the nonlinear analyses; (a), (b) and (c): time history analysis results under Altadena ground motion with magnified PGA of 1.0 g; and (d) push over analysis results.
Figure 3. Results of the nonlinear analyses; (a), (b) and (c): time history analysis results under Altadena ground motion with magnified PGA of 1.0 g; and (d) push over analysis results.
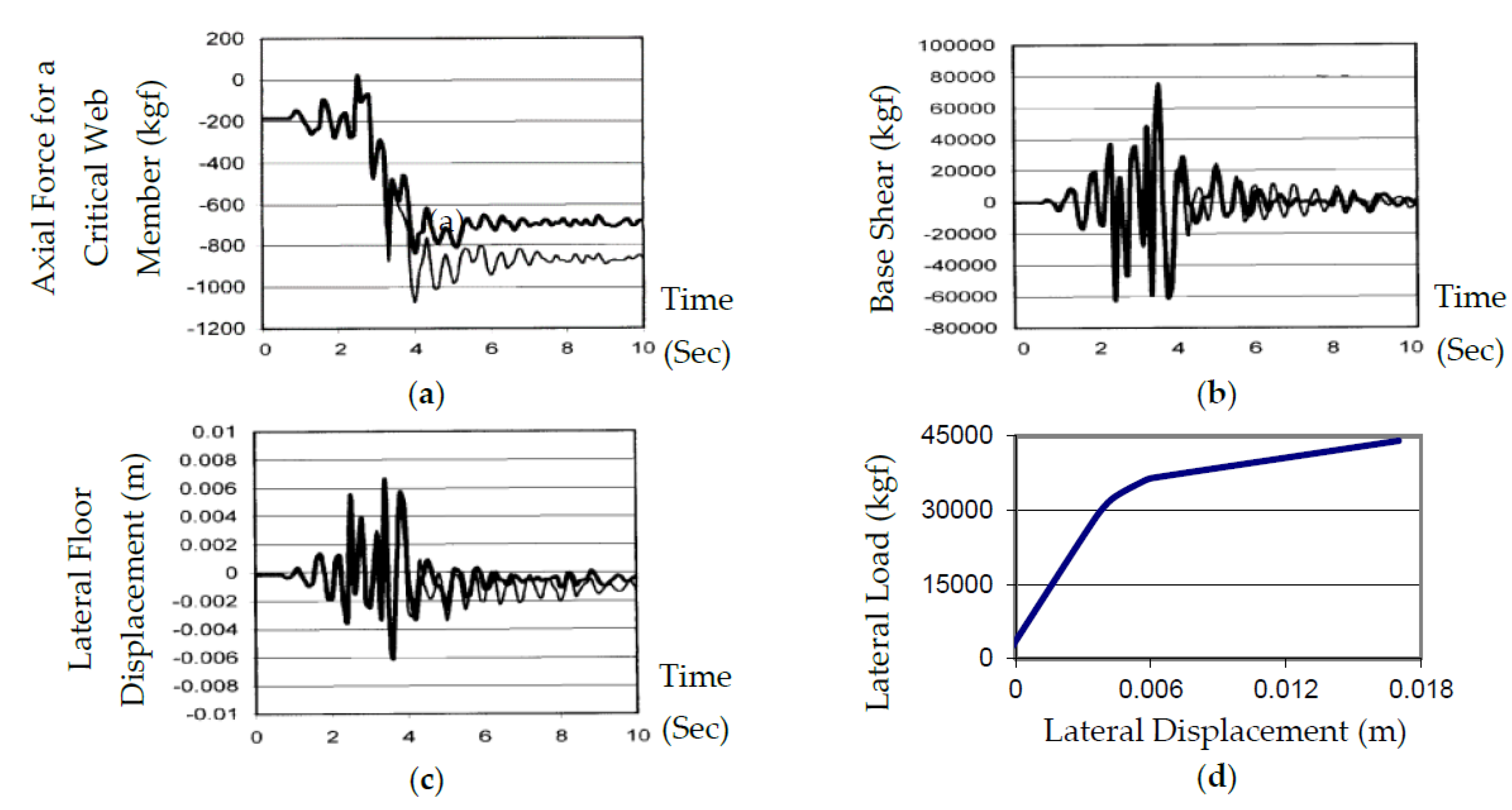
Preprints 79189 g003
Preprints 79189 g004
Figure 4. Selected results of the free vibration modes of the three-storey building; (a) mode 1; and (b) mode 7.
Figure 4. Selected results of the free vibration modes of the three-storey building; (a) mode 1; and (b) mode 7.
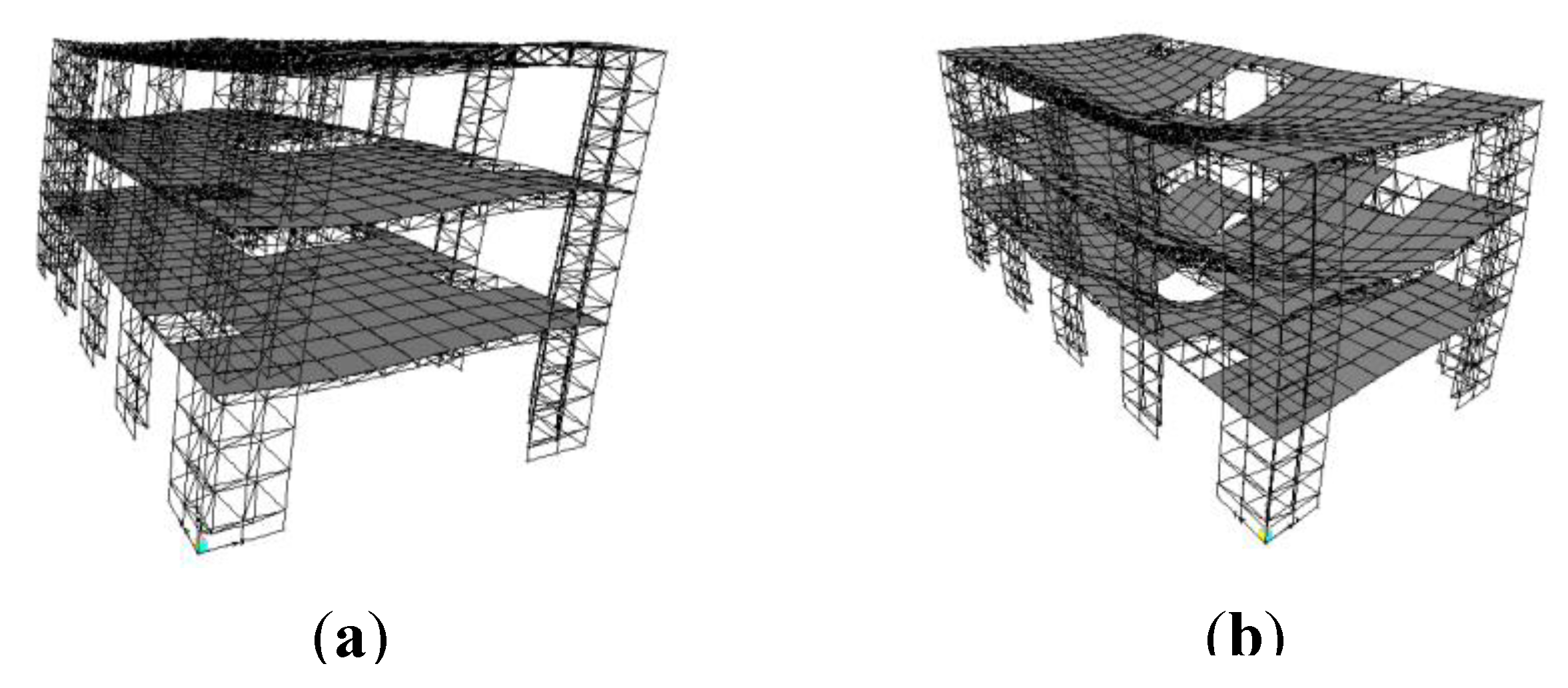
Preprints 79189 g004
Preprints 79189 g005
Figure 5. Results of composite double-layer grid spatial floor buildings: Double-layer grid of type (3)- plan view (a) and perspective view (d); double-layer square of square grid (c); moment frame combined with concentric bracing- plane view (b) and perspective view (e); vertical displacement contour for proposed double-layer grid floor (g); and comparison of weight per unit area of the three types of double-layer grid compared to braced moment frames (h).
Figure 5. Results of composite double-layer grid spatial floor buildings: Double-layer grid of type (3)- plan view (a) and perspective view (d); double-layer square of square grid (c); moment frame combined with concentric bracing- plane view (b) and perspective view (e); vertical displacement contour for proposed double-layer grid floor (g); and comparison of weight per unit area of the three types of double-layer grid compared to braced moment frames (h).
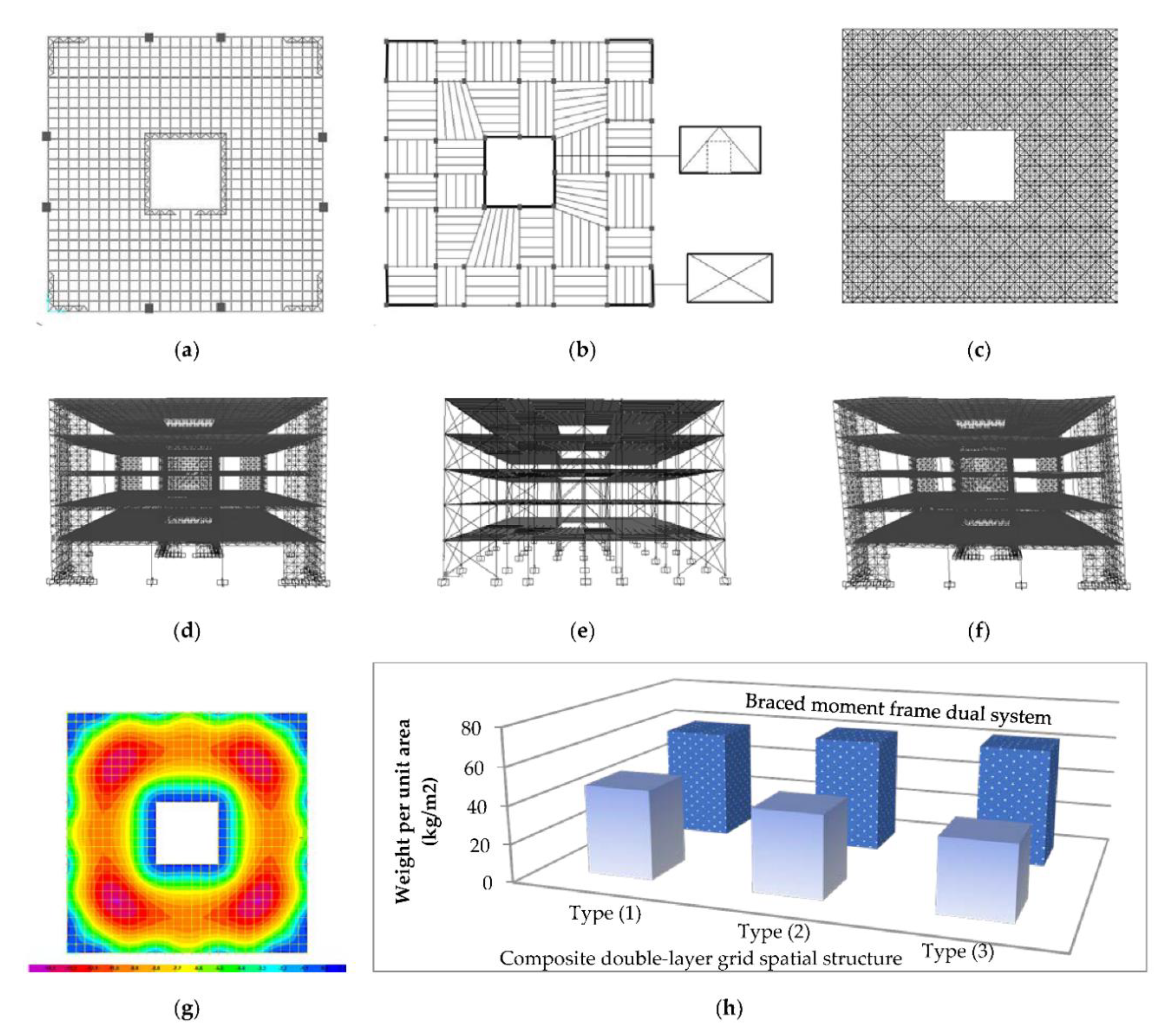
Preprints 79189 g005
Preprints 79189 g006
Figure 6. Modular double-layer spatial grid offshore structure: (a) deck; and (b) jacket type structure.
Figure 6. Modular double-layer spatial grid offshore structure: (a) deck; and (b) jacket type structure.
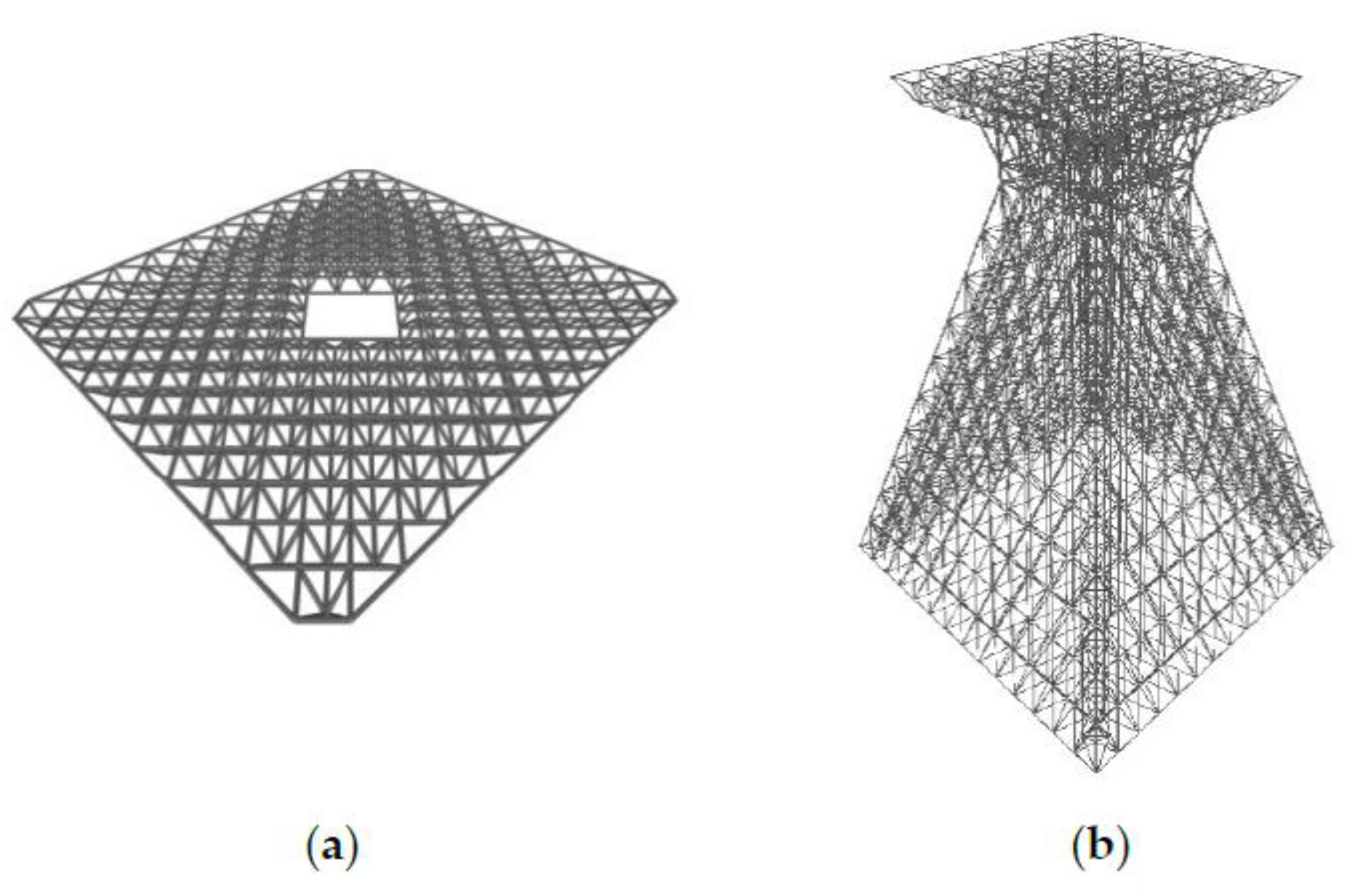
Preprints 79189 g006
Preprints 79189 g007
Figure 7. (a) Preferred spatial structure configuration for offshore tower; and (b) six sample vibration modes for the preferred spatial offshore tower.
Figure 7. (a) Preferred spatial structure configuration for offshore tower; and (b) six sample vibration modes for the preferred spatial offshore tower.
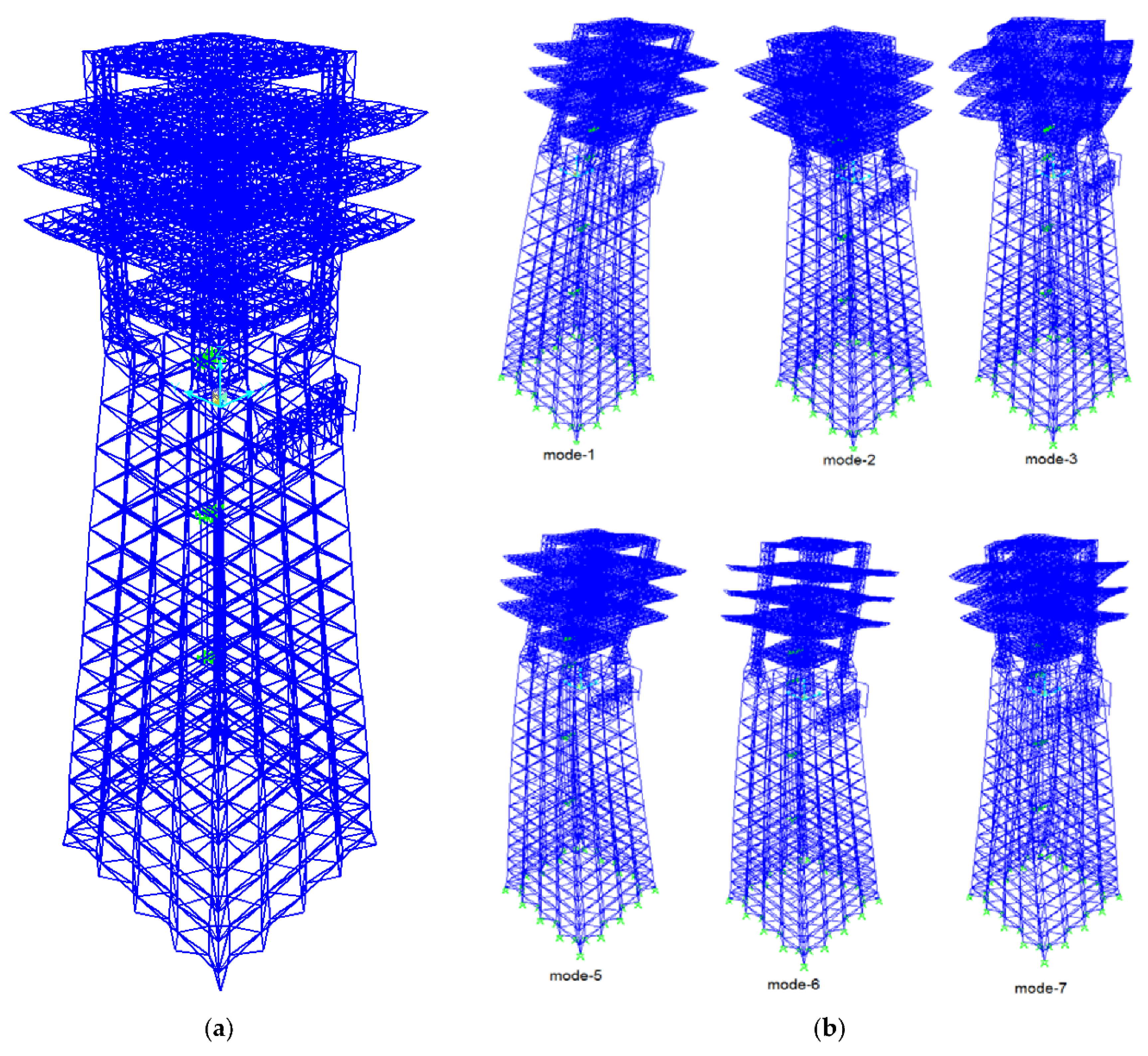
Preprints 79189 g007
Preprints 79189 g008
Figure 8. Three example design options for the base of offshore wind turbines inspired by offshore spatial grids.
Figure 8. Three example design options for the base of offshore wind turbines inspired by offshore spatial grids.
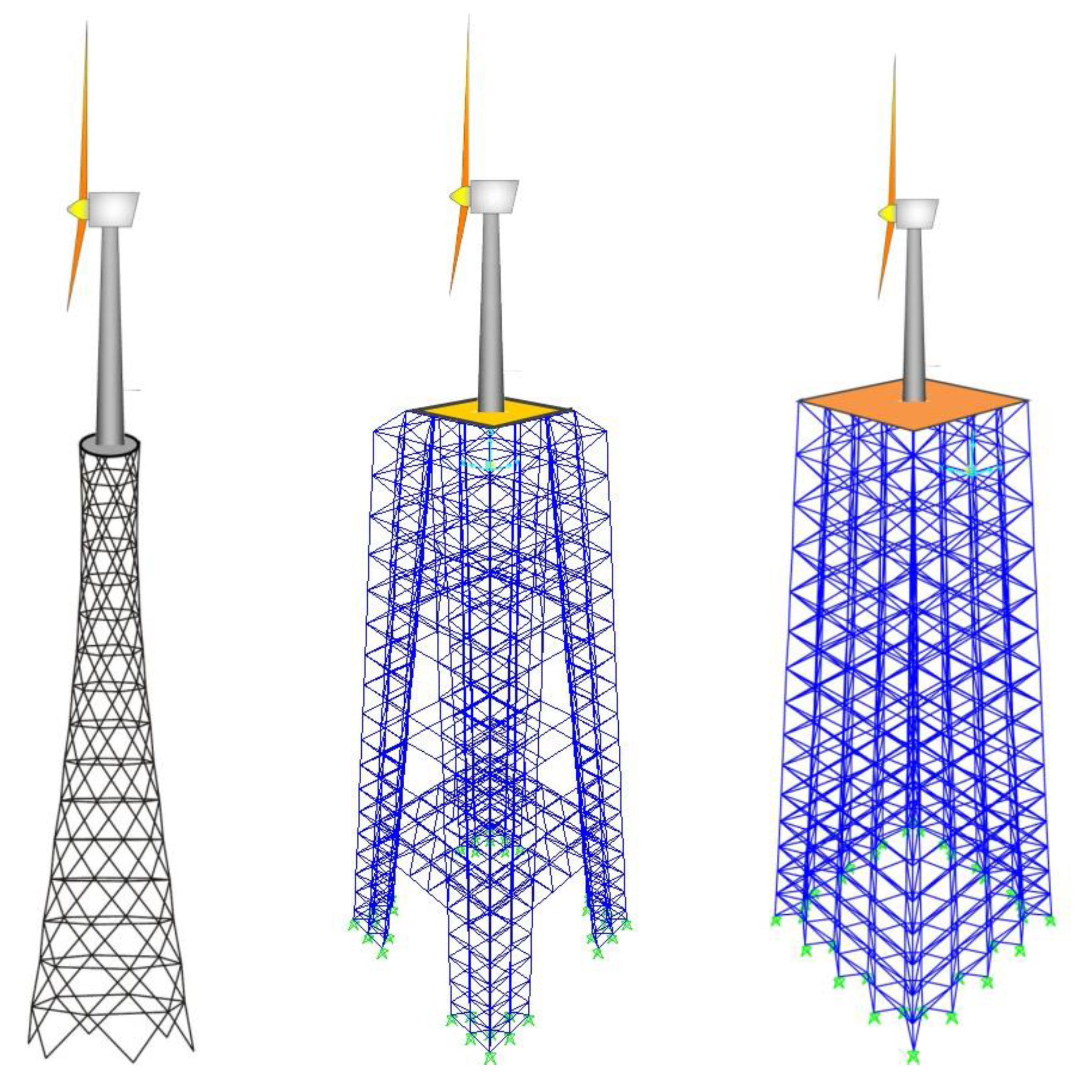
Preprints 79189 g008
Preprints 79189 g009
Figure 9. (a) Artistic impression of the domes (Gonbad) in the central Iranian desert (Kavir) of Koum by Madam Jane Dieulafoy; (b) digital model superimposed onto the picture.
Figure 9. (a) Artistic impression of the domes (Gonbad) in the central Iranian desert (Kavir) of Koum by Madam Jane Dieulafoy; (b) digital model superimposed onto the picture.
Preprints 79189 g009
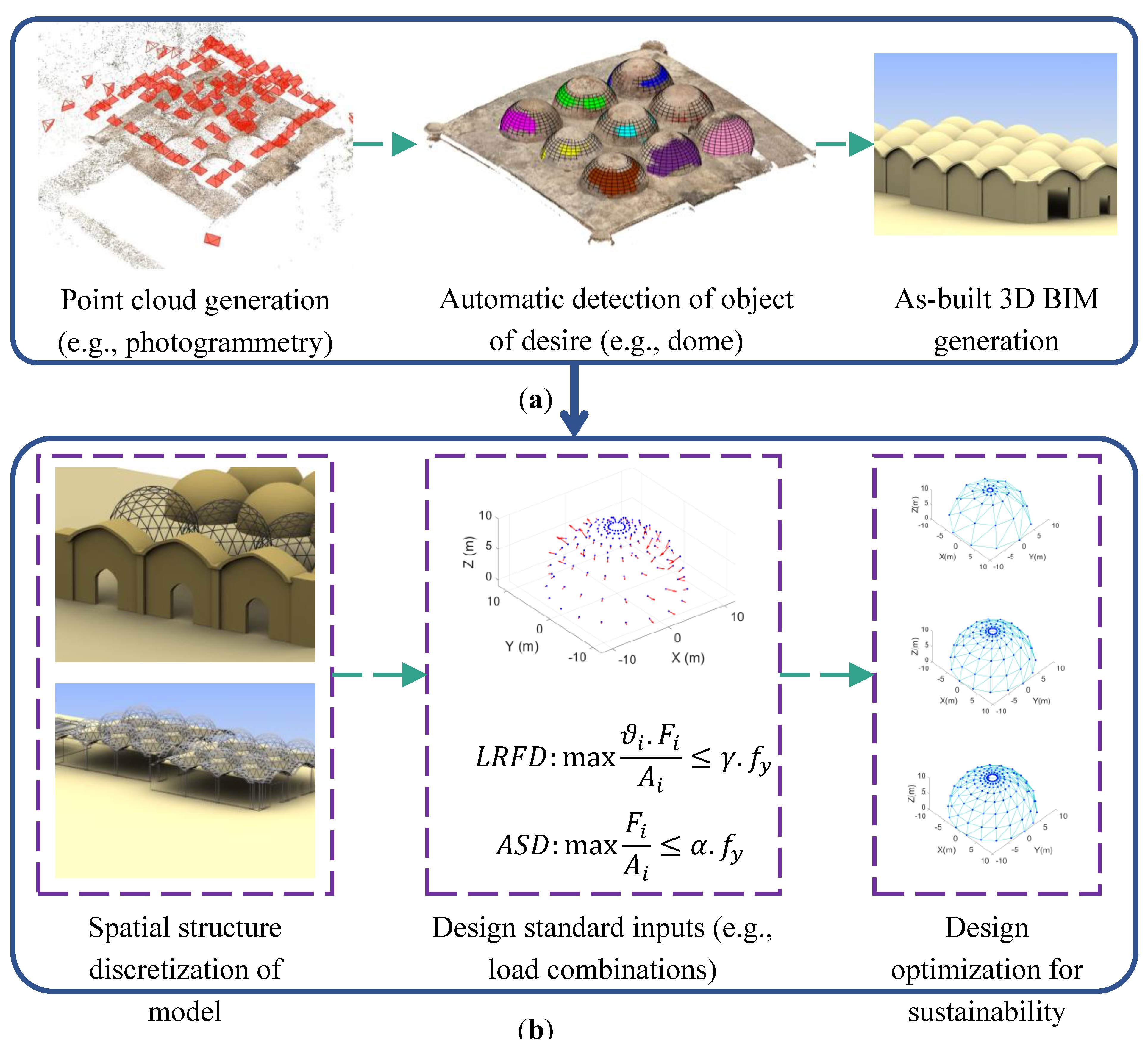
Preprints 79189 g010
Figure 10. Proposed spatial structure design optimization for geometry-preserving reconstruction considering sustainability: (a) automatic generation of 3D BIM using point clouds generated from optical instruments (e.g., laser scanners, or drones); and (b) design optimization for individual BIM components to minimize weight, embodied energy, and embodied Carbon.
Figure 10. Proposed spatial structure design optimization for geometry-preserving reconstruction considering sustainability: (a) automatic generation of 3D BIM using point clouds generated from optical instruments (e.g., laser scanners, or drones); and (b) design optimization for individual BIM components to minimize weight, embodied energy, and embodied Carbon.
Preprints 79189 g010
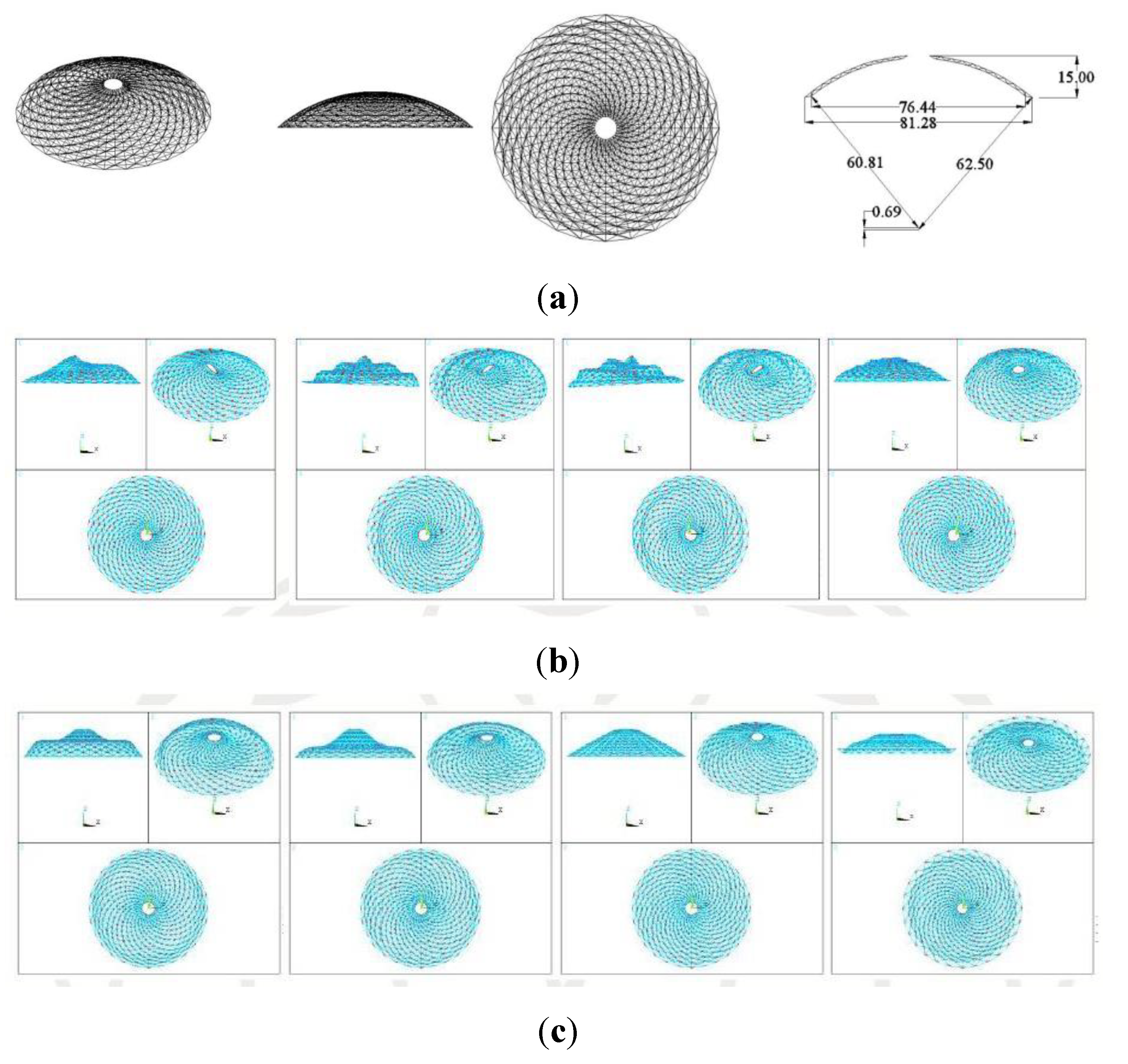
Preprints 79189 g011
Figure 11. (a) Lamella double-layered dome specifications; and modal shapes corresponding to the four vibration modes with larger modal participation in: (b) Horizontal-Direction (Modes No. 6, 88, 77 and 207 in the order of modal contribution); and (c) Vertical-Direction (Modes No. 21, 10, 5 and 51 in the order of modal contribution).
Figure 11. (a) Lamella double-layered dome specifications; and modal shapes corresponding to the four vibration modes with larger modal participation in: (b) Horizontal-Direction (Modes No. 6, 88, 77 and 207 in the order of modal contribution); and (c) Vertical-Direction (Modes No. 21, 10, 5 and 51 in the order of modal contribution).
Preprints 79189 g011
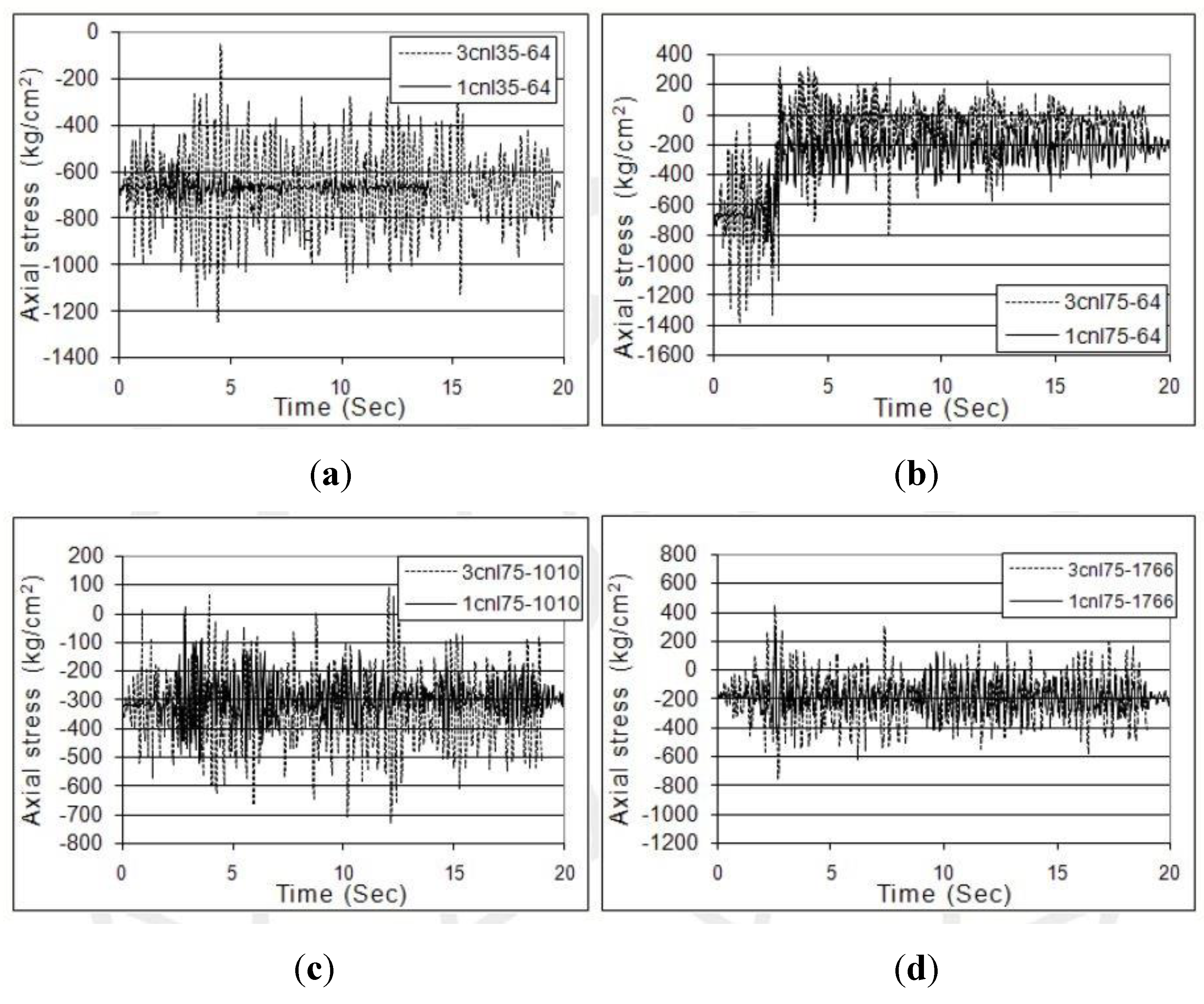
Preprints 79189 g012
Figure 12. Three component vs. single component nonlinear time history response of average axial stresses for selected members: Member No. 64, located at the uppermost outer layer ring with PGA (a) scaled 0.35g and (b) 0.75g; (c) Member No. 1010, a member of the internal layer at the second circumference from the top; and (d) Member No. 1766 , connecting a support to the adjacent outer layer node.
Figure 12. Three component vs. single component nonlinear time history response of average axial stresses for selected members: Member No. 64, located at the uppermost outer layer ring with PGA (a) scaled 0.35g and (b) 0.75g; (c) Member No. 1010, a member of the internal layer at the second circumference from the top; and (d) Member No. 1766 , connecting a support to the adjacent outer layer node.
Preprints 79189 g012
Preprints 79189 g013
Figure 13. Design of heritage domes reinforced using spatial structures.
Figure 13. Design of heritage domes reinforced using spatial structures.
Preprints 79189 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated