Prerpints.org logo
Preprint
Article

A Cascade Network for Pattern Recognition Based on Radar Signal Characteristics in Noise Environment

Altmetrics

Downloads

95

Views

18

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 July 2023

Posted:

13 July 2023

You are already at the latest version

Alerts
Abstract
Target recognition mainly includes three approaches: optical image-based, echo detection-based, and passive signal analysis-based methods. Among them, the passive signal-based method is closely integrated with practical applications due to its strong environmental adaptability. Based on passive radar signal analysis, we design an "end-to-end" model that cascades a noise estimation network with a recognition network to identify working modes in noise environment. The noise estimation network is implemented based on U-Net, which adopts a method of feature extraction and reconstruction to adaptively estimate the noise mapping level of the sample, which can help the recognition network to reduce noise interference. Focusing on the characteristics of radar signal, the recognition network is realized based on Multi-Scale Convolutional Attention Network (MSCANet). Firstly, the deep group convolution is used to isolate the channel interaction in the shallow network. Then, through the multi-scale convolution module, finer-grained features of the signal are extracted without increasing the complexity of the model. Finally, the self-attention mechanism is used to suppress the influence of low-correlation and negative-correlation channels and spaces. This method overcomes the problem that the conventional method is seriously disturbed by noise. We validated the proposed method in 81 kinds of noise environments, achieving an average accuracy of 94.65%. Additionally, we discussed the performance of six machine learning algorithms and four deep learning algorithms. Compared to these methods, proposed MSCANet achieved an accuracy improvement of approximately 17%. Our method demonstrates better generalization and robustness.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Through active or passive radiation such as light waves and microwaves, target recognition can be achieved. And radar is a necessary electronic device for most aerial targets. With the development of radar technology, airborne radar has possessed multiple capabilities such as aerial reconnaissance, target imaging, and firepower strike. Radar working mode is a manifestation of its function. Radar Mode Identification (RMI) refers to the process of obtaining radar style and parameters from unknown electronic signals to analyze radar functions. As far as we know, people tend to pay more attention to the optical features and echo characteristics of the target, ignoring the passive microwave signal [1,2]. However, it should be noted that compared to optical and echo features, passive radar signals have three advantages [3,4,5]: (1) signal reception is passive and has stronger stealth characteristics. (2) Radar signals are less affected by inclement weather such as rain, snow, and fog, making the signal more stable. (3) Radar signals can not only reflect the corresponding platform information, but also analyze the radar working mode to know the target’s intention. Therefore, this paper focuses on the passive radar signals to achieve recognizing working modes, which can help to quickly identify the target’s threats and direct decision making. 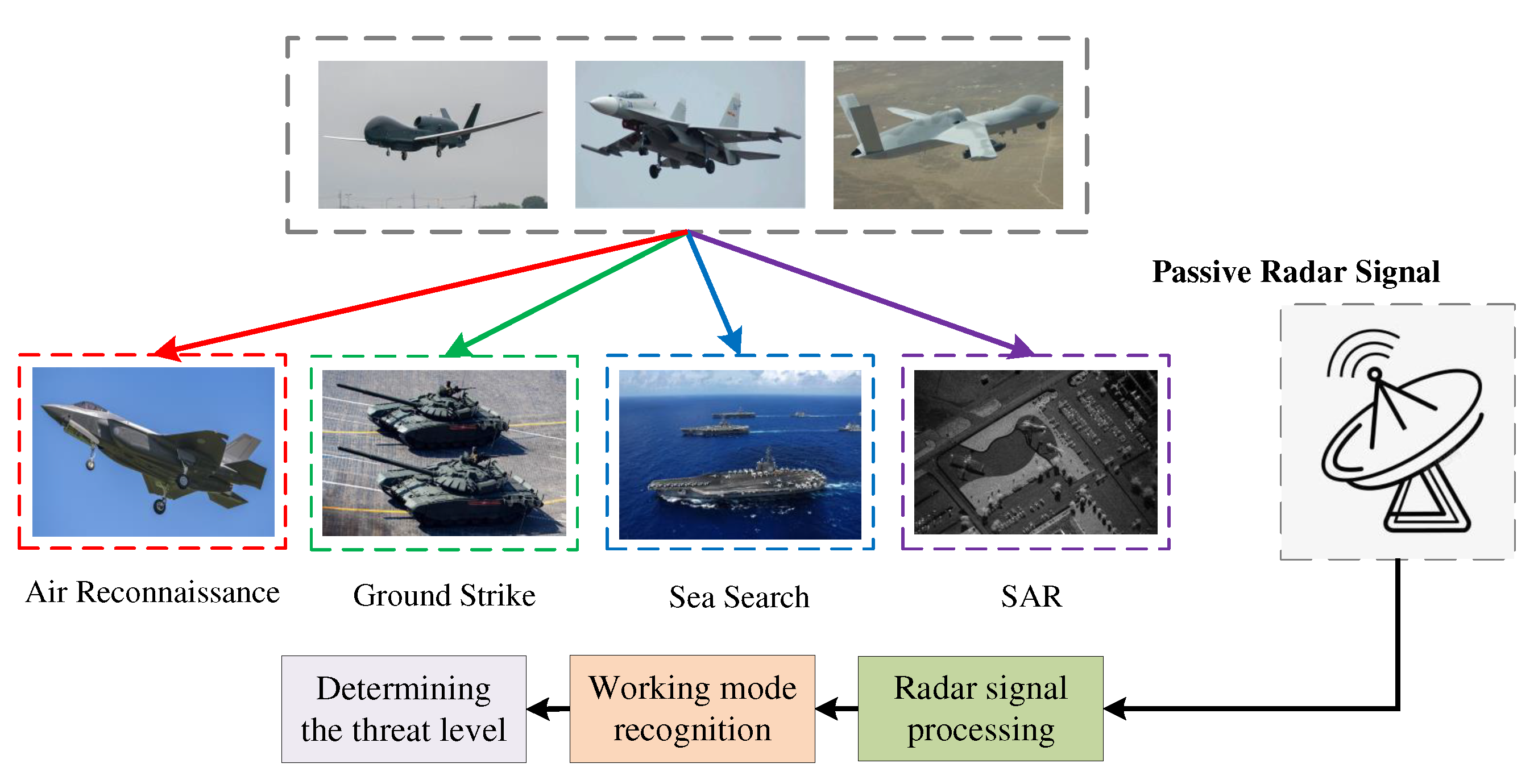Its application scenario is shown in Figure 1.
Nowadays, background signals are constantly increasing, and the impact of noise on signal processing is becoming more severe. In recent studies of working mode recognition [6,7,8], the scenarios with stable environments and small parameter ranges are mainly taking into account, but noise effects are not fully considered. It is well known that noise has a significant impact on signals, especially for airborne radar. Strong noise can cause the loss and errors of pulses, directly changing the pulse repetition frequency and leading to identification errors. Under high signal-to-noise ratio conditions, the signals are clear and the differences between working modes are apparent. A conventional deep learning network is capable of effectively extracting features for classification. Under low signal-to-noise ratio conditions, the following three challenges must be faced:
  • Due to the uncertainty of scenarios, radar pulses may originate from different noise environments or different radars, and their parameter ranges are beyond the scope of “training data”, belonging to “unknown signals”. This seriously interferes with machine learning algorithms that are purely data-driven.
  • As the signal-to-noise ratio decreases, a large amount of redundant or erroneous information will be mixed in the received radar pulses, resulting in wrong parameters. At this point, the effective parameters cannot be determined, and originally traceable signals become chaotic.
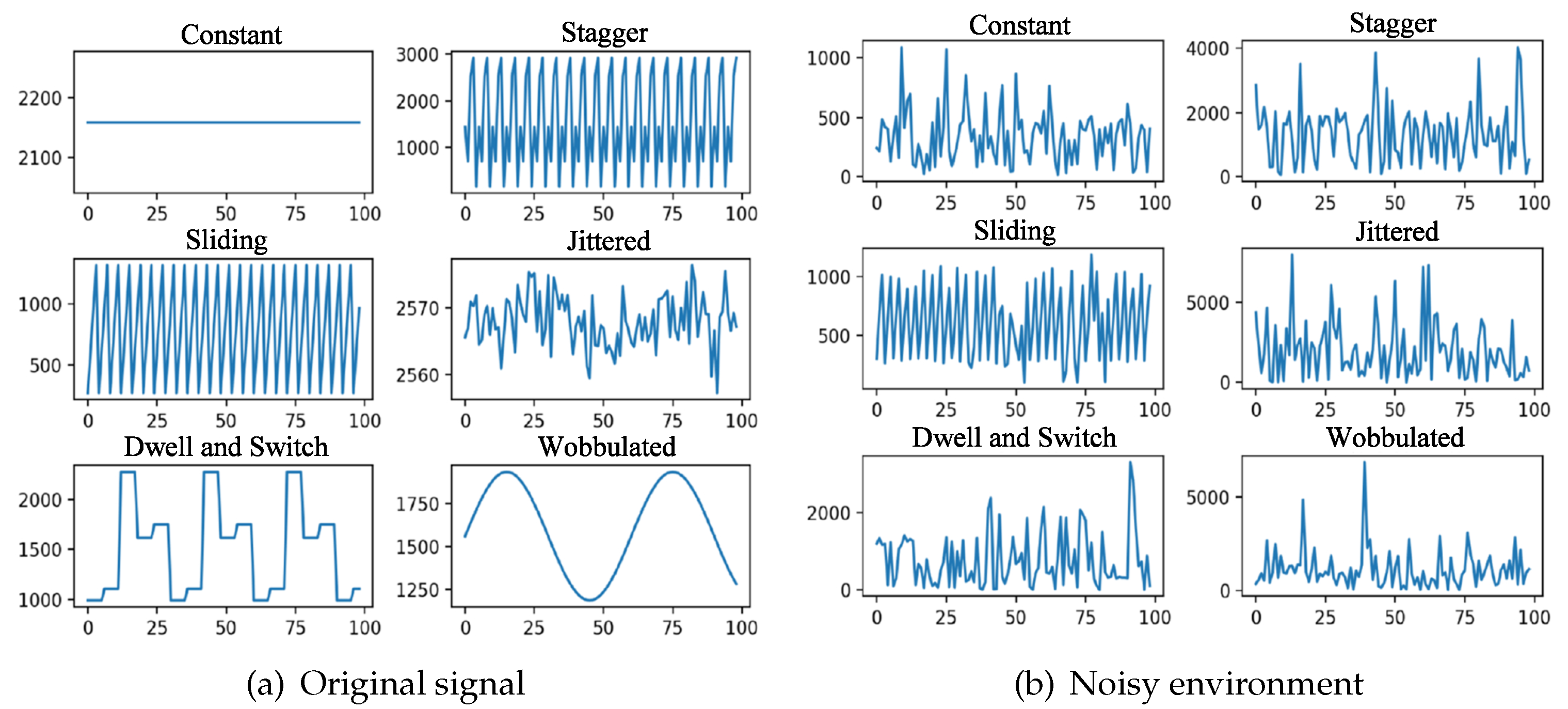
  • Defective radar signals differ from images in that the encoding and modulation styles of the signals are more diverse. The two types of inputs exhibit significant differences in terms of characteristics such as size, location, and shape. Noise has a more pronounced impact on signals, and conventional deep learning networks for computer vision are challenging to effectively process these differences. The comparison of the signal in a significant noise environment is shown in Figure 2. It can be seen that the radar pulse pattern is difficult to distinguish under noise.
In this context, a dual-network cascaded model based on latent-space noise encoding is proposed in this paper to address the aforementioned challenges. The main contributions of this paper are as follows:
  • We employ a cascaded learning approach with a noise estimation network and a recognition network, enhancing the algorithm’s adaptability in strong noise environments.
  • A noise estimation network based on U-Net is designed, which utilizes a symmetrical structure of up-sampling and down-sampling to extract and reconstruct noise features. The network achieves adaptive noise mapping relationships in different channel and spatial area.
  • The MSCANet, which is to address the characteristics of radar pulse signals, is presented. The network is augmented with both deep-wise group convolution, multi-scale convolution, and self-attention mechanisms, which serve to improve the network’s feature extraction capabilities and make the model more lightweight.
The rest of this paper is arranged as follows. Firstly, we review the relevant work in the field of radar working mode recognition in Section 2. In Section 3, the proposed algorithm is introduced with regard to various aspects, including noise encoding in latent space, group convolution method, multi-scale convolutional modules, and self-attention mechanism. Section 4 reports data sets, experimental designs, and experimental results to evaluate and compare the performance of the proposed algorithm with other recognition technologies. Section 5 concludes this paper.

2. Related Work

Radar signal recognition can be mainly classified into traditional expert knowledge-driven algorithms and data-driven algorithms represented by machine learning. With the diversification of radar systems and the complexity of electromagnetic space, traditional methods are gradually becoming ineffective, while data-driven algorithms have taken the lead in this field.
Data-driven methods optimize the known model by learning a large amount of data to achieve classification and recognition. In recent years, algorithms represented by deep learning have been widely used in computer vision, natural language processing and other fields. Convolutional Neural Network (CNN) [9], Recurrent Neural Network (RNN) [10] and self-attention mechanism [11] are three deep learning representative structures that each have advantages in radar signal recognition. Convolutional neural networks can extract the potential information of signals through feature mining, recurrent networks can preserve the semantic relationships, and self-attentive mechanisms are more advantageous in signal restoration.In practical scenarios, deep learning algorithms are usually limited by the following four aspects:
  • Recognition of unknown signals. [12,13] propose a comprehensive recognition approach based on both traditional classifiers and deep learning networks. By utilizing the classifier to assist in network training, the central vectors of known data are deduced and thus the feasibility of recognizing unknown signals through known ones is verified.
  • Few-shot learning problem. [14,15] explore the model training methods under the condition of few-shot learning respectively by using the generated adversarial network and the auto-encoder embedded with the feature extraction module, solving the problem of training data shortage.
  • Interpret-ability of recognition. The problem is a challenging research issue in various fields. From the perspective of integrating knowledge-driven and data-driven approaches, [16,17] have defined the feature representation of radar signals in deep learning networks, and have achieved embedded knowledge through prior knowledge assistance in network training.
  • Low Signal-to-Noise Ratio (SNR) condition. SNR is a critical factor in the field of signal processing [18], which must be considered. Reference [19] utilizes the characteristics of residual networks and adopts the naive method of deepening the network to improve recognition performance under low SNR, with no further improvement possible after network saturation. [20] employs a fusion of CNN and Long Short-Term Memory (LSTM) network to retain signal features and semantic relationships, but this method only focuses on short-term temporal dependencies and cannot extract global information. Literature [21] proposes a lightweight combinational neural network, which uses two networks for pre-recognition and fine recognition. SEBlock attention module is embedded in the network to suppress noise interference. This method is suitable for multi-label classification tasks.
We specifically focused on the challenges posed by low SNR environments in radiation source identification. Based on the aforementioned research, the main difficulty lies in extracting radar signal features in noisy environments. The above algorithms are essentially searching for differences among data, without considering the characteristics of radar signals. In other words, they are general methods in different fields, so their performance are significantly compromised when data is affected by noise.
Therefore, we propose a cascade network focusing on the characteristics of pulse signals in noisy environment. Among them, the noise encoding sub-network is built on the basis of U-Net. It is a classic network used for semantic segmentation in image processing, which has advantages in feature extraction and reconstruction due to its symmetric structure of up-sampling and down-sampling [22,23]. The recognition sub-network is an original design based on the characteristics of radar signals.

3. Radar Signal Detection in Noisy Environment

To find an appropriate method for measuring noise, the step is to establish a receive signal model under the noisy environment.As a passive receiver, it is impossible to know the signal processing method of the target.Therefore, a general representation of the received signal with added noise is as follows:
v I t = A + n I t = r t cos φ t
v Q t = n Q t = r t sin φ t
where n I t and n Q t are in-phase and quadrature components of the noise and have the same variance ψ 2 . A is the echo amplitude. The probability density functions for r t and φ t represent the modulus and phase of signal v t , respectively. Their joint probability density function is expressed as:
f r , φ = f n I , n Q ∂ n I ∂ r ∂ n I ∂ φ ∂ n Q ∂ r ∂ n Q ∂ φ = f n I , n Q cos φ − r sin φ sin φ r cos φ = f n I , n Q r t
with
f n I , n Q = 1 2 π ψ 2 e x p − n I 2 + n Q 2 2 ψ 2 = 1 2 π ψ 2 e x p − r cos φ − A 2 + r sin φ 2 2 ψ 2
Therefore, the probability density function of the modulus r alone can be expressed as:
f r = ∫ 0 2 π f r , φ d φ = r ψ 2 I 0 A r ψ 2 e x p − r 2 + A 2 2 ψ 2
where I 0 · is the modified zero-order Bessel function.
The target is detected when the modulus of the signal exceeds the threshold voltage V T . Considering the relationship between V T and false alarm probability P f , that is, V T = 2 ψ 2 ln 1 / P f . The detection probability P d can be written as:
P d = ∫ 2 ψ 2 ln 1 / P f ∞ r ψ 2 I 0 A r ψ 2 e x p − r 2 + A 2 2 ψ 2 d r
When the noise is Gaussian distribution and P d is much larger than P f , A, r and ψ in formula (6) are replaced by the signal-to-noise ratio (SNR), the formula can be approximated as follows:
P d = 0.5 × e r f c − ln P f − S N R + 0.5
with complementary error function e r f c · is:
e r f c x = 1 − 2 π ∫ 0 x e − y 2 d y
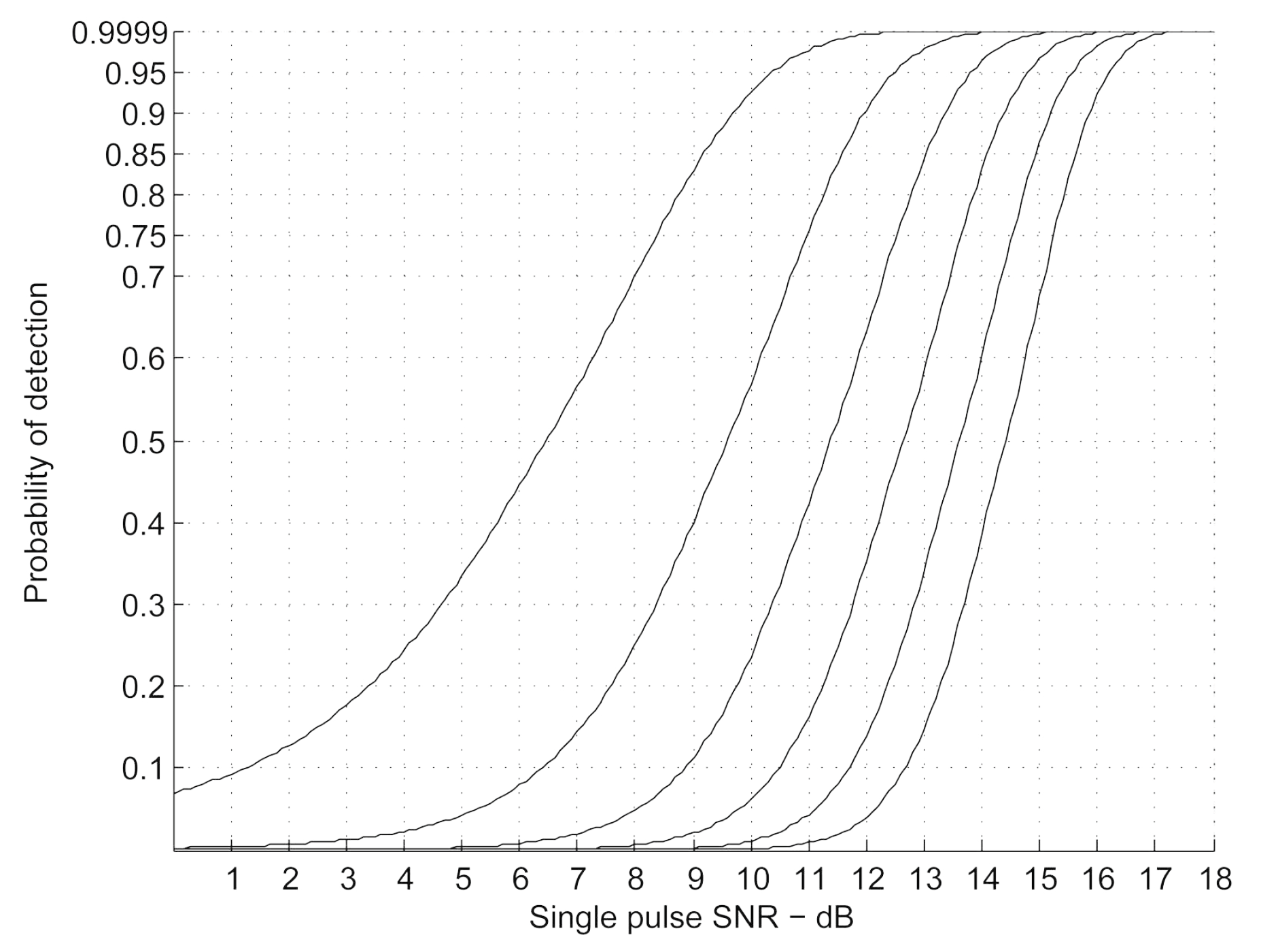
In summary, we can know that there will always be some loss or error radar pulse in noisy environment. The relationship between detection probability and SNR is shown in Figure 3.
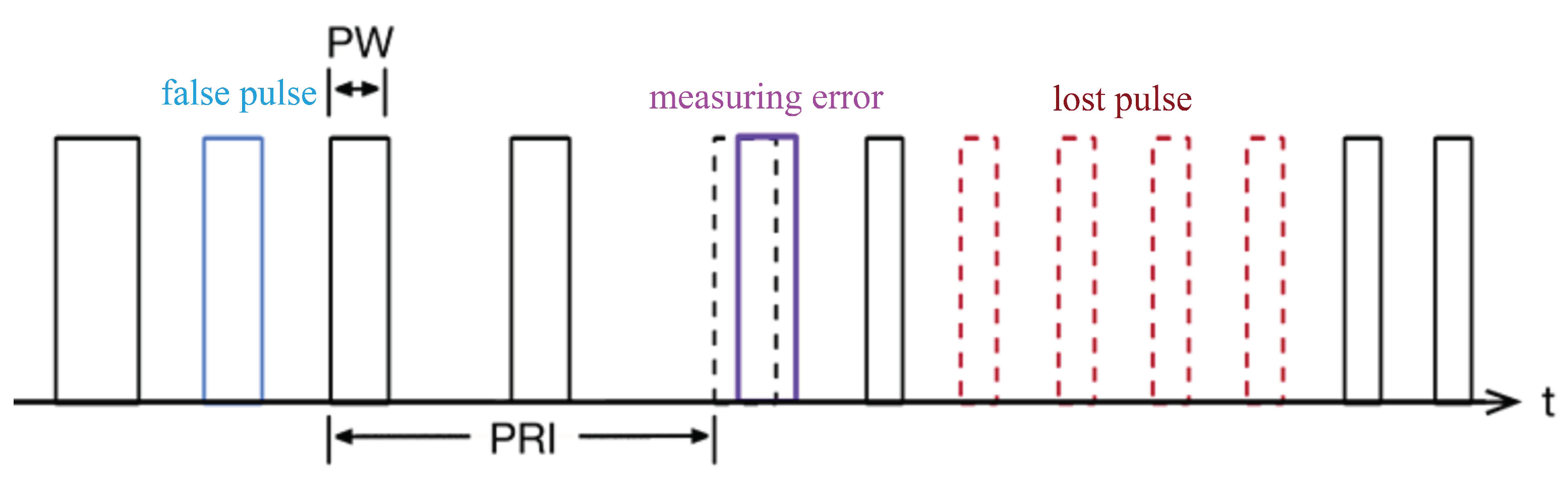
Through the changing pattern of radar pulse, we can analyze the radar working modes. But due to the interference of noise and the influence of hardware factors, radar pulse will have some deviation, error and loss. Equation (7) shows that the detection probability, false alarm probability, and SNR are related. As the SNR decreases, the pulse distortion becomes more severe, and the probabilities of false alarm and missed detection increase. Therefore, for convenience of expression, we convert the impact of SNR on radar full pulses into lost pulses and false pulses, as shown in Figure 4.

4. Algorithm Model and Implementation

4.1. Dual-Network Cascade Model

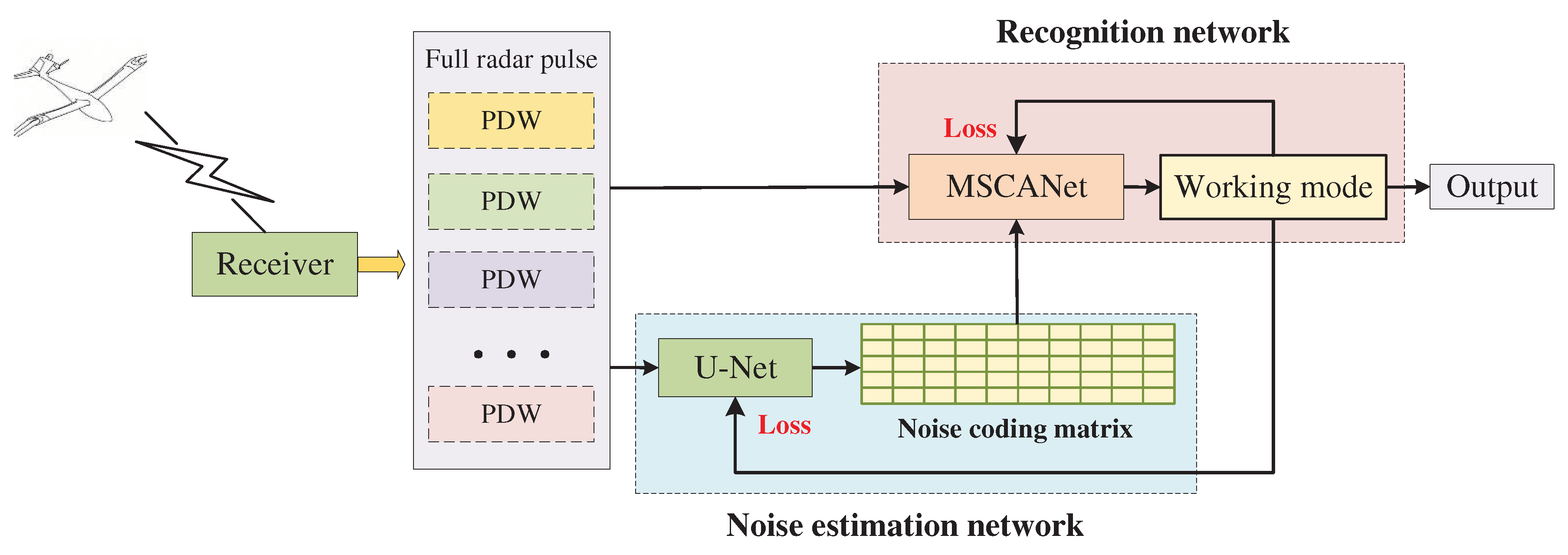
In this section, We designed an “end-to-end” recognition model with a dual-network cascade to address the problem of pulse pattern distortion in noisy environments. The model takes the full-pulse signal from the radar as input and outputs the mode recognition result.
In radar signal processing, the receiver can observe the received signal from multiple dimensions, such as radio frequency (RF), intermediate frequency (IF), base band, and full-pulse. Furthermore, according to the Fourier transform principle, feature extraction can be performed simultaneously from temporal and spectral domains. For example, in reference [24], the signal is transformed into a spectrogram, resulting in continuity on the feature map, greatly enhancing the effectiveness of convolutional layers. However, it should be noted that mode recognition relies more on the full-pulse data, which has more pronounced discreteness and weaker global self-correlation. As a result, noise more significantly disrupts the inherent pattern of the data, making conventional convolutional networks difficult to apply.
Therefore, we design the model into two parts. The first part is a noise estimation sub-network based on U-Net, which encodes the noise by down-sampling and up-sampling, and is used to adaptively estimate the sample’s noise level. The second part is a radar working mode recognition sub-network based on a multi-scale convolutional attention network, called MSCANet. It is trained using both the radar full pulse and noise coding information. The general diagram of the proposed scheme is shown in Figure 5.
Regarding to the optimization of networks, we adopt a cascaded approach to jointly train the noise estimation network and the classification recognition network to convergence, ensuring that both two networks are optimized for accurate identification of working mode in noisy environments. At this point, the objective function of cascaded training can be defined as the classification loss function:
L c = − 1 N ∑ i = 1 N y i ln y ^ i + 1 − y i ln 1 − y ^ i + γ 2 m ∑ l ∑ k ∑ j W k , j l 2
where y i represents the real label of N radar pulse samples within a batch size, y ^ i represents the prediction label. The second term of the formula is the regularization of the model, which is used to reduce the over-fitting phenomenon , the regularization coefficient γ is set to 0.001, and W k , j l 2 represents the jth convolution kernel corresponding to the kth feature map in the lth layer.

4.2. Noise Estimation Network Based on U-Net

Due to the uncertainty of noise environment, different signals are affected by noise to different extents. This irregular fluctuation is detrimental to recognition networks, therefore, a measure that can assess the level of signal noise is needed to help recognition networks filter out noise more effectively. In 2018, [25] firstly introduced the concept of noise level mapping into computer vision, and proposed FFDNet to help CNN complete image denoising and recognition. However, when the noise level of the evaluation is wrong, it will have a more adverse effect on the subsequent signal recognition. Therefore, in 2022, Du proposed a signal denoising classification network DNCNet [18] from the point of view of signals. The algorithm pre-positioned a 5-layer convolutional network to quantize the noise level, and then carried out denoising and identification. This method has better dynamic evaluation ability to noise.
On the basis of the above research, we design a sub-network of hidden space noise coding, which needs to meet the following requirements:
  • Each channel in radar full pulse is affected by noise to different degrees, so it is necessary to evaluate the noise separately.
  • The effect function of noise on discrete radar pulse can be defined as an indicative function rather than a continuous function, so the whole sequence cannot be evaluated by a continuous mapping relationship.
  • The purpose of noise evaluation is to help classification network to recognize working mode rather than to obtain certain information. The output noise coding sequence should match the input.
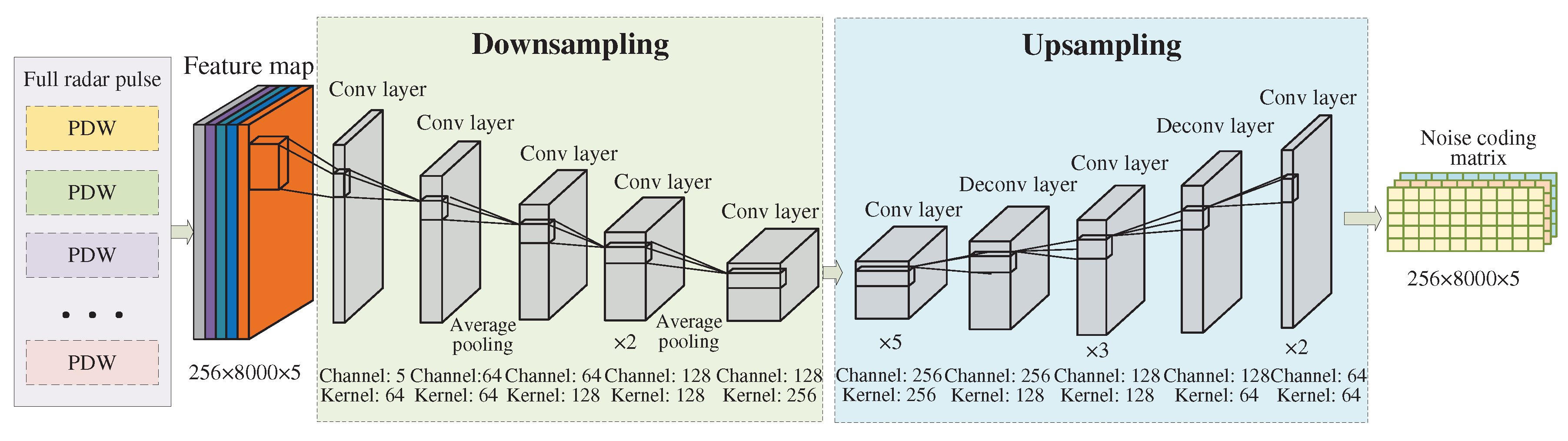
Based on the above requirements, we adopt U-Net structure, whose symmetrical down-sampling and up-sampling structure can ensure that the output noise code is consistent with the input size. And the coding point corresponds to the channel and time series in the pulse sequence. The process of sub-sampling can be regarded as the extraction of noise features, which consists of convolution and pooling. The up-sampling process is to restore the original size according to the noise characteristics, which is realized by convolution and deconvolution. This progressive reduction structure can extract and recover information by gradually increasing the receptive field of the network, and it is easier to grasp the noise features at different scales. The proposed noise estimation network is shown in Figure 6.
In detail, the input to the network is radar full pulses. The main structure consists of 16 convolutional layers, 2 deconvolution layers and 2 average pooling layers. In order to preserve the independence of each channel during sampling, the network adopts one-dimensional convolution, pooling and deconvolution, the kernel size is set to 3×1, the number of kernel is 64, 128 and 256 in a progressive order. The ReLU function is used as activation function to correct the gradient. The change of the the feature map size is realized by the Pooling layer and the deconvolution layer. And the cascade pooling is adopted during down-sampling, that is, the pooling size is greater than the step size, which can keep information interaction between adjacent data. The output of the network is a noise coding matrix with the same size as input, which can be used for adaptive evaluation of the sample noise level greatly.

4.3. Recognition Network Based on MSCANet

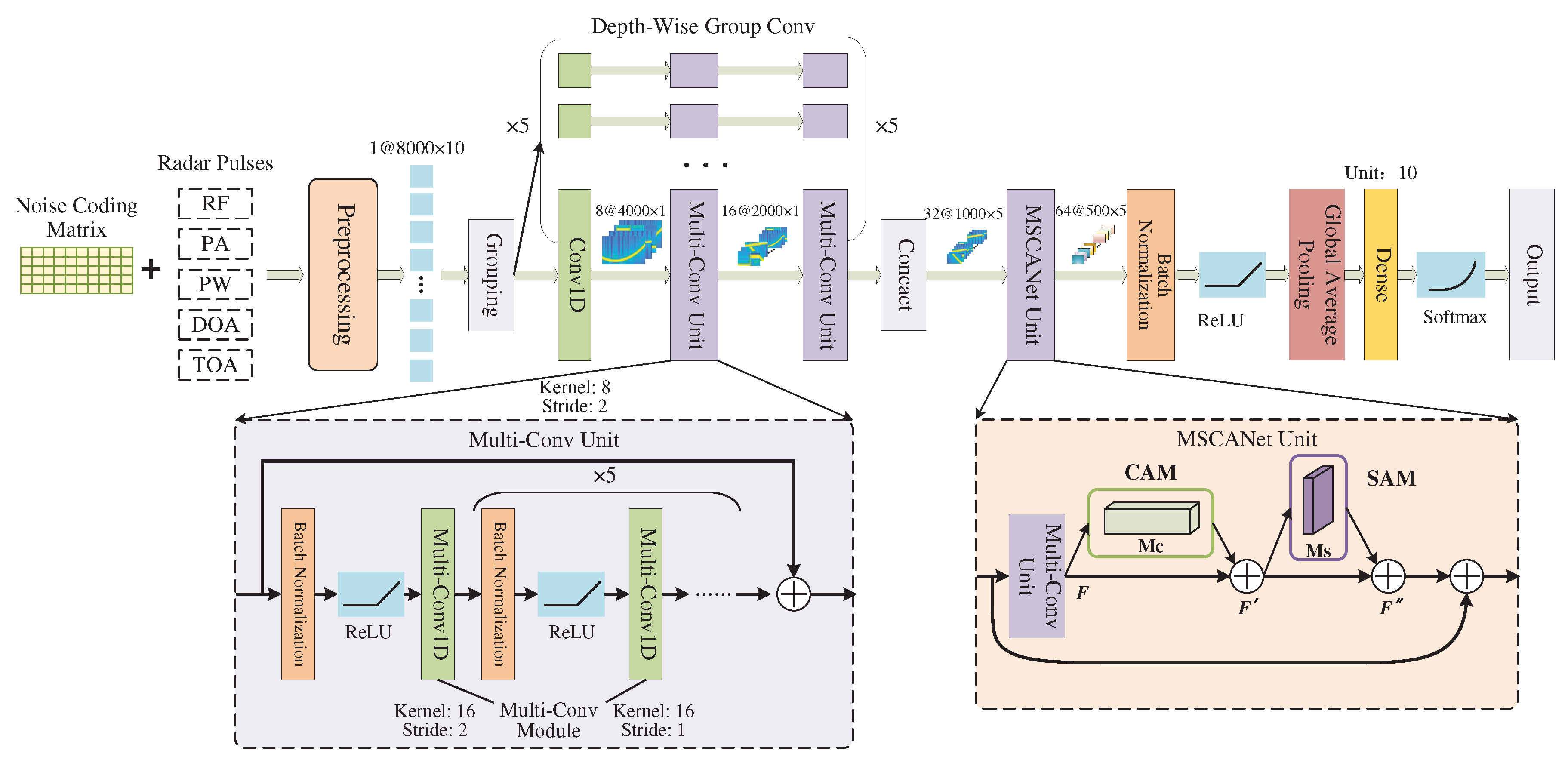
According to the characteristics of radar pulse and the influence of noise, we design the following network structures in MSCANet. (1) Depth-wise group convolution. Independent convolution kernels are used for each channel in the shallow network. (2) Multi-scale 1-D convolution. The multi-scale features of radar pulses are extracted by convolution kernel of multiple parallel mutual primes. (3) Channel attention module (CAM) and spatial attention module (SAM). Adaptive weights of channels and spatial regions are implemented, enabling the network to focus on high-impact features. The structure of MSCANet is illustrated in Figure 7.
The network also employs global average pooling to replace fully connected layers and adopts residual structures to establish shortcut connections between modules. Deeper networks are more efficient in extracting features, while the above structures help alleviate over-fitting in deep networks.

4.3.1. Depth-Wise Group Convolution

Radar pulse data is a set of discrete parameters on a time series, with no reliable correlations between channels. However, conventional convolution combines the feature maps of these channels, which is inefficient for extracting features from full-pulse data and results in substantial computational waste. Therefore, we adopt depth-wise group convolution to realize feature extraction.
Group convolution was firstly applied in AlexNet to solve the problem that a single GPU could not support simultaneous computation on feature maps. Therefore, designers split the channels and compute them separately on separate GPUs. Subsequently, with the prevalence of lightweight networks, reference [26] combined group convolution with ResNet to propose the ResNeXt network. In comparison to contemporaneous networks such as Inception v4 and Inception-ResNet v2, the proposed model exhibits simpler and more lightweight architecture at equivalent recognition accuracy on the ImageNet dataset.
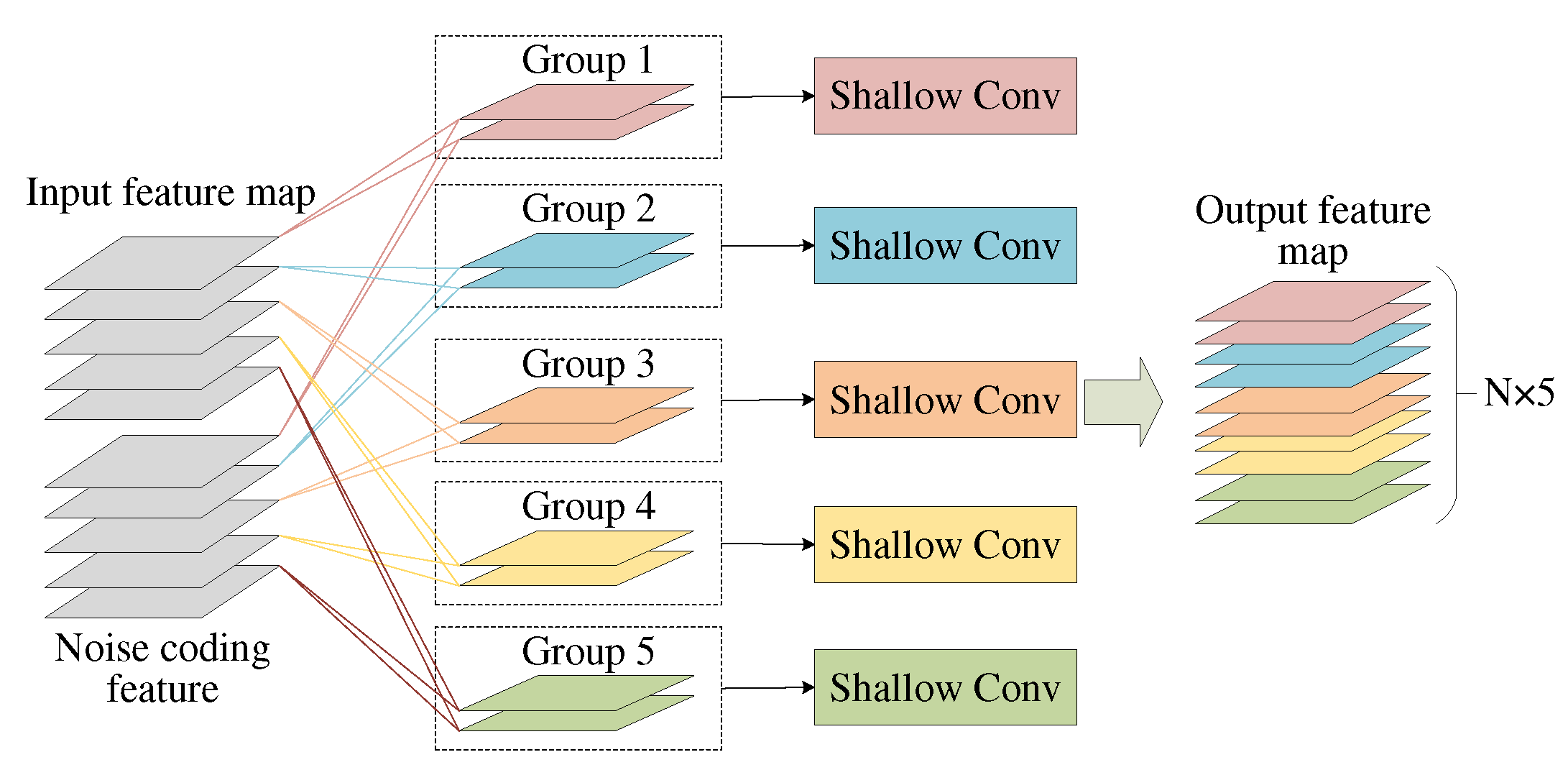
Using the same idea, we divide the pulse data into 5 groups, each group contains a dimension and the corresponding noise coding vector. Independent convolution kernel is used for feature extraction among the groups to ensure the independence of each channel in the shallow network. Channel concatenation is performed before the last convolution layer to preserve the correlation between channels. The specific structure is shown in Figure 8.
The advantage of depth-wise group convolution lies in not only isolating information interaction between different groups, but also reducing computational complexity and parameter quantity to 1 / 5 comparing with conventional convolution. This makes the network more lightweight and faster.
Taking 1-D convolution as an example in this paper, let C i n and C o u t represent input and output channel number respectively, K is the size of kernel, the computational complexity of kernel at a point for conventional convolution O 1 can be expressed as:
O 1 = C i n × K 2 + K 2 − 1 + 1 = C i n × 2 K 2 − 1 + 1
then, the computational complexity of the entire convolutional layer is:
O c = C o u t × O 1 × S o u t = C o u t × C i n × 2 K 2 − 1 + 1 × S o u t
where S o u t is the size of the output feature map. In the same way, the number of parameters for the convolution layer P c can be written as:
P c = C o u t × C i n × K + 1
When using depth-wise group convolution, assuming that the input feature map is split into g groups, the corresponding input and output feature map channels are reduced to 1 / g . Due to parallel calculations of g groups, this reduction is canceled out. However, corresponding to the change in the number of channels in the feature map, the number of channels in the convolution kernel also decreases to C i n / g . Therefore, the computational complexity O g and the number of parameters P g are expressed as:
O g = C o u t × C i n g × 2 K 2 − 1 + 1 × S o u t
P g = C o u t × C i n g × K + 1
It is not difficult to see that the computational complexity and the number of parameters are reduced to 1 / g approximately comparing to conventional convolution, which proves the advantage of deep-wise group convolution.

4.3.2. Multi-Scale 1-D Convolution

In convolution layer, using kernels of the same size will compute the same region in the feature map. The difference between the kernels lies in their kernel parameters, but their receptive fields are the same. This is not conducive to adapting to pulse patterns under uncertain noise. Inspired by the application of short-time Fourier transform (STFT) with different window functions [27,28], we use parallel multi-scale convolution kernel instead of conventional one. By using the parallel computation of multi-scale convolutional kernels, the network has different “perspectives”, so it can extract more scale signal features when the number of convolutional kernel is the same. This idea is also reflected in the Inception network for image recognition [29]. 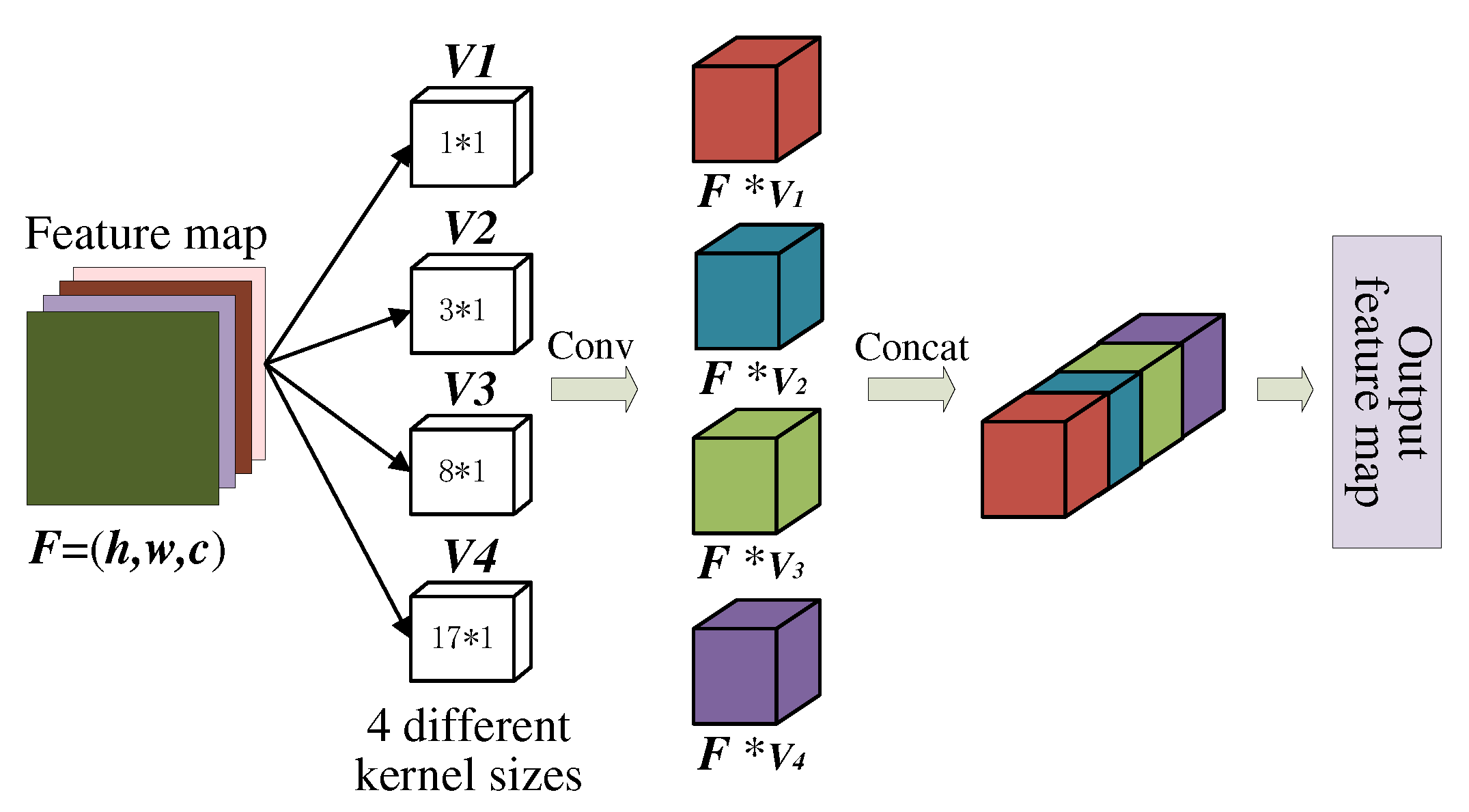Figure 9 shows the structure of the multi-scale convolution module.
In addition to using 1x1 convolutions to preserve the original feature map scale, the module adopts three types of 1-D convolution kernels with sizes of 3x1, 8x1, and 17x1 that are mutually prime. This design more efficiently extracts fine-grained features of the original signal. Different-scale convolution kernels are equivalent to mapping feature values at different window sizes. So the mapping z i j x y of the ith layer and jth feature map at location x , y can be expressed as:
z i j x y = f ∑ k = 1 K ∑ h H m − 1 ∑ w W m − 1 ω i j k h w z i − 1 k x + h y + w + b i j
where K is the number of feature maps at i − 1 layer, H m × W m is the size of the convolution kernel, ω i j k h w is the convolution kernel parameter matrix connected to the kth feature map at i − 1 layer, b i j is the bias, and f · is the ReLU activation function. Write the matrix of z i j x y as F , then the output feature map is:
F ′ = C o n c a t F ∗ V 1 , F ∗ V 2 , F ∗ V 3 , F ∗ V 4
where C o n c a t is a operation of channel concatenation. Different from the pyramid-type feature maps obtained by conventional convolution, multi-scale convolution can obtain more receptive fields of different sizes and have richer feature levels.

4.3.3. Self-Attention Mechanism

The influence of different parameters and regions on the operating modes in radar pulses varies greatly, but convolution is local and indiscriminate. Therefore, it is necessary to adopt different selection strategies. In order to extract signal features with emphasis and preserve semantic relationships, we introduce channel self-attention module (CAM) and spatial self-attention module (SAM) to achieve adaptive weight allocation, enabling the network to pay more attention to valuable channels and regions [30].
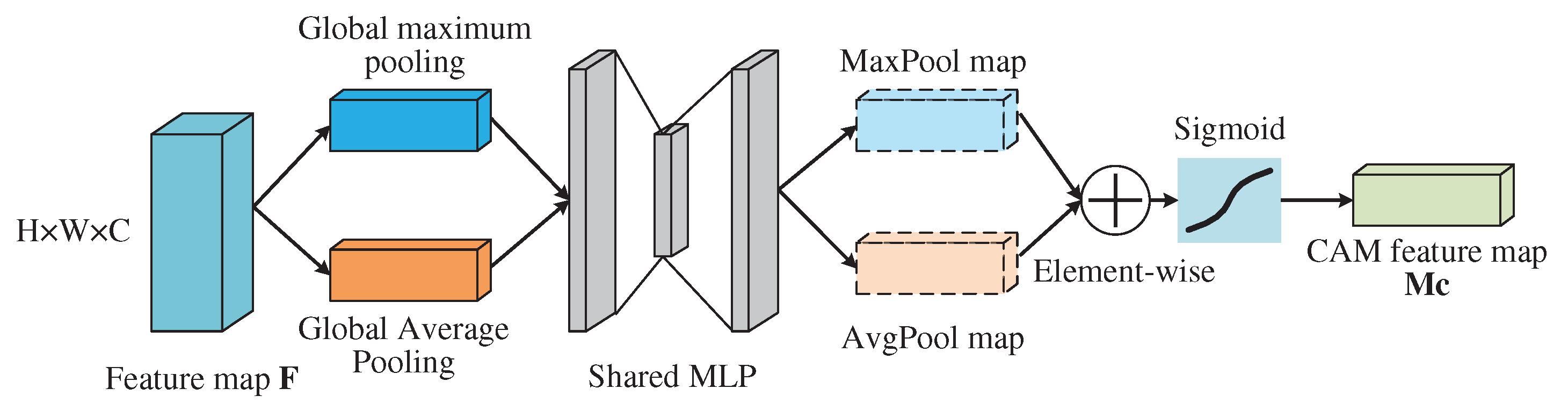
The structure of CAM is shown in Figure 10. Firstly, parallel maximum pooling and average pooling are utilized to compress the feature maps along the spatial dimensions, yielding channel-wise vectors and resulting in two 1 × 1 × C feature maps, where C represents the number of channels, H and W represent the height and width of the feature map respectively. Then, the obtained feature maps are input into a shared two-layer perceptron, with a ReLU activation function in between, and the number of neurons in the second layer equal to the number of output channels, which enhances the trainability of CAM. Finally, an element-wise operation is applied to the two kinds of pooling graphs, and the output feature map M c is written as:
M c F = f W 0 ⊗ W 1 ⊗ F avg c + W 0 ⊗ W 1 ⊗ F max c
where f · is sigmoid activation function, W 0 and W 1 are the weight vectors of the two-layer shared perceptron, ⊗ is Kronecker product. F a v g c and F m a x c represent global average pooling and global maximum pooling, respectively. The two pooling operations ensure that the model generates feedback on global region and maximum region of the feature map, so the performance is better than that of SENet [31] using only average pooling.
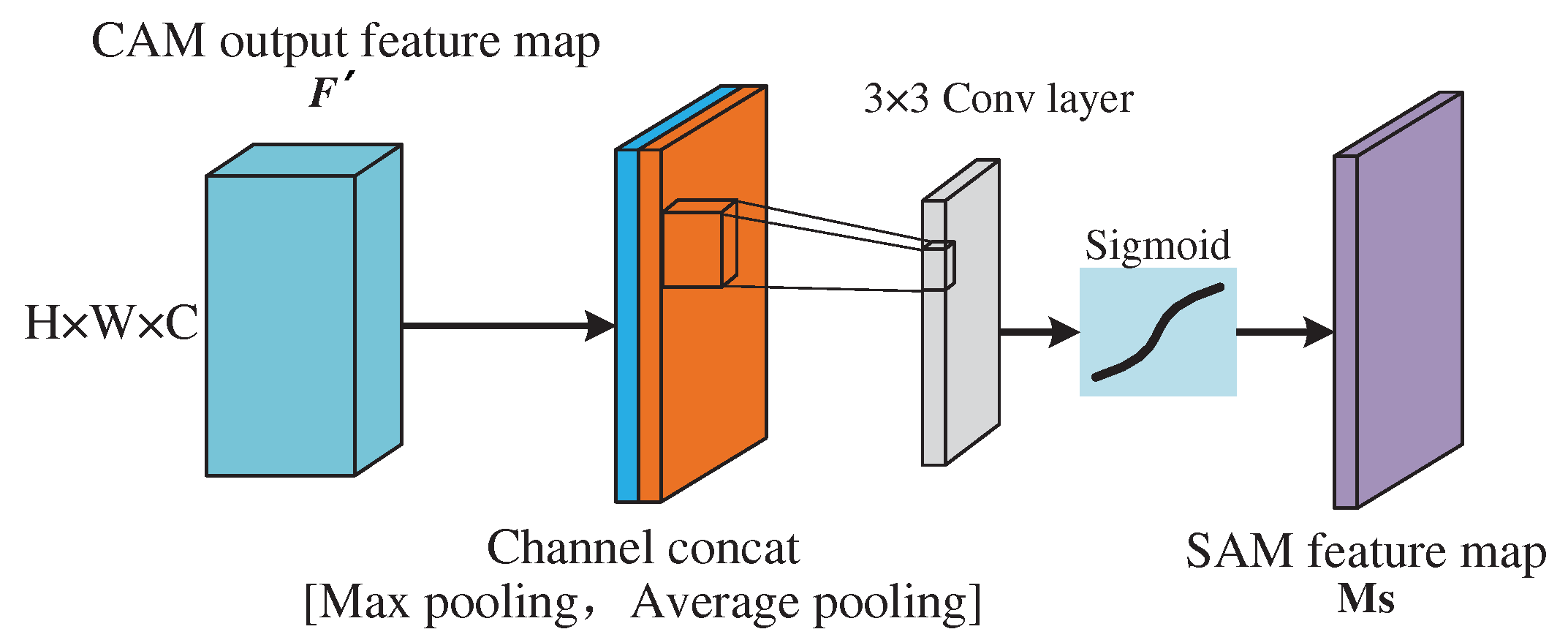
The structure of SAM module is shown in Figure 11. SAM is calculated on the basis of CAM, the module compresses the channel information and retains the attention to the spatial information. Firstly, global average pooling and global maximum pooling based on channel dimension are used to calculate feature maps. After it is splicing into H × W × 2 feature maps, the average pooling and maximum pooling information are extracted by 3×1 convolution, and the feature maps are reduced to 1 dimension again. The expression for M s is as follows:
M s F = f C o n v 1 D 3 F avg s , F max s
Where C o n v 1 D 3 is 1-D convolution of 3×1, F a v g s and F m a x s represent global average pooling and global maximum pooling, respectively.
What’s more, multi-scale convolution is used to obtain more multivariate feature maps, which better improves the performance of the self-attention mechanism. The CAM enables the network to focus on more efficient feature maps in multi-scale convolution, such as local information of modulation laws. The SAM can filter out the information redundancy or error area caused by interference at different sizes. All these can help the network to improve the recognition performance under significant noise environment.

5. Experiments and Results

In this section, the effectiveness of the proposed algorithm in significant noise environment is demonstrated through simulation experiments, which include four parts:
  • Considering different application scenarios, 10 kinds of typical radar working modes that have appeared are constructed for the demonstration of subsequent experiments.
  • The performance of traditional machine learning algorithms and deep learning algorithms is tested to prove the limitations of conventional artificial intelligence algorithms in noisy environments.
  • By introducing noise estimation sub-network, the performance of single classification model and dual-network cascade model is compared.
  • The performance of the proposed MSCANet network is compared with that of the classical deep learning network, and the influence of noise environment on radar working mode is analyzed.

5.1. Dataset

Due to the confidentiality of radar parameters, there is no available public data set at present. Therefore, on the basis of public literature [32,33,34] and referring to authoritative books such as Radar Manual, Airborne Radar Manual and Pulse Doppler Radar, we simulated and constructed radar full pulse data sets, namely RPDWS-I, which covers the typical modes of reconnaissance, search, tracking, moving target indication, SAR.
The dataset includes the following 10 kinds of radar working modes: Velocity Search (VS), Range While Search (RWS), Velocity-Range Search (VRS), Multiple-Target Tracking (MTT), Beam Riding (BR), Ground Moving Target Indication (GMTI), Ground Moving Target Tracking (GMTT), Sea Surface Search (SSS), Sea Surface Tracking (SST), Synthetic Aperture Radar (SAR). The training set includes 4,000 samples for each model. The test set has a total of 81 test environments, the range of miss pulse and false pulse is set to 0∼80%, the interval is 10%, 1000 samples for each environment. In order to present the experimental results succinctly and clearly, the baseline algorithm only tests the model performance under 0∼50% lost pulse and false pulse environments, the proposed algorithm is tested under all environments. The signal parameters in the data set are shown in Table 1, and the following parameter range and modulation style are confirmed in [35].

5.2. Performance of Conventional Artificial Intelligence Algorithms

Conventional artificial intelligence algorithms learn radar signal features in noisy environment by using noisy samples. Therefore, we randomly select 20% of the samples in the training set, and successively add 10∼30% ratio of the lost and false pulses as data enhancement measures to help the classifier extract data features in a noisy environment.

5.2.1. Traditional Machine Learning Algorithms

We selected 6 kinds of widely used machine learning classifiers for validation, as follows:
Linear support vector machine (SVM). The classifier uses linear kernel as a mapping function, which has the best effect in linearly separable data sets. However, the radar full pulse feature is high-dimensional data and linear indivisible, which cannot meet the requirements. Therefore, the model should have a certain tolerance for misclassification, the penalty factor C is set at 0.025.
Radial basis function (RBF) SVM. The classifier uses Gaussian kernel as a mapping function, which is suitable for high-dimensional and linearly inseparable full pulse features. Therefore, the focus of the research is to improve the recognition accuracy and avoid wrong classification, the standard deviation of the kernel parameter σ = 0.01 , and the penalty factor C = 1 .
Decision tree. In the algorithm, the data is divided by splitting the data set down into smaller, the number of splits being the depth of the decision tree. In this paper, Gini coefficient is used as the decision condition for dividing node data set. “Node” contains at least two samples, “leaf” contains at least one sample, and the maximum depth is 5.
Random forest. The algorithm is based on Bagging ensemble learning method, which divides the data set into multiple random subsets, trains on multiple base models, and finally gets the classification result by “voting”. Therefore, the algorithm can better eliminate the bias of a single model and prevent overfitting. In the algorithm, the base model is the Decision Tree classifier mentioned above, and the number of base models is 100.
Multi-layer perceptron (MLP). As an early neural network, MLP is mainly composed of fully connected layers. The maximum number of neurons in this paper is set at 1000.
Naive Bayes. Based on Bayes’ theorem, the posterior probability of classification is obtained by calculating prior probability, marginal likelihood estimation and likelihood estimation. The algorithm does not need to perform iterative calculation and has no preset parameters, which is suitable for large data sets.
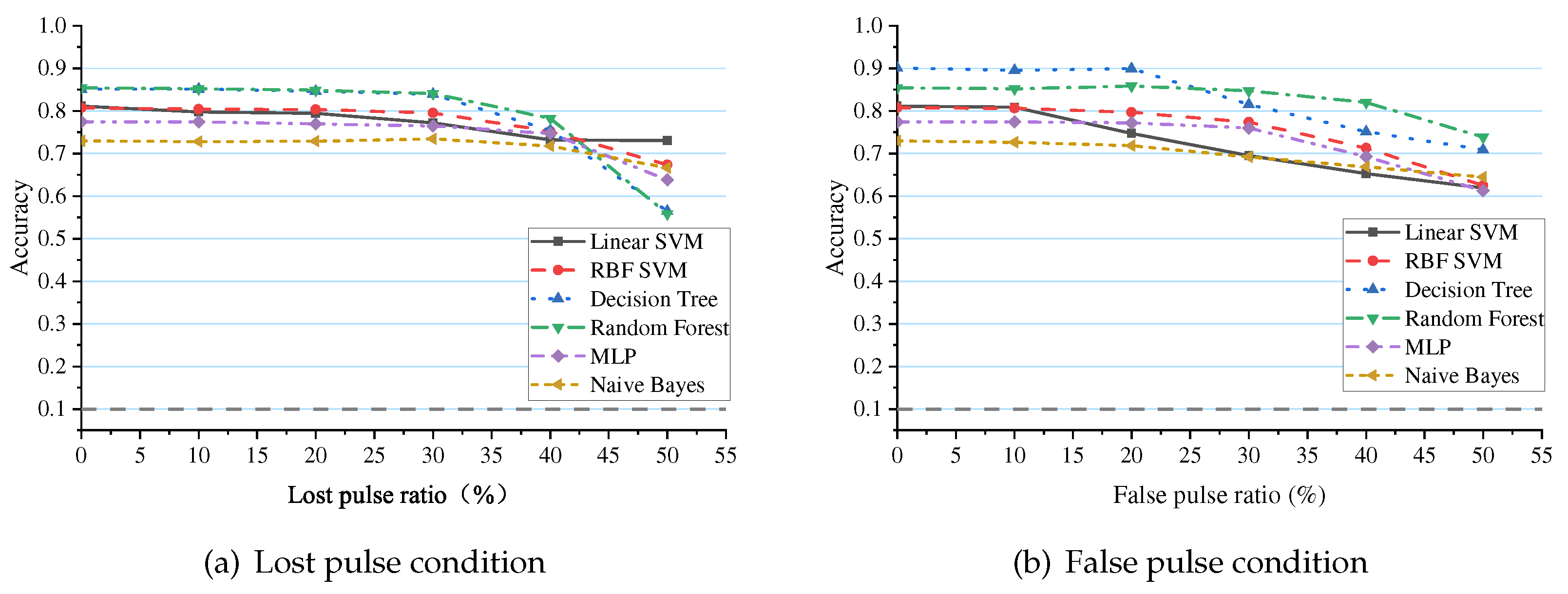
According to the above parameter settings, the performance of the classifiers is tested under different proportions of lost and false pulses. The results are shown in Figure 12. The gray dashed line represents the invalid recognition line. The average accuracy of six classifiers, including Linear SVM, RBF SVM, Decision Tree, Random Forest, MLP, and Naive Bayes, in identifying radar operating modes in a 0∼50% lost pulse environment are 77.2%, 77.3%, 78.4%, 78.9%, 74.5%, and 71.2%, respectively. In a 0∼50% false pulse environment, the average accuracy is 72.2%, 75.3%, 82.8%, 82.6%, 73.1%, and 69.6%, respectively. When the interference pulse ratio is below 30%, the recognition accuracy of the aforementioned classifiers remains relatively stable, but it significantly declines after exceeding 30%.
The results show that: (1) the overall recognition accuracy of the classifiers is not high, and the representation ability of traditional machine learning classifiers is not enough to support the extraction of radar features. (2) There is little difference in recognition ability between the two environments, and the classifier cannot take specific anti-interference measures for different environments. (3) The classifier relies heavily on the data distribution of the training set, and the recognition performance deteriorates significantly after it exceeds the range.

5.2.2. Conventional Deep Learning Algorithms

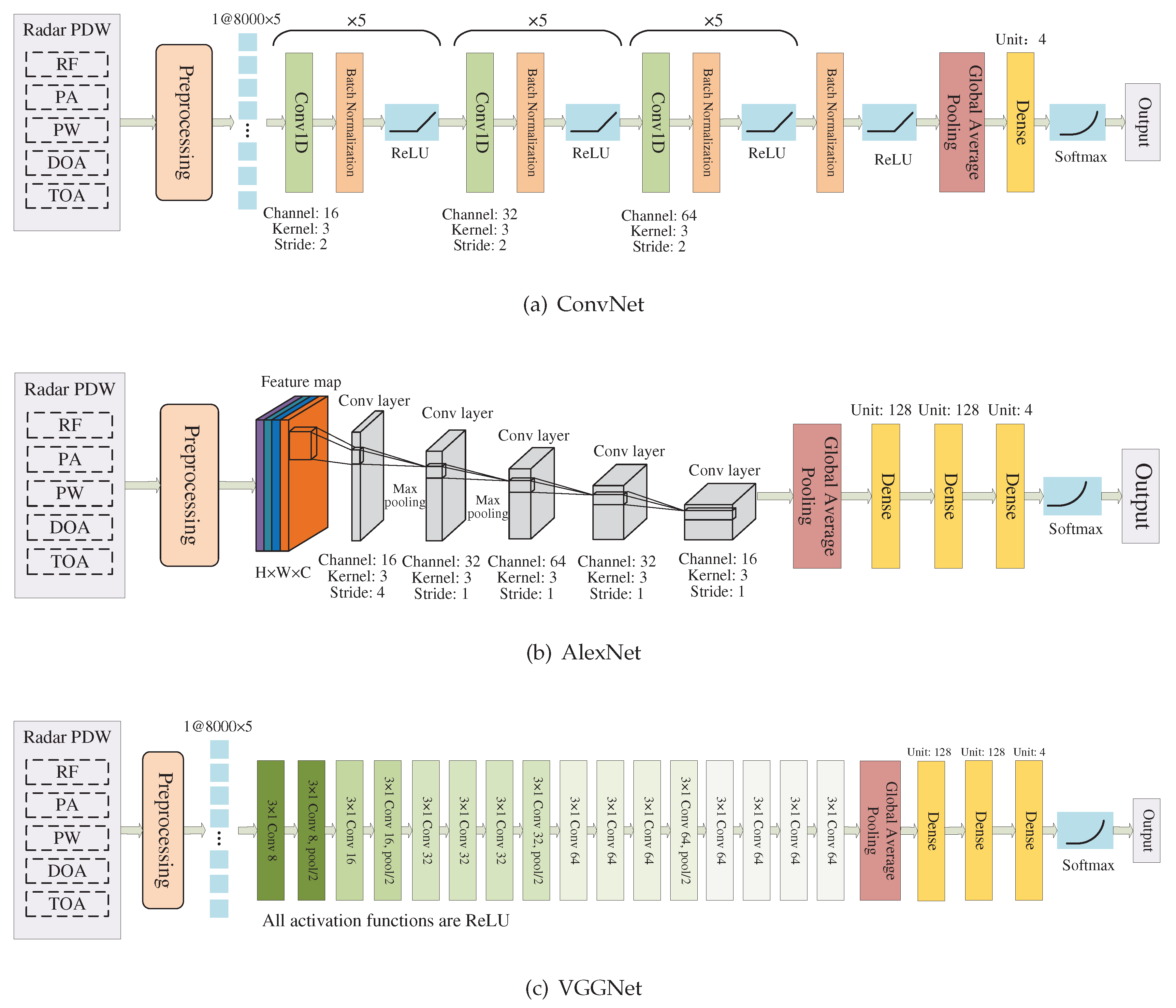
We selected 4 kinds of classic convolutional networks for testing, which have won championships in the ILSVRC competition and have been successfully applied in the field of radiation source identification. These models are ConvNet[12], ResNet[24], AlexNet[36], and VGGNet[37]. Among them, ResNet adopts the same basic structure as MSCANet, and the structures of ConvNet, AlexNet, and VGGNet are shown in Figure 13. To adapt to the radar pulse dataset, all convolution and pooling operations in the above networks are adjusted to 1-D. The networks use the Adam optimizer, and the learning rate decreases from 10 − 2 to 10 − 4 every 40 epochs. The batch size is set to 256, and each training consists of 160 epochs. The networks are regularized by L2 regularization with value of 10 − 4 .
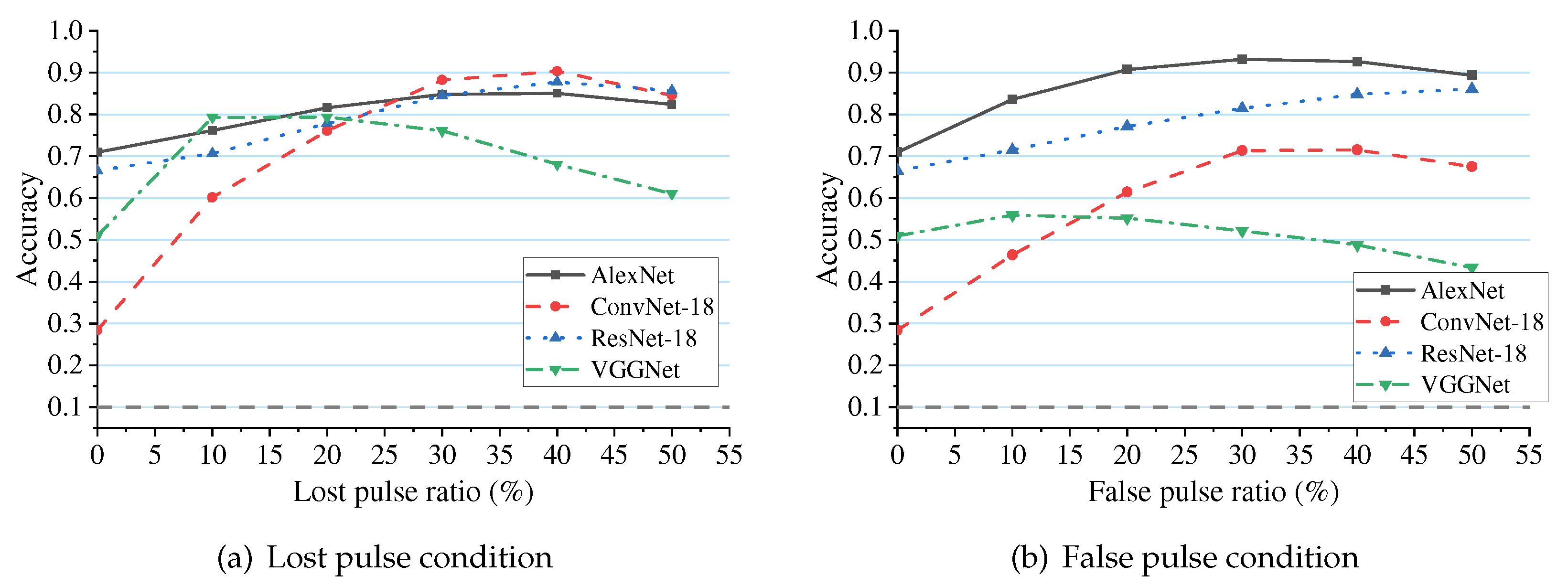
We conducted experiments in the same environment to test the deep learning algorithms. The accuracy of the four algorithms on the training set is shown in Table 2, all of which are above 90%. However, the performance of the networks on the test set is unstable, as shown in Figure 14.
It can be observed that AlexNet and ResNet-18 have better overall accuracy than ConvNet-18 and VGGNet, but they are still lower than the accuracy on the training set. All four networks exhibit a certain degree of overfitting. Although ConvNet-18 and VGGNet have deeper network structures compared to AlexNet, they lack effective measures to alleviate overfitting, resulting in worse test results. Deeper network structures can make the output closer to the training set, but it may not be effective for the test set. Although ResNet-18 also adopts a deep network structure, its residual connections help the network alleviate the overfitting problem.
A more concerning phenomenon is that the test accuracy of the four networks does not monotonically decrease but instead exhibits “peaks” at different positions. Due to the interference pulse ratio added in the training data ranging from 10% to 30%, when the test data has a similar distribution to the training data, the accuracy is relatively high, but the recognition ability declines in an ideal environment without interference. This means that the above four networks have not “learned” the true characteristics of radar working mode, but instead fitted the data distribution in the training set.

5.3. The Performance of Proposed Noise Estimation Sub-network

In order to verify the performance improvement brought by adaptive noise coding, we first introduce noise estimation sub-networks in different noise environments for testing. The model which combines the noise estimation sub-network and classification recognition network is called “cascade model”, and the single recognition network is denoted as “independent model”. This part of the experiment compares the recognition accuracy of the two kinds of models. The baseline models consist of ConvNet-18, AlexNet, VGGNet, and ResNet-18, which are mentioned above. To match the noise estimation sub-network, the cascaded models all adopt deep-wise group convolution.
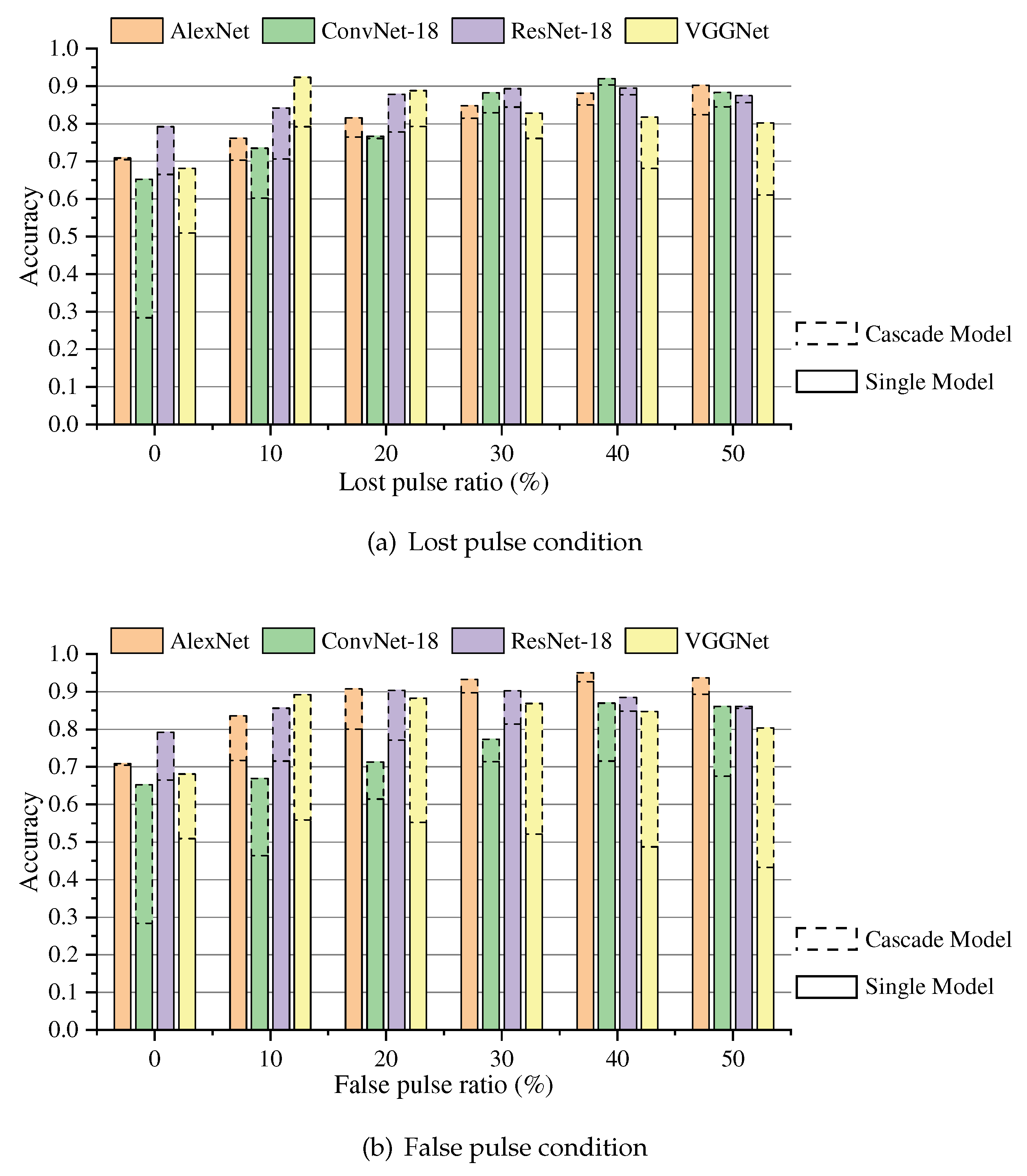
The results are shown in Figure 15. Compared with the independent model, the average recognition accuracy of the cascade models are improved by 10∼30%. And the fluctuation of recognition accuracy in different test environments is further reduced. The more noise affected the model, the more recognition rate improved after the introduction of noise estimation sub-network. This fully demonstrates that adaptive noise estimation can help recognition models to reduce noise interference.

5.4. The Performance of Proposed MSCANet

5.4.1. MSCANet Recognition Performance

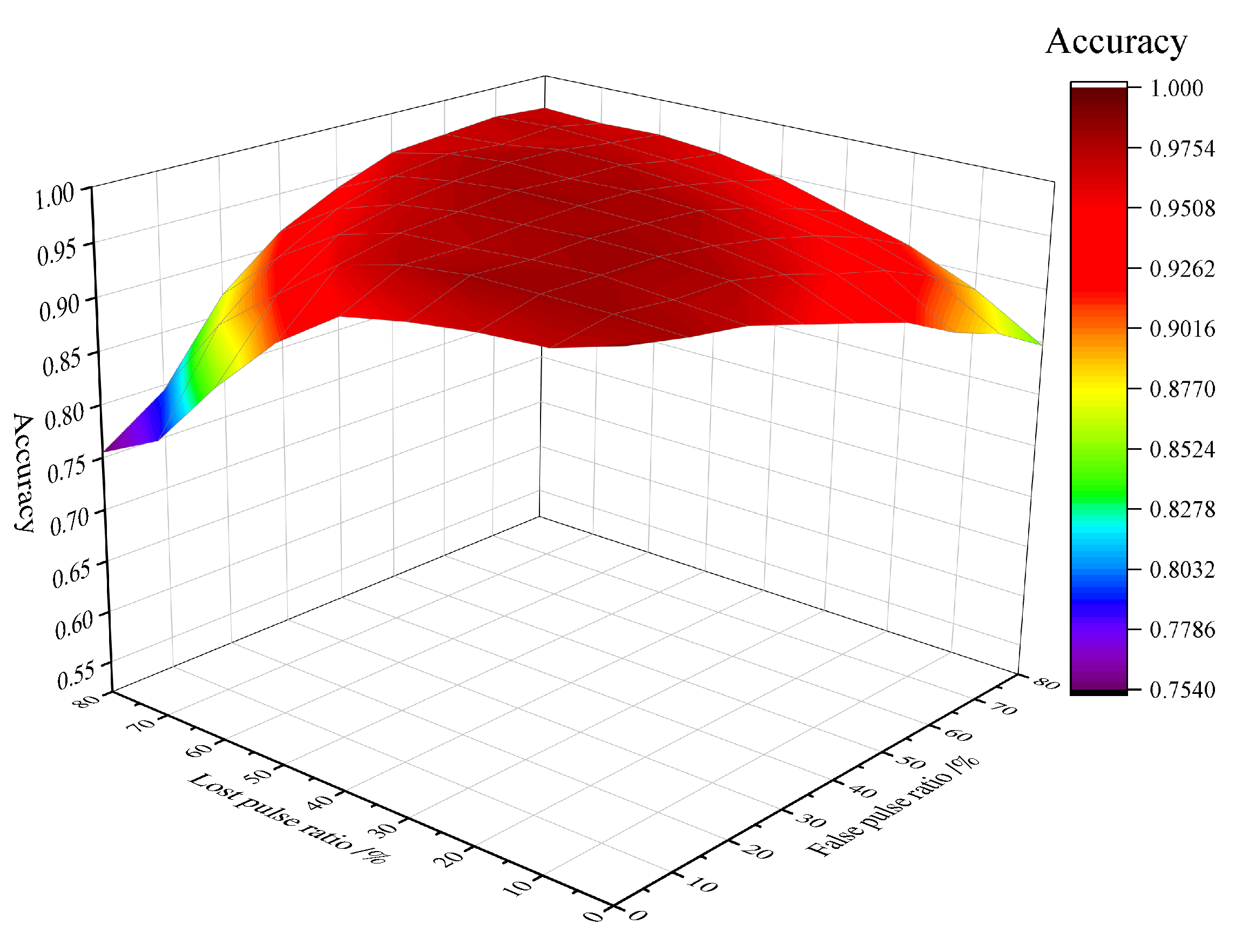
To demonstrate the recognition performance of MSCANet in complex environments, this part of experiment extends the ratio of lost pulse and false pulse to 0∼80%. The three-dimensional surface of recognition accuracy is shown in Figure 16.
Under different ratios of missed pulses and false pulses, MSCANet achieves an average recognition rate of 94.65%, and the surface of test accuracy is relatively flat, indicating stable recognition capability. In an ideal environment, the network achieves the highest recognition accuracy of 98.46%, which indicates that the network truly extracts recognition features from radar pulse patterns. It should be noted that the model is not immune to the interference of error terms, but in comparison to the baseline network, MSCANet demonstrates stronger anti-interference capabilities.
To validate the performance improvement of the proposed MSCANet, Table 3 provides a comparison of different networks under conditions of lost pulses and false pulses. It can be observed that: (1) MSCANet achieves an average accuracy improvement of 5% to 20% compared to other networks; (2) Except for AlexNet and MSCANet performing similarly under 40% and 50% false pulse conditions, MSCANet exhibits the best recognition performance in other environments. (3) MSCANet overcomes the issue of model overfitting, and the recognition accuracy decreases slowly as the environment deteriorates.
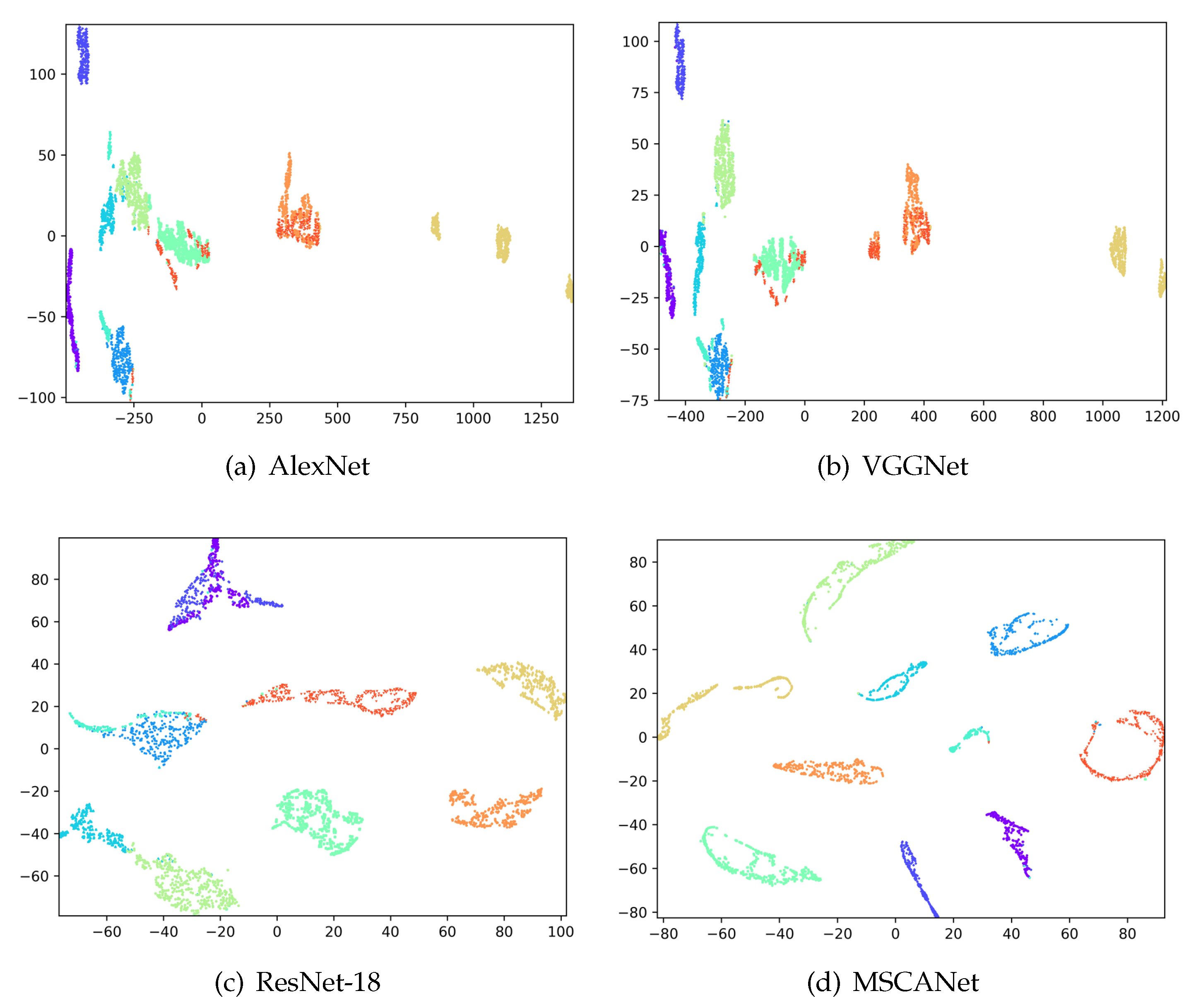
To visually demonstrate the feature extraction capability of the network, the output feature maps of the last convolutional layer in the pre-trained AlexNet, VGGNet, ResNet-18, and MSCANet models, are extracted for the same test samples. Principal Component Analysis (PCA) is used for dimensionality reduction and visualization, and the results are shown in Figure 17.
It can be observed that the sample of AlexNet and VGGNet are scattered and unevenly distributed, making them prone to confusion. The inter-cluster distance of ResNet-18 is relatively large, but there is overlap among some samples, resulting in incomplete classification. The results generated by the proposed MSCANet in this paper exhibit a neat distribution of the 10 classes, with strong intra-cluster aggregation and large inter-cluster distances. Therefore, it can be concluded that the proposed method outperforms other baseline models in UAV radar working mode recognition task.

5.4.2. Ablation Study

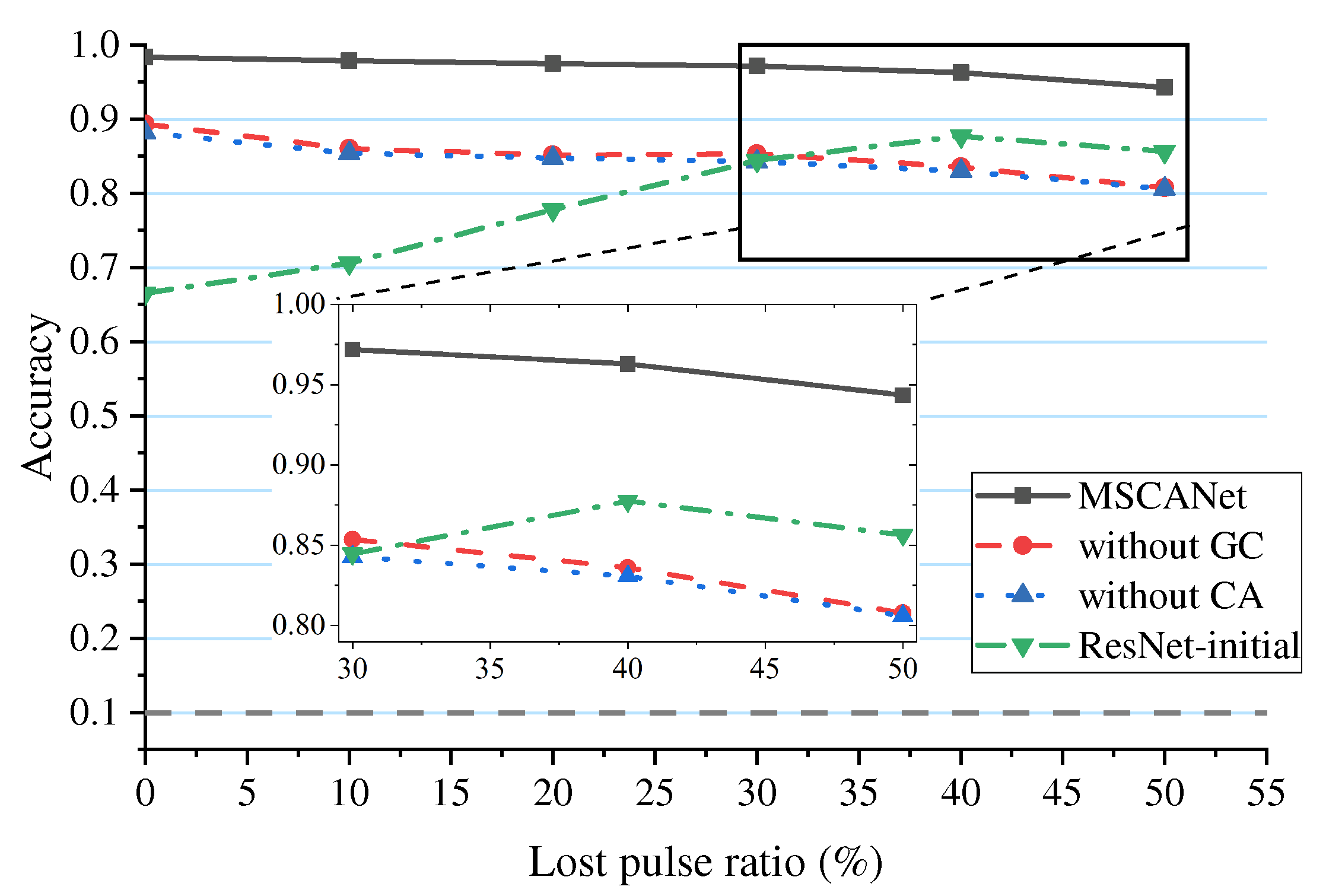
To further demonstrate the necessity of the deep group convolution, multi-scale convolution, and self-attention mechanism proposed in this paper, a set of ablation experiments is conducted to evaluate the network performance under different structures. Additionally, the performance improvement brought by noise encoding has been proven in the previous part and will not be reiterated here. This part of experiments is divided into four groups: (1) the complete structure MSCANet. (2) the network without the deep-wise group convolution structure, referred to as “without GC”. (3) a network without the multi-scale convolution and self-attention mechanism, referred to as “without CA”. (4) a conventional convolutional network without the above design structures, which degenerates into the initial deep residual network, referred to as “ResNet-initial”.
Taking the lost pulse environment as an example, the results are shown in Figure 18. It can be observed that, except for the initial ResNet-initial, the other three networks with the designed structures in this paper exhibit more stable recognition under different environments, and their recognition curves show a monotonically decreasing trend, which aligns with objective cognition. In terms of accuracy analysis, the average accuracy of the 4 structures are 96.9%, 85.0%, 84.4%, and 78.7% respectively. MSCANet has a significantly higher recognition capability than the other three networks. “Without GC” has slightly higher accuracy than “without CA”. “ResNet-initial” has the lowest accuracy.

6. Discussion

In this paper, to address the problem of radar mode recognition in high-noise environments, we proposed a dual-network cascaded model. The effectiveness of the proposed method is validated in 81 different noise environments. Our noise estimation sub-network effectively mitigates noise interference through adaptive noise coding. With the assistance of this structure, the proposed MSCANet is more suitable for feature extraction in radar pulse signals. This work is a further improvement compared with the latest research[38,39] on radar working mode recognition.
Under the same signal processing approach, the deep learning models, such as ConvNet[12], ResNet[24], AlexNet[36], and VGGNet[37], are superior to traditional machine learning classifiers, but the transferability of the algorithms in different noise environments is poor. We observed over-fitting on the test set through experiments. Taking VGGNet as an example, the recognition rate exhibits a clear peak as the noise increases, indicating that the network only matches the signal data distribution at the peak points. The addition of noise causes a single recognition model to fit the erroneous data with superimposed noise, failing to learn the true characteristics of the signal. Therefore, although it possesses some recognition ability, it cannot meet the practical requirements in terms of recognition accuracy and environmental adaptability.
Deep learning models have strong feature representation capabilities, but due to the uncertainty of noise, these models tend to exhibit varying degrees of over-fitting. Therefore, we designed a noise estimation network to define the impact of noise on the data. We synchronized the defined noise matrix with the pulse data as input to the recognition network, enabling the model to achieve a more multidimensional representation. At this point, the model no longer needs to focus on the impact of different noise environments but rather becomes more “focused” on the radar working mode classification task. Additionally, this also indicates that a single recognition network is difficult to simultaneously extract noise features and pulse regularity features.
In this paper, the noise estimation network and the recognition network are optimized using the same objective function. The improvement in the performance of one network in the cascaded model will enhance the performance of the other one, so as to establish the dependency between the noise law and the data law, and the global optimal decision is made by the model. It can be seen from the comparison experiments that this method not only improves the overall accuracy of the network but also significantly enhances the stability of recognition under different ratios of lost pulse and false pulse.
The structures such as deep-wise group convolution, multi-scale convolution and self-attention mechanism that we applied in MSCANet are all beneficial to radar working mode recognition. The details of the ablation experiment are shown in Table 4. Analyzing the results, we can draw the following conclusions: (1) the designed structures above can both improve the performance of radar working mode recognition, mainly by mitigating the interference caused by noise. (2) Deep-wise group convolution structure isolates the information interaction of shallow layers, making it easier for the last convolutional layer to eliminate redundant feature maps, resulting in a similar effect to feature selection. (3) The combination of multi-scale convolution and self-attention mechanism is more advantageous for selecting features of different scales, facilitating the extraction of the essential laws of radar working modes. (4) The design structures above have different emphases, and their effects on improving recognition capability can be combined. Therefore, MSCANet achieves the highest accuracy.

7. Conclusions

In significant noise environments, it is possible to know the working modes through the analysis of radar signals. In this work, a cascade model consisting of a noise estimation network based on U-Net and a recognition network based on MSCANet is proposed. The model employs adaptive noise encoding to help the network adapt to harsh noise environments. Three improved network structures, namely deep-wise group convolution, multi-scale convolution, and self-attention mechanism, are designed to extract and classify signal features in noisy environments. Experiments show that the proposed method improves the accuracy of conventional networks by approximately 17%. The average accuracy under noise conditions reaches to 94.65%. Compared to baseline networks such as AlexNet, ConvNet, ResNet, and VGGNet, the accuracy improvement ranges 5∼20%. The algorithm demonstrates better generalization and robustness. This work provides a new idea and method for the application of passive microwave signals.
In the future, we can focus on the following two parts: (1) Through the radar signal, it can not only identify the working modes, but also achieve aircraft type identification and fingerprint recognition. (2) There are many types of passive microwave signals. Therefore, future research will not be limited to radar signals. We can collect various types of radiation source signals, such as remote control signals, communication signals, and navigation signals, to achieve richer identification.

Author Contributions

Conceptualization, J.X. and J.P.; methodology, J.X.; validation, J.P. and M.D.; investigation, J.X.; writing—original draft preparation, J.X.; writing—review and editing, J.P. and M.D.; supervision, J.P.; project administration, J.P.; funding acquisition, J.P. All authors have read and agreed to the published version of the manuscript.

Funding

National Natural Science Foundation of China (No.62071476).

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Martino, D.; Andrea. Introduction to modern EW systems, second edition. ed.; Electronic warfare library, Artech House: Boston, MA, 2018; p. xi. 463p.
  2. E, W.M.; N., C.J.Y.; G., T.H. Command and Control for Multifunction Phased Array Radar. IEEE Transactions on Geoscience and Remote Sensing 2017, 55.
  3. Wang, S.; Gao, C.; Zhang, Q.; Dakulagi, V.; Zeng, H.; Zheng, G.; Bai, J.; Song, Y.; Cai, J.; Zong, B. Research and Experiment of Radar Signal Support Vector Clustering Sorting Based on Feature Extraction and Feature Selection. IEEE Access 2020, 8. [Google Scholar] [CrossRef]
  4. Weichao, X.; Huadong, L.; Jisheng, D.; Yanzhou, Z. Spectrum sensing for cognitive radio based on Kendall’s tau in the presence of non-Gaussian impulsive noise. Digital Signal Processing 2022, 123. [Google Scholar]
  5. Zhiling, X.; Zhenya, Y. Radar Emitter Identification Based on Novel Time-Frequency Spectrum and Convolutional Neural Network. IEEE COMMUNICATIONS LETTERS 2021, 25. [Google Scholar]
  6. Chi, K.; Shen, J.; Li, Y.; Wang, L.; Wang, S. A novel segmentation approach for work mode boundary detection in MFR pulse sequence. Digital Signal Processing 2022, 126. [Google Scholar] [CrossRef]
  7. Liao, Y.; Chen, X. Multi-attribute overlapping radar working pattern recognition based on K-NN and SVM-BP. The Journal of Supercomputing 2021. [Google Scholar] [CrossRef]
  8. Qihang, Z.; Yan, L.; Zilin, Z.; Yunjie, L.; Shafei, W. Adaptive feature extraction and fine-grained modulation recognition of multi-function radar under small sample conditions. IET Radar, Sonar & Navigation 2022, 16. [Google Scholar]
  9. Li, X.; Huang, Z.; Wang, F.; Wang, X.; Liu, T. Toward Convolutional Neural Networks on Pulse Repetition Interval Modulation Recognition. IEEE Communications Letters 2018, 22, 2286–2289. [Google Scholar] [CrossRef]
  10. Chen, W.; Chen, B.; Peng, X.; Liu, J.; Yang, Y.; Zhang, H.; Liu, H. Tensor RNN With Bayesian Nonparametric Mixture for Radar HRRP Modeling and Target Recognition. IEEE Transactions on Signal Processing 2021, 69, 1995–2009. [Google Scholar] [CrossRef]
  11. Ruifeng, D.; Ziyu, C.; Haiyan, Z.; Xu, W.; Wei, M.; Guodong, S. Dual Residual Denoising Autoencoder with Channel Attention Mechanism for Modulation of Signals. Sensors 2023, 23. [Google Scholar]
  12. Lutao, L.; Xinyu, L. Unknown radar waveform recognition system via triplet convolution network and support vector machine. Digital Signal Processing 2022, 123. [Google Scholar]
  13. Tao, X.; Shuo, Y.; Zhangmeng, L.; Fucheng, G. Radar Emitter Recognition Based on Parameter Set Clustering and Classification. Remote Sensing 2022, 14. [Google Scholar]
  14. Dong, Y.; Jiang, X.; Zhou, H.; Lin, Y.; Shi, Q. SR2CNN: Zero-Shot Learning for Signal Recognition. IEEE Transactions on Signal Processing 2021, 69, 2316–2329. [Google Scholar] [CrossRef]
  15. Wei, Z.; Da, H.; Minghui, Z.; Jingran, L.; Xiangfeng, W. Open-Set Signal Recognition Based on Transformer and Wasserstein Distance. Applied Sciences 2023, 13. [Google Scholar]
  16. Zheng, S.; Zhou, X.; Zhang, L.; Qi, P.; Qiu, K.; Zhu, J.; Yang, X. Towards Next-Generation Signal Intelligence: A Hybrid Knowledge and Data-Driven Deep Learning Framework for Radio Signal Classification. IEEE Transactions on Cognitive Communications and Networking 2023, pp. 1–1.
  17. Jiaji, L.; Weijian, S.; Zhian, D. New classes inference, few-shot learning and continual learning for radar signal recognition. IET Radar, Sonar & Navigation 2022, 16. [Google Scholar]
  18. Du, M.; Zhong, P.; Cai, X.; Bi, D. DNCNet: Deep Radar Signal Denoising and Recognition. IEEE Transactions on Aerospace and Electronic Systems 2022, 58, 3549–3562. [Google Scholar] [CrossRef]
  19. Han, J.W.; Park, C.H. A Unified Method for Deinterleaving and PRI Modulation Recognition of Radar Pulses Based on Deep Neural Networks. IEEE Access 2021, 9, 89360–89375. [Google Scholar] [CrossRef]
  20. Han, L.; Donghang, C.; Xiaojun, S.; Feng, W. Radar emitter recognition based on CNN and LSTM. In Proceedings of the The International society for optics and photonics, Vol. 11933; pp. 119331T–119331T–6. [Google Scholar]
  21. Shi, F.; Yue, C.; Han, C. A lightweight and efficient neural network for modulation recognition. Digital Signal Processing 2022, 123. [Google Scholar] [CrossRef]
  22. Pan, Z.S.; Wang, S.F.; Li, Y.J. Residual Attention-Aided U-Net GAN and Multi-Instance Multilabel Classifier for Automatic Waveform Recognition of Overlapping LPI Radar Signals. Ieee Transactions on Aerospace and Electronic Systems 2022, 58, 4377–4395. [Google Scholar] [CrossRef]
  23. Ronneberger, O.; Fischer, P.; Brox, T. , U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015; Lecture Notes in Computer Science, 2015; book section Chapter 28, pp. 234–241.
  24. Jifei, P.; Shengli, Z.; Lingsi, X.; Long, T. Embedding Soft Thresholding Function into Deep Learning Models for Noisy Radar Emitter Signal Recognition. Electronics 2022, 11. [Google Scholar]
  25. Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a Fast and Flexible Solution for CNN based Image Denoising. IEEE Trans Image Process 2018. [Google Scholar] [CrossRef]
  26. Xie, S.N.; Girshick, R.; Dollar, P.; Tu, Z.W.; He, K.M. Aggregated Residual Transformations for Deep Neural Networks. 30th Ieee Conference on Computer Vision and Pattern Recognition (Cvpr 2017) 2017, pp. 5987–5995.
  27. Yu, H.h.; Yan, X.p.; Liu, S.k.; Li, P.; Hao, X.h. Radar emitter multi-label recognition based on residual network. Defence Technology 2022, 18. [Google Scholar]
  28. Dadgarnia, A.; Sadeghi, M.T. Automatic recognition of pulse repetition interval modulation using temporal convolutional network. IET Signal Processing 2021, 15, 633–648. [Google Scholar] [CrossRef]
  29. Xing, D.; Yongfu, S.; Yupeng, S.; Huifeng, S.; Lei, Y. A Comparative Study of Different CNN Models and Transfer Learning Effect for Underwater Object Classification in Side-Scan Sonar Images. Remote Sensing 2023, 15. [Google Scholar]
  30. Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the Computer Vision – ECCV 2018, Lecture Notes in Computer Science; pp. 3–19.
  31. Jie, H.; Li, S.; Samuel, A.; Gang, S.; Enhua, W. Squeeze-and-Excitation Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence 2019, 42. [Google Scholar]
  32. Kun, C.; Jihong, S.; Yan, L.; Liyan, W.; Sheng, W. A novel segmentation approach for work mode boundary detection in MFR pulse sequence. Digital Signal Processing 2022, 126. [Google Scholar]
  33. Feng, H.C.; Tang, B.; Wan, T. Radar pulse repetition interval modulation recognition with combined net and domain-adaptive few-shot learning. Digital Signal Processing 2022, 127. [Google Scholar] [CrossRef]
  34. Hui, L.; Dong, J.W.; Dong, L.H.; Wei, C.T. Work Mode Identification of Airborne Phased Array Radar Based on the Combination of Multi-Level Modeling and Deep Learning. In Proceedings of the The 35th China Command and Control Conference; pp. 273–278.
  35. Skolnik, M.I. Radar handbook, 3rd ed.; McGraw-Hill: New York, 2008. [Google Scholar]
  36. Limin, G.; Xin, C. Low Probability of Intercept Radar Signal Recognition Based on the Improved AlexNet Model. Digital Signal Processing 2018. [Google Scholar]
  37. Das, G.A.; S., B.G.; V., C.P. Electrocardiogram signal classification using VGGNet: a neural network based classification model. International Journal of Information Technology 2022, 15.
  38. Tian, T.; Qianrong, Z.; Zhizhong, Z.; Feng, N.; Xinyi, G.; Feng, Z. Shipborne Multi-Function Radar Working Mode Recognition Based on DP-ATCN. Remote Sensing 2023, 15. [Google Scholar] [CrossRef]
  39. Xu, T.; Yuan, S.; Liu, Z.; Guo, F. Radar Emitter Recognition Based on Parameter Set Clustering and Classification. Remote Sensing 2022, 14. [Google Scholar] [CrossRef]
Preprints 79321 g001
Figure 1. Working mode recognition from the perspective of passive radar signal. The aircraft must employ corresponding radar working modes when conducting tasks such as air reconnaissance, ground strikes, sea search, and SAR imaging. The passive electronic receiver can intercept and process the signals, thereby analyzing the target’s intentions.
Figure 1. Working mode recognition from the perspective of passive radar signal. The aircraft must employ corresponding radar working modes when conducting tasks such as air reconnaissance, ground strikes, sea search, and SAR imaging. The passive electronic receiver can intercept and process the signals, thereby analyzing the target’s intentions.
Preprints 79321 g001
Preprints 79321 g002
Figure 2. Comparison of the signal in a noisy environment. (a) and (b) show six pulse modulation styles in ideal and noisy environments respectively.
Figure 2. Comparison of the signal in a noisy environment. (a) and (b) show six pulse modulation styles in ideal and noisy environments respectively.
Preprints 79321 g002
Preprints 79321 g003
Figure 3. The relationship between detection probability and SNR. The curve from left to right represents the decreasing probability of false alarms.
Figure 3. The relationship between detection probability and SNR. The curve from left to right represents the decreasing probability of false alarms.
Preprints 79321 g003
Preprints 79321 g004
Figure 4. The influence of noise on radar pulse. Lost pulses refer to pulses that are submerged in noise and do not reach the detection threshold. False pulses refer to pulses in which noise is erroneously detected as radar signals. Measurement error refers to the parameter drift generated compared with true pulses.
Figure 4. The influence of noise on radar pulse. Lost pulses refer to pulses that are submerged in noise and do not reach the detection threshold. False pulses refer to pulses in which noise is erroneously detected as radar signals. Measurement error refers to the parameter drift generated compared with true pulses.
Preprints 79321 g004
Preprints 79321 g005
Figure 5. The architecture of the proposed scheme.
Figure 5. The architecture of the proposed scheme.
Preprints 79321 g005
Preprints 79321 g006
Figure 6. Noise estimation network based on U-Net.
Figure 6. Noise estimation network based on U-Net.
Preprints 79321 g006
Preprints 79321 g007
Figure 7. Recognition network based on MSCANet. The network mainly consists of 5 parallel deep convolution modules and self-attention modules, which both adopt multi-scale convolutional units. Each convolutional unit contains 6 multi-scale convolution layers. The convolution layers are composed of 4 mutually prime convolution kernels, in combination with Batch Normalization layers and ReLU activation functions.
Figure 7. Recognition network based on MSCANet. The network mainly consists of 5 parallel deep convolution modules and self-attention modules, which both adopt multi-scale convolutional units. Each convolutional unit contains 6 multi-scale convolution layers. The convolution layers are composed of 4 mutually prime convolution kernels, in combination with Batch Normalization layers and ReLU activation functions.
Preprints 79321 g007
Preprints 79321 g008
Figure 8. The structure of depth-wise group convolution. A dimension of full pulses is programmed into a group with its corresponding noise coding vector. After passing through the shallow network, it is spliced by groups.
Figure 8. The structure of depth-wise group convolution. A dimension of full pulses is programmed into a group with its corresponding noise coding vector. After passing through the shallow network, it is spliced by groups.
Preprints 79321 g008
Preprints 79321 g009
Figure 9. The structure of the multi-scale convolution module.
Figure 9. The structure of the multi-scale convolution module.
Preprints 79321 g009
Preprints 79321 g010
Figure 10. The structure of channel self-attention module.
Figure 10. The structure of channel self-attention module.
Preprints 79321 g010
Preprints 79321 g011
Figure 11. The structure of spatial self-attention module.
Figure 11. The structure of spatial self-attention module.
Preprints 79321 g011
Preprints 79321 g012
Figure 12. Recognition performance of traditional machine learning classifiers. (a) under the condition of lost pulse, (b) under the condition of false pulse.
Figure 12. Recognition performance of traditional machine learning classifiers. (a) under the condition of lost pulse, (b) under the condition of false pulse.
Preprints 79321 g012
Preprints 79321 g013
Figure 13. The structures of conventional deep learning networks.
Figure 13. The structures of conventional deep learning networks.
Preprints 79321 g013
Preprints 79321 g014
Figure 14. Accuracy of deep learning networks in test set. (a) under the condition of lost pulse, (b) under the condition of false pulse.
Figure 14. Accuracy of deep learning networks in test set. (a) under the condition of lost pulse, (b) under the condition of false pulse.
Preprints 79321 g014
Preprints 79321 g015
Figure 15. Performance comparison between independent model and cascade model. The networks are tested in the environment of lost pulse and false pulse respectively. The dashed boxes in the figure represent the improvement in accuracy of the cascaded models compared to the independent models.
Figure 15. Performance comparison between independent model and cascade model. The networks are tested in the environment of lost pulse and false pulse respectively. The dashed boxes in the figure represent the improvement in accuracy of the cascaded models compared to the independent models.
Preprints 79321 g015
Preprints 79321 g016
Figure 16. MSCANet test accuracy surfaces in different environments. A total of 81 experimental environments are included in the figure, with x and y axes representing lost pulse and false pulse respectively, and z axes representing recognition accuracy.
Figure 16. MSCANet test accuracy surfaces in different environments. A total of 81 experimental environments are included in the figure, with x and y axes representing lost pulse and false pulse respectively, and z axes representing recognition accuracy.
Preprints 79321 g016
Preprints 79321 g017
Figure 17. Dimensionality reduction visualization of output features for different models. The points of different colors in the figure represent the 10 different working modes in the sample set. The stronger the clustering of points of the same type and the farther the distance between points of different types, the better the classification performance of the model.
Figure 17. Dimensionality reduction visualization of output features for different models. The points of different colors in the figure represent the 10 different working modes in the sample set. The stronger the clustering of points of the same type and the farther the distance between points of different types, the better the classification performance of the model.
Preprints 79321 g017
Preprints 79321 g018
Figure 18. Ablation experiment in lost pulse conditions. MSCANet is the network proposed in this paper. On this basis, “without GC” means the lack of deep-wise group convolution, “without CA” means the lack of multi-scale convolution and self-attention mechanism, “ResNet-initial” is the original network architecture with only residual connections.
Figure 18. Ablation experiment in lost pulse conditions. MSCANet is the network proposed in this paper. On this basis, “without GC” means the lack of deep-wise group convolution, “without CA” means the lack of multi-scale convolution and self-attention mechanism, “ResNet-initial” is the original network architecture with only residual connections.
Preprints 79321 g018
Table 1. RPDWS-I data set. Each working mode sample is random within the given range to simulate uncertain radar parameters.
Table 1. RPDWS-I data set. Each working mode sample is random within the given range to simulate uncertain radar parameters.
Working mode PRI(us) PW(us) Duty ratio(%) Pulse num in CPI Bandwidth(MHz) Modulation
VS 3.3∼10 1∼3 10∼30 500∼2000 0.3∼10 Consatnt
RWS 3.3∼10 1∼3 10∼30 500∼2000 0.3∼10 D & S
VRS 50∼165 1∼20 1∼25 30∼256 1∼10 Constant, D & S
MTT 3.3∼125 0.1∼20 0.1∼25 1∼64 1∼50 Stagger, Sliding
BR 3.3∼125 0.1∼20 0.1∼25 1∼64 1∼50 Wobbulated
GMTI 120∼500 2∼60 0.1∼25 20∼256 0.5∼15 Stagger
GMTT 62∼160 2∼40 0.1∼25 20∼256 0.5∼15 Stagger
SSS 1000∼2000 1∼200 0.1∼10 1∼8 0.2∼500 Stagger
SST 500∼1000 1∼200 0.1∼20 20∼256 0.2∼10 Stagger
SAR 100∼1000 3∼60 1∼25 70∼20000 10∼500 Constant
Table 2. Accuracy of deep learning networks in training set.
Table 2. Accuracy of deep learning networks in training set.
AlexNet ConvNet-18 ResNet-18 VGGNet
96.9% 90.7% 90.5% 99.7%
Table 3. Recognition accuracy of several networks in different environments.
Table 3. Recognition accuracy of several networks in different environments.
Model Lost pulse ratio (%) False pulse ratio (%) Process
time (s)		 Model
capacity
0 10 20 30 40 50 0 10 20 30 40 50
AlexNet 70.4 70.3 76.4 81.5 88.1 90.2 70.9 83.6 90.7 93.2 95.0 93.6 2.42 520K
ConvNet-18 65.2 73.5 76.6 82.8 92.1 88.3 65.2 66.8 71.3 77.3 86.9 86.1 11.46 954K
ResNet-18 79.1 84.2 87.7 89.3 89.4 87.5 79.1 85.6 90.3 90.2 88.4 86.1 11.93 1110K
VGGNet 68.0 92.3 88.7 82.8 81.7 80.1 68.1 89.2 88.2 86.9 84.7 80.3 9.15 1680K
MSCANet 98.4 97.8 97.5 97.1 96.2 94.3 98.4 97.8 97.1 95.4 93.7 92.1 14.50 849K
Table 4. Ablation Experimental results. “Noise Estimation” means noise estimation sub-network, “GC” means the deep-wise group convolution, “CA” means the multi-scale convolution and self-attention mechanism.
Table 4. Ablation Experimental results. “Noise Estimation” means noise estimation sub-network, “GC” means the deep-wise group convolution, “CA” means the multi-scale convolution and self-attention mechanism.
Model Noise Estimation GC GA Accuracy
1 √ √ √ 96.9%
2 × √ √ 83.3%
3 √ × √ 85.0%
4 √ √ × 84.4%
5 × × × 78.7%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated