Prerpints.org logo
Preprint
Article

An Electromechanical Jointed Approach for Contact Pair Fault Diagnosis of Oil-Immersed On-Load Tap Changer

This version is not peer-reviewed.

Submitted:

13 July 2023

Posted:

13 July 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
To address the problem of limited fault diagnosis accuracy in oil-immersed on-load tap changers (OLTC), this paper introduces a novel fault diagnosis method that combines the analysis of mechanical vibration signals and high-frequency current signals. The proposed approach aims to enhance the accuracy of fault diagnosis. To begin, an experimental platform is constructed to simulate the OLTC contact. Mechanical vibration signals and high-frequency current signals are collected from the testing platform under various operating states. These signals are then subjected to wavelet packet transform for denoising, followed by correlation analysis to capture the relationship between signals in different states. Based on these preliminary steps, the features of the signals are extracted and analyzed using ensemble empirical mode decomposition and the Hilbert-Huang transform. Subsequently, a support vector machine (SVM) is employed to analyze both the mechanical vibration signal and high-frequency current signal, enabling the classification of the OLTC contact state. The results demonstrate that the combination of characteristic analysis of mechanical vibration signals and high-frequency current signals provides a more comprehensive reflection of the actual OLTC contact state under different conditions. Through the SVM classification, the error between the predicted values and real values of the two types of signals remains below 10%, validating the efficiency and feasibility of the proposed method for fault diagnosis of OLTC contacts. These research findings serve as a reliable foundation for the diagnosis of operational states of on-site oil-immersed on-load tap changers, offering valuable insights for practical applications.
Keywords: 
Subject: 
Engineering  -   Electrical and Electronic Engineering

1. Introduction

The on-load voltage regulating transformer plays a crucial role in power systems by regulating voltage and reactive power flow to ensure smooth operations. The oil-immersed on-load tap changer (OLTC) is the key component of the on-load voltage regulating transformer responsible for voltage regulation. However, it is prone to wear, spark, and ablation during the tapping process, which can degrade its performance. Statistics show that between 2005 and 2015, faults caused by OLTC performance failure accounted for 20% to 41% of total faults in on-load voltage regulating transformers, with contact performance failure contributing to over half of these faults [1,2,3,4]. Therefore, real-time monitoring and diagnosis of the OLTC contact state are essential for understanding the operational status of the on-load voltage regulating transformer.
Currently, offline hanging core maintenance is the primary method for maintaining OLTC, but it is time-consuming and labor-intensive. To address this, online monitoring and fault diagnosis technology for OLTC has emerged, significantly reducing costs and improving maintenance efficiency. Various signal processing and fault diagnosis methods have been proposed by scholars, including short-time Fourier transform (STFT) [5], wavelet transform (WT) [6,7], empirical mode decomposition (EMD) [8,9], Hilbert transform (HT) [10,11,12], K-means cluster analysis [13,14], fuzzy C-means clustering (FCM) analysis [15,16], and others. These methods primarily rely on mechanical vibration signals for fault diagnosis of OLTC, but they haven't yielded satisfactory results.
While STFT analyzes vibration signals using time-domain localized window functions, its resolution cannot be optimized simultaneously in the time and frequency domains due to the limitations of the window function based on Heisenberg's uncertainty criterion. WT overcomes this limitation by allowing modifications in the window function with frequency, enabling analysis in the time-frequency domain. However, its analysis results are constrained by the choice of basic wavelet. EMD is an adaptive signal time-frequency processing method suitable for analyzing nonlinear and non-stationary signals. It addresses WT's limitations when selecting a basic wavelet and enhances the decomposition accuracy in the time-frequency domain. However, mode aliasing can occur when dealing with vibration signals containing significant pure white noise. K-means clustering analysis is a concise and efficient partition clustering algorithm for analyzing vibration signals, but its results are sensitive to the predetermined number of clusters (K). Fuzzy C-means (FCM) clustering analysis, as the primary method of unsupervised clustering, optimizes clustering results by eliminating the need to predefine K value compared to K-means clustering. However, it may encounter issues of local optimization during the clustering process.
Given the shortcomings of the aforementioned methods, this paper proposes a novel fault diagnosis method for OLTC contact by combining mechanical vibration signals and high-frequency current signals. The experimental platform simulating OLTC contact is established, and different signal states, including mechanical vibration signals and high-frequency current signals, are collected from the platform. Wavelet packet transform (WPT) is employed to denoise these signals, while correlation analysis is used to explore their relationships under different conditions. Subsequently, features from the signals are extracted and analyzed using ensemble empirical mode decomposition (EEMD) and Hilbert-Huang transform (HHT). Finally, support vector machine (SVM) is used to jointly analyze the mechanical vibration signal and high-frequency current signal, classifying the contact state of OLTC.

2. Experimental setup

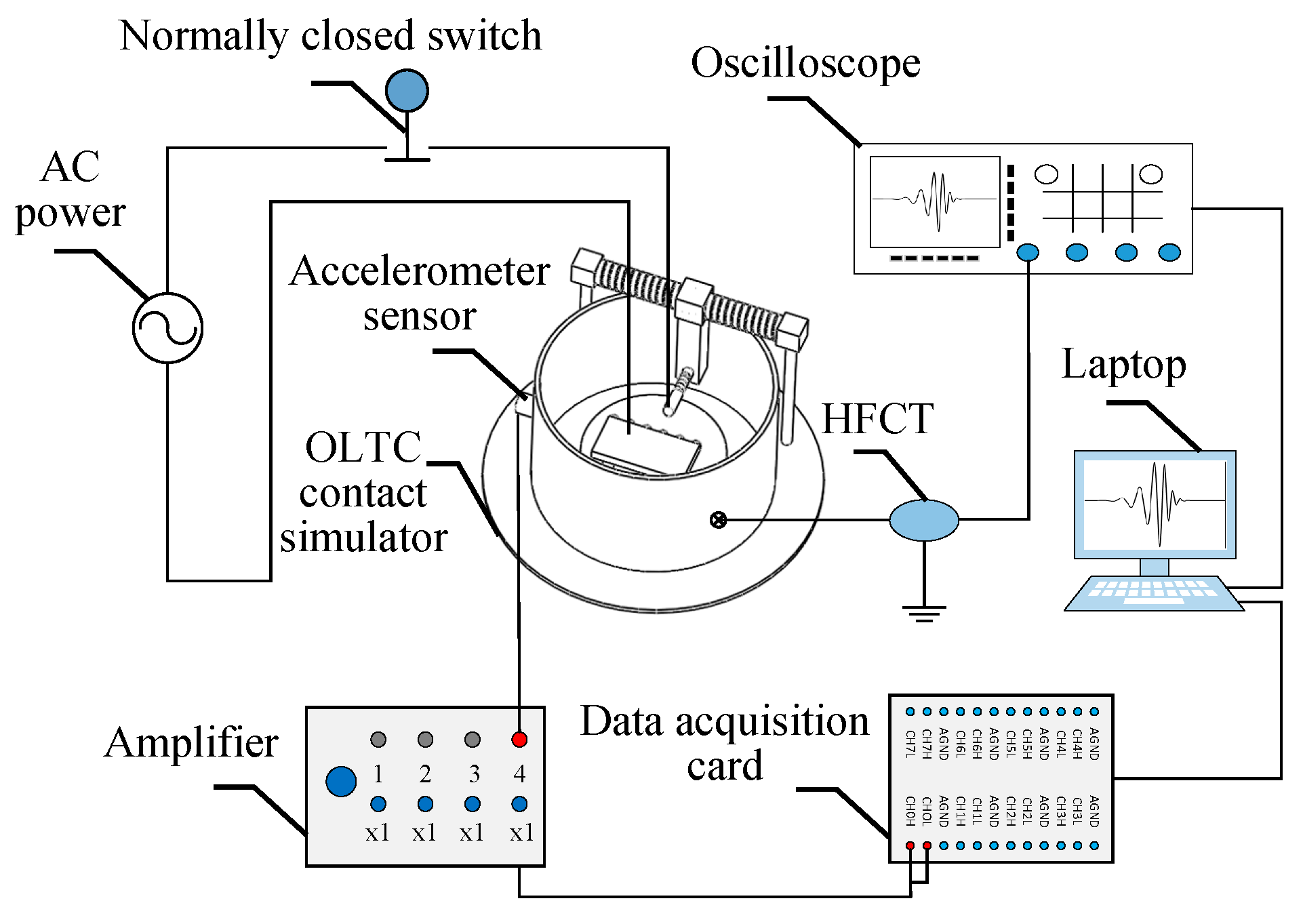
Oil immersed OLTC is the core device of on load voltage regulation transformer to complete the voltage regulation operation. It mainly adjusts the number of turns on the high-voltage side of the transformer through the switching of dynamic and static contacts, thus change the transformation ratio of on load voltage regulation transformer, so as to achieve the purpose of voltage regulation. With the increase of voltage regulation times, OLTC contacts will loose, wear and other faults. At the same time OLTC moving contacts and static contacts have the characteristics of current carrying sliding electrical contact in the tapping process, which is easy to produce sparks and ablation. Therefore, the experimental platform of OLTC contact simulation device is built in this paper. In order to simulate the actual structure and internal environment of oil immersed OLTC as much as possible, the contacts of the experimental device are made of silver copper alloy containing 2% silver. The transmission medium inside the oil tank of the experimental device selects Karamay 25 mineral oil, which is most commonly used in the oil tank of the on-site transformer, and insulating paper is pasted on the inner wall of the oil tank of the experimental device. Therefore, a laboratory test system for simulating actual operation of OLTC is built, as shown in Figure 1. The system includes:
(1) A contact switching device.
(2) A data acquisition system.
Details of the two parts are described as follows..
Based on the experimental platform of OLTC contact simulation device, the mechanical vibration signals and high-frequency current signals under four simulated states (normal, loose, slight wear and severe wear) are collected at the same time. Firstly, three CT1005LC accelerometer sensors are evenly installed on the outer wall of the simulation device at a spacing of 120°, and the height is kept horizontal with the position of moving and static contacts, so as to collect mechanical vibration signals under various states. Secondly, CT5204 amplifier is used to power the accelerometer sensors and amplify the collected mechanical vibration signal. Then, MCC1608G data acquisition card is used to convert the amplified mechanical vibration analog signal into digital signal. Finally, it is transmitted to the laptop through the data line for storage and analysis. For the acquisition of high-frequency current signals, firstly, the high-frequency current transducer (HFCT) is installed on the grounding cable of the experimental platform of OLTC contact simulation device to collect high-frequency current signals in four states. Secondly, the high-frequency current signal collected by HFCT is transmitted to MDO-2204 oscilloscope for display through BNC cable. Finally, the oscilloscope transmits the high-frequency current signal to the laptop through the USB data line for storage and analysis. The physical image of OLTC contact simulation device is shown in Figure 2.

3. Signal Acquisition and Preprocessing

3.1. Signal Acquisition

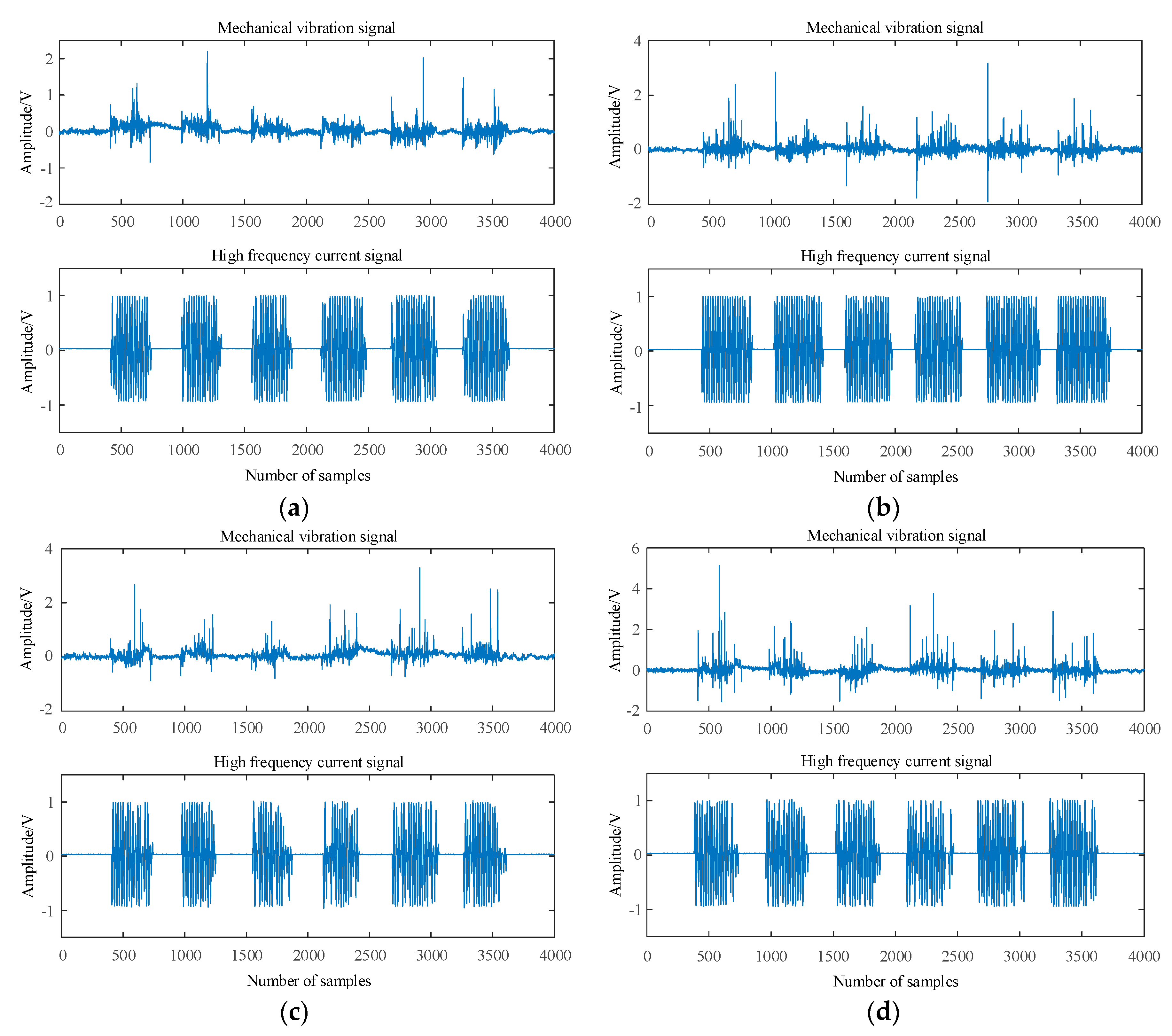
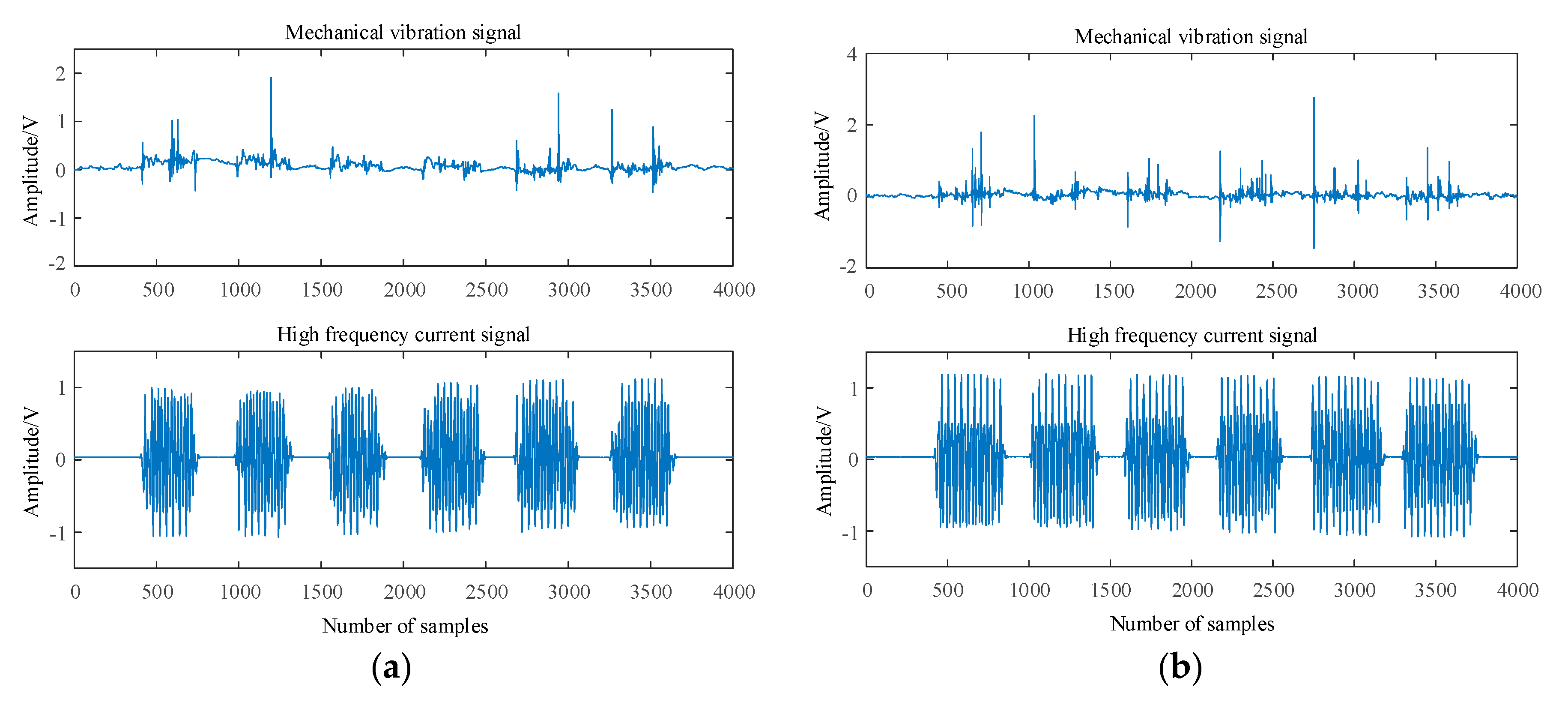
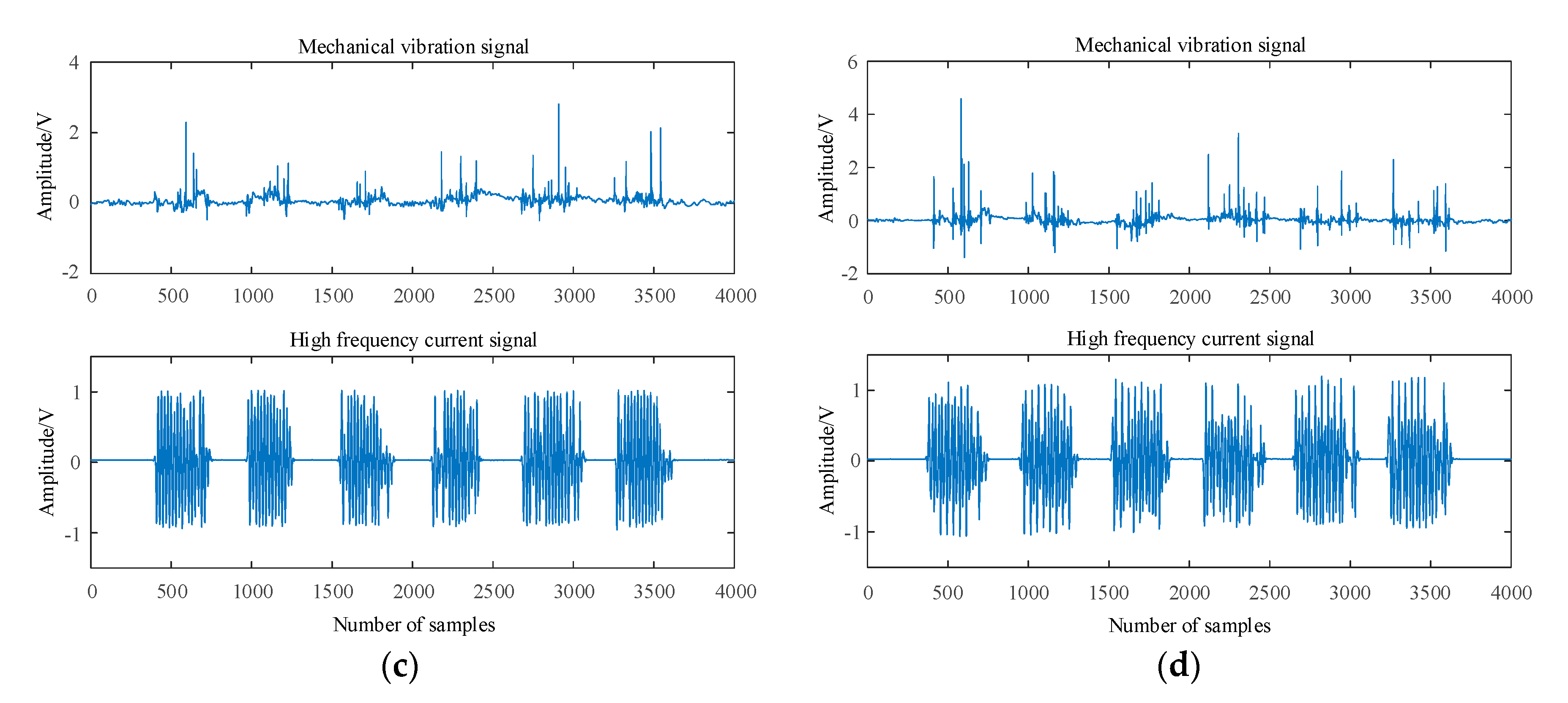
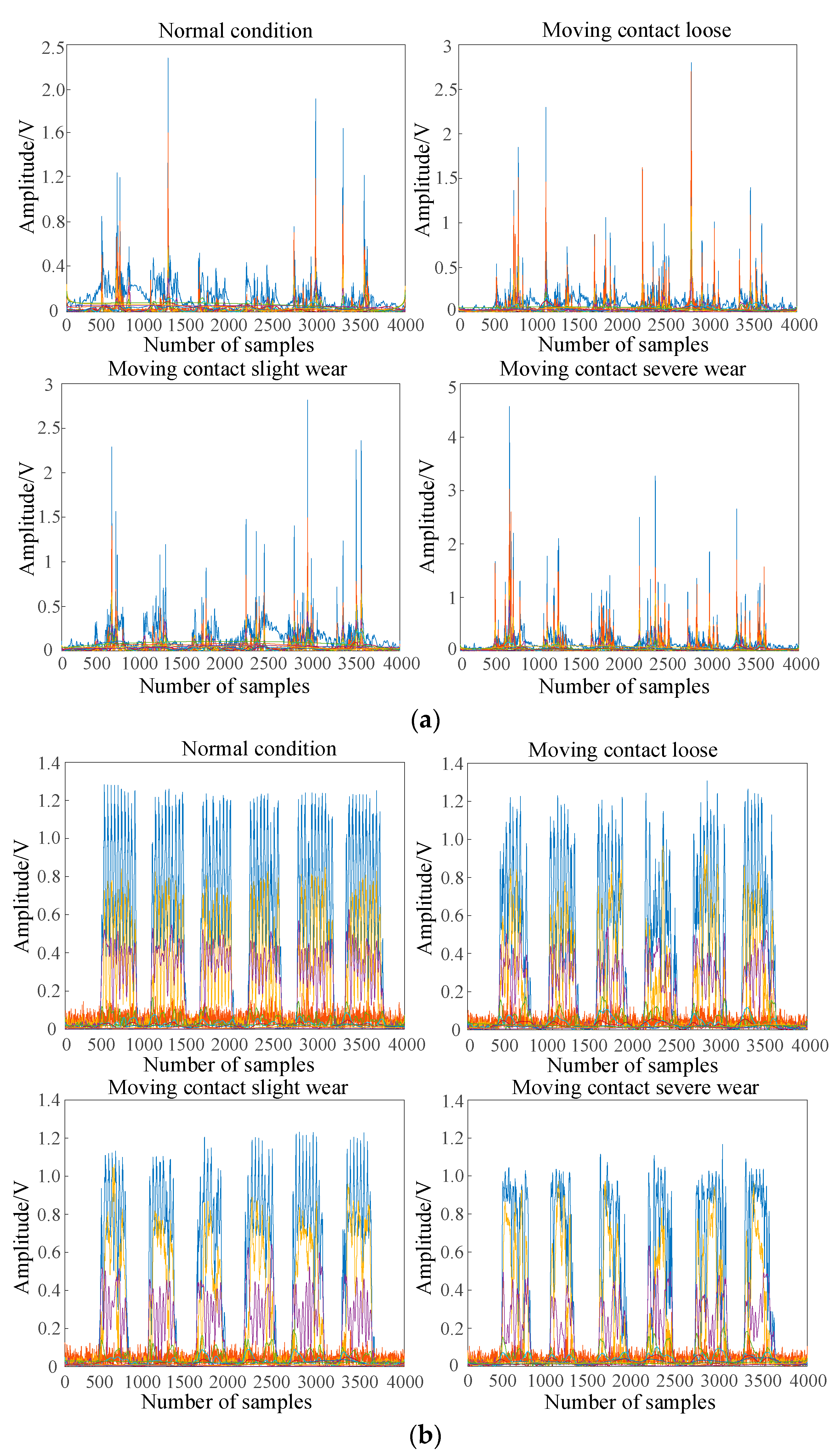
Based on the experimental platform of OLTC contact simulation device, the loose state of OLTC contact is simulated by manually loosening the contact. The single chip microcomputer control system is set to automatically switch the moving and static contacts back and forth for 3000 times to simulate the slight wear state of OLTC contacts. The moving and static contacts are automatically switched back and forth for 10000 times to simulate the severe wear fault state of OLTC contacts. The mechanical vibration signal and high-frequency current signal are collected at the same time under the four states of OLTC contact (normal, loose, slight wear and severe wear). In each state of OLTC contact, firstly, the vibration acceleration sensor and HFCT are used to collect the mechanical vibration signal and high-frequency current signal generated in the switching process of moving and static contacts of the experimental device at the same time. Secondly, the mechanical vibration signal is amplified by the amplifier and the data acquisition card to complete the analog-to-digital conversion, and saved to the laptop through the transmission line. The high-frequency current signal is collected by HFCT and displayed by oscilloscope and saved to the laptop. Finally, the electromechanical signals are analyzed in the laptop at the same time. The collected signals in four states are shown in Figure 3.

3.2. Signal Preprocessing

Due to the limitation of the experimental environment, the collected mechanical vibration signal and high-frequency current signal are affected by white noise and pulse interference. In order to improve the accuracy of OLTC contact fault diagnosis, wavelet packet transform (WPT) is used to denoise the two kinds of signals. WPT is a signal processing algorithm based on WT optimization. It solves the problem that WT cannot decompose high-frequency components and improves the processing ability of nonlinear and nonstationary signals.
Let x(t) be a signal whose corresponding decomposition coefficient is pln. G and H are the wavelet decomposition filter. G is related to the wavelet function, and H is related to the scale function. The mathematical expression is (1)~(3) [17,18,19]:
p 0 1 ( t ) = x ( t )
p l 2 n − 1 ( t ) = ∑ k H ( k − 2 t ) p l − 1 n ( t )
p l 2 n ( t ) = ∑ k G ( k − 2 t ) p l − 1 n ( t )
where t=1, 2, 3,…, 2L-l; n=1, 2, 3,…, 2l; L=log2N. Through the above analysis, the frequency fs of the original signal will be decomposed by WPT in n-layers, and the frequency domain is divided into 2n segments.
The corresponding frequency information of each decomposition is [0, fs/2n], [fs/2n, (2fs)/2n],…, [(k-1)fs/2n, (2kfs)/2n],…, [(2n-2)fs/2n, (2n-1)fs/2n], [(2n-1)fs/2n, fs]. The p generated by decomposition is the wavelet packet coefficient, and the original data of the signal is taken as the lowest wavelet packet coefficient. If there are many frequency signals, the signals of each frequency band can be decomposed as long as n is large enough. Secondly, by selecting the appropriate threshold and threshold function, the high-frequency component generated by decomposition is threshold quantized. Through repeated comparative experiments, this paper finally selects the heuristic threshold heursure and the threshold function ddencmp. Finally, the low-frequency component and the quantized high-frequency component are reconstructed as a whole to obtain the denoised signal, as shown in Figure 4.
As is shown in Figure 4, when OLTC contact evolves from normal state to serious wear fault state, the amplitude of mechanical vibration signal gradually increases and the signal component becomes more and more complex. The amplitude of high-frequency current signal remains basically unchanged, but the characteristic component of high-frequency current signal is gradually missing.

3.3. Relevance Analysis

In order to describe the relevance between the signals collected under various states when the OLTC contact evolves from the normal state to the fault state, it is necessary to analyze the relevance of the two types of signals collected by the OLTC contact under four states. In mathematical statistics, the related coefficient −1≤r≤1, and the greater the r value, the higher the relevance between the two signals. The related coefficient is defined as follows [20]:
r = n ∑ x y − ∑ x ∑ y n ∑ x 2 − ( ∑ x ) 2 n ∑ y 2 − ( ∑ y ) 2
where r represents the related coefficient; x and y represent two sets of signal data sets in different states; n represents the number of samples in the data sets.
In this paper, x specifically represents the mechanical vibration signal data sets and high-frequency current signal data sets collected by OLTC contacts under normal conditions, y represents the mechanical vibration signal data sets and high-frequency current signal data sets collected by OLTC contact under loose, slight wear and severe wear conditions. The relevance analysis results are shown in Table 1.
The analysis shows that with the increase of OLTC contact fault degree, the relevance between the collected mechanical vibration signal and high-frequency current signal in fault state and its corresponding signal in normal state gradually decreases. This shows that with the aggravation of the fault degree of OLTC contact, the characteristic components of the collected mechanical vibration signal and high-frequency current signal in the normal state and the characteristics of the collected mechanical vibration signal and high-frequency current signal in the fault state increase gradually.

4. Signal Feature Exaction

4.1. EEMD Based Signal Decomposition

In order to extract the feature quantity that can truly reflect the information contained in mechanical vibration signal and high-frequency current signal, this paper uses EEMD to decompose the mechanical vibration signal and high-frequency current signal after noise reduction.
EEMD is an improved signal decomposition method based on EMD. It adds evenly distributed white noise to the original signal and ensures that the white noise added in each independent test is different. Then carry out several independent tests, and finally calculate the average value of all tests, so as to cancel the noise contained in the signal. Therefore, EEMD can better improve the mode aliasing problem when EMD decomposes the signal, so as to improve the feature extraction accuracy of the signal. The steps of EEMD signal processing are as follows [21,22,23]:
The white noise signal ni(t) is added to the original signal x(t), i.e.
x 1 ( t ) = x ( t ) + n i ( t )
Decompose the added white noise signal x1(t) to generate intrinsic mode function (IMF), i.e.
x 1 ( t ) = ∑ j = 1 n c 1 j + r 1 n
Add different white noise signals in each independent test, and repeat step 1 and step 2 n times, i.e.
x i ( t ) = ∑ j = 1 n c i j + r i n
Calculate the mean value of each IMF obtained by n-times decomposition and take it as the final result, i.e.
c j = 1 n ∑ i = 1 n c i j
where n is the number of times to add white noise, c is the IMF value, and r is the decomposition residual component.

4.2. HT based signal feature extraction

HHT includes EMD and HT. Its purpose is to decompose the nonlinear non-stationary signal into IMF through EMD, and then use HT to extract the instantaneous frequency of the signal. In order to improve the mode aliasing problem in the process of EMD signal decomposition, EEMD is used to replace the EMD decomposition process to improve the accuracy of feature extraction. The process of HHT extracting signal features after optimization is as follows:
Firstly, the mechanical vibration signal and high-frequency current signal after noise reduction are decomposed by EEMD respectively to obtain the IMF component.
Secondly, HT the IMF component, and take the absolute value of the transformed signal to obtain its upper envelope, as shown in Figure 5.
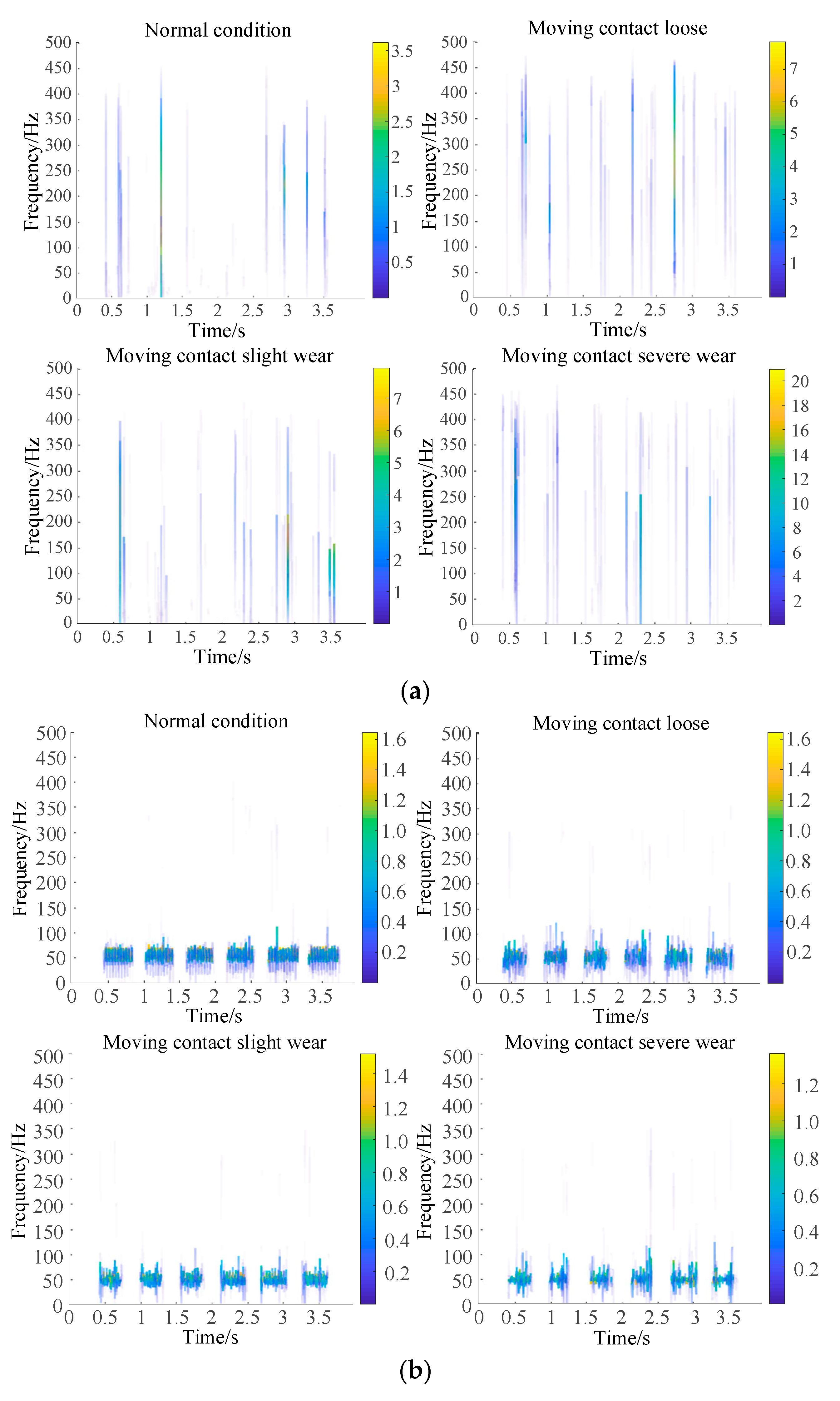
It can be seen from Figure 5 that when the OLTC contact evolves from the normal state to the fault state, the amplitude of the mechanical vibration signal gradually increases and the signal component becomes more and more complex. The amplitude of the high-frequency current signal and the fundamental frequency component represented by the purple part remain basically unchanged, but the characteristic components represented by the blue and yellow parts of the signal gradually decrease.
Then, HT the decomposed IMF component using the following formula, and obtain the corresponding Hilbert time-frequency spectrum [24], as shown in Figure 6.
H ( ω , t ) = Re ∑ i = 1 n a i ( t ) e j ∫ ω i ( t ) d t
It can be seen from Figure 6 that when the OLTC contact evolves from the normal state to the fault state, the frequency of the mechanical vibration signal is mainly concentrated in 0~450Hz, the signal component becomes more complex, and the energy corresponding to its frequency gradually increases. The frequency of high-frequency current signal is mainly concentrated between 0~100Hz, and its corresponding energy amplitude remains basically unchanged, but the frequency component decreases gradually.
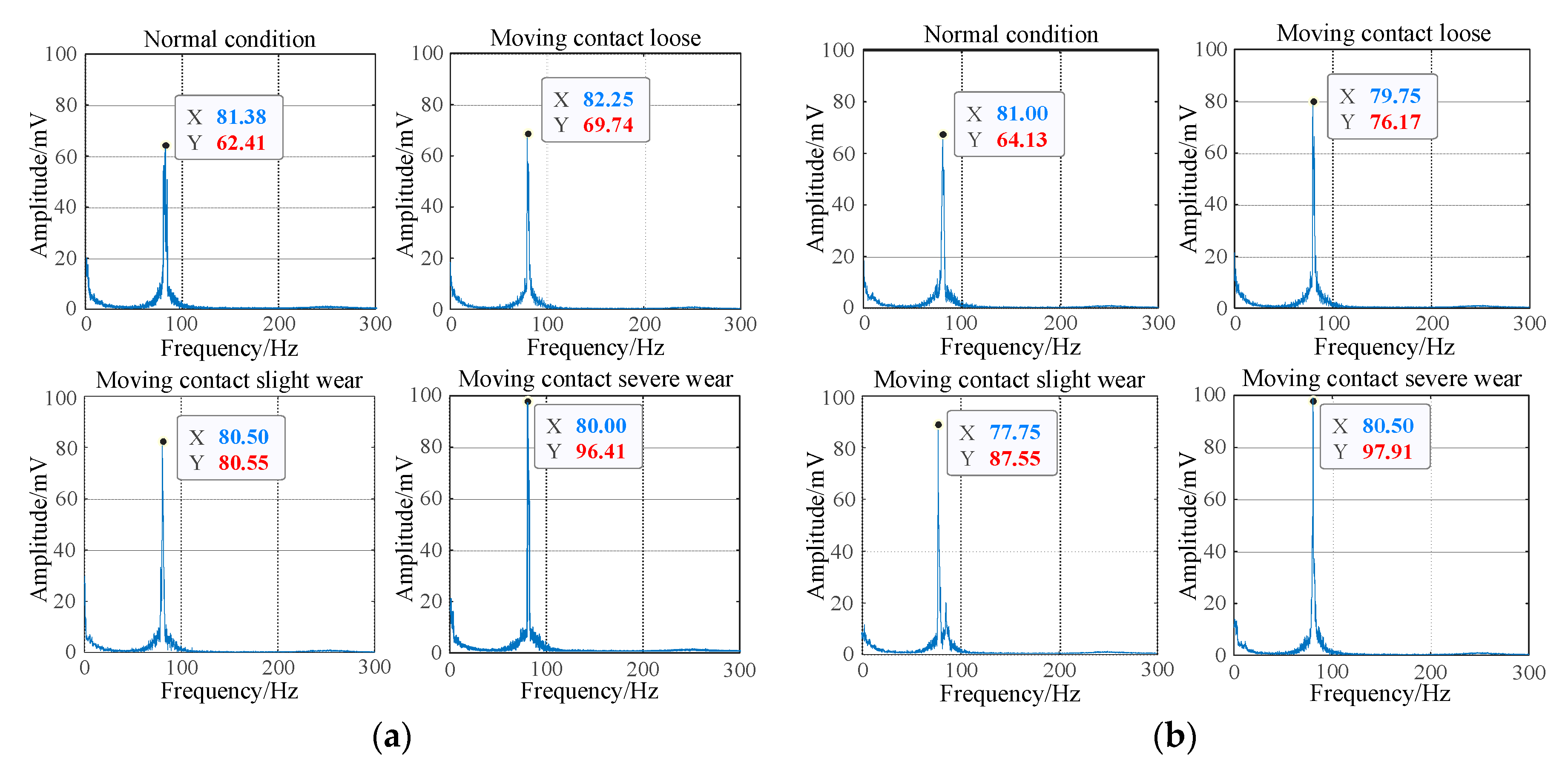
Finally, the Hilbert time-frequency spectrum is integrated on the time axis using the following formula to obtain the Hilbert marginal spectrum [25], as shown in Figure 7.
h ( ω ) = ∫ 0 T H ( ω , t ) d t
where T is the length of the signal sequence; H(ω,t) is the relationship among signal amplitude, frequency and time in the whole frequency range of the signal; h(ω) is the relationship between signal amplitude and frequency in the whole frequency range of the signal.
It can be seen from Figure 7 that when the OLTC contact evolves from the normal state to the fault state, the energy amplitude of the mechanical vibration signal gradually increases from 62.41mV to 96.41mV. The energy amplitude of high-frequency current signal gradually increases from 64.13mV to 97.91mV, and the energy amplitude of mechanical vibration signal and high frequency current signal is mainly concentrated between 0~100Hz.
The Hilbert marginal spectrum energy value is E(ω), and it can be finally obtained through (11) [26]:
E ( ω ) = ∫ ω 1 ω 2 h 2 ( ω ) d ω
where ω1 and ω2 is Hilbert marginal spectrum h(ω) frequency range.
Normalize the energy value and define the Hilbert marginal spectrum energy entropy according to the basic principle of information entropy, which can be expressed by the following formula [26]:
H j = − ε j log ε j
where εj is the ratio of IMF component energy to total energy in j layer.
By calculating the Hilbert marginal spectrum energy entropy of mechanical vibration signal and high-frequency current signal, and inputting it as mechanical characteristic quantity and electrical characteristic quantity into SVM algorithm for OLTC contact state diagnosis, the partial Hilbert marginal spectrum energy entropy of electromechanical signal are shown in Table 2 and Table 3.
It can be seen from Table 2 and Table 3 that when the oil immersed OLTC contact evolves from normal condition to fault state, the Hilbert marginal spectrum energy entropy of mechanical vibration signal and high-frequency current signal calculated by HHT gradually decreases. Because under normal conditions, the energy distribution of mechanical vibration signal and high-frequency current signal is relatively average and uncertain. In case of moving contact loose, wear and other faults, the mechanical vibration signal and high-frequency current signal resonate in the corresponding frequency band, and the corresponding marginal spectrum energy is concentrated in the frequency band, thus reducing the uncertainty of the marginal spectrum energy distribution, resulting in the reduction of the marginal spectrum energy entropy. Since the fault degree of OLTC contact under wear is more serious than that under loose condition, and the energy is more concentrated, the marginal spectrum energy entropy is smaller. Therefore, the marginal spectrum energy entropy obtained by HHT can be used as the input eigenvector of SVM algorithm to judge the working state and fault type of oil immersed OLTC contact.

5. Result Analysis

5.1. Analysis of Generation and Propagation Process of Electromechanical Signal

In order to extract the feature quantity that can truly reflect the information contained in mechanical vibration signal and high-frequency current signal, this paper uses EEMD to decompose the mechanical vibration signal and high-frequency current signal after noise reduction.
When the load of the on load voltage regulating transformer changes, in order to ensure the stability of the voltage at the output side, it is necessary to adjust the OLTC and change the number of winding turns at the high voltage side of the on load voltage regulating transformer to achieve the purpose of voltage regulation. When OLTC contact is in tapping operation, it has the characteristics of current carrying sliding electrical contact. The collision and wear of moving and static contacts are easy to produce mechanical vibration signals in the tapping process. The opening and closing operation of moving and static contacts are easy to produce arc phenomenon, resulting in the generation of high frequency current signal. However, the vibration of transformer core and winding will also produce mechanical vibration signals. Meanwhile, white noise and pulse interference are inevitable in the laboratory environment, which makes the components of collected mechanical vibration signal and high-frequency current signal more complex. Therefore, it is of great significance to analyze the propagation process of the two kinds of signals and preprocess the collected mechanical vibration signals and high-frequency current signals for noise reduction.
Firstly, the driving motor drives the OLTC to switch between moving contact and static contacts, then produces arc phenomenon, mechanical vibration signal and high-frequency current signal are generated at the same time. The generated mechanical vibration signal will not reach the inner wall of the oil chamber until it propagates for a certain distance in the insulating oil in the OLTC oil chamber. Because the oil chamber wall is relatively smooth, the vibration signal will be catadioptric when it reaches the oil chamber wall from the mineral oil in the oil chamber, which makes the vibration signal more complex. However, the damping of mineral oil in the oil chamber can reduce the complexity of vibration signal to a certain extent. When the vibration signal passes through the oil chamber wall and reaches the insulating oil in the transformer oil tank, catadioptric reflection will also occur, and the vibration of iron core and winding during transformer operation will also produce vibration signals in the transformer oil tank. Therefore, the components of vibration signals collected outside the transformer oil tank by vibration acceleration sensor are more complex. When the moving and static contacts of OLTC are tapped, arc phenomenon will occur. The high-frequency current signal can be collected by installing HFCT on the grounding cable of on load voltage regulating transformer, then the collected high-frequency current signal can be transmitted to MDO-2204 oscilloscope for display by BNC cable. Finally, the oscilloscope transmits the high-frequency current signal to the laptop through the USB data line for storage and analysis. In addition, the arc generated by the switching operation of OLTC moving and static contacts will decompose the mineral oil in the oil chamber, resulting in C2H2, H2, C2H4 and other fault gases, which will degrade the mineral oil in the OLTC oil chamber, reduce the insulation degree of mineral oil, affect its arc extinguishing effect and the transmission of mechanical vibration signal, and increase the complexity and acquisition difficulty of mechanical vibration signal. Therefore, it is of great significance to denoise the collected mechanical vibration signal and high-frequency current signal.

5.2. OLTC Contact Fault Classification Based on SVM

In order to diagnose the fault state of OLTC contact, this paper adopts the SVM algorithm with the characteristics of high efficiency and high classification accuracy in small sample data processing to analyze the mechanical vibration signal and high-frequency current signal at the same time [27,28,29]. In this paper, the Hilbert marginal spectrum energy entropy of electromechanical signal is taken as the input characteristic of SVM, and the relative energy amplitude is taken as the output of SVM. According to the experimental scheme, 20 groups of mechanical vibration signals and high-frequency current signals are collected in different states, each type of signal corresponds to 4 states, a total of 160 groups of data. The overall experimental data samples are small, which can give full play to the advantages of SVM in the classification and processing of small sample data.
SVM is a supervised learning method for solving binary classification problems. It has the characteristics of good generalization and avoiding falling into local minima. Its basic principle is to map the input space to the high-dimensional space according to the principle of structural risk minimization, and find an optimal hyperplane for classification, so as to maximize the difference of training data samples [30]. SVM algorithm includes two parts: data training and data testing. Its data training strategy is to maximize the interval of feature space, which can be transformed into a linear constrained convex quadratic programming problem. Suppose the data training set T={xi，yi}(i=1,2,…,l)，xi∈RN and yi∈R, nonlinear mapping Φ the data set xi is mapped to the high-dimensional feature space F by kernel function [31]. Then, the given data is analyzed by constructing a linear discriminant function f.
In the process of diagnosis, 120 groups of experimental data are selected for the training of SVM algorithm, and the remaining 40 groups of data are used for test classification. Therefore, the experimental data ratio between training set and test set is 120:40 (3:1). According to Hilbert time-frequency spectrum and Hilbert marginal spectrum, electromechanical signals have different energy amplitudes at the same frequency, so the relative energy amplitude is used to distinguish the state of OLTC contact. Because the input dimension of SVM algorithm in this paper is 3, the output dimension is 1 and the number of samples is small, the kernel function adopts Gaussian kernel function. After many comparisons, it can be obtained that the penalty factor C=50. Before the numerical test, all data sets are standardized and preprocessed using the maximum-minimum standardization method shown in equation (13). Finally, SVM algorithm is applied to train and test the mechanical vibration signal and high-frequency current signal at the same time. 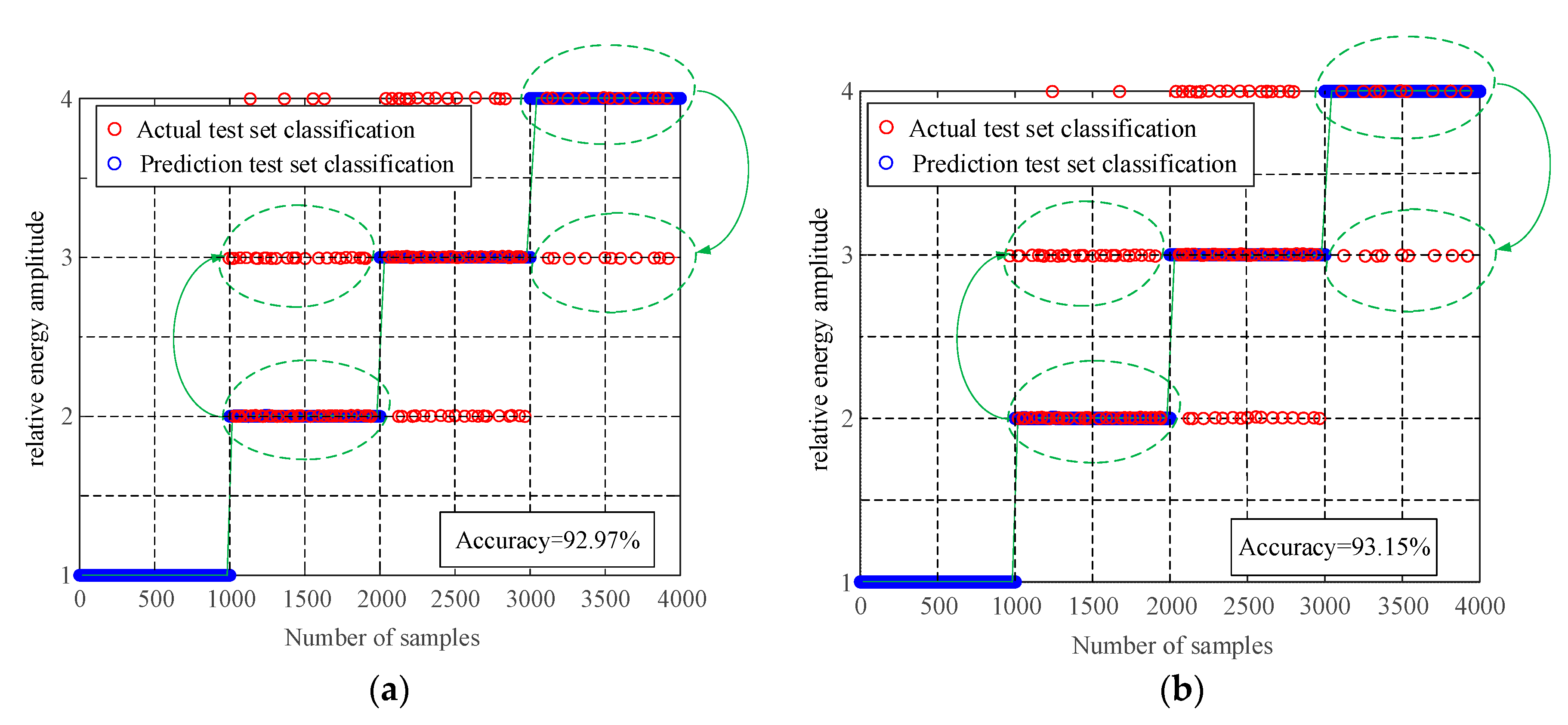The results are shown in Figure 8.
x ∗ = x − x min x max − x min
Based on the analysis in Figure 8, the SVM algorithm demonstrates accurate identification of the normal state and severe wear fault state of the OLTC contact based on the mechanical vibration signal. Despite some misclassification of individual data samples in the loose state and slight wear state of the OLTC contact, the overall accuracy of fault identification remains high at 92.97%. Regarding the high-frequency current signal, SVM also achieves accurate identification of the normal state and severe wear fault state of the OLTC contact. Although there are misclassified data samples during the loose state and slight wear state, the number of misclassifications is lower compared to the classification based on mechanical vibration signals. As a result, the overall accuracy of fault identification is relatively high at 93.15%. When considering the fault classification results obtained from both the mechanical vibration signal and high-frequency current signal using the SVM algorithm simultaneously, it is observed that although a small number of data are misclassified, they primarily occur in adjacent regions, with only a few isolated data points crossing boundaries. Hence, these errors are considered acceptable within the allowable range. The classification accuracy of both signals exceeds 90%, thereby validating the feasibility and efficiency of the proposed method in this study.

6. Conclusions

In this study, we utilized an experimental platform for OLTC contact simulation device. By employing vibration acceleration sensors and high-frequency current transformers (HFCTs), we simultaneously collected the mechanical vibration signal and high-frequency current signal of OLTC contact in four different states. Subsequently, we performed noise reduction preprocessing and feature extraction on the collected signals. Finally, we combined the mechanical vibration signal and high-frequency current signal to diagnose faults in the OLTC contact. The obtained results demonstrate that:
(1) As the OLTC contact transitions from a normal state to a fault state, there is a gradual increase in the amplitude of the mechanical vibration signal while the characteristic components of the high-frequency current signal gradually diminish.
(2) Through analysis of the Hilbert time-frequency spectrum and Hilbert marginal spectrum, it is observed that when the OLTC contact progresses from a normal state to a fault state, the frequency range of the mechanical vibration signal mainly concentrates between 0~450Hz, with a gradual increase in energy corresponding to its frequency. The frequency range of the high-frequency current signal primarily lies between 0~100Hz, exhibiting an increasing amplitude of energy as well.
(3) The results obtained from classifying OLTC contact faults indicate that electromechanical joint diagnosis allows for a more comprehensive analysis of the contact's condition. Moreover, the classification outcomes based on the SVM algorithm are more accurate, yielding error rates below 10%. These findings substantiate the feasibility and effectiveness of the electromechanical joint diagnosis method.

Author Contributions

S. L. contributed to conceptualization and proofread the article; L.D. wrote and revised the manuscript; S. L. proposed the main idea, contributed to conceptualization and proofread the article; Z. L and Y.K. summarized the references and proofread the article; Z.L. guided the writing and reference organization. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Gansu University Innovation Fund under contracts No. 2021B-111, the Doctoral foundation of colleges and universities in Gansu Province under contract No. 2021QB-061

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cai, Y.; Fang, R.; Peng, C.; Huang, W. On-load tap-changer mechanical fault diagnosis based on ANHGA-VMD and coupled hidden Markov model. High Voltage Technology. 2010, 8, 1–11. [Google Scholar]
  2. Liu, J.; Yu, S.; Chen, P.; Wang, F.; Ma, X.; Hu, X.; Qian, Y. Fault identification of energy storage spring of on-load tap-changer of transformer based on cluster analysis. High Voltage Apparatus 2020, 56, 159–165+172. [Google Scholar]
  3. Li, Q.; Zhao, T.; Zhang, L.; Lou, J. Mechanical fault diagnostics of on-load tap changer within power transformers based on hidden Markov model. IEEE Transactions on Power Deliver. 2012, 27, 596–601. [Google Scholar] [CrossRef]
  4. Wang, F.; Zeng, Q.; Zheng, Y.; Qian, Y. Mechanical fault diagnosis of on-load tap-changer based on Bayes estimation phase space fusion and CM-SVDD. Proceedings of the CSEE. 2020, 40, 58–368+402. [Google Scholar]
  5. Li, L.; Fu, X.; Cui, J.; Zhang, C.; Zhu, D.; Wu, K. Ground-penetrating radar soil layer information recognition based on envelope detection and STFT spectrum analysis. Journal of Geo-Information Science. 2020, 22, 316–327. [Google Scholar]
  6. Li, K.; Li, X.; Su, L.; Su, W. Bearing fault diagnosis based on DTCWT and GA improved sparse decomposition. Journal of Huazhong University of Science and Technology (Natural Science Edition). 2021, 49, 56–61. [Google Scholar]
  7. Zhang, X.; Li, L.; Liu, S.; Lei, J. Empirical wavelet transform based on energy peak location and its application in weak bearing fault diagnosis. Journal of Xi'an Jiaotong University. 2021, 55, 1–8. [Google Scholar]
  8. Duan, R.; Wang, F.; Zhou, L.; Yao, G. Detection of mechanical state of on load tap changer for converter transformer using narrowband noise assisted multiple empirical mode decomposition algorithm. Journal of Electrotechnics. 2017, 32, 182–189. [Google Scholar]
  9. Geng, C.; Wang, F.; Zhang, J. Modal parameters identification of power transformer winding based on improved Empirical Mode Decomposition method. Electric Power Systems Research. 2014, 108, 331–339. [Google Scholar] [CrossRef]
  10. Shi, Y.; Zhuang, Z.; Lin, J. Bearing fault diagnosis based on convolution sparse representation and isometric mapping. Vibration Test and Diagnosis. 2019, 39, 1081–1088+1138. [Google Scholar]
  11. Wu, C.; Zhang, D.; He, J. Protection scheme for VSC-MTDC based on low-frequency reactive power. Electric Power Systems Research. 2022, 204, 107703. [Google Scholar] [CrossRef]
  12. Zamani, R.; Mohammad, E.; Hamedani, G.; Hassan, H. A novel synchronous DGs islanding detection method based on online dynamic features extraction. Electric Power Systems Research. 2021, 195, 107180. [Google Scholar] [CrossRef]
  13. Zhou, X.; Wang, F.; Fu, J.; Lin, J.; Jin, Z. Mechanical condition monitoring of on load tap changer based on Chaos Theory and K-means clustering. Proceedings of the CSEE. 2015, 35, 1541–1548. [Google Scholar]
  14. Mehdi, B.; Ahmed, A. Clustering of transformer condition using frequency response analysis based on k-means and GOA. Electric Power Systems Research. 2022, 202, 107619. [Google Scholar] [CrossRef]
  15. Liu, J.; Li, Q.; Chen, W.; Yan, Y. Fault diagnosis method for tram fuel cell system based on multi class correlation vector machine and fuzzy C-means clustering. Proceedings of the CSEE. 2018, 38, 6045–6052. [Google Scholar]
  16. Wu, J.; Wu, Z.; Mao, X. Risk early warning method for distribution system with sources-networks-loads-vehicles based on fuzzy C-mean clustering. Electric Power Systems Research. 2020, 180, 106059. [Google Scholar] [CrossRef]
  17. Ding, Y.; He, Y.; Li, B.; Cui, J. Inverter fault diagnosis based on wavelet packet and quantum neural network. Journal of Chongqing University of Technology (Natural Science). 2021, 35, 152–158. [Google Scholar]
  18. Deng, M. Research on mechanical fault diagnosis of on load tap changer based on vibration signal. Transformer. 2018, 55, 26–29. [Google Scholar] [CrossRef]
  19. Liu, B.; Yu, Y.; Bai, X.; Ke, Z.; Wang, J. Research on transformer fault detection system based on vibration signal analysis. Electrical Automation. 2020, 42, 80–82+86. [Google Scholar]
  20. Stark, J A. Adaptive image contrast enhancement using generalizations of histogram equalization. IEEE Transactions on Image Processing. 2000, 9, 889–896. [Google Scholar] [CrossRef]
  21. Wu, Z.; Huang, N. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Advances in Adaptive Data Analysis. 2008, 1, 1–41. [Google Scholar] [CrossRef]
  22. Shao, Z.; Zheng, Q.; Liu, C. A feature extraction and ranking-based framework for electricity spot price forecasting using a hybrid deep neural network. Electric Power Systems Research. 2021, 200, 107453. [Google Scholar] [CrossRef]
  23. Ozgonenel, O.; Yalcin, T.; Guney, I. A new classification for power quality events in distribution systems. Electric Power Systems Research. 2013, 95, 192–199. [Google Scholar] [CrossRef]
  24. Huang, N.; Long, S.; Zheng, S. A new view of nonlinear water waves: The Hilbert spectrum. Annual Review of Fluid Mechanics 1999, 457–471. [Google Scholar] [CrossRef]
  25. Gao, A.; Zhu, Y.; Zhang, Y.; Cai, W. Partial discharge pattern recognition of transformers based on marginal spectrum image and deep residual network. Power System Technology. 2021, 45, 2433–2442. [Google Scholar]
  26. Yan, J.; Ma, H.; Zhu, H.; Zhang, Y.; Li, Y.; Xu, H. Transformer winding looseness diagnosis based on LMD marginal spectral energy entropy and FWA-SVM. Electrical Measurement and Instrumentation. 2021, 58, 74–80. [Google Scholar]
  27. Yu, M.; Zhao, W.; Wu, L.; Li, Y. Research on electric vehicle driving conditions based on K-means clustering and support vector machine. Journal of Chongqing Jiaotong University (Natural Science Edition). 2021, 40, 129–139. [Google Scholar]
  28. Abdelhalim, M.; Boubakeur, Z.; Mohammed, B. Fixed least squares support vector machines for flashover modelling of outdoor insulators. Electric Power Systems Research. 2019, 173, 29–37. [Google Scholar] [CrossRef]
  29. Yang, H.; Zhang, W.; Chen, J.; Wang, L. PMU-based voltage stability prediction using least square support vector machine with online learning. Electric Power Systems Research. 2018, 160, 234–242. [Google Scholar] [CrossRef]
  30. Li, Z.; Wang, H.; Qian, Y.; Huang, R.; Cui, Q. Pattern recognition of noisy partial discharge based on SURF. Journal of Electrotechnics. 2021, 10, 100–110. [Google Scholar]
  31. Yang, S.; Chen, S.; Li, G.; Jiang, J. Mechanical fault diagnosis of transformer on-load tap-changer based on variational modal decomposition and feature selection. Southern Power System Technology. 2019, 13, 39–47+59. [Google Scholar] [CrossRef]
Preprints 79367 g001
Figure 1. Schematic of OLTC switching signal acquisition system.
Figure 1. Schematic of OLTC switching signal acquisition system.
Preprints 79367 g001
Preprints 79367 g002
Figure 2. Physical image of OLTC contact simulation device.
Figure 2. Physical image of OLTC contact simulation device.
Preprints 79367 g002
Preprints 79367 g003
Figure 3. The original signal in four states. (a) Normal condition; (b) Moving contact loose; (c) Moving contact slight wear; (d) Moving contact severe wear.
Figure 3. The original signal in four states. (a) Normal condition; (b) Moving contact loose; (c) Moving contact slight wear; (d) Moving contact severe wear.
Preprints 79367 g003
Preprints 79367 g004aPreprints 79367 g004b
Figure 4. The original signal after noise reduction in four states. (a) Normal condition; (b) Moving contact loose; (c) Moving contact slight wear; (d) Moving contact severe wear.
Figure 4. The original signal after noise reduction in four states. (a) Normal condition; (b) Moving contact loose; (c) Moving contact slight wear; (d) Moving contact severe wear.
Preprints 79367 g004aPreprints 79367 g004b
Preprints 79367 g005
Figure 5. Hilbert upper envelope diagram in four states. (a) Upper envelope of mechanical vibration signal in four states; (b) Upper envelope of high-frequency current signal in four states.
Figure 5. Hilbert upper envelope diagram in four states. (a) Upper envelope of mechanical vibration signal in four states; (b) Upper envelope of high-frequency current signal in four states.
Preprints 79367 g005
Preprints 79367 g006
Figure 6. Hilbert time-frequency spectrum diagram in four states. (a) Time-frequency spectrum of mechanical vibration signal in four states; (b) Time-frequency spectrum of high-frequency current signal in four states.
Figure 6. Hilbert time-frequency spectrum diagram in four states. (a) Time-frequency spectrum of mechanical vibration signal in four states; (b) Time-frequency spectrum of high-frequency current signal in four states.
Preprints 79367 g006
Preprints 79367 g007
Figure 7. Hilbert marginal spectrum diagram in four states. (a) Marginal spectrum of mechanical vibration signal in four states; (b) Marginal spectrum of high-frequency current signal in four states.
Figure 7. Hilbert marginal spectrum diagram in four states. (a) Marginal spectrum of mechanical vibration signal in four states; (b) Marginal spectrum of high-frequency current signal in four states.
Preprints 79367 g007
Preprints 79367 g008
Figure 8. OLTC contact fault classification results. (a) Contact fault classification results of mechanical vibration signal SVM; (b) Contact fault classification results of high-frequency current signal SVM.
Figure 8. OLTC contact fault classification results. (a) Contact fault classification results of mechanical vibration signal SVM; (b) Contact fault classification results of high-frequency current signal SVM.
Preprints 79367 g008
Table 1. Relevance analysis results between different states of OLTC contacts.
Table 1. Relevance analysis results between different states of OLTC contacts.
OLTC moving contact status Related coefficient (r)
Mechanical vibration signal High frequency current signal
Normal condition 1 1
Loose state 0.565 0.634
Slight wear 0.470 0.553
Severe wear 0.261 0.319
Table 2. Hilbert marginal spectrum energy entropy of IMF component of vibration signal.
Table 2. Hilbert marginal spectrum energy entropy of IMF component of vibration signal.
IMF component Normal condition Moving contact loose Moving contact slight wear Moving contact severe wear
IMF1 2.9213 2.5627 2.3901 1.8172
IMF2 2.276 2.0142 1.9283 1.5116
IMF3 1.984 1.745 1.617 1.624
IMF4 1.7998 1.5637 1.3869 1.964
IMF5 1.507 1.3064 1.118 0.5927
IMF6 1.8617 1.014 0.9081 0.5677
IMF7 1.819 0.6592 0.4185 0.1278
IMF8 1.717 0.4237 0.605 0.0779
Table 3. Hilbert marginal spectrum energy entropy of IMF component of high-frequency current signal.
Table 3. Hilbert marginal spectrum energy entropy of IMF component of high-frequency current signal.
IMF component Normal condition Moving contact loose Moving contact slight wear Moving contact severe wear
IMF1 0.6691 0.4375 0.3017 0.1699
IMF2 0.4206 0.4062 0.2856 0.1428
IMF3 0.5013 0.3608 0.2601 0.1641
IMF4 0.3918 0.4120 0.3015 0.1329
IMF5 0.3216 0.3306 0.2590 0.0918
IMF6 0.2961 0.3014 0.2310 0.0764
IMF7 0.2654 0.2938 0.2045 0.1028
IMF8 0.3013 0.2237 0.2407 0.0839
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated