Prerpints.org logo
Preprint
Article

A Robust Integrated Watermarking Algorithm for Vector Geographic Data Copyright Protection

Altmetrics

Downloads

158

Views

57

Comments

0

Submitted:

12 July 2023

Posted:

13 July 2023

You are already at the latest version

Alerts
Abstract
Vector geographic data play an important role in the natural resources and environment sector and other location information services. This is also one of the types of data where the cost to create it is relatively large because of the difficulty in surveying, collecting, and authorizing. The rapid development of the Internet has created many advantages in the distribution, exploitation, and use of vector geographic data, but it also gives rise to many problems such as duplication, redistribution, forgery, and illegal data use. The theft on the Internet is becoming more and more sophisticated and the number of violations is increasing, showing the urgent need to research and develop an effective solution to protect the copyright of vector geographic data and prevent them from being illegally collected and used. Among the major studies and solutions, digital watermarking emerges as an effective method and is an active research area for copyright protection. Towards a good solution for copyright protection of vector geographic data, our study proposes a new algorithm with three main contributions, including: (1) generating short, pseudo-random meaningful watermarks to increase robustness and to enable automated as well as visual manual verifying; (2) building a uniformly distributed mapping between the vertex coordinates and the watermark bit indexes to increase the robustness of the watermarks; and (3) integrate two types of watermarks, namely, spatial domain-based watermarking and zero-watermarking to be resistant to most common attacks on geographic vector data. The algorithm also allows working on all types of vector geographic data, including points, polylines, and polygons.
Keywords: 
Subject: Environmental and Earth Sciences  -   Other

1. Introduction

Copyright protection is a very broad concept and therefore there are many solutions or techniques to implement. However, each technique usually only protects the author’s rights against certain attacks. Copyright protection techniques can be divided into two groups: precaution techniques; and accountability techniques [1]. Preventive techniques implement defensive methods such as encrypting data or controlling user access to prevent unauthorized users from accessing the data. Alternatively if unauthorized users can access the data, these techniques ensure they cannot exploit or utilize it. Accountability techniques perform post-checks, meaning that when in doubt or periodically, data can be checked to verify its copyright.
Digital watermarking is an accountability technique whose process is: (1) embedding copyright information (called watermark) into the data; (2) distributing the data to the user and assuming that the data will be subject to certain types of attacks (or transformations); and (3) detecting and extracting copyright information (embedded watermark) from data to verify copyright. Watermarking techniques are highly dependent on the protected object due to the different characteristics of these objects.
Vector geographic data represents the spatial and non-spatial properties of features that are geographically located on Earth. Usually, vector geographic data is organized into one or more layers, wherein each layer typically representing a type of feature with spatial properties such as points, polylines, or polygons. Maps are usually built by superimposing these layers of data. The main formats of vector geographic data are shapefile (.shp), geojson (.json), GeoPackage (.gpkg), or GeoDatabase.
Although the number of studies on digital watermarking to protect the copyright of vector geographic data in recent years has been quite large, it is still much less than the number of studies on digital watermarking to protect the copyright of multimedia data. This may be due to the ubiquity of multimedia data and the complexities arising from the nature of the vector geographic data (such as data structures, data analysis purposes, etc.).
To serve the purpose of copyright protection, watermarking techniques are needed to ensure stability/robustness against attacks, accidental or intentional modification. However, each current watermarking technique is only resistant to certain types of attacks, so an integrated solution is needed to increase resistance to many types of attacks. This paper will present our research results to form an integrated algorithm between spatial domain-based watermarking (specifically, watermarking embedded in the coordinates of vertices) and zero-watermarking (specifically, is a zero-watermark based on statistical properties), to create a stable/robust watermarking technique for copyright protection of vector geographic data. The algorithm contains three advantages, including (1) a technique to generate short, pseudo-random, and meaningful watermarks to increase durability and also be able to verify the watermark automatically and intuitively; (2) a uniformly distributed map between vertex coordinates and watermark bit indexes to increase the durability of watermark; and (3) the integration of two watermarking techniques to be able to resist many types of attacks.

2. Methodology

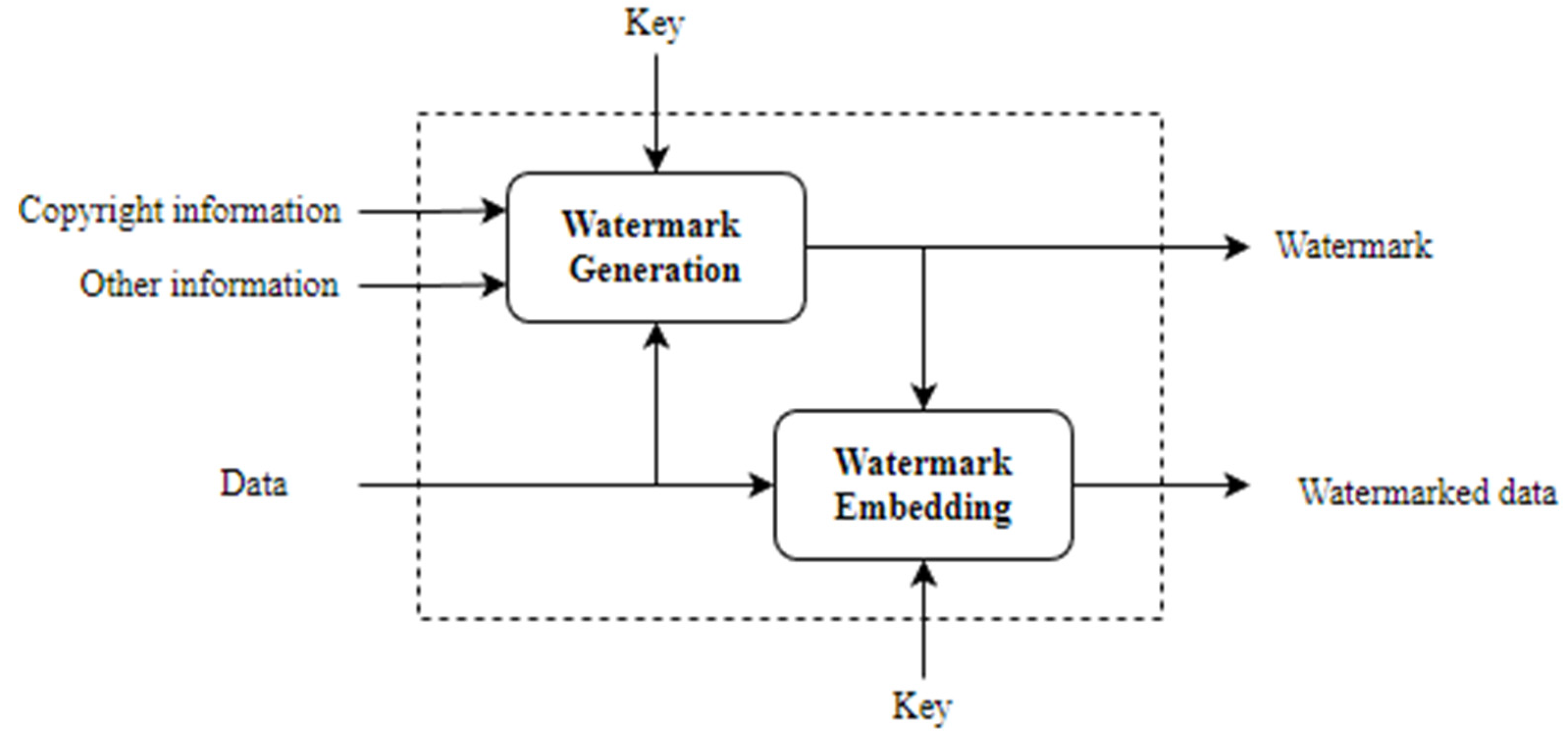
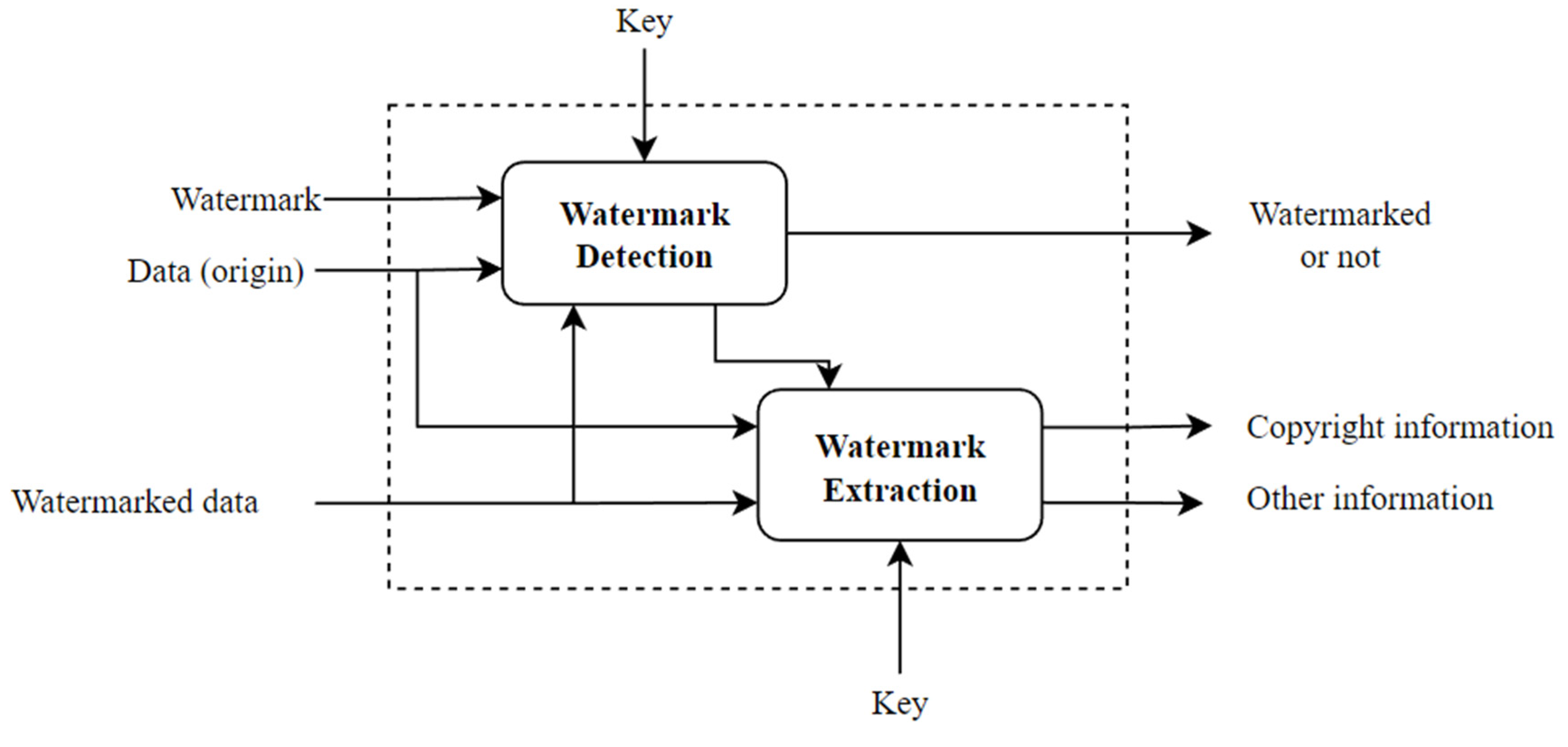
2.1. Watermarking Process for Copyright Protection

Watermark-based data copyright protection is accomplished by performing some operations on the data before transferring the data to the user. This work is called watermark embedding which consists of two steps: (1) watermark generation and (2) watermark embedding. Watermarks are generated from copyright information and some other information (e.g., user information). In some cases (e.g., in zero-watermarking) the generated watermark based on the data itself will be protected copyright. To increase security by eliminating the ability to visually view as well as statistically the adjacent information of the watermark, the watermark is often shuffled and may be encrypted by a key-using encryption algorithm [2]. The watermark is stored and in the case of a zero-watermarking can be sent to a trusted authenticated party. The watermark is then embedded into the data to create a product ready to be delivered to the user (called watermarked data). The procedure of copyright protection watermark embedding is shown in Figure 1.
The watermarked data is transferred to the user and is assumed to be subject to some accidental or intentional transformations or attacks. When verifying copyright is required, the process of detecting and extracting watermarks to prove copyright is performed. This process typically involves detecting if the data contains a watermark and then extracting the watermark to prove copyright. The input to the process will be data, which is needed to verify the copyright, and in some cases may need both watermark and the original data. The extracted watermark also needs the key to decrypt to get the copyright information. The watermark detection and extraction process are shown in Figure 2.

2.2. Analysis of Watermarking Techniques

Based on the embedding domains as well as the accuracy requirements of the watermarked data, watermarking techniques are divided into several categories such as spatial domain-based watermarking, frequency domain-based watermarking, reversible watermarking, lossless watermarking, and zero-watermarking. Research on watermarking using techniques of embedding information into the spatial domain (coordinates of objects) can be mentioned as [3,4,5,6,7,8,9], techniques of embedding information into the frequency domain such as [10,11,12]. Reversible watermarking techniques for vector geographic data are performed in [13,14,15,16,17,18]. In [19,20], the studies of watermarking without losing information based on the storage order are presented. Zero-watermarking techniques are studied in [21,22,23,24,25,26].
Watermarking algorithms often try to embed some information (watermark) into the data for the purpose of copyright protection by serving to detect and extract the watermark to prove the copyright of the owner. The embedding is based on the principle of finding redundant space in the data so that the watermark can be inserted without or with little effect on the data to be protected. The techniques for inserting or hiding this information into other information mainly used today include spectral modulation, least significant bit, or quantization index modulation techniques [27]. Note also that the watermark does not have to be embedded in the carrier data, and techniques of this kind are called zero-watermarking.
Based on the degree of stability of the watermark against attacks on the watermarked data, the watermarking algorithms can be classified into robust and fragile watermarking. Robust watermarking is useful for copyright protection while fragile watermarking is useful for integrity and authenticity issues. Based on the ability to see the watermark visually on the watermarked data, watermarking techniques are classified into visible and invisible watermarking. For multimedia data such as images or videos, visible watermarking is an effective way to explicitly identify data copyright. However, for vector geographic data, besides serving visual presentation, the data also serves many spatial analyses, therefore, the watermarking techniques on vector map data are mainly invisible watermarking, which is not seen by users. Based on the techniques of embedding watermarks into data, it is possible to divide watermarking algorithms into spatial domain-based watermarking and frequency domain-based watermarking. Spatial domain-based watermarking seeks to insert watermarks into the vertex coordinates or relations of geometric features, while frequency domain-based watermarking first, seeks to transfer geometric features from the spatial domain to the frequency domain using transformations such as Fourier transformation, Cosine transformation or wavelet transformation, then insert watermark into the coefficients, and finally convert back to the space domain using the corresponding inverse transformations. Based on whether original data is needed to verify watermarked data, watermarking algorithms are divided into blind and non-blind watermarking. With blind watermarking, extracting watermark information only needs the watermarked data itself, while with non-blind watermarking, extracting watermark information requires both original data and watermarked data.
Based on the influence as well as the ability to recover the original data from the watermarked data, watermarking algorithms are classified into lossy watermarking and lossless watermarking. Conventional watermarking techniques distort the original data and, in some cases, may be unacceptable (e.g., in geodesy, cartographic, military fields). Lossless watermarking attempts to preserve the original data and as such is suitable for copyright protection applications of highly accurate vector geographic data.
As analyzed in [19], the current studies of lossless watermarking for vector geographic data can be divided into three main categories. The first type is reversible watermarking which protects copyright by embedding watermark in the original data and it is possible to recover the original data from the watermarked data through watermark extraction. Unfortunately, the reversible watermarking technique has obvious defects that the watermark can only be used once because the reversible watermark information must be discarded after the watermark extraction. Therefore, this technique does not satisfy the requirement of copyright protection.
The second lossless watermarking technique is zero-watermarking, where the watermark is generated from the characteristics of the data without any modification to the original data. The generated watermark will be stored in an IPR (Intellectual Property Rights) repository for future proof of copyright. The main point of the method is to extract stable characteristics of the original data that are resistant to various types of attacks. There are two popular methods of extracting features that are based on statistical and geometrical features, respectively. For example, the map is divided into rings using concentric circles. The number of vertices in each belt is then counted to be used as information on statistical feature. These characteristics are further combined with copyright information to form zero-watermarks. Compared with reversible watermarking, zero-watermark achieves complete lossless information. However, the technique does not actually embed the watermark in the data, so there may be issues of trust in third parties in the proof of copyright.
The third technique is watermarking based on storage features. This method embeds the watermark by transforming the storage order of the vector data without changing the coordinate values, thus avoiding the defect of single-use limitation in reversible watermarking and avoiding the limitation of replying on a third-party in zero-watermarking. With this technique, the storage direction of a polyline is quantized by 0 or 1 corresponding to the storage characteristic of that polyline. To embed watermark, the watermark bit is considered whether consistent with the quantum value of the storage direction. If they are the same, the storage order of that polyline does not change. Otherwise, the storage order of that polyline is reversed. Compared with zero-watermarking, this technique actually embeds the watermark in the data.
The watermark itself can be classified into two groups as meaningful watermark and meaningless watermark. Meaningful watermarks are usually logo images that are easily visually inspected when extracted, while meaningless watermarks are often represented as a pseudo-random sequence of bits. Detecting the presence of meaningless watermarks often uses statistical correlations (e.g., the Pearson correlation coefficient). In addition, meaningless watermarks are usually much shorter than meaningful watermarks, so meaningless watermarks increase the robustness of watermarking techniques and are often used for small data sets. To improve the robustness of watermarking techniques and to ensure the security of the watermark, the watermark is often scrambled and can be encrypted by a cryptosystem before being embedded in the data. A contribution of this study is proposing a technique to generate a meaningful watermark with characteristics of a meaningless watermark, so can be detected and verified automatically with high accuracy. The generated watermark is also meaningful watermark, so can be verified visually by humans.

2.2.1. Spatial Domain-Based Techniques

The techniques use the spatial domain to embed watermark bits into the coordinates of vertices or other features such as distances, angles, or even the storage order of vector geographic data. To get a robust watermarking algorithm against common attacks such as feature deletion/addition, feature compression (simplification), vertex deletion/addition, algorithms try to embed watermark bits multiple times on the data and thus it is necessary to establish a one-to-many mapping of watermark bits to the vertices. For example, when we want to embed a watermark bit, the algorithm needs to establish a mapping that maps this bit to multiple vertices. This mapping needs to ensure that the watermark bits are embedded “uniformly” over the entire data set to prevent attacks such as data clipping. One contribution of this study is the construction of such a mapping.
Embedding watermark bits into vertices in vector geographic data can be done by one of the techniques such as least significant bit, quantization index modulation, or storage order.

2.2.2. Frequency Domain-Based Techniques

The frequency domain-based techniques organize the whole data or each feature (polyline or polygon) as a sequence of coordinates. Coordinate sequences are then converted to the frequency domain using one of the numerical transformations such as Fourier, Cosine, or Wavelet. The watermark bits will be embedded in the frequency domain coefficient values and then converted back into the space domain by the corresponding inverse digital transformations. In this way, the watermark bit is embedded and propagated into the coordinate sequence.
To ensure robustness, techniques using the frequency domain also use one-to-many mappings from the watermark bits into coordinate sequences as in the spatial domain-based technique. In general, techniques using frequency domain have higher stability than spatial domain techniques, but the accuracy of data after embedding watermark is lower.

2.2.3. Lossless Watermarking Techniques

Lossless watermarking techniques cannot embed watermark bits directly into the values of geometric objects in the data (whether directly or using frequency transformation) because this would reduce the accuracy of the data. Instead, these techniques seek to utilize the special characteristics of vector geographic data. A typical example is using the ordering of the vertices of a polyline or polygon to store a bit of information; for example, if the order is clockwise then the information bit is 1 and vice versa if the order is anti-clockwise then the information bit is 0.

2.2.4. Zero-Watermarking Technique

Zero-watermarking techniques actually do not embed watermarks in the data but are watermark generating techniques. Watermarks are generated based on the immutable characteristics of the data to ensure against attacks such as projection and CRS transformation. The generated watermark is a meaningless watermark that tries to characterize the data. This meaningless watermark may be saved by a trusted third party for future reference purposes. Some watermarking techniques also add the step of combining this meaningless watermark derived from data with copyright information to form a meaningful watermark.

3. Integrated Watermarking Algorithm

The proposed vector geographic data copyright protection integrated watermarking algorithm includes spatial domain watermarking, embedding watermarks in the coordinates of the vertices and zero-watermarking based on statistical characteristics. With the selection of embedded features as vertices, this watermarking is capable of embedding watermark on all types of vector geographic data including types of points, polylines, and polygons data. Moreover, in vector geographic data, the number of vertices is often more than the number of features, so in this watermarking technique, each bit of the watermark is embedded in the data more times and that means the watermark will be more stable.

3.1. Short, Pseudo-Random, and Meaningful Watermark Generation

By using the big character representation of a string as a meaningful watermark, the watermark can be verified by humans directly and its size remains small. For example, the watermark “CEID” and the watermark “HA NOI” as shown in Figure 3 have the size of only 114 and 168 bits respectively.
The big character representation of watermarks is generated using Pillow library. Without loss of generality, the bits representing the character are assigned the value 1 and the remaining bits are assigned the value -1. Thus, the watermark is represented by an array of bit values 1 and -1. Usually, the number of bits 1 and -1 of a watermark is not equal and therefore does not reflect randomness as if the watermark is randomly generated from bits 1 and -1. Our algorithm tries to make the number of bits 1 and -1 equal by padding bits 1 or -1 to the water as shown in Figure 4.
An Arnold’s transformation is applied to the watermark to generate a pseudo-random, watermark as shown in Figure 5.
The use of these watermarks makes automatic watermark detection and verification (using statistical indicators) unbiased and also allows intuitive manual verification.
Flatten the watermark into a vector and assume that the watermark is W = { w [ i ] , 0 ≤ i < N } , where w [ i ] is the watermark bit, i is the watermark bit index, N is the length of the watermark, and w [   i ] ∈ { − 1 , 1 } . The algorithm will embed each bit of this W   watermark in the vertices of the vector geographic data.

3.2. Watermark Embedded in the Vertices

Our procedure for embedding watermark’s bits in the coordinates of vertices is heavily based on the technique proposed by Wang et al. [3] but improves upon the determination of which watermark bit should be embedded in a vertex and then embeds that bit in the vertex coordinates based on the quantization technique.

3.2.1. Watermark Embedding

Vector geographic data contains vertices with coordinates. The vertex coordinates are the basis of the points, polylines, and polygons that are the basic feature classes in the vector geographic data. To obtain a strong watermarking algorithm against common attacks such as data slicing, data inversion, data simplification (compression), vertex addition, vertex deletion, we need to establish a mapping between the vertex coordinates and the watermark bit index such that the watermark bits are distributed “uniformly” over the vertex coordinate, and then watermark bits will be embedded in the corresponding vertex coordinates according to this mapping.
Assume that the vertex coordinates of the vector geographic data are the set V C = { v c i   | ( x i , y i ) , 0 ≤ i < M } , where v c i is the i-th vertex, ( x i , y i ) is the coordinates of the i-th vertex, and M is the number of vertices. The mapping between ( x i ,   y i ) and two watermark bit indexes ( i x ,   i y ) is established using the following equations:
i x = H a s h x i   %   N i y = H a s h y i   %   N
Thanks to the uniform distribution of a hash function, this map is also uniform distribution. It is a many-to-one mapping between the vertex coordinates and the watermark bit index. The watermark bits are embedded in the corresponding vertex coordinates using a quantization technique to ensure blind detection of the watermark bits. In the vast majority of cases, the number of vertex coordinates is much more than the length of the watermark. This leads to a many-to-one relationship mapping between the vertex coordinates and the watermark bit index, resulting in a watermark bit entry corresponds to multiple extracted watermark bits.

3.2.2. Watermark Detection

The watermark is extracted according to the reverse process of the watermark embedding process. The main steps to extract watermark are as follows: for certain vertex coordinates ( x i , y i ) , the watermark bit is extracted from ( x i , y i ) using a quantization algorithm, and the index for the watermark bit is calculated based on the mapping function.
Suppose the extracted watermark bits are the set W ′ = { w ′   [ i ] [ j ] , 0 ≤ i < N , 0 ≤ j < L i } and w [ i ] [ j ] ∈ { − 1 ,   1 } where w [ i ] [ j ] is the jth extracted watermark bit of the ith watermark bit index, N is the length of the watermark, L i represents the number of extracted watermark bits corresponding to the ith watermark bit index, and M is the number of vertices. Also L i ≥ 0 and ∑ i = 0 N − 1 L i = 2 ∗ M .
The basic principle of the watermark detection algorithm is first calculating the watermark W ″ with fixed length N based on the extracted watermark bits W ′ , then calculate the correlation coefficient between W ″ and the original watermark W to judge whether the watermark is contained in the data. Watermark W ″ = { w ″   [ i ] , 0 ≤ i < N } , w ″ [ i ] ∈ { − 1,1 } is determined by calculating t i = ∑ j = 0 L i − 1 w ′   i j and then calculating w ″ [ i ] according to the equation.
w ″ i = 1   i f   t i > 0   − 1   i f   t i < 0   1   o r − 1   r a n d o m l y   i f   t i = 0
The normalized correlation coefficient c 1 is calculated using the equation.
c 1 = ∑ i = 0 N − 1 w i ∗ w ″ [ i ] N
According to Wang et al. [3], threshold μ 1 = 4   ∗ 1 /   N can be used to detect watermark with the FPE is less than 0.0001. The watermark detection rule is as shown in the following expression.
n o n − w a t e r m a r k e d   d a t a c 1 ≤ μ 1   w a t e r m a r k e d   d a t a c 1 > μ 1
Wang et al. [3] also proposed other coefficient using extracted watermark bits W ’ directly instead of derivate watermark W ’ ’ (called the Adaptive Watermark Detection). This normalized correlation coefficient c 2 is calculated using the following equation.
c 2 = ∑ i = 0 N − 1 ∑ j = 0 L i − 1 w i ∗ w ′ [ i ] [ j ] 2 ∗ M
When a watermark is not contained in the detected data, for watermark bit index i , the extracted watermark bit w ′ i [ j ] is randomly equal to 1 and -1, and because the watermark W is pseudo-random, the mean and variance of w i ∗ w ′ [ i ] [ j ] can be expressed as E w i ∗ w ′ i j = 0 and V w i ∗ w ′ i j = 1 . According to the central limit theorem, correlation coefficient c 2 can be approximated by the normal distribution with a mean of 0 and a variance of 1 2 ∗ M as shown in the expression.
C 2 ~ N ( 0 , 1 2 ∗ M )
The threshold μ 2 = 4 ∗ 1 2 ∗ M is used to detect watermark with the FPE, e 1 = 1 − ϕ 4 = 0.000031671 < 0.0001 .
Our algorithm using both c 1 and c 2 and thresholds μ 1 , and μ 2 respectively, to state whether a detected data is watermarked or not. Moreover, manual visual inspection is also performed before concluding watermarked data for copyright protection purposes. The rule is shown in the following expression.
w a t e r m a r k e d   d a t a c 1 > μ 1   a n d   c 2 > μ 2   a n d   m a n u a l   v i s u a l   i n s p e c t i o n n o n − w a t e r m a r k e d   d a t a o t h e r s

3.3. Zero-Watermark Based on Statistical Properties

Zero-watermarking does not embed the watermark in vector geographic data but computes the stable features of the data which can then be used to prove the copyright of the data. Our algorithm uses the zero-watermarking technique based on statistical characteristics proposed by Xun et al. [25]. The algorithm divides the map into rings and counts the number of vertices in each round. Also, because it is based on vertices, the algorithm can work on all types of vector geographic data including point, polyline, and polygon data. In addition, when working with vertex data, the number of vertices in the vector geographic data is often much larger than the number of features of them, so the statistical properties are often more stable.

3.3.1. Zero-Watermark Embedding

Embedding zero-watermark is actually the process of generating watermark. First compute the coordinates of the center point, A v e P o i n t ( x ¯ , y ¯ ) , and the average distance, A v e D i s t a n c e , of all the vertices of the vector map dataset to the center point.
x ¯ = ∑ i = 1 M x i
y ¯ = ∑ i = 1 M y i
A v e D i s t a n c e = ∑ i = 1 M x i − x ¯ 2 + y i − y ¯ 2 M
where M is the number of vertices of the vector geographic data.
Next, we design a circle. The center of the circle is A v e P o i n t and the radius of the circle is twice A v e D i s t a n c e . Divide this circle into N (the size of the watermark) rings by concentric circles.
Finally, we count the number of vertices in each ring and consider it a statistical property of the vector geographic data. This data is stored in a vector Z of length N .
Let A v e N u m s is the average number of vertices for all rings. Vector Z ∗ is calculated using the formula.
Z i ∗ = 0 ,   Z i < A v e N u m s 1 ,   Z i ≥ A v e N u m s
Zero-watermark I is computed by XOR between Z ∗ and copyright information W
I = Z ∗ ⊕ W

3.3.2. Zero-Watermark Extraction

To extract the zero-watermark, first, based on the protected vector geographic data, we obtain the zero-watermark I from the third-party authoritative verifier. Next, based on the length of I , the vector map data is divided into rings and then counts the number of vertices in each ring to calculate Z ∗ as in the zero-watermark embedding procedure. copyright information is calculated according to the formula:
W ′ = Z ∗ ⊕ I

3.4. Integrate Watermarking Algorithm to Protect Copyright

The algorithm consists of two processes, the embedding watermarking process and the watermark extraction process from the vector geographic data that need to be authenticated.

3.4.1. Watermark Embedding Steps

Step 1. Generate pseudo-random watermark from a string.
Step 2. Embedding copyrighted images into data using watermarking algorithm embedded in vertex coordinates.
Step 3. Create zero-watermark according to zero-watermark algorithm based on statistical characteristics and send it to a trusted third-party (authoritative verifier).

3.4.2. Steps to Extract Watermark to Prove Copyright.

Step 1. Extract the watermark according to the watermarking algorithm embedded in the vertex coordinates. If the copyright information is enough to prove copyright, the process is over.
Step 2. Extract the watermark according to the zero-watermark algorithm based on the statistical features, if the copyright information is enough to prove the copyright, the process is over.
On the contrary, the conclusion is that there is not enough evidence to determine copyright.

4. Experiments

4.1. Generate Pseudo-Random Meaningful Watermark

Using the string “CEID” as copyright information, we convert it into the big character representation as shown in Figure 1.
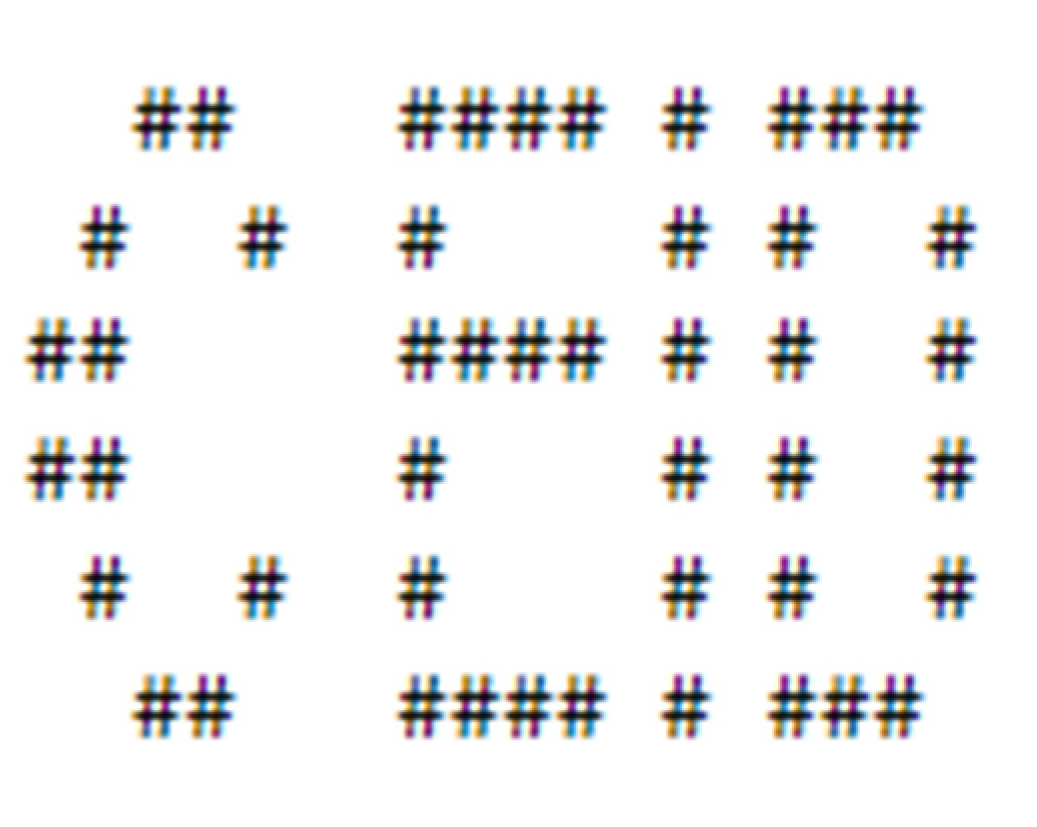
Preprints 79296 g006
Figure 6. Big character representation of CEID.
Figure 6. Big character representation of CEID.
Preprints 79296 g006
This big character representation is encoded in a matrix with 6 rows and 19 columns, Number -1 encodes the space and number 1 encodes the # character. The matrix is stored as a two-dimensional binary matrix 6 × 19 .
The matrix contains 47 bits value 1 and 67 bits value -1. To let the appearance of bits 1 and bits -1 be nearly the same, the padding technique is applied to this copyright image to let it have the nearly equal frequency of both 1 and -1 bits.
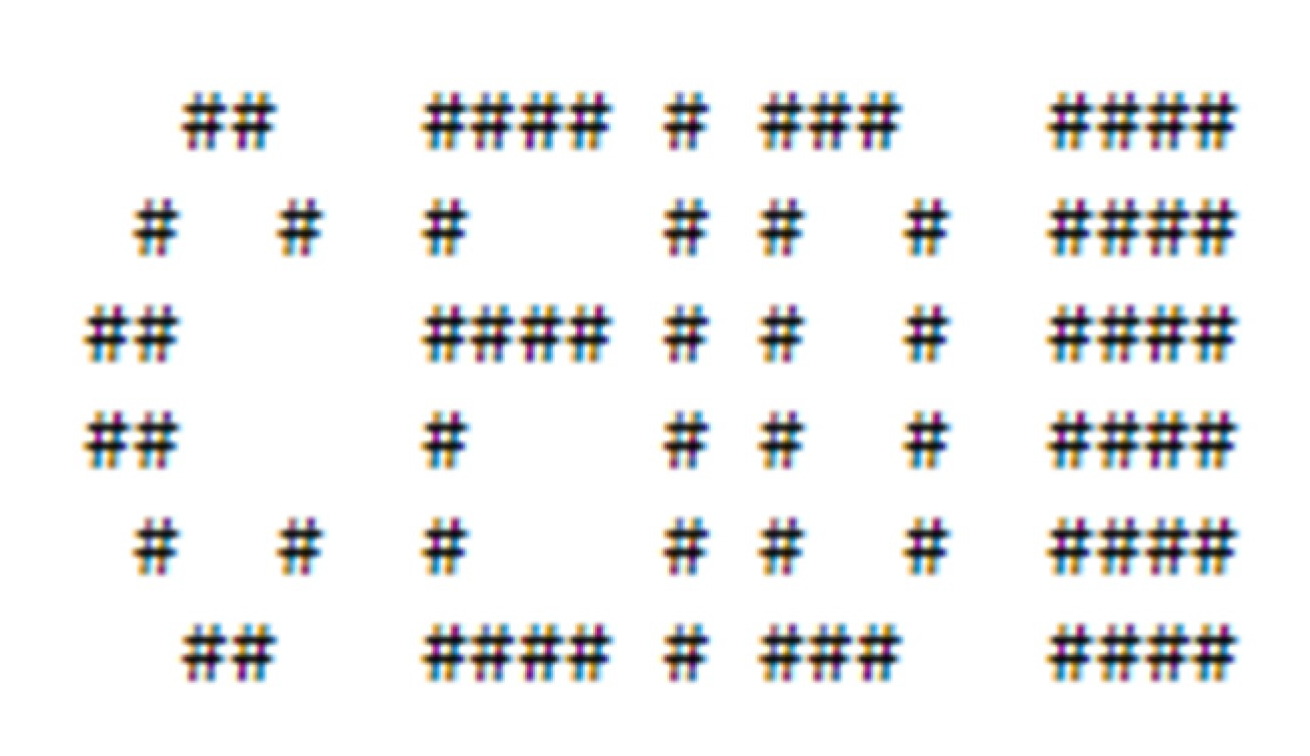
Preprints 79296 g007
Figure 7. Padding copyright image of CEID.
Figure 7. Padding copyright image of CEID.
Preprints 79296 g007
The size of the new copyright image is 6 × 24 and the frequencies of 1 and -1 bits in the padding copyright image now are 71 / 144 and 7 3 / 144 respectively.
Using Arnold’s transformation with 2 shuffled rounds, the shuffled copyright image or watermark seems to be a meaningless watermark. The watermark is shown in Figure 8.

4.2. Embedding and Detecting Watermark

We tested the algorithm on a number of vector geographic data belonging to twenty-five northern provinces of Vietnam including provincial administrative boundaries, main road network and population concentration points. The selection of data of all three types of points, polylines, and polygons is to test the algorithm’s ability to work with vector geographic data. We embedded the copyright information (called watermark) into the testing data to create layers of vector geographic data that have been embedded with copyright information with an error of 10 − 9 units (i.e., degree or meter depends on the map projection).

4.2.1. Experiment with a Polygon Vector Geographic Data

The polygon vector geographic data is the provincial administrative boundary data as shown in Figure 9.
This polygon data has 25 features (multi-polygons) with 39,797 vertices. So, the data has 79,594 coordinates, i.e., x and y coordinates. The copyright information is flattened into a 144-dimentional vector. Using our pseudo-uniformly distributed map, i.e., SipHash function, 79,594 coordinates are uniformly distributed into the watermark bit indexes, i.e., the set of { 1 ,   2 ,   … , 144 } . The number of coordinates embedding each watermark bit are shown in Table 1.
The distribution of coordinates for each watermark bit index is shown in Figure 10.
The watermark bits seem to be uniformly distributed into spatial vertices. Figure 11 shows a small area of the polygon data with vertices symbolized by the watermark bit index embedding in their x coordinates.
We tested the stability of the watermark against vertex deletion, feature deletion, and feature modification attacks by clipping the watermarked polygon data to keep a small area as shown in Figure 12.
Extracted watermark W ’ is extracted from clipped polygon data and then watermark W’’, normalized correlation coefficients ( c 1 ,   c 2 ) and thresholds ( μ 1 , μ 2 ) are calculated. The coefficient c 1 = 1.0 and the threshold μ 1 = 0.33333 ; the coefficient c 2 = 0.99210 and the threshold μ 2 = 0.04078 . The automatic watermark detection concludes that the data contains a watermark or copyright information. The watermark W ″ and the original watermark are applied to Arnold’s inverse transformation and shown side by side to verify visually (see Figure 13).

4.2.2. Experiment with Polyline Vector Geographic Data

The polyline vector geographic data is the major road network in twenty-five northern provinces of Vietnam as shown in Figure 14.
This polyline data has 241 features (multi-polylines) with 2,111 vertices. So, the data has 4,222 coordinates, i.e., x and y coordinates. The watermark is a 144-dimensional vector. Using our pseudo-uniformly distributed map, i.e., SipHash function, 4,222 coordinates are uniformly distributed into the watermark bit indexes, i.e., the set of { 1 ,   2 ,   … , 144 } . The number of coordinates embedding each watermark bit is shown in Table 2.
The distribution of coordinates for each watermark bit index is shown in Figure 15.
The watermark bits seem to be uniformly distributed into spatial vertices. Figure 16 shows a small area of the polygon data with vertices symbolized by the watermark bit index embedding in their x coordinates.
We tested the stability of the watermark against vertex deletion, feature deletion, and feature modification attacks by clipping the watermarked polyline data to keep a small area as shown in Figure 17.
Extracted watermark W ’ is extracted from clipped polygon data and then watermark W’’, normalized correlation coefficients ( c 1 ,   c 2 ) and thresholds ( μ 1 , μ 2 ) are calculated. The coefficient c 1 = 0.75 and the threshold μ 1 = 0.33333 ; the coefficient c 2 = 0.96648 and the threshold μ 2 = 0.14949 . The automatic watermark detection concludes that the data contains a watermark or copyright information. The watermark W ″ and the original watermark are applied to Arnold’s inverse transformation and shown side by side to verify visually (see Figure 18).

4.2.3. Experiment with Point Vector Geographic Data

The point vector geographic data is the population concentration places in twenty-five northern provinces of Vietnam as shown in Figure 19.
This point data has 341 features (points) and also 341 vertices. So, the data has 682 coordinates, i.e., x and y coordinates. The watermark is a 144-dimensional vector. Using our pseudo-uniformly distributed map, i.e., SipHash function, 682 coordinates are uniformly distributed into the watermark bit indexes, i.e., the set of { 1 ,   2 ,   … , 144 } . The number of coordinates embedding each watermark bit is shown in Table 3.
The distribution of coordinates for each watermark bit index is shown in Figure 20.
The watermark bits seem to be uniformly distributed into spatial vertices. Figure 21 shows a small area of the polygon data with vertices symbolized by the watermark bit index embedding in their x coordinates.
We tested the stability of the watermark against vertex deletion, feature deletion, and feature modification attacks by clipping the watermarked polyline data to keep a small area as shown in Figure 22.
Extracted watermark W ’ is extracted from clipped polygon data and then watermark W’’, normalized correlation coefficients ( c 1 ,   c 2 ) and thresholds ( μ 1 , μ 2 ) are calculated. The coefficient c 1 = 0.77778 and the threshold μ 1 = 0.33333 ; the coefficient c 2 = 1.0 and the threshold μ 2 = 0.18814 . The automatic watermark detection concludes that the data contains a watermark or copyright information. The watermark W ″ and the original watermark are applied to Arnold’s inverse transformation and shown side by side to verify visually (see Figure 23).

4.3. Embedding and Detecting Zero-Watermark

We also tested the algorithm’s resistance to coordinate system transformation attacks by embedding the watermark in all three data types (i.e., generating the zero-watermark) to generate the watermarked data. These watermarked data are then converted from the WGS-84 geographic coordinate system to the VN-2000 projected coordinate system. Applying the zero-watermark extraction procedure to these projected data, we get the results as shown in Figure 24.

5. Conclusions

The algorithm integrates two types of watermarks, including spatial domain watermark and zero-watermark, allowing the watermark to be more resistant to common attacks. By using meaningful watermarks and visual representation in the form of copyright images, the algorithm allows visual copyright identification from which there is more evidence for copyright verification than using only statistical characteristics.
The algorithm has been expressed into program code using Python language that can be easily implemented into real applications.

Acknowledgments

This article is the research result of the authors when implementing the project “Research and build technology to authenticate digital data of natural resources and environment with fee”, (code TNMT.2022.04.07).

References

  1. Wang, X.; Yan, H.; Zhang, L.; Zhang, X.; Li, P. An encryption algorithm for vector maps based on the Gaussian random and Haar transform. Journal of Spatial Science 2021, 1–16. [Google Scholar] [CrossRef]
  2. Mondal, B. Cryptographic image scrambling techniques. In Cryptographic and Information Security (pp. 37–65). CRC Press (2018).
  3. Wang, Y.; Yang, C.; Ren, N.; Zhu, C.; Rui, T.; Wang, D. An adaptive watermark detection algorithm for vector geographic data. KSII Transactions on Internet and Information Systems (TIIS) 2020, 14, 323–343. [Google Scholar] [CrossRef]
  4. Yan, H.; Zhang, L.; Yang, W. A normalization-based watermarking scheme for 2D vector map data. Earth Science Informatics 2017, 10, 471–481. [Google Scholar] [CrossRef]
  5. Wang, C.; Peng, Z.; Peng, Y.; Yu, L. Watermarking 2D vector maps on spatial topology domain. In 2009 International Conference on Multimedia Information Networking and Security (Vol. 2, pp. 71–74). IEEE (2009).
  6. Wang, Y.; Yang, C.; Zhu, C.; Ding, K. An efficient robust multiple watermarking algorithm for vector geographic data. Information 2018, 9, 296. [Google Scholar] [CrossRef]
  7. Voigt, M.; Busch, C. Feature-based watermarking of 2D vector data. In Security and Watermarking of Multimedia Contents V; SPIE, 2003; Volume 5020, pp. 359–366.
  8. Ren, N.; Wang, Q. S.; Zhu, C. Q. Selective authentication algorithm based on semi-fragile watermarking for vector geographical data. In 2014 22nd International Conference on Geoinformatics (pp. 1–6). IEEE (2014). [CrossRef]
  9. Wang, C.; Peng Z., Peng; Y., Yu; L., Wang, J.; Zhao, Q. Watermarking geographical data on spatial topological relations. Multimedia Tools and Applications 2012, 57, 67–89. [CrossRef]
  10. Zope-Chaudhari, S.; Venkatachalam, P.; Buddhiraju, K. M. Copyright protection of vector data using vector watermark. In 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS) (pp. 6110–6113). IEEE (2017).
  11. Wang, X.; Huang, D. J.; Zhang, Z. Y. A DCT-based blind watermarking algorithm for vector digital maps. In Advanced Materials Research (Vol. 179, pp. 1053–1058). Trans Tech Publications Ltd. (2011). [CrossRef]
  12. Liang, B.; Rong, J.; Wang, C. A vector maps watermarking algorithm based on dct domain. ISPRS Congr 2010, 38, 3. [Google Scholar]
  13. Hou, X.; Min, L.; Yang, H. A reversible watermarking scheme for vector maps based on multilevel histogram modification. Symmetry 2018, 10, 397. [Google Scholar] [CrossRef]
  14. Cao, L.; Men, C.; Ji, R. High-capacity reversible watermarking scheme of 2D-vector data. Signal, Image and Video Processing 2015, 9, 1387–1394. [Google Scholar] [CrossRef]
  15. Lin, Z. X.; Peng, F.; Long, M. A low-distortion reversible watermarking for 2D engineering graphics based on region nesting. IEEE Transactions on Information Forensics and Security 2018, 13, 2372–2382. [Google Scholar] [CrossRef]
  16. Qiu, Y. , Duan, H., Sun, J., & Gu, H. (2019). Rich-information reversible watermarking scheme of vector maps. Multimedia Tools and Applications 2019, 78, 24955–24977. [Google Scholar] [CrossRef]
  17. Qiu, Y.; Gu, H.; Sun, J. High-payload reversible watermarking scheme of vector maps. Multimedia Tools and Applications 2018, 77, 6385–6403. [Google Scholar] [CrossRef]
  18. Peng, F.; Yan, Z. J.; Long, M. A reversible watermarking for 2D vector map based on triple differences expansion and reversible contrast mapping. In International Conference on Security, Privacy and Anonymity in Computation, Communication and Storage (pp. 147–158). Springer, Cham (2017). [CrossRef]
  19. Ren, N.; Zhou, Q.; Zhu, C.; Zhu, A. X.; Chen, W. A Lossless Watermarking Algorithm Based on Line Pairs for Vector Data. Ieee Access 2020, 8, 156727–156739. [Google Scholar] [CrossRef]
  20. Zhou, Q.; Ren, N.; Zhu, C.; Tong, D. Storage feature-based watermarking algorithm with coordinate values preservation for vector line data. KSII Transactions on Internet and Information Systems (TIIS) 2018, 12, 3475–3496. [Google Scholar] [CrossRef]
  21. Li, A. B.; Zhu, A. X. Copyright authentication of digital vector maps based on spatial autocorrelation indices. Earth Science Informatics 2019, 12, 629–639. [Google Scholar] [CrossRef]
  22. Rani, A.; Bhullar, A. K.; Dangwal, D.; Kumar, S. A zero-watermarking scheme using discrete wavelet transform. Procedia Computer Science 2015, 70, 603–609. [Google Scholar] [CrossRef]
  23. Liu, Y.; Yang, F.; Gao, K.; Dong, W.; Song, J. A zero-watermarking scheme with embedding timestamp in vector maps for Big Data computing. Cluster Computing 2017, 20, 3667–3675. [Google Scholar] [CrossRef]
  24. Peng, Y. , & Yue, M. (2015). A zero-watermarking scheme for vector map based on feature vertex distance ratio. Journal of Electrical and Computer Engineering 2015, 2015, 35. [Google Scholar] [CrossRef]
  25. Xun, W. A. N. G.; Huang, D.; Zhang, Z. A robust zero-watermarking algorithm for vector digital maps based on statistical characteristics. Softw. Appl. Econ. Anal. Bus. Manag 2012, 7, 2349. [Google Scholar] [CrossRef]
  26. Zhou, Q.; Zhu, C.; Ren, N.; Chen, W.; Gong, W. Zero Watermarking Algorithm for Vector Geographic Data Based on the Number of Neighboring Features. Symmetry 2021, 13, 208. [Google Scholar] [CrossRef]
  27. Moulin, P.; Koetter, R. Data-hiding codes. Proceedings of the IEEE 2005, 93, 2083–2126. [Google Scholar] [CrossRef]
Preprints 79296 g001
Figure 1. The procedure to embed watermark for copyright protection.
Figure 1. The procedure to embed watermark for copyright protection.
Preprints 79296 g001
Preprints 79296 g002
Figure 2. The procedure to verify the copyright.
Figure 2. The procedure to verify the copyright.
Preprints 79296 g002
Preprints 79296 g003
Figure 3. Watermark “CEID” and “HA NOI”.
Figure 3. Watermark “CEID” and “HA NOI”.
Preprints 79296 g003
Preprints 79296 g004
Figure 4. Watermark “CEID” and “HA NOI” with roughly equal number of bits 1 and -1.
Figure 4. Watermark “CEID” and “HA NOI” with roughly equal number of bits 1 and -1.
Preprints 79296 g004
Preprints 79296 g005
Figure 5. Example of Short, pseudo-random, and meaningful watermarks.
Figure 5. Example of Short, pseudo-random, and meaningful watermarks.
Preprints 79296 g005
Preprints 79296 g008
Figure 8. The watermark contains copyright information of CEID.
Figure 8. The watermark contains copyright information of CEID.
Preprints 79296 g008
Preprints 79296 g009
Figure 9. The provincial administrative boundaries of twenty-five northern provinces of Vietnam.
Figure 9. The provincial administrative boundaries of twenty-five northern provinces of Vietnam.
Preprints 79296 g009
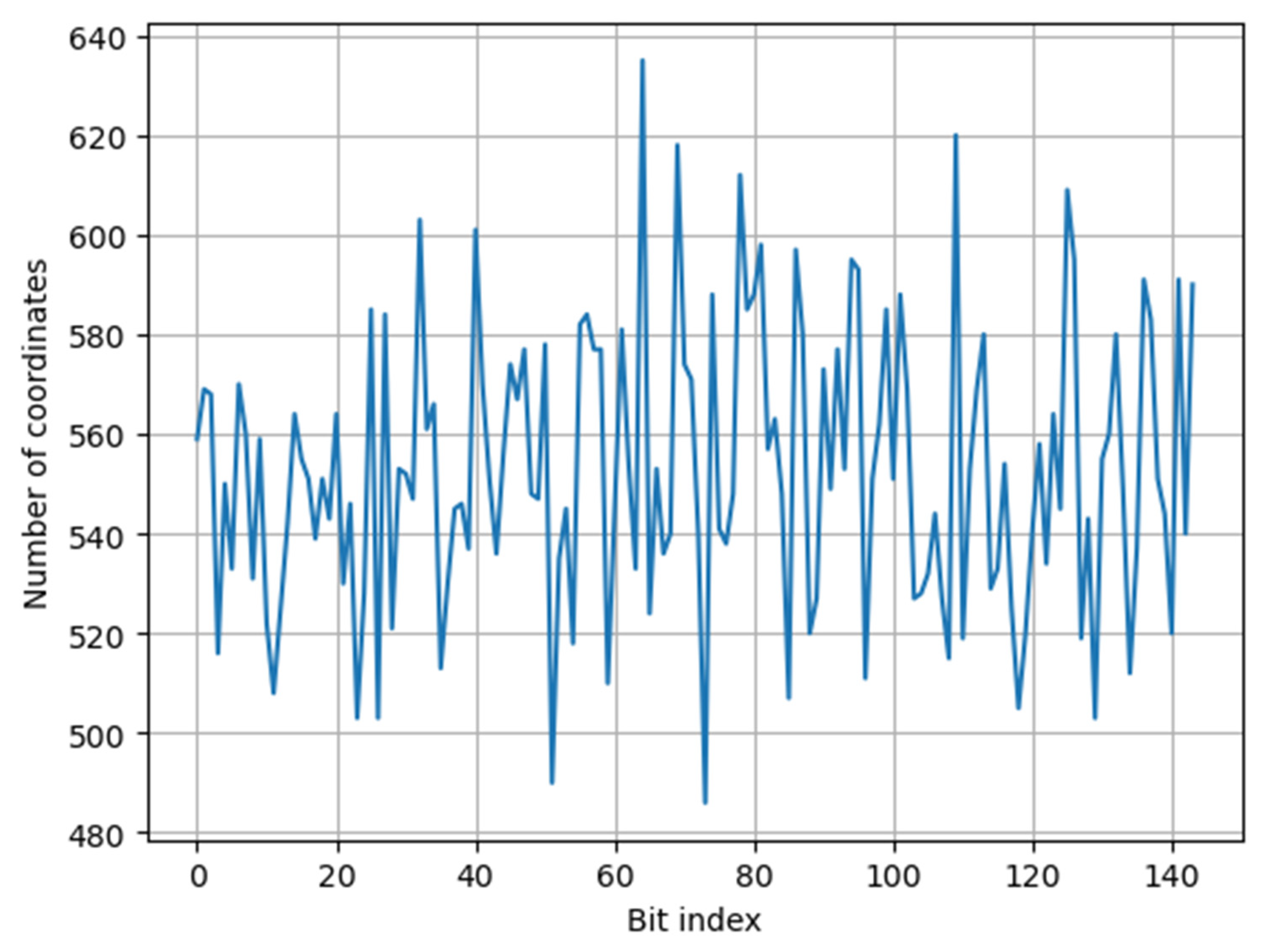
Preprints 79296 g010
Figure 10. The distribution of coordinates for each watermark bit index.
Figure 10. The distribution of coordinates for each watermark bit index.
Preprints 79296 g010
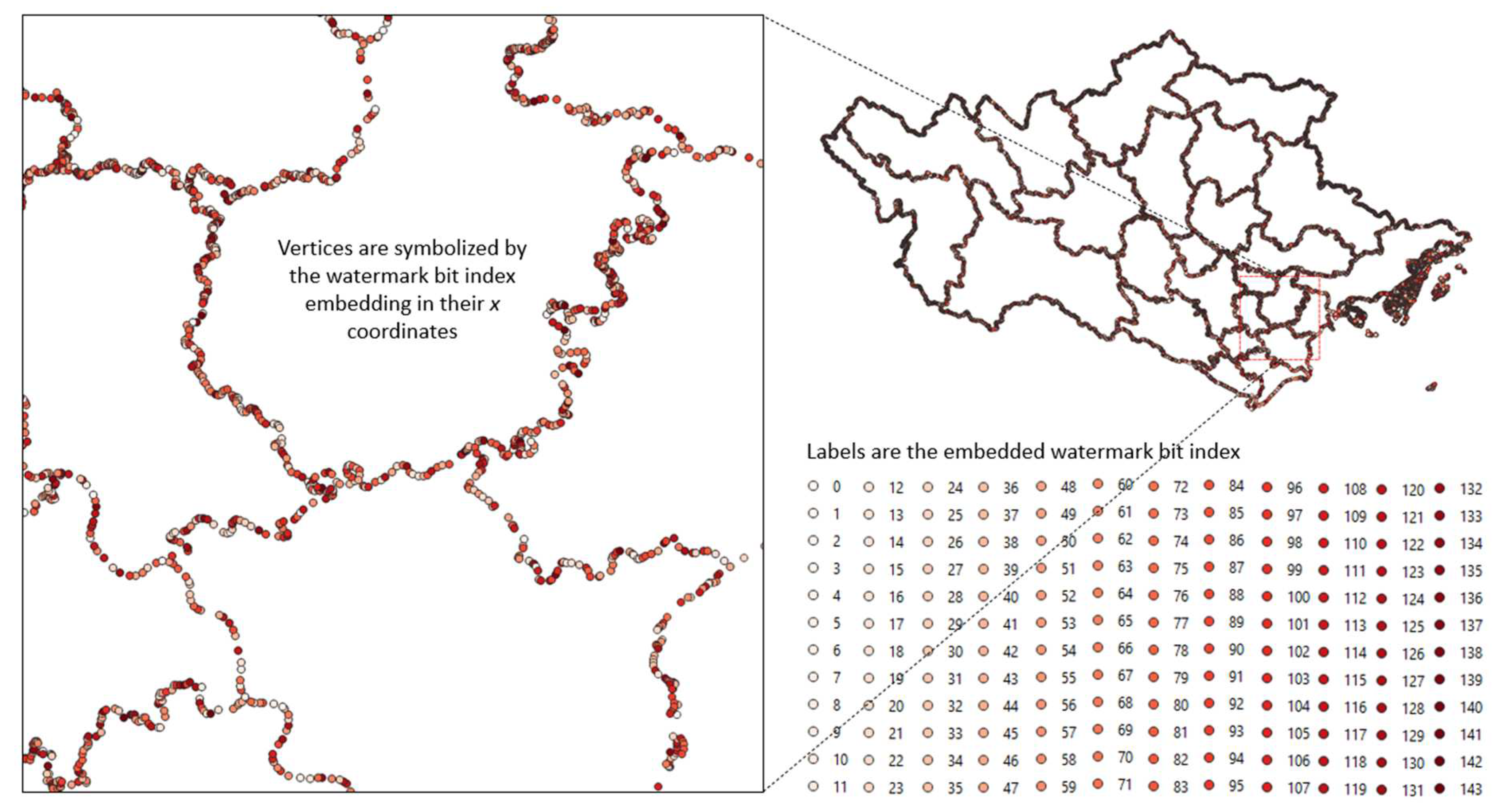
Preprints 79296 g011
Figure 11. Uniform spatial distribution of watermark bits to coordinates.
Figure 11. Uniform spatial distribution of watermark bits to coordinates.
Preprints 79296 g011
Preprints 79296 g012
Figure 12. A clipped area of watermarked polygon data.
Figure 12. A clipped area of watermarked polygon data.
Preprints 79296 g012
Preprints 79296 g013
Figure 13. (a) original watermark, and (b) watermark W ″ extracted from the data.
Figure 13. (a) original watermark, and (b) watermark W ″ extracted from the data.
Preprints 79296 g013
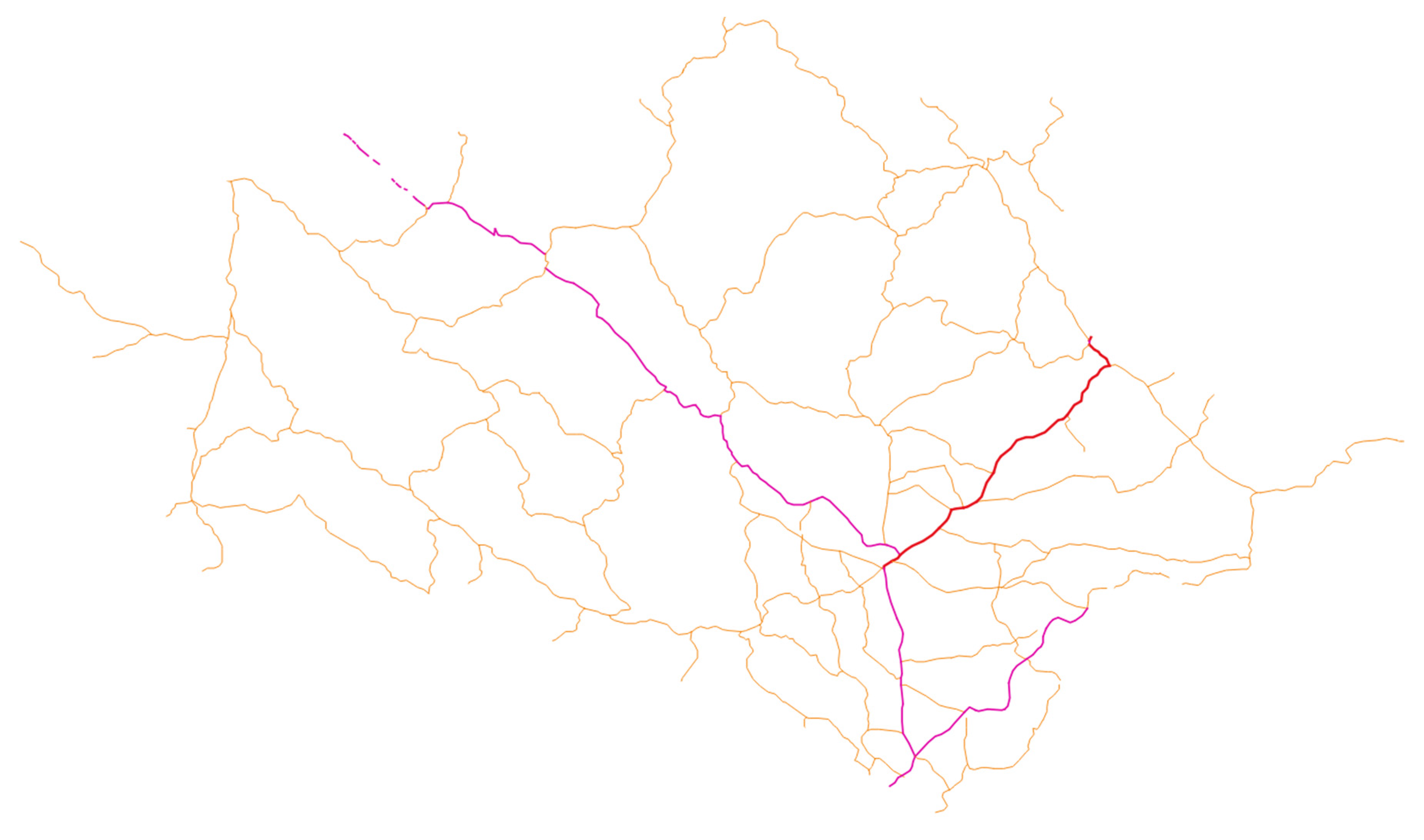
Preprints 79296 g014
Figure 14. The major road network of twenty-five northern provinces of Vietnam.
Figure 14. The major road network of twenty-five northern provinces of Vietnam.
Preprints 79296 g014
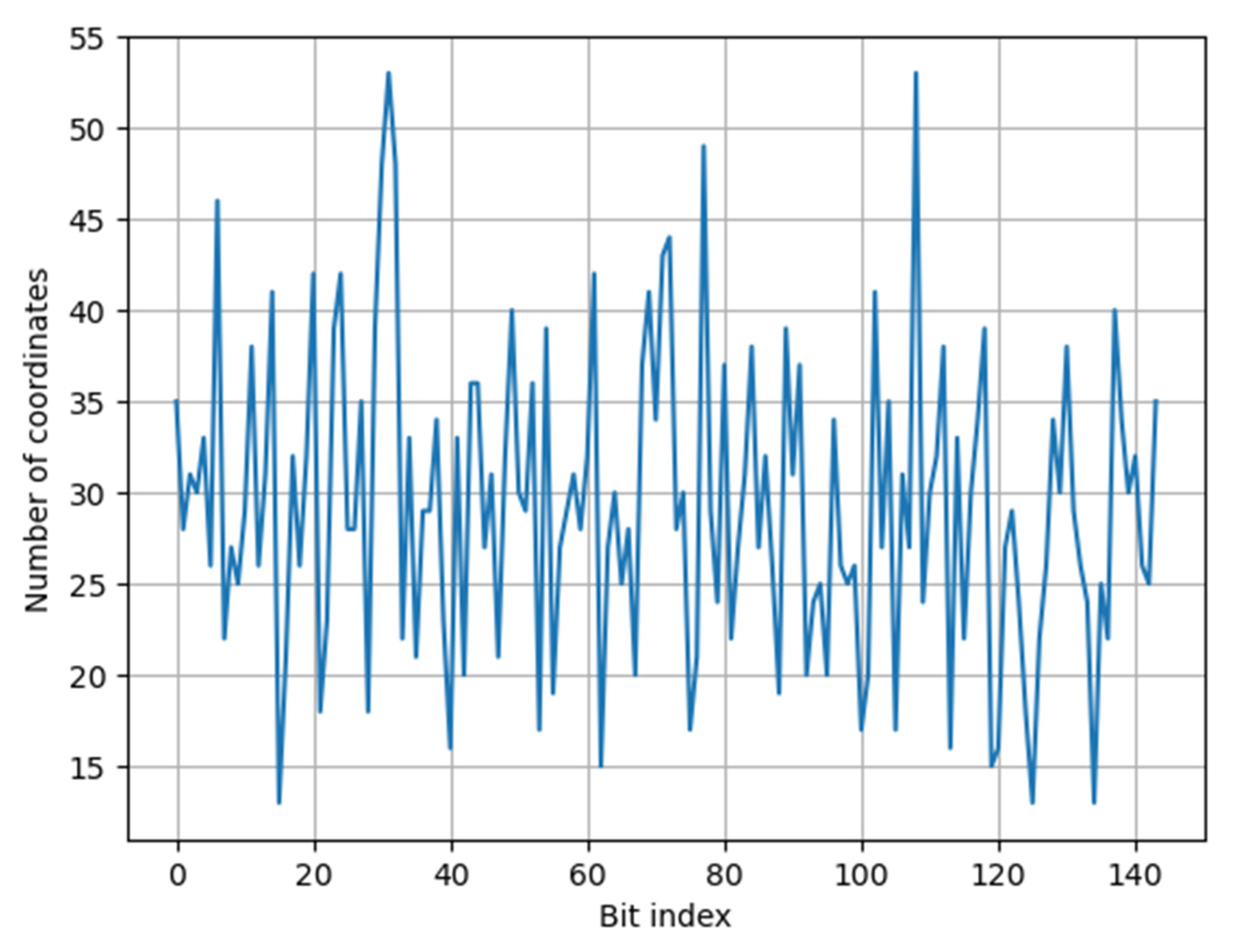
Preprints 79296 g015
Figure 15. The distribution of coordinates of polyline data for each watermark bit index.
Figure 15. The distribution of coordinates of polyline data for each watermark bit index.
Preprints 79296 g015
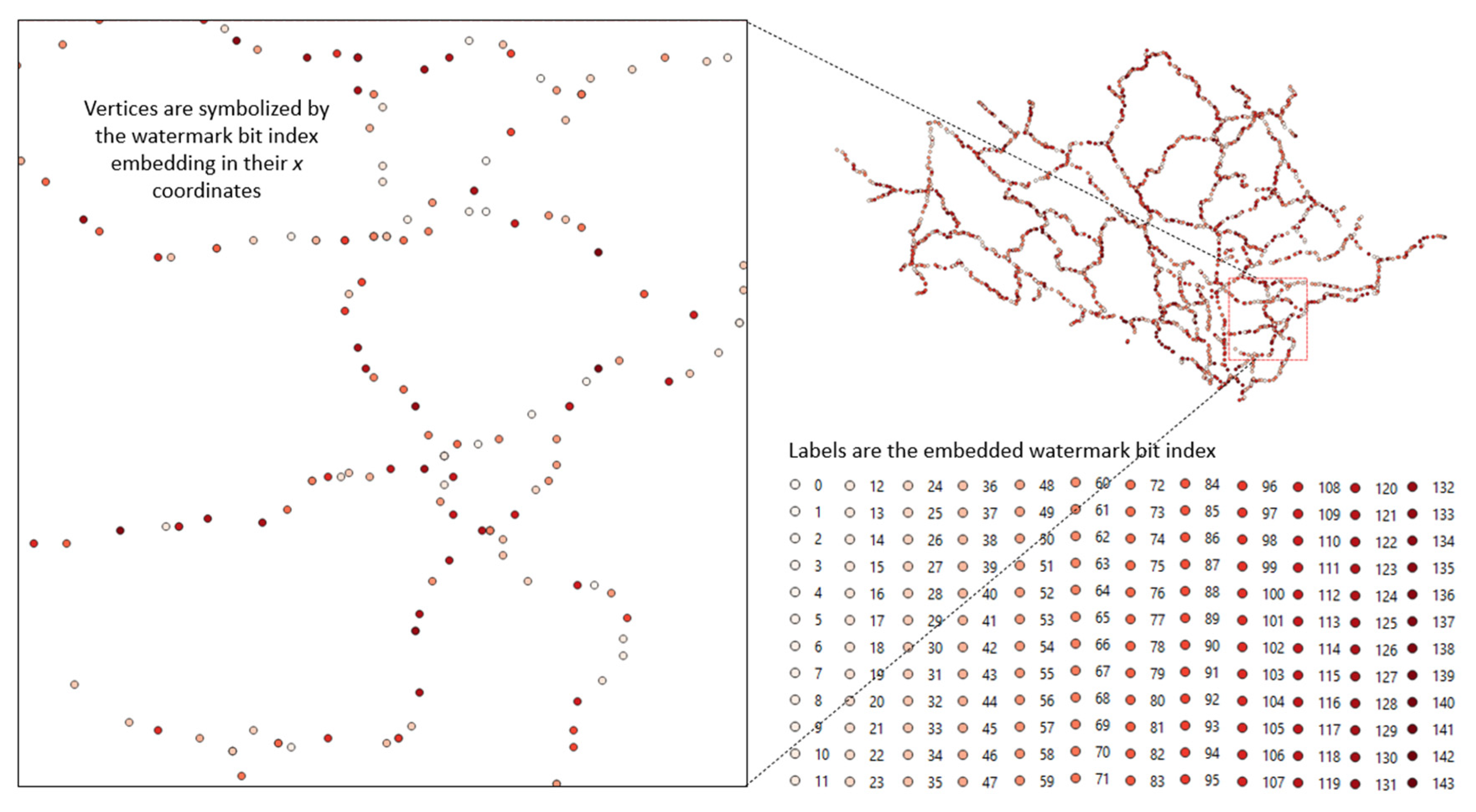
Preprints 79296 g016
Figure 16. Uniform spatial distribution of watermark bits to coordinates of the polyline data.
Figure 16. Uniform spatial distribution of watermark bits to coordinates of the polyline data.
Preprints 79296 g016
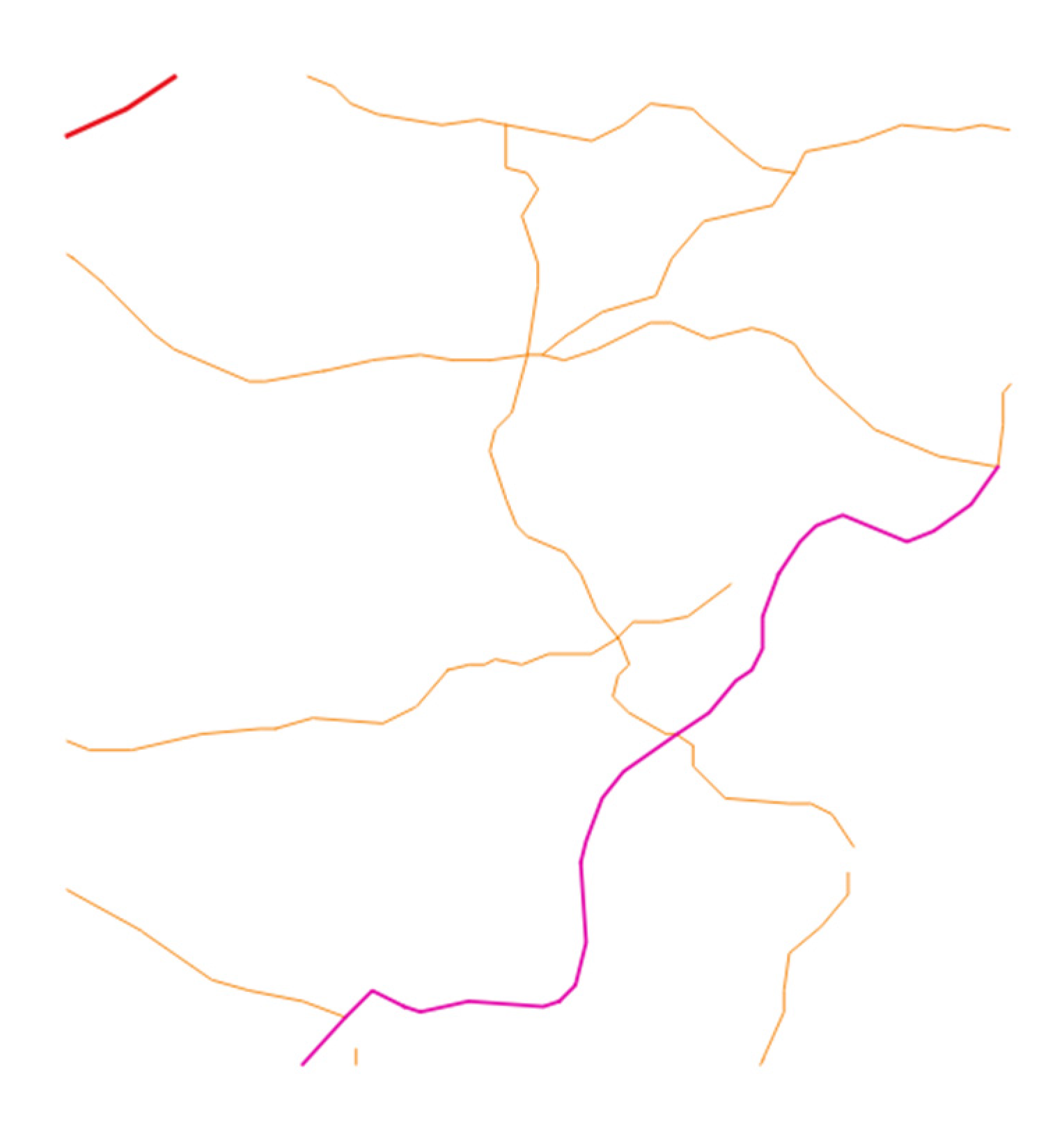
Preprints 79296 g017
Figure 17. A clipped area of watermarked polyline data.
Figure 17. A clipped area of watermarked polyline data.
Preprints 79296 g017
Preprints 79296 g018
Figure 18. (a) original watermark, and (b) watermark W ″ extracted from the polyline data.
Figure 18. (a) original watermark, and (b) watermark W ″ extracted from the polyline data.
Preprints 79296 g018
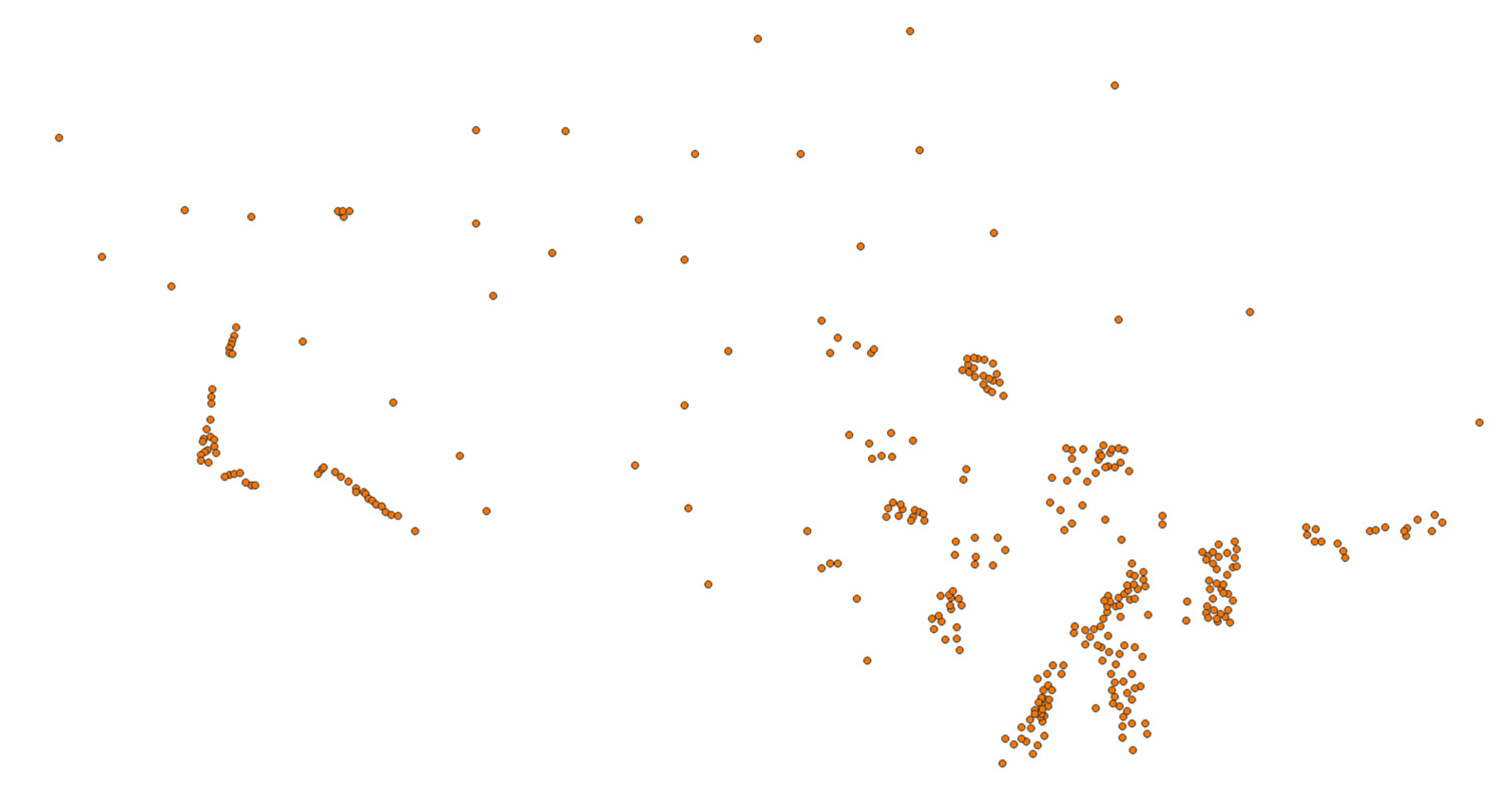
Preprints 79296 g019
Figure 19. The population concentration places of twenty-five northern provinces of Vietnam.
Figure 19. The population concentration places of twenty-five northern provinces of Vietnam.
Preprints 79296 g019
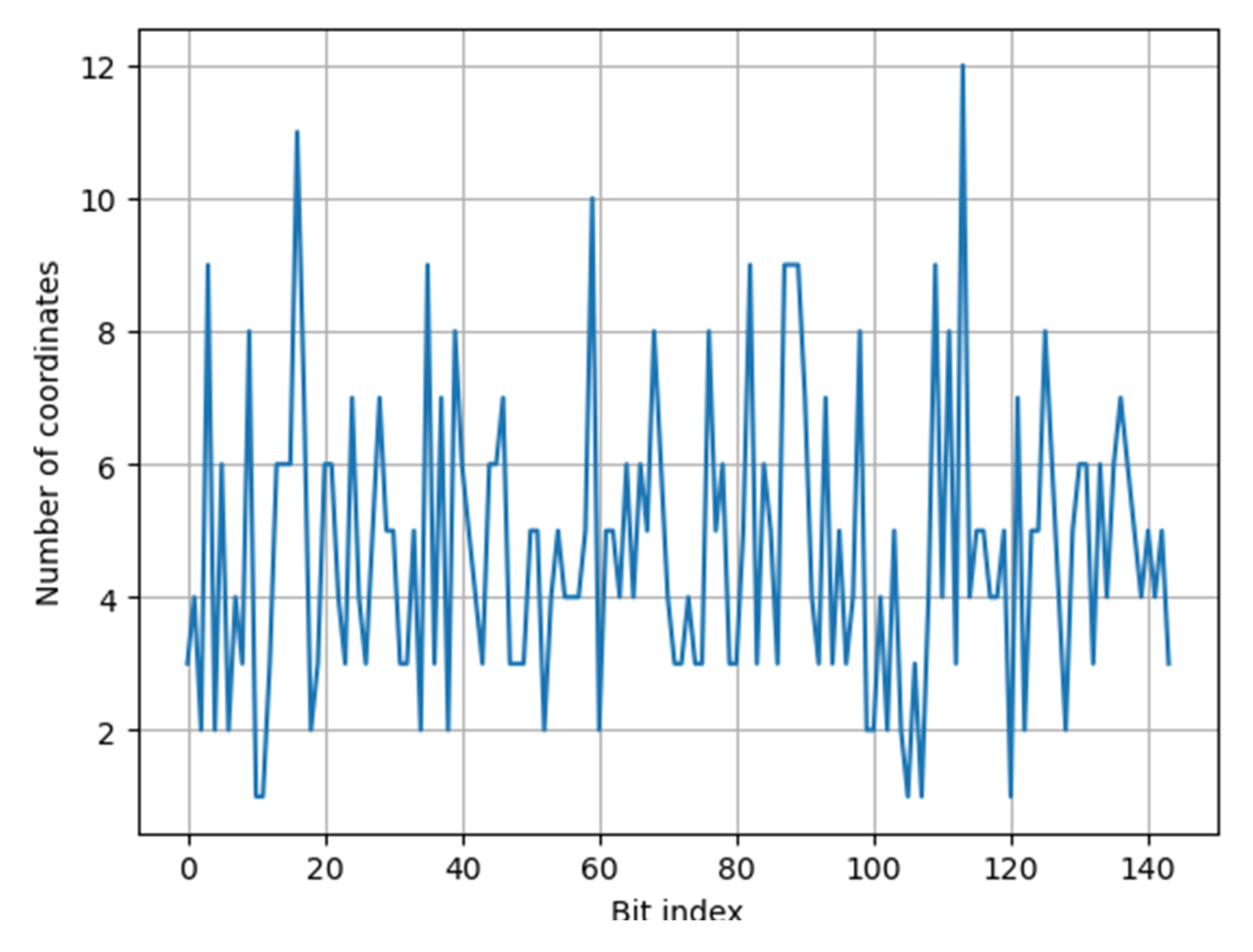
Preprints 79296 g020
Figure 20. The distribution of coordinates of point data for each watermark bit index.
Figure 20. The distribution of coordinates of point data for each watermark bit index.
Preprints 79296 g020
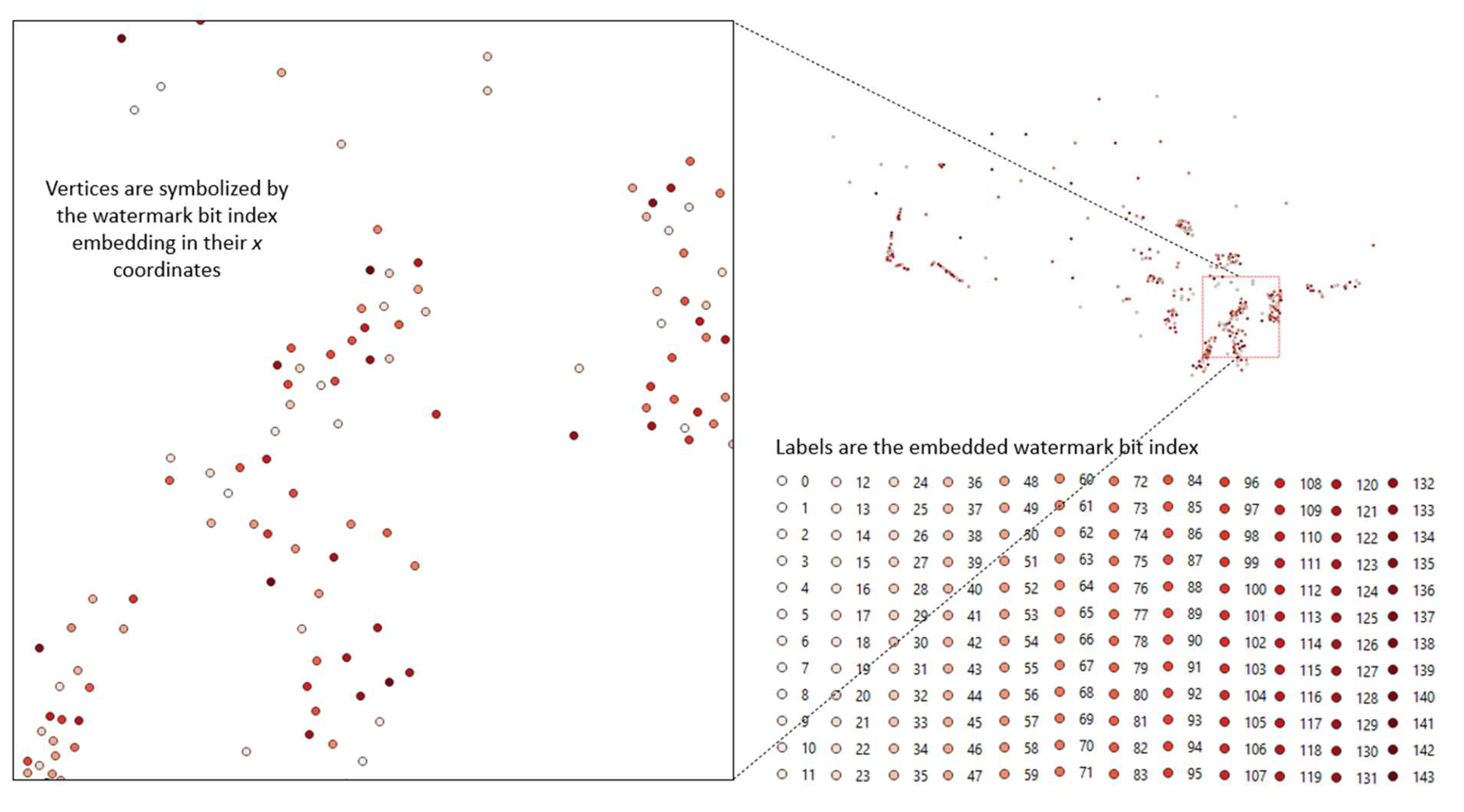
Preprints 79296 g021
Figure 21. Uniform spatial distribution of watermark bits to coordinates of the point data.
Figure 21. Uniform spatial distribution of watermark bits to coordinates of the point data.
Preprints 79296 g021
Preprints 79296 g022
Figure 22. A clipped area of watermarked point data.
Figure 22. A clipped area of watermarked point data.
Preprints 79296 g022
Preprints 79296 g023
Figure 23. (a) original watermark, and (b) watermark W ″ extracted from the point data.
Figure 23. (a) original watermark, and (b) watermark W ″ extracted from the point data.
Preprints 79296 g023
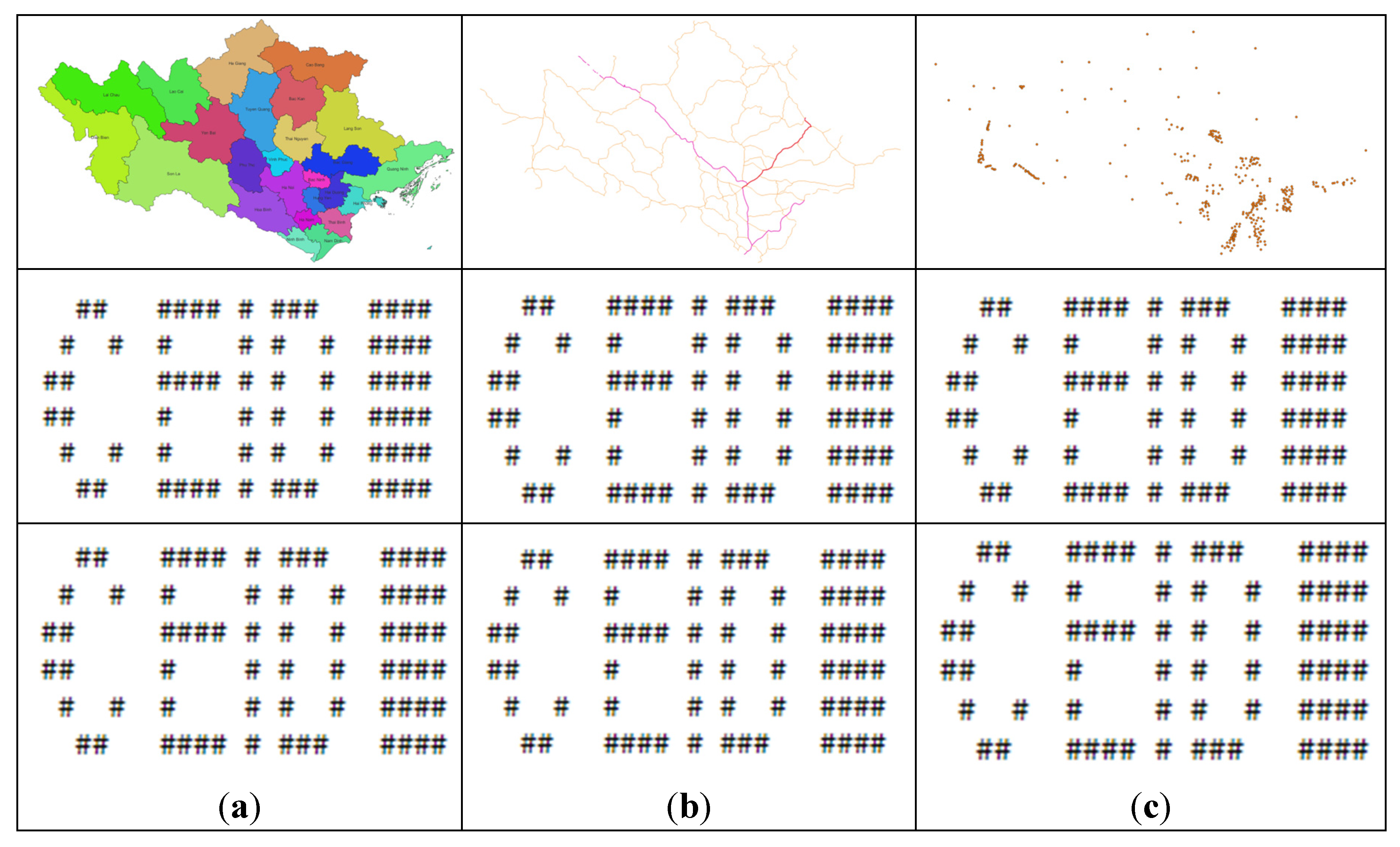
Preprints 79296 g024
Figure 24. The rows in columns (a), (b), (c) are projected data, original copyright information, and information extracted from the data.
Figure 24. The rows in columns (a), (b), (c) are projected data, original copyright information, and information extracted from the data.
Preprints 79296 g024
Table 1. The number of coordinates embedding each watermark bit.
Table 1. The number of coordinates embedding each watermark bit.
Bit index 0 1 2 3 4 5 6 7 8 9 10 11
No 559 569 568 516 550 533 570 560 531 559 522 508
Bit index 12 13 14 15 16 17 18 19 20 21 22 23
No 525 542 564 555 551 539 551 543 564 530 546 503
Bit index 24 25 26 27 28 29 30 31 32 33 34 35
No 528 585 503 584 521 553 552 547 603 561 566 513
Bit index 36 37 38 39 40 41 42 43 44 45 46 47
No 530 545 546 537 601 570 551 536 556 574 567 577
Bit index 48 49 50 51 52 53 54 55 56 57 58 59
No 548 547 578 490 535 545 518 582 584 577 577 510
Bit index 60 61 62 63 64 65 66 67 68 69 70 71
No 546 581 554 533 635 524 553 536 540 618 574 571
Bit index 72 73 74 75 76 77 78 79 80 81 82 83
No 540 486 588 541 538 548 612 585 588 598 557 563
Bit index 84 85 86 87 88 89 90 91 92 93 94 95
No 548 507 597 580 520 527 573 549 577 553 595 593
Bit index 96 97 98 99 100 101 102 103 104 105 106 107
No 511 551 562 585 551 588 569 527 528 532 544 527
Bit index 108 109 110 111 112 113 114 115 116 117 118 119
No 515 620 519 553 569 580 529 533 554 525 505 520
Bit index 120 121 122 123 124 125 126 127 128 129 130 131
No 541 558 534 564 545 609 595 519 543 503 555 560
Bit index 132 133 134 135 136 137 138 139 140 141 142 143
No 580 549 512 537 591 583 551 544 520 591 540 590
Table 2. The number of coordinates of polyline data embedding each watermark bit.
Table 2. The number of coordinates of polyline data embedding each watermark bit.
Bit index 0 1 2 3 4 5 6 7 8 9 10 11
No 35 28 31 30 33 26 46 22 27 25 29 38
Bit index 12 13 14 15 16 17 18 19 20 21 22 23
No 26 31 41 13 21 32 26 32 42 18 23 39
Bit index 24 25 26 27 28 29 30 31 32 33 34 35
No 42 28 28 35 18 39 48 53 48 22 33 21
Bit index 36 37 38 39 40 41 42 43 44 45 46 47
No 29 29 34 23 16 33 20 36 36 27 31 21
Bit index 48 49 50 51 52 53 54 55 56 57 58 59
No 32 40 30 29 36 17 39 19 27 29 31 28
Bit index 60 61 62 63 64 65 66 67 68 69 70 71
No 32 42 15 27 30 25 28 20 37 41 34 43
Bit index 72 73 74 75 76 77 78 79 80 81 82 83
No 44 28 30 17 21 49 29 24 37 22 27 31
Bit index 84 85 86 87 88 89 90 91 92 93 94 95
No 38 27 32 26 19 39 31 37 20 24 25 20
Bit index 96 97 98 99 100 101 102 103 104 105 106 107
No 34 26 25 26 17 20 41 27 35 17 31 27
Bit index 108 109 110 111 112 113 114 115 116 117 118 119
No 53 24 30 32 38 16 33 22 30 34 39 15
Bit index 120 121 122 123 124 125 126 127 128 129 130 131
No 16 27 29 24 18 13 22 26 34 30 38 29
Bit index 132 133 134 135 136 137 138 139 140 141 142 143
No 26 24 13 25 22 40 34 30 32 26 25 35
Table 3. The number of coordinates of point data embedding each watermark bit.
Table 3. The number of coordinates of point data embedding each watermark bit.
Bit index 0 1 2 3 4 5 6 7 8 9 10 11
No 3 4 2 9 2 6 2 4 3 8 1 1
Bit index 12 13 14 15 16 17 18 19 20 21 22 23
No 3 6 6 6 11 7 2 3 6 6 4 3
Bit index 24 25 26 27 28 29 30 31 32 33 34 35
No 7 4 3 5 7 5 5 3 3 5 2 9
Bit index 36 37 38 39 40 41 42 43 44 45 46 47
No 3 7 2 8 6 5 4 3 6 6 7 3
Bit index 48 49 50 51 52 53 54 55 56 57 58 59
No 3 3 5 5 2 4 5 4 4 4 5 10
Bit index 60 61 62 63 64 65 66 67 68 69 70 71
No 2 5 5 4 6 4 6 5 8 6 4 3
Bit index 72 73 74 75 76 77 78 79 80 81 82 83
No 3 4 3 3 8 5 6 3 3 5 9 3
Bit index 84 85 86 87 88 89 90 91 92 93 94 95
No 6 5 3 9 9 9 7 4 3 7 3 5
Bit index 96 97 98 99 100 101 102 103 104 105 106 107
No 3 4 8 2 2 4 2 5 2 1 3 1
Bit index 108 109 110 111 112 113 114 115 116 117 118 119
No 4 9 4 8 3 12 4 5 5 4 4 5
Bit index 120 121 122 123 124 125 126 127 128 129 130 131
No 1 7 2 5 5 8 6 4 2 5 6 6
Bit index 132 133 134 135 136 137 138 139 140 141 142 143
No 3 6 4 6 7 6 5 4 5 4 5 3
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated