A Conclusive Model-Fit Current-Voltage Characteristics Curves with Kink Effects

Preprint

Article

A Conclusive Model-Fit Current-Voltage Characteristics Curves with Kink Effects

Altmetrics

Downloads

131

Views

Comments

A peer-reviewed article of this preprint also exists.

Hsin-Chia Yang^*,Sung-Ching Chi

This version is not peer-reviewed

Submitted:

09 July 2023

Posted:

13 July 2023

You are already at the latest version

Alerts

Abstract

Current-voltage characteristics curves of NFinFET are presented and are fitted with the modi-fied current-voltage (I-V) formulas, where the modified term in the triode region is demon-strated to be indispensable. In the as-known I-V formula, important parameters need determin-ing to make both the measured data and the fitting data as close as possible. Those parameters include kN (associated with the sizes of the transistor and mobility), (associated with Early Voltage), and Vth (the threshold voltage). The differences between the measured data and the fit-ting data vary as the applied source-drain bias, proving that the mobility of the carriers is not consistently constant. On the other hand, a modified formula, called kink effect factor, is nega-tively or positively added simulating solitary heat waves, which disturb the propagation of car-riers and thus influence the Source-Drain current (IDS). The new statistical standard deviations () are then found to be effectively suppressed as the kink effect is taken into account.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Transistors fabricated in semiconductor industry successfully achieve various desired functions, including signal processing, data calculating, and decision-making. All the functions are associated with memory transferring at a comparable speed. So the size of transistor continues to shrink not mainly for the benefits of increasing number of integrated circuit (IC). The speed of IC’s somehow becomes the pursuing goal. Three concerns appear manifested in a sense. They are outrageous loss of controllability, unavoidable heat, and un-expected limitation of photolithograph. The controllability is closely related to leakage current due to proportional dimension shrinkage even though some adopted prevention including halo implant or pocket implant has been done at the planar device level. In addition, the promotion of electrical performance at the same scale using compressive or tensile stress technique is seriously taken into account as well. Unfortunately, channel lengths below tens of nanometers seem not to work out any more as desired no matter what has been taken. Instead of planar bulk silicon substrate, there comes the 3-D structural fin-like field effect transistor (FinFET), which make use of slim strip of epitaxial silicon as body substrate wrapped by insulator-separated gate poly-silicon. The strip of channel substrate gets depleted as the gate poly-silicon is applied with a bias. This bias causes the depletion region of the substrate strip impressively and effectively to block the leakage current in between Source and Drain. As for the generated heat, it is basically linked to the equivalent resistors, whose resistance is actually proportional to the length of the resistor and inversely dependent of the area of the cross section. The resistance of decreasing dimension soars up making the increasing Ohm’s heat tremendously degrade its electrical performance and thus competitively loss leading status. Therefore, the conduction of heat dominates the whole process flow and material choosing. Copper is thus preferred for its higher conductivity. The expose of ultra-violet ray suggests diffraction immunity, which is identified as the use of shorter wavelength, improvement of refraction angle (refractive index, n), and subtle design and combination of masks. Traditional optics and modern optics are both utilized or designed to resolve diffraction issues.

Furthermore, the electrical performances for any transistor have to be reliable and repeatable. Models are thus proposed to address the electrical performances and are able to fit the measured characteristics curves. And all the circuit designs, including analog and digital, rely solely on the established model. Research has to be paid to understand the electrical data. The most commonly used formulas have been posed for over many decades, and they surely reduce the tremendous work on the designing level. Therefore, the current-versus-voltage characteristic curves showing electrical performance of transistors are necessarily parameter-extracted in the model. Nevertheless, ones are still intrigued to know if the “modified” conventional formula is applicable for fitting repeated characteristic curves. [1,2,3,4,5,6,7,8,9,10,11,12,13,14] In the model, useful parameters are supposed to be constants even though they need interpreting. Some evidences in this paper do show some limitation. For example, the mobility is no longer reasonably treated as constant as the measured data are compared to the modified conventional formula.

Furthermore, one thing that causes attention is about carriers traveling in the crystallized silicon, which is diamond structure. The crystal thermally vibrates at certain temperature causing trouble to the carriers. As the carriers speed up, they confront more obstacles. More obstacles generate more heat and more friction, which may slow down the carriers, especially in the triode region. For example in our daily life, the rain falls at the almost constant terminal speed near the ground addressing the similar situation. The lattice interacts with the carriers and is energetically quantized as phonons, which is analogous to photons in electrical magnetic field. The analogy becomes good referencing facts that are readily explored.

In this study, the as-measured (I_DS, V_DS) data are referred to the transistors fabricated by 3-D FinFET structure process. The “modified” conventional I-V characteristic curve formulas in Equation (1) with λ (the inverse of the absolute value of Early voltage, V_A) is deliberately introduced in the triode region for V_DS is less than (V_GS-V_th), whereas Equation (2) is kept unchanged for the saturation regime. Delta deviation in Equation (3) for the whole fitting is suggested and effectively reduced the discrepancy between the fitting data and the measured data. In addition, a solution to a non-linear differential equation, called the sine-Gordon equation, is first proposed for addressing a solitary wave, which is some kind of phonons coming from quantized sound. The solution is proven to be Gaussian and is introduced to further reduce the delta deviation in the electrical characteristic curves, which is really encouraging.

2. Preparation of as Measured Data and Fitting

2.1. Preparation

The as measured (I_DS, V_DS) data is obtained through the probe station on the FinFET technology, which uses epitaxial silicon grown on silicon wafer and an dry-etched floated island “I” with two head ends as Source and Drain and the channel in between two ends. Dry oxidation of 14 angstroms on the slim sides followed by 4000 angstrom poly-silicon as Gate functions the transistor looking like a fin after dry-etching. The measured data and the self-generated data coming from the modified conventional formulas in Equations (1) and (2) as followed in the next paragraph are merged into one graph for comparison of fitting.

2.2. Fitting I_DS-V_DS and I_DS-V_GS

For MOSFET devices, the commonly conventional formulas are modified as follows:

\begin{array}{l} I_{D S} (T r i o d e) = k_{N} [(V_{G S} - V_{t h}) V_{D S} - \frac{V_{D S}^{2}}{2}] (1 + λ V_{D S}) \\ \begin{matrix}  \end{matrix} \begin{matrix}  \end{matrix} - α \exp [- β {(V_{D S} - χ)}^{2}] \end{array}

(1)

a n d

\begin{array}{l} I_{D S} (S a t u r a t i o n) = k_{N} \frac{{(V_{G S} - V_{t h})}^{2}}{2} (1 + λ V_{D S}) \\ \begin{matrix}  \end{matrix} \begin{matrix}  \end{matrix} - α \exp [- β {(V_{D S} - χ .)}^{2}] \end{array}

(2)

\begin{array}{l} w h e r e^{} \\ k_{N} = \frac{C_{o x} W μ}{L_{o}} \\ a n d \\ λ = \frac{1}{|V_{A}|} \end{array}

C_ox is the gate capacitance, W and L_o are the width and the length of the transistor, and μ is the mobility of carriers. Also V_A means Early Voltage, α is the kink effective coefficient, and β and χ are the corresponding speed-associated values.

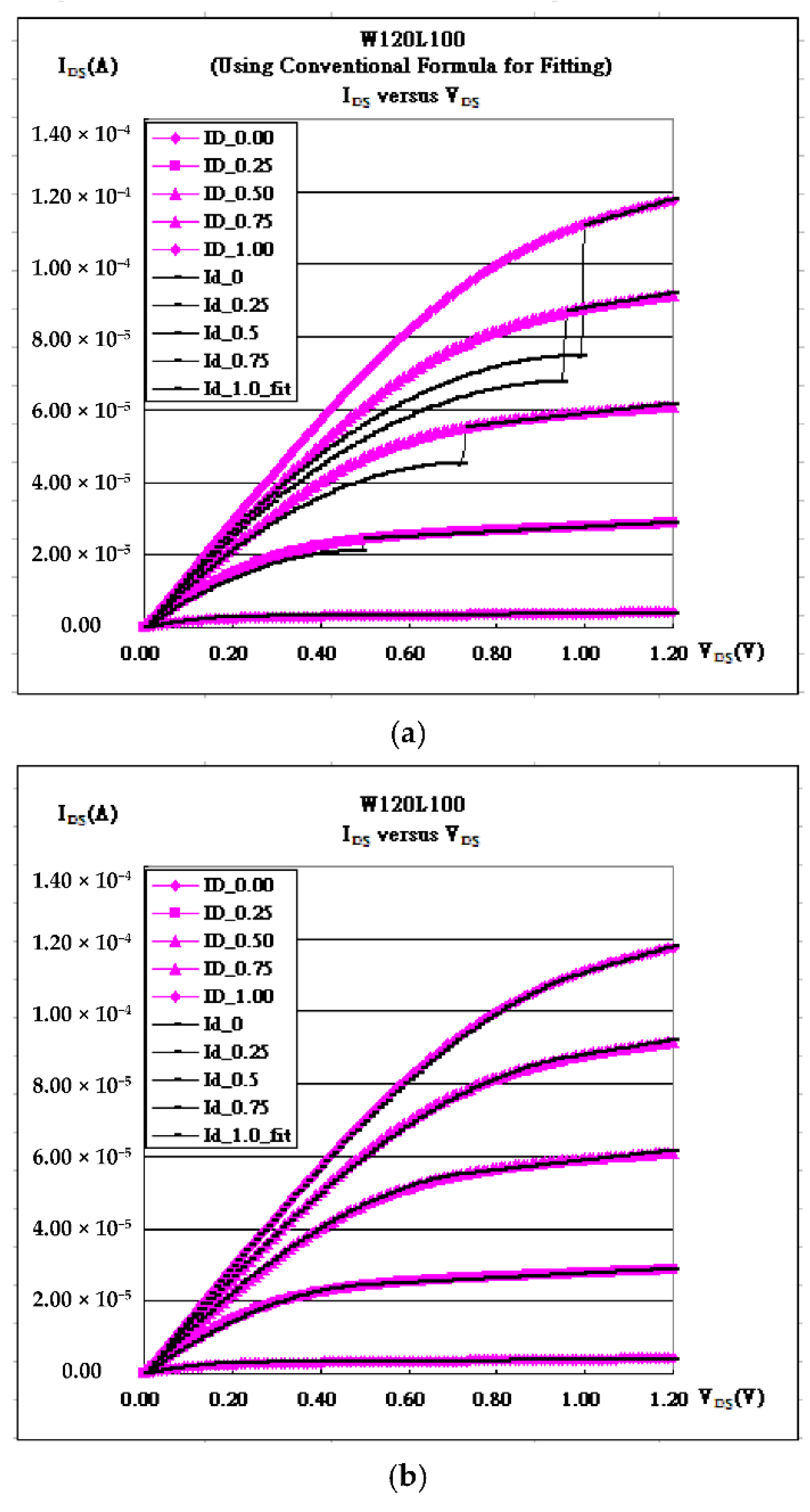
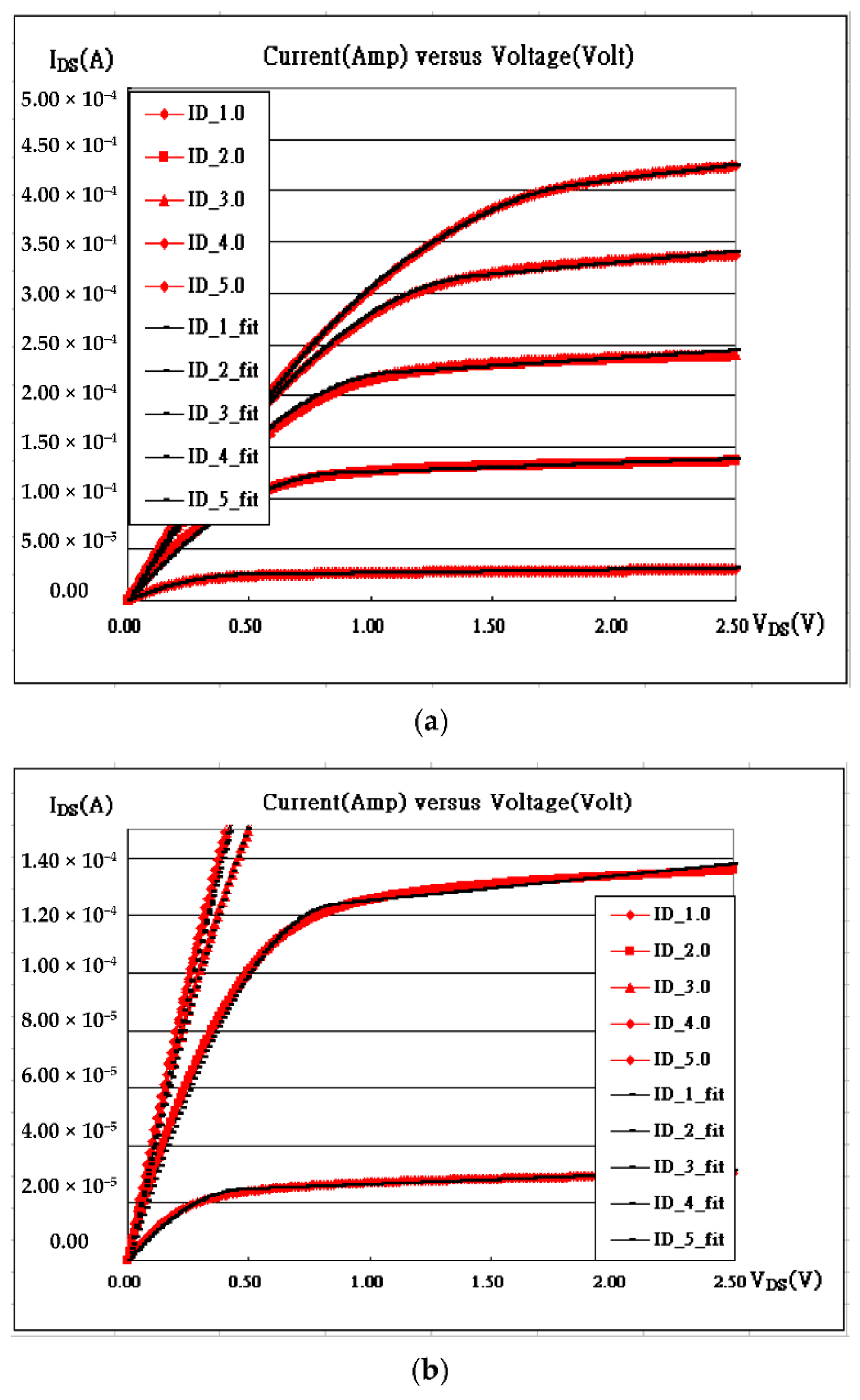
For one thing, it is worth mentioning that the term (1+λV_DS) in Equation (1) is necessarily added because, with or without it, the differences on fitting are demonstrated as in Figure 1.

2.3. The Delta Deviation

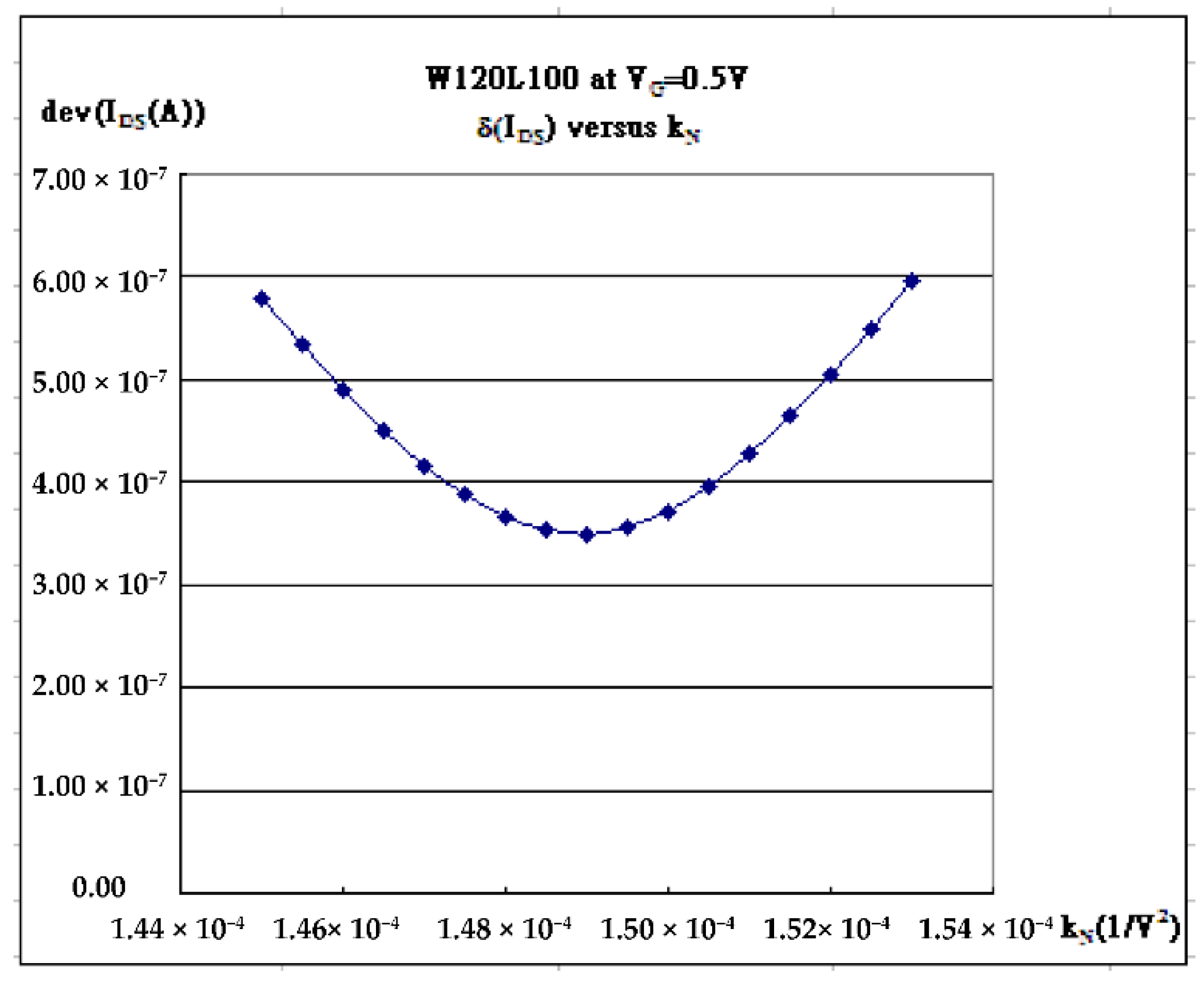
The fitting data by Equations (1) and (2) are deliberately used to fit the as-measured I-V characteristic curves. Those parameters are mainly determined predominantly according to the minimum delta (δ) in the following Equation (3):

δ = \sqrt{\frac{\sum_{i = 1}^{N} {(I_{f i t t i n g} - I_{m e a s u r e d})}_{i}^{2}}{N}}

(3)

For example, the final value of k_N is determined to be 1.49×10^-4(1/V²) through the smiling curve as the minimum delta is located in Figure 2. [15,16]

2.4. The kink effect

The non-linear differential equation addressing a moving electron scalar field in the strongly inversed layer is presented as follows:

\frac{\partial^{2} φ_{e}}{c^{2} \partial t^{2}} - \frac{\partial^{2} φ_{e}}{\partial x^{2}} + a \sin b φ_{e} = 0

(4)

which is named as sine-Gordon equation. [17] The moving electrons accelerated by the electrical field confront phonons with group velocity c of thousands of meters per second in the lattice [18]. The space-time variables are adjusted with respect to the referencing frame as follows:

φ_{e} (x, t) = f_{e} (x - v t) = f_{e} (ξ)

Equation (4) thus reduces to the following form:

\frac{\partial^{2} φ_{e}}{\partial ξ^{2}} - a {(1 - \frac{v^{2}}{c^{2}})}^{- 1} \sin b φ_{e} = 0

(5)

The non-linear solution of Equation (5) is expressed as

f_{e} (ξ) = \frac{4}{b} \arctan e^{\pm γ ξ}

(6)

\begin{array}{l} w h e r e \\ γ = {(1 - \frac{v^{2}}{c^{2}})}^{- 1 / 2} \end{array}

The speed of the electron, closely associated with current density (J=nev), is proportional to the derivative of the wave function with respect to ξ.

\begin{array}{l} \frac{d f (ξ)}{d ξ} = \frac{(4 / b) γ e^{γ ξ}}{1 + e^{2 γ ξ}} = \frac{(4 / b) γ}{e^{γ ξ} + e^{- γ ξ}} \\ \to (2 / b) γ (1 - \frac{γ^{2} ξ^{2}}{2}) \to (2 / b) γ \exp [- \frac{γ^{2} ξ^{2}}{2}] \end{array}

(7)

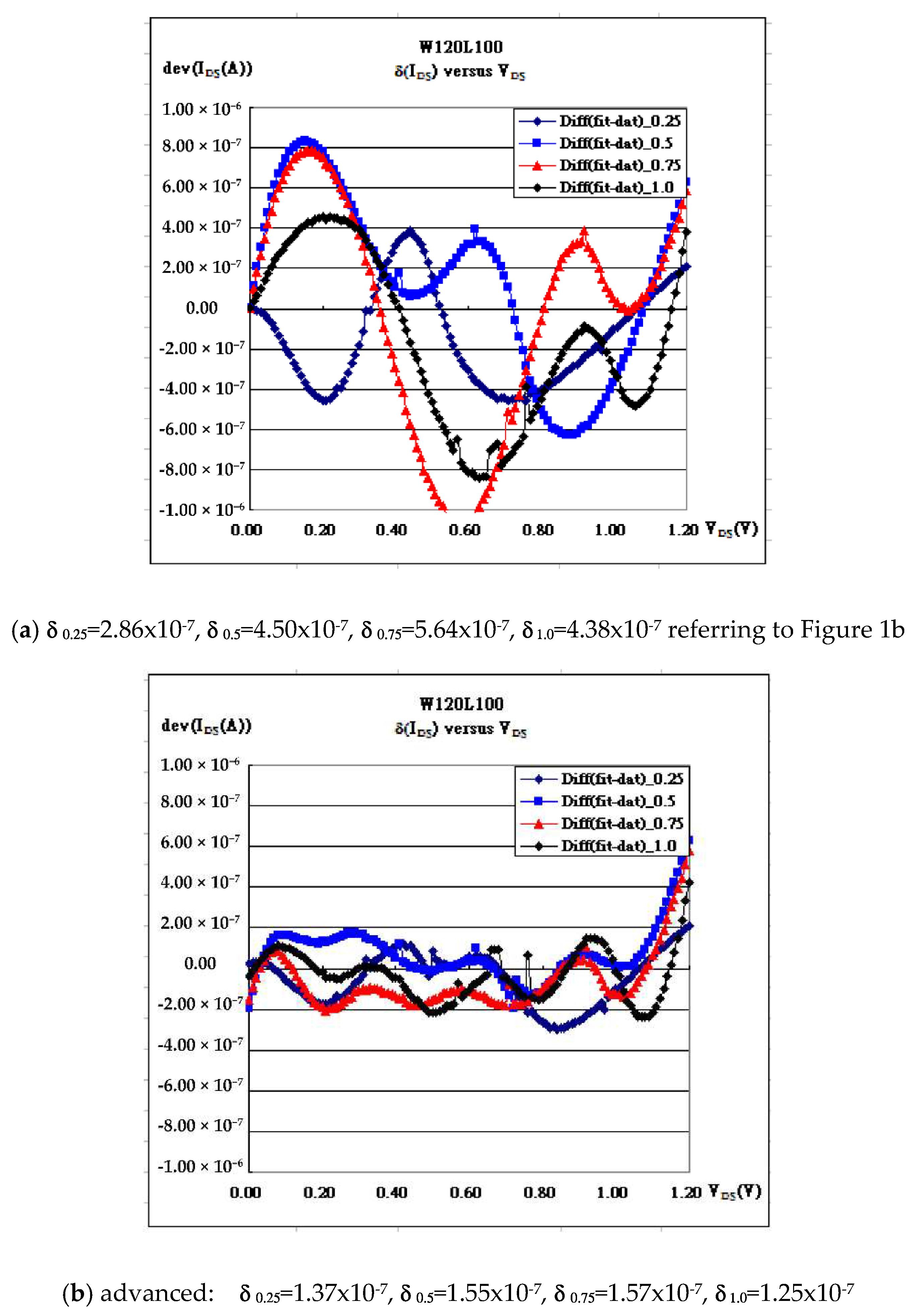
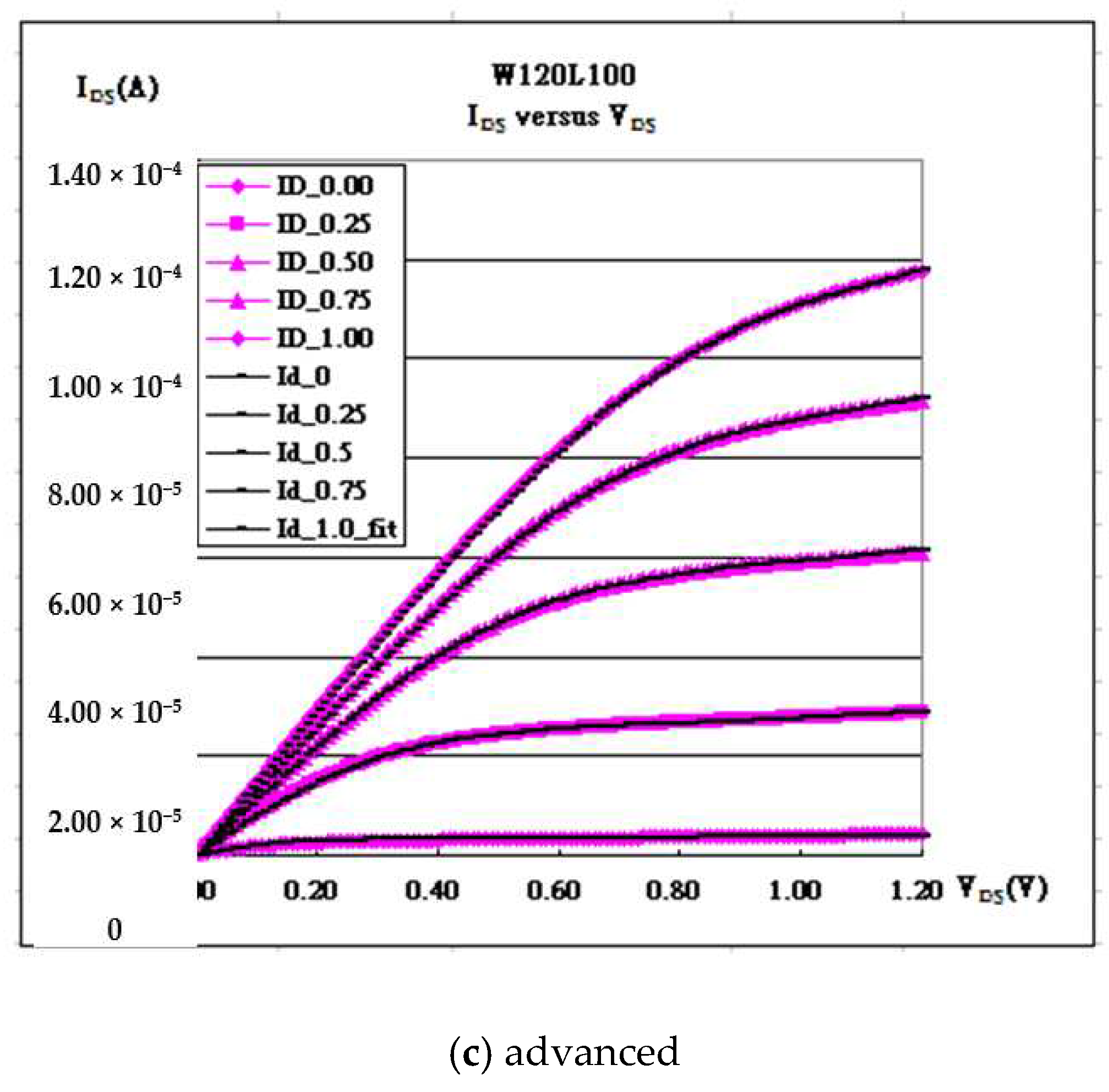
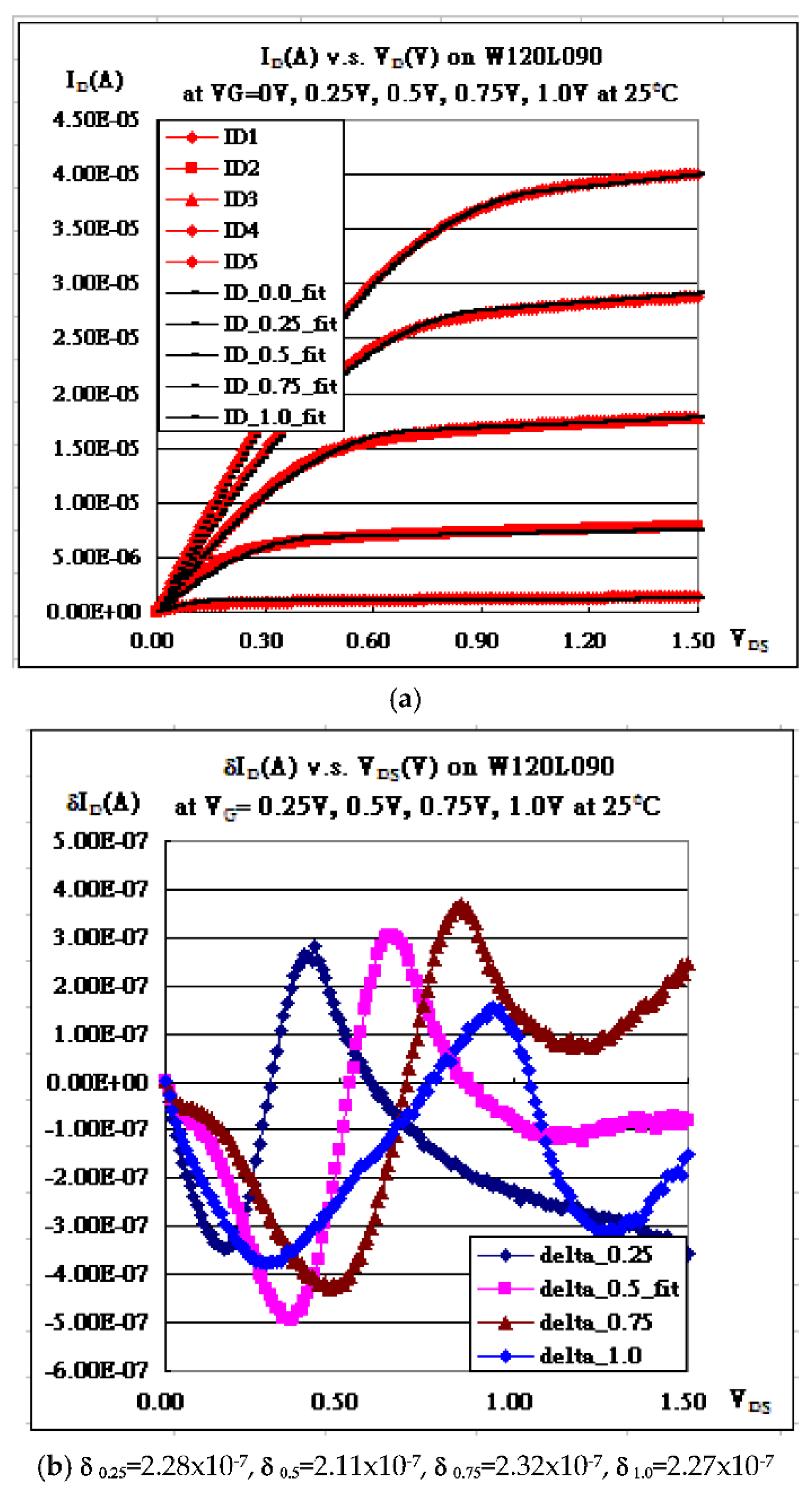
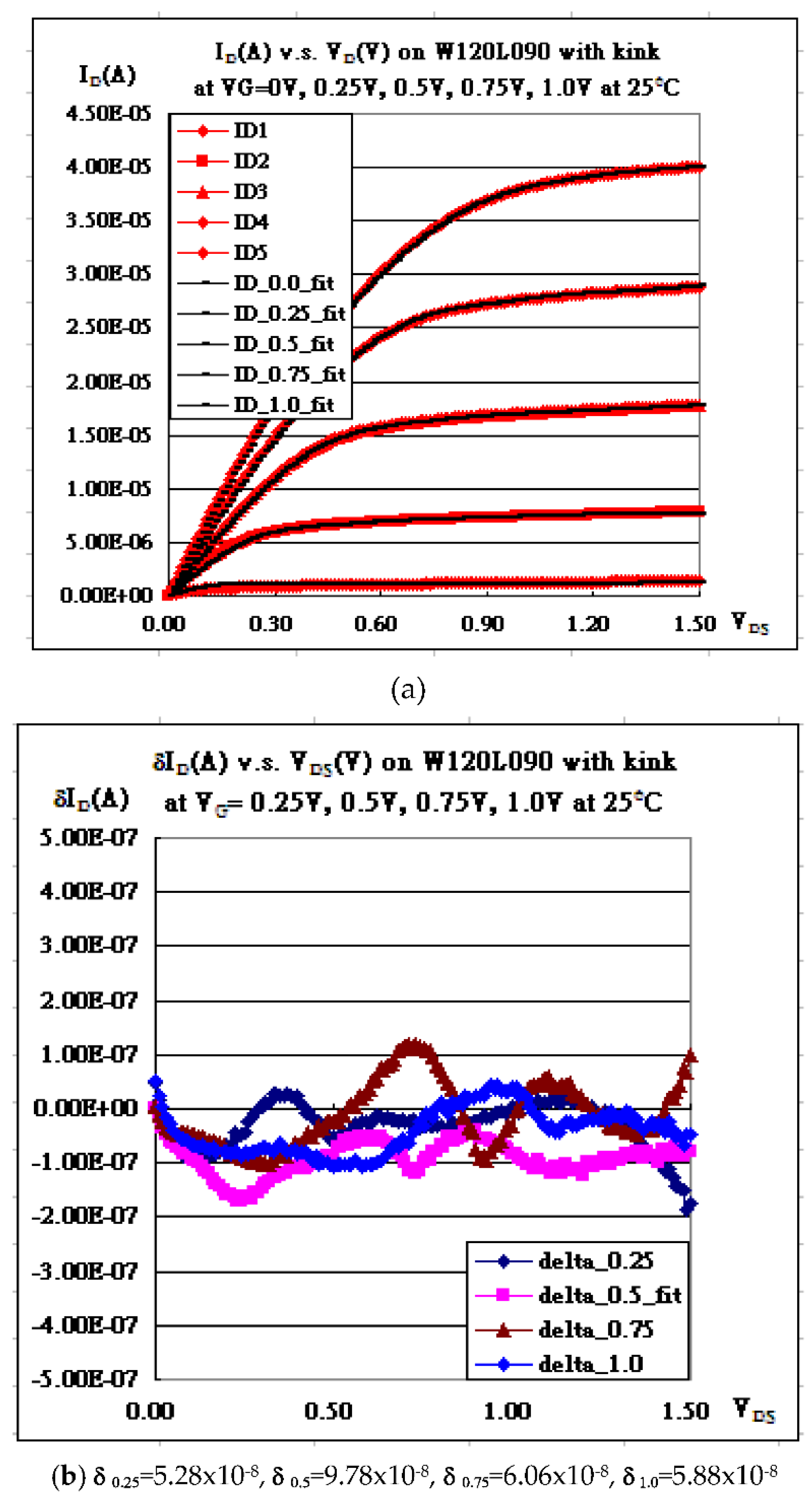
Therefore, the fine variations of I_DS in Figure 3a are to be easier modified by using the above Gaussian form, followed by Figure 3b with less minimum delta. The final fitting curves are then as shown in Figure 3c.

3. Application

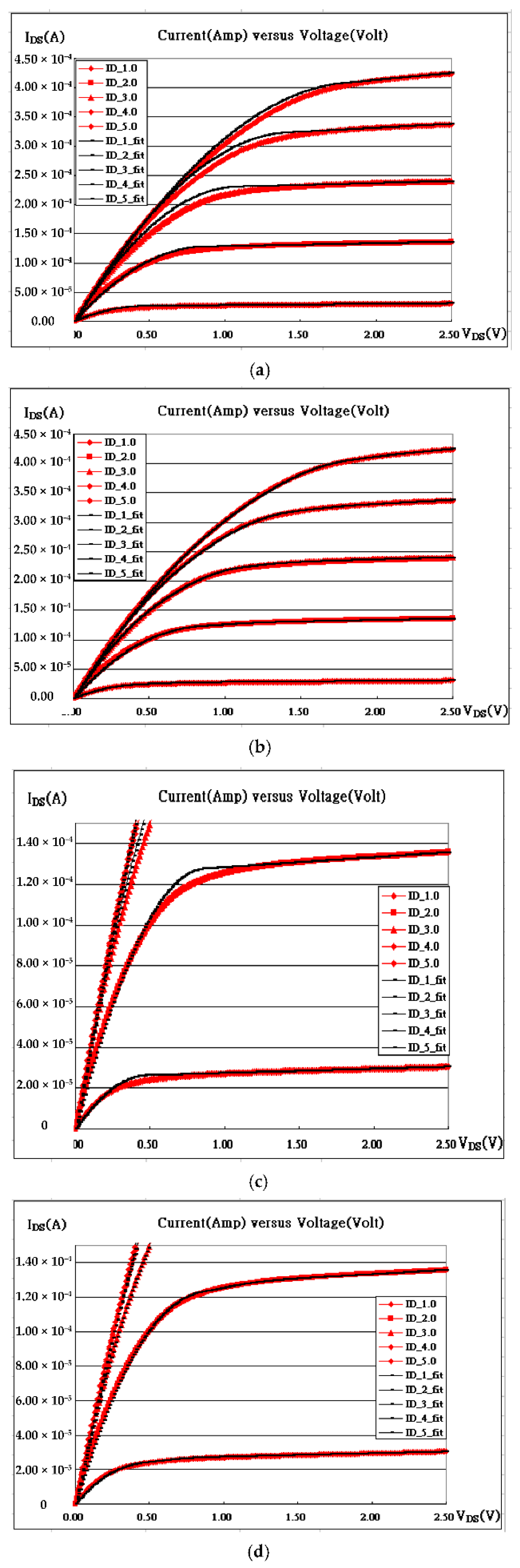
The minimum delta (δ) in Equation (3) can be used to determine the chosen parameters with or without taking kink effects into account, which are listed in Table 1 and Table 2. [8] In both tables, the minimum delta at different Gate biases requires different k_n, lambda (λ), and threshold voltages. For one thing, both Table 1 and Table 2 have reasonable delta trends; the higher the V_GS is, the higher the delta is because of larger scales. Furthermore, the fitting with kink effects is apparently superior to the one without. As referred to Figure 4, the fitting is not as good. Once the curves are enlarged in Figure 4b, the fitting curves do not consistently match the as measured data. Therefore, the minimum delta shown in Table 1 is usually at the order of 10^-6, except V_G=1.0 Volt.

With taking kink effects into account as shown in Table 2, the deviation (delta) can be suppressed as lowly as 10^-7., and the fitting is improved a lot in Figure 5. When turning off kink effects as shown in Figure 5a,b, the fitting curves are always lifted up at V_DS ～ (V_GS - V_th) as compared to the as measured data. To take care of the issue on which fitting curves are commonly lower than as-measured currents, the kink effects are thus considered. The solitary waves can be in thermal form, or maybe in phonons. The electron might be deflected because of the collisions with phonons, and those collisions may cause degradation of electrical performances. The item is thus introduced and subtracted, which is proportional to the exponential with the Gaussian form, as seen in Equation (1) and Equation (2). In Figure 5c,d, the fitting is really encouraging. The enlarged figure in Figure 5d does enhance the fitting.

4. Conclusions

The as measured data redrawn as characteristic curves can be fitted with the ones based on the modified conventional current-voltage formula. Even though it is quite engineering, such a fitting may be quite easy to be undertaken because all the parameters do not have to be the same and are easily adjusted. Instead, the trends or scales of some specific parameter always give some thoughts. On the other hand, the kink effect does really exist as referred to Figure 5a,c for 0.5 micron process and, furthermore, Figure 6a,b for 0.09 micron process, and it shall efficiently help to work out the fitting as referred to Figure 5b,d, and Figure 7a,b, where the minimum delta (δ) is proven to effectively reduce as expected.

Fitting with Kink effects gives the idea that the mobility implicitly shown in k_N varies all the time correlating to the subtractions in Figure 3a,b while the gate capacitance and the effective channel length and width shall be reasonably treated as fixed quantities. In the conventional model, the mobility included in k_N is supposed to be averagely constant, which is, in turn, unable to be convincing. Therefore, the mobility is then proven to be a variant along the strongly-inversed channel length. In addition, all the kink modified terms in Equation (7) for the fitting demonstrate that the values of (－γ²/2) are about tens, e.g., (－50). That is to say, the velocity of electron is quite the same order of the group velocity of the phonon, thousands of meters per second.[18]

Author Contributions

Conceptualization, H.C. Yang., and S.C. Chi.; methodology, H.C. Yang., and S.C. Chi.; software, H.C. Yang., and S.C. Chi; validation, H.C. Yang., and S.C. Chi; formal analysis, H.C. Yang., and S.C. Chi.; investigation, H.C. Yang., and S.C. Chi; resources, H.C. Yang., and S.C. Chi; data duration, H.C. Yang., and S.C. Chi.

Funding

Not available.

Institutional Review Board Statement

Not available.

Informed Consent Statement

Not available.

Data Availability Statement

No.

Conflicts of Interest

No.

References

Diab, A.; Torres Sevilla, G.-A.; Christoloveanu, S.; and Hussain, M.-M. Room to high temperature measurements of flexible SOI FinFETs with sub-20-nm fins. IEEE Trans. Electron. Devices 2014, 61, 3978. [Google Scholar] [CrossRef]
Wang, F.; Xie, Y.; Bernstein, K.; Luo, Y. Dependability analysis of nano-scale FinFET circuits. In Proceedings of the IEEE Computer Society Annual Symposium on Emerging VLSI Technologies and Architectures (ISVLSI'06), Karlsruhe, Germany, 2–3 March 2006; pp. 6, 399. [Google Scholar]
Huang, X.; Lee, W.-C.; Kuo, C.; Hisamoto, D.; Chang, L.; Kedzierski, J.; Anderson, E.; Takeuchi, H.; Choi, Y.-K.; Asano, K.; et al. Sub-50 nm P-channel FinFET. IEEE Trans. Electron. Devices 2001, 48, 880. [Google Scholar] [CrossRef]
Rudenko, T.; Kilchytska, V.; Arshad, M.K.M.; Raskin, J.-P.; Nazarov, A.; Flandre, D. On the MOSFET Threshold Voltage Extraction by Transconductance and Transconductance-to-Current Ratio Change Methods: Part II-Effect of Drain Voltage. IEEE Trans. Electron. Devices 2011, 58, 4180–4188. [Google Scholar] [CrossRef]
Takahashi, T.; Beppu, N.; Chen, K.; Oda, S.; Uchida, K. Self-heating effects and analog performance optimization of Fin-type field-effect transistors. Jpn. J. Appl. Phys. 2013, 52, 04CC03. [Google Scholar] [CrossRef]
Saitoh, M.; Yasutake, N.; Nakabayashi, Y.; Uchida, K.; Numata, T. Understanding of strain effects on high-field carrier velocity in (100) and (110) CMOSFETs under quasi-ballistic transport. In Proceedings of the 2009 IEEE International Electron Devices Meeting (IEDM), Baltimore, MD, USA, 7-9 December 2009; pp. 1–4. [Google Scholar]
Chen, C.W.; Wang, S.J.; Hsieh, W.C.; Chen, J.M.; Jong, T.; Lan, W.H.; Wang, M.C. Q-factor Performance of 28 nm-node High-k Gate Dielectric under DPN Treatment at Different Annealing Temperatures. Electronics 2020, 9, 2086. [Google Scholar] [CrossRef]
Lu, P.; Yang, C.; Li, Y.; Li, B.; Han, Z. Three-Dimensional TID Hardening Design for 14 nm Node SOI FinFETs. Eng 2021, 2, 620–631. [Google Scholar] [CrossRef]
Song, Y.S.; Tayal, S.; Rahi, S.B.; Kim, J.H.; Upadhyay, A.K.; Park, B.-G. Thermal-Aware IC Chip Design by Combining High Thermal Conductivity Materials and GAA MOSFET. In Proceedings of the 2022 5th International Conference on Circuits, Systems and Simulation (ICCSS), Nanjing, China, 13-15 May 2022; pp. 135–140. [Google Scholar]
Crupi, G.; Schreurs, D.M.M.-P.; Caddemi, A.; Angelov, I.; Homayouni, M.; Raffo, A.; Vannini, G.; Parvais, B. Purely analytical extraction of an improved nonlinear FinFET model including non-quasi-static effects. Microelectron. Eng. 2009, 86, 2283–2289. [Google Scholar] [CrossRef]
Li, Y.; Zhao, F.; Cheng, X.; Liu, H.; Zan, Y.; Li, J.; Zhang, Q.; Wu, Z.; Luo, J.; Wang, W. Four-Period Vertically Stacked SiGe/Si Channel FinFET Fabrication and Its Electrical Characteristics. Nanomaterials 2021, 11, 1689. [Google Scholar] [CrossRef] [PubMed]
Zhao, E.; Zhang, J.; Salman, A.; Subba, N.; Chan, J.; Marathe, A.; Beebe, S.; Taylor, K. Reliability challenges of high performance PD SOI CMOS with ultra-thin gate dielectrics. Solid State Electron. 2004, 48, 1703–1708. [Google Scholar] [CrossRef]
Zhao, Z.Q.; Li, Y.; Zan, Y.; Li, Y.L.; Li, J.J.; Cheng, X.H.; Wang, G.L.; Liu, H.Y.; Wang, H.X.; Zhang, Q.Z.; et al. Fabrication technique of the Si_0.5Ge_0.5 Fin for the high mobility channel FinFET device. Semicond. Sci. Technol. 2020, 35, 045015. [Google Scholar] [CrossRef]
Lee, J.; Park, T.; Ahn, H.; Kwak, J.; Moon, T.; Shin, C. Prediction Model for Random Variation in FinFET Induced by Line-Edge-Roughness (LER). Electronics 2021, 10, 455. [Google Scholar] [CrossRef]
Yang, H.-C.; Chi, S.-C. Process Corresponding Implications Associated with a Conclusive Model-Fit Current-Voltage Characteristic Curves. Appl. Sci. 2022, 12, 462. [Google Scholar] [CrossRef]
Yang, H.-C.; Chi, S.-C.; Liao, W.S. Comparison of Fitting Current–Voltage Characteristics Curves of FinFET Transistors with Various Fixed Parameter. Appl. Sci. 2022, 12, 10519. [Google Scholar] [CrossRef]
Lewis H. Ryder, Quantum Field Theory, Chapter 10.1 The sine-Gordon kink, p402, Published by the Press Syndicate of the University of Cambridge. ISBN 0 521 23764 5 hard covers.
Lacroix, D.; Traore, I.; Fumwron, S.; Jeandel, G. Phonon transport in silicon, influence of the dispersion properties choice on the description of the anharmonics resistive mechanisms. Eur. Phys. J. B 2009, 67, 15–25. [Google Scholar] [CrossRef]

Figure 1. I_DS-V_DS characteristic curves and the corresponding fitting (a) without taking the term (1+λV_DS) in Eq.(1) into account. (b) with taking the term (1+λV_DS) in Equation (1) into account.

Figure 2. I_DS-V_DS characteristic curves and the corresponding fitting with minimum delta (δ) skill in the following Equation (3).

Figure 3. (a) The subtraction values of I_DS-V_DS characteristic curves and the corresponding fitting without taking the Gaussian term into account. (b) with taking the Gaussian term into account. (c) the corresponding fitting in Figure 3b.

Figure 4. 0.25 micron process (a) I_DS-V_DS characteristic curves and the corresponding fitting without taking kink-effect factor into account. (b) Enlarged I_DS-V_DS characteristic curves and the corresponding fitting without taking kink-effect factor into account.

Figure 5. 0.25 micron process (a) I_DS-V_DS characteristic curves and the corresponding fitting by turning off kink-effect factor. (b) I_DS-V_DS characteristic curves and the corresponding fitting by turning on kink-effect factor. (c) Enlarged I_DS-V_DS characteristic curves and the corresponding fitting by turning off kink-effect factor. (d) Enlarged I_DS-V_DS characteristic curves and the corresponding fitting by turning on kink-effect factor.

Figure 6. 0.090 micron process (a) I_DS-V_DS characteristic curves and the corresponding fitting without taking kink-effect factor into account. (b) the corresponding fitting with minimum delta (δ).

Figure 7. 0.090 micron process (a) I_DS-V_DS characteristic curves and the corresponding fitting by turning on kink-effect factor. (b) the corresponding fitting with improved minimum delta (δ).

Table 1. Transistors Using 0.25 micron Process Technology without Kink Effect Factor.

Gate Bias	k_N	V_{th_fit}	λ	δ
V_G=1.00V	2.080×10^-4	0.5275	0.138	5.9311×10^-7
V_G=2.00V	3.181×10^-4	1.1437	0.073	1.6219×10^-6
V_G=3.00V	3.547×10^-4	1.9238	0.075	2.3925×10^-6
V_G=4.00V	2.859×10^-4	2.5900	0.079	2.3448×10^-6
V_G=5.00V	2.151×10^-4	3.2157	0.099	3.3145×10^-6

Table 2. Transistors Using 0.25 micron Process Technology with Kink Effect Factor.

Gate Bias	k_N	V_{th_fit}	λ	δ
V_G=1.00V	2.260×10^-4	0.5275	0.082	2.2803×10^-7
V_G=2.00V	3.365×10^-4	1.1437	0.040	6.5269×10^-7
V_G=3.00V	3.850×10^-4	1.9238	0.030	6.8806×10^-7
V_G=4.00V	3.060×10^-4	2.5900	0.044	7.6246×10^-7
V_G=5.00V	2.296×10^-4	3.2157	0.065	8.9941×10^-7

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Conclusive Model-Fit Current-Voltage Characteristics Curves with Kink Effects

Abstract

1. Introduction

2. Preparation of as Measured Data and Fitting

2.1. Preparation

2.2. Fitting IDS-VDS and IDS-VGS

2.3. The Delta Deviation

2.4. The kink effect

3. Application

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

2.2. Fitting I_DS-V_DS and I_DS-V_GS