Preprint
Review
Error Estimation through Computational Analysis of the Fluid Flow over Expanding Cylinder with Gyrotactic Microbe
Altmetrics
Downloads
105
Views
29
Comments
0
This version is not peer-reviewed
Submitted:
13 July 2023
Posted:
14 July 2023
You are already at the latest version
Alerts
Abstract
This study presents the numerical investigation of bioconvective nanofluid (NF) flow compris-ing gyrotactic microorganisms through convective boundary conditions (CBC) enclosing heat and mass transmission analysis above an inclined extending cylinder. Via appropriate transfor-mation, the set of Partial Differential Equations is transformed into a scheme of nonlinear ODEs. A new set of variables are presented in the directive to get the first-order convectional equations and, then solved numerically by using bvp4c. The influence of several factors on velocity, ener-gy, concentration, and the density of motile microorganisms (DMM) is investigated and exam-ined. The analysis describes and addresses all physical measures of concentration such as Skin Friction (SF), Sherwood number (SN), DMM, and Nusselt number (NN). The present conse-quences display a validation with published. For confirmation of bvp4c, the ND-solve approach is also applied. Error analysis is also examined for the confirmation of the mathematical model.
Keywords:
Subject: Computer Science and Mathematics - Applied Mathematics
1. Introduction
The study of boundary layer flow (BLF) towards an elongating surface was first introduced by Anderson [1] and has become a significant and exciting subject for research investigations because of its wide industrial application such as cooling capacity polymer, heat exchange properties such as thermal performance, wire coating-layer, liquids diffusivity, and chemical production sectors. Sakiadis [2,3] examined the BLF over the flat sheet. Further, Crane [4] expanded the study to analyze the changing extending sheet velocity and closed form analytically solutions obtained for Navier–Stokes system using two-dimensional flow. These initial assistances have been of excessive significance in wire performance and elastic fabrication industries. The heat dissemination of the melting liquid was deliberated [5], where the outcomes are revealed very imperatively in the development of conserving polymer sheets extracted through the die. Wang [6] amended the fluid dynamic problem outside the stretched tube, which is required for the manufacturing environment of cable and fiber pulling. Ishak [7] recently expanded the study of Wang to investigate the melting heat rate over a permeable surface. Keeping the applications of the stretching sheet, many researchers analyzed the fluid stream and heat transmission over the stretching sheet in different conditions. For this goal, the nanoparticles were introduced in the base fluid to increase the heat transport characteristics such as thickness, thermal efficiency, and diffusivity in the liquid.
Convective heat transfer (CHT) is the utmost efficient process for heat transmission in the liquefied. This framework can be improved by varying movement geometry, boundary constraints, or improving the thermal characteristics. For illustration, the accumulation of nanoparticles of higher thermal performance to the liquid upsurges the thermal characteristics of the base fluid.
NF technology has gained significant attention in recent years, particularly in the fields of production, physical science, and materials science. The concept of NF involves adding small quantities of nanoparticles to a base liquid, which enhances its thermal and electrical conductivity, viscosity, and other physical properties. These nanoparticles can be made from a variety of materials, including metals, ceramics, and carbon-based materials. Buongiorno [9] gave a mathematical form of the nanoparticles and determined that via basic mechanism permits us with prodigious suppleness in enlightening the thermal features. NFs have been widely used by mathematicians and researchers to study a wide range of practical problems in various fields. In industrial applications [10,11], NFs are used to progress the proficiency of heat transfer systems, which can lead to significant energy savings. In biomedical engineering [12], NFs have been used to develop new diagnostic and therapeutic techniques [13], such as targeted drug delivery systems. In solar thermal applications, NFs are also used to increase the adeptness of solar collectors [14,15,16,17] and increase the amount of energy that can be generated from solar power.
Many studies have been conducted to explore the limitations that control the nanoparticle's resistance to heat transfer by convection. That is correct. Nanomaterials, which are particles that range in size from 1 to 100 nanometers, are not self-propelled in the way that microorganisms are. Instead, their movement is largely determined by Brownian motion and thermophoresis. Brownian motion (BM) is the random movement of particles in a fluid, such as air or water, that arises from collisions with the molecules of the fluid. This motion causes the particles to move around randomly but in a generally confined area. In the case of nanomaterials, their movement is largely determined by the Brownian motion of the fluid in which they are suspended. Thermophoresis, on the other hand, is the movement of particles in a fluid that is caused by a temperature gradient. When the temperature is increased to a liquid containing nanomaterials, the particles move from space with higher temperature to spaces of low temperature. The higher-density microorganisms drop into the liquid and the microorganisms float up. The bioconvection procedure is a macroscopic vibration created by this replacement. Numerous studies appeared to demonstrate that the emergence of motile microorganisms (MM) in NF flow occurred [18]. The Fourier law has been used to study the issue of heat transmission, whereby was difficult to comprehend. Afterward, with Cattaneo and Later Christov, an improved version of the Fourier law (FL) was created and applied to discuss and examine the issue of heat transfer through a stretching sheet [19,20,21,22,23]. Temperature and concentration characteristics are unaffected via the bioconvection factor [16], whereas the buoyancy parameter has an impact on the density and velocity of MM. Growing the magnetic field, NN, the nanoparticle concentration, and density MM [24,25,26] although solar energy has no impact on the density of MM [27]. As a result of the mass slip, enhances the density of MM, heat, and fluid flow, whereas it modestly lowers the particle concentration [28,29]. The topic of this research is the bioconvection mechanism across a stretched cylinder. The time-dependent temperature slipstream of NF comprising MM along a flat tube demonstrates that motivation energy has a significant impact on nanoparticle mobility inside conventional fluids [30,31,32]. Recent research on the mechanics of NFs in various configurations [33-37]. The consequences of inner heat production or permeation with heat/mass transport of a NF comprising a MM across an inclined stretched cylinder were not addressed in any earlier studies. The main objective of this exploration is to explore the impact of incidence angle on stream heat transfer, which is crucial in numerous industries such as pipework, fiber optics, spherical plastic squeezing, transition phase of conductive sheets, polyethylene production, and condensation of electrical and automatic equipment.
The following are the existing work contributions: 1- The temperature and velocity of NF are explored across a stretched inclined cylinder containing microorganisms. 2- Using a proper transformation matrix, the set of PDEs is turned into ODEs. 3- The resultant ODEs are investigated numerically using bvp4c using the Mathematica software. 4- The inspiration of various factors on the movement, heat, nanoparticle concentration, and DMM is shown visually.
2. Mathematical Description
Consider a steady state uniform mixed convection NF movement past an inclined stretchable cylinder with velocity having radius a, containing GM (Gyrotacticn Microorganism) as described in Figure 1. The coordinates is used for this purpose. In figure 1 is the surface heat, is the fluid heat, is the ambient heat, and is the heat source subjected to the cylinder.
When a cylinder is immersed in an NF, a temperature difference may arise between the surface of the cylinder and the surrounding fluid. This temperature difference can create a buoyancy force (BF) due to the density difference between the warm and cool fluid. The warm fluid near the cylinder surface will become less dense and rise, while the cool fluid will sink, creating a convective flow. This flow is known as natural convection and is driven by the BF owing to the heat difference. In the presence of gravity, the BF owing to the temperature difference interacts with the gravitational force, resulting in a more complex flow pattern. The resulting flow can enhance heat transmission from the cylinder surface to the fluid, which can be beneficial in many engineering applications.
Ignoring the pressure gradients or external forces, the model equations are expressed as follows [16,17,18,19]:
With boundary Constraints at
Equations (1)-(4) are respectively, the continuity, movement, energy, and concentration equations. Where and are the x- and -component of velocities, whereas are indeed the density of fluid, nanomaterial, and microbes, correspondingly. Here, explores the concentration profile, is the capacity growth liquid coefficient, is the gravity, shows an angle of preference, depicts the mean volume of the microbes, is the DMM, represents the hotness of the liquid, are the dynamic and kinematic viscosity, respectively, is actual heat capacitance, depicts the BM coefficient, shows the thermophoresis measurement, is the diffusivity of the microbes, stands for the Chemotaxiscconstant, and is constantmmaximum cell swimmingsspeed.
The relevant non-dimensional conversion are applied to simplify the set of mathematical equations.
The transformed equation in ODEs are
with boundary constraint
here
is the curvature factor,
is Richardson's number,
is Buoyancy ratio factor,
is Prandtlnnumber,
is the bioconvection Rayleigh number
is Brownian motion factor,
is thermophoresispfactor,
is heat generation/absorption factor,
is Schmidtnnumber,
is bioconvectionnLewis number,
Pe is the Pecletnnumber,
and is the motile factor.
- 1.
- Physical quantities (Skin Friction (SF), Nusselt number (NN), and Sherwood number (SN)).
The dimensionless physical quantity of concentrations like SF, NN, SN is given below
- 2.
- Numerical procedure
The basic flow equations are converted in terms of PDEs. The PDEs are transformed to dimensionless form in terms of ODEs by using similarity transformations. The numerical results have been obtained vis bvp4c with 10-6 tolerance. For the verification of bvp4c, the ND-solve package is also applied and a good correlation is established as depicted in Figure 2a-d. Additionally, the existing work is compared with the previous as explored in Table 1. The calculation in Table 1 delivered an excellent clearance for and between the present and published work.
3. Error Analysis and Confirmation of RK4 Method
The dimensionless first-order differential equations are solved by the bvp4c package. It is implemented in various software packages such as MATLAB and Mathematica. By default, these packages use a certain working precision, which determines the accuracy of the numerical solution. Since we are interested in a numerical solution, the error estimations for the parameters are essential. The error is computed based on the difference of two different precision i.e., default work precision with working precision-22.
Indeed, logarithmic scales are often used to visualize small differences or changes that can span several orders of magnitude. By taking the logarithm of a variable, you compress its range of values and emphasize differences in the lower end of the scale, where they might otherwise be difficult to discern. In the case of real exponents [x], taking the logarithm base 10 of the absolute value of the exponent can be a useful transformation. This is because the absolute value ensures that the logarithm is always defined, even when the exponent is negative or zero. By using a logarithmic scale, you can compare values that differ by orders of magnitude, while still being able to see small differences near zero. In the figures below, we computed the error solutions for various physical model factors. Based on these estimates, our numerical answer is corrected since the error is too small, as seen in Figure 3a-d and Figure 4a-d.
4. Results and discussion
The bioconvection Lewis factor indicates the ratio of thermal diffusivity towards the diffusivity of microorganisms. The has no influence on Skin friction,, Nusselt Number, or SherwoodnNumber, as seen in Table 2. There is an upsurge inside the DMM. With raising quantity, the DMM declines (see Fig. 5a). Physically, raising reduces the diffusivity of microorganisms. Brownian motion denotes the molecular movement of deferred nanomaterials inside an NF. This movement is caused by the random movement of nanoparticles, which becomes more prominent as the temperature rises. Table 3 reveals that the has no upshot on SF or DMM, although it does reduce the NN (heat transfer by conduction). Figure 5b-c shows how affect the temperature and concentration profiles. It is witnessed that the temperature outline enhances (see Fig. 5b) while the concentration is declines (see Fig. 5c). Table 3demonstrates an escalation in the concentration of microchannel. Figure 5c depicts a drop in the concentration of nanoparticles far from the surface. Physically, enhance temperature, and accelerates the energy of the particles, which promotes motion and quick collisions, which enhances Brownianmmotion. While raising the concentration, the space for particle mobility is reduced, as it declines the possibility of collisions. The thermophoresis factor refers to the phenomena of a nanoparticle disparity reaction to the force of a heat variation. The TR gradient enhances this force, which enhances the heat inside the flow (see Fig. 5d). It is perceived that the concentration of the nanoparticles rises (see Fig. 5e). Table 4 demonstrates the influence of on SF, NN, SN, and DMM. This table demonstrates a drop in the NN with , followed by a rise in the thermal gradient as shown in Figure 5d. Table 4 indicates a rise in the Sherwood number, and Figure 11b indicates an increment in the nanoparticle concentration. Physically, raising the temperature raises the temperature gradients, which raises the transition force, and thus raises the convective heat transfer parameter.
Here, is the buoyancy-ratio factor. Table 5 shows that raising the factor leads to an increase in SF and a reduction throughout the NN, SN, as well as in DMM. Figure 5f and Figure 6a-c depict the influence of . The velocity of MM decreases (see Figure 5f), whereas the temperature, boundary layer flow concentration, and DMM rise as shown in Figure 6a-c, respectively.
The Peclet number Pe is the proportion of advective transportation rate versus mass diffusion rate. Table 6 indicates that when the Pe number increases, so does the concentration of MM While no significant effect was observed for SF, NN, and SN. Figure 6d depicts a decline in the fields of motile microorganisms as the Pe number increases.
The Prandtlnnumber Pr is indeed a nondimensional quantity that shows the relationship between the momentum diffusivity to the thermal diffusivity. This value compares the influence of the fluid viscosity to the associated heat conductivity. The magnitude of the number describes the characteristics of the fluid under investigation. Heat-transmitting fluids have strong heat capacity as well as low values. According to Table 7, raising the number has little impact on the skin friction but improves the Nusseltnnumber, Sherwoodnnumber, and DMM. If , the air may be designated a heat transmission fluid. The Carbon disulfide has a viscosity of 0.5 and a thermal conductivity of 0.149. for chloromethane is 5 and for water is 7. As the Pr number grows, the impact of viscosity improves, and the temperature rises while the concentration declines. Figure 6d-f depict the effect of . The heat is shown to be decreasing in Figure 6d. Physically, a rise in number indicates a reduction in heat flux, implying that the solvent has a higher heat capacity. Figure 6e demonstrates that the concentration of the microchannel rises further from the substrate, but the DMM decreases (see Figure 6f).
The Bioconvection Rayleigh Number , reflects the heat transmission in MM by natural convection. With rising number, there is an improvement in SF but a decline in the NN, SN, and DMM. Figure 7a depict a reduction in the velocity distribution as enhances. In addition, Figure 7b-d coincide with Table 8 and show a rise in temperature, nanoparticles concentration, and motile microorganisms performance when Rb enhances.
The Richardson number, , is a non-dimensional quantity that represents the buoyancy component to the stream sheared ratio. Table 9 illustrates that raising the, increase SF, NN, SN, and DMM. Figure 8a-d demonstrate a drop in the curves of velocity, temperature, boundary layer flow concentration, and DMM when , is increased.
The Schmidt number Sc is the relationship between the kinematic viscosity and the mass diffusion. Table 10 depicts the impact of Sc; a drop in the NN and an enhancement within SN. Figure 8e and 8f illustrate the increase inside the temperature distribution and a reduction in the nanoparticles concentration versus the rising number. In terms of physics, raising the Schmidt number enormously increases the dynamic viscosity of the density of the fluid with mass diffusivity which introduces the thickness of the mass transmission boundary layer. The proposed value for in the current investigation is very small, indicating that the molecules have a strong diffusivity, extremely small, and are unaffected by the viscosity of the media. Consequently, as the heat rises, so does the number, whereas the concentration declines, as increases.
The effect of the angle of inclination is shown in Table 11 to demonstrate the variance in these non-dimensional values as a function of the inclination angle. Varying the inclination angle significantly influences the movement, temperature, volume of nanoparticles, and the DMM as revealed in Figure 9a-d, respectively.
The curvature factor represents the distortion of the cylinder sheet about the size of the boundary layer. The surface area declines as the curvature factor enhances. Table 12 demonstrates an improvement in SF, NN, SN, and DMM as the curvature factor is increased owing to a consequent reduction area. Figure 9e-h explore how the curvature factor affects the velocity, temperature, volume of the NF away from the surface, and the MM profiles. For , the radius equals the thickness of the boundary layer, and the structure is axisymmetric; as grows, we reach the slender cylinder having a dense boundary layer. The heat source factor is a dimensionless factor that explores the quantity of heat created or absorbed in the medium. Table 13 shows that shifting the variation from absorption to generation causes a drop in the NN and a rise in the SN. The temperature as well as the concentration of nanomaterial enhancement are seen in Figure 10a and 10b. Table 14 shows that the bioconvection factor causes a slight improvement in the DMM. Figure 10c reveals a small decline in the MM (motile microorganisms) as the bioconvection factor is increased.
5. Conclusions
The laminar movement of an NF through an inclined cylinder in the context of generation/absorption, bioconvection, and in the presence of MM is investigated numerically. Through appropriate transformation, a network of PDEs is turned into a set of dimensionless ODEs, which are then computationally solved utilizing Mathematica Package bvp4c with an ND-solve approach. The simulation outcomes are consistent with earlier findings. The key points of this study are given below:
- ⮚
- SF rises as and are enhanced while it diminishes with enhancing and . Furthermore, SF is not influenced by other factors.
- ⮚
- The NN grows by enhancing and . When and are changed, the NN remains constant, but when other factors are improved, the NN decreases.
- ⮚
- The SN is only increased with increasing buoyancy factor . Although the SN is constant for and . The SN rises when the other factors are changed.
- ⮚
- The DMM reduces when Nr and Rb are enhanced and escalations with the other factors. On the other hand, the inclination angle has no impact.
- ⮚
- For angle <45o, the SPF, NN, and SN rise and decline for angle > 45o.
- ⮚
- As the curvature factor is increased, so does the velocity distribution. While it declines when and are enhanced.
- ⮚
- It is detected that the temperature profile upsurges with the growing values of BM, Richardson number, and Schmit number while the bioconvection factor has no effect.
- ⮚
- It is witnessed that the concentration of molecules increases with growing BM, Richardson number, thermophoretic number, and Schmit number while the bioconvection factor has no effect.
- ⮚
- The MM profile improves when , , and are enhanced while it decline with the swelling values of bio-convection number, Peclet number, Prandtl number as well as Richardson number.
Contributions
F.A.A and T.G. wrote the manuscript, E.A.I, and T.G. modeled the problem, W.K., and A.S.K. solved the problem. T.G. and A.S.K, have obtained the numerical computations.
Funding
Project number (RSPD2023R576), King Saud University, Riyadh, Saudi Arabia,
Acknowledgment
Researchers Supporting Project number (RSPD2023R576), King Saud University, Riyadh, Saudi Arabia,
Conflict of interest
The authors don't have any conflict of interest.
References
- Anderson, J.D. Ludwig Prandtl’s boundary layer. Phys Today 2005, vol. 58, pp. 42–48. [CrossRef]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for twodimensional and axisymmetric flow. AICHE J 1961, vol. 7, pp. 26-28. [CrossRef]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: II. The boundary layer on a continuous flat surface. AIChE J 1961, vol. 7, pp.221–225. [CrossRef]
- Crane, L.J. Flow past a stretching plate. Zeitschrift für angewandte Mathematik und Physik ZAMP 1970, vol. 21, pp. 645–652. [CrossRef]
- Dutta, B.K.; Roy, P.; Gupta, A.S. Temperature field in flow over a stretching sheet with uniform heat flux. Int Commun Heat Mass Transfer 1985, vol. 12, pp. 89–94. [CrossRef]
- Wang, C.Y. Fluid flow due to a stretching cylinder. Phys Fluids 1988, vol. 31, pp.466–474. [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Uniform suction/blowing effect on flow and heat transfer due to a stretching cylinder. Appl Math Model 2008, vol. 32, pp.2059–2066. [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles (No. ANL/MSD/CP- 84938; CONF-951135-29), (United States), Argonne National Lab.; 1995.
- Buongiorno, J. Convective transport in NFs. Journal of Heat Transfer 2006, vol. 128, pp. 240-250.
- Alanazi, M. M.; Hendi, A. A.; Raza, Q.; Rehman, M. A.; Qureshi, M. Z. A.; Ali, B.; & Shah, N. A. Numerical computation of hybrid morphologies of nanoparticles on the dynamic of nanofluid: The case of blood-based fluid. Axioms,2023, 12(2), 163. [CrossRef]
- Xian, H.W.; Sidik, N.A.C.; Najafi, G.J.J.O.T.A. Recent state of NF in automobile cooling systems. J Therm Anal Calorim 2019, pp.135, pp. 981–1008.
- Sheikhpour, M.; Arabi, M.; Kasaeian, A. Role of NFs in drug delivery and biomedical technology: Methods and applications. Nanotechnol Sci Appl 2020, vol. 13, pp. 47–59.
- Nagarajan, P.K.; Subramani, J.; Suyambazhahan, S. NFs for solar collector applications. Energy Procedia 2014, pp. 61, pp. 2416–2434.
- Mukhtar, S., & Gul, T. (2023). Solar Radiation and Thermal Convection of Hybrid Nanofluids for the Optimization of Solar Collector. Mathematics, 11(5), 1175. [CrossRef]
- Saidur, R.; Leong, K.Y.; Mohammed, H.A. A review on applications and challenges of NFs. Renewable Sustainable Energy Rev 2011, vol. 15, pp. 1646–1668.
- Wong, K.V.; De Leon, O. Applications of NFs: current and future. Adv Mech Eng 2010, vol. 2, vol. 519659- 519665.
- Sandeep, N.; Ashwinkumar, G.P. Impact of nanoparticle shape on magnetohydrodynamic stagnation-point flow of carreau nanoliquid: A comparative study. Proc Inst Mech Eng Part E: J Process Mech Eng 2021, vol. 09, pp. 544-556. [CrossRef]
- Akbar, N.S.; Khan, Z.H. Magnetic field analysis in a suspension of gyrotactic microorganisms and nanoparticles over a stretching surface. J Magn Magn Mater 2016, vol. 410, pp. 72–80. [CrossRef]
- Chakraborty, T.; Das, K.; Kundu, P.K. Framing the impact of external magnetic field on bioconvection of a NF flow containing gyrotactic microorganisms with convective boundary conditions. Alexandria Eng J 2018, vol. 57, pp. 61–71. [CrossRef]
- Acharya, N.; Das, K.; Kundu, P.K. Framing the effects of solar radiation on magneto-hydrodynamics bioconvection NF flow in presence of gyrotactic microorganisms. J Mol Liq 2016, vol. 222, pp. 28–37. [CrossRef]
- Uddin, M.J.; Yasser, A.O.; Bég, A.; Kabir, M.N. Numerical solutions for gyrotactic bioconvection in NFsaturated porous media with Stefan blowing and multiple slip effects. Comput Math Appl 2016, vol. 72, pp. 2562–2581.
- Tausif, S.M.; Das, K.; Kundu, P.K. Multiple slip effects on bioconvection of NF flow containing gyrotactic microorganisms and nanoparticles. J Mol Liq 2016, vol. 220, pp.518–526. [CrossRef]
- Aldabesh, A.; Khan, S.U.; Habib, D.; Waqas, H.; Iskander, T.M.; Khan, I. Unsteady transient slip flow of Williamson NF containing gyrotactic microorganism and activation energy. Alexandria Eng J 2020, vol. 59, pp. 4315–28. [CrossRef]
- Haq, F.; Kadry, S.; Chu, Y.M.; Khan, M.; Ijaz, K.M. Modeling and theoretical analysis of gyrotactic microorganisms in radiated nanomaterial Williamson fluid with activation energy. J Mater Res Technol 2020, vol. 9, pp. 10468–77. [CrossRef]
- Hussain, Arif, Malik, M.Y. MHD NF flow over stretching cylinder with convective boundary conditions and Nield conditions in the presence of gyrotactic swimming microorganism: A biomathematical model. Int Commun Heat Mass Transfer 2021, vol. 126, pp.105425-105436. [CrossRef]
- Shi, Q.H.; Hamid, A.; Khan, M.I. Numerical study of bio-convection flow of magneto-cross NF containing gyrotactic microorganisms with activation energy 2021. Vol. 11, pp. 16030-16045. [CrossRef]
- Yusuf, T.A.; Mabood, F.; Prasannakumara, B.C.; Sarris, I.E. Magneto-bioconvection flow of Williamson NF over an inclined plate with gyrotactic microorganisms and entropy generation. Fluids 2021, vol. 6, pp.109- 123. [CrossRef]
- Reddy, P.S. Impact of chemical reaction and double stratification on heat and mass transfer characteristics of NF flow over porous stretching sheet with thermal radiation. Int J Ambient Energy, 2020. pp. 1–11. [CrossRef]
- Sreedevi, P.; Reddy, P.S. Williamson hybrid NF flow over swirling cylinder with Cattaneo-Christov heat flux and gyrotactic microorganism. Waves Random Complex Medium 2021. Vol. 147, pp.1968537-9. [CrossRef]
- Elbashbeshy, E.M.A.; Hamada. G.; Asker, K.M. Flow and heat transfer over a stretching surface. Therm. Sci 2019, vol. 23, pp. 3105–16. [CrossRef]
Figure 1.
Configuration of the geometry and coordinates.
Figure 2.
a-d. Assessment of bvph4c and ND-solve for and . and
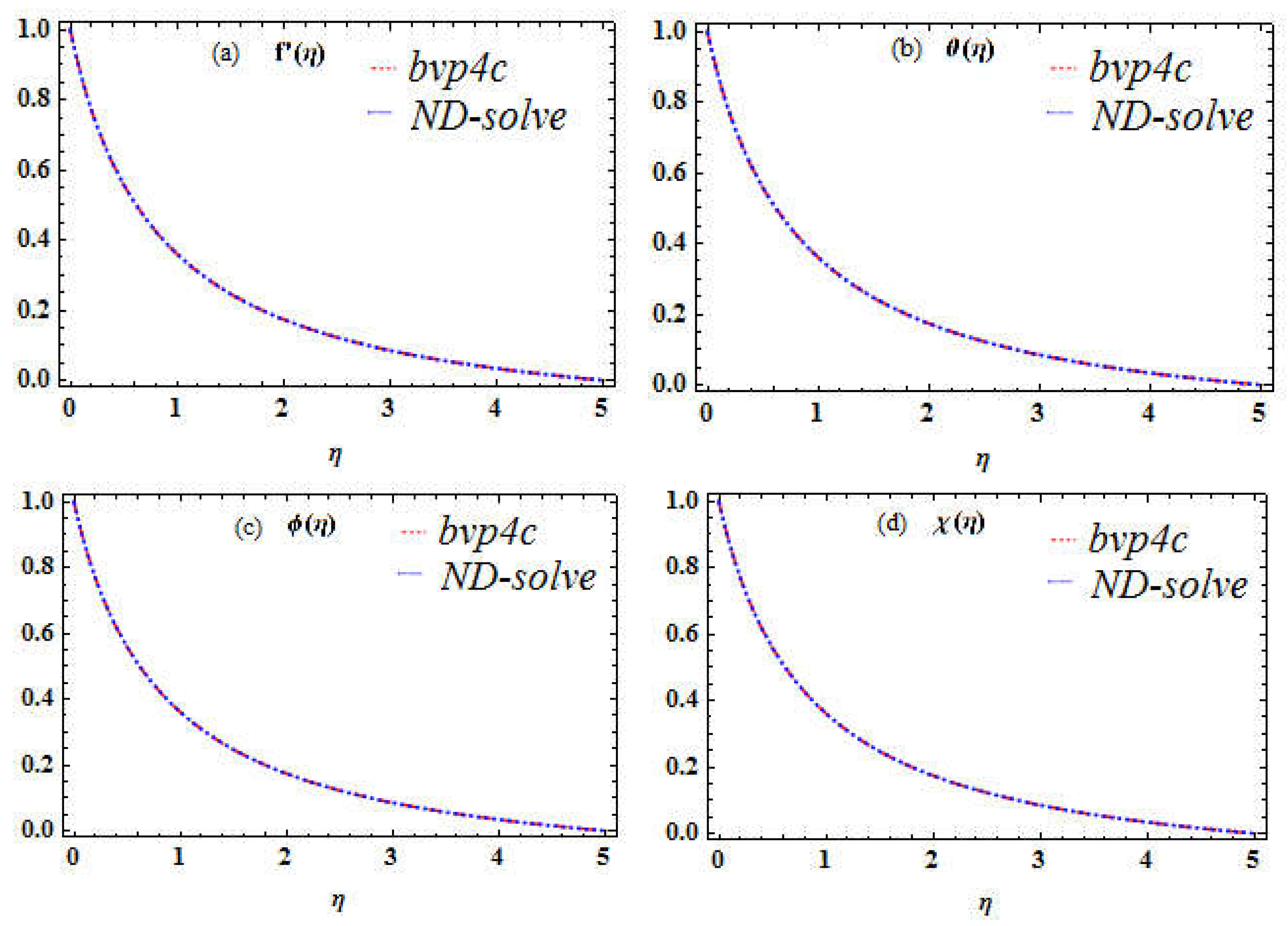
Figure 3.
a-d. Error estimation for velocity profile for different values of and
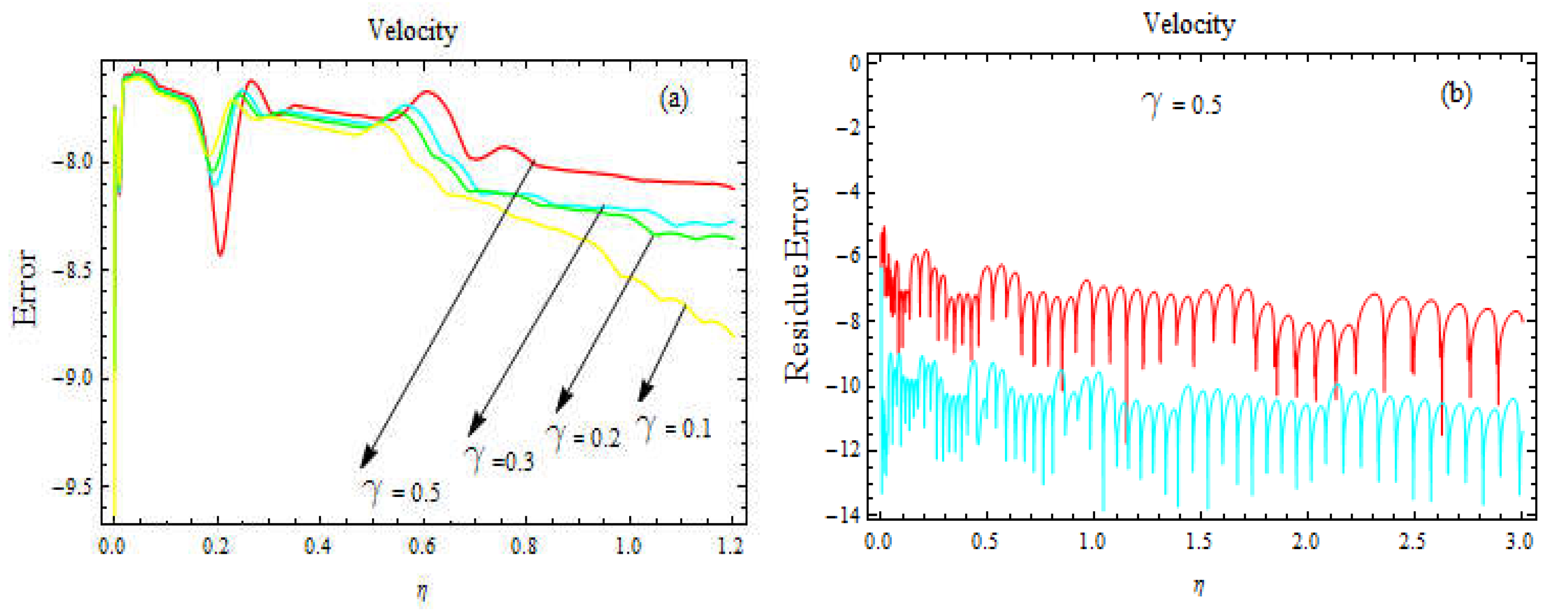
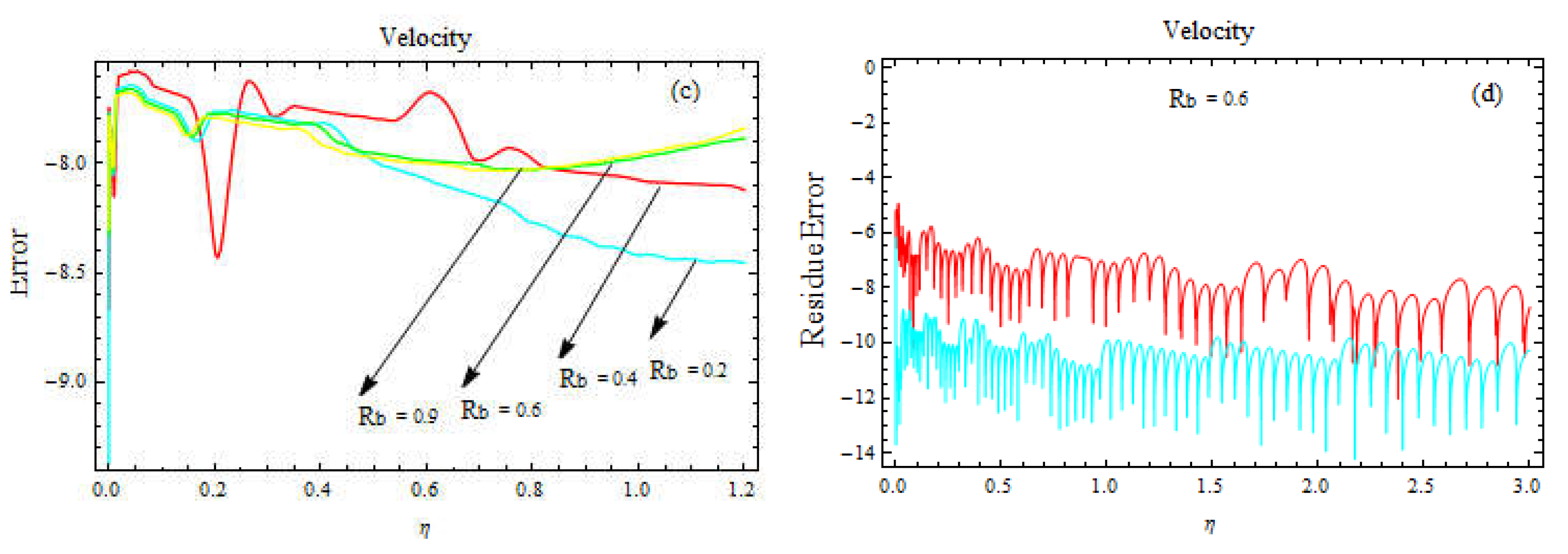
Figure 4.
a-d. Error estimation for velocity and temperature profiles for different values of and .
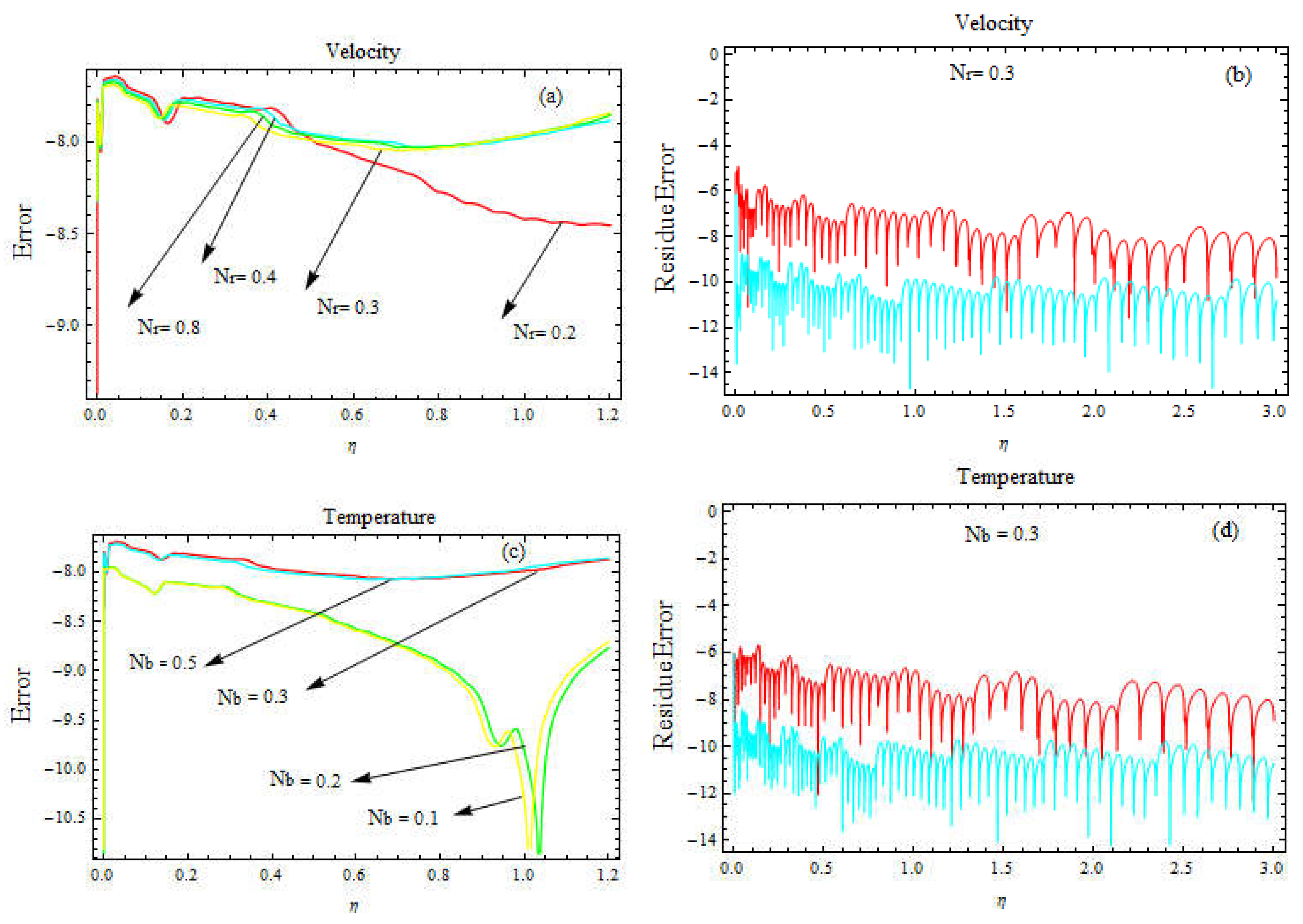
Figure 5.
a-f. Influence of on (b). on . (c). on . (d). on .(e). on . (f). on .
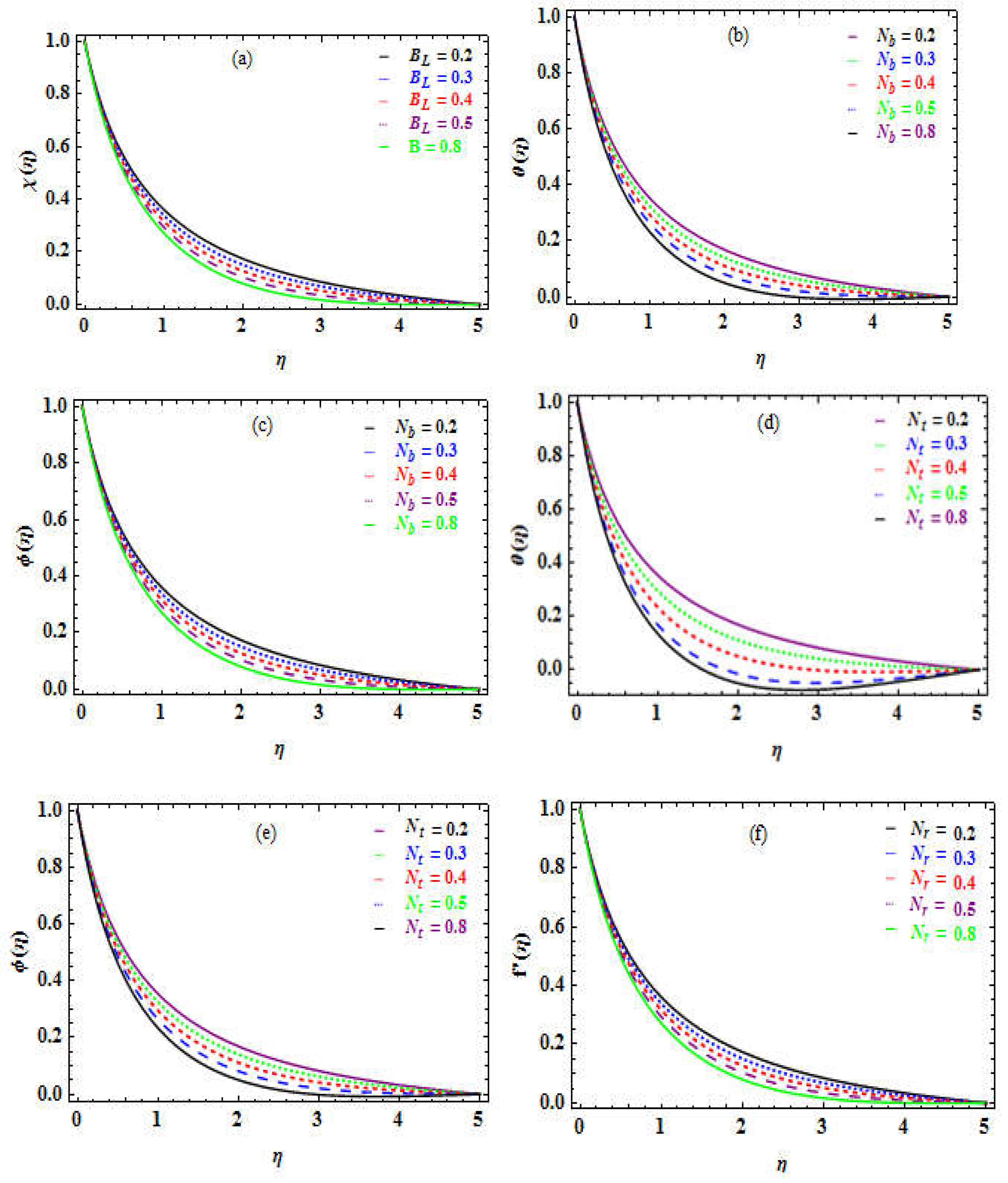
Figure 6.
a-h. Influence of (a) on (b) on (c) on (d) on (e) on (f). (h). on .
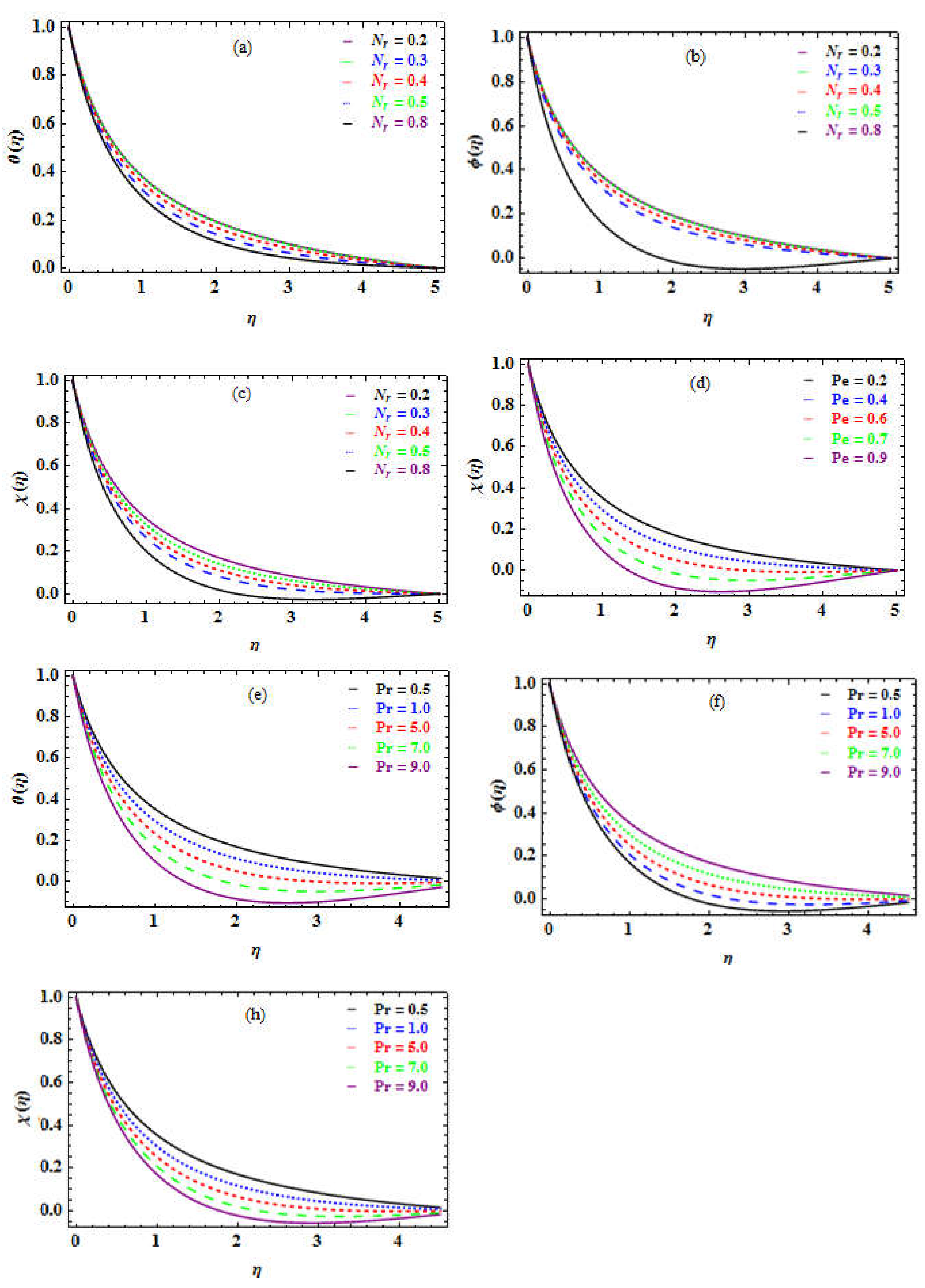
Figure 7.
a-d. Influence of .
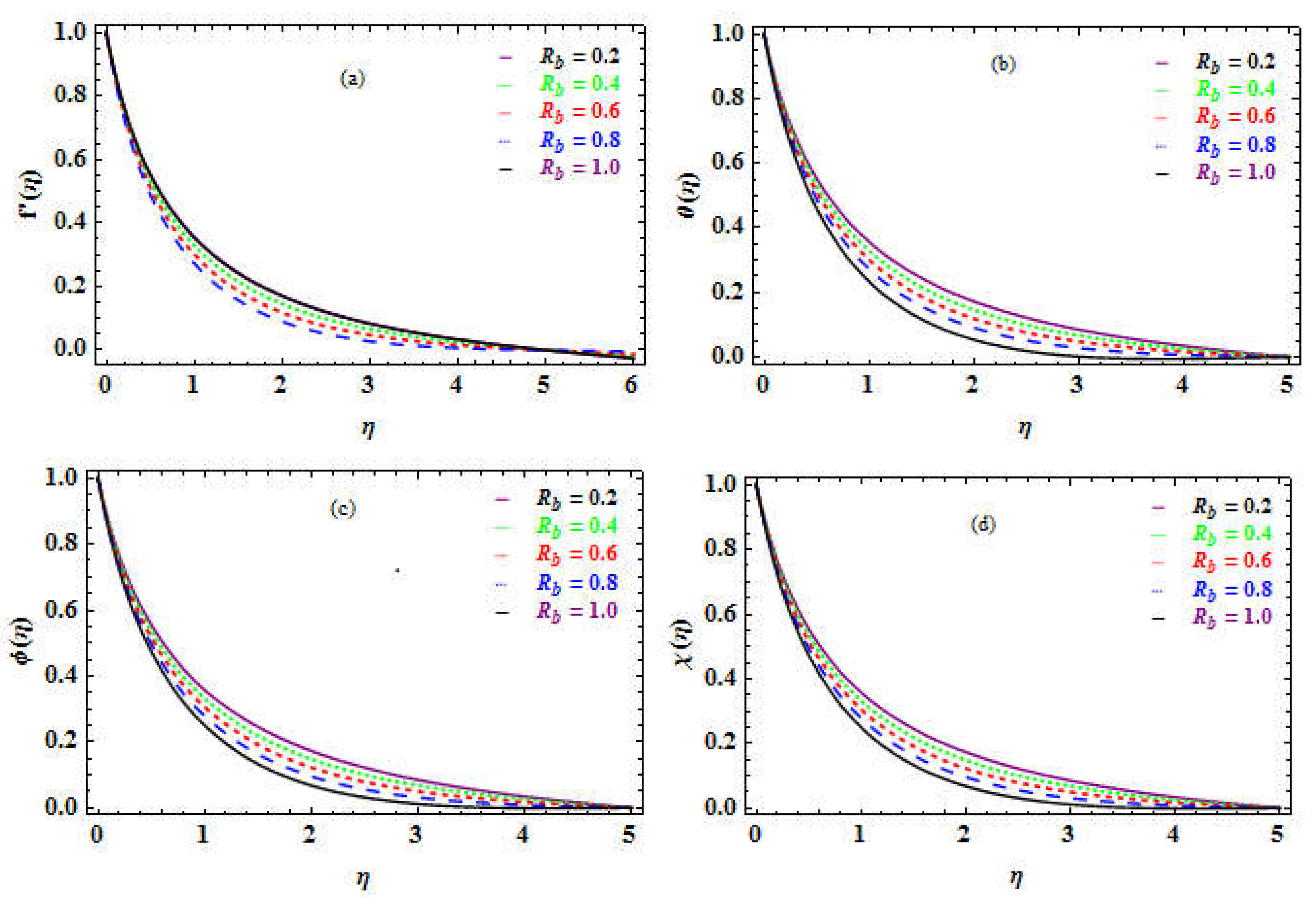
Figure 8.
a-f. Influence of and .
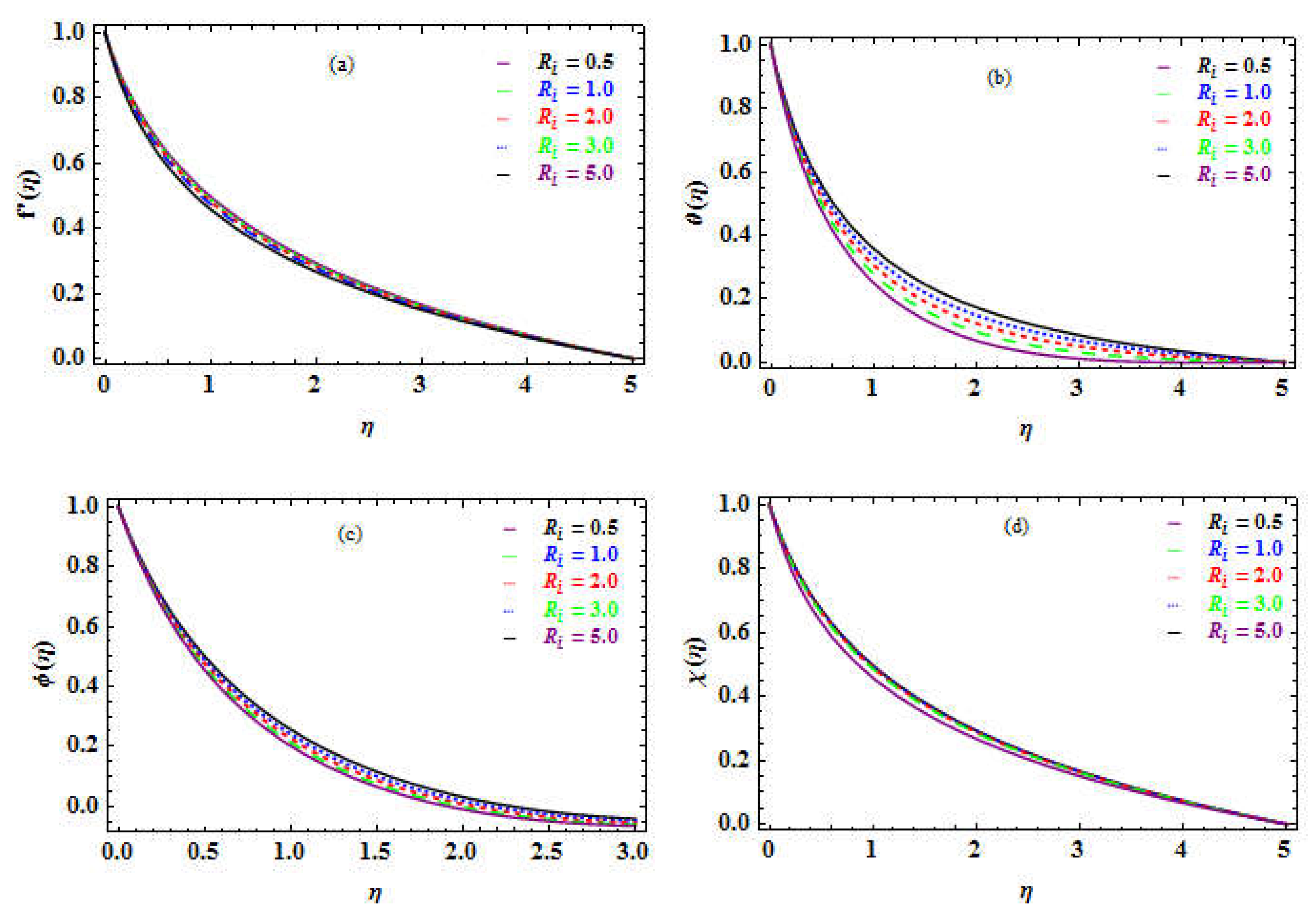
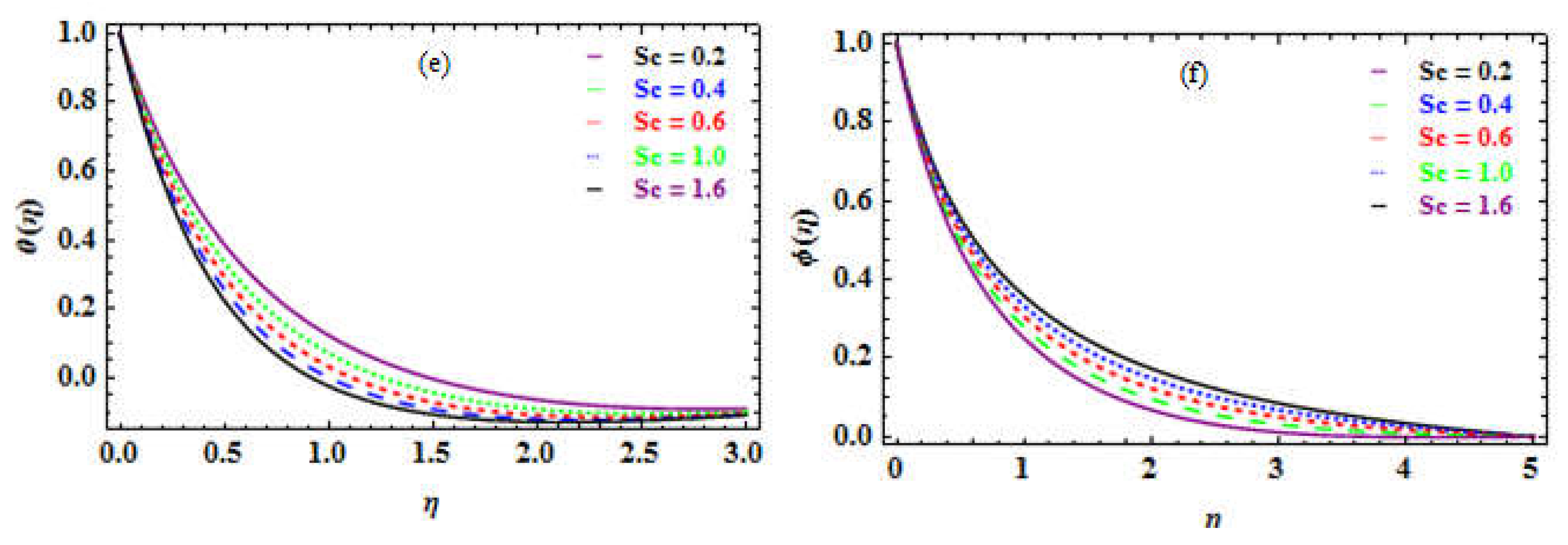
Figure 9.
a-h. Influence of and .
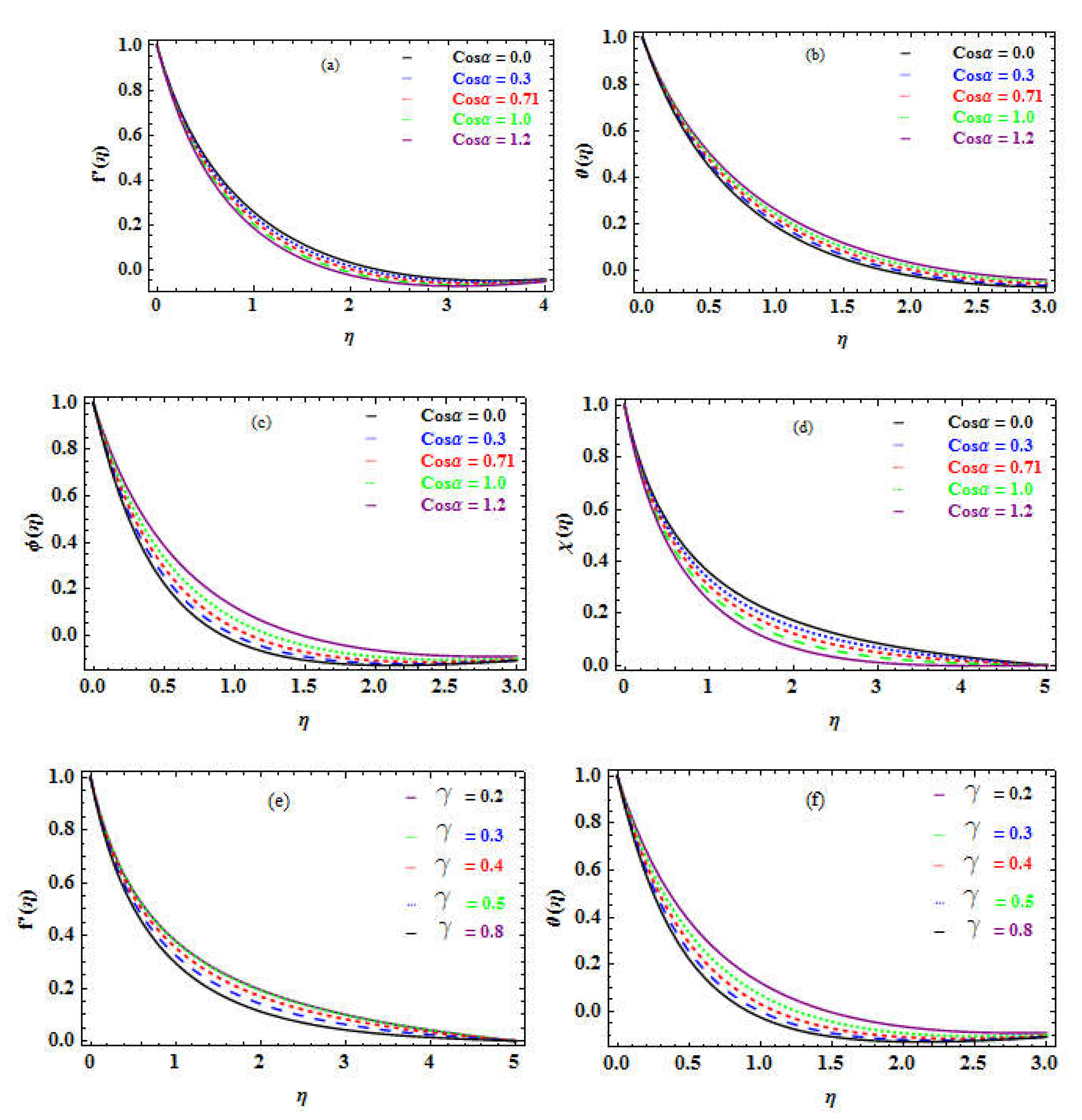
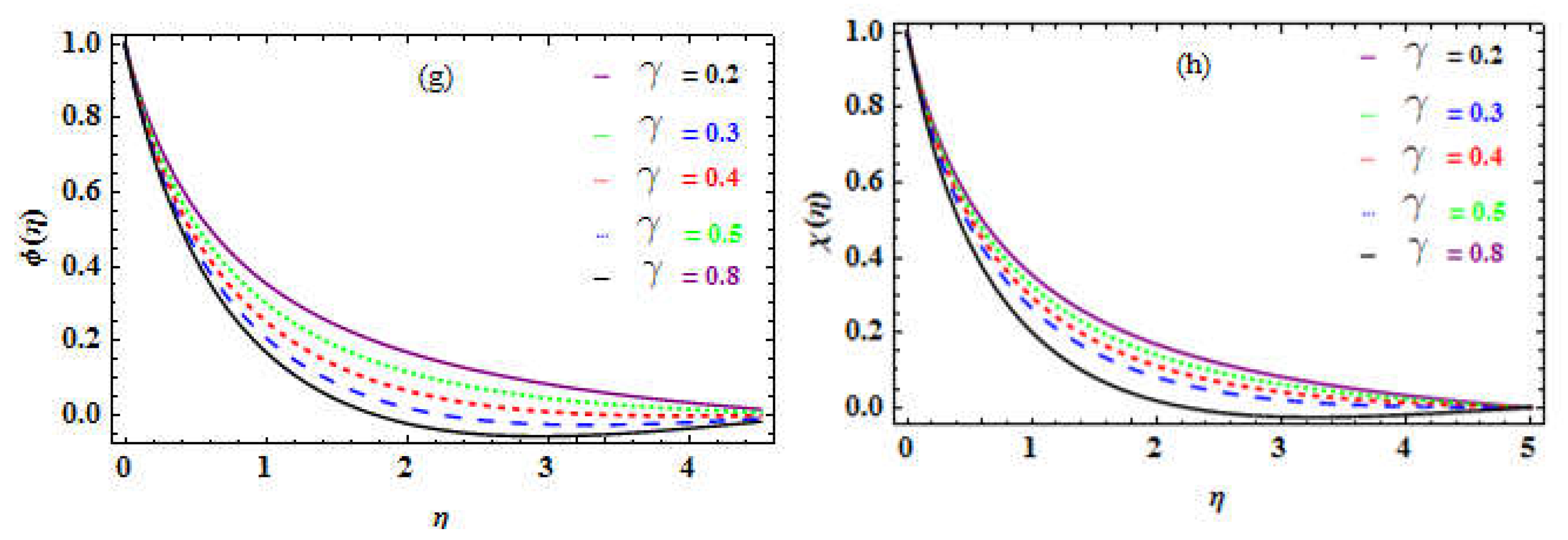
Figure 10.
a-c. Influence of and .
Table 1.
Impression of physical parameter on the physical quantities of interest and their confirmation.
Table 1.
Impression of physical parameter on the physical quantities of interest and their confirmation.
| Present work | Wang [6] | |||
|---|---|---|---|---|
| 0.2 | 1.4338 | 0.2701996 | 1.4331 | 0.2702 |
| 0.6 | 1.4328 | 0.5640398 | 1.4323 | 0.5640 |
| 2 | 1.4299 | 0.8224698 | 1.4298 | 0.8225 |
| 6 | 1.4285 | 2.9064991 | 1.4280 | 2.9065 |
| 15 | 1.4163 | 4.4648811 | 1.4157 | 4.4649 |
| 20 | 1.4042 | 7.57322885 | 1.4035 | 7.5733 |
Table 2.
Influence of onn, ,,, andd.
| 0.2 | 1.4338 | 0.2701 | 1.3266 | 1.6137 |
| 0.4 | 1.4338 | 0.2701 | 1.3266 | 1.7344 |
| 0.6 | 1.4338 | 0.2701 | 1.3266 | 1.8235 |
| 0.8 | 1.4338 | 0.2701 | 1.3266 | 1.8610 |
Table 3.
Influence of on , andd.
| 0.2 | 1.4353 | 0.6406 | 1.2765 | 0.7626 |
| 0.4 | 1.4343 | 0.6106 | 1.3173 | 0.7686 |
| 0.6 | 1.4328 | 0.5469 | 1.3479 | 0.7733 |
| 0.8 | 1.4299 | 0.3976 | 1.3657 | 0.7768 |
Table 4.
Influence of on , ,,, andd.
| 0.2 | 1.4338 | 0.5985 | 1.3331 | 0.9718 |
| 0.4 | 1.4328 | 0.5469 | 1.3479 | 0.9733 |
| 0.6 | 1.4291 | 0.4773 | 1.4244 | 0.9828 |
| 0.8 | 1.4252 | 0.4357 | 1.5063 | 0.9933 |
Table 5.
Influence of on , ,,, andd.
| 0.0 | 1.2812 | 0.3915 | 1.4674 | 1.6529 |
| 0.4 | 1.3351 | 0.3859 | 1.4486 | 1.6375 |
| 0.6 | 1.3726 | 0.3714 | 1.4339 | 1.6257 |
| 1.0 | 1.4727 | 0.3622 | 1.3867 | 1.5885 |
Table 6.
Influence of on , andd.
| 0.0 | 1.4443 | 0.3721 | 1.4266 | 1.6137 |
| 0.4 | 1.4442 | 0.3721 | 1.4267 | 1.9147 |
| 0.6 | 1.4441 | 0.3721 | 1.4267 | 3.2163 |
| 1.0 | 1.4439 | 0.3722 | 1.4268 | 3.5186 |
Table 7.
Influence of on , ,,, andd.
| 0.5 | 1.4313 | 0.5549 | 1.3463 | 0.9142 |
| 2 | 1.4379 | 0.5285 | 1.3556 | 1.1583 |
| 6 | 1.4442 | 0.3721 | 1.4266 | 1.6137 |
| 8 | 1.4452 | 0.2539 | 1.4746 | 1.8496 |
Table 8.
Influence of on , ,,, andd.
| 0.0 | 1.3218 | 0.3872 | 1.4516 | 1.6393 |
| 0.2 | 1.3351 | 0.3859 | 1.4486 | 1.6375 |
| 0.6 | 1.3888 | 0.3792 | 1.4362 | 1.6258 |
| 1.0 | 1.4579 | 0.3719 | 1.4189 | 1.5998 |
Table 9.
Influence of on , ,,, andd.
| 1.0 | 1.3218 | 0.3859 | 1.4486 | 1.6375 |
| 1.6 | 1.3351 | 0.3878 | 1.4682 | 1.6591 |
| 2.5 | 1.3888 | 0.3977 | 1.4846 | 1.6776 |
| 5.0 | 1.4579 | 0.4164 | 1.4988 | 1.6839 |
Table 10.
Influence of on , ,,, andd.
| 0.0 | 1.4551 | 0.7981 | 0.5134 | 1.4931 |
| 0.5 | 1.4533 | 0.7321 | 0.6242 | 1.5172 |
| 1.2 | 1.4498 | 0.6324 | 0.7869 | 1.5375 |
| 2.0 | 1.4443 | 0.3721 | 1.4266 | 1.6137 |
Table 11.
Influence of on , ,,, andd.
| 0.0 | 1.4571 | 0.3693 | 1.4237 | 1.5997 |
| 0.3 | 1.3351 | 0.3859 | 1.4486 | 1.6375 |
| 0.7 | 1.4591 | 0.3738 | 1.3999 | 1.5976 |
| 0.86 | 1.4573 | 0.3698 | 1.4225 | 1.5995 |
| 1.0 | 1.4612 | 0.3748 | 1.3956 | 1.5963 |
Table 12.
Influence of on , ,, andd.
| 1 | 1.4424 | 0.3778 | 1.4239 | 1.6147 |
| 2 | 1.9236 | 0.3623 | 2.1494 | 2.3147 |
| 4 | 2.5399 | 0.3591 | 2.8264 | 2.9697 |
| 6 | 2.9413 | 0.3717 | 3.5213 | 3.5994 |
Table 13.
Influence of on , ,,, andd.
| -0.1 | 1.4485 | 0.7297 | 1.3164 | 1.5899 |
| 0.0 | 1.4469 | 0.5677 | 1.3675 | 1.5962 |
| 0.1 | 1.4443 | 0.3721 | 1.4266 | 1.6137 |
| 0.3 | 1.4379 | 0.1473 | 1.4988 | 1.6253 |
Table 14.
Influence of on , ,,, andd.
| 0.1 | 1.4472 | 0.3678 | 1.4329 | 1.6134 |
| 0.3 | 1.4472 | 0.3678 | 1.4329 | 1.6383 |
| 0.6 | 1.4472 | 0.3678 | 1.4329 | 1.6633 |
| 0.9 | 1.4472 | 0.3678 | 1.4329 | 1.6882 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






