Prerpints.org logo
Preprint
Article

Optimization of Longitudinal Alignment of 4f System in a Compact Vectorial Optical Field Generator Based on a High-Resolution Liquid Crystal Spatial Light Modulator

Altmetrics

Downloads

95

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

13 July 2023

Posted:

14 July 2023

You are already at the latest version

Alerts
Abstract
Vectorial optical fields have sparked considerable interest with potential applications such as optical nano-fabrication, optical micromachining, quantum information processing, optical imaging, and so on. Traditional compact vectorial optical generators with amplitude modulation perform poorly in terms of diffraction effect reduction. In order to address this issue, the refractive 4f system in amplitude modulation is longitudinally aligned using an optimization approach presented in this research. The phase images used for longitudinal alignment are loaded into the liquid crystal spatial light modulator (SLM), and the distance between the lens and the mirror in the reflective 4f system is adjusted for longitudinal alignment by compensating for the neglected phase in the integrated module of the compact vectorial optical field generator. The spot images collected by the CCD are processed using the improved eight-direction Sobel operator, and the longitudinal alignment in the reflective 4f system is determined by the sharpness of the image. The sharpness of the lines' edges and the overall image are both enhanced after optimization compared to before optimization. The results show that the proposed method can significantly reduce the longitudinal alignment error of the reflective 4f system in the amplitude modulation of the compact vectorial optical field generator, lessen the diffraction effect, and improve the performance of the system.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

The polarization states of the vectorial optical field [1,2,3,4,5] regularly change with spatial changes, and a variety of polarization states will appear on the cross section of the optical field [6,7,8]. At present, complex vectorial optical field has been widely used in many fields such as optical micromanipulation technology [9,10], focal field engineering [11,12], quantum information processing [13,14], super-resolution microscopic imaging [15,16], optical trapping and manipulation [17,18,19,20], optical communication [21] and laser processing technology [22].
Due to its high resolution and ability to implement real-time control through programming, SLM is frequently employed in the construction of vectorial optical field generators. How to generate desired beams in complex optical systems has attracted great attention in various related fields. For example, a general-purpose vectorial optical field generator based on two high-resolution reflective SLMs is constructed, and it is capable of independently controlling the four degrees of freedom of the vectorial optical field at the pixel level [23]. At the same time, the pattern is designed to complete the alignment of the 4f system of the vectorial optical field generator. In order to convert linearly polarized beams into vectorial beams with arbitrary spatial polarization and phase distribution, Zhou, Y. proposed a compact optical module capable of efficiently generating vectorial vortex beams [24].In order to control the phase, amplitude, polarization ratio and retardation of the optical field in the spatial distribution, Chen, J. designed a compact vectorial optical field generator based on a high-resolution liquid crystal spatial light modulator that can generate arbitrarily complex vectorial beams by controlling the four degrees of freedom of the optical field while greatly reducing the spatial volume and number of optical elements [25].
In this work, the compact vectorial optical field generator based on the high-resolution liquid crystal spatial light modulator includes two 4f systems. The reflective 4f system relays the beam to the corresponding region of SLM for modulation, and the transmitted 4f system transmits the output optical field to the CCD for date collection. In the reference [25], the longitudinal alignment of the reflective 4f system has a significant inaccuracy in the amplitude modulation of the compact vectorial optical field generator. In order to address this issue, lessen the diffraction effect of the beam during propagation and make the obtained output optical field as clear and sharp as possible, it is necessary to optimize the longitudinal alignment of the reflective 4f system.

2. Experimental Device and Principle

2.1. Compact Vectorial Optical Field Generator

The experimental device of the compact vectorial optical field generator is shown in Figure 1, which is primarily composed of two 4f systems, the integrated module, CCD and SLM. The reflective 4f system consists of the large lens and the mirror and the transmitted 4f system consists of lenses 1 and 2. The integrated module, as shown in Figure 2, consists of a rectangular prism, one square half wave plate (HWP), two square quarter wave plates (QWPs), one polarizing beam splitter (PBS) and four non-polarizing beam splitters (NPBSs).
The fast axes of the three plates are 45 degrees from the horizontal direction. In order to avoid mutual crosstalk caused by the transmitted and reflected beams, the overlapping surface between NPBS 1 and NPBS 3 is blackened. The surface of PBS adjacent to NPBS 4 is also blackened due to the same reason. The collimated horizontally polarized He–Ne laser with the wavelength of 632.8 nm and diameter of 3 mm is used as the source. The SLM with 4K resolution is separated into four different sections that can independently and simultaneously modulate the vectorial beam’s four degrees of freedom. Figure 3 shows the locations of the beam to be modulated on each SLM section which are determined by the integrated module. Phase, amplitude, polarization ratio and retardation are modulated respectively in Section 1Section 2Section 3 and Section 4.
The optical path in the integrated module is shown in Figure 4. The incident beam is first directed by NPBS 1 to Section 1 of SLM for phase modulation. Subsequently, the reflected beam is relayed through the reflective 4f system to NPBS 2 and transmitted back to Section 2 of SLM. The SLM is a phase modulator, so the amplitude modulation is realized by the combination of the polarizing rotator and PBS. The polarizing rotator is composed of QWP and the Section 2 of SLM and the specific principle can be found in the reference [22]. The modulated beam reflected by the Section 2 of SLM will be directed from NPBS 2 to PBS with the optical axis in the vertical direction. Then the HWP changes the polarization of the beam to the horizontal direction. The beam is relayed by the same reflective 4f system to NPBS 3 and transmitted to the rear Section 3 of SLM for polarization ratio modulation. Here, QWP and the Section 3 of SLM constitute another polarizing rotator. The beam is reflected from the section 3 of SLM through NPBS 4 to the rectangular prism and relayed to NPBS 4 by the reflective 4f system, where the beam is modulated by the retardation after passing through the section 4 of SLM. At this time, the integrated module shown in Figure 2 completes the modulation of 4 degrees of freedom in the vectorial optical field. Finally, the beam is relayed to the CCD by a transmitted 4f system. In order to generate the correct vectorial optical field, the diffraction effect of the beam propagation must be reduced by the 4f system, which requires the longitudinal alignment of the 4f system [25].

2.2. 4f System

2.2.1. The Structure of 4f System

The beam can be transformed by the 4f system from the spatial domain to the frequency domain and then back to the spatial domain. The compact vectorial optical field generator consists of two 4f systems. One of them is the transmitted 4f system, as shown in Figure 5a. The transmitted 4f system consists of two lenses, both of which have a focal length of 20 cm. The other is a reflective 4f system, as shown in Figure 5b. The reflective 4f system consists of a lens with a focal length of 10 cm and a mirror.

2.2.2. The Longitudinal Alignment of the 4f System

First, the shear interferometer is used to determine whether the distance between lens and mirror is f [26]. It is generally possible to estimate if the distance between them has met the requirements when the highest interference fringe on the shear interferometer is observed to be parallel to the line of reference. When the distance of the object plane and the image plane to the lens both are f, the longitudinal alignment of the 4f system is theoretically complete. However, the distance between lens and mirror of the reflective 4f system is no longer an ideal distance due to the optical path difference and experimental error, the reflective 4f systems need to be slightly regulated. This includes the longitudinal alignment of the reflective 4f system for amplitude modulation. When the amplitude modulation region is longitudinally aligned, a specially aligned pattern is adopted. The corresponding aligned pattern is loaded in the amplitude modulation region of SLM and the position of the large lens and the mirror in the reflective 4f system is adjusted by the micrometer on the experimental platform. The data are collected by CCD after longitudinal alignment.

2.3. The Amplitude Modulation Principle of the Compact Vectorial Optical Field Generator

The first is phase modulation. Since SLM is a device with an external phase delay, the phase of the optical field can be directly adjusted. According to the reference [27], The optical field after phase modulation can be described by the Jones matrix as the following formula.
J 1 ( x , y ) = e j φ 1 ( x , y ) E i ( x , y ) [ 1 0 ] ,
In the formula (1), E i ( x , y ) is the amplitude intensity distribution of the incident optical field and φ 1 ( x , y ) is the phase information loaded into Section 1 of SLM.
The second is amplitude modulation. The polarizing direction of the optical field spins at a specific angle after the incident beam passes through the polarizing rotator before entering PBS. According to Malus’ law, the amplitude of the optical field is modified by PBS because of the angle between the polarizing direction of the optical field and the optical axis of PBS. The vertically polarizing beam generated by PBS is converted into a horizontally polarizing beam. The optical field after amplitude modulation can be represented by the Jones Matrices as the following formula.
J 2 ( x , y ) = M H W P M s M P R ( φ 2 ( x , y ) ) J 1 ( x , y ) = e j [ φ 1 ( x , y ) + φ 2 ( x , y ) 2 + π 2 ] E i ( x , y ) cos φ 2 ( x , y ) 2 [ 1 0 ] ,
In the formula (2), φ 2 ( x , y ) is the phase information loaded into Section 2 of SLM. M H W P , M s and M P R ( φ 2 ( x , y ) ) are the Jones Matrices for HWP, the reflection of PBS and the polarizing rotator, respectively, which can be given as the following:
M H W P = j [ 0 1 1 0 ] ,   M s = [ 0 0 0 1 ] ,   M P R ( φ 2 ( x , y ) ) = e j φ 2 ( x , y ) 2 [ − sin φ 2 ( x , y ) 2 − cos φ 2 ( x , y ) 2 cos φ 2 ( x , y ) 2 − sin φ 2 ( x , y ) 2 ] .
In fact, the beam has a distance from NPBS 2 to PBS in the integrated module during amplitude modulation and the distance is roughly 5mm in length for a polarization beam splitter. However, in the reference [25], when the reflective 4f system is longitudinally aligned during amplitude modulation, it is considered that the distance of the beam reflected from Section 2 of SLM to the large lens is the same as that from the large lens to Section 3 of SLM. Therefore, the optical path generated by the transmission of the beam in the integrated module is neglected. In order to get a better sharpness of the image observed by CCD, the phase modulation region on SLM can compensate for the neglected phase that is △ φ during longitudinal alignment of the reflective 4f system in amplitude modulation. The sum of the compensated phase and the phase generated by the transmission in the integrated module reaches 2 π , which can reduce the influence of this optical path on the reflective 4f system. The compensated phase can be calculated as the following:
φ = 2 π λ △ x = φ ′ + 2 n π ,   n = 0 , 1 , 2 ⋯ △ φ = 2 π − φ ′
In the formula (4), △ x is the transmission distance of the beam from NPBS 2 to PBS, λ is the wavelength and the phase delay that actually affects the 4f system is φ ′ . By calculation, the compensated phase should be 1.2188 π .

2.4. The Sharp Evaluation of the Image

In order to get a more accurate observation of the sharpness of the image after longitudinal alignment of the reflective 4f system in amplitude modulation, this paper uses an improved eight-direction Sobel operator to extract the contour of the image and evaluate the sharpness of the image by observing the edge of the contour. Compared with the traditional Sobel operator, the image contour is more accurate. Using the Sobel operator to detect the edge of the image is complicated, but it is less affected by noise and has a higher accuracy.
Compared with the traditional Sobel operator, the eight-direction Sobel operator is increased to eight directions based on the only horizontal and vertical directions of the template. The eight-direction Sobel operator proposed in the reference [28] uses a 5×5 directional template. Although the edge of the image is better detected, the influence of the noise is neglected, which worsens the overall detection effect, increases the overall calculation, and slows down the detection speed. In order to address this issue, this paper adopts a 3×3 directional template. The templates for each direction are as follows:
g 1 = [ − 1 0 1 − 2 0 2 − 1 0 1 ] ,   g 2 = [ − 2 − 1 0 − 1 0 1 0 0 2 ] ,   g 3 = [ − 1 − 2 − 1 0 0 0 1 2 1 ] ,   g 4 = [ − 1 0 1 − 2 0 2 − 1 0 1 ] ,   g 5 = [ 1 0 − 1 2 0 − 2 1 0 − 1 ] ,   g 6 = [ 2 1 0 1 0 − 1 0 − 1 − 2 ] ,   g 7 = [ 1 2 1 0 0 0 − 1 − 2 − 1 ] ,   g 8 = [ 0 1 2 − 1 0 1 − 2 − 1 0 ] .
In the formula (5), g 1 , g 2 , g 3 , g 4 , g 5 , g 6 , g 7 and g 8 respectively represent templates in the directions of 0°, 45°, 90°, 135°,180°,225°,270° and 315°.
Firstly, the image to be detected is convolved with eight directional templates to obtain the information about the contour of the image, which is G1, G2, G3, G4, G5, G6, G7 and G8. The gray value at each pixel point can be calculated as the following:
G a = G 1 2 + G 2 2 + G 3 2 + G 4 2 ,
G b = G 5 2 + G 6 2 + G 7 2 + G 8 2 ,
G ’ ( x , y ) = 1 2 G a + G b .
In the formula (8), G’(x, y) is the gray value at each pixel point. In order to improve the efficiency of operation, this paper uses the formula (9) instead of the formula (8) to reduce the amount of calculation. Finally, a suitable threshold value (T) is selected and the gray value of each pixel is performed as a threshold operation. If the gray value of a pixel is greater than or equal to 255, it is determined to be a contour point, otherwise, it is determined to be a non-contour point. The formulas for extracting the contour of the image are as the following:
G ’ ( x , y ) = 1 2 ( | G 1 | + | G 2 | + | G 3 | + | G 4 | ) ,
E ( x , y ) = { 0 , 255 , G ’ ( x , y ) < T G ’ ( x , y ) ≥ T .
In the formula (10), E ( x , y ) represents the gray value of the pixel after the threshold operation.

3. Experimental Results and Discussions

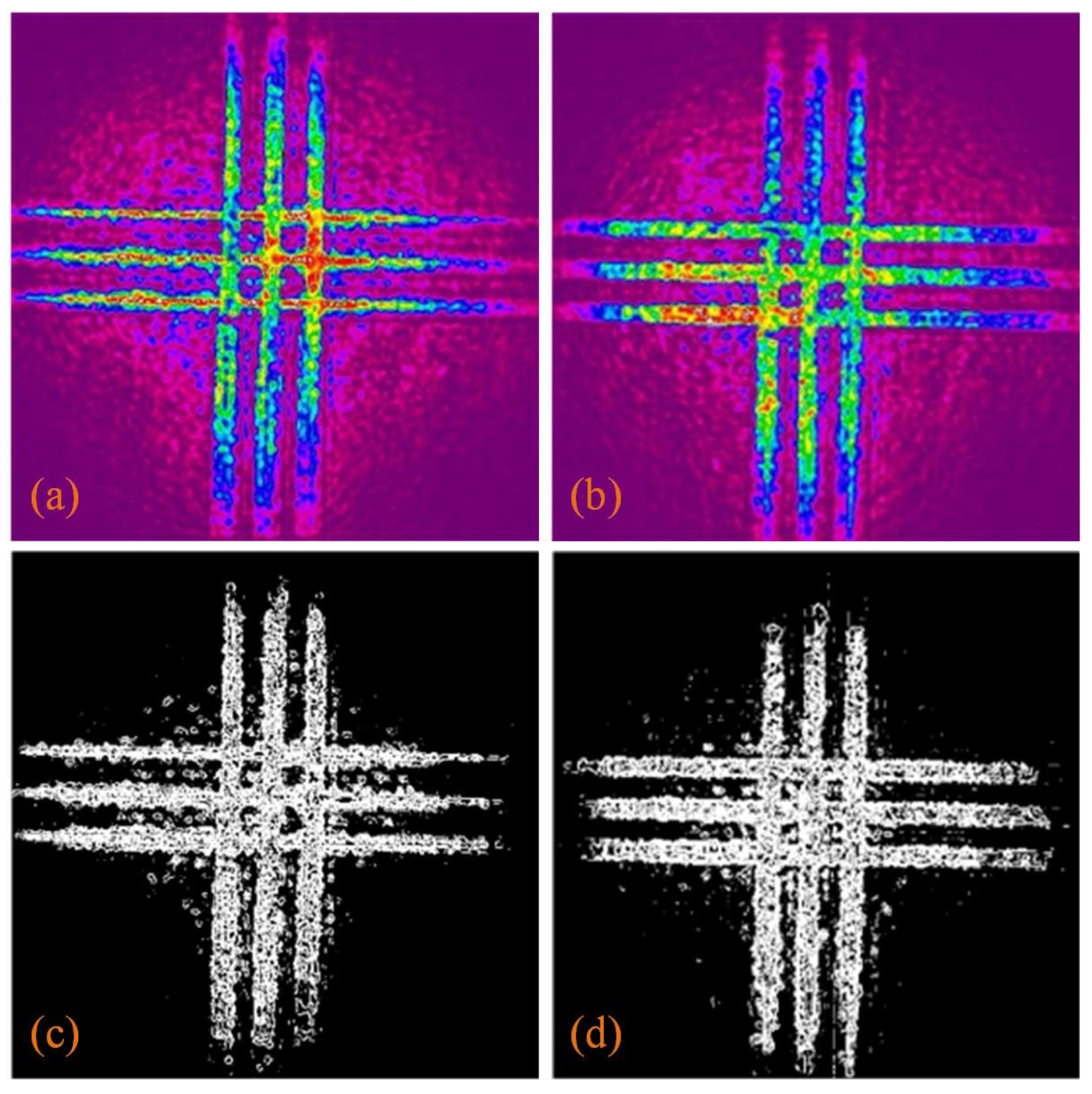
A specially aligned pattern is used for longitudinal alignment of the reflective 4f system in amplitude modulation. Figure 6 is the gray image loaded into SLM during longitudinal alignment and the pattern is composed of three pairs of horizontally and vertically crossed lines. Figure 6a is the gray image of the uncompensated phase, and Figure 6b is the gray image of the compensated phase. The finally optical field is collected by CCD [29]. When the reflective 4f system is longitudinally aligned in amplitude modulation, it is set to pass all light on the lines and suppress all light outside the lines.
The image of the optical spot with uncompensated phase collected by CCD is shown in Figure 7a, and the image of the optical spot with compensated phase is shown in Figure 7b, which correspond to the gray images of Figure 6a,b, respectively. The improved eight-direction Sobel operator is used to process two images of optical spots to obtain corresponding contours, as shown in Figure 7c,d. Compared with the contour without compensated phase, the edge of the contour of the three horizontal lines becomes significantly sharper and the sharpness of the overall image contour is improved. The diffraction effect of the optical field is reduced, and the degree of longitudinal alignment of the reflective 4f system in amplitude modulation is improved.

4. Conclusions

This paper presents an optimal method for the longitudinal alignment of the reflective 4f system in amplitude modulation of a compact vectorial optical field generator based on SLM. In this paper, the composition of the compact vectorial optical field generator, the optical path in the integrated module, the structure of 4f system, the principle of amplitude modulation in the compact vectorial optical field generator and the improved eight-direction Sobel operator are introduced. By compensating the neglected phase to optimize the reflective 4f system and using the improved eight-direction Sobel operator to process the optical spot images, the effect of longitudinal alignment can be more accurately judged. The experimental results show that compared with the contour without compensated phase, the edge of the contour of the three horizontal lines becomes significantly sharper and the sharpness of the overall image contour is improved. The diffraction effect of the optical field is lessened. The longitudinal alignment of the reflective 4f system is optimized in the amplitude modulation of the compact vectorial optical field generator. The amplitude modulation is a necessary process to build a vectorial optical field generator and generate complex vectorial optical fields. This method can improve the performance of the vectorial optical field generator.

Author Contributions

Conceptualization, M.L. and Y.L.; methodology, M.L. and Y.L.; software, M.L. and Y.L.; validation, M.L. and Y.L.; formal analysis, M.L.; investigation, Y.L.; resources, Y.L.; data curation, M.L.; writing—original draft preparation, M.L. and Y.L.; writing—review and editing, M.L. and Y.L.; visualization, Y.L.; supervision, Y.L.; project administration, M.L.; funding acquisition, M.L. and Y.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

Data will be made available on request.

Conflicts of Interest

The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Cheng, W.; Han, W.; Zhan, Q. Compact flattop laser beam shaper using vectorial vortex. Appl. Opt 2013, 52, 4608–4612. [Google Scholar] [CrossRef] [PubMed]
  2. Yao, A.M.; Padgett, M.J. Orbital angular momentum: origins, behavior and applications. Adv. Opt. Photonics. 2011, 3, 161–204. [Google Scholar] [CrossRef]
  3. Wang, X.L.; Cai, X.D.; Su, Z.E.; Chen, M.C.; Wu, D.; Li, L.; Liu, N.L.; Lu, C.Y. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 2015, 518, 516–519. [Google Scholar] [CrossRef] [PubMed]
  4. Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light-Sci. Appl. 2019, 8, 1–29. [Google Scholar] [CrossRef] [PubMed]
  5. Chen, J.; Wan, C.; Zhan, Q. Vectorial optical fields: recent advances and future prospects. Sci. Bull. 2018, 63, 54–74. [Google Scholar] [CrossRef]
  6. Zhan, Q. Cylindrical vector beams: from mathematical concepts to applications. Adv. Opt. Photonics. 2009, 1, 1–57. [Google Scholar] [CrossRef]
  7. Cheng, W.; Han, W.; Zhan, Q. W; Compact flattop laser beam shaper using vectorial vortex. Appl. Opt. 2013, 52, 4608–4612. [Google Scholar] [CrossRef]
  8. Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V. Roadmap on structured light. J. Opt. 2017, 19(1), 013001. [Google Scholar] [CrossRef]
  9. Tan, H.T.; Hu, H.Q.; Huang, L.; et al. Plasmonic tweezers for optical manipulation and biomedical applications. Analyst. 2020, 145, 5699–5712. [Google Scholar] [CrossRef]
  10. Ho, V. W.L.; Chang, Y.; Liu, Y.; et al. Optical Trapping and Manipulating with a Silica Microring Resonator in a Self-Locked Scheme. Micromachines. 2020, 11, 202. [Google Scholar] [CrossRef]
  11. Yu, Y.Z.; Zhan, Q.W. Optimization-free optical focal field engineering through reversing the radiation pattern from a uniform line source. Opt. Express. 2015, 23, 7527–7534. [Google Scholar] [CrossRef] [PubMed]
  12. Pan, Y.; Gao, X.Z.; Zhang, G.L. ; Spin angular momentum density and transverse energy flow of tightly focused kaleidoscope-structured vector optical fields. APL Photonics. 2019, 4, 096102. [Google Scholar] [CrossRef]
  13. Monroe, C. Quantum information processing with atoms and photons. Nature 2002, 416, 238–246. [Google Scholar] [CrossRef]
  14. Polino, E.; Valeri, M.; Spagnolo, N.; Sciarrino, F. Photonic quantum metrology. AVS Quantum Sci. 2020, 2, 024703. [Google Scholar] [CrossRef]
  15. Krüger, J.R.; Keller-Findeisen, J.; Geisler, C.; Egner, A. Tomographic STED microscopy. Biomed. Opt. Express. 2020, 11, 3139–3163. [Google Scholar] [CrossRef]
  16. Tamburini, F.; Anzolin, G.; Umbriaco, G.; Bianchini, A.; Barbieri, C. Overcoming the Rayleigh criterion limit with optical vortices. Phys. Rev. Lett. 2006, 97, 163903. [Google Scholar] [CrossRef]
  17. Harke, B.; Keller, J.; Ullal, C.K.; Westphal, V.; Schönle, A.; Hell, S.W. Resolution scaling in STED microscopy. Opt. Express. 2008, 16, 4154–4416. [Google Scholar] [CrossRef]
  18. Tan, H.T.; Hu, H.Q.; Huang, L.; Qian, K. Plasmonic tweezers for optical manipulation and biomedical applications. Analyst. 2020; 145, 5699–5712. [Google Scholar]
  19. Zhan, Q. ; Trapping metallic Rayleigh particles with radial polarization. Opt. Express. 2004, 12, 3377–3382. [Google Scholar] [CrossRef]
  20. Xue, Y.; Wang, Y.; Zhou, S.; Chen, H.W.; Rui, G.; Gu, B.; Zhan, Q. Focus shaping and optical manipulation using highly focused second-order full Poincaré beam. J. Opt. Soc. Amer. A. 2018, 35, 953–958. [Google Scholar] [CrossRef]
  21. Willner, A. E.; Huang, H.; Yan, Y.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics. 2015, 7, 66–106. [Google Scholar] [CrossRef]
  22. Rodrigo, J. A.; Alieva, T. ; Vector polymorphic beam. Sci. Rep. 2018, 8, 7698. [Google Scholar] [CrossRef] [PubMed]
  23. Han, W.; Yang, Y. F.; Cheng, W.; et al. Vectorial optical field generator for the creation of arbitrarily complex fields. Opt. Express. 2013, 21, 20692–20706. [Google Scholar] [CrossRef]
  24. Zhou, Y.; Li, X.; Cai, Y.; et al. Compact optical module to generate arbitrary vector vortex beams. Appl. Opt. 2020, 59, 8932–8938. [Google Scholar] [CrossRef] [PubMed]
  25. Chen, J.; Wang, Y.; Zhan, Q. W.; et al. Compact vectorial optical field generator based on a 10-megapixel resolution liquid crystal spatial light modulator. Opt. Commun. 2021, 495, 127112. [Google Scholar]
  26. Emilia, M.; Maurice, W.; Vincent, T. Simple phase-shifting lateral shearing interferometer. Opt. Express. 2014, 29, 1264–1266. [Google Scholar]
  27. Kenny, F.; Lara, D.; Rodríguez-Herrera, O. G.; et al. Complete polarization and phase control for focus-shaping in high-NA microscopy. Opt. Express. 2012, 20, 14015–14029. [Google Scholar] [CrossRef]
  28. Liu, W.; Wang, L. Quantum image edge detection based on eight-direction Sobel operator for NEQR. Quantum Inf Process. 2022, 21, 190. [Google Scholar] [CrossRef]
  29. Chen, J.; Wan, C. H.; Kong, L. J.; et al. Precise transverse alignment of spatial light modulator sections for complex optical field generation. Appl. Opt. 2017, 56, 2614–2620. [Google Scholar] [CrossRef]
Preprints 79402 g001
Figure 1. The experimental device of the compact vectorial optical field generator.
Figure 1. The experimental device of the compact vectorial optical field generator.
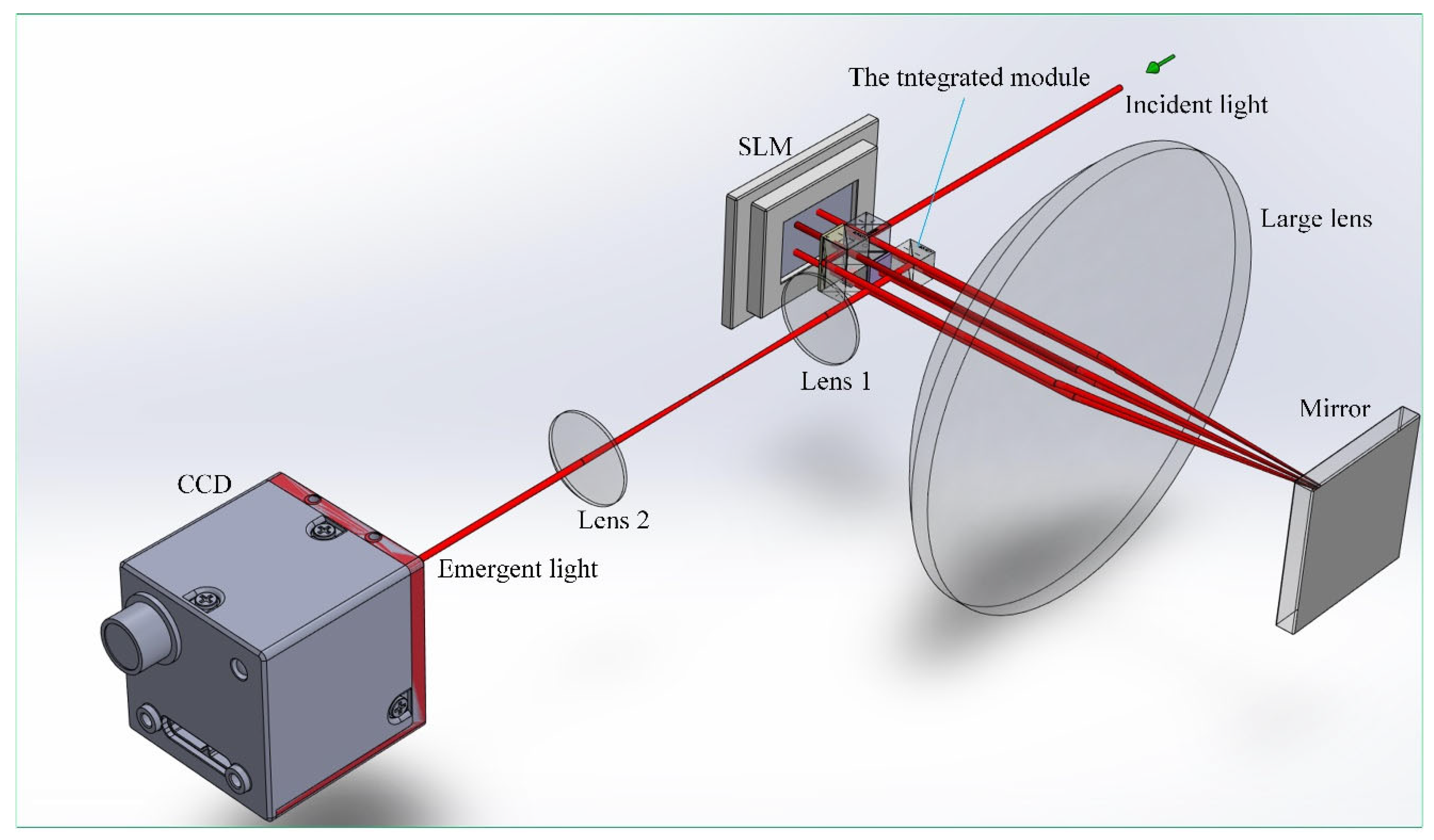
Preprints 79402 g001
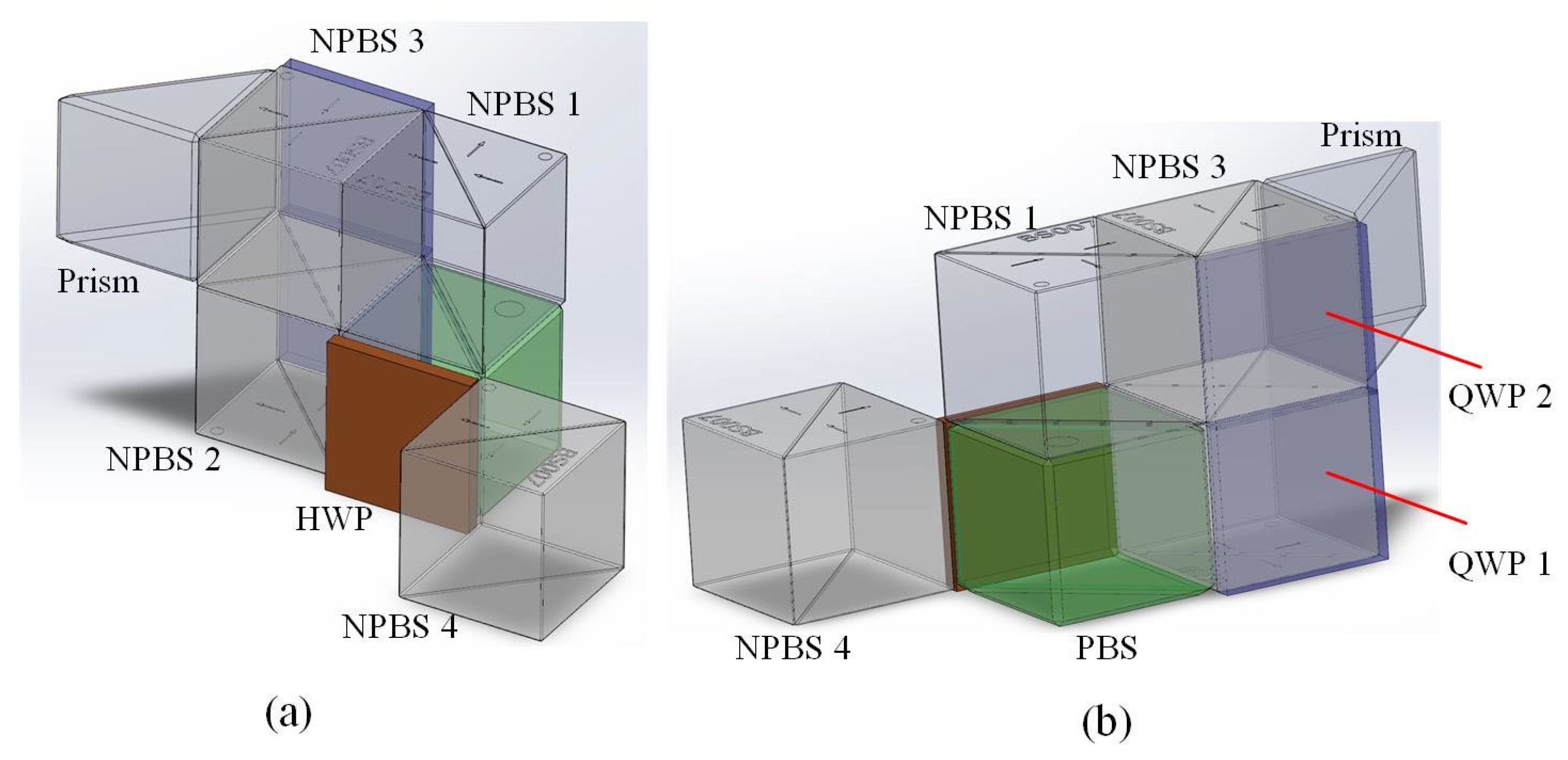
Preprints 79402 g002
Figure 2. (a) Front view of the integrated module; (b) Rear view of the integrated module.
Figure 2. (a) Front view of the integrated module; (b) Rear view of the integrated module.
Preprints 79402 g002
Preprints 79402 g003
Figure 3. The locations of the beam to be modulated on each SLM section.
Figure 3. The locations of the beam to be modulated on each SLM section.
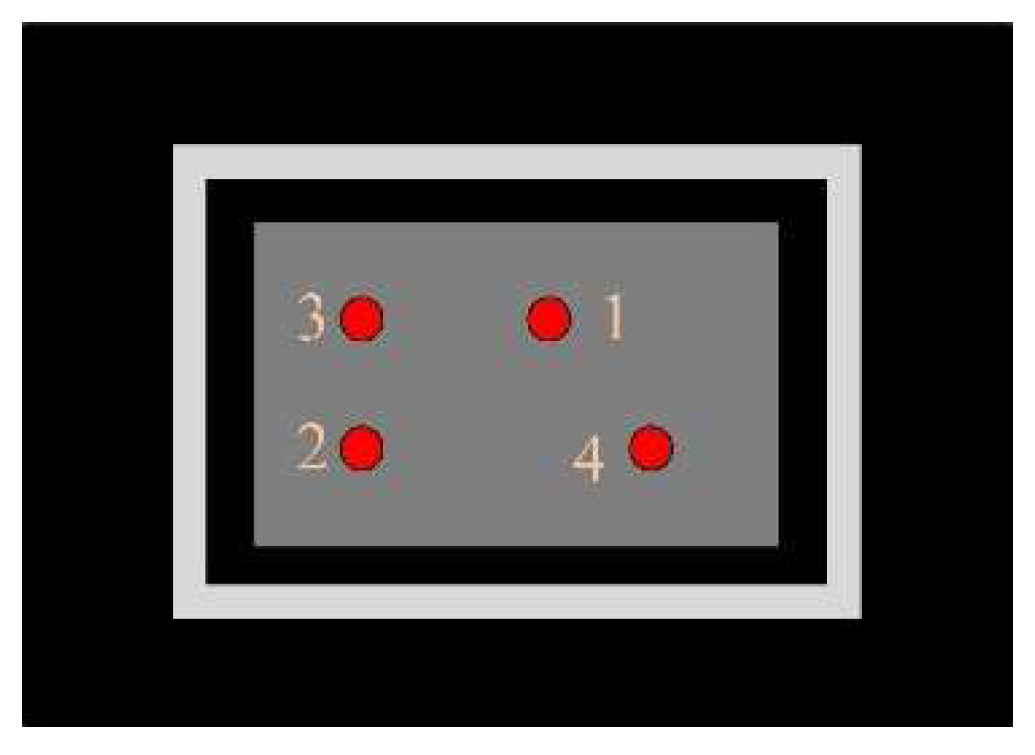
Preprints 79402 g003
Preprints 79402 g004
Figure 4. (a) Front view of the optical path in the integrated module; (b) Rear view of the optical path in the integrated module.
Figure 4. (a) Front view of the optical path in the integrated module; (b) Rear view of the optical path in the integrated module.
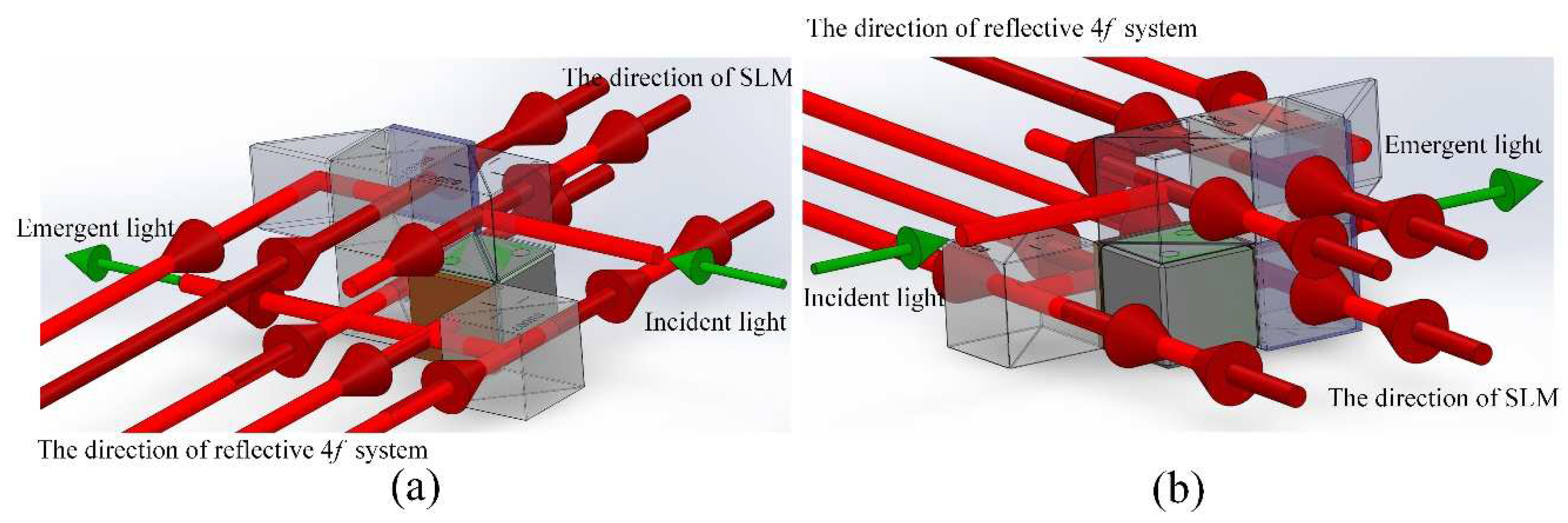
Preprints 79402 g004
Preprints 79402 g005
Figure 5. (a) The transmitted 4f system; (b) The reflective 4f system.
Figure 5. (a) The transmitted 4f system; (b) The reflective 4f system.
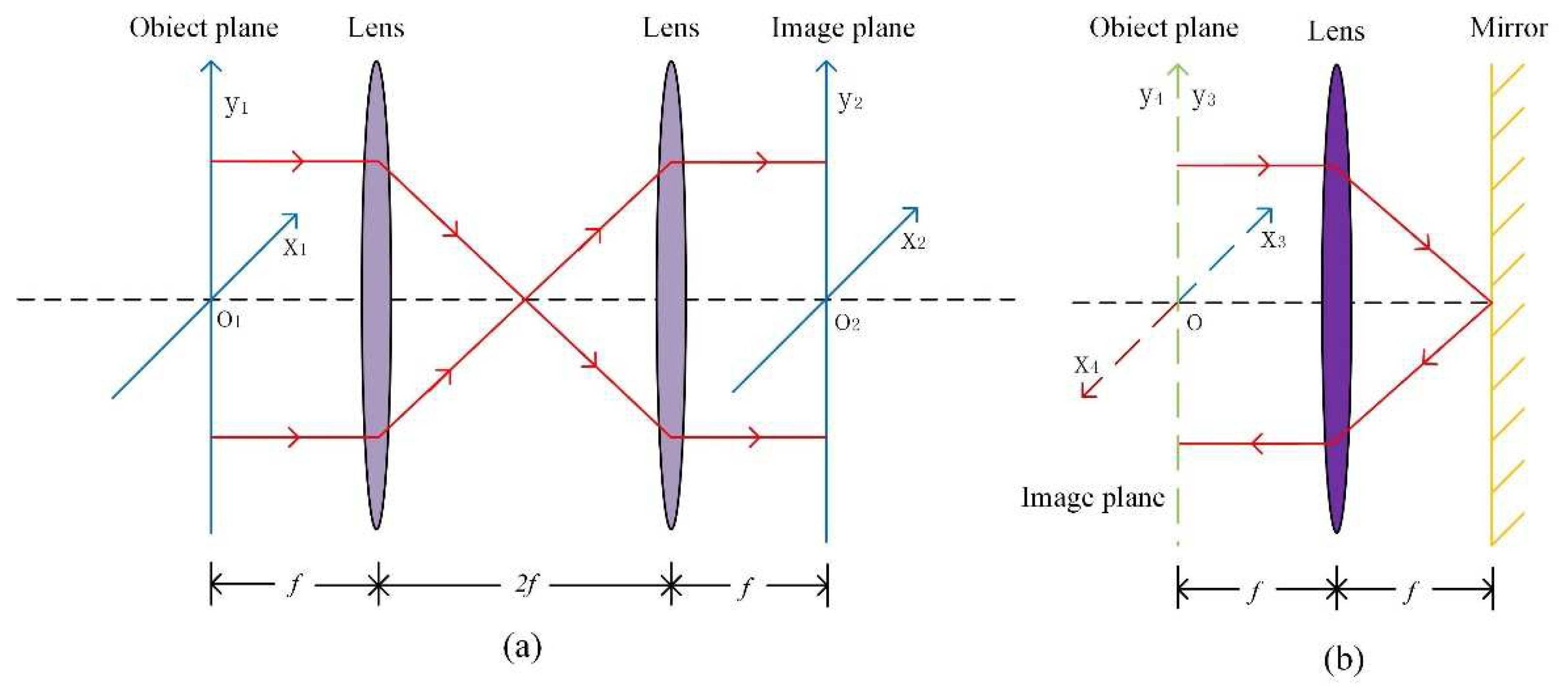
Preprints 79402 g005
Preprints 79402 g006
Figure 6. Longitudinally aligned gray images in amplitude modulation. (a) Uncompensated phase; (b) Compensated phase.
Figure 6. Longitudinally aligned gray images in amplitude modulation. (a) Uncompensated phase; (b) Compensated phase.
Preprints 79402 g006
Preprints 79402 g007
Figure 7. (a) The image of optical spot with uncompensated phase; (b) The image of optical spot with compensated phase; (c) Extract the contour from the image of optical spot with uncompensated phase; (d) Extract the contour from the optical of light spot with compensated phase.
Figure 7. (a) The image of optical spot with uncompensated phase; (b) The image of optical spot with compensated phase; (c) Extract the contour from the image of optical spot with uncompensated phase; (d) Extract the contour from the optical of light spot with compensated phase.
Preprints 79402 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated