Prerpints.org logo
Preprint
Article

Inverse Analysis Investigation by Gaussian Processes Optimisation of a Historical Concrete Bridge Relying on Dynamic Modal Measurements

Altmetrics

Downloads

106

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 July 2023

Posted:

14 July 2023

You are already at the latest version

Alerts
Abstract
In the broad field of Inverse Analysis and Structural Identification, it is nowadays of a large interest the study of Gaussian Processes, as a reliable and efficient optimisation method, particularly helpful toward the identification of a global optimum point, under the conditions of complicated functions to be optimised. In the present contribution, a specific case study is considered, focusing on a historical road reinforced concrete arched bridge, located in Northern Italy, employing dynamic modal properties, deciphered from in-situ measurements, previously acquired under operational traffic conditions, by a standard wired accelerometer system, placed at the deck level. Aiming at the identification and diagnosis of the bridge structure, three main methodological steps are herein considered: the adoption of a FEM model of the structure (in the linear dynamic framework), the definition of an appropriate discrepancy function, based on measured and numerically computed quantities (natural frequencies and mode shapes of the bridge), and the investigation of such a discrepancy function, toward a consistent selection of an optimisation strategy for the identification of sought parameters (Young’s moduli and mass densities of diverse elements of the structure). The presented developments, within the framework of methodological optimisation approach by Gaussian Processes, and achieved results display a rather efficient perspective, with reference to the considered case study, toward inverse analysis for structural diagnosis, in the context of strategic (historical) infrastructures.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

In a Structural Identification context, it is nowadays of a large and growing interest the possibility to effectively estimate model parameters, starting from experimental measurements, toward reliable model calibration, for subsequent employment and predictions. Within general and various approaches (see, e.g., [1,2]), a significant relevance is assumed by Gaussian Processes, employable toward the Inverse Analysis goal as optimisation tools, particularly advantageous, from a computational and robustness point of view, to tackle complicated identification problems featuring local minima difficulties (see, e.g.,[3,4,5,6,7]). Such approaches have been proven to be particularly efficient in various analyses, regarding different engineering application fields, such as Environmental Engineering (see, e.g., [8]) and Biomechanical Engineering (see, e.g., [9]).
Classical Inverse Analysis problems are usually tackled also in Civil Engineering research and applications, e.g. toward the identification of mechanical properties of structural elements, for design or diagnosis purposes. In this field, the suitable adoption of in situ testing and consistent computational modelling, and their reliable combination, represent a fundamental step together with numerical optimisation for robust and high quality parameter estimations (see, e.g., at a local structural scale [10,11] or at a global structural scale [12,13,14]). Within Civil Engineering application fields, the dynamic testing of structures in regular operative conditions plays a significant role toward Structural Health Monitoring purposes. Such research branch strictly correlates Inverse Analysis and Structural Identification during vibration experiments or operational state measurements of the structure, aiming at the estimation of modal properties of a structure by Operational Modal Analysis, as proposed, e.g., in [15,16,17,18,19,20,21,22,23].
In combination of innovative Inverse Analysis, based on Gaussian Processes optimisation, and dynamic modal input measurements, the present paper develops an investigation toward model calibration in a Structural Dynamics context for a Reinforced Concrete bridge. Specifically, the considered case study focuses on a historical reinforced concrete arched bridge, Brivio bridge, located in Northern Italy [24]. The bridge, both for hits historical value and its crucial, currently active, infrastructural role, has recently been the subject of a thorough study supported by experimental campaigns, followed by response signal processing and deciphering (see, e.g., [25,26,27,28]) and by property identification, model calibration and structural diagnosis (see, e.g., [29,30,31,32]).
The main goals of the present work aim at defining a complete and robust Inverse Analysis procedure able to efficiently tackle a complex structural identification problem relying on dynamic modal measurements only, taking advantage of a global optimisation approach, as provided by Gaussian processes. With specific reference to the considered case study, the investigation is devised for an efficient and automated methodology toward structural diagnosis or current operative condition assessment. Moreover, from a more general standpoint, the analysis procedure may be extended, either as a methodological guideline and application approach, to related structures in Civil Engineering research fields, combined to Structural Health Monitoring purposes.
The paper is organised as follows. In Section 2 the methodological approach adopted for Inverse Analysis is presented, focusing both on the Gaussian Processes strategy (Section 2.1) and on the specific selection of objective function to be investigated (Section 2.2). Section 3 describes the selected case study, namely Brivio bridge, from the structural, modelling and experimental testing standpoints. As an application of the proposed approach to the specific case study, in Section 4, the main results of the developed analyses are collected and discussed, providing relevant comments. Furthermore, general remarks are outlined in Section 5, gathering global observations and proposing possible future research perspectives, toward achieving effective Inverse Analysis procedures.

2. Inverse analysis investigation relying on dynamic modal measurements

According to the aims aforementioned in the Introduction, in the current section, the proposed methodology is discussed from a general point of view, both for the selected optimisation approach, namely Gaussian Processes (Section 2.1), and for a proper choice of the objective function, to be minimised within an Inverse Analysis strategy, specifically conceived to rely only on dynamic modal measurements, toward structural mechanical parameter estimation (Section 2.2).

2.1. Methodological optimisation approach by Gaussian Processes

Gaussian Processes represent a reliable and efficient optimisation method, particularly helpful toward the identification of a global minimum point, under conditions of severely complicated functions to be optimised. In the current section, a brief theoretical introduction to the approach is provided; further details may be found, e.g., in [3,4,5,6], also illustrated by applications, e.g., in [8,9].
Gaussian Processes can be illustrated by a linear regression model, which consists of a combination between a linear function of model parameter vector w and a non–linear function of input data vector x :
y ( w , x ) = ∑ m = 1 M w m φ m ( x )
where φ m ( x ) is a fixed set of basis functions of the input data variables (e.g., polynomial or radial basis functions [33,34]).
For N given learning training patterns ( x n , t n ) , being x n the input vector and t n the observation response value for n = 1 , ⋯ , N , model parameter vector w of the linear combination may be obtained by the penalised least–squares method, namely:
w = ( Φ T Φ + α I ) − 1 Φ T t
where Φ N × M is a method design matrix, with elements defined as φ m ( x n ) , and I is the identity matrix of order M. Regularisation parameter α (usually called hyperparameter, in the process jargon) can be computed by using a validation set or by maximising the evidence of dataset p ( t | α ) , with respect to α , within a Bayesian inference framework [5].
The Gaussian Process model shall consistently be derived by reformulating the linear model in terms of a dual representation, where the learning process is achieved by a minimisation of a regularised error, defined through a N × N symmetric Gram matrix:
K = Φ Φ T = k ( x , x ′ )
where elements of the matrix correspond to a kernel function k ( x , x ′ ) . Such definition allows for a prediction associated to a new input vector x * , namely:
G P ( x * | x , t , α ) = k * ( x , x * ) T ( K + α I ) − 1 t
where k * ( x , x * ) holds the role of a covariance vector between a new input x * and the whole set of other inputs.
Therefore, a Gaussian Process approach may be interpreted, according to Bayesian theory, as a dual representation of a linear combination model, while the kernel function may be conceived as a covariance function. Consistently, the regression model allows for the prediction of target variable y ( x * ) , for each new input vector x * . The evaluation of conditional distribution p ( y | t ) , associated to Gaussian Process, requires the definition of relevant mean and covariance, as:
x * ¯ = k T C − 1 t
σ 2 ( x * ) = x * ¯ − k T C − 1 k
C ( x , x ′ ) = K + 1 β I
where β is the variance parameter of the target distribution and C N × N is the covariance matrix, defining likelihood of input x and x ′ , which should give rise to strongly correlated values of y ( x ) and y ( x ′ ) in the output space.
Any function suitable to generate a specific non–negative covariance matrix can be used as a covariance kernel function for any ordered set of input vectors; a stationary, non–isotropic squared exponential covariance function may be selected, as given by:
k ( x , x ′ ) = ν exp − 1 2 ∑ m = 1 M γ m ( x m − x m ′ ) 2 + b
where ν controls the vertical scale of the problem, γ m provides a different scaling factor for each m–th dimension, b represents the deviation control factor. Such hyperparameters display a rather important role, directly related to the model sensitivity with respect to the input parameters, therefore allowing to measure the importance of the input parameters.
The definition of a covariance function allows for the Gaussian Process prediction of new input vectors, provided that hyperparameters are effectively calibrated, e.g. by the maximisation of a log–likelihood function:
δ = β , ν , γ 1 , ⋯ , γ M , b T
log p ( t | δ ) = 1 2 log | C | − 1 2 t C − 1 t − N 2 log 2 π
as possibly efficiently optimised by gradient based algorithms (e.g., a Levenberg–Marquart Algorithm or a Trust Region Algorithm).

2.2. Study on the objective function

In a Inverse Analysis approach, a fundamental step is the proper selection of an objective function f ( θ ) , as a measure of the discrepancy between the numerical model and the real object; therefore, the minimisation of such a function shall lead to obtain the sought parameters ( θ ) of the model.
In the present study, according to a previous selection [29], the objective function is based on dynamic modal properties of the structure under consideration (mode shapes u ( θ ) i and mode frequencies ω ( θ ) i ), while the sought parameters are selected as material Young’s moduli and densities of diverse structural elements ( θ = E 1 , ⋯ , E N , ρ 1 , ⋯ , ρ M ). Consequently, the discrepancy function consists of a vector of differences between the calculated eigenvectors, i.e. mode shapes of the structure ( u ( θ ) n u m i ), and eigenvalues, i.e. related to modal frequencies ( ω ( θ ) n u m i ), of the model and, respectively, eigenvectors ( u e x p i ) and eigenvalues ( ω e x p i ) obtained from experiments on a real object, namely in one possible mathematical form:
f ( θ ) = ∑ i = 1 n u ( θ ) n u m i − u e x p i 2 1 / 2 ∥ u e x p ∥ + ∑ i = 1 n ω ( θ ) n u m i − ω e x p i 2 1 / 2 ∥ ω e x p ∥
The proper matching correspondence for eigenvectors and eigenvalues with real counterparts may be found by Modal Assurance Criterion (MAC) computations [35], also improved by a priori (i.e., before objective function evaluation) pairing, ensuring a regularisation effect:
MAC i j = u ( θ ) n u m i ∥ u ( θ ) n u m i ∥ T u e x p j ∥ u e x p j ∥
In order to further deepen the study on the objective function, to allow for better computational performance of the minimisation algorithm, in view of adoption of Gaussian Processes, a second definition of discrepancy function is conceived, providing an additional contribution to Equation (11), namely:
f * ( θ ) = f ( θ ) + F ∑ j = 1 m v j ρ j ρ ¯ − 1
where F acts as a penalty coefficient, v j is the ratio of the volume for a given material structural element to the volume of the entire structure, and ρ ¯ is an average reference material mass density.
In following Section 4, the results of the study on the objective function are presented, highlighting the differences and advantages with respect to each choice of the discrepancy function, either by Equation (11) or Equation (13), with the aim to achieve an effective adoption of Gaussian Processes as an Inverse Analysis optimisation approach.

3. Case study: a historical concrete bridge

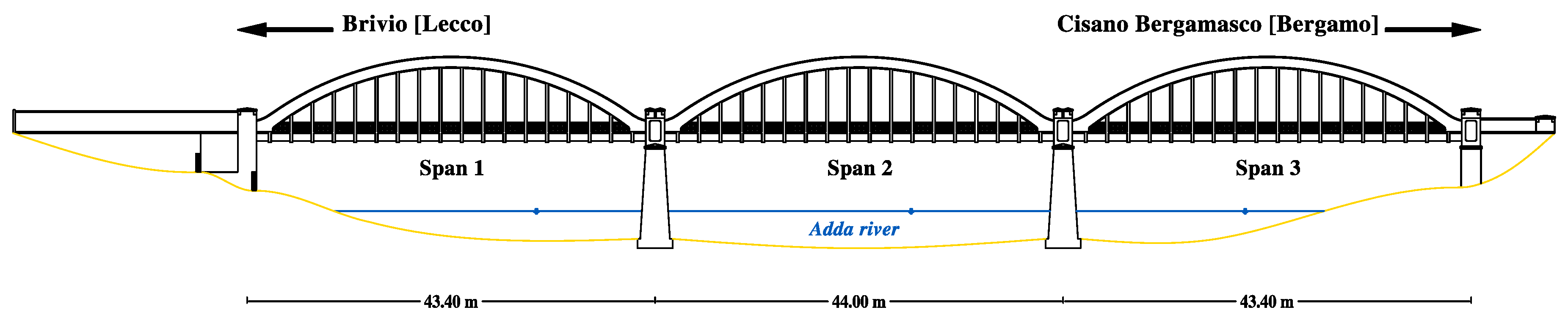
The case study considered in the present work refers to a specific road infrastructure: Brivio bridge, a historical reinforced concrete three–span arched bridge [24]. The bridge, built in 1917, displays a significant historical and structural value, and currently preserves its full daily traffic infrastructural functionality, then keeping a key role in the local territory, between Brivio (province of Lecco) and Cisano Bergamasco (province of Bergamo), in the Lombardia region, Northern Italy, over the Adda river (Figure 1).
In the current section, brief descriptions of Brivio bridge (Figure 2) from a structural standpoint, of the developed FEM model (Figure 3) and of a previously carried out experimental campaign are provided, for a proper understanding of the Inverse Analysis procedure (source reference and detailed information may be found in [24,25,26,27,29]).
The reinforced concrete road bridge consists of three arched spans, supported by characteristic twin parabolic arches and with hanging underneath straight deck. The structure shows full symmetry, with respect to its mid–longitudinal plane. The average height of the deck is about 8 m above water level (Adda river, flowing out of the Lecco branch of Como lake and going down toward the Po valley). The central span, supported by two pillars in the bed of the river, is 44 m long, while the lateral spans, connected to the river banks, are 43.4 m long, summing up to a total length of 130.8 m (in the sequel, for the sake of simplicity: “Span 1” for the lateral span toward Brivio, “Span 2” for the central one, “Span 3” for the lateral span toward Cisano Bergamasco, as also shown in Figure 2). The twin parabolic arches of the bridge are designed on a geometry with a 42.80 m span and a 8.00 m rise. The cross section of each arch structural element displays a rectangular shape, built with a constant width (0.60 m) and a variable height (from 1.37 m, at the impost, to 1.25 m, at the crown), being the whole profile of each arch symmetric, with respect to the vertical axis at half span. Each arch is connected to the corresponding other, on their upper central part, by eight transverse beams, and to the bridge deck through a system of sixteen reinforced concrete hangers (at each side, at each span), with a rectangular cross section (0.32 m × 0.60 m). The road deck is 9.2 m wide, as designed for two roadway lanes, contoured by two sidewalks (each 0.8 m wide), built as cantilevers. Two main longitudinal girders (section 0.45 m × 1.00 m) are placed in each span of the bridge, at a respective transverse distance of 8.60 m, and are joined by further secondary beam elements (section 0.20 m × 0.55 m) installed at a distance equal to 2 m, symmetrically located with respect to the vertical longitudinal plane of the bridge; between this girder system, transverse grid beam connections (section 0.30 m × 0.75 m) are employed, approximately every 2.30 m. Such grid substructure is completed, at the deck level, by a reinforced concrete slab, with a thickness of 0.15 m. The intermediate supports of the spans, inside the river bed, are constituted by two concrete piers, built with a tapered cross section (maximum dimensions, at the base, equal to 12.8 m × 3.8 m, respectively in the transverse and longitudinal directions). The pier foundation system is set on forty–eight reinforced concrete piles (square cross section with a 0.35 m side), with a driving depth ranging from 13 m to 16 m. Supporting reinforced concrete slabs (height equal to 1 m) are placed above both the intermediate piers and the abutments.
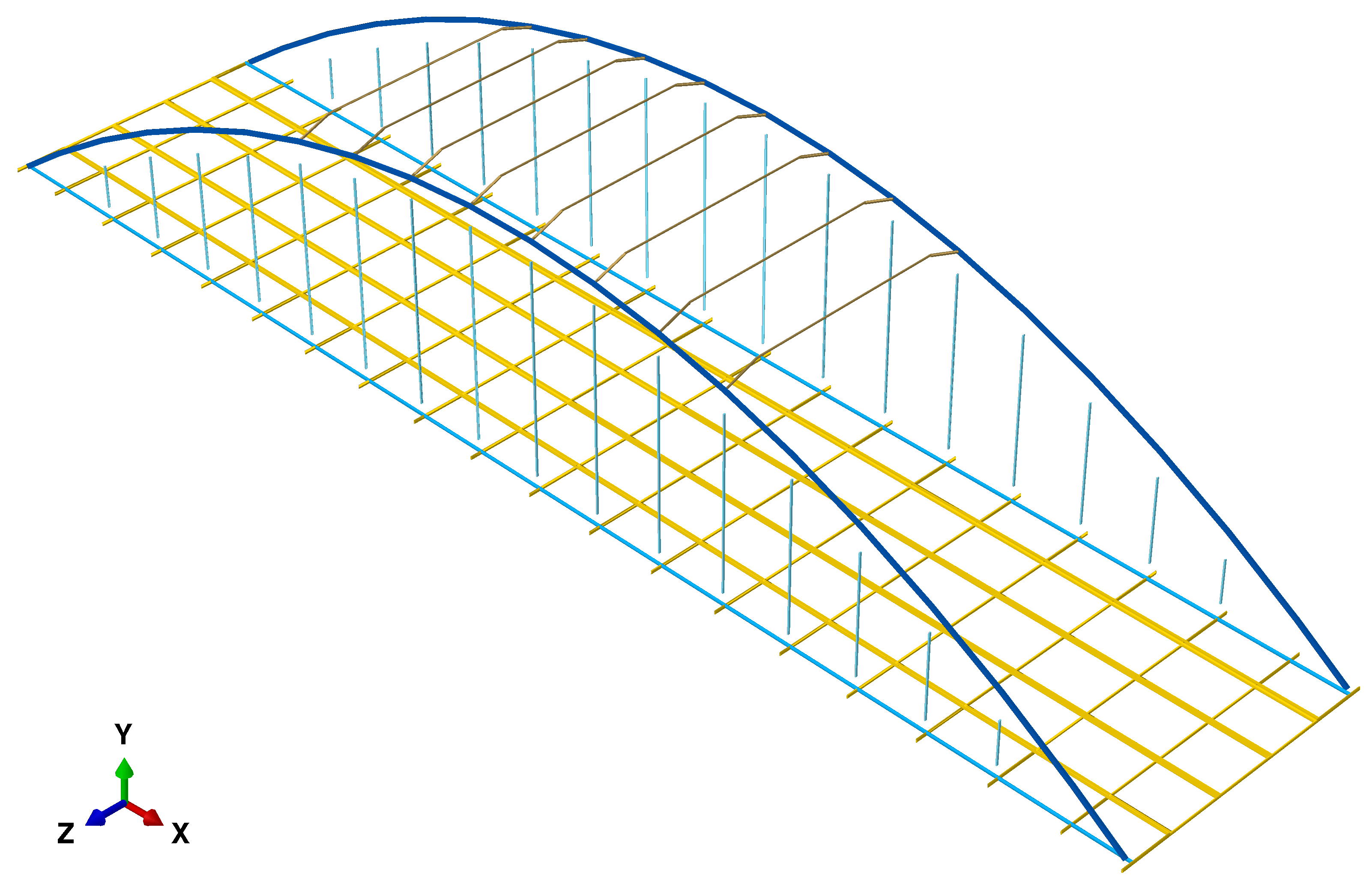
Consistently with the above–provided synoptic technical description, a linear elastic FEM model of Brivio bridge (single span, referring to Span 1, see Figure 3) is adopted, as originally developed in [29], employing the Abaqus finite element code, then combined with Python and Matlab self–implemented routines.
The model is conceived as a three–dimensional frame structure composed by beam finite elements, realised as an assembly of five principal structural components: deck, longitudinal deck girders, arches, hangers and upper transverse beams, as also highlighted in Figure 3, together with the reference coordinate system (x for the longitudinal axis, y for the vertical axis and z for the transverse horizontal axis of the bridge). The mechanical constitutive parameters are selected consistently with the five underlying structural components, although only nine parameters (five Young’s moduli and four mass densities) are finally adopted as sought parameters in the Inverse Analysis problem, according to a sensitivity analysis study previously developed in [29] and as reported in Table 1 and Table 2. The geometrical features of the FEM model are carefully assumed as in [29]. The deck is modelled by a meshing grid of 254 beams, the arches are built by 70 elements, whereas 24 elements are employed for the upper beams. Moreover, the deck–hanger and the hanger–arch joints are reproduced by the implementation of rigid link models. Globally, the FEM model of the bridge sums up to 380 beam elements and 1680 degrees of freedom, keeping a significantly reduced size for the computational model, in view of the computational burden for repetitive runs within the Inverse Analysis optimisation. Further, non–structural mass components, e.g. referring to the asphalt layer, are also included in the model. In defining the boundary conditions, the model is implemented as simply supported at the deck with combined elastic supports (linear spring elements), namely with two z–axis rotational springs at both extremities and two translational springs (at x–axis, horizontal, and y–axis, vertical, respectively), set at the second edge.
In order to feed the optimisation procedure in the Inverse Analysis methodology, the numerical counterparts computed on the FEM model are compared with experimentally obtained quantities (i.e., identified experimental mode shapes and modal frequencies). Operational experimental campaigns were performed on Brivio bridge between 11 and 13 June 2014 (see details reported in [25,26,27]). Several instrumentation systems were adopted during the test phases, in particular: ten uniaxial wired piezoelectric accelerometers, seven wireless sensors, four QDaedalus system total stations and a laser scanner; simultaneous dynamic testing and measurement of the structure, under regular operational traffic loading conditions, were defined also according to diverse setups. In the present work, experimentally identified quantities are acquired from previously processed data, while details on experimental identification and response signal processing may be found, respectively, in [29] and [28], with reference both to single span and whole bridge analysis.

4. Analysis results

In the current section, the computed results are presented, as based on the previously described methodology, objective function choice and FEM model. In particular, as a key term in understanding and solving the Inverse Analysis problem, the discrepancy function is analysed according to four configurations:
  • 9D search domain, based on the complete set of parameters,
    θ = [ E 1 , E 2 , E 3 , E 4 , E 5 , ρ 1 , ρ 2 , ρ 3 , ρ 4 ] ;
  • 5D search domain, based on a reduced set of parameters, limited to Young’s moduli,
    θ = [ E 1 , E 2 , E 3 , E 4 , E 5 ] ;
  • 2D search domain, based on a reduced set of parameters, limited to averaged Young’s modulus and mass density,
    θ = [ E ¯ , ρ ¯ ] ;
  • 4D search domain, based on a simplified beam model characterised by two structural components, respectively associated to Young’s modulus and mass density values,
    θ = [ E 1 , E 2 , ρ 1 , ρ 2 ] .
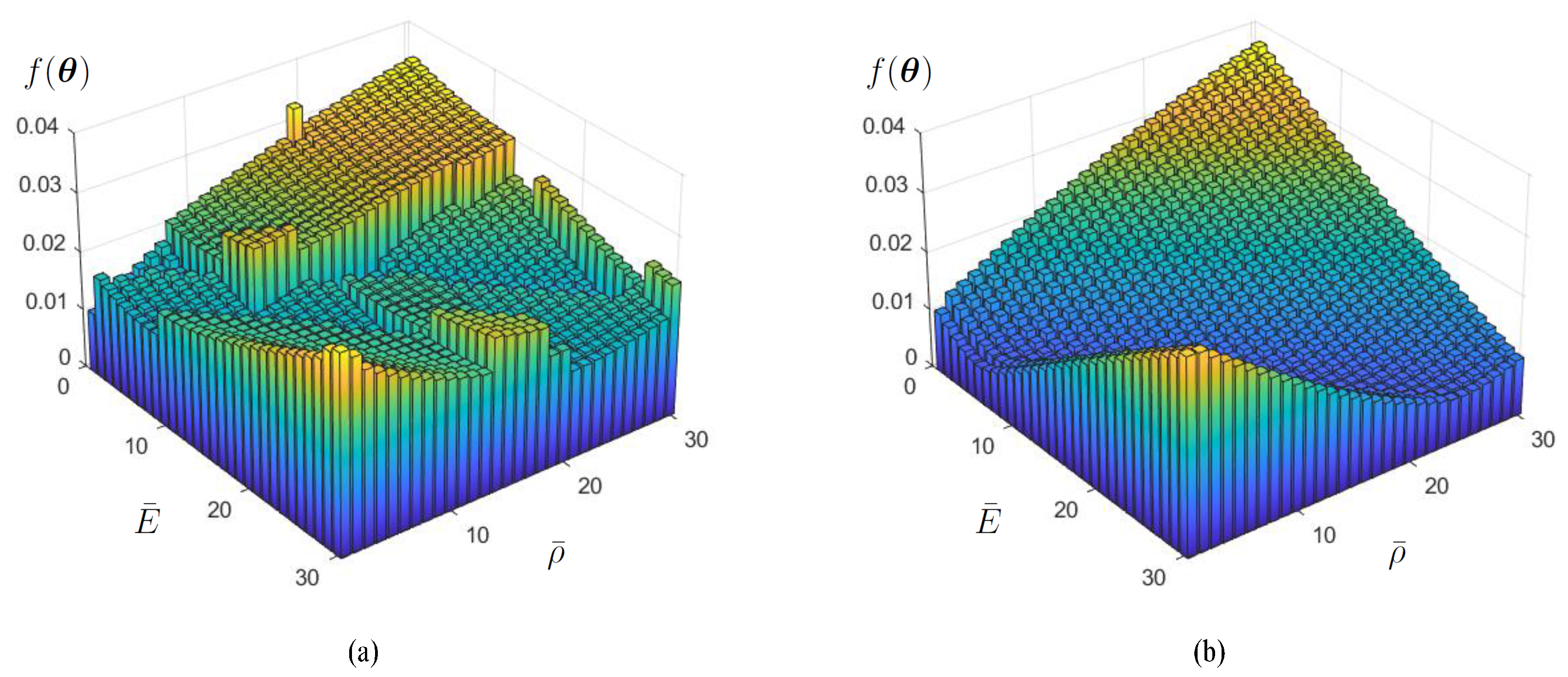
By limiting the problem to a two–parameter space (configuration 3), it is possible to observe that a mode adjustment in the modal pairing, as inner loop in the objective function evaluation, leads to a very irregular and discontinuous objective function (see Figure 4a). On the contrary, by selecting a priori the appropriate modes, without the possibility of changing them in the fitting process, namely by introducing a MAC regularisation as proposed in Section 2.2, a continuous target function may effectively be obtained (see Figure 4b).
Therefore, on the basis of such preliminary analyses, the introduction of a regularisation procedure turns out to be a necessary step in view of the application of Gaussian Processing, to reduce abrupt function discontinuities. However, also in such a regularised approach (see Figure 4b), the employment of Gaussian Processes still appears to be less feasible, due to the intrinsic “ill–posedness” condition of the objective function, linked to the identification based just on modal properties, as displayed by the “valley” of possible “realisations”, i.e. by the couple of parameters equally satisfying the minimisation problem. Therefore, such an issue may lead to an impractical or misleading application of Gaussian Processing optimisation, suggesting for an improvement of objective function definition toward achieving an automated identification method.
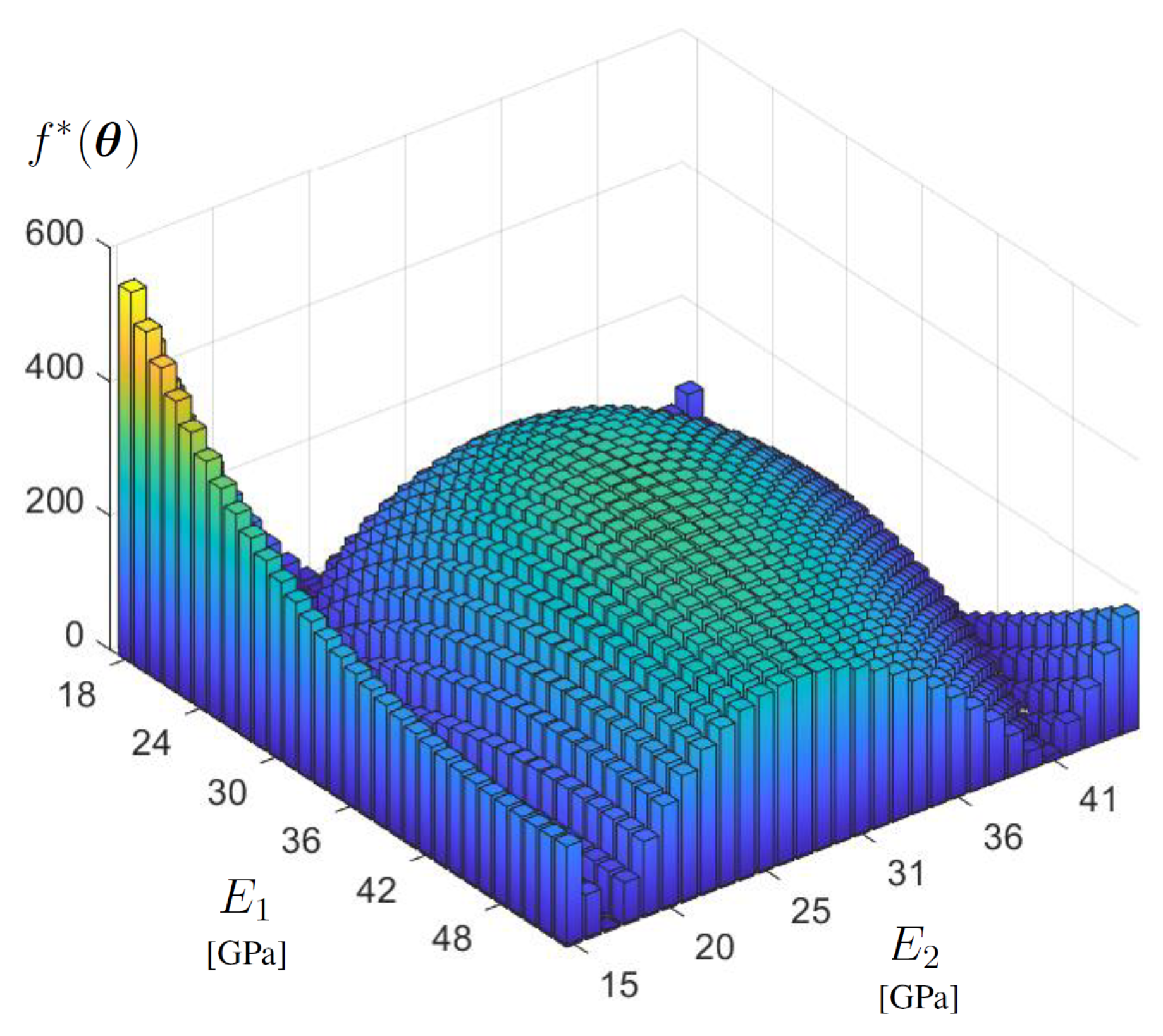
In a further step, adopting a 5D parameter space (configuration 2), Young’s moduli of diverse structural components are considered as model parameters to be calibrated, while mass densities are assumed at a fixed value, as previously estimated in [29], aiming at temporarily excluding the “realisation valley” issue. 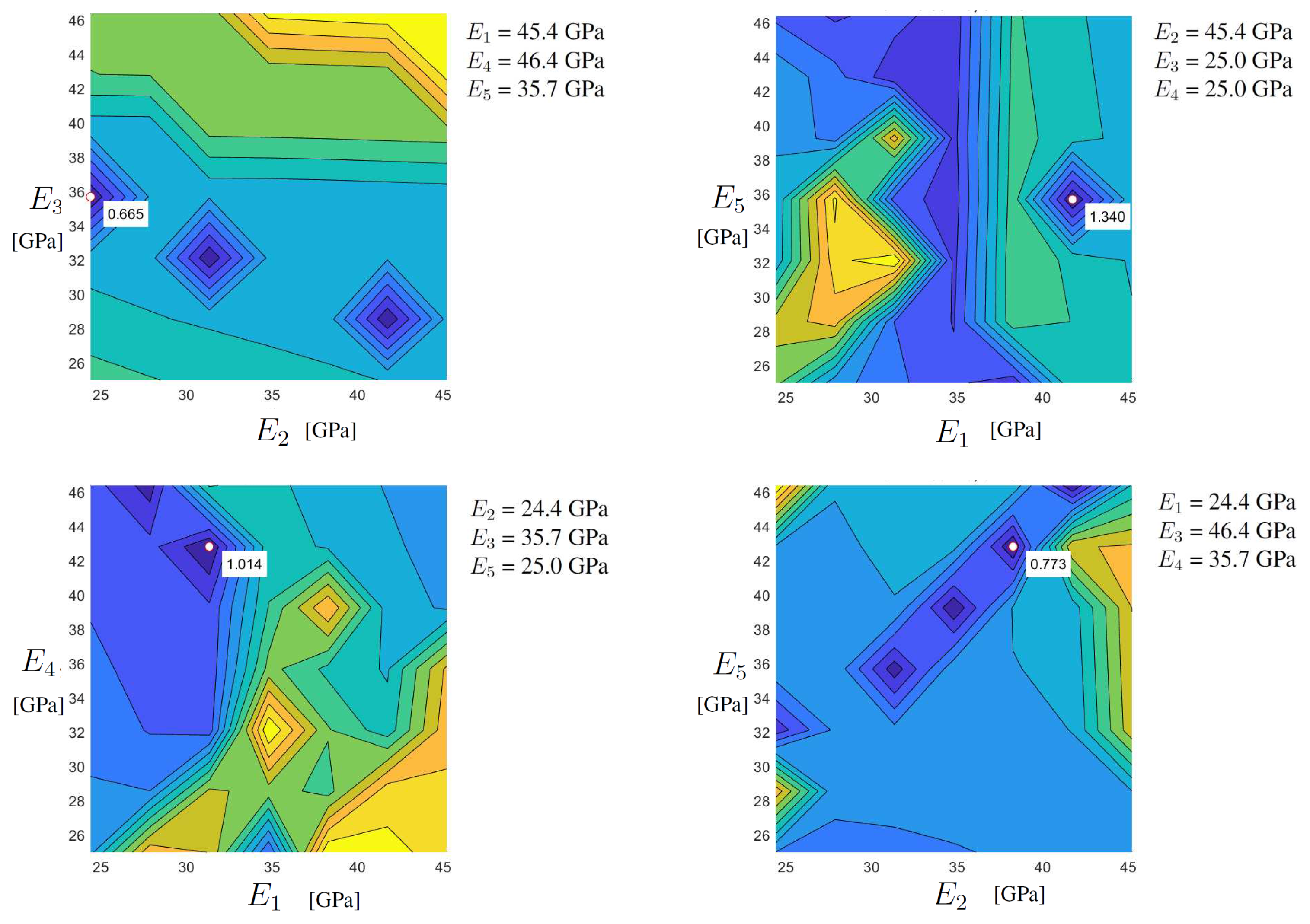In order to prepare the appropriate number of learning points, required for Gaussian Processes implementation, numerical evaluations of the FEM model and of the discrepancy function are produced over a regular grid in the search domain for 57 = 16,807 points (i.e., for 7 scanning values, for each of the 5 sought parameters). 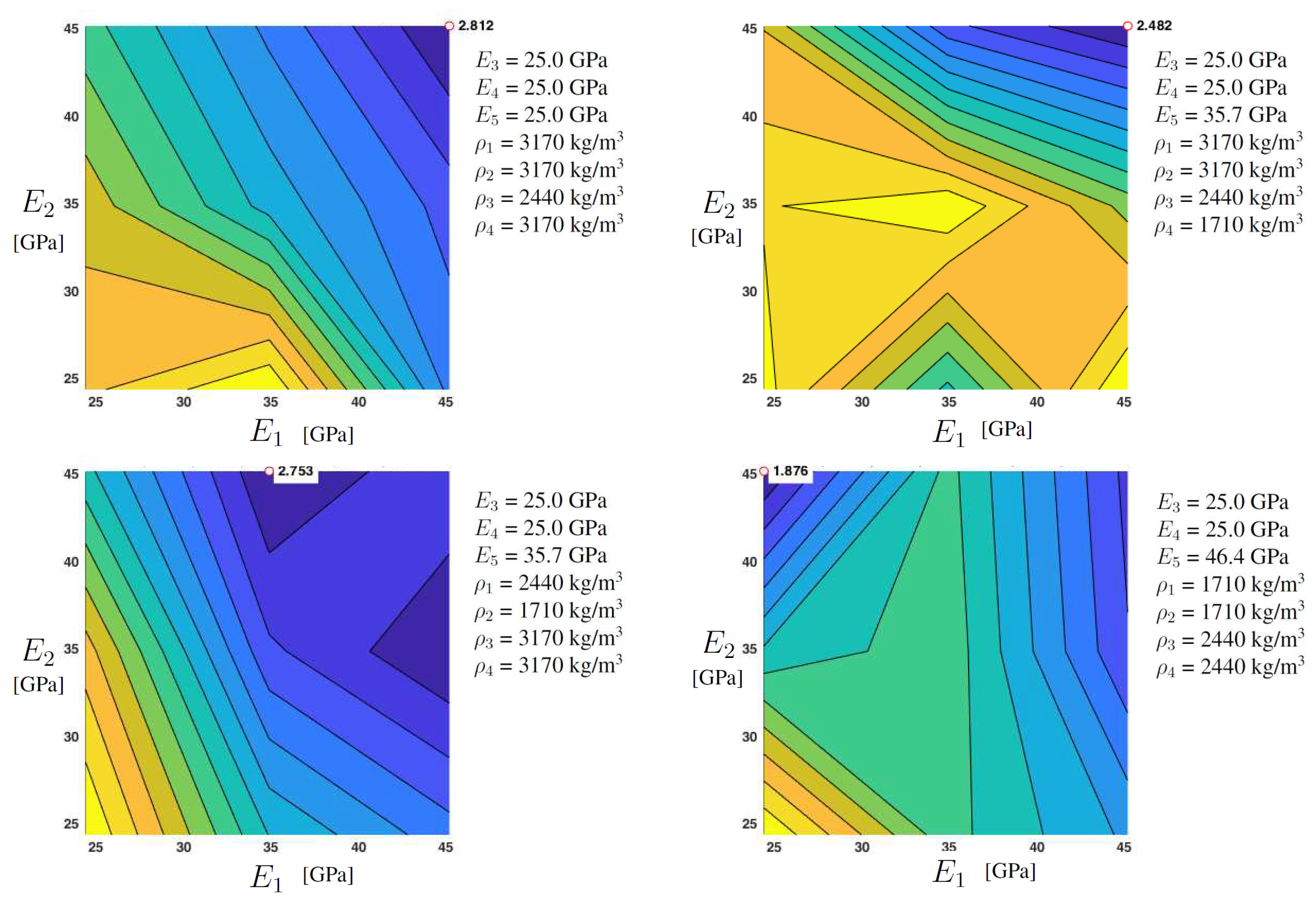Such an investigation of the objective function highlights non–satisfactory minima conditions, such as minimum points in non–feasible parameter space locations and equivalent minimum points, namely for a negligible variation of discrepancy function value, associated to significantly different parameter vector estimations (see Table 3). The highlighted behaviour may be interpreted as a lack of observed quantities (e.g., for missing data about mode shapes of other parts of the bridge, as bridge arches) in the objective function and/or as a reduced sensitivity, with respect to the sought parameters. The issue can further be confirmed by investigating the shape of the objective function, for example through cross section representations, where several irregularities and local minima may be observed (see the example cross sections collected in Figure 5).
Similar results are obtained in the original 9D parameter space (configuration 1), analysed with a regular grid of 39 = 19,638 points (i.e., for 3 scanning values, for each of the 9 sought parameters), as depicted in Figure 6 with four sample cross sections of the objective function, also highlighting non–feasible locations for minimum points at the search domain boundaries.
In consideration of the observed features of the employed objective function, in view of a proper choice of the minimisation algorithm to tackle the identification problem, it is worth to mention that the selection of “local algorithms” to find the global minimum (rather related to the “best” minimum within the possible combination of sought parameters) exhibits practical difficulties, while the use of “global algorithms” (including Gaussian Processes), associated with a large computational cost, may not guarantee the estimation of parameters at feasible values, due to a possible mismatch between “global” numerical minimum and “best” parameter combination from a structural standpoint.
An attempt to improve the identification behaviour of the objective function is developed by introducing a penalty term related to the mass densities of the structural components, as proposed in Section 2.2. In order to validate the novel approach, a pseudo–experimental configuration is developed in a 4D parameter space, on a simplified beam model (configuration 4), namely by adopting two beam structural components, each characterised by an associated Young’s modulus and mass density. Consistently, Figure 7 displays an example of the modification effect produced on the objective function shape by the introduction of the mass density penalty term.
For testing the numerical procedure, within the validation scheme, one parameter value (specifically ρ 2 ) is kept at a fixed value, while the other three parameters are estimated, using pseudo–experimental data, at varying penalty coefficient F. For two diverse reference structural configurations, four identification tests are conducted, as respectively reported in Table 4 and Table 5. However, the computed results, even for elevated penalty coefficient values, do not allow to ensure for correct parameter estimations neither for a robust identification procedure. Therefore, the modified formulation of the objective function may be deemed as only partially improved, although not effective in defining a fully reliable automated calibration methodology in the present context, at this stage of development.

5. Conclusions

In the present paper, a methodology for model calibration relying on dynamic modal measurements is sought. The Inverse Analysis problem has been tackled in an application case study devoted to a reinforced concrete road arched bridge, Brivio bridge (1917), of a significant historical and infrastructural interest for Structural Health Monitoring assessment in the present operative conditions.
In particular, within the general framework of Inverse Analysis approaches, an optimisation strategy based on Gaussian Processes has been selected and discussed, as an innovative method to tackle a demanding identification problem, both from computational efficiency and capability in searching for a “global” minimum. The choice of a promising optimisation approach has been coupled with multiple and improving definitions of a suitable objective function, as a central element in an Inverse Analysis problem. Moreover, considering the specific case study, particular attention has been devoted in the adoption of a FEM model apt to computationally generate numerical counterparts of the dynamic modal properties of the bridge structure, previously acquired out of an experimental campaign.
Further, with reference to the case study of Brivio bridge and, at the same time, providing observations of a more general validity, the investigation has been focused on the peculiar features and behaviour of the objective function, with possible regularisations and modifications, also at varying size of the parameter optimisation space. From the analysis results some main comments may be derived:
  • in relying on dynamic modal measurements, as experimental data for identification problem, a regularisation criterion (e.g., by a fixed Modal Assurance Criterion) is required to reduce abrupt discontinuity jumps in the discrepancy function shape;
  • the exploitation of modal properties, as a unique experimental source, intrinsically exhibits a “non–well posedness” condition, in terms of multiple “realisations”, in aiming at a joint estimation of stiffness and mass properties of a structural system, namely leading to the identification of the correlated parameters;
  • incomplete modal dynamic measurements (e.g. just at the deck level) may lead to a non–effective and non–robust identification procedure, consequently difficult to be tackled by optimisation algorithms, also including Gaussian Processes;
  • the introduction of penalty and regularisation terms in the discussed objective functions may lead to improved computational performances, however not sufficiently effective to provide a robust approach to be adopted in an automated identification procedure, toward structural assessment and diagnosis.
Despite the computational difficulties highlighted by the on–going analysis, the deepening and improved understanding on the objective function behaviour, for the tackled problem, confirm the validity of Inverse Analysis approaches toward Structural Identification and Structural Health Monitoring, with possible extensions, in future developments, to the insertion of additional sources of measurements.
Moreover, additional and corroborating studies, which may act just on the pure modelling side, based on pseudo–experimental results, relying on a full control of the underlying FEM modelling, for a digital replication of the infrastructure, may help in guidelining appropriate optimisation paths and variable choices, and needed measurement data, in the identification process, to investigate the role of “well-posedness”, of the scheduled optimisation task, and associated reliability of the optimisation algorithm that is being employed. This is concomitantly under current research investigation, as separately reported for first encouraging outcomes in companion paper [36].

Acknowledgments

The financial support by “Fondi di Ricerca d’Ateneo ex 60%”, “STaRs – Azione 2 Visiting e Fellow” and “PRIN Life–long optimized structural assessment and proactive maintenance with pervasive sensing techniques” at the University of Bergamo is gratefully acknowledged.

References

  1. A. Tarantola, Inverse Problem Theory. Siam, 2005.
  2. G. Maier, V. Buljak, T. Garbowski, G. Cocchetti, G. Novati, Mechanical characterization of materials and diagnosis of structures by inverse analyses: Some innovative procedures and applications. International Journal of Computational Methods, 11, 1343002, 2014. [CrossRef]
  3. C.E. Rasmussen, C.K.I. Williams, Gaussian Processes for Machine Learning. MIT Press, 2006.
  4. D. Sivia, J. Skilling, Data Analysis: A Bayesian Tutorial, 2nd Edition. Oxford Science Publications, 2006.
  5. C.M. Bishop, Pattern Recognition and Machine Learning. Springer, 2007.
  6. M. Alvarez, N. Lawrence, Sparse Convolved Gaussian Processes for Multi–Output Regression. D. Koller, D. Schuurmans, Y. Bengio, L. Bottou eds. Twenty–Second Annual Conference on Neural Information Processing Systems (NIPS), Vancouver, Canada, December 8-10, 2008. 8 December.
  7. T. Garbowski, Stochastic model reduction applied to inverse analysis. J.P.M. de Almeida, P. Díez, C. Tiago, N. Parés eds. VI International Conference on Adaptive Modeling and Simulation (ADMOS 2013), Lisbon, Portugal, June 3-5, 2013. 3 June.
  8. M. Adamski, M. Czechlowski, K. Durczak, T. Garbowski, Determination of the Concentration of Propionic Acid in an Aqueous Solution by POD–GP Model and Spectroscopy. Energies, 14, 8288, 2021. [CrossRef]
  9. K. Zaborowicz, T. Garbowski, B. Biedziak, M. Zaborowicz, Robust Estimation of the chronological age of children and adolescents using tooth geometry indicators and POD–GP. International Journal of Environmental Research and Public Health, 19, 2952, 2022. [CrossRef]
  10. T. Garbowski, G. Maier, G. Novati, Diagnosis of concrete dams by flat–jack tests and inverse analyses based on proper orthogonal decomposition. Journal of Mechanics of Materials and Structures, 6, 181–202, 2011. 2011.
  11. T. Gajewski, T. Garbowski, Calibration of concrete parameters based on digital image correlation and inverse analysis. Archives of Civil and Mechanical Engineering, 14, 170–180, 2014. [CrossRef]
  12. D. Ribeiro, R. Calçada, R. Delgado, M. Brehm, V. Zabel, Finite element model updating of a bowstring–arch railway bridge based on experimental modal parameters. Engineering Structures, 40, 413–435, 2012. [CrossRef]
  13. C. Bendon, M. Dilena, A. Morassi, Ambient vibration testing and structural identification of a cable–stayed bridge. Meccanica, 51, 2777–2796, 2016. [CrossRef]
  14. F. Shabbir, P. Omenzetter, Model updating using genetic algorithms with sequential technique. Engineering Structures, 120, 166–182, 2016. [CrossRef]
  15. J.E. Mottershead, M.I. Friswell, Model updating in structural dynamics: A survey. Journal of Sound and Vibration, 167, 347–375, 1993. [CrossRef]
  16. C.P. Fritzen, D. Jennewein, T. Kiefer, Damage detection based on model updating methods. Mechanical Systems and Signal Processing, 12, 163–186, 1998. [CrossRef]
  17. E. Reynders, System identification methods for (Operational) Modal Analysis: Review and comparison. Archives of Computational Methods in Engineering, 19, 51–124, 2012. [CrossRef]
  18. F. Ubertini, C. Gentile, A.L. Materazzi, Automated modal identification and its application to bridges. Engineering Structures, 46, 264–278, 2013. [CrossRef]
  19. C. Rainieri, G. Fabbrocino, Operational Modal Analysis of Civil Engineering Structures. Springer, 2014.
  20. F. Pioldi, R. Ferrari, E. Rizzi, Output–only modal dynamic identification of frames by a refined FDD algorithm at seismic input and high damping. Mechanical Systems and Signal Processing, 68–69, 265–291, 2016. [CrossRef]
  21. F. Pioldi, R. Ferrari, E. Rizzi, Earthquake structural modal estimates of multi–storey frames by a refined Frequency Domain Decomposition algorithm. JVC/Journal of Vibration and Control, 23, 2037–2063, 2017. [CrossRef]
  22. F. Pioldi, R. Ferrari, E. Rizzi, Seismic FDD modal identification and monitoring of building properties from real strong–motion structural response signals. Structural Control and Health Monitoring, 24, e1982, 2017. [CrossRef]
  23. R. Cardoso, A. Cury, F. Barbosa, A robust methodology for modal parameters estimation applied to SHM. Mechanical Systems and Signal Processing, 95, 24–41, 2017. [CrossRef]
  24. L. Santarella, E. Miozzi, Ponti Italiani in Cemento Armato (in Italian). Hoepli, 1948.
  25. R. Ferrari, D. Froio, E. Chatzi, C. Gentile, F. Pioldi, E. Rizzi, Experimental and numerical investigations for the structural characterization of a historic RC arch bridge. M. Papadrakakis, V. Papadopoulos, V. Plevris eds. 5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Greece, May 25-27, 2015. 25 May.
  26. R. Ferrari, F. R. Ferrari, F. Pioldi, E. Rizzi, C. Gentile, E. Chatzi, R. Klis, E. Serantoni, A. Wieser, Heterogeneous sensor fusion for reducing uncertainty in structural health monitoring. M. Papadrakakis, V. Papadopoulos, G. Stefanou eds. 1st ECCOMAS Thematic Conference on Uncertainty Quantification in Computational Sciences and Engineering (UNCECOMP 2015), Crete Island, Greece, May 25-27, 2015. 25 May.
  27. R. Ferrari, F. Pioldi, E. Rizzi, C. Gentile, E. Chatzi, E. Serantoni, A. Wieser, Fusion of wireless and non-contact technologies for the dynamic testing of a historic RC bridge. Measurement Science and Technology, 27, 124014, 2016. [CrossRef]
  28. A. Cornaggia, R. Ferrari, M. Zola, E. Rizzi, C. Gentile, Signal Processing Methodology of Response Data from a Historical Arch Bridge toward Reliable Modal Identification. Infrastructures, 7, 74, 2022. [CrossRef]
  29. R. Ferrari, D. Froio, E. Rizzi, C. Gentile, E. Chatzi, Model updating of a historic concrete bridge by sensitivity and global optimization–based Latin hypercube sampling. Engineering Structures, 1, 139–160, 2019. [CrossRef]
  30. G. Zonno, C. Gentile, Assessment of Similar Reinforced Concrete Arch Bridges by Operational Modal Analysis and Model Updating. Lecture Notes in Civil Engineering, 156, 853–868, 2021. [CrossRef]
  31. P. Borlenghi, C. Gentile, G. Zonno, Monitoring Reinforced Concrete Arch Bridges with Operational Modal Analysis. Lecture Notes in Civil Engineering, 200, 361–371, 2022. [CrossRef]
  32. P. Borlenghi, C. Gentile, M. Pirrò, Continuous Dynamic Monitoring and Automated Modal Identification of an Arch Bridge. Lecture Notes in Civil Engineering, 254, 166–176, 2023. [CrossRef]
  33. J. Nocedal, S.J. Wright, Numerical Optimization. Springer, 1999.
  34. M.D. Buhmann, Radial Basis Functions. Cambridge University Press, 2003.
  35. R.J.Allemang, The Modal Assurance Criterion – Twenty Years of Use and Abuse. Sound and Vibration, 2003, 14–21, 2003.
  36. A. Cornaggia, T. Garbowski, G. Cocchetti, R. Ferrari, E. Rizzi, Optimised structural modelling for Inverse Analysis parameter identification relying on dynamic measurements. M. Papadrakakis, M. Fragiadakis eds. 9th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2023), Athens, Greece, June 12-14, 2023, submitted. 12 June.
Preprints 79502 g001
Figure 1. Brivio bridge (1917): downstream view of the road three–span arched bridge crossing the Adda river; Brivio (Lecco) right bank (left), Cisano Bergamasco (Bergamo) left bank (right). Picture taken by author E.R. on 7 July 2022.
Figure 1. Brivio bridge (1917): downstream view of the road three–span arched bridge crossing the Adda river; Brivio (Lecco) right bank (left), Cisano Bergamasco (Bergamo) left bank (right). Picture taken by author E.R. on 7 July 2022.
Preprints 79502 g001
Preprints 79502 g002
Figure 2. Brivio bridge (1917): schematic representation of downstream front.
Figure 2. Brivio bridge (1917): schematic representation of downstream front.
Preprints 79502 g002
Preprints 79502 g003
Figure 3. FEM model of Brivio bridge (single span); colours identify diverse elements of the structure for sought material parameters.
Figure 3. FEM model of Brivio bridge (single span); colours identify diverse elements of the structure for sought material parameters.
Preprints 79502 g003
Preprints 79502 g004
Figure 4. Normalised bar plot of the objective function in the 2D parameter space (configuration 3): (a) without MAC regularisation, (b) with MAC regularisation.
Figure 4. Normalised bar plot of the objective function in the 2D parameter space (configuration 3): (a) without MAC regularisation, (b) with MAC regularisation.
Preprints 79502 g004
Preprints 79502 g005
Figure 5. Selected cross sections of the objective function in the 5D parameter space (configuration 2).
Figure 5. Selected cross sections of the objective function in the 5D parameter space (configuration 2).
Preprints 79502 g005
Preprints 79502 g006
Figure 6. Selected cross sections of the objective function in the 9D parameter space (configuration 1).
Figure 6. Selected cross sections of the objective function in the 9D parameter space (configuration 1).
Preprints 79502 g006
Preprints 79502 g007
Figure 7. Three–dimensional cross section of the objective function in the 4D parameter space (configuration 4), with penalty mass density factor F = 1000.
Figure 7. Three–dimensional cross section of the objective function in the 4D parameter space (configuration 4), with penalty mass density factor F = 1000.
Preprints 79502 g007
Table 1. Material input parameters and search domain for the Inverse Analysis problem, based on the FEM model.
Table 1. Material input parameters and search domain for the Inverse Analysis problem, based on the FEM model.
Parameter Lower Upper Reference
bound bound value
Deck elastic modulus, E 1 [GPa] 24.4 45.4 34.9
Main longitudinal girders elastic modulus, E 2 [GPa] 24.4 45.4 34.9
Parabolic arches elastic modulus, E 3 [GPa] 25.0 46.4 35.7
Hangers elastic modulus, E 4 [GPa] 25.0 46.4 35.7
Upper transverse beams elastic modulus, E 5 [GPa] 25.0 46.4 35.7
Deck mass density, ρ 1 [kg/m3] 1710 3170 2440
Main longitudinal girders mass density, ρ 2 [kg/m3] 1710 3170 2440
Parabolic arches mass density, ρ 3 [kg/m3] 1710 3170 2440
Hangers mass density, ρ 4 [kg/m3] 1710 3170 2440
Table 2. Base FEM model parameters, at fixed values, not included in the Inverse Analysis search domain.
Table 2. Base FEM model parameters, at fixed values, not included in the Inverse Analysis search domain.
Parameter Reference value
Upper transverse beams mass density, ρ 5 [kg/m3] 2440
I–support translational (x–axis) spring stiffness, k 1 [kN/m] 10−5
I–support translational (y–axis) spring stiffness, k 2 [kN/m] 1010
I–support rotational spring stiffness, k 3 [kNm] 10−5
II–support rotational spring stiffness, k 4 [kNm] 10−5
Table 3. Seven best values of the objective function, by grid search, and corresponding parameters in the 5D search domain (configuration 2).
Table 3. Seven best values of the objective function, by grid search, and corresponding parameters in the 5D search domain (configuration 2).
f ( θ ) [-] 0.005990 0.006053 0.006098 0.006114 0.006118 0.006184 0.006210
E 1 [GPa] 45.2 45.2 45.2 45.2 45.2 45.2 45.2
E 2 [GPa] 24.4 34.8 24.4 27.9 27.9 27.9 45.2
E 3 [GPa] 35.7 32.1 35.7 35.7 35.7 35.7 28.6
E 4 [GPa] 46.4 42.8 42.8 42.8 39.3 46.4 42.8
E 5 [GPa] 35.7 42.8 35.7 46.4 46.4 42.8 39.3
Table 4. First test case for effectiveness of mass density penalty term in objective function, evaluated in 4D parameter space (configuration 4).
Table 4. First test case for effectiveness of mass density penalty term in objective function, evaluated in 4D parameter space (configuration 4).
Reference Test 1 Test 2 Test 3 Test 4
f * ( θ ) [–] – 0.4901 0.8349 2.8628 13.2080
F [–] – 0 10 100 1000
E 1 [GPa] 33.74 38.02 38.02 36.81 36.81
E 2 [GPa] 28.38 31.55 31.55 31.55 31.55
ρ 1 [kg/m3] 2235 2524 2524 2441 2441
ρ 2 [kg/m3] 2147 2400 2400 2400 2400
Table 5. Second test case for effectiveness of mass density penalty term in objective function, evaluated in 4D parameter space (configuration 4).
Table 5. Second test case for effectiveness of mass density penalty term in objective function, evaluated in 4D parameter space (configuration 4).
Reference Test 1 Test 2 Test 3 Test 4
f * ( θ ) [–] – 0.3955 0.9702 5.5767 18.2130
F [–] – 0 10 100 1000
E 1 [GPa] 38.00 36.81 36.81 38.02 39.22
E 2 [GPa] 29.00 27.41 27.41 27.41 27.41
ρ 1 [kg/m3] 2300 2193 2193 2276 2359
ρ 2 [kg/m3] 2500 2400 2400 2400 2400
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated