PP-JPEG: A Privacy-Preserving JPEG Image Tampering Localization

Preprint

Article

PP-JPEG: A Privacy-Preserving JPEG Image Tampering Localization

Altmetrics

Downloads

107

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

This preprints belongs to the Topic

Computer Vision and Image Processing

Submitted:

15 July 2023

Posted:

17 July 2023

You are already at the latest version

Alerts

Abstract

The widespread availability of digital image processing softwares has given rise to various forms of image manipulation and forgery which can pose a significant challenge in different fields such as law enforcement, journalism etc,. it can also lead a privacy concern. We are proposing a privacy-preserving framework to encrypt images before processing them is vital to maintain the privacy and confidentiality of sensitive images, especially those used for purpose of Investigation. To address these challenges, we propose a novel solution that detects image forgeries while preserving the privacy of the images. Our method proposes a privacy-preserving framework that encrypts the images before processing them, making it difficult for unauthorized individuals to access them. The proposed method utilizes a compression quality analysis in the encrypted domain to detect the presence of forgeries in images if the forged portion (dummy image) has a compression quality different from the original image (featured image) in the encrypted domain. This approach effectively localizes the tampered portions of the image, even for small pixel blocks of size 10x10 in the encrypted domain. Furthermore, the method identifies the featured image's JPEG quality using the first minima in the energy graph.

Keywords:

Subject: Computer Science and Mathematics - Security Systems

1. Introduction

The advancement of highly advanced digital image processing software has made it effortless to create manipulated images without any noticeable signs [1]. Consequently, people are losing faith in the trustworthiness and authenticity of digital images. This erosion of trust in digital imagery has far-reaching implications, impacting various domains such as journalism, forensics, and legal proceedings. Hence, the development of technologies that can determine whether an image has been altered is becoming more crucial than ever.

Joint Photographic Experts Group (JPEG) [2] is the most widely used image format. Human eyes have a higher sensitivity for low-frequency signals than high-frequency ones [3]. By reducing the high-frequency information, JPEG compression allows images to retain a high compression ratio and obtain satisfactory image quality. For a tampered JPEG image, the tampered region usually has a different JPEG compression from the authentic region. The tampered digital image is generally challenging to be identified by human eyes; however, it is usually left behind some hidden clues or statistical artifacts [4]. Based on these clues or artifacts, JPEG digital forensic technologies have undergone continuous development and improvement.

We present a technique for detecting tampering in low-quality and high-quality images in the encrypted domain. This approach detects tampering when a low-quality JPEG image is injected into a higher-quality JPEG image and vice versa. It can come from combining two separate photographs of people into a single composite image, for example, or by splicing one person’s head onto another person’s body. In this method, part of the image is explicitly determined to be compressed at a different quality than the rest of the image.

In this paper, a passive approach is proposed for the detection of image forgery [5], which is based on examining the difference in JPEG qualities between the forged portion and the remaining parts of the image in the encrypted domain. The original image is referred to as the "featured" image, while the manipulated portion is denoted as the "dummy" image. The method presented in this study involves the identification and localization of the forged portion by re-saving the forged image at different image qualities and determining the range of JPEG qualities that yield the highest forgery detection rates. Through experimentation involving various combinations of dummy and featured image qualities, the obtained results were analyzed to ascertain the most effective techniques for localizing image forgery in an encrypted domain.

A comparative analysis of the proposed work is done with Singh et al. [6]. Singh et al. [6] and present work focuses on digital image forensic techniques for JPEG images and primarily addresses the detection of forgeries based on compression quality differences. Existing work proposes a method that analyzes the similarity between the featured image and the forged portion, referred to as a dummy image. While the paper explores various attack scenarios and demonstrates robustness, it does not specifically address privacy concerns. In contrast, the present paper recognizes the widespread availability of image manipulation tools and the need for privacy in sensitive image applications. It proposes a privacy-preserving framework that encrypts images before processing, ensuring the confidentiality of the data. By utilizing compression quality analysis in the encrypted domain, the method effectively detects forgeries while preserving privacy. It also highlights the importance of localization and identifies the JPEG quality of the featured image, contributing the forgery detection in the encrypted domain. Overall, the present works stands out for its emphasis on privacy and the development of a novel solution that addresses image forgery detection while maintaining the privacy and confidentiality of sensitive images. It provides a valuable contribution in the context of investigations, where privacy concerns are paramount.

Our contributions include developing a novel approach to passive image forgery detection and exploring resaving at different image qualities to improve forgery localization. Following are the key contributions:

The proposed method was evaluated using various scenarios of copy-move forgeries in the encrypted domain. Copy-move forgeries involve duplicating an pasting a portion of an image onto another part of the same image. The testing included different combinations of high-quality dummy and low-quality featured image, low-quality and dummy-high-quality featured image, and equal JPEG quality for dummy and featured images. Pixel block sizes were varied from $50 \times 50$ to as small as $10 \times 10$ . The results of the testing indicate that the proposed method was effective in localizing the tampered portions of the image in the encrypted domain, despite the variations in quality levels and small pixel block sizes. These findings suggest that the proposed method may be useful for detecting and locating copy-move forgeries in images in an encrypted domain.
The forgery detection results were analyzed and it was found that the quality of the featured image can be predicted from these plots. Specifically, the featured image quality corresponds to the first minima in the energy plot.

The rest of the paper is organized as follows. In Section 2, we review the related work. Section 3 presents a brief overview of paillier encryption. Section 4 describes the system and the threat model of the architecture, details of the proposed PP-JPEG and the solution. The security analysis are done in Section 5. The performance validation of the proposed scheme is outlined in Section 6, which presents the experiments conducted. Furthermore, Section 7 concludes the work and discusses the future scope of the research.

2. Related Work

Various techniques have been studied in the field of detecting image forgery. Here, we provide a concise overview of some of these approaches.

Farid et al. [7] proposed a framework technique for detecting tampering in low-quality JPEG images. Singh et al. [6] proposed a framework that can detect forgeries in images. The framework works by identifying the forged portion of the image, called the ghost image. It has a compression quality different from that of the cover image.

Luckas et al. [8] introduced a method for image forgery detection by analyzing the unique photo response non-uniformity (PRNU) pattern associated with each camera, enabling the detection of potential manipulations. This technique is effective when the camera source is known or when other images from the same camera are available for comparison.

Amerini et al. have proposed [9] a step forward in this direction by analyzing how a single or double JPEG compression can be revealed and localized using convolutional neural networks (CNNs). In their paper, Zhou et al. propose [10] a new method to detect tampering in manipulated images using a two-stream Faster R-CNN network. This method combines two streams, one that extracts features from the RGB image and another that leverages noise features to detect inconsistencies between authentic and tampered regions. The two streams are combined using a bilinear pooling layer for improved accuracy. The method outperforms others and achieves state-of-the-art performance on four standard image manipulation datasets while also robust to resizing and compression.

Rahmati et al. propose a new method [11] for detecting double JPEG compression in images using a convolutional auto-encoder and convolutional neural network. The method outperforms previous algorithms on standard datasets and is robust to JPEG compression quality factors perturbations. Results are based on small-sized image patches. This paper proposes a new method [12] for image forgery detection using a convolutional neural network (CNN) specifically designed for image splicing and copy-move detection. The CNN is initialized using a high-pass filter set from the spatial rich model (SRM) to capture subtle tampering artifacts. The pre-trained CNN is used as a patch descriptor to extract dense features, and a feature fusion technique is used for SVM classification. Experimental results show that the proposed method outperforms some state-of-the-art methods in detecting image forgery.

This paper proposes a method [13] for detecting copy-move forgery in images using a reduced feature-based algorithm. It uses stationary wavelet transform to obtain the low approximation band of the subject image and then extracts significant features using block-based DCT and SVD. The approach only extracts three feature vectors to reduce computational overhead but still achieves precise detection of forged areas and is robust against post-processing attacks. Diallo et al. [14] proposes a framework for detecting image forgery, which considers various transformations such as compression and resizing. The framework is based on a convolutional neural network and considers the image quality for the application. It shows results in image forgery detection. This paper addresses [15] privacy and tampering issues in medical imaging and bioinformatics caused by cloud computing. Image tampering detection is proposed using a deep learning architecture to identify tampered components efficiently. The proposed approach is evaluated on the MICC-F220 dataset using k-fold cross-validation.

Our proposed image tamper detection scheme is highly robust and efficient, capable of detecting tampering in encrypted images with all possible combinations of JPEG quality for both dummy and featured images. By operating in an encrypted domain, our scheme ensures the privacy and security of the images while providing reliable tamper detection.

3. Preliminaries

3.1. Paillier Encryption

The Paillier cryptosystem, created and named after Pascal Paillier in 1999, is an asymmetric cryptographic algorithm used for public key cryptography with homomorphic properties [16].

3.1.1. Key Generation

Choose two large prime numbers p and q, and a random value g where g is a generator of

Z_{n}^{*}

. Set

n = p \cdot q

and

λ = lcm (p - 1, q - 1)

. Public key is

(n, g)

, private key is

μ = L {(g^{λ} mod n^{2})}^{- 1} mod n

, where

L (x) = (x - 1) / n

3.1.2. Encryption

To encrypt message m, choose random r such that

0 \leq r < n

and compute

c = g^{m} \cdot r^{n} mod n^{2}

. c is the encrypted message.

3.1.3. Decryption

To decrypt message c, compute

m = L (c^{λ} mod n^{2}) \cdot μ mod n

3.1.4. Homomorphic Properties

Paillier encryption supports additive homomorphism, which means that given two encrypted messages

c_{1}

and

c_{2}

that represent messages

m_{1}

and

m_{2}

, respectively, we can compute an encrypted message

c_{3}

that represents the sum of

m_{1}

and

m_{2}

, without decrypting any of the values.

This is done by simply multiplying

c_{1}

and

c_{2}

together, modulo

n^{2}

. That is:

c_{3} = c_{1} \cdot c_{2} mod n^{2}

When we decrypt

c_{3}

using the private key, we get the sum of

m_{1}

and

m_{2}

modulo n:

m_{1} + m_{2} \equiv Dec (c_{1} \cdot c_{2} mod n^{2}) (mod n)

We can also compute a scalar multiplication of an encrypted message

c_{1}

with a plaintext value a, by raising

c_{1}

to the power of a, modulo

n^{2}

c_{2} = c_{1}^{a} mod n^{2}

When we decrypt

c_{2}

, we get the plaintext value

m_{2}

that is equal to

a \cdot m_{1}

modulo n:

m_{2} \equiv a \cdot m_{1} (mod n)

These homomorphic properties make Paillier encryption a useful tool for secure computation on encrypted data, as it allows for the manipulation of data without the need to decrypt it first.

4. The Proposed Framework

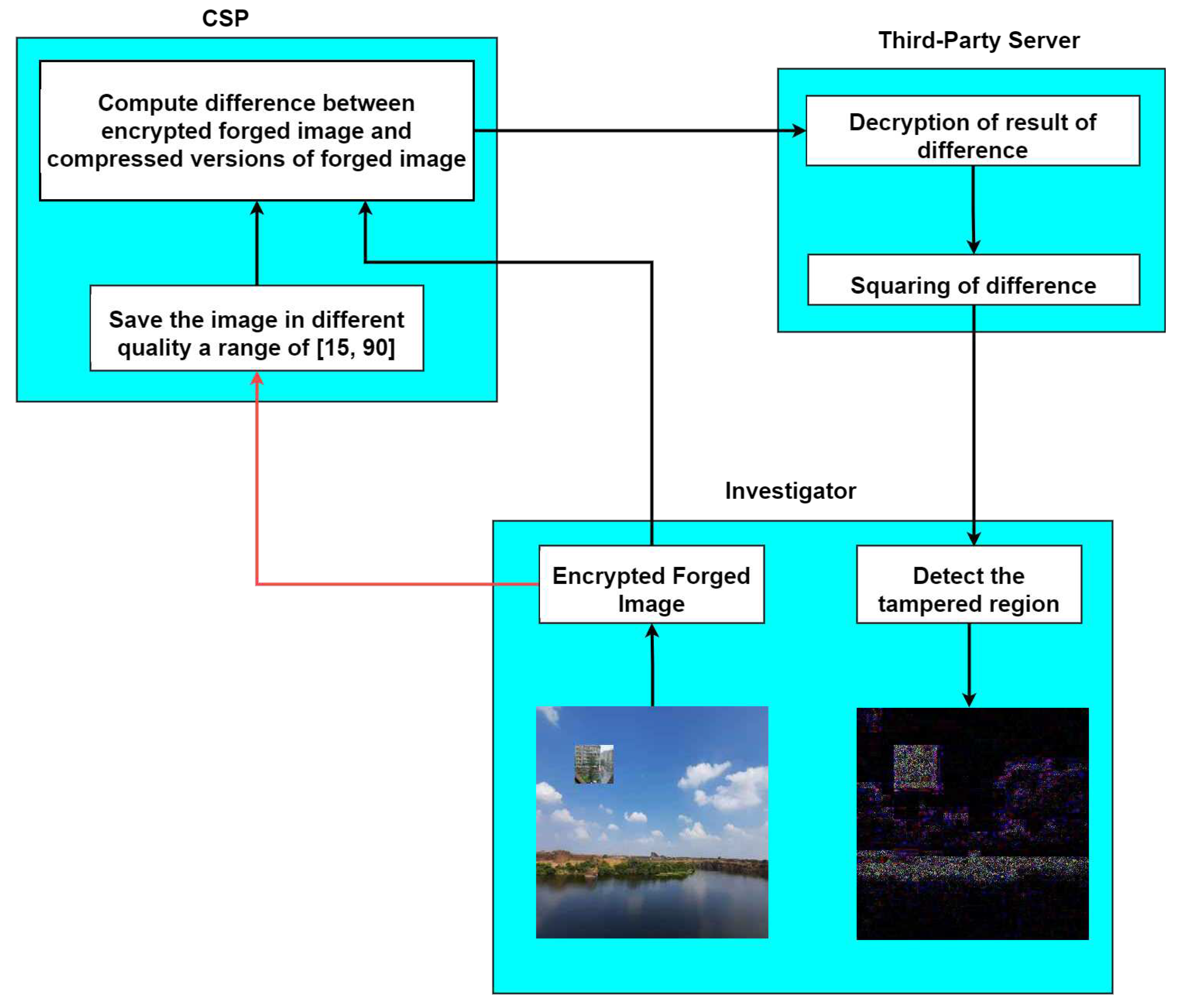
Our proposed framework consists of three entities: the system model, the threat model, and the proposed methodology. These entities are shown in Figure 1.

4.1. System Model and Threat Model

The system model defines the structure of the system being analyzed, while the threat model identifies potential security threats. The proposed methodology outlines the steps used to assess and mitigate these threats within the system. This comprehensive framework provides an effective approach for addressing security concerns.

Investigator : As an Investigator the role is to identify the forged region in an encrypted image without compromising the confidentiality of the image content. The forged images, denoted as $I {(x, y)}_{F}$ , are created by copying and pasting a portion of an image onto another region within the same image, and then saving the resulting image at different JPEG qualities [17]. To perform this task, the encrypted forged image is outsourced to a Cloud Service Provider (CSP), who is assumed to be honest but curious.

To maintain confidentiality, the image is encrypted using Paillier encryption, a public-key encryption scheme that supports homomorphic operations. The CSP follows the proposed protocol for detecting forged regions, but may also be interested in learning about the content of the image. However, since Paillier encryption is semantically secure, the encryption scheme reveals no information about the underlying image content. This ensures the privacy of the original image while allowing the identification of any tampered regions. It is assumed that the Investigator is a reliable and trusted entity.
Cloud Service Provider(CSP) : Cloud Service Provider is an entity that resaves the encrypted forged image at different JPEG qualities and computes the difference between the encrypted forged image with the resaved image of different qualities. This ensures the confidentiality of the original image content throughout the process. Once the CSP has computed the encrypted differences, they can outsource them to a third-party server for further analysis. We are considering communication channel to be insecure between investigator and CSP, implying that the CSP is deemed to be an honest yet curious entity.
Third-Party Server: As a Third-Party Server, the primary responsibility is to assist the Investigator in detecting forged regions in an encrypted image. This involves decrypting the encrypted difference between the resaved image received from the Cloud Service Provider.

Once decrypted, the difference must be squared to amplify it before being sent back to the Investigator. His role is to ensure that the decryption process is performed securely and that the squared difference is sent back to the Investigator without any loss of data or privacy concerns. The third-party server is assumed to be a trusted entity.

4.2. Proposed Methodology

The proposed methodology presents a framework for verifying the integrity of an image in an encrypted domain, as shown in Figure 1. This method utilizes the properties of JPEG compression to detect tampered regions in images while maintaining the confidentiality of the original image content. The following steps outline the detailed process:

Investigator

To verify the integrity of a potentially tampered image, the Investigator follows these steps:

Step 1: Investigator is provided with an image to check the integrity. For example, let’s say a portion of 30 by 30 of an image with a JPEG quality 50 called as a dummy image, pasted on the featured image originally at quality 80 that image is considered to be as a forged image.

Step 2: Forged image is encrypted using the public key of Paillier encryption [18]

E (I {(x, y)}_{F})

. It is sent to the CSP.

CSP

Step 3: The integrity of the forged image,

E (I {(x, y)}_{F})

is checked by resaving at different JPEG qualities

E (I {(x, y)}_{F q})

where, q is the quality of the image. We have done this for a range of [15, 90] with a step size of 5.

Step 4: To compute the difference image

E (S)

in the encrypted domain, the operations involved are addition and scalar multiplication that is supported by pailler encryption. The sum of two plaintexts

I_{1}

and

I_{2}

is equivalent to the decrypted product of corresponding ciphertexts

E (I_{1})

and

E (I_{2})

. The product of a scalar s with a plaintext

I_{1}

is equivalent to the decrypted exponentiation of the corresponding ciphertext

E (I_{1})

with the scalar. The difference image

E (S)

is obtained by computing between the encrypted forged image

E (I)

and the resaved image

E (I^{q})

as follows:

Difference in Plaintext Domain:

S (x, y) = [{(I {(x, y)}_{F i} - I {(x, y)}_{F i}^{q}]}_{i = 1, 2, 3}

(1)

Difference in Encrypted Domain:

E (S (x, y)) = [{(E (I {(x, y)}_{F i}) \times {(E (I {(x, y)}_{F i}^{q}))}^{- 1}]}_{i = 1, 2, 3}

(2)

where,

E (I {(x, y)}_{i})

and

E (I {(x, y)}_{i}^{q})

represents the pixel value at

(x, y)

co-ordinates of the

i^{t h}

color channel of the forged image and resaved forged image respectively. Here, the

i^{t h}

value represents the R, G and B channels respectively.

Third-Party Server

Step 5: After receiving the encrypted difference

E (S)

from the CSP, the third-party server decrypts it using the private key of the Paillier encryption scheme. As squaring cannot be performed in the encrypted domain, the decrypted difference is squared to amplify the difference as follows:

D (S (x, y)) = {(D e c [E (S (x, y))])}_{i = 1, 2, 3}^{2}

(3)

Here,

D e c

represents the decryption operation and

D (S (x, y))

represents the squared difference value at the

(x, y)

co-ordinate of the

i^{t h}

color channel.

Investigator

Step 6: The decrypted and squared difference image

D (S)

is received from the third-party server and converted to RGB format. This step allows the forged regions to be visualized more clearly, and the tampered portions of the image can be identified with greater detail in the experimental Section 6.

5. Security Analysis

Paillier encryption is a form of homomorphic encryption that is semantically secure and probabilistically correct, and it can be useful in privacy-preserving protocols [16].

Theorem 1.

If the Paillier encryption is semantically secure, PP-JPEG is also semantically secure.

Proof.

The proof of semantic security in Paillier encryption is based on the decisional composite residuosity assumption (DCR). DCR states that given a composite number n and a random number a, it is computationally infeasible to determine whether

gcd (a, n) = 1

a^{λ (n)} = 1 mod n^{2}

, where

λ

is the Carmichael function.

To prove the semantic security of Paillier encryption, we will show that given any two plaintexts

m_{1}

and

m_{2}

, the difference between their corresponding ciphertexts

C_{1}

and

C_{2}

is statistically indistinguishable from a uniformly random value in

Z_{n^{2}}

Let’s consider the ciphertexts:

C_{1} = (g^{m_{1}} \cdot r^{n}) mod n^{2}

C_{2} = (g^{m_{2}} \cdot r^{n}) mod n^{2}

where: - g is a generator of the group - n is the public key modulus - r is a random value chosen during encryption -

mod

denotes the modulus operation

The difference between the two ciphertexts can be expressed as:

(C_{1} \cdot C_{2}^{- 1}) mod n^{2}

[(g^{m_{1}} \cdot r^{n}) \cdot (g^{- m_{2}} \cdot r^{- n})] mod n^{2}

g^{m_{1} - m_{2}} mod n^{2}

Now, let’s consider a hypothetical attacker who is trying to distinguish between two ciphertexts

C_{1}

and

C_{2}

without knowing the corresponding plaintexts.

The attacker can compute the value

g^{m_{1} - m_{2}} mod n^{2}

based on the ciphertexts. However, under the DCR assumption, this value is computationally indistinguishable from a uniformly random value in

Z_{n^{2}}

, unless the factorization of n is known. Therefore, the attacker cannot gain any information about the difference between the plaintexts

m_{1}

and

m_{2}

solely based on the ciphertexts. This demonstrates the semantic security of the Paillier encryption scheme. In conclusion, the Paillier encryption scheme is semantically secure under the decisional composite residuosity assumption (DCR). Without knowledge of the private key, an attacker cannot determine the corresponding plaintext from the ciphertext, as the difference between ciphertexts reveals no information about the plaintexts. □

Theorem 2.

If the Paillier encryption is probabilistically correct, PP-JPEG is also probabilistically correct.

Proof.

Let m be the plaintext message, r be a random value, g be a generator of the group, and n be the public key modulus.

The ciphertext C is computed as:

C = (g^{m} \cdot r^{n}) mod n^{2}

Where · denotes multiplication,

mod

denotes the modulus operation, and all operations are performed within the group.

This formula ensures the probabilistic correctness of Paillier encryption, as the random value r is added to the plaintext before encryption and removed during decryption. The resulting ciphertext C is a representation of the encrypted message that cannot be easily reversed to obtain the original plaintext without knowing the private key. □

6. Experimental Analysis

Our experiments were conducted using Intel(R) Xeon(R) Silver 4214R CPU @ 2.40GHz. We considered various scenarios to test the effectiveness of our proposed method against a range of possible attack scenarios. We tested the method on different combinations of dummy and featured images, such as high quality dummy image with low quality featured image, low quality dummy image with high quality featured image, and dummy and featured images with the same quality. Additionally, we examined the method’s ability to detect even small forgeries by testing it on dummy images of sizes ranging from

50 \times 50

10 \times 10

pixels. Results for each of these scenarios are presented in the following section:

6.1. Result Analysis

1.

In the first scenario, there are three conditions where the forgery portion size in all the conditions is

50 \times 50

as shown in Figure 2. The first condition involves a dummy image with higher quality than the featured image, while the second condition involves the featured image having higher quality than the dummy image and the third condition involves the featured image having equal quality of the dummy image.

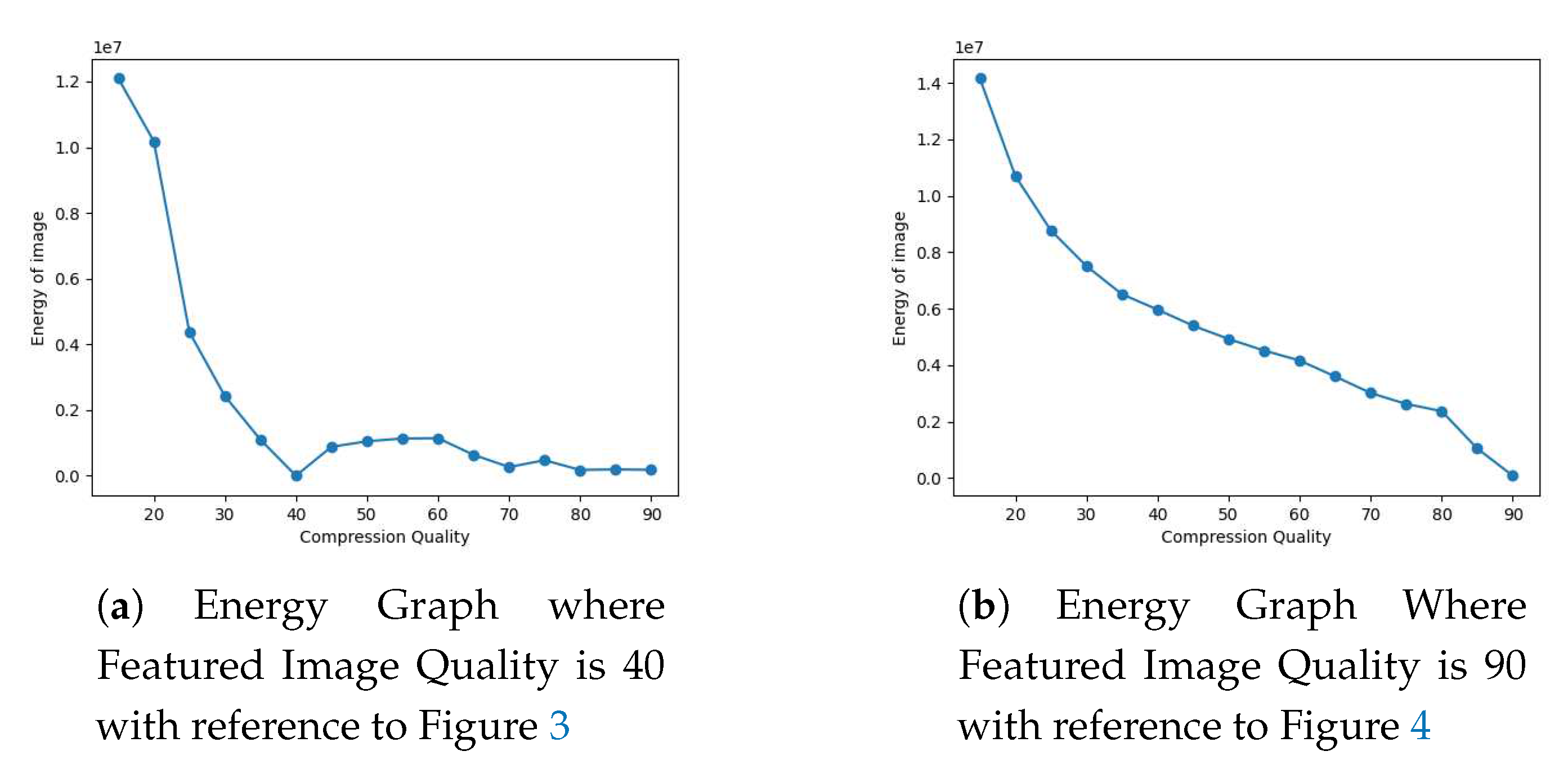
(a): In Figure 3, the featured image quality is 40 and dummy image quality is 70 of size $50 \times 50$ inserted at coordinate (50, 50).
(b): In Figure 4, the featured image quality is 90 and dummy image quality is 70 of size $50 \times 50$ inserted at coordinate(50, 50).
(c): In Figure 5, the featured image quality is 90 and dummy image quality is 90 of size $50 \times 50$ inserted at coordinate (90, 90).

2.

In the last scenario, there are three conditions where the forgery portion size in all conditions is

10 \times 10

as shown in Figure 6. The first condition involves a dummy image with higher quality than the featured image, while the second condition involves the featured image having higher quality than the dummy image. and the third condition involves the featured image having equal quality of the dummy image.

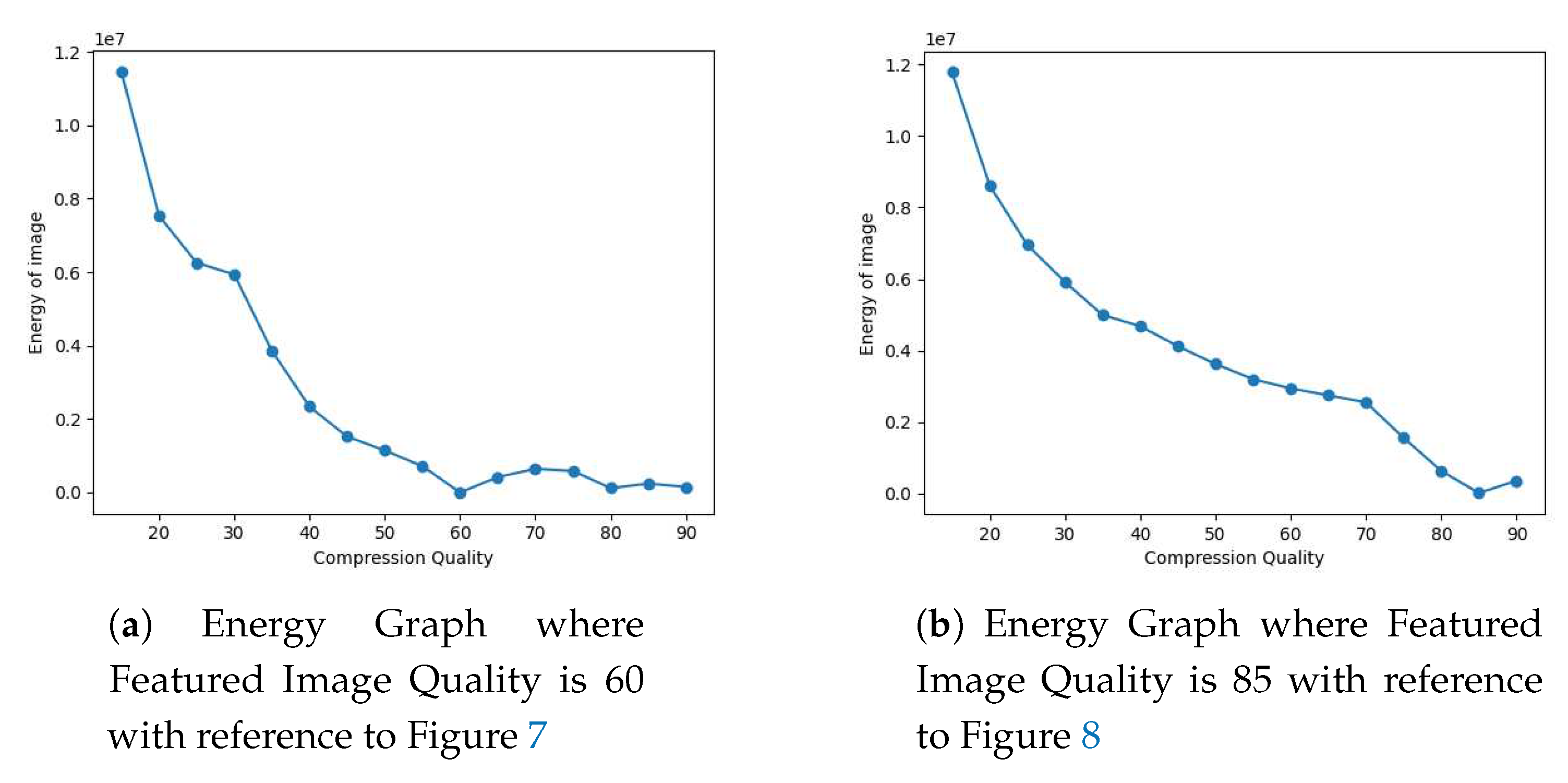
(a): In Figure 7, the featured image quality is 60 and dummy image quality is 85 of size $10 \times 10$ inserted at coordinate (90, 90).
(b): In Figure 8, the featured image quality is 85 and dummy image quality is 60 of size $10 \times 10$ inserted at coordinate (90, 90).
(c): In Figure 9, the featured image quality is 90 and dummy image quality is 90 of size $10 \times 10$ inserted at coordinate (90, 90).

By varying the JPEG quality of resaved images, we analyzed different combinations of dummy and featured images. Through experimentation and testing with different sizes of forged portions, we determined that the detection of forged regions was effective for a range of JPEG quality and potential combinations of dummy and featured images.

We also analyze the different experimental scenarios based on the difference between the energy of forged and resaved version of the image as shown in Equation (4), where P(x,y) is the energy of the image.

P (x, y) = \sum_{d = 1}^{d i m} \sum_{x = 1}^{r o w s} \sum_{y = 1}^{c o l} S (x, y, d)

(4)

where,

P (x, y)

represents the sum of the amplified pixel values

{(D e c [E (S (x, y))])}_{i = 1, 2, 3}^{2}

of the difference image obtained in Equation (1). The first minima in graphs of "energy of image" against its "compression quality" indicate the quality of the featured image. In the Figure 10 and Figure 11 the first minima occur at compression quality corresponds to the quality of the featured image along with that the minute forgeries can be identified using our proposed scheme.

7. Conclusion and Future Work

In this paper, we have described an privacy preserving framework for detecting tampering in JPEG image in the encrypted domain. In our experiments, we found that combining two different JPEG images of different quality is quite likely to lead to forgery detection. The energy graph can be used to determine the quality of the featured image. As shown in the energy graph, the quality of the featured image is the first minima. However, the chances of forgery detection are quite low with the same JPEG quality. No matter whether the images were captured from the same camera device or not, this holds true. In future work, we can extend to other image formats out paper focuses on JPEG images, there are many other image formats. It would be interesting to explore how the proposed approach could be adapted to work with other image formats, such as PNG, BMP, or TIFF.

Funding

Not applicaple.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Abidin, A.B.Z.; Majid, H.B.A.; Samah, A.B.A.; Hashim, H.B. Copy-move image forgery detection using deep learning methods: a review. 2019 6th international conference on research and innovation in information systems (ICRIIS). IEEE, 2019, pp. 1–6.
Wallace, G.K. The JPEG still picture compression standard. IEEE transactions on consumer electronics 1992, 38, xviii–xxxiv. [Google Scholar]
Jiansheng, M.; Sukang, L.; Xiaomei, T. A digital watermarking algorithm based on DCT and DWT. Proceedings. The 2009 International Symposium on Web Information Systems and Applications (WISA 2009). Citeseer, 2009, p. 104.
Rocha, A.; Scheirer, W.; Boult, T.; Goldenstein, S. Vision of the unseen: Current trends and challenges in digital image and video forensics. ACM Computing Surveys (CSUR) 2011, 43, 1–42. [Google Scholar] [CrossRef]
Al-Qershi, O.M.; Khoo, B.E. Passive detection of copy-move forgery in digital images: State-of-the-art. Forensic science international 2013, 231, 284–295. [Google Scholar] [CrossRef] [PubMed]
Singh, D.; Singh, P.; Jena, R.; Chakraborty, R.S. An image forensic technique based on JPEG ghosts. Multimedia Tools and Applications 2022, pp. 1–17.
Farid, H. Exposing digital forgeries from JPEG ghosts. IEEE transactions on information forensics and security 2009, 4, 154–160. [Google Scholar] [CrossRef]
Lukáš, J.; Fridrich, J.; Goljan, M. Detecting digital image forgeries using sensor pattern noise. Security, Steganography, and Watermarking of Multimedia Contents VIII. International Society for Optics and Photonics, 2006, Vol. 6072, p. 60720Y.
Amerini, I.; Uricchio, T.; Ballan, L.; Caldelli, R. Localization of JPEG double compression through multi-domain convolutional neural networks. 2017 IEEE Conference on computer vision and pattern recognition workshops (CVPRW). IEEE, 2017, pp. 1865–1871.
Zhou, P.; Han, X.; Morariu, V.I.; Davis, L.S. Learning rich features for image manipulation detection. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 1053–1061.
Rahmati, M.; Razzazi, F.; Behrad, A. Double JPEG compression detection and localization based on convolutional auto-encoder for image content removal. Digital Signal Processing 2022, 123, 103429. [Google Scholar] [CrossRef]
Rao, Y.; Ni, J. A deep learning approach to detection of splicing and copy-move forgeries in images. 2016 IEEE international workshop on information forensics and security (WIFS). IEEE, 2016, pp. 1–6.
Kumar, S.; Mukherjee, S.; Pal, A.K. An improved reduced feature-based copy-move forgery detection technique. Multimedia Tools and Applications 2023, 82, 1431–1456. [Google Scholar] [CrossRef]
Diallo, B.; Urruty, T.; Bourdon, P.; Fernandez-Maloigne, C. Robust forgery detection for compressed images using CNN supervision. Forensic Science International: Reports 2020, 2, 100112. [Google Scholar] [CrossRef]
Doegar, A.; Hiriyannaiah, S.; Siddesh, G.; Srinivasa, K.; Dutta, M. Cloud-based fusion of residual exploitation-based convolutional neural network models for image tampering detection in bioinformatics. BioMed Research International 2021, 2021, 1–12. [Google Scholar] [CrossRef]
Paillier, P. Public-key cryptosystem based on discrete logarithm residues. EUROCRYPT 1999 1999. [Google Scholar]
Kabeen, K.; Gent, P. Image Compression and Discrete Cosine Transform. College of Redwoods.
Sridokmai, T.; Prakancharoen, S. The homomorphic other property of Paillier cryptosystem. 2015 International Conference on Science and Technology (TICST). IEEE, 2015, pp. 356–359.

Figure 1. An overview of the proposed methodology.

Figure 2. Forged image where the forgery portion is

50 \times 50

Figure 2. Forged image where the forgery portion is

50 \times 50


(a) Featured Image	(b) Dummy Image	(c) Forged Image

Figure 3. The Forged Portion is

50 \times 50

where the Featured Image Quality is 40 and Dummy Image Quality is 70.

Figure 3. The Forged Portion is

50 \times 50

where the Featured Image Quality is 40 and Dummy Image Quality is 70.

Figure 4. The Forged Portion is

50 \times 50

where the Featured Image Quality is 90 and Dummy Image Quality is 70.

Figure 4. The Forged Portion is

50 \times 50

where the Featured Image Quality is 90 and Dummy Image Quality is 70.

Figure 5. The Forged Portion is

50 \times 50

where the Featured Image Quality is 90 and Dummy Image Quality is 90.

Figure 5. The Forged Portion is

50 \times 50

where the Featured Image Quality is 90 and Dummy Image Quality is 90.

Figure 6. Forged Image where the Forgery Portion is

10 \times 10

Figure 6. Forged Image where the Forgery Portion is

10 \times 10


(a) Featured Image	(b) Dummy Image	(c) Forged Image

Figure 7. The Forged Portion

10 \times 10

where the Featured Image Quality is 60 and Dummy Image Quality is 85.

Figure 7. The Forged Portion

10 \times 10

where the Featured Image Quality is 60 and Dummy Image Quality is 85.

Figure 8. The Forged Portion

10 \times 10

where the Featured Image Quality is 85 and Dummy Image Quality is 60.

Figure 8. The Forged Portion

10 \times 10

where the Featured Image Quality is 85 and Dummy Image Quality is 60.

Figure 9. The Forged Portion is

10 \times 10

where the Featured Image Quality is 90 and Dummy Image Quality is 90.

Figure 9. The Forged Portion is

10 \times 10

where the Featured Image Quality is 90 and Dummy Image Quality is 90.

Figure 10. Energy Graph for the forgery portion

50 \times 50

Figure 10. Energy Graph for the forgery portion

50 \times 50

Figure 11. Energy Graph for the forgery portion

10 \times 10

Figure 11. Energy Graph for the forgery portion

10 \times 10

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

PP-JPEG: A Privacy-Preserving JPEG Image Tampering Localization

Abstract

1. Introduction

2. Related Work

3. Preliminaries

3.1. Paillier Encryption

3.1.1. Key Generation

3.1.2. Encryption

3.1.3. Decryption

3.1.4. Homomorphic Properties

4. The Proposed Framework

4.1. System Model and Threat Model

4.2. Proposed Methodology

5. Security Analysis

6. Experimental Analysis

6.1. Result Analysis

7. Conclusion and Future Work

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe