Prerpints.org logo
Preprint
Article

Influence of Humidity and Temperature on Mechanical Properties of Corrugated Board – Numerical Investigation

Altmetrics

Downloads

202

Views

120

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 July 2023

Posted:

17 July 2023

You are already at the latest version

Alerts
Abstract
Paper is a material whose mechanical properties are highly dependent on humidity and temperature. Which naturally also builds the relationship between the stiffness and strength of corrugated board and changing weather conditions. In this paper, attention is focused on the dependence of the physical properties of the cardboard on changes in humidity and temperature, which undergo dynamic fluctuations both during the production of corrugated board and during its storage. Two techniques were used to test this effect, namely numerical homogenization and global sensitivity analysis. Both methods were implemented to determine the theoretical relationships between the change in humidity and/or temperature in each layer of corrugated board and its global bending, compression and shear stiffness. The procedure was used to analyze different types of 5-ply and 3-ply cardboard. The obtained results allowed to build a complete map of the relationship between the change in humidity of selected layers and the strength characteristics of the full assembly.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

Introduction

The earliest paper-like material used for writing by the Egyptians, Romans and Greeks from 3000 B.C.E. was papyrus. A cheap grade or recycled papyri were also utilized for packaging, e.g. wrapping merchandise. In terms of production, i.e. macerating and blending fibers papyrus is not a true paper, the paper, as we know it, was developed in China in 105 C.E. Chinese cognizance about papermaking reached North Africa in 750, the first recorded use of wrapping paper was in 1035, the first European paper mill was built in the 1100s on the Mediterranean coast. Papermaking reached Germany in the 1300s, France in the 1400s, and England in the early 1490s. The first paper mill in the U.S. was constructed in 1690. The papermaking machine, the wood pulping method and lithographic printing were three significant technological advances made in the 1800s that helped pave the way for the mass production of paper packaging at the turn of the century (Twede 2005).
Technological progress and the needs of the packaging sector, which have been growing rapidly over the years and driving the industry, have resulted in the global pulp and paper market being valued at USD 351.5 billion in 2021, and is projected to exceed approximately USD 380.12 billion by 2030 (Precedence 2022). This has also been the rationale behind the paper industry's pursuit of efficient, profitable, and simple solutions, which has in turn sparked a vibrant growth of research in the area. A matter of strength evaluation of paperboard or corrugated cardboard containers is the subject of ongoing, comprehensive studies.
As early as the 1950s (Kellicutt and Landt 1952; Maltenfort 1956) and 1960s (McKee et al. 1963) analytical formulae were derived and used for the calculations of corrugated box compressive strength. They are still widely applied because they lead to quick and easy solutions, however only for simple standard boxes. This fact has been an impulse for further development of the approach through the years (Allerby et al. 1985; Garbowski and Knitter-Piątkowska 2022). With the development of computer methods and the increase in computing power, numerical methods, such as finite element method (FEM) have become common to evaluate the load-bearing capacity of cardboard boxes (Park et al. 2020) as well as the material parameters of cardboard or paperboard itself (Domaneschi et al. 2017). When testing corrugated board, it is essential to know the material properties of each constituent layer, which is a demanding task due to anisotropy of the paper. The procedure that allows for facilitating one single layer, therefore getting substantial savings in computational time while maintaining the accuracy of the results, is called homogenization (Suarez et al. 2021). The fundamental physical testing, such as, e.g. box compression test (BCT), bending stiffness (BS), or the edge crush test (ECT) allows to assess the strength of the corrugated board or box itself (Czechowski et al. 2021; Jamsari et al. 2019). To assess the behavior of the corrugated board box during handling and transport, it can also be subjected to experiments by loading it with an impact load (Johst et al. 2023).
Molded pulp products, such as paperboard and corrugated board, offer an environmentally friendly alternative to diverse petroleum-based packaging systems. One of the most important advantages that make cardboard packaging superior to the plastic one is the possibility of its recycling for further various uses. The study (Sobotková et al. 2021) investigated the feasibility of using post-consumer recycled paper to produce paper plates for furniture design. The main materials used were cardboard and office paper. Multiple recycling leading to loss of quality of cellulose fibers from corrugated board, and consequently reducing the mechanical properties of paper can be partially offset by the addition of bamboo powder (Chen et al. 2022). Various methods are also being developed and enhanced to recover cellulose fibers from gloss art paper (Hafid et al. 2023) or food service waste, such as disposable coffee cups (Triantafillopoulos and Koukoulas 2020). However, the poor mechanical strength of old corrugated container (OCC) paper hinders its widespread use. To solve this problem, it has been proposed to construct a dense cross-linked network of carboxymethylcellulose inside OCC papers (Yang et al. 2023) to enable exceptional mechanical performance and water resistance. An algorithm that determines the best corrugated cardboard composition based on the packaging's geometry and the material utilized, allowing for more environmentally conscious corrugated cardboard production using components, e.g. from multiple recycling processes was proposed in (Mrówczyński et al. 2022). The effect of using recycled fibers on the thickness, modulus of elasticity and bending stiffness of a handsheet was discussed in (Ham et al. 2020). In the extensive literature on the subject, one can also find discussions on the main interactions and challenges affecting package design decisions (Berry et al. 2022), the rapid prototyping and advances in tooling, providing future opportunities for more efficient molds and more effective packaging (Debnath et al. 2022) or the different types of molded fiber products in terms of natural fiber sources, manufacturing processes, current and emerging applications, and environmental sustainability of molded products (Zhang et al. 2022).
The factors that reduce the strength of cardboard packaging such as different ventilation openings and holes or shifts on flaps (Mrówczyński et al. 2021), moisture and temperature cannot be overlooked. The impact of the last two will be discussed in detail in this paper. The contact with water or moisture has a very destructive effect on the mechanical properties of the cardboard. Water-soaked corrugated board can easily collapse, causing irreversible shape distortion. In order to make the cardboard water-repellent, a hydrolysis-resistant polyester-based thermoplastic polyurethane was proposed in (Cataldi et al. 2019). The mechanical strength reduction of the carton occurs especially when transporting and storing fresh products in high relative humidity conditions, in order to reduce moisture loss in, e.g. fruit and preserve its quality (Berry et al. 2019; Fadiji et al. 2018). Changes in the mechanical properties of various fibrous materials widely used in packaging applications due to changes in moisture content were investigated by means of a tensile test in (Nienke et al. 2022). To meet the demands of cold chain logistics, it is necessary to develop corrugated packaging that is suitable for high moisture environments. The papers (Su et al. 2023; Yang et al. 2023) investigate the mechanism of damage during cold chain transport. The effect of temperature and relative humidity on the moisture content of the undulating substrate was experimentally investigated and presented in (Wang 2018). Improving the water resistance of corrugated board products can also be achieved by spraying them with coatings such as polymeric, mineral-filled polymeric, and hybrid silica sol-gel products (Marinelli et al. 2022). Temperature, whether during production, molding or usage, has a significant impact on the behavior of cardboard products. The ultrasound-induced temperature rise during the embossing process results in the structural changes of paperboard, and, in consequence, changes of the mechanical properties of the board (Kaeppeler et al. 2020). The change in fiber structure can be characterized by subjecting the samples to selected physical and visual analyses. The dimensional stability of press-formed cardboard trays during heating and cooling was investigated in (Niini et al. 2021). The effect of heat input during folding on paperboard tray stiffness based on compression and torsion tests was evaluated in (Niini et al. 2022). The use of higher folding temperatures was proved to increase the strength and stiffness of the trays. A study to evaluate the creep behavior of corrugated packaging under two environmental conditions of standard and refrigeration at a constant load for twelve hours was reported in (Fadiji et al. 2019).
In this study, attention is focused on the dependence of the physical properties of the cardboard, particularly Young’s modulus, on changes in humidity and temperature, which undergo dynamic fluctuations both during the production of corrugated board and during its storage. The experiments are conducted numerically exploiting numerical homogenization and sensitivity analysis. Both methods are implemented to determine the theoretical relationships between the change in humidity and/or temperature in each layer of corrugated board and its global bending, compression and shear stiffness. The procedure is used to analyze several different types of 5-ply and 3-ply cardboard with various profiles of a corrugated web. The obtained results allow to build a map of the relationship between the change in humidity of selected layers and the strength characteristics of the full assembly.

Methods and Materials

Workflow of the Study

The paper investigates the influence of changes in temperature and relative humidity (RH) of individual layers of paper(s) on the mechanical properties of various types of 3- and 5-layer cardboard. Crucial part of the study was to determine the relationship between the temperature and the relative humidity and particular mechanical constants of papers. The relationship was assumed based on the literature research and is described in details in Influence of relative humidity and temperature on mechanical properties - literature study subchapter.
The homogenization method of computational mechanics was used to assess the influence on the mechanical properties of cardboard expressed by the change in its stiffnesses of representative volume elements (RVE). The computational method used was the Garbowski and Gajewski homogenization technique (Garbowski and Gajewski 2021), see Numerical homogenization subchapter.
In the main part of the work, corrugated board type B, C and BC are presented. Other cases are also presented in the Appendix, i.e. corrugated board type E, EB, BB, also taking into account different layer thicknesses, including unsymmetric cases.
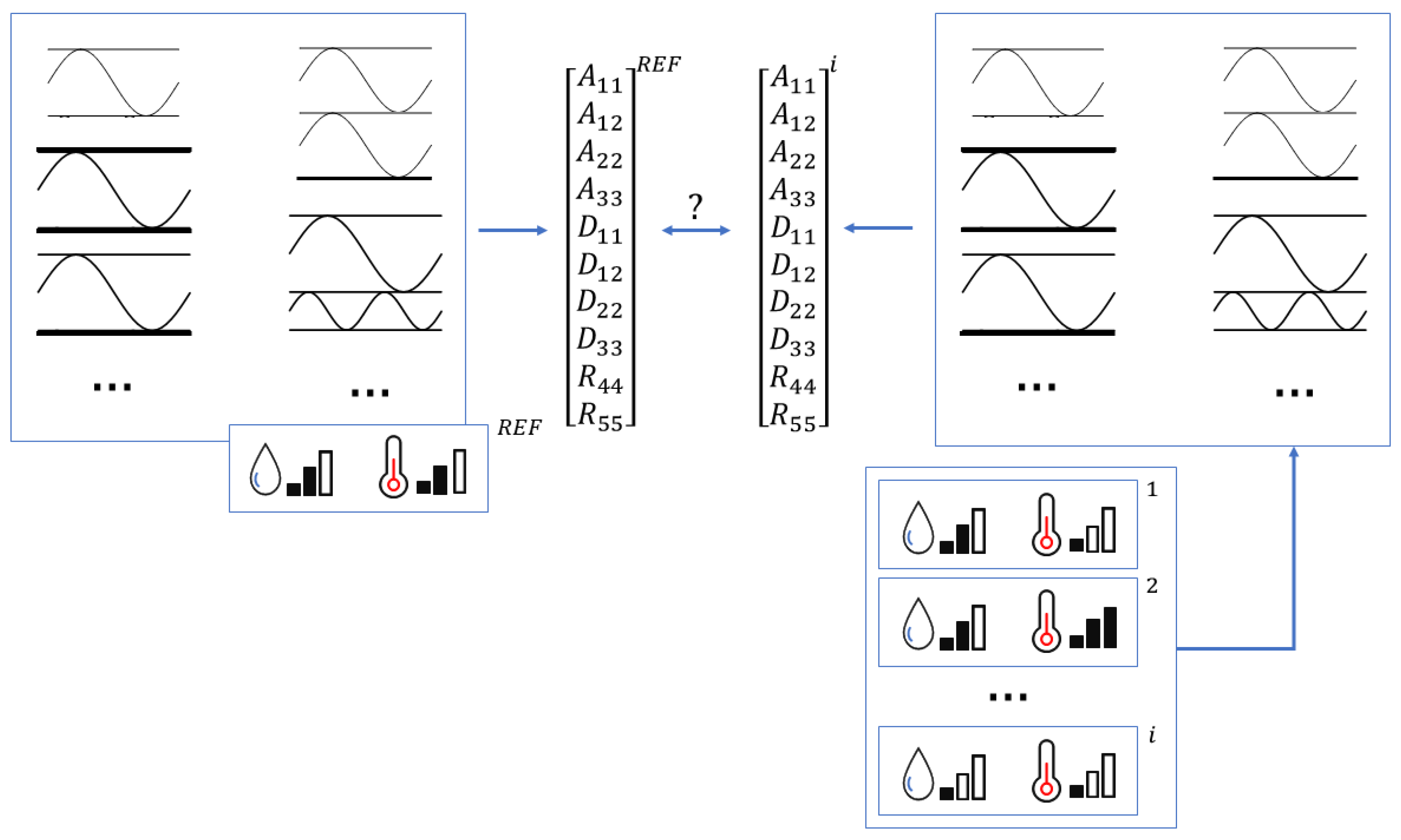
In Figure 1, the conceptual scope of the performed study was presented. The left part of the scheme represents the reference computational cases, namely, computed according to the laboratory conditions, i.e., 23 o C temperature and 50% RH. On the contrary, the right part of the scheme displays the cases with modified temperature and/or modified RH in regard to the reference values. For each case the representative stiffnesses of RVE were computed and compared with the reference case.

Influence of Relative Humidity and Temperature on Mechanical Properties—Literature Study

Since several decades, the influence of temperature and relative humidity on paper, paperboard and corrugated board has been considered and studied (Benson 1971). More recently, other works considered specific behaviors as: combined effects of moisture and temperature (Linvill and Östlund 2014), also observing reversed effects on longitudinal and tangential elastic moduli; the effect of moisture for various grammage paperboard (Marin et al. 2020a; Marin et al. 2020b); combined response during processing and heating phases (Askfelt and Ristinmaa 2017); effects of temperature and humidity on honeycomb structured paperboard (Wang et al. 2013); effects and possible defect formation in packaging paperboard due to temperature and humidity (Fadiji et al. 2018).
Despite several detailed studies, neither general validity models nor a complete database appear to be available in the literature, particularly with reference to anisotropic constitutive modelling. In view of a practical engineering methodological application, in the current paper, linearized interpolating relationships were assumed, as supported by experimental data and curves by the above-mentioned references. The assumed models, relating mechanical constitutive parameters to temperature and relative humidity variations, can be formulated by equations as:
E = E r e f 1 + α 1 T − T r e f + α 2 R H − R H r e f   ,
G = G r e f 1 + α 3 T − T r e f + α 4 R H − R H r e f   ,
where E and G represent, respectively, a longitudinal and tangential elastic modulus, T is the current temperature, R H holds for the relative humidity, r e f subscript denotes reference laboratory-controlled conditions, and α i are interpolation parameters from literature available data (where α 1 = -0.0045714·1/°C, α 2 = -0.0031429·1/%, α 3 = +0.0034615·1/°C, and α 4 = -0.0028846·1/%,). In consideration of the above-described physical behavior, it is worth to note that the numerical values of such interpolation parameters are material-dependent and mutually temperature- and relative humidity-dependent. Specific mechanical parameters for the analysis study cases considered in the present paper are given in the subsequent section Model setup.
Further research investigated the influence of temperature and relative humidity of paperboard strength (see, e.g., (Linvill and Östlund 2014)), as a relevant behavior for loading capacity and buckling resistance, particularly in packaging configurations, in order to ensure sufficient supporting and standing capacity. Nevertheless, such features are not deepened in the present work, according to the main focus of the study, devoted to mechanical elastic stiffnesses of the corrugated board.
An additional key point toward the understanding and assessment of the influence of temperature and relative humidity on corrugated board structure, is the proper selection of representative scenarios for typical conditions of temperature and relative humidity, both during processing stages and in storage environments. While coupled hygro-thermo-mechanical analyses would turn out of scope for the present investigation, some literature cases were considered, namely, climatic conditions (Lamb and Rouillard 2017), processing drying phases (Östlund 2006), relative humidity and related moisture content variations (Wang 2018), and packaging configurations (Fadiji et al. 2016).
In this paper, the reference, ambient laboratory-controlled, conditions were assumed as temperature equal to 23°C and relative humidity pairing to 50%, as reported in Table 1, tougher with the further investigated scenarios, also in agreement with standardized procedures (ISTA 2011). No detailed data could be found regarding temperature gradients through corrugated board layers during processing phases from practical observations. The classic storage conditions (hot-humid, hot-dry, cold-humid) were combined with processing conditions, at higher temperature, for various relative humidity levels (from humid to dry state), also with temperature gradients (for complete numerical description, see Table 1). It is worth to notice that the latter were considered only for 5-ply boards (labels s1-s3 and p1-p12 in Table 1), while 3-ply boards were restricted to testing conditions without temperature gradients due to reduced total thickness (labels s1-s3 and p1-p4, in Table 1).

Model Setup

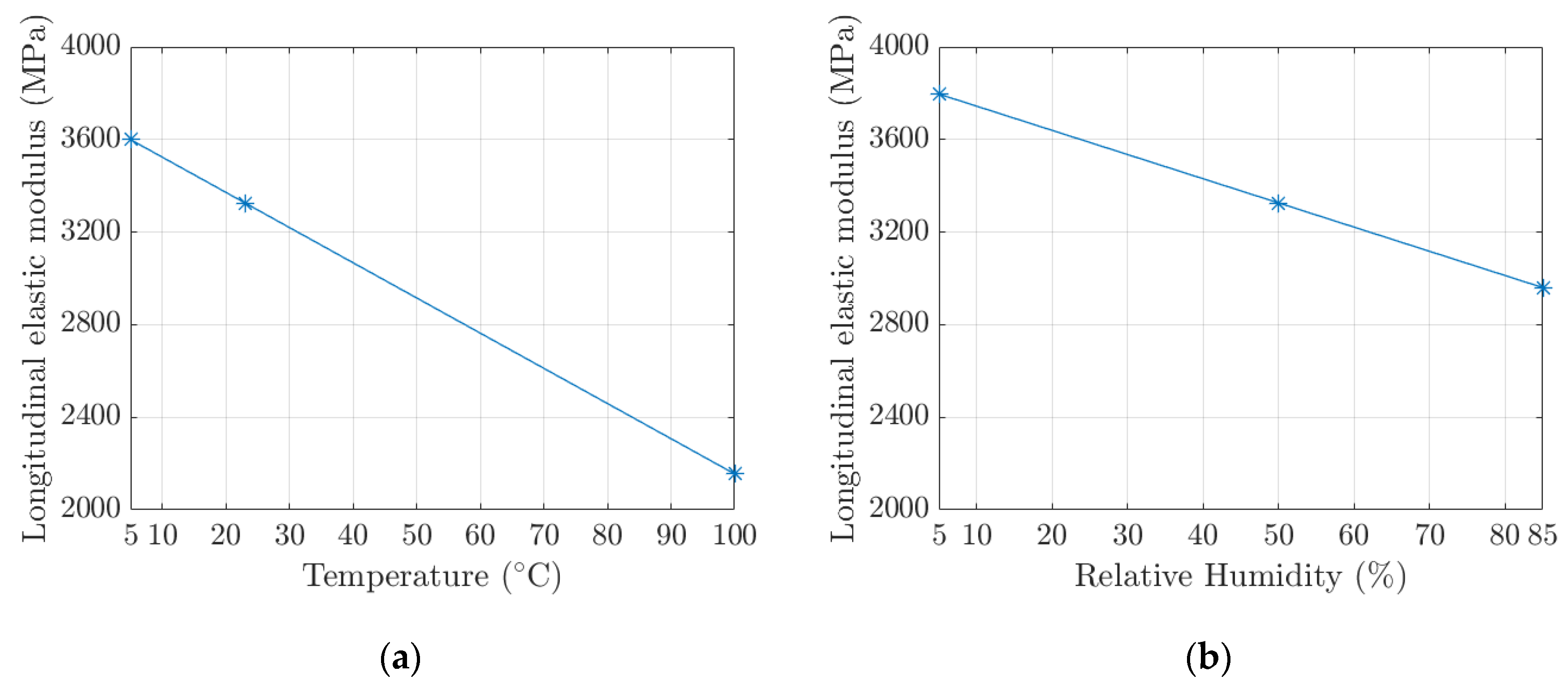
With reference to the aforementioned modelling approach (section Influence of relative humidity and temperature on mechanical properties - literature study), the constitutive mechanical parameters were selected for an orthotropic material model as in (Biancolini 2005; Garbowski and Gajewski 2021), here reported in Table 2, together with examples of temperature and relative humidity relationships sketched in Figure 2.
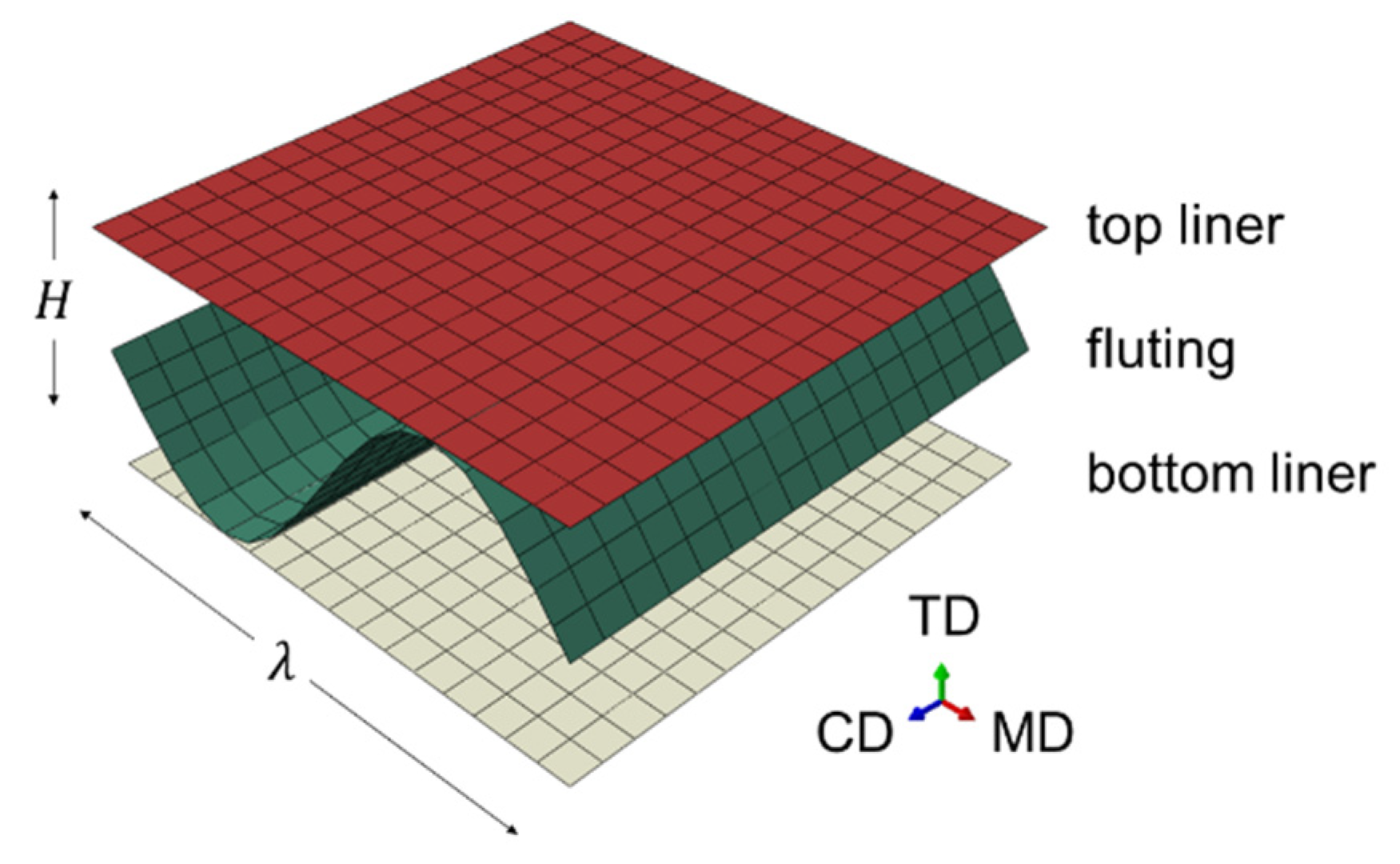
The numerical model, built within the Finite Element Method (FEM) scheme for subsequent homogenization, was developed for the three main considered geometries, namely: board type B, C and BC, defined on a one-period Representative Volume Element (RVE), characterized by axis topology (see Figure 3 and references (Biancolini 2005; Garbowski and Gajewski 2021)). In particular, fluting period ( λ ) and total height ( H ) were selected to 6.78 mm and 2.44 mm, respectively, for board type B, while equal to 8.00 mm and 3.51 mm, respectively, for board type C. For board type BC, fluting period was 8.00 mm and total height was 5.95 mm.
Within the FEM context, the paperboard layers were modelled by classic general purpose four-node shell elements, and the computational size of each model was summing up, respectively, to 969 nodes, 896 elements and 5814 degrees of freedom, for type B and C 3-ply boards, while to 1936 nodes, 1536 elements and 11616 degrees of freedom, for type BC 5-ply board.

Numerical Homogenization

One of the crucial elements of the paper is the numerical homogenization method used. The homogenization method enables computing the effective stiffnesses of the laminate composite. Due to employing the technique to different layered corrugated boards, one may easily compare the representative mechanical properties between specific boards. Here, the method of Garbowski and Gajewski was used (Garbowski and Gajewski 2021). In this section, the brief overview of the method will be presented, for more details see the original paper (Garbowski and Gajewski 2021).
The method partially bases on the FEM approach; however, it does not require solving the system of equations, which is characteristic of this technique. The method ensures the equivalence of the strain energy between the shell element and the three-dimensional reference representative volume element.
The finite element degrees of freedom for RVE are considered in a decoupled form, by separating the external (index e ) and internal (index i ) nodes:
K   u = F   → K e e K e i K i e K i i u e u i = F e 0   .
where K is the global stiffness matrix, u is a nodal displacement vector and F is the external nodal load vector.
In the present paper, the RVE is considered as the periodic element of the corrugated board, i.e., a single unit with one flute period in MD and with the same length in CD, see Figure 3. In the method, the static condensation is performed and internal nodes are omitted from further consideration.
Therefore, from static condensation the total energy of elastic deformation, E , is computed from the following:
E = 1 2 u e T   F e
The positions of external nodes may be computed by the generalized constant strains according to the relation, which for a single node takes:
u x u y u z θ x θ y i = x 0 y / 2 z / 2 0 x z 0 y z / 2 0 y x / 2 0 z / 2 0 y z x z / 2 0 0 0 x / 2 y / 2 − x 2 / 2 − y 2 / 2 − x y / 2 0 0 0 0 0 0 − y − x / 2 0 0 0 0 0 x 0 y / 2 i ε x ε y γ x y γ x z γ y z κ x κ y κ x y i .
Now, the total energy of elastic deformation for external nodes may be written by the following:
E = 1 2 u e T   K   u e = 1 2 ϵ e T   A e T   K   A e   ϵ e ,
Which for shell in bending, traction and transverse shearing may be rewritten as
E = 1 2 ϵ e T   H k   ϵ e a r e a ,
in which the laminate stiffness matrix, H k , is stated in discrete form:
H k = A e T   K   A e a r e a .
The matrix H k can be also expressed by the submatrices A, B, D, and R as follows:
H k = A 3 × 3 B 3 × 3 0 B 3 × 3 D 3 × 3 0 0 0 R 2 × 2
in which A is traction and shear effective stiffnesses, B is coupled traction-bending effective stiffnesses, D is bending and torsional effective stiffnesses and R is transverse shear effective stiffness.

Results and Discussion

Following the above devised methodology, described in Section Methods and Materials, therefore employing global sensitivity, on the selected representative scenarios, and numerical homogenization, the current section gathers the most meaningful results. These results refer to variation of homogenized stiffnesses, as influenced by temperature and relative humidity, as affecting the corrugated board layers. Such results are here reported, with normalization to percentage variations for ease of comparison, in graphical form (see Figure 4, Figure 5, Figure 6 and Figure 7) and numerical values (see Table 3, Table 4, Table 5 and Table 6), together with some relevant observations. Changes in effective stiffnesses can be clearly represented in multi-axis polar diagrams. Therefore, the figures were presented as polar plots for easier comparison between case-to-case outcome. Additional numerical results are collected in the Appendix, for further deeper case studies. In particular, Figure 4, Figure 5 and Figure 6 and related Table 3, Table 4 and Table 5 compare the storing (s1-s3) and processing (p1-p4) scenarios, respectively for B, C and BC board types. Figure 7 and associated Table 6 display results for processing (p5-p12) scenarios, with temperature gradients through layers, for BC board type.
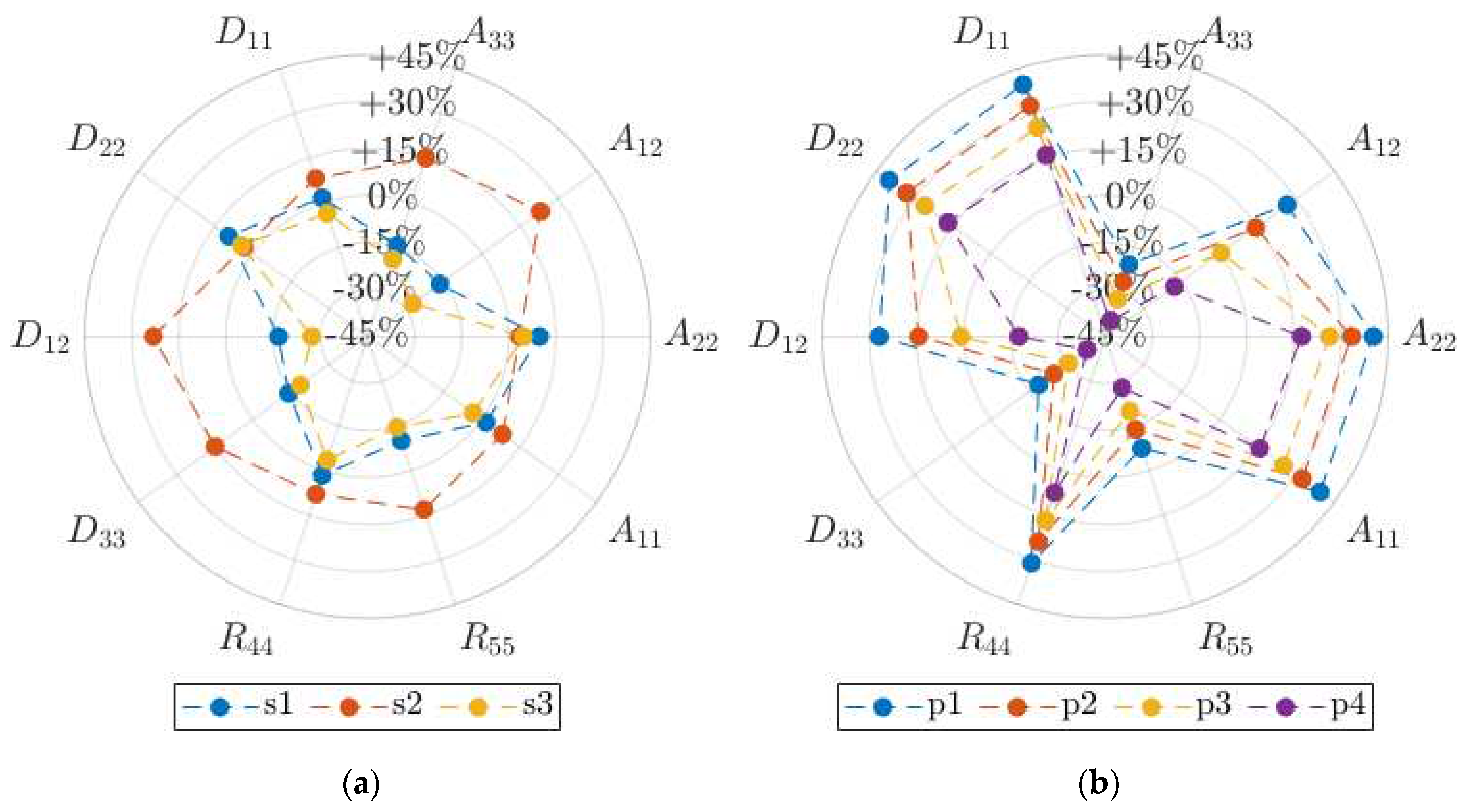
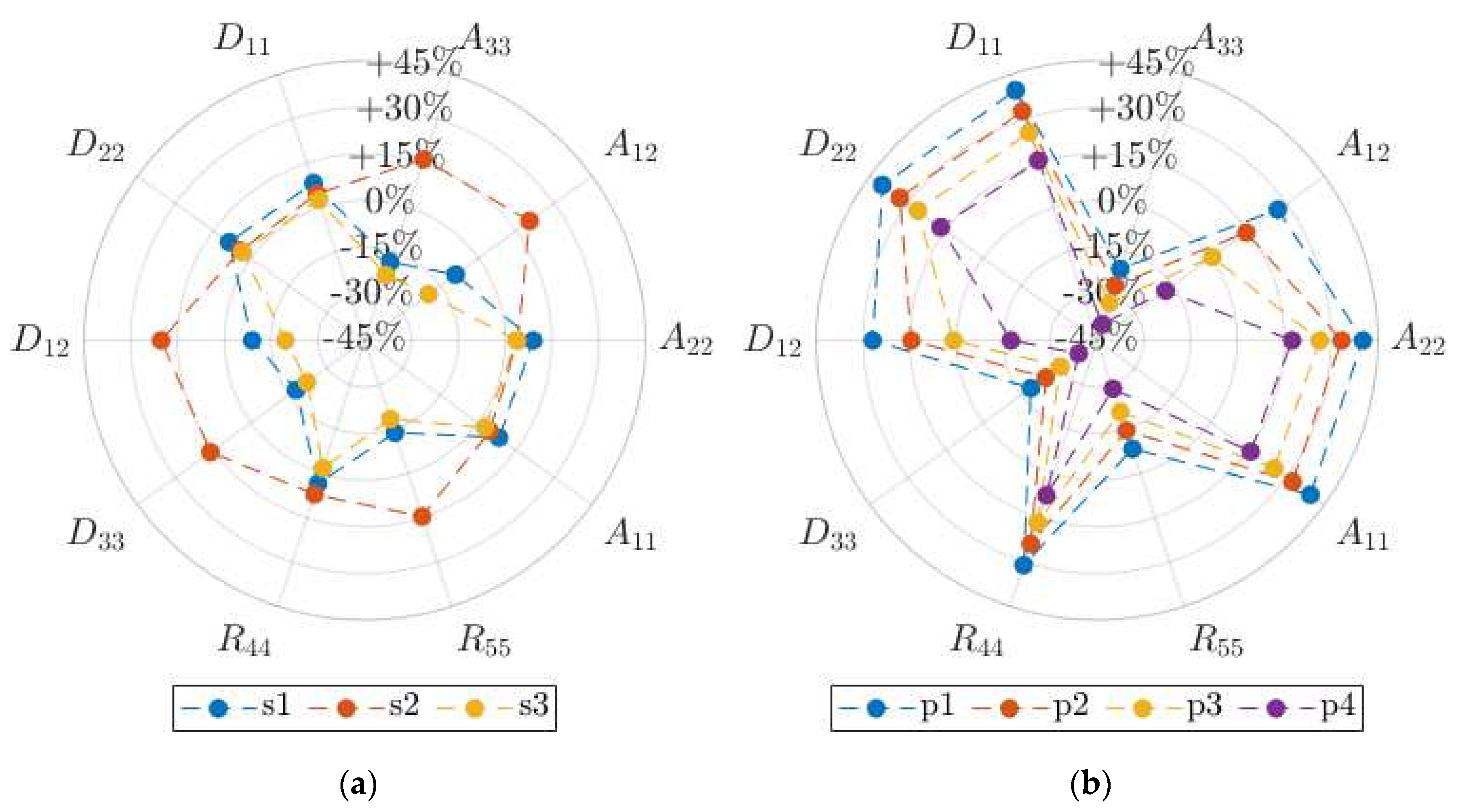
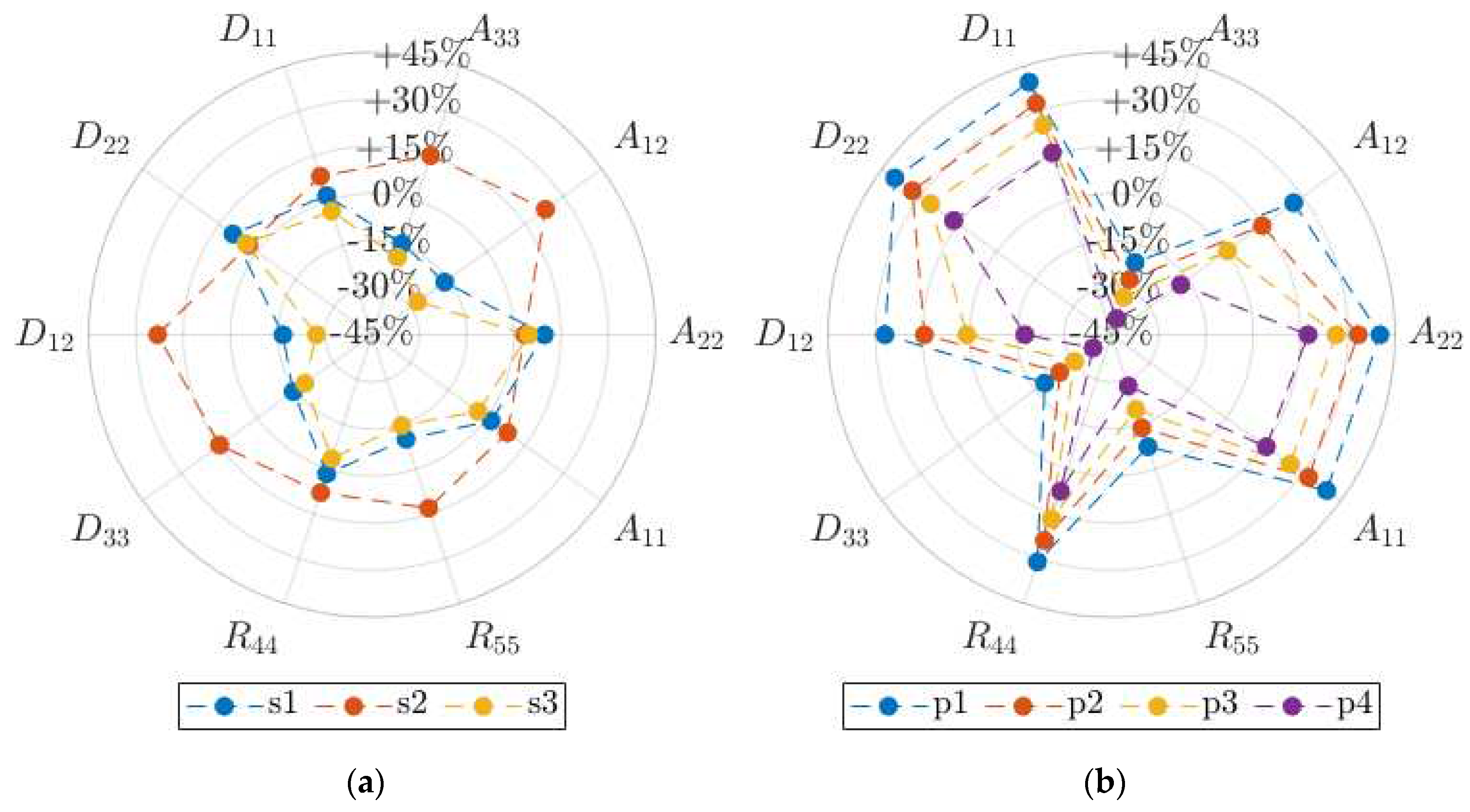
From graphical and, in details, from numerical results, it is possible to observe that diverse board types, i.e., B and C for 3-ply geometries and BC for 5-ply geometry, are subjected to similar influence effect by modifications of both temperature and relative humidity, namely displaying similar trends on stiffness variations. Therefore, such result allows for possible extension of the observed effects to various geometries, specifically focusing on mechanical, rather than geometrical, behavior.
Although it was not possible to specifically distinguish between influences caused by temperature or relative humidity variations, due to their intrinsic combined relationship on constitutive parameters, clear differences are highlighted between storing and processing scenarios. At this stage, it is worth to mention that diverse trends are obtained for each type of homogenized stiffness, namely for traction and shear, traction-bending, bending and torsional, and transverse shear stiffnesses, however with regular and smooth variation for each specific quantity. A comparison between storing and processing conditions displays more evidenced variations in the processing situations on the specific stiffness parameters, while the storing cases present more averaged modifications. This is especially visible while using the polar plots with multi-axes representing the particular effective stiffness. Giving the example, scenario s2 (5°C and 85% RH) in Figure 6a is almost perfectly convex and above 0, what means that all stiffnesses are approximately equally increased. While in Figure 6b, the “star shape” is visible with dashed lines crossing the 0% level, what means that some of the stiffnesses were increased (e.g.  A 12 ,   R 44 ), while the others were decreased (e.g. A 11 , D 11 ).
In particular, for storage conditions, while limited variations are observed between hot moderate humid and hot dry conditions, significant changes are produced by the reversal of temperature and humidity environment, such as in cold humid configuration. On the contrary, for drying processes at constant temperature, regular trends are observed, as a consequence of humidity variation, without any abrupt change in the homogenized stiffnesses.
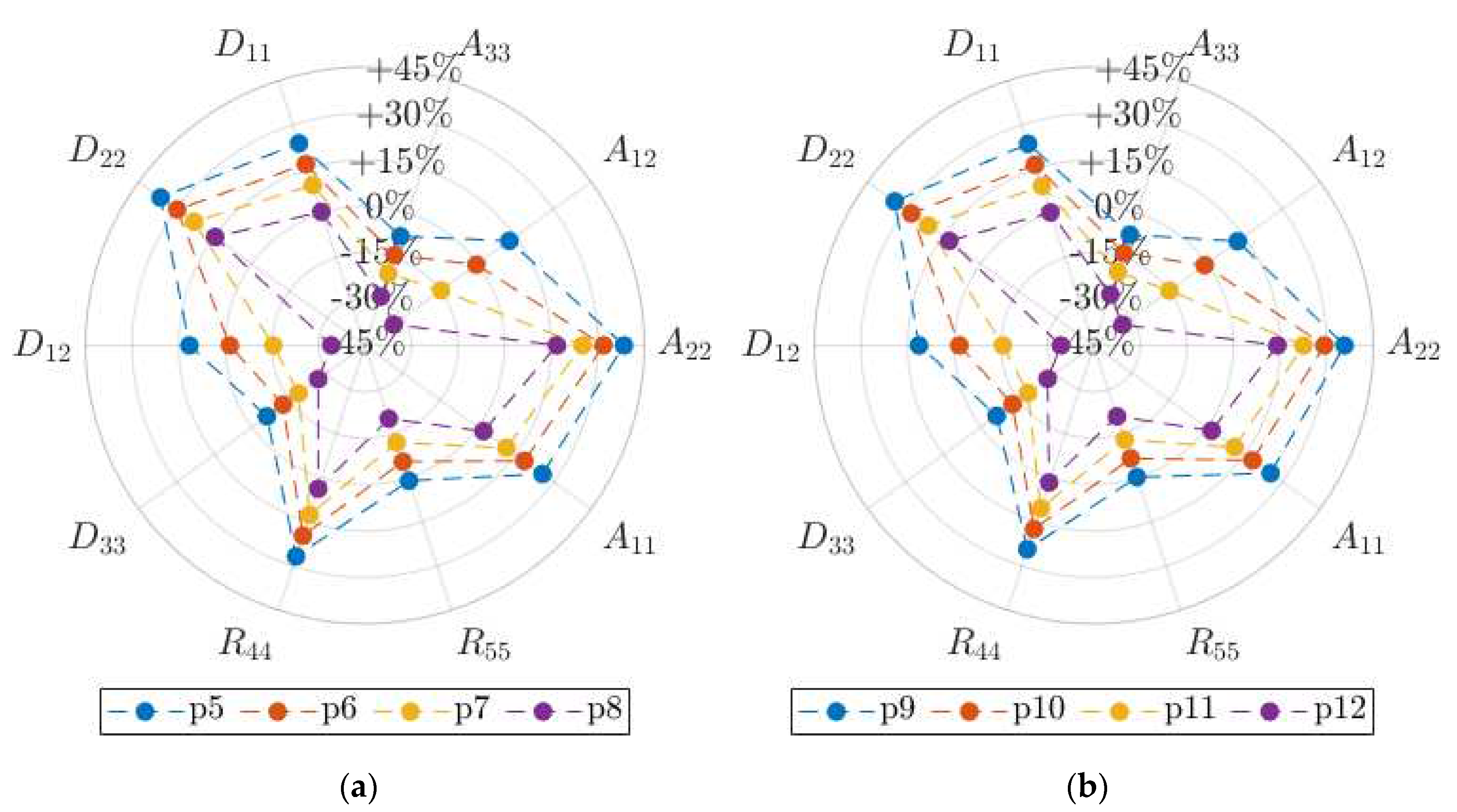
Additional comments may be derived by the discussion of results computed on the scenarios, for 5-ply boards, with temperature gradients through the layers. Particularly, the presence of a temperature gradient reduces the effects of stiffnesses changes, with increasing and smoother influence provided by less sharp temperature gradients.
The above-mentioned observed behaviors and the consequent reasoning appear to be of significant scientific and industrial interest for proper understanding of the mechanical influence of temperature and relative humidity of corrugated board, particularly toward its use in box manufacturing and various practical applications, therefore involving structural performance capacity. The possible rise of defects, during processing stages, and damages or deformations, in storage configurations, may consistently be interpreted as effects of changes of mechanical stiffnesses, particularly in uneven conditions, which may alter, in transient conditions, the paperboard inner structural behavior and response.

Conclusions

  • The influence of different humidity and temperature on the mechanical properties of cardboard appears not to be deeply investigated in the state-of-the-art. For example, on the basis of scientific literature, although a general understanding is clearly provided, it is difficult to predict precisely, and for specific material, how a change in temperature or humidity of a single layer of paper will affect the mechanical properties of a particular corrugated cardboard.
  • In this work, based on computational analyzes, developed by numerical homogenization and global sensitivity, it was systematically calculated how the change in temperature and/or relative humidity of individual layers of paper affects the change in the effective mechanical stiffnesses of 3- and 5-ply corrugated cardboards.
  • The most interesting and realistic examples, in storing and processing conditions, of analyzed calculation cases of changes in temperature and/or relative humidity of paper layers of corrugated boards were discussed. Those cases are: (1) very high storing temperature – moderate relative humidity, (2) low storing temperature – high relative humidity (3) very high storing temperature – low relative humidity, (4) very high processing temperature – varying relative humidity levels, (5) very high processing temperature with gradients – varying relative humidity levels. All results were compared to reference cases, namely to the cardboards in laboratory conditions, 23°C temperature and 50% relative humidity.
  • Temperature and relative humidity influence displayed coupled effects, however supported by regular trends, smoothened by gradient configurations, to be considered as advantageous features in processing stages against occurrence of defect formations.
  • Storing and processing conditions showed different trends in stiffness variations, with more evident and uneven effects produced by the latter, which, therefore, may be proposed as a more delicate/weak stage, requiring and suggesting for specific higher attention.
  • Diverse types of board presented similar results and trends, allowing for general validity observations, possibly to be extended as guidelines in the investigation and understanding of the considered physical conditions and phenomena.
  • The overall changes in mechanical stiffnesses for various, though realistic, scenarios highlighted global significant effects (approximately up to 40% variations), which confirm the need of specific insights and understanding of the presented problem, fostering for devoted consideration of the observed results in practical applications.
  • The changes in mechanical stiffnesses may be interpreted as sources of defects and damages in corrugated board, therefore requiring proper understanding and modelling of the temperature-relative humidity scenario (also with reference to possible transient stages and gradient fields). This has the consequent influence on constitutive mechanical parameters, and effects on structural behavior, as proposed in the methodology devised by this paper.
Article submitted:

Appendix

In order to present a wider set of cases of practical interest, this section collects numerical results for corrugated board types E (Table 7), C with different liner thicknesses (Table 8), EB (Table 9 and Table 10), and BB (Table 11 and Table 12). The results were obtained by the computational methodology devised in the paper. For stiffness definitions and temperature and relative humidity scenarios, as labelled in the tables, please, see the descriptions in the article text.
Table 7. Stiffness percentage variations (%), with respect to the reference conditions, for type E corrugated board, in scenarios s1-p4.
Table 7. Stiffness percentage variations (%), with respect to the reference conditions, for type E corrugated board, in scenarios s1-p4.
Stiffness s1 s2 s3 p1 p2 p3 p4
A 11 8.0 4.7 2.5 39.3 32.2 24.9 15.6
A 22 8.9 4.0 3.7 40.2 33.3 26.3 17.4
A 12 -9.2 20.3 -19.9 26.3 13.8 0.2 -18.2
A 33 -18.6 16.3 -22.9 -20.8 -26.6 -32.4 -39.6
D 11 8.2 4.6 2.7 39.6 32.5 25.2 15.9
D 22 8.7 4.3 3.3 40.0 33.0 26.0 16.9
D 12 -8.9 20.2 -19.6 26.9 14.4 0.9 -17.5
D 33 -18.0 16.1 -22.3 -19.5 -25.3 -31.1 -38.3
R 44 3.4 7.3 -1.9 31.3 24.1 16.7 7.4
R 55 -14.5 14.7 -19.0 -11.0 -17.0 -23.1 -30.7
Table 8. Stiffness percentage variations (%), with respect to the reference conditions, for type C corrugated board with different liner thicknesses, in scenarios s1-p4.
Table 8. Stiffness percentage variations (%), with respect to the reference conditions, for type C corrugated board with different liner thicknesses, in scenarios s1-p4.
Stiffness s1 s2 s3 p1 p2 p3 p4
A 11 8.2 4.6 2.7 39.5 32.4 25.2 15.8
A 22 8.8 4.2 3.5 40.1 33.1 26.1 17.1
A 12 -9.0 20.2 -19.7 26.6 14.1 0.6 -17.8
A 33 -18.5 16.3 -22.9 -20.8 -26.6 -32.3 -39.6
D 11 8.2 4.6 2.8 39.6 32.5 25.3 16.0
D 22 8.6 4.3 3.2 39.9 32.9 25.8 16.6
D 12 -8.8 20.2 -19.6 27.0 14.5 1.0 -17.4
D 33 -18.1 16.1 -22.4 -19.5 -25.3 -31.2 -38.4
R 44 2.9 7.4 -2.4 29.6 22.5 15.3 6.0
R 55 -14.5 14.8 -19.0 -10.1 -16.3 -22.5 -30.2
Table 9. Stiffness percentage variations (%), with respect to the reference conditions, for type EB corrugated board, in scenarios s1-p4.
Table 9. Stiffness percentage variations (%), with respect to the reference conditions, for type EB corrugated board, in scenarios s1-p4.
Stiffness s1 s2 s3 p1 p2 p3 p4
A 11 1.1 8.3 -4.0 26.8 19.6 12.3 3.2
A 22 9.8 3.3 4.9 40.7 34.1 27.5 19.2
A 12 -17.2 23.2 -27.7 11.6 -1.8 -15.9 -34.9
A 33 -12.9 14.4 -17.4 -4.2 -10.8 -17.4 -25.5
D 11 1.1 8.2 -4.0 26.6 19.4 12.2 3.2
D 22 9.8 3.4 4.8 40.6 34.1 27.5 19.1
D 12 -17.2 23.2 -27.8 11.3 -2.0 -16.2 -35.1
D 33 -12.6 14.3 -17.1 -3.7 -10.3 -16.8 -24.9
R 44 1.5 8.0 -3.6 26.7 19.7 12.6 3.6
R 55 -9.9 12.9 -14.5 0.8 -5.6 -12.0 -20.0
Table 10. Stiffness percentage variations (%), with respect to the reference conditions, for type EB corrugated board, in scenarios p5-p12.
Table 10. Stiffness percentage variations (%), with respect to the reference conditions, for type EB corrugated board, in scenarios p5-p12.
Stiffness p5 p6 p7 p8 p9 p10 p11 p12
A 11 25.7 18.5 11.3 2.3 25.4 18.3 11.1 2.1
A 22 39.1 32.5 25.9 17.6 36.9 30.3 23.8 15.5
A 12 11.4 -1.9 -16.0 -34.8 11.2 -2.0 -16.1 -34.9
A 33 -4.3 -10.9 -17.4 -25.4 -4.6 -11.1 -17.6 -25.6
D 11 24.6 17.5 10.4 1.4 24.4 17.3 10.2 1.3
D 22 37.5 30.9 24.3 16.0 35.7 29.1 22.5 14.2
D 12 11.0 -2.2 -16.2 -35.0 10.7 -2.4 -16.4 -35.2
D 33 -3.4 -9.9 -16.4 -24.4 -4.1 -10.6 -17.0 -24.9
R 44 26.7 19.7 12.6 3.6 25.2 18.2 11.2 2.3
R 55 0.8 -5.7 -12.1 -20.0 -0.2 -6.6 -12.9 -20.8
Table 11. Stiffness percentage variations (%), with respect to the reference conditions, for type BB corrugated board, in scenarios s1-p4.
Table 11. Stiffness percentage variations (%), with respect to the reference conditions, for type BB corrugated board, in scenarios s1-p4.
Stiffness s1 s2 s3 p1 p2 p3 p4
A 11 1.4 8.2 -3.8 27.4 20.2 13.0 3.8
A 22 9.7 3.4 4.8 40.6 34.0 27.4 19.1
A 12 -16.9 23.2 -27.4 12.4 -0.9 -15.1 -34.1
A 33 -13.9 14.8 -18.4 -6.8 -13.4 -19.8 -27.8
D 11 1.4 8.2 -3.7 27.5 20.3 13.0 3.9
D 22 9.6 3.5 4.6 40.5 33.9 27.2 18.8
D 12 -16.9 23.1 -27.4 12.4 -0.9 -15.1 -34.2
D 33 -13.6 14.6 -18.2 -6.5 -13.0 -19.5 -27.4
R 44 1.1 8.2 -4.0 25.7 18.7 11.7 2.9
R 55 -8.9 12.6 -13.5 3.8 -2.8 -9.4 -17.5
Table 12. Stiffness percentage variations (%), with respect to the reference conditions, for type BB corrugated board, in scenarios p5-p12.
Table 12. Stiffness percentage variations (%), with respect to the reference conditions, for type BB corrugated board, in scenarios p5-p12.
Stiffness p5 p6 p7 p8 p9 p10 p11 p12
A 11 24.3 17.1 10.0 1.0 23.8 16.7 9.6 0.6
A 22 38.1 31.6 25.0 16.6 35.2 28.6 22.0 13.7
A 12 11.4 -1.8 -15.8 -34.5 11.0 -2.1 -16.0 -34.7
A 33 -6.0 -12.5 -18.8 -26.7 -5.5 -11.8 -18.2 -26.0
D 11 22.4 15.4 8.3 -0.7 22.1 15.1 8.0 -0.9
D 22 35.8 29.3 22.6 14.2 33.8 27.2 20.6 12.2
D 12 10.7 -2.4 -16.3 -34.9 10.4 -2.6 -16.5 -35.1
D 33 -4.5 -10.9 -17.2 -25.1 -5.0 -11.3 -17.6 -25.4
R 44 25.7 18.7 11.7 2.8 22.8 15.9 9.0 0.2
R 55 3.5 -3.1 -9.6 -17.8 1.8 -4.6 -11.0 -18.9

References Cited

  1. Allerby, I.M., Laing, G.N., Cardwell, R.D. (1985). “Compressive strength—From components to corrugated containers,” Appita Conf. Notes, 1–11.
  2. Askfelt, H., Ristinmaa, M. (2017). “Response of moist paperboard during rapid compression and heating,” Applied Mathematical Modelling, 42, 114-132. [CrossRef]
  3. Benson, R.E. (1971). “Effects of relative humidity and temperature on tensile stress-strain properties of kraft linerboard”. Tappi J 54(5), 699-703.
  4. Berry, T.M., Ambaw, A., Defraeye, T., Coetzee, C., and Opara, U.L. (2019). “Moisture adsorption in palletised corrugated fibreboard cartons under shipping conditions: A CFD modelling approach,” Food Bioprod. Process. 114, 43-59. [CrossRef]
  5. Berry, T.M., Defraeye, T., Shrivastava, C., Ambaw, A., Coetzee, C., and Opara, U.L. (2022). “Designing ventilated packaging for the fresh produce cold chain,” Food Bioprod. Process. 134, 121-149. [CrossRef]
  6. Biancolini, M.E. (2005). “Evaluation of equivalent stiffness properties of corrugated board,” Composite Structures, 69, 322-328. [CrossRef]
  7. Cataldi, P., Profaizer, M., and Bayer, I.S. (2019). “Preventing water-induced mechanical deterioration of cardboard by a sequential polymer treatment,” Ind. Eng. Chem. Res. 58, 6456-6465. [CrossRef]
  8. Chen, H., Wang, Y., Qiu, J., Song, J., Wang, J., Liu, M., Wo, Q., Jiang, L., and Yang, T. (2022). “Properties and application of kraft pulp prepared from waste bamboo powder,” BioResources 17(4), 6262-6276. [CrossRef]
  9. Czechowski, L., Kmita-Fudalej, G., Szewczyk,W., Gralewski, J., and Bienkowska, M. (2021). “Numerical and experimental study of five-layer non-symmetrical paperboard panel stiffness,” 14(23), 7453. [CrossRef]
  10. Debnath, M., Sarder, R., Pal, L., and Hubbe, M.A. (2022). “Molded pulp products for sustainable packaging: Production rate challenges and product opportunities,” BioResources 17(2), 3810-3870. [CrossRef]
  11. Domaneschi, M., Perego, U., Borgqvist, E., and Borsari, R. (2017). “An industry-oriented strategy for the finite element simulation of paperboard creasing and folding,” Packag. Technol. Sci. 30(6), 269–294. [CrossRef]
  12. Fadiji, T., Coetzee, C.J., Opara, U.L. (2016). “Compression strength of ventilated corrugated paperboard packages: Numerical modelling, experimental validation and effects of vent geometric design,” Biosyst. Eng. 151, 231-247. [CrossRef]
  13. Fadiji, T., Berry, T.M., Coetzee, C.J., Opara, U.L. (2018). “Mechanical design and performance testing of corrugated paperboard packaging for the postharvest handling of horticultural produce,” Biosyst. Eng. 171, 220-244. [CrossRef]
  14. Fadiji, T., Coetzee, C.J., Opara, U.L. (2019). “Analysis of the creep behaviour of ventilated corrugated paperboard packaging for handling fresh produce — An experimental study,” Food Bioprod. Process. 117, 126-137. [CrossRef]
  15. Garbowski, T., Gajewski, T. (2021). “Determination of Transverse Shear Stiffness of Sandwich Panels with a Corrugated Core by Numerical Homogenization,” Materials 14(8), 1976. [CrossRef]
  16. Garbowski, T., Knitter-Piątkowska, A. (2022). “Analytical determination of the bending stiffness of a five-layer corrugated cardboard with imperfections,” Materials 15(2), 663. [CrossRef]
  17. Hafid, H.S., Omar, F.N., Bahrin, E.K., and Wakisaka, M. (2023). “Extraction and surface modification of cellulose fibers and its reinforcement in starch-based film for packaging composites,” Bioresour. Bioprocess. 10, 7-26. [CrossRef]
  18. Ham, C.H., Youn, H. J., and Lee, H. L. (2020). “Influence of fiber composition and drying conditions on the bending stiffness of paper,” BioResources 15(4), 9197-9211. [CrossRef]
  19. International Safe Transit Association. (2011) ISTA Procedure 2A 11-11: packaged-products 150 lb (68 kg) or less.
  20. Jamsari, M.A., Kueh, C., Gray-Stuart, E.M., Dahm, K., and Bronlund, J.E. (2019). “Experimental and numerical performance of corrugated fibreboard at different orientations under four-point bending test,” Packag. Technol. Sci. 32(11), 555–565. [CrossRef]
  21. Johst, P., Kaeppeler, U., Seibert, D., Kucher, M., and Böhm, R. (2023). “Investigation of different cardboard materials under impact loads,” BioResources 18(1), 1933-1947. [CrossRef]
  22. Kaeppeler, U., Hünniger, J., Hofmann, A., Berlich, A., and Engisch, L. (2020). “Thermal influence on the mechanical properties of cardboard during an ultrasonic-assisted embossing process,” BioResources 15(3), 5110-5121. [CrossRef]
  23. Kellicutt, K., and Landt, E. (1952). “Development of design data for corrugated fiberboard shipping containers,” Tappi J. 35, 398–402.
  24. Lamb, M.J., Rouillard, V. (2017). “Static and Dynamic Strength of Paperboard Containers Subjected to Variations in Climatic Conditions,” Packag. Technol. Sci., 30, 103-114. [CrossRef]
  25. Linvill, E., Östlund, S. (2014). “The Combined Effects of Moisture and Temperature on the Mechanical Response of Paper,” Experimental Mechanics, 54, 1329-1341. [CrossRef]
  26. Maltenfort, G. (1956). “Compression strength of corrugated containers,” Fibre Contain. 41, 106–121.
  27. Marin, G., Nygårds, M., Östlund, S. (2020a). “Elastic-plastic model for the mechanical properties of paperboard as a function of moisture”, Nordic Pulp & Paper Research Journal, 35(3), 353-361. [CrossRef]
  28. Marin, G., Nygårds, M., Östlund, S. (2020b). “Stiffness and strength properties of five paperboards and their moisture dependency”, Tappi Journal, 19(2), 71-85.
  29. Marinelli, A., Diamanti, M.V., Lucotti, A., Pedeferri, M.P., and Del Curto, B. (2022). “Evaluation of coatings to improve the durability and water-barrier properties of corrugated cardboard,” Coatings, 12, 10-24. [CrossRef]
  30. McKee, R.C., Gander, J.W., and Wachuta, J.R. (1963). “Compression strength formula for corrugated boxes,” Paperboard Packag. 48, 149–159.
  31. Mrówczyński, D., Garbowski, T. and Knitter-Piątkowska, A. (2021). “Estimation of the Compressive Strength of Corrugated Board Boxes with Shifted Creases on the Flaps,” Materials 14(18), 5181. [CrossRef]
  32. Mrówczyński, D., Knitter-Piątkowska, A., and Garbowski, T. (2022). “Optimal design of double-walled corrugated board packaging,” Materials 15, 2149. [CrossRef]
  33. Nienke, T., Kwade, A., and Eggerath, D. (2022). “Influence of moisture, temperature and bleaching on the mechanical properties of coated fiber-based substrates,” Coatings 12, 1287-1299. [CrossRef]
  34. Niini, A., Tanninen, P., Varis, J., and Leminen, V. (2021). “Effects of press-forming parameters on the dimensional stability of paperboard trays,” BioResources 16(3), 4876-4890. [CrossRef]
  35. Niini, A., Tanninen, P., Laukala, T., Varis, J., and Leminen, V. (2022). “A folding method to increase the rigidity of paperboard tray packages,” BioResources 17(1), 1427-1441. [CrossRef]
  36. Östlund, M., (2006). “Modeling the Influence of Drying Conditions on the Stress Buildup During Drying of Paperboard,” Journal of Engineering Materials and Technology, 128, 495-502. [CrossRef]
  37. Park, J., Park, M., Choi, D.S., Jung, H.M. and Hwang, S.W. (2020). “Finite element-based simulation for edgewise compression behavior of corrugated paperboard for packing of agricultural products,” Appl. Sci. 10(19), 6716. [CrossRef]
  38. Precedence Research (2022). “Pulp and Paper Market Size, Growth, Trends,” Report 2022-2030 (https://www.precedenceresearch.com/pulp-and-paper-market), accessed 4 July 2023.
  39. Sobotková, A., Šimek, M., Pařil, P., Fictum, L., and Szökeová, S. (2021). “Mechanical and physical properties of boards made from recycled paper,” BioResources 16(2), 3952-3963. [CrossRef]
  40. Su, H., Huang, C., Li, C., Zhao, Y., Zheng, D., and Duan, Q. (2023). “Failure mechanism of the corrugated medium under simulated cold chain logistics,” ACS Omega 8(26), 23673–23682. [CrossRef]
  41. Suarez, B., Muneta, M.L.M., Sanz-Bobi, J.D., and Romero, G. (2021). “Application of homogenization approaches to the numerical analysis of seating made of multi-wall corrugated cardboard,” Compos. Struct. 262, 113642. [CrossRef]
  42. Triantafillopoulos, N., and Koukoulas, A. A. (2020). “The future of single-use paper coffee cups: Current progress and outlook,” BioResources 15(3), 7260-7287. [CrossRef]
  43. Twede, D. (2005). “The origins of paper based packaging,” in: Proceedings of the 12th Conference on Historical Analysis and Research in Marketing 12, 288-300.
  44. Wang, D. (2018). “Elastic modulus prediction of corrugating medium under different temperature and relative humidity,” IOP Conf. Ser.: Mater. Sci. Eng. 439, 042043-042050. [CrossRef]
  45. Wang, D., Wang, J., Liao, Q. (2013). “Investigation of mechanical property for paper honeycomb sandwich composite under different temperature and relative humidity,” Journal of Reinforced Plastics and Composites, 32(13), 987-997. [CrossRef]
  46. Yang, W., Ding, Y., Liang, J., Li, C., Bian, H., Dai, H., and Hu, C. (2023). “Constructing carboxymethyl cellulose-metal ion crosslinked networks in old corrugated recycled paper enhances its strength and wet stability,” Cellulose 30, 3901–3913. [CrossRef]
  47. Zhang, Y., Duan, C., Bokka, S.K., He, Z., and Ni, Y. (2022). “Molded fiber and pulp products as green and sustainable alternatives to plastics: A mini review,” J. Bioresour. Bioprod. 7, 14-25. [CrossRef]
Preprints 79627 g001
Figure 1. The conceptual scope of the performed study: reference cases vs. cases with modified temperature and/or modified RH.
Figure 1. The conceptual scope of the performed study: reference cases vs. cases with modified temperature and/or modified RH.
Preprints 79627 g001
Preprints 79627 g002
Figure 2. Examples of constitutive parameter variation laws: (a) longitudinal elastic modulus vs. temperature; (b) longitudinal elastic modulus vs. relative humidity.
Figure 2. Examples of constitutive parameter variation laws: (a) longitudinal elastic modulus vs. temperature; (b) longitudinal elastic modulus vs. relative humidity.
Preprints 79627 g002
Preprints 79627 g003
Figure 3. Corrugated board geometric representative volume element model for homogenization, with highlighted geometric parameters (period ( λ ) and total height ( H )), sections (liners and fluting), and material orientation (Machine Direction, Transverse Direction, Cross Direction) reference system.
Figure 3. Corrugated board geometric representative volume element model for homogenization, with highlighted geometric parameters (period ( λ ) and total height ( H )), sections (liners and fluting), and material orientation (Machine Direction, Transverse Direction, Cross Direction) reference system.
Preprints 79627 g003
Preprints 79627 g004
Figure 4. Stiffness percentage variations, with respect to the reference conditions, for type B corrugated board in (a) storing scenarios, s1-s3, and (b) processing scenarios, p1-p4.
Figure 4. Stiffness percentage variations, with respect to the reference conditions, for type B corrugated board in (a) storing scenarios, s1-s3, and (b) processing scenarios, p1-p4.
Preprints 79627 g004
Preprints 79627 g005
Figure 5. Stiffness percentage variations, with respect to the reference conditions, for type C corrugated board in (a) storing scenarios, s1-s3, and (b) processing scenarios, p1-p4.
Figure 5. Stiffness percentage variations, with respect to the reference conditions, for type C corrugated board in (a) storing scenarios, s1-s3, and (b) processing scenarios, p1-p4.
Preprints 79627 g005
Preprints 79627 g006
Figure 6. Stiffness percentage variations, with respect to the reference conditions, for type BC corrugated board in (a) storing scenarios, s1-s3, and (b) processing scenarios, p1-p4.
Figure 6. Stiffness percentage variations, with respect to the reference conditions, for type BC corrugated board in (a) storing scenarios, s1-s3, and (b) processing scenarios, p1-p4.
Preprints 79627 g006
Preprints 79627 g007
Figure 7. Stiffness percentage variations with respect to the reference conditions, for type BC corrugated board in (a) processing scenarios with one-layer-temperature gradient, p5-p8, and (b) processing scenarios with two-layer-temperature gradient, p9-p10.
Figure 7. Stiffness percentage variations with respect to the reference conditions, for type BC corrugated board in (a) processing scenarios with one-layer-temperature gradient, p5-p8, and (b) processing scenarios with two-layer-temperature gradient, p9-p10.
Preprints 79627 g007
Table 1. Temperature and relative humidity main scenarios considered for the numerical analyses (scenarios s1-p4 apply to 3-ply cardboard models; scenarios s1-p12 apply to 5-ply cardboard models).
Table 1. Temperature and relative humidity main scenarios considered for the numerical analyses (scenarios s1-p4 apply to 3-ply cardboard models; scenarios s1-p12 apply to 5-ply cardboard models).
Scenario Label Scenario Description Temperature (°C) Relative Humidity (%)
ref laboratory-controlled conditions 23 50
s1 storage, extreme heat, moderate humidity 60 30
s2 storage, cold, humid 5 85
s3 storage, extreme heat, dry 60 15
p1 processing, humid 100 70
p2 processing, ambient humidity 100 50
p3 processing, moderate humidity 100 30
p4 processing, dry 100 5
p5 processing, temperature gradient, humid 100
70 (top liner)		 70
p6 processing, temperature gradient, ambient humidity 100
70 (top liner)		 50
p7 processing, temperature gradient, moderate humidity 100
70 (top liner)		 30
p8 processing, temperature gradient, dry 100
70 (top liner)		 5
p9 processing, temperature gradient, humid 100
70 (top liner and fluting)		 70
p10 processing, temperature gradient, ambient humidity 100
70 (top liner and fluting)		 50
p11 processing, temperature gradient, moderate humidity 100
70 (top liner and fluting)		 30
p12 processing, temperature gradient, dry 100
70 (top liner and fluting)		 5
Table 2. Thicknesses and material properties of liners and fluting adopted in the reference, laboratory-controlled, conditions; after (Garbowski and Gajewski 2021).
Table 2. Thicknesses and material properties of liners and fluting adopted in the reference, laboratory-controlled, conditions; after (Garbowski and Gajewski 2021).
Layer t
(mm)		 E 1
(MPa)		 E 2
(MPa)		 ν 12
(-)		 G 12
(MPa)		 G 13
(MPa)		 G 23
(MPa)
liners 0.29 3326 1694 0.34 859 429.5 429.5
fluting 0.30 2614 1532 0.32 724 362 362
Table 3. Stiffness percentage variations (%), with respect to the reference conditions, for type B corrugated board, in scenarios s1-p4.
Table 3. Stiffness percentage variations (%), with respect to the reference conditions, for type B corrugated board, in scenarios s1-p4.
Stiffness s1 s2 s3 p1 p2 p3 p4
A 11 8.1 4.7 2.6 39.4 32.3 25.1 15.7
A 22 8.9 4.1 3.7 40.2 33.3 26.3 17.4
A 12 -9.1 20.3 -19.8 26.5 14.1 0.5 -17.9
A 33 -18.6 16.3 -22.9 -20.8 -26.6 -32.4 -39.6
D 11 8.2 4.6 2.7 39.6 32.5 25.2 15.9
D 22 8.7 4.3 3.3 40.0 33.1 26.0 16.9
D 12 -8.9 20.2 -19.6 26.9 14.4 0.9 -17.5
D 33 -17.8 16.0 -22.1 -18.8 -24.7 -30.5 -37.8
R 44 3.5 7.1 -1.8 31.1 23.9 16.7 7.4
R 55 -13.4 14.4 -17.9 -7.5 -13.8 -20.0 -27.8
Table 4. Stiffness percentage variations (%), with respect to the reference conditions, for type C corrugated board, in scenarios s1-p4.
Table 4. Stiffness percentage variations (%), with respect to the reference conditions, for type C corrugated board, in scenarios s1-p4.
Stiffness s1 s2 s3 p1 p2 p3 p4
A 11 8.2 4.6 2.7 39.5 32.4 25.1 15.8
A 22 9.0 4.0 3.7 40.2 33.4 26.4 17.5
A 12 -9.0 20.3 -19.7 26.6 14.1 0.6 -17.8
A 33 -18.5 16.3 -22.9 -20.8 -26.5 -32.3 -39.5
D 11 8.2 4.6 2.7 39.6 32.5 25.3 15.9
D 22 8.7 4.2 3.3 40.0 33.1 26.0 16.9
D 12 -8.9 20.2 -19.6 26.9 14.5 1.0 -17.4
D 33 -17.8 16.1 -22.2 -18.8 -24.7 -30.5 -37.8
R 44 3.5 7.1 -1.8 31.0 23.8 16.6 7.4
R 55 -13.8 14.6 -18.4 -8.3 -14.5 -20.8 -28.6
Table 5. Stiffness percentage variations (%), with respect to the reference conditions, for type BC corrugated board, in scenarios s1-p4.
Table 5. Stiffness percentage variations (%), with respect to the reference conditions, for type BC corrugated board, in scenarios s1-p4.
Stiffness s1 s2 s3 p1 p2 p3 p4
A 11 1.7 8.1 -3.4 28.3 21.1 13.8 4.6
A 22 9.7 3.4 4.7 40.6 34.0 27.3 18.9
A 12 -16.5 23.0 -27.1 13.4 0.1 -14.1 -33.2
A 33 -14.5 15.0 -19.0 -8.7 -15.1 -21.5 -29.4
D 11 1.6 8.1 -3.6 28.0 20.7 13.5 4.3
D 22 9.6 3.5 4.5 40.5 33.8 27.1 18.7
D 12 -16.7 23.1 -27.3 13.0 -0.3 -14.6 -33.6
D 33 -14.1 14.8 -18.6 -7.7 -14.2 -20.6 -28.5
R 44 1.6 7.9 -3.5 26.7 19.7 12.7 3.8
R 55 -10.0 13.1 -14.6 1.2 -5.3 -11.8 -19.9
Table 6. Stiffness percentage variations (%), with respect to the reference conditions, for type BC corrugated board, in scenarios p5-p12.
Table 6. Stiffness percentage variations (%), with respect to the reference conditions, for type BC corrugated board, in scenarios p5-p12.
Stiffness p5 p6 p7 p8 p9 p10 p11 p12
A 11 25.7 18.5 11.3 2.2 25.3 18.2 11.0 1.9
A 22 38.4 31.8 25.1 16.8 35.7 29.2 22.5 14.1
A 12 12.5 -0.6 -14.7 -33.5 12.3 -0.9 -14.9 -33.6
A 33 -7.9 -14.3 -20.6 -28.4 -7.4 -13.7 -20.0 -27.7
D 11 23.7 16.6 9.5 0.4 23.5 16.4 9.2 0.2
D 22 36.3 29.7 23.0 14.6 34.2 27.6 20.9 12.5
D 12 11.5 -1.5 -15.5 -34.2 11.3 -1.7 -15.7 -34.4
D 33 -6.0 -12.4 -18.6 -26.4 -6.3 -12.6 -18.8 -26.6
R 44 26.7 19.7 12.6 3.7 24.3 17.4 10.4 1.6
R 55 1.0 -5.5 -12.0 -20.1 -0.2 -6.6 -12.9 -20.9
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated