Prerpints.org logo
Preprint
Article

Optimised Structural Modelling For Inverse Analysis Parameter Identification Relying On Dynamic Measurements

Altmetrics

Downloads

112

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 July 2023

Posted:

18 July 2023

You are already at the latest version

Alerts
Abstract
In the context of Inverse Analysis in Civil Engineering, parameter identification and model calibration, of a structural system, relying on dynamic measurements, are subjects of a growing research interest. In the present contribution, the topic is tackled with reference both to simplified structural numerical examples and to a specific case study, namely a historical road three-span reinforced concrete arched bridge, with vibrational data previously acquired by standard wired accelerometers on the deck, under operational traffic conditions. In particular, the present work aims at focussing on the identification issues, concerning the definition of a maximum allowable threshold number of sought material parameters (e.g., Young’s moduli and mass densities of different structural components), with respect to the amount of available measurement data, and the investigation of the inverse analysis discrepancy function to be optimised, in order to set the intrinsic issue of multiple “realizations”, in case of a plain use of modal properties, and in view of forming a well–posed optimisation problem. Structural modelling, sensitivity analysis and numerical optimisation approaches are herein combined toward a robust and efficient identification strategy, to be effectively employed in structural assessment and diagnosis, also with respect to originally available or enriched sets of experimental data. The proposed methodology, and collected results, shall outline an efficient identification procedure, in view of automated inverse analysis, practically oriented to the dynamic assessment and structural diagnosis in the Civil Engineering context, as applied e.g. to strategic bridge infrastructures.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Inverse Analysis approaches assumed, since several years, a significant role in scientific and engineering research, as a reliable methodology toward parameter identification and model calibration (see, e.g., [1,2]). Nowadays, a growing interest, supported by computational advancements, is exhibited in the context of both Solid and Structural Mechanics, fostering engineering problem–oriented developments (see, e.g., [3,4,5,6,7]).
Within such a framework, a complete Inverse Analysis setup may be devised in eight main steps, as described in the following.
  • Selection of the parameters to be estimated in the investigated problem, namely choice of the sought quantities to be identified, toward assessment and calibration of the specific behaviour and model.
  • Design of the experiment, as the best suitable experimental procedure to collect response data as source of information for a subsequent identification phase.
  • Test simulation, by computational modelling, to effectively reproduce the experimental phenomena, in a reliable manner, to evaluate numerical counterparts of experimental measurements.
  • Definition of a feasible “search domain”, namely of a constrained space of the underlying system parameters, with limits possibly suggested by experts or guidelines, to be adopted within the identification procedure.
  • Sensitivity analysis (see, e.g., [8]) of the investigated problem, with respect to the sought parameters, in order to efficiently understand the specific influence of the selected parameters (possibly, to be reduced) on the system behaviour and, specifically, on the observed quantities.
  • Formulation of an appropriate “discrepancy function”, to be minimised, as a scalar norm between measured and computed quantities, therefore forming a function of the input sought parameters, possibly also accounting for sources of uncertainty.
  • Selection and implementation of a minimisation algorithm, in order to handle, in a robust and efficient manner, the foreseen optimisation problem of inverse identification, selecting for instance among mathematical programming methods, evolutive methods or artificial intelligence methods.
  • Validation and accuracy checks, developed to test and confirm the effectiveness of the specific devised approach, either on pseudo–experimental (necessary validation condition) or real experimental measurement data.
The current state of the art, in the context of aforementioned Inverse Analysis approaches, presents several contributions, particularly within Industrial Engineering applications, e.g., for material characterisation and diagnosis of metallic structural components [9,10,11,12,13], for mechanical characterisation of advanced materials [14,15], and for biomechanical identification [16]. With shared methodologies, in recent years, a growing interest has been exerted for Inverse Analysis also in Civil Engineering context, as, e.g., in material characterisation of concrete structures [17,18], in bridge and infrastructure analysis [19,20,21], and in structural identification [22,23,24].
Such a renewed research branch displays significant advantages, by the adoption of the Inverse Analysis methodology, in experimental or operational state measurements of the structure, toward the estimation of modal properties of a structure, specifically by Operational Modal Analysis, as proposed, e.g., in [25,26,27,28,29,30,31]. Pursuing the goals of this research branch, the present paper sets an Inverse Analysis problem based on modal properties, first on a simple archetypal structure and, then, on a specific case study, namely a historical reinforced concrete arched bridge, that is Brivio bridge (1917) [32], located in Northern Italy. The bridge, given its still crucial infrastructural role and historical value, has been subjected, in recent years, to monitoring experimental campaigns and to subsequent response signal processing (see, e.g., [33,34,35,36]) and structural modelling and identification (see, e.g., [37,38]), as also enquired in the present contribution and in companion work [39].
Within the subject of Inverse Analysis relying on dynamic measurements, the present investigation aims at defining and developing a robust parameter identification procedure, supported by a proper selection of the sought model parameters, the measurement data and the discrepancy function formulation. The main goals of the contribution shall point out to a general guideline procedure, numerically applied on an archetypal structure, to be further investigated on the specific real case study of Brivio bridge, for structural validation, particularly toward understanding the current structural behaviour, and reassuring the associated model calibration/updating, in view of diagnosis and Structural Health Monitoring (SHM) goals.
The article is organised in two main sections, as follows. Section 2 sets the Inverse Analysis problem on a characteristic structural example, analysing the most effective selection of input parameters, measured data and discrepancy function. In subsequent Section 3, account taken of the previously discussed methodological results, an optimised structural modelling and consistent Inverse Analysis approach is investigated with reference to the specific case study of Brivio bridge, toward SHM aims. Furthermore, Section 4 collects closing global observations, highlighting the central role of Inverse Analysis as a reliable general methodology for model calibration and structural assessment, then proposing possible future developments in the context of dynamic modal measurements and processing.

2. Parameter Identification Relying on Dynamic Measurements: Problem Setup

According to the implementation stages of an Inverse Analysis problem described in the Introduction, in the current section, the problem setup is first devised and investigated with reference to an archetypal structure, namely a pinned-pinned beam, relying on dynamic modal pseudo–experimental measurements. Advantageously exploiting the basic structural configuration, the reference pseudo–experimental solution and the identification analyses are developed by standard methods of Structural Dynamics, both for uniform beams [40,41,42] and stepped beams [42,43,44], i.e., with varying material, or geometrical, parameters along the beam axis.
The selection of the discrepancy function, ω ( θ ) , as the objective function measuring the discrepancy between the description of the numerical model and the real object, to be minimised in order to estimate the sought parameters ( θ ) of the model, is operated in accordance with previous choice [37], also adopted in companion paper [39]. Consistently, the dynamic modal properties of the structure are considered as mode shapes u ( θ ) i and mode frequencies f ( θ ) i , while the model parameters are selected, for diverse structural elements, as material Young’s moduli and/or densities ( θ = E 1 , ⋯ , E N ; ρ 1 , ⋯ , ρ N ). Consequently, the discrepancy function may be written, in vectorial form, by the following equation:
ω ( θ ) = ∑ i = 1 n u ( θ ) n u m i − u e x p i 2 1 / 2 ∥ u e x p ∥ + ∑ i = 1 n f ( θ ) n u m i − f e x p i 2 1 / 2 ∥ f e x p ∥
where experimental quantities may equivalently be substituted by pseudo–experimental counterparts.
The investigation of the objective function and Inverse Analysis problem on the archetypal structure is developed either in a two–dimensional parameter space (i.e. uniform beam, parameters θ = E , ρ ) and in a four–dimensional parameter space (i.e. stepped beam, parameters θ = E 1 , E 2 , ρ 1 , ρ 2 ), leading to the following observations.
  • The adoption of modal properties, as a unique source of measurement data, intrinsically brings in a “non–well posedness” condition, in terms of multiple “realisations”, in terms of ratios between stiffness and mass properties of a structural system, namely leading to the identification of the correlated parameters, as also shown by the “valley” of minima in the discrepancy function plot for a two–dimensional parameter space (see Figure 1).
  • Uniqueness of the optimisation problem may be found, in a two–dimensional parameter space, fixing either one of the two constitutive parameters or their ratio. Therefore, in a practical application case study, additional evaluations or measurements shall be required, to possibly estimate specific mechanical parameters at the local scale (e.g., by material testing) or from global scale measurements devised by experimentally controlled static or dynamic testing of the structure.
  • The enlargement of the parameter space size further exhibits a correlation between parameters, namely a possible balancing effects or multiple mathematically equivalent “realisations”. Such an observation is graphically depicted in Figure 2, where three–dimensional cross sections of the discrepancy function, analysed in a four–dimensional parameter space, reveal possible “valleys” of minima, also in terms of ratios between stiffness or mass density parameters (Figure 2a and Figure 2b, respectively).
  • Therefore, a robust Inverse Analysis procedure shall require complemented measurement data, suitable to assess the behaviour of diverse structural components and capable to estimate, possibly in a sequential procedure, both stiffness and mass density properties, for instance also considering experimental static or dynamic loading tests on the structure.

3. Optimised Structural Modelling on the Case Study of a Historical Concrete Bridge

After the prodromal investigation of the Inverse Analysis problem on a simplified archetypal structure, as briefly delineated in Section 2, one aim of the present work is to extend the validity of the methodology toward real application case studies. Therefore, in the current section a specific case study is considered, namely a historical reinforced concrete three–span arched road bridge, namely Brivio bridge (1917) [32]. Such an infrastructure, completed around the end of World War I, still holds nowadays an important role and historical value, while also keeping its key traffic infrastructural functionality, in connecting the provinces of Lecco (Brivio territory) and Bergamo (Cisano Bergamasco territory), in the Lombardia region, Northern Italy, over the Adda river.
The following brief description of Brivio bridge structure (Figure 3 and Figure 4) is here intended for a proper understanding of relevant numerical modelling, sensitivity analysis and Inverse Analysis stages. Detailed information may be found in references [32,33,34,35,37] and in companion paper [39].
The reinforced concrete road bridge consists of three arched spans, coupled to twin parabolic arches and with tied hanging underneath straight deck. The structure shows full symmetry, with respect to its mid–longitudinal plane, with the following characteristic lengths: average height of the deck above water level equal to 8 m; central span length equal to 44 m; lateral spans pairing to 43.4 m; total length of 130.8 m. Lateral spans (“Span 1” toward Brivio, “Span 3” toward Cisano Bergamasco) are connected to the river banks, while the central one (“Span 2”) is supported by two pillars within the river bed, with pier foundation system set on reinforced concrete piles. The twin parabolic arches of the bridge are designed on a geometry with a 42.80 m span and a 8.00 m rise, being the whole profile symmetric with respect to the vertical axis at half span. The upper central part of each arch is connected to the respective corresponding one by eight transverse beams, while the bridge deck is linked to the arches, at each side, at each span, through a system of sixteen reinforced concrete hangers. The road deck, 9.2 m wide, provided with two roadway lanes and two cantilever sidewalks, is built by two main longitudinal girders, joined by secondary beam elements and transverse grid beam connections, and completed by a reinforced concrete slab at the deck level.
In order to analyse, for sensitivity and Inverse Analysis, the bridge structure, a linear elastic FEM model of Brivio bridge (single span, referring to Span 1, see Figure 5, originally developed in [37]) is employed, within the software environments of Abaqus finite element code and Python and Matlab self–implemented routines.
The model is developed as a three–dimensional frame structure built by beam finite elements, practically composed as an assembly of five principal structural components: deck, main longitudinal deck girders, arches, hangers and upper transverse beams. Consistently, a constitutive material is associated to each structural type, with regard to Young’s moduli and mass densities, as reported in Table 1 and also highlighted in Figure 5. The geometrical characteristics of the FEM model are adopted as in [37] and companion paper [39]. The global computational size and cost of the FEM model is kept rather limited, in view of repetitive runs in Inverse Analysis optimisation loops, summing up to 380 beam elements and 1680 degrees of freedom (254 beam elements for the deck grid, 70 beam elements for the arches, 24 beam elements for the upper beams, deck–hanger and hanger–arch joints modelled by rigid links, added non–structural mass components). The boundary conditions are realised by a simply supported deck configuration, with combined elastic supports (linear spring elements), implemented by two z–axis rotational springs, at both extremities, and two translational springs (at x–axis, horizontal, and y–axis, vertical, respectively set at the second edge (reference coordinate system: x for the longitudinal axis, y for the vertical axis and z for the transverse horizontal axis of the bridge, as also depicted in Figure 5).
To the aim of properties identification, the sought parameters and search domain are selected, according to previous work in [37], as in Table 1, while measured quantities are considered relying on dynamic modal measurements (also consistently with aforementioned discrepancy function, Equation 1), namely investigating structural vibration modes and natural frequencies.
With reference to the base FEM model, in Figure 6, it is possible to observe the first sixteen structural vibration modes of Brivio bridge, clearly involving the whole set of structural components, particularly at deck and arch levels. Such an observation highlights the quest of complete measurements, for several modes, considering both deck beams and arches, in order to fully characterise the current structural behaviour of the bridge and to reliably estimate the associated material parameters. For each vibration mode, the relevant natural frequency, evaluated at the reference parameter values, is reported in Table 2, second column.
Further analyses, developed on the numerical model of Brivio bridge, allow for first additional guidelining observations, as in the following.
  • Among the selected modelling parameters, for material and boundary condition standpoints, with reference to the selected measurements and discrepancy function, a major role is assumed by nine mechanical constitutive parameters, namely Young’s moduli ( E 1 , ⋯ , E 5 ) and mass densities ( ρ 1 , ⋯ , ρ 4 ) of the structural components, as pointed out by previous sensitivity analyses in [37].
  • Global property measurement, such as for natural frequency, may suffer reduced sensitivity effects, causing significant difficulties in specific parameter identification. This particular condition can be observed from the numerical results in Table 2, third and fourth columns, where the global frequency variation is computed for a 30% range variation on parabolic arches elastic modulus ( E 3 ) and mass density ( ρ 3 ), with variation gain on the results approximately reduced by one order of magnitude.
  • According to the previous point, in order to ensure a robust and reliable parameter identification procedure, specific requirements are expected in the measuring stages, namely significantly reducing noise effects and providing complete structural observations, possibly complemented by local detailing measurements and estimations.
  • As a complementary global source of measurement information, vibration modes can carry similar observations, as the above–mentioned for natural frequencies, both on sensitivity effects and complete measurement requirements. As an example, the results reported in Figure 7 graphically represent the numerical results for the second vibration mode of the bridge at the base configuration and for a 30% range variation of various specific parameters, without, however, structurally meaningful mode shape variations.
  • The effect of boundary conditions on the mode shapes and natural frequencies appears to be less sensitive with respect to material parameters of bridge structural components (see, also, sensitivity analysis in [37]). However, the influence of mechanical parameters of elastic boundary conditions can rule a contribution approximately of one order of magnitude lower, though not negligible on a global scale structural behaviour (see, for an example, Table 2, fifth column). Therefore, particular attention is required in setting numerical model definition also regarding the boundary conditions, in order to produce a reliable numerical instrument, avoiding biased parameter fitting, in Inverse Analysis methodology for structural assessment and diagnosis.

4. Conclusions

In the present paper, an Inverse Analysis methodology for structural parameter identification, relying on dynamic modal measurements, is investigated. The problem has been tackled, by analytical and numerical tools, first on a simplified archetypal structure, for problem setup and understanding, then on a specific application case study, regarding a reinforced concrete historical road arched bridge, Brivio bridge (1917). The global aim of such a research work is the definition of a robust, efficient and reliable methodology, supported by Inverse Analysis approaches, toward parameter identification, structural assessment and diagnosis in Structural Health Monitoring contexts, possibly in automatised operational conditions, for Civil Engineering structures and infrastructures.
In particular, the analysis of an archetypal simplified structure has highlighted the intrinsic “non–well posedness” condition, in terms of multiple “realisations”, of the identification problem relying only on dynamic modal measurements, with respect to the estimation of both stiffness and mass density properties. The correlation effect between sought parameters, therefore the non–uniqueness of the solution, has been observed also in a larger size parameter space, highlighting ratio compensation effects among stiffness values and mass density values of diverse structural parts/components.
Such conditions would consistently require, in order to develop a robust and reliable identification methodology, two specific interventions at experimental design: the introduction of local measurements on material properties, as additional source of information within the discrepancy function; the adoption of a specifically conceived experimental structural testing, either in static or dynamic configurations, under controlled loading conditions, suitable for direct or stepwise identification of structural properties and assessment of current structural behaviour.
The investigation conducted on an archetypal simplified structure has then been extended to the real case study of Brivio bridge (1917), with the adoption of a numerical FEM model, as more case–oriented specifically considered in companion paper [39]. The consideration of dynamic modal measurements, namely vibration structural modes and natural frequencies, further than the features observed on the archetypal structure, has highlighted the reducing sensitivity of global measurements at increasing model complexity and parameter space size. Moreover, the effect of the boundary conditions has presented a strict requirement in the level of refinement and accuracy for the numerical model of the structure, in a high–fidelity detailing, in order to avoid biased parameter fitting, toward, instead, reliable estimation of parameters characteristic of the complete current behaviour of the structure under investigation.
Consistently, in view of a thorough and reliable application of such an Inverse Analysis methodology to a practical case study (i.e. with further investigation on Brivio bridge or to other similar structures), several hints may be proposed as guidelines: the adoption of high precision and reduced noise experimental measurements; the introduction of complete measurements, suitable to observe the full structural behaviour, in particular for non–principal structural elements (e.g. arches, secondary beams and hangers); the definition of an optimised and detailed numerical model, also with respect to the number of selected sought parameters; the enrichment of the identification procedure by introduction of local material testing and/or global measurements under experimentally load controlled conditions, in a static or, preferably, dynamic regime.
The proposed methodology, results and observation of the present paper gather a first insight on the structural identification problem relying on dynamic modal measurements, both from a conceptual point of view and for a preliminary application standpoint on Brivio bridge, specific subject of investigation in companion paper [39]. In future developments, the highlighted hints may lead to subsequent researches, particularly focussing on the “well–posedness” conditions of the Inverse Analysis problem, on the optimisation of the modelling stages, and on the development of a thorough and reliable methodology for parameter estimation within the current context of Structural Dynamics for infrastructures. Such a perspective may, therefore, aim at defining a guideline approach, particularly suitable for identification and prognosis stages in an innovative Structural Health Monitoring framework, supported by algorithmic tools of Inverse Analysis.

Acknowledgments

The financial support by “Fondi di Ricerca d’Ateneo ex 60%”, “STaRs – Azione 2 Visiting e Fellow” and “PRIN Life–long optimized structural assessment and proactive maintenance with pervasive sensing techniques” at the University of Bergamo is gratefully acknowledged.

References

  1. A. Tarantola, Inverse Problem Theory. Siam, 2005. [CrossRef]
  2. R.C. Aster, B. Bochers, C.H. Thurber, Parameter Estimation and Inverse Analysis. Elsevier, 2013.
  3. H.D. Bui, Inverse Problems in the Mechanics of Materials: An Introduction. CRC Press, 1994.
  4. Z. Mróz, G.E. Stavroulakis eds., Parameter Identification of Materials and Structures. Springer, 2005.
  5. V. Buljak, Inverse Analysis with Model Reduction. Springer, 2012. [CrossRef]
  6. T. Garbowski, Stochastic model reduction applied to inverse analysis. J.P.M. de Almeida, P. Díez, C. Tiago, N. Parés eds. VI International Conference on Adaptive Modeling and Simulation (ADMOS 2013), Lisbon, Portugal, June 3-5, 2013.
  7. V. Buljak, G. Cocchetti, A. Cornaggia, T. Garbowski, G. Maier, G. Novati, Materials Mechanical Characterizations and Structural Diagnoses by Inverse Analyses. G.Z. Voyiadjis ed. Handbook of Damage Mechanics, Springer, 619–642, 2015.
  8. M. Kleiber, H. Antúnez, T.D. Hien, P. Kowalczyk, Parameter Sensitivity in Nonlinear Mechanics. Wiley, 1997.
  9. M. Bocciarelli, V. Buljak, C.K.S. Moy, S.P. Ringer, G. Ranzi, An inverse analysis approach based on a POD direct model for the mechanical characterization of metallic materials. Computational Materials Science, 95, 302–308, 2014. [CrossRef]
  10. F. Arizzi, E. Rizzi, Elastoplastic parameter identification by simulation of static and dynamic indentation tests. Modelling and Simulation in Materials Science and Engineering, 22, 035017, 2014. [CrossRef]
  11. V. Buljak, G. Cocchetti, A. Cornaggia, G. Maier, Assessment of residual stresses and mechanical characterization of materials by “hole drilling” and indentation tests combined and by inverse analysis. Mechanics Research Communications, 68, 18–24, 2015. [CrossRef]
  12. V. Buljak, G. Cocchetti, A. Cornaggia, G. Maier, Estimation of residual stresses by inverse analysis based on experimental data from sample removal for “small punch” tests. Engineering Structures, 136, 77–86, 2017. [CrossRef]
  13. V. Buljak, G. Cocchetti, A. Cornaggia, G. Maier, Parameter identification in elastoplastic material models by Small Punch Tests and inverse analysis with model reduction. Meccanica, 53, 3815–3829, 2018. [CrossRef]
  14. G. Cocchetti, M.R. Mahini, G. Maier, Mechanical characterization of foils with compression in their planes. Mechanics of Advanced Materials and Structures, 21, 853–870, 2014. [CrossRef]
  15. V. Buljak, S. Bavier–Romero, A. Kallel, Calibration of Drucker–Prager cap constitutive model for ceramic powder compaction through inverse analysis. Materials, 14, 4044, 2021.
  16. K. Zaborowicz, T. Garbowski, B. Biedziak, M. Zaborowicz, Robust estimation of the chronological age of children and adolescents using tooth geometry indicators and POD–GP. International Journal of Environmental Research and Public Health, 19, 2952, 2022. [CrossRef]
  17. T. Garbowski, G. Maier, G. Novati, Diagnosis of concrete dams by flat–jack tests and inverse analyses based on proper orthogonal decomposition. Journal of Mechanics of Materials and Structures, 6, 181–202, 2011. [CrossRef]
  18. T. Gajewski, T. Garbowski, Calibration of concrete parameters based on digital image correlation and inverse analysis. Archives of Civil and Mechanical Engineering, 14, 170–180, 2014. [CrossRef]
  19. D. Ribeiro, R. Calçada, R. Delgado, M. Brehm, V. Zabel, Finite element model updating of a bowstring–arch railway bridge based on experimental modal parameters. Engineering Structures, 40, 413–435, 2012. [CrossRef]
  20. C. Bendon, M. Dilena, A. Morassi, Ambient vibration testing and structural identification of a cable–stayed bridge. Meccanica, 51, 2777–2796, 2016.
  21. T. Garbowski, A. Pożarycki, Multi–level backcalculation algorithm for robust determination of pavement layers parameters. Inverse Problems in Science and Engineering, 25, 674–693, 2017. [CrossRef]
  22. B. Miller, Application of neural networks for structure updating. Computer Assisted Mechanics and Engineering Sciences, 18, 191–203, 2011.
  23. F. Shabbir, P. Omenzetter, Model updating using genetic algorithms with sequential technique. Engineering Structures, 120, 166–182, 2016. [CrossRef]
  24. M. Crognale, V. Gattulli, A. Paolone, F. Potenza, A damage identification procedure for steel truss. A. Carcaterra, A. Paolone, G. Graziani eds. Proceedings of XXIV AIMETA Conference 2019 (AIMETA 2019), Roma, Italy, September 15-19, 2020.
  25. J.E. Mottershead, M.I. Friswell, Model updating in structural dynamics: A survey. Journal of Sound and Vibration, 167, 347–375, 1993. [CrossRef]
  26. E. Reynders, System identification methods for (Operational) Modal Analysis: Review and comparison. Archives of Computational Methods in Engineering, 19, 51–124, 2012. [CrossRef]
  27. C. Rainieri, G. Fabbrocino, Operational Modal Analysis of Civil Engineering Structures. Springer, 2014.
  28. F. Pioldi, R. Ferrari, E. Rizzi, Output–only modal dynamic identification of frames by a refined FDD algorithm at seismic input and high damping. Mechanical Systems and Signal Processing, 68–69, 265–291, 2016. [CrossRef]
  29. F. Pioldi, R. Ferrari, E. Rizzi, Earthquake structural modal estimates of multi–storey frames by a refined Frequency Domain Decomposition algorithm. JVC/Journal of Vibration and Control, 23, 2037–2063, 2017. [CrossRef]
  30. F. Pioldi, R. Ferrari, E. Rizzi, Seismic FDD modal identification and monitoring of building properties from real strong–motion structural response signals. Structural Control and Health Monitoring, 24, e1982, 2017. [CrossRef]
  31. R. Cardoso, A. Cury, F. Barbosa, A robust methodology for modal parameters estimation applied to SHM. Mechanical Systems and Signal Processing, 95, 24–41, 2017. [CrossRef]
  32. L. Santarella, E. Miozzi, Ponti Italiani in Cemento Armato (in Italian). Hoepli, 1948.
  33. R. Ferrari, D. Froio, E. Chatzi, C. Gentile, F. Pioldi, E. Rizzi, Experimental and numerical investigations for the structural characterization of a historic RC arch bridge. M. Papadrakakis, V. Papadopoulos, V. Plevris eds. 5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Greece, May 25-27, 2015. [CrossRef]
  34. R. Ferrari, F. Pioldi, E. Rizzi, C. Gentile, E. Chatzi, R. Klis, E. Serantoni, A. Wieser, Heterogeneous sensor fusion for reducing uncertainty in structural health monitoring. M. Papadrakakis, V. Papadopoulos, G. Stefanou eds. 1st ECCOMAS Thematic Conference on Uncertainty Quantification in Computational Sciences and Engineering (UNCECOMP 2015), Crete Island, Greece, May 25-27, 2015.
  35. R. Ferrari, F. Pioldi, E. Rizzi, C. Gentile, E. Chatzi, E. Serantoni, A. Wieser, Fusion of wireless and non-contact technologies for the dynamic testing of a historic RC bridge. Measurement Science and Technology, 27, 124014, 2016. [CrossRef]
  36. A. Cornaggia, R. Ferrari, M. Zola, E. Rizzi, C. Gentile, Signal processing methodology of response data from a historical arch bridge toward reliable modal identification. Infrastructures, 7, 74, 2022. [CrossRef]
  37. R. Ferrari, D. Froio, E. Rizzi, C. Gentile, E. Chatzi, Model updating of a historic concrete bridge by sensitivity and global optimization–based Latin hypercube sampling. Engineering Structures, 1, 139–160, 2019. [CrossRef]
  38. G. Zonno, C. Gentile, Assessment of similar reinforced concrete arch bridges by Operational Modal Analysis and model updating. Lecture Notes in Civil Engineering, 156, 853–868, 2021. [CrossRef]
  39. T. Garbowski, G. Cocchetti, A. Cornaggia, R. Ferrari, E. Rizzi, Inverse analysis investigation by Gaussian Processes optimisation of a historical concrete bridge relying on dynamic modal measurements. M. Papadrakakis, M. Fragiadakis eds. 9th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2023), Athens, Greece, June 12-14, 2023.
  40. R.W. Clough, J. Penzien, Dynamics of Structures. Computer & Structures, Inc., 1995.
  41. A.K. Chopra, Dynamics of Structures. Prentice Hall, 2012.
  42. C.Y. Wang, C.M. Wang, Structural vibration. CRC Press, 2014.
  43. N.J. Taleb, E.W. Suppiger, Vibration of stepped beams. Journal of the Aerospace Sciences, 28, 295–298, 1961.
  44. S.K. Jang, C.W. Bert, Free vibration of stepped beams: exact and numerical solutions. Journal of Sound and Vibration, 130, 342–346, 1989. [CrossRef]
Preprints 79505 g001
Figure 1. Normalised plot of the objective function, for the archetypal structure, in a 2D parameter space.
Figure 1. Normalised plot of the objective function, for the archetypal structure, in a 2D parameter space.
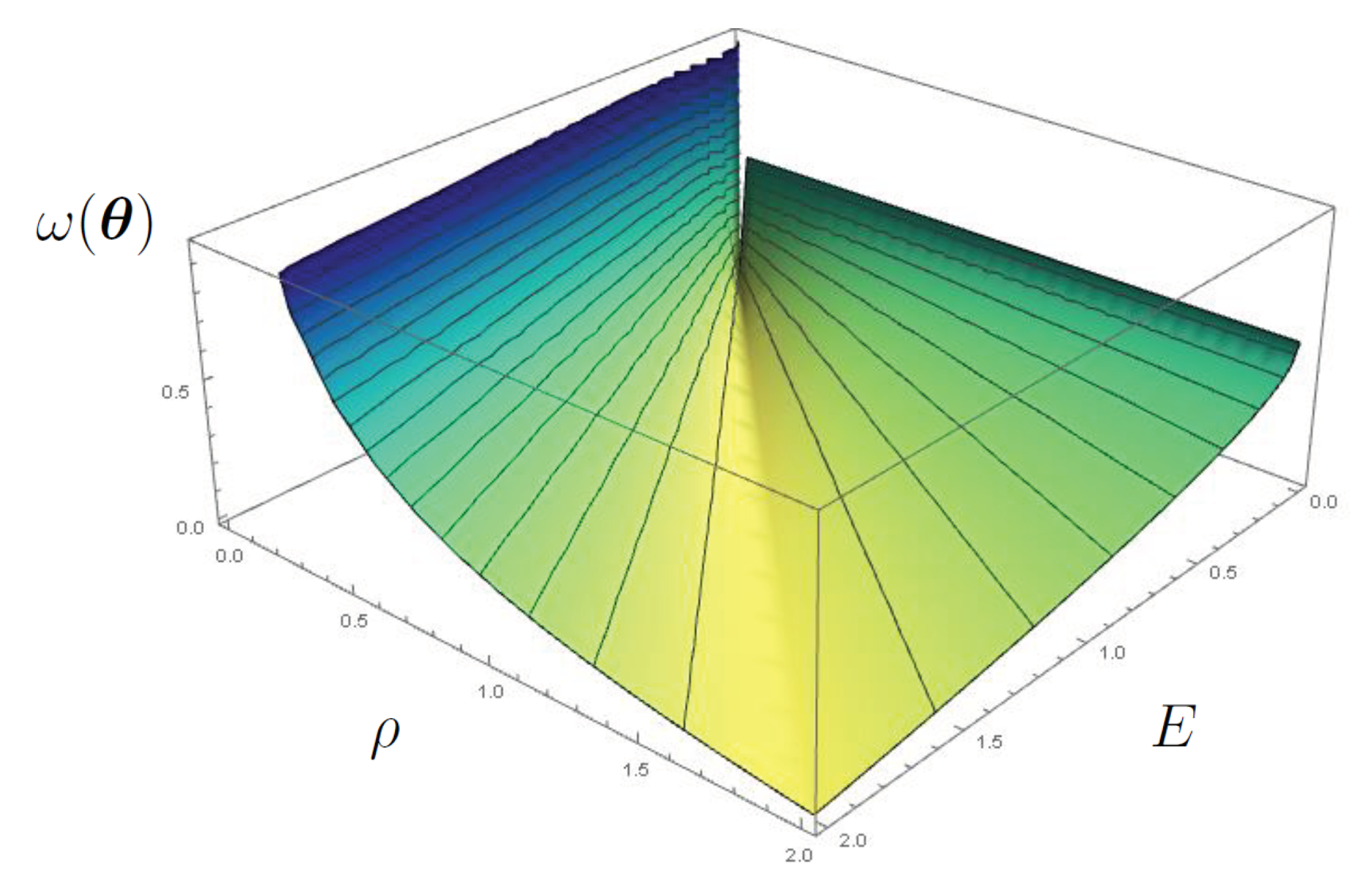
Preprints 79505 g001
Preprints 79505 g002
Figure 2. Three–dimensional cross sections of the objective function, for the archetypal structure, in a 4D parameter space.
Figure 2. Three–dimensional cross sections of the objective function, for the archetypal structure, in a 4D parameter space.
Preprints 79505 g002
Preprints 79505 g003
Figure 3. Brivio bridge (1917): (a) downstream view of the road three–span arched bridge crossing the Adda river; Brivio (Lecco) right bank (left), Cisano Bergamasco (Bergamo) left bank (right); (b) zoomed upstream view of Span 1 (toward Brivio). Pictures taken by author E.R. on 7 July and 9 May 2022, respectively.
Figure 3. Brivio bridge (1917): (a) downstream view of the road three–span arched bridge crossing the Adda river; Brivio (Lecco) right bank (left), Cisano Bergamasco (Bergamo) left bank (right); (b) zoomed upstream view of Span 1 (toward Brivio). Pictures taken by author E.R. on 7 July and 9 May 2022, respectively.
Preprints 79505 g003
Preprints 79505 g004
Figure 4. Brivio bridge (1917): schematic representations of downstream front and bottom section–top views.
Figure 4. Brivio bridge (1917): schematic representations of downstream front and bottom section–top views.
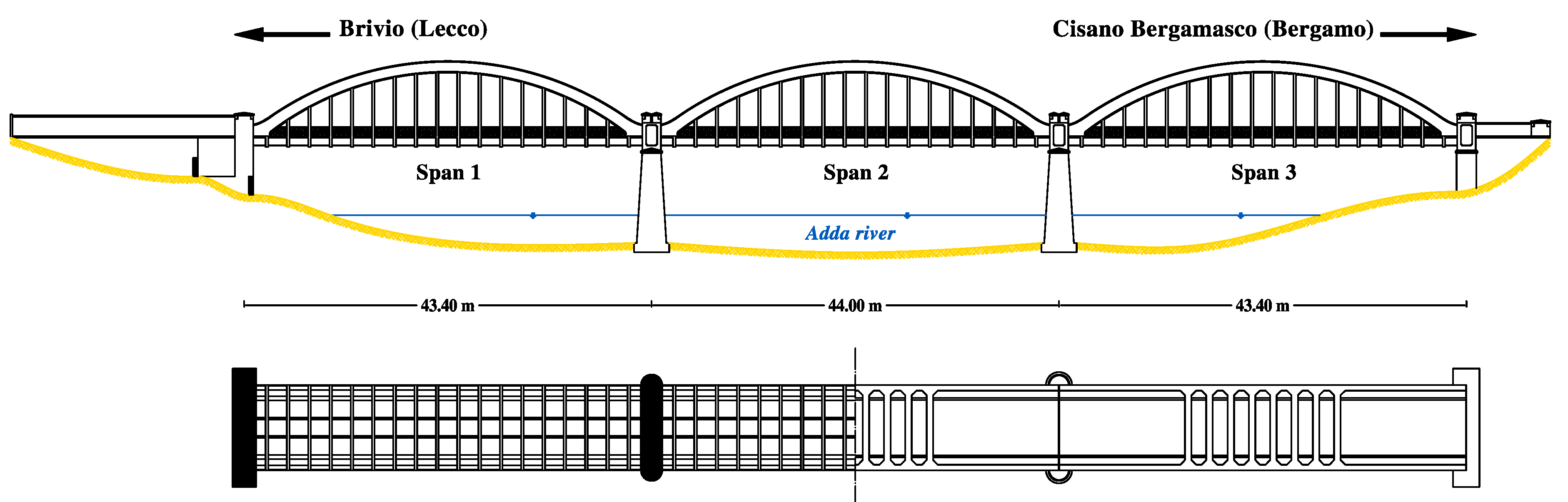
Preprints 79505 g004
Preprints 79505 g005
Figure 5. FEM model of Brivio bridge (single span); diverse elements of the structure for sought material parameters identified by colours, boundary conditions by symbols.
Figure 5. FEM model of Brivio bridge (single span); diverse elements of the structure for sought material parameters identified by colours, boundary conditions by symbols.
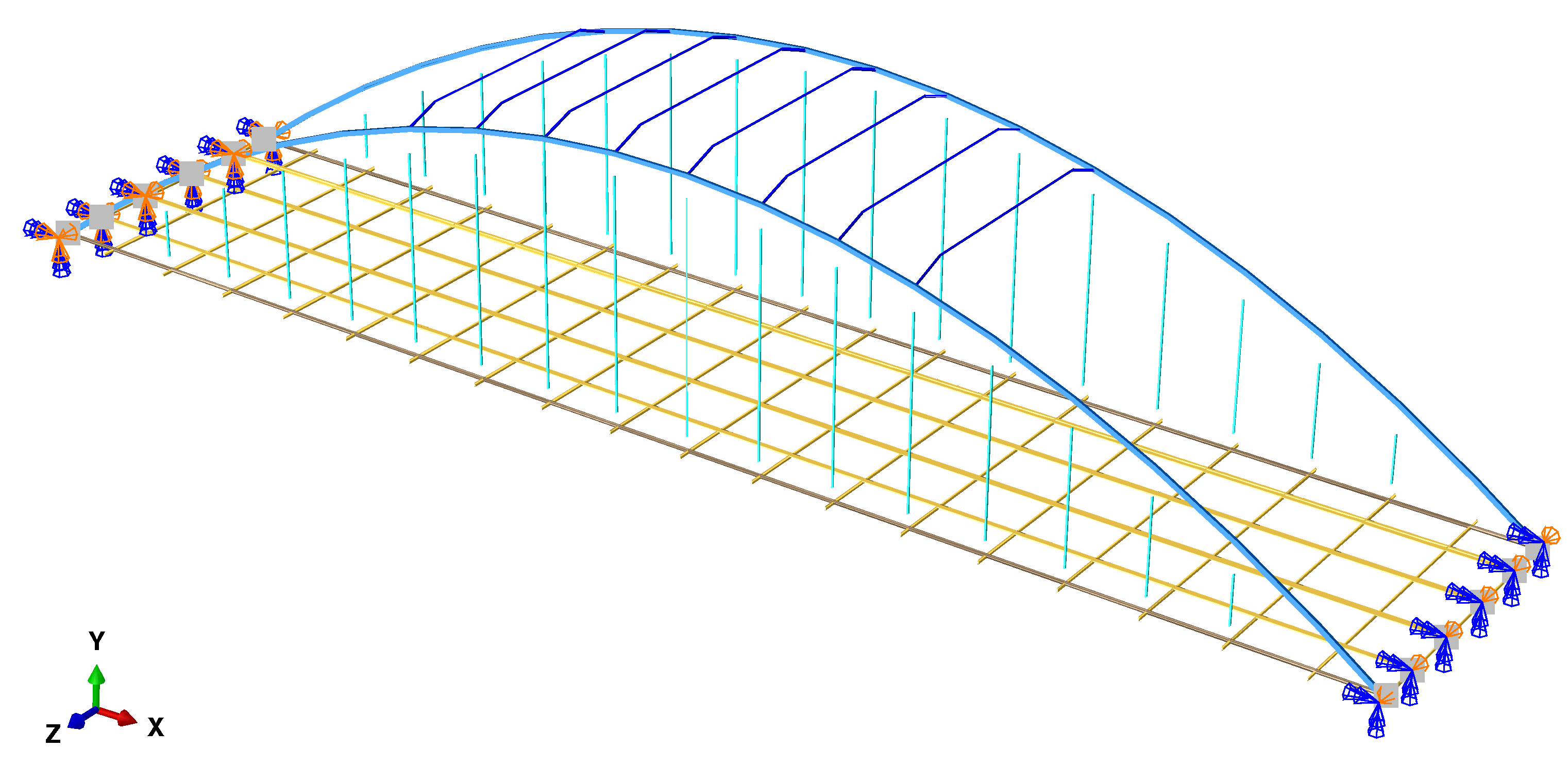
Preprints 79505 g005
Preprints 79505 g006
Figure 6. First sixteen vibration modes of the FEM base model (parameters set at reference value) of the bridge.
Figure 6. First sixteen vibration modes of the FEM base model (parameters set at reference value) of the bridge.
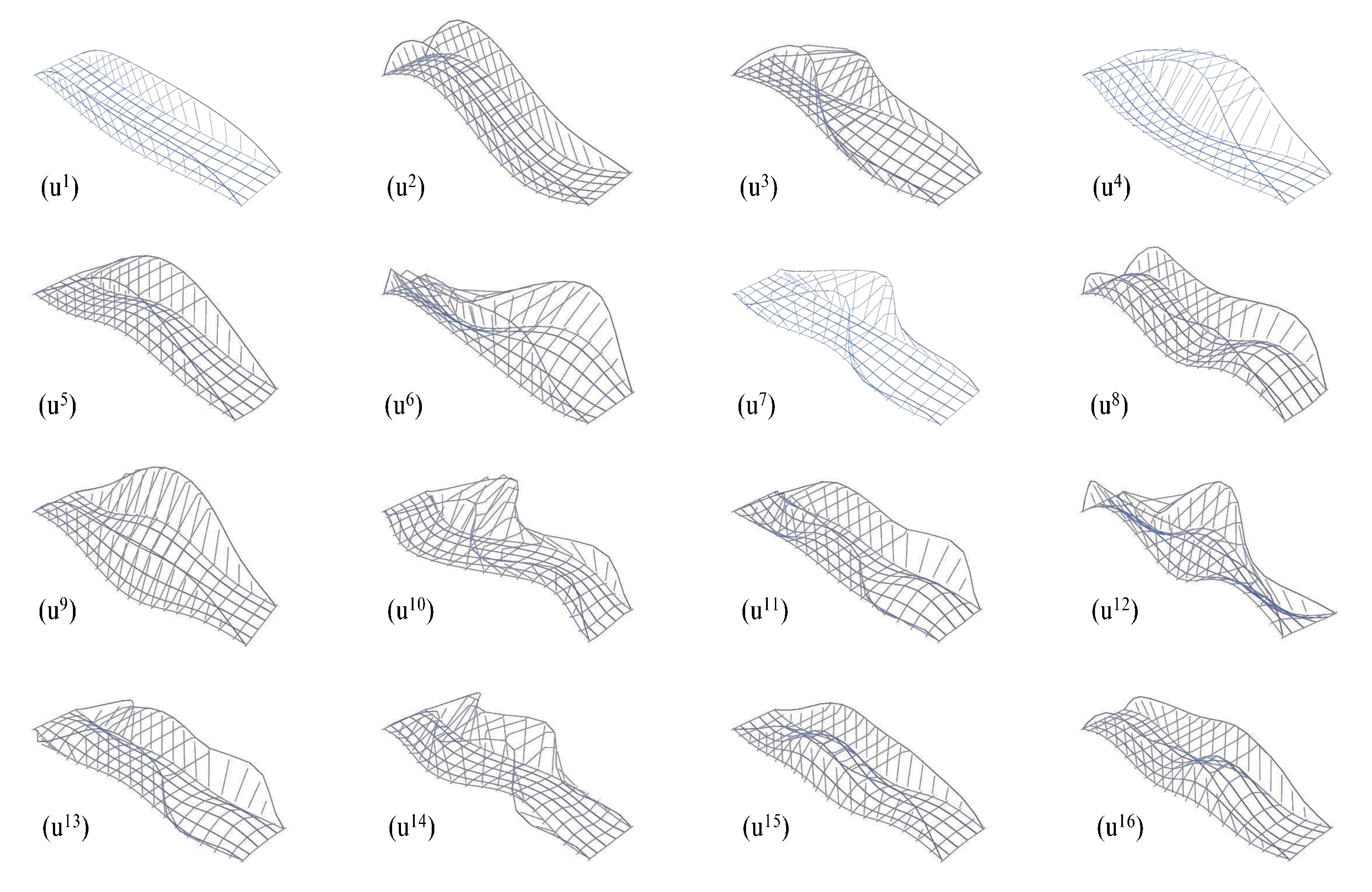
Preprints 79505 g006
Preprints 79505 g007
Figure 7. Second vibration mode of the FEM model of the bridge, with parameters set at reference values and with possible variations.
Figure 7. Second vibration mode of the FEM model of the bridge, with parameters set at reference values and with possible variations.
Preprints 79505 g007
Table 1. Material input parameters and search domain for the sensitivity analysis and Inverse Analysis problem, based on the FEM model, after [37].
Table 1. Material input parameters and search domain for the sensitivity analysis and Inverse Analysis problem, based on the FEM model, after [37].
Parameter Lower Upper Reference
bound bound value
Deck elastic modulus, E 1 [GPa] 24.4 45.4 34.9
Main longitudinal girders elastic modulus, E 2 [GPa] 24.4 45.4 34.9
Parabolic arches elastic modulus, E 3 [GPa] 25.0 46.4 35.7
Hangers elastic modulus, E 4 [GPa] 25.0 46.4 35.7
Upper transverse beams elastic modulus, E 5 [GPa] 25.0 46.4 35.7
Deck mass density, ρ 1 [kg/m3] 1710 3170 2440
Main longitudinal girders mass density, ρ 2 [kg/m3] 1710 3170 2440
Parabolic arches mass density, ρ 3 [kg/m3] 1710 3170 2440
Hangers mass density, ρ 4 [kg/m3] 1710 3170 2440
Upper transverse beams mass density, ρ 5 [kg/m3] 1710 3170 2440
I–support translational (x–axis) spring stiffness, k 1 [kN/m] 10−7 10−3 10−5
I–support translational (y–axis) spring stiffness, k 2 [kN/m] 108 1012 1010
I–support rotational spring stiffness, k 3 [kNm] 10−7 10−3 10−5
II–support rotational spring stiffness, k 4 [kNm] 10−7 10−3 10−5
Table 2. First sixteen natural frequencies of the FEM base model (parameters set at reference values) of the bridge, and percentage variations for possible parameter variations.
Table 2. First sixteen natural frequencies of the FEM base model (parameters set at reference values) of the bridge, and percentage variations for possible parameter variations.
Frequency [Hz] Reference parameter values E 3 +30% ρ 3 +30% k 2 +30%
f 1 2.5312 +1.28% −4.22% +0.07%
f 2 3.7908 +3.53% −2.91% +0.01%
f 3 3.9781 +4.41% −5.30% +0.06%
f 4 5.4889 +1.52% −1.42% +0.08%
f 5 5.8677 +3.72% −1.77% +0.30%
f 6 6.4903 +1.63% −4.26% +0.00%
f 7 7.7809 +4.66% −6.00% +0.18%
f 8 7.8392 +4.08% −2.36% +0.15%
f 9 8.8131 +2.41% −2.80% +0.16%
f 10 10.311 +1.84% −5.40% +0.01%
f 11 10.325 +4.03% −2.99% +0.10%
f 12 10.672 +3.73% −4.45% +0.28%
f 13 10.888 +4.45% −5.72% +0.23%
f 14 12.139 +1.38% −4.10% +0.06%
f 15 12.160 +4.05% −1.55% +0.01%
f 16 12.490 +2.43% −1.46% +0.09%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated