Submitted:
16 July 2023
Posted:
18 July 2023
You are already at the latest version
Abstract
Keywords:
Introduction
Method and Materials
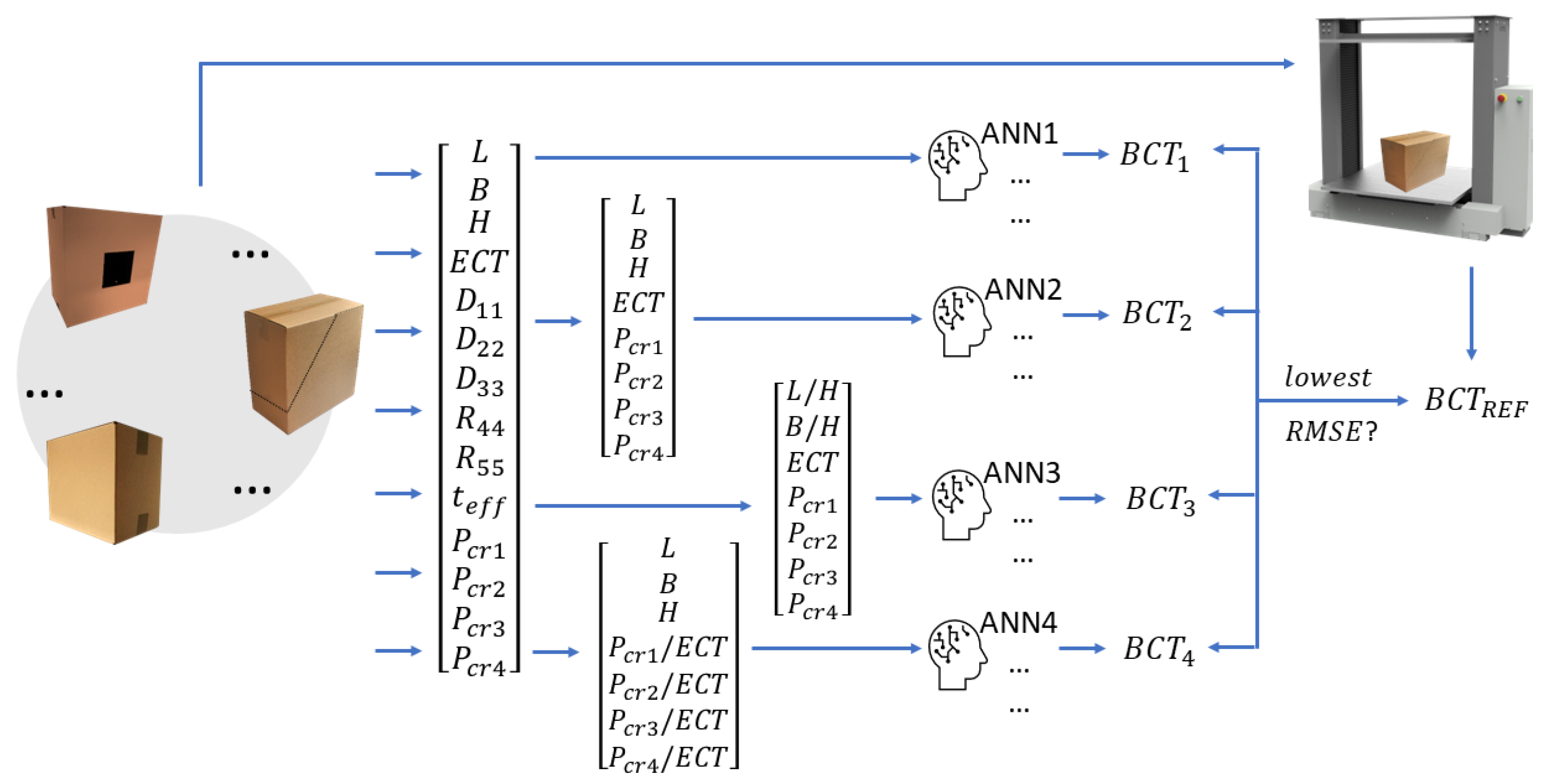
Framework of the study
Data collected for use in an artificial neural networks
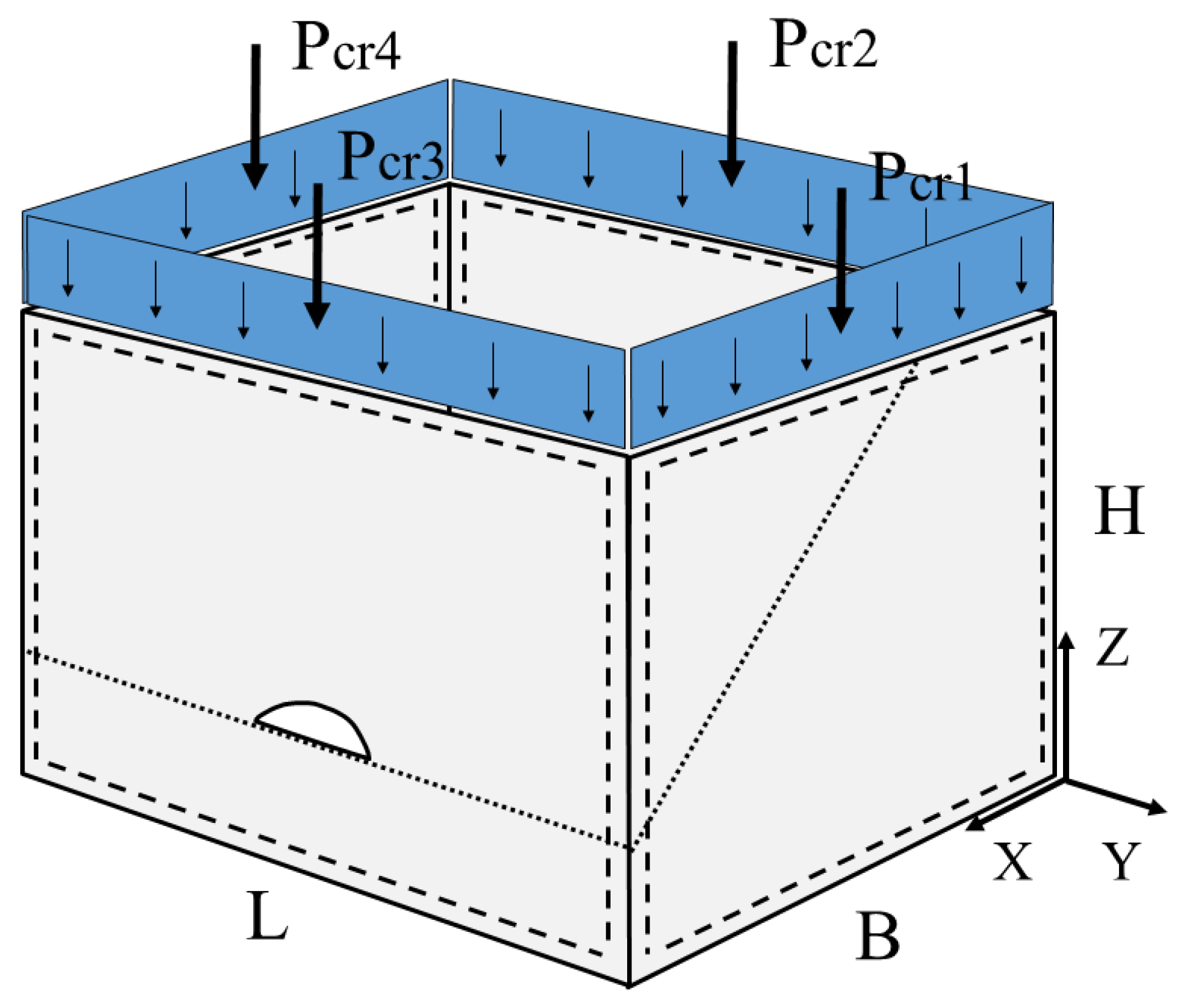
- box dimensions (from to ): width, , length, , and height,
- specification of the box geometry, i.e., character of the flaps (no flaps, traditional flaps or offset flaps), presence and geometry of holes, and presence and technical details of perforations (type of cutting knife, etc.)
- effective material properties of the corrugated cardboard expressed as laminate composite constants, i.e., – bending stiffness in the machine direction, – bending stiffness in the cross-machine direction, – twisting bending stiffness, and – transverse shear stiffnesses in horizontal and vertical directions, respectively (in regard to box orientation)
- index and effective thickness of the cardboard as the laminate composite,
- critical forces of all four side walls loaded vertically in their plane,
Assessment of the load capacity of the packaging
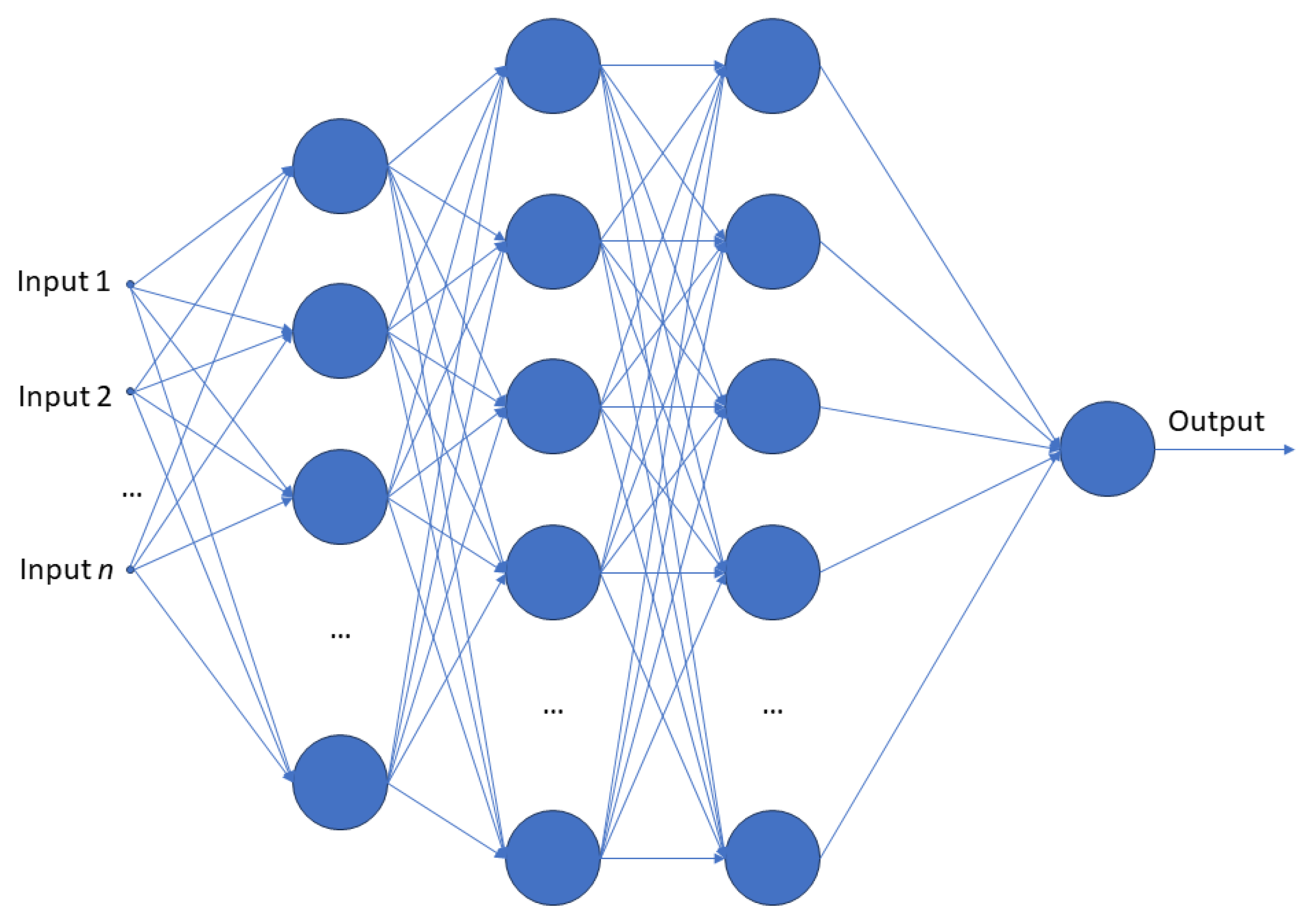
Artificial neural network used
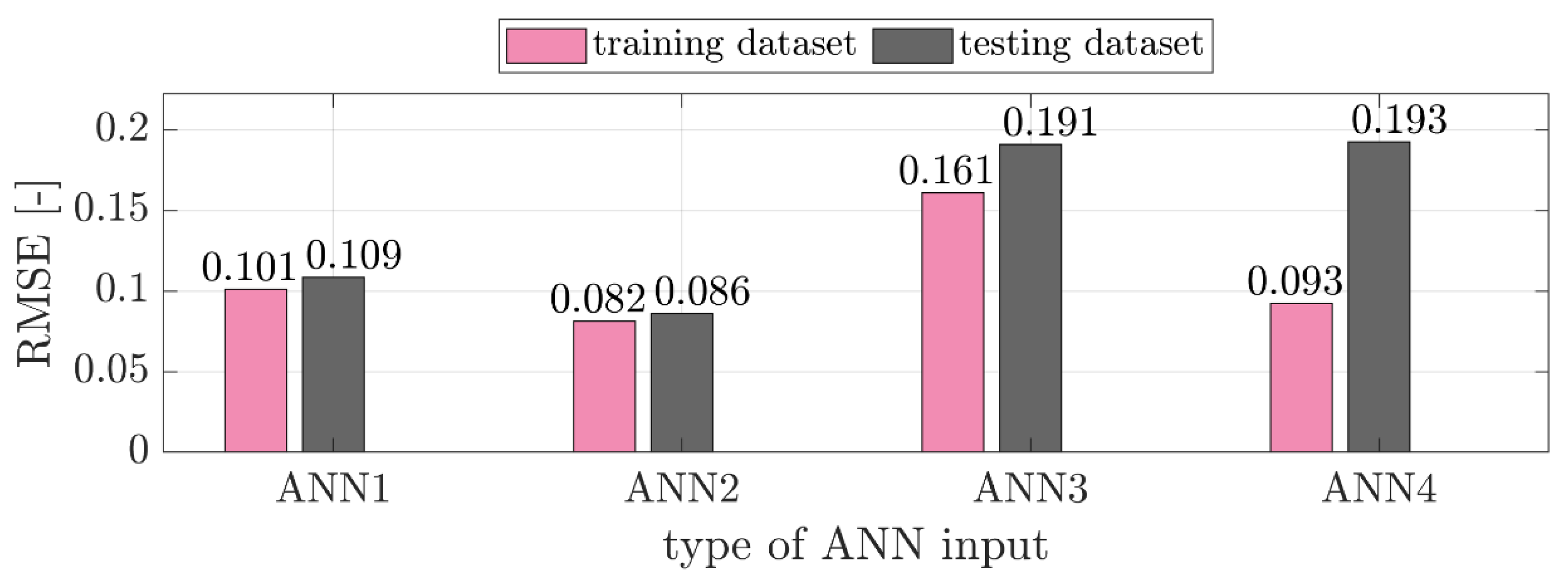
Results and Discussion
- ANN1: Packaging dimensions (, and ), representative properties of cardboard as an orthotropic composite (, , , and ), , effective thickness and critical forces of load-bearing panels (, , and )
- ANN2: Packaging dimensions (, and ), and critical forces of load-bearing panels (, , and )
- ANN3: Ratios of packaging dimensions ( and ), , and critical forces of load-bearing panels (, , and )
- ANN4: Packaging dimensions (, and ) and critical forces of load-bearing panels in relation to (, , and )
Conclusions
References
- Simon, JW. A Review of Recent Trends and Challenges in Computational Modeling of Paper and Paperboard at Different Scales. Archives of Computational Methods in Engineering 2020; 28: 2409-2428. [CrossRef]
- Coffin, DW. Historical perspectives of corrugated box testing for 2020. TAPPI Journal 2020; 19(3): 161-73. [CrossRef]
- Nagasawa S, Yamashita Y, Abdul~Hamid D, Fukuzawa Y, Hine A. Out-of-plane shearing characteristics of coated paperboard. International Journal of Mechanical Sciences 2010; 52(9): 1101-1106. [CrossRef]
- Borgqvist E, Wallin M, Ristinmaa M, Tryding J. An anisotropic in-plane and out-of-plane elasto-plastic continuum model for paperboard. Composite Structures 2015; 126: 184-195. [CrossRef]
- Harrysson A, Ristinmaa M. Large strain elasto-plastic model of paper and corrugated board. International Journal of Solids and Structures 2008; 45(11-12): 3334-3352. [CrossRef]
- Lindström SB, Karabulut E, Kulachenko A, Sehaqui H, Wågberg L. Mechanosorptive creep in nanocellulose materials. Cellulose 2012; 19: 809-819. [CrossRef]
- Östlund M, Borodulina S, Östlund S. Influence of Paperboard Structure and Processing Conditions on Forming of Complex Paperboard Structures. Packaging Technology and Science 2011; 24(6): 331-341. [CrossRef]
- Leminen V, Tanninen P, Mäkelä P, Varis J. Combined effect of paperboard thickness and mould clearance in the press forming process. BioResources 2013; 8(4): 5701-5714. [CrossRef]
- Nygårds M, Just M, Tryding J. Experimental and numerical studies of creasing of paperboard. International Journal of Solids and Structures 2009; 46(11-12): 2493-2505. [CrossRef]
- Nagasawa S, Komiyama Y, Mitsomwang P. Finite Element Analysis of Corrugated Board on Rotary Creasing Process. Journal of Advanced Mechanical Design, Systems, and Manufacturing 2013; 7(2): 103-114. [CrossRef]
- Huang H, Hagman A, Nygårds M. Quasi static analysis of creasing and folding for three paperboards. Mechanics of Materials 2014; 69(1): 11-34. [CrossRef]
- Borgqvist E, Wallin M, Tryding J, Ristinmaa M, Tudisco E. Localized Deformation in Compression and Folding of Paperboard. Packaging Technology and Science 2016; 29(7): 397-414. [CrossRef]
- Suarez B, Muneta MLM, Sanz-Bobi JD, Romero G. Application of homogenization approaches to the numerical analysis of seating made of multi-wall corrugated cardboard. Composite Structures 2021; 262: 113642. [CrossRef]
- Johansson S, Engqvist J, Tryding J, Hall SA. 3D Strain Field Evolution and Failure Mechanisms in Anisotropic Paperboard. Experimental Mechanics 2021; 61: 581-608. [CrossRef]
- Johansson S, Engqvist J, Tryding J, Hall SA. Microscale deformation mechanisms in paperboard during continuous tensile loading and 4D synchrotron X-ray tomography. Strain 2022; 58: e12414. [CrossRef]
- Hahn EK, Ruvo dA, Westerlind BS, Carlsson LA. Compressive strength of edge-loaded corrugated board panels. Experimental Mechanics 1992; 32: 259-265. [CrossRef]
- Biancolini ME, Brutti C. Numerical and experimental investigation of the strength of corrugated board packages. Packaging Technology and Science 2003; 16(2): 47-60. [CrossRef]
- Åslund PE, Hägglund R, Carlsson LA, Isaksson P. Modeling of global and local buckling of corrugated board panels loaded in edge-to-edge compression. Journal of Sandwich Structures & Materials 2014; 16(3): 272-292. [CrossRef]
- Tanninen P, Leminen V, Kainusalmi M, Varis J. Effect of process parameter variation on the dimensions of press-formed paperboard trays. BioResources 2016; 11(1): 140-158. [CrossRef]
- Fadiji T, Coetzee CJ, Berry TM, Linus Opara U. Investigating the role of geometrical configurations of ventilated fresh produce packaging to improve the mechanical strength - Experimental and numerical approaches. Food Packaging and Shelf Life 2019; 20: 100312. [CrossRef]
- Hägglund R, Carlsson LA. Packaging performance. In: Östlund S, Niskanen K., eds. Mechanics of Paper Products De Gruyter, Berlin. 2nd ed. 2021 (pp. 37-67).
- Jamialahmadi A, Trost T, Östlund S. A Proposed Tool to Determine Dynamic Load Distribution between Corrugated Boxes. Packaging Technology and Science 2011; 24(6): 317-329. [CrossRef]
- Korin C, Ristinmaa M, Ottosen NS. Analytical prediction of package collapse - consideration of windows in the package. Nordic Pulp & Paper Research Journal 2018; 29(4): 717-724. [CrossRef]
- Robertsson K, Borgqvist E, Wallin M, et al. Efficient and accurate simulation of the packaging forming process. Packaging Technology and Science 2018; 31(8): 557-566. [CrossRef]
- Lindberg G, Kulachenko A. Tray forming operation of paperboard: A case study using implicit finite element analysis. Packaging Technology and Science 2021; 35(2): 183-198. [CrossRef]
- Fadiji T, Coetzee CJ, Linus Opara U. Compression strength of ventilated corrugated paperboard packages: Numerical modelling, experimental validation and effects of vent geometric design. Biosystems Engineering 2016; 151: 231-247. [CrossRef]
- Di Russo FM, Desole MM, Gisario A, Barletta M. Evaluation of wave configurations in corrugated boards by experimental analysis (EA) and finite element modeling (FEM): the role of the micro-wave in packaging design. The International Journal of Advanced Manufacturing Technology 2023; 126: 4963-4982. [CrossRef]
- Urbanik TJ, Frank B. Box compression analysis of world-wide data spanning 46 years. Wood and Fibre Science 2006; 38(3): 399-416.
- Frank, B. Corrugated Box Compression - A Literature Survey. Packaging Technology and Science 2014; 27(2): 105-128. [CrossRef]
- Coffin, DW. Some observations towards improved predictive models for box compression strength. TAPPI Journal 2015; 14(5): 537-545.
- Marin G, Srinivasa P, Nygårds M, Östlund S. Experimental and finite element simulated box compression tests on paperboard packages at different moisture levels. Packaging Technology and Science 2021; 34(4): 229-243. [CrossRef]
- Garbowski T, Gajewski T, Grabski JK. The Role of Buckling in the Estimation of Compressive Strength of Corrugated Cardboard Boxes. Materials 2020; 13(20): 4578. [CrossRef]
- Garbowski T, Gajewski T, Grabski JK. Estimation of the Compressive Strength of Corrugated Cardboard Boxes with Various Openings. Energies 2021; 14(1): 155. [CrossRef]
- Garbowski T, Gajewski T, Grabski JK. Estimation of the Compressive Strength of Corrugated Cardboard Boxes with Various Perforations. Energies 2021; 14(4): 1095. [CrossRef]
- Mrówczyński D, Garbowski T, Knitter-Piątkowska A. Estimation of the Compressive Strength of Corrugated Board Boxes with Shifted Creases on the Flaps. Materials 2021; 14(8): 5181. [CrossRef]
- Mrówczyński D, Gajewski T, Garbowski T. Sensitivity Analysis of Open-Top Cartons in Terms of Compressive Strength Capacity. Materials 2023; 16(1): 412. [CrossRef]
- Garbowski T, Mrówczyński D, Grabski JK. Modified Compression Test of Corrugated Board Fruit Tray: Numerical Modeling and Global Sensitivity Analysis. Materials 2023; 16(3): 1121. [CrossRef]
- Nygårds M, Sjökvist S, Marin G, Sundström J. Simulation and experimental verification of a drop test and compression test of a gable top package. Packaging Technology and Science 2019; 32(7): 325-333. [CrossRef]
- Waszczyszyn Z, Ziemiański L. Neural networks in mechanics of structures and materials - new results and prospects of applications. Computers & Structures 2001; 79(22-25): 2261-2276. [CrossRef]
- Miller B, Ziemiański L. Optimization of dynamic behavior of thin-walled laminated cylindrical shells by genetic algorithms and deep neural networks supported by modal shape identification. Advances in Engineering Software 2020; 147: 102830. [CrossRef]
- Stręk AM, Dudzik M, Kwiecień A, Wańczyk K, Lipowska B. Verification of Application of ANN Modelling in Study of Compressive Behaviour of Aluminium Sponges. Engineering Transactions 2019; 67(2): 271-288. [CrossRef]
- Gravett DZ, Mourlas C, Taljaard VL, Bakas N, Markou G, Papadrakakis M. New fundamental period formulae for soil-reinforced concrete structures interaction using machine learning algorithms and ANNs. Soil Dynamics and Earthquake Engineering 2021; 144: 106656. [CrossRef]
- Ariza-Garcia MA, Redondo S, Llorens DP, Calvo B, Rodriguez~Matas JF. A predictive tool for determining patient-specific mechanical properties of human corneal tissue. Computer Methods in Applied Mechanics and Engineering 2017; 317: 226-247. [CrossRef]
- Zaborowicz K, Biedziak B, Olszewska A, Zaborowicz M. Tooth and Bone Parameters in the Assessment of the Chronological Age of Children and Adolescents Using Neural Modelling Methods. Sensors 2021; 21(18): 6008. [CrossRef]
- Cieślińska K, Zaborowicz K, Zaborowicz M, Biedziak B. Evaluation of the Second Premolar’s Bud Position Using Computer Image Analysis and Neural Modelling Methods. International Journal of Environmental Research and Public Health 2022; 19(22): 15240. [CrossRef]
- Boniecki P, Koszela K, Piekarska-Boniecka H, et al. Neural identification of selected apple pestsl. Computers and Electronics in Agriculture 2015; 110: 9-16. [CrossRef]
- Boniecki P, Raba B, Pilarska AA, et al. Neural Reduction of Image Data in Order to Determine the Quality of Malting Barley. Sensors 2021; 21(17): 5696. [CrossRef]
- Araujo G, Andrade FAA. Post-Processing Air Temperature Weather Forecast Using Artificial Neural Networks with Measurements from Meteorological Stations. Applied Sciences 2022; 12(14): 7131. [CrossRef]
- Boniecki P, Sujak A, Niedbala G, Piekarska-Boniecka H, Wawrzyniak A, Przybylak A. Neural Modelling from the Perspective of Selected Statistical Methods on Examples of Agricultural Applications. Agriculture 2023; 13(14): 762. [CrossRef]
- Adamopoulos S, Karageorgos A, Rapti E, Birbilis D. Predicting the properties of corrugated base papers using multiple linear regression and Artificial Neural Networks. Drewno. Wood. Research papers. Reports. Announcements 2016; 59(198): 61-72. [CrossRef]
- Garbowski T, Knitter-Piątkowska A, Grabski JK. Estimation of the Edge Crush Resistance of Corrugated Board Using Artificial Intelligence. Materials 2023; 16(4): 1631. [CrossRef]
- Archaviboonyobul T, Chaveesuk R, Singh J, Jinkarn T. An analysis of the influence of hand hole and ventilation hole design on compressive strength of corrugated fiberboard boxes by an artificial neural network model. Packaging Technology and Science 2020; 33(4-5): 171-181. [CrossRef]
- Technical Association of the Pulp & Paper Industry, Inc. Peachtree Corners Standard conditioning and testing atmospheres for paper, board, pulp handsheets, and related products, Test Method TAPPI/ANSI T 402 sp-21. 2021.
- Wierzbicki T, Abramowicz W. On the Crushing Mechanics of Thin-Walled Structures. Journal of Applied Mechanics 1983; 50(4a): 727-734. [CrossRef]
- Setoodeh S, Abdalla MM, Ijsselmuiden ST, Gürdal Z. Design of variable-stiffness composite panels for maximum buckling load. Composite Structures 2009; 87(1): 109-117. [CrossRef]
- Timoshenko SP, Gere JM. Theory of Elastic Stability. New York: McGraw-Hill. 2nd ed. 1961.
- Wang CM, Wang CY, Reddy JN. Exact solutions for buckling of structural members. Boca Raton: CRC Press. 2005.
- Bažant Z, Cedolin L. Stability of Structures. Singapore: World Scientific. 2nd ed. 2010.
- McKee RC, Gander JW, Wachuta JR. Compression strength formula for corrugated boxes. Paperboard Packaging 1963; 48(8): 149-159.
- Buchanan JS, J D, W TG. Combined board characteristics that determine box performance. Paperboard Packaging 1964; 49(9): 74-85.

| Type/No. of input | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| ANN1 | ||||||||||||||
| ANN2 | ||||||||||||||
| ANN3 | ||||||||||||||
| ANN4 |
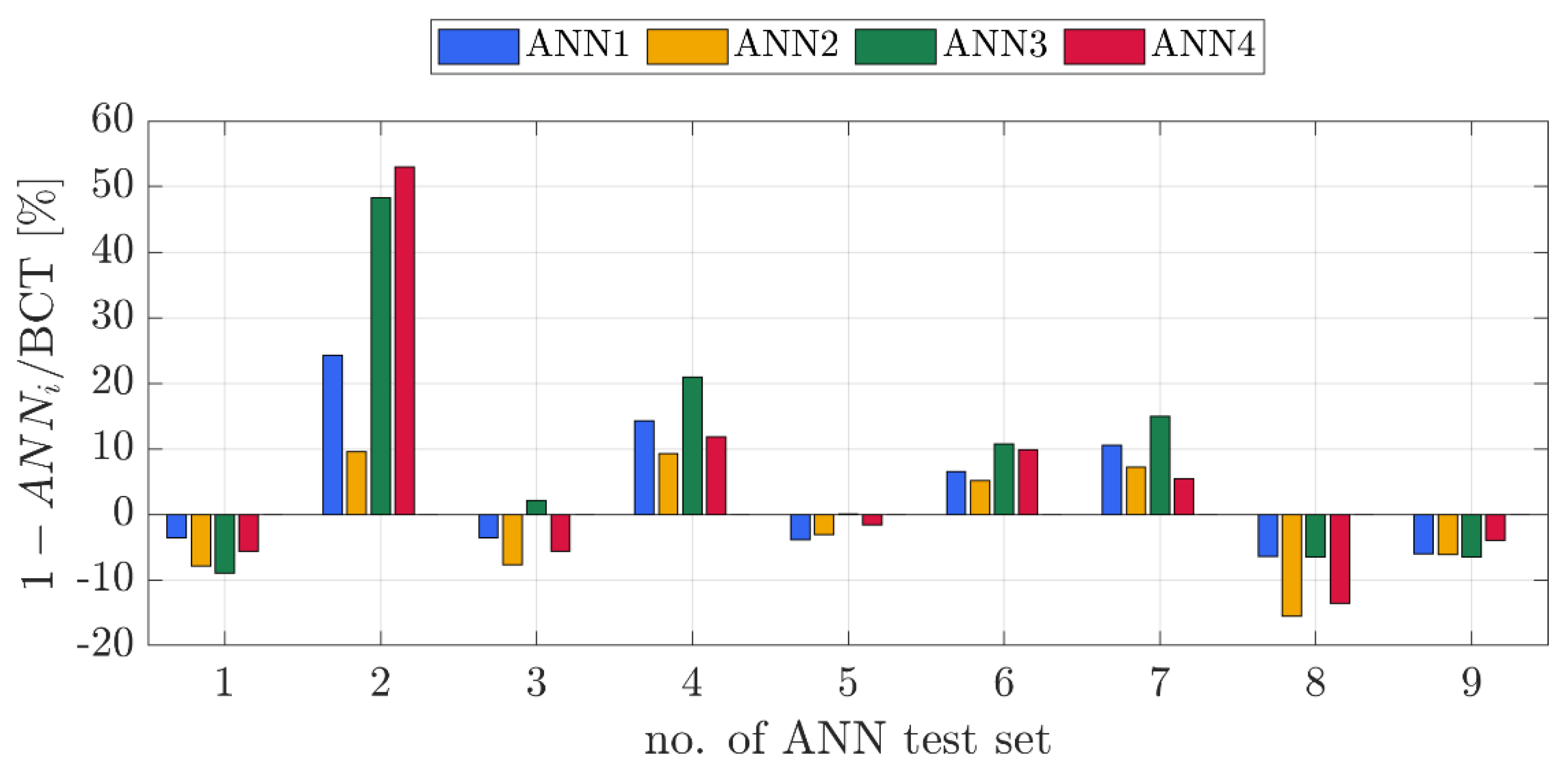
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| BCT [N] | 1903 | 697 | 1902 | 1606 | 1033 | 933 | 899 | 2078 | 1869 |
| ANN1 [N] | 1834 | 866 | 1834 | 1834 | 993 | 9935 | 993 | 1944 | 1757 |
| ANN2 [N] | 1752 | 763 | 1755 | 1755 | 1001 | 980 | 963 | 1755 | 1755 |
| ANN3 [N] | 1733 | 1033 | 1942 | 1942 | 1033 | 1033 | 1033 | 1942 | 1747 |
| ANN4 [N] | 1795 | 1066 | 1795 | 1795 | 1016 | 1024 | 947 | 1795 | 1795 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





