Preprint
Article
Unveiling Strong Dependence of Geometrical Aspect Ratio on the Magneto-Structural Properties of Co2Mn-Based Microwires
Altmetrics
Downloads
120
Views
67
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
17 July 2023
Posted:
18 July 2023
You are already at the latest version
Alerts
Abstract
The present study illustrates the strong effect of geometrical parameters on the magneto-structural properties of Co2MnSi glass-coated microwires prepared using the Taylor-Ulitovsky method. Thus, two samples with different geometrical aspect ratios (ρ= d / D) have been fabricated, where d is the metallic nuclei diameter and D is the total diameter of the Co2MnSi microwire. The XRD analysis shows a significant change by modifying the aspect ratio, for ρ = 0.46 the main peak with miller indices (220) is recognized as an A2-type disordered cubic structure. Meanwhile, in the sample with a low aspect ratio, ρ = 0.31, the perfect L21 ordered cubic structure is attained. In addition, a decrease in average grain size from 36.62 nm to 28.07 nm by increasing the aspect ratio from 0.46 to 0.31 is observed. The magnetic characterization has been done in a wide range of temperatures and magnetic fields. Both of Co2MnSi samples show ferromagnetic behavior in a whole measuring temperatures range. A significant increase in coercivity and normalized reduced remanence by decreasing the aspect ratio is observed. The change in the magnetic properties is attributed to the modification in the microstructure, which is induced during the fabrication process. Such a dependence on the microstructure and magnetic properties on the ρ-ratio can be associated either with the internal stresses distribution and magnitude or with different quenching rates of microwires with different aspect ratios. The current findings demonstrate the tunability of microstructure and magnetic properties of Co2MnSi-glass-coated microwires simply, by a small modification in the geometric properties during the manufacturing process and without excreting any additional post-processing. The variation in geometric parameters of Co2MnSi glass-coated microwires allows us to tune magnetic properties and structure, which is essentially advantageous for sensing devices development.
Keywords:
Subject: Chemistry and Materials Science - Metals, Alloys and Metallurgy
1. Introduction
Investigations of innovative materials, particularly half-metals displaying ferromagnetism at a wide range of temperatures, have intensified due to the development of a new generation of spintronic devices [1]. Among the most extensively studied materials are the Heusler alloys, defined as magnetic intermetallic. The Heusler alloys present a vast family of ternary intermetallic compounds with a variety of magnetic phenomena. Several of such compounds are well known for their unique properties, such as high Curie temperature, half metallicity, and excellent tenability for metallic Heusler alloys, in particular, are of great interest due to the high spin-polarized current close to the Fermi level, which is predicted to increase the efficiency of spintronic devices. This can be exploited to enhance the efficiency of spin-injecting and information storage devices [2,3]. Depending on the nature of magnetic sub-lattices, a Heusler alloy is called either half Heusler compounds or full Heusler compounds [4,5].
Their generic formula is X2YZ. In general, X and Y are d-group transition metal elements. X is usually a transition metal 3d (Fe, Co, Ni, Cu, Zn), 4d (Ru, Rh, Pd, Ag, Cd), or 5d (Ir, Pt, Au). The position of Y is usually occupied by 3d (Ti, V, Cr, Mn), 4d (Y, Zr, Nb), 5d (Hf, Ta), or by lanthanides (Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) or actinides (U). While, Z is the p-group main elements III-B (Al, Ga, In, Tl), IV-B (Si, Ge, Sn, Pb), or V-B (As, Sb, Bi) [6,7]. The parent phase may be stabilized by the covalent link created by the p-d orbital hybridization between p and d-group atoms. One of the most attractive materials for multiple-function applications are Co2-based full/half-Heusler alloys with high Curie temperatures (Tc > 1100 K), high magnetic moments, distinct electronic structures, and low Gilbert damping constants (= 0.004) [4,8]. Because of their distinctive electronic band structures, some Co2-based full Heusler alloys also exhibit a significant anomalous Hall effect, in addition to half-metallic ferromagnetism [9]. Accordingly, Co2-based Heusler alloys have attracted the scientific community's attention and, therefore, have been widely explored experimentally. Over the past ten years, a theoretical and experimental study has been conducted to fully understand the crystalline structure [10,11]. Thus, two crystalline phases of Heusler alloys can be found: the high-symmetry austenite phase, which has the simplest structure as a cubic L21 (high-ordered phase) or B2 structure (disorder phase), and the less-symmetrical martensitic phase [6].
Using the appropriate manufacturing and synthesis procedures, alloys can acquire the ordered austenitic structure. In some cases, the L21 phase can be obtained by annealing the alloys at high temperatures for several hours, followed by a long cooling procedure to create a solid-state reaction [12]. In this instance, the formation of this phase is promoted by the homogenization of the chemical composition and the removal of the impurities in produced alloys [13,14]. Other synthesized techniques, like melt spinning or atomization can also be used to obtain the L21 phase in Heusler alloys by rapid solidification. These procedures consist of quenching the molten alloy at a high cooling rate to eliminate the formation of other phases and promote the formation of the ordered one [14,15,16,17]. Otherwise, the formation of nanocrystalline powder alloys can lead to reach the fully ordered L21 structure. Alternatively, mechanical alloying consisting of milling of a mixture of the constituent elements of the desired alloy in a ball milling for several hours or even days can be used. Hereafter, the obtained powders can be consolidated into bulk materials by hot pressing or sintering [18]. It should be noted that the composition of the alloy and the processing techniques employed have a significant impact on the attainment of the L21 structure [15]. Depending on the material's desired qualities and intended applications, different processing conditions may be suitable.
Co2Mn-based alloys with an L21 structure exhibit a ferromagnetic ordering, which makes them attractive for various magnetic applications [5,19]. In addition, this ordered structure exhibits, making it suitable for high-temperature applications [20]. Moreover, to describe the mechanical stability of alloys exhibiting an L21-ordered structure, the stability of some elastic constants against external forces was examined. When analyzing the elastic constants and other related mechanical excellent mechanical properties, such as high strength, good ductility, and high fracture toughness, were observed [21]. Such properties are suitable for thermoelectric applications and development of devices based on spintronic.
Recently, Taylor-Ulitovsky technique involving rapid melt quenching has been successfully used for the fabrication of thin glass-coated magnetic microwires from Heusler alloys [22,23]. The Taylor-Ulitovsky process allows preparing of a substantial amount (up to several km) of metallic microwires covered by glass coating from a few grams of master alloy within a few minutes [22,24,25]. As discussed elsewhere, such fabrication technique provides a favorable surface-to-volume ratio, tunable diameter, d, of the metallic nucleus, and glass-coating thickness. Additionally, the internal stress magnitude is tunable by the ratio, ρ, between the metallic nucleus diameter, d, and total diameter, D [22]. The preferably axial origin of such internal stresses substantially affects the magnetic anisotropy and particularly the easy magnetization axis of glass-coated microwires [24,26]. Besides, the ability to fabricate glass-coated microwires with various structures (such as amorphous, nanocrystalline, and granular) offers a special advantage for researching the impact of various microstructures on the physical properties of the same material [25,26].
In our previous investigations, we attempted to obtain a high degree of ordered Co2Mn-based glass-coated microwires prepared by the Taylor-Ulitovsky technique [27,28,29]. We evaluated various parameters, such as excreting annealing treatments [30] and varying chemical composition, to improve the structured ordered degree [31]. High-ordered L21 structure is attained at Co2MnGe as described elsewhere [19]. Recently, a strong dependence of the geometrical aspect ratio on magneto-structural properties of Heusler glass-coated microwires was discussed [31]. Therefore, the main objective of the present study is to illustrate the influence of the aspect ratio change on the magneto-structural behavior of the well know Co2MnSi alloys for multifunctional applications.
2. Materials and Methods
Two significant steps are involved in the production of Co2MnSi glass-coated microwires. First of all, the melting process begins by melting the nominal high purity (Co (99.99%), Mn (99.9%), and Si (99.9%)) elements in an arc melting furnace. The alloy components were weighed according to the desired composition and placed in a water-cooled copper mold. Manganese was supplemented with an extra two weight percent to compensate for the losses that can be caused by its evaporation during the production process. The melting procedure was repeated five times to attain an alloy with higher homogeneity and a uniform microstructure [16,27,28]. At this stage, the Co2MnSi alloy has solidified into an ingot, permitting us to proceed to the manufacturing of Co2MnSi glass-coated microwires through the Taylor-Ulitovsky technique [26,27,28] Afterwards, the obtained metal ingot (normally a few grams) is again subjected to melting inside a Pyrex glass tube by a high-frequency inductor (normally 350-500 kHz). The glass capillary softened glass is then formed from the softened glass, which is picked up by a spinning pick-up spool [32]. Hereafter, a microwire with a metallic core completely coated in a continuous, thin, and flexible glass covering is fashioned as the molten metallic alloy fills the glass capillary. In this fabrication process, a combined microwire having a glass capillary over a metallic nucleus inside of it is susceptible to rapid solidification, as it passes through a stream of coolant water [33]. Although the diameter of the metallic nucleus is constrained by the starting amount of the master alloy droplet, the amount of glass employed in the process is balanced by the continual passing of the glass tube through the inductor zone. One of the advantages of the Taylor-Ulitovsky procedure is that it allows for the preparation of microwires with a very thin glass coating, normally a few micrometers in thickness. The metallic nucleus diameter, d, and glass-coating thickness can be adjusted by the speed at which the wire is drawn and by the glass, tube feed rate. For this, we are producing two types of Co2MnSi glass-coated microwires with different geometrical parameters (varying the diameters of nucleus and core-shell), where the diameter of the metallic nuclei, d, and the total wire D is tuned by adjusting the speed of wire drowning and pick-up bobbin rotation [30]. This manufacturing process is particularly advantageous for alloys containing manganese as it protects against oxidation by the surrounding glass layer due to the rapid solidification [27]. Therefore, this procedure proves suitable for the production of such materials, while achieving desired results in terms of quality control. The origins of mechanical internal stresses in glass-coated ferromagnetic microwire are attributed to several factors, such as the difference in the thermal expansion coefficients of metallic alloy solidifying inside the glass coating, the quenching stresses related to the rapid quenching of the metallic alloy and the drawing stresses [22,24,34]. The stresses induced by the difference in the thermal expansion coefficients of metallic alloy and the glass coating are the largest one, being an order of magnitude higher than the other stresses [22,34]. The ratio of the metallic nucleus to the entire diameter (d/D) can be used to estimate the first type of stress; glass shell-induced stress. It implies that raising the d/D lowers the stresses caused by the shell [22,24,31,34].
Henceforward, from the optical microscope, we can extract the diameters of microwires after their production; one with aspect ratio ρ = d/D total = 0.46 and the other with ρ = d/D total = 0.31. Therefore, in this work, two groups of Co2MnSi glass-coated microwires with different d/D; (10.2 µm/ 22.2 µm) and (7.4 µm/ 23.2 µm) were produced and investigated.
For investigating the microstructure, morphology and composition of the obtained glass-coated microwires, we used a scanning electron microscope, attached with an energy-dispersive spectrometry (EDX) device. In addition, their structural analysis has been scrutinized by using a BRUKER X-ray diffractometer (D8 Advance, Bruker AXS GmbH, Karlsruhe, Germany), executed with Cu Kα (λ = 1.54 Å) radiation. The magnetic studies of the Co2MnSi glass-coated microwires are performed by means a Physical Property Measurement System (PPMS) (Quantum Design Inc., San Diego, CA). The measurements of the magnetization curves were executed parallel to the wire axis, where the easy magnetization axis is expected due to the shape magnetic anisotropy, and performed at a varied range of temperature (5- 300 K) and magnetic fields (50 Oe - 1kOe). In order to examine the potential magnetic phase transition or irreversibility, zero-field cooling (ZFC), field cooling (FC), and field heating (FH) protocols were used. The findings are expressed as the normalized magnetization, M/M5K, where M5K is the magnetic moment obtained at 5 K.
3. Results
3.1. Microstructure analysis
In order to investigate the aspect ratio effect in Co2MnSi glass coated microwires (GCMWs) produced using the Taylor-Ulitovsky process, two microwires with different d/D characteristics were selected. The first microwire shows the average metal core (d) and total (D) diameters 7.4 and 23.8 μm, respectively. On the other hand, the second microwire present the average metal core (d) and total (D) diameters 10.2 and 22.2 μm , respectively. We conducted an EDX/SEM study to determine the real chemical composition of the produced glass-coated microwires, where the output results are provided in Table 1. The real chemical composition is determined by analyzing ten distinct locations. From such experiments we determined that the average chemical composition of (GCMW-A) corresponds to Co49.55Mn25.1Si25.02 and Co51Mn23.9Si25.1 for (GCMW-B), which are close to expected composition (Co50Mn25Si25) and confirms the stoichiometric ratio (2:1:1), as listed in Table 1.
In addition, XRD structure analysis was conducted, to explore the order state of Co2MnSi-GCMWs and to study the impact of the aspect ratio on the crystalline structure. The representative findings are illustrated in Figure 1. The (111) and (200) superlattice reflections are clearly observed at 2Ө = 27.67⁰ and 32⁰ positions in the XRD diffractogram for GCMW-A. As described in our previous publications [15,17,30], such XRD diffractograms are attributed to fully ordered cubic L21 austenitic structure. Nevertheless, these two superlattices' diffraction (111) and (200) peaks are significantly weaker, as- compared to other elements belonging to the same period of the periodic table [35]. The intensities of these peaks may therefore be essentially undetectable if the majority or all of the elements in the presented alloys belongto the same period in the elemental periodic table. Commonly, these two XRD diffraction lines will not appear either if samples demonstrate such a disorder cubic A2 crystal structure [36]. Given that Mn (3d54s2) and Co (3d⁷4s²) belong to the same period (period 4)of the studied alloy, GCMW-B may have a disordered phase with the cubic A2 type structure. Moreover, in this diffractogram, we can observe the absence of a (400) peak around 2Ө = 65⁰, which is ordinarily expected to be present in the A2 structure. This strengthens the possibility that the crystallites are too fine to be recognized by X-rays, as has been noticed previously [31,37]. Furthermore, similar scattering effects of the constituent elements (Co, Mn, and Si) can explain the nonappearance of some peaks [38]. Subsequently, when comparing both of the XRD spectra, the well-defined diffraction patterns presented in GCMW-A express a high crystallinity. The intensity of the diffraction peak then weakens with increasing the aspect ratio of the GCMW's nucleus and metal diameters, as reported and discussed in our previous investigations [31]. This proves that, with relatively low crystallinity, the crystalline size diminishes relating to GCMWs-B. It is important to note that superstructure peaks intensities can be affected by various types of atomic disorders [19].
As we know, Co2MnSi compounds can be described as X2YZ Heusler alloys-types. Therefore, for a deeper understanding of the L21 and A2 phases, the arrangement of atoms in both crystal structures can be conferred. It can be realized that the L21-type belongs to the cubic Fm3¯m space group, which is made up of four interpenetrated face-centered cubic (FCC) sublattices. Considering the X2YZ type, in our case Co (X), Mn (Y), and Si (Z) occupy the following Wyckoff positions; Si (Z) is the main group element with the highest electronegativity which occupies: 4a (0 0 0), Mn (Y) is the lower valence transition metal atom with smallest electronegativity and occupies: 4b (0.5 0.5 0.5), and Co the transition metal (X) atoms are of intermediate electronegativity and occupy 8c (0.25 0.25 0.25) and (0.75 0.75 0.75) [39].
Theoretically under 2θ ranging, (220) and (400) are the main reflection peaks of the L21 structure, although (111) and (200) sublattices are responsible for the orderly stacking of X, Y, and Z atoms. Heusler alloys with an ordered cubic L21 structure are specifically identified by the existence of super lattice reflection peaks; the presence of (111) peak indicates the chemical ordering of atoms in octahedral positions, (200) peak implies the order for atoms in tetrahedral positions, whereas (220) peak is a principal reflection that is independent of the state of the order. Wherefore, the diffractogram of GCMW-B confirms the disordered A2-type cubic structure with no ordered reflection. A random distribution of atoms over lattice sites ultimately leads to the formation of an A2 (bcc) disorder structure [40].
Crystallographic parameters, such as the space group, cell parameters, crystallite size, and Strukturbericht designation of two cubic phases of GCMW-A and GCMW-B are provided in Table 2.
3.1. Magnetic properties (M-H behavior)
Magnetic properties of Co2-Mn-Si glass-coated microwires are linked to their structure. Precisely, the combination of a metallic nucleus and a glass coating affects the magnetic properties. A magnetic study was conducted to study the magnetic properties of the current samples. For better comparison the M-H loops of both GCMWs, the magnetic hysteresis (M-H) loops are normalized and expressed as M/M5K, where M5K is the maximal magnetic moment attained at 5K (lower temperature). Figure 2 recapitulates the magnetic hysteresis behavior of Co2MnSi glass-coated microwires over a temperature range of 5 K and 300 K. As illustrated in Figure 2, all samples, with different geometrical parameters, exhibit a ferromagnetic behavior.
Generally, coercivity, Hc, is an essential parameter in magnetic materials characterization, as it determines their practical utility for specific applications. The coercivity of ferromagnetic glass-coated microwires can vary depending on several factors, including the composition of the metallic nucleus, the dimensions of the microwire, and the manufacturing process conditions. It is important to note that the choice of ferromagnetic material, in combination with the microwire dimensions and the specific application requirements, determines the coercivity of glass-coated microwires. Therefore, the coercivity can be tailored by selecting appropriate core materials and optimizing the fabrication process of the microwires [31,41]. Table 3 summarizes the Hc values of GCMW-A and GCMW-B for a wide range of temperatures from 5 to 300K. For GCMW-A, the coercivity values vary between 8.5 and 11.2 Oe. However, Hc values fluctuate between 5.3 to 9.2 Oe, for GCMW-B. The differences between the highest and lowest value of the coercivity can indicate the stability of Hc with the temperature. Thus, the GCMWs-A shows higher thermal stability compared to GCMW-B, where, ΔHc = 2.7 Oe for B-sample and 3.9 Oe for the GCMW-B sample.
Considering that increasing factor i.e., P = Hc (A)/ Hc (B). P > 1 indicates that GCMWs-A shows a higher Hc value as- compared to GCMW-B. As shown in Table 3 the P factor has a monotonic increase with Temperature, where by decreasing the temperature from 300 to 20 K the P increase from 1.1 to 1.8 at T = 20 K. A decrease in the P factor from 1.8 to 1.6 is observed below T = 20 K and is related to strong changes in the magnetic behavior of GCMW-A and GCMW-B at low temperatures. The current results and behavior of Hc and P with T (K) indicate a strong dependence on the magnetic properties of the aspect ratio.
3.2. Magnetic properties (ZFC, FC and FH magnetization behavior)
To investigate the impact of the microstructure ordering on the magnetothermal behavior of Co2MnSi-GCMWs samples zero field cooling (ZFC), field cooling (FC), and field heating (FH) magnetizations curves have been performed at different temperatures and magnetic fields. All magnetic curves are normalized to M/M5K for better comparison of the studied samples.
By applying a low external magnetic field, i.e. H = 50 Oe during measuring the ZFC, FC, and FH curves for the ordered sample( GCMW-A) and the disordered sample (GCMW-B) a notable differences are observed, as illustrated in Figure 3. Both samples show large irreversibility : the magnetization curves start to decrease by decreasing the temperature from 350 K to 5 K. The characteristic point, such as the irreversible temperature (Tirr) for the ordered sample shifted to the low temperature (Tirr ≥ 120 K), however Tirr ≈ 175 K) for the disordered sample. ZFC, FC, and FH magnetic curves appear perfectly matched at a temperature range from 350 K to 70 K, and below T = 70 K a notable mismatching between the FC and ZFC is detected. For the ordered sample, a notable mismatching between ZFC, FC, and FH curves is observed (see Figure 3a). Assuming the differences between magnetization curves as (ΔM), thus ΔM between ZFC and FC&FH is much higher than ΔM between FH and FC, for the ordered sample at all measuring temperatures . In contrast, ΔM ≈ zero for the disordered sample at a temperature range of 350-70 K.
Upon further increasing of the external magnetic field from 50 Oe to 200 Oe a slight change in the magnetic behavior of the disordered sample is observed, where ΔM between ZFC and FC&FH increased a little bit. However, for the ordered sample ΔM for ZFC, FC, and FH curves is almost zero at temperature range 350-260 K (see Figure 4a). In addition, FC and FH curves are overlapping ZFC curves for temperatures below 260 K. Moreover additional transition point is appeared at T = 35 K, where the behavior of ZFC, FC, and FH curves start changing, increase by decreasing temperature from 35 to 5K.
The increasing of the external magnetic field up to 1 kOe during measuring ZFC, FC, and FH magnetic curves has a strong effect on the magnetic behavior of disordered sample. In the ordered sample (GCMW-A) ZFC, FC, and FH curves show perfect matching with two flipping points at T = 85 K and T = 45 K, where the magnetic behavior changed as described in Figure 5a. Meanwhile, the disordered sample shows inhomogeneous magnetic behavior, where ZFC, FC, and FH loss their matching. In addition, a notable characteristic temperature is observed at which the magnetic behavior is changing. As illustrated in Figure 5b for disordered samples the magnetic behavior of ZFC, FC, and FH can be divided into two main parts depending on the temperature range. The first part is initially for the temperature range 350-225 K, where FC and FH follow a monotonic increase by decreasing the temperature to reach the maximum value at T = 225 K. Then below this temperature decreasing in FC and FH curves are observed by further decreasing of the temperature reach the minimum at 5 K (see Figure 5b). The most interesting point is that the thermal magnetic behavior of the disordered sample shows an opposite tendency of the ordered one by changing the applied field from 50 Oe to 1000 Oe.
4. Discussion
There are several parameters of the Taylor-Ulitovsky fabrication method that affect the metallic nucleus diameter, d, and glass coating thickness of the produced glass-coated microwires. Among these factors are the speed at which the wire is drawn and the glass tube feed or the ingot temperature [22,34]. There are several sources o the internal stresses, such as the difference in the thermal expansion coefficients of metallic alloy solidifying inside the glass coating, the quenching stresses related to the rapid quenching of the metallic alloy and the drawing stresses [22,24,34]. The stresses induced by the difference in the thermal expansion coefficients of metallic alloy and the glass coating are the largest one, being an order of magnitude higher than the othe stresses [22,34]. As thicker is glass-coating as stronger are internal stresses. Accrodingly, the internal stresses can be modified by the ratio of the metallic nucleus to the entire diameter /D. Thus, raising the d/D ratio diminishes the stresses caused by the shell [22,24,34]. However, it must be taken into account that the quenching rate of the metallic alloy is affected by the thickness of the insulating glass-coating [22]. Therefore, the crystalline structure can be also affected by the glass-coating thickness [22,42,43,44]. Additionally, the influence of the internal stresses on crystallization process must be related to the non-equilibrium thermodynamics: the crystals nucleation and growth are affected by the atomic diffusion in the presence of the stress [45]. From studies of Co2MnSi microwires, we can deduce that decreasing the d/D ratio from 0.46 (GCMW-B) to 0.31 (GCMW-A) can lead to enhancing the crystallinity and the degree of structural order from a disordered A2 type to an ordered L21 cubic structure. Furthermore, changing the geometrical parameters has a huge effect on the magnetic behavior. When compared to GCMW-B, the magnetic behavior of GCMW-A can be significantly modified by applying a moderate magnetic field of 200 Oe instead of 50 Oe. This can be explained by the sensitivity of GCMW-A to small magnetic field changes. However, substantial variations in the magnetic behavior of GCMW-B by applying 1 kOe are detected. Thus, such modification in GCMW-B magnetic behavior is correlated with the X-ray diffraction results, owing to the disordered A2 cubic structure. Moreover, the magnetization curves in GCMW-A tend to overlap gradually by increasing the magnetic field application from 50 Oe to 1 kOe. Therefore, glass-coated Co2MnSi microwires are sensitive to changing temperature and applied magnetic field, as demonstrated by the magnetic behavior of the GCMW-A sample, making them an appropriate candidate for use as sensing materials.
The current results illustrate the strong dependence of the microstructure and thermomagnetic properties of rather well-known Heusler alloys, i.e., Co2MnSi-based glass coating microwires on its geometric parameters. The ability to tailor the magnetic & structure properties of Heusler –based glass-coated microwires makes these smart systems promising for different applications.
5. Conclusions
In summary, in the current study, we illustrate the effect of changing geometrical parameters during the manufacturing process of Co2MnSi glass-coated microwires on the structure and magnetic properties. Two Co2MnSi microwires coated with glass are produced employing the Taylor Utilovsky method by changing the diameters of the core and total microwire. First microwire GCMW-A shows the average metal core (d) and total (D) diameters of 10.2 and 22.2 μm, respectively. However, the second one present the average metal core (d) and total (D) diameters of 7.4 and 23.8 μm, respectively. From X-ray analysis, we remark that GCMW-A exhibits an L21 cubic ordered structure with Fm3¯m space group, whereas, GCMW-B demonstrates an A2 cubic disordered structure with Im3¯m space group. By comparing both of the XRD diffractograms, the well-defined diffraction patterns presented in GCMW-A express a high crystallinity. Thus, the intensity of the diffraction peak declines with increasing the aspect ratio. This proves that, with relatively low crystallinity, the crystalline size diminishes relating to GCMW-B from 36.62 to 28.02 nm. Regarding the magnetic properties, both samples display dissimilar magnetic responses with the temperature and applied magnetic field. Firstly, by applying 50 Oe the ZFC-FC-FH magnetization curves express an irreversible magnetic behavior, accompanied by a mismatching between the ZFC and FH curves. Furthermore, when applying an extra magnetic field of 200 Oe, no change was perceived, for the (M, T) curves of GCMW-B. However, applying an additional magnetic field in GCMW-A, reduces the gap occurring between ZFC and FH magnetization curves. While applying a stronger magnetic field of 1kOe, ZFC and FH magnetization curves in GCMW-A coincide and express a strong change and mismatching in GCMW-B, relating to the disordered crystalline structure that occurred. Because of the extraordinary thermal stability of the coercivity values of GCMW-A and GCMW-B, Co2MnSi microwires, can be combined in generators, sensors, transformers, and actuators for application potentials.
Author Contributions
Conceptualization, A.W., M.S. and A.Z.; methodology, V.Z.; validation, M.S., V.Z. and A.Z.; formal analysis, M.S. and A.W.; investigation, M.S., A.W. and A.Z.; resources, V.Z. and A.Z.; data curation, M.I.; writing—original draft preparation, M.S., A.W. and A.Z.; writing—review and editing, M.S., A.W. and A.Z.; visualization, M.S., A.W. and M.I.; supervision, V.Z and A.Z.; project administration, V.Z. and A.Z.; funding acquisition, V.Z. and A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish MICIN, under PID2022-141373NBI00, by EU under “INFINITE” (Horizon Europe) project and by the Government of the Basque Country, under PUE_2021_1_0009 and Elkartek (MINERVA, ZE-KONP and MAGAF) projects and by under the scheme of “Ayuda a Grupos Consolidados” (Ref.: IT1670-22). MS wish to acknowledge the funding within the Maria Zambrano contract by the Spanish Ministerio de Universidades and European Union –Next Generation EU (“Financiado por la Unión Europea-Next Generation EU”). We also wish to thank the administration of the University of the Basque Country, which not only provides very limited funding, but even expropriates the resources received by the research group from private companies for the research activities of the group. Such interference helps keep us on our toes.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank for technical and human support provided by SGIker Magnetic Measurements Gipuzkoa (UPV/EHU/ ERDF, EU).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Manna, K.; SUN, Y.; Muechler, L.; et al. Heusler, weyl and berry. Nat Rev Mater 2018, 3, 244–256. [Google Scholar] [CrossRef]
- Sheron, T.; Kesong, Y.; Marc A, Meyers. Heusler alloys: Past, properties, new alloys, and prospects. Prog Mater Sci 2023, 132, 101017. [Google Scholar] [CrossRef]
- Balke, B.; Wurmehl, S.; Fecher, G.; Felser, C.; Kübler, K. Rational design of new materials for spintronics: Co2FeZ (Z=Al, Ga, Si, Ge). Sci Technol Adv Mater 2008, 9, 1. [Google Scholar] [CrossRef] [PubMed]
- Galanakis, I. Theory of Heusler and Full-Heusler Compounds. In: Heusler Alloys, Felser, C., Hirohata, A.; Eds.; Springer Series in Materials Science: Cham, 2016, 222. [Google Scholar] [CrossRef]
- Trudel, S.; Gaier, O.; Hamrle, J.; Hillebrands, B. Magnetic Anisotropy, Exchange and Damping in Cobalt-Based Full-Heusler Compounds: An Experimental Review. J. Phys. D. Appl. Phys. 2010, 43, 193001. [Google Scholar] [CrossRef]
- Graf, T.; Felser, C.; Parkin, S.S.P. Simple Rules for the Understanding of Heusler Compounds. Prog. Solid State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
- Adem, U.; Dincer, I.; Aktürk, S.; Acet, M.; Elerman, Y. Phase Formation Characteristics and Magnetic Properties of Bulk Ni2MnGe Heusler Alloy. J. Alloys Compd. 2015, 618, 115–119. [Google Scholar] [CrossRef]
- Hazra, B.K.; Kaul, S.N.; Srinath, S.; Raja, M.M. Uniaxial Anisotropy, Intrinsic and Extrinsic Damping in Co2FeSi Heusler Alloy Thin Films. J. Phys. D. Appl. Phys. 2019, 52, 325002. [Google Scholar] [CrossRef]
- Yu, L.; Li, Z.; Zhu, J.; Liu, H.; Zhang, Y.; Cao, Y.; Xu, K.; Liu, Y. Electrical and Magnetic Transport Properties of Co2VGa Half-Metallic Heusler Alloy. Mater. 2022, 15. [Google Scholar] [CrossRef]
- Bentouaf, A.; Hassan, F.H.; Reshak, A.H.; Ai¨ssa, B.; Ai¨ssa, A. First-Principles Study on the Structural, Electronic, Magnetic and Thermodynamic Properties of Full Heusler Alloys Co 2 VZ (Z = Al, Ga). J. Electron. Mater. 2017, 46, 130–142. [Google Scholar] [CrossRef]
- Dong, Z.; Luo, J.; Wang, C.; et al. Half-Heusler-like compounds with wide continuous compositions and tunable p- to n-type semiconducting thermoelectrics. Nat Commun. 2022, 13, 35. [Google Scholar] [CrossRef] [PubMed]
- Enkatesan, A.; Govindan, S.; R. Kalaimani, K.; Kuppan, R.; Impact of annealing temperature on structural and magnetic properties of Co2FeSn Heusler alloy. J Magn Magn Mater 2020, 508, 166731. [Google Scholar] [CrossRef]
- Matyja, E.; Prusik, K.; Zubko, M.; Świec, P.; Dercz, G.; Loskot, J. Crystallization Kinetics and Structure Evolution during Annealing of Ni-Co-Mn-In Powders Obtained by Mechanical Alloying. Mater. 2023, 16, 645–2023. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.J.; Boyer, C.; Niewczas, M. Magnetic and structural properties of Co2MnSi based Heusler compound. J. Alloys Compd. 2018, 12, 018. [Google Scholar] [CrossRef]
- Wederni, A.; Ipatov, M.; Pineda, E.; Suñol, J.-J.; Escoda, L.; González, J.M.; Alleg, S.; Khitouni, M.; Żuberek, R.; Chumak, O.; et al. Magnetic Properties, Martensitic and Magnetostructural Transformations of Ferromagnetic Ni–Mn–Sn–Cu Shape Memory Alloys. Appl. Phys. 2020, 126, 320. [Google Scholar] [CrossRef]
- Wederni, A.; Ipatov, M.; González, J.M.; Khitouni, M.; Suñol, J.J. Ni-Mn-Sn-Cu Alloys after Thermal Cycling: Thermal and Magnetic Response. Materials 2021, 14. [Google Scholar] [CrossRef]
- Wederni, A.; Ipatov, M.; Pineda, E.; Escoda, L.; González, J.-M.; Khitouni, M.; Suñol, J.-J. Martensitic Transformation, Thermal Analysis and Magnetocaloric Properties of Ni-Mn-Sn-Pd Alloys. Processes 2020, 8, 1582. [Google Scholar] [CrossRef]
- Dhanal, S. V; Devadi, H.; Akkimardi, V.G.; Kori, S.A. INDIAN JOURNAL OF SCIENCE AND TECHNOLOGY Ni-Mn-Al Heusler Alloy Samples Preparation by Mechanical Alloying Method and Study of Their Investigated Properties. Prop. Indian J. Sci. Technol. 2022, 15, 1997–2003. [Google Scholar] [CrossRef]
- Salaheldeen, M.; Wederni, A.; Ipatov, M.; Zhukova, V.; Zhukov, A. Preparation and Magneto-Structural Investigation of High Ordered (L21 Structure) Co2MnGe Microwires. Processes 2023, 11, 1138. [Google Scholar] [CrossRef]
- Liu, S.; Cao, P.; Lin, D.Y.; Tian, F. Stability of L21 (NiM)2TiAl (M=Co, Fe) in High-Entropy Alloys. J. Alloys Compd. 2018, 764, 650–655. [Google Scholar] [CrossRef]
- Sofi, S.A.; Gupta, D.C. Exploration of Electronic Structure, Mechanical Stability, Magnetism, and Thermophysical Properties of L21 Structured Co2XSb (X = Sc and Ti) Ferromagnets. Int. J. Energy Res 2020, 44, 2137–2149. [Google Scholar] [CrossRef]
- Zhukov, A.; Corte-Leon, P.; Gonzalez-Legarreta, L.; Ipatov, M.; Blanco, J.M.; Gonzalez, A.; Zhukova, V. Advanced Functional Magnetic Microwires for Technological Applications. J. Phys. D Appl. Phys. 2022, 55, 253003. [Google Scholar] [CrossRef]
- Ulitovsky, AV.; Maianski, I M.; Avramenco, A I. Method of continuous casting of glass coated microwire, Patent No 128427(USSR), 15.05.60, Bulletin, No 10, p. 14.1960.
- Chiriac, H.; and Ovari, T-A. Amorphous glass-covered magnetic wires: Preparation, properties, applications. Prog. Mater. Sci. 1996, 40, 333–407. [Google Scholar] [CrossRef]
- Baranov, S.A.; Larin, V.S.; Torcunov, A.V. Technology, Preparation and Properties of the Cast Glass-Coated Magnetic Microwires. Crystals 2017, 7, 136. [Google Scholar] [CrossRef]
- Shevyrtalov, S.; Rodionova, V.; Lyatun, I.; Zhukova, V.; Zhukov, A. Post-Annealing Influence on Magnetic Properties of Rap idly Quenched Ni-Mn-Ga Glass-Coated Microwires. IEEE Trans. Magn. 2021, no 7, P1–6. [Google Scholar] [CrossRef]
- Salaheldeen, M.; Talaat, A.; Ipatov, M.; Zhukova, V.; Zhukov, A. Preparation and Magneto-Structural Investigation of Nanocrystalline CoMn-Based Heusler Alloy Glass-Coated Microwires. Processes 2022, 10, 2248. [Google Scholar] [CrossRef]
- Salaheldeen, M.; Ipatov, M.; Corte-Leon, P.; Zhukova, V.; Zhukov, A. Effect of Annealing on the Magnetic Properties of Co2MnSi-Based Heusler Alloy Glass-Coated Microwires. Metals 2023, 13, 412. [Google Scholar] [CrossRef]
- Salaheldeen, M.; Zhukova, V.; Wederni, A.; Ipatov, M.; Zhukov, A. Magnetic Properties of Co2MnSi-based Heusler Alloy Glass-coated Microwires. IEEE Trans. Magn. 2023. [Google Scholar] [CrossRef]
- Salaheldeen, M.; Wederni, A.; Ipatov, M.; Gonzalez, J.; Zhukova, V.; Zhukov, A. Elucidation of the Strong Effect of the Annealing and the Magnetic Field on the Magnetic Properties of Ni2-Based Heusler Microwires. Crystals 2022, 12. [Google Scholar] [CrossRef]
- Salaheldeen, M.; Wederni, A.; Ipatov, M.; Zhukova, V.; Lopez Anton, R.; Zhukov, A. Enhancing the Squareness and Bi-Phase Magnetic Switching of Co2FeSi Microwires for Sensing Application. Sensors 2023, 23, 5109. [Google Scholar] [CrossRef]
- Nematov, M.G.; Baraban, I.; Yudanov, N.A.; Rodionova, V.; Qin, F.X.; Peng, H.X.; Panina, L.V. Evolution of the magnetic anisotropy and magnetostriction in Co-based amorphous alloys microwires due to current annealing and stress-sensory applications. J. Alloys Compd. 2020, 2020. 837, 155584. [Google Scholar] [CrossRef]
- Alam, J.; Nematov, M.; Yudanov, N.; Podgornaya, S.; Panina, L. High-Frequency Magnetoimpedance (MI) and Stress-MI in Amorphous Microwires with Different Anisotropies. Nanomaterials 2021, 11, 1208. [Google Scholar] [CrossRef] [PubMed]
- Astefanoaei, I.; Radu, D.; Chiriac, H. Internal stress distribution in DC joule-heated amorphous glass-covered microwires. J. Phys. Condens. Matter. 2006, 18, 2689–2716. [Google Scholar] [CrossRef]
- Ahmad, A.; Mitra, S.; Srivastava, S.K.; Das, A.K. Size-Dependent Structural and Magnetic Properties of Disordered Co2FeAl Heusler Alloy Nanoparticles. J. Magn. Magn. Mater. 2019, 474, 599–604. [Google Scholar] [CrossRef]
- Elphick, K.; Frost, W.; Samiepour, M.; Kubota, T.; Takanashi, K.; Sukegawa, H.; Mitani, S.; Hirohata, A. Heusler Alloys for Spintronic Devices: Review on Recent Development and Future Perspectives. Sci. Technol. Adv. Mate. 2021, 22, 235–271. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Xu, Z.; Fu, X.; Lu, Z.; Xiong, R. Magnetic and Structural Properties of Sputtered Thick Co2FeSi Alloy Films. J. Magn. Magn. Mater. 2023, 570, 170557. [Google Scholar] [CrossRef]
- Zhang, X.; Han, L.; Dehm, G.; Liebscher, C.H. Microstructure and Physical Properties of Dual-Phase Soft Magnetic Fe-Co-Ti-Ge Alloys. J. Alloys Compd. 2023, 945, 169282. [Google Scholar] [CrossRef]
- Zhang, Y.; He, X.; Xu, K.; Kang, Y.; Sun, H.; Liu, H.; Cao, Y.; Wei, S.; Li, Z.; Jing, C. Structural Ordering, Magnetic and Electrical Transport Properties in Ni60-XFe13+xGa27 Heusler Alloys. J. Alloys Compd. 2023, 936, 168242. [Google Scholar] [CrossRef]
- Mahat, R.; Karki, U.; Kc, S.; Law, J.Y.; Franco, V.; Galanakis, I.; Gupta, A.; Leclair, P. Effect of Mixing the Low-Valence Transition Metal Atoms Y = Co, Fe, Mn, Cr, V, Ti, or Sc on the Properties of Quaternary Heusler Compounds Co_{2-X}Y_{x}FeSi (0). Phys. Rev. Mater. 2022, 6. [Google Scholar] [CrossRef]
- Salaheldeen, M.; Garcia-Gomez, A.; Ipatov, M.; Corte-Leon, P.; Zhukova, V.; Blanco, J.M.; Zhukov, A. Fabrication and Magneto-Structural Properties of Co2-Based Heusler Alloy Glass-Coated Microwires with High Curie Temperature. Chemosens. 2022, 10, 225. [Google Scholar] [CrossRef]
- Zhukov, A.; Ipatov, M.; Talaat, A.; Blanco, J.M.; Hernando, B.; Gonzalez-Legarreta, L.; Suñol, J.J.; Zhukova, V. Correlation of Crystalline Structure with Magnetic and Transport Properties of Glass-Coated Microwires. Crystals 2017, 7, 41. [Google Scholar] [CrossRef]
- Klein, P.; Varga, R.; Badini-Confalonieri, G.A.; Vazquez, M. Domain Wall Dynamics in Amorphous and Nanocrystalline FeCoMoB Microwires. J. Nanosci. Nanotechnol. 2012, 12, 7464–7467. [Google Scholar] [CrossRef] [PubMed]
- Zhukov, A.; González, J.; Blanco, J.M.; Vázquez, M.; Larin, V. Microwires Coated by Glass: A New Family of Soft and Hard Magnetic Materials. J Mater Res. 2000, 15, 2107–2113. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. I. Phys. Rev. 1931, 37, 405. [Google Scholar] [CrossRef]
Figure 1.
Room temperature X-ray diffraction (XRD) diffractograms of Co2MnSi for GCMWs-A and GCMWs-B. The inset illustrate the different atoms distributions of Co, Mn and Si in L21 and A2 structure.
Figure 1.
Room temperature X-ray diffraction (XRD) diffractograms of Co2MnSi for GCMWs-A and GCMWs-B. The inset illustrate the different atoms distributions of Co, Mn and Si in L21 and A2 structure.
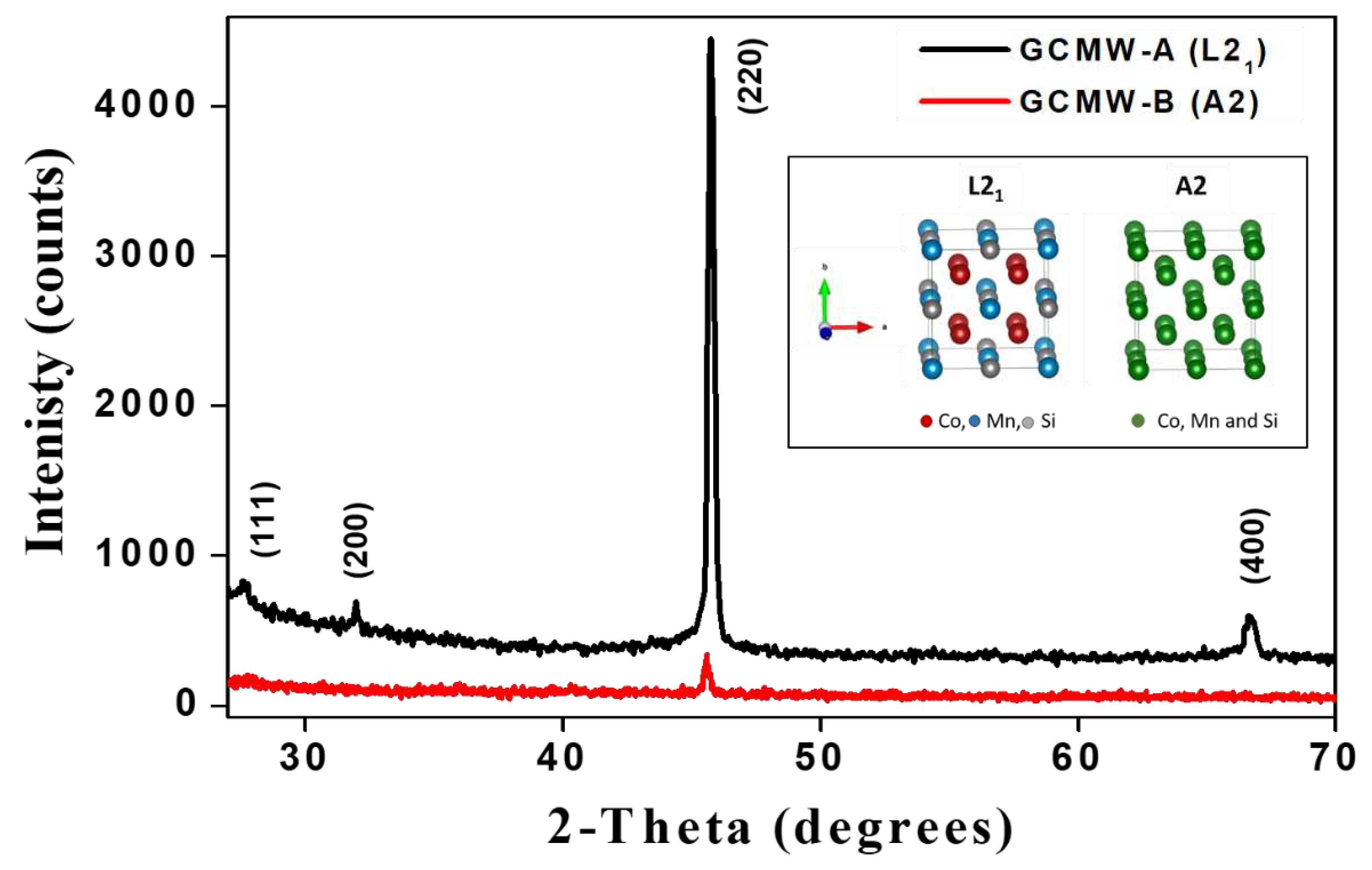
Figure 2.
Hysteresis loops measured at 5 K and 300 K for Co2MnSi GCMW-A and GCMW-B. (The insets show the low scale M-H loops of samples).
Figure 2.
Hysteresis loops measured at 5 K and 300 K for Co2MnSi GCMW-A and GCMW-B. (The insets show the low scale M-H loops of samples).
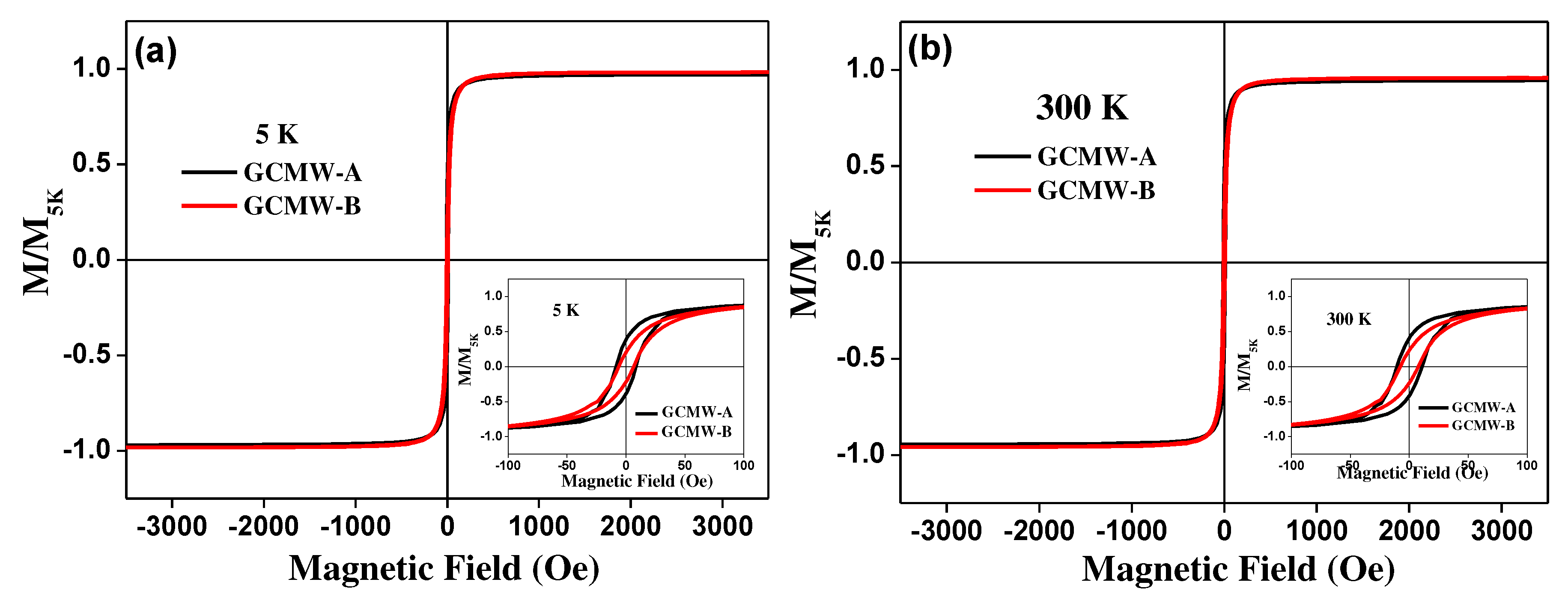
Figure 3.
Temperature dependence of magnetization M/M5K (H) for prepared Co2MnSi glass-coated microwires A and B with applied external magnetic field of 50 Oe.
Figure 3.
Temperature dependence of magnetization M/M5K (H) for prepared Co2MnSi glass-coated microwires A and B with applied external magnetic field of 50 Oe.
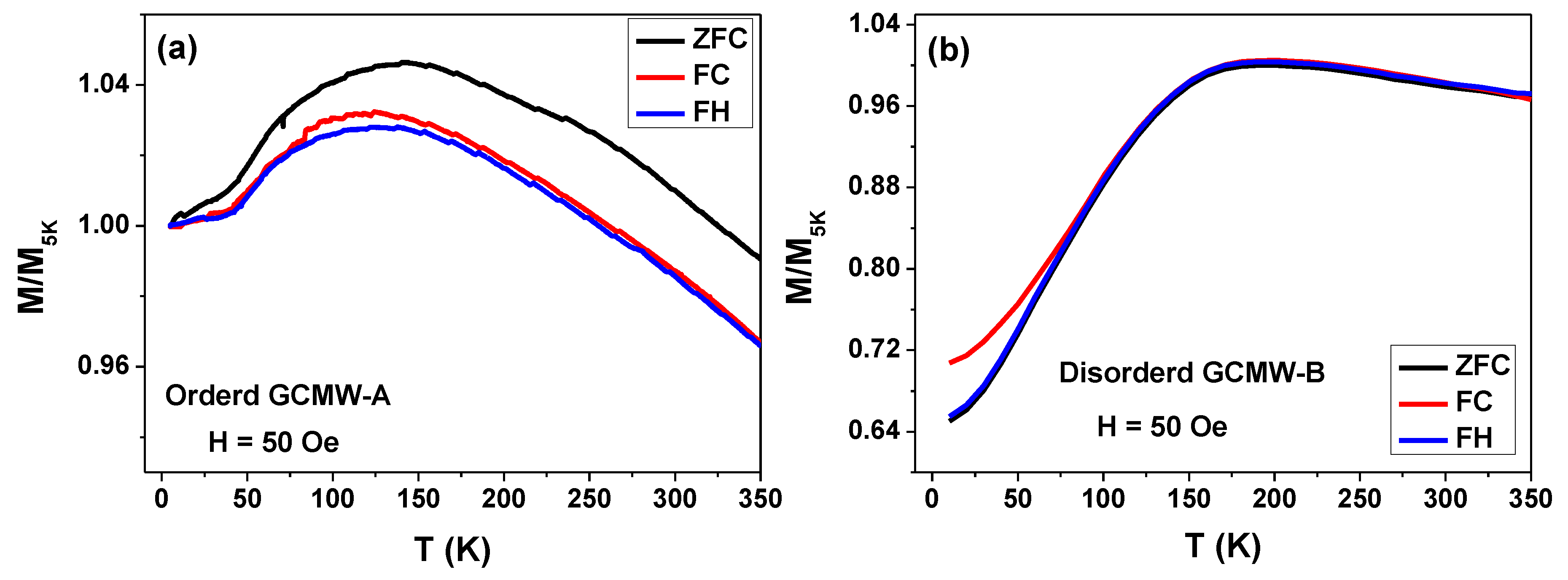
Figure 4.
Temperature dependence of magnetization M/M5K (H) for prepared Co2MnSi glass-coated microwires A and B with applied external magnetic field of 200 Oe.
Figure 4.
Temperature dependence of magnetization M/M5K (H) for prepared Co2MnSi glass-coated microwires A and B with applied external magnetic field of 200 Oe.
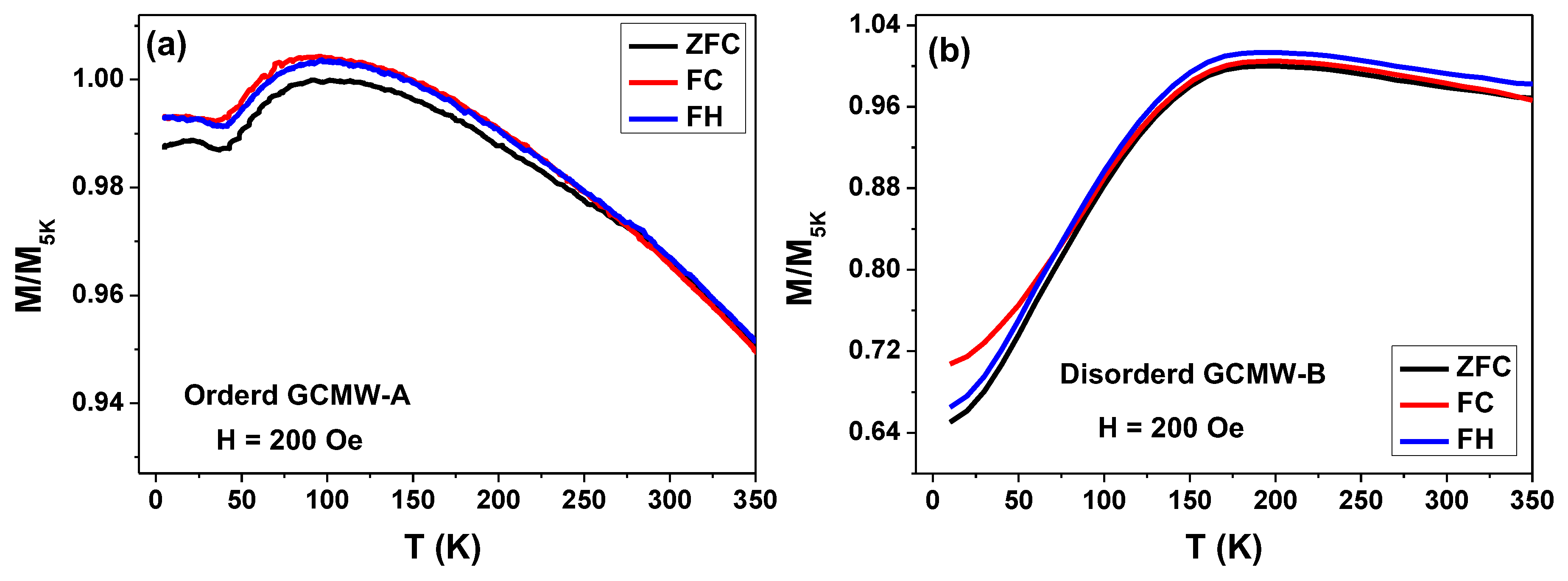
Figure 5.
Temperature dependence of magnetization M/M5K (H) for synthesized Co2MnSi glass-coated microwires A and B with applied external magnetic field of 1 kOe.
Figure 5.
Temperature dependence of magnetization M/M5K (H) for synthesized Co2MnSi glass-coated microwires A and B with applied external magnetic field of 1 kOe.
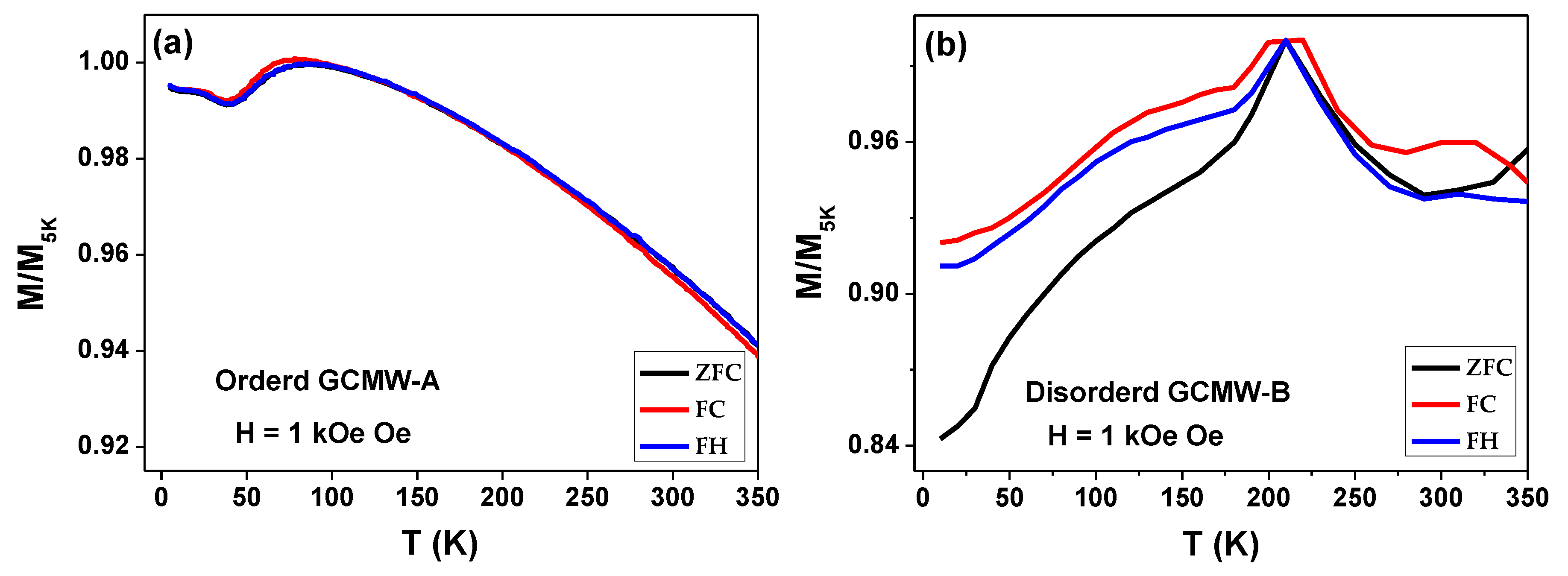
Table 1.
Chemical compositions and different aspect ratio of Co2MnSi glass-coated microwires (GCMWs-A and GCMWs-B).
Table 1.
Chemical compositions and different aspect ratio of Co2MnSi glass-coated microwires (GCMWs-A and GCMWs-B).
| Sample | Aspect ratio (ρ) | Chemical composition |
|---|---|---|
| GCMW-A | 0.31 | Co49.55Mn25.1Si25.02 |
| GCMW-B | 0.46 | Co51Mn23.9Si25.1 |
Table 2.
Crystallographic information of prepared Co2MnSi glass-coated microwires (GCMW-A and GCMW-B).
Table 2.
Crystallographic information of prepared Co2MnSi glass-coated microwires (GCMW-A and GCMW-B).
| Sample | Crystallite size (nm) | Space group | Cell parameters | Strukturbericht Designation |
|---|---|---|---|---|
| GCMWs-A | 36.62 | Fm3¯m (FCC) | a = 5.62 A⁰ | L21 |
| GCMWs-B | 28.07 | Im3¯m (BCC) | a = 2.87 A⁰ | A2 |
1 Tables may have a footer.
Table 3.
Coercivity dependence on temperature of prepared Co2MnSi glass-coated microwires (GCMW-A and GCMW-B).
Table 3.
Coercivity dependence on temperature of prepared Co2MnSi glass-coated microwires (GCMW-A and GCMW-B).
| T(K) | GCMW-A | GCMW-B | P factor |
|---|---|---|---|
| Hc (Oe) | Hc (Oe) | Hc (A)/ Hc (B) | |
| 5 | 11.2 ±0.5 | 7.2±0.5 | 1.6 |
| 20 | 9.7±0.5 | 5.3±0.5 | 1.8 |
| 50 | 9.6±0.5 | 7.1±0.5 | 1.4 |
| 100 | 9.7±0.5 | 6.8±0.5 | 1.4 |
| 150 | 8.5±0.5 | 6.5±0.5 | 1.3 |
| 200 | 9.7±0.5 | 8.2±0.5 | 1.2 |
| 250 | 9.1±0.5 | 8.4±0.5 | 1.1 |
| 300 | 10±0.5 | 9.2±0.5 | 1.1 |
| ΔHc | 2.7 | 3.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated









