5.1. Dedicated Fleet Pricing Problem
In this section, we describe the pricing problem in detail. Let
(
) for
be the dual variables associated with constraints (22) and
(
),
be the dual variables associated with constraints (23). Let
,
be the reduced cost of a complete path
q that is operated by a type
k truck, i.e., a closed loop route that starts and ends at the depot. The pricing problem without strengthened cuts for the problem
can be formulated as follows.
We first write down the calculation of
in (
41) explicitly,
. Here, we use
to denote the number of layovers spent on path
q. A feasible route in
is an elementary path starting and ending at the depot in which every node is visited exactly once, i.e., no loops or subtours exists. However, not all elementary paths are feasible as they may violate the time windows, truck capacities, battery capacity, or the intra-node distance constraints. The recharging time and layover time should be applied on the elementary paths if necessary to check if time windows of the shipments are respected. These resource constraints are required to be defined and traced while extending the paths. The functions that record the constraint-related resources are called
resource extension functions (REFs , see Desaulniers et al. (1998)).
Problem (
41) aims at finding a feasible dedicated fleet route with vehicle type
k with the minimum reduced cost. The arc cost
for
is replaced by a defined edge cost
, where
. In order to include the three types of cuts, the reduced cost of the pricing problem needs to be adjusted accordingly. Firstly, let
be the dual value associated with the 2-path cuts (
39) and
be the dual value associated with the generalized multistar cuts (
40). Then, for a given shipment candidate set
S,
and
are subtracted from the reduced cost
of all arcs
, such that
. Therefore, we have the modified reduced cost for columns of type-k vehicle in the RMP as follows.
Similarly, consider a violated SR inequality of the form (
35), defined by a subset of three shipments
,
, and
as its associated dual value. Since
is negative, it will act as a penalty. Because the terms of SR inequalities are summed over the “rows", the penalties cannot be added directly to each arc. The value
must be subtracted from the reduced cost
each time a new column
q is passed to the master problem but the column revisits shipments in
that define the violated SR cuts. Therefore, an additional resource is required for each violated SR cut to indicate the regeneration times of the shipments. Note that we know such a column is regenerated only if completed, because the total demands fulfilled and other shipments on route could possibly change the left-hand side of the cuts. We have the updated reduced cost for the type-k column as below.
In this setting, the subproblem corresponds to an elementary shortest path problem with resource constraints (ESPPRC) that can be solved by dynamic programming using a labeling algorithm, see Feillet et al. (2004). This well-known method has been successfully applied to many problems in routing and scheduling. Compared with labeling algorithms for other VRP variants in the literature, solving the pricing problem for MVRPC is differentiated by the following factors: 1) multiple REFs are extended separately by truck type k; 2) additional resource constraints are extended to satisfy the working time regulations, recharging needs, and recharger information; 3) necessary layovers and recharging add difficulties to the dominance tests. Moreover, we must be careful about the complexity arisen by these additional constraints. In fact, Dror (1994) has proved that the ESPPRC is strongly NP-hard for VRPTW.
Theorem. The ESPPRC for MVRPC is strongly NP Hard, whereas the SPPRC without elementarity can be solved by route-relaxed dynamic programming in pseudo-polynomial time.
Proof. The idea of NP-hardness proof is attributable to Dror (1994). The dynamic programming backward recurrence for a type-k truck of ESPPRC for MVRPC can be stated as:
where
denotes the minimal reduced cost of the partial route going from the depot up to node
i,
S is the node set selected for route
q, and
t is the time ready to leave node i while
is the time spent on the arcs to travel and service. From the constructions of the recurrent function and the graph
G, if there exists a feasible shortest path solution from 0 to
for VRPTW on graph G, then there is also a feasible ESPPRC solution satisfying the constraints in (
44) for MVRPC. Since the shortest path problem is NP-hard, and we found a polynomial transformation from Dror (1994) to our elementary path problem, our problem is NP-hard as well. Note that, the exact dynamic programming approach in solving ESPPRC yields an exponential number of possible states
.
However, if we shrink the state space by retaining only the m closest shipments to the current end point of the partial path q, which can be visited before i, and relax the elementary path requirement, then the dynamic programming algorithm only explores a pseudo-polynomial number of states between 0 and ). This method is called ng-relaxation. Another known relaxed method is state relaxation where only the solutions with minimal cost are stored and extended at each state. Details refer to Baldacci et al. (2011); Righini and Salani (2008). Therefore, SPPRC is solvable by a route-relaxed method, which gives the lower bound to the solution. This will lead to the effective labeling algorithms we discuss in the following sections. □
We first review the basic concept of labeling algorithm (Irnich and Desaulniers (2005)). In this method, labels are generated and updated to represent partial paths that start at the depot 0. Starting from an initial label associated with node 0, paths are constructed iteratively by extending its label and its descendants forward/backward on graph G. These extensions of a label relay the updates of REFs along an arc. In each iteration, a new extended label is checked for feasibility with respect to the defined critical resource (Feillet et al. (2004)) constraints. If the label breaks any critical resource, it is discarded. To avoid enumerating all feasible partial paths, different dominance criteria are developed and applied to speed up the labeling algorithms. This concept is similar to pruning a tree while eliminating partial paths that cannot generate solutions better than the current bounded minimal reduced cost and pruning for further fathom. When labels are generated in one direction from the origin to the destination, a so-called mono-directional labeling search is performed.
Probably inspired by the method of Divide and Conquer, Righini and Salani (2008) designed a new bidirectional labeling algorithm, in which forward and backward labeling are performed simultaneously often yielding considerable computational time reduction. In this case, the critical resources have to be non-decreasing along the path. In other words, the triangle inequality must be satisfied. For MVRPC, this is indeed the fact, because time windows, truck capacities, layover time accumulations, and total required electricity are all suitable monotone resources. However, the intra-node distance constraint (18) does not satisfy the triangle inequality, i.e., even if for the current partial path q with end node i, j could also be feasible for later extensions of the path. Moreover, a midpoint is required to be specified. For instance, if we choose time windows as the resource, any can be a candidate midpoint. Bidirectional labeling algorithm works in three steps. First, labels are extended forward from the sink to the midpoint M; second, labels are extended from destination backward to M; third, two labels are merged and checked for feasibility.
We will discuss how to develop efficient mono-directional and bidirectional labeling algorithms for MVRPC in the following sections.
5.2. Mono-directional Labeling Algorithm
In this section, we describe the mono-directional labeling algorithm for the ESPPRC, where the reduced cost of the subproblem is defined by (
43) with the three strengthened cuts. The labeling algorithm seeks to find a negative reduced-cost route that is feasible with respect to truck capacities, time windows and the current U.S. hours of service regulations.
The forward label search concept discussed here involves a relaxation technique, in which the state space explored by the exact dynamic programming method is projected onto a lower dimensional space, so that certain “non-critical" nodes are allowed to be visited several times. Different from normal VRPTW or EVRPTW, the pricing problem of MVRPC requires additional resources to keep track of the accumulated work time since the last layover and the remaining time to reach the next customer
j. Goel and Irnich (2014) has illustrated that it is effective to use the minimal layover time when updating the time REFs and add necessary hours to each layover later on to avoid waiting time. We adopt the same idea and incorporate the possible recharging time for EV routes. In a forward mono-directional labeling algorithm for MVRPC, each label
L corresponds to a partial path
q starting at the depot 0 up to a node
. In the following descriptions of labeling algorithms, we will keep using
as a duplicate of the depot, which is the destination of each route. For a type-k truck, a label
is defined by the following attributes:
|
Reduced cost of partial path q. |
|
Accumulated demand fulfilled by partial path q. |
|
Number of recharges performed along path q. |
|
Service start time at node when reached through partial |
| |
path q. |
|
Accumulated electricity consumption (in hours) from depot or a |
| |
recharger up to node i along the partial path q. Note this resource |
| |
is renewable. |
|
A dummy resource variable that records the number of times any |
| |
critical shipment is visited along path q. The path is |
| |
elementary only if . |
|
Accumulated elapsed time (hours) since the last layover (or depot |
| |
if no layover). |
|
Accumulated working time (hours) since the last layover (or depot |
| |
if no layover). |
|
Number of layovers the driver has taken up to node i. |
|
The latest possible time point to which the end of the last layover |
| |
period can be extended to i without violating any |
| |
resource constraint. |
|
A vector that stores the visited nodes along partial path q. |
To further shrink the searching space, we introduce the idea of unreachable nodes, see Feillet et al. (2004). In the pricing problem of MVPRC, our considered critical resources obey the triangle inequality. Then, we can identify the nodes that cannot be visited by any extension of because the time window and the capacity constraints are violated. These nodes are called unreachable by the label. If a label is assigned by an ICV, all of the available rechargers will not be considered in the search algorithm, and the corresponding REFs are set as 0. When a node is set as unreachable by a label, the dummy resource variable , i.e., as if the node n had been visited. Feillet et al. (2004) observed that setting to 1 will not change the structure of the label search but will reduce the computational time. Therefore, we define another attribute as the infeasible set that cannot be extended from the current state . That is, . In addition, we introduce as a candidate set of arcs that are feasible to be explored. Its definition will be introduced later in the section on implementation strategies.
In the initial state at node 0, all attributes of the label
L are set to 0 except for
, which is equal to
∞. The extension of a label
=
,
,
,
,
,
,
,
,
,
,
,
along an arc
is performed for each vehicle type
k using the following REFs:
While updating the time resource
, we need to consider the possible recharging time and the viable layover time. We first define an alert indicator
passing through the arc
to check whether or not the service hours regulation is broken, where
. A direct extension from
i to
j can be performed only if
, otherwise, a layover must be added since the service hours regulation is about to be violated. Considering the two situations, we define the REF for
as:
Note that in REF (49),
for all partial path
q that travels by ICV. Next, we define a function named
to measure the feasibility status of
for the current label
. If the time window and capacity resources are not violated, then this function returns 1, otherwise, it returns 0.
REF (53) explains how prolonged layover period(s) can be added to a partial path. For every non-depot start node on a partial path, we assume it is delivered at its beginning time window
. The layover periods are specified whenever needed with the minimum hours
as shown in REFs (
48) and (52). By this scheduling policy, we avoid times during which the driver is not productive. However, this may also cause early arrivals due to time window constraints at subsequent shipments and thus miss some valid routes. By lengthening the duration of the layover periods between
, we allow the possibility of measuring the before-missed routes. However, the arrival time at already routed subsequent shipments may be pushed out of their respective time windows. We therefore must calculate the resource values of
indicating the maximum amount by which the duration of a layover can be extended without violating any resource constraints. REF (54) says that the latest end time
of the last layover can be updated by minimizing values between the current latest time
and the latest possible end time of the last layover without violating node
j’s time window. In some cases,
is allowed to be deferred, such that we use the term
to represent the arrival time at
i. Let the term
be the work and potential layover period between
i and
j. As shown in (54),
is the truncated working time left after an immediate layover. Then, the duration of the latest layover can be lengthened by any value less than or equal to
. In other words, at each state, only if the following condition (
56) is satisfied can we continue extending the label.
Because, if a layover is applied on the corresponding arc
the layover period can only be adjusted between
. For arcs
that do not take any layover either because the work time limit is never hit or because layovers have been taken in previous states, based on our policy, the current time can still be adjusted to satisfy the time window constraints for subsequent nodes. Therefore, whether or not there is a layover added on the arc, we need to check the following condition to ensure adjusting the time resource
is feasible.
When checking whether or not a new label extension from
i to
j satisfies the time window resource constraint, we initially need to check if
is feasible. Next, suppose (
56) and (
57) are not violated under the defined situations, we should update the current route time
to ensure the earliest acceptable time
is respected.
In each label extension, the REFs defined in (
45)-(
58) are updated by the following sequence.
The label =, , , , , , , , , , , resulting from this extension is deemed feasible if , , , and for all . If failed to pass any feasibility check, it is dropped.
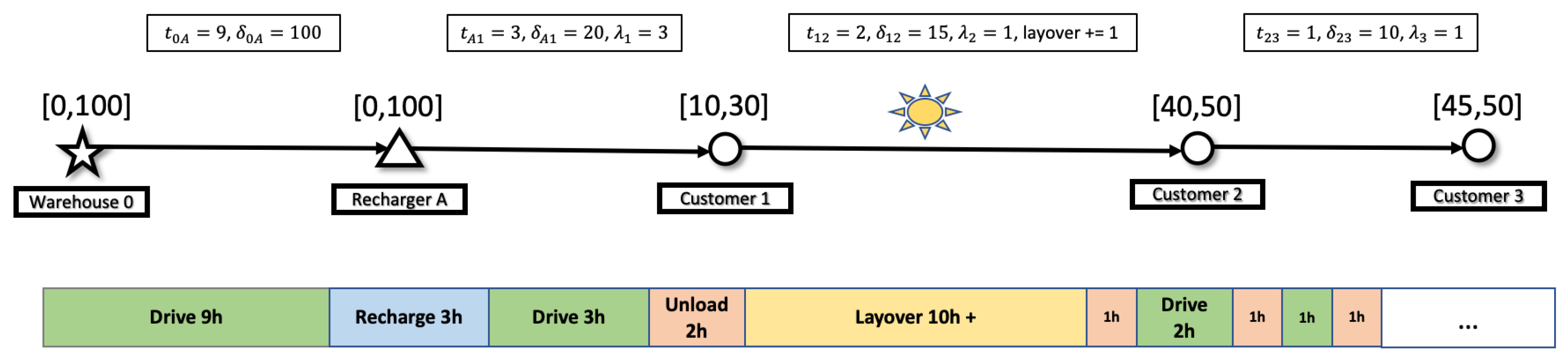
Example 2. Figure 1 illustrates an example of extending a partial path following the above defined REFs. For a fully rested driver at depot, we set and assume all the EVs are fully charged to a battery level of . We also assume the accumulated demands of customer 1,2,3 fit the EV capacity . The time window for each node is given, e.g. . The travel time, electric consumption, and service time are stored in parameters , , and , respectively. The “sun" on the arc from customer 1 to customer 2 means there is a layover required. Given the charging rate , maximum-allowed working time before a layover , and layover period , the forward path generated by updating the corresponding time-related REFs in the network is as follows:

The forward propagation starts from the depot 0, then through recharger A and customer 1. No time adjustment is performed on these two states due to and both time windows are fitted. When reaching customer 2, a layover is enforced because the accumulated work time . In addition, the current time needs to be adjusted since otherwise the path would have arrived before otherwise. Similarly, is adjusted. The numbers are calculated recursively by updating and .
Note that all REFs are non-decreasing functions. Hence, a standard dominance rule can be applied here, see Desaulniers et al. (1998). Another useful dominance rule arising by introduction of the layover constraint can be derived from the results of Tilk (2016).
Proposition 5.1 (Rule 1.)
. Define two labels and associated with the same node i. Then, label is dominated by label only if all the following conditions are satisfied and at least one of the inequalities is strict. Therefore, can be discarded.
Proposition 5.2 (Rule 2.)
. Define two labels and associated with the same node i. Then, label is dominated by label only if all the following conditions are satisfied and at least one of the inequalities is strict. Therefore, can be discarded.
Recall that the resource
only stores the visiting information for “critical" shipments, i.e., the shipments visited more than once are marked as critical and the labeling algorithm repeats until all the optimal routes are elementary. The so-called decremental state-space relaxation (DSSR) was initially proposed by Righini and Salani (2008). Let
be the set of critical shipments found in the current iteration. Let
be the set of critical shipments in the optimal solutions discovered by the DSSR labeling algorithm, where non-elementarity is allowed. In each iteration, we update the set
by
. This iteration procedure is repeated until the sets
becomes empty, and we reach an optimal solution for the ESPPRC. Algorithm 1 shows a generic version of this forward labeling algorithm for the pricing problem of MVRPC.
is the list of forward states associated with node
i.
is the set of nodes to be checked and extended. And
is the set of critical shipments found up to the current iteration plus the unreachable nodes for each. The function
returns the set of nodes that cause the cycles in the current
n optimal paths. The parameter
n is set to 3 in our study.
|
Algorithm 1:Bounded forward search with decremental state-space relaxation |
 |
5.3. Bidirectional Labeling Algorithm
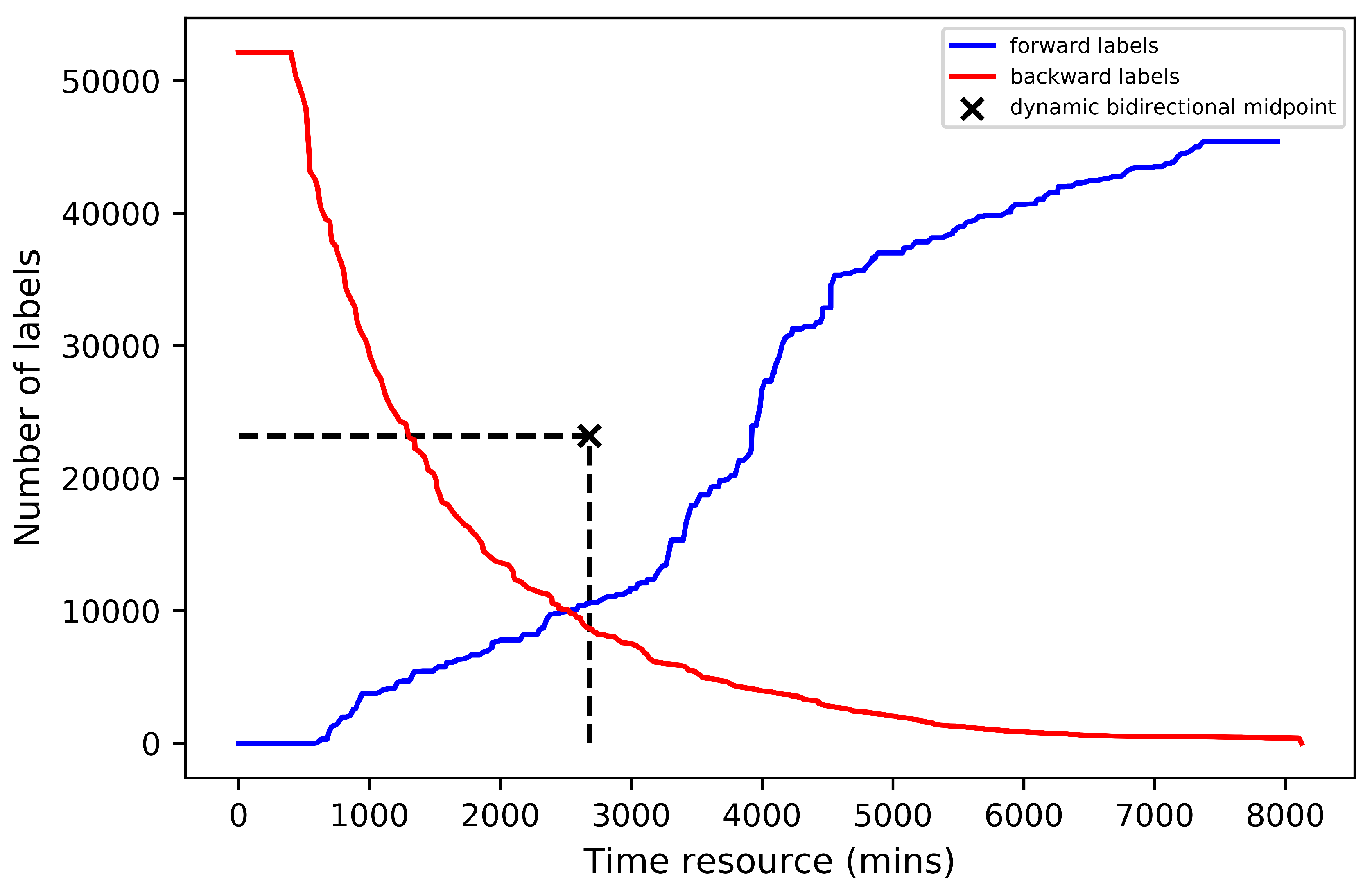
Bidirectional labeling algorithms are widely used in solving the pricing problems of VRP variants. They are especially beneficial in mitigating the explosion of labels, see Tilk et al. (2017). It has been observed in Righini and Salani (2006) and many more recent works that the bidirectional labeling algorithms are usually superior to their mono-directional counterparts and lead to substantially improved computational times for solving related SPPRC. When running a bidirectional algorithm, both forward partial paths and backward partial paths are created and extended alternatively. Each direction is processed up to a so-called “halfway point" (Righini and Salani (2006)). The halfway point is the midpoint of the domain of a monotone critical resource, e.g. for our case. Recall that along a partial path the time-related and load-related resources are all monotone. Along a forward path, the arrival times and the accumulated demands are non-decreasing. This standard bidirectional search mechanism with fixed halfway point has been adopted as almost a quasi-standard for solving ESPPRC. However, when it comes to renewable resources, such as EV recharging, Tilk et al. (2017) observed the number of forward and backward labels can differ significantly due to the fixed halfway point setting. Since MVRPC involves two renewable resources, i.e., EV recharging and replenishment layovers, we decide to adopt a dynamic halfway point scheme as in Tilk et al. (2017) to combat the potential unbalanced extensions. In our work, we choose to use time windows as the critical resource because it considers the layover resources and is more restrictive than the demand resource. In fact, the more restrictive the monotone resource is, the more effective is bidirectional labeling.
It is worth noting that the relaxed bounded bidirectional search with forward and backward propagations may result in either feasible or infeasible complete paths because of cycles. As can be seen from
Figure 2, both forward and backward extensions can result in cyclic partial paths (top); even if the two partial paths are elementary, because certain shipments may occur in both paths, a cycle can be produced by joining them (e.g., shipment
k in the bottom panel). This issue can be addressed by a modified DSSR feasible check, which will be discussed later.
5.3.1. Dynamic Halfway Points
We start with the definitions of necessary components for the bidirectional search. The upper bound of the halfway point of the time resource is initialized as . is the halfway point for the forward search, which indicates half of the latest possible return time to the depot. Then, the forward search proceeds as in Algorithm 1 only if its does not pass the forward halfway point . As for the backward extension, the search direction is against the travel direction. The extension of the critical resource will be proceeded towards the lower bound of the halfway point , which is initialized as . Let be the adjusted backward time resource. Every time a forward label is extended, the backward halfway point is updated by the following rule to . Alternatively, when a backward label is extended, the forward halfway point is updated to . Note that the forward halfway point remains non-decreasing whereas the backward halfway point remains non-increasing. The two alternative updating steps ensure that , which guarantees the optimality. In addition, the initial values of and restrict the evolution of the dynamic halfway point to lie in the interval . If we initialize , then this becomes the standard fixed bidirectional labeling algorithm.
5.3.2. Backward Resource Extension Functions
Although the REFs for backward search are defined similar to the forward search, some adaptions need to be made. Consider a backward path traveled by an EV,
, that requires a visit to the recharger
. Then,
is named the “next recharger" of
q, which implies there is no additional recharging visit between node
i and
. The amount of electricity consumed from
i to
varies while we extend the label backwards. We need an additional resource
for the sake of merging forward and backward labels. This resource is the maximum available recharging time for
, assuming that all time windows along path
are respected. Moreover, whether the working hours hit the limit is unknown as well because it depends on the schedules from 0 to
i, which are performed by the forward search. For a type-k backward path
, the label
is defined by the following attributes:
,
,
,
,
,
,
,
,
,
,
,
,
. In order to use the similar REFs definitions as in forward labeling procedure, we need the following adaptions.
|
Reduced cost of partial path q. |
|
Residual space on the truck, which equals to the accumulated |
| |
demand from except at the last node i. |
|
Negative number of recharges along path q except at node i. |
|
Latest arrival time at without breaking any time window. |
|
Accumulated electricity consumption from or a recharger back |
| |
to node i along the path q. Note this resource is renewable. |
|
A dummy resource variable that records the number of times any |
| |
critical shipment is visited along path q except node i. |
| |
Let the value be 1 if unreachable, which indicates |
| |
or . |
|
Accumulated elapsed time (hours) from the next layover ( if no |
| |
layover) to i. |
|
Accumulated working time (hours) from the next layover ( if no |
| |
layover) to i. |
|
Negative number of layovers the driver has taken from to i. |
|
The latest possible time to which the end of last layover period |
| |
can be extended to j without violating any resource constraint. |
|
Maximum flexible period that can be used for the next recharge |
| |
that satisfies the time windows while running EV on the path. |
|
A vector that stores the visited nodes along backward path q. |
The backward labeling procedure starts from node
with the initial values assigned to each resource of
, where
,
,
(and
if
), and the other resources are all set to 0. REFs for
,
,
,
,
are defined the same as
,
,
,
,
. If the backward path is assigned by an ICV, then
. Again, nodes are
unreachable to the current label if and only if the time window and/or the truck capacity are violated.
is also the same as before except that we use
to substitute
in the forward labeling procedure. Other resources of a label
along a backward arc
are extended towards
by the following REFs. Moreover, we introduce the feasible arcs list
on the inverted network, follow the same logic as forward search. Details are elaborated in
Section 5.4.1. Note that the extension will be proceeded from
backwards before
hitting the lower bound of the halfway point
.
REFs (
59), (63)-(65) are similar to their forward counterparts, yet are propagated in an inverted direction. The unloading times at the current
j are not taken into account in computing the resources. Furthermore, when the recharging activity happens right before a layover (in the reversed chronological order), the recharging time
at recharger
i should not be considered in the calculations of
. The reason is that this activity happened before the layover period and the truncated elapsed time should only track the driving and unloading time afterwards. When checking the time resource feasibility, each time window at shipment
i will be shifted by
to
. Since the time windows for the rechargers are relaxed, a labeling extension to rechargers always satisfies the time window constraint. Moreover, even without any layover associated with a backward arc
, the current time
, which may be greater than
, can be adjusted to fit into the time window if and only if
. Therefore, the updated current time for the backward path is:
The sequence of extending and checking the backward REFs are the same as discussed for the forward labeling procedure. The resulting label , , , , , ,
, , , , , is deemed feasible if , , , , and for all . If failed to pass any feasibility check, it is dropped. Now let us consider another straightforward example which shows the consistency and difference between forward and backward labeling.
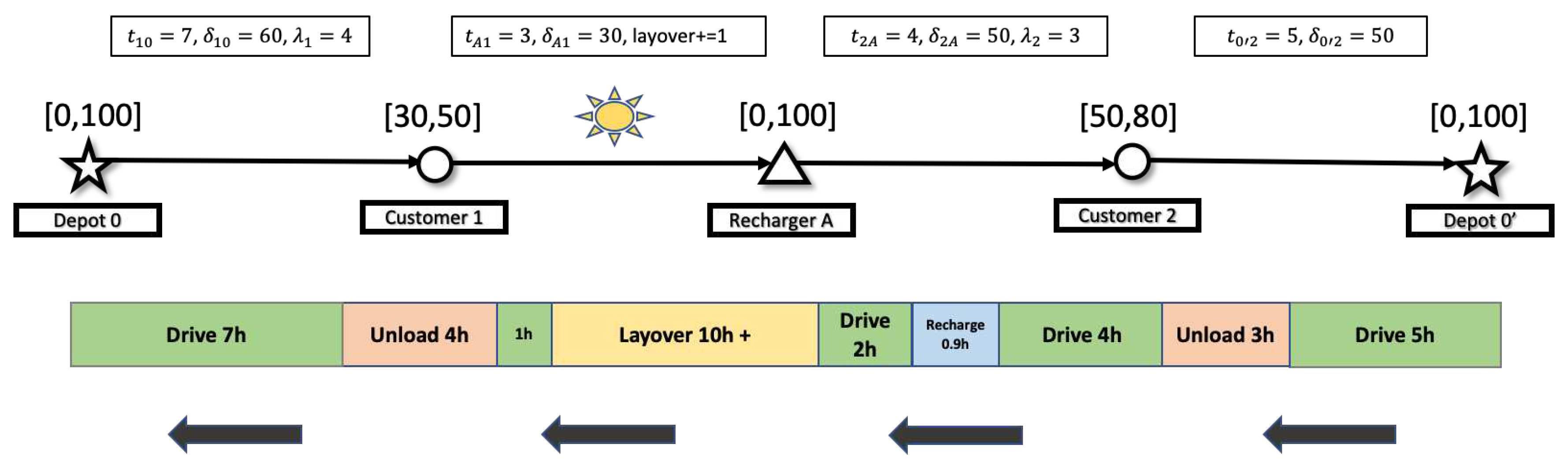
Example 3. Figure 3 shows another complete EV route with a single visit to rechargers. The route is built by the backward extension. Other configurations are the same as Example 2 except for the parameter values. In this example, the route generated from the backward propagation can be exactly reproduced by the forward extension. However, the detailed schedules (arrival time and layovers) may or may not be different. This allows generation of diverse columns while keeping the number of labels lower than mono-directional searches. The aroused issues such as infeasible routes after merging the partial paths can be offset by the framework of dynamic halfway points.
The backward extension starts from the copy of depot , then the extension follows the above-defined REFs and the depicted time windows, travel time, power consumption, and unloading time. After the first two extensions, this label arrives at node 1. The resource needs to be adjusted to fit in the time window. Also, the resource is updated reflecting a minimum recharging of the power consumed on arc . indicates how much additional electricity can be assumed on the paths ahead, which have not yet been determined. The extension along arc yields , , , , . This example illustrates how recharging time should be eliminated from the calculation . In fact, recharging is not taken into account for the hours of service regulation and is only used for tracking the current time. Indeed, even if the recharge at A was additionally required for up to units of time due to other possible extensions, would be set at . The adjusted time would still fit into the time window, which is set at .
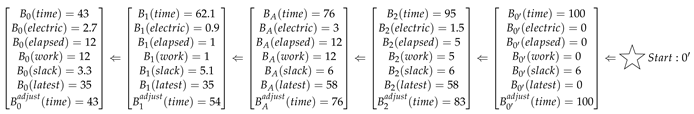
To avoid explosion of backward labels, the two dominance rules introduced in Rule 1. and Rule 2. are still valid for the backward counterparts. The only difference is that certain non-decreasing monotone resources become non-increasing. To apply the two dominance rules, apart from changing all resources from to , we need the following adaptions. First, the signs of the time resource (), the number of recharges resource (), and the layover resource ()) are switched from ≤ to ≥. Also, the sign of is reversed from ≥ in forward search to ≤. Second, according to Desaulniers et al. (2016), all strictly negative values of are equally good. Therefore, REF (60) can be strengthened to . Similarly, REF (62) for the layover resource can be strengthened in the same way to . Finally, the dominance criteria for the backward resource is added, i.e., for label dominated by label .
5.3.3. Merge Forward and Backward Paths
In bidirectional labeling algorithms, labels are propagated to the halfway point. If either bound of the dynamic halfway point stays at the initial position, then a mono-directional labeling search is performed. Sometimes, it is also beneficial to make an adjustment such that more columns with negative reduced cost can be priced, although in the most cases halfway points are updated towards the middle of the critical resource. Once the forward labeling and the backward labeling extensions are completed, forward and backward labels are joined together at the halfway point to form complete paths. Suppose there are two labels and representing a forward and a backward path, respectively, ending at node i. Merging these two labels yields a complete origin to destination path with reduced cost . The path is feasible if and only if the following conditions are fulfilled:
- 1.
, where is the set of critical shipments that maintain elementarity.
- 2.
The path respects the vehicle capacity: .
- 3.
-
The path is feasible with respect to the time resource. The feasibility should be considered by two distinct cases.
-
Case 1.
The backward path from to visits at least 1 recharger, i.e., , and .
-
Case 2.
-
The backward path from to visits no recharger, i.e.,
, and
.
- 4.
The accumulated working time does not break the hours of service regulation: .
After the merge, we perform a final dominance test with Rule 1. and Rule 2. for all merged routes. The non-dominated routes with negative reduced cost are candidate columns for the RMP.
5.3.4. Generic Structure of the Algorithm
The bidirectional labeling algorithm updates the two bounds of the halfway points towards each other. Apart from the extension mechanism introduced in the previous sections, it is important to determine criteria for how to alternate between forward and backward labeling so that the overall performance of the algorithm can be guaranteed. An ideal strategy is to choose the direction which may minimize the overall computational time. Tilk et al. (2017) suggest that a heuristic be added by choosing the direction with smaller number of already generated labels. This heuristic is also added in a function of our algorithm, which is named
.
if it chooses to do a forward extension. Otherwise,
. However, purely relying on this simple heuristic may cause too many infeasible merges. To overcome the issue, we collect
and
that are produced in the current iteration, such that no merge is possible for those labels, and store them into a list
. After finishing the procedures of merge and feasibility check, the algorithm will extend the labels from
in a monotone direction until they approach the depot (0 for backward and
for forward). In particular, if infeasibility has arisen due to the violation of service hour regulation, we continue forward extension from this state in the following iterations. For simplicity, we denote the operations for the forward REFs (
45)-(
58) as
and the corresponding operations for the backward REFs as
. Let
equal 1 if the merge of a forward and a backward label at node
i passes all the conditions, and equals 0 otherwise. Once a complete route is merged, we store the feasible route
q in a set
F. The selected routes in
F with negative reduced cost will finally be passed to
in the RMP. With these additional notations, the bounded bidirectional labeling framework is given in Algorithm 2. The forward and backward functions are shown in Algorithm 3.
|
Algorithm 2:Bounded bidirectional labeling algorithm |
 |
|
Algorithm 3:Forward and backward search steps |
 |
5.5. Modified Dominance Criteria
Consider the dedicated fleet pricing problem of the format (
41). Recall that the 2-path inequality and the multistar inequality are both robust, The reduced cost changed by adding them to the RMP can be decomposed by arcs on the subproblem network, as shown in (
42). However, applying the SR inequality interrupts the search space and the feasibility of the generated columns, see Jepsen et al. (2008). The dominance criteria developed in Rule 1. and Rule 2. are no longer valid. The two rules need to be modified to capture the dual values invoked by the SR inequality (
35). During the execution of the modified algorithm, we need only to consider non-dominated paths.
By solving the separation problem (
38), we get a SR inequality (
35) with the modified reduced cost shown in (
43). Set
is of cardinality three and
. Using the notations of labels, we can express the coefficient of the dual value
applied on the current partial path by
. Then, the first improvement on the two dominance criteria is produced by substituting the conditions
and
by
. In fact, this means the possible space of extensions for label
is larger than that for label
. As further cuts are identified and added, Rule 1. and Rule 2. will not be effective as in the initial stage because penalties had already been imposed. Therefore, rare conditions in the two rules are satisfied. In order to overcome this problem, we note the following property of (
43).
Therefore, we define
after the last dual penalty has been applied on the reduced cost by delivering
demands through set
S. In the case that
dominates
,
, and
. Thus,
, given
. Only demands after the last penalty towards the target node will be affected, see Jepsen et al. (2008). Considering two labels
and
, then the larger the
, the sooner will the corresponding label incur another penalty to the reduced cost. We define the following set:
where
denotes combinations of the set
S found by the separation optimization that induce active SR inequality (
35). The dominance criterion Rule 1. can be strengthened to:
Proposition 5.3 (Rule 3.).
Define two labels and associated with the same node i. Then, label is dominated by label only if all the following conditions are satisfied and at least one of the inequalities is strict. Therefore, can be discarded. denotes the modified reduced cost of label q imposed with SR inequalities.
Proof. Consider any possible extension
. Because for any
we have
, the future coefficients for the dual variables maintain the following relationship.
Since
, the left-hand side of
69 is at most one unit larger than the right-hand side, which means label
can conduct at most one more
penalty to the reduced cost than
. This lead to:
Because we allow multiple SR inequalities to be added in a single iteration, this indicates is satisfied. The other conditions are ensured by Rule 1. Hence, label is dominated by label . □
By similar adjustment of Rule 2. we can reach a modified dominance criteria Rule 4.
5.6. Branching Rules
When the subproblem does not pass any columns with negative reduced cost to the RMP, the LP solver provides us the optimal solution for the linear relaxation of the set partitioning reformulation. If the solution is integer and all the constraints are respected, this solution is also optimal for MVRPC. Otherwise, the solution is fractional and a branch-and-bound tree must be explored. Additional columns could be generated at each branch. In our implementation, we refer to the best-bound strategy used by Desrochers et al. (1992) and Dabia et al. (2019,a). Note that all the branching decisions are made based on the arc-flow formulation
. The variables are projected by equation (
25). The branching strategy can be separated into multiple levels: (i) we start with branching on the outsourcing decision variable
. The algorithm finds the
that is closest to 0.5 in each iteration and creates two branches
and
. When the variables
are integers for all
, we proceed to the next level of branching. (ii) The algorithm branches on the number of vehicles
over all vehicle types and sizes. Two branches are created,
and
, where
is the optimal fractional solution at the current branch. (iii) If the number of total vehicles is an integer, then we decide to branch on the number of routes per truck type
k. We choose the truck type
k for which the fractional part of the number is closest to 0.5. Thereafter, a branch is created,
and
. (iv) If the previous two numbers are both integers, we start branching on the number of recharges. First, we choose to branch on the fractional portion of the total number of visits to
that closest to 0.5. Then, a branch on each location of the recharger is created follow the same logic. For every branch created up to this stage, the decision is imposed by adding the associated inequality to the RMP. The corresponding dual values of the added inequality need to be transferred to the reduced cost of the related columns. Each time the past four branching strategies are utilized, the current solution is no longer feasible, which means a reoptimization is required on the linear relaxation.
Next, branching decisions are taken on the arcs of the subproblem network. (v) we check the pair of such that is closest to 0.5, and imposes two branches and . (v) Finally, among all arcs with a fractional value in the current solution, we choose several close to 0.5. Ties are broken by preferring arcs with higher cost . Incident arcs to j on vehicle k are removed temporarily from the graph G if is set to 1. The branch-and-bound tree is enumerated according to the impact of the branching decisions on the two child nodes of the candidates. In other words, each time we reoptimize the RMP, the increase of the lower bounds of the two child nodes are measured, and the maximum is chosen as the next move. The number of branch candidates is set as 20 in our study. We adopt the hybrid search technique used by Desaulniers et al. (2016), in which subtrees will be explored only if their father nodes’ lower bound is within a gap of of the current best lower bound.
This process is repeated until the entire search tree is explored.