Closed Form Solutions to a Class of Pursuit Problems Using Geometric Analogies

Preprint

Article

Closed Form Solutions to a Class of Pursuit Problems Using Geometric Analogies

Altmetrics

Downloads

184

Views

Comments

This version is not peer-reviewed

Submitted:

25 January 2024

Posted:

25 January 2024

You are already at the latest version

Alerts

Abstract

This article studies a class of pursuit problems admitting both a simple geometric solution as well as a more general analytic treatment. The results are specialized to demonstrate solutions to certain elementary problems typically posed to high schoolers, although a full analytic treatment, requiring some more comfort with geometry and calculus, is typically avoided at that stage.

Keywords:

Subject: Physical Sciences - Other

I. Introduction

Pursuit problems are of critical importance in several engineering and science applications today, including navigation, warfare, and so on. The study of these problems were first motivated by the problems of navigating ships in the age of exploration [1,3]. The Apollonius pursuit problem was defined as that of finding whether a ship leaving from a point A with a constant velocity v_A will intercept another ship leaving from point B with a constant velocity v_B. The situation of adaptive pursuit, where the pursuer maneuvers their “ship” adaptively according to position of the pursuee, was first studied by Bouguer [6], who derived the so-called “radiodrome” as the curve of best pursuit.

More recently, this problem has been generalized in various ways, for example, allowing for variable speeds of the pursuer and the pursued, adaptive strategies for the pursued, energy constraints on the pursuer and pursued, as well as errors in observation and imperfect information. For a detailed survey on these various generalizations and constraints, we refer the reader to [2,5,6,7,8] and references therein.

In this work, we look at a class of pursuit problems admitting a simple geometrical argument for establishing the locus and further generalize the result using analytic arguments. We demonstrate that certain popular challenge problems typically posed to senior high school or freshmen undergraduate students in physics admit simple solutions as special cases of these results.

II. Problem setup and main results

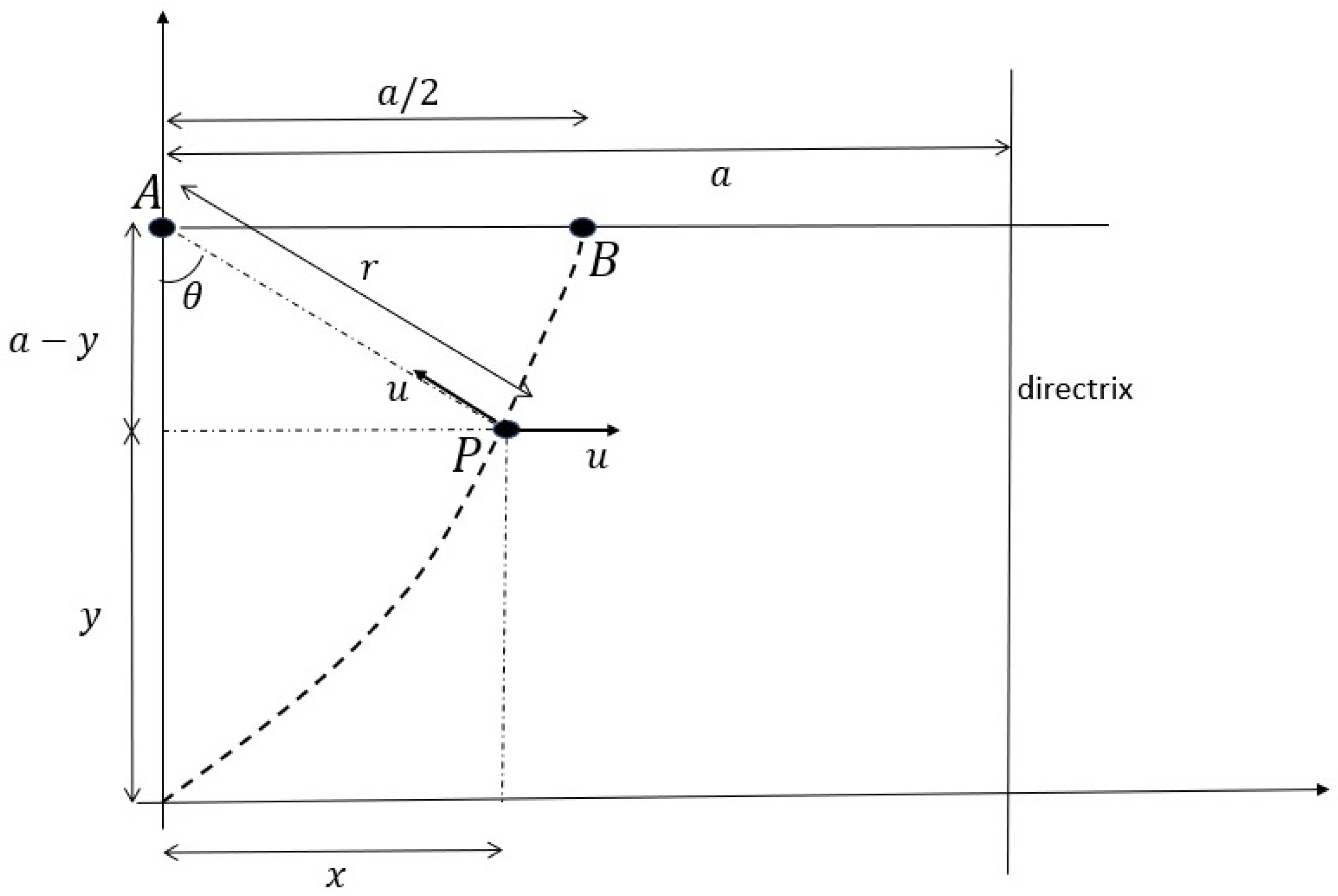
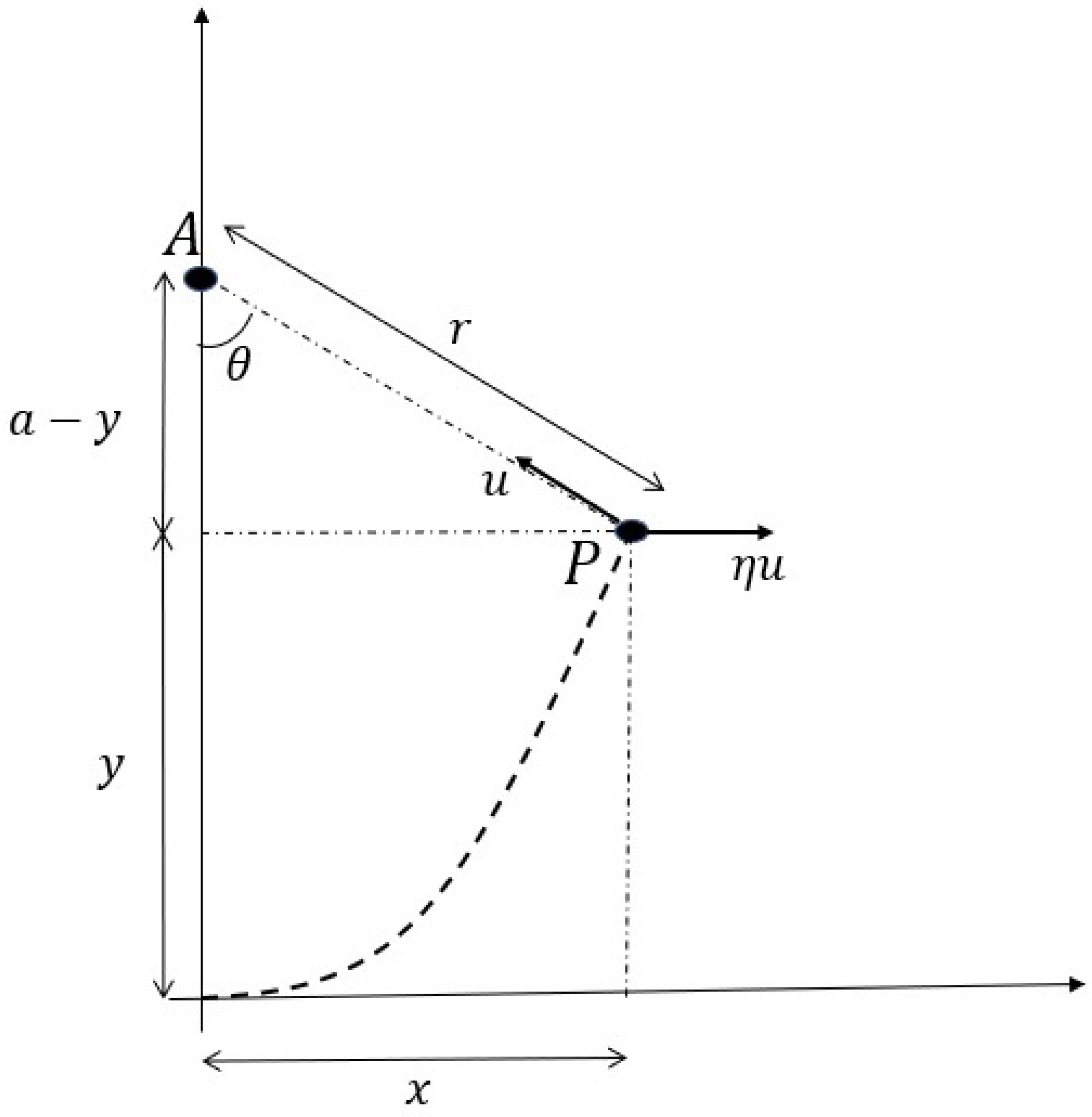
The main setup of our problem is illustrated in Figure 1 and Figure 2. A pursuer P wishes to catch a stationary “prey” A by always approaching A with speed

η u

pointing towards

A,

while drifting in the x direction with constant speed

η u .

The problem now is to find the trajectory of P and decide if P will ever be able to catch

A .

The general solution to this problem for

η \in

in presented in Theorem 1 and requires an analytic treatment; however, for the special case

η = 1,

it can be argued geometrically that the trajectory is a conic section, without delving into any analytic derivation [4,5]. The critical observation that makes this argument possible is that for this case (see Figure 1), the component of the velocity of P along the x axis remains identical to the component of the velocity of P in the instantaneous direction of

A,

each being equal to

u (1 - sin θ) .

Therefore, the total amount of drift in the x direction till any time t is equal to the reduction in the distance between P and A till

t .

This observation immediately enables us to prove the following lemma.

Lemma 1.

Suppose a point

P,

starting from the origin

(0, 0),

wishes to reach the point A

(0, a)

by always trying to approach A at speed

u,

as shown in Figure 1. However, there is a constant “current” of the same speed u towards the positive x direction, which causes the path of P to drift. Then, the resultant locus of P is a parabola with focus at

A,

given by the equation

x = \frac{a}{2} [1 - {(\frac{a - y}{a})}^{2}]

for

y \in [0, a] .

Geometric proof of Lemma 1.

Consider a line parallel to the y-axis, at a distance a (i.e., the line satisfying

y = a

). By the previous arguments, the distance of the man from this line remains equal to his distance from

A .

This leads us immediately to conclude, from elementary geometry, that the locus of the path is a parabola with focus at A and directrix given by the line

y = a .

Moreover, the final point B lies on the perpendicular drawn from the focus to the directrix and is therefore the vertex. The length of the latus rectum is then given by

2 a,

and the parabola “opens” in the negative x direction with vertex at

(a / 2, a) .

The equation of the path is then given by

\begin{matrix} \frac{{(a - y)}^{2}}{x - \frac{a}{2}} = - 2 a \\ i . e ., & x = \frac{a}{2} - \frac{{(a - y)}^{2}}{2 a} \\ i . e ., & x = \frac{a}{2} [1 - {(\frac{a - y}{a})}^{2}] . \end{matrix}

(1)

□

Finding the time dependence of the motion [9,10], however, requires some additional effort. To that end, note that since the positive y component of the velocity is given by

u cos θ = u (a - y) / \sqrt{x^{2} + {(a - y)}^{2}},

we have

\begin{matrix} d t & = \frac{\sqrt{x^{2} + {(a - y)}^{2}}}{u (a - y)} d y \\ = \frac{\sqrt{\frac{{(2 a - y)}^{2} y^{2}}{4 a^{2}} + {(a - y)}^{2}}}{u (a - y)} d y . \end{matrix}

Setting

z : = (a - y) / a,

we then have

\begin{matrix} \frac{u d t}{a} & = - \sqrt{1 + \frac{{(1 + z)}^{2} {(1 - z)}^{2}}{4 z^{2}}} d z \\ = - \frac{1 + z^{2}}{2 z} d z . \end{matrix}

The integrated equation of motion is then given by

\frac{2 u t}{a} = \int_{1 - \frac{y}{a}}^{1} (z^{- 1} + z) d z .

(2)

Integrating eq. (2) and re-arranging leads to

t = \frac{a}{4 u} [1 - {(\frac{a - y}{a})}^{2} - 2 log (\frac{a - y}{a})] .

(3)

We now tackle the general case where the speed of the current [13,14,17] is given by

η u

for

η \in .

As a first step, we present the following elementary result, which is a popular problem posed in elementary kinematics (see, for example, [12]).

Lemma 2.

For

| η | < 1,

the pursuer reaches the point A, as depicted in Figure 2, at time

t_{f} = a / (u (1 - η^{2})) .

Proof.

From Figure 2, we have

\dot{x} = η u - u sin θ

and

\dot{r} = η u sin θ - u .

Eliminating

θ

between these relations leads to

η \dot{x} + \dot{r} + (1 - η^{2}) u = 0 .

Integrating this equation with the initial conditions

x (0) = 0,

r (0) = a

leads to

\begin{matrix} r = a - η x - (1 - η^{2}) u t . \end{matrix}

(4)

Setting

r (t_{f}) = x (t_{f}) = 0

in (4) leads to the result. □

Remark II.1.

We note that eqn (4) holds in general for any

η .

However,

t_{f}

is finite only for

| η | < 1 .

Remark II.2.

We can use eqn (4) to provide a second proof of Lemma 1 as follows. Setting

η = 1

in (4) leads to

\begin{matrix} r = a - x \\ i . e ., & x^{2} + {(a - y)}^{2} = {(a - x)}^{2} \\ i . e ., & 2 a x = a^{2} - {(a - y)}^{2}, \end{matrix}

which yields eqn (1) on dividing both sides by

2 a .

We now establish the most general result of this section.

Theorem 1.

The equation of path of the pursuer, with

x,

y,

r,

and

θ

as depicted in Figure 2, is given by

x = \frac{a}{2} [{(\frac{a - y}{a})}^{1 - η} - {(\frac{a - y}{a})}^{1 + η}] .

(5)

Further, the time dependence of the path [18] is given by

t = \{\begin{matrix} \frac{a}{2 u} [\frac{2}{1 - η^{2}} - (\frac{1}{1 - η}) {(\frac{a - y}{a})}^{1 - η} - (\frac{1}{1 + η}) {(\frac{a - y}{a})}^{1 + η}], & | η | \neq 1 \\ \frac{a}{4 u} [1 - {(\frac{a - y}{a})}^{2} - 2 log (\frac{a - y}{a})], & | η | = 1 . \end{matrix}

(6)

The path equation (5) holds for

y \in [0, a]

for

| η | \leq 1

and

y \in [0, a)

for

| η | > 1,

while (6) holds for

y \in [0, a]

for

| η | < 1

and

y \in [0, a)

for

| η | \geq 1 .

Corollary 1.1.

We note here that Theorem 1 immediately recovers the result [17] of Lemma 1 by setting

η = 1 .

In addition, setting

y = a

in (6) (for

| η | < 1

) leads to

t_{f} = \frac{a}{u (1 - η^{2})},

which recovers the result of Lemma 2.

Proof of Theorem 1.

We start from eqn (4). Setting

x = r sin θ

in (4) and solving for r leads to

\begin{matrix} r = \frac{a + (η^{2} - 1) u t}{1 + η sin θ} . \end{matrix}

(7)

Now, going back to Figure 2, we note that the

θ

component of the velocity is given by

η u cos θ,

whence, we have

\begin{matrix} r \dot{θ} = η u cos θ . \end{matrix}

(8)

Eliminating r between (7) and (8) lets us write down a linear differential equation in

θ

and

t,

\begin{matrix} \dot{θ} = \frac{η u cos θ (1 + η sin θ)}{a + (η^{2} - 1) u t} \end{matrix}

(9)

Integrating (9) leads to

\begin{matrix} \int_{0}^{t} \frac{d τ}{a + (η^{2} - 1) u τ} = \int_{0}^{θ} \frac{d ϕ}{η u cos ϕ (1 + η sin ϕ)} . \end{matrix}

(10)

The LHS of (9) equals

\frac{1}{(η^{2} - 1) u} log \frac{a + (η^{2} - 1) u t}{a},

while the RHS, with the substitution

z sin ϕ,

can be written as

\begin{matrix} \int_{0}^{sin θ} \frac{d z}{η u (1 - z^{2}) (1 + η z)} \\ \overset{(a)}{=} & \frac{1}{η u} (A \int_{0}^{sin θ} \frac{d z}{1 - z} + B \int_{0}^{sin θ} \frac{d z}{1 + z} + C \int_{0}^{sin θ} \frac{d z}{1 + η z}) \\ = & \frac{1}{η u} (- A log (1 - sin θ) + B log (1 + sin θ) + (C / η) log (1 + η sin θ)) . \end{matrix}

(11)

Here,

(a)

is obtained through a standard partial fraction decomposition (see, for example, [16]) and the constants

A,

B,

and C are obtained as

\begin{matrix} A & = lim_{z \to 1} \frac{1}{(1 + z) (1 + η z)} = \frac{1}{2 (1 + η)}, \end{matrix}

(12)

\begin{matrix} B & = lim_{z \to - 1} \frac{1}{(1 - z) (1 + η z)} = \frac{1}{2 (1 - η)}, \end{matrix}

(13)

\begin{matrix} C & = lim_{z \to - 1 / η} \frac{1}{1 - z^{2}} = \frac{η^{2}}{η^{2} - 1} . \end{matrix}

(14)

Substituting (12), (13), (14), and (11) into (10) leads to

\begin{matrix} \frac{a + (η^{2} - 1) u t}{a} & = {({(1 - sin θ)}^{- \frac{1}{2 (1 + η)}} {(1 + sin θ)}^{\frac{1}{2 (1 - η)}} {(1 + η sin θ)}^{\frac{η^{2}}{η^{2} - 1}})}^{\frac{η^{2} - 1}{η}} \\ = (1 + η sin θ) {(1 - sin θ)}^{\frac{1 - η}{2 η}} {(1 + sin θ)}^{- \frac{1 + η}{2 η}} . \end{matrix}

Rearranging leads to

\begin{matrix} \frac{a + (η^{2} - 1) u t}{1 + η sin θ} & = a {(1 - sin θ)}^{\frac{1 - η}{2 η}} {(1 + sin θ)}^{- \frac{1 + η}{2 η}} \\ = a {(1 - {sin}^{2} θ)}^{\frac{1 - η}{2 η}} {(1 + sin θ)}^{- 1 / η} \\ = a {(cos θ)}^{\frac{1}{η} - 1} {(1 + sin θ)}^{- 1 / η} . \end{matrix}

(15)

Now, from Figure 2, we have

cos θ = (a - y) / r

and

sin θ = x / r .

Therefore, continuing (15), we have

\begin{matrix} \frac{a + (η^{2} - 1) u t}{1 + η sin θ} & = a r {(a - y)}^{\frac{1}{η} - 1} {(r + x)}^{- 1 / η} . \end{matrix}

Now, using (7) leads to

\begin{matrix} {(r + x)}^{1 / η} & = a {(a - y)}^{\frac{1}{η} - 1}, \end{matrix}

which simplifies to

\begin{matrix} r = a^{η} {(a - y)}^{1 - η} - x . \end{matrix}

(16)

Squaring (16) and using

r^{2} = x^{2} + {(a - y)}^{2}

yields

a - y = a^{2 η} {(a - y)}^{1 - 2 η} - 2 x {(\frac{a}{a - y})}^{η} .

Finally, solving for x yields

\begin{matrix} x & = \frac{(a - y) (a^{2 η} {(a - y)}^{- 2 η} - 1)}{2 {(\frac{a}{a - y})}^{η}} \\ = \frac{a}{2} [{(\frac{a - y}{a})}^{1 - η} - {(\frac{a - y}{a})}^{1 + η}], \end{matrix}

(17)

which establishes the equation of the path [20]. Using this equation of path in (16) yields

\begin{matrix} r & = \frac{a}{2} [2 {(\frac{a - y}{a})}^{1 - η} - {(\frac{a - y}{a})}^{1 - η} + {(\frac{a - y}{a})}^{1 + η}] \\ = \frac{a}{2} [{(\frac{a - y}{a})}^{1 - η} + {(\frac{a - y}{a})}^{1 + η}] . \end{matrix}

(18)

Now, using (7), we have, for

| η | \neq 1,

\begin{matrix} (η^{2} - 1) u t & = r (1 + η sin θ) - a \\ \overset{(a)}{=} r + η x - a \\ \overset{(b)}{=} \frac{a}{2} [(1 + η) {(\frac{a - y}{a})}^{1 - η} + (1 - η) {(\frac{a - y}{a})}^{1 + η} - 2], \end{matrix}

which simplifies to

t = \frac{a}{2 u} [\frac{2}{1 - η^{2}} - (\frac{1}{1 - η}) {(\frac{a - y}{a})}^{1 - η} - (\frac{1}{1 + η}) {(\frac{a - y}{a})}^{1 + η}],

establishing the time dependence for

| η | \neq 1 .

Here,

(a)

follows by using

x = r sin θ,

and

(b)

follows by substituting the expressions for r and x from (18) and (17), respectively. Note that the time dependence for the case

η = 1

was already established in (3). We demonstrate here an additional sanity check that seems to corroborate this result. We have, for

z > 0,

\begin{matrix} lim_{η \to 1} [\frac{2}{1 - η^{2}} - (\frac{1}{1 - η}) z^{1 - η} - (\frac{1}{1 + η}) z^{1 + η}] \\ = & lim_{η \to 1} (\frac{1 - z^{1 - η}}{1 - η} + \frac{1 - z^{1 + η}}{1 + η}) \\ = & \frac{1 - z^{2}}{2} - log z . \end{matrix}

(19)

Setting

z = (a - y) / a

recovers the time dependence expression for

η = 1 .

□

Remark II.3.

Note that the analysis leading to (19) is merely a sanity check and not a rigorous proof, since we did not argue that t has to be continuous in

η

for each

y .

This can, however, be argued fairly easily from elementary results on ordinary differential equations; we point the interested reader to [15] and references therein.

III. Other pursuit problems

In this section, we briefly comment on a class of pursuit problems which are commonly stated in the following form. Referring again to Figure 2, suppose the point A moves horizontally with speed

η u

and the pursuer P always points their velocity vector towards

A,

but there is no “current”. Clearly, the problem is equivalent to the setting in Theorem 1, but observed from a frame moving in the x direction with velocity

η u .

Accordingly, for the scenario where A moves in the positive x direction, the x coordinate of P will be given by

- (x - η u t),

according to the notation used in Section II, and

t (y)

will remain unchanged. Thus, for this problem, we have, using (5) and (6),

\begin{matrix} x & = \{\begin{matrix} \frac{a}{2} [\frac{1}{1 + η} {(\frac{a - y}{a})}^{1 + η} - \frac{1}{1 - η} {(\frac{a - y}{a})}^{1 - η} + \frac{2 η}{1 - η^{2}}], & | η | \neq 1, \\ \frac{a}{4} [{(\frac{a - y}{a})}^{2} - 2 log (\frac{a - y}{a}) - 1], & η = 1, \\ \frac{a}{4} [1 - {(\frac{a - y}{a})}^{2} + 2 log (\frac{a - y}{a})], & η = - 1 . \end{matrix} \end{matrix}

(20)

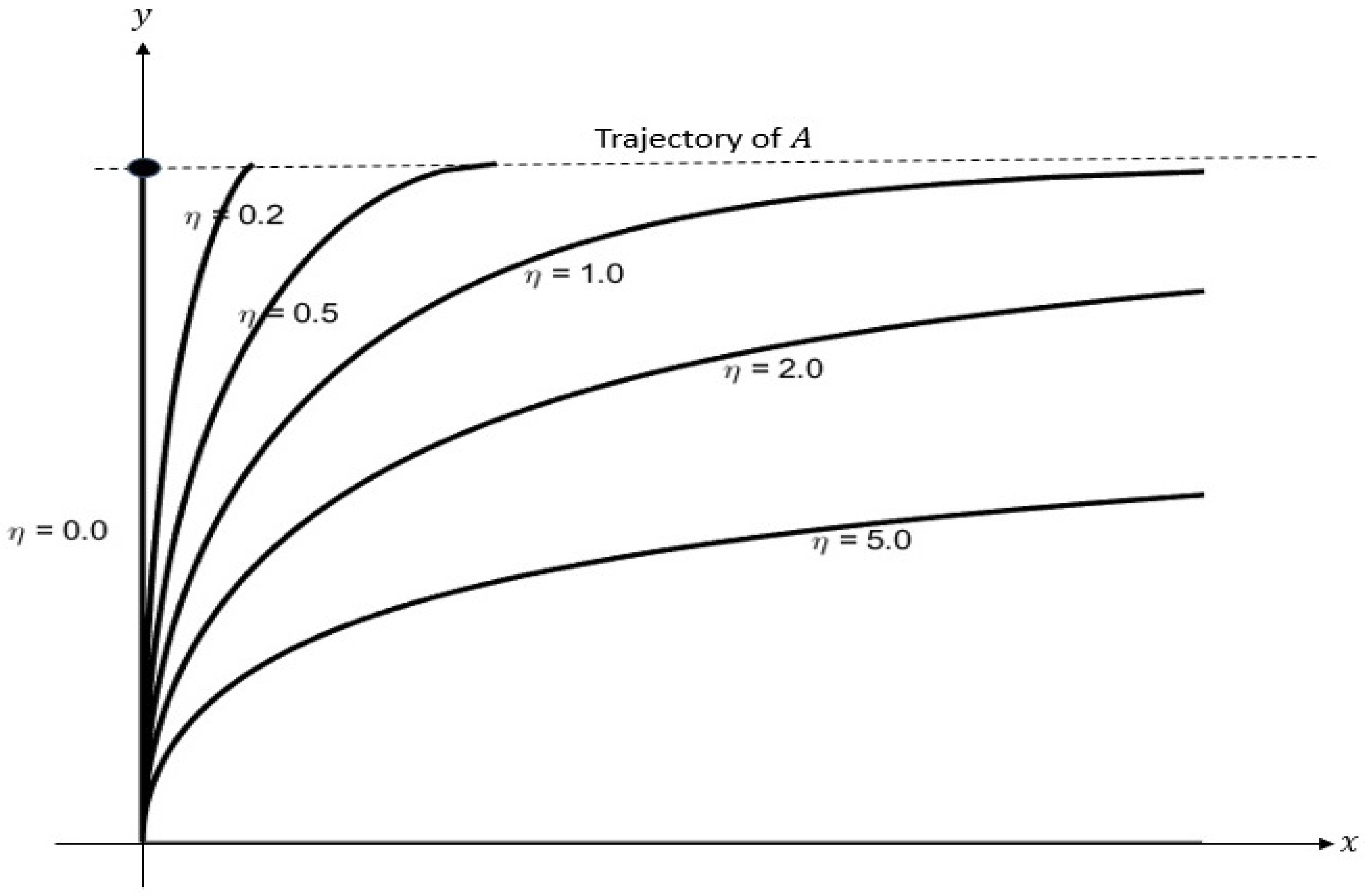
Figure 3 plots the pursuit trajectories (20) for various values of

η .

For

| η | \geq 1,

the trajectory approaches the trajectory of A asymptotically, while for

| η | < 1,

the pursuer “catches” the prey at

x = a η / (1 - η^{2}) .

Remark III.1.

This problem illustrates an interesting kinematic phenomenon: the trajectory in the first problem (Theorem 1) for

η = 1

is a finite segment of a parabola with no asymtotes, while the trajectory for the same problem observed from a different frame has an asymptote (

y = a

) and “looks” quite different (cf. Figure 3), even though the frames move with uniform velocity with respect to one another.

IV. Discussions

The settings explored in this work can be generalized to include various scenarios, as allued to in the introduction. A geometric solution, while it may not be feasible in a general setting, might still provide a useful starting point and provide insights critical to solving many such problems. Bernhart [19] and others [7,21,22] have performed in-depth treatment specifically of the geometric properties and aspects of pursuit curves.

References

E. Kasner and F. Supnick, “The Apollonian packing of circles”, Proceedings of the National Academy of Sciences USA 29(11), pp. 378–384, 1943.
P. Zhao, P. B. Vyas, S. Mcdonnell, P. Bolshakov-Barrett, A. Azcatl, C. L. Hinkle, P. K. Hurley, R. M. Wallace and C. D. Young, “Electrical characterization of top-gated molybdenum disulfide metal-oxide-semiconductor capacitors with high-k dielectrics”, Microelectronic Engineering 147, pp. 151-154, 2015. [CrossRef]
Isaac Weintraub, Eloy Garcia, and Meir E. Pachter, “Optimal guidance strategy for the defense of a non-manoeuverable target in 3-dimensions”, IET Control Theory & Applications 14(11), pp. 1531–1538, 2020.
Ali Saadat, Pratik B. Vyas, Maarten L. Van de Put, Massimo V. Fischetti, Hal Edwards, and William G. Vandenberghe “Channel Length Scaling Limit for LDMOS Field-Effect Transistors: Semi-classical and Quantum Analysis”, 2020 32nd International Symposium on Power Semiconductor Devices and ICs (ISPSD), pp. 443-446, 2020.
Pratik B. Vyas, Ninad Pimparkar, Robert Tu, Wafa Arfaoui, Germain Bossu, Mahesh Siddabathula, Steffen Lehmann, Jung-Suk Goo, and Ali B. Icel, “Reliability-Conscious MOSFET Compact Modeling with Focus on the Defect-Screening Effect of Hot-Carrier Injection”, 2021 IEEE International Reliability Physics Symposium (IRPS), pp. 1-4, 2021.
Pierre Bouguer, “Sur de nouvelles courbes auxquelles on peut donner le nom de lignes de poursuite”, Mémoires de mathématique et de physique tirés des registres de l’Académie royale des sciences, pp. 1–15, 1732.
J. C. Barton and C. J. Eliezer, “On Pursuit Curves”, The Journal of the Australian Mathematical Society B41: Applied Mathematics (3), pp. 358–371, 2000.
C. Hoenselaers, “Chasing Relativistic Rabbits”, General Relativity and Gravitation (4), pp. 351–360, 1995.
Pratik B. Vyas, Charisse Zhao, Sefa Dag, Ashish Pal, El Mehdi Bazizi, and Buvna Ayyagari-Sangamalli, “Next Generation Gate-all-around Device Design for Continued Scaling Beyond 2 nm Logic”, 2023 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), pp. 57-60, 2023.
Pratik B. Vyas, Charisse Zhao, Sefa Dag, Ashish Pal, El Mehdi Bazizi, and Buvna Ayyagari-Sangamalli, “Modeling of SiC transistor with counter-doped channel”, Solid State Electronics 200, pp. 108548, 2023. [CrossRef]
Richard P. Feynman, Robert B. Leighton, and Matthew Sands, The Feynman Lectures on Physics, Vol. 1 (Addison-Wesley, 1964), p. 3–10.
I. E. Irodov, Problems in General Physics (Mir Publishers, 1988).
Pratik B. Vyas, Maarten L. Van de Putt, and Massimo V. Fischetti, “Quantum Mechanical Study of Impact of Surface Roughness on Electron Transport in Ultra- Thin Body Silicon FETs”, 2018 IEEE 13th Nanotechnology Materials and Devices Conference (NMDC), pp. 1-4, 2018.
Pratik B. Vyas, Maarten L. Van de Put, and Massimo V. Fischetti, “Master-Equation Study of Quantum Transport in Realistic Semiconductor Devices Including Electron-Phonon and Surface-Roughness Scattering”, Phys. Rev. Appl. 13, pp. 014067, 2020. [CrossRef]
Erwin Kreyszig, Advanced Engineering Mathematics (3rd ed.) (New York: Wiley, 1972.
Richard Courant, Differential and Integral Calculus, Vol. 1 (London: Blacktie & Son Limited, 1961.
P. B. Vyas, C. Naquin, H. Edwards, M. Lee, W. G. Vandenberghe, and M. V. Fischetti, “Theoretical simulation of negative differential transconductance in lateral quantum well nMOS devices”, Journal of Applied Physics 121, pp. 044501, 2017. [CrossRef]
Pratik B. Vyas, Maarten L. Van de Put, and Massimo V. Fischetti, “Simulation of Quantum Current in Double Gate MOSFETs: Vortices in Electron Transport”, 2018 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), pp. 1-4, 2018.
Arthur Bernhart, “Curves of general pursuit”, Scripta Mathematica 24, 1959.
Pratik B. Vyas, Ashish Pal, Gregory Costrini, Plamen Asenov, Sarra Mhedhbi, Charisse Zhao, Victor Moroz, Benjamin Colombeau, Bala Haran, El Mehdi Bazizi, and Buvna Ayyagari-Sangamalli, “Materials to System Co-optimization (MSCO^TM) for SRAM and its application towards Gate-All-Around Technology”, 2023 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), pp. 53-56, 2023.
A. Guha and S. K. Biswas, “On Leonardo da Vinci’s cat and mouse problem”, Bulletin of the Institute of Mathematics and its Applications 30(1, 2), pp. 12–15, 1994.

Figure 1. Schematic description of problem setup for Lemma 1.

Figure 2. Schematic description of problem setup for Theorem 1.

Figure 3. Pursuit curves.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Closed Form Solutions to a Class of Pursuit Problems Using Geometric Analogies

Abstract

I. Introduction

II. Problem setup and main results

III. Other pursuit problems

IV. Discussions

References

MDPI Initiatives

Important Links

Subscribe