Prerpints.org logo
Preprint
Article

Nonlocal Hydrodynamical Model with Viscosive Damping and Generalized Drude-Lorentz Term

Altmetrics

Downloads

106

Views

17

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

19 July 2023

Posted:

20 July 2023

You are already at the latest version

Alerts
Abstract
The response of plasmonic metal particles to an electromagnetic wave undergoes significant features at the nanoscale level. Different properties of the internal composition of a metal, such as its ionic background and the free electron gas, begin to manifest more prominently. As the dimensions of the nanostructures decrease, the classical local theory gradually becomes inadequate. Therefore, Maxwellʹs equations need to be supplemented with a relationship determining the dynamics of current density which is the essence of nonlocal plasmonic models. In this field of physics, the standard (linearized) hydrodynamic model (HDM) has been widely adopted with great success, serving as the basis for a variety of simulation methods. However, ongoing efforts are also being made to expand and refine it. Recently, the GNOR (general nonlocal optical response) modification of the HDM has been used, with the intention of incorporating the influence of electron gas diffusion. Clearly, from the classical description of fluid dynamics, a close relationship between viscosive damping and diffusion arises. This offers a relevant motivation for introducing the GNOR modification in an alternative manner. The standard HDM and its existing GNOR modification also do not include the influence of interband electron transitions in the conduction band and other phenomena that are part of many refining modifications of the Drude‐Lorentz and other models of metal permittivity. In this article, we present a modified version of GNOR‐HDM that incorporates the viscosive damping of the electron gas and a generalized Drude‐Lorentz term. In the selected simulations, we also introduce Landau damping which corrects the magnitude of the standard damping constant of the electron gas based on the size of the nanoparticle. We have chosen a spherical particle as a suitable object for testing and comparing HD models and their modifications because it allows finding precise analytical solutions for the interaction and, simultaneously, it is a relatively easily fabricable nanostructure in practice. Our contribution also includes our own analytical method for solving the HDM interaction of a plane wave with a spherical particle. This method forms the core of calculations of the characteristic quantities, such as the extinction cross‐sections and the corresponding components of electric fields and current densities.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Metallic nanoparticles are currently being intensively studied both in terms of describing their interaction with electromagnetic radiation and also of utilizing their unique properties. Their application as plasmonic nanostructured materials can find use in various fields, such as sensors utilizing the effect of phosphorescence [1], extraordinary optical transmission (EOT) [2], photothermal applications [3], Raman spectroscopy (SERS) [4,5], designs of highly sensitive gas sensors [6,7,8,9], unique anti-reflective coatings to enhance the efficiency of solar cells [10], integrated optical or quantum signal processing [11], battery research [12,13], biomedical applications [4,14,15], and even in designing metamaterials with unique properties such as negative refractive index [16], among others.
The existing research and development of new applications in the aforementioned directions necessarily relies on adequately precise calculations. At the current level of knowledge, approximate solutions in the form of quasistatic models appear insufficient [17,18], even though in the early days of plasmonics, these theories provided many satisfactory explanations [19]. A fundamental breakthrough for the entire field of plasmonics was represented by Mie’s theory [20] which accurately determined the position and value of resonant extinction maxima and associated quantities characterizing the behavior of spherical particles interacting with incident electromagnetic waves.
The demand for accuracy in description, and thus the relevance of simulations derived from them, increases in parallel with the growing technological capabilities of preparation of nanostructures and nanostructured surfaces [21,22,23]. As an example, sensor applications based on SERS technology can be mentioned, where the sensitivity of the sensor relies on the amplification of the field at the specifically designed site where the binding of the detected molecule is intended to occur.
Just as the quasistatic theory has proven to be inadequate, the classical solutions of Maxwell’s equations now also appear unsatisfactory, particularly when a high precision of the results is required to simulate the interaction of plasmonic nanostructures with electromagnetic waves. Based on numerous experiments, it is becoming evident that standard simulations, in some cases, significantly overestimate the intensity of the electromagnetic field in the vicinity of sharp edges and interfaces of nanostructures [24]. In the case of nanostructures with characteristic dimensions on the order of a few nanometers, as mentioned above, the classical theory also inaccurately determines the position of resonant maxima for characteristic quantities.
These shortcomings can become a significant problem in practice. A clear example can be found in sensor applications, where in addition to accurately determining the resonant frequency, the intensity of the electric field in specific detection locations of the sensor also plays a significant role. The mentioned requirements for high calculation accuracy have given rise to the need to incorporate nonlocal response.
In contrast to the classical description (Maxwell’s equations and Ampere’s law), the nonlocal theory assumes a more complex relationship between current density and electric field evolution than a simple proportional relationship. The most widely used nonlocal model in the field of plasmonics has become the so-called standard hydrodynamic model (HDM) [25]. However, there are also alternative nonlocal models [26,27].
Using the HDM, Mie theory has already been generalized [28,29], and several other analytical solutions have been found for metallic interfaces [30], such as the generalized Fresnel equations [31,32]. For the structure of an infinitely long cylinder, the need for finding an accurate solution has been demonstrated, as the so-called curl-free approximation exhibits significant numerical drawbacks in the form of spurious resonances below the plasma frequency [33].
While the standard HDM has become a successful mathematical tool for predicting various phenomena, such as the blue shift of the main extinction maximum in gold and silver spherical nanoparticles with diameters smaller than 10 nm, theoretical research in this field continues with the aim of achieving the most accurate description. Recently, a modification of HDM called GNOR (general nonlocal optical response) has been proposed [34,35] which incorporates the diffusion of the electron gas. The influence of Landau (Kreibig) damping, which is inversely proportional to the nanoparticle size [36,37,38], is also being discussed. Simultaneously, efforts are being made to find solutions for a more accurate nonlinearized form of HDM [39,40], and the question of viscosive damping of the electron gas is gaining prominence [41,42,43]. The hydrodynamic model itself is based on the concept of a jellium model which can be interpreted as the electron fluid moving with respect to a positively charged background of metal ions. From this perspective, the question directly arises of how much of the overall material response of a metal belongs to the electron fluid itself and how much to the ion background. The standard HDM, for example, does not consider the influence of energy transitions of electrons within the conduction band, and thus this response is implicitly attributed from a mathematical perspective to the ion background of a metal. From the description of fluid dynamics, there is also a well-known connection between diffusion and viscosive damping, which suggests incorporating the influence of diffusion in an alternative way, different from the GNOR modification. These aforementioned insights are, in our opinion, a relevant stimulus for considering further possible modifications of the hydrodynamic model, which is also the main goal of our article.
The contributions of our article are thus numerous. Among other things, we provide a relatively detailed mathematical procedure for solving HDM in the case of the interaction of a metallic spherical particle with a planar wave. We also compare selected calculations between the classical (Mie) and nonlocal HD models. However, the main contribution lies in presenting a possible approach for further generalizing the standard HDM through the modification of the existing GNOR-HDM by incorporating viscosive damping and considering the general form of the Drude-Lorentz term. Furthermore, in analogy with the previous approach, we compare the computations obtained by solving each variant of the HDM.
The rest sections of the article are organized as follows. In the second section of the article, we briefly recapitulate the procedure of solving the problem of the interaction between a plane wave and a spherical metal nanoparticle within the framework of the HD model, and subsequently present important new results in the form of an explicit expression for the field expansion coefficients. In the third section, the effective extinction cross sections of gold and silver particles determined according to the classical Mie theory and the standard HD model are compared. Additionally, the influence of Kreibig damping on the behavior of the mentioned quantities is briefly analyzed. The fourth section is dedicated to the generalization of the GNOR-HDM, so that the new model incorporates viscosive damping of the electron gas and the general Drude-Lorentz term. Furthermore, the procedure for the possible solution of our modified GNOR-HDM is discussed. The final fifth section of the article is focused on comparing the results of individual variants of HD models, with the emphasis on comparing the calculations of selected quantities using the standard HD model and our generalized GNOR-HDM, also referred to as the HD model with viscosive damping. The paper is concluded with the conclusions together with possible future activities.

2. Review of Standard Hydrodynamic Model and Calculation Procedure

In this section, we would like review the standard hydrodynamic model calculation procedure [29], and subsequently also show our implementation of the technique (Section 3) which will be later used for the generalized hydrodynamic model (Section 4). From a mathematic point of view, the HD model and its modifications represents a system of two linear differential equations for the vector functions of the electric field E and the induced current density   J . In this article, we will use simplified notation for vector functions E ≡ E r , θ , φ , ω , J ≡ J r , θ , φ , ω , where ω is the angular frequency and r , θ , and   φ are the spherical coordinates (see Figure 1).
In the traditional HDM, the electrical field and the current density are given by the solutions of the wave equation and the hydrodynamic equation-of-motion [38]. We will concentrate here on the specific spherical geometry of a nanoparticle although some parts of the calculation are more general (primarily the determination of the nonlocal wave number). Clearly, derived expansion coefficients of the fields are generally dependent on the particle shape and analytically can be determined only for a spherical geometry considered here.
The basic HD model can be formulated with Equations (1) and (2) as follows:
β 2 ∇ ∇ . J + ω ω + i γ J = i ω ω p 2 ε 0 E ,
∇ × ∇ × E − ω 2 c 2 ε t − ε e g E = i ω μ 0 J .
Here, the constants ε 0 , μ 0 , and c represent vacuum permittivity, vacuum permeability, and the speed of light, respectively. Next quantities of HD model ε e g   and ε t indicate the permittivity of electron gas and the total permittivity of a metal, respectively.
Next assumption is concerned with the expression for the permittivity of an electron gas. The HDM modification unfortunately provides no clue which particular form should represent the electron gas permittivity. Clearly, one possibility is to use the expression often formulated in literature, for example in [45,46]. This expression for the electron gas permittivity is, in fact, the Dude-Lorentz relation for the permittivity, and can be stated as follows:
ε e g = ε ∞ − ω p 2 ω ω + i γ .
Here, the difference ε t − ε e g   has the meaning of permittivity of the ionic background of the metal. Other parameters of the HD model are the plasma angular frequency   ω p , the attenuation constant γ , and the nonlocal constant β 2 ≡ 3 / 5 v F 2 , where v F   is the Fermi velocity. At this point, it is appropriate to provide specific values of the parameters. According to [38], for gold, the values are ω p = 1.3673 · 10 16 H z , γ = ω p / 127 and v F = 1.39 · 10 6 m · s − 1 , in the case of silver, the values are ω p = 1.3627 · 10 16 H z , γ = ω p / 360 and v F = 1.39 · 10 6 m · s − 1 . The mentioned values of parameters are used in the analysis of selected quantities in the third and fifth part of this article.
For solving this system of equations, at first, it is necessary to determine both longitudinal and transversal wave numbers, as applied, e.g. in [29]. We note that while the longitudinal wave number belongs to the electric field with the vector of electric intensity oscillating in the direction of the wave vector of the field, the transversal wave number belongs to the field which oscillates perpendicularly with respect to the direction of propagation. Following [29], the transversal and longitudinal field components can be described as Et = ∇×Ψ and El = ∇Φ, respectively, where Et is the transversal electric field, Ψ is some vector function, El is the longitudinal electric field and Φ some scalar function. Although these assumptions are not absolutely general, they are typically used (as in Equation (1)) and allow us obtaining the analytical results, as required. It should be also noted that there exists also an alternative procedure based on the mathematical theory of generalized functions [2], but this approach brings another difficulty connected with the fulfillment of the boundary conditions and thus is not very practical. A reader can find a classification of HD models from the perspective of such generalized function (including also the derivation of Green functions) in [47]. Returning back to our approach, for the spherical geometry considered, Et is therefore necessarily a spherical vector function and Φ function satisfies the scalar wave equation. The fields Et and El hence satisfy the following Equations (4) and (5), respectively; this follows from definition of vector spherical harmonics.
∆ E l = − k l 2 E l ,
∆ J l = − k l 2 J l .
Further, these relations (4) and (5) will be substituted into Equations (1) and (2), to obtain the following equations
− β 2 k l 2 J l + ω ω + i γ J l + J t = i ω ω p 2 ε 0 E l + E t ,
k t 2 E t − ω 2 c 2 ε t − ε e g E l + E t = i ω μ J l + J t .
These two equations can be further converted to describe the longitudinal and transversal fields separately. This will enable assuming the fields can be described by scalar functions and hence the mathematical operators of rotation and gradient can be applied to them, providing for the longitudinal case
− β 2 k l 2 J l + ω ω + i γ J l = i ω ω p 2 ε 0 E l ,
− ω 2 c 2 ε t − ε e g E l = i ω μ J l ,
and similarly, for the transversal field and transversal wave number
  ω ω + i γ J t = i ω ω p 2 ε 0 E t ,
k t 2 E t − ω 2 c 2 ε t − ε e g E t = i ω μ J t .
This will further allow expressing the longitudinal wave number from Equations (8) and (9), and correspondingly the transversal wave number, from Equations (10) and (11), as
k t 2 = ω 2 c 2 ε t − ε e g   − ω p 2 ω ω + i γ ,
  k l 2 = 1 β 2 ω ω + i γ − ω p 2 ε t − ε e g .
Unfortunately, if we assume that ε e g   is zero, as it follows from standard Maxwell equations, then nonphysical results appear, specifically the extinction cross section will follow wrong functional dependence and the extinction maxima will not follow correct spectral position for bigger particles, in accordance with the Mie theory. Here, we will track the calculation method, introduced in [29], to obtain the correct results. The idea of this technique is based on expressing the unknown permittivity of an electron gas ε e g   as   − ω p 2 / ω ω + i γ (see Equations (3) and (12)). Applying that, the transversal wave number follows the predictions for the electric and magnetic fields from the Mie theory [48]. HD model, however, as compared to the standard Mie theory, considers also the longitudinal wave number (which often has significantly larger value). Clearly, from the wave number formulas, one can further proceed with the calculations of the scattered field around a particle and the induced field in a particle (i.e. the absorbed field).
First, we must specify the proper boundary conditions. Although Maxwell boundary conditions allow discontinuity of the tangential magnetic field component, the Mie theory assumes their continuity. The same boundary conditions are used in the case of solving HDM in [29]. Second, the tangential electric field is naturally continuous on the boundary of a particle. Finally, the last boundary condition determines the zero normal component of the electric current density on the particle boundary. Overall, following the expansion of the fields in the spherical coordinates ( θ , φ ), we obtain five boundary conditions on the particle boundary
E θ i n c a + E θ s a = E θ p a ,       E φ i n c a + E φ s a = E φ p a ,
H θ i n c a + H θ s a = H θ p a ,       H φ i n c a + H φ s a = H φ p a ,
J r a = 0 .
Here, E φ p a , E θ p a   and H φ p a ,   H θ p a are the components of the total electric and magnetic field inside a particle, in the directions of spherical coordinates φ and θ , respectively. Similarly, E φ s a , E θ s a   and H φ s a ,   H θ s a are the components of the scattered fields, and E φ i n c a , E θ i n c a   and H φ i n c a ,   H θ i n c a represents the incident fields. All fields are considered on a surface of a particle. Before starting the determination of expansion coefficients of the fields, let us make some remarks. We will follow the procedure of decomposing the transversal fields into series of vector spherical wave functions M and N of both even (index e) and odd (index o) components which we will denote as M n m e h     M n m e ,     N n m e h ,     N n m e ,     M n m o h ,     M n m o ,     N n m o h ,     N n m o . Here, the index n belongs to the radial part whereas the index m represents the azimuthal part of the wave function, respectively.
In order to describe the longitudinal fields, it is necessary to find the solution of Equation (5) in spherical coordinates. We will thus define the scalar even and odd functions Φ n m e     and Φ n m o . It is also convenient to distinguish the mentioned functions according to the wave number in the argument of their radial functions, therefore we add the given wave number as the superscript of the respective functions. The index n takes values from 1,2…∞, the index m should be restricted only to the values -1 or 1 because we consider the case of a single spherical particle and an incident plane wave. Clearly, in the case of a Gaussian beam (or an evanescent wave), this symmetry is broken. The vector functions with no upper index are expressed with radial spherical Bessel functions j n r , vector functions with index h include spherical Hankel function of the first type h n r . Index o denotes odd function s i n ( m φ ) and index e denotes even function   c o s ( m φ ) .
The mathematical form of the vector spherical harmonics in the spherical coordinates r , θ, and φ are well known and can be found, for example in [20] or [49]. The explicit expression of the gradient of the Φ n m e k l     and Φ n m o k l functions necessary for the decomposition of the longitudinal fields is thus as follows:
∇ Φ n m e k l = k l cos ⁡ m φ P n , m cos ⁡ θ d   j n k l r d   k l r cos ⁡ m φ d d θ P n , m cos ⁡ θ r − 1 j n k l r − sin ⁡ m φ m   P n , m cos ⁡ θ sin ⁡ θ r − 1 j n k l r ,
∇ Φ n m o k l = k l sin ⁡ mφ ⁡ P n , m cos ⁡ θ d   j n k l r d   k l r sin ⁡ m φ d d θ P n , m cos ⁡ θ r − 1 j n k l r cos ⁡ m φ m   P n , m cos ⁡ θ sin ⁡ θ r − 1 j n k l r .
(18)
Using the vector harmonics M and N and the gradients of the scalar functions mentioned above, it is hence possible to decompose the fields. For the selected index m and n, the following relations can be found:
E n , m i n c = M n m o k 0 − i N n m e k 0 ,
H n , m i n c = M n m e k 0 + i N n m o k 0 ,
    E n , m p = B e M m n e k t + B o M m n o k t − i A e M m n e k t − i A o M m n o k t + C e ∇ Φ m n e k l + C o ∇ Φ m n o k l ,      
H n , m p = k t ω μ 0 A e M n m e k t + A o M n m o k t + i B e N n m e k t + i B o N n m o k t ,
J m , n = − T i A e M m n e k t + i A o M m n o k t − i B e N n m e k t − i B o N n m o k t + S C e ∇ Φ m n e k l + C o ∇ Φ m n o k l ,
E n , m s = − β e M n m e h , k 0 − β o M n m o h , k 0 + i α e N n m e h , k 0 + i α o N n m o h , k 0 ,  
  H n , m s = − k 0 ω μ 0 i β e M n m e h , k 0 + i β o M n m o h , k 0 + i α e N n m e h , k 0 + i α o N n m o h , k 0 .
Relations (19) and (20) hold for the incident plane wave, see Figure 1, and its electric and magnetic components, respectively. The electric and magnetic fields and the induced current density inside the particle can be determined by Equations (21)–(23). Similarly, to the incident field around the particle, relations for the scattered field can be established in the form of Equation (24) for the electric field and (25) for the magnetic field.
The individual wave numbers are marked as follows: k 0 is the (vacuum) wave number of the incident and scattered field, k t and k l are the wave numbers of the transversal and longitudinal fields inside the nanoparticle. Parameters S and T take the following form S = i ω ε 0 ε t + ε e g , T = i ω ε 0 ε t + ε e g − i k t 2 μ ω . To obtain the total fields E , H and current density J , it is necessary to sum the components in Equations (19)–(25), over all n and m. Before summation, one must determine 10 unknown coefficients, A e , A o , B e , B o , α e , α o , β e , β o , C e , C o by substituting the components from Equations (19)–(25) into Equations (14)–(16). In our situation of the nonlocal case, the gradients in Equations (17) and (18) will be applicable. Next, we can proceed with solving five boundary conditions using the finding that the expansion coefficients A o , B e , α o , β e , C o   are, in fact, zero. That implies from the fact that we have only five linear equations for the ten unknowns. It is thus possible to determine the expansion coefficients in the form shown below. Here, it is convenient to define the following effective labelling: j n k t = j n k t a , h n k 0 = h n k 0 a , Z n j , k 0 = d k 0 r j n k 0 r d k 0 r | a , d j n k l = d j n k l r d k l r | a , and similarly for other indices. The expansion coefficients A e n , α e n ,   D e n ,   B o n   ,   β o n , after some algebraic manipulation, take the following form:
A e n = k 0 k t Z n h , k 0 j n k 0 − Z n j , k 0 h n k 0 k 0 2 k t 2 k 0 2   Z n h , k 0 j n k t − Z n j , k t h n k 0 + h n k 0 j n k l j n k t   T   n   n + 1 a   S   k l   d j n k l   ,
α e n = j n k 0 h n k 0 − k t j n k t k 0 h n k 0 A e n   ,
D e n = i   T   n n + 1 j n k t k t   a   S   k l   d j n k l A e n   ,
B o n = Z n j , k 0 h n k 0 − Z n h , k 0 j n k 0 Z n j , k t h n k 0 − Z n h , k 0 j n k t   ,
(29)
β o n = Z n j , k t j n k 0 − Z n j , k 0 j n k t Z n j , k t h n k 0 − Z n h , k 0 j n k t .
(30)
In order to facilitate the reader’s possible work with deriving these expansion coefficients of the fields, we present here their explicit expressions. Now, from the knowledge of the α e n and β o n coefficients, it is clearly possible to evaluate the effective cross-section of extinction:
σ e x t = 2 π k 0 2 ∑ n = 1 ∞ 2 n + 1 R e α e n + β o n   .
The expansion coefficients A e n , α e n ,   D e n ,   B o n   ,   β o n   are also necessary for calculation of induced current density in a particle, electric and magnetic fields in the surroundings and within the volume of a particle. The coefficients have a general form for the spherical particle, therefore parametric modifications of the HD model would change only the formulas for the wave numbers and electron gas permittivities.
One possible modification of the HD model is the so-called General nonlocal optical response (GNOR) theory [34,38]. This theory should unify quantum-pressure convection effects and induced charge-diffusion kinetics. GNOR well describes also size-depending damping and corresponding frequency shifts. This effect could be easily added to our model, too. Another possible modification assumes that the attenuation of electron gas oscillations is related to the ratio between the particle surface and its volume. It is generally considered to be the attenuation due to the formation of an electron-hole pair at the interface which has a direct effect on energy loss of plasmon modes. Phenomenologically, this effect can be considered by the introduction of the so-called Landau attenuation [37]; this is also done further in this paper. The decay constant then depends on the radius of a spherical particle. The effect of this attenuation on the spectral behavior of the extinction will be shown in the next section.

3. Model Implementation - Comparison of Local and Standard Nonlocal HD Model

In this section, we will briefly show the results of our implementation of the standard nonlocal HD model, presented in the previous section, in comparison with the local method, to demonstrate the differences and thus the correct implementation of the HDM. For such demonstration, we will use the quantity of the extinction cross section which allows identifying positions of the resonance maxima and revealing the extent to which the spherical particle interacts with incident electromagnetic radiation. Let us note that the absorption spectra play dominant role especially for small particles (below 10 nm in radius). Figure 2 and Figure 3 display comparison of the extinction cross section between Mie’s and HDM results, for a spherical gold (Figure 2) and silver (Figure 3) particle in vacuum and water environment.
As is seen and is well known, HD theory predicts a significant blue shift of the position of extinction maxima, in comparison to the Mie theory. As one can see, these differences are more significant in water environment. As expected, in water environment, both models predict circa three times larger extinction maxima and also maximum spectral shifts towards longer wavelengths. Concerning the nonlocality, a blue shift of the nonlocal curve is slightly more significant in water environment. Further, in Figure 4, again for the cases of vacuum and water environment, we can follow the effect of Landau’s damping, incorporated to our standard HD model. Evidently, it modifies the shape of the extinction spectra curve, as compared to the standard HDM. Also, Landau’s damping changes the local maximum extinction values and also values of the extinction for shorter wavelengths (both decrease) whereas for longer wavelengths, a more relaxed declination to zero value is visible, in comparison with the standard HD model without Landau’s damping.
Finally, in Figure 5 and Figure 6, we can see main differences in distribution of X–component of the electric field calculated by Mie’s theory and standard HD model, for two selected wavelengths ( λ = 527.3   nm - maximum prediction for the Mie model, and λ = 486   nm for the HD model). It is apparent that, in accordance with the results of others [24], the HD model predicts smaller values of the electric field inside a particle (and also in its vicinity). Let us also note an interesting fact that the electric field is weaker around particle surface for the HD model.

4. Nonlocal Hydrodynamic Model with Viscosive Damping and Generalized Drude-Lorentz Term

The standard HDM, analyzed in the previous section, is based on the perception of an electron gas as a charged continuum which can be described, in a certain approximation with a model, relying on the equations of motion of a fluid flow. Recently, an extension of the HDM has been proposed that includes the diffusion of an electron gas; a phenomenon occurring regularly in liquids and gases. Within the physics of fluids, the Stokes-Navier equations play a crucial role, which, among other issues, establishes a close connection between diffusion and viscosive damping. Therefore, it is natural to generalize the standard HDM by introducing viscosive damping of the electron fluid. Starting from the derivation of HDM in [25] and the Stokes-Navier equations for the case of convective form [50], it is straightforward to arrive at the initial Equation (32), which can be further modified to find the generalized variant of HDM.
ρ m − i ω + v ⋅ ∇ v = − e ρ e E + v × B − ρ m γ v − ρ m i ω β 2 ∇ ∇ · v + μ v △ v + 1 3 μ v ∇ ∇ · v .
The left-hand side of Equation (32) represents the total derivative of the velocity vector v of the electron fluid with respect to time. The first term on the right-hand side represents the Lorentz force acting on an individual volume element of the electron fluid. The second term is the standard damping term, the third term is the standard nonlocal expression, and the last two terms of the equation involve viscosive damping. The individual parameters of the model are as follows: B is the magnetic field, ρ m is the mass density of the electron fluid, e is the charge of the electron, ρ e   is the charge density, β   is the same nonlocal constant as in the standard HDM, and terms μ v and 1 3 μ v represent the relevant damping terms of viscosive attenuation in the convective form of the Navier-Stokes equation.
To proceed further, it is first convenient to assume the behavior of the electron gas density in the form: n r , t   ≈ n 0 + n 1 r , t , where n 0 is a constant equilibrium density and n 1 r , t is a linear deviation. Subsequently, it is possible to linearize the Equation (32), which leads to neglecting the influence of the magnetic field and introducing an approximate expressions for the current density, charge density and mass density as: J ≈ e n 0 v , ρ e ≈ e n 0 , and ρ m ≈ m e n 0 , where m e is the electron mass. If we multiply Equation (32) by the term − e / m e and perform the mentioned linearization, we obtain:
ω 2 + i ω γ J = i n 0 ω e 2 m e E − β 2 ∇ ∇ · J + i ω m e n 0 μ v ∆ J + i ω 3 m e n 0 μ v ∇ ∇ · J .
If we introduce a new damping parameter, γ v = μ v m e n 0 , which is analogous to kinematic viscosity in the classical approach, and further, according to the common definition, the plasma frequency ω p = e 2 n 0 m e ε 0 , then by straightforward adjustments of Equation (33), we obtain a modified novel version of the first equation of the standard HDM as follows:
β 2 − 1 3 i ω γ v ∇ ∇ · J − i ω γ v ∆ J + ω ω + i γ J = i ω ω p 2 ε 0 E .
Now the question arises whether it is possible to further generalize Equation (34). Since the HDM can be considered as a more sophisticated version of the Drude model for the electron dispersion in a metal, it is worth considering a similar modification approach as in the case of the actual Drude model. As it is well known, the original Drude model of the permittivity of a metal can be modified by the additional Lorentzian terms, resulting in the Drude-Lorentz model [51,52], to account for intraband (within the conduction band) and interband (between bands) electron energy transitions. By a simple analysis of the first equation of the HDM, i.e. the current Equation (34), by substituting the transverse fields, it can be determined that precisely the term ω ω + i γ J is the crucial for the Drude-type response of the permittivity ε e g of a free electron gas. Let us assume a generalization: ω ω + i γ   →   ω ω + i γ + ξ ω , where ξ ω is an as-yet undetermined function. For better clarity, let us denote U = ω ω + i γ + ξ ω and introduce an HDM with viscosive damping and a generalized Drude-Lorentz term in the following form:
 
  β 2 − i 1 3 ω γ v ∇ ∇ · J − i ω γ v ∆ J + U J = i ω ω p 2 ε 0 E ,
∇ × ∇ × E − k 0 2 ε t − ε e g , v E = i ω μ 0 J .
The generalized HDM defined by Equations (35) and (36) includes the three unknown parameters γ v ,   U ,   ε e g , v for which it will be necessary to establish the three conditions. The term ε e g , v has a similar meaning as ε e g   in the case of classical HDM, representing the permittivity of the electron gas, but it is generally different from ε e g . The total permittivity ε t of the metal is the same as in the classical HDM and is determined by tabulated values [53]. All these three parameters are clearly frequency dependent, however, for the sake of clarity in the mathematical notation, it will not be shown here.
Finding a solution for the generalized HDM is possible in a similar way as for the classical HDM. From Equation (36), it is possible to express the relationship for current density J and substitute it into Equation (35). In this way, an equation for the total electric field E only is obtained, which can be solved separately for its transverse and longitudinal components. In the case of a transverse field, it is advantageous to use the relationships between vector spherical harmonics ∇ × M = k t N ,   ∇ × N = k t M   and operator identities: ∇ × ∇ × Ψ = ∇ ∇ · Ψ − ∆ Ψ , ∇ · ∇ × Ψ = 0 , valid for any vector function Ψ . In the case of a longitudinal field, it is beneficial to use the identities ∇ ∇ · ∇   φ = ∇ ∆ φ and ∇ × ∇ φ = 0 . Based on the mentioned procedure, the relationships for the transversal and longitudinal wave numbers can be obtained in the following form:
k t 4 − i U ω γ v + k 0 2 ε t − ε e g , v k t 2 − i k 0 2 ω γ v ω p 2 − U ε t − ε e g , v = 0 ,
k l , v 2 = 1 β 2 + 4 3 i ω γ v U − ω p 2 ε t − ε e g , v .
Equations (37) and (38) serve as a starting point for finding the additional relationships for the parameters γ v ,   U   , and   ε e g , v . The classical HDM already includes a closely unspecified parameter ε e g . However, to ensure that the HDM solution is not too far from the experimentally measured values, a condition k t = k 0 ε t has been introduced for the transverse wave number [29] which is widely utilized and which will be also applied here. Considering that the standard solution of Equation (37) as a quadratic equation would provide only one condition, it seems reasonable to proceed by evaluating the brackets in (37), which allows us to obtain a pair of additional expressions without the need for introducing ad hoc parameters. One possibility is to set the second term in Equation (37) equal to k t     and the third term equal to zero. However, it can be easily verified that such a solution implies a zero value for the longitudinal wave number and therefore the absence of the nonlocal response. One option is to set the second term in Equation (37) equal to k t 2 and the third term equal to zero. However, such a solution implies a zero value for the longitudinal wave number, and therefore the absence of a nonlocal response. Therefore, as a solution, it is suggested to set the first bracket in Equation (37) to zero and assign the value of k t 4 to the last term in Equation (37). From Equation (37), we can easily obtain two conditions in the following form:
i ω γ v k 0 2 ε t − ε e g , v − U = 0 ,
U ε t − ε e g , v − ω p 2 = i ω γ v k 0 2 ε t 2 .
To establish the final condition, it is possible to start from the following consideration. Let us assume that the diffusion phenomenon is well phenomenologically described by the GNOR modification [34] of the HDM, although the magnitude of the diffusion constant D may still be the subject of investigation [38]. Thanks to the fact that the fourth term in the right-hand side of Equation (32) is responsible for the diffusion according to the classical description of fluid dynamics, this diffusion is indeed included in Equation (32). From the comparison of the GNOR model with the classical HD, it follows that diffusion manifests only in the change of the nonlocal parameter as: β 2 → β 2 + D γ − i ω . Under the assumption that diffusion is the main accompanying phenomenon caused by viscosive damping, it can be presumed that such viscosive damping will manifest in a similar way, primarily through a certain change in the nonlocal constant β . Based on the mentioned considerations and Equation (38), the third condition can be written in the following form:
γ v = − 3 4 i D ω − 1 γ − i ω .
From the given conditions (39), (40) and (41), the relationships for the parameters   U   and   ε e g , v can be derived. Specifically, from Equations (39) and (41), it is straightforward to obtain the following relationship for ε e g , v as:
ε e g , v = ε t − 4 3 U D γ − i ω k 0 2 .
Subsequently, from Equations (42), (40), and (41), the relationship for U can be derived in the following form:
U = k 0 3 4 D γ − i ω ω p 2 + i ω k 0 2 ε t 2 1 2 .
From the above Equations (41)–(43), it is finally possible to determine the longitudinal wave number defined by (38). As mentioned before, for the transverse wave number, the relationship k t = k 0 ε t holds. The value of the diffusion constant can be approximated as D ~ v F 2 / γ   according to [38,53] which we have also used in our calculations. It remains to mention that the expansion coefficients of the fields, including the substitution relations denoted by S and T , given in the second section, can be still used in the same form, but with a logical replacement of k l , ε e g , and ω ω + i γ by k l , v ,   ε e g , v , and U .

5. Results of HDM with Generalized Drude-Lorentz Term and Viscosive Damping

In this section, we turn to the results of the generalized HD model. From the outcome of our simulations, it is possible to come up with the following findings. First, in Figure 7, our viscosive damping generalization of the HDM model in comparison with the standard HDM, for a gold spherical nanoparticle, provides the extinction cross-section (standard HDM and our HDM-Vis.D. model) for a gold spherical particle (3 nm) in vacuum (Figure 7a) and water (Figure 7b). Additionally, the HDM-Vis.D. model has caused a small red correction to the blue shift of extinction local maxima (about 2 to 5 nm). Also, local maxima for gold spherical particles, for smallest particles, have disappeared, in comparison with the results from the standard HDM.
This is visible in Figure 7 where a blue curve, which represents the hydrodynamical model with viscosive damping, reaches in both cases (vacuum or water) higher values. Our model predicts a red correction to the blue shift about 3 nm in both cases (vacuum or water), the extinction cross-section in main resonance peak, as predicted from our model, has about 5 % higher value. Both HDM models also show that the resonance maximum is larger and narrower in the case of water surroundings. It is also seen in Figure 7 that both models converge to the same values in the case of water environment for shorter wavelengths (350 – 450 nm).
Next, Figure 8 shows a similar comparison of both models, now for a silver spherical nanoparticle in vacuum and water environment. The permittivity spectral dependence is for a silver obtained by the Drude-Lorentz dispersion model. In Figure 8, we can notice again weak differences between calculated values of the two models, as expected. Similarly, to gold, our model again predicts a red correction to the blue shift, somewhat higher values of extinction at the resonance peak (more noticeable for vacuum) and larger half-width values (also more obvious for vacuum)
Further, Figure 9. shows additional modification of calculations of the extinction spectra which are represented in Figure 7. This modification, the Landau damping, denotes additional size-dependent damping of localized plasmons on the interface of a metal structure. Figure 9 shows that the extinction cross-section of a gold spherical particle in water environment has almost the same value on shorter wavelengths (between 350-400 nm), similarly to Figure 7, whereas a particle in vacuum exhibits little differences between the two model predictions, on these short wavelengths.
The HDM model with both viscosive and Landau damping again predicts corrections to the blue shift for both cases of surrounding environment and it also shows slightly larger values in the resonance maxima, as compared to Figure 7. It is clearly visible that additional inclusion of Landau damping into the model causes lowering of resonance maxima and slower convergence to zero values of the extinction cross-section for long wavelengths (up to 650 nm).
As we can see in Figure 10, again our model with both viscosive and Landau damping, compared to the standard HDM, predicts corrections of blue shift and slightly larger resonance maximum value. Clearly, silver particles exhibit stronger influence of Landau damping, thus the resonance maxima peak is significantly larger and also narrower (compared to Figure 7). Descent of the extinction out of the resonance wavelength up to 400 nm is surprisingly faster. Our model with viscosive and Landau damping predicts new although very weak resonance on shorter wavelengths, this effect is maybe caused by Drude-Lorentz model for metal permittivity data.
Next, Figure 11 shows the calculated X-component of the electric field for our HDM with viscosive damping and classical HDM at the frequency of the resonant maximum of the HDM. At the first glance on the figures, a difference in the negative field values is noticeable. The calculated profile of the electric field inside a particle using HDM can help us evoking the idea of the direction of the incident plane wave, but this deduction using the field distribution in particle calculated by HDM with viscosive damping is not so apparent.
Figure 12 represents the electric current distribution in the plane cut of a spherical particle in axes X and Y. Both graphs display symmetric distribution of the current density in X and Y direction. At the first sight, these current profiles are very similar, but more detailed view reveals us that our HDM with viscosive damping predicts higher absolute values of the current density, and area around maxima value is situated out of the center of a particle (in the middle of each hemisphere) while classical HDM provides the maxima values near the center of a particle. It can be also mentioned that classical HDM predicts a slower descent to zero values of the current density near the boundary of a particle.
In Figure 13, when comparing the X-component electric fields calculated by the HDM and our HDM with viscosive damping, we can notice three major differences. The first distinction is that our model predicts only a twice stronger positive maximum value than the maximum negative value whereas the classical HDM predicts this ratio about three. Next thing concerns the majority of the area inside a particle which exhibits an inverse value of the field, i.e. where the HDM calculations display negative values, our model shows positive values and conversely. The last difference is related to close vicinity of a particle, in the case of the classical HDM, the particle is surrounded by a region with maximum positive values of the field whereas positive values of the field obtained by our model are located mainly in Y axes direction.
Figure 14 shows the density of the energy displayed in a plane cut defined by X and Y axes. How a reader can see, now the classical HDM predicts a large range of the energy density values than in the previous case with a vacuum environment. If we compare maximum and minimum values of the energy density within a particle, we find that the classical HDM predicts an unusually large difference of these values, moreover, they are visible areas inside the particle of a near zero density. Our model, however, predicts a different shape of distribution density of energy inside a particle and a significantly larger minimal value.
Also, Figure 15 shows a very similar situation as Figure 13, however our model predicts larger attenuation (positive maxima values) in comparison with the classical HDM. Figure 15b, corresponding to the HDM with viscosive dumping, displays that the lowest values of the X component of the electric field are located outside a particle whereas the HDM predicts that these values are located inside a particle and their absolute values are larger as compared to the HDM with viscosive dumping.
Next, Figure 16 shows us the distribution of the energy density in the plane cut defined by X and Y axes. Differences between the HDM and our model are clearly visible. HDM predicts that the areas with a maximal energy density are located mainly inside a particle and its vicinity. It can be further read from the figures that our model predicts higher values of the lowest energy density. The lowest energy is in both cases of HD models located inside a particle but the area of the highest energy density calculated by our model is oriented diagonally mainly outside of a particle.
As a reader can see from Figure 17, both models predict different distributions of the current density but every calculated pattern is symmetric by the X axis and antisymmetric by the Y axis. A next finding from these calculations is that our model shows two times larger current density which is situated near the edge of a particle whereas the area with a largest current density calculated by the HDM is located near the center of a particle. Next interesting point is that our model also shows that inside a particle there is a large area where the current density is nearly zero.
Additionally, Figure 18 displays, similarly to Figure 16, the X component of the electric field but now for a water environment and at the different wavelength. Although these two cases are not directly comparable, we can see that the shape of the field distribution of the electric field is similar to that predicted with the HDM. In contrast to the HDM calculation, however, of our model shows the opposite distribution of positive and negative values of the electric field in a particle. Very apparent is also a different distribution of the electric field outside of a particle, as it is determined by our model in comparison with the HDM. Again, our model predicts significantly smaller negative and positive values of the electric field.
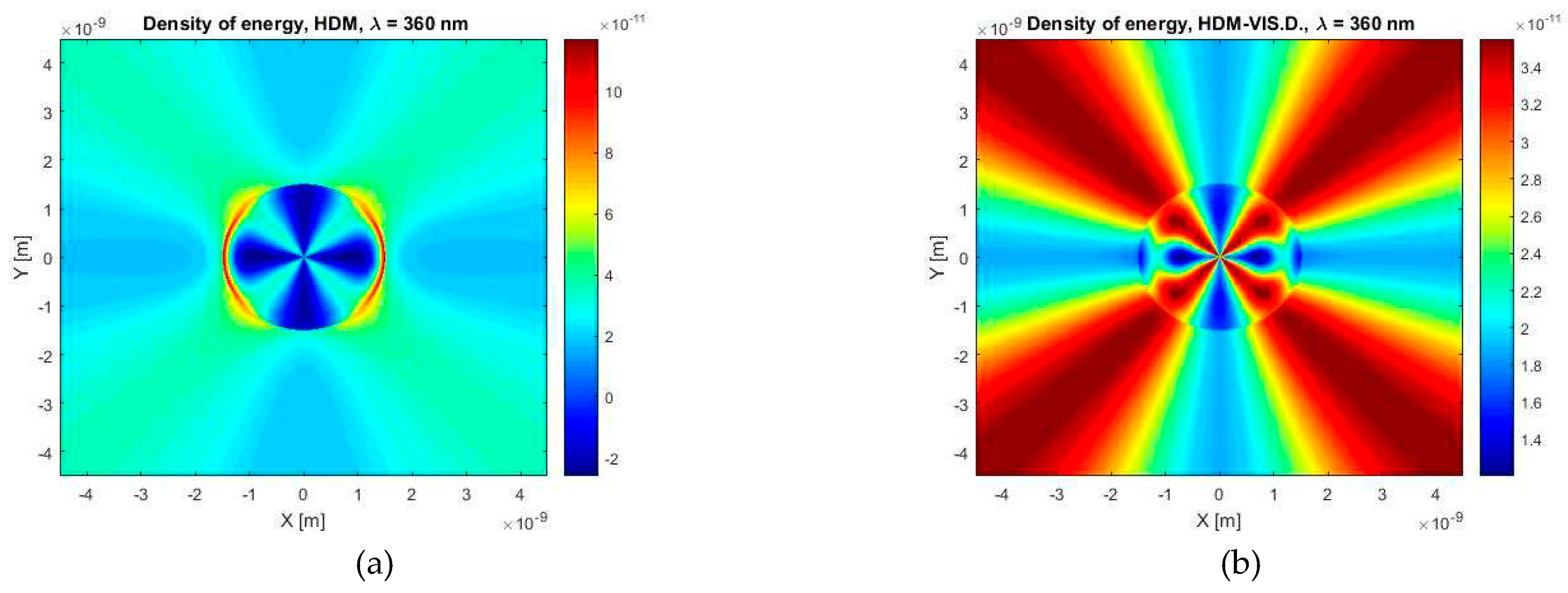
Finally, Figure 19 shows quite important data, demonstrating another disadvantage of the classic HDM. It should be noted that the same formula was used for these calculations of energy density as for the calculations shown in Figure 16. A quite strange findings is that standard HDM shows negative values of energy density in same places inside a particle volume; these unphysical values are not found applying the same calculations for gold particle. The standard HDM unlike our model displays large energy densities on the edge of a particle which is about three times larger than the maximum density calculated by our model. With these presented results we clearly demonstrated the applicability of our presented HD model with viscosive damping and generalized Drude-Lorentz term.

6. Conclusions

In this article, we have studied theoretically and numerically the linearized nonlocal plasmonic interaction of light with a simple spherical metallic nanoparticle. We have concentrated on understanding the interaction and developing a simple model capable of predicting the longitudinal nonlocal response based on the linearized hydrodynamic model, generalizing the standard nonlocal HD model. Using this model, we have studied the electric field interaction with a nanoparticle immersed in dielectric surrounding media (such as air or water). Our generalization conveys on the inclusion of the generalized Drude-Lorentz term and viscosive current damping in connection to Landau damping. We have demonstrated the applicability of our extended model by comparing the extinction cross-section predictions of both gold and silver spherical nanoparticles. The results confirm the generally assumed conclusion that metallic particles with a few nanometers in diameter possess a blue resonance shift. It was also found that the HD model predicts a lower electric field intensity inside and around the particle. The modification in the form of Landau’s attenuation corrects the blue shift and affects the shape of the spectral course of the extinction.

Author Contributions

Methodology, M.B. and I.R.; Software, M.B.; Validation, M.B.; Formal analysis, M.B.; Investigation, M.B. and I.R.; Writing—original draft, M.B. and I.R.; Supervision, I.R.; Project administration, I.R. All authors have read and agreed to the published version of the manuscript.

Funding

The research has been performed with the support of the Czech Science Foundation, grant number GA21-05259S, and the MEYS of the Czech Republic grant number CZ.02.1.01/0.0/0.0/16_019/0000778 of the European Structural and Investments Funds.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data available from the authors upon the personal request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ostrowski, J.C.; Mikhailovsky, A.; Bussian, D.A.; Summers, M.A.; Buratto, S.K.; Bazan, G.C. Enhancement of phosphorescence by surface-plasmon resonances in colloidal metal nanoparticles: the role of aggregates. Adv. Funct. Mater. 2006, 16, 1221–1227. [Google Scholar] [CrossRef]
  2. Landström, L.; Brodoceanu, D.; Piglmayer, K.; Bäuerle, D. Extraordinary optical transmission through metal-coated colloidal monolayers. Appl. Phys. A 2006, 84, 373–377. [Google Scholar] [CrossRef]
  3. Indhu, A.R.; Keerthana, L.; Dharmalingam, G. Plasmonic nanotechnology for photothermal applications – an evaluation. Beilstein J. Nanotechnol. 2023, 14, 380–419. [Google Scholar] [CrossRef] [PubMed]
  4. Tian, F.; Bonnier, F.; Casey, A.; Shanahan, A.E.; Byrne, H.J. Surface enhanced Raman scattering with gold nanoparticles: effect of particle shape. Anal Methods 2014, 6, 9116–9123. [Google Scholar] [CrossRef]
  5. Balčytis, A.; Nishijima, Y.; Krishnamoorthy, S.; Kuchmizhak, A.; Stoddart, P.R.; Petruškevičius, R.; Juodkazis, S. From fundamental toward applied SERS: shared principles and divergent approaches. Adv. Opt. Mater. 2018, 6, 1800292. [Google Scholar] [CrossRef]
  6. Proença, M.; Rodrigues, M.S.; Borges, J.; Vaz, F. Gas sensing with nanoplasmonic thin films composed of nanoparticles (Au, Ag) dispersed in a CuO matrix. Coatings 2019, 9, 337. [Google Scholar] [CrossRef]
  7. Rodrigues, M.S.; Borges, J.; Lopes, C.; Pereira, R.M.S.; Vasilevskiy, M.I.; Vaz, F. Gas sensors based on localized surface plasmon resonances: synthesis of oxide films with embedded metal nanoparticles: theory, simulation, and sensitivity enhancement strategies. Appl. Sci. 2021, 11, 5388. [Google Scholar] [CrossRef]
  8. Long, N.V.; Teranishi, T.; Yang, Y.; Thi, C.M.; Cao, Y.; Nogami, M. Iron oxide nanoparticles for next generation gas sensors. Int. J. Metall. Mater. Eng. 2015, 1. [Google Scholar] [CrossRef] [PubMed]
  9. Tittl, A.; Giessen, H.; Liu, N. Plasmonic gas and chemical sensing. Nanophotonics 2014, 3, 157–180. [Google Scholar] [CrossRef]
  10. Temple, T.L.; Bagnall, D.M. Optical properties of gold and aluminium nanoparticles for silicon solar cell applications. J. Appl. Phys. 2011, 109, 084343. [Google Scholar] [CrossRef]
  11. Chang, D.E.; Sørensen, A.S.; Hemmer, P.R.; Lukin, M.D. Quantum optics with surface plasmons. Phys. Rev. Lett. 2006, 97, 053002. [Google Scholar] [CrossRef] [PubMed]
  12. Zhu, Z.; Ni, Y.; Lv, Q.; Geng, J.; Xie, W.; Li, F.; Chen, J. Surface plasmon mediates the visible light–responsive lithium–oxygen battery with Au nanoparticles on defective carbon nitride. Proc. Natl. Acad. Sci. 2021, 118, e2024619118. [Google Scholar] [CrossRef]
  13. Marques Mota, F.; Yu, S.; Chae, K.; Che Mohamad, N.A.R.; Kim, D.H. An analysis of the promise of Li–O2 and Li–S batteries incorporating plasmonic metal nanostructures. Mater. Today Energy 2022, 27, 101033. [Google Scholar] [CrossRef]
  14. Wu, T.; Shao, Y.; Wang, Y.; Cao, S.; Cao, W.; Zhang, F.; Liao, C.; He, J.; Huang, Y.; Hou, M.; et al. Surface plasmon resonance biosensor based on gold-coated side-polished hexagonal structure photonic crystal fiber. Opt. Express 2017, 25, 20313. [Google Scholar] [CrossRef]
  15. Chen, J.; Gong, M.; Fan, Y.; Feng, J.; Han, L.; Xin, H.L.; Cao, M.; Zhang, Q.; Zhang, D.; Lei, D.; et al. Collective plasmon coupling in gold nanoparticle clusters for highly efficient photothermal therapy. ACS Nano 2022, 16, 910–920. [Google Scholar] [CrossRef]
  16. Parsons, J.; Hendry, E.; Sambles, J.R.; Barnes, W.L. Localized surface-plasmon resonances and negative refractive index in nanostructured electromagnetic metamaterials. Phys. Rev. B 2009, 80, 245117. [Google Scholar] [CrossRef]
  17. Fan, X.; Zheng, W.; Singh, D.J. Light scattering and surface plasmons on small spherical particles. Light Sci. Appl. 2014, 3, e179–e179. [Google Scholar] [CrossRef]
  18. Dutta, A.; Tiainen, V.; Toppari, J.J. Numerical study on the limit of quasi-static approximation for plasmonic nanosphere; Bikaner, India, 2020; p. 050012.
  19. Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, 2007; ISBN 978-0-387-33150-8. [Google Scholar]
  20. Quinten, M. Optical Properties of Nanoparticle Systems: Mie and Beyond; Wiley-VCH: Weinheim, Germany, 2011; ISBN 978-3-527-41043-9. [Google Scholar]
  21. Baig, N.; Kammakakam, I.; Falath, W. Nanomaterials: A review of synthesis methods, properties, recent progress, and challenges. Mater. Adv. 2021, 2, 1821–1871. [Google Scholar] [CrossRef]
  22. Qiao, J.; Qi, L. Recent progress in plant-gold nanoparticles fabrication methods and bio-applications. Talanta 2021, 223, 121396. [Google Scholar] [CrossRef]
  23. Liu, Y.; Plate, P.; Hinrichs, V.; Köhler, T.; Song, M.; Manley, P.; Schmid, M.; Bartsch, P.; Fiechter, S.; Lux-Steiner, M.Ch.; et al. Size- and density-controlled deposition of Ag nanoparticle films by a novel low-temperature spray chemical vapour deposition method—research into mechanism, particle growth and optical simulation. J. Nanoparticle Res. 2017, 19, 141. [Google Scholar] [CrossRef]
  24. Toscano, G.; Raza, S.; Yan, W.; Jeppesen, C.; Xiao, S.; Wubs, M.; Jauho, A.-P.; Bozhevolnyi, S.I.; Mortensen, N.A. Nonlocal response in plasmonic waveguiding with extreme light confinement. Nanophotonics 2013, 2, 161–166. [Google Scholar] [CrossRef]
  25. Hiremath, K.R.; Zschiedrich, L.; Schmidt, F. Numerical solution of nonlocal hydrodynamic Drude model for arbitrary shaped nano-plasmonic structures using Nédélec finite elements. J. Comput. Phys. 2012, 231, 5890–5896. [Google Scholar] [CrossRef]
  26. McMahon, J.M.; Gray, S.K.; Schatz, G.C. Calculating nonlocal optical properties of structures with arbitrary shape. Phys. Rev. B 2010, 82, 035423. [Google Scholar] [CrossRef]
  27. Ginzburg, P.; Zayats, A.V. Localized surface plasmon resonances in spatially dispersive nano-objects: phenomenological treatise. ACS Nano 2013, 7, 4334–4342. [Google Scholar] [CrossRef] [PubMed]
  28. García De Abajo, F.J. Nonlocal effects in the plasmons of strongly interacting nanoparticles, dimers, and waveguides. J. Phys. Chem. C 2008, 112, 17983–17987. [Google Scholar] [CrossRef]
  29. David, C.; García De Abajo, F.J. Spatial nonlocality in the optical response of metal nanoparticles. J. Phys. Chem. C 2011, 115, 19470–19475. [Google Scholar] [CrossRef]
  30. Benedicto, J.; Pollès, R.; Ciracì, C.; Centeno, E.; Smith, D.R.; Moreau, A. Numerical tool to take nonlocal effects into account in metallo-dielectric multilayers. J. Opt. Soc. Am. A 2015, 32, 1581. [Google Scholar] [CrossRef]
  31. David, C.; Mortensen, N.A.; Christensen, J. Perfect Imaging, Epsilon-near zero phenomena and waveguiding in the scope of nonlocal effects. Sci. Rep. 2013, 3, 2526. [Google Scholar] [CrossRef]
  32. Pitelet, A.; Mallet, É.; Centeno, E.; Moreau, A. Fresnel coefficients and Fabry-Perot formula for spatially dispersive metallic layers. Phys. Rev. B 2017, 96, 041406. [Google Scholar] [CrossRef]
  33. Raza, S.; Toscano, G.; Jauho, A.-P.; Wubs, M.; Mortensen, N.A. Unusual resonances in nanoplasmonic structures due to nonlocal response. Phys. Rev. B 2011, 84, 121412. [Google Scholar] [CrossRef]
  34. Mortensen, N.A.; Raza, S.; Wubs, M.; Søndergaard, T.; Bozhevolnyi, S.I. A generalized non-Local optical response theory for plasmonic nanostructures. Nat. Commun. 2014, 5, 3809. [Google Scholar] [CrossRef] [PubMed]
  35. Svendsen, M.K.; Wolff, C.; Jauho, A.-P.; Mortensen, N.A.; Tserkezis, C. Role of diffusive surface scattering in nonlocal plasmonics. J. Phys. Condens. Matter 2020, 32, 395702. [Google Scholar] [CrossRef] [PubMed]
  36. Karimi, S.; Moshaii, A.; Abbasian, S.; Nikkhah, M. Surface plasmon resonance in small gold nanoparticles: introducing a size-dependent plasma frequency for nanoparticles in quantum regime. Plasmonics 2019, 14, 851–860. [Google Scholar] [CrossRef]
  37. Khurgin, J.B.; Sun, G. Landau Damping—The ultimate limit of field confinement and enhancement in plasmonic structures. In Quantum Plasmonics; Bozhevolnyi, S.I., Martin-Moreno, L., Garcia-Vidal, F., Eds.; Springer Series in Solid-State Sciences; Springer International Publishing: Cham, 2017; ISBN 978-3-319-45819-9. [Google Scholar]
  38. Raza, S.; Bozhevolnyi, S.I.; Wubs, M.; Asger Mortensen, N. Nonlocal optical response in metallic nanostructures. J. Phys. Condens. Matter 2015, 27, 183204. [Google Scholar] [CrossRef]
  39. Huynh, D.-N.; Moeferdt, M.; Matyssek, C.; Wolff, C.; Busch, K. Ultrafast three-wave-mixing in plasmonic nanostructures. Appl. Phys. B 2016, 122, 139. [Google Scholar] [CrossRef]
  40. Moeferdt, M.; Kiel, T.; Sproll, T.; Intravaia, F.; Busch, K. Plasmonic modes in nanowire dimers: a study based on the hydrodynamic Drude model including nonlocal and nonlinear effects. Phys. Rev. B 2018, 97, 075431. [Google Scholar] [CrossRef]
  41. Petrov, A.S.; Svintsov, D. Viscosity-limited drift instabilities in two-dimensional electron systems. Phys. Rev. Appl. 2022, 17, 054026. [Google Scholar] [CrossRef]
  42. Diaw, A.; Murillo, M.S. A Viscous quantum hydrodynamics model based on dynamic density functional theory. Sci. Rep. 2017, 7, 15352. [Google Scholar] [CrossRef]
  43. Tokatly, I.; Pankratov, O. Hydrodynamic theory of an electron gas. Phys. Rev. B 1999, 60, 15550–15553. [Google Scholar] [CrossRef]
  44. Scholl, J.A.; Koh, A.L.; Dionne, J.A. Quantum plasmon resonances of individual metallic nanoparticles. Nature 2012, 483, 421–427. [Google Scholar] [CrossRef] [PubMed]
  45. Alabastri, A.; Tuccio, S.; Giugni, A.; Toma, A.; Liberale, C.; Das, G.; Angelis, F.; Fabrizio, E.; Zaccaria, R. Molding of plasmonic resonances in metallic nanostructures: dependence of the non-linear electric permittivity on system size and temperature. Materials 2013, 6, 4879–4910. [Google Scholar] [CrossRef] [PubMed]
  46. Wubs, M. Classification of scalar and dyadic nonlocal optical response models. Opt. Express 2015, 23, 31296–31312. [Google Scholar] [CrossRef] [PubMed]
  47. Eremin, Y.A. Scattering|Scattering Theory. In Encyclopedia of Modern Optics; Elsevier, 2005; pp. 326–330. ISBN 978-0-12-369395-2. [Google Scholar]
  48. Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Scattering, Absorption, and Emission of Light by Small Particles; Cambridge University Press, 2002; ISBN 978-0-521-78252-4. [Google Scholar]
  49. Batchelor, G.K. An Introduction to Fluid Dynamics, 1st ed.; Cambridge University Press, 2000; ISBN 978-0-521-66396-0. [Google Scholar]
  50. West, P.R.; Ishii, S.; Naik, G.V.; Emani, N.K.; Shalaev, V.M.; Boltasseva, A. Searching for better plasmonic materials. Laser Photonics Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef]
  51. Rakić, A.D.; Djurišić, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271. [Google Scholar] [CrossRef]
  52. Handbook of Optical Constants of Solids II; Palik, E.D. (Ed.) Academic Press: Boston, 1991; ISBN 978-0-12-544422-4. [Google Scholar]
  53. Kreibig, U.; Fragstein, C.V. The limitation of electron mean free path in small silver particles. Zeitschrift für Physik. 1969, 224, 307–323. [Google Scholar] [CrossRef]
Preprints 79946 g001
Figure 1. Schematic representation of a plane wave interacting with a spherical metallic particle. A plane wave with the electric intensity E i n c and wave vector k i n c is incident along the Z-axis onto a spherical particle. The electric field E i n t is induced within the particle and simultaneously the scattered electric field E s c a is formed in vicinity of a particle.
Figure 1. Schematic representation of a plane wave interacting with a spherical metallic particle. A plane wave with the electric intensity E i n c and wave vector k i n c is incident along the Z-axis onto a spherical particle. The electric field E i n t is induced within the particle and simultaneously the scattered electric field E s c a is formed in vicinity of a particle.
Preprints 79946 g001
Preprints 79946 g002
Figure 2. Comparison of the extinction cross sections of a gold spherical particle with a diameter of 3 nm according to the classical Mie theory and the nonlocal HD model, (a) for a vacuum environment and (b) for a water environment.
Figure 2. Comparison of the extinction cross sections of a gold spherical particle with a diameter of 3 nm according to the classical Mie theory and the nonlocal HD model, (a) for a vacuum environment and (b) for a water environment.
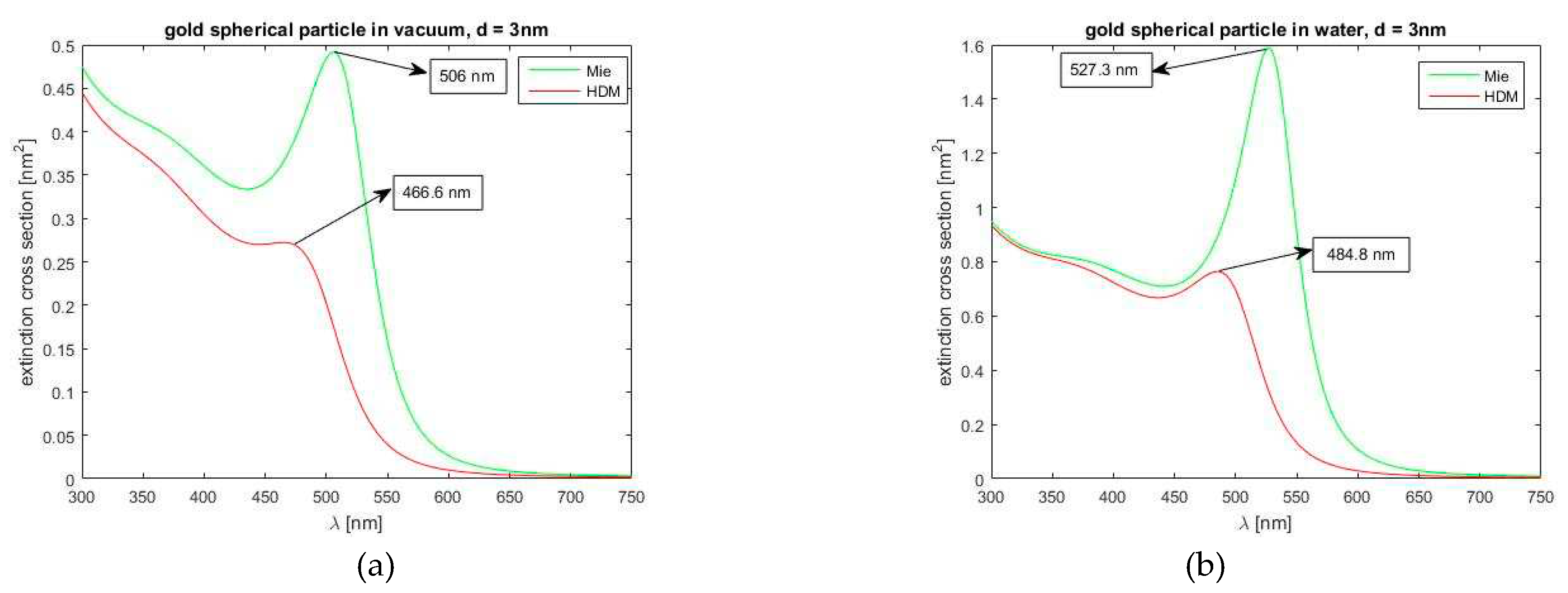
Preprints 79946 g002
Preprints 79946 g003
Figure 3. Comparison of the extinction cross-sections of a silver spherical particle with a diameter of 3 nm according to the classical Mie theory and the nonlocal HD model, (a) for a vacuum environment and (b) for a water environment.
Figure 3. Comparison of the extinction cross-sections of a silver spherical particle with a diameter of 3 nm according to the classical Mie theory and the nonlocal HD model, (a) for a vacuum environment and (b) for a water environment.
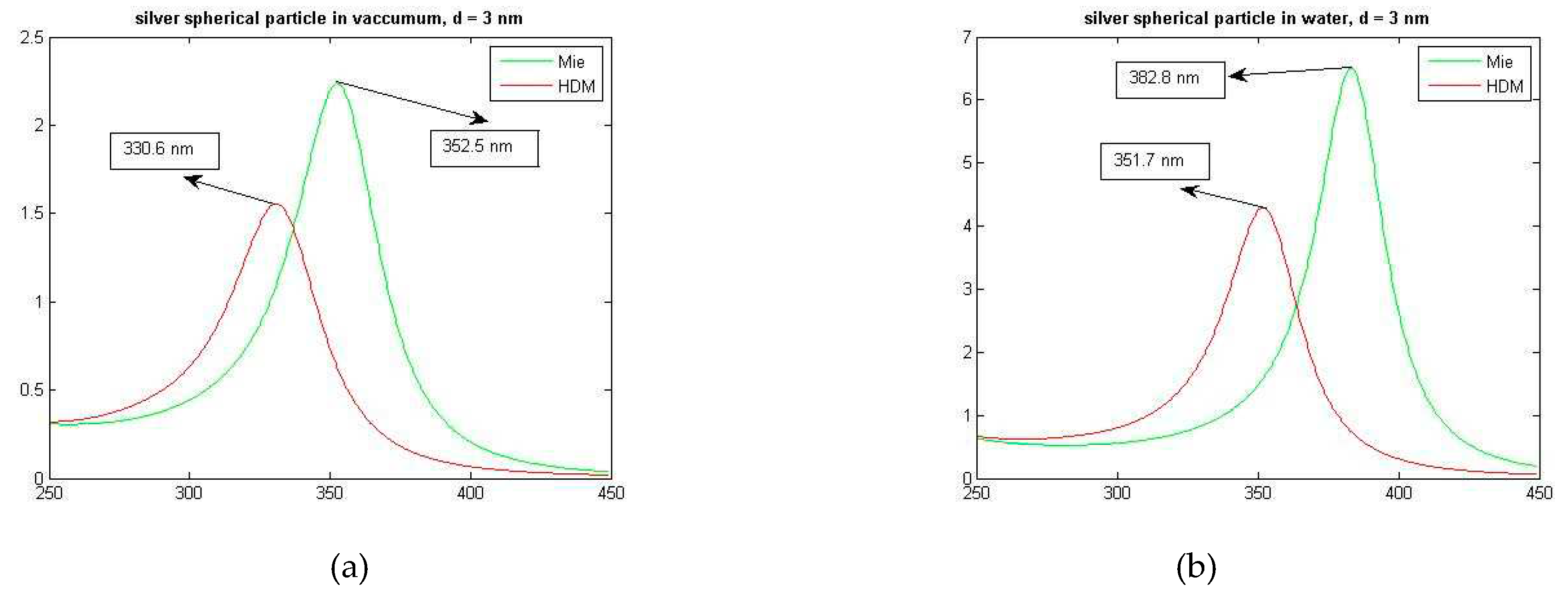
Preprints 79946 g003
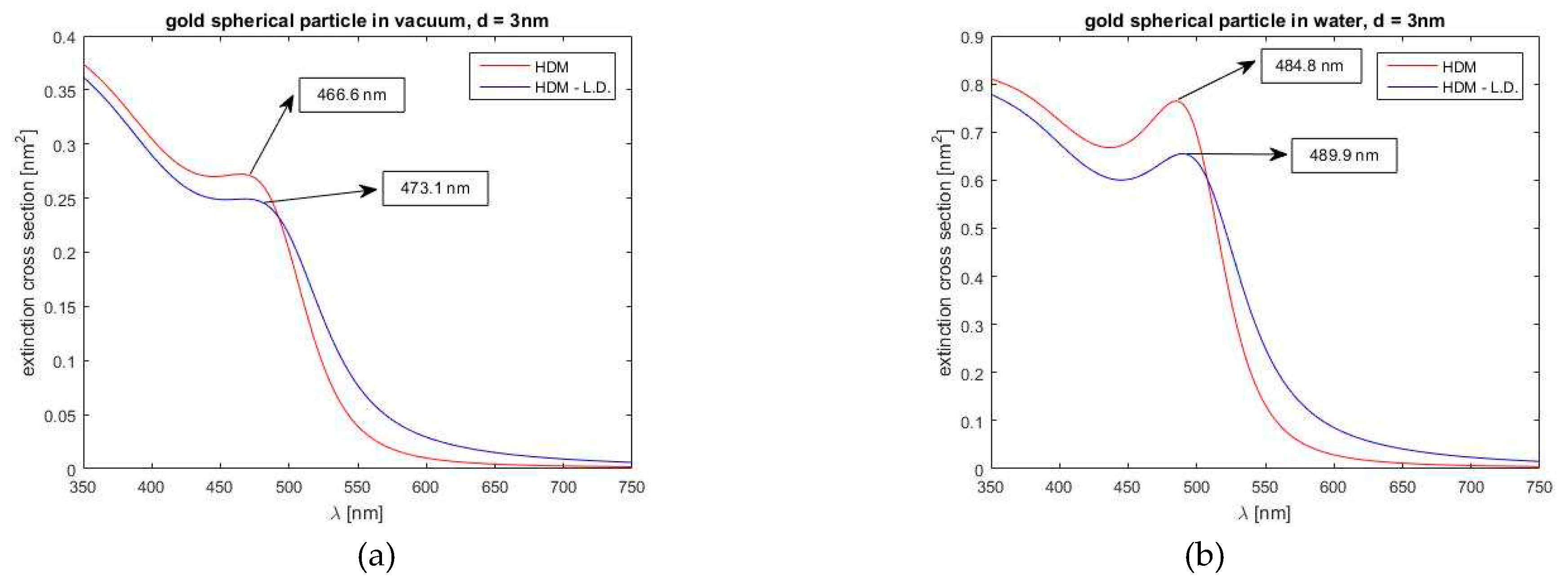
Preprints 79946 g004
Figure 4. Comparison of the extinction cross-sections of a silver spherical particle with a diameter of 3 nm according to the standard HDM and the HDM – L.D. (HDM with Landau damping) model, (a) for a vacuum environment and (b) for a water environment.
Figure 4. Comparison of the extinction cross-sections of a silver spherical particle with a diameter of 3 nm according to the standard HDM and the HDM – L.D. (HDM with Landau damping) model, (a) for a vacuum environment and (b) for a water environment.
Preprints 79946 g004
Preprints 79946 g005
Figure 5. The X-component of the electric field calculated for the wavelength of λ = 527.3 nm and the case of a gold spherical particle with a diameter of 3 nm in a water environment, according to (a) Mie theory and (b) HDM.
Figure 5. The X-component of the electric field calculated for the wavelength of λ = 527.3 nm and the case of a gold spherical particle with a diameter of 3 nm in a water environment, according to (a) Mie theory and (b) HDM.
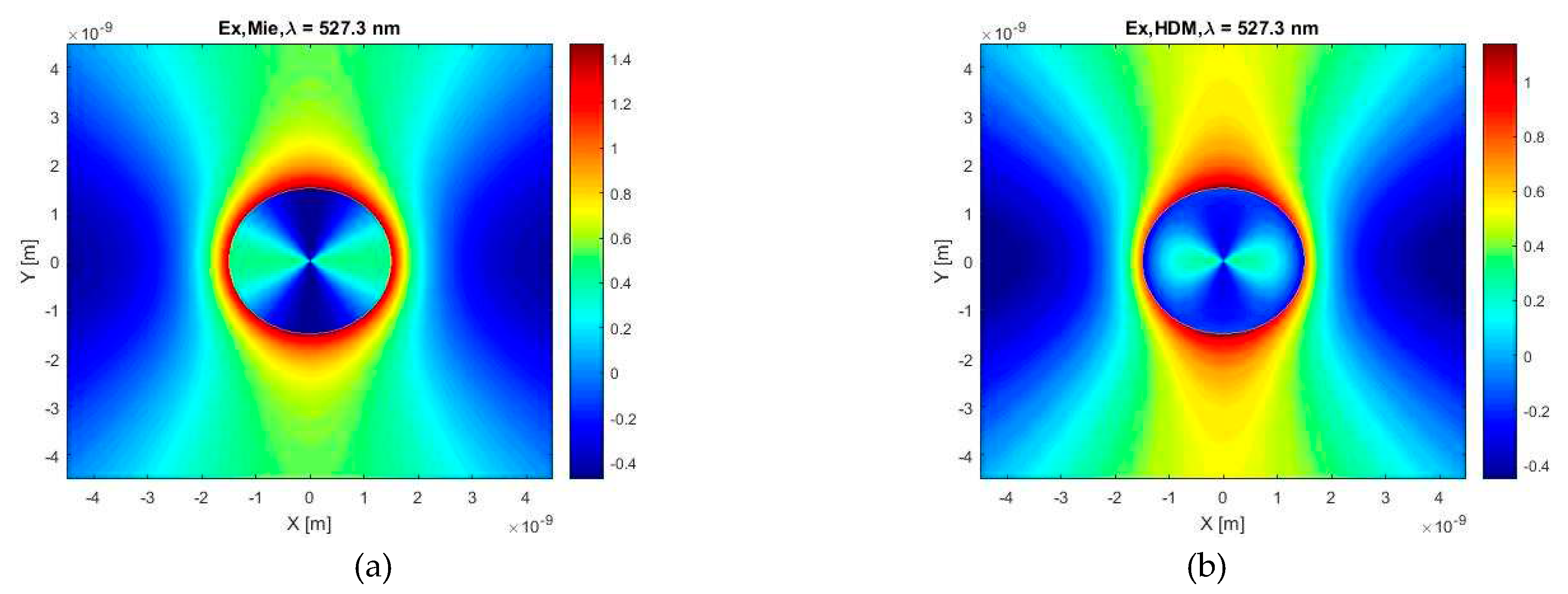
Preprints 79946 g005
Preprints 79946 g006
Figure 6. The X-component of the electric field calculated for a wavelength of λ = 486 nm and the case of a gold spherical particle with a diameter of 3 nm in a water environment, according to (a) Mie theory and (b) HDM.
Figure 6. The X-component of the electric field calculated for a wavelength of λ = 486 nm and the case of a gold spherical particle with a diameter of 3 nm in a water environment, according to (a) Mie theory and (b) HDM.
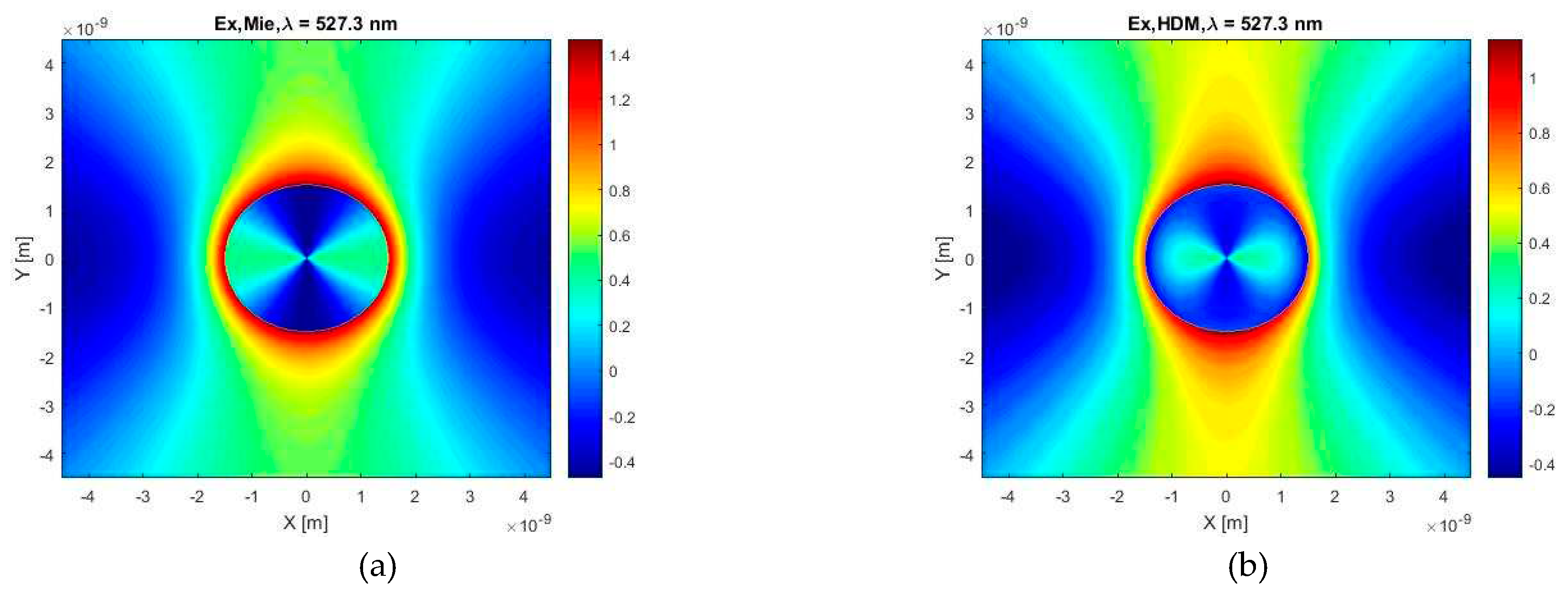
Preprints 79946 g006
Preprints 79946 g007
Figure 7. Comparison of the extinction cross-sections of a gold spherical particle with a diameter of 3 nm according to the HDM and the and HDM-Vis.D model: (a) for a vacuum environment and (b) for a water environment.
Figure 7. Comparison of the extinction cross-sections of a gold spherical particle with a diameter of 3 nm according to the HDM and the and HDM-Vis.D model: (a) for a vacuum environment and (b) for a water environment.
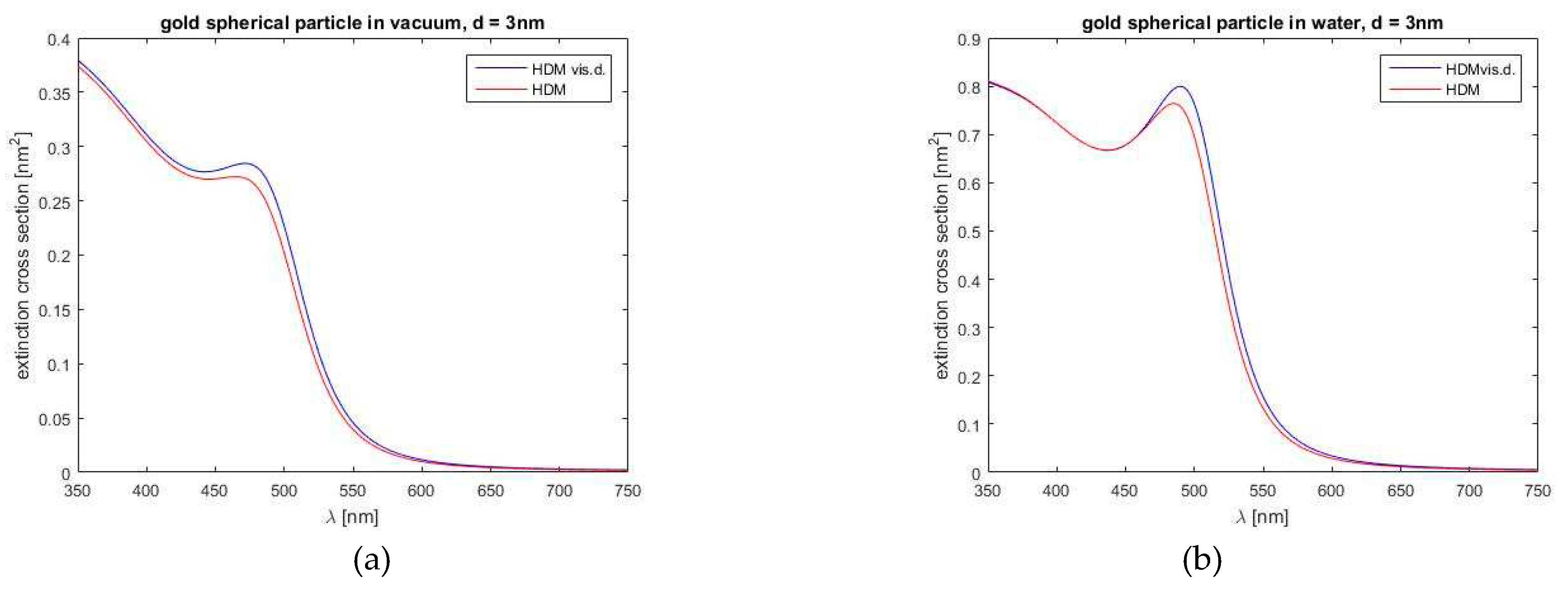
Preprints 79946 g007
Preprints 79946 g008
Figure 8. Comparison of the extinction cross-sections of a silver spherical particle with a diameter of 3 nm according to the HDM and the and HDM-Vis.D. model: (a) for a vacuum environment and (b) for a water environment.
Figure 8. Comparison of the extinction cross-sections of a silver spherical particle with a diameter of 3 nm according to the HDM and the and HDM-Vis.D. model: (a) for a vacuum environment and (b) for a water environment.
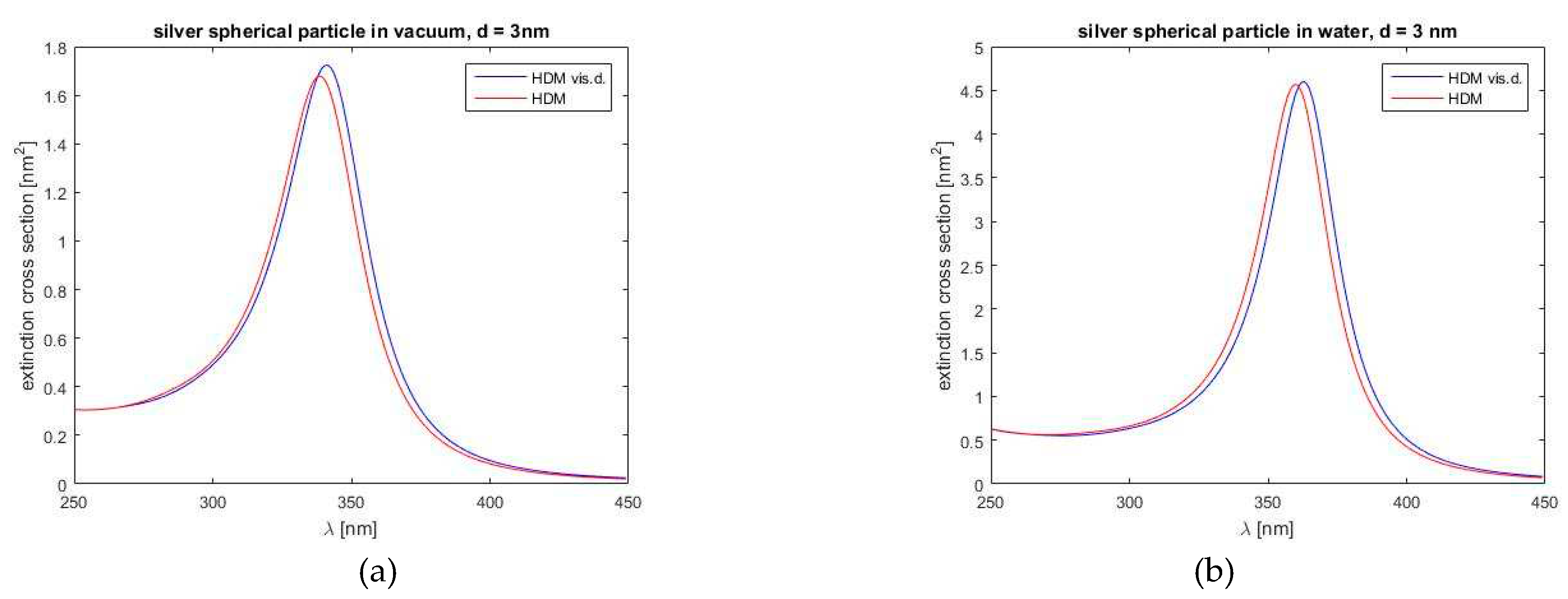
Preprints 79946 g008
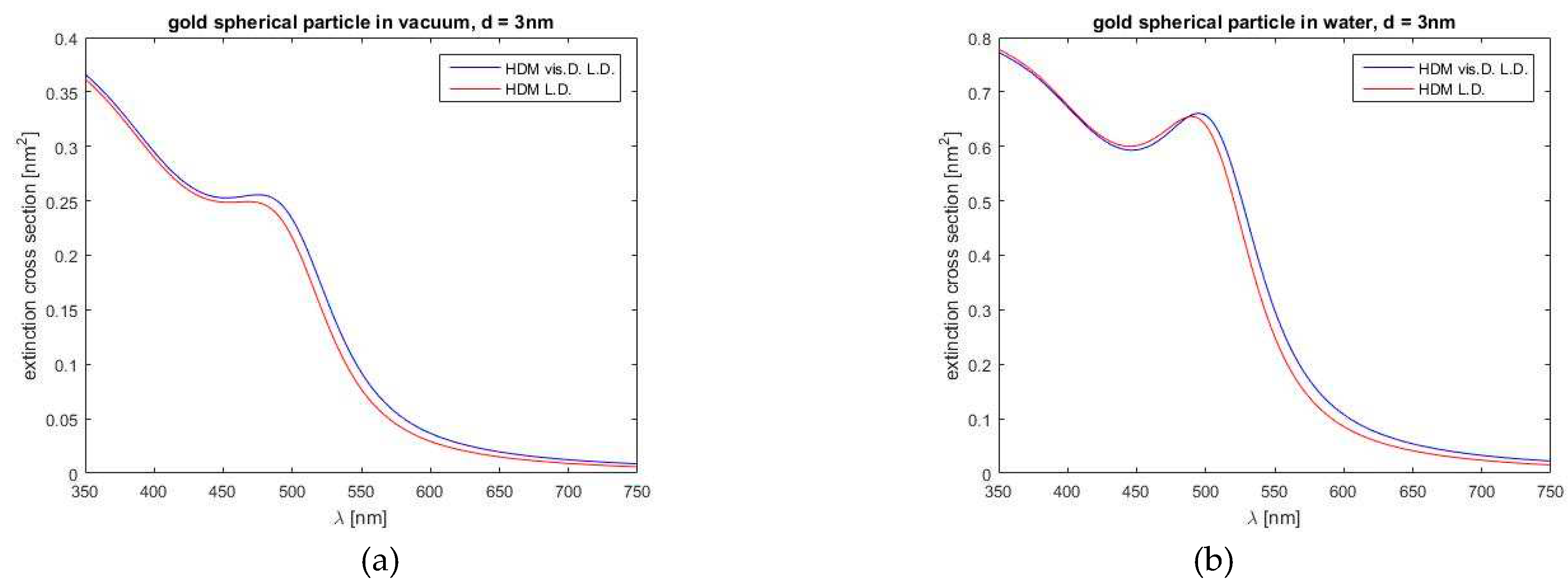
Preprints 79946 g009
Figure 9. Comparison of the extinction cross-sections of a gold spherical particle with a diameter of 3 nm according to the HDM L.D and the HDM-Vis.D. L.D. (both HDM and HDM-Vis.D. with Landau damping): (a) for a vacuum environment and (b) for a water environment.
Figure 9. Comparison of the extinction cross-sections of a gold spherical particle with a diameter of 3 nm according to the HDM L.D and the HDM-Vis.D. L.D. (both HDM and HDM-Vis.D. with Landau damping): (a) for a vacuum environment and (b) for a water environment.
Preprints 79946 g009
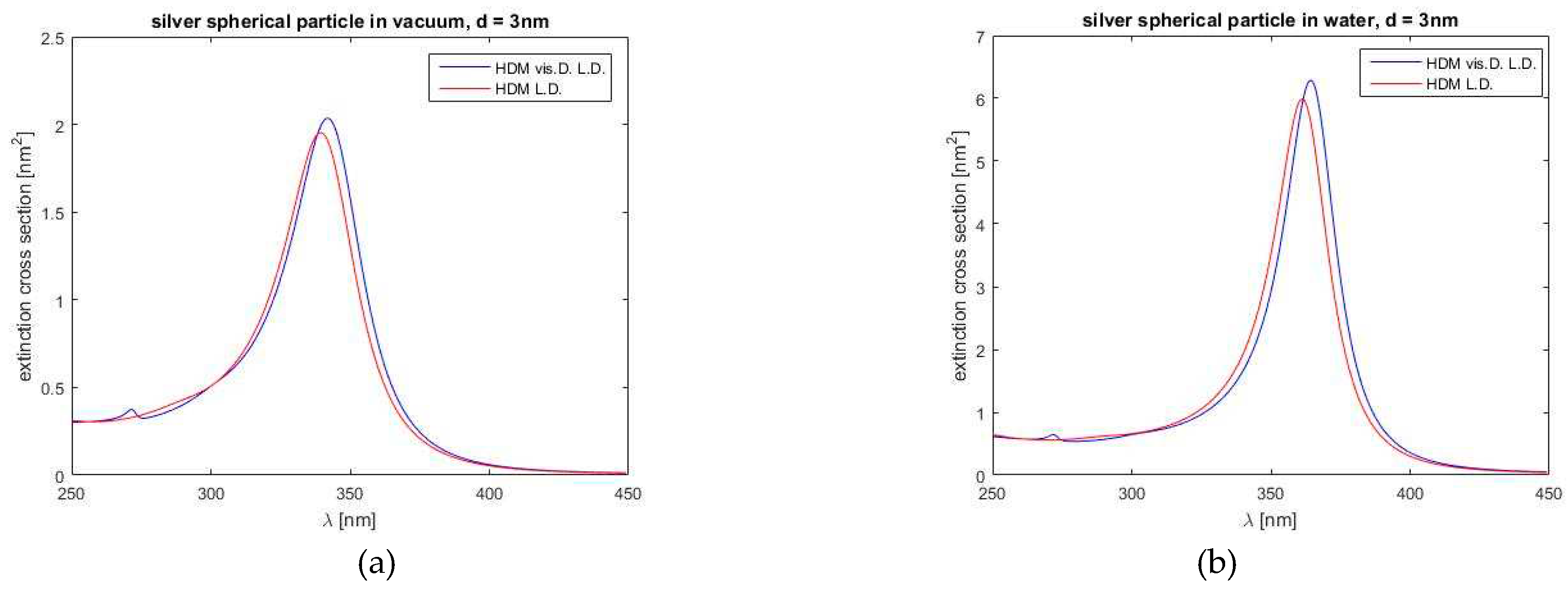
Preprints 79946 g010
Figure 10. Comparison of the extinction cross-sections of a silver spherical particle with a diameter of 3 nm according to the HDM L.D and the HDM-Vis.D. L.D. (both HDM and HDM-Vis.D. with Landau damping): (a) for a vacuum environment and (b) for a water environment.
Figure 10. Comparison of the extinction cross-sections of a silver spherical particle with a diameter of 3 nm according to the HDM L.D and the HDM-Vis.D. L.D. (both HDM and HDM-Vis.D. with Landau damping): (a) for a vacuum environment and (b) for a water environment.
Preprints 79946 g010
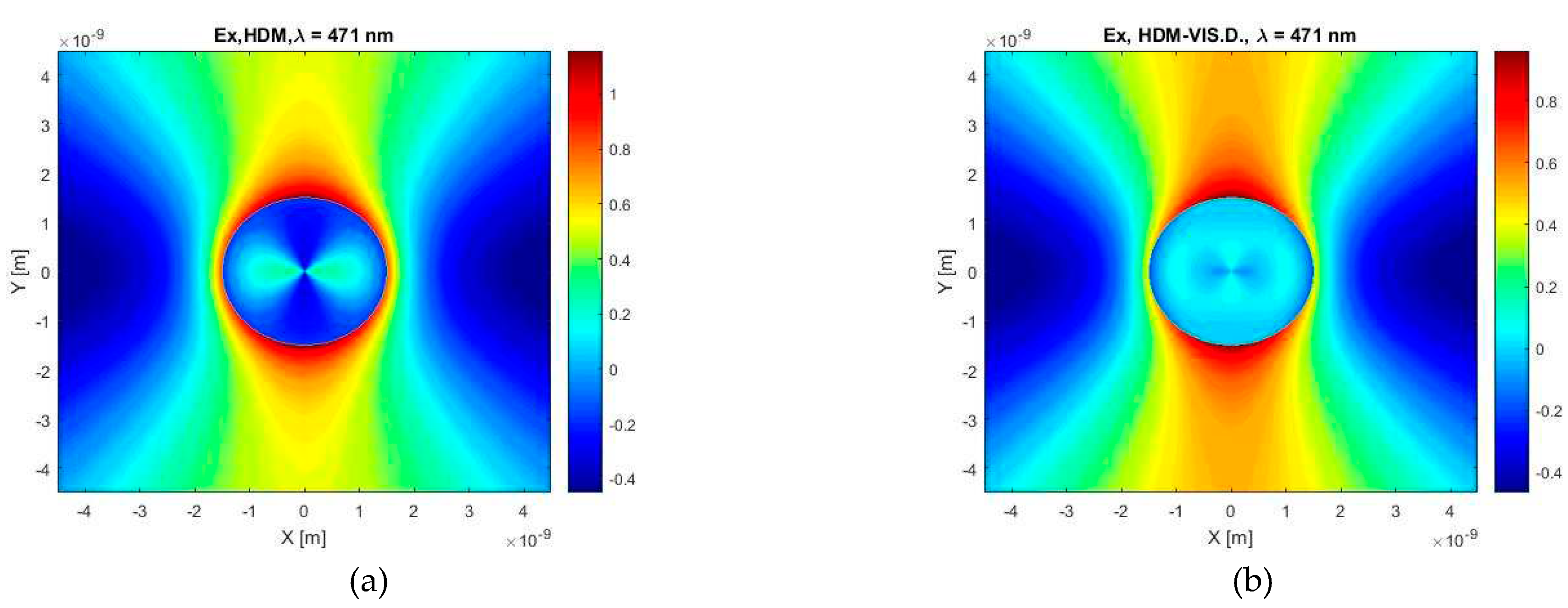
Preprints 79946 g011
Figure 11. The X-component of the electric field calculated for the wavelength of λ = 471 nm and the case of a gold spherical particle with a diameter of 3 nm in a vacuum environment, according to (a) HDM and (b) HDM–Vis.D.
Figure 11. The X-component of the electric field calculated for the wavelength of λ = 471 nm and the case of a gold spherical particle with a diameter of 3 nm in a vacuum environment, according to (a) HDM and (b) HDM–Vis.D.
Preprints 79946 g011
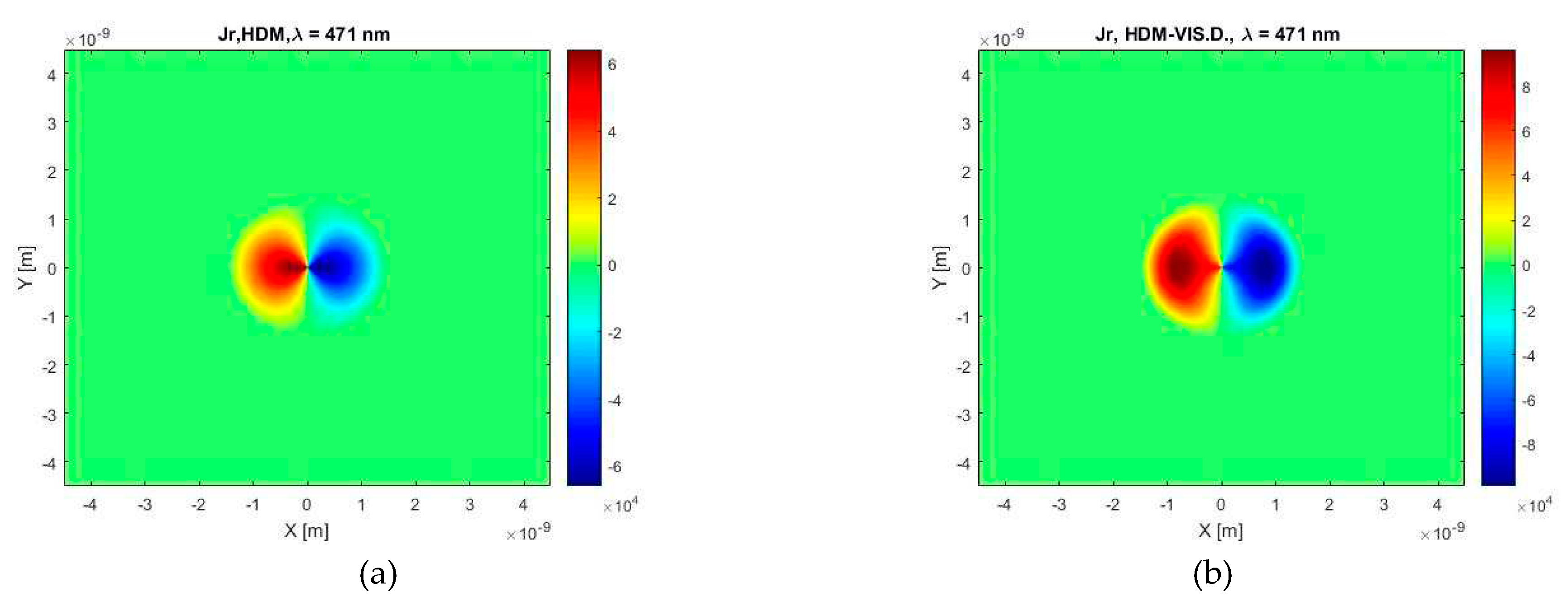
Preprints 79946 g012
Figure 12. The radial component of the current density calculated for the wavelength of λ = 471 nm and the case of a gold spherical particle with a diameter of 3 nm in a vacuum environment, according to (a) HDM and (b) HDM–Vis.D.
Figure 12. The radial component of the current density calculated for the wavelength of λ = 471 nm and the case of a gold spherical particle with a diameter of 3 nm in a vacuum environment, according to (a) HDM and (b) HDM–Vis.D.
Preprints 79946 g012
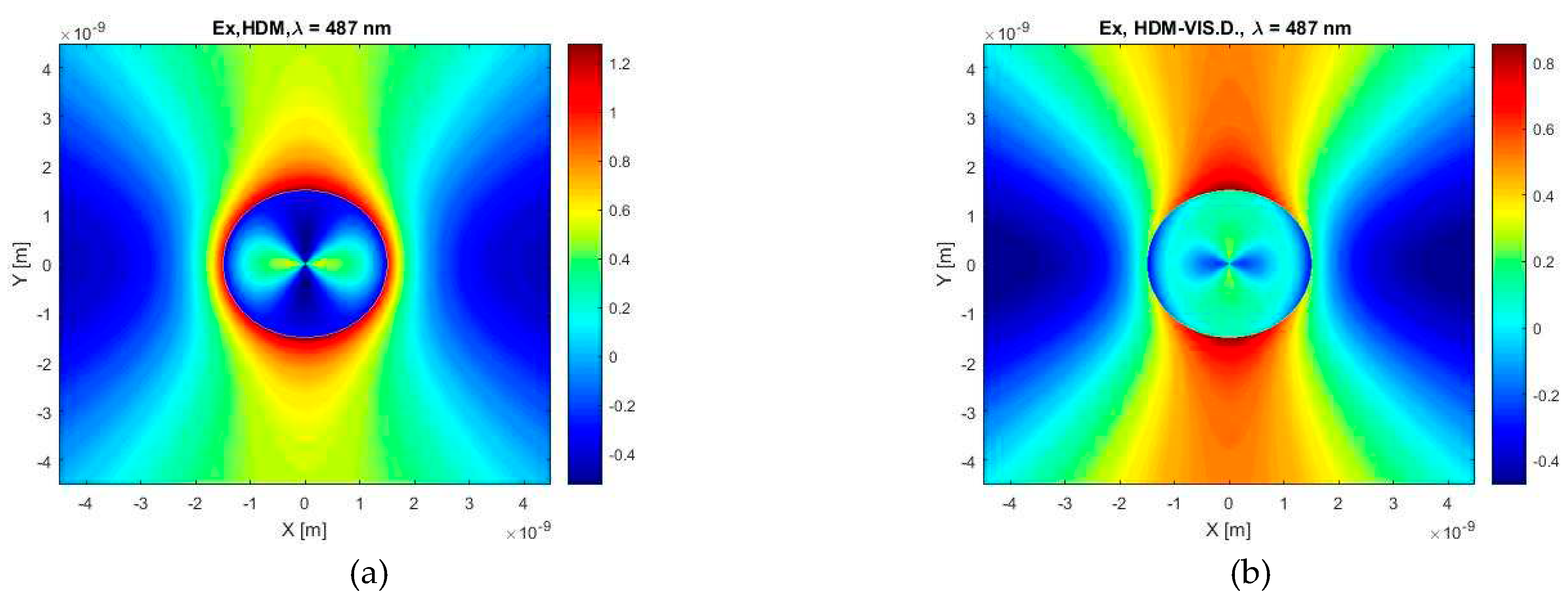
Preprints 79946 g013
Figure 13. The X-component of the electric field calculated for the wavelength of λ = 487 nm and the case of a gold spherical particle with a diameter of 3 nm in a water environment, according to (a) HDM and (b) HDM–Vis.D.
Figure 13. The X-component of the electric field calculated for the wavelength of λ = 487 nm and the case of a gold spherical particle with a diameter of 3 nm in a water environment, according to (a) HDM and (b) HDM–Vis.D.
Preprints 79946 g013
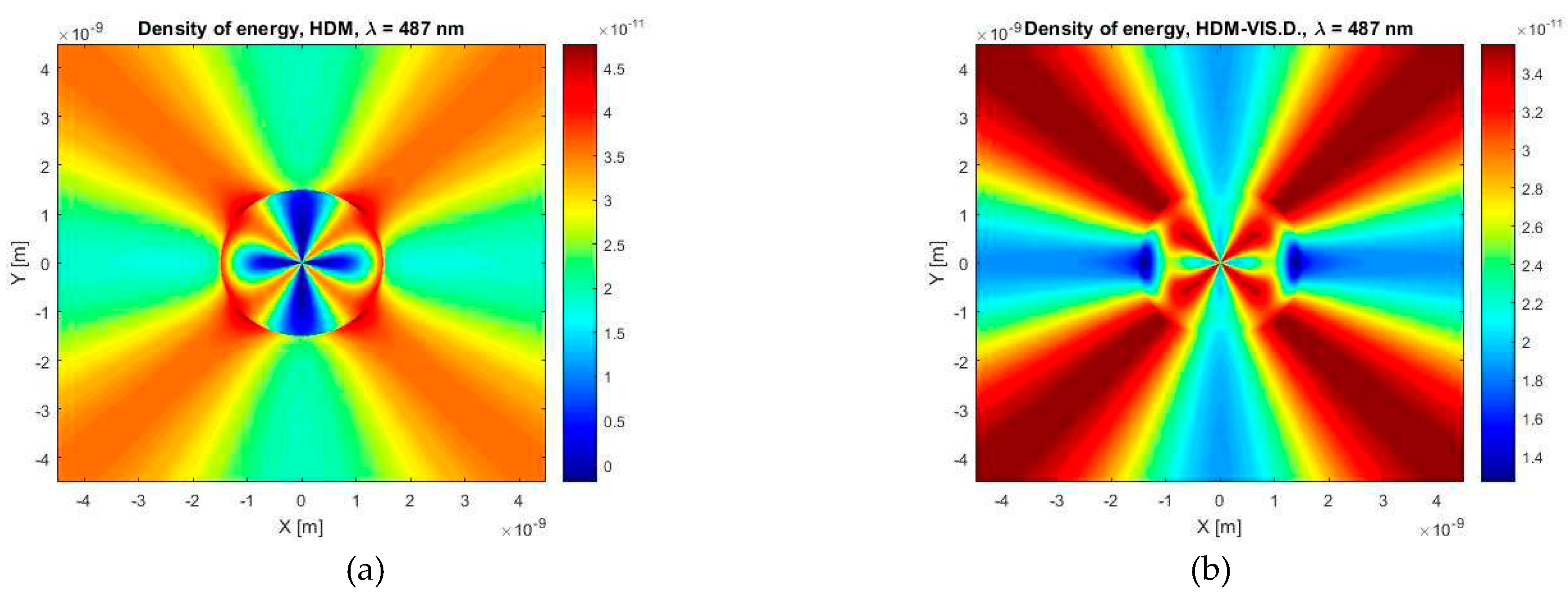
Preprints 79946 g014
Figure 14. The density of electromagnetic field energy calculated for the wavelength of λ = 487 nm and the case of a gold spherical particle with a diameter of 3 nm in a water environment, according to (a) HDM and (b) HDM–Vis.D.
Figure 14. The density of electromagnetic field energy calculated for the wavelength of λ = 487 nm and the case of a gold spherical particle with a diameter of 3 nm in a water environment, according to (a) HDM and (b) HDM–Vis.D.
Preprints 79946 g014
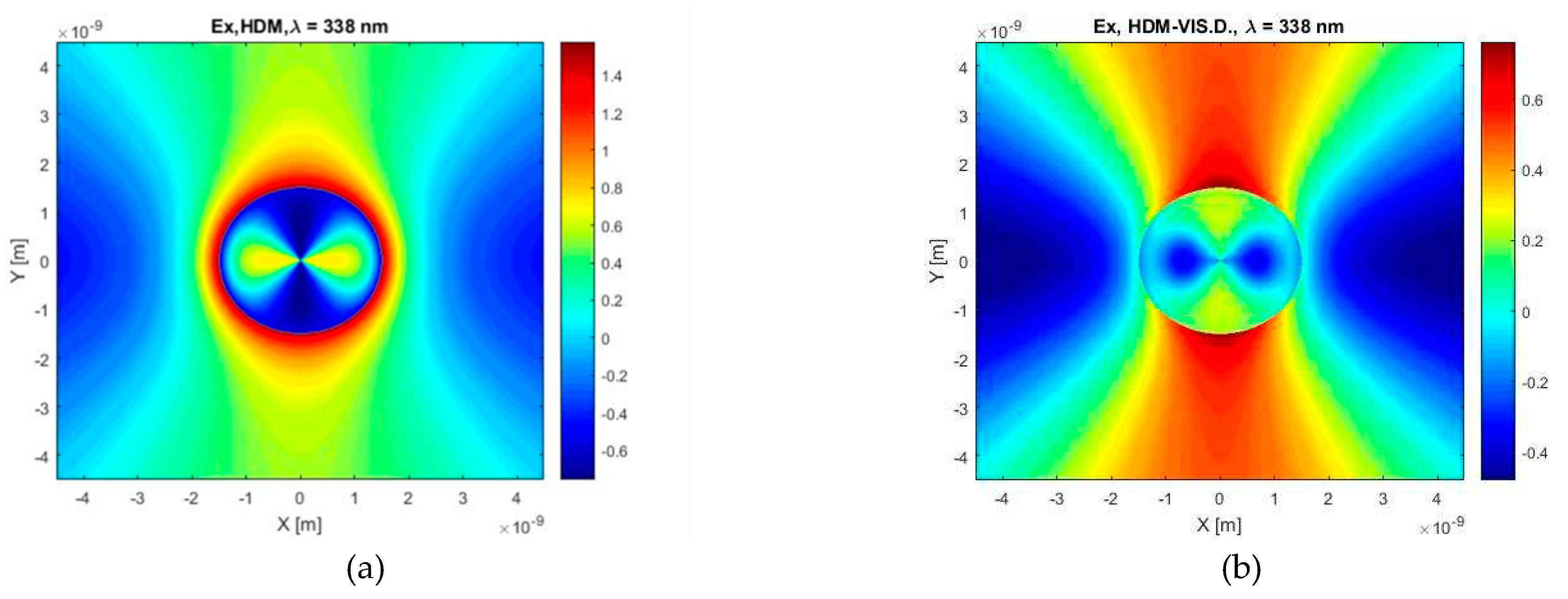
Preprints 79946 g015
Figure 15. The X-component of the electric field calculated for the wavelength of λ = 338 nm and the case of a silver spherical particle with a diameter of 3 nm in a vacuum environment, according to (a) HDM and (b) HDM–Vis.D.
Figure 15. The X-component of the electric field calculated for the wavelength of λ = 338 nm and the case of a silver spherical particle with a diameter of 3 nm in a vacuum environment, according to (a) HDM and (b) HDM–Vis.D.
Preprints 79946 g015
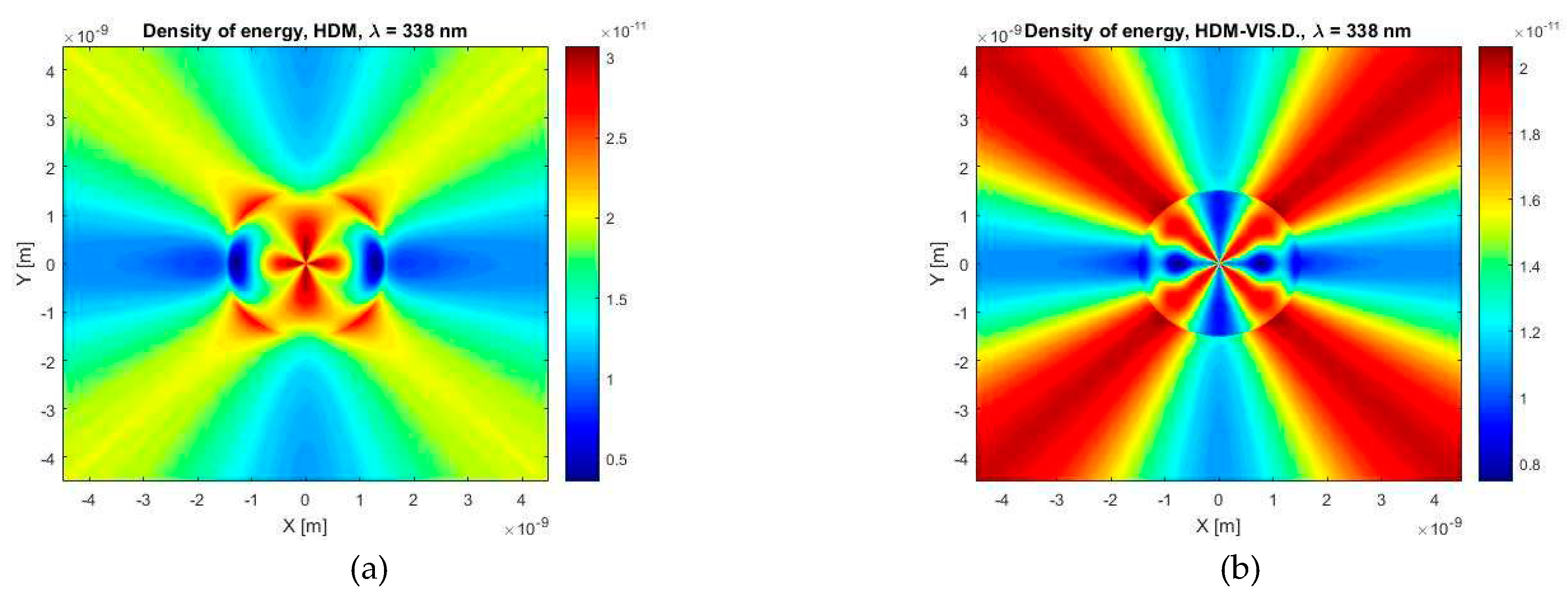
Preprints 79946 g016
Figure 16. The density of electromagnetic field energy calculated for the wavelength of λ = 338 nm and the case of a silver spherical particle with a diameter of 3 nm in a vacuum environment, according to (a) HDM and (b) HDM–Vis.D.
Figure 16. The density of electromagnetic field energy calculated for the wavelength of λ = 338 nm and the case of a silver spherical particle with a diameter of 3 nm in a vacuum environment, according to (a) HDM and (b) HDM–Vis.D.
Preprints 79946 g016
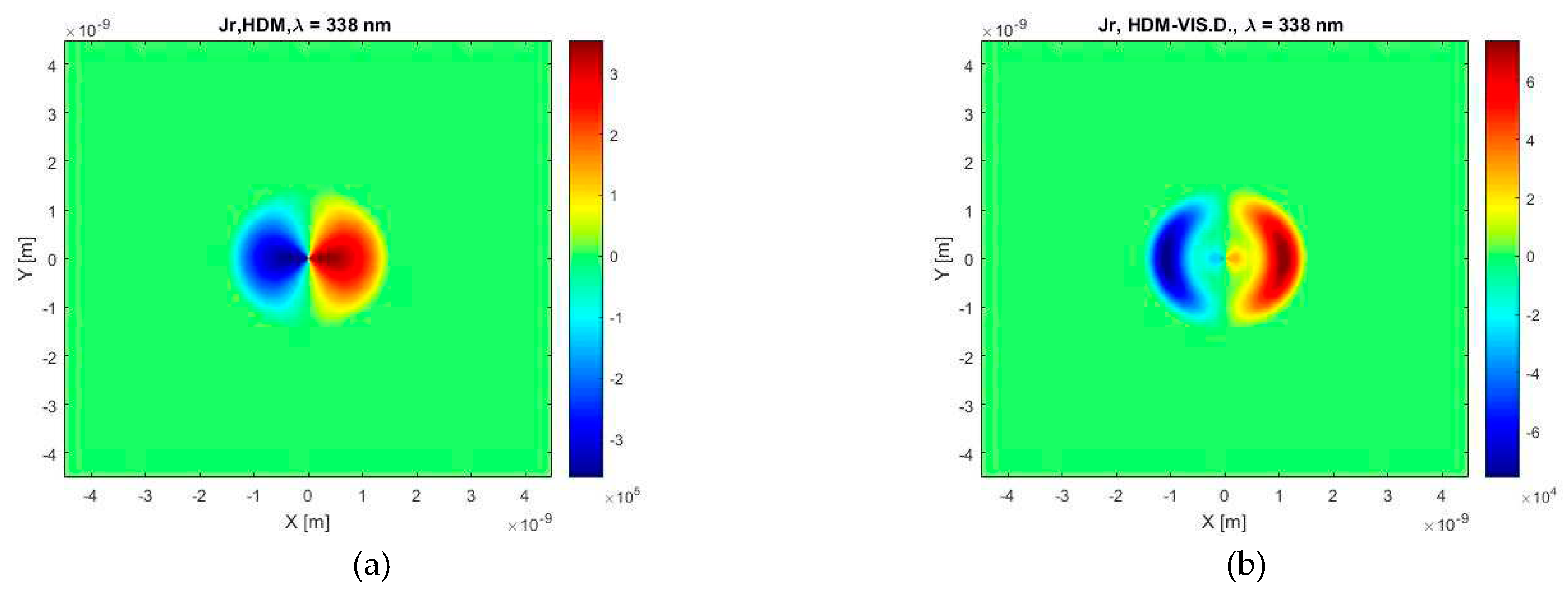
Preprints 79946 g017
Figure 17. The radial component of the current density calculated for the wavelength of λ = 338 nm and the case of a silver spherical particle with a diameter of 3 nm in a vacuum environment, according to (a) HDM and (b) HDM–Vis.D.
Figure 17. The radial component of the current density calculated for the wavelength of λ = 338 nm and the case of a silver spherical particle with a diameter of 3 nm in a vacuum environment, according to (a) HDM and (b) HDM–Vis.D.
Preprints 79946 g017
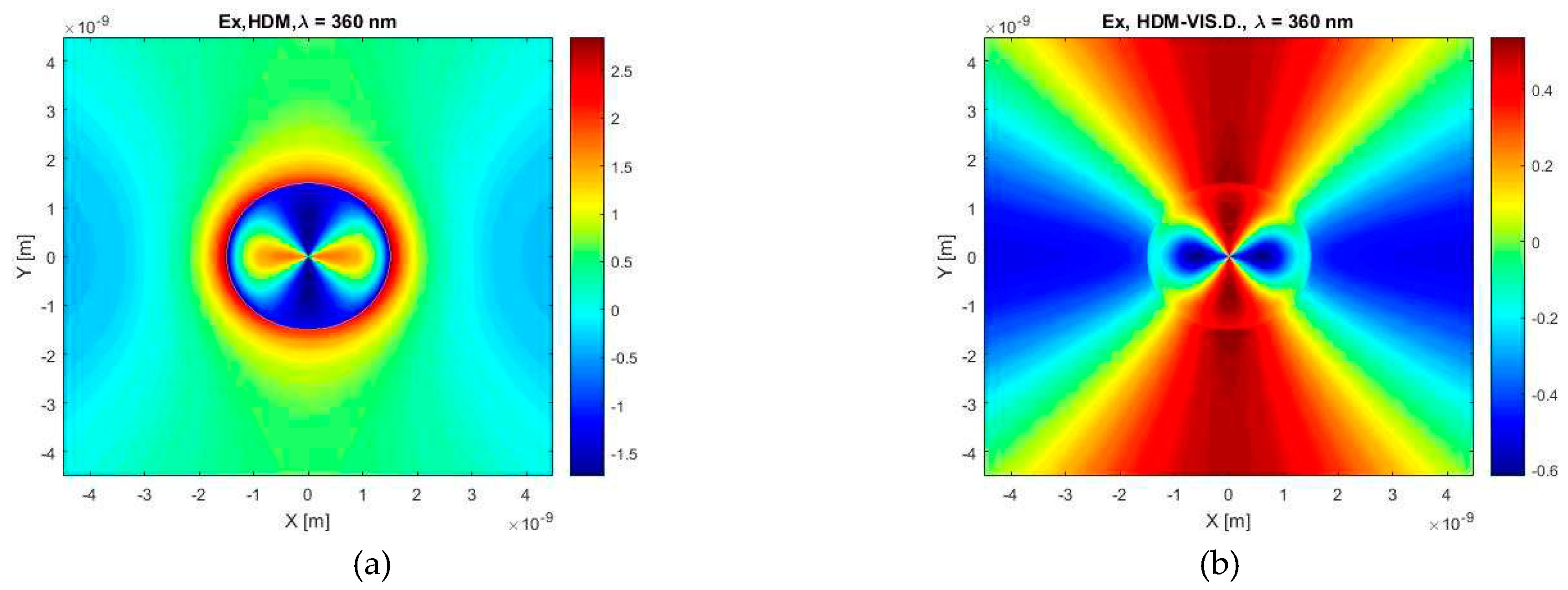
Preprints 79946 g018
Figure 18. The X-component of the electric field calculated for the wavelength of λ = 360 nm and the case of a silver spherical particle with a diameter of 3 nm in a water environment, according to (a) HDM and (b) HDM–Vis.D.
Figure 18. The X-component of the electric field calculated for the wavelength of λ = 360 nm and the case of a silver spherical particle with a diameter of 3 nm in a water environment, according to (a) HDM and (b) HDM–Vis.D.
Preprints 79946 g018
Preprints 79946 g019
Figure 19. The density of electromagnetic field energy calculated for the wavelength of λ = 360 nm and the case of a silver spherical particle with a diameter of 3 nm in a water environment, according to (a) HDM and (b) HDM–Vis.D.
Figure 19. The density of electromagnetic field energy calculated for the wavelength of λ = 360 nm and the case of a silver spherical particle with a diameter of 3 nm in a water environment, according to (a) HDM and (b) HDM–Vis.D.
Preprints 79946 g019
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated