Preprint
Article
The Rise and Fall of Omicron BA.1 Variant as Seen in Wastewater Supports Epidemiological Model Predictions
Altmetrics
Downloads
122
Views
50
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.pdf (814.29KB )
This version is not peer-reviewed
Preprints on COVID-19 and SARS-CoV-2
Submitted:
18 July 2023
Posted:
20 July 2023
You are already at the latest version
Alerts
Abstract
The COVID-19 pandemic caused by the SARS-CoV-2 virus has inflicted significant mortality and morbidity worldwide. Continuous virus mutations have led to the emergence of new variants. The Omicron BA.1 sub-lineage prevailed as the dominant variant globally at the beginning of 2022 but was subsequently replaced by BA.2 in numerous countries. Wastewater-based epidemiology (WBE) offers an efficient tool for capturing viral shedding from infected individuals, enabling early detection of potential pandemic outbreaks without relying solely on community cooperation and clinical testing resources. This study integrated RT-qPCR assays for detecting general SARS-CoV-2 and its variants levels in wastewater into a modified triple susceptible-infected-recovered-susceptible (SIRS) model. The emergence of the Omicron-BA.1 variant was observed, replacing the presence of its predecessor, the Delta variant. Comparative analysis between the wastewater data and the modified SIRS model effectively described the BA.1 and subsequent BA.2 waves, with the decline of the Delta variant aligning with its diminished presence below the detection threshold in wastewater. This study demonstrates the potential of WBE as a valuable tool for future pandemics. Furthermore, by analyzing the sensitivity of different variants to model parameters, we are able to deduce real-life values of cross-variant immunity probabilities, emphasizing the asymmetry in their strength.
Keywords:
Subject: Public Health and Healthcare - Health Policy and Services
1. Introduction
T The COVID-19 pandemic due to SARS-CoV-2 is responsible for huge mortality and severe morbidity, and the virus is still circulating globally [1,2]. Meanwhile, the SARS-CoV-2 virus is undergoing mutations resulting in the continuous emergence of new variants [3,4,5]. The Omicron (B.1.1.529) variant was first detected in South Africa in November 2021 and had undergone significant mutations compared to its previous variants, which were considered to have increased virulence and pathogenicity. Due to its numerous mutations and transmissibility rate, it could spread rapidly [6,7,8]. Globally, the BA.1 sub-lineage emerged as the predominant variant; however, it was gradually supplanted by BA.2 in numerous countries [9,10]. Analysis of SARS-CoV-2-positive sample sequences in Israel revealed the prevailing dominance of the BA.2 variant between March 2022 and June 2022 [11]. Until now, Omicron and sister lineages are currently the dominant variants circulating globally, accounting for >98% of viral sequences shared on GISAID after February 2022 [12]
Wastewater-based epidemiology (WBE) captures viral shedding from infected individuals, irrespective of clinical presentation; it can be used as a convenient tool that provides virus prevalence in a population [13,14,15,16,17,18,19]. The utilization of such a tool allows for the early detection and warning of potential pandemic outbreaks, circumventing the reliance on community cooperation and clinical testing resources. Previous Studies conducted in our lab systematically monitored SARS-CoV-2 variant occurrence in wastewater by employing the reverse transcriptase quantitative polymerase chain reaction (RT-qPCR) method [17,18,20]. This virus surveillance facilitated the development of a double susceptible-infected-recovered (SIR) model specifically tailored for the Delta and Omicron variants [20].
In light of the widespread transmission of the Omicron virus of concern across the globe, the aim of this research is to enable quick assessment of the spread of SARS-CoV-2 variants via WBE [20] and, in parallel use SIR model for predicting the possible future behavior of the variant, which can be verified by RT-qPCR in return. Therefore, WBE data can be used to optimize prediction modeling for infectious agents, including the virus spread in the population.
2. Materials and Methods
2.1. Wastewater Samples
Composite 24 h influent wastewater samples were obtained from the Beer Sheva municipality wastewater treatment plant in Israel. The samples were collected twice a week using an autosampler from December 2021 to July 2022. Samples were transported to the lab under chilled conditions and stored at 4 °C until further processing.
2.2. RNA Extraction
RNA was extracted from the wastewater samples using a Zymo Environ Water RNA kit (Zymo Research R2042) according to the manufacturer protocol, including the viral enrichment step as described previously by Yaniv et al. (2022) [20]. The MS2 phage, present in undetectable levels in Israeli wastewater, served as an external control during the experiment by spiking the samples with 105 copies. The RNA samples were eluted using 35 μL of RNase-free water and preserved at a temperature of -80 °C.
2.3. RT-qPCR
Taq-Man RT-qPCRs assays for detecting and quantifying Sars-Cov-2 in wastewater samples were performed as previously described [17,18,20] using Applied Biosystems Thermocycler (Thermo Scientific). The primer and probes used by Yaniv et al. (2022) [17,18,20] and listed in Table 1. Following the manufacturer's protocol, the assay used One Step PrimeScript III RT-qPCR mix RR600 (TAKARA, Japan). The reaction mixture contains 0.5 μM primers concentration and 0.2 μM probs concentration and added 5 μL of RNA sample to the total volume of 20 μL. RNA copy number per Liter of wastewater was calculated using calibration curves and Equation presented in the supplementary and following Yaniv et al. (2022) [20].
3. Results
3.1. Wastewater Portrait of SARS-CoV-2
The wastewater of Beer-Sheva, Israel's fourth largest city, has been continuously monitored since the beginning of the COVID-19 pandemic, as detailed in previous publications [17,18,20]. The detection of general SARS-CoV-2 levels was carried out utilizing the CDC's N2 set, while the specific identification of the Delta and Omicron BA.1 variants was achieved through the utilization of the Delta S∆157 and Omicron Ins214 S sets developed by Yaniv et al. (2021, 2022) [17,20]. This study monitored general SARS-CoV-2 and the shifting of variants from the end of December 2021 till July 2022 (Fig.1). Delta variant copy number declined and was undetectable after the beginning of February 2022. From the beginning of January 2022, omicron BA.1 was the dominant variant. The peak of omicron BA.1 was reached at the end of January till the beginning of February 2022. Omicron BA.1 decreased to an undetectable level in the wastewater after April 2022. The remaining high level of overall SARS-CoV-2 (through N gene monitoring) is probably due to the emerge of the omicron BA.2 variant in Israel during February 2022 and followed by BA.4 and BA.5 in the mid of April [11], which is undetectable by the Omicron Ins214 S probe that was used in this study (Figure 1S) [20]. The WBE data presented in Figure 1 may help develop and optimize prediction modeling for infectious agents, including viruses spread in the population.
3.2. Remodeling
Soon after the omicron BA.1 outbreak, omicron BA.2 emerged [11]. It is essential to include it, too, as it has a larger basic reproduction number (R0) than BA.1 while inducing strong protection against BA.1 and similar protection as BA.1 against Delta. We, therefore, present here a triple susceptible-infected-recovered-susceptible (SIRS) model [22,23] that accounts for an (exponentially decaying) time-dependent waning immunity and cross-variant immunization [20].
We define the following time-dependent variables:
- , and are the fractions of actively infected populations in Delta, Omicron-BA.1, and Omicron-BA.2, respectively.
- , and are the effective fractions of susceptible populations to Delta, Omicron-BA.1, and Omicron-BA.2 infections, respectively, henceforth "susceptibilities". These variables present an average over the diverse immunity presented in the population, although, in the original SIR model, they simply present the fraction of population that is neither actively infected nor recovered.
- , and are the fractions of recovered population from Delta, Omicron-BA.1, and Omicron-BA.2, respectively. The contribution of recovered individuals from previous outbreaks is accounted for in the initial conditions.
In addition, we use the following (time-independent) parameters:
- , and are the infection time-period of Delta, Omicron-BA.1, and Omicron-BA.2, respectively.
- , and are the basic reproduction numbers of Delta, Omicron-BA.1, and Omicron-BA.2, respectively.
- , , and are the corresponding characteristic waning-immunity times, based on exponential decay of the immunity.
The model equations are as follows:
where , and take the following expressions, accounting for cross-variant immunization,
In Eqs. (1)-(3), the first term on the right-hand-side (RHS) of each equation represents an infection rate while the second term accounts for the recovery rate. In Eqs. (4)-(6), the first term on the RHS in each equation is the same recovery rate, while the second term is a waning-immunity rate.
In Eqs. (7)-(9), represents the relative mean protection against Delta infection that a newly recovered individual from Omicron gained, and similarly represents the relative mean protection against Omicron infection that a newly recovered individual from Delta gained; , , and have a corresponding meaning.
To minimize free-parameters, and due to the similarity between Omicron-BA.1 and Omicron-BA.2, we use , . Asymmetric cross-immunization, supported by antibody immunology studies [24,25], implies , i.e., the protection against Omicron due to Delta past infection is higher than the protection against Delta due to Omicron past infection. However, these antibody immunity assays do not account for the full complexity of the immune system, such as the T-cell immunity, and so are an underestimate of the immunity against Delta due to Omicron past infection. Hence, the estimated ratio used in our previous publication [20], which stems from these immunity assays, is an underestimate, which we correct here to be 0.6 to fit better the wastewater data. (In the SI of Yaniv et al (2022) [20]) we considered also 0.5, closer to the ratio used here.)
To account for immunity gained from past pandemic waves and vaccination, the initial recovered fraction of Delta is set to a non-zero value, thereby determining the initial susceptibilities () associated with the three variants.
In addition, we use the following parameter values that fall within the acceptable range of known values to roughly fit the observed data:
-
Basic reproduction numbers
-
Infection periods(days)(days)(days)
-
Characteristic waning-immunity times(days)(days)
-
Cross immunity probabilities,,,
The following initial conditions are taken: , , , . The entrance of BA.2 is modelled as a (Dirac-delta function) source rate at day 34 with value (), introduced on the RHS of Eq. (3).
Eqs. (1)-(9) form a set of non-linear differential equations and are therefore solved numerically. The results for the active infections (, and ), scaled to the observed wastewater peak concentration of the Omicron-BA.1 wave, are shown in figure 2.
Figure 2.
SARS-CoV-2 variants copy number from the model, scaled to the observed wastewater concentrations (Figure 1).
Figure 2.
SARS-CoV-2 variants copy number from the model, scaled to the observed wastewater concentrations (Figure 1).
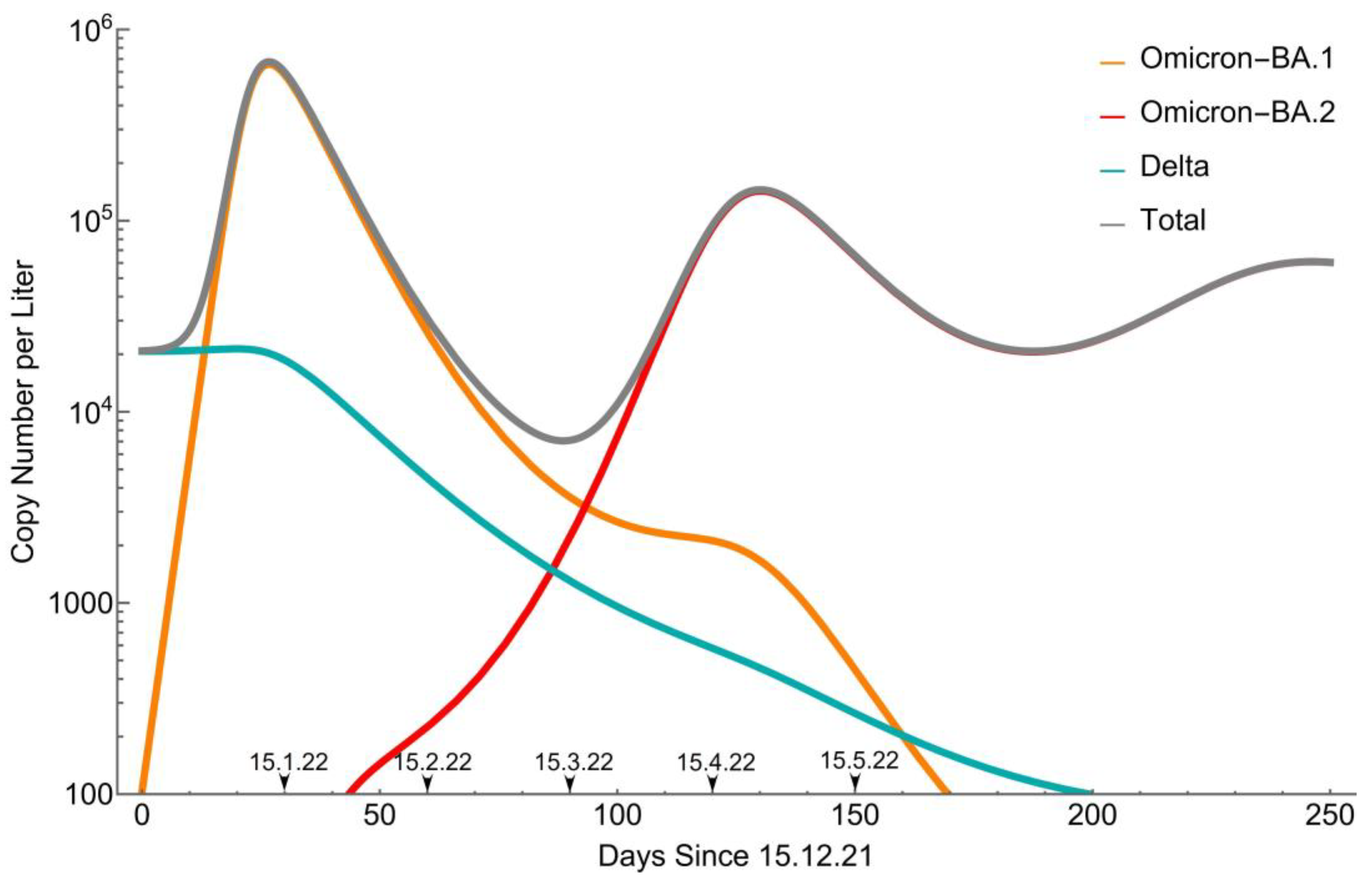
Comparing to the wastewater data (figure 1), the BA.1 wave is well described. The subsequent BA.2 wave, roughly 4+ months later, is consistent with the total wastewater viral count and MOH infection data [26]. Soon after BA.1 has peaked, there was a strong drop of Delta, consistent with it going below the detection threshold. This drop continues even after BA.1 dropped to low values, since the BA.2 wave keeps it down. In absolute terms, according to the model Delta is not eradicated completely, but it is kept extremely low.
The BA.2 wave keeps BA.1 dropping too, but not at a constant pace, and we can observe a “shoulder” of it roughly when BA.2 peaks, reminiscent of the “shoulder” in wastewater data (end March-early April). In the absence of BA.2, we would have had a second BA.1 wave coming due to the BA.1 waning immunity, and the “shoulder” is simply the signature left from this hypothetical wave before the BA.2 wave suppresses it. Note that, surprisingly, BA.1 is not detected in wastewater for the subsequent few weeks in April and emerges briefly at end-April (figure 1), which is clearly not predicted by the model.
In figures S2-S4, we perform sensitivity analysis to the variation of a few parameters: (i) (figure S2), ranging from 30%-60% above [10], showing relatively weak sensitivity of all variants. (ii) and (figure S3), ranging from 40% to 70% of and (respectively), thus describing strong asymmetric cross-immunities between the pairs BA.1 and Delta and BA.2 and Delta. The analysis shows strong sensitivity of the faith of Delta but very weak sensitivity of the two other variants. (iii) (figure S3), ranging from just 117.5% to 91% of , thus describing slight asymmetric cross-immunities between BA.1 and BA.2. The analysis shows strong effects on BA.1 and BA.2 and weaker effects on Delta. In particular, the timing of the BA.2 wave is very sensitive to this value, which in turn influences the appearance of the shoulder/peak in BA.1.
The presented model is based on homogeneous infection spreading model and cannot describe spatial (geographic) non-uniformity [27,28,29,30]. We suspect that the brief (single detection) emergence of BA.1 on end-April results from a late infection of one of the city neighborhoods. Unfortunately, the data for different neighborhoods is unavailable to us, so we cannot confirm this hypothesis. Nevertheless, this suggests that detection at multiple locations, even within the same city, could give insight into the spreading pattern of disease [31].
4. Discussion
Monitoring of Israel’s 4th largest city (Beer-Sheva) was performed through wastewater analysis to determine SARS-CoV-2 levels in wastewater. With escalated global infection, the Omicron-BA.1 variant appeared in the wastewater and eradicated the presence of its predecessor, the Delta variant. Comparing the wastewater data (figure 1) and the modified SIRS model (figure 2), the BA.1 wave is well described. The subsequent BA.2 wave, roughly 4+ months later, is consistent with the total wastewater viral count. Soon after BA.1 has peaked, there was a strong drop of Delta consistent with it going below the detection threshold in wastewater. This drop continues even after BA.1 dropped to low values since the BA.2 wave keeps it down. In absolute terms, according to the model, Delta is not eradicated completely but is kept extremely low.
This study demonstrated that WBE data can help optimize prediction modeling for infectious agents, including virus spread in the population, and may be useful for future pandemics. Due to the high sensitivity of the different variants to some of the model parameters (as seen in the SI, figures S2-S4), we were able to roughly deduce real-life values of cross-variant immunity probabilities in terms of the strength of their asymmetry. Specifically, we suggest that the protection against Delta due to an Omicron past infection is lower by about 40% than the protection against Omicron due to a Delta past infection, and that the protection against Omicron-BA.2 due to an Omicron-BA.1 past infection is higher by about 10% than the protection against Omicron-BA.1 due to an Omicron-BA.2 past infection. Increasing the number of variants detected simultaneously and the detection accuracy, and improving the model, in particular accounting for geographic inhomogeneities in the disease spread, can improve the estimates of model parameters. Preparation for future pandemics should include these issues.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Equation S1: Equation for RNA copy number per Liter of wastewater for raw samples calculation; Figure S1: Primer and probe illustration in Omicron Variants; Figure S2: Sensitivity analysis to the basic reproduction number of BA.2; Figure S3: Sensitivity analysis to the Delta—BA.1 and Delta—BA.2 pairs cross-immunity parameters; Figure S4: Sensitivity analysis to the BA.1—BA.2 pair.
Author Contributions
Conceptualization, Michal Liddor Naim, Yu Fu and Ariel Kushmaro; Formal analysis, Michal Liddor Naim, Yu Fu, Itay Bar-Or, Robert Marks, Qun Sun and Rony Granek; Methodology, Rony Granek; Supervision, Ariel Kushmaro; Visualization, Michal Liddor Naim, Yu Fu and Marilou Shagan; Writing – original draft, Michal Liddor Naim, Yu Fu and Rony Granek; Writing – review & editing, Itay Bar-Or, Robert Marks, Qun Sun, Rony Granek and Ariel Kushmaro.
Funding
We would like to acknowledge funding from Ben Gurion University through The Corona Challenge Covid-19 and funding from the Israeli Ministry of Health.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to acknowledge funding from Ben Gurion University, The Corona Challenge Covid-19 (https://in.bgu.ac.il/en/corona-challenge/Pages/default.aspx) and funding from the Israeli Ministry of Health. We thank Electra Company, which holds WWTP of Beer-Sheva management, especially Nikolay Schipunov. We gratefully acknowledge Esti Kramarsky-Winter assistance with comments and scientific editing of the manuscript.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
References
- WHO COVID-19 Weekly Epidemiological Update - Edition 144 2023.
- Wang, H.; Paulson, K.R.; Pease, S.A.; Watson, S.; Comfort, H.; Zheng, P.; Aravkin, A.Y.; Bisignano, C.; Barber, R.M.; Alam, T.; et al. Estimating Excess Mortality Due to the COVID-19 Pandemic: A Systematic Analysis of COVID-19-Related Mortality, 2020–21. The Lancet 2022, 399, 1513–1536. [CrossRef]
- Goswami, S.; Gupta Bakshi, U.; Bhattacharya, S. SARS-CoV-2 and Its Variants. In COVID-19 and SARS-CoV-2: The Science and Clinical Application of Conventional and Complementary Treatments; CRC Press, 2022; pp. 49–60 ISBN 978-1-00-317851-4.
- Farheen, S.; Araf, Y.; Tang, Y.; Zheng, C. The Deltacron Conundrum: Its Origin and Potential Health Risks. J. Med. Virol. 2022, 94, 5096–5102. [CrossRef]
- Tao, K.; Tzou, P.L.; Nouhin, J.; Gupta, R.K.; De Oliveira, T.; Kosakovsky Pond, S.L.; Fera, D.; Shafer, R.W. The Biological and Clinical Significance of Emerging SARS-CoV-2 Variants. Nat. Rev. Genet. 2021, 22, 757–773. [CrossRef]
- Kannan, S.; Shaik Syed Ali, P.; Sheeza, A. Omicron (B.1.1.529) - Variant of Concern - Molecular Profile and Epidemiology: A Mini Review. Eur. Rev. Med. Pharmacol. Sci. 2021, 25, 8019–8022. [CrossRef]
- Karim, S.S.A.; Karim, Q.A. Omicron SARS-CoV-2 Variant: A New Chapter in the COVID-19 Pandemic. The Lancet 2021, 398, 2126–2128. [CrossRef]
- Singh, A.K.; Misra, A. Impact of COVID-19 and Comorbidities on Health and Economics: Focus on Developing Countries and India. Diabetes Metab. Syndr. 2020, 14, 1625–1630. [CrossRef]
- Callaway, E. Heavily Mutated Omicron Variant Puts Scientists on Alert. Nature 2021, 600, 21–21. [CrossRef]
- Chatterjee, S.; Bhattacharya, M.; Nag, S.; Dhama, K.; Chakraborty, C. A Detailed Overview of SARS-CoV-2 Omicron: Its Sub-Variants, Mutations and Pathophysiology, Clinical Characteristics, Immunological Landscape, Immune Escape, and Therapies. Viruses 2023, 15, 167. [CrossRef]
- Kliker, L.; Zuckerman, N.; Atari, N.; Barda, N.; Gilboa, M.; Nemet, I.; Abd Elkader, B.; Fratty, I.S.; Jaber, H.; Mendelson, E.; et al. COVID-19 Vaccination and BA.1 Breakthrough Infection Induce Neutralising Antibodies Which Are Less Efficient against BA.4 and BA.5 Omicron Variants, Israel, March to June 2022. Eurosurveillance 2022, 27. [CrossRef]
- WHO COVID-19 Weekly Epidemiological Update - Edition 115 2022.
- Collivignarelli, M.C.; Collivignarelli, C.; Carnevale Miino, M.; Abbà, A.; Pedrazzani, R.; Bertanza, G. SARS-CoV-2 in Sewer Systems and Connected Facilities. Process Saf. Environ. Prot. 2020, 143, 196–203. [CrossRef]
- Martin, J.; Klapsa, D.; Wilton, T.; Zambon, M.; Bentley, E.; Bujaki, E.; Fritzsche, M.; Mate, R.; Majumdar, M. Tracking SARS-CoV-2 in Sewage: Evidence of Changes in Virus Variant Predominance during COVID-19 Pandemic. Viruses 2020, 12, 1144. [CrossRef]
- La Rosa, G.; Bonadonna, L.; Lucentini, L.; Kenmoe, S.; Suffredini, E. Coronavirus in Water Environments: Occurrence, Persistence and Concentration Methods - A Scoping Review. Water Res. 2020, 179, 115899. [CrossRef]
- Westhaus, S.; Weber, F.-A.; Schiwy, S.; Linnemann, V.; Brinkmann, M.; Widera, M.; Greve, C.; Janke, A.; Hollert, H.; Wintgens, T.; et al. Detection of SARS-CoV-2 in Raw and Treated Wastewater in Germany – Suitability for COVID-19 Surveillance and Potential Transmission Risks. Sci. Total Environ. 2021, 751, 141750. [CrossRef]
- Yaniv, K.; Ozer, E.; Lewis, Y.; Kushmaro, A. RT-QPCR Assays for SARS-CoV-2 Variants of Concern in Wastewater Reveals Compromised Vaccination-Induced Immunity. Water Res. 2021, 207, 117808. [CrossRef]
- Yaniv, K.; Ozer, E.; Shagan, M.; Lakkakula, S.; Plotkin, N.; Bhandarkar, N.S.; Kushmaro, A. Direct RT-QPCR Assay for SARS-CoV-2 Variants of Concern (Alpha, B.1.1.7 and Beta, B.1.351) Detection and Quantification in Wastewater. Environ. Res. 2021, 201, 111653. [CrossRef]
- Maida, C.M.; Tramuto, F.; Giammanco, G.M.; Palermo, R.; Priano, W.; De Grazia, S.; Purpari, G.; La Rosa, G.; Suffredini, E.; Lucentini, L.; et al. Wastewater-Based Epidemiology as a Tool to Detect SARS-CoV-2 Circulation at the Community Level: Findings from a One-Year Wastewater Investigation Conducted in Sicily, Italy. Pathogens 2023, 12, 748. [CrossRef]
- Yaniv, K.; Ozer, E.; Shagan, M.; Paitan, Y.; Granek, R.; Kushmaro, A. Managing an Evolving Pandemic: Cryptic Circulation of the Delta Variant during the Omicron Rise. Sci. Total Environ. 2022, 836, 155599. [CrossRef]
- Dreier, J.; Störmer, M.; Kleesiek, K. Use of Bacteriophage MS2 as an Internal Control in Viral Reverse Transcription-PCR Assays. J. Clin. Microbiol. 2005, 43, 4551–4557. [CrossRef]
- Nill, F. Endemic Oscillations for SARS-CoV-2 Omicron -- A SIRS Model Analysis. Chaos Solitons Fractals 2023, 173, 113678. [CrossRef]
- Goncalves, S.; Abramson, G.; Gomes, M.F.C. Oscillations in SIRS Model with Distributed Delays. 2009. [CrossRef]
- Laurie, M.T.; Liu, J.; Sunshine, S.; Peng, J.; Black, D.; Mitchell, A.M.; Mann, S.A.; Pilarowski, G.; Zorn, K.C.; Rubio, L.; et al. SARS-CoV-2 Variant Exposures Elicit Antibody Responses With Differential Cross-Neutralization of Established and Emerging Strains Including Delta and Omicron. J. Infect. Dis. 2022, 225, 1909–1914. [CrossRef]
- Suryawanshi, R.K.; Chen, I.P.; Ma, T.; Syed, A.M.; Brazer, N.; Saldhi, P.; Simoneau, C.R.; Ciling, A.; Khalid, M.M.; Sreekumar, B.; et al. Limited Cross-Variant Immunity after Infection with the SARS-CoV-2 Omicron Variant Without Vaccination; Infectious Diseases (except HIV/AIDS), 2022;
- Data Resources - COVID-19 Data Tracker - IsraeliMinistryofHealthDashboard Available online: https://datadashboard.health.gov.il/portal/dashboard/corona.
- Tsori, Y.; Granek, R. Epidemiological Model for the Inhomogeneous Spatial Spreading of COVID-19 and Other Diseases. PLOS ONE 2021, 16, e0246056. [CrossRef]
- Tsori, Y.; Granek, R. Spatio-Temporal Spread of COVID-19: Comparison of the Inhomogeneous SEPIR Model and Data from South Carolina. PLOS ONE 2022, 17, e0268995. [CrossRef]
- Dos Santos, J.P.C.; Monteiro, E.; Ferreira, J.C.; Teixeira Lemes, N.H.; Rodrigues, D.S. Well Posedness and Qualitative Analysis of a SEIR Model with Spatial Diffusion for COVID-19 Spread. SSRN Electron. J. 2022. [CrossRef]
- La Torre, D.; Liuzzi, D.; Marsiglio, S. Geographical Heterogeneities and Externalities in an Epidemiological-macroeconomic Framework. J. Public Econ. Theory 2022, 24, 1154–1181. [CrossRef]
- Yaniv, K.; Shagan, M.; Lewis, Y.E.; Kramarsky-Winter, E.; Weil, M.; Indenbaum, V.; Elul, M.; Erster, O.; Brown, A.S.; Mendelson, E.; et al. City-Level SARS-CoV-2 Sewage Surveillance. Chemosphere 2021, 283, 131194. [CrossRef]
Figure 1.
RT-qPCR of SARS-CoV-2, Delta, and Omicron BA.1 variants in Beer-Sheva wastewater. From mid-December 2021 to July 2022. The gray area illustrates the overall SARS-CoV-2 variants using N gene sets. The blue columns indicate the detection of the Delta variant using the SΔ157 set, while the orange columns represent the detection of the Omicron variant of concern using the Ins214S set.
Figure 1.
RT-qPCR of SARS-CoV-2, Delta, and Omicron BA.1 variants in Beer-Sheva wastewater. From mid-December 2021 to July 2022. The gray area illustrates the overall SARS-CoV-2 variants using N gene sets. The blue columns indicate the detection of the Delta variant using the SΔ157 set, while the orange columns represent the detection of the Omicron variant of concern using the Ins214S set.
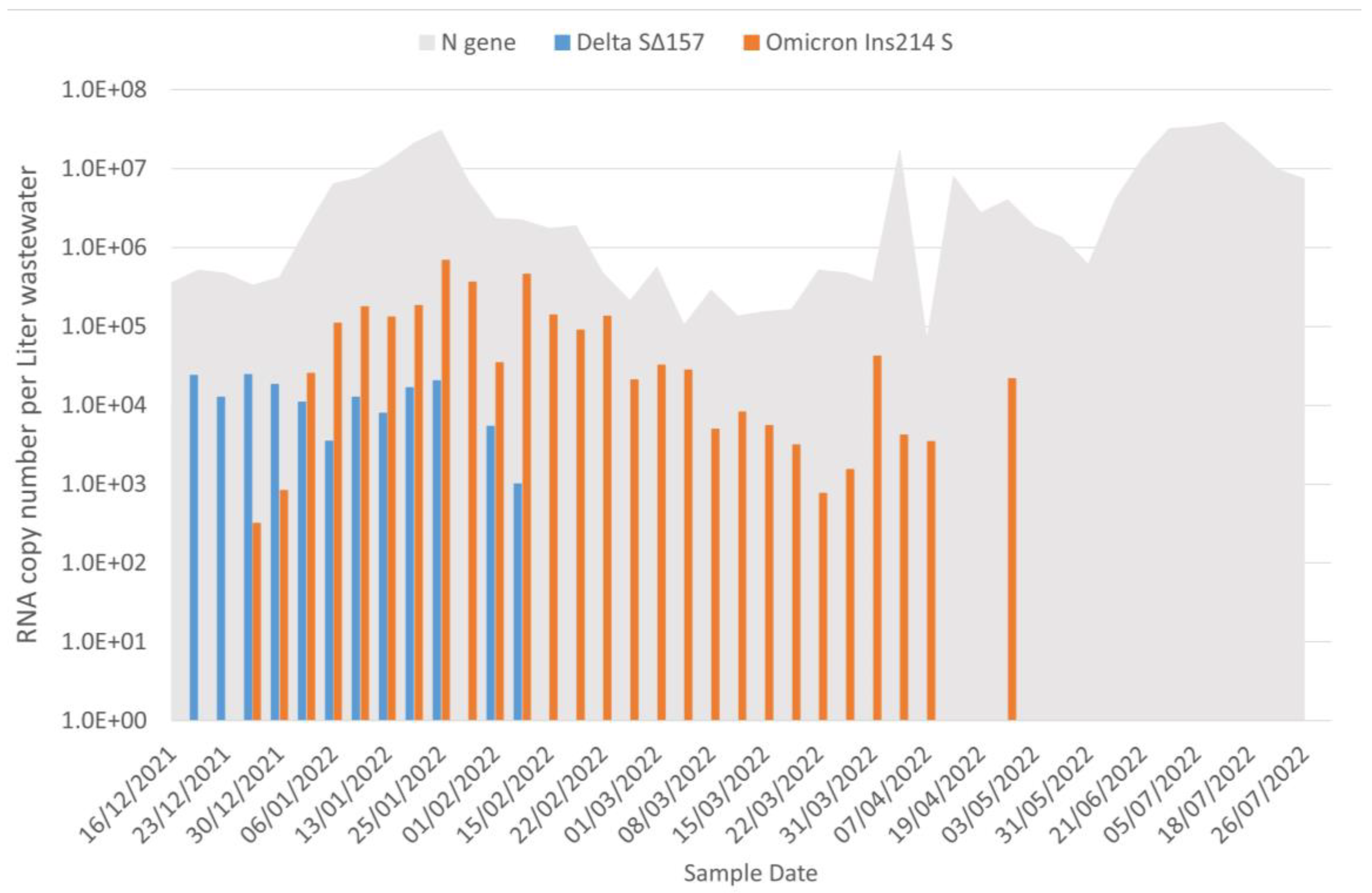
Table 1.
List of primers and probs sequences used in this study.

† NCBI database; ‡ GISAID database; * Positions listed for each sequence are from the relevant accession number. Forward and Reverse primers names of Delta correspond to the nucleotides position on the original sequence, when aligned together with the variants of concern.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







