Prerpints.org logo
Preprint
Article

Multi-Objectives Nonlinear Interval PageRank Algorithm Based on the Constrained Interval Arithmetic

Altmetrics

Downloads

107

Views

16

Comments

0

This version is not peer-reviewed

Submitted:

17 July 2023

Posted:

20 July 2023

You are already at the latest version

Alerts
Abstract
This paper presents a novel algorithm, the multi-objective nonlinear interval PageRank (MONIPR) Algorithm. This algorithm extends the conventional PageRank (PR) algorithm, integrating nonlinear interval computation and multi-objective considerations into the computation process. The MONIPR algorithm bridges a research gap in integrating nonlinear interval approaches and multi-objective problems into the PR algorithm, which were traditionally treated separately. In addition, this research adopts the constrained interval arithmetic proposed to address the limitations of the conventional PR algorithm, which tends to overlook uncertainties and results in deterministic outcomes. In addition, we use a numerical example to demonstrate the proposed algorithm, contrasting it with the conventional approaches. A numerical example demonstrates the algorithm's performance by comparing the rank intervals obtained with the traditional crisp Markov chain and PR algorithm. The results highlight the ability of the proposed algorithm to provide a range of possible rank intervals, considering both uncertainty and multi-objectives. The findings suggest potential applications in decision-making, uncertainty quantification, and systems analysis.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

The PageRank (PR) algorithm, initially developed by [1], revolutionizes the ranking of web pages based on their importance. This algorithm assigns a numerical weight to each element of a hyperlinked set of documents, thereby determining its relative importance within the set [2]. Since its introduction, several enhancements and modifications have been suggested to adapt the original algorithm for various contexts. For instance, [3] discussed the integration of edge weights into computation via the edge-weighted personalized PR. [4] addressed an inverse problem for PR by identifying a perturbation in an existing network's structure that yields a desired PR. Nonlinear approaches were also introduced by [5,6] to boost the performance and robustness of the PR algorithm. While the PR algorithm was initially designed for web applications, it can be expanded to other fields, like stochastic processes and multi-criteria decision-making (MCDM), due to it is a special case of the Markov chain. As such, it is crucial to consider more realistic scenarios, such as nonlinearity, uncertainty, and multiple objectives, to expand the PR algorithm's applications.
Despite the commonplace practice of utilizing interval or fuzzy numbers to denote problem uncertainty in existing literature, these methods do not extend seamlessly to the PR algorithm. The power iterative method employed by the PR algorithm tends to inflate results with each multiplication of interval or fuzzy numbers, leading to results that exceed rational bounds. Constrained interval arithmetic, as suggested by [7], solves this persistent dependency issue, circumventing the traditional tendency of interval arithmetic to overestimate the resultant interval width in the presence of dependencies. This approach has found applications in computing control invariant sets for constrained nonlinear systems [8] and has been utilized across various fields.
The PR algorithm's nonlinear approach has shown potential, with studies by [5] suggesting that a nonlinear formula be employed due to link correlations or dependencies. Similarly, [6] improved the ranking system's performance and robustness by incorporating nonlinearity into the PR algorithm. While significant strides have been made in the evolution of the PR algorithm, there remains a lack of thorough exploration into the integration of interval computation and nonlinear approach into the PR algorithm. Current research typically handles these aspects separately [5,6,7,8], creating a research gap in this interdisciplinary domain. Moreover, past studies have not adequately addressed the importance of considering multiple objectives for determining the importance of a factor, whether for web pages, criteria weights, or other considerations.
Hence, this paper aims to develop a novel algorithm, named the multi-objectives nonlinear interval PR (MONIPR) algorithm, to integrate nonlinear interval computation and multi-objectives considerations into the PR algorithm. The proposed algorithm extends the traditional PR algorithm to account for different update forms and nonlinear functions to derive. In addition, the derived result can also consider multi-objectives to reflect complex decision-making situations. Then, we provide a numerical example to demonstrate the proposed algorithm and justify it by comparing it with the conventional methods, offering a more comprehensive and flexible method for applying the PR algorithm.
The rest of the paper is organized as follows. Section 2 introduces the PR Algorithm and the methods to account for uncertainty and nonlinearity. Section 3 presents the detail of the proposed algorithm by using the mathematical representation. In Section 4, a numerical example is used to demonstrate the practical application of the proposed algorithm and compare the results with the conventional methods. Section 5 contains a comprehensive discussion of the previous sections' results. Finally, we give the conclusion in the last section.

2. The PR Algorithm

The PR algorithm is a widely used method to rank webpages based on their PR scores [1]. Since its proposal, the algorithm has seen extensive theoretical development and practical applications in various fields. The theoretical framework of the PR algorithm has undergone significant advancement. Early on, the algorithm was based on counting the number and quality of links to a page, thereby determining a rough estimate of the page's importance [2]. However, recent research has expanded upon these foundations and introduced more sophisticated models to respond to the need in practice. In another attempt to adapt the algorithm to modern needs, [9] introduced the adapted PR Algorithm (APA) for urban network analysis. This model challenged the traditional idea of an equal chance of jumping from one node to another, making data from neighboring nodes more likely than data from nodes further away.
A unique approach by [10] extended the concept of PR to time-sensitive networks. Traditionally, PR is based on a steady state of a random walk on a fixed network. They extended the algorithm's applicability to dynamic, temporal networks, thereby opening up possibilities for ranking nodes based on their importance over time. [11] developed new algorithms for personalized PR estimation and search. Their bidirectional approach demonstrated significant speed improvements over existing estimators and could effectively handle large-scale network searches. [12] developed a multi-label graph-based feature selection (MGFS) algorithm using PR. They constructed a correlation distance matrix and a feature-label graph to calculate the importance of each feature, a technique that proved effective in reducing the dimensionality of multi-label data.
In addition, [13] built upon the original algorithm by developing a massively parallel framework for personalized PR (PPR) computations which is named Delta-Push. Their method addressed the challenges of operating on large graphs, which cannot be easily handled with traditional methods due to memory limitations. They successfully reduced communication rounds and costs, which are crucial for large-scale computations. [5] argued for using a nonlinear formula for static-rank computation due to link correlation or dependence. Their work provided new insights into how static-rank computations should be viewed and conducted, shifting away from the linearity of traditional models.
Next, we introduce the theory of the PR algorithm as follows. Assume the Internet as a directed graph where each website is a node, and the links between websites are edges and denote this graph as G(V, K), where V is the set of websites and K is the set of links. The number of nodes n is the total number of web pages. Initially, every webpage has an equal rank and is represented as a vector PR of size n, where P R i = 1 / n for every webpage i. This signifies that a user is equally likely to be on any webpage. The damping factor d is the probability that the person will continue clicking on links at each step. The usual value of d is 0.85 to indicate 15% of the time, jumping to a page chosen at random.
The PR of a webpage i is updated based on the PR of all webpages j that link to i. The update rule is as follows:
P R ' i = 1 − d / n + d × ∑ j P R j / L j
where PR'(i) is the new PageRank of a webpage i, PR(j) is the current PR of webpage j, and L(j) is the number of outgoing links from webpage j. The sum is over all webpages j that has a link to webpage i. Then, the process is repeated until the PR values converge. Although the PR algorithm is most used for webpage-related applications, it can be considered a special Markov chain case. Hence, the PR algorithm also accounts for these fields that use the Markov chain.
Let each page corresponds to a state in the Markov chain. The probability of moving from state i to state j is given by:
P ( i ,   j )   =   1 / L ( i )
if there is a link from i to j, and 0 otherwise. This forms a transition probability matrix P, where P(i, j) is the element in the ith row and jth column. Then, we can calculate P ' ( i ,   j ) as a new probability matrix by the weighted average of two probability matrices as follows:
P ' ( i ,   j )   =   d × P ( i ,   j )   +   ( 1 − d ) / n
This new transition probability matrix P' corresponds to a random surfer who, with probability d, follows the links on the current page with probability ( 1 − d ) and jumps to a random page. Since P' is a stochastic matrix and the corresponding Markov chain is ergodic, which ensures the existence of the steady-state status. In other words, if we let π be a row vector that represents the distribution of PRs, it satisfies the following:
π   =   π P '
and, therefore, a special case of the Markov chain.
For the nonlinear PR algorithm, [6] proposed the mathematical representation, called nonlinearRank, as follows:
s i t + 1 = 1 − c + c × s j t θ
where s i t is the score of node i at time t, c is the damping factor, s j t θ represents the θ-norm of the scores of the neighboring nodes j at time t, θ is a tunable parameter that controls the nonlinearity. In Equation (5), the θ-norm of a vector is defined as:
s j t θ = Σ j s j t θ 1 / θ
where the summation Σ j is over all neighboring nodes j that link to node i. The final score of each node is defined as the steady value after the convergence of s i t . The final ranking of nodes in nonlinearRank, denoted as R n , will be obtained by sorting s i in descending order when s i reaches the stable state.
For the interval PR algorithm, [14] proposed the algorithm as follows. Let M : = M _ , M ¯ be the interval link matrix, we need to calculate the center point of the interval matrix, M c , as:
M c = 1 / 2 × 1 − m × A ¯ + A _ + m / n × S
where n denotes the number of pages in the web graph, m denotes the damping factor, A is the original link matrix of size n × n , where A i , j represents the link from page j to page i, and S is the teleportation matrix of size n × n and represents the probability of randomly transitioning to any page in the graph. It is usually constructed as
S = 1 / n × J
where J is a matrix of ones of size n × n .
Then, we need to calculate the radius matrix ∆, where
∆ = 1 / 2 * 1 − m * A ¯ − A _ + m / n * S
and it represents the distance from the center matrix to the endpoints of the interval matrix.
Next, we can compute the interval matrix M, which represents the range of link matrices, as:
M = M c − ∆ , M c + ∆
and we can find the set of eigenvectors X ' :
X ' = x ∈ R n | ∃ M ~ ∈ M , M ~ x = x , 1 T x = 1 , x ≥ 0
Finally, we can calculate the interval hull X ' : = [ x _ ' , x ¯ ' ] as the result of the interval PR algorithm, where
x _ i ' = m i n x ∈ X ' x i
x ¯ i ' = m a x x ∈ X ' x i
Based on the content of the interval PR algorithm above, it uses the concept of the interval Markov chain to derive the results directly instead of using the power iteration method to derive the results gradually.
Beyond web searches, the PR algorithm has found relevance in many practical applications, such as citation analysis [15] and biology [16]. The application of the PR algorithm has even reached the realm of scientific publication ranking, where [6] introduced nonlinearity to enhance the ranking of significant scientific papers. [17] optimized memory performance for the FPGA implementation of the PR algorithm, a notable contribution to enhancing the speed of the algorithm's execution and improving system performance. [18] examined the PR algorithm from a system-oriented perspective, analyzing algorithm design factors such as work activation, data access pattern, and scheduling. Their research introduced a push-based, data-driven PR implementation, outperforming standard PR algorithm implementations by 28 times. This was a significant step in understanding how the algorithm's efficiency can be optimized and also formed a basis for designing new scalable algorithms. In addition, [19] applied the algorithm to reduce communication in PR computations, an approach that significantly improved execution time and communication volume.
Then, [20] demonstrated an innovative use of the PR algorithm in fraud detection among financial institutions. Recognizing the privacy constraints and data confidentiality issues in sharing information among institutions, they used secure multiparty computation (MPC) techniques to compute the PR values for combined transaction graphs jointly. This novel application ensures that each institution learns only the PR values of its accounts, ensuring privacy and security. In a unique application, [21] proposed using the PR algorithm to evaluate and optimize swarm behavior based on the local behavior of individual entities in the swarm. They showed that the PR algorithm could be used to assess the importance of nodes in the local state space of a swarm of robots. The performance of the swarm significantly improved when each robot implemented the evolved policy. Their research showed that the PR algorithm could optimize swarm behavior efficiently and flexibly, even in large swarms.
Despite its success, the PR algorithm still needs to be revised to account for more complicated situations. Hence, the paper proposes a multi-objective nonlinear interval RP algorithm to address these issues simultaneously.

3. Multi-Objectives Nonlinear Interval PR Algorithm

The constrained interval arithmetic extends traditional interval arithmetic by incorporating constraints on variable values. Compared to conventional interval arithmetic, constrained interval arithmetic provides several advantages. Firstly, it allows for the representation of more intricate constraints. Secondly, it can solve problems that are challenging or impossible to tackle with traditional interval arithmetic. Lastly, it allows for reasoning about the behavior of programs under constraints.
Let the basic operations on intervals be defined as follows:
Addition of two intervals I 1 = a 1 , b 1 and I 2 = a 2 , b 2 is defined as:
I 1 ⊕ I 2 = a 1 + a 2 , b 1 + b 2
Subtraction of I 2 from I 1 is defined as:
I 1 ⊖ I 2 = a 1 − b 2 , b 1 − a 2
Multiplication of I 1 and I 2 is defined as:
I 1 ⊗ I 2 = m i n a 1 a 2 , a 1 b 2 , b 1 a 2 , b 1 b 2 , m a x a 1 a 2 , a 1 b 2 , b 1 a 2 , b 1 b 2
Division of I 1 by I 2 ( I 2 ≠ 0,0 ) is defined as:
I 1 ⊘ I 2 = I 1 ⊗ 1 / b 2 , 1 / a 2 ,   i f a 2 > 0   a n d   b 2 > 0
The constraint C is a logical condition involving intervals. For example, let C : I 1 ⊕ I 2 ≤ I 3 where I 1 , I 2 , and I 3 are intervals. If we calculate I 1 ⊗ I 2 ⊗ I 3 , the aim in constrained interval arithmetic is to perform interval operations while ensuring the constraint C are satisfied, i.e., I 1 ⊗ I 2 ⊗ I 3 ∩ C . The constrained interval arithmetic can be computationally expensive because interval methods often involve operations on intervals as opposed to point values, and these operations can be computationally costly.
Now let us detail the proposed algorithm step-by-step. Let us consider a graph G with n nodes, where each node i is a tank with a rank denoted as an interval R i = r i − , r i + and the interval path weight W i j = w i j − , w i j + , where Wij denotes the path weight from the ith tank to the jth tank. Note that in this paper, we use "tank" to indicate the PR algorithm's webpage or the Markov chain's node to analogy for an object with a certain capacity level. In addition, each tank i has an initial rank interval R i and connections C i j to other tanks j. Each tank i casts a vote V i j for its connected tanks j based on a transformation function T ∙ of its rank r and the connection weight w i j . The update value V i j can be considered as one of the three forms (I)-(III):
V i j = T R i × W i j   (I)
V i j = T R i × W i j   (II)
V i j = R i × T W i j   (III)
where the transformation function T ∙ can be linear, exponential, logarithmic, or sigmoid, as shown in Table 1.
After receiving votes, each tank i distributes its votes across its outgoing connections C i j to other tanks j, taking into account the total weight W i of its outgoing connections. The interval distributed vote D i j which reflects the influence or recommendation from one tank to another is calculated as:
D i j = W i j W i × V i
The rank interval R i of each tank i is updated based on the received votes D i j and a damping factor d, where is assumed to be 0.85 here. The new rank interval R i ' is calculated as:
R i ' = 1 − d n + d × ∑ j D i j
The rank intervals of the tanks are adjusted by considering a two-objectives optimization problem to derive the final rank interval R i ' ' as:
R i ' ' = k 1 × r i − + k 2 × E i − , k 1 × r i + + k 2 × E i +
where k1 and k2 are weights of the ranks and entropy objectives, respectively.
The two-objectives optimization problem is formulated as:
m i n , m a x       r i ,   ∀ i
m i n , m a x     − Σ P r i × l o g 2 P r i
s . t .       r i ⊂ r i − , r i + ,   ∀ i
∑ r i = 1
where E i = − ∑ r i × l o g 2 r i denots the entropy function, which accounts for the amount of uncertainty or randomness in a probability distribution. Then, the above steps are continuous until the ranks are convergent, e.g., a b s R i ' ' − R i < ε , where ε = 0.0001 here. Note that although we only consider a different objective, i.e., the entropy function, here, for simplicity, we can extend the idea for multi-objectives with the same process above.

4. Numerical Example

Our problem at hand is one rooted in the world of simulation, concerning an intricate network of interconnected tanks, designated as tanks A, B, C, and D, as shown in Figure 2. The values for each tank represent their initial states and are provided as intervals, reflecting the inherent uncertainty of real-world scenarios or the outcomes of group decisions. In the beginning, Tank A has an initial state in the interval [0.2, 0.6], Tank B within the interval [0.2, 0.4], Tank C falls in [0.1, 0.3], and Tank D ranges between [0.2, 0.5]. The intervals here signify that the initial states can be any value within the given range, addressing the imprecision that often accompanies real-life situations.
Tank A connects exclusively to Tank B, with a constant transfer rate interval of [1.0, 1.0], denoting a completely certain and unvarying connection. Tank B has more complexity, linking Tank A with a transfer rate of [0.3, 0.5] and to Tank C with a transfer rate of [0.5, 0.7]. This means that in every iteration, Tank B will transfer a fraction of its content within these ranges to Tanks A and C, respectively. Tank C is at the center of a network of connections. It is connected to Tank A with a rate of [0.2, 0.4], to itself with a rate of [0.2, 0.4], and to Tank D with a transfer rate of [0.3, 0.5]. The self-connection signifies some form of retention or recycling process, where a portion of its content is not transferred to another tank but is retained or reprocessed within the tank itself. Tank D, finally, is interconnected with Tanks A, B, and C with the same transfer rate of [0.2, 0.4] for each connection.
First, our benchmark models use the crisp Markov chain and PR algorithm. The initial vector of the Makov chain π = [ 0.32,0.24,0.16,0.28 ] ' , which is the normalized midpoint vector of the tanks. Then, we can use the midpoint of the path weights to form the probability matrix:
P = 0 1 0 0 0.4 0 0.6 0 0.3 0 0.3 0.4 0.4 0.3 0.3 0 )
Then, we can calculate the steady-state status of the Markov chain. On the other hand, the weights for pages are [ 0.32,0.24,0.16,0.28 ] , and the connection weights are assumed to be the uniform distribution as used in the PR algorithm. Their results are shown in Table 2.
Next, we will use the proposed algorithm to address the problem as follows. Here, we use three different types of the updating form, as shown in Equations (18)–(20), and four nonlinear functions in our numerical examples. Type (I) applies the transformation function directly to the rank before multiplying by the path weight. It tends to provide more disparity in results when using nonlinear transformation functions (logarithmic, exponential, sigmoid), as these functions accentuate the difference in ranks. For example, in the exponential scenario, the rank intervals for all tanks widen considerably compared to the linear scenario. Type (II) applies the transformation function to the product of rank and path weight. This calculation method considers the connection's rank and weight in the transformation. The impact is significant in the exponential and sigmoid scenarios, where the rank of Tank 1 increases notably. This method might highlight the influence of the higher-weight connections when combined with the ranks. Type (III) multiplies the rank with the transformed path weight. This method emphasizes the role of the path weight while keeping the ranks linear. The difference is noticeable in the logarithmic scenario, where the rank intervals narrow slightly compared to Types (I) and (II).
Then, we entail the different results with respect to different nonlinear functions, as shown in Table N. First, the linear function will obtain the same rank intervals for all three vote calculation types (I, II, III). This suggests that when the transformation function is linear, the order of operations does not affect the outcome. The logarithmic function somewhat reduces the disparity in weights, as evident from the closer rank intervals obtained compared to the linear function. For types (I) and (II), we observe very similar results, while Type (III) shows slightly higher rank intervals for Tank 1 and Tank 4, implying a stronger emphasis on connection weights. The exponential function increases the rank disparity, causing rank intervals to widen. In types (I) and (III), we observe similar patterns, with Tank 3 always having the highest rank. However, Type (II) shows different results, with Tank 1 and Tank 3 having more comparable rank intervals. This suggests that applying the exponential transformation to the product of rank and weight may lead to a more balanced influence distribution in specific network configurations. Last, the sigmoid function concentrates ranks toward middle values. While Tanks 1 and 3 still have higher ranks, the gap between all tanks is reduced, suggesting a balanced influence distribution. In Type (II), all tanks have almost equal ranks, indicating that applying the sigmoid function to the product of rank and weight can strongly level out rank differences.
In summary, the choice of transformation function and its application to either the rank, connection weight, or their product (updating types I, II, III) can significantly affect the final rank intervals. The logarithmic and sigmoid functions tend to reduce rank disparity, while the exponential function increases it. The effect of the exponential function is more pronounced when the transformation function is applied to the product of rank and connection weight (Type II). Therefore, the selection of the transformation function and updating types should consider both the characteristics of the network and the desired outcome, e.g., preserving rank disparity or aiming for a more egalitarian distribution of influence.
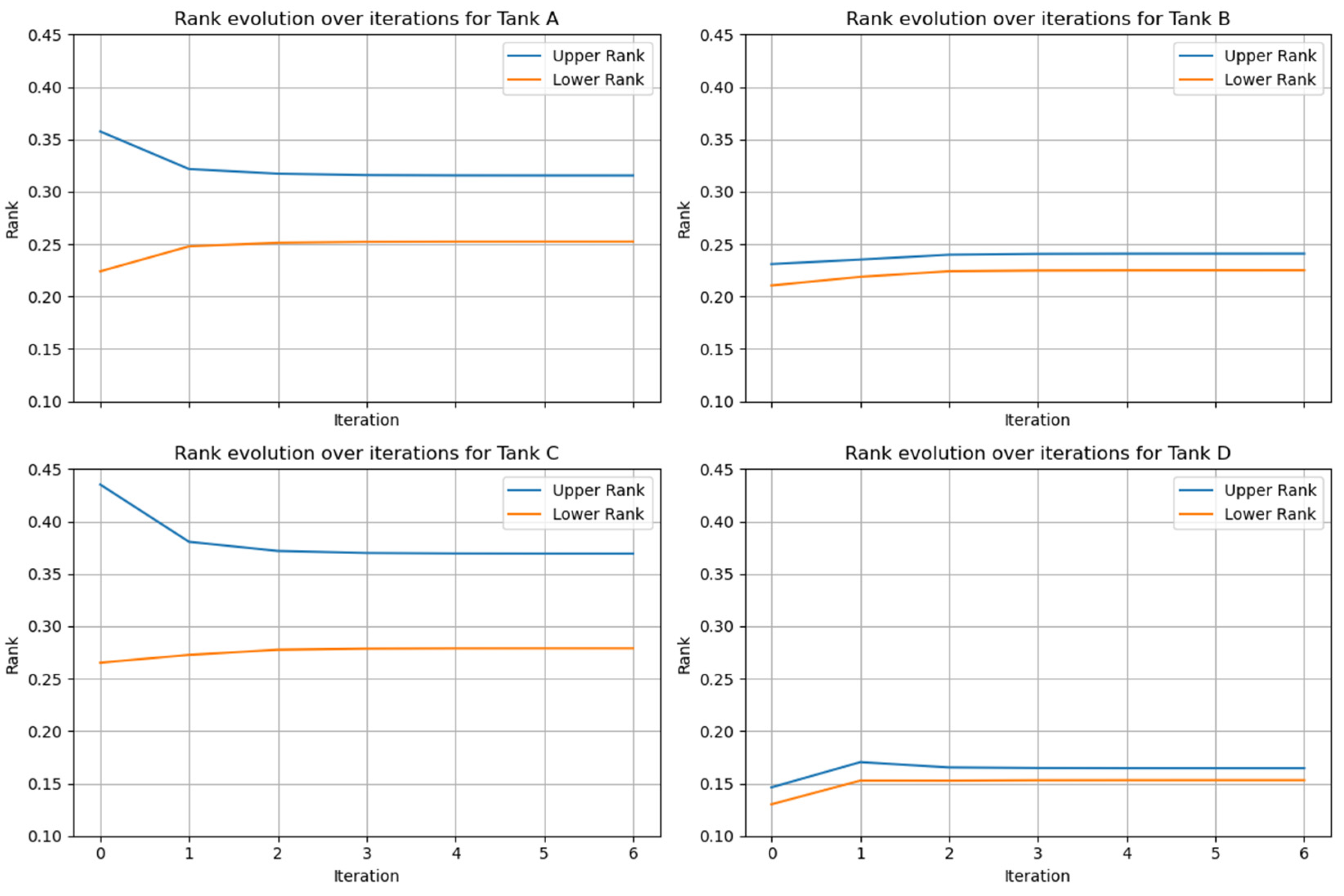
We can also observe the interval rank change with the different iterations to understand the convergent situation. For example, the rank evolution over iterations for different tanks can be depicted as shown in Figure 3, and it can be seen that all tanks are gradually convergent to the steady-state status, and Tanks B and D show less sensitivity compared to Tanks A and C.
The uncertainty and variability in the tanks' behavior depend significantly on the chosen update function and equation type. This underlines the importance of these choices when modeling real-world systems with uncertainties.

5. Discussions

In the numerical example, the initial vector was selected as the midpoint of each tank's initial state interval, normalized to add up to 1. The probability matrix was formed using the midpoints of the path weights. This provides a crisp baseline against which we can compare the results obtained by the proposed method. The crisp Markov chain and PR algorithm results are deterministic and do not account for the uncertainty or imprecision inherent in the system. This limitation is addressed in the proposed approach using constrained interval arithmetic which provides a range of possible values rather than a single value. As shown in Table N, the proposed method is able to account for the uncertainty in the ranks and connection weights to provide a range of possible ranks for each tank. The results also vary based on the transformation function and the Type of forms used.
From Table 2, it can be seen that the linear function results in the same rank intervals for all three calculation types, i.e., [0.2524, 0.3155] for Tank 1, [0.2250, 0.2409] for Tank 2, [0.2790, 0.3694] for Tank 3, and [0.1532, 0.1646] for Tank 4. The logarithmic function reduces the disparity in weights, yielding slightly closer rank intervals compared to the Linear function. For example, Tank 1's rank interval for the three types ranges from [0.2535, 0.3141] to [0.2574, 0.3137]. The exponential function increases rank disparity, causing rank intervals to widen. Tank 1's rank interval, for example, expands to range from [0.2591, 0.3153] to [0.3000, 0.3017]. Last, the sigmoid function results in rank intervals that are close to each other, concentrating the ranks towards a middle value. For Tank 1, the rank interval ranges from [0.2601, 0.3139] to [0.3017, 0.3017].
We can observe that the interval results of the proposed algorithm do not necessarily include the crisp results of the Markov chain and PR algorithm. The reasons are that the provided information is not entirely considered by the Markov chain nor the PR algorithm. For example, the Markov chain does not consider the random jumping effect, and the PR algorithm ignores the path weights of pages. In addition, the most critical factor is that we use an additional objective, i.e., the entropy function, to account for another objective that we might concern to derive the ranks of the tanks. It gives us a more flexible way to consider multi-objectives in the PR algorithm or Markov chain. Compared to the interval PR algorithm [14], we follow the power iteration method which is used in the conventional PR algorithm, rather than consider the problem as the interval/fuzzy Markov chain.
We should highlight that the function's appropriateness depends on the problem's context. The linear function could be the most suitable if the problem setting suggests a linear or steady change. A logarithmic function may be better if initial changes have more substantial impacts. An exponential function would be more suitable if there is an understanding of the system's rapid, compounding growth or decay. If the changes in the system occur slowly at first, rapidly in the middle, and then slowly again, a sigmoid function would be appropriate. These properties of different functions also provide the flexibility of the proposed algorithm in various applications.
In addition, the numerical example results also indicate that updating equations' types play a critical role. As usual, Type (II) is a natural extension of the nonlinear PR algorithm, where the network structure and the tank values interact iteratively to produce the final result. However, types (I) and (III) also can be used for the specific situation. Therefore, each equation type represents a different approach to structuring the PR computation and could be used depending on the specifics of the problem and the requirements of the particular implementation. Compared to [6]'s method, our method proposes different nonlinear functions adaptation in the PR algorithm rather than the LP-norms for the scores.
Last, the proposed algorithm focuses on a two-objective optimization problem, incorporating the entropy function as an additional objective. Further research may consider different objectives to reflect the problem. However, the appropriate weights between objectives might be another challenge.

6. Conclusion

In this paper, we propose a novel algorithm that employs constrained interval arithmetic to calculate the tank interval ranks, considering the initial states' uncertainty and connection weights. We also account for different types and nonlinear functions to reflect the complexity between states. In addition, the entropy function is also accounted for in calculating the interval ranks of the tanks. We have compared the results with the traditional crisp Markov chain and PR algorithm through a numerical example. The comparison reveals that the proposed algorithm captures the uncertainty in the tanks' behavior, providing a range of possible rank intervals for each tank. The different transformation functions and updating types lead to varying interval ranks, allowing for a flexible representation to conduct the complex system and justify the usefulness of the proposed method.

References

  1. S. Brin and L. Page, "The anatomy of a large-scale hypertextual Web search engine," Computer Networks and ISDN Systems, vol. 30, no. 1, pp. 107–117, Apr. 1998. [CrossRef]
  2. L. Page, S. Brin, R. Motwani, and T. Winograd, "The PageRank Citation Ranking : Bringing Order to the Web," presented at the The Web Conference, Nov. 1999. Accessed: Jun. 26, 2023. [Online]. Available: https://www.semanticscholar.org/paper/The-PageRank-Citation-Ranking-%3A-Bringing-Order-to-Page-Brin/eb82d3035849cd23578096462ba419b53198a556.
  3. W. Xie, D. Bindel, A. Demers, and J. Gehrke, "Edge-weighted personalized pagerank: Breaking a decade-old performance barrier," in Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2015, pp. 1325–1334.
  4. H. S. Bhat and B. Sims, "InvestorRank and an Inverse Problem for PageRank".
  5. B. Lu, S. Shi, Y. Ma, and J.-R. Wen, "Nonlinear Algorithms for Static-Rank Computation," Jun. 2023.
  6. L. Yao, T. Wei, A. Zeng, Y. Fan, and Z. Di, "Ranking scientific publications: the effect of nonlinearity," Sci Rep, vol. 4, no. 1, Art. no. 1, Oct. 2014. [CrossRef]
  7. W. Lodwick, "Constrained Interval Arithmetic," Mar. 1999.
  8. J. M. Bravo, D. Limon, T. Alamo, and E. F. Camacho, "On the computation of invariant sets for constrained nonlinear systems: An interval arithmetic approach," Automatica, vol. 41, no. 9, pp. 1583–1589, Sep. 2005. [CrossRef]
  9. T. Agryzkov, M. Curado, F. Pedroche, L. Tortosa, and J. F. Vicent, "Extending the Adapted PageRank Algorithm Centrality to Multiplex Networks with Data Using the PageRank Two-Layer Approach," Symmetry, vol. 11, no. 2, Art. no. 2, Feb. 2019. [CrossRef]
  10. P. Rozenshtein and A. Gionis, "Temporal PageRank," in Machine Learning and Knowledge Discovery in Databases, P. Frasconi, N. Landwehr, G. Manco, and J. Vreeken, Eds., in Lecture Notes in Computer Science. Cham: Springer International Publishing, 2016, pp. 674–689. [CrossRef]
  11. P. Lofgren, S. Banerjee, and A. Goel, "Personalized PageRank Estimation and Search: A Bidirectional Approach," in Proceedings of the Ninth ACM International Conference on Web Search and Data Mining, in WSDM '16. New York, NY, USA: Association for Computing Machinery, Feb. 2016, pp. 163–172. [CrossRef]
  12. A. Hashemi, M. B. Dowlatshahi, and H. Nezamabadi-pour, "MGFS: A multi-label graph-based feature selection algorithm via PageRank centrality," Expert Systems with Applications, vol. 142, p. 113024, Mar. 2020. [CrossRef]
  13. G. Hou, X. Chen, S. Wang, and Z. Wei, "Massively parallel algorithms for personalized pagerank," Proc. VLDB Endow., vol. 14, no. 9, pp. 1668–1680, May 2021. [CrossRef]
  14. H. Ishii and R. Tempo, "Fragile link structure in PageRank computation," in Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Dec. 2009, pp. 121–126. [CrossRef]
  15. M. Franceschet, "PageRank: standing on the shoulders of giants," Commun. ACM, vol. 54, no. 6, pp. 92–101, Jun. 2011. [CrossRef]
  16. T. Chakraborty, T. Ghosh, and P. K. Dan, "Application of Analytic Hierarchy Process and heuristic Algorithm in Solving Vendor Selection Problem," 2011, [Online]. Available: https://core.ac.uk/display/28782708.
  17. G. Pandurangan, P. Raghavan, and E. Upfal, "Using PageRank to Characterize Web Structure," in Computing and Combinatorics, O. H. Ibarra and L. Zhang, Eds., in Lecture Notes in Computer Science. Berlin, Heidelberg: Springer, 2002, pp. 330–339. [CrossRef]
  18. S. Zhou, C. Chelmis, and V. K. Prasanna, "Optimizing memory performance for FPGA implementation of pagerank," in 2015 International Conference on ReConFigurable Computing and FPGAs (ReConFig), Dec. 2015, pp. 1–6. [CrossRef]
  19. J. J. Whang, A. Lenharth, I. S. Dhillon, and K. Pingali, "Scalable Data-Driven PageRank: Algorithms, System Issues, and Lessons Learned," in Euro-Par 2015: Parallel Processing, J. L. Träff, S. Hunold, and F. Versaci, Eds., in Lecture Notes in Computer Science. Berlin, Heidelberg: Springer, 2015, pp. 438–450. [CrossRef]
  20. S. Beamer, K. Asanović, and D. Patterson, "Reducing Pagerank Communication via Propagation Blocking," in 2017 IEEE International Parallel and Distributed Processing Symposium (IPDPS), May 2017, pp. 820–831. [CrossRef]
  21. A. Sangers et al., "Secure Multiparty PageRank Algorithm for Collaborative Fraud Detection," in Financial Cryptography and Data Security, I. Goldberg and T. Moore, Eds., in Lecture Notes in Computer Science. Cham: Springer International Publishing, 2019, pp. 605–623. [CrossRef]
  22. M. Coppola, J. Guo, E. Gill, and G. C. H. E. de Croon, "The PageRank algorithm as a method to optimize swarm behavior through local analysis," Swarm Intell, vol. 13, no. 3, pp. 277–319, Dec. 2019. [CrossRef]
Preprints 79677 g001
Figure 2. The interdependencies between the tanks.
Figure 2. The interdependencies between the tanks.
Preprints 79677 g001
Preprints 79677 g002
Figure 3. The rank evolution over iterations.
Figure 3. The rank evolution over iterations.
Preprints 79677 g002
Table 1. Transformation functions in this paper.
Table 1. Transformation functions in this paper.
Function Formula Description
linear x The rank is unchanged. This will maintain the current disparity in ranks.
logarithmic log ⁡ x + 1 The rank increases logarithmically. This can result in a leveling effect, reducing the disparity in weights.
exponential e x The rank increases exponentially. This can lead to more disparity in ranks.
sigmoid 1 1 + e − x The rank increases following a sigmoid curve. This can concentrate the ranks towards a middle value.
Note that we adjust the formula of the logarithmic function to avoid generating the negative ranks.
Table 2. The comparison between different methods and functions.
Table 2. The comparison between different methods and functions.
Functions Tank 1 Tank 2 Tank 3 Tank 4
Crisp Markov chain 0.2635 0.3008 0.3112 0.1245
Crisp PR algorithm 0.2845 0.3128 0.2845 0.1181
Linear (I) [0.2524, 0.3155] [0.2250, 0.2409] [0.2790, 0.3694] [0.1532, 0.1646]
Linear (II) [0.2524, 0.3155] [0.2250, 0.2409] [0.2790, 0.3694] [0.1532, 0.1646]
Linear (III) [0.2524, 0.3155] [0.2250, 0.2409] [0.2790, 0.3694] [0.1532, 0.1646]
Logarithmic (I) [0.2535, 0.3141] [0.2262, 0.2421] [0.2802, 0.3667] [0.1536, 0.1636]
Logarithmic (II) [0.2545, 0.3147] [0.2244, 0.2409] [0.2799, 0.3669] [0.1543, 0.1645]
Logarithmic (III) [0.2574, 0.3137] [0.2224, 0.2402] [0.2798, 0.3636] [0.1565, 0.1663]
Exponential (I) [0.2591, 0.3153] [0.2282, 0.2460] [0.2872, 0.3667] [0.1461, 0.1515]
Exponential (II) [0.3000, 0.3017] [0.2249, 0.2268] [0.3202, 0.3256] [0.1495, 0.1513]
Exponential (III) [0.2764, 0.3070] [0.2261, 0.2389] [0.2968, 0.3421] [0.1554, 0.1573]
Sigmoid (I) [0.2601, 0.3139] [0.2293, 0.2471] [0.2880, 0.3637] [0.1469, 0.1510]
Sigmoid (II) [0.3017, 0.3017] [0.2235, 0.2258] [0.3225, 0.3230] [0.1495, 0.1523]
Sigmoid (III) [0.2890, 0.3042] [0.2234, 0.2275] [0.3072, 0.3264] [0.1612, 0.1612]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated