Prerpints.org logo
Preprint
Article

Distributed Subgraph Query Processing Using Filtering Scores on Spark

Altmetrics

Downloads

97

Views

22

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

19 July 2023

Posted:

20 July 2023

You are already at the latest version

Alerts
Abstract
As various services have been generating large scale graphs to represent multiple relationships between objects, studies have been conducted to obtain subgraphs with particular patterns. In this paper, we propose a distributed query processing method to efficiently search a subgraph for a large graph on Spark. To reduce unnecessary processing costs, the search order is determined by filtering scores using the probability distribution. The partitioned queries are searched in parallel in the distributed graph of each slave node according to the search order, and the local search results obtained from each slave node are combined and returned. The query is partitioned in triplets based on the determined search order. The performance of the proposed method is compared with the performance of existing methods to demonstrate its superiority.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

1. Introduction

A graph G=(V, E) comprises a set V of vertices and a set E of edges to represent multiple relationships between objects in social media, biological networks, and the Internet of Things (IoT) [1,2,3,4]. A graph is used with the objective of analyzing interactions, detecting anomaly patterns, and providing recommendation services [5,6,7,8]. In the IoT, for example, data transmission and control flows among connected devices (“things”) are modeled as graphs that are analyzed to identify anomalies or to group things used by the interactions. Since large amounts of graphs have been generated in respect of social media, the IoT, and so on, systems have been developed to partition and store graphs to perform distributed processing [9,10,11,12].
Distributed parallel processing methods have been proposed to effectively process large amounts of graph big data [13,14,15,16]. Pregel proposed a bulk synchronous parallel model for the parallel processing of large graphs [17,18]. Pregel computations consist of a sequence of iterations, called supersteps. Parallel such as MapReduce [19,20,21], which is a programming model for processing large amounts of data in distributed parallel computing, simplify the design and implementation of large capacity data processing systems; however, they may result in inefficient processing because they do not support efficient data mining and machine learning algorithms. To resolve this problem, GraphLab has been proposed, and it supports asynchronous processing while ensuring data consistency in a distributed shared memory environment [22]. PowerGraph processes a graph analysis algorithm by repeatedly executing a gather-apply-scatter (GAS) model to reduce network communication and processing costs [23]. GraphX is a widely used large capacity data processing engine that is used to perform parallel processing of graph data and simplify the implementation and application of algorithms [24,25]. GraphX implemented on top of Spark uses resilient distributed datasets (RDDs), which are collections of objects that are partitioned across a cluster to provide in-memory storage abstraction.
Subgraph queries are frequently used in application areas that use large graphs to determine which subgraph matches a certain pattern [26,27,28,29,30,31]. In social media, for example, subgraph queries are performed to obtain a user graph with a particular relation or identify communities that have similar interactions. In the IoT, subgraph queries are used to detect anomaly patterns among objects or identify IoT devices that perform similar actions. In protein–protein interaction networks, subgraph queries are used to identify a particular protein structure. Subgraph query processing requires performing a subgraph isomorphism test to identify a graph that structurally matches the query in all graphs [28,31]. The subgraph isomorphism test compares all possible subgraphs in a large graph and is therefore NP-complete.
To solve NP-compete problems occurring in subgraph query processing, filtering and verification [32,33,34,35] and path based query processing [36,37,38] have been proposed. The filtering and verification is divided into a filtering stage and a verification stage. The filtering stage extracts the candidate set for the graphs. The verification stage performs the subgraph isomorphism test for the candidate set. To extract a candidate set, building indices by extracting features of the graphs is required. Commonly used features include paths, trees, and cycles, and hash table information is occasionally used. When a query is entered, a candidate set that matches the features of the query is extracted through the constructed index. The validation stage performs a subgraph isomorphism test for the extracted candidate set to verify whether they actually match the query. Commonly used subgraph isomorphism test algorithms include VF2 [39], GraphQL [40], and GADDI [41], among others [42]. The filtering and verification requires additional costs for building and managing the index for each feature for the entire graph. Furthermore, as the subgraph isomorphism test is an NP-complete problem, the cost may vary greatly depending on the method of filtering the candidate set.
The path based query processing method searches subgraphs without executing a subgraph isomorphism test algorithm [36,37,38,43,44]. Starting from a vertex in the graph that matches the query, all paths are searched for the connected neighbor vertices to check whether they match the vertex of the query. The search is performed for all connected vertices, and if a vertex that matches the query is obtained, then the vertex ID is recorded, and the ID of the vertex recorded at the end of the search becomes the path of the subgraph matching the query. In [37], a new query processing method was proposed to partition a query into segments of triplets in Spark. In the head segment, which corresponds to the first search order, a vertex that matches the label of the head segment vertex is obtained in each graph and selected as the starting vertex. The labels of the neighbor vertices of the selected starting vertex are checked to obtain a triplet matching the segment and return it to the master. Then, a search for the partitioned segment is performed, and the master gathers the results sent from the nodes. In this method, however, there are no special criteria for selecting the starting vertex, and a cost model that can reduce the processing cost is not built. Therefore, the problem with this method is that the processing cost increases if several vertices match the label of the head segment, which is the starting vertex, or if the degree of the pertinent vertex is large.
In this paper, we propose a distributed query processing method to search a subgraph with the same label as a query on Spark. Through a probability density function of the degree that can occur at each vertex based on the statistical information collected for the graph, the probability of the degree of the pertinent vertex appearing scores the probability that the search is not required. This value is a probability that can filter out the vertices that do not need to be searched owing to the difference in the degree between the query and the graph. As the probability of becoming filtered increases, it is possible to search with less cost. The query is partitioned with the vertices in the order from the highest filtering probability to the lowest, thereby searching the partitioned subqueries. The contributions of this paper are as follows.
  • We predict the filtering score to avoid the vertices that do not need to be searched, based on the statistical information of the graph.
  • We determine the search order that determines the priority of the vertices to be searched among the vertices of the query through the filtering score.
  • We partition the query into subqueries according to the filtering score for distributed query processing in Spark.
This paper is organized as follows. Section 2 presents previous studies related to this research, and Section 3 explains the proposed path based distributed subgraph query processing method. Section 4 discusses the performance evaluation to confirm the superiority of the proposed method. Finally, Section 5 provides the concluding statements.

2. Related Work

Spark has a programming model for distributed data processing similar to MapReduce. Spark uses a data type called an RDD to overcome data volatility in memory and efficiently perform distributed processing [25,45]. An RDD comprises data stored in a distributed manner across many nodes and allows for parallel processing. Moreover, it can recover on its own, even in the event of a failure. An RDD is not processed at one node. It is divided into smaller units called partitions that are distributed and processed at multiple nodes. Spark’s GraphX is a submodule that supports distributed and parallel graph processing of large data [24]. GraphX generates RDDs by dividing vertices and edges into two tables: VertexRDD and EdgeRDD. The divided RDDs are partitioned using the vertex-cut method on each node. The Diver program serves as the master and instructs walkers to perform tasks through the cluster manager. The workers that received the task instructions perform the parallel processing of the partitioned VertexRDD and EdgeRDD.
In [37], a distributed graph path querying that operates without the need to build extensive indices in Spark was proposed. In this framework, an input query is partitioned into such triplets. Once the query partitioning of the master is finished, the partitioned subgraphs are disseminated to all slaves, and each slave searches the received triplet. A vertex in the partitioned query is selected as the starting vertex of the search, and the search is performed along the direction of the edge connected to that vertex. The edge direction is recorded in the vertex information table, and the information of the vertices approached along the edge is read to obtain the information of the neighbor vertices and the edge direction. Once the search for a particular triplet is finished, each slave sends the search result to the master, and the master records it and instructs the slave to obtain the next triplet. In the master table, the search results are stored, thereby recording and accumulating the searched vertices. When the search for all partitioned queries is finished, the accumulated vertices in the master’s table become the searched path.
GraphCache is a caching system for undirected labeled graphs to support subgraph and supergraph queries [33]. GraphCache consists of three modules: method M, query processing runtime, and cache manager. The main objective of method M is a subgraph isomorphism test. The cache manager deals with the management of data and metadata stored in the cache. GraphCache introduces a number of graph cache replacement strategies including a hybrid graph cache replacement policy. The query processing runtime executes queries and monitors the key. The query processing runtime consists of the resource/thread manager, the internal subgraph/supergraph query processors, the logic for candidate set pruning, and the statistics monitor. The internal subgraph/supergraph query processors check whether the query is a subgraph or supergraph of previous queries and execute queries using cached queries and their answer sets.
HGraph is a parallel and distributed tool for processing large scale graphs on top of Hadoop and Spark [15]. HGraph consists of the application layer, the execution layer, and the distributed storage layer. The application layer supports the APIs for implementing a program for large scale graph processing. The distributed storage layer is based on the Hadoop File System (HDFS) and Spark RDD. HGraph uses two types of operators: unary operators and binary operators. Unary operators are logical graph operators that take a single input graph. Binary operators perform operations on two input graphs. HGraph operators run in memory and switch to the local disk when both the physical and virtual memory are completely saturated.
In [46], query processing algorithms are proposed based on a worst-case optimal join algorithm in a continuously changing large graph. To support distributed processing of the recent worst-case optimal join algorithms, three distributed algorithms are introduced: BiGJoin, Delta-BiGJoin, and BiGJoin-S. BiGJoin is a distributed algorithm for static graphs that achieves a subset of theoretical guarantees. Each operation that BiGJoin performs on each tuple corresponds to an operation in the serial execution of generic join. Therefore, BiGJoin inherits its computation and communication optimality from generic join. Delta-BiGJoin is a distributed algorithm for dynamic graphs in insert only environments. BiGJoin and Delta-BiGJoin are implemented in Timely Dataflow, which is a distributed data parallel dataflow system in which one connects dataflow operators describing computation using dataflow edges describing communication. BiGJoin-S is a distributed algorithm for static graphs that achieves all theoretical guarantees, including balancing the workload between distributed workers on any input instance.
MapReduce based multiple subgraph query processing (MSP) was proposed to process multiple graph queries in Hadoop [47]. MSP uses structure based partitioning and an integrated graph index (IGI) to reduce the query search space. The structure based data partition stores the subgraphs with similar labels and structures on one node to improve the default partition provided by MapReduce. The IGI created by the method proposed in [48] keeps all neighborhood information of the graphs to extract common subgraphs. MSP performs two MapReduce operations: the first partitions the graphs and creates an index for each partition; the second processes subgraph queries and index maintenance. For query processing, MSP checks whether all edges of the query exist in that IGI. If all the edges are not present in the IGI, the query is filtered. In the validation, only the necessary IGIs are loaded based on the preprocessing phase.

3. The Proposed Distributed Subgraph Query Processing

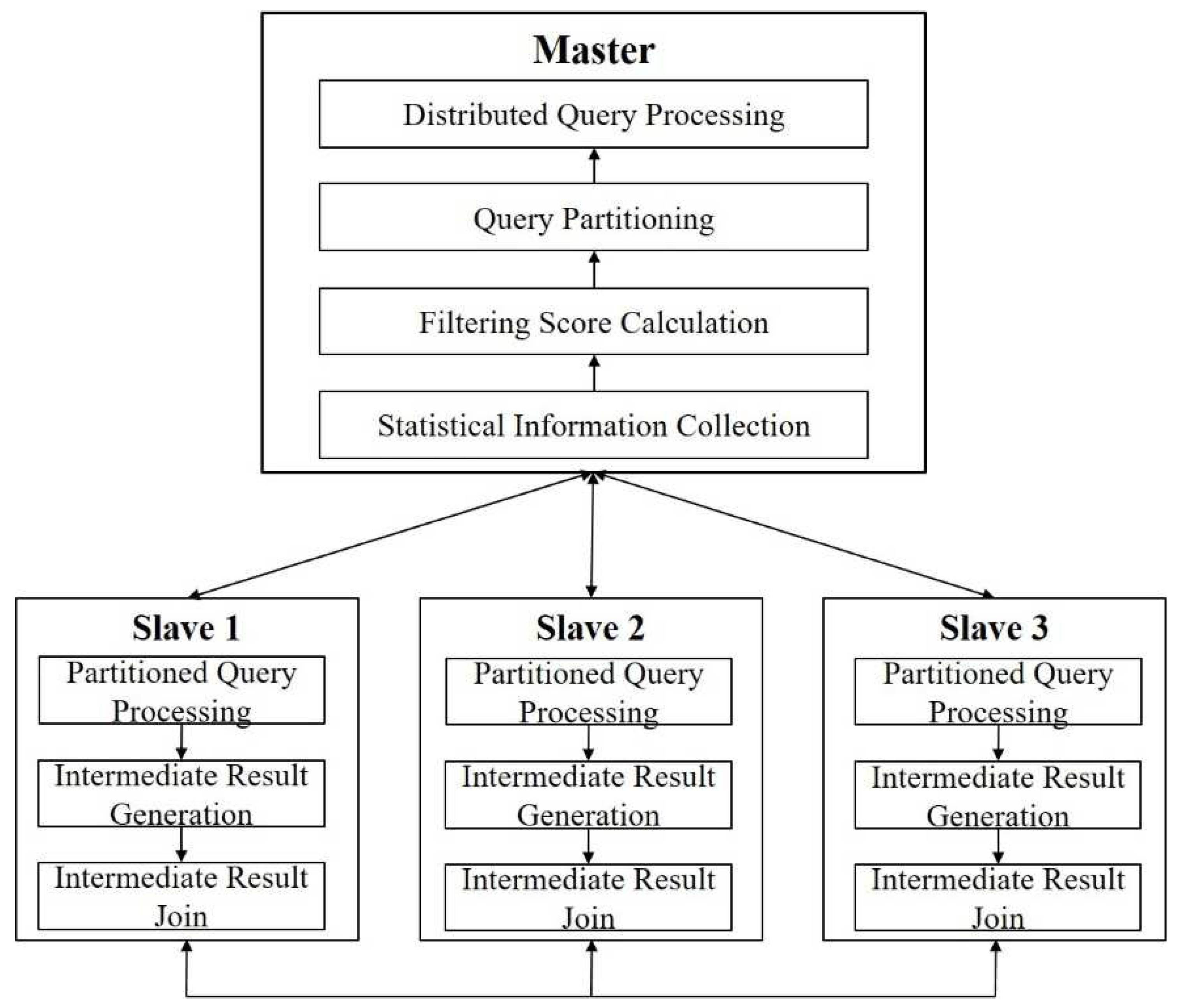
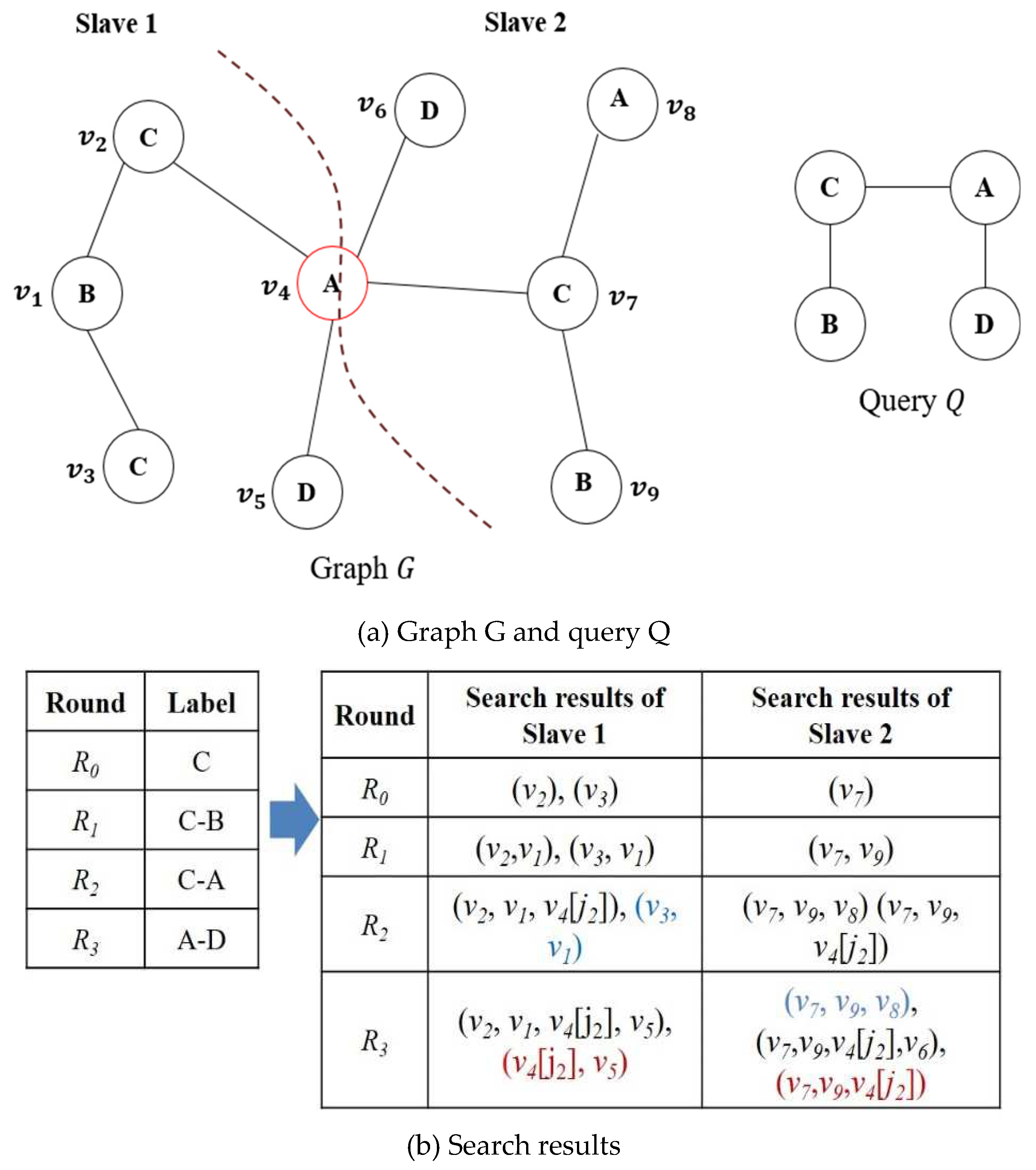
3.1. Overall Architecture

In the case of a path subgraph query, searching for a certain vertex can have a significant impact on the search to minimize candidate results that satisfy partial query conditions. If there are countless starting vertices that are searched first, numerous parallel searches are performed, leading to a larger number of unnecessary searches than the number of vertices actually required for the search. Furthermore, even if the search is performed starting with an appropriate number of vertices, the connected neighbor vertices all have to be searched, indicating that there are countless cases to search according to the number of connected edges. Therefore, the proposed method calculates the filtering score to search for the subgraph that matches the query with a smaller number of searches, while reducing unnecessary searches. A vertex with a high filtering score can filter more unnecessary searches. If the search is performed in the search order of the vertices from the highest to the lowest score, the search time can be reduced further. The filtering score is calculated through the probability density functions considering the data distribution characteristics.
Figure 1 shows the overall architecture of the subgraph query processing method on Spark. In the distributed environment, the graph is distributed according to the partition policy and stored in multiple slave nodes, and the statistics are collected for the entire graph. The collected statistics include the number of vertices for each label and the degree of each label. As the search order has a significant impact on the performance in the path query, we compute a filtering score to determine the search order for query processing. The filtering score is calculated based on the statistical information to reduce unnecessary searches. The parallel searches are performed at each slave node in Spark according to the determined search order. The query is partitioned into triplets according to the filtering score to perform parallel searches. As the data are distributed and stored in different nodes, it is necessary to join the results that have been locally searched in each slave node. The search results are transmitted for joining through communication between the slave nodes, and the results are finally joined at one slave node.

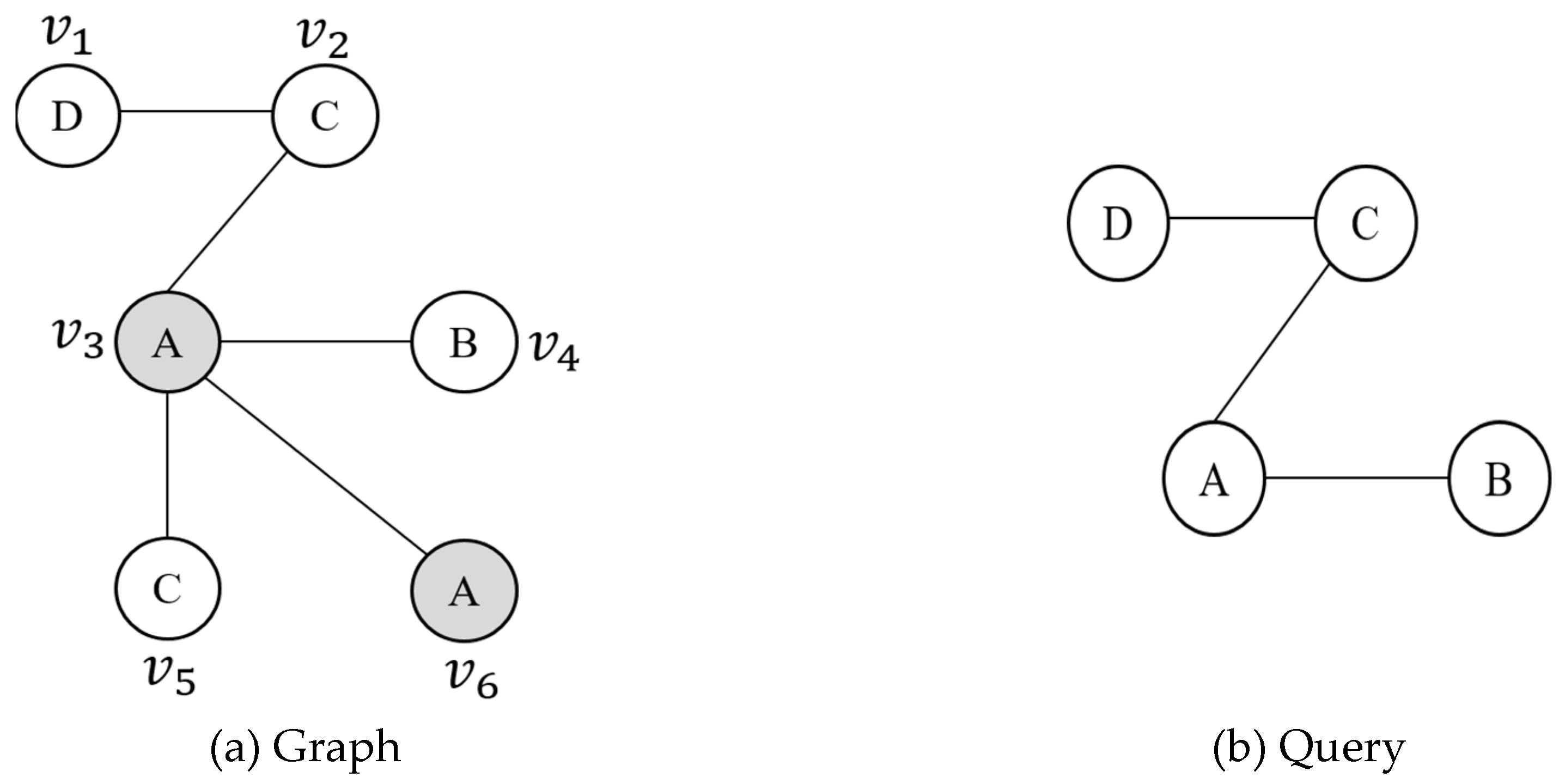
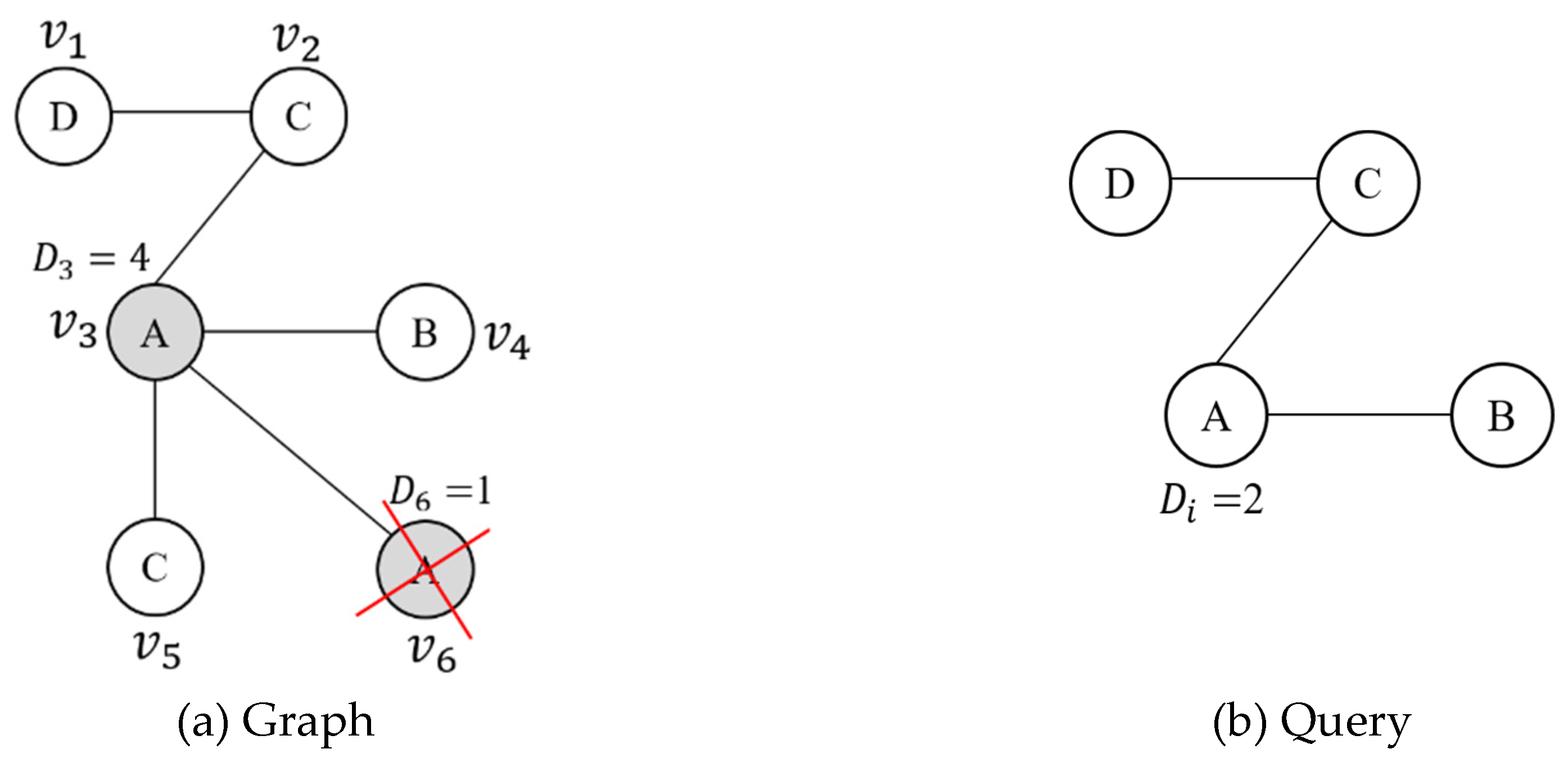
3.2. Filtering Score

Statistical information regarding the graph is collected to calculate the filtering score used for determining the search order. The information collected as statistics includes the graph’s labels and degree. In general, path subgraph queries first search for vertices with the same label as vertices included in the query. In the graph, vertices with fewer labels matching the query can produce relatively fewer candidate result sets than vertices that do not. Therefore, it is necessary to first search for vertices that match the labels included in the query less. It is efficient to exclude the vertices with a smaller degree than the degree of the query because even if they are searched, they pertain to paths that are not likely to develop into the query. We calculate the probability of a particular degree occurring at a certain vertex and use it for the cost prediction of the path.
Suppose G and Q are the vertices of a graph and a query with the same label. If matching vertices are searched starting with every G, then as the number of labels L increases, the number of vertices where the search starts will increase linearly. In Figure 2, more searches are required in the case of searching for the path starting with v 4 , where the number of the same labels is 1 in Figure 2 (a), compared to the case of searching for the path starting with v 3 and v 6 , where the number of the same labels is 2. Therefore, our proposed method collects the statistics for the number of labels at each vertex of G, and the vertices with a small number of labels are selected as the starting vertices.
When vertices matching the query are searched, vertices having smaller degrees than the degree of the query vertex do not need to be searched. For example, if vertices with the label A of the query are searched, as shown in Figure 3, v 3 and v 6 will be searched. If the degree of vertex v i is D i , D 3 and D 6 are 4 and 1, respectively. Since the degree of the vertex with the label A of the query is 2, v 3 with degree 4 has to be searched, but v 6 with degree 1 has no possibility of becoming the query result. Vertices having degrees smaller than the degree of the query can be filtered out. Therefore, we calculate the filtering score for avoiding the vertices to be searched depending on the difference in the degree.
When real world data are modeled as a graph, the distribution of the vertices and their edges shows a particular tendency depending on which data are used. Simply, the normal distribution will be shown where the vertices of the graph and the edges connected to the vertices are evenly distributed. However, many graph applications show a power-law distribution where a small number of vertices has many edges [23,49,50]. If the vertices of the graph and the edges connected to the vertices show a certain distribution, we herein calculate the probabilistic filtering scores that will be excluded from the search and determine the search order to decide which vertices of the query will be searched with higher priorities. The search order is determined based on the filtering score, and the filtering score is calculated in two cases. The first case divides a normal distribution where the vertices of the graph and their degrees are evenly distributed and a case of showing a power-law distribution where the degrees are concentrated on a certain vertex. Subsequently, the degree of the pertinent vertex is predicted through the probability density function of the corresponding distribution, and the probabilistic search order is determined based on the predicted value. The second case determines the search order of the vertices through the average degree of the vertices having the label corresponding to the query.
The proposed method defines a filtering score to determine the search order for query processing. The filtering score is the filtering probability calculated through the probability density function and the proportion of a certain label in the total labels obtained through the statistics collection stage. The filtering probability considers different probability density functions because it can show a different distribution depending on the graph characteristics. The first method calculates through the probability density function of a normal distribution, denoted by normalFS. The second method calculates through the probability density function of a power-law distribution, denoted by powerFS. The last method calculates using the average degree of a particular label without considering the probabilistic distribution of data, denoted by avgDgFS.
Assuming that the vertices of the graph and their degrees follow an evenly distributed normal distribution, Equation (1) shows the probability density function f x , where x is the degree of the vertices with label L as a variable for calculating the probability density function, μ is the average degree of the vertices, and σ is the standard deviation of the degree of the vertices.
f x = 1 σ 2 π e − ( x − μ ) 2 2 σ 2
Assuming that a vertex v i with the same label L exists in the graph and query, G L ( v i ) and Q L ( v i ) in the probability density function denote the probability that the corresponding degree will occur, respectively, and the area of Q L ( v i ) ~ G L ( v i ) is the probability that can filter, without searching, the vertex G L ( v i ) that has a smaller degree than the degree of Q L ( v i ) according to the aforementioned difference in the degree. Therefore, the area from the degree of G to that of Q L ( v i ) for the selection of the starting vertex is called F P N D ( v i ) , as shown in Equation (2).
F P N D v i = ∫ G L ( v i ) Q L ( v i ) 1 σ 2 π e − ( x − μ ) 2 2 σ 2 d x
According to [51], the relation between the vertices and their degrees in a graph of the real world follows a power-law distribution, and the probability that such vertices and degrees occur is generally P ( d ) ∝ d − α , with   α ≈ 2 . Furthermore, [52] showed that a power-law distribution can be expressed as a probability distribution called a zeta distribution or Pareto distribution. If the vertices and edges in the power-law distribution have an exponential relationship of 2, then the variable s in the zeta function can be specified as 2. The zeta function converges to a specific value, and the probability density function of the Pareto distribution can be expressed as Equations (3) and (4). Therefore, the probability density function of the power-law distribution can be represented by Equation (5).
ζ γ = ∑ k = 1 ∞ 1 k γ
ζ 2 = ∑ k = 1 ∞ 1 k 2 = π 2 6
f x = 6 ( π x ) 2
Let v j be the vertices of the graph having the same label as the query. In the probability density function, G L ( v i ) and Q L v i represent the probability that the corresponding degree will occur, and the area of G L ( v i ) ~ Q L ( v i ) is the probability that can filter, without searching, the vertex G L ( v i ) that has a smaller degree than Q L ( v i ) based on the aforementioned difference in the degree. Therefore, the area from the degree of G L ( v i ) to that of Q L ( v i ) is called F P P D ( v i ) , as shown in Equation (6), for the selection of the starting vertex.
F P P D v i = ∫ G L ( v i ) Q L ( v i ) 6 ( π x ) 2 d x
When a query is entered as an input, the filtering score is calculated for all vertices of Q based on the collected statistical information. For the filtering score, we consider the value calculated using the three methods explained in the previous section and the proportion of a certain label in all labels collected in the statistics collection stage. The filtering scores are classified into normalFS, powerFS, and avgDgFS according to the distribution characteristics, as shown in Equations (7)~(9), respectively. Table 1 shows the description of the parameters in Equations (7)~(9).
n o r m a l F S v i = V L V a l l × F P N D ( v i )
p o w e r F S v i = V L V a l l × F P P D ( v i )
a v g D g F S v i = V L V a l l × A D L ( v i )

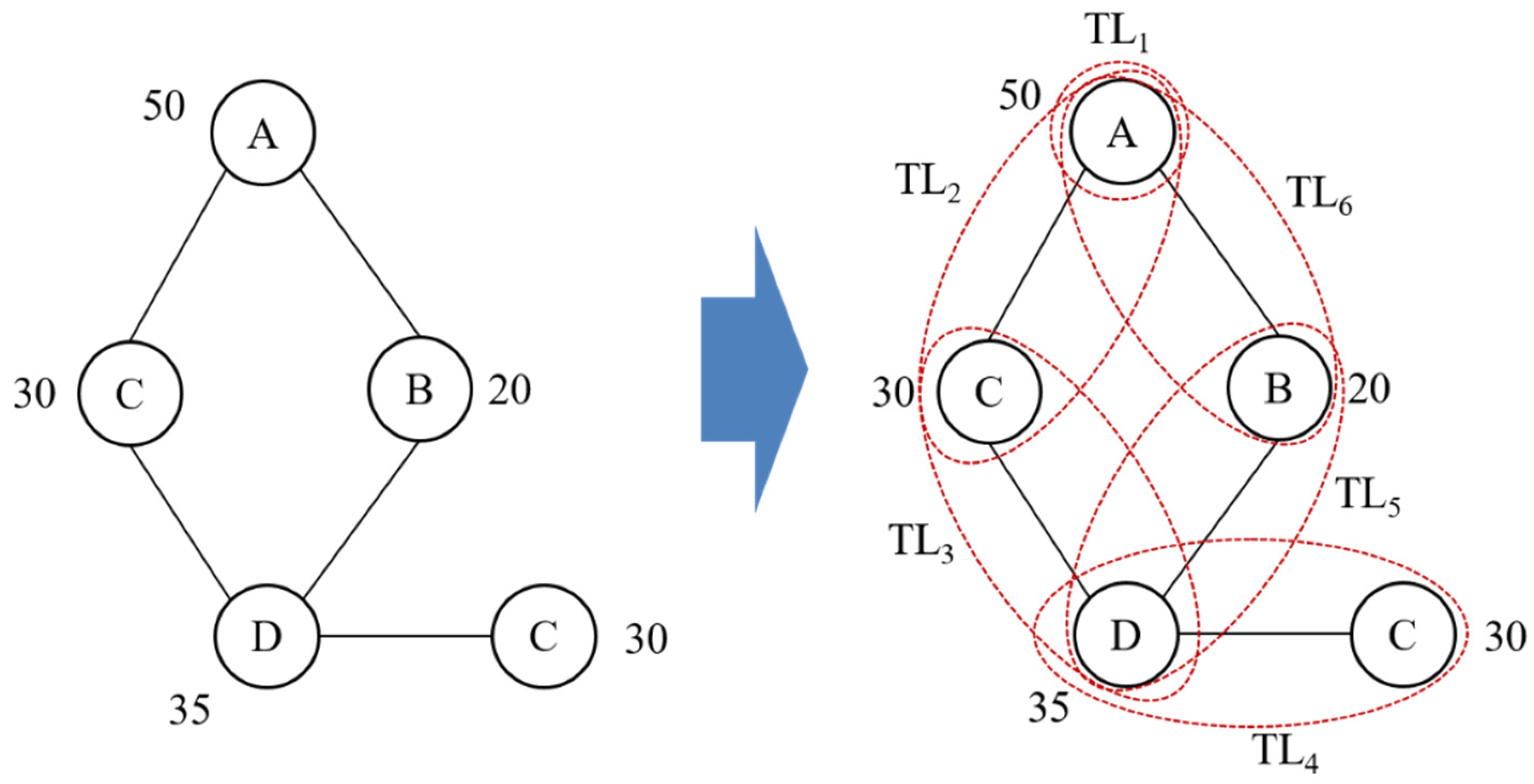
3.3. Query partitioning

A vertex that has the highest filtering score among the vertices of the query is selected as the starting vertex, and the query is partitioned into triplets comprising a vertex having the next highest filtering score among the neighbor vertices connected to the starting vertex. The triplet consists of < T V i , E i , H V i > . Here, T V i stores tail vertex information with the highest filtering score in the query, H V i stores head vertex information with high filtering score among neighbor vertices of T V i , and E i stores edge information. The initial start vertex is set to NULL by T V i and E i . Query partitioning is performed for all neighbor vertices connected to the starting vertex. When the partitioning with the neighbor vertices is finished, the same operation is performed at the vertex with the next highest filtering score among the vertices connected to the neighbor vertices of the starting vertex.
Algorithm 1 shows the query partitioning. Once the starting vertex and the search order are determined, they are registered as a round in accordance with the determined search order. The round represents the search order of performing a parallel process at each slave node, and the next round is performed only after finishing the previous round. The starting vertex with the highest filtering score is registered as R 0 . The vertex that has the next highest score among the neighbor vertices connected to the starting vertex is registered as the next round. When the round registration for all neighbor vertices connected to the starting vertex is finished, the same operation is performed for the neighbor vertices of the starting vertex. As a result, all vertices of the query are partitioned in the order from the highest to the lowest filtering score and the partitioned triplets are registered in qRound.
Algorithm 1 Query partitioning
Preprints 79941 i001
Figure 4 shows the process of dividing a query into triplets. First, we construct triplets by finding the highest vertex in the query graph and performing a depth-first search (DFS) based on that vertex. Suppose query Q consists of five vertices and the number next to the vertex is the filtering score. Since the vertex with label A has the highest filtering score, we set the vertex with label A as the starting vertex and add the initial triplet T L 1 to qRound. When the starting vertex is selected, triplets are added to qRound while continuously performing DFS based on the filtering score. With a vertex with label A as the starting vertex, a neighbor vertex with a high filtering score is selected as T L 2 and added to qRound. While this process is repeated until DFS is finished, triplets for the query are registered in qRound.

3.4. Distributed Query Processing

The proposed method works as a master-slave architecture in a Spark environment. The master node calculates a filtering score through statistical information collection. The query is partitioned based on the filtering score and the query processing rounds are registered. The master node instructs each slave node to perform the query according to the search order. The slave nodes that have received the instruction perform the search in their own partitions and record the results in the result table. Each slave node generates intermediate results according to the search order registered in the qRound and combines the intermediate results generated from each slave through join operations to deliver the final results to the master node.
Algorithm 2 represents a distributed query processing process performed in a slave. Triplets are stored in the qRound according to the order in which query processing is performed. Each slave searches the graph according to the triplet order registered in the qRound, generating intermediate results with matching labels. When the first round R 0 is performed for the subgraph query, each slave node searches all vertices with the label selected as the starting vertex. After that, in the second round R 1 , the neighbor vertex with the label of R 1 connected to the vertex with the label of the starting vertex is searched. The next round is searched through the ID of the vertex recorded in the search result. When R 0 is performed according to the query processing rounds, each slave node searches for all vertices with the label selected as the starting vertex. Subsequently, R 1 is performed, and the neighbor vertices with the label R 1 connected to the vertex labeled as the starting vertex are searched and recorded. In the next round, the search is performed based on the ID of the vertices recorded in the search results. Based on this, the search is only performed for the neighbors of the vertices obtained in the previous round, and the processing cost can be efficiently reduced because there is no need to search again from the vertices that were not needed in the previous search. Each slave stores partitions divided by a vertex-cut method, and the vertex that becomes the basis for division is replicated to each slave. When we encounter replication vertices while searching a graph using triplets according to the qRound order, we set a join tag because query processing is no longer possible on the current slave node. Candidate results in slave nodes are joined based on the vertex to which the join tag is assigned.
Algorithm 2 Distributed Query Processing
Preprints 79941 i002
Figure 5 shows the intermediate search results by round. As a result of performing   R 1 , v 1 connected to v 3 can be searched, but the graph has no vertex with a label A connected to v 3 - v 1 in R 2 . Therefore, ( v 3 , v 1 ) is excluded in the result of R 2 . As ( v 3 , v 1 ) has been removed in R 3 , there is no need to search for the vertices with a label D connected to v 1 . If a vertex due to the graph partitioning is encountered in the process of searching according to the round in each partition, there may be more vertices connected to the pertinent vertex in the replicated partition, but this information cannot be known in the current partition. Therefore, a join tag is marked on the corresponding vertices of all partitions that have replicated the vertex, and the next search is commenced. The join tag is used when sending/receiving the search result between the slave nodes after the local search. The join tag is a mark used to store only intermediate results that require joins to avoid storing unnecessary intermediate results. In R 2 , a replicated v 4 is obtained, and a join tag is marked. As the vertex with a join tag indicates that there is a path in another partition, the search begins again at the vertex with the join tag in R 3 , which is the next round. As such, owing to the method of performing the next round only for the results of the previous round, there is the advantage that the size of the table recording the results is gradually reduced, and unnecessary searching is not performed.
Figure 6 shows the results of such search result joins. When the partitioned query searches are finished, an intermediate search result table is created in each partition, and the intermediate result tables are sent/received using communications between the partitions for the join. Because the search is performed asynchronously in each partition, the completion time of each search is different. The partitions that have finished searching already and are in the waiting state send their intermediate result tables if there is another partition that has finished the search. As the cost required for the communication increases as the size of the table increases, the communication cost can be reduced if a table of a small size is transmitted. The partition that has received the intermediate result performs the join with its own intermediate result table.

4. Performance Evaluation

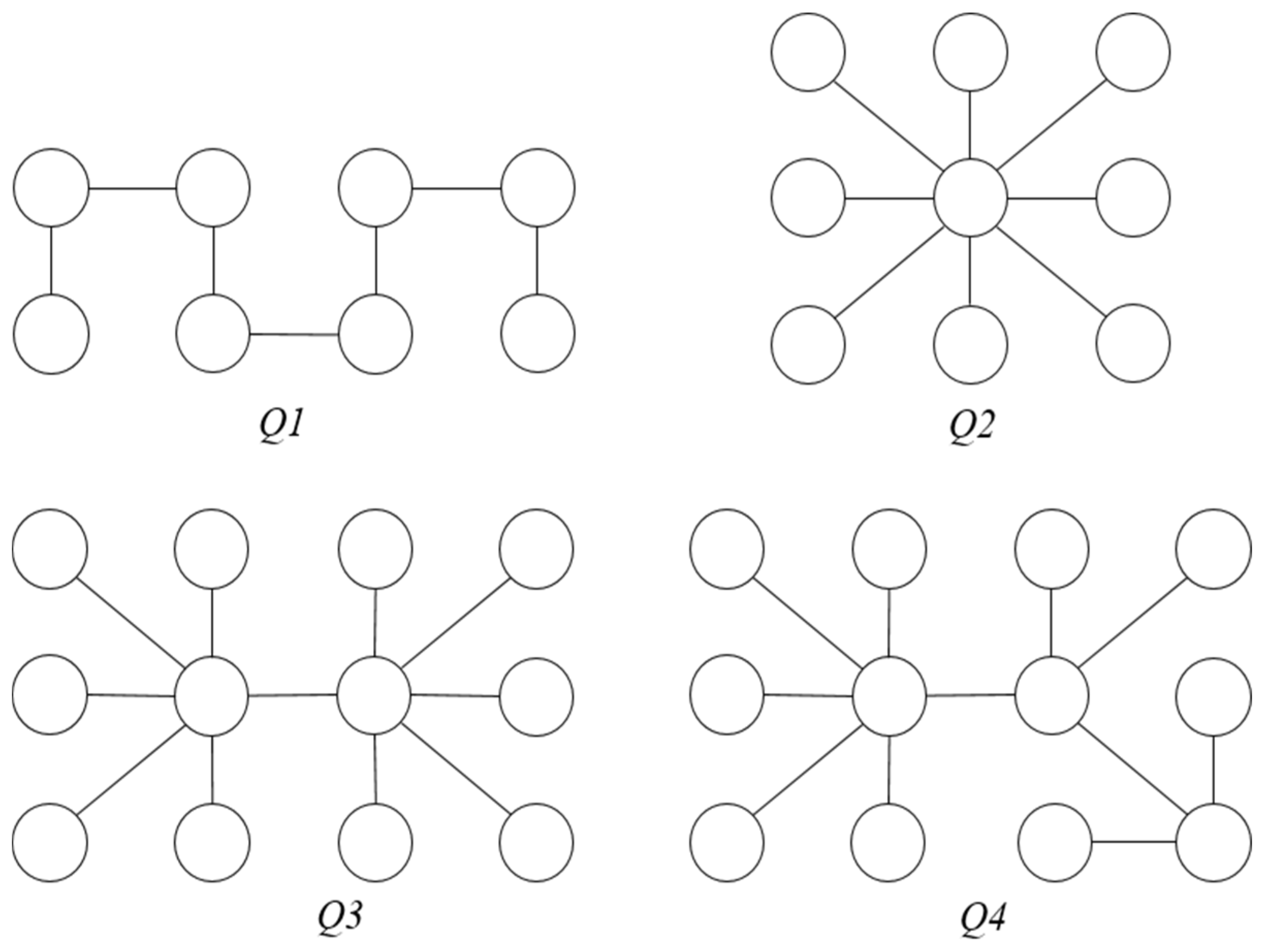
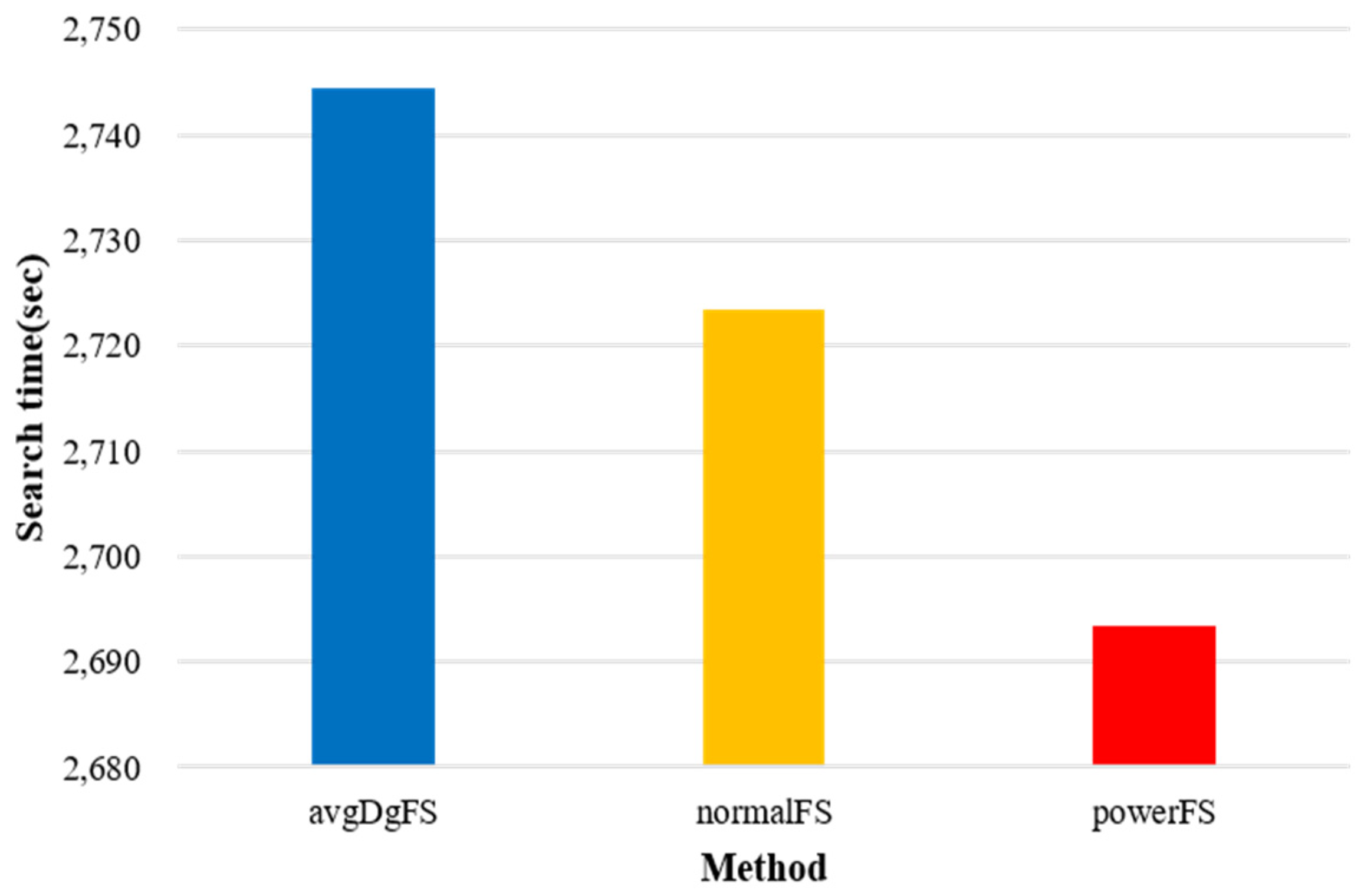
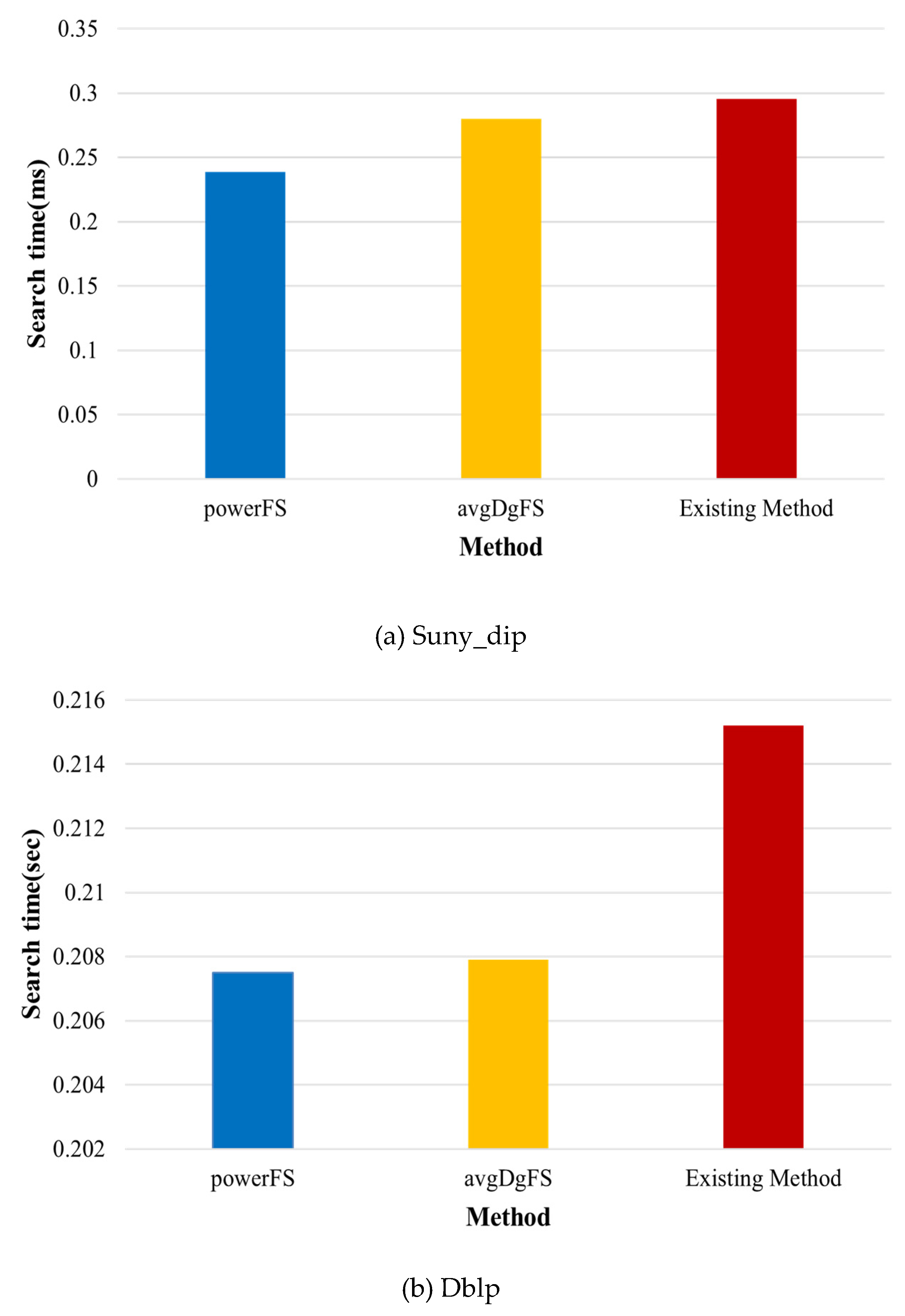
4.1. Analysis

Various distributed query methods have been proposed to effectively perform subgraph search on large graphs. Distributed subgraph query processing methods are divided into filtering and verification and pathbased processing according to the query processing technique. GraphCache [33] is a representative filtering and verification method to improve graph query processing through caching data. When a query similar to a previously performed query comes in, it generates a candidate result using the cached query and the query execution result, and performs a verification phase to generate the final result. However, when a new query that has not been previously performed is requested, the filtering phase is performed. MSP [47] is an FTV that processes multiple subgraph queries through MapReduce framework. MSP uses an index called IGI, which is available in the filtering phase and the verification phase in a distributed environment. IGI integrates common subgraphs to reduce the cost of processing multiple queries. When edge labels integrate different vertices, instead of adding vertices and edges separately, we reduce the size of the IGI by adding edge information to the vertices. During the verification phase, HDFS does not load all the IGIs, but only the required IGIs. HGprah[15] is a prototype tool for distributed graph processing in Hadoop and Spark. HGraph has a master-slave structure, and the master manages the workflow, and the actual distributed processing is performed through the slave. HGraph does not provide a separate query processing method and uses Hadoop and Spark's execution engine. DWJ [46] is a method for processing both static and dynamic queries in a distributed environment based on the worst-case optimal join algorithm. [46] proposed a path based processing method that supports both static and dynamic queries in a distributed environment based on the worst-case optimal join algorithm. It constructs an edge index to access outgoing and incoming neighbors based on each vertex. DWJ can be applied to directional queries with specific patterns and provides an extended function for using static query results for dynamic query processing. [37] performs path based query processing in a master/slave environment. The master divides the query into triplets and delivers them to all slaves. Each slave selects a specific vertex based on the received triplets and performs a search along the direction of the edge connected to the vertex. When the search for one triplet is completed, each slave transmits the search result to the master and expands the search area based on the other triplet. Therefore, it constructs an index and does not perform an isomorphism test. However, since the search is performed based on the arbitrary vertices included in the query, unnecessary comparisons are performed to produce results satisfying the query.
The filtering and verification method generates a candidate set through an index in the filtering step. Since the candidate set contains results corresponding to false positives, it is verified through the verification step. The filtering and verification method requires the cost of constructing and managing the index for the graph, and there is a cost difference depending on the method of verifying the candidate set. Path based processing creates a set of candidates that match queries while exploring neighbor vertices based on a specific vertex without constructing an index. The search is performed for all connected vertices, and if a vertex matching the query is found, the vertex ID is recorded, and up to the ID of the vertex recorded at the end of the search is a subgraph matching the query. However, existing path based processing has not presented a method for generating candidate results that satisfy queries at minimal cost. That is, it performs random comparison without presenting a criterion for determining which vertex is good to start processing the query based on. The search cost increases linearly if the number of vertices matching the label of the vertex that begins processing the query is large or if the degrees of those vertices are large. The proposed method computes filtering scores to reduce the cost of exploring neighbor vertices in the process of generating a set of candidates satisfying the query. The query is divided into triplets based on the vertex with a high filtering score among the vertices included in the query. The master delivers the search order to each slave, and the slab performs the search on its partition and generates an intermediate result. It generates a final result by performing a join operation on the calculated intermediate result in each slave. In this case, in order to reduce the transmitted intermediate result, a slave with a small size of the intermediate result delivers the intermediate result to another slave.
Table 2 shows the results of comparative analysis of the characteristics of the existing methods and the proposed method for processing distributed subgraph queries. Methodology, FAV , and Path represent a query processing method, filtering and verification, and a path based processing technique, respectively. Environment is a system environment that performs queries, and GraphCache does not provide distributed processing, but the proposed and other methods support distributed processing. Query Type represents the type of query supported by each method, and Random represents the support of arbitrary subgraph searches on labeled graphs. Most methods are random, but DWJ only supports subgraph searches with specific patterns on diversity graphs. Index represents an index used for query processing in each method. The filtering and verification method uses indexes, but path based methods do not use indexes. Since HGraph is a framework for distributed subgraph processing, it does not specifically present a specific index or query processing method. Verification indicates whether an isomorphism test is performed on a candidate set, and only the filtering and verification method performs Verification. The search order indicates whether it provides a search order of vertices for query processing, and other methods except for the proposed method do not provide a separate processing order. In particular, the filtering and verification method quickly generates a candidate set through an index, but a verification step must be performed for all candidate sets.

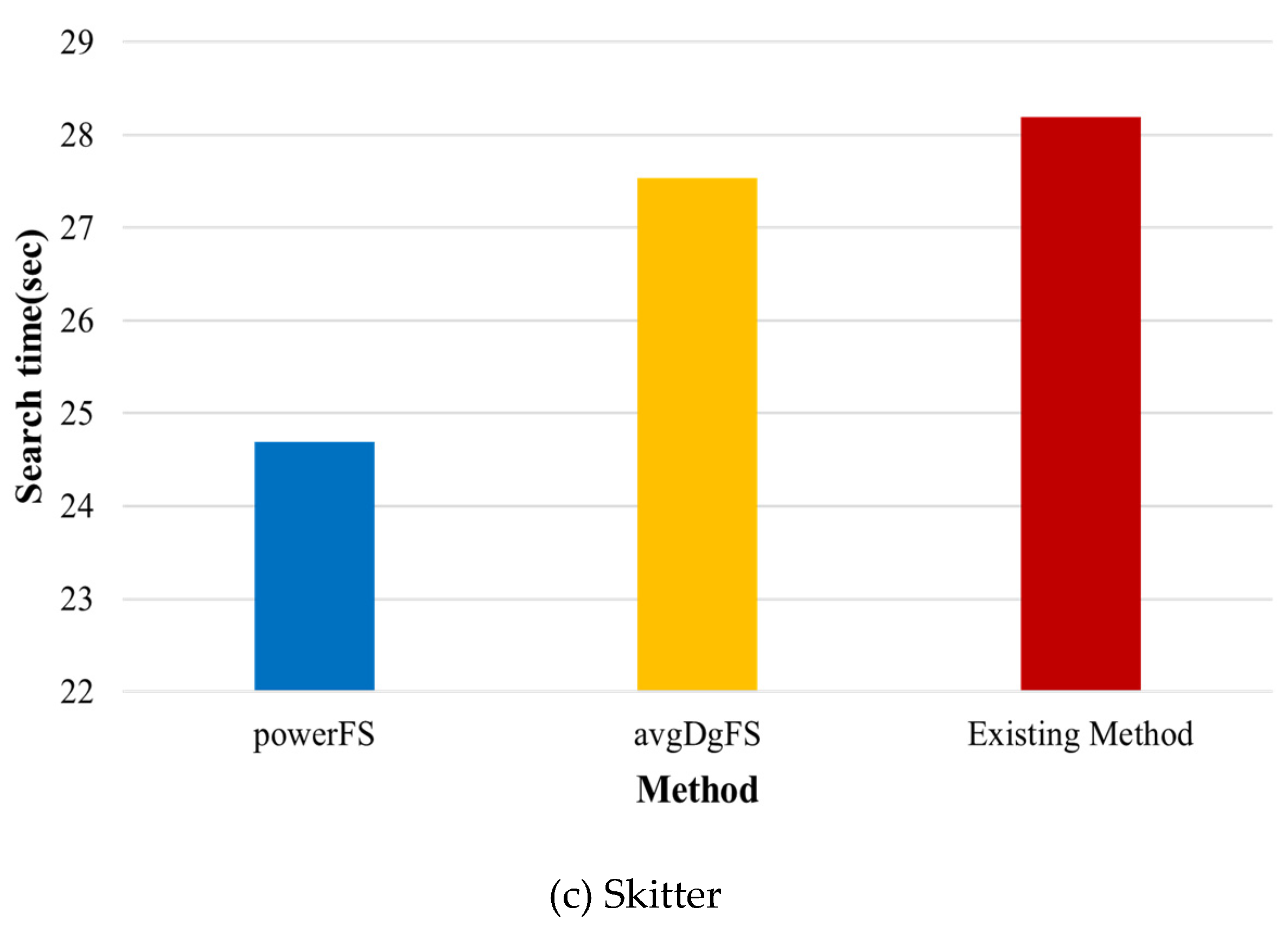
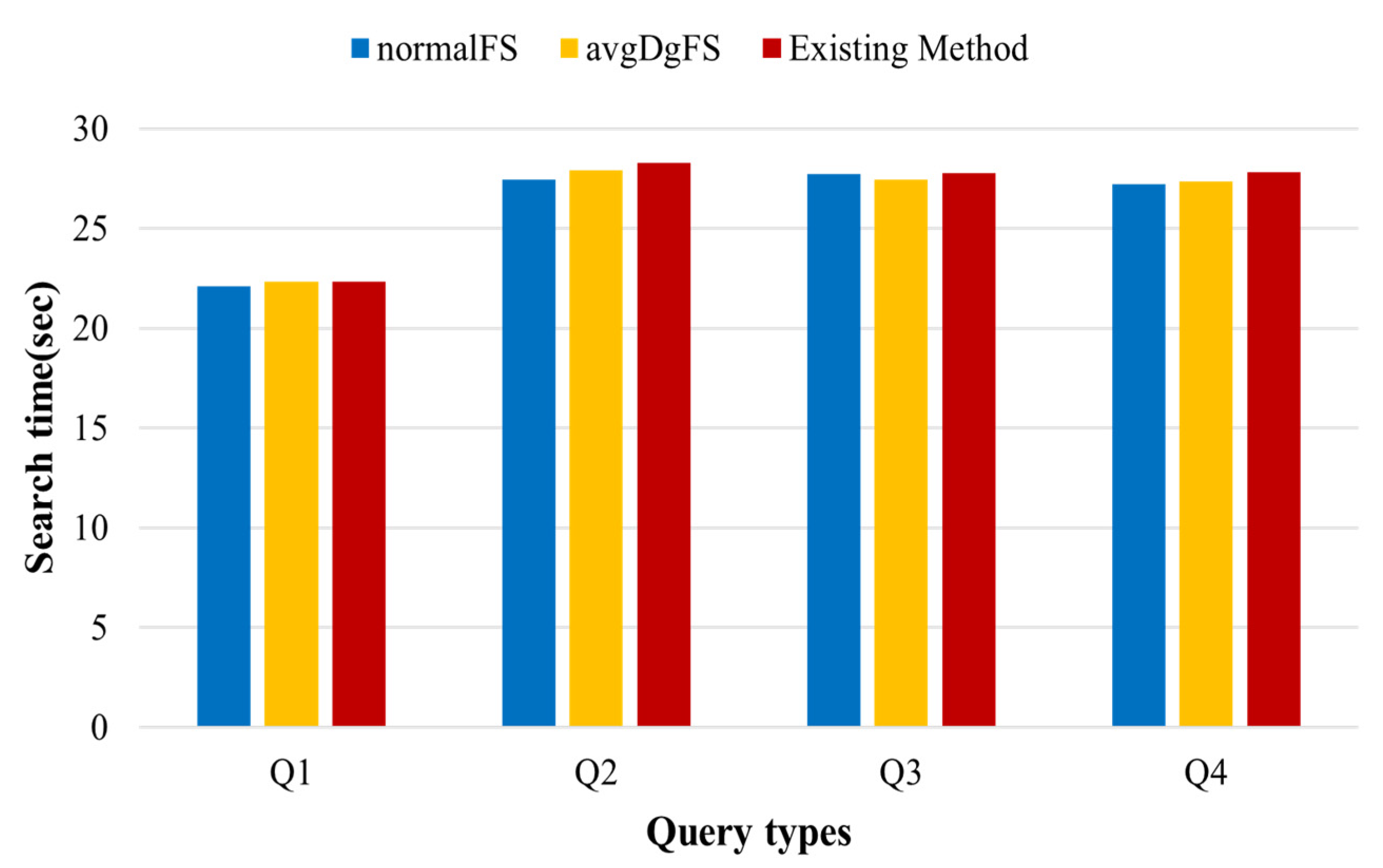
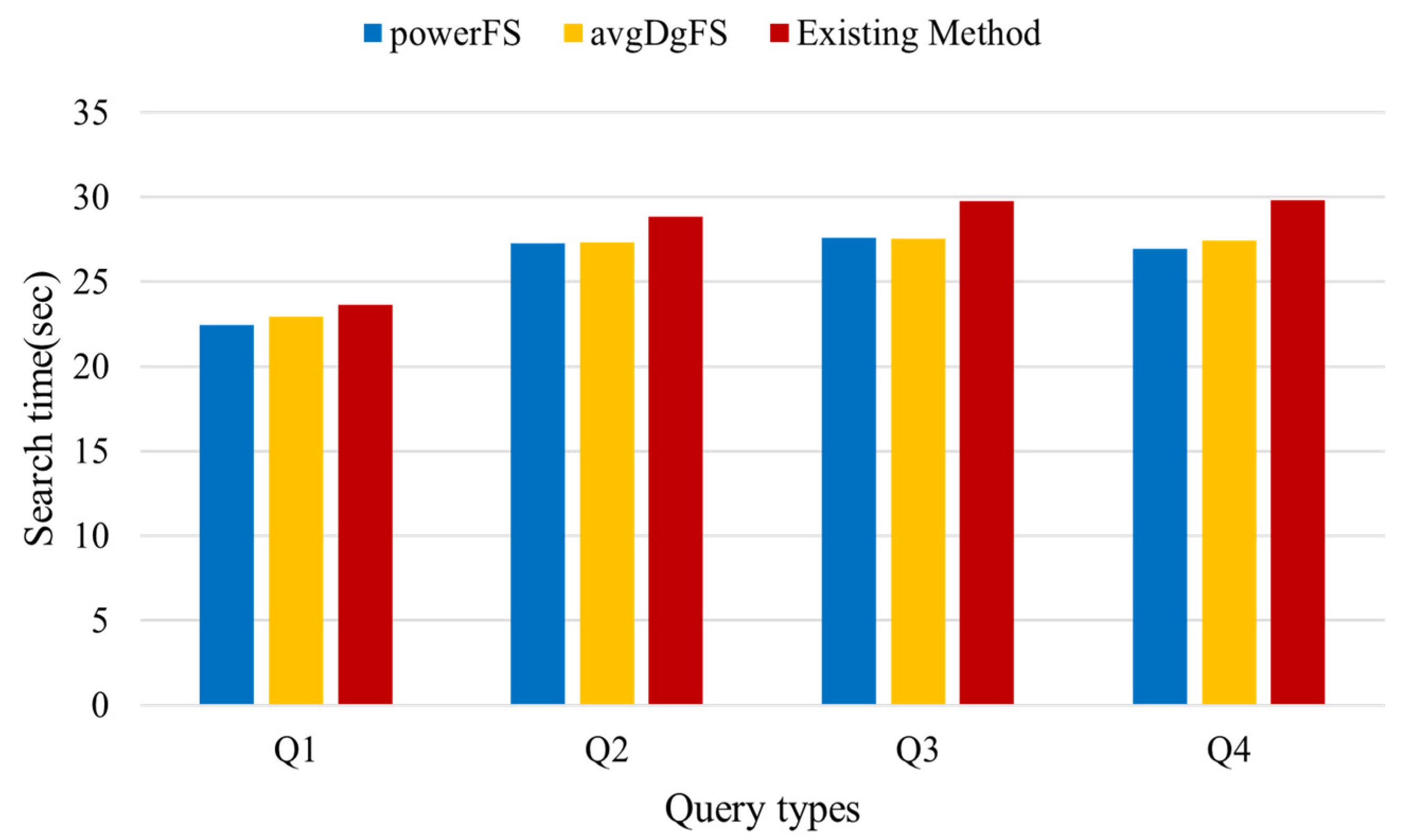
4.2. Evaluation Results

To demonstrate the superiority of the proposed method, we performed self-performance evaluation according to various distributions of graphs in various datasets and compared the performance with existing schemes. Table 3 shows the performance evaluation environment, comprising an Intel(R) Core(TM) i7-6700 CPU 3.40GHz processor, and 30GB memory. In order to perform the experimental evaluation in a distributed environment, we constructed three Spark based clusters and implemented them through Scala in GraphX. To evaluate the query processing performance across a variety of datasets, we used real datasets provided by Stanford [53] and randomly generated datasets created through the graph generator software GTgraph [54], as shown in Table 4. Suny_dip is a biology dataset, comprising approximately 20,000 vertices and 70,000 edges. Dblp is a coauthor network dataset, comprising approximately 400,000 vertices and 1 million edges. Skitter is an Internet topology dataset, comprising approximately 1.7 million vertices and 11 million edges. GTgraph is a randomly generated dataset with the same number of vertices and edges as the skitter dataset. The datasets were generated such that the vertices and their degrees would be evenly generated. Various methods for processing subgraph queries have been proposed. Query processing methods performed in a single server environment do not incur communication costs to distribute queries and sign up for distributed query processing results. However, query processing methods performed in a single server environment increase query processing time because they perform query processing while visiting vertices sequentially. Therefore, distributed processing methods are required to improve the processing performance of large subgraph queries. Various schemes have been proposed for the distributed processing of subgraph queries. However, they have various conditions and purposes of subgraph queries and different distributed environments. [46] supports query processing for a specific connected pattern for a directed graph in a Timely Dataflow environment [37] provides a query processing method for any subgraph in a Spark environment, similar to the proposed method.
To show the superiority of distributed query processing using the proposed filtering scores, we compared the proposed distributed query processing scheme with an scheme proposed in [37] . Query processing performance depends on the dataset and query types used in the experiment. Therefore, we defined four query types for the randomly generated dataset and the real dataset and compared the average search time required for query processing by generating 10 queries for each query type. Figure 7 shows the query types used to compare the search time. Queries Q1~Q4 show large structural differences. Query Q1 has a structure, wherein one vertex and another vertex are simply connected; Q2 has a structure of concentration on one vertex; Q3 has a structure of concentration on two vertices; finally, Q4 is a query with a structure, wherein a simple structure is mixed with a structure of concentration on a small number of vertices.
Figure 8 shows the search times according to the distribution of the graph in the randomly generated dataset and real dataset. In the calculation for the degree, Case 1 is divided into a normal distribution and a power-law distribution according to the distribution, and the score is calculated based on the probability of the degree of the query occurring in each distribution. The normal distribution and power-law distribution are denoted by normalFS and powerFS, respectively. Case 2 is a method of calculating the score based only on the average degree in the graph, and it is denoted by avgDgFS. The dataset generated randomly through GTGraph was used as the normal distribution data in the experiment, and the real dataset was used as the power-law distribution dataset. Regardless of the data, Case 1, wherein the score was calculated based on the probability density function’s filtering probability and the number of labels, demonstrated better performance than Case 2, wherein the score was calculated based on the average data and the degree. This was because the graph’s vertices and degrees followed a certain distribution. The average value provided only the baseline value and did not compensate for the values outside the baseline. Conversely, the calculation using the probability density function in Case 1 showed excellent performance in most cases because it provides paths that can perform the query with a smaller number of searches using the statistical information of the real dataset.
Figure 9 shows the search time according to the datasets. In relatively small Sunny_dip and dblp datasets, the order in which query processing is performed by filtering scores does not have a significant impact, but the proposed method shows slightly better performance. The existing method [37] begins the search based on vertices with matching labels without any special search order, which results in more candidate results in datasets with many vertices and edges, such as Skitter, resulting in poor performance than the proposed method. The time required for determining the search order by calculating the filtering score through the collected statistical information and partitioning the query was not long compared to the search time. The proposed method performs better than the existing method because it performs path comparison based on vertices that are likely to generate not many candidate results through filtering scores. In the proposed method, powerFS considering the power-law distribution shows superior performance compared to avgDgFS considering the average degree. In particular, the larger the graph, the more power-law distribution characteristics are, the more performance differences occur in the Skitter dataset.
Figure 10 shows the search time among query types in the randomly generated dataset. Since a query compare vertices that exist in a structurally simple path based on a particular vertex, a large set of candidates does not occur. Therefore, there is not much difference in performance between the existing method and the proposed method. It may be seen that query processing time increases because there are more neighbor vertices to be compared in queries Q2~Q4 than Q1. The existing method [37] increases the search time compared to the proposed method because the number of vertices to be compared increases as the search range expands when there are many vertices that match a specific label. However, the proposed method improves query processing performance compared to the existing method because it extends the search range based on vertices that are believed to generate a small set of candidates through filtering scores even if the query is complex. Although the difference in the search time is not large between the queries, the performances of normalFS and avgDgFS in the proposed method are excellent in terms of the search methods. The performance difference was not large between the query types in the randomly generated dataset. In addition, a simple form of query did not show a large difference in the performance evaluation of the real dataset.
Figure 11 shows the search time between query types in the real dataset. The real data set has various distributions of vertices with specific labels based on specific vertices. Therefore, when the filtering score is applied according to the query type, there is a large difference in performance. Query Q1 searches only one neighbor vertex based on a particular vertex, and query Q2 compares multiple neighbor vertices based on one vertex, but only needs to expand the search scope once. Therefore, determining the search order through Q1 and Q2 filtering scores does not have much effect on performance. However, the proposed method can reduce the number of vertices to be compared next based on the starting vertex, resulting in some performance improvement over the existing method. Since queries Q3 and Q4 extend the search range based on specific vertices, reducing the number of vertices to be compared while generating candidate results has a significant impact on performance. Existing methods should compare all neighbor vertices for each vertex if there are many vertices in the graph that match the label of the vertex included in the query. Therefore, if the vertex to be compared increases, such as Q3 and Q4, the performance is degraded. However, the proposed method can reduce the vertices to be searched additionally for a relatively small set of candidates because filtering scores determine the order to be searched. As a result, the more complex the query is, the more performance the proposed method is relatively better than the existing method. In the case of Q4, the most noticeable performance difference was shown in the comparison with the existing method. The proposed method shows strength in queries of a mixed structure, such as Q4, because the search method of paths that can create the query with a small number of searches involves predicting the probability of each vertex occurring in the graph for the query, rather than random searching.

5. Conclusions

In this paper, we proposed a distributed query processing method to search a subgraph on Spark. In this method, the filtering score is calculated to eliminate unnecessary searches in the query search through the distribution of the vertices of the graph and their edges. Based on the calculated filtering score, the vertex that can be filtered most is selected as the starting vertex, and the search is performed by partitioning the query into subqueries of smaller units depending on the filtering score. This facilitates a faster search for the subgraphs compared to the existing methods. In the evaluation results, the proposed method demonstrates a performance improvement compared to the existing methods in the real dataset. Although the absolute performance improvement does not appear to be high, the relative performance has been proven to be excellent because there is no disk I/O in Spark, a distributed in-memory environment. The proposed method is difficult to apply in other distributed environments because subgraphs are processed through filtering scores on Spark. In the future, we will conduct research to apply the proposed method to heterogeneous graphs and to reduce the cost of join computation in a distributed environment. In addition, to demonstrate the relative superiority of distributed query processing methods, we will conduct performance evaluations with state-of-the-art studies using datasets with varying configurations of vertices and edges on a single server.

Author Contributions

Conceptualization, K.B., M.K., D.C., H.L., and J.Y.; methodology, K.B., M.K., D.C., J.L., and J.Y.; software, M.K., H.L., and D.C.; validation, K.B., M.K., D.C., and J.L.; formal analysis, K.B., M.K., and J.Y.; writing—original draft preparation, K.B., M.K., and J.L.; writing—review and editing, K.B. and J.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2022R1A2B5B02002456), by the Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korean government (MSIT) (No.2014-3-00123, Development of High Performance Visual Big Data Discovery Platform for Large-Scale Realtime Data Analysis), and by the Cooperative Research Program for Agriculture Science and Technology Development (Project No. PJ016247012022), Rural Development Administration, Republic of Korea.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Bok, K.; Jeong, J.; Choi, D.; Yoo, J. Detecting Incremental Frequent Subgraph Patterns in IoT Environments. Sensors 2018, 18, 1–16. [Google Scholar] [CrossRef] [PubMed]
  2. Bok, K.; Yoo, S.; Choi, D.; Lim, J.; Yoo, J. In-Memory Caching for Enhancing Subgraph Accessibility. Appl. Sci. 2020, 10, 1–18. [Google Scholar] [CrossRef]
  3. Michail, D.; Kinable, J.; Naveh, B.; Sichi, J.V. JGraphT - A Java Library for Graph Data Structures and Algorithms. ACM Trans. Math. Softw. 2020, 46, 1–29. [Google Scholar] [CrossRef]
  4. Nguyen, V.; Sugiyama, K.; Nakov, P.; Kan, M. FANG: leveraging social context for fake news detection using graph representation. Commun. ACM 2022, 65, 124–132. [Google Scholar] [CrossRef]
  5. Saeed, Z.; Abbasi, R.A.; Razzak, M.I.; Xu, G. Event Detection in Twitter Stream Using Weighted Dynamic Heartbeat Graph Approach. IEEE Comput. Intell. Mag. 2019, 14, 29–38. [Google Scholar] [CrossRef]
  6. Lee, J.; Bae, H.; Yoon, S. Anomaly Detection by Learning Dynamics from a Graph. IEEE Access 2020, 8, 64356–64365. [Google Scholar] [CrossRef]
  7. anturk, D.; Karagoz, P.; SgWalk: Location Recommendation by User Subgraph-Based Graph Embedding. IEEE Access 2021, 9, 134858–134873. [CrossRef]
  8. Guo, Q.; Zhuang, F.; Qin, C.; Zhu, H.; Xie, X.; Xiong, H.; He, Q. A Survey on Knowledge Graph-Based Recommender Systems. IEEE Trans. Knowl. Data Eng. 2022, 34, 3549–35646. [Google Scholar] [CrossRef]
  9. Mukherjee, A.; Chaki, R.; Chaki, N. An Efficient Data Distribution Strategy for Distributed Graph Processing System. In Proceedings of International Conference on Computer Information Systems and Industrial Management, Barranquilla, Colombia, 15-17 July 2022. [Google Scholar]
  10. Choi, D.; Han, J.; Lim, J.; Han, J.; Bok, K.; Yoo, J. Dynamic Graph Partitioning Scheme for Supporting Load Balancing in Dis-tributed Graph Environments. IEEE Access 2021, 9, 65254–65265. [Google Scholar] [CrossRef]
  11. Davoudian, A.; Chen, L.; Tu, H.; Liu, M. A Workload-Adaptive Streaming Partitioner for Distributed Graph Stores. Data Sci. Eng. 2021, 6, 163–179. [Google Scholar] [CrossRef]
  12. Ayall, T.; Liu, H.; Zhou, C.; Seid, A.M.; Gereme, F.B.; Abishu, H.N.; Yacob, Y.H. Graph Computing Systems and Partitioning Techniques: A Survey. IEEE Access 2022, 10, 118523–118550. [Google Scholar] [CrossRef]
  13. Liu, N.; Li, D.; Zhang, Y.; Li, X. Large-scale graph processing systems: a survey. Frontiers Inf. Technol. Electron. Eng. 2020, 21, 384–404. [Google Scholar] [CrossRef]
  14. Bouhenni, S.; Yahiaoui, S.; Nouali-Taboudjemat, N.; Kheddouci, H. A Survey on Distributed Graph Pattern Matching in Massive Graphs. ACM Comput. Surv. 2022, 54, 1–35. [Google Scholar] [CrossRef]
  15. Adoni, W.Y.H.; Tarik, N.; Krichen, M.; El Byed, A. HGraph: Parallel and Distributed Tool for Large-Scale Graph Processing. In Proceedings of International Conference on Artificial Intelligence and Data Analytics, Riyadh, Saudi Arabia, 6-7 April 2021. [Google Scholar]
  16. Fan, W.; He, T.; Lai, L.; Li, X.; Li, Y.; Li, Z.; Qian, Z.; Tian, C.; Wang, L.; Xu, J.; Yao, Y.; Yin, Q.; Yu, W.; Zeng, K.; Zhao, K.; Zhou, J.; Zhu, D.; Zhu, R. GraphScope: A Unified Engine For Big Graph Processing. Proc. VLDB Endow. 2021, 14, 2879–2892. [Google Scholar] [CrossRef]
  17. Malewicz, G.; Austern, H.M.; Bik, J.A.; Dehnert, J.; Horn, I.; Leiser, N.; Czajkowski, G.M. Pregel: a system for large-scale graph processing. In Proceedings of ACM SIGMOD International Conference on Management of data, Indianapolis, Indiana, USA, 6-10 June 2010. [Google Scholar]
  18. Xu, Q.; Wang, X.; Li, J.; Zhang, Q.; Chai, L. Distributed Subgraph Matching on Big Knowledge Graphs Using Pregel. IEEE Access 2019, 7, 116453–116464. [Google Scholar] [CrossRef]
  19. Dean, J.; Ghemawat, S. MapReduce: Simplified data processing on large clusters. Commun. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
  20. Su, Q.; Huang, Q.; Wu, N.; Pan, Y. Distributed subgraph query for RDF graph data based on MapReduce. Comput. Electr. Eng. 2022, 102, 108221. [Google Scholar] [CrossRef]
  21. Angles, R.; López-Gallegos, F.; Paredes, R. Power-Law Distributed Graph Generation With MapReduce. IEEE Access 2021, 9, 94405–94415. [Google Scholar] [CrossRef]
  22. Low, Y.; Gonzalez, J.; Kyrola, A.; Bickson, D.; Guestrin, C.; Hellerstein, J. Distributed GraphLab: A Framework for Machine Learning in the Cloud. Proc. VLDB Endow. 2012, 5, 716–727. [Google Scholar] [CrossRef]
  23. Gonzalez, J.; Low, Y.; Gu, H.; Bickson, D.; Guestrin, C. PowerGraph: Distributed graph-parallel computation on natural graphs. In Proceedings of USENIX Symposium on Operating Systems Design and Implementation, Hollywood, CA, USA, 8-10 October 2012. [Google Scholar]
  24. Xin, R.S.; Gonzalez, J.; Michael, F.J.; Ion, S. Graphx: A resilient distributed graph system on spark. In Proceedings of International Workshop on Graph Data Management Experiences and Systems, New York, NY, USA, 24 June 2013. [Google Scholar]
  25. Zaharia, M.; Xin, R.S.; Wendell, P.; Das, T.; Armbrust, M.; Dave, A.; Meng, X.; Rosen, J.; Venkataraman, S.; Franklin, M.J.; Ghodsi, A.; Gonzalez, J.; Shenker, S.; Stoica, I. Apache spark: a unified engine for big data processing. Commun. ACM 2016, 59, 56–65. [Google Scholar] [CrossRef]
  26. Talukder, N.; Zaki, M.J. A distributed approach for graph mining in massive networks. Data Min. Knowl. Discov. 2016, 30, 1024–1052. [Google Scholar] [CrossRef]
  27. Tian, Y.; McEachin, R.C.; Santos, C.; States, D.J.; Patel, J.M. SAGA: a subgraph matching tool for biological graphs. Bioinform. 2006, 23, 232–239. [Google Scholar] [CrossRef] [PubMed]
  28. Zhu, L.; Yao, Y.; Wang, Y.; Hei, X.; Zhao, Q.; Ji, W.; Yao, Q. A novel subgraph querying method based on paths and spectra. Neural Comput. Appl. 2019, 31, 5671–5678. [Google Scholar] [CrossRef]
  29. Liang, Y.; Zhao, P. Workload-Aware Subgraph Query Caching and Processing in Large Graphs. In Proceedings of IEEE International Conference on Data Engineering, Macao, China, 8-11 April 2019. [Google Scholar]
  30. 30-22. Sun, S.; Luo, Q. 11 April 2019, 30-22. Sun, S.; Luo, Q. Scaling Up Subgraph Query Processing with Efficient Subgraph Matching. In Proceedings of IEEE International Conference on Data Engineering, Macao, China, 8-11 April 2019.
  31. Luaces, D.; Viqueira, J.R.R.; Cotos, J.M.; Flores, J.C. Efficient access methods for very large distributed graph databases. Inf. Sci. 2021, 573, 65–81. [Google Scholar] [CrossRef]
  32. Cheng, J.; Ke, Y.; Ng, W. Efficient query processing on graph databases. ACM Trans. Database Syst. 2009, 34, 1–48. [Google Scholar] [CrossRef]
  33. Wang, J.; Ntarmos, N.; Triantafillou, P. GraphCache: a caching system for graph queries. In Proceedings of International Conference on Extending Database Technology, Venice, Italy, 21-24 March 2017. [Google Scholar]
  34. Li, Y.; Yang, Y.; Zhong, Y. An Incremental Partitioning Graph Similarity Search Based on Tree Structure Index. In Proceedings of International Conference of Pioneering Computer Scientists, Engineers and Educators, Taiyuan, China, 18-21 September 2020. [Google Scholar]
  35. Wangmo, C.; Wiese, L. Efficient Subgraph Indexing for Biochemical Graphs. In Proceedings of International Conference on Data Science, Technology and Applications, Lisbon, Portugal, 11-13 July 2022. [Google Scholar]
  36. Khuller, S.; Raghavachari, B.; Young, N. Balancing minimum spanning trees and shortest-path trees. Algorithmica 1995, 14, 305–321. [Google Scholar] [CrossRef]
  37. Balaji, J.; Sunderraman, R. Distributed Graph Path Queries Using Spark. In Proceedings of Annual Computer Software and Applications Conference, Atlanta, GA, USA, 10-14 June 2016. [Google Scholar]
  38. Wei, F. TEDI: efficient shortest path query answering on graphs. In Proceedings of ACM SIGMOD International Conference on Management of Data, Indianapolis, Indiana, USA, 6-10 June 2010. [Google Scholar]
  39. Cordella, L.P.; Foggia, P.; Sansone, C.; Vento, M. A (sub)graph isomorphism algorithm for matching large graphs. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1367–1372. [Google Scholar] [CrossRef]
  40. He, H.; Singh, A.K. Graphs-at-a-time: query language and access methods for graph databases. In Proceedings of ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 10-12 June 2008. [Google Scholar]
  41. Zhang, S.; Li, S.; Yang, J. GADDI: distance index based subgraph matching in biological networks. In Proceedings of Inter-national Conference on Extending Database Technology, Saint Petersburg, Russia, 24-26 March 2009. [Google Scholar]
  42. Ullmann, J.R. An algorithm for subgraph isomorphism. J. ACM 1976, 23, 31–42. [Google Scholar] [CrossRef]
  43. Zhang, X.; Chen, L. Distance-aware selective online query processing over large distributed graphs. Data Sci. Eng. 2017, 2, 2–21. [Google Scholar] [CrossRef]
  44. Jing, N.; Huang, Y.W.; Rundensteiner, E.A. Hierarchical encoded path views for path query processing: An optimal model and its performance evaluation. IEEE Trans. Knowl. Data Eng. 1998, 10, 409–432. [Google Scholar] [CrossRef]
  45. Zaharia, M.; Xin, R.S.; Wendell, P.; Das, T.; Armbrust, M.; Dave, A.; Meng, X.; Rosen, F.; Venkataraman, S.; Franklin, M.J.; Ghodsi, A.; Gonzalez, J.; Shenker, S.; Stoica, I. Apache Spark: a unified engine for big data processing. Commun. ACM 2016, 59, 56–65. [Google Scholar] [CrossRef]
  46. Ammar, K.; McSherry, F.; Salihoglu, S.; Joglekar, M. Distributed Evaluation of Subgraph Queries Using Worst-case Optimal and Low-Memory Dataflows. Proc. VLDB Endow. 2018, 11, 691–704. [Google Scholar] [CrossRef]
  47. Fathimabi, S.; Subramanyam, R B. V.; Somayajulu, D.V.L.N. MSP: Multiple Sub-graph Query Processing using Structure-based Graph Partitioning Strategy and Map-Reduce. J. King Saud Univ. Comput. Inf. Sci. 2019, 31, 22–34. [Google Scholar]
  48. Cheng, J.; Ke, Y.; Fu, A.W.; Yu, J.X. Fast graph query processing with a low-cost index. VLDB J. 2021, 20, 521–539. [Google Scholar] [CrossRef]
  49. Sala, A.; Zheng, H.; Zhao, B.Y.; Gaito, S.; Rossi, G.P. Brief announcement: revisiting the power-law degree distribution for social graph analysis. In Proceedings of Annual ACM Symposium on Principles of Distributed Computing, Zurich, Switzerland, 5-28 July 2010. [Google Scholar]
  50. Zhang, S.; Jiang, Z.; Hou, X.; Li, M.; Yuan, M.; You, H. DRONE: An Efficient Distributed Subgraph-Centric Framework for Processing Large-Scale Power-law Graphs. IEEE Trans. Parallel Distributed Syst. 2023, 34, 463–474. [Google Scholar] [CrossRef]
  51. Faloutsos, M.; Faloutsos, P.; Faloutsos, C. On power-law relationships of the internet topology. ACM SIGCOMM Comput. Commun. Rev. 1999, 29, 251–262. [Google Scholar] [CrossRef]
  52. Goldstein, M.L.; Morris, S.A.; Yen, G.G. Problems with fitting to the power-law distribution. Eur. Phys. J. B. 2005, 41, 255–258. [Google Scholar] [CrossRef]
  53. Stanford Large Network Dataset Collection, Available online:. Available online: https://snap.stanford.edu/data (accessed on 15 January 2021).
  54. GTgraph, Available online:. Available online: http://www.cse.psu.edu/~kxm85/software/GTgraph (accessed on 5 October 2021).
Preprints 79941 g001
Figure 1. Overall architecture of the proposed query processing.
Figure 1. Overall architecture of the proposed query processing.
Preprints 79941 g001
Preprints 79941 g002
Figure 2. Difference in the number of labels.
Figure 2. Difference in the number of labels.
Preprints 79941 g002
Preprints 79941 g003
Figure 3. Difference in the degree.
Figure 3. Difference in the degree.
Preprints 79941 g003
Preprints 79941 g004
Figure 4. An example of query partitioning.
Figure 4. An example of query partitioning.
Preprints 79941 g004
Preprints 79941 g005
Figure 5. Search results by round.
Figure 5. Search results by round.
Preprints 79941 g005
Preprints 79941 g006
Figure 6. Joining of search results.
Figure 6. Joining of search results.
Preprints 79941 g006
Preprints 79941 g007
Figure 7. Query types according to the structure.
Figure 7. Query types according to the structure.
Preprints 79941 g007
Preprints 79941 g008
Figure 8. Search time according to the graph distribution.
Figure 8. Search time according to the graph distribution.
Preprints 79941 g008
Preprints 79941 g009aPreprints 79941 g009b
Figure 9. Comparison of search time according to the dataset.
Figure 9. Comparison of search time according to the dataset.
Preprints 79941 g009aPreprints 79941 g009b
Preprints 79941 g010
Figure 10. Comparison of search times among query types in randomly generated data.
Figure 10. Comparison of search times among query types in randomly generated data.
Preprints 79941 g010
Preprints 79941 g011
Figure 11. Comparison of search time between query types in real data.
Figure 11. Comparison of search time between query types in real data.
Preprints 79941 g011
Table 1. Description of the parameters.
Table 1. Description of the parameters.
Parameters Description
F P N D ( v i ) Filtering probability of normal distribution
F P P D ( v i ) Filtering probability of power-law distribution
V L Number of vertices with label L in graph G
V a l l Total number of vertices in graph G
A D L ( v i ) Average degree of collected labels
Table 2. Characteristic comparison of distributed query processing schemes.
Table 2. Characteristic comparison of distributed query processing schemes.
Schemes Methodology Environment Query Type index Verification Search Order
GraphCache[33] FAV Single Random G C i n d e x , M i n d e x 0 X
MSP[47] FAV Hadoop Random IGI 0 X
HGraph[15] - Hadoop, Spark Random - - X
DWJ[46] Path Timely Dataflow Directed Edge index X X
SPQ[37] Path Spark Random X X X
Proposed Path Spark Random X X Filtering score
Table 3. Performance evaluation environment.
Table 3. Performance evaluation environment.
Parameter Value
Processor Intel(R) Core(TM) i7-6700 CPU 3.40GHz
Memory 30G
Number of clusters 3
Programming language Scala
Table 4. Datasets used in the performance evaluation.
Table 4. Datasets used in the performance evaluation.
Dataset Vertices Edges Description
suny_dip 22,596 69,148 Biology data
dblp 425,961 1,049,866 Coauthor network
skitter 1,696,415 11,095,298 Internet topology
GTgraph 1,696,415 11,095,298 Randomly generated graph
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated