Preprint
Article
Planning of Innovative Changes in Development of the Socio-Economic Systems
Altmetrics
Downloads
113
Views
39
Comments
0
This version is not peer-reviewed
Transmission Clusters and Containment Measures in Global Different Regions during COVID-19 Pandemic
Submitted:
19 July 2023
Posted:
21 July 2023
You are already at the latest version
Alerts
Abstract
Abstract: The planning of innovative changes in socio-economic systems should focus on the effective utilization of the existing potential for innovative development. This research proposes a method for strategic planning of innovative changes, which enables the determination of development goals, approaches to problem-solving, and a system of indicators to optimize plans for innovative change. The stages of organizing innovative activities, aligned with the mechanism of project development and implementation, are identified. The technique is improved through a system of analytical indicators that assess the state of innovative activity and the scientific and technical level of innovations. The establishment of admissible sets of elementary processes and their combinations leading to innovative changes is also discussed. The planning algorithm is adapted to the type of innovative behavior and the state of the innovation potential within the socio-economic system. The potential for innovation in socio-economic systems is exemplified by the case of Ukraine, with the determination of the strategy for its innovative development in relation to the potentially optimal state.
Keywords:
Subject: Business, Economics and Management - Economics
1. Introduction
Innovation planning plays a crucial role in enabling organizations and individuals to identify and prioritize new ideas, technologies, and processes that drive growth and enhance competitiveness. This research paper aims to provide a comprehensive overview of innovation planning in the field of computer science, including its definitions, benefits, and best practices.
Objectives are determination of the foundations of innovative activity in the conditions of functional digitalization of production, based on the activation of the implementation of information and communication technologies of the digital economy to ensure the development of economic systems.
While there are various models concerning innovation changes, they all share a common understanding that innovation activities can be broadly described and visualized through process models. Although innovation studies are not a new topic, an increasing number of studies are being conducted in response to evolving innovation forms and changing global situations. Some models describe the life cycle of innovation as a function consisting of three distinct phases: emergence, growth, and maturity (Howard and Guile 1992; Mitrova et al. 2015; Perani and Sirilli 2008). Other studies emphasize the characteristics of innovation defined by different stages of development. Linear models of innovation typically distinguish the discovery (invention), definition of possible application spheres, development, design, and use as phases of the innovation process (Niosi 1999; Godin 2006; Meissner 2015; Carayannis et al. 2015).
In the context of computer science, it is essential to establish a clear definition of innovation planning. Innovation planning refers to the process of identifying, evaluating, and prioritizing potential technological, organizational, or business innovations that drive growth and success. This process involves a range of activities such as brainstorming sessions, idea generation workshops, market research, and the development of plans and strategies for implementing and scaling new innovations. This paper presents a discussion on the necessity and constant refinement of the development strategy, including innovative design, based on planning and environmental forecasting.
Organizations may encounter several key challenges when implementing innovation planning. One challenge is the difficulty of identifying and prioritizing the most promising ideas and technologies, particularly in fast-moving industries where trends and technologies rapidly change. Organizations must adopt a proactive approach to innovation planning by continuously monitoring market trends and actively seeking out new ideas and technologies to drive growth and success. Another challenge is the inherent risk associated with innovation. While innovation can bring significant benefits, it also carries a level of risk as new ideas and technologies may not always succeed. Organizations must carefully assess the potential risks and rewards of each innovation before allocating resources for implementation. Additionally, the allocation of resources for innovation poses another challenge, especially for organizations with limited resources. Implementing new ideas and technologies often requires significant investments in terms of time and money.
To overcome these challenges, organizations need to prioritize their innovation efforts and allocate resources to initiatives that offer the highest potential for success. Adopting a structured and systematic approach to innovation planning is crucial. This approach can involve the use of tools and techniques such as roadmapping, which visualizes an organization's innovation goals and plans. Roadmapping helps identify key milestones, resources, dependencies, track progress, and adjust plans as necessary. In summary, innovation planning is a critical aspect of computer science that helps organizations and individuals identify and prioritize new ideas, technologies, and processes to drive growth and enhance competitiveness. While innovation planning brings significant benefits, it also presents challenges, including the difficulty of identifying and prioritizing promising ideas and technologies, the risks associated with innovation, and the need to allocate resources effectively. To address these challenges, organizations must adopt a structured and systematic approach to innovation planning, such as roadmapping, to track progress and adjust plans accordingly.
Functions of Innovations in Planning
When considering the planning process, it is crucial to include the following functions of innovations:
Firstly, innovation functions within the system include:
- -
- innovations serve as a channel to translate the achievements of human intelligence and the results of new information technologies into management practice. They contribute to the intellectualization and increased scientific intensity of management activities;
- -
- innovations expand the range of administrative functions of public authorities and enhance the quality of their implementation. They contribute to satisfying the needs of individuals and society as a whole;
- -
- innovations enable the attraction of new resources for management, allowing the execution of management functions with fewer labor, resources, and time;
- -
- concentrating innovations in the management sphere aligns the structure and essence of public administration with the social needs of post-industrial societies. Innovations are integral to this alignment.
Secondly, innovation primarily affects the functions of management itself, leading to the restructuring of the entire system. These functions include:
- -
- goal-setting functions associated with the need for planning, forecasting, and programming socio-economic development. The primary goal is to improve the quality of life for people. This function is realized through the economic and social transformation of society and systemic reform of public administration;
- -
- regulation functions, primarily implemented in market economies and the social sphere. Regulation differs fundamentally from administrative management in terms of goals and technology, forming a new functional imperative for the state's economy in a market environment;
- -
- stimulation function, involving the purposeful impact of the management subject on socio-economic processes in line with the implementation of state and social interests.
Thirdly, the functions of public authorities in organizing innovations within management are essential when considering their influence on society. Researchers have identified the following main functions of state bodies in the innovation sphere:
- -
- accumulation of funds for research and innovation;
- -
- coordination of innovative activities among government bodies;
- -
- stimulation of innovations and establishment of sanctions for their absence;
- -
- creation of a regulatory and legal framework for innovative processes in public administration;
- -
- staffing of innovative activities;
- -
- formation of scientific and innovative infrastructure;
- -
- institutional support of innovation processes;
- -
- ensuring a socio-centric and human-centered orientation of innovations;
- -
- raising the social status of innovative activity;
- -
- regional regulation of innovation processes;
- -
- study and implementation of international experience as an essential resource for managerial innovations [14].
2. Materials and Methods
In the process of planning innovations, the main focus is on making a reasonable choice of the main directions of innovation. Strategy, in the context of innovation management, refers to a conscious and thoughtful set of norms and rules that underlie the development and adoption of strategic decisions affecting the future state of the enterprise. It serves as a means of connecting the enterprise with the external environment. The development of measures and plans, such as programs and projects, is an essential aspect of strategy to achieve the intended goals. These plans should consider the scientific, technical, and production potential of the enterprise, as well as its market and sales opportunities. The management of the innovation process entails the crucial task of developing and implementing the innovation strategy of the economic entity, which is subordinate to the general strategy. The innovation strategy establishes the goals of innovation, determines the means to achieve them, and identifies the sources of funds for innovation. (Figure 1) [6,22].
An economic unit engaging in innovative activities can apply various types of strategies, depending on its goals, the theory of the product life cycle, market position, and ongoing scientific and technical policies.
The methodology for strategic planning of innovative changes enables the determination of the development goals of the object of strategic planning, approaches to solving problems, and a system of indicators that optimize strategic plans for innovative changes. An innovative strategic development plan typically consists of a set of innovative projects or a "portfolio" of projects. The selection of promising projects, resource allocation, and determination of final results based on specific criteria are crucial in this process.
Projects involving innovative changes are characterized by significant information complexity and a high degree of uncertainty in the initial stages. Effectively managing such projects requires well-structured information about the upcoming work stages.
At this stage, it becomes necessary to establish permissible sets of elementary processes and their combinations that lead to the emergence of innovative products of appropriate quality. From these permissible sets, a realized set of innovations is selected, forming an innovative change. When considering an individual enterprise as the object at the first level, it becomes part of a higher-level set with specific characteristics at the subsequent level.
The degree of achievement of innovative goals for enterprises depends significantly on the optimality of the organizational form of the innovator.
The innovative behavior of socio-economic systems (CES) is diverse, and various classification features can be used to analyze it. According to L. G. Ramenskiy, there are four types of innovative behavior for enterprises based on their goals: violets, commutants, patents, and explorents.
Socio-economic systems are classified as complex systems. Planning complex systems in the economy requires considering several properties to ensure the adequacy of the constructed plans. Table 1 presents the most important properties and characteristics of complex systems in the economy.
Each stage of the planning process corresponds to specific features of the state of the socio-economic system, which in turn characterize the type and strategy of the innovation system (Figure 2).
These characteristics provide insights into the nature and behavior of complex systems in the economy, highlighting their interconnectedness, adaptability, and inherent unpredictability.
According to the approach mentioned, strategic behavior in complex systems can be categorized into the following types:
Exploitative Stage: This stage involves the emergence of a system in a market economic environment and the formation of its initial structure. These are small systems characterized by dedication, a strong commitment to the idea, highly skilled employees, and competent leadership. These systems allocate significant resources to research and development (R&D).
Patent Stage: Patent systems, also referred to as "sly foxes," can vary in size. The strategy at this stage is to differentiate products and focus maximum effort on a narrow market segment. Patents leverage differences in product quality, services, and advertising. The primary focus is to determine and deliver consumer value. Development in this stage can take two directions:
- -
- stagnation or moderate growth within the occupied market segment. If the market segment's volume stagnates, the system's growth stops; otherwise, it expands in size;
- -
- change of strategy and transformation into a larger violet system.
Violet Stage: Systems exhibiting innovative violet behavior are characterized by a large number of employees, multiple branches and subsidiaries, and a wide range of products. These systems make significant investments in R&D and maintain extensive marketing networks. Violet products are known for their excellent quality, standardization, unification, and manufacturability, resulting in lower prices due to mass production. Typical representatives of this type are multinational companies that create oligopolistic markets. Violets can further evolve into "proud lions," "mighty elephants," and "hulking hippos" based on their evolutionary development stages.
Proud lions focus on a narrow but massive range of highly demanded goods, displaying the most dynamic pace of development, large-scale production, and R&D expenditures.
Mighty elephants exhibit average dynamic development and extended diversification to compensate for a potential loss of a leader's position in the region, aiming for stability. This type prefers implementing successful innovations rather than creating them from scratch.
Hulking hippos comprise small systems oriented towards meeting local and national needs, characterized by wide diversification. They transition smoothly to the commutative behavioral type, actively participating in the routinization of new products through imitative activity, as imitation is cheaper than independent innovation.
Commutative Stage: This stage involves the ability to search for strategic partners through engagement with switching systems. Small firms, which cater to local, narrow-group, or even individual demands, play a unifying and connecting role in the economy. These firms undertake tasks that are not of interest to violets, patents, or exporters, hence the term "commutants." They facilitate the diffusion of innovations while also routinizing them. Small firms actively promote new products, technologies, and services based on innovations, accelerating the diffusion process. The commutative stage also encompasses a venture type of behavior observed in systems with flexible and mobile structures. These systems excel in the speed of new product development, surpassing the capabilities of large enterprises. These ventures often engage in product production and transfer their developments to other systems. Due to their small scale, these systems have a limited number of employees.
Each system type (viola, commutators, patents, ventures, and exporters) possesses unique characteristics and varying degrees of strategy implementation to achieve product competitiveness (refer to Table 2 for details).
To determine the market segment of an innovator, the "Costs - Use Value" matrix (Figure 3) can be utilized. This matrix helps analyze the relationship between costs and the value of a product.
The analysis of Figure 3 reveals that explorative strategies face the greatest challenges. Surviving in the market requires simultaneously improving the quality of goods and reducing their costs. However, relying solely on partial improvements can leave other strategies vulnerable. Research indicates that the improvement of quality is a crucial factor for the success of new products in the market.
To remain competitive in a specific market segment, when technology advancements or production organization improvements are not possible, enterprises often have to reduce the price of their goods and decrease profit margins. Switching enterprises and patents, while maintaining production costs, can enhance the quality of manufactured goods by introducing innovations. Violent strategies involve implementing innovative approaches to enhance technology, production organization, labor, and management. Those who fail to innovate in a timely manner in terms of products and processes are eventually ousted from the market due to the objective law of competition.
| Indicator | Type of competitive behavior (classification by L. G. Ramensky) | |||
|---|---|---|---|---|
| Violent | Patient | Explorative | Commute | |
| 1. Level of competition | Tall | Low | Middle | Middle |
| 2. The novelty of the industry | Mature | New | New | Mature |
| 3. Types of needs served | Bulk, standard | Massive, but non-standard | Innovative | Local |
| 4. Production profile | Massive | Specialized | Experimental | Universal small |
| 5. Company size | Large | Large, medium, small | Medium and small | Small |
| 6. Stability of the company | Tall | Tall | Low | Low |
| 7. Expenditure on R&D | Tall | Middle | Tall | Absent |
| 8. Competitive advantage | High performance | Adaptation to a specific market | Leading the way in innovation | Flexibility |
| 9. Dynamism of development | Tall | Middle | Tall | Low |
| 10. Costs | Low | Middle | Low | Low |
| 11. Product quality | Middle | Tall | Middle | Middle |
| 12. Assortment | Middle | Narrow | Individual orders | Narrow |
| 13. Type of R&D | Improving | Adaptive | Breakthrough | Absent |
| 14. Sales network | Own or controlled | Own or controlled | Absent | Absent |
The variety of corporate strategies and organizational forms of business entities offers numerous strategic positions and options for selecting competitive strategies with an innovative focus. To navigate this decision space effectively, it is crucial to adequately assess the firm's position in the market and identify its strategic competitive behavior.
3. Results
The effectiveness of managing the organization of innovative activities within business entities is evident through the synergistic interaction of various stages associated with the process of developing, implementing, and promoting innovations. Additionally, these stages are closely connected with changing the mental resource of employees, including the formation of corporate culture, business image, labor motivation system for innovation development and implementation, and corporate social responsibility.
Six stages of organizing innovative activity have been identified, aligned with the mechanism of developing and implementing investment projects:
1) planning of idea carriers; 2) determination of basic and functional strategies, as well as establishing a system of goals for their implementation; 3) assessment of innovative potential; 4) formation of the structure, regulations, and criteria for implementing and controlling innovations; 5) development and examination of innovative projects; 6) preparation of an innovation program and an innovation budget, including an assessment of innovation effectiveness. The success of an innovation project is reflected in the interdependence between technology, operating costs, sales volume, and the price of the new product or service being offered. This is manifested through growth rates of economic value added and financial efficiency. From a societal perspective, the resource intensity of the innovation program decreases.
Table 4 presents a general grouping of the developed system of analytical indicators that enable the assessment of an economic entity's innovation activity. These indicators cover the scientific and technical level of innovation, the specific manifestation of the innovation process, and different aspects of evaluating innovation effectiveness.
The socio-economic system (SES) has been chosen as the subject of research, and it is important to consider multiple levels within the SES:
- -
- macro-level: This represents the country as a whole (concept);
- -
- meso-level: This refers to regions (plan);
- -
- micro-level: This pertains to individual enterprises (program).
Creating a computer-mathematical model for innovation planning in computer science can involve the use of optimization techniques. Optimization techniques are mathematical approaches that aim to find the best solution to a given problem by maximizing or minimizing a specific objective function.
One approach to developing a computer-mathematical model for innovation planning is utilizing linear programming. Linear programming involves optimizing a linear objective function while adhering to a set of linear constraints. In the context of innovation planning, the objective function could represent the expected value or impact of a specific innovation, while the constraints could reflect the available resources and limitations of the organization.
The integral indicator R, which represents the quality index of the evaluated program, can be defined as the sum of the products of the values of complex criteria () and their corresponding weight characteristics , as shown in formula (1):
Here:
- weight characteristics of the importance of complex criteria ;
- is the number of the complex criterion;
- values of complex criteria
Complex criteria are typically derived from mathematical operations performed on a group of p initial indicators ,, where , which describe the object being evaluated. The formulation for complex criteria is given as:
To assess the compliance of programs (plans), a set of complex criteria can be selected based on a system of analytical indicators for assessing innovative activities (Table 4). Weight characteristics of importance are then assigned to each complex criterion, considering the number of indicators included in each group. The obtained data is as follows:
- scientific and technical level of innovation, ;
- innovation process, ;
- efficiency of innovation activity, ;
To normalize the real assessment according to the b_ij criterion, the formula (2) is used:
Here:
- is an expert assessment set for the particular criterion for assessing on a point scale;
- is the maximum possible value of the expert assessment for a particular criterion for assessing on a point scale;
- is the minimum possible value of the expert assessment for a particular criterion for assessing on a point scale.
Weighting coefficients w_ij are then established for specific assessment criteria, considering their partial contribution to the overall assessment (Table 5, Table 6 and Table 7).
Calculations of particular criteria by types of innovative behavior, with the establishment of appropriate weighting factors, are given in Table 8.
The normalization of the estimates obtained was carried out by an expert method, the calculations of which are presented in Table 9. The values of complex criteria for various types of innovative behavior are given in Table 10.
To assess the complex coefficients of the criteria, the classification of the system of indicators is used, given in Table 11.
The values of the complex coefficients show that venture capitalists, violets, and exporters have a significant scientific and technical level of innovation (), violets are far superior to all in the innovation process (), switches have the lowest indicator of the innovation process, and the efficiency of innovation () has a spread the least significant by types of behavior.
The calculated integral indicators for various types of innovative behavior are given in Table 12
The integral indicator, which serves as a comprehensive measure for assessing the level of innovativeness, holds significant importance for violets but is least relevant for commutants (see Figure 4).
In the field of computer science, there exist several key metrics that organizations can utilize to gauge the effectiveness of their innovation planning endeavors. One such metric is the quantity of new ideas or technologies generated. This metric aids organizations in tracking the output of their innovation planning efforts and evaluating whether they are generating a sufficient volume of ideas. Another metric is the success rate of new ideas or technologies, which enables organizations to assess the quality of their ideas and identify areas for improvement. Additionally, the impact of new ideas or technologies on the organization is a vital metric that involves measuring their financial impact, operational efficiency, and customer satisfaction. Furthermore, the level of employee engagement in the innovation process serves as a fourth metric, which helps organizations evaluate the level of buy-in and support for innovation among employees while identifying potential barriers to innovation. To summarize, organizations can employ several key metrics, including the quantity of new ideas or technologies generated, the success rate of these ideas or technologies, their impact on the organization, and the level of employee engagement, to effectively measure the effectiveness of their innovation planning efforts in computer science. By tracking these metrics, organizations can gain valuable insights and identify areas for improvement.
Through our analysis, we have discovered that the choice of an innovative behavior model for a firm's planning depends on environmental factors. Once a certain level is reached, welfare no longer plays a primary role in determining the model of innovative behavior within the socio-economic system. On the contrary, the endowment of scientific research potential becomes the determining factor for the type of innovative behavior in systems with a sufficient level of welfare. Even against the backdrop of relatively high welfare, a relatively low level of research resources prevents the acquisition of a specific role function. For further calculations, we present an innovative model based on generalized average data, which incorporates all the criteria of the considered socio-economic systems.
The effective utilization of existing potential for innovative development in socio-economic systems is the solution to the key tasks of planning innovative activities.
There exist several key strategies that organizations can employ to effectively implement innovation planning in the field of computer science. One strategy involves establishing an innovation team or task force, comprising a diverse group of individuals responsible for identifying and evaluating potential innovations, as well as developing and implementing plans for their execution. This team should encompass individuals with varying skills and perspectives to ensure a comprehensive approach to innovation planning.
Another strategy is adopting a structured approach to innovation planning, such as roadmapping. As previously mentioned, roadmapping entails creating a visual representation of an organization's innovation goals and plans. This aids organizations in identifying crucial milestones, allocating resources, and understanding dependencies while allowing them to track progress and adjust plans accordingly.
Encouraging a culture of innovation represents a third strategy. This entails providing employees with the necessary resources and support to generate and test new ideas, as well as recognizing and rewarding innovative thinking. Organizations may also consider implementing processes and practices that foster continuous improvement and experimentation, such as design thinking or agile methodologies.
The fourth strategy involves leveraging external sources of innovation, such as partnerships, collaborations, and external research and development. By engaging with external organizations, companies can access a broader pool of ideas and expertise, while also potentially gaining entry into new markets and technologies.
To summarize, there are several key strategies that organizations can employ to effectively implement innovation planning in computer science. These include establishing an innovation team or task force, adopting a structured approach to innovation planning, fostering a culture of innovation, and leveraging external sources of innovation. By following these strategies, organizations can effectively identify and prioritize new ideas and technologies that drive growth and enhance competitiveness.
Now, let us proceed with calculating the potential of socio-economic systems for innovation using Ukraine as an example. The innovative potential of socio-economic systems comprises three main components: financial, material and technical, and personnel.
For the calculation of Ukraine's innovative potential in socio-economic systems, we propose the use of two indicators for each component.
- Personnel Component:
The following indicators characterize the proportion of individuals engaged in innovative activities within the total population:
Number of individuals employed in science and scientific services as a percentage of the total labor force (P).
Employment in medium and high-tech production as a percentage of the total labor force (F).
- 2.
- Financial Component:
Indicators within this group characterize the physical volumes of financing in the innovation sphere, such as the share of investments relative to GDP and the share of investments in the total volume:
Total expenditures on research and development (R&D) as a percentage of GDP (E).
Share of the volume of sold innovative products (goods and services) in the total volume of sold products (goods and services) of industrial enterprises, expressed as a percentage (I).
- 3.
- Material and Technical Component:
Indicators within this group characterize the number of organizations involved in scientific activities and possessing a material and technical basis for innovation:
Share of industrial enterprises that have introduced innovations (products and/or technological processes) in the total number of industrial enterprises, expressed as a percentage (T).
Number of registered patent applications for inventions and utility models per year, per total workforce (Y).
All data are given for the period 2012-2021 in Table 13.
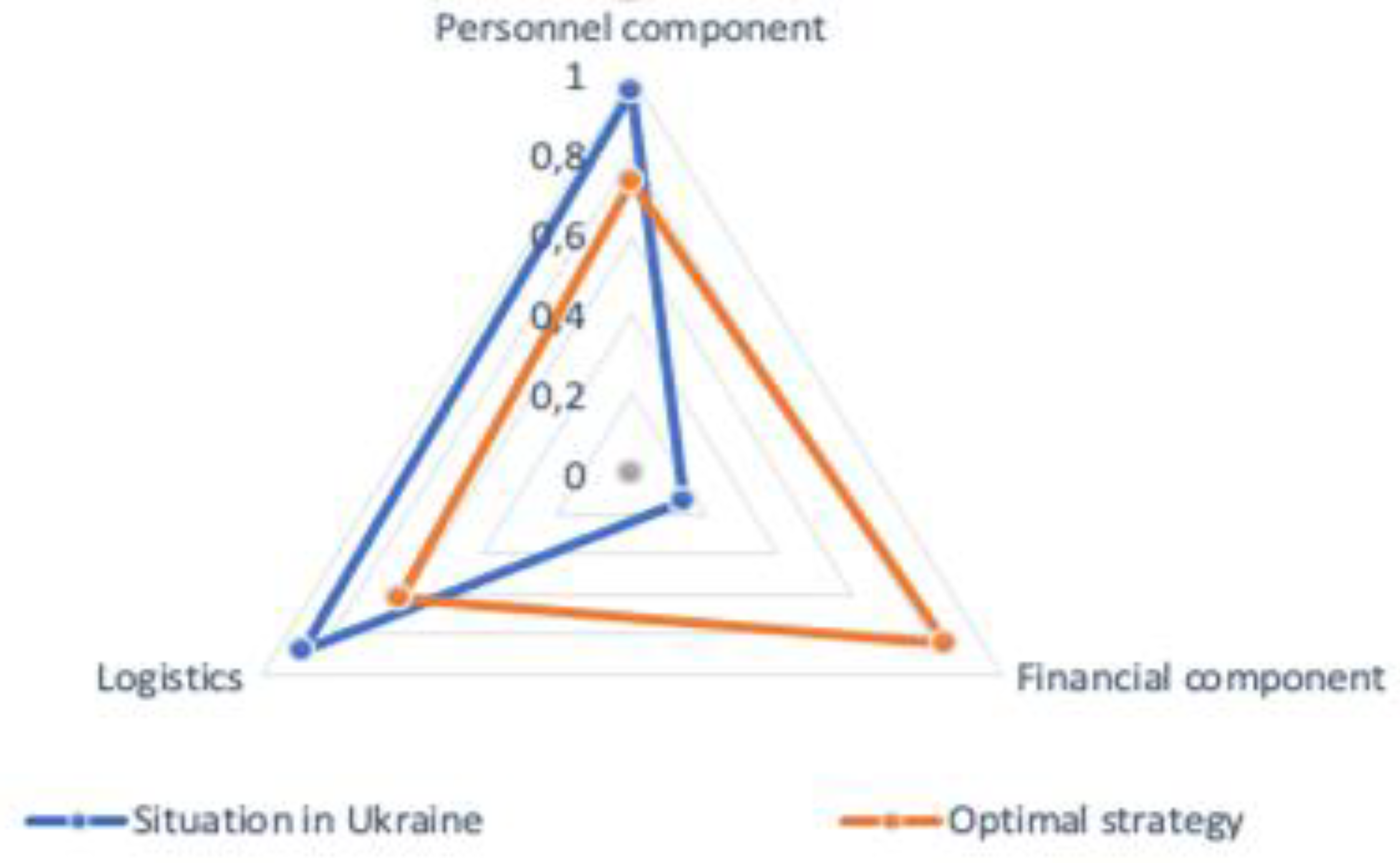
The constructed innovative profile of Ukraine was analyzed using an optimal strategy, which was derived from all considered socio-economic systems based on the highest integral indicator of viability and overall performance, visually resembling the optimal strategy (see Figure 5).
This approach enables the determination of the type of innovative behavior by considering a set of criteria. It also aids in identifying the diffusion process, which results from the increased production of innovative products consumed by the market.
The strategy for the innovative development of Ukraine, in relation to the potentially optimal state, is characterized by a lag in terms of the financial component and well-being level. In conditions of a low financial component, the innovation process is formally restricted. The absence of a deficit in research resources encourages the active utilization of closed innovations aimed at improving and modernizing already existing products within the domestic market. As prosperity grows, it becomes possible to independently create new innovations not only for the domestic market but also for the international market.
Understanding the growth rate of costs in the R&D cycle and their share in the total investment in technological development for new product production and commercialization is crucial for effective innovation management and planning.
The assessment of the scientific and technical factors pertaining to Ukraine's national security should be conducted with the aim of achieving conditions that would allow the country to secure a prominent position in the global economy.
In order to address this optimization problem, the model can identify a set of innovations that maximize the expected value or impact, taking into account the available resources and limitations. Alternatively, decision analysis techniques like decision trees or expected value analysis can be employed. These techniques involve evaluating potential outcomes associated with different decisions and their corresponding probabilities, ultimately selecting the decision with the highest expected value. Within the context of innovation planning, decision analysis techniques can be used to assess potential outcomes of various innovations and identify those that offer the greatest expected value or impact.
To summarize, a computer-mathematical model for innovation planning in computer science can be created using optimization techniques such as linear programming or decision analysis. By defining an objective function and constraints, and solving the optimization problem, the model can identify a set of innovations that maximize the expected value or impact considering the available resources and limitations.
To formulate the equations for an innovation planning model using optimization techniques, it is necessary to define the objective function and constraints and express them as mathematical equations.
The objective function represents the goal of the innovation planning process, which could involve maximizing the expected value or impact of the innovations. This function needs to be defined in terms of variables that represent the different innovations under consideration. For instance, if the goal is to maximize the expected value of the innovations, the objective function might be expressed as follows:
Maximize: E = sum(p[i] * v[i]) for i = 1 to n
Here, E is the expected value, p[i] is the probability of success for innovation i, and v[i] is the value of innovation i.
The constraints represent the available resources and limitations of the organization, such as budget, personnel, and time. These constraints should also be defined in terms of variables that represent the innovations. For example, if there is a budget constraint, it can be expressed as:
sum(c[i] * x[i]) <= B
In this equation, c[i] represents the cost of innovation i, x[i] is a binary variable indicating whether innovation i is selected (1) or not selected (0), and B represents the budget.
Once the objective function and constraints have been defined, a mathematical optimization solver can be employed to determine the optimal solution for the problem at hand.
To construct equations for an innovation planning model using optimization techniques, the objective function and constraints must be explicitly defined and expressed mathematically. The objective function signifies the goal of the innovation planning process, while the constraints represent the available resources and limitations within the organization. Solving these equations enables the identification of the set of innovations that maximizes the expected value or impact, considering the given resources and limitations.
When creating an innovation planning model using optimization techniques, several additional factors should be considered. One such factor is the level of complexity inherent in the model. While more intricate models may encompass greater detail and nuance, they can also pose challenges in terms of solvability and resource requirements. Thus, striking a balance between model complexity and solution tractability is crucial.
Another consideration relates to the data and assumptions utilized in constructing the model. Employing accurate and up-to-date data is vital to ensure the validity and reliability of the results. Additionally, careful consideration of the assumptions made during model construction is necessary, as they can significantly impact the outcomes.
An alternative approach to address the problem of planning random innovations through functional programming involves leveraging a functional programming language such as Haskell or ML. This approach entails implementing a model capable of generating and evaluating random innovations. To achieve this, a set of functions representing different aspects of innovation, such as value, risk, and feasibility, can be defined.
These functions would accept inputs representing the characteristics of an innovation and produce outputs corresponding to the respective values for these aspects. For instance, a function called "value" could be established to take an innovation as input and return a value between 0 and 1, indicating its potential value. Similarly, a function called "risk" could be defined to assess the potential risk of an innovation, also yielding a value between 0 and 1.
To generate and evaluate random innovations, functional programming techniques like recursion and higher-order functions can be utilized. These techniques enable iterating over a substantial number of random samples and assessing their characteristics using the defined functions. Subsequently, statistical or machine learning techniques can be employed to analyze the results, identify emerging patterns and trends, and inform decision-making.
In summary, an alternative solution for planning random innovations through functional programming involves employing a functional programming language to implement a model that generates and evaluates random innovations using functions representing various aspects of innovation. By utilizing functional programming techniques to iterate over a significant number of random samples and analyze the outcomes, patterns and trends can be identified to support decision-making in the field of computer science.
Sure, here's an example of how you might create a mathematical model for innovation planning in MATLAB, taking into account financial, logistics, and human resources criteria.
% Define the objective function
c = [wi_financial*financial_scores wi_logistics*logistics_scores wi_human_resources*human_resources_scores];
% Define the constraints
A = [financial_constraints; logistics_constraints; human_resources_constraints];
b = [financial_constraints_values; logistics_constraints_values; human_resources_constraints_values];
% Define the bounds
x0_bounds = [0, 1];
x_bounds = repmat(x0_bounds, num_options, 1);
% Solve the linear programming problem
options = optimoptions('linprog','Algorithm','simplex');
res = linprog(c, A, b, [], [], x_bounds(:,1), x_bounds(:,2), [], options);
% Print the results
fprintf("Optimal solution: %f\n", res.x);
fprintf("Optimal value: %f\n", res.objval);
In this example, the objective function is defined as a linear combination of financial, logistics, and human resources scores. Each score is multiplied by a weight that represents the importance of the corresponding criterion for the organization. The constraints are defined by matrices A and B, representing the financial, logistics, and human resources constraints, along with the corresponding constraint values.
The variable bounds are specified as lower and upper bounds, and the optimization algorithm employed to solve the problem is the simplex method. The algorithm selection is achieved using the optimoptions function in conjunction with the linprog function. Solving this optimization problem yields the optimal selection of options that maximize the overall score while adhering to the constraints.
It should be noted that this is a simplified example and may require adjustments based on the specific requirements and criteria of the organization. For instance, the financial, logistics, and human resources scores and constraints can be more intricate, and the weights can be tailored to reflect the organization's specific priorities. Moreover, it is essential to consider the possibility of inaccuracies and uncertainties in the available data when interpreting the results.
Additionally, this model assumes linearity between the criteria and the innovation options, which may not always hold true. In cases where the relationship is nonlinear, alternative optimization methods such as nonlinear programming or heuristics may be more appropriate.
Overall, this model offers a framework for organizations to assess and strategize their innovation efforts by considering multiple criteria, including financial, logistics, and human resources. By leveraging this model, organizations can make more informed decisions regarding the pursuit of innovations and enhance resource allocation efficiency.
Now, let's delve into the code and model in greater detail:
The objective function is expressed as a linear combination of the financial, logistics, and human resources scores. Each score is multiplied by a weight, denoted as wi_financial, wi_logistics, and wi_human_resources, respectively. These weights should be positive and sum up to 1.
The model's constraints are defined by matrices A and B. Matrix A encompasses the financial, logistics, and human resources constraints, while the vector b contains the corresponding constraint values. The constraints can include factors like budget limitations, resource availability, or regulatory compliance.
The variables are bounded by lower and upper bounds. In this case, the lower bound is set to 0, and the upper bound is set to 1, reflecting the binary nature of the variables where options are either selected or not.
To solve the optimization problem, the linprog function from MATLAB's Optimization Toolbox is employed. The simplex method, a widely used technique for linear optimization problems, is utilized as the underlying algorithm.
4. Conclusions
Planning for innovative changes is an integral part of competitive strategy development. The planning process for innovative changes should encompass multiple stages. The organization of innovative activities must be aligned with the mechanisms for developing and implementing investment projects. Projects involving innovative changes are characterized by significant information complexity and a high degree of uncertainty. To effectively manage such innovative projects, well-structured information regarding the upcoming tasks is essential. The choice of an innovative behavior model depends on environmental factors. The evaluation of program (plan) compliance is based on a system of analytical indicators designed for assessing innovative activities comprehensively. The conducted studies provide a basis for developing fundamental models of innovative systems and modeling methods to address planning problems. Consequently, the research formulates the problem of planning innovation activity as an optimization problem for the allocation of limited resources. Additionally, a search method for solving the optimization problem of planning innovation activity is proposed.
Author Contributions
methodology, I. D., A. A; approaches, I. D.; system of indicators, A. A; stages of organization of innovative activity, I. D.; the mechanism of development and implementation of innovative projects, A. A; establishing admissible sets of elementary processes and their combinations, I. D.; Calculation of the innovative potential of socio-economic systems on the example of Ukraine, A. A; the strategy of innovative development of Ukraine regarding the potentially optimal state, I. D.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
In this section, you can acknowledge any support given which is not covered
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lyashenko, V.І. Regulation of development of economic systems: theory, regimes, institutes: monograph. 2006; 668 p.
- Starish, O.G. Systemology: Pidruch. 2005, 232 p.
- Mocherny, S.V. Methodology of economic development. 2001, 416 p.
- Erokhina E., A. The theory of economic development: a system-synergetic approach [Electronic resource]./E. A. Erokhina - Access mode. Available online: www.coast.ru/referats/library/ek.lit.agava.ru/eroh.
- Grazhevska, N.І. Economic systems of the era of global changes. 2008, 431 p.
- Karenov, R.S. Strategic management.2006. - P. 5.
- Bovin, A.A.; Cherednikova, L.E.; Yakimovich, V.A. Management of innovations in the organization: Textbook. allowance. S. 2009, 194–195. [Google Scholar]
- Karenov, R.S. Innovation management. S. 1997, 18–20. [Google Scholar]
- Ivasenko, A.G.; Nikonova, Y.I.; Sizova, A.O. Innovation management: Textbook. allowance. S. 2009, 174–175. [Google Scholar]
- Gunin, V.N.; Barancheev, V.P.; Ustinov, V.A.; Lyapina, S.Y. Management of innovations: 17-module program for managers "Management of the development of the organization." Module 2000, 7. P. 76.
- Gililov M., V. Methods and tools for assessing the innovative activity of business entities [Text]: author. dis. for a job. learned. step. Cand. econom. Sciences (08.00.05)/M. V. Gililov - Federal State Educational Institution. higher professional education "Ivanovo State Power Engineering University named after IN AND. Lenin ". 2000, 26 p.
- Morozova, N.I. Planning the development of territorial socio-economic systems according to the criterion of the quality of life of the population/N. I. Morozova/magazine "Regional economy: theory and practice" 2011, 32, 52–59. [Google Scholar]
- Christmann, G.B.; Ibert, O.; Jessen, J.; Walther, U.J. Innovations in spatial planning as a social process – phases, actors, conflicts. European Planning Studies 2020, 28, 496–520. [Google Scholar] [CrossRef]
- Green, P.L.; Plsek, P.E. Coaching and leadership for the diffusion of innovation in health care: a different type of multi-organization improvement collaborative. Journal on Quality Improvement 2002, 28(2), 55–71. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Illustrates the strategic aspect of innovative strategic planning [8].
Figure 1.
Illustrates the strategic aspect of innovative strategic planning [8].
Figure 2.
Types of Strategic Behavior in Complex Systems:.
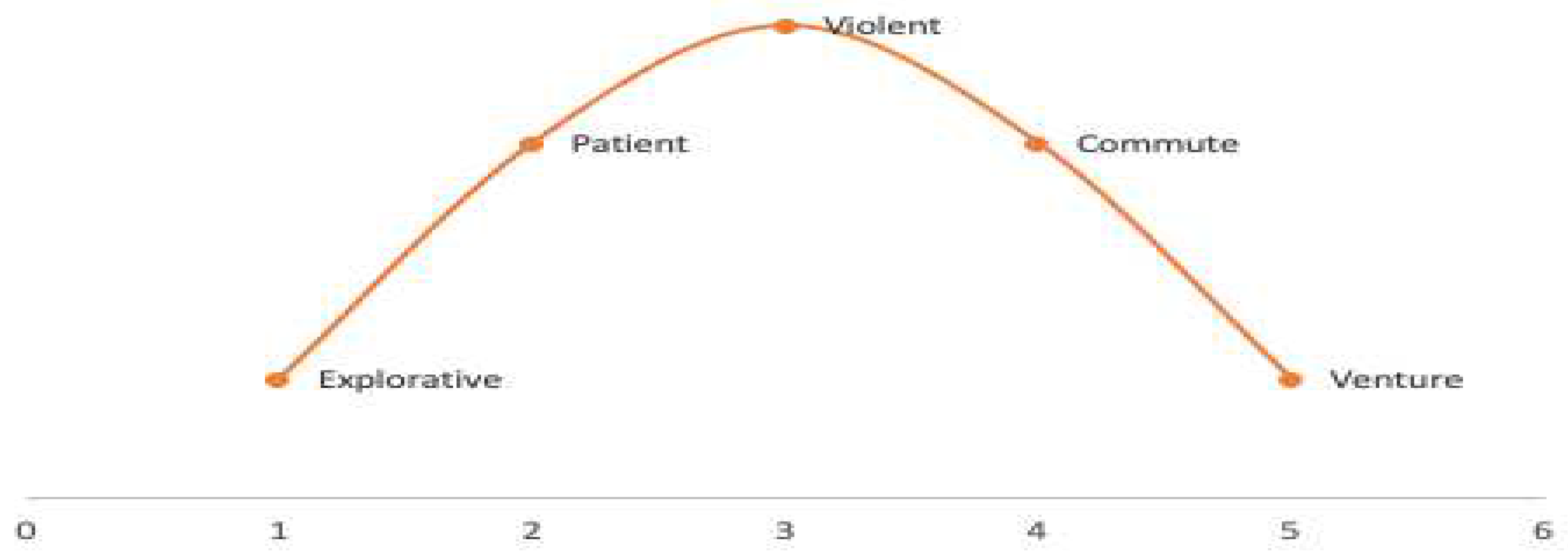
Figure 3.
Matrix for choosing a strategy for innovators.
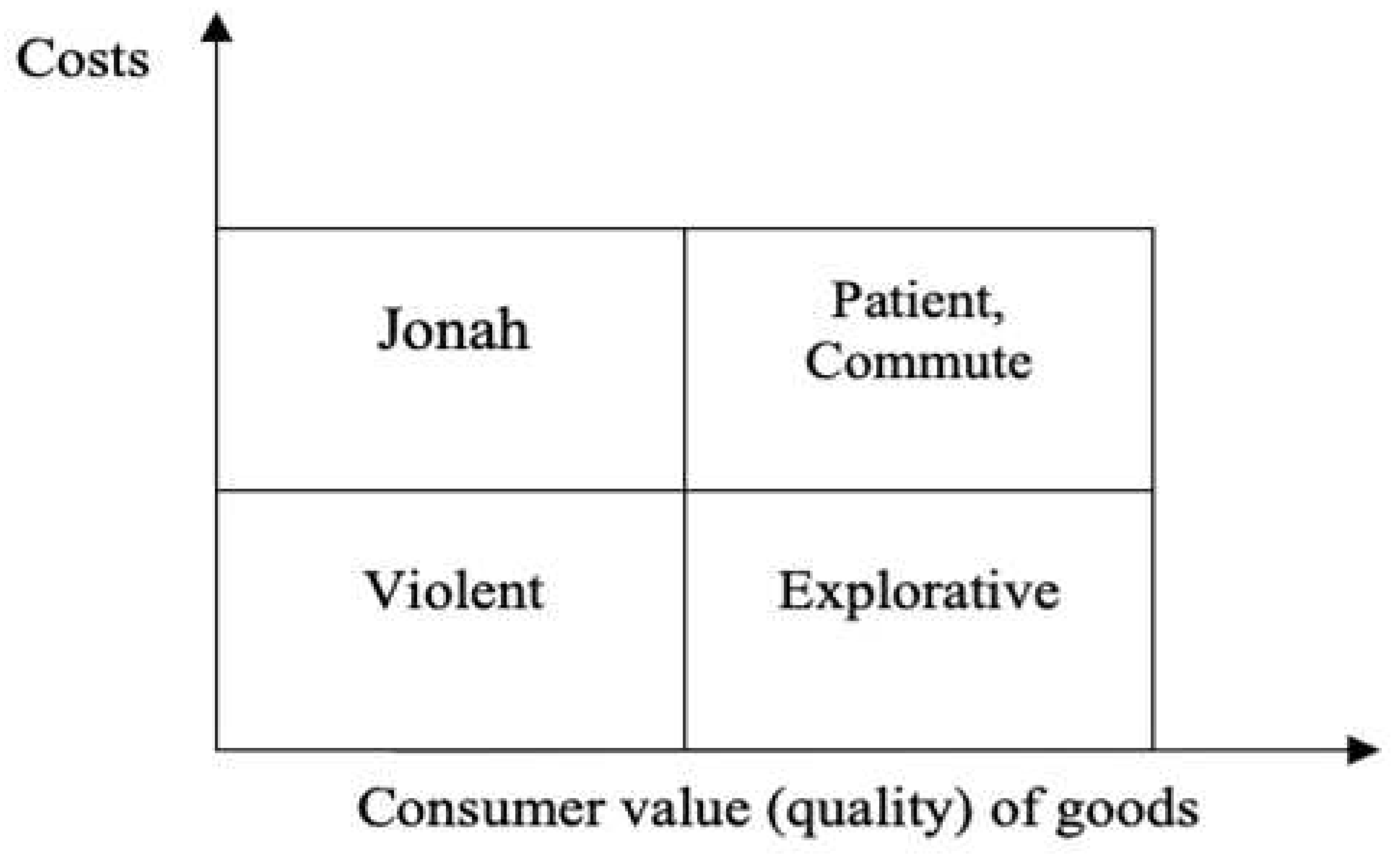
Figure 4.
Analysis of strategies for various states of the socio-economic system.
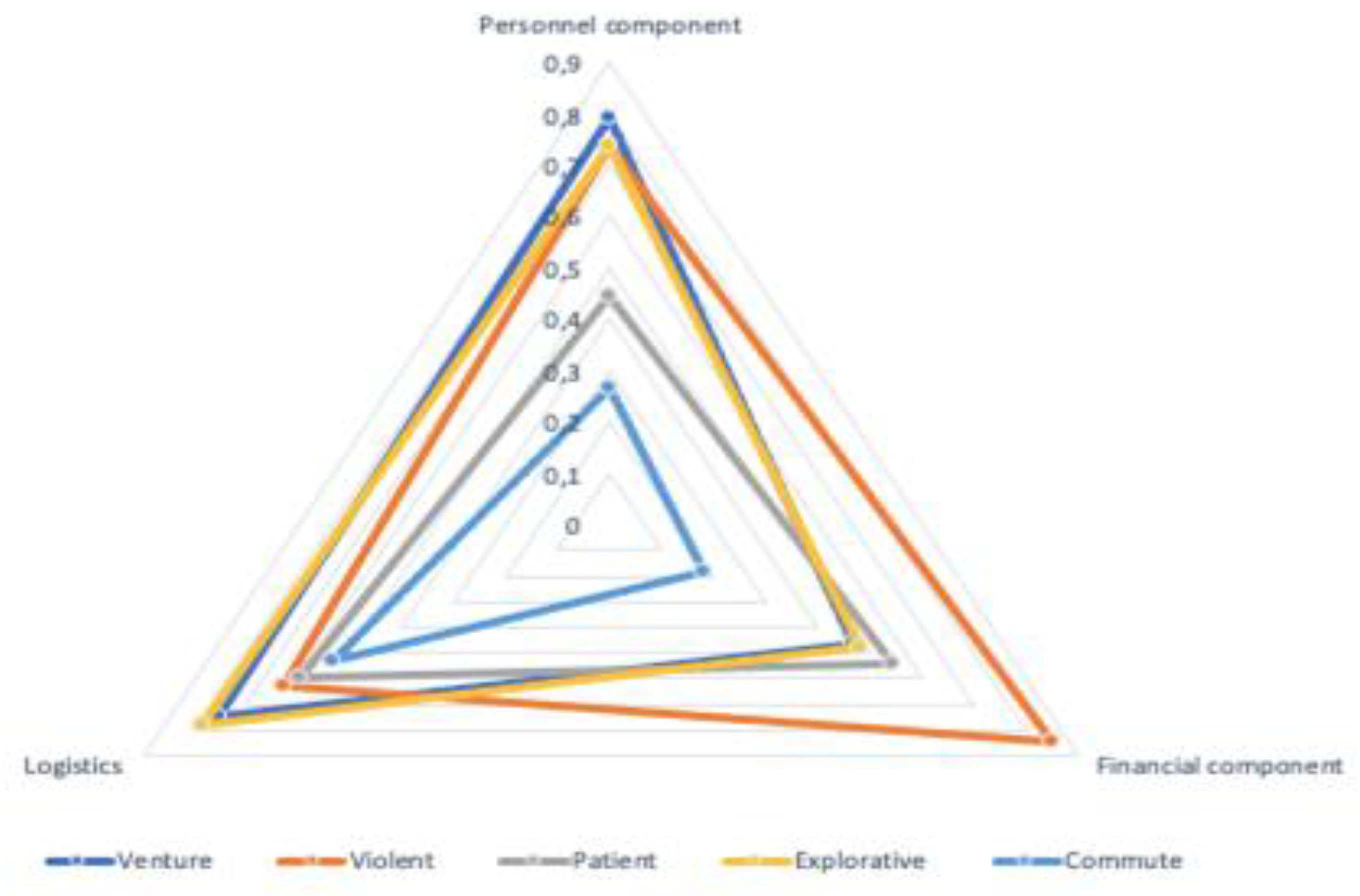
Figure 5.
Presents a comparative analysis of the strategies for Ukraine.
| Properties | Characteristics of Complex Systems in the Economy: |
| Integrity | A change in any component of the system affects the other components and the system as a whole. The system exhibits unity among its elements, self-preservation in content, and self-reproduction in form. A system with signs of self-organization becomes more stable and gains the ability to develop. |
| Hierarchy and heterarchy | The components of the system are strictly subordinated, forming a systemic structure with levels of constituent parts. Each system can be considered as an element of a higher-level system (supersystem) and as a subsystem. Elements can belong to multiple subsystems through interconnections. |
| Integrity or synergy (emergence) |
The system possesses properties that are absent in its individual elements. Synergistic relationships between the elements result in an overall effect greater than the sum of the effects of the individual elements. |
| Openness (mass character) |
The system functions through the exchange of energy and information flows with other systems and its environment. |
| Dynamism | The system undergoes changes in parameters and structure under the influence of external factors. It has a purpose and functions that involve interactions with other systems and the environment, as well as overcoming internal contradictions. |
| Resilience and adaptability | The system can maintain its structure, functionality, and purposeful existence in the presence of internal contradictions and external influences. However, the equilibrium of a system is relatively stable, and the significant influence of the external environment can lead to the emergence of multiple centers of disequilibrium. |
| Fractality | The functioning and development of the system are independent of the scale of observation. Changes in higher-level systems result in similar changes in the subsystems. The functioning of the components is interconnected, and the violation of functional complementarity disrupts the integrity of the system. |
| Self-organization and self-development | The system has the ability to change its internal structure under the influence of internal or external factors. This process involves the formation of dissipative structures and the pursuit of dynamic equilibrium. |
| Non-linearity (Randomness and uncertainty) |
Complex systems exhibit a probabilistic nature due to the interaction of numerous external and internal factors. Economic and mathematical models based on probability theory are often used to study them. The development of a system is characterized by cyclical periods of progress and degradation. As the complexity of the system increases, cross-cyclic phenomena may occur, where the phases of development of some components overlap with the regression of others. It is challenging to isolate and study phenomena in such systems in their purest form due to their interaction with the environment. |
| Type of innovative behavior | Characteristic | Features of the |
| Venture | Systems with flexible and mobile structures operate at the stages of growth of inventive activity. The advantage is the high speed of new product development, with which large enterprises cannot compete | They do not organize the production of products, but transfer their developments to other systems. The number of employees is small |
| Explorative | Medium or small systems that enter the market with a fundamentally new product, subsequently forming a new industry | They are distinguished by their dedication, high professional level of employees and leaders, high expenditures on R&D, the results of which are qualitatively new products and new technologies |
| Violent | Large systems that carry out mass production, operating in the market with their own or acquired new products, are ahead of the competition due to mass production and the effect of scale. They are characterized by forceful competitive and innovative behavior. | The systems are large in size, have a large number of employees, many branches and subsidiaries, and a full range of products. They are distinguished by high costs from R&D, production, marketing and distribution networks. High quality products due to the high level of standardization and unification. Many violets are TNCs, create an oligopolistic market |
| Patient | Large, medium, small systems produce new or modernized products with unique characteristics and adapted to narrow segments of a wide market | In specialized production, the stock of competitiveness of a product is ensured by the consumer value of the product and full compliance with consumer expectations. An occupied narrow niche should be distinguished by unique technological experience, a special distribution network, and the historical prestige of the trademark. |
| Commute | Small systems carry out the diffusion of innovations created by other innovative organizations, adapting them to the requirements of the local market | Satisfying the local needs of local markets or even individual demand, "bind the economy across the entire space", which contributes to the diffusion of changes in their diffusion through imitation activities and the introduction of new types of services, creating on the basis of new technologies |
Table 4.
The system of analytical indicators for assessing innovative activities [11].
Table 4.
The system of analytical indicators for assessing innovative activities [11].
| Complex criterions (Ki) | Number of indicators | Of these, by stages of innovation | ||
|---|---|---|---|---|
| I | II | III | ||
| 1. Scientific and technical level of innovation () | 19 | 5 | 9 | 5 |
| 1.1. Progressiveness | 7 | 2 | 4 | 1 |
| 1.2. Technicality | 5 | 2 | 3 | - |
| 1.3. Competitiveness | 1 | - | - | - |
| 1.4. Legal security | 4 | 1 | 1 | 2 |
| 1.5. Manufacturability | 2 | - | 1 | 1 |
| 2. Innovative process () | 25 | 9 | 11 | 5 |
| 2.1. Innovative activity | 2 | - | - | 2 |
| 2.2. Intensity | 4 | 1 | 3 | - |
| 2.3. Saturation | 7 | 2 | 4 | 1 |
| 2.4. Complexity | 5 | 3 | - | 2 |
| 2.5. Duration | 3 | 1 | 2 | - |
| 2.6. Completeness of coverage | 4 | 2 | 2 | - |
| 3. Effectiveness of innovation̆ activity () | 16 | 1 | 1 | 14 |
| 3.1. Commercialization | 1 | - | - | 1 |
| 3.2. Wide range and versatility of application | 1 | - | - | 1 |
| 3.3. Financial | 6 | - | - | 6 |
| 3.4. Investment | 4 | - | - | 4 |
| 3.5. Incentives | 3 | - | - | 3 |
| All groups | 60 | 15 | 21 | 24 |
Table 5.
Scoring system for a complex criterion K1.
| Essence of a particular criterion | The value of a particular criterion | ||
|---|---|---|---|
|
Progressiveness |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Technicality |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Competitiveness |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Legal security |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Manufacturability |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 |
Table 6.
Scoring system for a complex criterion K2.
| Weight coefficient |
Private criterion bij | Essence of a particular criterion | The value of a particular criterion |
|---|---|---|---|
|
Innovative activity |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Intensity |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Saturation |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Complexity |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Duration |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Completeness of coverage |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 |
Table 7.
Scoring system for a complex criterion K3.
| Weight coefficient wij | Private criterion bij | Essence of a particular criterion | The value of a particular criterion |
|---|---|---|---|
|
Commercialization |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Wide range and versatility of application |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Wide range and versatility of application |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Investment |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 | ||
|
Incentives |
average performance | 10 | |
| dynamic reproduction | 5 | ||
| steadiness | 0 |
Table 8.
Calculation of the assessment of private criteria.
| Weight coefficient |
|||||
|---|---|---|---|---|---|
| Venture | Violent | Patient | Explorative | Commute | |
| criterion | |||||
| 0,368 | 10 | 10 | 5 | 10 | 0 |
| 0,263 | 10 | 5 | 5 | 10 | 5 |
| 0,053 | 10 | 5 | 5 | 0 | 5 |
| 0,211 | 5 | 10 | 5 | 5 | 5 |
| 0,105 | 10 | 5 | 5 | 10 | 0 |
| criterion | |||||
| 0,08 | 10 | 5 | 5 | 10 | 5 |
| 0,16 | 10 | 5 | 5 | 10 | 0 |
| 0,25 | 5 | 10 | 5 | 0 | 0 |
| 0,2 | 5 | 10 | 5 | 5 | 0 |
| 0,12 | 0 | 10 | 10 | 5 | 5 |
| 0,16 | 0 | 10 | 5 | 5 | 5 |
| criterion | |||||
| 0,0625 | 5 | 10 | 10 | 10 | 5 |
| 0,0625 | 0 | 10 | 5 | 0 | 5 |
| 0,375 | 10 | 10 | 10 | 10 | 10 |
| 0,25 | 10 | 5 | 5 | 10 | 0 |
| 0,1875 | 5 | 0 | 0 | 5 | 5 |
Table 9.
Normalization of the obtained estimates.
| Venture | Violent | Patient | Explorative | Commute | |
|---|---|---|---|---|---|
| criterion | |||||
| 0,368 | 1 | 1 | 0,5 | 1 | 0 |
| 0,263 | 1 | 0,5 | 0,5 | 1 | 0,5 |
| 0,053 | 1 | 0,5 | 0,5 | 0 | 0,5 |
| 0,211 | 0,5 | 1 | 0,5 | 0,5 | 0,5 |
| 0,105 | 1 | 0,5 | 0,5 | 1 | 0 |
| criterion | |||||
| 0,08 | 1 | 0,5 | 0,5 | 1 | 0,5 |
| 0,16 | 1 | 0,5 | 0,5 | 1 | 0 |
| 0,25 | 0,5 | 1 | 0,5 | 0 | 0 |
| 0,2 | 0,5 | 1 | 0,5 | 0,5 | 0 |
| 0,12 | 0 | 1 | 1 | 0,5 | 0,5 |
| 0,16 | 0 | 1 | 0,5 | 0,5 | 0,5 |
| criterion | |||||
| 0,0625 | 0,5 | 1 | 1 | 1 | 0,5 |
| 0,0625 | 0 | 1 | 0,5 | 0 | 0,5 |
| 0,375 | 1 | 1 | 1 | 1 | 1 |
| 0,25 | 1 | 0,5 | 0,5 | 1 | 0 |
| 0,1875 | 0,5 | 0 | 0 | 0,5 | 0,5 |
Table 10.
Complex criteria values.
| Venture | Violent | Patient | Explorative | Commute | |
|---|---|---|---|---|---|
| 0,7895 | 0,737 | 0,4475 | 0,7365 | 0,2635 | |
| 0,465 | 0,85 | 0,545 | 0,48 | 0,18 | |
| 0,75 | 0,625 | 0,59375 | 0,78125 | 0,53125 |
Table 11.
Criteria significance level classification.
| Significance level of the criterion | Complex criterion value |
|---|---|
| Absolutely significant | 1-0,99 |
| Significant in the long run | 0,85-0,98 |
| Significant in the medium term | 0,75-0,84 |
| Relatively significant | 0,65-0,74 |
| Insignificantly | < 0,65 |
Table 12.
Integral indicator.
| Venture | Violent | Patient | Explorative | Commute |
|---|---|---|---|---|
| 0,6436765 | 0,754329 | 0,52706 | 0,641443 | 0,299902 |
Table 13.
Innovative parameters for calculating the socio-economic system of Ukraine.
| Year | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.Personnel component | ||||||||||
| The number of people employed in science and scientific services (thousands people) – x1 | 19261,4 | 19314,2 | 18073,3 | 16443,2 | 16276,9 | 16156,4 | 16360,9 | 16578,3 | 16590,2 | 16602 |
| Employment in high-tech production (thousands people) - x2 | 504,1 | 493,6 | 456,0 | 422,9 | 428,1 | 415,8 | 437,9 | 421,6 | 418,7 | 415,7 |
| 2.Financial component | ||||||||||
| Total expenditures on R&D (mln.UAH) - x3 |
9419,9 | 10248,5 | 9487,5 | 11003,6 | 11530,7 | 13379,3 | 16773,7 | 16773,7 | 16891,1 | 17009,4 |
| Costs for innovations, (mln.UAH) - x4 |
11480,6 | 9562,6 | 7695,9 | 13813,7 | 23229,5 | 9117,5 | 12180,1 | 14220,9 | 14320,5 | 14420,7 |
| 3. Logistics | ||||||||||
| Share of industrial enterprises that introduced innovations -x5 | 2181 | 2002 | 1729 | 1655 | 1503 | 1376 | 1491 | 1503 | 1493 | 1482 |
| Number of registered patent applications for inventions and utility models per year – x6 | 44876 | 45910 | 50234 | 63266 | 73690 | 73411 | 83654 | 82914 | 83495 | 84079 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






