CKM Matrix Parameters from an Algebra

Preprint

Article

CKM Matrix Parameters from an Algebra

Altmetrics

Downloads

149

Views

Comments

A peer-reviewed article of this preprint also exists.

TEJINDER PAL SINGH^*,

ADITYA ANKUR PATEL

TEJINDER PAL SINGH^*,

ADITYA ANKUR PATEL

This version is not peer-reviewed

Submitted:

20 July 2023

Posted:

21 July 2023

You are already at the latest version

Alerts

Abstract

We report a theoretical derivation of the Cabibbo-Kobayashi-Maskawa (CKM) matrix parameters and the accompanying mixing angles. These results are arrived at from the exceptional Jordan algebra applied to quark states, and from expressing flavor eigenstates (i.e. left-chiral states) as superposition of mass eigenstates (i.e. the right-chiral states) weighted by square-root of mass. Flavor mixing for quarks is mediated by the square-root mass eigenstates, and the mass ratios used have been derived in earlier work from a left-right symmetric extension of the standard model. This permits a construction of the CKM matrix from first principles. There exist only four normed division algebras, they can be listed as follows - the real numbers $\mathbb{R}$, the complex numbers $\mathbb{C}$, the quaternions $\mathbb{H}$ and the octonions $\mathbb{O}$. The first three algebras are fairly well known; however, octonions as algebra are less studied. Recent research has pointed towards the importance of octonions in the study of high energy physics. Clifford algebras and the standard model are being studied closely. The main advantage of this approach is that the spinor representations of the fundamental fermions can be constructed easily here as the left ideals of the algebra. Also the action of various Spin Groups on these representations too can be studied easily. In this work, we build on some recent advances in the field and try to determine the CKM angles from an algebraic framework. We obtain the mixing angle values as $\theta_{12}=11.093^o, \theta_{13}=0.172^o, \theta_{23}=4.054^o$. In comparison, the corresponding experimentally measured values for these angles are $13.04^o \pm 0.05^o, 0.201^o \pm 0.011^o, 2.38^o \pm 0.06^o $. The agreement of theory with experiment is likely to improve when running of quark masses is taken into account.

Keywords:

Subject: Physical Sciences - Nuclear and High Energy Physics

1. Introduction

There has been occasional interest in the last few decades as to the significance of octonions for understanding the standard model of particle physics [1]. Research on this topic has picked up significant pace in the last seven years or so, since the publication of Furey’s Ph. D. thesis [2], and also the discovery by Todorov and Dubois-Violette [3] that the exceptional groups

G_{2}, F_{4}, E_{6}

contain symmetries of the standard model as maximal sub-groups. This has given rise to the hope that octonions could play a significant rule in the unification of electroweak and strong interaction, and in turn their unification with gravitation. Octonionic chains can be used to generate a Clifford algebra, and spinors made as minimal left ideals of Clifford algebras possess symmetries observed in the standard model [2,4].

We have proposed a left-right symmetric extension of the standard model, based on complex split bioctonions, which incorporates gravitation [5]. This is consistent with unification based on an

E_{8} \times E_{8}

symmetry, and the breaking of this symmetry reveals the standard model [6,7]. Chiral fermions arise after symmetry breaking; left-handed fermions are eigenstates of electric charge and right-handed fermions are eigenstates of the newly introduced

U (1)

quantum number - square root of mass. By expressing charge eigenstates as superpositions of square-root mass eigenstates one is able to theoretically derive the observed mass ratios of quarks and charged leptons [8,9,10,11,12].

In the present paper we extend these methods to provide a theoretical derivation of the CKM matrix parameters for quark mixing, and the accompanying mixing angles. Also, we show that the complex Clifford algebra

C l (9)

is the algebra of unification. Further, we conclude from our investigations that our universe possesses a second 4D spacetime with its own distinct light-cone structure. Distances in this space-time are invariably microscopic and only quantum systems can access this second space-time.

This paper is organised as follows. Sections 2, 3, 4 review a few basics of group representations, Clifford algebras, and the octonions. Sections 5 and 6 briefly recall earlier work on particle representations made from the octonions, and our own work on derivation of mass ratios from the exceptional Jordan algebra. Section 7 is the heart of the paper; the space of minimal ideals is constructed and the role of

S U {(2)}_{L}

and

S U {(2)}_{R}

symmetry elucidated. The triality property of the spinor and vector reps of

S O (8)

is used to motivate the methodology for theoretical derivation of the CKM matrix parameters. The calculation of these matrix parameters and mixing angles is then carried out in Section 8. Conclusions are in Section 9.

2. A few basics

To engage in the study of the Clifford Algebras, mass ratios and their application to the Standard Model itself, we first need a basic introduction to some mathematical concepts. A basic review has been done in the following subsequent sections about some of the required concepts.

2.1. Algebra

An Algebra (A, + , . , F) over a Field F is defined to be a vector space over the field, equipped with a bi-linear operation that follows the following properties:-

m : A \times A ⟶ A

(1)

(a, b) ⟶ a . b a, b, a . b \in A

(2)

( $α$ a).( $β$ b) = $α β$ (a.b) $α$ , $β$ ∈ F ; a, b ∈ A
(a + b).c = (a.c) + (b.c) a,b,c ∈ A.
((a.b).c) = (a.(b.c))

An Ideal I is defined as a subspace of A which survives multiplication by any element of A. A left ideal is defined as:-

a \in I, \forall b \in A \Rightarrow (b . a) \in I

(3)

2.2. Group Representations

If there is a homomorphism from a group G to a group of operators $U (G)$ on a vector space V, then $U (G)$ forms a representation of group G on V.
The dimension of the representation is the same as the dimension of the vector space.

g \in G \overset{U}{⟶} U (g)

(4)

U (g) e_{i} = D {(g)}_{i}^{j} e_{j} i, j = 1, 2 - - d i m (V)

(5)

Here, the D are the matrix representation of G on the vector space V. As a representation is a homomorphism it must preserve the group operation, so we have:-

U (g_{1}) U (g_{2}) = U (g_{1} . g_{2})

(6)

D (g_{1}) D (g_{2}) = D (g_{1} . g_{2})

(7)

If for a representation

U (G)

of G on V, there exists a subspace

V_{1}

in V such that :-

U (g) | x_{1} 〉 \in V_{1} \forall x_{1} \in V_{1}

(8)

then such a subspace is called an invariant subspace of V with respect to the group representation

U (G)

. The trivial invariant subspaces of V are V itself, and the space of null vectors. A subspace which does not have any non-trivial invariant subspace is called minimal or proper. The representation

U (G)

on V is called irreducible if there is no non-trivial invariant subspace in V; otherwise the representation is reducible [13].

2.3. The Standard Model

The gauge group of the Standard Model is given below, also the forces and their respective carriers are presented in the Table 1.

G_{S M} = S U {(3)}_{c} \times S U {(2)}_{L} \times U {(1)}_{Y}

(9)

A representation of the gauge group G acts on a finite-dimensional Hilbert space V.
Particles then live in the irreducible invariant subspace of V as their basis vectors.

3. Clifford Algebras

A Clifford algebra

C l (p, q)

over

R

is defined to be an associative algebra, generated by n elements

e_{i}

. These n generators exhibit the properties:

{e_{i}, e_{j}} = e_{i} e_{j} + e_{j} e_{i} = 2 η_{i j}

(10)

e_{i}^{2} = 1 e_{j}^{2} = - 1

(11)

Here i runs from 1 to p, j runs from 1 to q. The multiplication also called the Clifford product can be realised in terms of dot product and wedge product of vectors. An example is:-

x y = x . y + x \land y

(12)

The signature becomes irrelevant when we form the algebra over

C

as the field. For a vector v (a linear combination of generators) we have :-

v^{2} = - | | v | | \Rightarrow v^{- 1} = \frac{- v}{| | v | |}

(13)

3.1. Pin and Spin Groups

There is a natural automorphism in the Clifford Algebra, for all vectors in the Clifford Algebra, given by:-

\begin{matrix} v ⟶ \tilde{v} = - v \end{matrix}

(14)

Let us denote this automorphism as

α

. It partitions the algebra into two parts, firstly we have the part that is the product of even number of vectors, given as:

C l^{e v e n} (n) = {α (x) = x; \forall x \in C l (n)}

(15)

The other part contains odd number of vectors as product.

C l^{o d d} (n) = {α (x) = - x; \forall x \in C l (n)}

(16)

For a non-null vector u, we can define an inverse given by:-

\begin{matrix} \forall u \in V \subset C l (V) \end{matrix}

(17)

\begin{matrix} \exists u^{- 1} \in C l^{*} (V) : u^{- 1} = - \frac{u}{∥ \vec{u} ∥} \end{matrix}

(18)

Here

C l^{*} (V)

is the group of elements that have inverses. The definition of inverse of vector can be extended to the inverse of the product of the vectors. Thus, we can define two groups as done below [14,15]:-

Pin = \{a \in C l^{*} (V) : a = u_{1} u_{2} - - - u_{r}, u_{j} \in V, | u_{j} | = 1\}

(19)

Spin = P i n \cap C l^{e v e n} (n) = {a \in C l (n) : a = u_{1} - u_{2 r}; u_{j} \in V, | u_{j} | = 1}

(20)

The action of both these groups on V can be defined by the Twisted Adjoint Action:-

{\tilde{A d}}_{a} x = α (a) x a^{- 1} \in V \forall x \in V .

(21)

{(α (a) v a^{- 1})}^{2} = v^{2} \forall v \in V

(22)

As both these group preserve the magnitude of the vectors, they are orthogonal and special orthogonal transformations.

Pin ⟶ O (n)

(23)

Spin ⟶ S O (n)

(24)

3.2. Representations of Clifford Algebras

The real and complex Clifford algebras have matrix representations. Here however, we will focus on representations of complex Clifford Algebras. The representations of the even subalgebra can be similarly obtained by the identity [16,17]:-

C l^{e v e n} (n) ≅ C l (n - 1); n \geq 1

(25)

The matrix representations are given below, here

M_{p} (C)

represents a

p \times p

matrix with complex entries.

C l (n) ≅ M_{p} (C) p = 2^{\frac{n}{2}}; n = e v e n

(26)

C l (n) ≅ M_{p} (C) \oplus M_{p} (C) p = 2^{\frac{n - 1}{2}}; n = o d d

(27)

Again notice that for the odd case, the total representation gets reduced to two irreducible representations. Especially look at the case of

n = 3, 7 \mod 8

. The irreducible subspace on which matrices act is represented by P. These

M_{n} (F)

act on n-dimensional irreducible space. The choice of volume element can split the algebra into two parts [17,18], total space also gets partitioned into two irreducible subspaces. For dimensions 3 and 7, there are two choices of the irreducible spaces, Positive pinor space (

P_{+}

) and Negative Pinor Space (

P_{-}

C l (n) ≅ C l^{+} (n) \oplus C l^{-} (n) ≅ E n d_{C} (P_{+}) \oplus E n d_{C} (P_{-})

(28)

P = P_{+} \oplus P_{-}

(29)

Now look at the case for the complexified Dirac Algebra

C \otimes C l (1, 3)

, it is equivalent to complex Clifford Algebra

C l (4)

. We need to study the usual spinors, so we look at the matrix representations of

C l^{e v e n} (4)

. We know that

C l^{e v e n} (4) ≅ C l (3)

. For those cases, where the even subalgebra gets partitioned into two, we similarly get Positive Spinor Space ( $S_{+}$ ) and Negative Spinor Space ( $S_{-}$ ).

C l^{e v e n} (4) ≅ C l (3) ≅ M_{2} (C) \oplus M_{2} (C)

(30)

S = S_{+} \oplus S_{-} = S_{L} \oplus S_{R}

(31)

These are the matrix representations of the spin groups that act on the spinor space. The total spinor space is the vector sum of the positive and negative spinor spaces. Both spaces are 2 dimensional and indeed these spaces are interpreted as the Left Handed Weyl Spinor and Right Handed Weyl Spinor. Keeping this information in mind, we will construct two irreducible subspaces in higher dimensions, brief outline is discussed below. For the

C l (8)

algebra we look at its even subalgebra.

C l^{e v e n} (8) = C l (7) = M_{8} (C) \oplus M_{8} (C)

(32)

n = 7

, the representation space can be decomposed into two irreducible subspaces. This fact can be used later to include spin and other things in the analysis.

4. Octonions

A generic complex octonion can be represented as :

C \otimes O = \sum_{n = 0}^{7} A_{n} e_{n}

(33)

Here

A_{n}

are complex coefficients and

e_{n}

are octonionic units, with properties

e_{0}^{2} = 1

and

e_{i}^{2} = - 1

. So

e_{0} = 1

and rest are the imaginary octonionic units. In general octonionic multiplication is non-associative; an example is given:

e_{3} (e_{4} (e_{6} + i e_{2})) = - 1 + i e_{7}

(34)

(e_{3} e_{4}) (e_{6} + i e_{2}) = - 1 - i e_{7}

(35)

To tackle this problem of the octonions, we need to define an order of multiplication on a product of octonions. It leads to chain of octonions, made from maps.

e_{1} (e_{2} (e_{3} (e_{4})))) ⟶ \overset{\leftarrow}{e_{1} e_{2} e_{3} e_{4}}

(36)

\overset{\leftarrow}{- - e_{i} e_{j} - -} f = - (\overset{\leftarrow}{- - e_{j} e_{i} - -} f)

(37)

We will work with octonionic chains only. Octonionic multiplication is represented by the Fano Plane given below. An example multiplication is given by:-

e_{7} e_{1} = e_{3} and e_{1} e_{7} = - e_{3}

(38)

e_{i} e_{j} + e_{j} e_{i} = 0

(39)

The octonionic chains form a representation of the Clifford Algebras and hence we are interested in their study. They form a representation of

C l (6)

[2].

The generators of the Clifford Algebra can be constructed from the octonionic imaginary units as shown in Furey’s work [2]. The Fano plane in Figure 1, lists down the method to multiply octonionic units.

C l (6) ≅ C \otimes \overset{\leftarrow}{O}

(40)

The 64 dim

C l (6)

algebra is fully generated by the set : {

\overset{\leftarrow}{i e_{1}}, \overset{\leftarrow}{i e_{2}}, \overset{\leftarrow}{i e_{3}}, \overset{\leftarrow}{i e_{4}}, \overset{\leftarrow}{i e_{5}}, \overset{\leftarrow}{i e_{6}}

}. These are the generators of the Clifford Algebra and act as the underlying vector space structure.

\overset{\leftarrow}{e_{1} e_{2} e_{3} e_{4} e_{5} e_{6}} f = \overset{\leftarrow}{e_{7}} f

(41)

5. Minimal Left Ideals

The generators of

C l (6)

can be used to make elements of maximally totally isotropic space (MTIS). An element of maximally totally isotropic space has a quadratic norm equal to zero [19]. This space for Maximally Isotropic Subspace follows the algebraic structure given below:-

{q_{i}, q_{j}} f = q_{i} (q_{j} f) + q_{j} (q_{i} f) = 0

(42)

{q_{i}^{†}, q_{j}^{†}} f = q_{i}^{†} (q_{j}^{†} f) + q_{j}^{†} (q_{i}^{†} f) = 0

(43)

{q_{i}, q_{j}^{†}} f = δ_{i j} f

(44)

The

a^{†}

represents Hermitian conjugation. It is basically the complex conjugation

a^{*}

and octonionic conjugation

\tilde{a}

done simultaneously. The elements of the MTIS can be constructed from the generators of

C l (6)

. One choice is given below [2,5]. The six generators give rise to six elements with a quadratic norm equal to zero. There can be other equivalent choices also [19].

q_{1} = \frac{1}{2} (- e_{5} + i e_{4}) q_{1}^{†} = \frac{1}{2} (e_{5} + i e_{4})

(45)

q_{2} = \frac{1}{2} (- e_{3} + i e_{1}) q_{2}^{†} = \frac{1}{2} (e_{3} + i e_{1})

(46)

q_{3} = \frac{1}{2} (- e_{6} + i e_{2}) q_{3}^{†} = \frac{1}{2} (e_{6} + i e_{2})

(47)

We construct quantities out of these isotropic vectors, the Nilpotent given as [2]:-

q = q_{1} q_{2} q_{3} q^{†} = q_{3}^{†} q_{2}^{†} q_{1}^{†}

(48)

q^{2} = 0 {(q^{†})}^{2} = 0

(49)

We also have the Idempotent given as:-

p = q q^{†} p^{'} = q^{†} q

(50)

p^{2} = p {(p^{'})}^{2} = p^{'}

(51)

We act on idempotent by the q and

q^{†}

operators and get various algebraic states and the minimal left ideals. These states are later classified according to the transformations they undergo [2,20].

5.1. Symmetry Transformations

We first look at the transformations of such kind that Maximally isotropic Space is closed. Operator transforms of type :-

e^{i ϕ_{k} g_{k}} | e^{- i ϕ_{k} g_{k}} ϕ_{k} \in R

(52)

[g_{k}, \sum_{i} b_{i} q_{i}] = \sum_{j} c_{j} q_{j} [g_{k}, \sum_{i} b_{i}^{'} q_{i}^{†}] = \sum_{j} c_{j}^{'} q_{j}^{†}

(53)

We can make Hermitian operators by the following procedures:-

q = c_{1} q_{1} + c_{2} q_{2} + c_{3} q_{3} a n d q^{'} = c_{1}^{'} q_{1} + c_{2}^{'} q_{2} + c_{3}^{'} q_{3}

(54)

Charge Operator has a

U (1)

symmetry: Q =

\frac{1}{3} \sum_{i} q_{i}^{†} q_{i}

, and SU(3) generators :

Λ_{1} = - q_{2}^{†} q_{1} - q_{1}^{†} q_{2} Λ_{2} = i q_{2}^{†} q_{1} - i q_{1}^{†} q_{2}

(55)

Λ_{3} = q_{2}^{†} q_{2} - q_{1}^{†} q_{1} Λ_{4} = - q_{1}^{†} q_{3} - q_{3}^{†} q_{1}

(56)

Λ_{5} = - i q_{1}^{†} q_{3} + i q_{3}^{†} q_{1} Λ_{6} = - q_{3}^{†} q_{2} - q_{2}^{†} q_{3}

(57)

Λ_{7} = i q_{3}^{†} q_{2} - i q_{2}^{†} q_{3} Λ_{8} = - \frac{1}{\sqrt{3}} (q_{1}^{†} q_{1} + q_{2}^{†} q_{2} - 2 q_{3}^{†} q_{3})

(58)

A general Hermitian operator can be written as :

\sum_{H} H = r_{0} Q + r_{i} \sum_{i = 1}^{8} Λ_{i}

(59)

We see that the idempotent remains unaffected by these operations:

e^{i \sum H} q q^{†} e^{- i \sum H} = (1 + i \sum H + - -) q q^{†} (1 - i \sum H - -) = q q^{†} = p

(60)

Hence it is identified as a neutrino. The down isospin family can be obtained via complex conjugation of all the particles. Operators for that family also get complex conjugated and then are used to identify the particles.

5.2. Particle Representations

We have the symmetry groups

S U (3)

and

U (1)

of the Standard Model; we now look at the action of these groups on the elements of the Minimal Left Ideals and see how they transform. Depending upon their transformations and eigenvalues we label them accordingly [2], as shown in Table 2. We look at their charges obtained by the action of the Q operator and also observe the action of

S U (3)

generators to classify them.

The

{\bar{d}}_{i}

and

u_{j}

have indices running from 1 to 3, representing the three coloured up and anti-down quarks. The Left Ideal present above gives another Left Ideal after the complex conjugation. This time it gives isospin down family. Observe that transition from one family to other can be done by the complex conjugation. Now the creation operator and the annihilation operator reverse their roles, we also get a new idempotent.

Hence we have a representation of one generation of standard model particles under the unbroken symmetry

S U {(3)}_{c} \times U {(1)}_{e m}

[2].

6. Split Bioctonions and Mass Ratios

Split Bioctonions are simply two copies of octonions in the same algebra. They can be constructed from the generators in the

C l (7)

algebra [5]

C l (7) ≅ C l (6) \oplus C l (6)

(61)

Observe that the spinor representations of

C l^{e v e n} (8)

again give us the positive and negative spinor space.

C l^{e v e n} (8) ≅ C l (7) ≅ M_{8} (C) \oplus M_{8} (C)

(62)

6.1. Construction

The seven generators of Cl(7) given as :

\{e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}, e_{7}\}

can be arranged in the manner given below; keeping in mind the non- associativity of the octonions we will use the octonionic chains [5]:-

ω = \overset{\leftarrow}{e_{1} e_{2} e_{3} e_{4} e_{5} e_{6} e_{7}}

(63)

e_{8} = \overset{\leftarrow}{e_{1} e_{2} e_{3} e_{4} e_{5} e_{6}}

(64)

(1, e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}, e_{8}) \oplus ω (1, - e_{1}, - e_{2}, - e_{3}, - e_{4}, - e_{5}, - e_{6}, - e_{8})

(65)

ω^{2} = 1

(66)

This

e_{8}

acts as an octonionic unit and

ω

as a pseudoscalar that commutes with every octonionic unit, and hence with every element of the

C l (7)

algebra. It is the analog of the split complex number which squares to one but is neither one not minus one. To generate the system with opposite parity look at an example given below:-

\overset{\leftarrow}{e_{1} e_{2} e_{4} e_{5} e_{6} e_{7}} = - \overset{\leftarrow}{e_{1} e_{2} e_{3} e_{3} e_{4} e_{5} e_{7} e_{6} e_{6}} = - \overset{\leftarrow}{e_{3} e_{1} e_{2} e_{3} e_{4} e_{5} e_{6} e_{7}} = - e_{3} ω = - ω e_{3}

(67)

C l (6)

algebra can be used to construct a left sided ideal. It is similar to an irreducible space; action (left multiplication) of various elements of algebra on the elements in ideal keeps the space of Ideal closed, similar to the working of irreducible space. The two sets of Octonions can now be used to construct ideals that represent states of opposite chirality, similar to positive and negative spinor states. By the complex conjugation of the two chiral families we can also construct the antiparticle sates. We can do so by defining the idempotents and nilpotents as earlier and do our analysis. But notice this time for the second copy of the octonions the generators have a negative sign. This helps us to introduce the chirality into the problem. From the first copy of the octonions we get the Left Handed Neutrino family and its right handed anti-particle’s family. Similarly from the second copy we can get Right Handed Neutrino family and its left handed anti-particle’s family [5].

6.2. Mass Ratios

We construct all three families from a single real octonionic family by a set of transformations. Both cases for Dirac and Majorana Neutrino have been analysed [9]. The solution of Dirac Equation in

(9, 1)

spacetime, is connected with the eigenvalue problem of the Hermitian octonionic matrices as explained in [21,22]. The eigenvalues thus calculated give us square root mass ratios of various fundamental fermions.

6.2.1. Hermitian Octonionic Matrices

The quarks have different representations for different colours. Octonions are difficult to work with, quaternions are much easier to deal with. To make the problem simpler we take the representations of neutrino and electron and choose the colour state of quarks accordingly; such that only one quaternionic copy is used for one family of the fermions. Now this complex quaternionic representation is mapped to real octonionic representation by a mapping given below [9]:-

C \otimes H ⟶ R \otimes O

(68)

(a_{0} + i a_{1}) + (a_{2} + i a_{3}) e_{4} + (a_{4} + i a_{5}) e_{5} + (a_{6} + i a_{7}) e_{7}

(69)

↓

(70)

a_{0} + a_{1} e_{1} + a_{5} e_{2} + a_{3} e_{3} + a_{2} e_{4} + a_{4} e_{5} + a_{7} e_{6} + a_{6} e_{7}

(71)

Once we have the real representation for one family, we do an internal rotation about some axis and get real octonionic representation for all the three families. We can use these representations to fill the entries in

3 \times 3

Octonionic Hermitian Matrices. The uniqueness of the axis used for transformation and similar matters are already discussed earlier[9]. It is observed that the ratios of the square root mass of the positron, the up quark and the down quark is 1 : 2 : 3. Motivated by this information we can define a new quantity as the Gravi charge. The ratio of Gravi Charges will then be:-

e^{+} : u : d = \frac{1}{3} : \frac{2}{3} : 1

(72)

The Gravi- charges can be negative also. These Gravi - Charges are then used on the diagonals of these octonionic Hermitian matrices. These

3 \times 3

Octonionic Hermitian Matrices are referred as Exceptional Jordan Matrices and they form the exceptiomal Jordan Algebra, with a specified Jordan product [23].

A o B = \frac{1}{2} (A B + B A)

(73)

We fill the entries in the matrices accordingly with the diagonals filled with the Gravi-charge.

X_{ν} = [\begin{matrix} 0 & V_{τ} & {\bar{V}}_{μ} \\ {\bar{V}}_{τ} & 0 & V_{ν} \\ V_{μ} & {\bar{V}}_{ν} & 0 \end{matrix}] X_{e} = [\begin{matrix} \frac{1}{3} & V_{\bar{τ}} & {\bar{V}}_{\bar{μ}} \\ {\bar{V}}_{\bar{τ}} & \frac{1}{3} & V_{e^{+}} \\ V_{\bar{μ}} & {\bar{V}}_{e^{+}} & \frac{1}{3} \end{matrix}]

(74)

X_{u} = [\begin{matrix} \frac{2}{3} & V_{t} & {\bar{V}}_{c} \\ {\bar{V}}_{t} & \frac{2}{3} & V_{u} \\ V_{c} & {\bar{V}}_{u} & \frac{2}{3} \end{matrix}] X_{d} = [\begin{matrix} 1 & V_{\bar{b}} & {\bar{V}}_{\bar{s}} \\ {\bar{V}}_{\bar{b}} & 1 & V_{\bar{d}} \\ V_{\bar{s}} & {\bar{V}}_{\bar{d}} & 1 \end{matrix}]

(75)

These matrices satisfy the characteristic equation given as [23] :-

A^{3} - (t r A) A^{2} + σ (A) A - (d e t A) I = 0

(76)

The definition and explanation for each quantity are presented in appendix A. The exact nature of these matrices in the context of Standard Model is still not completely understood. However some results do suggest that the

{OP}^{2}

space is crucial for our understanding of the spinors, and these spaces are closely related to these Hermitian Matrices [24]. These matrices with real octonionic entries can be further decomposed as given [21]:

A = \sum_{i}^{3} λ_{i} P_{λ_{i}}

(77)

P_{λ_{i}} o P_{λ_{j}} = 0 = \frac{1}{2} (P_{λ_{i}} P_{λ_{j}} + P_{λ_{j}} P_{λ_{i}})

(78)

\Rightarrow A o P_{λ} = λ P_{λ}

(79)

It gives us an eigenmatrix equation. These eigenvalues are used to calculate the square root masses of various fundamental fermions [9], as shown in the Figure 2 below.

6.2.2. Inclusion Of Gravity

The mass ratios of the up-quark , down-quark, and positron motivated us to extend the gauge group to

S U {(3)}_{g r a v} \times S U {(2)}_{R} \times U_{g} (1)

. This U(1) symmetry is similar to the usual

U (1)

, with Gravi-Charge as the quantity analogous to the electric charge. We can group the particles with up-isospin together as done earlier and proceed as given below:-

e^{+} : u : \bar{d} = \frac{1}{3} : \frac{2}{3} : 1

(80)

We have the following families that are expected to observe the

S U {(2)}_{R}

symmetry:-

(\begin{matrix} u \\ e^{-} \end{matrix}) (\begin{matrix} ν_{e} \\ d \end{matrix})

(81)

Notice the swapping of the down quark and electron. This structure can be extended to all three generations. Now we are working in the

C l (7)

algebra, it has two copies of the

C l (6)

algebra; one copy can be used to construct the octonionic representations of the gravitationally inactive particles that transform according to the normal standard model gauge group. The second copy of the

C l (6)

can be used to construct a new minimal left ideal for this new extension to the gauge group, which will then have the following octonionic representation for the various gravitationally active particles. The minimal left ideal and the right handed nilpotents, and the Idempotent for these spinors that are gravitationally active are then given below:-

q_{1} = \frac{- ω}{2} (- e_{5} + i e_{4}) q_{1}^{†} = \frac{- ω}{2} (e_{5} + i e_{4})

(82)

q_{2} = \frac{- ω}{2} (- e_{3} + i e_{1}) q_{2}^{†} = \frac{- ω}{2} (e_{3} + i e_{1})

(83)

q_{3} = \frac{- ω}{2} (- e_{6} + i e_{2}) q_{3}^{†} = \frac{- ω}{2} (e_{6} + i e_{2})

(84)

q_{R} = q_{1} q_{2} q_{3} q_{R}^{†} = q_{3}^{†} q_{2}^{†} q_{1}^{†}

(85)

p_{R} = q_{R} q_{R}^{†}

(86)

This helps us to generate the following particle eigenstates :-

ν_{e, R} = \frac{i e_{8} + 1}{2}

(87)

V_{e^{+} 1} = ω \frac{(- e_{5} - i e_{4})}{2}

(88)

V_{e^{+} 2} = ω \frac{(- e_{3} - i e_{1})}{2}

(89)

V_{e^{+} 3} = ω \frac{(- e_{6} - i e_{2})}{2}

(90)

V_{u_{1}} = \frac{e_{4} + i e_{5}}{2}

(91)

V_{u_{2}} = \frac{e_{1} + i e_{3}}{2}

(92)

V_{u_{3}} = \frac{e_{2} + i e_{6}}{2}

(93)

V_{\bar{d}} = ω \frac{(i + e_{8})}{2}

(94)

7. Space Of Minimal Left Ideals

The complete space related to minimal left ideals is not used in the

C l (6)

algebra. We intend to use it fully. We already have information about the square root mass ratios. We know that

p = q q^{†}

is idempotent, and

q_{i}^{†}

are the ladder operators. By using this we can construct a left ideal and by the right multiplication on this space of left ideal we can span the whole space of the Algebra [20,25].

7.1. Patterns in The Standard Model

To study the standard model the first thing to do is to introduce vector spaces (or the Hilbert space) which are later made into an algebra. The underlying complex vector space

(V, h)

establishes a natural isomorphism between vector space dual and its conjugate. h here is the inner product on the vector space. We, therefore have the following relations [20]:-

\begin{matrix} V^{- 1} ≅ V^{†} ≅ \bar{V} \end{matrix}

(95)

The Table 3 represents the vector space required to explain the appropriate symmetries [20]. The space

χ_{e m}

represents one vector that corresponds to a charge of

\frac{e}{3}

and the space

χ_{c}

represents a 3-dimensional complex vector space that have three basis vectors given as

{r, g, b}

. For the electromagnetic space the charges add up for the tensor product of such spaces, they appear as numbers in the exponential associated with the U(1) symmetry. By the above relations we then have information about the dual space or the conjugate space. We have the space

{\bar{χ}}_{e m}

which has the charge equal to

\frac{- e}{3}

; and the dual colour space which now has the vectors as

{\bar{r}, \bar{g}, \bar{b}}

. We can use our knowledge of how particles transform under various symmetry transformations and define the internal elctro-colour space for various particles as done in Table 4. This will later help us to develop isomorphisms between exterior algebra related to the internal space and the elements of the

C l (6)

algebra.

For the colour space of fermions, we can use the exterior powers of the

χ_{c}

to represent different fermions. The colour space

χ_{c}

and its dual (or conjugate)

{\bar{χ}}_{c}

have the basis as given below:-

χ_{c} = {r, g, b} {\bar{χ}}_{c} = {\bar{r}, \bar{g}, \bar{b}}

(96)

For the exterior algebra of the vectors of the colour space and its dual, we have the following relation:-

Λ^{- k} χ_{c} = Λ^{k} {\bar{χ}}_{c}

(97)

With this knowledge we have the following isomorphisms:-

Λ^{0} χ_{c} ≅ C

(98)

Λ^{1} χ_{c} ≅ χ_{c}

(99)

Λ^{2} χ_{c} ≅ {\bar{χ}}_{c} : {r \land g \to \bar{b}, g \land b \to \bar{r}, r \land b \to \bar{g}}

(100)

Λ^{3} χ_{c} ≅ C : r \land g \land b

(101)

The representations of particles in exterior algebra is given in Table 5. For the simplification of the notation define :-

χ = {\bar{χ}}_{e m} \otimes {\bar{χ}}_{c}

(102)

Note that the Hilbert space is equipped with

h = h_{e m} \otimes h_{c}

, and the space is 3 dimensional.

We choose a basis of the isotropic vectors for the newly defined space

χ

{q_{1}, q_{2}, q_{3}}

, and its dual basis for the space

\bar{χ}

{q_{1}^{†}, q_{2}^{†}, q_{3}^{†}}

. So the total Hilbert space can be seen as

χ^{†} \oplus χ

and other particles are the elements of the exterior algebra defined by this space. These vectors are the Grassmann numbers, they indeed define a basis for the exterior powers of the

χ

(wedging kind of replaced by the Clifford product).

7.2. Algebra for the Standard Model

We construct an algebra over the space

χ^{†} \oplus χ

and generate a basis of null vectors [20]. The two chiral spaces are the maximally isotropic subspaces for the inner product. So from our previous knowledge and definitions in the earlier section, we have the following:-

χ = {q_{1}, q_{2}, q_{3}} χ^{†} = {q_{1}^{†}, q_{2}^{†}, q_{3}^{†}}

(103)

{q_{i}^{†}, q_{j}^{†}} = 0 {q_{i}, q_{j}} = 0 {q_{i}, q_{j}^{†}} = δ_{i j}

(104)

q = q_{1} q_{2} q_{3} q^{†} = q_{3}^{†} q_{2}^{†} q_{1}^{†}

(105)

p = q q^{†} p^{'} = q^{†} q

(106)

Here p and

p^{'}

are the idempotents; q and

q^{†}

are the nilpotents as defined earlier. We can now define an orthonormal basis using these null vectors, by the following construction:-

χ^{†} \oplus χ = {e_{1}, e_{2}, e_{3}, {\tilde{e}}_{1}, {\tilde{e}}_{2}, {\tilde{e}}_{3}}

(107)

e_{j} = q_{j} + q_{j}^{†}

(108)

{\tilde{e}}_{j} = i (q_{j}^{†} - q_{j})

(109)

e = e_{1} e_{2} e_{3} \tilde{e} = {\tilde{e}}_{1} {\tilde{e}}_{2} {\tilde{e}}_{3}

(110)

e_{i}^{2} = {\tilde{e}}_{i}^{2} = 1

(111)

e \tilde{e} = - \tilde{e} e

(112)

Observe that we could have chosen

- {\tilde{e}}_{j}

as the orthonormal vector instead of

e_{j}

, this will change the definition of null vectors in terms of the orthonormal vectors. Here however we choose the above given definitions.

7.3. Ideals and Representations

C l^{e v e n} (7) ≅ C l (6) ≅ M_{8} (C)

(113)

We know that the

C l (7)

spinors have representations as the elements of the

C l (6)

algebra. We construct left ideals in the

C l (6)

algebra and now left multiply various elements of the

C l (6)

algebra with the elements of the left ideal; as the space is closed, the resulting space is invariant. It gives us the matrix representations of the elements of

C l (6)

. Following the earlier framework [2], we will act with the creation operators on the Idempotents to create the particles and thus get the representation of particles in the algebra. A basis of the minimal left ideal or the action of all creation operators on one idempotent can be written as [20]:-

{p, q_{23}^{†} p, q_{31}^{†} p, q_{12}^{†} p, q_{321}^{†} p, q_{1}^{†} p, q_{2}^{†} p, q_{3}^{†} p}

(114)

On the simplification of the above given basis in terms of the

q_{i}

’s we have:-

{q q^{†}, - q_{1} q^{†}, - q_{2} q^{†}, - q_{3} q^{†}, q^{†}, q_{23} q^{†}, q_{31} q^{†}, q_{12} q^{†}}

(115)

We left act on this algebraic basis using various creation and annihilation operators. It will give us the representations of the algebra as the endomorphisms on the underlying vector space. For the Algebraic ideal A, we have:-

ρ : A ⟶ ρ (A)

(116)

ρ (A) : b \in A ⟶ ρ (A) (b) \in A

(117)

ρ (A) ≅ E n d_{C} (A ≅_{v e c} C^{8})

(118)

Using the above information we have :-

[\begin{matrix} q q^{†} \\ - q_{1} q^{†} \\ - q_{2} q^{†} \\ - q_{3} q^{†} \\ q^{†} \\ q_{23} q^{†} \\ q_{31} q^{†} \\ q_{12} q^{†} \end{matrix}] \overset{q_{1}^{†}}{⟶} [\begin{matrix} 0 \\ 0 \\ - q_{1} q_{2} q^{†} \\ - q_{1} q_{3} q^{†} \\ q_{1} q^{†} \\ q q^{†} \\ 0 \\ 0 \end{matrix}]

(119)

So the action of

q_{1}^{†}

can be reprsented as :-

[\begin{matrix} 0 \\ 0 \\ - q_{1} q_{2} q^{†} \\ - q_{1} q_{3} q^{†} \\ q_{1} q^{†} \\ q q^{†} \\ 0 \\ 0 \end{matrix}] = [\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & - 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & - 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}] [\begin{matrix} q q^{†} \\ - q_{1} q^{†} \\ - q_{2} q^{†} \\ - q_{3} q^{†} \\ q^{†} \\ q_{23} q^{†} \\ q_{31} q^{†} \\ q_{12} q^{†} \end{matrix}]

(120)

Matrix reprsentation of the

q_{1}^{†}

and other null vectors is therefore given below:-

q_{1}^{†} = [\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & - i σ_{2} \\ - i σ_{2} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}] q_{2}^{†} = [\begin{matrix} 0 & 0 & 0 & σ_{3}^{-} \\ 0 & 0 & - σ_{3}^{-} & 0 \\ 0 & - σ_{3}^{+} & 0 & 0 \\ σ_{3}^{+} & 0 & 0 & 0 \end{matrix}]

(121)

q_{3}^{†} = [\begin{matrix} 0 & 0 & 0 & - σ_{-} \\ 0 & 0 & σ_{+} & 0 \\ 0 & - σ_{+} & 0 & 0 \\ σ_{-} & 0 & 0 & 0 \end{matrix}]

(122)

σ_{+} = [\begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix}] σ_{-} = [\begin{matrix} 0 & 0 \\ 1 & 0 \end{matrix}] σ_{3}^{+} = [\begin{matrix} 1 & 0 \\ 0 & 0 \end{matrix}] σ_{3}^{-} = [\begin{matrix} 0 & 0 \\ 0 & 1 \end{matrix}]

(123)

With the matrix definitions of the null vectors we have matrix representations for other defined elements as given below, the nilpotents, idempotents and the orthonormal vectors respectively.

q^{†} = [\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ σ_{3}^{+} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}] q = [\begin{matrix} 0 & 0 & σ_{3}^{+} & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}]

(124)

p = [\begin{matrix} σ_{3}^{+} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}] p^{'} = [\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & σ_{3}^{+} & 0 \\ 0 & 0 & 0 & 0 \end{matrix}]

(125)

The orthonormal vectors are given below :-

e_{1} = [\begin{matrix} 0 & 0 & i σ_{2} & 0 \\ 0 & 0 & 0 & - i σ_{2} \\ - i σ_{2} & 0 & 0 & 0 \\ 0 & i σ_{2} & 0 & 0 \end{matrix}] e_{2} = [\begin{matrix} 0 & 0 & 0 & 1_{2} \\ 0 & 0 & - 1_{2} & 0 \\ 0 & - 1_{2} & 0 & 0 \\ 1_{2} & 0 & 0 & 0 \end{matrix}]

(126)

e_{3} = [\begin{matrix} 0 & 0 & 0 & i σ_{2} \\ 0 & 0 & i σ_{2} & 0 \\ 0 & - i σ_{2} & 0 & 0 \\ - i σ_{2} & 0 & 0 & 0 \end{matrix}] {\tilde{e}}_{1} = [\begin{matrix} 0 & 0 & σ_{2} & 0 \\ 0 & 0 & 0 & σ_{2} \\ σ_{2} & 0 & 0 & 0 \\ 0 & σ_{2} & 0 & 0 \end{matrix}]

(127)

{\tilde{e}}_{2} = [\begin{matrix} 0 & 0 & 0 & - i σ_{3} \\ 0 & 0 & i σ_{3} & 0 \\ 0 & - i σ_{3} & 0 & 0 \\ i σ_{3} & 0 & 0 & 0 \end{matrix}] {\tilde{e}}_{3} = [\begin{matrix} 0 & 0 & 0 & - i σ_{1} \\ 0 & 0 & i σ_{1} & 0 \\ 0 & - i σ_{1} & 0 & 0 \\ i σ_{1} & 0 & 0 & 0 \end{matrix}]

(128)

To compute the inner product between various orthonormal vectors use the matrix multiplication :-

\vec{a} . \vec{b} = \frac{1}{2} (a b + b a)

(129)

7.3.1. SU(2) Symmetry

We will first partition this 8-dimensional space into a vector sum of two irreducible spaces of dimension 4. Then these 4 dimensional spaces have to be further decomposed into irreducible subspaces, defined to be of different chirality. To proceed, we need to define new matrix operators; for the weak isospin

\frac{1}{2}

and

- \frac{1}{2}

, we use an isospin operator (it decomposes the space into two irreducible representations).

e = [\begin{matrix} 0 & 1_{4} \\ - 1_{4} & 0 \end{matrix}] \tilde{e} = i [\begin{matrix} 0 & 1_{4} \\ 1_{4} & 0 \end{matrix}]

(130)

e \tilde{e} = i [\begin{matrix} 1_{4} & 0 \\ 0 & - 1_{4} \end{matrix}]

(131)

The

\frac{1 \pm e \tilde{e}}{2}

operator partitions the

C^{8}

space into two

C^{4}

spaces. We have the chirality operator given below :-

Γ^{5} = - i e_{1} {\tilde{e}}_{1} = [\begin{matrix} 1_{2} & 0 & 0 & 0 \\ 0 & - 1_{2} & 0 & 0 \\ 0 & 0 & - 1_{2} & 0 \\ 0 & 0 & 0 & 1_{2} \end{matrix}]

(132)

This operator can be used to define projectors on left and right chiral subspaces of two irreducible representations. Minus sign of the chirality operator represents the left chiral subspace. We need to mix the left chiral subspace of the particles for a given

S U_{L} (2)

doublet. We can define a new basis of null vectors for the excited weak iso-spin states as given below [20]:-

w_{u} = [\begin{matrix} 0 & 1_{2} & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & - 1_{2} \\ 0 & 0 & 0 & 0 \end{matrix}] w_{d} = [\begin{matrix} 0 & 0 & - 1_{2} & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & - 1_{2} \\ 0 & 0 & 0 & 0 \end{matrix}]

(133)

w_{o} = [\begin{matrix} σ_{+} & 0 & 0 & 0 \\ 0 & - σ_{+} & 0 & 0 \\ 0 & 0 & - σ_{+} & 0 \\ 0 & 0 & 0 & σ_{+} \end{matrix}]

(134)

{w_{i}, w_{j}} = 0 {w_{i}^{†}, w_{j}^{†}} = 0 {w_{i}, w_{j}^{†}} = δ_{i j}

(135)

We have the matrix representations of the various elements; we can make the following identifications:-

[\begin{matrix} p \\ w_{o}^{†} p \\ w_{u}^{†} p \\ w_{u}^{†} w_{o}^{†} p \\ w_{d}^{†} p \\ w_{d}^{†} w_{o}^{†} p \\ w_{d}^{†} w_{u}^{†} p \\ w_{d}^{†} w_{u}^{†} w_{o}^{†} p \end{matrix}] = [\begin{matrix} p \\ q_{23}^{†} p \\ q_{31}^{†} p \\ q_{12}^{†} p \\ q_{321}^{†} p \\ q_{1}^{†} p \\ q_{2}^{†} p \\ q_{3}^{†} p \end{matrix}]

(136)

w_{u}^{†}

represents the creation of left chiral subspace for an up-isospin particle from the idempotent, similarly

w_{d}^{†}

represents a creation of left chiral subspace for a down-isospin particle.

w_{d}^{†} w_{u}^{†}

represents a creation of right chiral subspace of a down-isospin particle [20]. Observe the following decomposition, due to isospin projectors and later projections due to the chirality operator.

W_{C^{j}}

represents j dimensional complex space.

W_{C^{8}} = W_{C^{4}}^{1} \oplus W_{C^{4}}^{2}

(137)

W_{C^{8}} = W_{C^{2}, R}^{1} \oplus W_{C^{2}, L}^{1} \oplus W_{C^{2}, L}^{2} \oplus W_{C^{2}, R}^{2}

(138)

= {p, w_{o}^{†} p} \oplus {w_{u}^{†} p, w_{u}^{†} w_{o}^{†} p} \oplus {w_{d}^{†} p, w_{d}^{†} w_{o}^{†} p} \oplus {w_{d}^{†} w_{u}^{†} p, w_{d}^{†} w_{u}^{†} w_{o}^{†} p}

(139)

= {p, q_{23}^{†} p} \oplus {q_{31}^{†} p, q_{12}^{†} p} \oplus {q_{321}^{†} p, q_{1}^{†} p} \oplus {q_{2}^{†} p, q_{3}^{†} p}

(140)

We now define

S U (2)

symmetry generators, these will only mix the left chiral space for both fermions.

T_{1} = \frac{1}{2} (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 1_{2} & 0 \\ 0 & 1_{2} & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}) T_{2} = \frac{- i}{2} (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & - 1_{2} & 0 \\ 0 & 1_{2} & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix})

(141)

T_{3} = \frac{1}{2} (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & - 1_{2} & 0 & 0 \\ 0 & 0 & 1_{2} & 0 \\ 0 & 0 & 0 & 0 \end{matrix})

(142)

[T_{i}, T_{j}] = i ϵ_{i j k} T_{k}

(143)

Observe that no mixing takes place for the right chiral space.

7.3.2. Complete Space of Ideals

The complete basis of the Algebra

C l (6)

in terms of the minimal left ideal can be written as given below, the initial basis is expanded via the right multiplication on that ideal.

{[\begin{matrix} p & p q_{23} & p q_{31} & p q_{12} & p q_{321} & p q_{1} & p q_{2} & p q_{3} \\ q_{23}^{†} p & q_{23}^{†} p q_{23} & q_{23}^{†} p q_{31} & q_{23}^{†} p q_{12} & q_{23}^{†} p q_{321} & q_{23}^{†} p q_{1} & q_{23}^{†} p q_{2} & q_{23}^{†} p q_{3} \\ q_{31}^{†} p & q_{31}^{†} p q_{23} & q_{31}^{†} p q_{31} & q_{31}^{†} p q_{12} & q_{31}^{†} p q_{321} & q_{31}^{†} p q_{1} & q_{31}^{†} p q_{2} & q_{31}^{†} p q_{3} \\ q_{12}^{†} p & q_{12}^{†} p q_{23} & q_{12}^{†} p q_{31} & q_{12}^{†} p q_{12} & q_{12}^{†} p q_{321} & q_{12}^{†} p q_{1} & q_{12}^{†} p q_{2} & q_{12}^{†} p q_{3} \\ q_{321}^{†} p & q_{321}^{†} p q_{23} & q_{321}^{†} p q_{31} & q_{321}^{†} p q_{12} & q_{321}^{†} p q_{321} & q_{321}^{†} p q_{1} & q_{321}^{†} p q_{2} & q_{321}^{†} p q_{3} \\ q_{1}^{†} p & q_{1}^{†} p q_{23} & q_{1}^{†} p q_{31} & q_{1}^{†} p q_{12} & q_{1}^{†} p q_{321} & q_{1}^{†} p q_{1} & q_{1}^{†} p q_{2} & q_{1}^{†} p q_{3} \\ q_{2}^{†} p & q_{2}^{†} p q_{23} & q_{2}^{†} p q_{31} & q_{2}^{†} p q_{12} & q_{2}^{†} p q_{321} & q_{2}^{†} p q_{1} & q_{2}^{†} p q_{2} & q_{2}^{†} p q_{3} \\ q_{3}^{†} p & q_{3}^{†} p q_{23} & q_{3}^{†} p q_{31} & q_{3}^{†} p q_{12} & q_{3}^{†} p q_{321} & q_{3}^{†} p q_{1} & q_{3}^{†} p q_{2} & q_{3}^{†} p q_{3} \end{matrix}]}_{8 \times 8}

(144)

Now we can identify 4-dimensional spaces using the Classifier spaces, Isospin spaces and Spinor chiral spaces with various particles [25]. We use the elements from row 1, and row 5 to assign the electric charge to the two 4-dimensional column spinors present in a column by calculating the total electric charge from the product of the creation and the annihilation operators. We identify these basis with the following particle spaces, remember that these are now complex numbers on which

M_{8} (C)

can act from the left.

{[\begin{matrix} ν_{R_{1}} & u_{R_{1}}^{r} & u_{R_{1}}^{b} & u_{R_{1}}^{g} & {\bar{e}}_{L_{1}} & {\bar{d}}_{L_{1}}^{\bar{r}} & {\bar{d}}_{L_{1}}^{\bar{b}} & {\bar{d}}_{L_{1}}^{\bar{g}} \\ ν_{R_{2}} & u_{R_{2}}^{r} & u_{R_{2}}^{b} & u_{R_{2}}^{g} & {\bar{e}}_{L_{2}} & {\bar{d}}_{L_{2}}^{\bar{r}} & {\bar{d}}_{L_{2}}^{\bar{b}} & {\bar{d}}_{L_{2}}^{\bar{g}} \\ ν_{L_{1}} & u_{L_{1}}^{r} & u_{L_{1}}^{b} & u_{L_{1}}^{g} & {\bar{e}}_{R_{1}} & {\bar{d}}_{R_{1}}^{\bar{r}} & {\bar{d}}_{R_{1}}^{\bar{b}} & {\bar{d}}_{R_{1}}^{\bar{g}} \\ ν_{L_{2}} & u_{L_{2}}^{r} & u_{L_{2}}^{b} & u_{L_{2}}^{g} & {\bar{e}}_{R_{2}} & {\bar{d}}_{R_{2}}^{\bar{r}} & {\bar{d}}_{R_{2}}^{\bar{b}} & {\bar{d}}_{R_{2}}^{\bar{g}} \\ e_{L_{1}} & d_{L_{1}}^{r} & d_{L_{1}}^{g} & d_{L_{1}}^{b} & {\bar{ν}}_{R_{1}} & {\bar{u}}_{R_{1}}^{\bar{r}} & {\bar{u}}_{R_{1}}^{\bar{b}} & {\bar{u}}_{R_{1}}^{\bar{g}} \\ e_{L_{2}} & d_{L_{2}}^{r} & d_{L_{2}}^{g} & d_{L_{2}}^{b} & {\bar{ν}}_{R_{2}} & {\bar{u}}_{R_{2}}^{\bar{r}} & {\bar{u}}_{R_{2}}^{\bar{b}} & {\bar{u}}_{R_{2}}^{\bar{g}} \\ e_{R_{1}} & d_{R_{1}}^{r} & d_{R_{1}}^{g} & d_{R_{1}}^{b} & {\bar{ν}}_{L_{1}} & {\bar{u}}_{L_{1}}^{\bar{r}} & {\bar{u}}_{L_{1}}^{\bar{b}} & {\bar{u}}_{L_{1}}^{\bar{g}} \\ e_{R_{2}} & d_{R_{2}}^{r} & d_{R_{2}}^{g} & d_{R_{2}}^{b} & {\bar{ν}}_{L_{2}} & {\bar{u}}_{L_{2}}^{\bar{r}} & {\bar{u}}_{L_{2}}^{\bar{b}} & {\bar{u}}_{L_{2}}^{\bar{g}} \end{matrix}]}_{C h a r g e}

(145)

7.3.3. Left Action on the Space of Ideals

Now we have arranged our total complex ideal space in such a manner that left multiplication will only cause transformation within an ideal. We have already shown our

S U (2)

generators and their intended action on an ideal (a

C^{8}

column, basically). It is important to notice that

C l (6) ≅ C l (4) \otimes C l (2)

, now

C l (4)

represents the Dirac Algebra and

C l (2)

represents the spin algebra. Essential transformations will basically be Lorentzian in nature and

S U (2)

transformations. Thus if we want to include spin in our analysis, we can do so by looking at the algebra

C l (4) \otimes C l (2) \otimes C l (2) ≅ C l {(4)}_{D i r a c} \otimes C l {(2)}_{I s o - s p i n} \otimes C l {(2)}_{S p i n}

and the left action of various elements of

C l (8)

algebra on the ideals of the

C l (8)

7.3.4. Right Action on the Space of Ideals

Looking at the total space of ideals, we see that a right multiplication by

M_{8} (C)

will permute the columns. It can basically change the colour space of various quarks. So here, essential transformations for us will be

S U (3)

transformations. The matrices that can do so will form one-to-one correspondence with Gell-Mann’s

S U (3)

matrices [25].

7.4. Cl(7) Algebra

We have :-

C l (7) = C \times O \oplus ω (C \times O) = C l (6) \oplus C l (6)

(146)

With the above information, we proceed for the extended gauge group

S U {(3)}_{g r a v} \times S U {(2)}_{R} \times U_{g} (1)

. With this we can define a new internal space, as done earlier for all the particles. It is done in Table 6.

As done earlier, we will again define a space

χ

as done below:-

χ ≅ {\bar{χ}}_{g e m} \otimes {\bar{χ}}_{g r a v}

(147)

The space

χ_{g e m}

assigns

- \frac{1}{3}

units of the Gravi-Charge to the particles. We again have three null basis vectors for this tensor product space. Every basis represents a Gravi Charge of

\frac{1}{3}

and each three anti-colour related to

S U {(3)}_{g r a v}

. Gravi-Charge is additive in nature and it will add up for a product of the null basis vectors. For

χ

space we denote the basis as :

{q_{i}^{†}}_{i = 1, 2, 3}

each basis vector has Gravi-Charge equal to

\frac{1}{3}

and one gravi anti-colour. We then have the total space as

χ \oplus χ^{†}

, with their basis vectors as given below:-

χ = {q_{1}^{†}, q_{2}^{†}, q_{3}^{†}} χ^{†} = {q_{1}, q_{2}, q_{3}}

(148)

With this notation, we can proceed further and classify particles according to the representations of the exterior algebra. It has been done in Table 7 and Table 8.

Now for the other copy of the

C l (6)

we can use the complex conjugated vector space and similarly,

p^{'}

as the idempotent. The new basis will then be:-

{p^{'}, q_{23} p^{'}, q_{31} p^{'}, q_{12} p^{'}, q_{321} p^{'}, q_{1} p^{'}, q_{2} p^{'}, q_{3} p^{'}}

(149)

{q^{†} q, q_{1}^{†} q, q_{2}^{†} q, q_{3}^{†} q, - q, q_{32}^{†} q, q_{13}^{†} q, q_{21}^{†} q}

(150)

Similarly, we can define the complete space of ideals as defined earlier.

{[\begin{matrix} p^{'} & p^{'} q_{32}^{†} & p^{'} q_{13}^{†} & p^{'} q_{21}^{†} & p^{'} q_{321}^{†} & p^{'} q_{1}^{†} & p^{'} q_{2}^{†} & p^{'} q_{3}^{†} \\ q_{23} p^{'} & q_{23} p^{'} q_{32}^{†} & q_{23} p^{'} q_{13}^{†} & q_{23} p^{'} q_{21}^{†} & q_{23} p^{'} q_{321}^{†} & q_{23} p^{'} q_{1}^{†} & q_{23} p^{'} q_{2}^{†} & q_{23} p^{'} q_{3}^{†} \\ q_{31} p^{'} & q_{31} p^{'} q_{32}^{†} & q_{31} p^{'} q_{13}^{†} & q_{31} p^{'} q_{21}^{†} & q_{31} p^{'} q_{321}^{†} & q_{31} p^{'} q_{1}^{†} & q_{31} p^{'} q_{2}^{†} & q_{31} p^{'} q_{3}^{†} \\ q_{12} p^{'} & q_{12} p^{'} q_{32}^{†} & q_{12} p^{'} q_{13}^{†} & q_{12} p^{'} q_{21}^{†} & q_{12} p^{'} q_{321}^{†} & q_{12} p^{'} q_{1}^{†} & q_{12} p^{'} q_{2}^{†} & q_{12} p^{'} q_{3}^{†} \\ q_{321} p^{'} & q_{321} p^{'} q_{32}^{†} & q_{321} p^{'} q_{13}^{†} & q_{321} p^{'} q_{21}^{†} & q_{321} p^{'} q_{321}^{†} & q_{321} p^{'} q_{1}^{†} & q_{321} p^{'} q_{2}^{†} & q_{321} p^{'} q_{3}^{†} \\ q_{1} p^{'} & q_{1} p^{'} q_{32}^{†} & q_{1} p^{'} q_{13}^{†} & q_{1} p^{'} q_{21}^{†} & q_{1} p^{'} q_{321}^{†} & q_{1} p^{'} q_{1}^{†} & q_{1} p^{'} q_{2}^{†} & q_{1} p^{'} q_{3}^{†} \\ q_{2} p^{'} & q_{2} p^{'} q_{32}^{†} & q_{2} p^{'} q_{13}^{†} & q_{2} p^{'} q_{21}^{†} & q_{2} p^{'} q_{321}^{†} & q_{2} p^{'} q_{1}^{†} & q_{2} p^{'} q_{2}^{†} & q_{2} p^{'} q_{3}^{†} \\ q_{3} p^{'} & q_{3} p^{'} q_{32}^{†} & q_{3} p^{'} q_{13}^{†} & q_{3} p^{'} q_{21}^{†} & q_{3} p^{'} q_{321}^{†} & q_{3} p^{'} q_{1}^{†} & q_{3} p^{'} q_{2}^{†} & q_{3} p^{'} q_{3}^{†} \end{matrix}]}_{8 \times 8}

(151)

As done earlier, we can get a matrix representation of the elements of

C l (6)

by the left action of various elements on the left ideal. We have a method to compute the

U (1)

charges using the classifier space. We have employed this method to assign electric charges to 4 dimensional column vectors and hence classify the various subspaces of the complete space of ideals as particles. We use the same method and classify particles according to the Gravi- Charges.

7.4.1. Right Adjoint Action

The right action have a similar working.

M_{8} (C)

acting from right can permute the columns and hence can cause colour changes for coloured particles. We have similar matrices for such transformation as we defined earlier for

S U (3)

. Here too, we can do the same for

S U {(3)}_{g r a v}

, the gravi-colour symmetry.

7.4.2. Left Adjoint Action

For the left action of the elements of the algebra, the space of ideals is closed. This gives us the matrix representations of the algebraic elements. But now we want our spinors such that they are

S U {(2)}_{R}

active, it means that their right chiral space mixes due to

S U {(2)}_{R}

. We can define a new basis of gravi weak isospin null vectors and similarly a set of

S U (2)

generators.

{\bar{ω}}_{u} = [\begin{matrix} 0 & - 1_{2} & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1_{2} \\ 0 & 0 & 0 & 0 \end{matrix}] {\bar{ω}}_{d} = [\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ - 1_{2} & 0 & 0 & 0 \\ 0 & - 1_{2} & 0 & 0 \end{matrix}]

(152)

{\bar{ω}}_{o} = - [\begin{matrix} σ_{+} & 0 & 0 & 0 \\ 0 & - σ_{+} & 0 & 0 \\ 0 & 0 & - σ_{+} & 0 \\ 0 & 0 & 0 & σ_{+} \end{matrix}]

(153)

{{\bar{w}}_{i}, {\bar{w}}_{j}} = 0 {{\bar{w}}_{i}^{†}, {\bar{w}}_{j}^{†}} = 0 {{\bar{w}}_{i}, {\bar{w}}_{j}^{†}} = δ_{i j}

(154)

\begin{matrix} [\begin{matrix} p^{'} \\ q_{23} p^{'} \\ q_{31} p^{'} \\ q_{12} p^{'} \\ q_{321} p^{'} \\ q_{1} p^{'} \\ q_{2} p^{'} \\ q_{3} p^{'} \end{matrix}] ⟶ [\begin{matrix} p^{'} \\ {\bar{ω}}_{o}^{†} p^{'} \\ {\bar{ω_{u}}}^{†} p^{'} \\ {\bar{ω_{u}}}^{†} {\bar{ω_{o}}}^{†} p^{'} \\ {\bar{ω_{d}}}^{†} p^{'} \\ {\bar{ω_{d}}}^{†} {\bar{ω_{o}}}^{†} p^{'} \\ {\bar{ω}}_{d}^{†} {\bar{ω}}_{u}^{†} p^{'} \\ {\bar{ω}}_{d}^{†} {\bar{ω}}_{u}^{†} {\bar{ω}}_{o}^{†} p^{'} \end{matrix}] ⟶ [\begin{matrix} W_{1 R} \\ W_{1 L} \\ W_{2 L} \\ W_{2 R} \end{matrix}] \end{matrix}

(155)

Interpret these new null vectors as follows:

{\bar{ω}}_{u}^{†}

as the creation operator of left chiral subspace of the gravi weak up isospin particle,

{\bar{ω}}_{d}^{†}

as the creation operator to generate the left chiral subspace of the gravi weak down isospin particle. Similarly,

{\bar{ω}}_{d}^{†} {\bar{ω}}_{u}^{†}

generates the right chiral subspace for gravi weak down isospin particle. With these definitions for null basis we can define an orthonormal basis too, as defined earlier.

\bar{u_{j}} = {\bar{ω}}_{j} + {\bar{ω}}_{j}^{†}

(156)

\bar{u_{j}^{'}} = i ({\bar{ω}}_{j}^{†} - {\bar{ω}}_{j})

(157)

We have the following set of orthonormal vectors:-

{{\bar{u}}_{u}, {\bar{u}}_{d}, {\bar{u}}_{o}, {\bar{u^{'}}}_{u}, {\bar{u^{'}}}_{d}, {\bar{u^{'}}}_{o}}

(158)

We now check the action of the SU(2) operator constructed from the

{\bar{u}}_{i}

and

{\bar{u}}_{i}^{'}

. Define the new SU(2) generators as the following:-

\begin{matrix} {\bar{T}}_{1} = \frac{1}{2} [\begin{matrix} 0 & 0 & 0 & 1_{2} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1_{2} & 0 & 0 & 0 \end{matrix}] {\bar{T}}_{2} = \frac{- i}{2} [\begin{matrix} 0 & 0 & 0 & 1_{2} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ - 1_{2} & 0 & 0 & 0 \end{matrix}] \end{matrix}

(159)

{\bar{T}}_{3} = \frac{1}{2} [\begin{matrix} 1_{2} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & - 1_{2} \end{matrix}]

(160)

[{\bar{T}}_{i}, {\bar{T}}_{j}] = i ϵ_{i j k} {\bar{T}}_{k}

(161)

Look carefully; it does not mix the left chiral components of the spinors from the two irreducible representations of different chirality. Hence it gives us the gravitationally active right chiral spinors.

7.4.3. Particle Identification

Now we can proceed further and identify the various particles in the new complete space of ideals.

\begin{matrix} {[\begin{matrix} ν_{R_{1}} & u_{R_{1}}^{r} & u_{R_{1}}^{b} & u_{R_{1}}^{g} & {\bar{d}}_{L_{1}} & {\bar{e}}_{L_{1}}^{\bar{r}} & {\bar{e}}_{L_{1}}^{\bar{b}} & {\bar{e}}_{L_{1}}^{\bar{g}} \\ ν_{R_{2}} & u_{R_{2}}^{r} & u_{R_{2}}^{b} & u_{R_{2}}^{g} & {\bar{d}}_{L_{2}} & {\bar{e}}_{L_{2}}^{\bar{r}} & {\bar{e}}_{L_{2}}^{\bar{b}} & {\bar{e}}_{L_{2}}^{\bar{g}} \\ ν_{L_{1}} & u_{L_{1}}^{r} & u_{L_{1}}^{b} & u_{L_{1}}^{g} & {\bar{d}}_{R_{1}} & {\bar{e}}_{R_{1}}^{\bar{r}} & {\bar{e}}_{R_{1}}^{\bar{b}} & {\bar{e}}_{R_{1}}^{\bar{g}} \\ ν_{L_{2}} & u_{L_{2}}^{r} & u_{L_{2}}^{b} & u_{L_{2}}^{g} & {\bar{d}}_{R_{2}} & {\bar{e}}_{R_{2}}^{\bar{r}} & {\bar{e}}_{R_{2}}^{\bar{b}} & {\bar{e}}_{R_{2}}^{\bar{g}} \\ d_{L_{1}} & e_{L_{1}}^{r} & e_{L_{1}}^{g} & e_{L_{1}}^{b} & {\bar{ν}}_{R_{1}} & {\bar{u}}_{R_{1}}^{\bar{r}} & {\bar{u}}_{R_{1}}^{\bar{b}} & {\bar{u}}_{R_{1}}^{\bar{g}} \\ d_{L_{2}} & e_{L_{2}}^{r} & e_{L_{2}}^{g} & e_{L_{2}}^{b} & {\bar{ν}}_{R_{2}} & {\bar{u}}_{R_{2}}^{\bar{r}} & {\bar{u}}_{R_{2}}^{\bar{b}} & {\bar{u}}_{R_{2}}^{\bar{g}} \\ d_{R_{1}} & e_{R_{1}}^{r} & e_{R_{1}}^{g} & e_{R_{1}}^{b} & {\bar{ν}}_{L_{1}} & {\bar{u}}_{L_{1}}^{\bar{r}} & {\bar{u}}_{L_{1}}^{\bar{b}} & {\bar{u}}_{L_{1}}^{\bar{g}} \\ d_{R_{2}} & e_{R_{2}}^{r} & e_{R_{2}}^{g} & e_{R_{2}}^{b} & {\bar{ν}}_{L_{2}} & {\bar{u}}_{L_{2}}^{\bar{r}} & {\bar{u}}_{L_{2}}^{\bar{b}} & {\bar{u}}_{L_{2}}^{\bar{g}} \end{matrix}]}_{M a s s} \end{matrix}

(162)

This has been done using the classifier space, weak force generators and

S U (3)

operations. This will give us the following gravi-weak isospin doublets

S U {(2)}_{R}

as given below.

First generation

\begin{matrix} {(\begin{matrix} u \\ e^{-} \end{matrix})}_{R} {(\begin{matrix} ν \\ d \end{matrix})}_{R} \end{matrix}

(163)

Second Generation

\begin{matrix} {(\begin{matrix} t \\ μ^{-} \end{matrix})}_{R} {(\begin{matrix} ν_{μ} \\ b \end{matrix})}_{R} \end{matrix}

(164)

Third Generation

\begin{matrix} {(\begin{matrix} c \\ τ^{-} \end{matrix})}_{R} {(\begin{matrix} ν_{τ} \\ s \end{matrix})}_{R} \end{matrix}

(165)

7.5. Triality and Cl(8) Algebra

The basic reason to look into the

C l (8)

algebra is to use the Triality mapping. Triality mapping is, generally a very interesting object to study. Some authors have pointed towards its importance in studying three generations [2,16].

C l^{e v e n} (8) ≅ C l (7) ≅ M_{8} (C) \oplus M_{8} (C)

(166)

As explained earlier,

M_{8} (C) \oplus M_{8} (C)

acts on a spinor space

S_{8}^{+} \oplus S_{8}^{-}

. Both

S_{8}^{+}

and

S_{8}^{-}

are 8-dimensional complex spinor spaces. The eight generators of the

C l (8)

algebra give us the vector representation denoted by

V_{8}

. These can be considered as the basis vectors of the underlying vector space. Triality denoted by

t_{8}

is defined as the following mapping [16]:-

t_{8} : S_{8}^{+} \times S_{8}^{-} \times V_{8} ⟶ C

(167)

So it basically takes three complex vector spaces and gives us a number as an output. Now focus on the space of the ideals for the

C l (8)

algebra. We have earlier seen that even subalgebra of

C l (8)

is same as

C l (7)

and we know that

C l (7) ≅ C l (6) \oplus C l (6)

, so the subspace - the even subalgebra of

C l (8)

is the same as the direct sum of the left ideal space of the two copies of

C l (6)

7.5.1. Space of Ideals in Cl(8)

We require an 8-dimensional null basis to get the complete maximally totally isotropic subspace of the null vectors. To the 6-dimensional vector space of

χ \oplus χ^{†}

add a two-dimensional space S, for the two spin vectors. Our final underlying space will then be

χ \oplus χ^{†} \oplus S

. To describe this new space, we also add

{q_{4}, q_{4}^{†}}

to the pre-existing set of null vectors. Now any element in ideal will be a product from these 8 vectors, then we have [25]:-

C l (8) ≅ C l (4) \otimes C l (2) \otimes C l (2) ≅ C l {(4)}_{D i r a c} \otimes C l {(2)}_{I s o - s p i n} \otimes C l {(2)}_{S p i n}

(168)

{q_{1}, q_{2}, q_{3}, q_{4}, q_{1}^{†}, q_{2}^{†}, q_{3}^{†}, q_{4}^{†}}

(169)

q = q_{1} q_{2} q_{3} q_{4} q^{†} = q_{4}^{†} q_{3}^{†} q_{2}^{†} q_{1}^{†}

(170)

p = q q^{†} p^{'} = q^{†} q

(171)

Here q and

q^{†}

are the nilpotents, the p and

p^{'}

are the idempotents. We use p as the idempotent; from our previous information we know the importance of

C l^{e v e n} (8)

, so we can write the

C l^{e v e n} (8)

ideal subspace as [25]:-

C l (8) = [\begin{matrix} E v e n_{1} & O d d \\ O d d & E v e n_{2} \end{matrix}] \Rightarrow C l^{e v e n} (8) = [\begin{matrix} E v e n_{1} & 0 \\ 0 & E v e n_{2} \end{matrix}]

(172)

The

E v e n_{1}

part of the complete space of the ideal of

C l (8)

is given below:-

[\begin{matrix} p & p q_{32} & p q_{13} & p q_{21} & p q_{4321} & p q_{41} & p q_{42} & p q_{43} \\ q_{23}^{†} p & q_{23}^{†} p q_{32} & q_{23}^{†} p q_{13} & q_{23}^{†} p q_{21} & q_{23}^{†} p q_{4321} & q_{23}^{†} p q_{41} & q_{23}^{†} p q_{42} & q_{23}^{†} p q_{43} \\ q_{31}^{†} p & q_{31}^{†} p q_{32} & q_{31}^{†} p q_{13} & q_{31}^{†} p q_{21} & q_{31}^{†} p q_{4321} & q_{31}^{†} p q_{41} & q_{31}^{†} p q_{42} & q_{31}^{†} p q_{43} \\ q_{12}^{†} p & q_{12}^{†} p q_{32} & q_{12}^{†} p q_{13} & q_{12}^{†} p q_{21} & q_{12}^{†} p q_{4321} & q_{12}^{†} p q_{41} & q_{12}^{†} p q_{42} & q_{12}^{†} p q_{43} \\ q_{1234}^{†} p & q_{1234}^{†} p q_{32} & q_{1234}^{†} p q_{13} & q_{1234}^{†} p q_{21} & q_{1234}^{†} p q_{4321} & q_{1234}^{†} p q_{41} & q_{1234}^{†} p q_{42} & q_{1234}^{†} p q_{43} \\ q_{14}^{†} p & q_{14}^{†} p q_{32} & q_{14}^{†} p q_{13} & q_{14}^{†} p q_{21} & q_{14}^{†} p q_{4321} & q_{14}^{†} p q_{41} & q_{14}^{†} p q_{42} & q_{14}^{†} p q_{43} \\ q_{24}^{†} p & q_{24}^{†} p q_{32} & q_{24}^{†} p q_{13} & q_{24}^{†} p q_{21} & q_{24}^{†} p q_{4321} & q_{24}^{†} p q_{41} & q_{24}^{†} p q_{42} & q_{24}^{†} p q_{43} \\ q_{34}^{†} p & q_{34}^{†} p q_{32} & q_{34}^{†} p q_{13} & q_{34}^{†} p q_{21} & q_{34}^{†} p q_{4321} & q_{34}^{†} p q_{41} & q_{34}^{†} p q_{42} & q_{34}^{†} p q_{43} \end{matrix}]

(173)

The

E v e n_{2}

part of the complete space of the ideal of

C l (8)

is given below:-

[\begin{matrix} q_{4}^{†} p q_{4} & q_{4}^{†} p q_{432} & q_{4}^{†} p q_{413} & q_{4}^{†} p q_{421} & q_{4}^{†} p q_{321} & q_{4}^{†} p q_{1} & q_{4}^{†} p q_{2} & q_{4}^{†} p q_{3} \\ q_{234}^{†} p q_{4} & q_{234}^{†} p q_{432} & q_{234}^{†} p q_{413} & q_{234}^{†} p q_{421} & q_{234}^{†} p q_{321} & q_{234}^{†} p q_{1} & q_{234}^{†} p q_{2} & q_{234}^{†} p q_{3} \\ q_{314}^{†} p q_{4} & q_{314}^{†} p q_{432} & q_{314}^{†} p q_{413} & q_{314}^{†} p q_{421} & q_{314}^{†} p q_{321} & q_{314}^{†} p q_{1} & q_{314}^{†} p q_{2} & q_{314}^{†} p q_{3} \\ q_{124}^{†} p q_{4} & q_{124}^{†} p q_{432} & q_{124}^{†} p q_{413} & q_{124}^{†} p q_{421} & q_{124}^{†} p q_{321} & q_{124}^{†} p q_{1} & q_{124}^{†} p q_{2} & q_{124}^{†} p q_{3} \\ q_{123}^{†} p q_{4} & q_{123}^{†} p q_{432} & q_{123}^{†} p q_{413} & q_{123}^{†} p q_{421} & q_{123}^{†} p q_{321} & q_{123}^{†} p q_{1} & q_{123}^{†} p q_{2} & q_{123}^{†} p q_{3} \\ q_{1}^{†} p q_{4} & q_{1}^{†} p q_{432} & q_{1}^{†} p q_{413} & q_{1}^{†} p q_{421} & q_{1}^{†} p q_{321} & q_{1}^{†} p q_{1} & q_{1}^{†} p q_{2} & q_{1}^{†} p q_{3} \\ q_{2}^{†} p q_{4} & q_{2}^{†} p q_{432} & q_{2}^{†} p q_{413} & q_{2}^{†} p q_{421} & q_{2}^{†} p q_{321} & q_{2}^{†} p q_{1} & q_{2}^{†} p q_{2} & q_{2}^{†} p q_{3} \\ q_{3}^{†} p q_{4} & q_{3}^{†} p q_{432} & q_{3}^{†} p q_{413} & q_{3}^{†} p q_{421} & q_{3}^{†} p q_{321} & q_{3}^{†} p q_{1} & q_{3}^{†} p q_{2} & q_{3}^{†} p q_{3} \end{matrix}]

(174)

We know that there is a volume element in

C l (7)

algebra that can partition the algebra into two parts. Here the

C l^{e v e n} (8)

gets partitioned into two parts depending upon whether the element is self-dual or not. So by this, we can assign different spins to both the even parts. Let us assign spin up to

E v e n_{1}

and spin down to

E v e n_{2}

part of the

C l^{e v e n} (8)

. By our previous arguments, we know that a correspondence can be established between each even part of the

C l (8)

algebra and two copies of

C l (6)

, so we can identify a given subspace of even subalgebra by particles from one generation with two different definite spins. Let us make some identifications; for example, for the

S U {(2)}_{L}

active particles we can identify the

E v e n_{1}

part as :-

A^{↑} = {[\begin{matrix} ν_{R_{1}}^{↑} & u_{R_{1}}^{r ↑} & u_{R_{1}}^{b ↑} & u_{R_{1}}^{g ↑} & {\bar{e}}_{L_{1}}^{↑} & {\bar{d}}_{L_{1}}^{\bar{r} ↑} & {\bar{d}}_{L_{1}}^{\bar{b} ↑} & {\bar{d}}_{L_{1}}^{\bar{g} ↑} \\ ν_{R_{2}}^{↑} & u_{R_{2}}^{r ↑} & u_{R_{2}}^{b ↑} & u_{R_{2}}^{g ↑} & {\bar{e}}_{L_{2}}^{↑} & {\bar{d}}_{L_{2}}^{\bar{r} ↑} & {\bar{d}}_{L_{2}}^{\bar{b} ↑} & {\bar{d}}_{L_{2}}^{\bar{g} ↑} \\ ν_{L_{1}}^{↑} & u_{L_{1}}^{r ↑} & u_{L_{1}}^{b ↑} & u_{L_{1}}^{g ↑} & {\bar{e}}_{R_{1}}^{↑} & {\bar{d}}_{R_{1}}^{\bar{r} ↑} & {\bar{d}}_{R_{1}}^{\bar{b} ↑} & {\bar{d}}_{R_{1}}^{\bar{g} ↑} \\ ν_{L_{2}}^{↑} & u_{L_{2}}^{r ↑} & u_{L_{2}}^{b ↑} & u_{L_{2}}^{g ↑} & {\bar{e}}_{R_{2}}^{↑} & {\bar{d}}_{R_{2}}^{\bar{r} ↑} & {\bar{d}}_{R_{2}}^{\bar{b} ↑} & {\bar{d}}_{R_{2}}^{\bar{g} ↑} \\ e_{L_{1}}^{↑} & d_{L_{1}}^{r ↑} & d_{L_{1}}^{g ↑} & d_{L_{1}}^{b ↑} & {\bar{ν}}_{R_{1}}^{↑} & {\bar{u}}_{R_{1}}^{\bar{r} ↑} & {\bar{u}}_{R_{1}}^{\bar{b} ↑} & {\bar{u}}_{R_{1}}^{\bar{g} ↑} \\ e_{L_{2}}^{↑} & d_{L_{2}}^{r ↑} & d_{L_{2}}^{g ↑} & d_{L_{2}}^{b ↑} & {\bar{ν}}_{R_{2}}^{↑} & {\bar{u}}_{R_{2}}^{\bar{r} ↑} & {\bar{u}}_{R_{2}}^{\bar{b} ↑} & {\bar{u}}_{R_{2}}^{\bar{g} ↑} \\ e_{R_{1}}^{↑} & d_{R_{1}}^{r ↑} & d_{R_{1}}^{g ↑} & d_{R_{1}}^{b ↑} & {\bar{ν}}_{L_{1}}^{↑} & {\bar{u}}_{L_{1}}^{\bar{r} ↑} & {\bar{u}}_{L_{1}}^{\bar{b} ↑} & {\bar{u}}_{L_{1}}^{\bar{g} ↑} \\ e_{R_{2}}^{↑} & d_{R_{2}}^{r ↑} & d_{R_{2}}^{g ↑} & d_{R_{2}}^{b ↑} & {\bar{ν}}_{L_{2}}^{↑} & {\bar{u}}_{L_{2}}^{\bar{r} ↑} & {\bar{u}}_{L_{2}}^{\bar{b} ↑} & {\bar{u}}_{L_{2}}^{\bar{g} ↑} \end{matrix}]}_{C h a r g e}

(175)

Similarly, the

E v e n_{2}

part can be identified by the second generation

S U {(2)}_{L}

particle eigenstates. We replace the particles with the corresponding second generation particles.

{ν, \bar{ν}} ⟶ {ν_{μ}, {\bar{ν}}_{μ}}

(176)

{e, \bar{e}} ⟶ {μ, \bar{μ}}

(177)

{u, d} ⟶ {c, s}

(178)

{\bar{u}, \bar{d}} ⟶ {\bar{c}, \bar{s}}

(179)

However, this family will have opposite sign of spin, let us denote the second generation

S U {(2)}_{L}

active family with down spin as

B^{↓}

. Similarly, third generation family with up spin can be represented as

C^{↑}

. So the total

S U {(2)}_{L}

active vector spaces

(C^{8} \times C^{8})

with different spins available to us can be listed below as following:-

{A^{↑}, A^{↓}, B^{↑}, B^{↓}, C^{↑}, C^{↓}}

(180)

Now observe the following:-

C l (9) = C l (7) \otimes C l (2) = (C \times O \oplus ω (C \times O)) \otimes C l (2) = C l (8) \oplus C l (8)

(181)

Now we can use one copy of

C l (8)

to construct the representations for left active

S U {(2)}_{L}

particles. The other copy of

C l (8)

can be used to construct the right active

S U {(2)}_{R}

particles. Both copies will give us the spin up and spin down particles. For

S U {(2)}_{R}

active particles we can use the complexified space of ideals and use the

p^{'}

as idempotent. We do the similar procedure, now again the

C l^{e v e n} (8)

algebra will get partitioned into two subalgebras denoting different spins. An example of particle identification of different gravi-charges and

S U {(2)}_{R}

active first generation is present below:-

\begin{matrix} P^{↑} = {[\begin{matrix} ν_{R_{1}}^{↑} & u_{R_{1}}^{r ↑} & u_{R_{1}}^{b ↑} & u_{R_{1}}^{g ↑} & {\bar{d}}_{L_{1}} & {\bar{e}}_{L_{1}}^{\bar{r ↑}} & {\bar{e}}_{L_{1}}^{\bar{b} ↑} & {\bar{e}}_{L_{1}}^{\bar{g} ↑} \\ ν_{R_{2}}^{↑} & u_{R_{2}}^{r ↑} & u_{R_{2}}^{b ↑} & u_{R_{2}}^{g ↑} & {\bar{d}}_{L_{2}}^{↑} & {\bar{e}}_{L_{2}}^{\bar{r} ↑} & {\bar{e}}_{L_{2}}^{\bar{b} ↑} & {\bar{e}}_{L_{2}}^{\bar{g} ↑} \\ ν_{L_{1}}^{↑} & u_{L_{1}}^{r ↑} & u_{L_{1}}^{b ↑} & u_{L_{1}}^{g ↑} & {\bar{d}}_{R_{1}}^{↑} & {\bar{e}}_{R_{1}}^{\bar{r} ↑} & {\bar{e}}_{R_{1}}^{\bar{b} ↑} & {\bar{e}}_{R_{1}}^{\bar{g} ↑} \\ ν_{L_{2}}^{↑} & u_{L_{2}}^{r ↑} & u_{L_{2}}^{b ↑} & u_{L_{2}}^{g ↑} & {\bar{d}}_{R_{2}}^{↑} & {\bar{e}}_{R_{2}}^{\bar{r} ↑} & {\bar{e}}_{R_{2}}^{\bar{b} ↑} & {\bar{e}}_{R_{2}}^{\bar{g} ↑} \\ d_{L_{1}}^{↑} & e_{L_{1}}^{r ↑} & e_{L_{1}}^{g ↑} & e_{L_{1}}^{b ↑} & {\bar{ν}}_{R_{1}}^{↑} & {\bar{u}}_{R_{1}}^{\bar{r} ↑} & {\bar{u}}_{R_{1}}^{\bar{b} ↑} & {\bar{u}}_{R_{1}}^{\bar{g} ↑} \\ d_{L_{2}}^{↑} & e_{L_{2}}^{r ↑} & e_{L_{2}}^{g ↑} & e_{L_{2}}^{b ↑} & {\bar{ν}}_{R_{2}}^{↑} & {\bar{u}}_{R_{2}}^{\bar{r} ↑} & {\bar{u}}_{R_{2}}^{\bar{b} ↑} & {\bar{u}}_{R_{2}}^{\bar{g} ↑} \\ d_{R_{1}}^{↑} & e_{R_{1}}^{r ↑} & e_{R_{1}}^{g ↑} & e_{R_{1}}^{b ↑} & {\bar{ν}}_{L_{1}}^{↑} & {\bar{u}}_{L_{1}}^{\bar{r} ↑} & {\bar{u}}_{L_{1}}^{\bar{b} ↑} & {\bar{u}}_{L_{1}}^{\bar{g} ↑} \\ d_{R_{2}}^{↑} & e_{R_{2}}^{r ↑} & e_{R_{2}}^{g ↑} & e_{R_{2}}^{b ↑} & {\bar{ν}}_{L_{2}}^{↑} & {\bar{u}}_{L_{2}}^{\bar{r} ↑} & {\bar{u}}_{L_{2}}^{\bar{b} ↑} & {\bar{u}}_{L_{2}}^{\bar{g} ↑} \end{matrix}]}_{M a s s} \end{matrix}

(182)

Similarly, the second family will be represented by Q and the third family by R, both present as spin up and spin down. The three mass families with different spins that transform according to

S U {(3)}_{g r a v} \times S U {(2)}_{R} \times U {(1)}_{g}

can be represented as:-

{P^{↑}, P^{↓}, Q^{↑}, Q^{↓}, R^{↑}, R^{↓}}

(183)

7.5.2. Triality Operator

The action of the triality operator on

C l (8)

representations [16,20,26] can be seen as:-

T r i a l : {V_{8}, S_{8}^{+}, S_{8}^{-}} ⟶ {S_{8}^{+}, S_{8}^{-}, V_{8}}

(184)

T r i a l : (\begin{matrix} A^{↑} & 0 \\ 0 & B^{↓} \end{matrix}) = (\begin{matrix} C^{↑} & 0 \\ 0 & A^{↓} \end{matrix})

(185)

where

{A, B, C}

represents the usual

S U {(2)}_{L}

active generations. Now look at the

C l (9)

algebra. It gives us the spin up and spin down for both flavour as well as mass eigenstates; one that transforms according to

S U {(2)}_{L}

and the other transforms according to

S U {(2)}_{R}

. If

{P, Q, R}

are the three generations that transform according to

S U {(2)}_{R}

, then total space for us is:-

\begin{matrix} (\begin{matrix} A^{↑} \oplus A^{↓} \\ B^{↑} \oplus B^{↓} \\ C^{↑} \oplus C^{↓} \end{matrix}) \oplus (\begin{matrix} P^{↑} \oplus P^{↓} \\ Q^{↑} \oplus Q^{↓} \\ R^{↑} \oplus R^{↓} \end{matrix}) \end{matrix}

(186)

O = 1 \otimes T r i a l

(187)

Now if we operate the operator O on our total space, we can group various mass and flavour families in a given

C l (9)

algebra by permuting the rows. This gives us a theoretical framework to construct the CKM matrix.

8. CKM Matrix Parameters

Let us focus our attention on one generation that transforms according to

S U {(3)}_{g r a v} \times S U {(2)}_{R} \times U {(1)}_{g}

. Here we have eight mass eigenstates or the particles in one generation, considering the two particles that transform according to

S U {(3)}_{g r a v}

. Here we develop some isomorphisms to make further progress. As we already had octonionic representations of various particles, and quaternionic representations of particles from one generation; it was natural to proceed with them. However, those methods did not yield any significant progress, which forced us to adopt the method given below.

8.1. Gravi-Charge Operator

We can develop an isomorphism from the space of representations (space of ideals) of one generation of mass eigenstates to a 8-dimensional complex vector space. For some definite spin, suppressing the spin, we can write the above argument of isomorphism for all the particles for three generations as given below:-

{P, Q, R} ⟶ C^{8} \oplus C^{8} \oplus C^{8}

(188)

We can now act on this space of

C^{8} \oplus C^{8} \oplus C^{8}

with an operator G- the Gravi - Charge Operator, to assign the gravi charges to various particles.

G = M_{8} (C) \oplus M_{8} (C) \oplus M_{8} (C)

(189)

M_{8} (C) = [\begin{matrix} g_{1} & 0 & 0 & 0 & 0 \\ 0 & g_{2} & 0 & 0 & 0 \\ 0 & 0 & g_{3} & 0 & 0 \\ 0 & 0 & 0 & g_{4} & 0 \\ 0 & 0 & 0 & 0 & - - \end{matrix}]

(190)

This matrix

M_{8} (C)

will be used three times for three mass families. So the Gravi-charge operator only has diagonal entries. It acts on linear column vectors that are

S U {(2)}_{R}

mass eigenstates and assign them a gravi charge.

8.2. Mass and Gravi-Charge

Now before moving further, we make some assumptions:-

Mass is a derived quantity. Gravi-charge is more fundamental.
The mass operator will be constructed from the Gravi-charge Operator, and the gravi-charge eigenvectors are weighed accordingly by the value of the square root of the mass of respective particles to make them massive eigenvectors.

8.3. Left Handed Quarks

We now look only at a part of the operator G and its action on down, charm and strange quarks, and similarly, the action on up, charm and top quarks. The operator G can be reduced to a small matrix representation as given below:-

G = (\begin{matrix} g & 0 & 0 \\ 0 & g & 0 \\ 0 & 0 & g \end{matrix})

(191)

It acts on

S U {(2)}_{R}

active mass eigenstates and gives the gravi-charges.

{u, c, t} \in C^{3}

(192)

{d, s, b} \in C^{3}

(193)

Observe that

C^{3}

vector space is needed for both families of quarks.

Figure 3. Basis vectors of reduced vector space

C^{3}

act as

S U {(2)}_{R}

active quarks. The space is used for

S U {(2)}_{L}

active quarks.

Figure 3. Basis vectors of reduced vector space

C^{3}

act as

S U {(2)}_{R}

active quarks. The space is used for

S U {(2)}_{L}

active quarks.

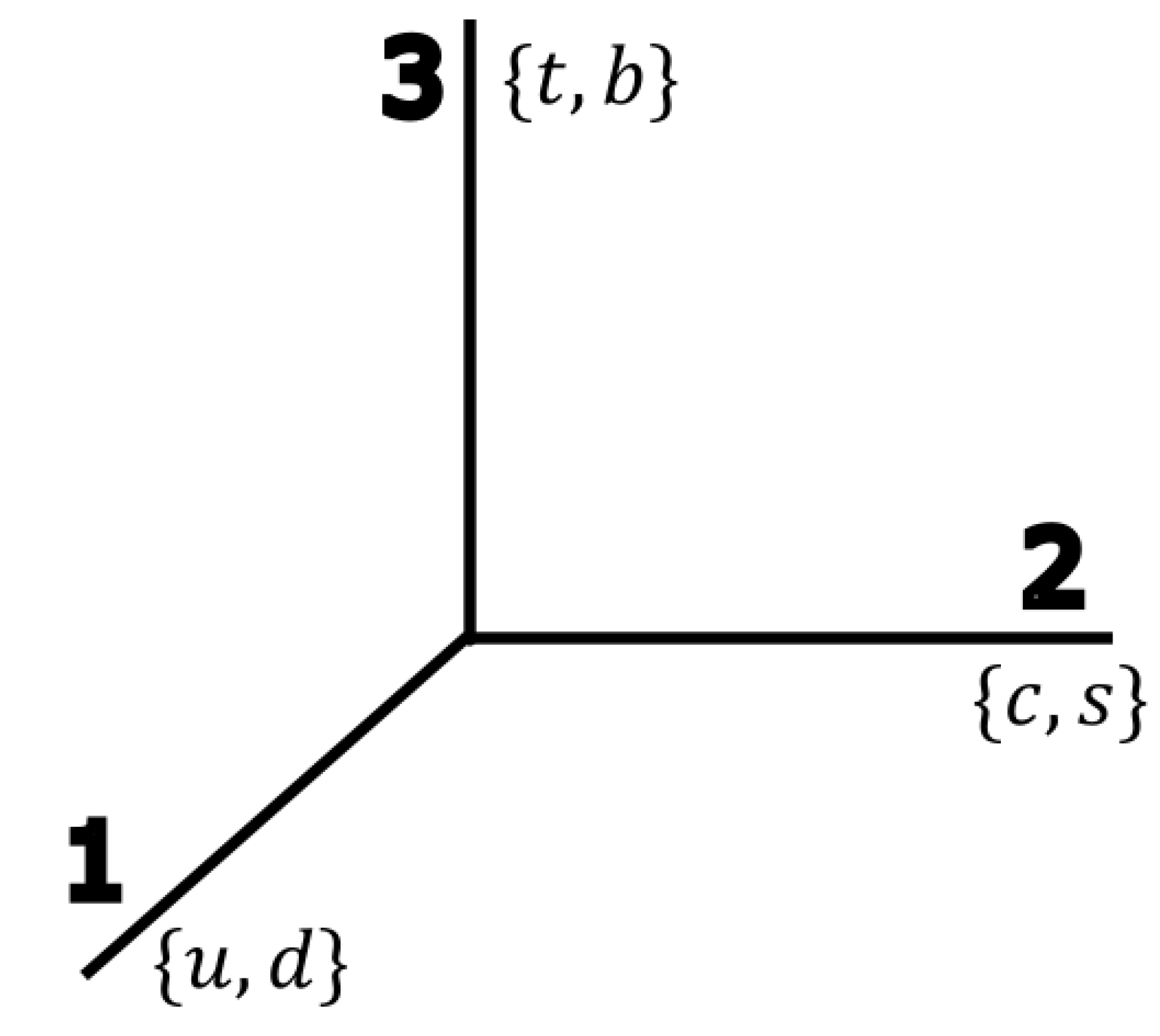
We will use this later, when one axis will represent one quark from the up isospin family and one from the down isospin family. This is done to observe the transformation between quark states. The right handed up quarks (eigenstates of the gravi charge operators) are given by:-

u_{g, R} = (\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}) c_{g, R} = (\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}) t_{g, R} = (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})

(194)

We can define massive quark vectors as :-

u_{m, R} = (\begin{matrix} \sqrt{m_{u}} \\ 0 \\ 0 \end{matrix}) c_{m, R} = (\begin{matrix} 0 \\ \sqrt{m_{c}} \\ 0 \end{matrix}) t_{m, R} = (\begin{matrix} 0 \\ 0 \\ \sqrt{m_{t}} \end{matrix})

(195)

Now in nature, we see a left handed quark, an

S U {(2)}_{L}

active left handed quark vector is present. We propose that it is a linear combination of massive quark vectors. So a normalised left handed vector can be represented by :

e_{q}^{'} = \frac{1}{\sqrt{m_{u} + α^{2} m_{c} + β^{2} m_{t}}} (\begin{matrix} \sqrt{m_{u}} \\ α \sqrt{m_{c}} \\ β \sqrt{m_{t}} \end{matrix})

(196)

By varying

α

and

β

, we can change the contribution of various massive vectors to the given

S U {(2)}_{L}

active left handed quark vector. The same can be done for the down-quark family. However, it should be kept in mind that only the integer linear combination of massive quark vectors can be done.

8.4. CKM Matrix

Now observe these two left handed vectors:-

e_{1}^{'} = \frac{1}{\sqrt{m_{u} + α^{2} m_{c} + β^{2} m_{t}}} (\begin{matrix} \sqrt{m_{u}} \\ α \sqrt{m_{c}} \\ β \sqrt{m_{t}} \end{matrix})

(197)

e_{2}^{'} = \frac{1}{\sqrt{m_{d} + a^{2} m_{s} + b^{2} m_{b}}} (\begin{matrix} \sqrt{m_{d}} \\ a \sqrt{m_{s}} \\ b \sqrt{m_{b}} \end{matrix})

(198)

We try a set of values

α = β = a = b = 1

. With this choice, for

e_{1}

the probability of it being in a top quark gravi eigenstate is

99.33 %

. Similarly for

e_{2}

the probability of it being in bottom quark gravi eigenstate will then be equal to

97.7 %

. So let us identify

e_{1}

and

e_{2}

; as left handed top quark (

e_{t}

) and a left handed bottom quark (

e_{b}

), respectively. Now let us see the decay of flavour eigenstate of bottom quark to a flavour eigenstate of top quark :

e_{b}^{'} ⟶ e_{t}^{'}

e_{t}^{'} = \frac{1}{\sqrt{m_{u} + m_{c} + m_{t}}} (\begin{matrix} \sqrt{m_{u}} \\ \sqrt{m_{c}} \\ \sqrt{m_{t}} \end{matrix}) e_{b}^{'} = \frac{1}{\sqrt{m_{d} + m_{s} + m_{b}}} (\begin{matrix} \sqrt{m_{d}} \\ \sqrt{m_{s}} \\ \sqrt{m_{b}} \end{matrix})

(199)

These vectors can be rotated into each other by the application of normal rotation matrices.

Figure 4.

S U {(2)}_{L}

active particles and their projections

Figure 4.

S U {(2)}_{L}

active particles and their projections

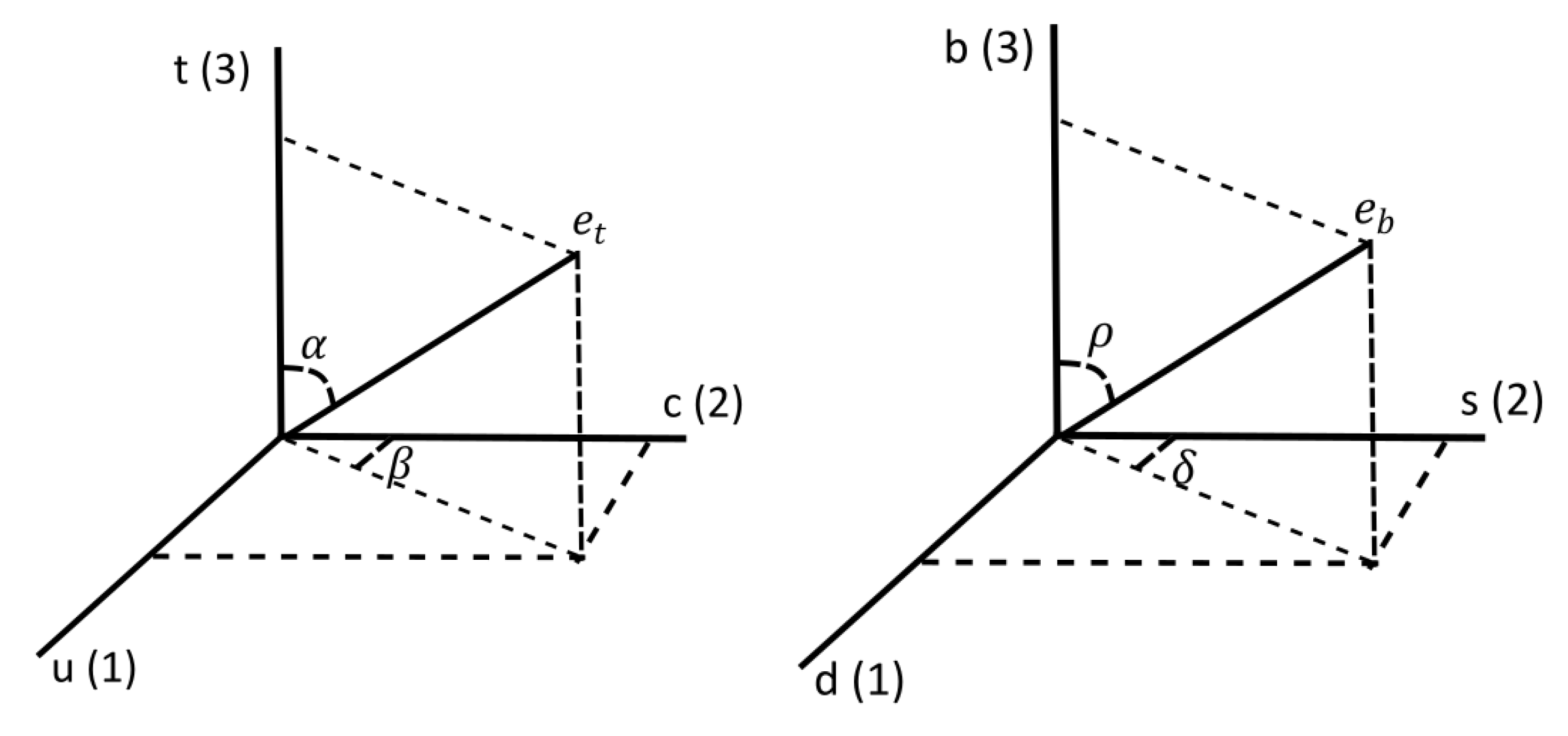
Here u represents the matrices acting on vectors in the space of the up-isospin particles, and similarly d represents the matrices acting on the space of down-isospin particles.

e_{t}^{'} = R_{12}^{u} (- β) R_{23}^{u} (- α) R_{23}^{d} (ρ) R_{12}^{d} (δ) e_{b}^{'} = V e_{b}^{'}

(200)

R_{12}^{d} (δ) = (\begin{matrix} c o s (δ) & - s i n (δ) & 0 \\ s i n (δ) & c o s (δ) & 0 \\ 0 & 0 & 1 \end{matrix}) c o s (δ) = \frac{\sqrt{m_{s}}}{\sqrt{m_{s} + m_{d}}}

(201)

R_{23}^{d} (ρ) = (\begin{matrix} 1 & 0 & 0 \\ 0 & c o s (ρ) & - s i n (ρ) \\ 0 & s i n (ρ) & c o s (ρ) \end{matrix}) c o s (ρ) = \frac{\sqrt{m_{b}}}{\sqrt{m_{b} + m_{s} + m_{d}}}

(202)

R_{12}^{u} (- β) = {(R_{12}^{u} (β))}^{T} = (\begin{matrix} c o s (β) & s i n (β) & 0 \\ - s i n (β) & c o s (β) & 0 \\ 0 & 0 & 1 \end{matrix}) c o s (β) = \frac{\sqrt{m_{c}}}{\sqrt{m_{u} + m_{c}}}

(203)

R_{23}^{u} (- α) = {(R_{23}^{u} (α))}^{T} = (\begin{matrix} 1 & 0 & 0 \\ 0 & c o s (α) & s i n (α) \\ 0 & - s i n (α) & c o s (α) \end{matrix}) c o s (α) = \frac{\sqrt{m_{t}}}{\sqrt{m_{u} + m_{c} + m_{t}}}

(204)

Now we use the numerical values of the square root masses of various quarks obtained from the eigenvalues of

3 \times 3

octonionic Hermitian matrices, as shown in Figure 2. By that substitution, we obtain:-

V_{i j} = (\begin{matrix} 0.9813 & - 0.1924 & - 0.0030 \\ 0.1917 & 0.9789 & - 0.0707 \\ 0.0165 & 0.0688 & 0.9975 \end{matrix})

(205)

| V_{i j} | = (\begin{matrix} 0.9813 & 0.1924 & 0.0030 \\ 0.1917 & 0.9789 & 0.0707 \\ 0.0165 & 0.0688 & 0.9975 \end{matrix})

(206)

The code used to obtain the above CKM matrix using square root mass as projections; is presented in the Appendix B. Every element of

V_{i j}

represents a projection of quark j on quark i. Its square represents the probability of transitioning from quark j to quark i in standard particle physics.

8.4.1. Standard CKM Matrix

In standard QFT textbooks [27], it is given that the CKM matrix is just a unitary transformation from mass eigenstates to states that are weak iso-spin doublets. The weak isospin doublets are

S U {(2)}_{L}

active. The weak interaction doublets are given below :

(\begin{matrix} u \\ d^{'} \end{matrix}) (\begin{matrix} c \\ s^{'} \end{matrix}) (\begin{matrix} t \\ b^{'} \end{matrix})

(207)

The CKM matrix can then be written as:-

(\begin{matrix} d^{'} \\ s^{'} \\ b^{'} \end{matrix}) = (\begin{matrix} V_{u d} & V_{u s} & V_{u b} \\ V_{c d} & V_{c s} & V_{c b} \\ V_{t d} & V_{t s} & V_{t b} \end{matrix}) (\begin{matrix} d \\ s \\ b \end{matrix})

(208)

The

{d, s, b}

represents the mass eigenstates. Each entry in the CKM matrix written as

V_{i j}

represents the transition of j quark to i quark by weak interactions. The CKM matrix is parameterised using three Euler angles

{θ_{12}, θ_{13}, θ_{23}}

and a phase factor

δ_{13}

[28] as given below:-

(\begin{matrix} c_{12} c_{13} & s_{12} c_{13} & s_{13} e^{- i δ_{13}} \\ - s_{12} c_{23} - c_{12} s_{23} s_{13} e^{i δ_{13}} & c_{12} c_{23} - s_{12} s_{23} s_{13} e^{i δ_{13}} & s_{23} c_{13} \\ s_{12} s_{23} - c_{12} c_{23} s_{13} e^{i δ_{13}} & - c_{12} s_{23} - s_{12} c_{23} s_{13} e^{i δ_{13}} & c_{23} c_{13} \end{matrix})

(209)

The experimental determination of the entries of the CKM matrix gives the values [17]:-

(\begin{matrix} | V_{u d} | & | V_{u s} | & | V_{u b} | \\ | V_{c d} | & | V_{c s} | & | V_{c b} | \\ | V_{t d} | & | V_{t s} | & | V_{t b} | \end{matrix}) = (\begin{matrix} 0.97370 \pm 0.00014 & 0.2245 \pm 0.0008 & 0.00382 \pm 0.00024 \\ 0.221 \pm 0.004 & 0.987 \pm 0.011 & 0.0410 \pm 0.0014 \\ 0.0080 \pm 0.0003 & 0.0388 \pm 0.0011 & 1.013 \pm 0.030 \end{matrix})

(210)

This yields the following experimentally determined values of the angles and the complex phase [29] :-

θ_{12} = 13.04 \pm 0.05

(211)

θ_{13} = 0.201 \pm 0.011

(212)

θ_{23} = 2.38 \pm 0.06

(213)

δ_{13} = 68.8 \pm 4.5

(214)

8.4.2. Theoretical Determination Of CKM matrix angles

With the values of the CKM matrix obtained from the theoretical considerations, we calculated the following values of the CKM Euler angles:-

θ_{12} = 11.093

(215)

θ_{13} = 0.172

(216)

θ_{23} = 4.054

(217)

We have no information about phase in our analysis so far. Further assumptions and research is required in this direction. The values obtained are in reasonable agreement with the measured values. Basically, the off-diagonal matrix elements are different from the experimentally determined values and hence are the reason for these values of the angles. A correction to mass matrices and hence to the masses of particles itself, is required to obtain better values. This is because we have used mass ratios derived in the asymptotically free limit, whereas mixing angles are likely impacted by the running of masses.

8.4.3. CKM parameters using Mass as projections

Instead of using the square root mass as the projections, we tried using mass. With this new definition our

S U {(2)}_{L}

active particles will be given by :-

e_{b}^{'} ⟶ e_{t}^{'}

(218)

e_{t}^{'} = \frac{1}{\sqrt{m_{u}^{2} + m_{c}^{2} + m_{t}^{2}}} (\begin{matrix} m_{u} \\ m_{c} \\ m_{t} \end{matrix})

(219)

e_{b}^{'} = \frac{1}{\sqrt{m_{d}^{2} + m_{s}^{2} + m_{b}^{2}}} (\begin{matrix} m_{d} \\ m_{s} \\ m_{b} \end{matrix})

(220)

e_{t}^{'} = R_{12}^{u} (- β_{1}) R_{23}^{u} (- β_{2}) R_{23}^{d} (α_{2}) R_{12}^{d} (α_{1}) e_{b}^{'} = V e_{b}^{'}

(221)

We use the same machinery, and rotate the vectors into each other by application of rotation matrices. It gives us following matrix required for the transformation :-

V_{i j} = (\begin{matrix} 0.9984 & - 0.0559 & 0.2228 \times 10^{- 5} \\ 0.0559 & 0.9982 & 0.1236 \times 10^{- 2} \\ - 0.7134 \times 10^{- 5} & - 0.1234 \times 10^{- 2} & 0.9998 \end{matrix})

(222)

The code to obtain the above given CKM matrix is presented in the Appendix C. With the above values of the various CKM matrix elements we obtain the following values of the CKM parameters :

θ_{12} = 3.205

(223)

θ_{13} = 0.00013

(224)

θ_{23} = 0.071

(225)

The above values are very different from experimentally obtained values. This thus provides us with additional justification for using the square root mass values over the mass values; while constructing the massive and the

S U {(2)}_{L}

active left handed vectors.

8.4.4. Connection between mass eigenstates and weak-isospin doublets

Observe that the physically massive vectors used in the above calculations are a linear combination of gravi-charge eigenstates of the right handed quarks. Also, observe that as we have developed an isomorphism between the vector space of ideals to this new vector space

C^{8} \oplus C^{8} \oplus C^{8}

, for

S U {(2)}_{R}

active mass eigenstates, we can do a similar mapping for the space of the

S U {(2)}_{L}

active flavour eigenstates. So for the three left handed quarks of same colour of

S U_{c} (3)

, we will need the following space to describe them

C \oplus C \oplus C

, just as for mass eigenstates. This time however, instead of the Gravi-charge operator, another diagonal operator corresponding to the electric charge will act on this space. Let us use the same

C^{3}

for both left and right active states (suppressing the colour for both

S U {(3)}_{c}

and

S U {(3)}_{g r a v}

). Then we can interpret the CKM matrix as a transformation that rotates the normalised mass eigenstates of the gravi-charge vectors to the normalised left handed flavour eigenstates. This connection can be done because of the triality. Triality allows for the mixing of various families in the spinor representations of the

C l (8)

algebra.

(\begin{matrix} d_{L} \\ s_{L} \\ b_{L} \end{matrix}) = (\begin{matrix} V_{u d} & V_{u s} & V_{u b} \\ V_{c d} & V_{c s} & V_{c b} \\ V_{t d} & V_{t s} & V_{t b} \end{matrix}) (\begin{matrix} d_{g, R} \\ s_{g, R} \\ b_{g, R} \end{matrix})

(226)

We have to use the normalised mass eigenstates and hence the gravi-charge eigenvectors.

9. Summary and Discussion

As is evident from the analysis in the previous sections, the complex Clifford algebra

C l (9)

is one of great significance. It is the algebra of unification of the standard model with gravitation, via a left-right symmetric extension of the standard model. We also note that

C l (9)

has dimension 512, and its irrep is

16 \times 16

matrices with complex number entries. If we assume the diagonal entries of these matrices to be real, their dimensionality is reduced to

512 - 16 = 496

, which is precisely the dimension of the

E_{8} \times E_{8}

symmetry group

(248 + 248)

proposed by us earlier for unification [6]. Hence there is consistency between

E_{8} \times E_{8}

symmetry and the algebra

C l (9)

vis a vis unification. Prior to left-right symmetry breaking which breaks unification in this theory, the coupling constant is simply unity, and the role of the emergent

U (1)

charge is played by this coupling constant divided by 3. Thus the fundamental entities prior to symmetry breaking are lepto-quark states which all have an associated charge

1 / 3

: these are neither bosonic nor fermionic in nature, and the charge value

1 / 3

is evident when one finds the eigenmatrices corresponding to the Jordan eigenvalues in the exceptional Jordan eigenvalue problem. For these eigenmatrices see the Appendix in [9]. The neutrino family, the up quark family, the down quark family and the electron family, all are expressed as different superpositions of three basis states which all have an associated charge

1 / 3

. This means that the left-chiral families are electric charge eigenstates expressed as superposition of pre-unification basis states, and right-chiral families are square-root mass eigenstates expressed as superposition of pre-unification basis states. This fact permits electric charge eigenstates to be expressed as superpositions of square-root mass eigenstates which in turn allows mass ratios to be determined theoretically.

We recall from above that the unification algebra

C l (9)

is written as a direct sum of two copies of

C l (8)

. On the other hand

C l (9)

can also be written as

C l (9) = C l (7) \otimes C l (2) = [C l (6) \otimes C l (2)] \oplus [C l (6) \otimes C l (2)]

. This last expression has profound implications for our understanding of space-time structure in quantum field theory. Recall that each of the two

C l (6)

represents one generation of standard model chiral quarks and leptons; the first

C l (6)

for left-chiral particles and the second

C l (6)

for right-chiral particles. In so far as the

C l (2)

are concerned, the second

C l (2)

(associated with right chiral fermions) is used to generate the Lorentz algebra

S L (2, C)

of 4D space-time (via complex quaternions with one quaternionic imaginary kept fixed), which includes the Lorentz boosts and the three-dimensional

S U {(2)}_{R}

rotations. Gauging of this

S U {(2)}_{R}

symmetry can be used to achieve Einstein’s general relativity on a 4D space-time manifold [30]. As for the first

C l (2)

, the one associated with left-chiral fermions, the

S U {(2)}_{L}

rotations describe weak isospin. However, undoubtedly, this

C l (2)

has its own set of Lorentz boosts, which along with the weak isospin rotations generate a second 4D spacetime algebra

S L (2, C)

distinct from the first, familiar 4D spacetime. In spite of its counterintuitive nature this second spacetime is also an element of physical reality, and there is definitive evidence for it in our earlier work [7,11,12]. In this second space-time, distances are at most of the order of the range of the weak force, and only microscopic quantum systems access this second space-time. Classical systems do not access it - their penetration depth into this space-time is much less than one Planck length. Our universe thus has two 4D space-times, which have resulted from the symmetry breaking of a 6D space-time, consistent with the equivalence

S L (2, H) ≃ S O (1, 5)

. See also [31,32,33,34]. The second space-time also obeys the laws of special relativity, and has a causal light-cone structure. A quantum system travels from a space-time point A to another space-time point B through both space-times, but gets to B much faster through the second space-time, on a time scale of the order

L / c \sim 10^{- 26}

s where

L \sim 10^{- 16}

cm is the range of the weak force. This is true even if B is located billions of light years away from A, and this offers a convincing resolution of the EPR paradox as to how quantum influences manage to arise nonlocally. These influences are local through the second space-time. In spirit our resolution could be compared to the ER=EPR proposal, but unlike the latter, our resolution has a sound mathematical basis. Moreover our resolution was not invented with the express purpose of understanding quantum nonlocality but is an indirect implication of the algebraic unification of standard model with gravitation. The weak force is seen as the geometry of this second space-time.

Acknowledgments

We would like to thank Abineet Parichha, for his valuable feedback and suggestions.

Appendix A

The

3 \times 3

Hermitian Octonionic Matrices, known as the exceptional Jordan algebra satisfy the characteristic equation given as [15,23] :-

A^{3} - (t r A) A^{2} + σ (A) A - (d e t A) I = 0

(A1)

For the definition of each part look at an example shown here.

A = (\begin{matrix} p & a & \bar{b} \\ \bar{a} & m & c \\ b & \bar{c} & n \end{matrix})

(A2)

p, m, n \in R a, b, c \in O

(A3)

t r A = p + m + n

(A4)

σ (A) = p m + p n + m n - {| a |}^{2} - {| b |}^{2} - {| c |}^{2}

(A5)

d e t A = p m n + b (a c) + \bar{b (a c)} - {n | a |}^{2} - {m | b |}^{2} - p {| c |}^{2}

(A6)

The real eigenvalues of the

3 \times 3

Hermitian Octonionic matrix satisfy a modified characteristic equation given by:-

d e t (λ I - A) = λ^{3} - (t r A) λ^{2} + σ (A) λ - d e t (A) = r

(A7)

r^{2} + 4 Φ (a, b, c) r - {| [a, b, c] |}^{2} = 0

(A8)

Φ (a, b, c) = \frac{1}{2} R e ([a, \bar{b}] c)

(A9)

[a, b, c] = (a b) c - a (b c)

(A10)

The

[a, b, c]

is the associator it is a measure of the associativity of the algebra involved. Now for our case the mass matrix has only quaternionic entries. In that case

r = 0

, and we have the usual characteristic equation that gives us real roots. These real roots are then used to calculate the mass ratios [9].

Appendix B

Here in this code we use mass eigenstates weighted by square-root of mass. The method is explained in the section

8.4

. The identifications used in the code are written below :

e_{t}^{'} = R_{12}^{u} (- β) R_{23}^{u} (- α) R_{23}^{d} (ρ) R_{12}^{d} (δ) e_{b}^{'} = V e_{b}^{'}

(A11)

A 12 T ⟶ R_{12}^{u} (- β)

(A12)

A 23 T ⟶ R_{23}^{u} (- α)

(A13)

B 23 ⟶ R_{23}^{d} (ρ)

(A14)

B 12 ⟶ R_{12}^{d} (δ)

(A15)

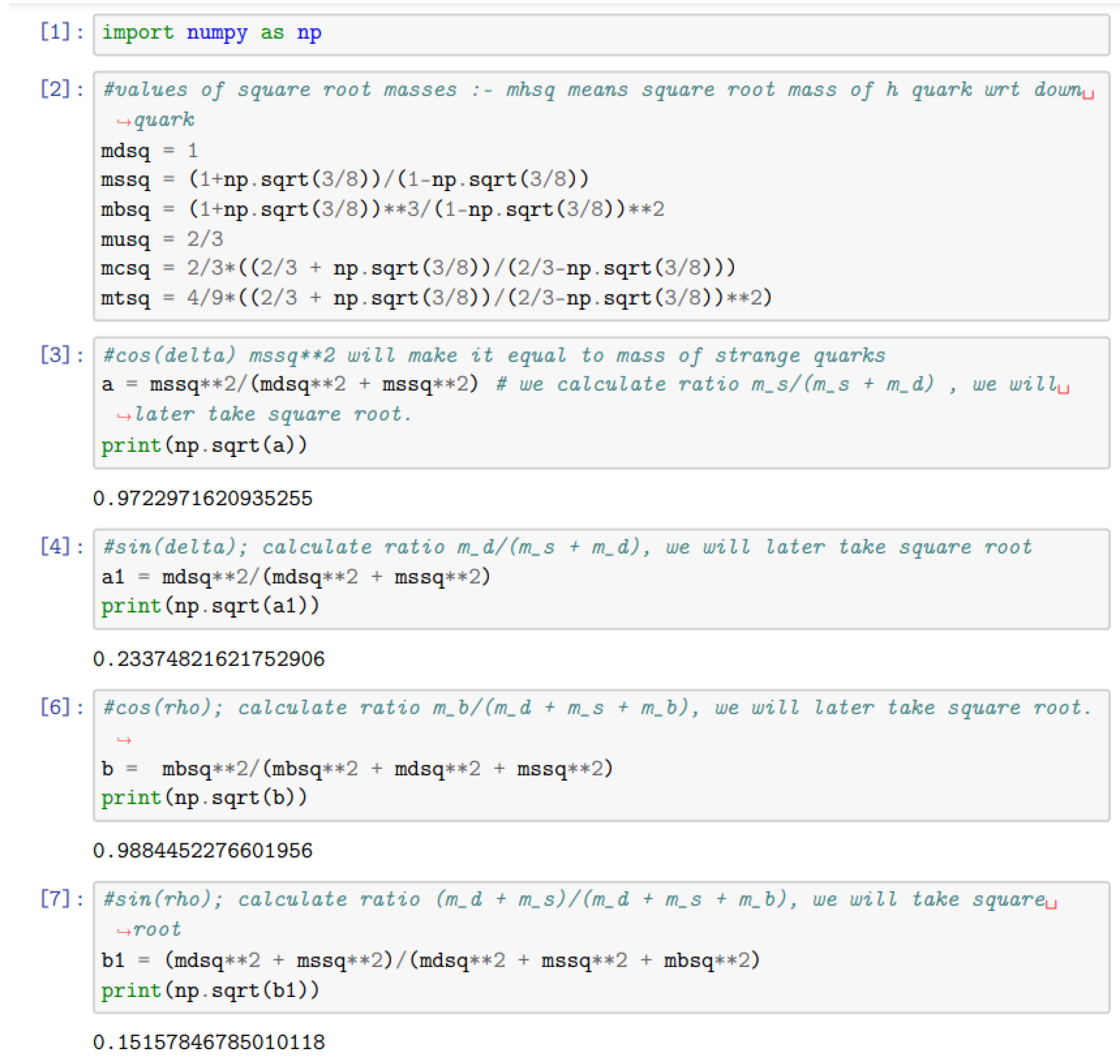
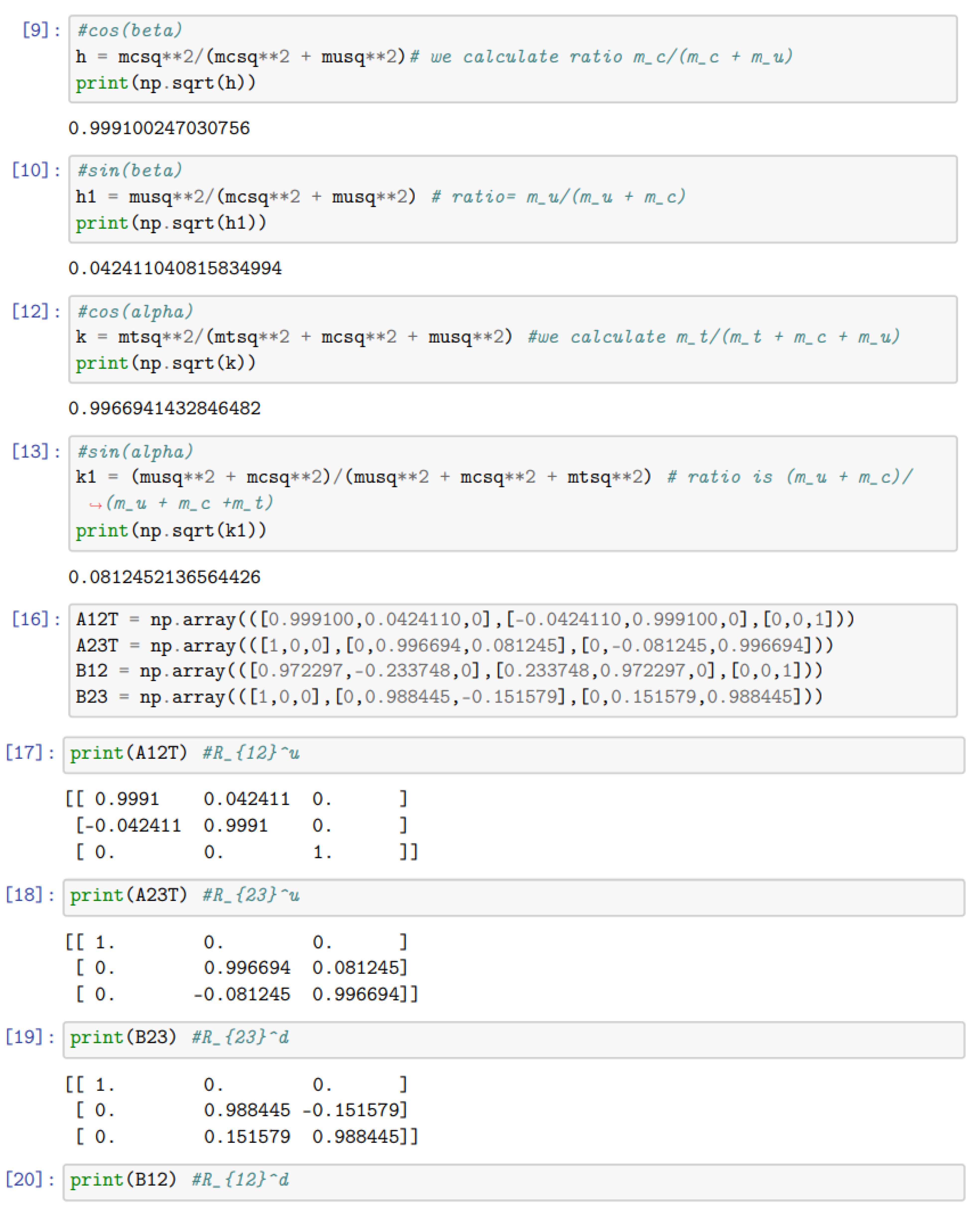
These values are reported in the earlier section.

Appendix C

Here is a code for computing CKM matrix parameters and mixing angles with mass eigenstates weighted by mass (instead of square root of mass). The definitions of rotation matrices and the mass vectors correspondingly get changed.

e_{t}^{'} = R_{12}^{u} (- β_{1}) R_{23}^{u} (- β_{2}) R_{23}^{d} (α_{2}) R_{12}^{d} (α_{1}) e_{b}^{'} = V e_{b}^{'}

(A16)

P 12 T ⟶ R_{12}^{u} (- β_{1})

(A17)

P 23 T ⟶ R_{23}^{u} (- β_{2})

(A18)

Q 23 ⟶ R_{23}^{d} (α_{2})

(A19)

Q 12 ⟶ R_{12}^{d} (α_{1})

(A20)

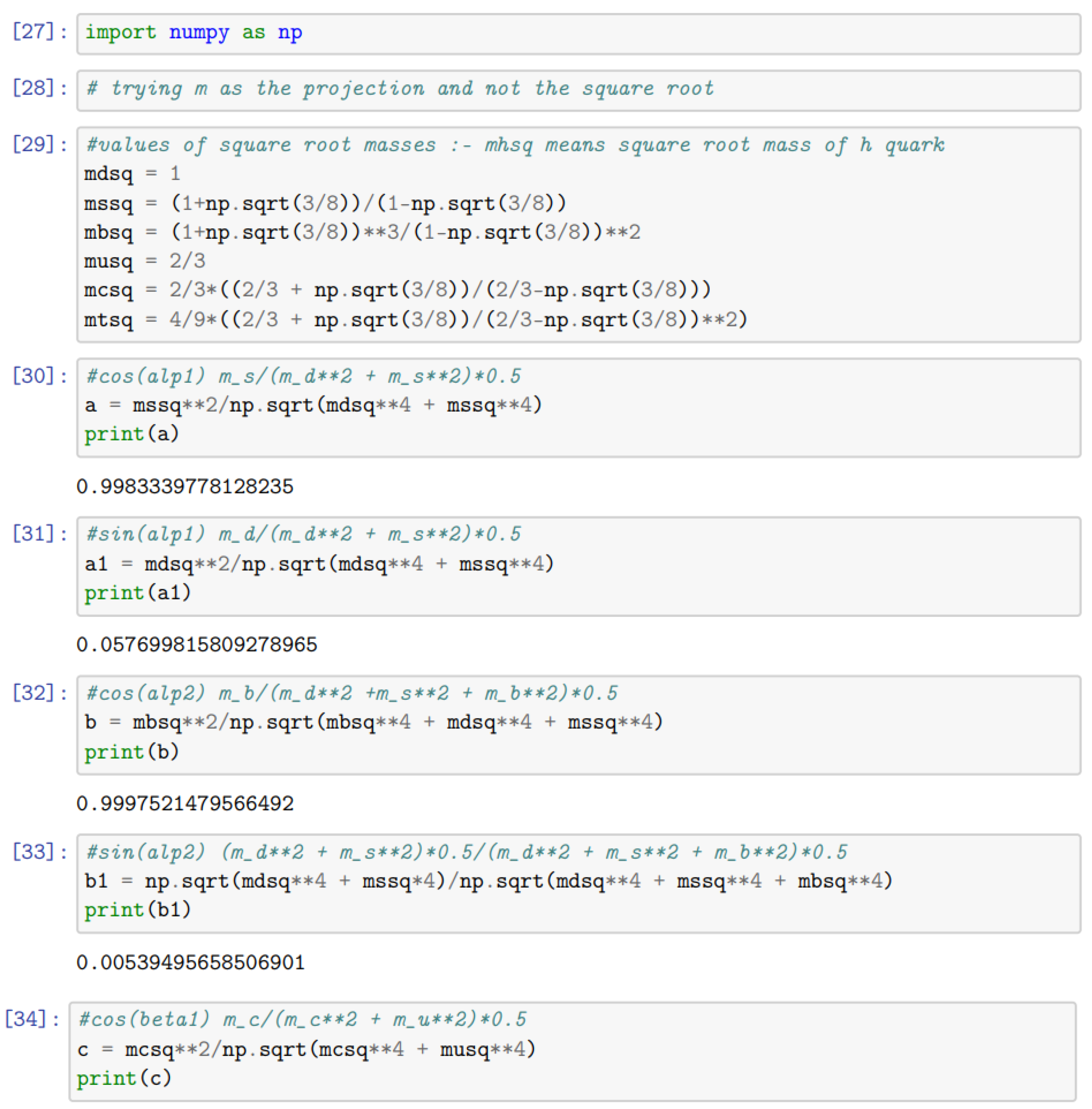
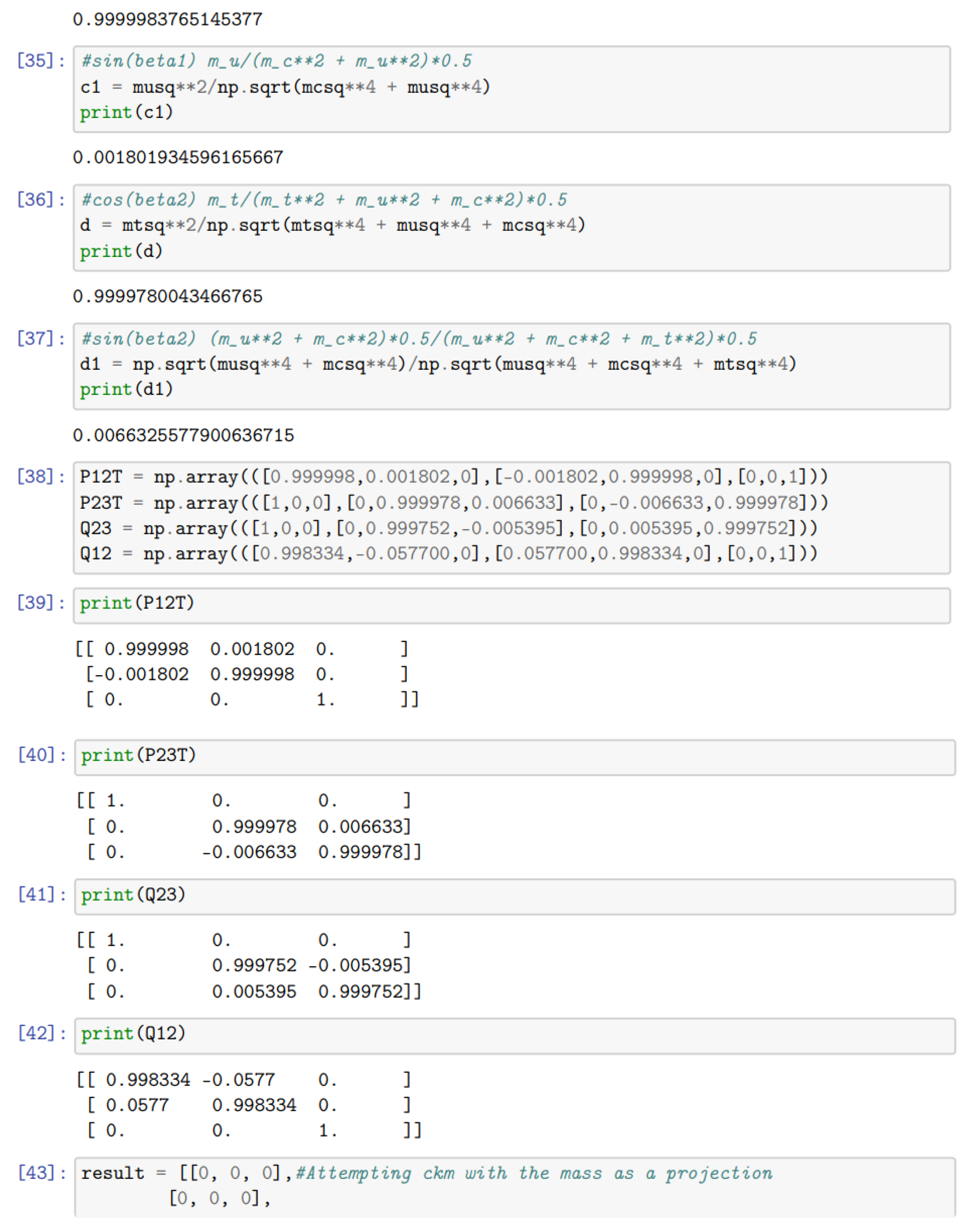
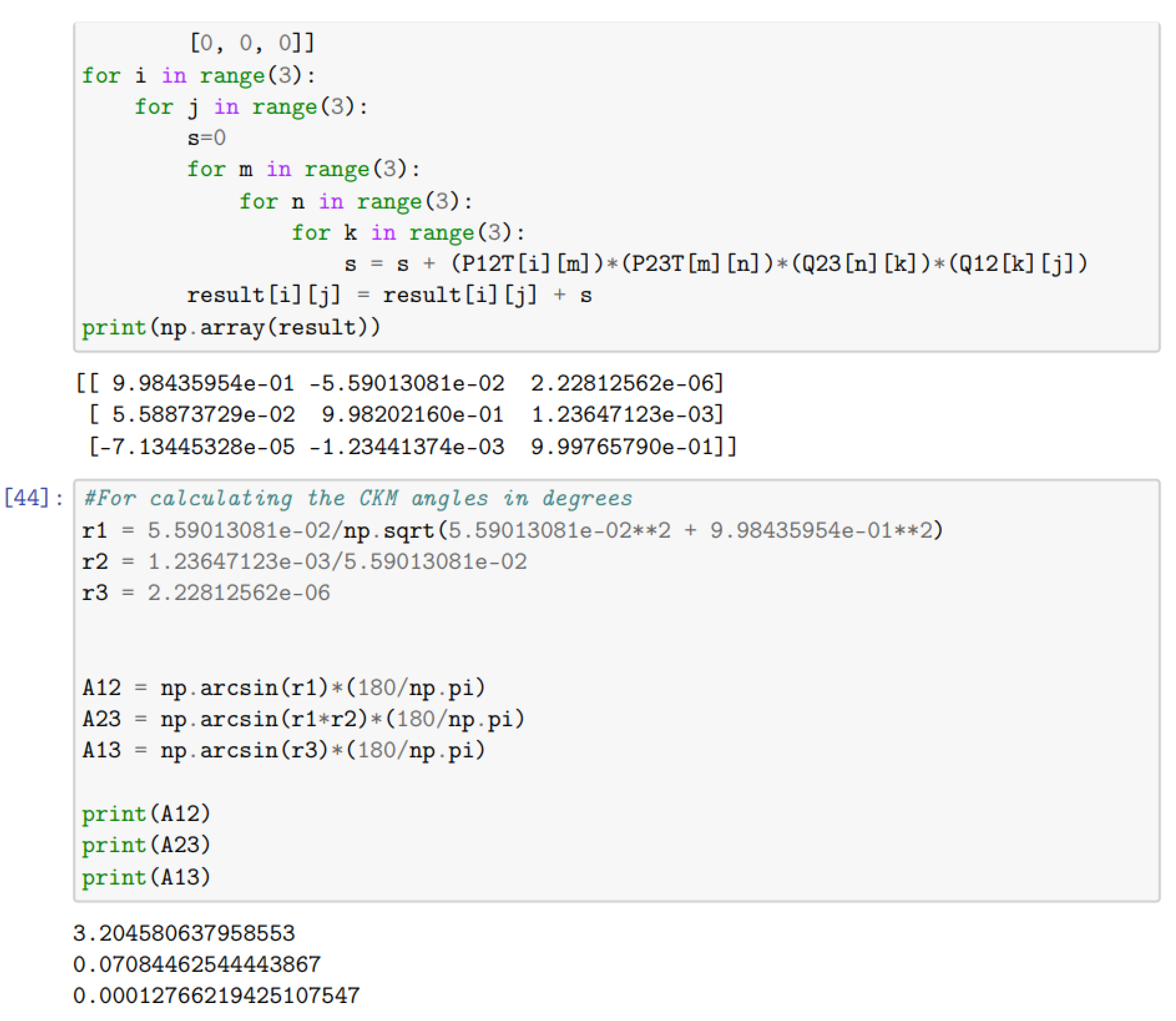
Here it can be seen that the values obtained for the CKM parameters are very different from the experimentally seen values. It justifies our choice of using the square root mass as more fundamental quantity over the mass of the fermions. References

References

Günaydin, M.; Gürsey, F. Quark structure and octonions. Journal of Mathematical Physics 1973, 14, 1651. [Google Scholar] [CrossRef]
Furey, C. Standard model physics from an algebra? arXiv 2016, arXiv:1611.09182. [Google Scholar]
Todorov, I.; Dubois-Violette, M. Deducing the symmetry of the standard model from the automorphism and structure groups of the exceptional Jordan algebra. Int. J. Mod. Phys. A 2018, 33, 1850118. [Google Scholar] [CrossRef]
Furey, C. Charge quantization from a number operator. Phys. Lett. 2015, B742, 195. [Google Scholar] [CrossRef]
Vaibhav, V.; Singh, T.P. Left-right symmetric fermions and sterile neutrinos from complex split biquaternions and bioctonions. Adv. Appl. Clifford Algebras 2023, 33, 32. [Google Scholar] [CrossRef]
Kaushik, P.; Vaibhav, V.; Singh, T.P. An E₈×E₈ unification of the standard model with pre-gravitation, on an octonion-valued twistor space. arXiv 2022, arXiv:2206.06911.
Raj, S.; Singh, T.P. A Lagrangian with E8×E8 symmetry for the standard model and pre-gravitation I. – The bosonic Lagrangian, and a theoretical derivation of the weak mixing angle. arXiv 2022, arXiv:2208.09811.
Singh, T.P. Quantum gravity effects in the infra-red: a theoretical derivation of the low energy fine structure constant and mass ratios of elementary particles. The European Physical Journal Plus 2022, 137, 664. [Google Scholar] [CrossRef]
Bhatt, V.; Mondal, R.; Vaibhav, V.; Singh, T.P. Majorana Neutrinos, Exceptional Jordan Algebra, and Mass Ratios for Charged Fermions. J. Phys. G: Nucl. Part. Phys. 2022, 49, 045007. [Google Scholar] [CrossRef]
Singh, T.P. Why do elementary particles have such strange mass ratios? – The role of quantum gravity at low energies. Physics 2022, 4, 948–969. [Google Scholar]
Singh, T.P. The exceptional Jordan algebra, and its implications for our understanding of gravitation and the weak force arXiv 2023, arXiv:2304.01213.
Singh, T.P. Gravitation, and quanum theory, as emergent phenomena https://www.preprints.org/manuscript/202302.0253/v1 to be published in J. Phys. Conf. Series. 2023. [Google Scholar]
Tung, W.K. Group Theory in Physics (World Scientific, 1985).
Gallier, J. Clifford Algebras, Clifford Groups, and a Generalization of the Quaternions. arXiv 2014, arXiv:0805.0311.
Harvey, F.R. Spinors and Calibrations: 9 (Perspectives in mathematics) (Elsevier Science, 1990).
Baez, J.C. The octonions. Bull. Am. Math. Soc. 2002, 39, 145. [Google Scholar]
Zyla, P.A.; Barnett, R.M.; Beringer, J.; et al. (Particle Data Group) Review of particle physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar]
Todorov, I. Clifford algebras and spinors. Bulg. J. Phys. 2011, 38, 3. [Google Scholar]
Ablamowicz, R. Construction of Spinors via Witt Decomposition and Primitive Idempotents: A Review; Springer: Dordrecht, Netherlands, 1995; pp. 113–123. [Google Scholar]
Stoica, O.C. Leptons, quarks, and gauge from the complex Clifford algebra Cl(6) (the standard model algebra). Advances in Applied Clifford Algebras 2018, 28, 52. [Google Scholar] [CrossRef]
Dray, T.; Manogue, C.A. The exceptional Jordan eigenvalue problem. IJTP 1999, 38, 2901. [Google Scholar]
Manogue, C.A.; Dray, T. Octonions, E₆, and Particle Physics. J. Phys. Conf. Ser. 2010, 254, 012005. [Google Scholar] [CrossRef]
Dray, T.; Manogue, C.A. The octonionic eigenvalue problem. Adv. Appl. Clifford Algebras 1998, 8, 341. [Google Scholar] [CrossRef]
Boyle, L. The standard model, the exceptional Jordan algebra, and triality. arXiv 2020, arXiv:2006.16205.
Gillard, A.B.; Gresnigt, N.G. The Cl(8) algebra of three fermion generations with spin and full internal symmetries. arXiv 2019, arXiv:1906.05102.
Lounesto, P. Clifford Algebras and Spinors London Mathematical Society Lecture Note Series (Cam- bridge University Press, 2nd edition, 2001).
Griffiths, D. Introduction to elementary particles Weak Interactions, Chapter 10, pages 301–341 (John Wiley Sons, Ltd, 1987).
Chau, L.L.; Keung, W.Y. Comments on the parametrization of the Kobayashi-Maskawa matrix. Phys. Rev. Lett. 1984, 53, 1802. [Google Scholar] [CrossRef]
Amsler, C.; et al. (Particle Data Group) Review of particle physics. Physics Letters 2008, B667, 1.
Woit, P. Euclidean twistor quantization arXiv:2104.05099 [hep-th].
Chester, D.; Rios, M.; Marrani, A. Beyond the standard model with six-dimensional spinors. Particles 2023, 6, 144. [Google Scholar] [CrossRef]
Trayling, G. A geometric approach to the Standard Model. arXiv 1999 arXiv:hep-th/9912231.
Trayling, G.; Baylis, W.E. A geometric basis for the standard-model gauge group. J. Phys. A Math. Theor. 2001, 34, 3309. [Google Scholar]
Trayling, G.; Baylis, W.E. The Cl(7) Approach to the Standard Model In: Ablamowicz, R. (ed.) Clifford Algebras: Applications to Mathematics, Physics, and Engineering, pp. 547 Birkhauser Boston, Boston (2004).

Figure 1. The Fano Plane [16]

Figure 2. The square root of mass of fermions with respect to the down quark.[9]

Table 1. Forces and force carriers

Force	Gauge Boson	Symbol
Electromagnetism	Photon	$γ$
Weak Force	W and Z bosons	$W^{+}, W^{-}, Z$
Strong Force	Gluons	g

Table 2. (a)Up-Isospin particles ; (b)Down-Isospin Particles .

Q	$Λ$	$P^{u}$	Particle	$- Q^{*}$	$- Λ^{*}$	$P^{d}$	Particle
0	1	p	$ν$	0	1	$p^{'}$	$\bar{ν}$
$\frac{1}{3}$	$\bar{3}$	$q_{i}^{†} p$	$\bar{d_{i}}$	$- \frac{1}{3}$	3	$q_{i} p^{'}$	$d_{i}$
$\frac{2}{3}$	3	$q_{i}^{†} q_{j}^{†} p$	$u_{i}$	$- \frac{2}{3}$	$\bar{3}$	$q_{i} q_{j} p^{'}$	$\bar{u_{i}}$
1	1	$q_{i}^{†} q_{j}^{†} q_{k}^{†} p$	$e^{+}$	$- 1$	1	$q_{i} q_{j} q_{k} p^{'}$	$e^{-}$

Table 3. Internal Space for various Symmetry.

Force/Charge	Internal space	Dimension	Symmetry
Electromagnetism	$χ_{e m}$	1	U(1)
Strong	$χ_{c}$	3	SU(3)
Weak Hypercharge	$χ_{Y}$	1	U(1)
Weak- Electromagnetism	$χ_{e w}$	2	U(2)

Table 4. Internal Space of Particles

Particle	Internal Space
$e^{-}$	$χ_{e m}^{3}$
$\bar{u}$	$χ_{e m}^{2} {\bar{χ}}_{c}$
d	$χ_{e m} χ_{c}$
$ν$	C
$\bar{ν}$	C
$\bar{d}$	$χ_{e m}^{- 1} {\bar{χ}}_{c}$
u	$χ_{e m}^{- 2} \bar{χ_{c}}$
$e^{+}$	$χ_{e m}^{- 3}$

Table 5. Particles as the representations of the Exterior Algebra.[20]

Particles	Vectors in Exterior Space
$e^{-}$	$Λ^{3} \bar{χ}$
$\bar{u}$	$Λ^{2} \bar{χ}$
d	$Λ^{1} \bar{χ}$
$ν$	$Λ^{0} \bar{χ}$
$\bar{ν}$	$Λ^{0} χ$
$\bar{d}$	$Λ^{1} χ$
u	$Λ^{2} χ$
$e^{+}$	$Λ^{3} χ$

Table 6. New Symmetry Group

Force/Charge	Internal space	Dimension	Symmetry
Gravi-Electromagnetism	$χ_{g e m}$	1	U(1)
Gravi-Strong	$χ_{g r a v}$	3	SU(3)
Gravi-Weak Hypercharge	$χ_{g}$	1	U(1)
Gravi Weak- Electromagnetism	$χ_{g - e w}$	2	U(2)

Table 7. Internal Space due to extended Symmetry Group

Particle	Internal Space
d	$χ_{g e m}^{3}$
$\bar{u}$	$χ_{g e m}^{2} {\bar{χ}}_{g r a v}$
$e^{-}$	$χ_{g e m} χ_{g r a v}$
$\bar{ν}$	$C$
$ν$	$C$
$e^{+}$	$χ_{g e m}^{- 1} {\bar{χ}}_{g r a v}$
u	$χ_{g e m}^{- 2} χ_{g r a v}$
$\bar{d}$	$χ_{g e m}^{- 3}$

Table 8. Particles in Exterior Algebra

Particle	Vectors in Exterior Space
d	$Λ^{3} \bar{χ}$
$\bar{u}$	$Λ^{2} \bar{χ}$
$e^{-}$	$Λ^{1} \bar{χ}$
$\bar{ν}$	$Λ^{0} \bar{χ}$ ≅ $C$
$ν$	$Λ^{0} χ$ ≅ $C$
$e^{+}$	$Λ^{1} χ$
u	$Λ^{2} χ$
$\bar{d}$	$Λ^{3} χ$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

CKM Matrix Parameters from an Algebra

Abstract

1. Introduction

2. A few basics

2.1. Algebra

2.2. Group Representations

2.3. The Standard Model

3. Clifford Algebras

3.1. Pin and Spin Groups

3.2. Representations of Clifford Algebras

4. Octonions

5. Minimal Left Ideals

5.1. Symmetry Transformations

5.2. Particle Representations

6. Split Bioctonions and Mass Ratios

6.1. Construction

6.2. Mass Ratios

6.2.1. Hermitian Octonionic Matrices

6.2.2. Inclusion Of Gravity

7. Space Of Minimal Left Ideals

7.1. Patterns in The Standard Model

7.2. Algebra for the Standard Model

7.3. Ideals and Representations

7.3.1. SU(2) Symmetry

7.3.2. Complete Space of Ideals

7.3.3. Left Action on the Space of Ideals

7.3.4. Right Action on the Space of Ideals

7.4. Cl(7) Algebra

7.4.1. Right Adjoint Action

7.4.2. Left Adjoint Action

7.4.3. Particle Identification

7.5. Triality and Cl(8) Algebra

7.5.1. Space of Ideals in Cl(8)

7.5.2. Triality Operator

8. CKM Matrix Parameters

8.1. Gravi-Charge Operator

8.2. Mass and Gravi-Charge

8.3. Left Handed Quarks

8.4. CKM Matrix

8.4.1. Standard CKM Matrix

8.4.2. Theoretical Determination Of CKM matrix angles

8.4.3. CKM parameters using Mass as projections

8.4.4. Connection between mass eigenstates and weak-isospin doublets

9. Summary and Discussion

Acknowledgments

Appendix A

Appendix B

Appendix C

References

MDPI Initiatives

Important Links

Subscribe