Visual Odometer Based on Image Region Texture Weights of ORB Features

ORB (Oriented FAST and Rotated Brief) features are the most commonly used features in visual SLAM and visual odometry that have high computational speed, and rotation scale invariance. However, due to the homogenization of ORB features, the corner properties of specific features are poor in some artificial environments, and it can lead to poor matching performance when the environmental texture is not rich. The underlying reason is that the pixel grayscale changes in the less-richly textured regions on the image are not obvious, leading to a certain degree of mis-matching in the matching process. At the same time, when the camera motion speed is low, there is much overlap between adjacent frames. This results in minimal or almost no changes in the projection of feature points, and the system is highly sensitive to errors, In this case, even small errors can cause significant fluctuations in the calculation results. In response to the above issues, an improved feature point method for stereo vision mileage calculation is proposed to solve the problem of system stability deterioration when cameras move at low speeds in artificial envi-ronments. Firstly, weight calculation based on different texture regions is used to solve the problem of low corner properties of feature points caused by environmental texture differences. Then, keyframes are used for motion model estimation to improve the system's stability under low-speed motion. The experimental results of the dataset showed that the key frame rate was optimal between 10% and 12%, and the positioning accuracy was higher than these open-source systems compared with three common open-source VO systems.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

Unmanned driving has brought great convenience in ore mining and transportation, car driving, factory production, and agriculture [1,2], and localization algorithms are the basis and key to realizing unmanned driving. Currently, Simultaneous Localization and Mapping (SLAM) is commonly used and is divided into two types, laser-based and vision-based, depending on the sensor [3]. Laser SLAM started earlier than vision SLAM; while the technology of both products is relatively mature, but the cost is higher, while vision SLAM is receiving more and more attention due to the richer environmental information and low sensor cost [4].

Visual SLAM consists of five main components: sensor information acquisition, visual odometry, back-end optimization, Loop Closure Detection, and mapping [5]. The task of visual odometry is to estimate the motion of cameras between adjacent images, and its accuracy directly affects the performance of SLAM systems. Most of these visual odometry systems are feature-based, i.e., after extracting certain image features and representing them with descriptors, the camera motion is represented by matching between images in order to compute the conversion matrix between frames [6].

In this paper, the feature extraction algorithm is selected as ORB (Oriented FAST and Rotated Brief) features, which combines the FAST (Features from Accelerated Segment Test) extraction algorithm and BRIEF (Binary Robust Independent Elementary Features) descriptor, which makes it highly computationally fast and rotation invariant and scale-invariant and is currently the most commonly used feature operator in visual SLAM [7]. In the extraction process of ORB features, the feature points are usually concentrated, and in order to match more conveniently and also to calculate the minimization reprojection error more accurately, it should try to make the feature points evenly distributed in the whole image that is, homogenization [8,9,10].

Both domestic and foreign scholars have provided unique insights on the improvement of ORB features; for example, Mur-Artal R et al. proposed the introduction of quadtree homogenization to improve the homogeneity of ORB feature point extraction, but the extraction rate of feature points is still low in weak texture regions [11]. , proposed an improved algorithm to improve the extraction rate of feature points by introducing adaptive thresholding, but the problem of low feature point uniformity was not effectively solved [12]. Chen Mianshu et al. improved the uniformity of feature point extraction based on the idea of grid division and hierarchical determination of key points but reduced the real-time performance of the system [13]. Yao Jinjin et al. proposed to set different quadtree depths for different pyramid layers to improve the computational efficiency, and the extraction time was reduced by 10% compared with the traditional algorithm, but the enhancement of the underlying texture image was not obvious [14]. Zhao Cheng et al. used quadtree homogenization and adaptive thresholding to reduce the degree of aggregation of feature points in texture information-rich regions and improve the homogeneity of feature point extraction [15]. However, because its adaptive thresholding depends on the image texture, it still does not solve the problem of poor matching accuracy of feature points in low-texture regions.

In response to the above research status, the main contributions of this paper are:

(1) To propose a matching algorithm based on the weight of feature point response values by studying the homogenization of ORB features in visual odometry.

(2) Incorporating a predictive motion model in the keyframes bit pose estimation.

2. Visual Odometry

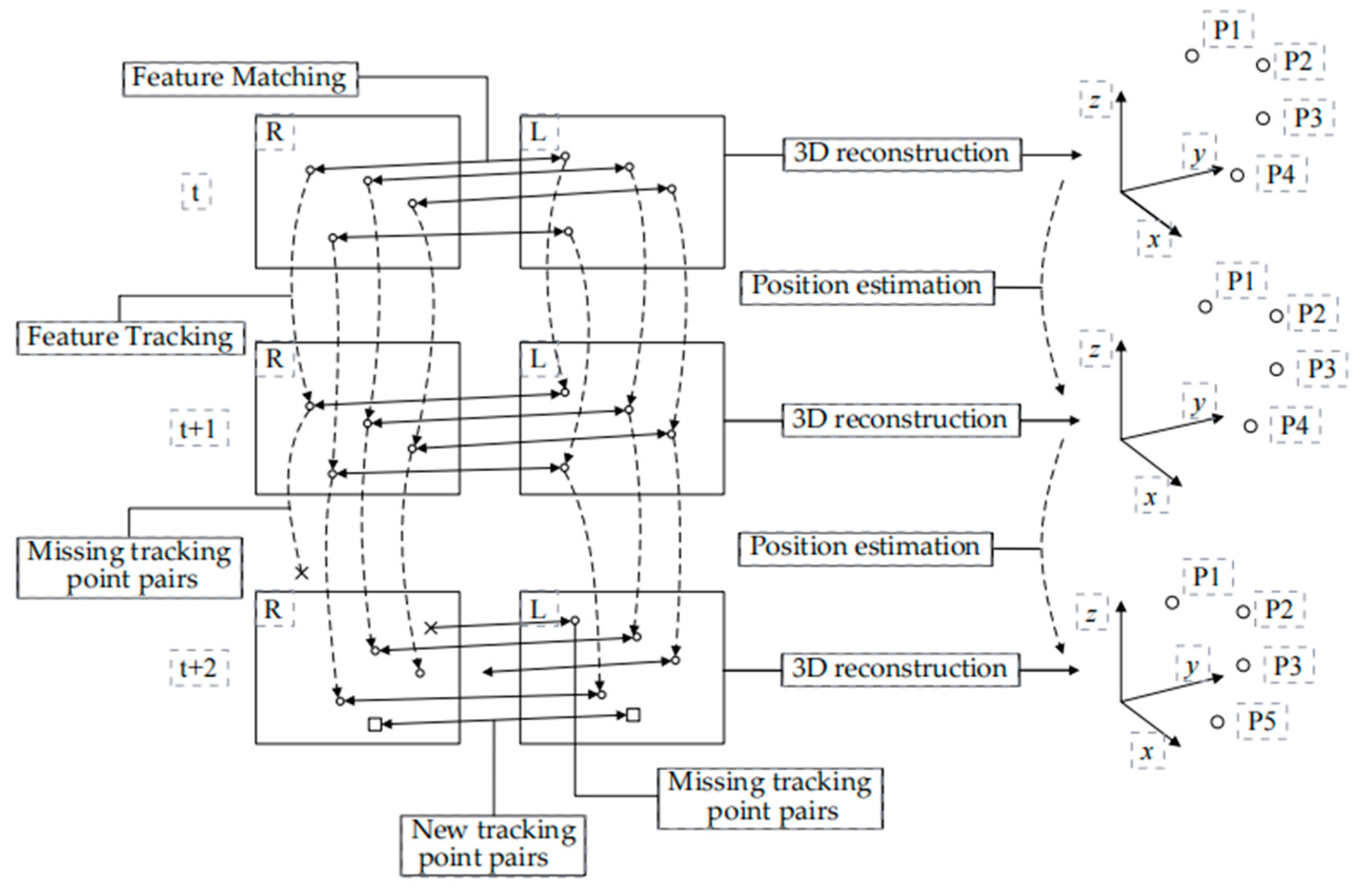
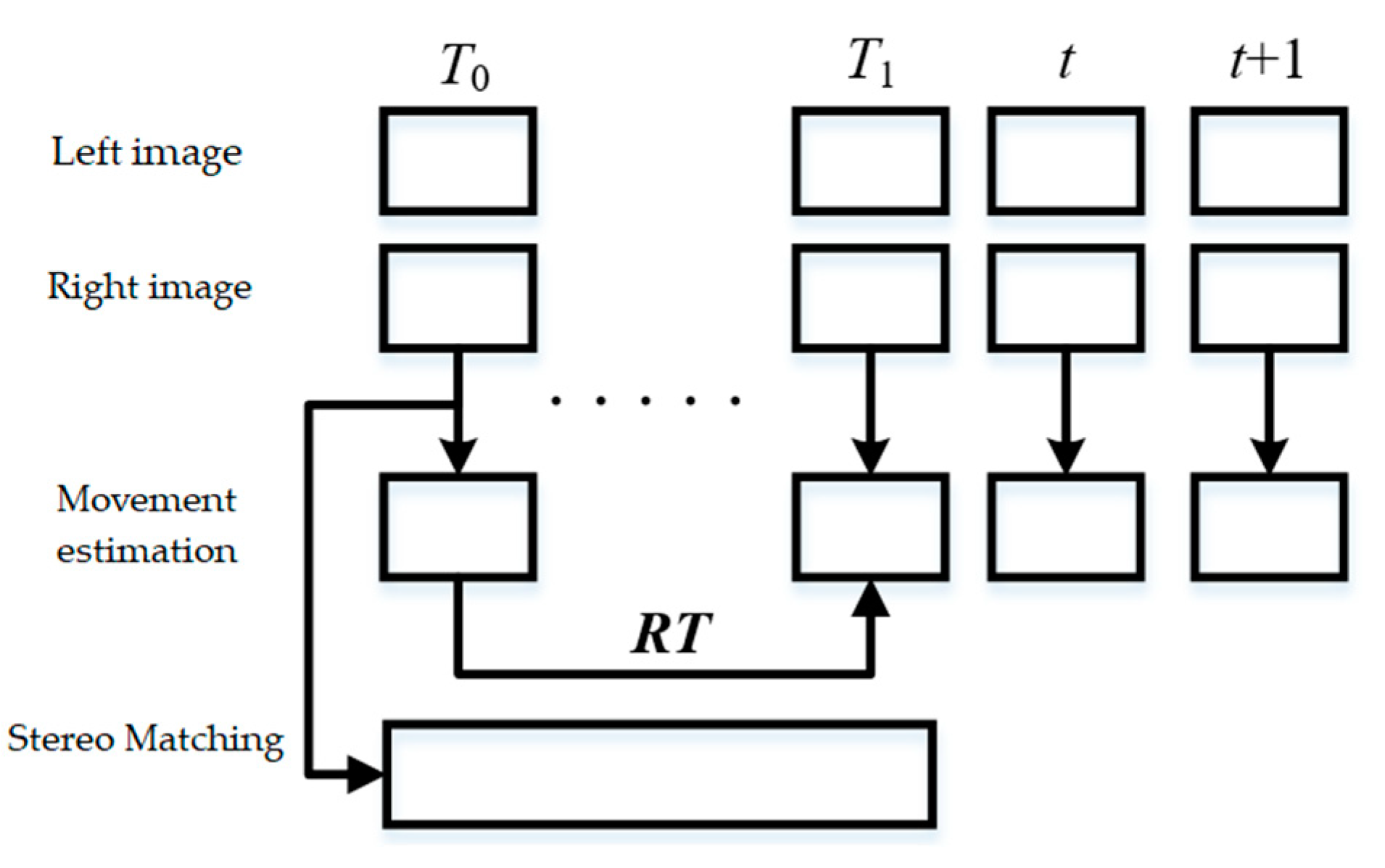
2.1. System Framework

A complete stereo vision odometry system consists of four parts [16]: image acquisition and preprocessing, feature extraction and matching, feature tracking and 3D reconstruction, and motion estimation. The system flowchart is shown in Figure 1, and the specific processes are as follows: extracting feature points on the left and right eye images; matching feature points based on Euclidean distance and polar line constraints; reconstructing the 3D coordinates of matched feature point pairs; tracking feature points in the next frame of the image pair; and calculating the camera pose by solving the minimum reprojection error problem for the feature points.

2.2. ORB algorithm parameters selection

ORB features are used to reduce the computation time and mismatch rate [17]. It is necessary to select the appropriate scale parameter in openCV with the number of s pyramid layers N. Assuming that the original map is at layer 0, the scale of layer i is:

S_{i} = s^{i}

(1)

where s is the initial scale. Then the image size of the ith layer is:

S_{i} = (\frac{H}{s_{i}}) \times (\frac{W}{s_{i}})

(2)

H \times W

is the size of the original image. From the above equation, it can be seen that the scale parameter determines the size of each layer of the pyramid, and the larger the scale parameter is, the smaller the image of each layer is, i.e., the scaling ratio is approximately larger. In order to select a suitable combination of parameters, this paper conducts experiments under different parameter combinations using 05 image sequences from the KITTI database.

The results of the parameter comparison are shown in Figure 2. The vertical coordinates represent the variation of the number of pyramid layers from 2 to 8, and the horizontal coordinates represent the variation of the scale parameter from 1.2 to 1.8. The color in each square in the figure then represents the size of the corresponding result. The total time from extraction to matching of ORB features with different combinations of parameters is given in Figure 2(a). From the results, it is seen that the computation time increases as the number of pyramid layers increases, while it decreases when the scale parameter becomes larger. This indicates that the image size of each layer becomes smaller after the scale parameter becomes larger, which leads to a shorter time for computing feature points on the image.

The false match rate when matching ORB feature points with different combinations of parameters is given in Figure 2(b). From the results, it is seen that the false match rate decreases significantly when the number of pyramid layers increases, which indicates that the feature points can ensure a good matching correct rate when the number of pyramid layers is large. Similarly, when the scale parameter becomes larger, there is a small increase in the false match rate, which indicates that the false match of feature points increases when the image size of each layer in the pyramid becomes smaller.

Combined with the above analysis, the scale parameter is chosen 1.8 and the number of image pyramid layers is chosen 8 when ORB features are used in this paper under the comprehensive consideration of computational efficiency and correct matching rate.

3. Improvement of ORB features

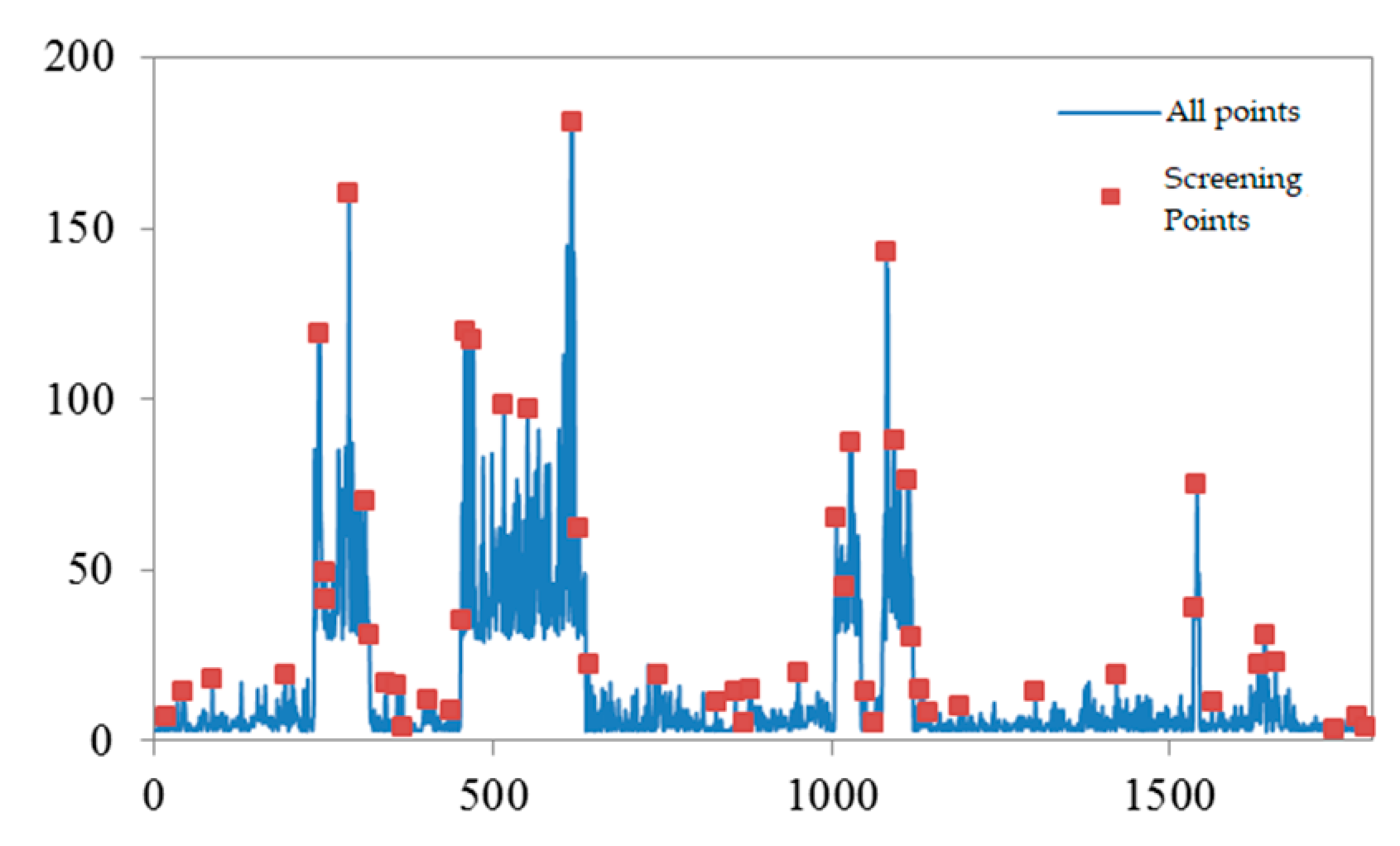
3.1. Calculation of different texture area weights

In the actual extraction process of ORB features, it is necessary to divide the image into several smaller regions for extracting feature points, while the number of feature points in each region is consistent so that the calculation results can be guaranteed to be more accurate. The main steps are as follows [18]:

1. segmentation of the image;

2. tracting feature points;

3. axing the extraction condition and extracting again if the number of feature points in the region is less than the minimum threshold;

If the number of features is greater than the maximum threshold, select a few of them with the largest Harris response value, and discard the rest.

Figure 3(a) image resolution is 1226*370, which is the road screen when the 05 image sequence of the KITTI dataset is not a region. As seen in the figure, the feature points are mainly concentrated in the plants as well as the outlines of the houses, which not only leads to mismatching and reduces the correct matching rate; but also makes the calculation results cause large errors.

First, the image is segmented so that its feature points can be distributed as evenly as possible in the graph. For an image of original size

W \times H

, given the segmentation coefficients

s_{w}

s_{w}

for width and height, the width and height of the image are divided equally as follows:

n_{w} = \frac{W}{s_{w}}, n_{h} = \frac{W}{s_{h}}

(3)

The FSAT parameter for the first feature extraction in each region after segmentation is 30, and if no feature points are extracted, the parameter is changed to 3 and extracted again. A total of 1862 feature points were extracted, and the result shows that the extracted feature points are more evenly distributed in the image after region segmentation. The next step is to filter the feature points according to their Harris response values in each region and keep the points with the largest response values in each region, and the results are shown in Figure 3(b).

The above screening process results in the retention of only the local optimums because the response values of feature points in each region are compared. The relationship between the response values of feature points before and after screening is given in Figure 4. The blue curve in the figure indicates the response values of all 1862 feature points, and the red dots indicate the response values of the final feature points obtained after the screening. From the figure, it can be seen that a considerable number of feature points are local response value extremes, but their response values are still low in the whole, which indicates that the corner point nature of these points is not obvious compared with other points.

While point feature homogenization ensures that feature points are distributed as evenly as possible, it also makes the corner point properties of some feature points poor. This method works well in the case of rich textures; less rich environmental textures lead to poor matching of feature points. To solve the above problem, the image regions are differentiated [19]. For the image

I (x, y)

, calculate the matrix:

G = {\sum (\frac{\partial I}{\partial x} \frac{\partial I}{\partial y})}^{T} (\frac{\partial I}{\partial x} \frac{\partial I}{\partial y})

(4)

The two eigenvalues of the matrix G represent the texture information of the region. When both eigenvalues are larger, it means that the region is a high-texture region, and vice versa, it means that the region is a low-texture region [20].

For different texture regions, different weights are given. That is, the weights should be small for low-texture areas of the image, while for high-texture areas of the images, the weights should be large. Definition of weights:

w = \min (e i g e n v a l u e (G))

(5)

The weight values are determined by the grayscale gradient of the pixel points in the local region of the image. This results in feature points with weights that are uniformly distributed over the image, ready for feature tracking and motion estimation.

3.2. Keyframe-based predictive motion model

Stereo-matching aims to find the corresponding projection points of the same spatial point in images acquired from different viewpoints [21]. The parallel binocular vision system uses a polar constraint to perform feature matching between the left and right images. From the pair-pole geometry, let the projection points of the same spatial point P on the left and right images be P1 and P2, then the corresponding point P2 of the point P1 must be on the polar line l2 corresponding to P1. For the parallel binocular system, for the same spatial point, the polar line is on the same line; that is, it is P2 on the extension line of the polar line where P1 is located so that when searching for the matching point, it is only necessary to search in the domain of the polar line.

For the feature matching problem of inter-frame images, the robustness and real-time performance of the visual odometry are not guaranteed if we rely only on the unique constraint to reduce the error, and the method of estimating the motion model to narrow the search range is currently used in the front and back frame feature point matching to solve the above problem [22]. The method is to estimate the motion model of the system based on the images at moment t-1 and moment t. The position of the feature points in the image at moment t in moment t+1 is calculated under this motion model, and the best matching points are searched around this position.

However, in the above method, the overlap between adjacent frames increases for slower vehicles, resulting in almost no change in the projection of feature points, leading to high sensitivity of the system to errors. In this paper, we propose to use keyframes for motion model estimation to solve this problem. These keyframes are characterized by easy identification of feature points between adjacent keyframes, and the mean Euclidean distance between the current frame and the 3D coordinates of all matching points of the previous keyframe are considered as keyframes only when they are within a certain threshold.

d_{\min} < d_{k_{i}, k_{i - 1}} < d_{\max}

(6)

where

d_{\min}

- the minimum value of the distance threshold;

d_{\max}

- the maximum value of the distance threshold;

d_{k_{i}, k_{i - 1}}

- the mean value of the Euclidean distance of the 3D coordinates of all matching points of the ith keyframe and the i-1st keyframe.

The specific steps are as follows:

Let the first frame of the input be the reference frame, and the subsequent consecutive frames are calculated with the selected reference frame in Euclidean distance until the one that meets the condition is the current keyframe. After using the current frame, the above operation is repeated to find all the keyframes. As shown in Figure 6, T0 indicates the reference keyframe and T1 indicates the current keyframe. The motion calculated from the two keyframes is used to estimate the motion model of the current frame and the next frame, and this motion model is used to calculate the position of the feature points in the image at moment t in moment t+1 and the best matching points are cycled around that position early.

3.3. 3D reconstruction

The 3D reconstruction is first performed using the matched pairs of feature points on the image, and then a second projection, called reprojection, is performed using the coordinates of the computed 3D points and the computed camera matrix. For a three-dimensional point P, the projection is:

d_{i} p_{i} = K (R P_{i} + t)

(7)

Measurement errors are always inevitable due to the imperfect accuracy of measuring instruments and the influence of human factors and external conditions. Therefore, there is a certain projection error between the projection points, which is called reprojection error, referring to the difference between the projection and reprojection of the real three-dimensional space points on the image plane, and in order to deal with the problem of errors in these projection points, the number of observations is often more than the number of observations necessary to determine the unknown quantity, that is, to make redundant observations.

Redundant observations can also cause contradictions between observation results, and these contradictions require optimization of the model to find the most reliable results of the observed quantities and to evaluate the accuracy of the measurement results [25]. The reprojection error of the point feature is calculated as follows:

e_{p} = p - h (ξ, P)

(8)

By constructing a least squares problem with the reprojection error of all points as a cost function, Eq:

ξ = \arg \min_{ξ} {\sum_{i} ‖p_{i} - \frac{1}{d_{i}} K \exp (ξ^{\land}) p_{i}‖}^{2}

(9)

For the calculation of the minimized reprojection error, the texture weight values of the feature points are added:

ξ = \arg \min_{ξ} {\sum_{i} w ‖p_{i} - \frac{1}{d_{i}} K \exp (ξ^{\land}) p_{i}‖}^{2}

(10)

Before calculating the least squares optimization problem, it is necessary to know the derivative of each error term with respect to the optimization variables, i.e., linearization:

e (x + Δ x) \approx e (x) + J Δ x

(11)

When the pixel coordinate error

e

is two-dimensional and the camera pose

x

is six-dimensional,

J

is a 2 × 6 matrix. Transforming to the spatial point sitting under the camera coordinates is marked as

P'

, taking out its first three dimensions:

P' = {(\exp (ξ^{\land}) P)}_{1 : 3} = {[X', Y', Z']}^{T}

(12)

Then the camera projection model is:

d u = K P'

(13)

Eliminating d yields:

u = f_{x} \frac{X'}{Z'} + c_{x}, v = f_{y} \frac{Y'}{Z'} + c_{y}

(14)

Consider the derivative of the change in

e

with respect to the amount of perturbation:

\frac{\partial e}{\partial δ ξ} = \lim_{δ ξ \to 0} \frac{e (δ ξ \oplus ξ)}{δ ξ} = \frac{\partial e}{\partial P'} \frac{\partial P'}{\partial δ ξ}

(15)

Where

\oplus

denotes the left multiplicative perturbation on the Lie algebra. With the relationship between the variables obtained, it is deduced that:

\frac{\partial (T P)}{\partial P'} = {(T P)}^{⊙} = [\begin{matrix} I & - P'^{\land} \\ 0^{T} & 0^{T} \end{matrix}]

(16)

By taking the first 3 dimensions in the definition of

P'

and multiplying the two terms together, we obtain the 2 × 6 Jacobi matrix:

\frac{\partial e}{\partial δ ξ} = - [\begin{matrix} \frac{f_{x}}{Z'} & 0 & \frac{f_{x} X'}{Z'^{2}} & \frac{f_{x} X' Y'}{Z'^{2}} & f_{x} + \frac{f_{x} X'^{2}}{Z'^{2}} & - \frac{f_{x} Y'}{Z'} \\ 0 & \frac{f_{y}}{Z'} & - \frac{f_{y} Y'}{Z'^{2}} & - f_{y} - \frac{f_{y} Y'^{2}}{Z'^{2}} & \frac{f_{y} X' Y'}{Z'^{2}} & \frac{f_{y} X'}{Z'} \end{matrix}]

(17)

This Jacobi matrix describes the first-order variation of the reprojection error with respect to the Lie algebra of camera poses. For the derivative of e with respect to

P

e

spatial point:

\frac{\partial e}{\partial P} = \frac{\partial e}{\partial P'} \frac{\partial P'}{\partial P}

(18)

Regarding the second item, by definition:

P' = \exp (ξ^{\land}) P = R P + t

(19)

Then:

\frac{\partial e}{\partial P} = - [\begin{matrix} \frac{f_{x}}{Z'} & 0 & - \frac{f_{x} Y'}{Z'} \\ 0 & \frac{f_{y}}{Z'} & - \frac{f_{y} Y'}{Z'^{2}} \end{matrix}] R

(20)

So, the two derivative matrices of the observed camera equations with respect to the camera pose and feature points are obtained.

4. Experimental verification

4.1. System Validation

The visual odometer system built in this paper was experimented with using the KITTI dataset, which uses data obtained from GPS and inertial guidance system measurements as the reference path, the image acquisition frequency is 10Hz, the image resolution is 1241*376, and the camera parameters are shown in Table 1:

Because different distance thresholds yield different keyframe intervals, it is necessary to know and find the effect of different keyframe intervals on the accuracy of the system. The KITTI dataset 01 image sequence has a total of 1101 frames of binocular images, and the statistics of different keyframe rates are shown in Table 2 for five sets of experiments; 05 sequence has a total of 2761 frames, and eight sets of experiments, and the statistics of different keyframe rates are shown in Table 3.

The average translation error and rotation error of the system at different keyframe intervals for 01 sequence and 05 sequence are counted in Figure 7(a) and (b). It can be seen from the results that the average translation error and rotation error have the same trend. The error of the system first decreases and then increases as the key frame rate becomes larger, mainly because the keyframe used becomes less effective when the interval is small, and when the interval is too large, the use of uniform motion. The actual motion of the vehicle cannot be accurately described, and the effect is not very good. From the statistical results, the keyframe rate should be selected at 10%-12%.

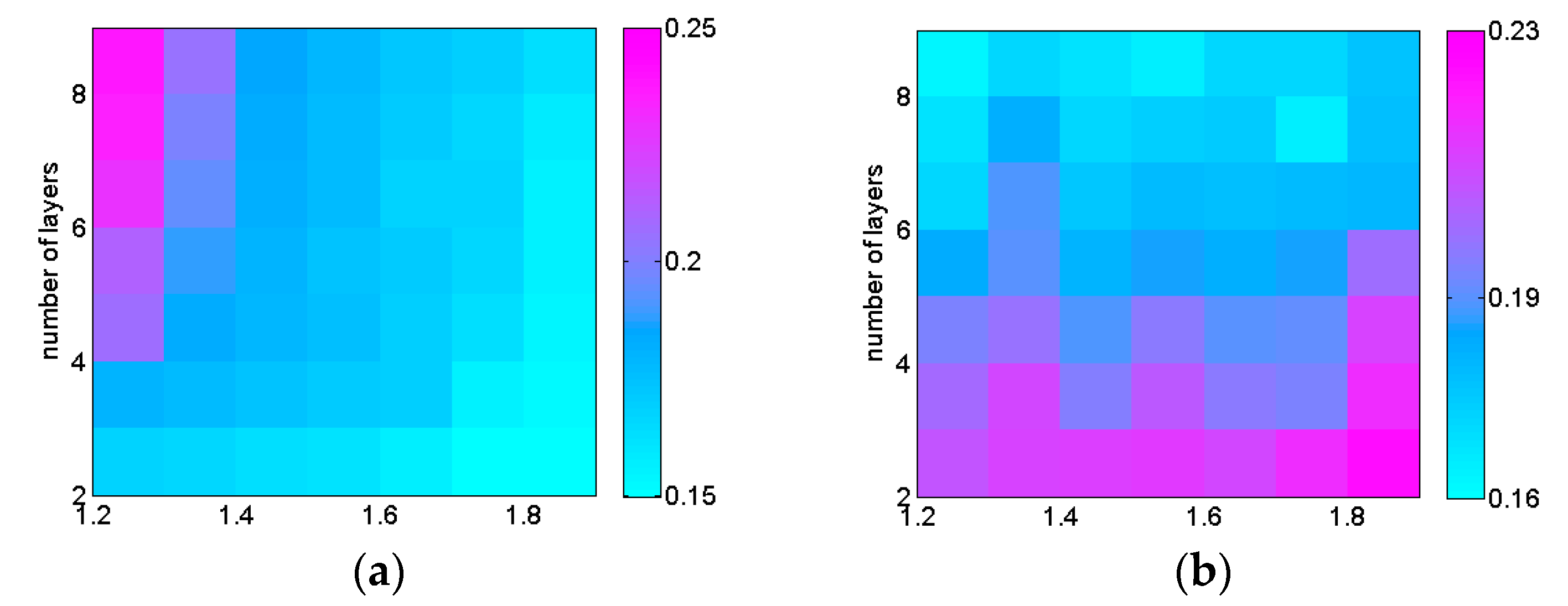
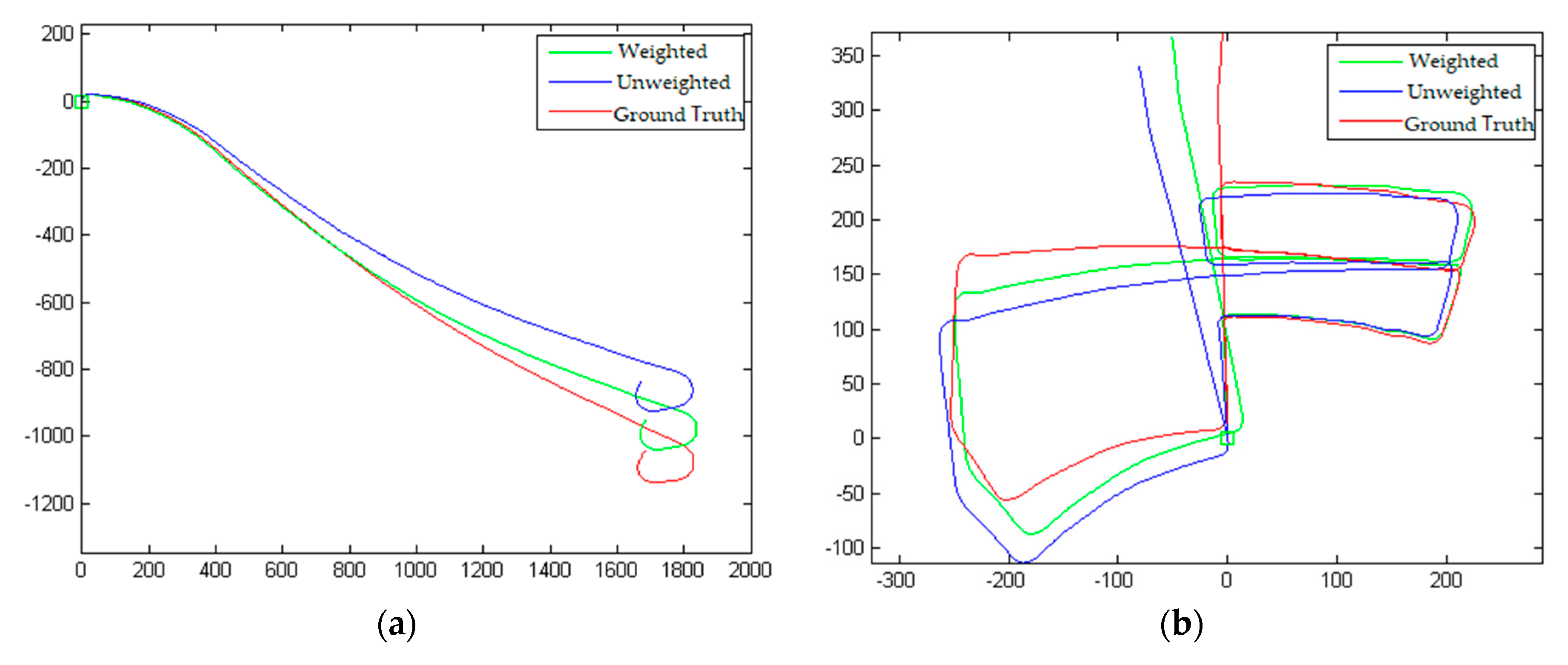
4.2. Verify texture weighting impact

The computational results of 01 and 05 image sequences without weighting (VISO2) and with weighting are compared in Figure 8, where the coordinate unit is m. The environment of 01 image sequence is a highway and that of 05 image sequence is a small highway. The red path represents the groundtruth, the blue path is the calculation result when there is no weight, and the green path is the calculation result when there is weight. From the figure, it can be seen that the calculated results with weights are better than those without weights in both experiments, which initially verifies the effectiveness of this method.

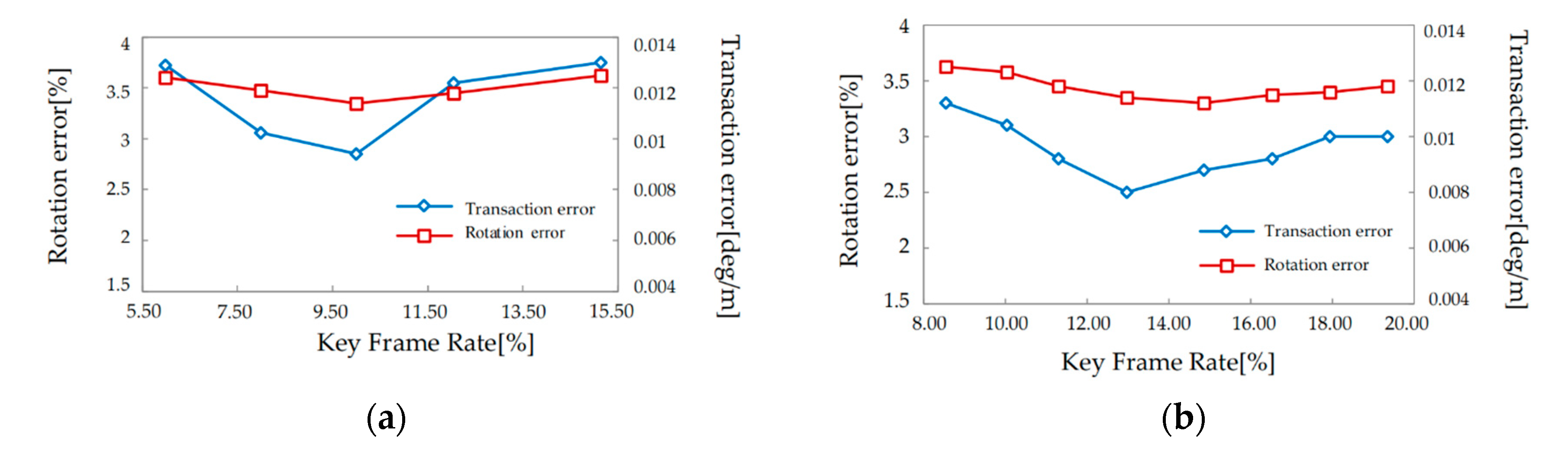
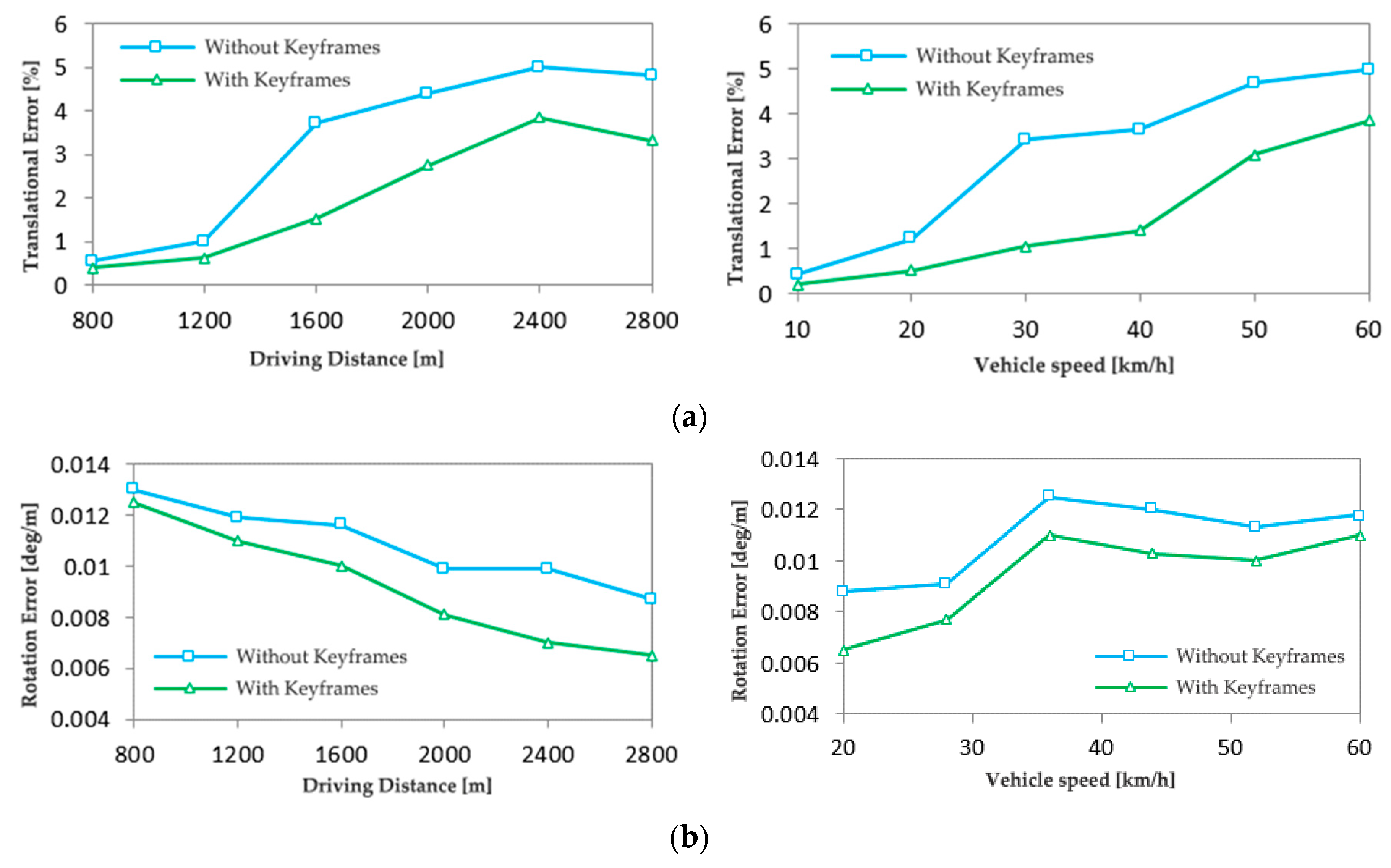
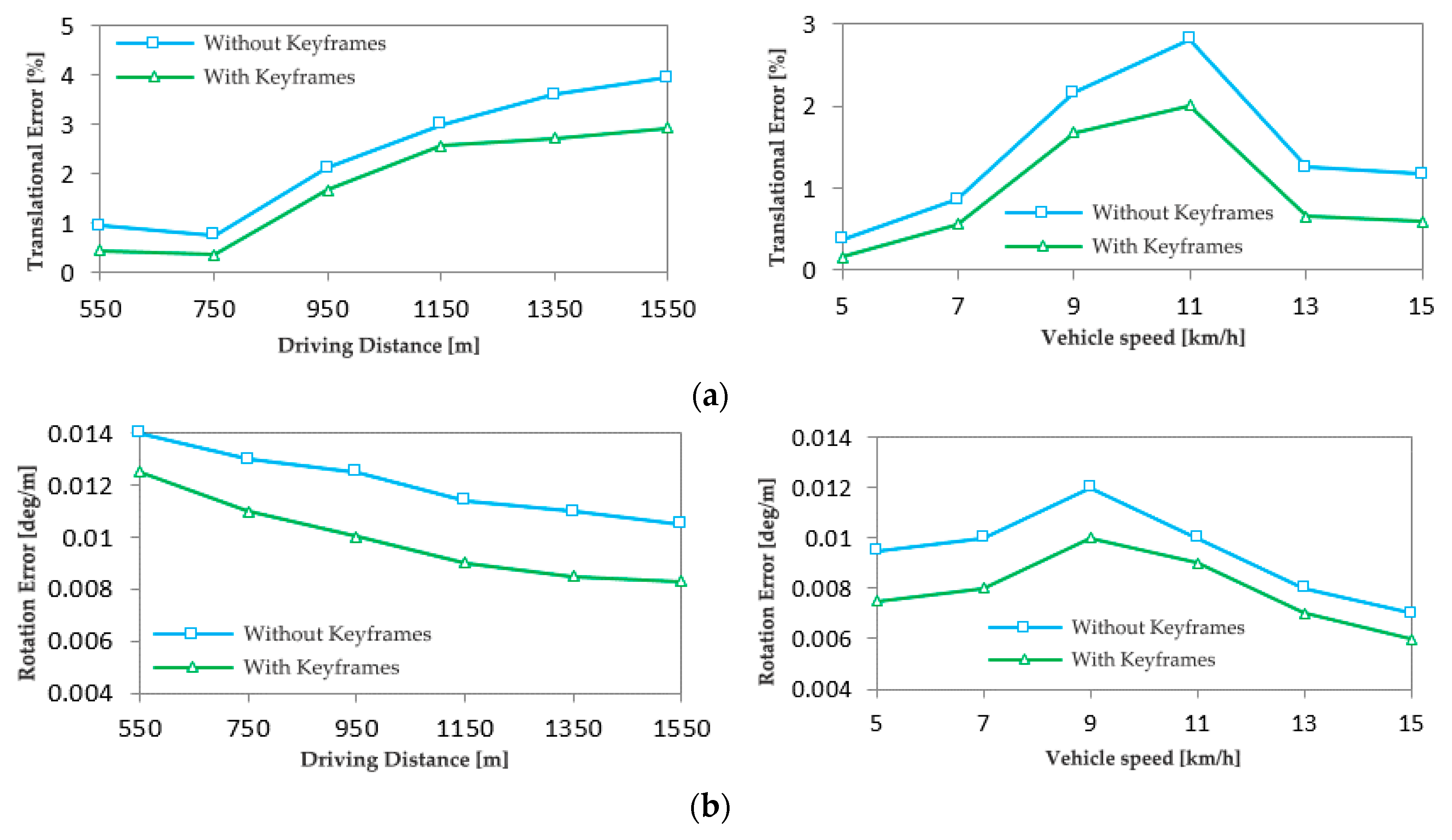
4.3. Verification of keyframes

Comparing the calculation results with and without keyframes, Figure 9 and Figure 10 give a comparison of the translation error and rotation error of the 01 and 05 image sequences. From the experimental results, the average translation error of the 01 image sequence calculated with keyframes in Figure 9 is 2.8%, the maximum translation error is 3.8%, the average rotation error is 0.0095deg/m, and the maximum rotation error is 0.0125deg/m. The average translation error for the 05 image sequence calculated with keyframes in Figure 10 is 2.2%, the maximum translation error is 2.9%, the average rotation error is 0.0087deg/m, and the maximum rotation error is 0.0125deg/m. The method of adding keyframes for inter-frame feature matching greatly reduces systematic error at low speeds.

The reason for the gradual increase in positioning error of the above two methods is that visual odometry is a relative positioning method, so the error of the system increases with mileage.

To further verify the performance of the system, a comparative analysis was done with the current common VISO2[23], VISO2+GP[24], and TGVO[25] open-source systems, and the system performance was described using a boxplot of the relative positioning error. The upper and lower sides of the rectangular box in the boxplot represent the upper and lower quartiles of the data, the end lines of the upper and lower extensions of the rectangular box represent the maximum and minimum observations, the horizontal line in the rectangular box represents the median of the data, and the outlier points are represented by the scatter points on the outside of the observations. Comparative experiments were conducted on four data sets, KITTI_00, KITTI_01, KITTI_05, and KITTI_007, and the results are shown in Figure 11.

As seen from the results in Figure 11, the visual odometers proposed in this paper all show good performance with average relative errors of 2.3%, 2.2%, 3.5% and 3.4%, respectively. In Table 4, the statistics of the time used by the visual odometer system for each main process in the calculation process in ms, Min represents the shortest time used, Max represents the longest time used, and Avg represents the average time used for each frame.

The above experiments demonstrate that the point feature-based visual odometry proposed in this paper has some improvement in localization accuracy in the dataset experiments compared with several other common open-source VO systems.

5. Conclusions

In response to the problem that the feature point method leads to poor stability of vehicle driving in complex environment, the visual odometer based on improved ORB features is proposed to obtain better results.

Propose the calculation of weights for different texture regions, with high matching weights for high texture regions and low matching weights for low texture regions, so that feature points can be evenly dispersed throughout the image and better matching results.
Using the predicted motion model of keyframes, i.e., the motion of feature points between adjacent keyframes is obvious so that the system is more stable and less prone to errors when the vehicle is driving at slow speed. The test using KITTI dataset shows that the key frame rate reaches 10%-12% error minimum. When comparing the translation and rotation errors with and without keyframes using the KITTI dataset, the presence of keyframes clearly shows a reduction in translation and rotation errors.
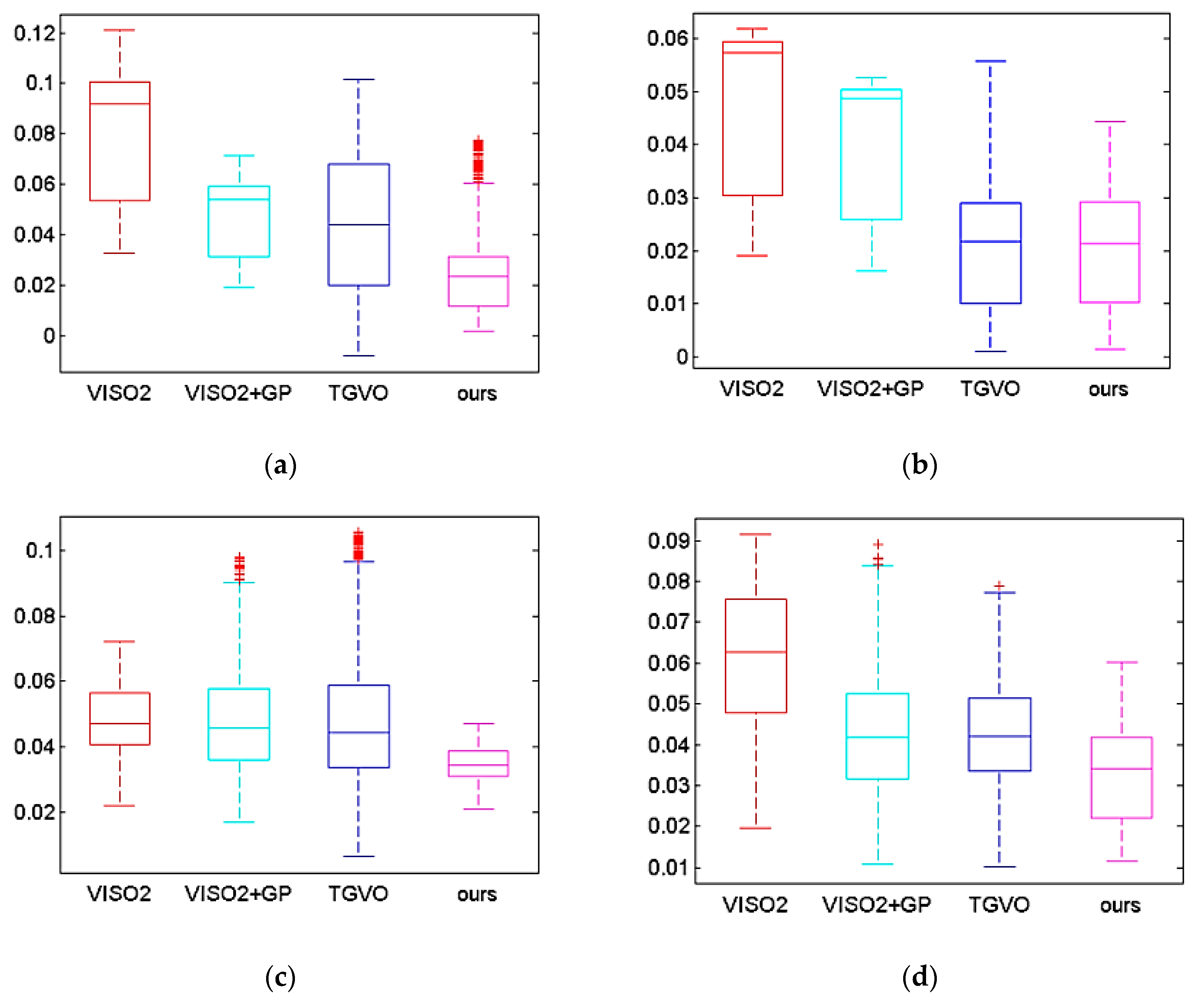
This system compares the performance of the VISO2, VISO2+GP, and TGVO verification systems, and the comparison experiments were conducted on four sequences of the KITTI dataset, and the errors were lower than those of the above three systems.

References

Li, S.; Wang, G.; Yu, H.; Wang, X. Engineering Project: The Method to Solve Practical Problems for the Monitoring and Control of Driver-Less Electric Transport Vehicles in the Underground Mines. World Electr. Veh. J. 2021, 12, 64. [Google Scholar] [CrossRef]
Boersma, R.; Van Arem, B.; Rieck, F. Application of Driverless Electric Automated Shuttles for Public Transport in Villages: The Case of Appelscha. World Electr. Veh. J. 2018, 9, 15. [Google Scholar] [CrossRef]
Zhang, C.; Lei, L.; Ma, X.; Zhou, R.; Shi, Z.; Guo, Z. Map Construction Based on LiDAR Vision Inertial Multi-Sensor Fusion. World Electric Vehicle Journal. 2021, 12, 261. [Google Scholar] [CrossRef]
Ma, F.W.; Shi, J.Z.; Ge, L.H.; et al. Research progress of monocular vision odometer for unmanned vehicles. Journal of Jilin University (Engineering Edition) 2020, 50, 765–775. [Google Scholar]
Zeng, Q.H.; Luo, Y.X.; Sun, K.C.; et al. A review on the development of SLAM technology for vision and its fused inertia[J]. Journal of Nanjing University of Aeronautics and Astronautics 2022, 54, 1007–1020. [Google Scholar]
Zhou, F.Y.; Gu, P.L.; Wan, F.; et al. Methods and techniques for multi-motion visual odometry. Journal of Shandong University (Engineering Edition) 2021, 51, 1–10. [Google Scholar]
Campos, C.; Elvira, R.; Rodríguez, J.J.; et al. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual-Inertial and Multi-Map SLAM. IEEE Transactions on Robotics 2020, 37, 1874–1890. [Google Scholar] [CrossRef]
Chen, Z.; Liu, L. Navigable Space Construction from Sparse Noisy Point Clouds. IEEE Robotics and Automation Letters 2021, 6, 4720–4727. [Google Scholar] [CrossRef]
Zhang, B.; Zhu, D. A Stereo SLAM System with Dense Mapping. IEEE Access 2021, 9, 151888–151896. [Google Scholar] [CrossRef]
Seichter, D.; Köhler, M.; Lewandowski, B.; Wengefeld, T.; Gross, H.M. Efficient RGB-D Semantic Segmentation for Indoor Scene Analysis[C]. 2021 IEEE International Conference on Robotics and Automation (ICRA), 2021: 13525-13531.
Raúl Mur-Artal, J.M.; Montiel, M.; Tardós, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System[J]. IEEE Transactions on Robotics 2015, 3, 1147–1163. [Google Scholar] [CrossRef]
Bei, Q.; Liu, H.; Pei, Y.; Deng, L.; Gao, W. An Improved ORB Algorithm for Feature Extraction and Homogenization Algorithm[C]. 2021 IEEE International Conference on Electronic Technology, Communication and Information (ICETCI), 2021: 591-597.
Chen, J.S.; Yu, L.L.; Li, X.N.; et al. Loop detection based on uniform ORB[J]. Journal of Jilin University (Engineering and Technology Edition), 2022: 1-9.
Yao, J.J.; Zhang, P.C.; Wang, Y.; et al. An algorithm for uniform distribution of ORB features based on improved quadtrees[J]. Computer Engineering and Design 2020, 41, 1629–1634. [Google Scholar]
Zhao, C. Research on the uniformity of SLAM feature points and the construction method of semantic map in dynamic environment[D]. Xi’an University of Technology, 2022.
Lai, L.; Yu, X.; Qian, X.; Ou, L. 3D Semantic Map Construction System Based on Visual SLAM and CNNs[C]. IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, 2020: 4727-4732.
Ranftl, R.; Bochkovskiy, A.; Koltun, V. Vision Transformers for Dense Prediction[C]. 2021 IEEE/CVF International Conference on Computer Vision (ICCV), 2021: 12159-12168.
Li, G.; Zeng, Y.; Huang, H.; et al. A Multi-Feature Fusion Slam System Attaching Semantic In-Variant to Points and Lines[J]. Sensors 2021, 21, 1196. [Google Scholar] [CrossRef] [PubMed]
Fan, X.N.; Gu, Y.F.; Ni, J.J. Application of improved ORB algorithm in image matching[J]. Computer and Modernization 2019, 282, 5–10. [Google Scholar]
Xu, H.; Yang, C.; Li, Z. OD-SLAM: Real-Time Localization and Mapping in Dynamic Environment through Multi-Sensor Fusion[C]. 2020 5th International Conference on Advanced Robotics and Mechatronics (ICARM), 2020:172-177.
Xu, H.; Yang, C.; Li, Z. OD-SLAM: Real-Time Localization and Mapping in Dynamic Environment through Multi-Sensor Fusion[C]. 2020 5th International Conference on Advanced Robotics and Mechatronics (ICARM). 2020(7): 75604-75614.
Zhao, L.; Liu, Z.; Chen, J.; Cai, W.; Wang, W.; Zeng, L. A Compatible Framework for RGB-D SLAM in Dynamic Scenes[J]. IEEE Access 2019, 7, 75604–75614. [Google Scholar] [CrossRef]
Geiger, A.; Ziegler, J.; Stiller, C. StereoScan: Dense 3d reconstruction in real-time[J]. IEEE Intelligent Vehicles Symposium 2011, 32, 963–968. [Google Scholar]
Geiger, A. Are we ready for autonomous driving? The KITTI vision benchmark suite[C]// Computer Vision and Pattern Recognition. IEEE, 2012:3354-3361.
Kitt, B.; Geiger, A.; Lategahn, H. Visual odometry based on stereo image sequences with RANSAC-based outlier rejection scheme[C]// Intelligent Vehicles Symposium. IEEE, 2010: 486-492.

Figure 1. Block diagram of stereo vision odometer system.

Figure 2. Calculation time and mismatch rate under different parameter matching. (a) Calculation time / 10-2s; (b) False match rate.

Figure 3. Features Distribution. (a) Distribution of original features; (b) Region segmentation results.

Figure 4. ORB Feature Harris Response Value.

Figure 6. Motion model estimation based on keyframe.

Figure 7. Comparison of errors at different key frame rates. (a)KITTI_01; (b)KITTI_05.

Figure 8. Comparison of Dataset Results. (a)KITTI_01; (b)KITTI_05.

Figure 9. Error contrast diagram of sequence 01. (a) Translation error; (b) Rotation error.

Figure 10. Error contrast diagram of sequence 05. (a) Translation error; (b) Rotation error.

Figure 11. Relative error contrast diagram. (a)KITTI_00; (b)KITTI_01; (c)KITTI_05; (d)KITTI_07.

Table 1. Binocular camera parameters.

Focal length/mm	Coordinates of main point	Aberration factor	Baseline /m
718.86	(607.19,185.22)	0.00	0.54

Table 2. Key frame interval statistics of sequence 01.

Serial number	Number of frames	Key Frame Count	Key Frame Rate(%）
1	1101	66	5.99
2	1101	88	8.00
3	1101	110	10.00
4	1101	133	12.05
5	1101	167	15.15

Table 3. Key frame interval statistics of sequence 05.

Serial number	Number of frames	Key Frame Count	Key Frame Rate(%）
1	2761	236	8.55
2	2761	277	10.03
3	2761	312	11.30
4	2761	358	12.97
5	2761	410	14.85
6	2761	456	16.52
7	2761	495	17.93
8	2761	534	19.34

Table 4. Algorithm calculation time statistics table.

Time(ms)	Min	Max	Avg
Feature extraction and matching	14.6	34.6	20.7
3D reconstruction	5.1	12.6	8.5
Movement estimation	2.9	10.7	6.4
Total time	23.9	52.3	35.6

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer