Prerpints.org logo
Preprint
Article

Estimation of nutrient loads in an agricultural area: Case study of the Lobo Basin in Côte d'Ivoire (West Africa)

Altmetrics

Downloads

166

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

20 July 2023

Posted:

21 July 2023

You are already at the latest version

Alerts
Abstract
Eutrophication in the Lobo watershed remains a major problem. The work carried out has focused on chemical and biological analyzes in the lake or in its immediate environment: they did not sufficiently take into account the diffuse transfer of nutrients over the entire watershed. This study aims to assess the nutrient (N and P) loads in the Lobo watershed, an agricultural area, to understand the spatio-temporal impacts of land management practices on eutrophication. The methodology uses two steps: streamflow calibration and nutrient (N and P) estimation using the Soil and Water Assessment Tool (SWAT) watershed model. Thus, the nutrient inputs were estimated based on the levels of N and P in every kilogram of NPK-type fertilizers applied by farmers. The average quantities of N and P applied to the crops were 47.24 kg N/ha and 21.25 kg P/ha. Results show a good performance on flow calibration as evidenced by evaluation criteria R2, NSE and PBIAS of 0.63, 0.62 and -8.1, respectively. The yields of inorganic N and soluble P varied from 0 to 0.049 kg N/ha and from 0 to 0.31 kg P/ha. These results show that the crops’ in-organic nitrogen requirements were higher than the demands for soluble phosphorus. Simulations relating to the organic N transfer revealed values ranging from 0.2 to 5 kg N/ha, while the transport of organic phosphorus was estimated to vary from 0.3 to 1.3 kg P/ha.
Keywords: 
Subject: Environmental and Earth Sciences  -   Water Science and Technology

1. Introduction

FAO statistics show that agriculture, hunting, fishing and forestry supported 2.57 billion people at the start of the new millennium. This figure represents 42 percent of humanity, including those who work within these sectors and their families. Agriculture is essential for the economy in most developing countries and even in industrialized countries like the USA, where agricultural exports reached $177 billion in 2021[1]. Today, few countries are able to experience significant economic growth without agricultural development.
In Côte d'Ivoire, one estimate about 60% the population living in rural areas, and the agricultural sector occupies 30.7% of the Gross Domestic Product (GDP). Thus, the State of Côte d'Ivoire has set up several Government agencies structures such as National Rural Development Support Agency (ANADER in french), the National Center for Agronomic Research of Cote d'Ivoire (CNRAin french), the Marketing of Food Products Office (OCPV in french) and the Development of Rice Cropping National Office (ONDR in french) to oversee and assist with agricultural management and development for sustainable agricultural growth and self-sufficiency of foods. Faced with the rising demand linked to population growth, the Government of Côte d'Ivoire uses these agencies to encourage traditional farmers and industrialists to use chemicals to increase their agricultural productivity. However, a lack of training linked to insufficient resources in the sustainable use of chemicals and loose policy on environmental protection and quality standards have led to increased usage of agricultural inputs. This irresponsible usage means that these inputs are now polluting the water bodies and river networks of Côte d'Ivoire, causing major eutrophication problems. Several previous published studies [2,3,4,5] demonstrated eutrophication of the Lobo water body based on analyzed biological and physico-chemical parameters. These studies, although important didn’t alow us to understand deeply the eutrophication phenomenon in the Lobo basin because the samples were punctual at the level of the reservoir but failed to relate critical sources in the drainage areas to the water quality problem. To address the lack of on-site data in that context, methodologies based combining hydrological models and Geographic Information Systems (GIS) are supposed to be more efficient. Watershed Hydrological models are commanded by mathematical formulas in link with physically-based process and conceptual models. The basin hydrologic functioning includes an analogy and a concept. In the analogy, soils and groundwater are considered as reservoirs whose rate of emptying depends on the filling. The physically-based models are directly linked to physical processes [6,7]. The principle of calculation is based on precise physical and empirical representations of natural processes. Empirical models [8] such as the USLE (Universal Soil Loss Equation) erosion model [9], derived from laboratory or field experiments. These models are global: this the case of the GR4 model which can represent the watershed in a single entity for global assessment [10]. However, global-scale models are not suitable for studying the hydrological processes of an agricultural watershed because they do not consider the watershed variability spatial of phenomena like runoff or erosion. So, they cannot take into account the land uses effects in processes. Thus, semi-distributed models such as the Soil and Water Assessment Tool (SWAT), come in addition to overcome this lack by now, considering topography, land cover, soil and soil management practices in the basin.
This study aims to assess the nutrient loads from agricultural practices in the Lobo watershed to understand the spatio-temporal evolution of nutrient transport processes using the SWAT model. The assessment is based on the amounts of fertilizer applied to each crop.

2. Materials and Methods

2.1. Materials

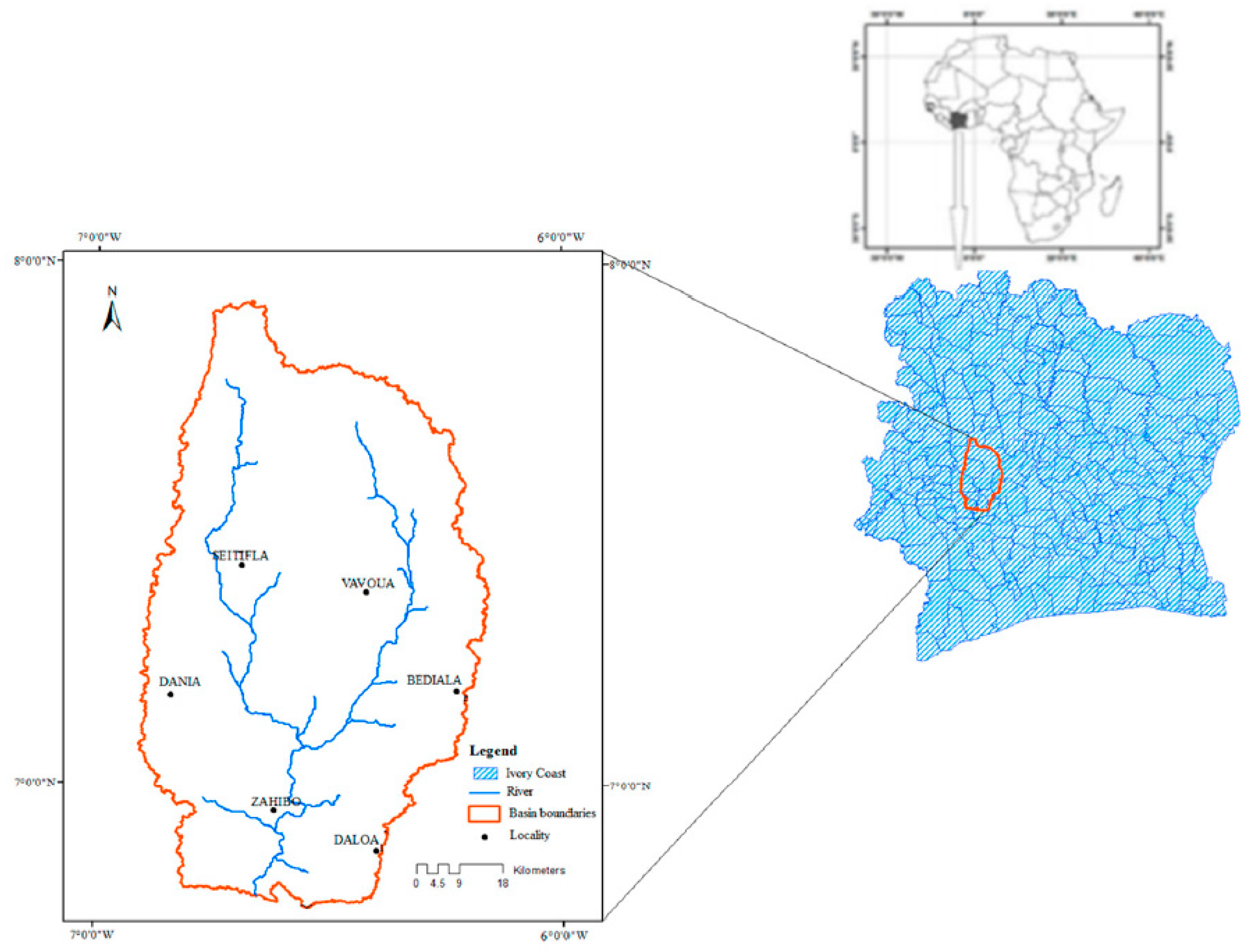
2.1.1. Study area

The Lobo watershed at Nibéhibé is located in west-central Côte d'Ivoire between 6°00 and 7°00 West longitude and 6°54 and 8°00 North latitude. It covers about 6,442.66 km2 as area (Figure 1). The plateaus about 200 to 400 m altitude compose the relief. This makes it a little bit contrast [11]. The underlying geology is primarily composed of granites. The peaks of precipitation are observed in the month of September with 275 mm and in May with 150 mm. This makes it possible to define two seasons: a dry season and a rainy season. The dry season is from November to February while the rainy season is observed from March to October. The average annual rainfall recorded in the study area was 1335 mm from 1991-2020. This value of rain amount recorded annually is lower than reported [12] in that findings showed 1437,4 mm as annual rainfall from 1943 to 2010 in the same basin using the GR4J model, or a decrease of 7.14%.
The study area's vegetation is composed of dense moist semi-deciduous forest and cleared mesophilic forest. Ferralitic soil, strongly or moderately desaturated, governs this area. The main activity is agriculture based on coffee, cocoa, rubber, oil palm and food crops [13]. the drinking water supply comes from the Lobo reservoir exploited by SODECI.

2.1.2. Data

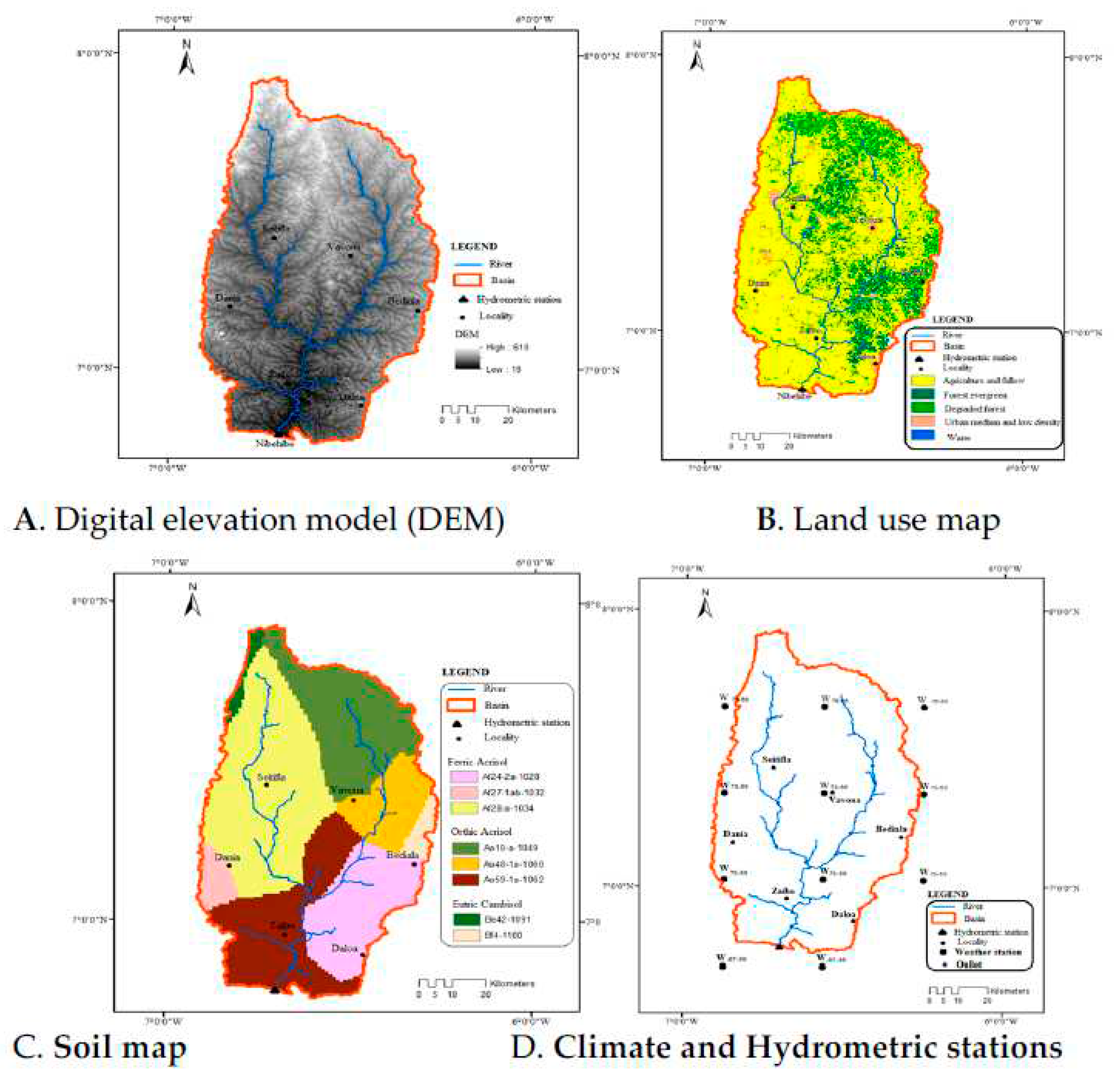
Data used in this study were Digital Elevation Model (DEM), land use map, soil map, soil physicochemical and biological properties, climate and agronomic data. The Figure 2 shows essential input data for the SWAT model.

Digital Elevation Model (DEM)

The Digital Elevation Model (DEM) of 30 m x 30 m resolution, in the Northern Hemisphere projection UTM Zone 30, downloaded from the website https://search.earthdata.nasa.gov/search has been used to extract the hydrographic network and delineate the watershed.

Land use map

The land use map has been obtained throughout four (4) February 22, 2018 sentinel-2 satellite images treatment using ENVI 4.7. These images include four (4) bands that are 2, 3, 4 and 8 and were obtained from the website https://scihub.copernicus.eu/dhus/#/home. For this study we considered Five classes of land use: forest evergreen (11%), degraded forest (9%), agriculture and fallow (77%), urban (0.5%), and water (2.5%).

Soil data

To run the SWAT model, we need texture, available water content, hydraulic conductivity, bulk density, and organic carbon content of different soil layers. These data are available in the FAO database [15] and have been completed by physicochemical properties obtained after field sampling and in-laboratory analyses. The dominant soil of the basin is the sandy-clay-loam about 38%, followed by the sandy-loam soil (32%) of the basin.

Hydro-climate data

The climate date at a daily time step were obtained from the swat model website http://globalweather.tamu.edu/. These data include minimum and maximum temperatures, precipitation, relative humidity, solar radiation and wind speed. These data were The use of these data is justified by the fact that in the watershed, there are few data available that can allow adequate hydrological modeling of the watershed. Some authors such as Mbungu and Kahaigili [16] believe that global gridded climatological datasets (GGCDs) could be combined with hydrological modelling to understanding hydrological processes in data-scarce environments. Therefore, for this study, we have used Eleven (11) climatic stations over the period 1979-2014. As for the flow data, stream gauge data were collected from the National Drinking Water Office (ONEP in french) for the period from 1981 to 1994 at Nibehibé hydrometric station.

Agronomic data

The types of fertilizers, the doses applied to each type of crop, the types of crops, agricultural practices and agricultural calendars on the watershed were used in this study (http://www.cnra.ci/listefiche.php).

2.1.3. Computer software

The computer tools used in this study consist of QSWAT 1.9 in the QGIS 2.6.1 interface, SWATCUP 2019, ENVI 4.7 and the WGN program. QSWAT 1.9 made it possible to delimit the watershed into sub-watersheds and to extract the hydrographic network and to simulate the water flow and the nutrients transfer. SWATCUP 2019 was used to calibrate the water flow. ENVI 4.7 has been useful in the processing of satellite images for obtaining land use. As for the WGN program, it made it possible to calculate the statistical parameters from the climatic data.

2.2. Methods

The methodology based upon the SWAT (Soil and Water Assessment Tool) model was structured into two main stages: flow calibration and nutrient estimation.

2.2.1. Flow calibration

Model and software description SWAT Model description

SWAT is a semi-distributed agro-hydrological model [17] with a daily time step. SWAT is used for evaluating water quality and quantity, agricultural practices management, surface and subsurface water management and sediment, nutrient and pesticide transfer. SWAT is used worldwide by a large scientists community.
This model is based on the water balance equation which is as follows [18]:
SWt = SWo + Σ (Rday +IRR– Qsurf – Ea – Wseep), (Eq.1)
where SWt is the final soil water content (mm) of the day, SWo is the in soil initial water content (mm), Rday is the daily rainfall (mm), IRR is irrigation volume added to the soil (mm), Qsurf is the surface runoff volume (mm), Ea is the actual evapotranspiration (mm), and Wseep is percolation loss from the soil profile into the shallow aquifer (mm).

SWAT-CUP and SUFI-2 algorithm

Uncertainties may occur while setting up and running the model. Uncertainties come either from measurement errors or from the model itself [19,20,21]. To be used efficiently, the model’s performance must be tested. This study tested the correlation between observed data and simulated outputs statistically and graphically. Thus, Swat-cup (SWAT Calibration Uncertainty Program) was used to optimize the flow model. The program is the most widely used tool by the SWAT community. SWAT-CUP allows to perform calibration, uncertainty and global sensitivity analysis automatically (Table 1). Several methods are integrated into the SWAT-CUP program. We have Sequential Uncertainty Fitting version 2 (SUFI-2) [22,23], Generalized Likelihood Uncertainty Estimation (GLUE) [24], Particle Swarm Optimization (PSO) [25], Parameter Solution (PARASOL) [26] and Markov Chain Monte Carlo (MCMC) [27].
Because of its simplicity in its use, the SUFI 2 method has permitted to perform global parameter sensitivity analysis, uncertainty analysis and calibration [28].

Global sensitivity analysis

The analysis of global sensitivity begins with the definition of the objective function. Objcetive functions wthin SUFI2 include R2, Chi2, NS, and R2 multiplied by the line regression coefficient b, bR2, and SSQR (sum of squared errors) coefficients. But for this study, NS and R2 coefficients were the objective functions used. NS is used to analyse the strength of the model predictions and while R2 coefficient is related to the correlation between simulations and observed values. Then, the values of the parameters to be optimized, are chosen based on Equation 2 [29]:
bj,abs _min ≤ bj ≤ bj,abs_max , j=1…m (Eq.2),
where bj is the jth parameter and m is the number of parameters to be estimated.
The parameter global sensitivity in each simulation is accounted by the sensitivity matrix J, of g (bj) [29] :
Jij = ∆gi/∆bj i=1…C2n (Eq.3),
where bj is the parameter, g is global sensitivity and i is all possible combinations of two simulations and j is the number of columns (number of parameters).
Latin Hypercube sampling is the sampling method used in this study. It makes it possible to calculate the global sensitivity by calculating a multiple regression system of the parameters considered [29]:
g = α + ∑ i = 1 m β i b i (Eq.4),
where α = σ s σ m , β = μ s μ m . σ s and σ m are considered to be the respective standard deviations of the simulated and observed data; μ s and μ m are the averages of the simulated and observed data.
The relative impact of each parameter on the flow is identified from a statistical test. This impact is noted bi. The global sensitivity is related to the variation of the objective function which depends on the observed variation of the parameter considered when all parameters change.

Uncertainty analysis

P-factor and R-factor are used to calculate the uncertainties at 2.5% (Xl) and 97.5% (Xu) percentiles of the cumulative distribution at each point. P-factor indicates the percentage of observed data bracketed by 95PPU. R-factor is the average thickness of the 95PPU band obtained from the standard deviation of the observed data [20].

Calibration analysis

We chose NSE, R2 and PBIAS as objective functions to analyze the performance and accuracy of the simulations. The PBIAS measures the percentage of bias. When PBIAS is 0, the simulation is said to be accurate. A positive PBIAS shows an underestimation of the model, while negative values indicate an overestimation of the model bias [30]. Its use makes it possible to refine and make more precise the predictions of the model [31] in [32,33,34,35,36,37,38,39,40,41,42,43]. NSE (equation 5) varies from -∞ to 1 (for a strong link between observed and simulated values). Equation (6) is used to calculate PBIAS. Moriasi et al. [35] made the classification of model performance:
PBIAS <± 10: very good performance model;
±10<PBIAS<±15: good performance model;
± 15 <PBIAS < ± 25: satisfactory performance;
PBIAS > ± 25: unsatisfactory performance.
R2 is calculated according to equation (7); it varies from 0 to 1, 1 representing a perfect simulation [44]. A value greater than 0.5 is often accepted because it expresses a good restitution of the observed data [32].
N S E = 1 − ∑ i = 1 n Q i o b s − Q i s i m 2 ∑ i = 1 n Q i o b s − Q m e a n 2 (Eq. 5)
P B I A S = ∑ i = 1 n Q i o b s − Q i s i m * 100 ∑ i = 1 n Q i o b s 2 (Eq. 6)
R ² = ( ∑ i = 1 n Q i o b s − Q i s i m ( Q i s i m − Q i s i m ¯ ) ) ² ∑ i = 1 n ( Q i o b s − Q i o b s ¯ ) ² ∑ i = 1 n ( Q i s i m − Q i s i m ¯ ) ² (Eq. 7)
with Qiobs observed flow, Qisim simulated flow, Qmean average observed flow, Q i o b s ¯ average observed flow and Q i s i m ¯ average simulated flow.

Model setup

The model implemented follows the methodology adopted by Koua et al (2019) [45]. The Lobo watershed in Nibéhibé covers an area of 6,442.66 km2. The delimitation of the watershed and the extraction of the hydrographic network was possible thanks to the processing of the DEM under QSWAT. The D8 algorithm [46] integrated in QGIS makes it easy to extract watershed boundaries and river network using QSWAT. This step is followed by the integration of meteorological data, land use, pedology and their physico-chemical properties. Then, the hydrological response units (HRU) combining land use type, soil type and slope in a sub-basin were calculated. HRUs are the basis for calculating for the SWAT model. They highlight the differences in evapotranspiration and other hydrological conditions between different types of land cover. the multiple HRU method of the SWAT model made it possible to constitute 163 HRUs. After that, QSWAT established the various input data tables. This made it possible to integrate information relating to the watershed, pedology, hydrometeorology, the HRUs themselves, water resources and their use, watershed management, wetlands, septic tanks, different reservoirs on the watershed, and the watershed master file. At this stage, the hydrological simulation of the Lobo watershed can be done.

Streamflow calibration process

The flow calibration at a monthly time step was possible by using observed data at the Nibéhibé hydrometric station using the SUFI-2 method [22,23] in the SWAT-CUP program [47]. For this study, ten (10) flow parameters have been used. These parameters were the CN2 expressing the humidity conditions II, the quantity of water available in the soil SOL_AWC, the ESCO factor which translates the compensation coefficient of the soil evaporation, RCHRG_DP which is the fraction of percolation water from the deep aquifer, the re-evaporation coefficient of groundwater GW_REVAP, ALPHA_BF (Baseflow alpha factor), the water depth threshold in the shallow aquifer depth GWQMN required for return flow to occur, the water depth threshold in the shallow aquifer REVAPMN for revaporation to occur, the groundwater delay time GW_DELAY, the CANMX (Maximum storage of canopy). Flow calibration was performed over the period 1981 to 1994. A total of 500 iterations were performed during the monthly water flow simulation process. Then, the Nash–Sutcliffe coefficient (NSE), the percentage of bias (PBIAS) and the R2 determination coefficient were calculated in order to judge the robustness of the SWAT model on this watershed.

2.2.2. Nutrient loads estimation

While reservoir eutrophication processes are significantly influenced by nutrient contents in the water, there exists little information upon the reservoir water quality. Because of the lack of observation data on nitrogen and phosphorus, the estimation of nutrient inputs to the reservoir was made on the basis of the quantity of NPK fertilizers applied to crops in the watershed because these nutrients come from NPK chemical fertilizers [3,4]. Data relating to fertilizers, such as the amount, duration, and frequency of application, were integrated into SWAT according to crops by sub-basin and HRU. The mineral fertilizers are of the xN-yP-zK formula, x, y and z representing respectively the proportions in percentage (%) of N, P and K (Potassium) in 1 kg of fertilizer used. If the fertilizer formula is known, the quantities of N, P and K are determined (Eq. 8 & 9) [48]:
N ( K g ) K g f e r t = % N f e r t × 1 K g ( f e r t ) / 100 (Eq. 8)
P ( K g ) K g f e r t = % P f e r t × 1 K g ( f e r t ) / 100 (Eq. 9)
For this study, only N and P quantities were estimated.
From the soil, the crops take Nitrogen in the form of nitrates [48]. Nitrate transportation within the watershed is done via surface runoff, lateral flow, or percolation. The amount of nitrate contained in runoff is assessed from the nitrate concentration in moving water. This concentration is a proportion of the nitrate mass in the runoff volume [48]. It is calculated according to Eq. 10:
C o n c N O 3 , m o b i l e = N O 3 l y . ( 1 − e x p − w m o b i l e 1 − θ e . S A T l y w m o b i l e , (Eq. 10),
where C o n c N O 3 , m o b i l e is the concentration of nitrate in mobile water for a given soil layer (Kg N/mm H2O), N O 3 l y expresses the quantity of nitrate (Kg N/ha), w m o b i l e is the amount of mobile water in the layer (mm H2O), θ e is the porosity fraction on which the anion exclusion depends, S A T l y is the water content when the soil layer is saturated (mm H20).
The amount of mobile water in the soil layer is assumed equal to that lost by runoff, lateral flow or percolation and can be estimated by equations 11 and 12.
w m o b i l e = Q s u r f + Q l a t , l y + w p e r c , l y for top 10 mm (Eq. 11)
w m o b i l e = Q l a t , l y + w p e r c , l y for lower soil layers, (Eq. 12)
Q s u r f is the depth of surface water runoff on the given day (mm H2O), Q l a t , l y is the height of water escaping from the layer laterally (mm H2O), w p e r c , l y is the amount of percolation water in the underlying soil layer on the given day (mm H2O).
Surface runoff transports nutrients to the top 10 mm above the soil. Equation 13 was used to calculate the amount of nitrate in runoff.
N O 3 s u r f = β N O 3 . C o n c N O 3 , m o b i l e . Q s u r f , (Eq. 13)
N O 3 s u r f is the quantity of nitrate retained during surface runoff (Kg N/ha), β N O 3 represents the nitrate percolation coefficient, C o n c N O 3 , m o b i l e expresses the concentration of nitrate in the runoff water for the top 10 mm of soil (Kg N/mm H2O), Q s u r f is the runoff height of the given day (mm H2O).
Surface runoff allows organic nitrogen mostly attached to sediments transfer to the main channel in the watershed. The amount of organic nitrogen transported with thesediments to the watercourse is calculated using Equation 14 [49,50]:
o r g N s u r f = 0.001 . C o n C o r g N . s e d a r e a h r u . ε N s e d (Eq. 14),
where o r g N s u r f is the amount of organic nitrogen contained in surface runoff transported in Kg N/ha, C o n C o r g N is the concentration in g N/tonne of soil organic nitrogen in the first 10 mm above soil (g N/metric ton soil), sed is the amount of sediment produced on the given day (metric tons), area is the HRU area (ha), and ε N s e d is the nitrogen enrichment rate.
The nitrogen enrichment rate is estimated according to Menzel [51]. Thus, the equation 15 was used to calculate the nitrogen enrichment rate:
ε N s e d = 0.78 . ( C o n c s e d , s u r q ) (Eq. 15),
where C o n c s e d , s u r q is the in runoff sediment concentration (Mg sed/m3 H2O).
The concentration of sediment in surface runoff is calculated according to equation 16 :
C o n c s e d , s u r q = s e d 10 . a r e a h r u . Q s u r f (Eq. 16),
where sed where sed is the amount of sediment on a given day (metric tons), a r e a h r u is the HRU area (ha), and Q s u r f is the amount of runoff on a given day (mm H2O).
The movement of soluble phosphorus in the soil is by diffusion. Due to its low mobility, transfer by surface runoff only concerns soluble phosphorus stored in the top 10 millimeters of soil [50]. The amount of soluble P transferred is calculated from Equation 17:
P s u r f = P s o l u b l e , s u r f . Q s u r f ρ b . d e p t h s u r f . k d , s u r f (Eq. 17),
where P s u r f is the quantity of soluble phosphorus retained during runoff, expressed in Kg P/ha, P s o l u b l e , s u r f is the quantity of soluble phosphorus in solution in the first 10 mm (Kg P/ha), Q s u r f is the quantity of surface water runoff on the day in question (mm H20), ρ b is the soil density over the first 10 mm expressed in Mg/m3, d e p t h s u r f is the depth of the surface layer (10 mm), and k d , s u r f is the partition coefficient of phosphorus in the soil (m3/Mg).
Surface runoff to the main channel allows the organic and mineral phosphorus attached to soil particles transfer. All the nutrients parameters were integrated in SWAT model and nutrients flows were simulated running one time only the model with stream flow calibrated parameters.

3. Results

3.1. Streamflow parameter global sensitivity

The parameter global sensitivity analysis has showed that GW_REVAP, GWQMN, RCHRG_DP, ESCO and CN2 are the most sensitive parameters to the flow (Table 2). It is noted that the most sensitive among these parameters mentioned above are those related to the groundwater flow (GW_REVAP, GWQMN and RCHRG_DP). This sensitivity analysis showed a possible connection between groundwater and surface water within the watershed.

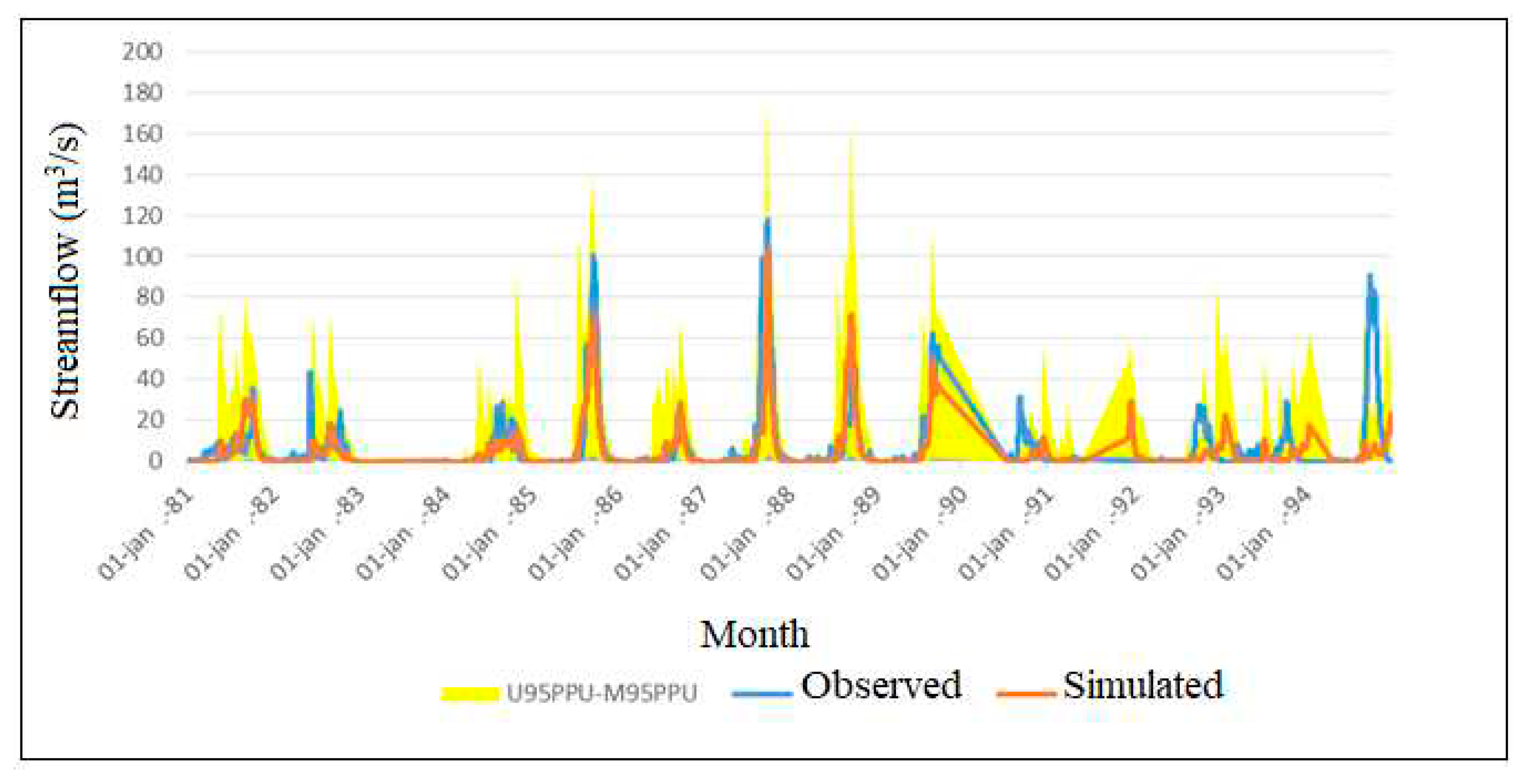
3.2. Streamflow calibration and uncertainty

The analysis of the results showed that the SWAT model is suitable for flow evaluation in the Lobo watershed at Nibéhibé. Indeed, R2, NSE and PBIAS had values of 0.63, 0.62 and -8.1 respectively. The values of P_factor and R_factor were 0.48 and 0.52 (Table 3).
The graph in Figure 3 shows the results of the water flow calibration. SWAT model predictions generally follow the trend of observed flow. However, we note a shift in the flow peaks at the end of the simulation period (1981-1994).
From January 1, 1981 to January 1, 1990, the model has globally reproduced the observed fow correctly. But, from January 1, 1990 to December 31, 1994, the opposite is observed. Indeed, the SWAT model could not reproduce the peak flows and overestimated the base flow.
The uncertainties on the predictions are highlighted by P-factor and R-factor. The P-factor and R-factor values obtained were 0.48 and 0.52, respectively. This situation is explained by the fact that the SWAT model could not faithfully restore the peakflow from January 01, 83 to January 01, 85.

3.3. Nutrients fluxes

3.3.1. Nutrients requirements for crops

After integrating the different crops and fertilizers used in Lobo watershed, the SWAT model estimated the average nutrient requirement (N and P) of the main crops grown in the watershed (Table 4). We note that the average needs observed by the CNRA is 41 Kg/ Ha for nitrogen and 28 Kg/Ha for phosphorus. One notices an overestimation of N of + 15% and an underestimation of P of -24% compared to CNRA results.

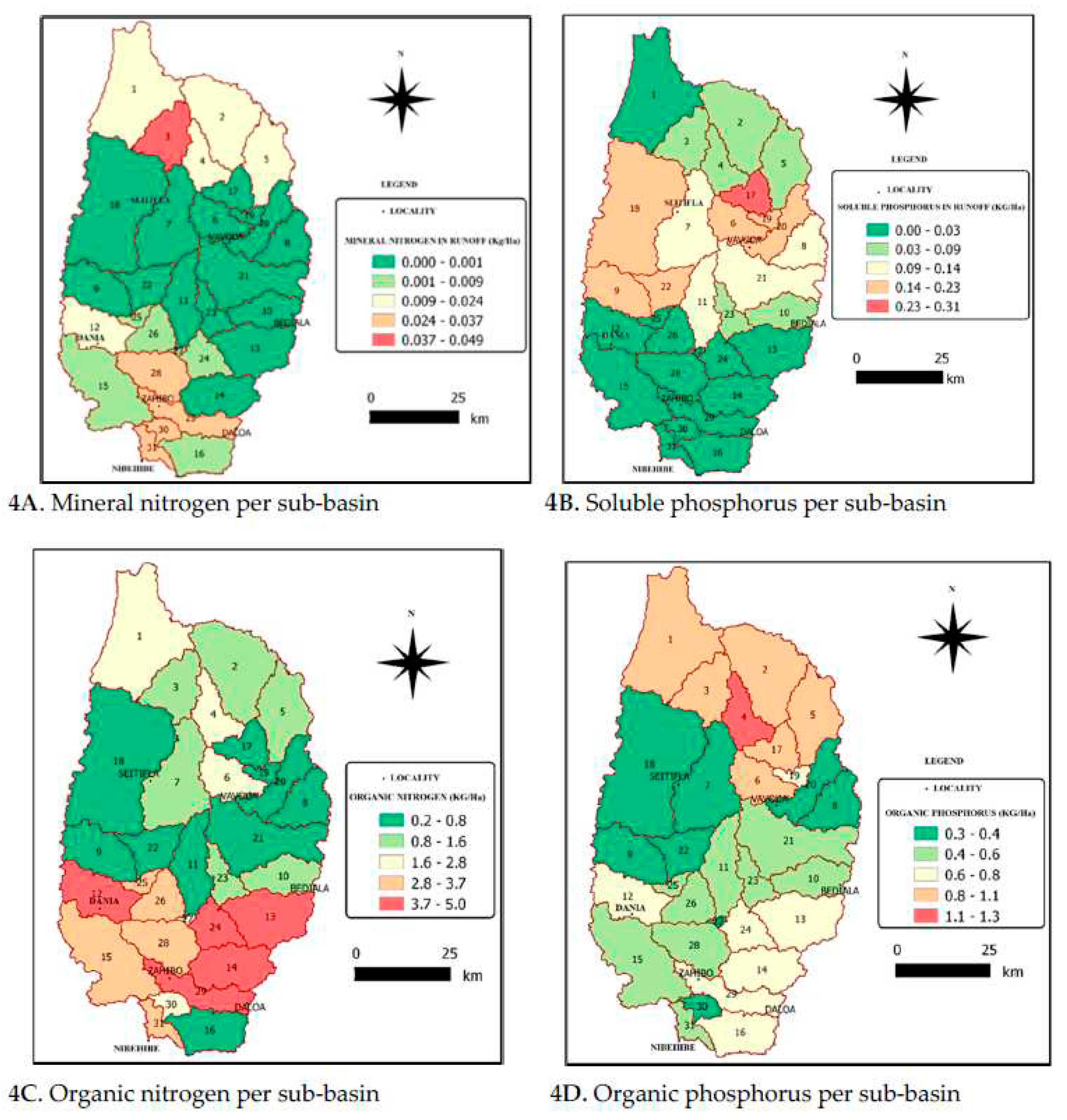
3.3.2. Mineral nitrogen and soluble phosphorus transferred per sub-basin

The mineral nitrogen and soluble phosphorus spatial distribution on the basis of fertilizers used by crop type is presented in Figure 4A and Figure 4B. In Figure 4A, the variations in mineral nitrogen vary from 0 to 0.049 Kg/Ha. The highest mineral nitrogen fluxes are observed overall in the northern part of the watershed. The sub-basins concerned are 1, 2, 3, 4 and 5. Sub-basin 3 presents the largest contribution (0.049 Kg/Ha) of the entire Lobo catchment area taken in Nibéehibé. The south and southwest parts also show high flows but a little less compared to the north part. These quantities of nitrogen per hectare vary from 0 to 0.037 Kg/Ha. The sub-basins with large quantities are sub-basins 28, 29 (containing the Lobo water reservoir), 30 and 31. It is generally observed that the mineral nitrogen inputs over the entire watershed are weak. Figure 4B shows the spatial variation in soluble phosphorus levels by sub-watershed. The soluble phosphorus flux varies from 0 to 0.31 Kg/Ha. The higher values are observed in the central, eastern and western parts of the basin with rates of up to 0.31 Kg/Ha. It is also noted that the flows of mineral nitrogen are lower than those of phosphorus. This difference stems from the NPK fertilizer formula used.

3.3.3. Organic Nitrogen and organic phosphorus transferred per sub-basin

The simulation of organic nitrogen transport by sub-basin revealed inputs varying from 0.2 to 5 Kg/Ha (Figure 4C). One notes that the sub-basins in the southern part, except sub-basin 16, present a greater contribution of organic nitrogen and organic phosphorus than those of sub-basins located in the central and northern areas. The sub-basins with higher rates of organic nitrogen and organic phosphorus are 12, 13, 14, 24 and 29 with values reaching 3.7 to 5 Kg/Ha. As for organic phosphorus, it is shown in Figure 4D. Unlike the distribution of organic nitrogen, we observe higher amounts only in the northern part of the watershed.
The sub-basins with high inputs are 1, 2, 3, 4, 5, 6 and 17 with rates varying between 0.8 and 1.3 Kg/Ha. The results of this study show that the contributions of nutrients of exogenous and organic origin remain higher than those of mineral origin.

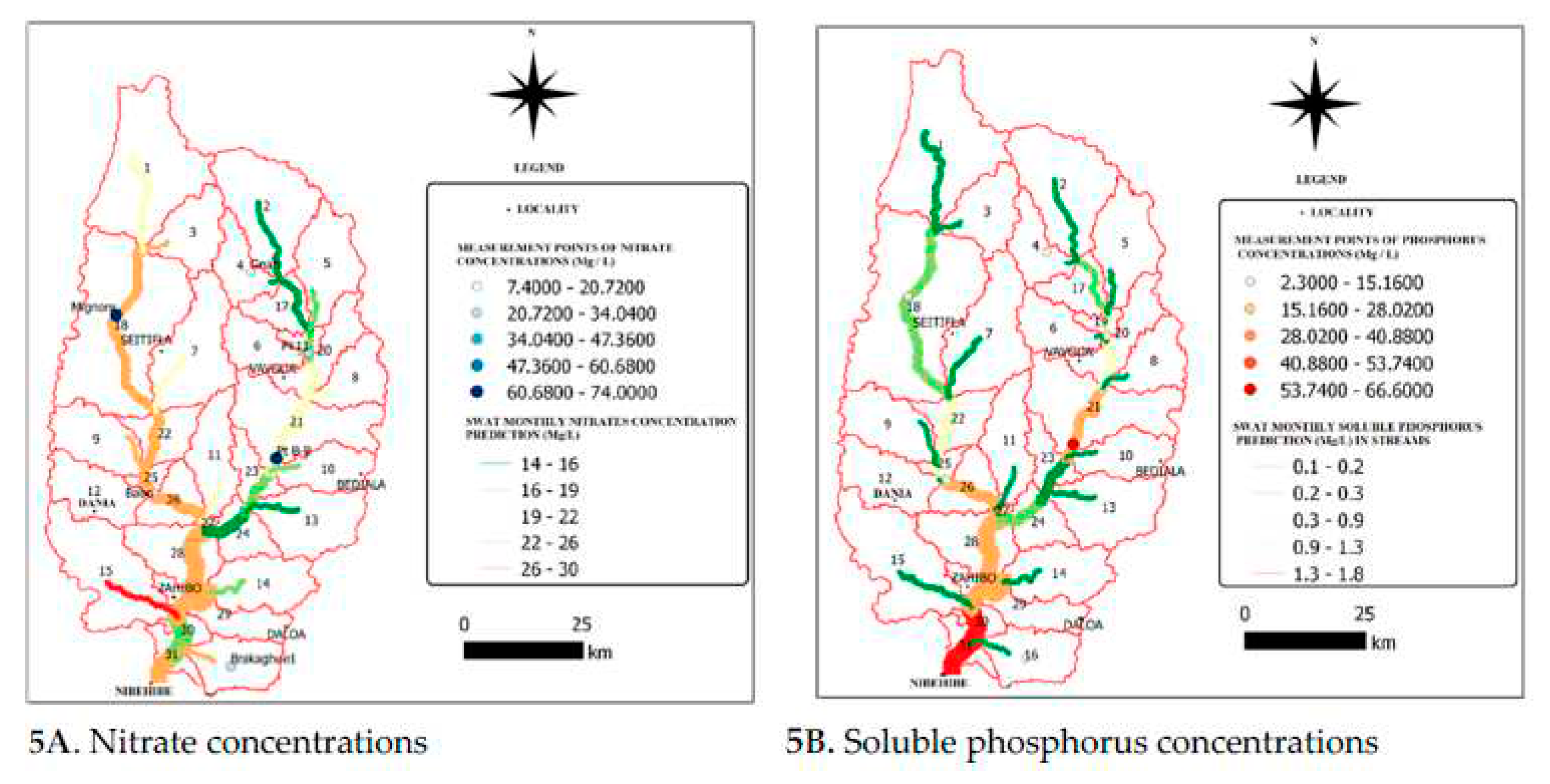
3.3.4. Nitrates and soluble phosphorus concentrations in streams

The monthly mean nitrate concentrations in mg/L were also estimated by the SWAT model. The predictions showed values ranging from 14 to 30 mg/L (Figure 5A). The result showed that the left bank and downstream part of the Lobo river is more vulnerable to an excessive intake of nitrates. This excessive inflow is extended to the outlet of the watershed (Nibéhibé) through sub-basin 29 where the Lobo water reservoir is located. Sub-basin 15 is the most vulnerable with concentrations up to 30 mg/L. Figure 5B presents the monthly average concentrations of soluble phosphorus in mg/L. The values vary from 0.1 to 1.8 mg/L (Figure 5B). The rivers in sub-watersheds 30 and 31 have the highest soluble phosphorus concentrations (1.3-1.8 mg/L). Sub-basins 21, 26, 28 and 29 also recorded high concentrations (0.9-1.3 mg/L). One noted that both for nitrates and soluble phosphorus, the sub-basin 29 containing the Lobo water reservoir recorded a significant contribution. A sampling campaign carried out made it possible to measure nitrate and phosphorus concentrations in surface water in the watershed. The measurement points have been represented on the maps of Figure 5A and Figure 5B.
These measurements revealed nitrate concentrations ranging from 7.4 to 74 mg/L and phosphorus ranging from 2.3 to 66.6 mg/L. In the absence of historical data that can be used to calibrate nutrient inputs (N and P), these measurement points were superimposed on the spatial distribution map in order to verify the robustness of the SWAT model predictions. It appears that high concentration points (dark blue for nitrates and red for phosphorus) coincide with areas of streams where predictions show a high value (orange and red). The points of high concentrations may remain the same over the years. However, the amount of nitrates and phosphorus accumulated can increase significantly over the years.

4. Discussion

The observed flow data used for this study are mostly available for the period 1981-1994. It is assumed that there is no major land use and rainfall trend over this period. In ungauged hydrological catchments where there is a scarcity of historical data, this hypothesis makes it possible to simulate flow and nutrient dynamics [52]. The study revealed that flow parameters such as GW_REVAP, GWQMN, RCHRG_DP, ESCO and CN2 impact the water flow the most. The same conclusion was made by Anoh et al. [53] in the Taabo watershed bordering that of Lobo. Along the same lines, Dakhlalla et al. [54] showed through a study on the evaluation of flow, nutrients and sediments transfer parameters sensitivity and uncertainty that hydrological parameters such as GWQMN, ESCO and CN2 are sensitive to flow. ESCO and CN2 are also parameters considered to significantly influence streamflow in western Mississippi [55]. Moreover, CN2, being a parameter very sensitive to runoff, a decrease in precipitation impacts surface runoff which will modify the values of CN2 [56,57,58] in [59]. However, a parameter can be identified as not sensitive. But, this does not really mean that it does not influence the flow in the watershed [60].
The values of R2, NSE and PBIAS of 0.63, 0.62 and -8.1 respectively, highlighted the capacity of the SWAT model according to the evaluation criteria proposed by Moriasi et al. [35]. Upon the Taabo watershed, similar results were obtained by Anoh et al. [61]. Indeed, the average NSE obtained by these authors was 0.7 during the calibration period. A PBIAS value of -8.1 obtained in this study showed a very good performance of the model [35]. For flow, any P-factor > 0.7 and R-factor < 1.5 are considered acceptable. Therefore, the uncertainties on the flow predictions are considered acceptable [62]. P-factor has a value of 0.48 which is therefore less good since the wish is for this value to be close to 1 [29]. On the other hand, R-factor of 0.52 is acceptable. A model is said to be perfect when R-factor is close to 0. Very often, these values are very difficult to reach. This is why some authors recommend a balance between these two parameters [29]. In our case, P-factor is 0.48 and R-factor 0.52. There is a certain balance between these parameters. The prediction uncertainties are therefore acceptable. Despite these shortcomings of the model, the results obtained in this study constitute a solid basis for hydrological modeling in the region with a view to the fight against the eutrophication of surface water facing the population of this region. Compared with the results of the [63], the predictions of SWAT show an underestimation of the N rates of -9.9% and of -5.55% for P rates. The results show low inorganic nitrogen levels. These low inorganic nitrogen levels in the Lobo watershed have also been highlighted by the work of [3,4]. This could be explained by the fact that the recommendations of agricultural advisers to farmers regarding chemical fertilizers are respected. Then, nature, including crops, is able to digest the applied fertilizers, and only a small amount remains in the environment. The flows of mineral nitrogen are lower than those of phosphorus. This difference stems from the NPK fertilizer type used. Indeed, surveys carried out with ANADER (National Agency for Rural Development Support) and CIDT (Ivorian Textile Development Company) revealed that all agricultural activities practiced in the watershed use NPK fertilizer. In fact, NPK-10-18-18 fertilizer is used equally well for Coffee, Cocoa and cotton. But coffee and cocoa are the main industrial crops in this region of Cote d'Ivoire. This fertilizer formula contains 18% phosphorus against 10% nitrogen in 1 kg of this fertilizer, hence the high soluble phosphorus levels relative to nitrogen. Leakage of nitrogen and phosphorus by the SWAT model takes place outside the root zone, i.e., primarily by infiltration for nitrates and runoff for phosphorus, although the model estimates that a fraction of nitrogen migrates by leaching in runoff [64]. The variability of nitrogen and phosphorus leaks between sub-basins is conditioned by the vulnerability of soils to runoff and infiltration. Thus, soils favorable to runoff generate higher transfers of phosphorus and reduce those of nitrogen by reducing infiltration and promoting denitrification [65]. In general, the levels of mineral nitrogen are low compared to the levels of phosphorus. This is because nitrogen is almost always one of the deficient nutrients in cultivated soils with fragile organic status and particularly in ferralitic and ferruginous soils [66]. The contributions of nutrients of exogenous and organic origin remain higher than those of mineral origin. These results are in accordance with the work of [3] who showed that the fertilizer used by farmers throughout the Lobo watershed was manure, mainly used in the Séguéla area located to the north of the basin. According to Maïga et al. (2001) [3], the nutrient losses are of natural origin. Thus, natural fertilizers could provide 10 to 50 Kg/Ha for nitrogen (N) and 0.15 to 0.75 Kg/Ha for phosphorus (P) per hectare in the Lobo watershed. SWAT model simulations gave values lower than measured values in the field. However, the results have proved that the points of high concentrations fit well in the area of high nutrient concentrations predicted by the SWAT model. But, the amount of nitrates and phosphorus accumulated can increase significantly over the years. This explains the concentrations measured in the field, which reached as high as 74 mg/L for nitrates and 66.6 mg/L for phosphorus, the level above water quality criteria set by the World Health Organization (WHO) which stipulates that water with more than 50 mg/L of nitrates is considered polluted. In addition, most unpolluted freshwater contains between 10 and 50 μg/L [67] in [68]. This shows the state of pollution (eutrophication) of the Lobo water reservoir located in sub-basin 29, which is used for drinking water supply to Daloa city and around. These results agree with those of [4] who highlighted the eutrophication phenomenon of the Lobo reservoir. These authors have strived to examine the causes and consequences of such a phenomenon. In the same vein, [69] showed that the Lobo undergoes very advanced permanent eutrophication. The study carried out by [3] highlighted phosphorus values that can reach 0.066 mg/l. The OECD (Organization for Economic Cooperation and Development) threshold values between 0.035 and 0.1 mg/l classify Lobo reservoir in the category of hypereutrophic lakes [70]. The eutrophication phenomenon results from a primary overproduction in the water body, that is, an intense photosynthetic activity causing algal and plant development (autotrophic organisms), more significant than the consumption capacity of heterotrophic organisms (microorganisms, fish and crustaceans). There is then an imbalance between the trophic levels of the ecosystem. So, excess plant matter clutters the water body [70]. When the water body is invaded by floating macrophytes, they cover the surface of the water and limit the penetration of sunlight. The dead plant material settles at the bottom of the basin which it fills. This explains the black color of tap water mentioned by [5].

5. Conclusions

Considering the criteria for evaluating the flow setting, we note that the SWAT model is capable of simulating transfers in the Lobo watershed at Nibéhibé. The evaluation criteria R2, NSE and PBIAS had values of 0.63, 0.62 and -8.1 respectively. P-factor P and R-factor gave 0.48 and 0.52. On the basis of these values obtained, it appears that the SWAT model is indicated for the simulation of flows and nutrient transfers in tropical agricultural watersheds, in particular that of the Lobo.. The estimation of the average quantities of N and P applied to the crops gave 47.24 Kg/Ha of N and 21.25 Kg/Ha of P. The flows of inorganic N and soluble P vary from 0 to 0.049 Kg/Ha for inorganic N and from 0 to 0.31 Kg/Ha for soluble phosphorus. The northern and southern parts of the basin are more vulnerable to a large input of inorganic N when the central part remains vulnerable to the soluble phosphorus transfer. Simulations relating to the organic N transfer revealed values ranging from 0.2 to 5 Kg/Ha, the southern part showing the highest fluxes. As for the flow of organic phosphorus, they vary from 0.3 to 1.3 Kg/Ha. Unlike organic N, the greatest amounts are observed in the north. By comparing the flows of mineral (inorganic) nutrients with those of organic nutrients, one can say that the eutrophication observed in the Lobo water reservoir (sub-basin 29) would mainly have an exogenous origin (domestic, etc.) and organic. Predictions of nitrates concentrations and soluble phosphorus in the stream made using the SWAT model revealed concentrations of nitrates between 14 and 30 mg/L and soluble phosphorus between 0.1 and 1.8 mg/L. Field measurement points with high concentrations usually fall in areas of the stream with high concentrations simulated by SWAT. Apart from the limitations of this study related to the quality and quantity of the input data, it allowed us to gain a spatial understanding of the evolution and distribution of nutrients in the watershed. It also made it possible to identify the major inflow areas that would further contribute to eutrophication in the Lobo reservoir. These results constitute a solid basis which can serve as a basis in the fight against the phenomenon of eutrophication of water bodies in the watersheds of Côte d'Ivoire.

Author Contributions

Conceptualization, J.-J.T.K. and R.S.; methodology, J.-J.T.K.; software, R.S, T.A., Y.D. and J.J.; validation, J.-J.T.K., R.S. and Y.D.; writing—original draft preparation, J.-J.T.K; writing—review and editing, J.-J.T.K. R.S and J.J; supervision, J.J; project administration, J.J; funding acquisition, J.-J.T.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded in part by J. William Fulbright Foreign Scholarship, grant number PS00285574.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

All the data used in this paper can be traced back to the cited references.

Acknowledgments

I acknowledge support given by The Spatial Science Laboratory at Texas A& M University (TAMU) in College Station (Texas) that provided me an office and a computer for this study during my Fulbright mobility.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Economic Research Service, U.S. Department of Agriculture. Available online: https://www.ers.usda.gov/topics/international-markets-u-s-trade/u-s-agricultural-trade/ (accessed on 20 January 2023).
  2. Komelan, Y. Eutrophisation des réservoirs d'eau en Côte d'Ivoire et gestion de leur bassin versant : cas de Lobo à Daloa. Master thesis, EIER, Ouagadougou, 1999.
  3. Maïga, A.; Denyigba, K.; Allorent, J. Eutrophisation des petites retenues d'eau en Afrique de l'Ouest : Causes et conséquences : cas de la retenue d'eau de la Lobo en Côte d'Ivoire. Sud Sciences & Technologies 2001, 7, 16–29. [Google Scholar]
  4. Dié. Renforcement de l'alimentation en eau potable de la ville de Daloa à partir du barrage de Buyo en Côte d'Ivoire. Master thesis, EIER, Ouagadougou, 2006.
  5. Ohou-Yao, M.; Séka, A.; Mambo, V.; Yapo, O.; Konan, K.; Houénou, P. Contamination des eaux de puits traditionnels par les nitrates sur le bassin versant de la Lobo (Buyo, sud-ouest de la Côte d’Ivoire). J. Appl. Biosci. 2014, 78, 6654–6665. [Google Scholar] [CrossRef]
  6. Chocat, B. Amenagement urbain et hydrologie. La Houille Blanche 1997, 7, 12–19. [Google Scholar] [CrossRef]
  7. Refsgaard, J.C. Parameterization, calibration, and validation of distributed hydrological models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
  8. Refsgaard, J.C.; Storm, B. Construction, calibration, and validation of hydrological models. In Distributed Hydrologic Modeling, 2nd ed.; Abbot, M. B, Ed.; Kluwer Academic Publishers: Dordrecht, Netherlands, 1996; pp. 41–54. [Google Scholar]
  9. Wischmeier, W. H.; Smith D. D. Predicting Rainfall Erosion Losses. Agriculture Handbook 537, United States Department of Agriculture, Science and Education Administration, 1978; 58 p.
  10. Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. Journal of Hydrology 2003, 279, 275–289. [Google Scholar] [CrossRef]
  11. Avenard, J. M. Aspect géomorphologique. In L’Environnement naturel de Côte d'Ivoire, 2nd ed.; Avenard, J.M., Eldin, M., Girard, G., Sircoulon, J., Touchebeuf, P., Guillaumet, J.L., Adjanohoun, Perraud A., Eds.; ORSTOM: Paris, France, 1971; pp. 11–72. [Google Scholar]
  12. Yao, A.B.; Goula, B.T.A.; Kouadio, Z.A.; Kouakou, K.E.; Kane, A.; Sambou, S. Analyse de la variabilité climatique et quantification des ressources en eau en zone tropicale humide : cas du bassin versant de la Lobo au Centre-ouest de la Côte d’Ivoire. Rev. Ivoir. Sci. Technol 2012, 19, 136–157. [Google Scholar]
  13. Brou, Y.T. Climat, mutations socio-économiques et paysages en Côte d’Ivoire. Mémoire de synthèse des activités scientifiques présenté en vue de l’obtention de l’Habilitation à Diriger des Recherches, Université des Sciences et Techniques de Lille, France, 2005.
  14. Koua, T.J.-J.; Dhanesh, Y.; Jeong, J.; Srinivasan, R.; Anoh, K.A. Implementation of the Semi-Distributed SWAT (Soil and Water Assessment Tool) Model Capacity in the Lobo Watershed at Nibéhibé (Center-West of Côte D’Ivoire). Journal of Geoscience and Environment Protection 2021, 9, 21–38. [Google Scholar] [CrossRef]
  15. Harmonized world soil database version1.1. Available online: http://www.fao.org/fileadmin/templates/nr/documents/HWSD/HWSD_Documentation.pdf (Accessed on September 2012).
  16. Mbungu, W.B; Kashaigili, J.J. Assessing the Hydroology of a Data-Scarce Tropical Watershed Using the Soil and Water Assessment Tool: Case of the Little Ruaha River Watershed in Iringa, Tanzania. Open Journal of Modern Hydrology 2017, 7, 65–89. [Google Scholar] [CrossRef]
  17. Arnold, J.G.; Srinivasan, R.; Muttiah, R.; Williams, J.R. Large area hydrologic modeling and assessment. Part I: Model development. J. Am. Water Res. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
  18. Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, R. Soil and Water Assessment Tool. Theoretical Documentation, Version 2005. Agricultural Research Service, Grassland, Soil and Water Research Laboratory, Temple, USA, 2005.
  19. Refsgaard, J.C.; Van der Sluijs, J.P.; Højberg, A.L.; Vanrolleghem, P. A. Uncertainty in the environmental modelling process – a framework and guidance. Environmental Modelling & Software 2007, 22, 1543–1556. [Google Scholar]
  20. Schuol, J.; Abbaspour, K.C.; Srinivasan, R.; Yang, H. Modeling blue and green water availability in Africa. Water Resources Research, 2008, 44, 1–18. [Google Scholar] [CrossRef]
  21. Bastin, L.; Cornford, D.; Jones, R.; Heuvlink, G.; Pebesma, E.; Stasch, C.; Nativi, S.; Mazzetti, P.; Williams, M. Managing uncertainty in integrated environmental modelling: The UncertWeb framework. Environmental Modelling & Software 2013, 39, 116–134. [Google Scholar]
  22. Abbaspour, K.C.; Johnson, C.A.; Van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone Journal 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
  23. Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
  24. Beven, K.; Binley, A. The future of distributed models – model calibration and uncertainty prediction. Hydrological Processes 1992, 6, 279–298. [Google Scholar] [CrossRef]
  25. Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the sixth international symposium on micro machine and human science. Nagoya, Japan, 4-6 October 1995. [Google Scholar]
  26. Van Griensven, A.; Meixner, T. Methods to quantify and identify the sources of uncertainty for river basin water quality models. Water Sci. Technol. 2006, 53(1), 51–59. [Google Scholar] [CrossRef]
  27. Kuczera, G.; Parent, E. Monte Carlo assessment of parameter uncertainty in conceptual catchment models: the Metropolis algorithm. J. Hydrol. 1998, 211, 69–85. [Google Scholar] [CrossRef]
  28. Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
  29. Abbaspour, K.C. SWAT calibration and uncertainty programs – a user manual. Swiss Federal Institute of Aquatic Science and Technology, EAWAG, Duebendorf, Switzerland, 2015.
  30. Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrologic Eng. 1999, 4(2), 135–143. [Google Scholar] [CrossRef]
  31. Coffey, M.E.; Workman, S.R.; Taraba, J.L.; Fogle, A.W. Statistical procedures for evaluating daily and monthly hydrologic model predictions. Transaction of the ASABE. 2004, 47, 59–68. [Google Scholar] [CrossRef]
  32. Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W. A.; Srinivasan, R. Validation of the SWAT model on a large river basin with point and nonpoint sources. JAWRA. 2001, 37(5), 1169–1188. [Google Scholar]
  33. Chu, T.W.; Shirmohammadi, A.; Montas, H.; Sadeghi, A. Evaluation of the SWAT model’s sediment and nutrient components in the piedmont physiographic region of Maryland. ASABE. 2004, 47(5), 1523–1538. [Google Scholar] [CrossRef]
  34. Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: historical development, applications, and future research directions. Transactions of the ASABE. 2007, 50(4), 1211–1250. [Google Scholar] [CrossRef]
  35. Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Transactions of the ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
  36. Schuol, J.; Abbaspour, K.C.; Srinivasan, R.; Yang, H. Estimation of freshwater availability in the West African sub-continent using the SWAT hydrologic model. J. Hydrol. 352, 30–49. [CrossRef]
  37. Sintondji, L.O.; Awoye, H. R.; Agbossou, K. E. Modélisation du bilan hydrologique du bassin versant du Klou au Centre-Bénin : Contribution à la gestion durable des ressources en eau. Bulletin de la recherche agronomique du Bénin 2008, 59, 35–48. [Google Scholar]
  38. Rollo, N. Modélisation des dynamiques de pollution diffuse dans le bassin versant de la rivière d’Auray : quantification, caractérisation et gestion des apports nutritifs terrigènes. Thèse de Doctorat, Université de Nantes, 2012.
  39. Vilaysane, B.; Takara, K.; Luo, P.; Akkharath, I.; Duan, W. Hydrological stream flow modelling for calibration and uncertainty analysis using SWAT model in the Xedone river basin, Lao PDR. Procedia Environ. Sci. 2015, 28, 380–390. [Google Scholar] [CrossRef]
  40. Aouissi, J.; Benabdallah, S.; Chabaâne, Z.; Cudennec, C. Evaluation of potential evapotranspiration assessment methods for hydrological modelling with SWAT-application in data-scarce rural Tunisia. Agric. Water Manag. 2016, 174, 39–51. [Google Scholar] [CrossRef]
  41. Havrylenko, S.B.; Bodoque, J.M.; Srinivasan, R.; Zucarelli, G.V.; Mercuri, P. Assessment of the soil water content in the Pampas region using SWAT. Catena 2016, 137, 298–309. [Google Scholar] [CrossRef]
  42. Maliehe, M.; Mulungu, D.M. Assessment of water availability for competing uses using SWAT and WEAP in South Phuthiatsana catchment, Lesotho. Physics and Chemistry of the Earth, 2017, Parts A/B/C.
  43. Molina-Navarro, E.; Anderson, H.; Nielsen, A.; Thodsen, H.; Trolle, D. The impact of the objective function in multi-site and multi-variable calibration of the SWAT model. Environ. Model. Softw. 2017, 93, 255–267. [Google Scholar] [CrossRef]
  44. Tolson, B.A.; Shoemaker, C.A. Watershed modeling of the Cannonsville Basin using SWAT 2000, Model development, calibration and validation for the prediction of the flow, sediment and phosphorus transport to the Cannonsville reservoir. Technical Report, School of Civil and Environmental Engineering, Cornell University, Ithaca, New York, 2004.
  45. Koua, T.J.; Kouassi, K.H.; Anoh, K.A. Analysis of the SWAT (Soil and Water Assessment Tool) Semi-distributed Model Input Data for the Hydrological Simulation of the Lobo Water Reservoir (Central West of Côte d'Ivoire). Journal of Geography, Environment and Earth Science International 2019, 23, 1–20. [Google Scholar] [CrossRef]
  46. Jenson, S.; Domingue, J. Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis. Photogramm. Eng. Remote Sensing 1998, 54, 1593–1600. [Google Scholar]
  47. Abbaspour, K.C. Swat-Cup2: SWAT Calibration and Uncertainty Programs Manual. Version 2.: Swiss Federal Institute of Aquatic Science and Technology, EAWAG, Duebendorf, Switzerland, 2011.
  48. Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and water assessment tool theoretical documentation, version 2005. Grassland, Soil and Water Research Laboratory – Agricultural Research Service. Blackland Research Center – Texas Agricultural Experiment Station. Texas Water Resources Institute, College Station, 2011.
  49. McElroy, A.D.; Chu, S.Y.; Nebgen, J.W.; Aleti, A.; Bennett, F.W. Loading functions for assessment of water pollution from nonpoint sources. Environ. Prot. Tech. Serv. 1976, 76–151. [Google Scholar]
  50. Williams, J.R.; Hann, R.W. Optimal operation of large agricultural watersheds with water quality constraints. Texas Water Resources Institute, Texas A & M Univ., 1978.
  51. Menzel, R.G. Enrichment ratios for water quality modeling. In CREAMS: A Field Scale Model for Chemicals, Runoff, and Erosion from Agricultural Management Systems, 2nd ed Knisel, W.G., Eds; U.S. Dept. Agric. Conserv. Res., USA, 1980, pp. 486-492.
  52. Alemayehu, T.; Gupta, H.V.; van Griensven, A.; Bauwens, W. On the Calibration of Spatially Distributed Hydrologic Models for Poorly Gauged Basins: Exploiting Information from Streamflow Signatures and Remote Sensing-Based Evapotranspiration Data. Water 2022, 14, 1252. [Google Scholar] [CrossRef]
  53. Anoh, K.; Koua, T.; Eblin, S.; Kouamé, K.; Jourda, J. Modelling Freshwater Availability Using SWAT Model at a Catchment-Scale in Ivory Coast. Journal of Geoscience and Environment Protection 2017, 5, 70–83. [Google Scholar] [CrossRef]
  54. Dakhlalla, A.O.; Parajuli, B.P. Assessing model parameters sensitivity and uncertainty of streamflow, sediment, and nutrient transport using SWAT. Inf. Process. Agric. 2019, 6, 61–72. [Google Scholar] [CrossRef]
  55. Xu, H.; Taylor, R. G.; Kingston, D. G.; Jiang, T.; Thompson, J. R.; Todd, M. C. Hydrological modeling of River Xiangxi using SWAT2005: a comparison of model parameterizations using station and gridded meteorological observations. Quat. Int. 2010, 226, 54–59. [Google Scholar] [CrossRef]
  56. Strauch, M.; Bernhofer, C.; Koide, S.; Volk, M.; Lorz, C.; Makeschin, F. Using precipitation data ensemble for uncertainty analysis in SWAT streamflow simulation. J. Hydrol 2012, 414-415, 413–424. [Google Scholar] [CrossRef]
  57. Vu, M.T.; Srinivasan, R.; Liong, S.Y. SWAT use of gridded observations for simulating runoff – a Vietnam river basin study. Hydrol. Earth Syst. Sci. 2012, 16, 2801–2811. [Google Scholar] [CrossRef]
  58. Tuo, Y.; Duan, Z.; Disse, M.; Chiogna, G. Evaluation of precipitation input for SWAT modeling in Alpine catchment: A case study in the Adige river basin (Italy). Sci. Total Environ 2016, 573, 668–82. [Google Scholar] [CrossRef]
  59. Shen, Z.; Chen, L.; Liao, Q.; Liu, R.; Hong, Q. Impact of spatial rainfall variability on hydrology and nonpoint source pollution modeling. J. Hydrol 2012, 472–473, 205–215. [Google Scholar] [CrossRef]
  60. Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B.A. Continental-scale hydrology and water quality model for Europe: calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
  61. Anoh, K.; Koua, T.; Kouamé, K.; Jourda, J.; Laurent, F. Modelling water flow in a complex watershed in humid a tropical area using SWAT: a case study of Taabo watershed in Ivory Coast. Int. J. River Basin Manag. 2018, 16(2), 157–167. [Google Scholar] [CrossRef]
  62. Dosso, M. Etude de la consommation d'engrais en Côte d'Ivoire. Rept. 2015, 29 p.
  63. Bioteau, T.; Bordenave, P.; Laurent, F.; Ruelland, D. Evaluation des risques de pollution diffuse par l'azote d'origine agricole à l'échelle de bassins versants : intérêts d'une approche par modélisation avec SWAT. Ingénieries-EAT 2002, 32, 3–13. [Google Scholar]
  64. Laurent, F.; Ruelland, D.; Chapdelaine, M. Simulation de l’effet de changements de pratiques agricoles sur la qualité des eaux avec le modèle SWAT. Journal of Water Science 2007, 20, 395–408. [Google Scholar] [CrossRef]
  65. Maliki, R.; Bernard, M.; Padonou, E.; Englehart, C.; Sinsin, B. A.; Aho, N. Effet combiné de NPK et de trois différents mulchs d’origine végétale sur la production maïsicole et la fertilité des sols au Sud-Bénin. BRAB 2017, 10–26. [Google Scholar]
  66. Wetzel, R.G. Limnology: Lake and River Ecosystems. 3rd Ed.; Academic Press, San Diego, 2001, 1006 p.
  67. Koua, T. Apport de la modélisation hydrologique et des Systèmes d’Information Géographique (SIG) dans l’étude du transfert des polluants et des impacts climatiques sur les ressources en eau : cas du bassin versant du lac de Buyo (Sud-ouest de la Côte d'Ivoire). PhD Thesis, Felix Houphouet Boigny University of Cocody, Abidjan, Cote d’Ivoire, 11 December 2014. [Google Scholar]
  68. Koukougnon, W.G. Milieu urbain et accès à l’eau potable : Cas de Daloa (Centre-Ouestde la Cote d’Ivoire). PhD Thesis, Felix Houphouet Boigny University of Cocody, Abidjan, Cote d’Ivoire, 2012. [Google Scholar]
  69. OECD, Organization for Economic Co-Operation and Development. Eutrophication of Waters. Monitoring, Assessment and Control, 1982, 154 p.
  70. Dassi, C.; Mosi, L.; Narh, C. A.; Quaye, C. Distribution and Risk of Mycolactone-Producing Mycobacteria Transmission within Buruli Ulcer Endemic Communities in Côte d’Ivoire. Trop. Med. Infect. Dis. 2017, 2, 2–17. [Google Scholar] [CrossRef] [PubMed]
Preprints 80088 g001
Figure 1. Location of Lobo basin in Côte d'Ivoire [14].
Figure 1. Location of Lobo basin in Côte d'Ivoire [14].
Preprints 80088 g001
Preprints 80088 g002
Figure 2. Essential input data for the SWAT model.
Figure 2. Essential input data for the SWAT model.
Preprints 80088 g002
Preprints 80088 g003
Figure 3. Flow calibration result at Nibéhibé hydrometric station.
Figure 3. Flow calibration result at Nibéhibé hydrometric station.
Preprints 80088 g003
Preprints 80088 g004
Figure 4. Annual mean spatial distribution of nutrients per sub-basin over the period 1981-1994.
Figure 4. Annual mean spatial distribution of nutrients per sub-basin over the period 1981-1994.
Preprints 80088 g004
Preprints 80088 g005
Figure 5. Spatial distribution of monthly mean nitrate and soluble phosphorus concentrations over the period 1981-1994.
Figure 5. Spatial distribution of monthly mean nitrate and soluble phosphorus concentrations over the period 1981-1994.
Preprints 80088 g005
Table 1. SWAT-CUP methods.
Table 1. SWAT-CUP methods.
Algorithm Description
SUFI-2 In SUFI 2, it is considered that the uncertainty on the simulations is observed in a uniform way. The sources of uncertainties are the driving variables, the conceptual model, parameters and measured data.
GLUE In this method, once the general probability has been defined, all the parameters are randomly sampled from the previous distribution. The parameters are thus grouped either into a behavioral set, or into a non-behavioral set by comparing them to a given threshold probability. The parameters are then weighted according to their behavior. Finally, the uncertainty is predicted.
PSO Here, the uncertainty prediction method is based on stochastic population optimization. The optimization is done from random sampling of parameters.
PARASOL During PARASOL method, a global optimization criterion (GOC) is first fixed. The method seeks to minimize the objective functions (OF) or GOC from the Shuffle Complex algorithm (SCE-UA).
MCMC MCMC proceeds with a random sampling which adapts to the posterior distribution.
Table 2. Summary of selected SWAT parameters global sensitivity and parameters’ fitted values for simulating streamflow.
Table 2. Summary of selected SWAT parameters global sensitivity and parameters’ fitted values for simulating streamflow.
Global sensitivity rank Parameter Parameter description Fitted value Minimum value Maximum value
1 v__GW_REVAP Groundwater revaporation coefficient 0.1649 0.02 0.2
2 a__GWQMN Threshold depth of water in the shallow aquifer required for return flow to occur (mm) -162 -1000 1000
3 a__RCHRG_DP Deep aquifer percolation fraction -0.0205 -0.05 0.05
4 v__ESCO Soil evaporation compensation factor 0.5465 0.5 0.8
5 r__CN2 SCS runoff curve number fonction 0.081 -0.1 0.1
6 a__GW_DELAY Groundwater delay (days) -28.83 -30 60
7 a__REVAPMN Threshold depth of water in the shallow aquifer for "revap" to occur (mm) 370.50 -750 750
8 v__ALPHA_BF Baseflow alpha factor (days) 0.945 0.00 1.00
9 r__SOL_AWC Available water capacity of the soil layer -0.0143 -0.05 0.05
10 v__CANMX Maximum canopy storage 14.1749 0.00 15.00
a: add parameter value to an existing value; v: Replace the given value with another; r: Multiply the existing parameter value by (1 + a given value of the same parameter).
Table 3. Mean monthly streamflow simulated and observed over 1981-1994 and summary statistics.
Table 3. Mean monthly streamflow simulated and observed over 1981-1994 and summary statistics.
Parameter simulated
R2 0.63
NSE 0.62
PBIAS -8.1
P_factor 0.48
R_factor 0.52
Table 4. Nutrients requirements for crops.
Table 4. Nutrients requirements for crops.
Crop Fertilizer (NPK) Quantity (Kg/Ha) N quantity (Kg/Ha) P quantity (Kg/Ha)
Cotton 15-15-15 200 30 13.2
Cocoa tree 0-23-19 500 00 50.6
Coffee 12-06-20 784 94.08 79.34
Cashew 11-22-16 81.6 8.2 9.69
Rice 12-24-18 200 24 21.12
Banana 25-04-23 200 50 4.224
Corn 15-15-15 250 37.5 16.5
Observed mean (CNRA) 41 Kg/Ha 28 Kg/Ha
SWAT 47.24 Kg/Ha 21.25 Kg/Ha
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated