Prerpints.org logo
Preprint
Article

Effectiveness of Travelling Slice Modeling in Representing the Continuous Casting Process of Large Product Sections

Altmetrics

Downloads

112

Views

18

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 July 2023

Posted:

24 July 2023

You are already at the latest version

Alerts
Abstract
In metal continuous casting process is important to estimate the temperature evolution of casted section along machine from meniscus (point in which liquid metal is poured) to cutting machine where product is cut at commercial length. Particularly in the case of large sections, a convenient approximated model to achieve this goal with a feasible computational effort, is the so called travelling slice: the transversal section of casted product is subjected to different thermal boundary conditions (e.g. thermal flux, radiation, convection) that are found during the movement at constant speed from meniscus to the end of machine. In the case of an axisymmetric section, a comparison with the exact solution can be easily achieved. The article will show pros and cons of both, namely the far lower computational cost of travelling slice model without losing precision. Results confirm the validity of the travelling slice approach also at low casting speed and huge dimensions.
Keywords: 
Subject: Engineering  -   Metallurgy and Metallurgical Engineering

1. Introduction

Nowadays the great part of metals with an engineering application, steel among others, is produced by continuous casting process. At begin of 20th century the widely used casting technique was the ingot one: a quantity of molten metal was poured in a container that was removed when was achieved the complete solidification. After pioneering experiments in ‘30s, the steel continuous casting process became an industrial viable solution from ‘50s and its share never stop growing in the following decades: in 2021 the 97% of worldwide steel was produced by continuous casting. The reasons why continuous casting process took over are several: most important is the higher productivity compared to other methods. The development of this production technique led to the need of comprehension of the phenomena related to processes: since most of them (e.g. solidification, segregation, defect generation) are temperature driven, a tool to evaluate the thermal field plays an important role. Theoretically a model to describe such process should be tridimensional; in this case the computational cost, both in terms of resources as well as time needed to get the results, is high (examples of 3D modeling applied to metal casting processes are [1,2]). To overcome these issues, a quicker bidimensional approach named travelling slice has been tested and became widely used. First attempts to study this problem dates back to ‘70s and during ‘80s FE thermomechanical models appears. In the following years many people worked on this issue and several ways have been explored. Latest developments lead to the use of deep learning techniques in the solidification of steel [3]. One of the earliest studies in which the travelling slice has been used is [4]; later on other authors widened the method including also phase transformations [5] and hot tearing criteria in order to estimate crack formation: see [6,7,8]. Although such modeling is common in literature review, an evaluation on its limits is still missing. Some decades ago, the continuous casting technology were limited to relatively small sections, nowadays an increase of casted product size (up to 1200 mm diameter with the forecast to go beyond in the forthcoming years) is observed, see [9], and this could question the validity of this modeling. Great part of authors relies on the correctness of the assumption on the negligible heat conduction in casting direction: in this regard [10,11] could be cited. The purpose of the article is to verify the truthfulness of this statemen, spanning a wide range of product sizes and casting speeds.

2. Numerical modeling of the continuous casting process

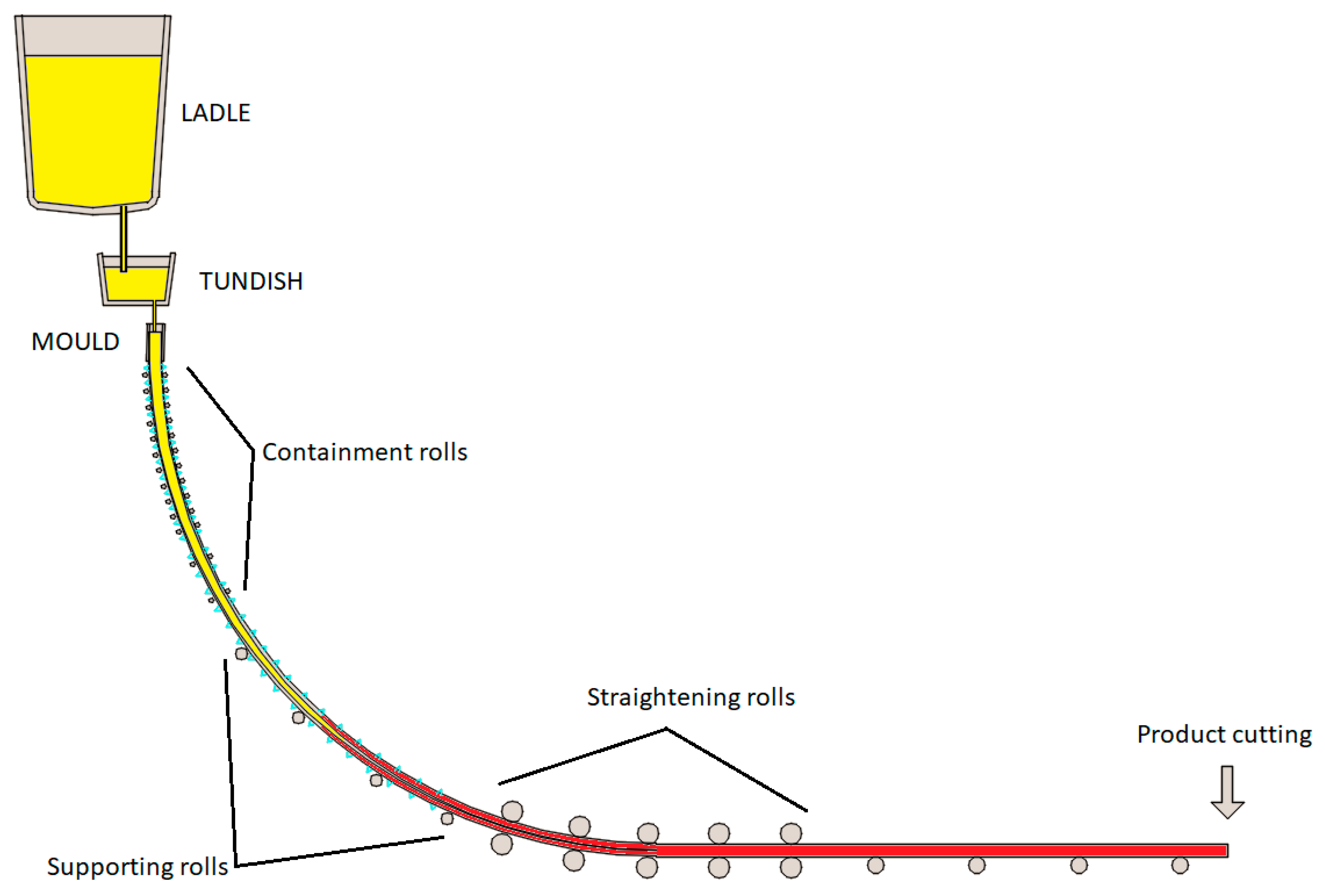
The modeling of steel continuous casting process shall be multiphysics due to the complexity of phenomena which occur: thermal (solidification of molten metal, withdraw of latent and sensible heat), mechanical (interaction between casted product and mould, friction, effect on the shape of pressure of the part which is still liquid), metallurgical (grain growth in consequence of solidification, precipitation of secondary phases or carbides) and chemical (segregation of solutes, decomposition of lubricant). The above-mentioned fields are linked each other and make the problem non linear; a common root of all of them is that are temperature dependent. In a steel continuous casting plant (schematic representation of a continuous caster is given in Figure 1). The core equipment is represented by the mould where in short time and small volume, compared to overall dimensions, a big amount of energy (order of magnitude: tens of MJ) is withdrawn from molten metal. This component is made by copper, due to its high thermal conductivity, and cooled by water. The thermal exchange between metal and mould depends essentially by contact status; in early stage, when metal is too soft and not yet able to bear mechanical loads, the adherence is high as well as the withdrawn of energy. Moving downward metal become stiffer and a gap between it and mould is created, so thermal exchange is lessened and rate of growth of solidified shell diminishes. At mould exit the solidified thickness must be enough to withstand the pressure exerted by inside metal which is still liquid.
As can be understood, heat exchange inside mould plays a significant role in the whole process; moreover the great part of defects on the casted material, such cracks and pin-holes, born here and are related to uneven heat extraction (see [12]).
What happens in the short space between solidified shell and mould surface is one of the most studied energy transfer mechanism of the whole steel casting process; it can be represented by a thermal resistances model in which each of them are the bodies (water, mould, lubricant, gap, shell, molten steel) crossed by heat. A comprehensive treating could be found in [13]; an interesting analysis on peak fluxes is given in [14]. If each thermal resistance is known, starting from molten steel temperature could be determined all others in between and the thermal flux: this is the so called fully coupled or direct approach where both temperatures and flux are output; however, one of the greater difficulties of such modeling is to estimate the resistance value of gap. Several studies on the gap formation in mould have been carried out: only in some particular cases, like round shape, problem is less complicated and a numerical approach could be done (see [15,16]). For other common shapes such as square (billet) and rectangles (bloom and slab), the computational cost for the gap estimation increases dramatically and different way shall be chosen: the problem decoupling. In this latter one the thermal flux becomes an input, shifting the complexity on the convenient mathematical description of the heat withdrawn from mould, which depends by several parameters as casting speed, lubrication, material; e.g. for steel two lubricants are typically used (powder or mineral oil) and specific grades (the peritectic ones) shows differences in energy exchange (a quantification could be found in [17]). To solve this issue come to help mixed analytical-empirical models, see for example [18], so thermal flux is now established and no more dependent from contact status; this is a strong assumption, anyhow it permits the analysis to be performed in a feasible time. Typically, the mould flux trend in monotonically decreasing moving from meniscus to exit, again [13,18]) could be consulted, although this statement in not widely agreed and a degree of uncertainty still remains.

3. Travelling slice model

3.1. Model statement

As mentioned in the previous paragraph, the model has to take into account firstly the thermal aspect of continuous casting process. Analysis is transient and with temperature dependent thermal properties, see [10], and time/temperature dependent boundary conditions. In other words, Fourier’s equation shall be solved over the whole calculation domain:
∂ T ∂ t = λ ρ c ∇ 2 T
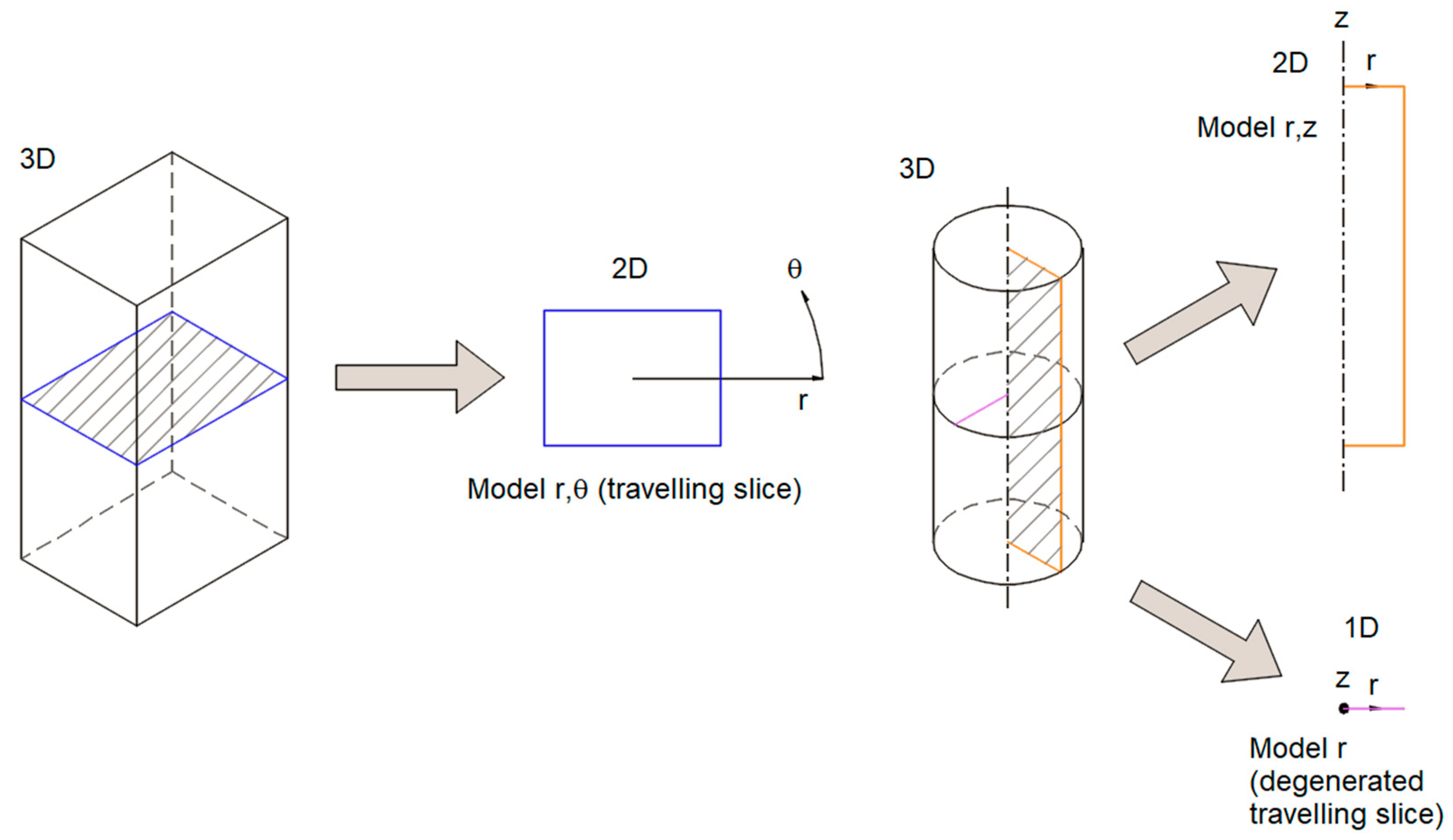
where T is temperature, t is time, λ, ρ and c are respectively the thermal conductivity, the volumic mass and specific heat of metal that is casted. Following the physics of the steel continuous casting process the model should be tridimensional. In fact, even though geometry remains constant in the casting direction (z axis), boundary conditions changes along z.
The most natural choice is that of following a growing mesh strategy, where new elements are added at domain too during simulation; such approach is less often adopted due to a higher complexity. As mentioned before, a good computational alternative, is that of adopting a plane model (in the plane perpendicular to the z axis containing the product section) which moves in z direction obeying the following law:
z t + ∆ t = z t + v · ∆ t
where t is time, Δt is time increment and v is casting speed. According to this approach, generally called travelling slice model, boundary conditions start below a certain level, that could be chosen arbitrarily (e.g. 0), and casted product move in negative z direction; this means that all nodes above 0 shall have fixed temperature in order to avoid thermal fluxes in the domain part which is not yet been casted. As the nodes move below the aforementioned level, the fixed temperature condition is removed. In the particular case of a casted product whose shape is round, axisymmetry permits Equation (1) to be solved exactly according to a 2D model. In the latter case the approximated travelling slice model degenerates into a 1D model (as visible in Figure 2).
This favorable condition makes possible a comparison between the two models to be easily performed with a reduced computational effort, which permits a parametric analysis to be carried out. It will be thus possible to verify in a wide range of product dimension and speed casting, the correctness of the hypothesis that heat conduction, namely energy transfer, in casting direction is negligible.

3.2. Boundary and initial conditions

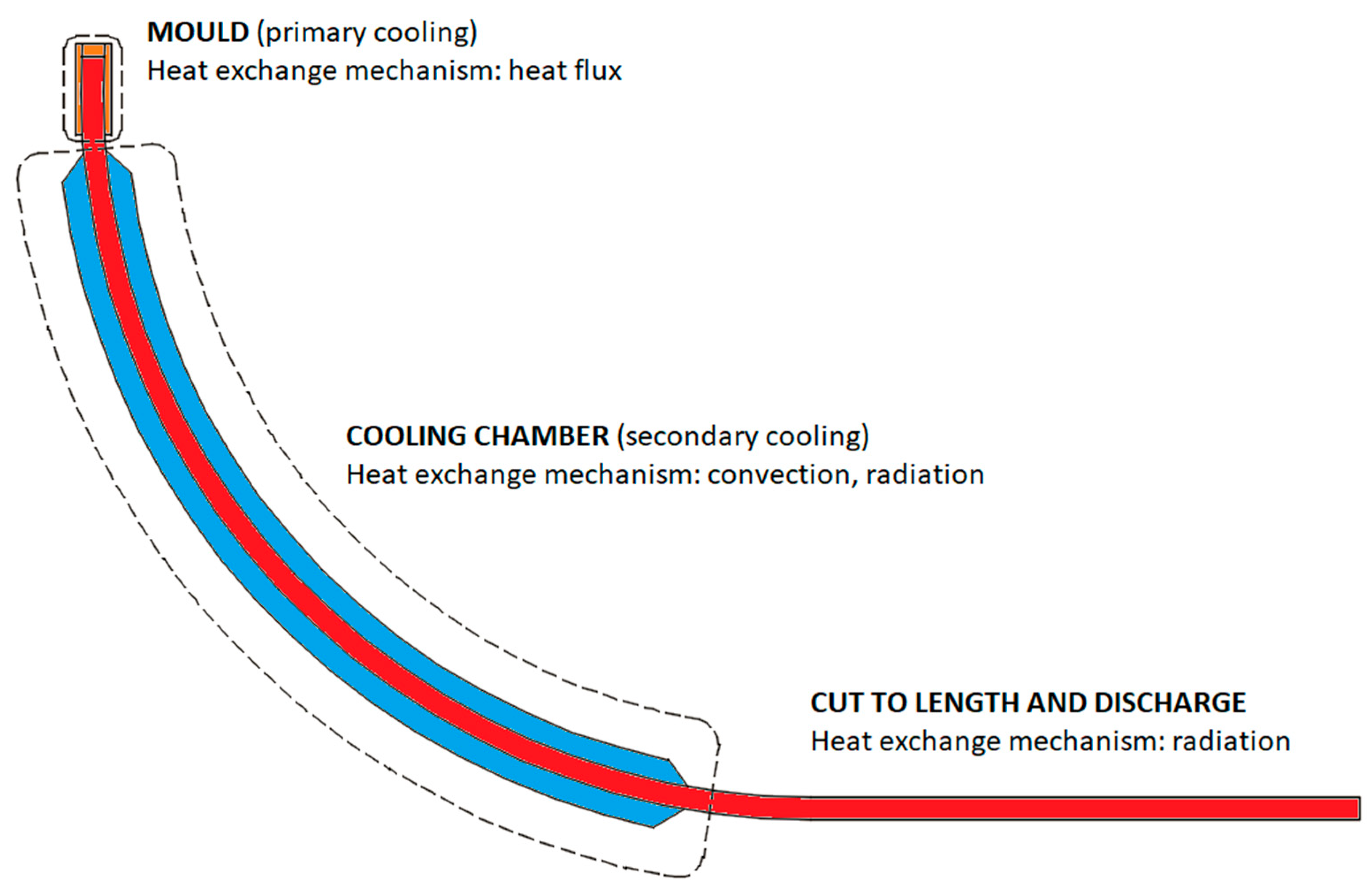
In a steel continuous casting machine there are three different kinds of thermal exchange, each predominant in a certain part of it (as visible in Figure 3).
Thermal flux is withdrawn from mould in order to start solidification; from a technical point of view this is called primary cooling. When mould is left, casted product pass through a cooling chamber in which energy is removed by arrays of water sprays (or air-mist for slabs); here two concurring heat transfer mechanisms take place: convection with cooling media and radiation. In this zone occurs the secondary cooling. In the last part of machine cooling continues thanks to radiation only.
Since models are transient, an initial condition shall be given; this is a fixed temperature in all nodes of calculation domain. For steel continuous casting pouring temperature is the sum of liquidus temperature (which is dictated by chemical composition) and a certain superheat, namely the overheating respect to liquidus, typically in the range 20÷50 °C. This is done to avoid solidification in other devices (tundish and submerged entry nozzle if present) prior to mould where steel shall remain in liquid phase, otherwise technological issues could occur and stop the casting process or make it troublesome.

3.2.1. Mould

As said before, thermal flux must be considered an input if a decoupled analysis is chosen, otherwise it becomes an output of the model; in this paper first approach is used, as done in most published papers. From a global perspective, thermal flux acts on the domain borders; it is a Neumann’s boundary condition expressed as follows:
∂ T ∂ t = λ ρ c ∇ 2 T q "   = − λ ∇ T · n
where n is the unit vector perpendicular to surface.
From a mathematical point of view the above one is function of time and coordinates (for shapes as billets, blooms and slabs):
q "   = f ( t i m e ,   c o o r d i n a t e s )
(3’)
Thermal flux distributions are typically empiric: there are several references, however a first outlook could be found in [20,21].

3.2.2. Cooling chamber

The cooling of casted product, started in mould, continues in this zone in which heat is withdrawn both by convection and radiation. Typical boundary condition could be written as:
q " = − α T , c o o l i n g   f l o w   r a t e T s u r f − T ∞
where T s u r f is the surface temperature and T ∞   the temperature outside the boundary layer. Temperature dependence is due to include radiation effects avoiding the fourth power exponent, making simpler its numerical treatment; for this reason, α shall be considered an equivalent heat transfer coefficient. As for mould heat fluxes, also for heat transfer coefficients several measuring tests have been conducted, resulting in a wide range of empiric correlations (see [20,21,22,23,24] for details).
Cooling chamber is divided in sectors fed with different water flow rates; first one just after mould is called “foot rolls” (where cooling is intense), followed by “mobile” and a number of “fixed” till end depending on machine layout and productivity. Higher is the casting speed (means productivity), longer is the cooling chamber. The flow rate decreasing law is chosen to guarantee a smooth cooling path without excessive reheating on product surface passing from a sector to the subsequent one. Shall be pointed out that aim of secondary cooling is to ensure the complete solidification before product cutting.

3.2.3. Cut to length and discharge

In this part the casted product is not anymore subjected to forced cooling: it loses energy by radiation only. In some layouts hoods are present to have a passive control on how much temperature is left on the product prior to subsequent plastic deformation processes; in such case radiation losses are lessen in order to maintain a certain enthalpic level in it.

4. Case study

Following the concepts shown till now, in the case of an axi-symmetric product section, the plane model will be compared with the 1D travelling slice model. As mentioned before, recently an increase of casted product size has been observed. It is therefore of great interest to analyze also these cases. For this purpose, three different casted shapes were investigated, all rounds with diameters of 200 mm, 850 mm and 1200 mm respectively. The case of 200 mm round represents the traditional small size product. Three values of casting speed were made to vary in a range of industrial interest (from 2 m/min to 3 m/min). The 850 mm case represents a typical size of more recent steelmaking plant to fed the subsequent hot forging process. The adopted casting speed is 0.20 m/min. Nowadays very big sections have been introduced as an alternative and more efficient process compared to ingot casting. The case of 1200 mm will be thus considered. Two values of casting speed are taken into account: 0.08 m/min and 0.04 m/min; this latter one, although is outside industrial range, has been considered to stress the “travellig slice” model to see if it fails.
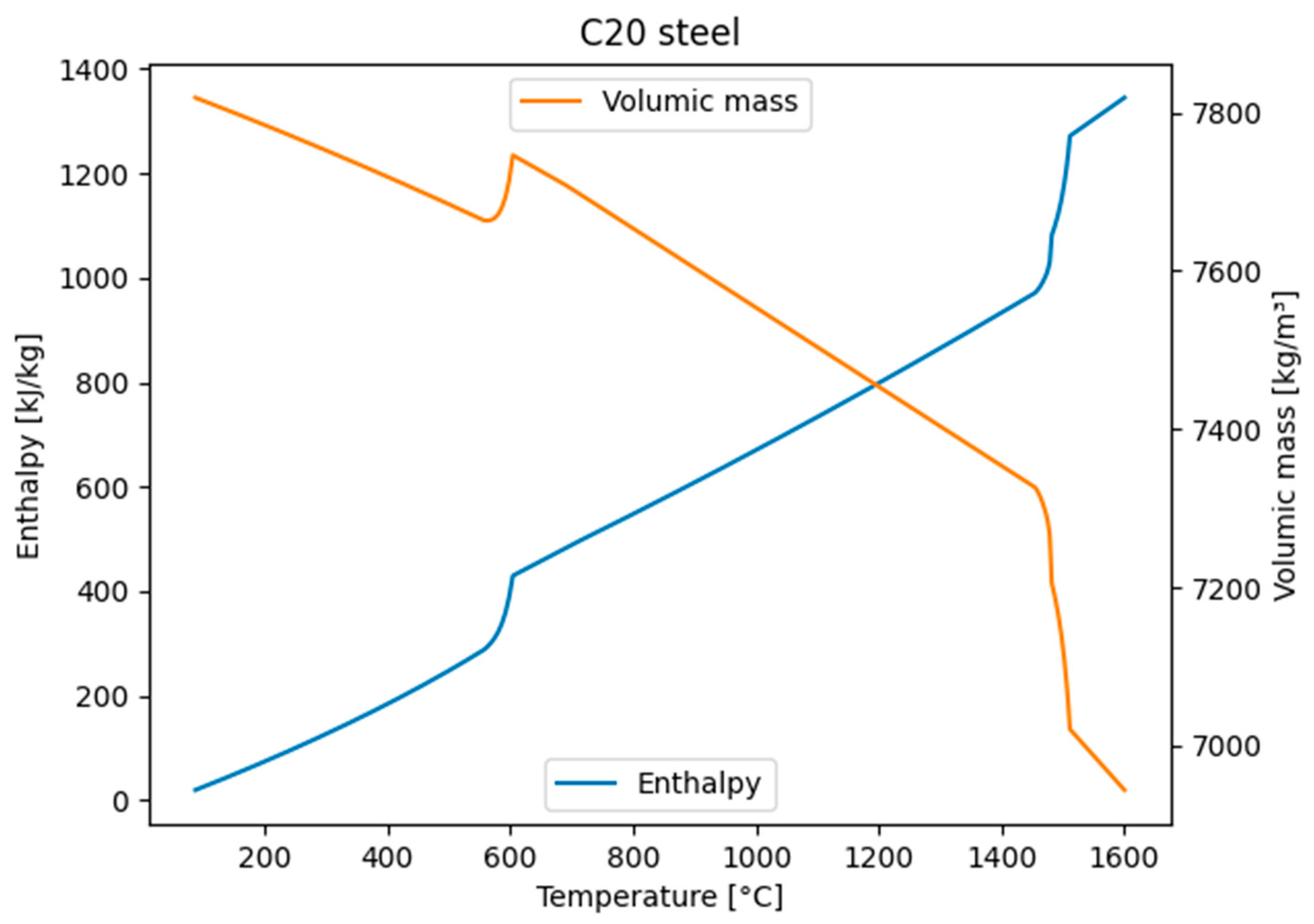
Steel composition is given in Table 1, as well as its characteristics in Table 2. In Figure 4 the values of enthalpy and volumic mass are reported for different temperatures. This is a common structural steel, widely used for round bar, rebar and beam production.
Boundary conditions are listed in Table 3, Table 4 and Table 5 for the three product diameters considered in this work. In particular, the thermal flux acting in mould and the heat transfer coefficient (HTC) in the subsequent regions are reported. It must be observed that as casted section increases, a less intense cooling is required, due to lower casting speed and higher energy stored in the liquid steel. As pointed out previously, in the discharge section the heat cooling is mainly governed by radiation.

5. Result and discussion

Figure 5 represents the computed temperatures (surface and core) for the three cases of Ø 200 mm; both surface and core temperature are given. It is visible a similar trend for all speeds, although with different values; moreover, is visible the complete solidification is reached before for lower speed, in totally agreement with plant operations and reference [26].
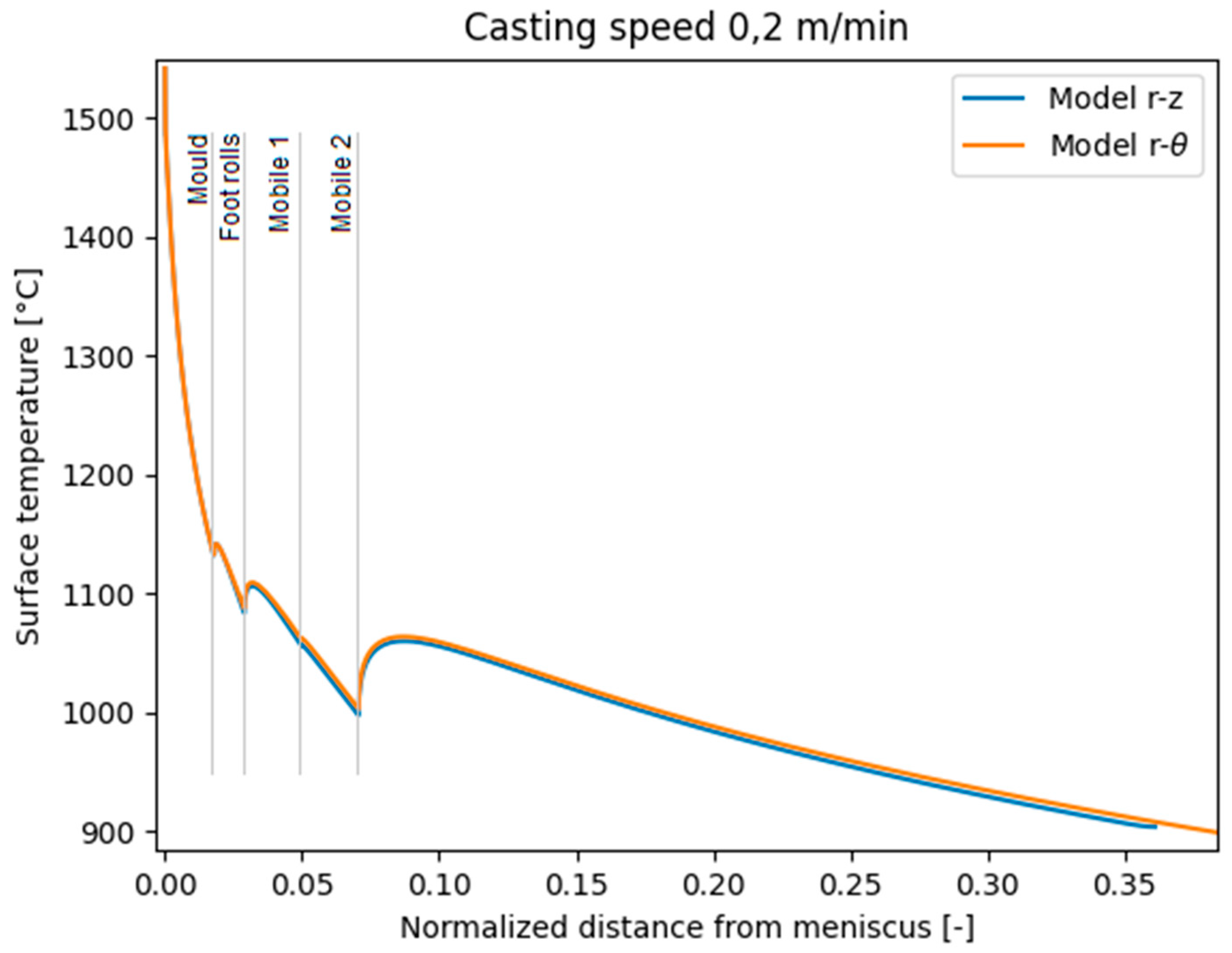
Figure 6 compares both models for Ø 850 mm casted at 0.20 m/min: the agreement between them is significant, since the two curves are practically overlapped; in Table 6 could be find the relative error for all sections and all casting speeds.
Please note that the comparison is given in the only points present in all cases: mould exit and foot rolls (these two are common in Table 3, Table 4 and Table 5). Relative error is far under the acceptable threshold for the purposes of an industrial use.
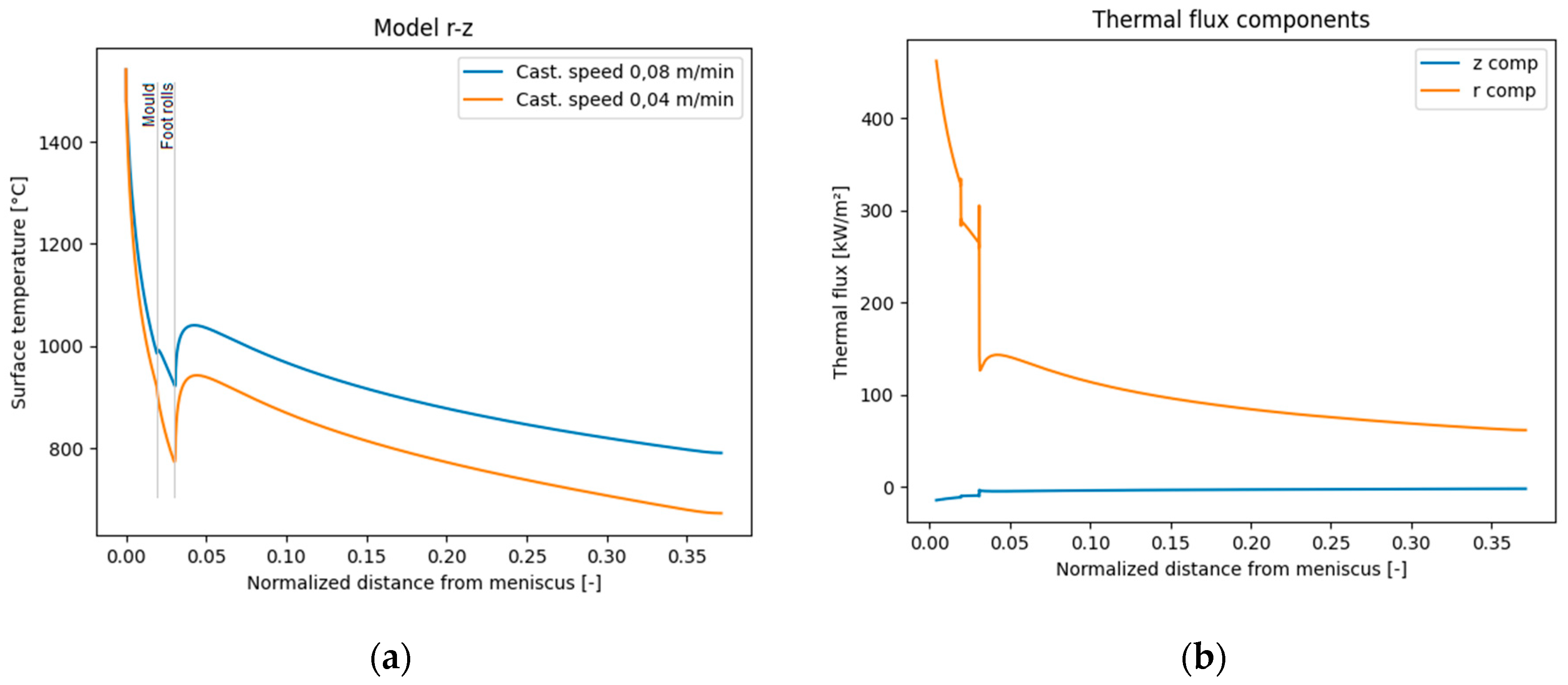
Figure 7 relates to the biggest section, the Ø 1200 mm one. It must be pointed out that casting speed in such case, namely 0.08 m/min, is approaching the lower operational limit in continuous casting process. As said in previous paragraph, a case at 0.04 m/min has been done only with the purpose of investigating the applicability of the travelling slice model at very low casting speed; boundary conditions were different in the mould (average heat flux 316 kW/m²) but not in foot rolls, where same HTC (see Table 5) has been taken: for this reason the computed surface temperature results low from an operational perspective. Moreover, it is visible that radial heat flux is always far bigger than axial one, confirming the correctness of neglecting this latter one (which is the fundamental hypothesis of travelling slice modeling). If this assumption is true for a such slow casted section, it will be even more so in case of smaller and quicker sections.
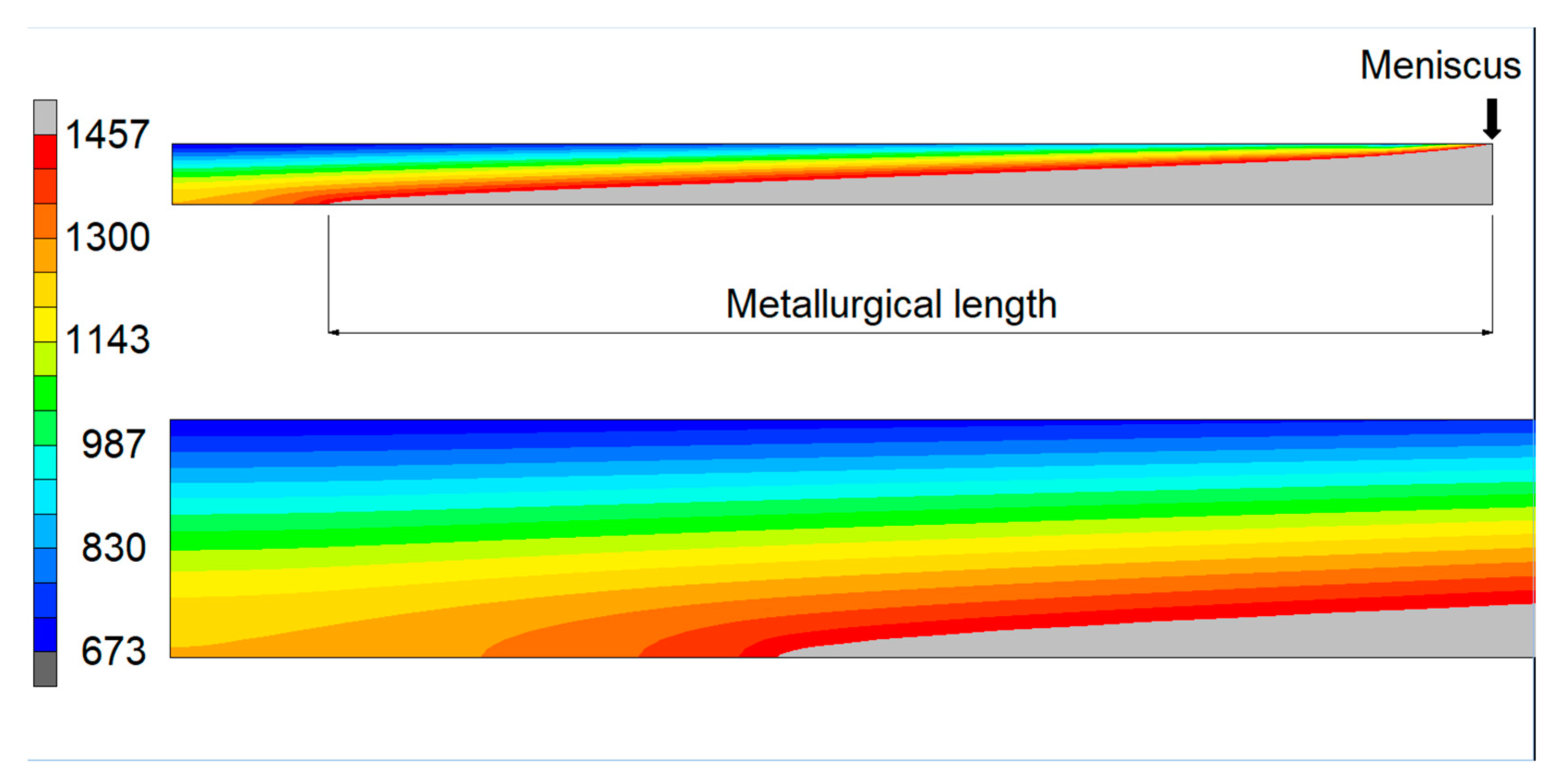
Figure 8 shows the thermal field for Ø 1200 mm casted at 0.04 m/min, making visible the “liquid pool end” that occurs where the entire section is completely solidified (all domain is under solidus temperature).
It shall be noted that travelling slice model gives same metallurgical length of model bidimensional model, making again itself as a reliable approach in modeling the continuous casting process.

6. Conclusions

In this work, the validity of the travelling slice model is analyzed, particularly in the case of large diameter product and low casting speeds. Only in the case of round section a comparison with an exact model is possible with a reasonable computational cost. Two different models (1D travelling slice approximated model and 2D axisymmetric exact one) have been developed and compared. The results show the validity of the “travelling slice “model in a wide range of product dimensions and casting speed. Surface temperature comparison shows practically the overlap of profiles coming from both models with a relative error that is always less than 1.5% also in case of casting speed outside the industrial range. Moreover, the component of thermal flux along casting direction is always a negligible portion of total flux, thus confirming the validity of travelling slice model. It can be thus stated that also in case of big sections and low productivity the travelling slice could be a reliable choice to model the continuous casting process. It shall be highlighted that the computational cost of the exact 2D model is far higher the 1D approximated one; the ratio of calculation time for the same casted profile is proportional to 103 in favor of travelling slice model (on the same hardware).

Author Contributions

Conceptualization, G. B.; methodology, G. B. and F. D. B.; validation, G. B.; formal analysis, G. B.; investigation, G. B. and F. D. B.; writing—original draft preparation, G. B.; writing—review and editing, F.D.B. Both authors have read and agreed to the published version of the manuscript.

Conflicts of Interest

G. B. declares to be an employee of Danieli & C. Officine Meccaniche SpA headquartered in Buttrio (Italy). F. D. B. declares no conflicts of interest.

References

  1. Dong, Q.; Zhang, J.; Yin, Y.; Wang, B. Three-dimensional numerical modeling of macrosegregation in continuously cast billets. Metals 2017, 7, 209. [Google Scholar] [CrossRef]
  2. Yang, J.; Xie, Z.; Meng, H.; Hu, Z.; Liu, W.; Ji, Z. 3D transient heat transfer simulation and optimization for initial stage of steel continuous casting process. ISIJ Int. 2023, 63, 862–869. [Google Scholar] [CrossRef]
  3. Koric, S.; Abueidda, D. Deep learning sequence method in Multiphysics modeling of steel solidification. Metals, 2021, 11, 494. [Google Scholar] [CrossRef]
  4. Han, H.N.; Lee, J.; Yeo, T.; Won, Y. M.; Kim, K.; Oh, K. H.; Yoon, J. A finite element model for 2-dimensional slice of cast strand. ISIJ Int., 1999, 39, 445–454. [Google Scholar] [CrossRef]
  5. Koric, S.; B. G. Thomas, B. G. Efficient thermo-mechanical model for solidification processes. Int. J. Numer. Meth. Engng., 2006, 66, 1955–1989. [Google Scholar] [CrossRef]
  6. Heger, J. Finite element modelling of mechanical phenomena connected to the technological process of continuous casting of steel. Acta Polytech 2004, 44, 15–20. [Google Scholar] [CrossRef]
  7. Kong, Y.; Chen, D.; Liu, Q.; Long, M. A prediction model for internal cracks during slab continuous casting. Metals 2019,, 9, 587. [Google Scholar] [CrossRef]
  8. Li, C.; Thomas, B. G. Thermo-mechanical finite element model of shell behavior in continuous casting of steel. Modeling of Casting, Welding and Advanced Solidification Processes X, San Destin, FL, May 25-30, 2003, 385-392. 25 May.
  9. Nian, Y.; Zhang, L.; Zhang, C.; Ali, N.; Chu, J.; Li, J.; Liu, X. Application status and development trend of continuous casting reduction technology: a review. Processes, 2022, 10, 2669. [Google Scholar] [CrossRef]
  10. Wang, E.; He, J.; FE numerical simulation for influence of mold taper on thermomechanical behavior of steel billet in continuous casting process. J. Mater. Sci. Technol., 2001, 17 suppl. 1, s8-s12.
  11. Fang, Q.; Ni, H.; Zhang, H.; Wang, B.; Liu, C. Numerical study on solidification behavior and structure of continuously cast U71Mn steel. Metals, 2017, 7, 483. [Google Scholar] [CrossRef]
  12. Kwon, S. H.; Won, Y. M.; Back, G. S.; Kim, H.; Lee, J. S.; Kim, D. G.; Heo, Y. U.; Yim, C. H. Prediction model for degree of solid-shell unevenness during initial solidification in the mold. ISIJ Int., 2021, 61, 2534–2539. [Google Scholar] [CrossRef]
  13. Saraswat, R.; Maijer, D. M.; Lee, P. D.; Mills, K. C. The effect of mould flux properties on thermo-mechanical behavior during billet continuous casting. ISIJ Int., 2007, 47, 95–104. [Google Scholar] [CrossRef]
  14. Mills, K. C.; Fox, A. B. The role of mould fluxes in continuous casting – So simple yet so complex. ISIJ Int., 2003, 43, 1479–1486. [Google Scholar] [CrossRef]
  15. Vynnycky, M. Air gaps in vertical continuous casting in round moulds. J. Eng. Math., 2010, 68, 129–152. [Google Scholar] [CrossRef]
  16. Vynnycky, M. Applied mathematical modelling of continuous casting process: a review. Metals, 2018, 8, 928. [Google Scholar] [CrossRef]
  17. Jolivet, J. M.; Le Papillon, Y.; Bellavia, L. Development of high productivity casting of conventional and thin slabs, RFCS publications, 2009, EUR 23887 Final Report.
  18. Alizadeh, M.; Jahromi, A. J.; Abouali, O. New analytical model for local heat flux density in the mold in continuous casting of steel. Comput. Mater. Sci., 2008, 44, 807–812. [Google Scholar] [CrossRef]
  19. Mills, K. C.; Karagadde, S.; Lee, P. D.; Yuan, L.; Shahbzian, F. Calculation of physical properties for use in models of continuous casting processes – Part 2: steels. ISIJ Int., 2016, 56, 274–281. [Google Scholar] [CrossRef]
  20. AA. VV. The making, shaping and treating of steel (MSTS). The AISE Steel Foundation, Pittsburg, PA. 2003.
  21. Assuncao, C.; Tavares, R.; Oliveira, G. Improvement in secondary cooling of continuos casting of round billets through analysis of heat flux distribution. Ironmak. Steelmak 2015, 42, 1–8. [Google Scholar] [CrossRef]
  22. Wang, W.; Zhang, H.; Nakajima, K.; Lei, H.; Tang, G.; Wang, X.; Mu, W.; Jiang, M. Prediction of final solidification position in continuous casting bearing steel billets by slice moving method combined with Kobayashi approximation and considering MnS and Fe3P precipitation. ISIJ Int., 2021, 61, 2703–2714. [Google Scholar] [CrossRef]
  23. Long, M.; Chen, H.; Chen, D.; Yu, S.; Liang, B.; Duan, H. A combined hybrid 3-D/2-D model for flow solidification prediction during slab continuous casting. Metals, 2018, 8, 182. [Google Scholar] [CrossRef]
  24. Milkowska-Piszczek, K.; Falkus, J. Control and design of the steel continuous casting process based on advanced numerical models. Metals, 2018, 8, 581. [Google Scholar] [CrossRef]
  25. Cai, S. W.; Wang, T. M.; Xu, J. J.; Li, J.; Cao, Z. Q.; Li, T. J. Continuous casting novel mould for round steel billet optimized by solidification shrinkage simulation. Mater. Res. Innov. 2011, 15, 29–35. [Google Scholar] [CrossRef]
  26. Chen, Y.; Peng, Z.; Wu, L.; Zhao, L.; Wang, M.; Bao, Y. High-precision numerical simulation for effect of casting speed on solidification of 40Cr during continuous billet casting. Metall. Ital. 2015, 1, 47–51. [Google Scholar]
Preprints 80218 g001
Figure 1. Sketch of a typical curved continuous casting machine. Molten steel in yellow, solidified steel in red. Cyan triangles: spray cooling.
Figure 1. Sketch of a typical curved continuous casting machine. Molten steel in yellow, solidified steel in red. Cyan triangles: spray cooling.
Preprints 80218 g001
Preprints 80218 g002
Figure 2. Different modeling strategies.
Figure 2. Different modeling strategies.
Preprints 80218 g002
Preprints 80218 g003
Figure 3. Prevailing heat exchange mechanisms in a continuous casting machine.
Figure 3. Prevailing heat exchange mechanisms in a continuous casting machine.
Preprints 80218 g003
Preprints 80218 g004
Figure 4. Enthalpy and volumic mass trend for the selected steel.
Figure 4. Enthalpy and volumic mass trend for the selected steel.
Preprints 80218 g004
Preprints 80218 g005
Figure 5. Surface (a) and core (b) temperatures for Ø 200 mm.
Figure 5. Surface (a) and core (b) temperatures for Ø 200 mm.
Preprints 80218 g005
Preprints 80218 g006
Figure 6. Comparison of both models on surface temperature (casted section Ø 850 mm).
Figure 6. Comparison of both models on surface temperature (casted section Ø 850 mm).
Preprints 80218 g006
Preprints 80218 g007
Figure 7. Surface temperature at different casting speed (a) and thermal flux components at 0.04 m/min for Ø 1200 mm (b).
Figure 7. Surface temperature at different casting speed (a) and thermal flux components at 0.04 m/min for Ø 1200 mm (b).
Preprints 80218 g007
Preprints 80218 g008
Figure 8. Thermal field in [°C] on whole domain (top) and particular of “liquid pool end” (bottom) for Ø 1200 mm.
Figure 8. Thermal field in [°C] on whole domain (top) and particular of “liquid pool end” (bottom) for Ø 1200 mm.
Preprints 80218 g008
Table 1. Steel chemical composition.
Table 1. Steel chemical composition.
Element Concentration [%] Element Concentration [%]
C 0.210 Mn 1.500
Cr 0.020 Ni 0.020
Mo 0.002 Si 0.200
Cu 0.035 Al 0.045
P 0.010 S 0.002
V 0.003 Fe balance
Table 2. Some physical parameters of selected steel.
Table 2. Some physical parameters of selected steel.
Parameter Value
Liquidus temperature 1541 °C
Solidus temperature 1457 °C
Solidification range 84 °C
Latent heat 297.66 kJ/kg
Table 3. Detail of applied boundary conditions for each zone for both models (cast section Ø 200).
Table 3. Detail of applied boundary conditions for each zone for both models (cast section Ø 200).
Zone Length [m] Boundary condition
Mould (steel level) 0.68 Thermal flux according to [25]
Foot rolls 0.35 HTC = 1410÷1523 W/m²·K (depending on speed)
Mobile 1.90 HTC = 720÷795 W/m²·K (depending on speed)
Fixed 1 2.30 HTC = 320÷390 W/m²·K (depending on speed)
Fixed 2 1.15 HTC = 269÷309 W/m²·K (depending on speed)
Discharge 28.6 Radiation to environment
Table 4. Detail of applied boundary conditions for each zone for both models (cast section Ø 850).
Table 4. Detail of applied boundary conditions for each zone for both models (cast section Ø 850).
Zone Length [m] Boundary condition
Mould (steel level) 0.64 Average thermal flux = 548 kW/m²
Foot rolls 0.40 HTC = 331 W/m²·K
Mobile 1 0.75 HTC = 251 W/m²·K
Mobile 2 0.75 HTC = 242 W/m²·K
Discharge 32.46 Radiation to environment
Table 5. Detail of applied boundary conditions for each zone for both models (cast section Ø 1200).
Table 5. Detail of applied boundary conditions for each zone for both models (cast section Ø 1200).
Zone Length [m] Boundary condition
Mould (steel level) 0.64 Average thermal flux = 413 kW/m²
Foot rolls 0.40 HTC = 296 W/m²·K
Discharge 33.96 Radiation to environment
Table 6. Relative error on the computed surface temperature for all studied cases in two points.
Table 6. Relative error on the computed surface temperature for all studied cases in two points.
Case Mould exit Foot rolls
Ø 200 mm – 2.00 m/min 0.19% -0.74%
Ø 200 mm – 2.50 m/min 0.19% 0.51%
Ø 200 mm – 3.00 m/min 0.28% -0.59%
Ø 850 mm – 0.20 m/min 0.09% -0.28%
Ø 1200 mm – 0.08 m/min 0.20% 0.43%
Ø 1200 mm – 0.04 m/min -0.87% 1.15%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated