Prerpints.org logo
Preprint
Article

FSI Application in the Parametric Analysis of Blade-Disc Connection of Turbojet Engine Compressor

Altmetrics

Downloads

112

Views

19

Comments

0

This version is not peer-reviewed

Submitted:

21 July 2023

Posted:

27 July 2023

You are already at the latest version

Alerts
Abstract
In the following work, the assessment of the strength properties of the critical area of the rotor stage of the turbine jet engine was undertaken. This is the place of fixing the blade in the rotor disc. An important aspect of this issue are characteristic geometrical dimensions and operating factors e.g., change in rotor speed. In this paper, the assessment of the strength properties of the existing trapezoidal blade-disc connection was undertaken using parametric analysis considering FSI. Virtual models of the compressor rotor stage were developed, including parametric blade-disc connections and discrete models for FEM and CFD analyses. In the parametric analysis of the blade-disc connection, one-way fluid-structure coupling was used. The parametric analysis was aimed at assessing selected geometric parameters in terms of their impact on the maximum reduced stresses in the blade root. It was examined how the adopted value of the friction coefficient influences the maximum reduced stresses in the rotor stage of the compressor.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Issues related to the design of rotor systems, including compressors, are solved in many areas. These areas are frequency analyses [1,2]. These studies, in addition to numerical analyzes, are carried out by way of experiment. To eliminate overlapping frequencies of components, for example discs and blades. The work of these elements in the same frequencies leads to fatigue problems. This issue was developed in the work [3]. The paper proposed a three-dimensional equivalent notch model, which proved to be more convenient than the traditional crack simulation model. The article presents the effect of cracking on the strength of the rotor system. The vibration characteristics of the design of the blade-disc connection structure were analyzed in the work [4] using cycle analysis method with the aid of ANSYS software. The results show that under the influence of prestress, the stiffness and natural frequency of the blade structures increased with a gradual increase in rotational speed. This influence weakened when the rotational speed reached a certain range. Damage tolerance analysis could be exploited more and more to study, understand, and calculate the residual life of a component when a crack occurs in service [5]. In this paper, the authors are presented the results of a systematic crack propagation analysis campaign performed on a compressor-blade-like structure. The possibility of reducing the rate of crack propagation in low-cycle fatigue was investigated. Another significant problem in compressors is the stall, which limits the operating range and stability of the compressor and has a significant impact on the life of the rotor blades. In the article [6] investigates the relationship between stall pressure wave and its induced non-synchronous blade vibration, which will be meaningful for stall resonance avoidance at the early design phase.
Nowadays, there are works solving the problem of strength calculations of rotor assemblies using artificial neural networks. In the article [7] the process of selecting and optimizing artificial neural networks based on the example of determining the stress distribution in a disk-drum structure compressor stage of an aircraft turbine engine. The presented algorithm allows the determination of von Mises stress values which can be part of the penalty function for further mass optimization of the structure.
The critical area of the rotor stage structure of a turbine jet engine is the place where the blade is attached to the disc rim. And this area is the main interest of the author in the following work. The most common type of connection used in fans and rotor stages of axial compressors is a trapezoidal root with a cross-section like an isosceles trapezoid. The method of attaching the blade depends largely on the type of supporting structure. In the case of disc structures, the blades are fixed in specially made channels parallel or diagonal to the axis of rotation of the engine, and in the case of drum or drum-disc structures, in channels turned circumferentially [8,9].
The main dimensional loads in the root are centrifugal forces acting on the weight of the part of the blade located above the root (they cause tension in cross-section and pressure of the mating surfaces of the root and the disc rim) and aerodynamic forces acting on the blade, causing bending and twisting. In the case of perimeter-fixed trapezoidal roots, the greatest tensile force acts in the 0-0 cross-section (Figure 1). The maximum tensile stresses in this section are a function of:
σ r = f F r ,   b , c
where F r   is the resultant loading force of the part of the blade above the section of dimensions b and c [10].
An important aspect in the methods of designing blade connections with discs is the use of numerical methods and parametric models to optimize and assess the impact of specific variables on the strength and operation of such a structure [11,12,13,14,15,16,17,18]. Parameters, in this case, may be characteristic geometric dimensions and operating factors, e.g., such as rotational speeds or pressures affecting the distribution of aerodynamic loads acting on the blade.
Considering several types of loads require the use of advanced tools, such as coupled analyzes examining the fluid-structure interaction (FSI). An example of the use of FSI coupling in the analysis of rotor assemblies is a publication by Sun Tao et al. [19], where the authors presented the methodology of mentioned method in the analysis of the centrifugal compressor rotor stage and the impact of the applied coupling on the stress distribution in the rotor blade.
In the following work, the assessment of the strength properties of the existing trapezoidal blade-disc connection was undertaken using parametric analysis considering the FSI. The analysis was based on the relationship between the selected geometrical parameters and the maximum stresses reduced in the structure. The analysis algorithm is shown in Figure 2.
The main stages of the analysis included: development of a virtual model, including parametric blade-disc connection and discrete models for FEM and CFD analyses, performing numerical structural-flow analyses and applying them to the analysis of the parametric model.

2. Object of research

For numerical research, a virtual model of the rotor stage of the axial compressor was developed. For this purpose, curves were used to map the scanned object, which was the blade of the high-pressure compressor of turbine jet engine. First, the blade was modeled, and then the root. Due to the small angle of twisting the blade, it was limited to a few of its cross-sections, which in this case was sufficient to reproduce the correct geometry of the blade (Figure 3). It should be noted that in the case of modeling planes, the appropriate number of curves should be selected to obtain a non-distorted modeled surface. The high-pressure compressor support element with a disc-drum design was mapped using the available engine technical documentation.
The developed geometric model of the compressor blade was also the starting point for the preparation of a virtual model for numerical flow simulation. Taking into account the repeatability of elements in the rotor stage (Figure 4a) and the fact that the Fluent program allows the use of periodic boundary conditions, in the case of rotating machines, it was limited to the construction of a small, repeating fragment of the rotor palisade (Figure 4b). These boundary conditions allow interference between successive elements of the model to be considered. In the model under consideration, the compressor stage had 68 rotor blades, so the angle of the modeled design area was 5.29°.
Discretization of the rotor stage structure was limited to generating a finite element grid of the slice (Figure 5a) including one blade (Figure 5b). Due to the possibility of using a condition of cyclic symmetry. In addition, in sensitive areas of the structure, such as the connection area, appropriate mesh compaction has been introduced (Figure 5c). The discrete model is shown in Figure 5.
The condition of cyclic symmetry [20,21] used in FEM calculations of rotating discs and blades allows to shorten the calculation time. This is because that the cyclically symmetrical structure contains sectors of repetitive shape, arranged circumferentially around the axis of symmetry. The FEM model of such a construction is one basic sector divided into finite elements. The remaining sectors are calculated based on the performance of the basic sector using the combined Fourier series [20].
The boundary conditions for the CFD task were given during the creation of the design area geometry and mesh generation (Figure 6). It consisted in indicating suitable surfaces in the calculation area, representing selected boundary conditions [22]: Inlet (in the inlet to the compressor stage) – in the boundary condition: Pressure Inlet; Outlet (in the outlet from the compressor stage) – in the boundary arrange: Pressure Outlet; Hub (disc/load-bearing structure) – in boundary condition: Wall; Shroud (outer cover) – in boundary condition: Wall. In addition, because in the analyzed case only the repeating element of the rotor stage was considered, the periodic boundary conditions were imposed. They allow to consider the interference between subsequent elements of the model.

3. Parametric analysis with FSI

FSI is a multiphysical study of the interaction of fluid that flows around the solid structure, considering the effect of the reverse interaction, i.e., the impact of structural deformation on flow parameters. Fluid-structure interaction is a method that requires the calculation with using computational fluid dynamics (CFD) and the combination of fluid flow results with a structural analysis model. Analyses of this type should be considered wherever the flow of fluid can exert pressure as well as thermal load on the structure. The coupling allows fluids and structural models to exchange information and shows how fluid flow can cause structure deformation (and vice versa, how structure deformations can affect flow in the ambient zone). Modelling approaches may vary depending on the degree of physical coupling between fluid and solid and the level of accuracy required. When stresses and deformations are taken into account, the analysis includes data provided by simulations from flow and structural analysis. The application of the appropriate FSI coupling for analysis depends on the degree of physical coupling of the solution field between the liquid and the solid [8,13]. Strongly physically coupled fields require strong numerical coupling. Full couplings are then used. Solution fields that are relatively independent can be solved by using a weaker numerical coupling, using one-way fluid-structure coupling.
In the parametric analysis of the blade-disc connection, one-way fluid-structure coupling was used. In the first place, the pressure distribution on the blade was determined and then the resulting data were implemented for structural analysis. ANSYS Workbench software was used for calculations. A diagram of the one-way analysis is shown in Figure 7.
The classic design of the high-pressure compressor rotor stage was tested. Considered two characteristic speed ranges of turbine engines: the idle range (65%N2) and the maximum rotor speed (100%N2). The parametric analysis was carried out to evaluate selected geometrical parameters in terms of their impact on the maximum reduced stresses in the connection. Due to the condition of maintaining the dimensions of the engine, parameters that could change the radial dimensions of the rotor stage were not considered. The parameter P1 – width angle (i.e., the angle of inclination of the side surfaces of the blade root) and the parameter P2 – angle defining the thickness of the blade root were selected. They are presented in Figure 8.

4. Results

4.1. Influence of the blade root width angle (P1) on the maximum reduced stresses

The parameter P1 defines the angle of inclination of the side surfaces of the trapezoidal blade root. Table 1 shows the effect of changing the value of this parameter on the maximum reduced stresses in the rotor stage of the axial compressor at fixed values of other parameters. The parameter P1 varied from 92° to 98°. The assumed constant value of P2 was 1.26°, 1.4° and 1.6° respectively.
In the case of reduced stresses (Table 1) at P2 = 1.26° and 65% N2, the lowest values were obtained in the range of variation of the breech width angle from 93° to 95°, while the highest values occurred at the angle of 98°. Depending on the value of aerodynamic loads (150 and 200 kPa) they were 500 ÷ 540 MPa. Increasing the rotational speed to 100% N2 resulted in an increase in the maximum stress values in the stage to the level of 1160 MPa at a pressure of 150 kPa and to about 1180 MPa at a pressure of 200 kPa. In the angle variation range from 94° to 96°, maximum reduced stress values were obtained for a lower flow load (pressure 150 kPa). However, for a higher load of 200 kPa, the maximum values were obtained for the extreme values of the P1 parameter, i.e., 92° and 98°, and the lowest for the values of 95°.
For parameter P2 of 1.4°, the maximum stress values occurred for a width angle of 94° to 95°. They did not exceed 630 MPa at idle speed. In the case of maximum rotor speed, the higher values were occurred for P1 = 92° and over 1400 MPa.
Increasing the value of the P2 parameter to 1.6° had a significant impact on the character of the course and the values of reduced stress for both assumed rotational speeds. Relatively high stress values were achieved, especially at maximum rotational speed. The lowest values of about 1700 MPa were obtained for P1 = 98°, and the largest, over 1900 MPa for P1 = 92°. These are values that significantly exceed the strength of the material used.

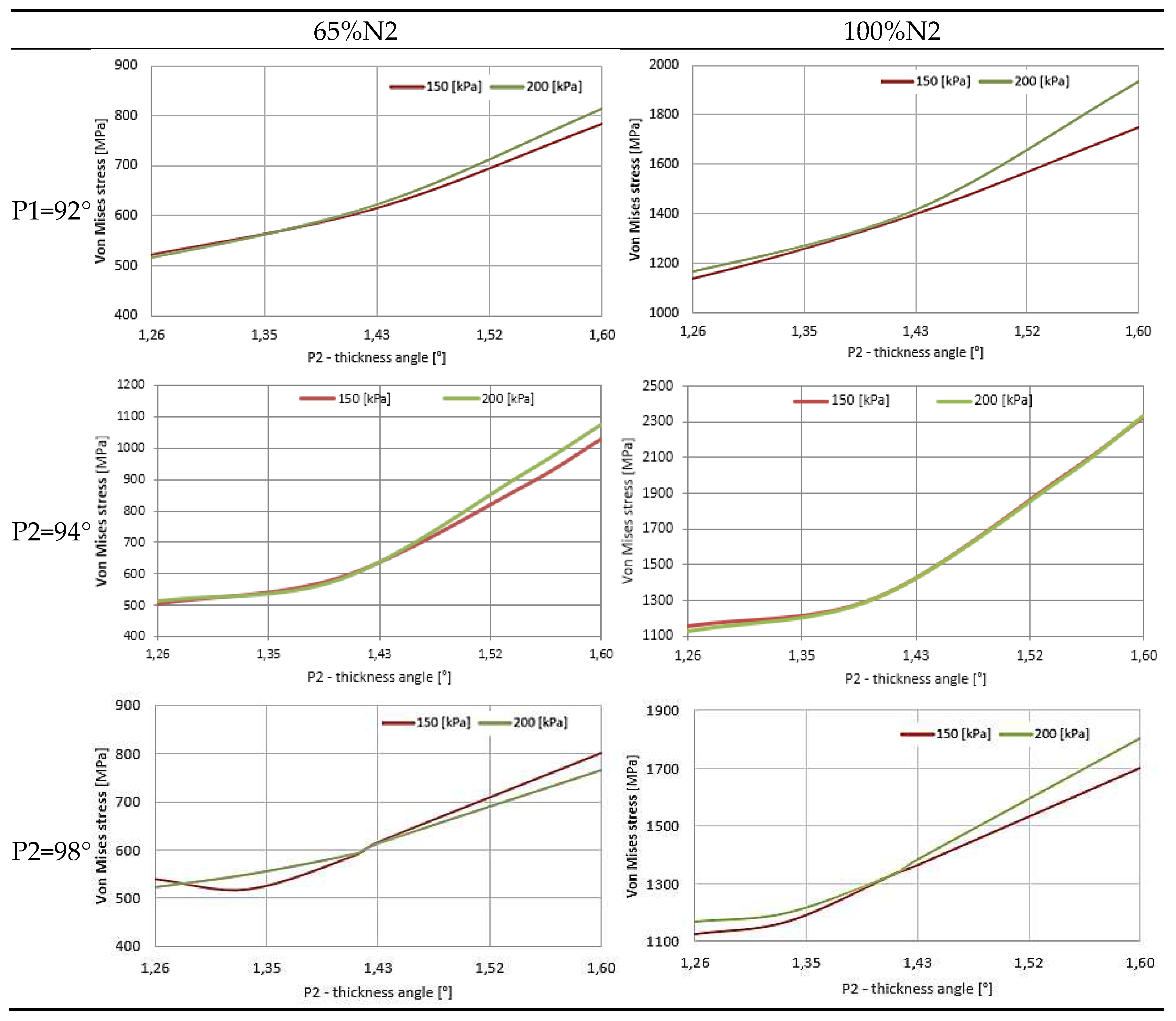
4.2. The influence of the blade root thickness angle (P2) on the maximum reduced stresses

The next stage of the parametric analysis included the assessment of the impact of changes in the P2 parameter (thickness angle) on the stresses reduced in the structure, assuming constant values of the P1 parameter. The results of the analysis are presented in Table 2. They include two rotational speeds (65%N2 and 100%N2), three values of the parameter P1: 92°, 94° and 98° and two flow loads (150 kPa and 200 kPa).
In all considered cases, the values of reduced stresses increased with the increase of P2. In the first of the three cases considered, where P1 = 92°, the reduced stresses increased from about 500 MPa for P2 = 1.26° to over 800 MPa for P2 = 1.6° at 65%N2. In the case of maximum rotor speed and P2 = 1.6°, the stresses value increased to almost 2000 MPa. The greatest growth occurred after the angle of the thickness of 1.4° was exceeded. The pressure value also had an additional effect, with the greatest differences visible in the range of large values of the P2 parameter (above 1.5°).
With the value of P1 = 94°, the smallest stresses occurred for parameter P2 in the range from 1.26° to about 1.4°. After exceeding 1.4°, stress value increased significantly. The course of parameter changes is similar for both rotor speeds. In this case, increasing the angle of the blade root width caused an increase in stresses by about 10% compared to the first case.
The value of the reduced stresses at P1 = 98° and rotational speed of 65%N2, varied from 500 MPa to about 800 MPa. The values of reduced stresses in the angle range (1.26°÷1.33°) remained constant and obtained 1170÷1200 MPa at maximum speed (100%N2). Only after exceeding the value of P2 = 1.33° their values reach 1800 MPa.

4.3. Coefficient of friction

In the analysis of the classic structure, where the rotor blade and the load-bearing element are connected by a root, friction occurring on the surfaces of contacting and cooperating elements plays an important role. In the adopted methodology, they were considered by using in the calculations the appropriate type of contact, i.e., contact with friction, which in ANSYS software is defined as Frictional [24]. The value of the friction coefficient defined in the program depends on the type of material from which the cooperating components are made. Usually, this value is determined experimentally, but a numerical solution can also be sought. To check how much influence, the adopted value of the friction coefficient has on the maximum stresses reduced in the rotor stage of the compressor, several numerical simulations were carried out. The load was assumed to be centrifugal force set by the appropriate rotational speed of the rotor. The obtained results are shown in Figure 9.
The analysis was carried out in the range of the friction coefficient 0÷0.5. The results are presented for four selected rotational speeds, the values of which correspond to the actual operating ranges of the turbine engine compressor rotor. In this case, the speed of 15183 rpm corresponds to 100%N2, i.e., the maximum rotational speed of the high-pressure rotor. Trend lines have a similar course for rotational speeds less than the maximum rotor speed. The value of reduced stress decreases with the increase of the coefficient of friction. It increases slightly after exceeding 0.35÷0.4. It is also seen that the local minimum changes with increasing speed. An increase in the coefficient of friction from 0.1 to 0.3 causes a decrease in maximum stress values by about 5%, depending on the value of rotation speed. It can also be seen that the increase in rotational speeds causes the optimal point of the curve to shift towards higher coefficients of friction. Therefore, taking the friction coefficient values in the range of 0.1÷0.3 for the calculation will not critically affect the maximum values of reduced stresses in the compressor rotor stage.
The above analysis also considered the case without friction, i.e., one in which the coefficient of friction is equal to 0 (in ANSYS, the contact conditions adopted in this way are equivalent to another available type of contact, the so-called Frictionless [24]). However, it should be remembered that this is only a theoretical case. In an existing construction, in the blade-disk connection between adjacent surfaces, there will always be at least minimal friction.

5. Conclusions

A trapezoidal type of connection for circumferential fastening was analyzed, which is the most used type of blade-disc connection in rotor assemblies of high-pressure compressors. The analysis provided information on the influence of selected combinations of geometrical parameters P1, P2 and the coefficient of friction on the course of changes and the values of maximum reduced stresses in the compressor rotor stage. Two types of loads are considered. Mass load due to rotational speed and aerodynamic load as pressure distribution on the blade.
For lower values of P2 and lower values of rotational speeds N2, the choice of the optimum angle P1 should be related to the angle range P 1 ≤ 95 o . Considering the maximum rotor speeds, the angle P1 should be greater than 94 o . It can be concluded that the parameter P1 should have a value of about 95 o . The effect of P2 on reduced stresses is more monotonic than P1. The aerodynamic load analysis provided information not only on the influence on stresses, but also on the change in the position of the load extreme, considering the tested parameters. Analyses of the influence of the coefficient of friction showed the possibility of reducing stress by appropriate selection of this parameter.
It can be stated that the obtained results specified the ranges in which the values of selected geometrical parameters of the blade-disc connection should be located. They provided an important indication in the field of manufacturing technology related to the need to maintain high accuracy of the connection, because a small dimensional deviation significantly affects the values of stresses reduced in the rotor stage.

Author Contributions

Conceptualization, O.G. and A.K.; writing—original draft preparation, O.G. and A.K; writing—review and editing, O.G. and A.K.; supervision, A.K. and O.G.; project administration, A.K. and O.G.; funding acquisition, A.K and O.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Military University of Technology, Warsaw, Poland, under research project No. UGB 822/2023.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable

Data Availability Statement

Not applicable

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pan, H.; Wu, Y.; Zhao, T. Study on Influence of Multi-Parameter Variation of Bladed Disk System on Vibration Characteristics. Appl. Sci. 2021, 11, 3084. [Google Scholar] [CrossRef]
  2. Hui, M.; Di, W.; Xingyu, T.; Bangchun, W. Vibration response analysis of blade-disk dovetail structure under blade tip rubbing condition. Journal of Vibration and Control 2016, 23. [Google Scholar] [CrossRef]
  3. Li, Z.; Zhao, T.; Kou, H.; Zhang, H.; Yuan, H. Vibration Characteristics of MultiStage Blade–Disk–Shaft Integrated Structure with Three-Dimensional Crack. Journal of Vibration Engineering & Technologies 2021, 9, 597–611. [Google Scholar] [CrossRef]
  4. Chunjie, W.; Shunguang, S.; Xiao, Z. ; Vibration analysis of blade-disc coupled structure of compressor. Frontiers of Energy and Power Engineering in China 2008, 2, 302–305. [Google Scholar] [CrossRef]
  5. Canale, G.; Kinawy, M.; Maligno, A.; Sathujoda, P.; Citarella, R. Study of Mixed-Mode Cracking of Dovetail Root of an Aero-Engine Blade Like Structure. Appl. Sci. 2019, 9, 3825. [Google Scholar] [CrossRef]
  6. Xinwei, Z.; Qiang, Z.; Shuhua, Y.; Hongkun, L. Rotating Stall Induced Non-Synchronous Blade Vibration Analysis for an Unshrouded Industrial Centrifugal Compressor, Sensors 2019, 19, 4995. Sensors 2019, 19, 4995. [Google Scholar] [CrossRef]
  7. Kozakiewicz, A.; Kieszek, R. ; Artificial Neural Network Structure Optimisation in the Pareto Approach on the Example of Stress Prediction in the Disk-Drum Structure of an Axial Compressor. Materials 2022, 15, 4451. [Google Scholar] [CrossRef]
  8. Szczeciński, S.; et al. Aircraft turbine engines, construction-operation-diagnostics; Scientific Library of the Institute of Aviation: Warsaw, Poland, 2010; p. 428. [Google Scholar]
  9. Dżygadło, Z.; et al. Turbine engine rotor assemblies; WKL: Warsaw, Poland, 1982. [Google Scholar]
  10. Lipka, J. Strength of rotating machines; WNT: Warsaw, Poland, 1967. [Google Scholar]
  11. Kozakiewicz, A.; Grzejszczak, O. An influence of selected geometric parameters on strength properties of compressor’s jet engine blade joint. Mechanic 2016, 7, 740–741. [Google Scholar] [CrossRef]
  12. Kozakiewicz, A.; Grzejszczak, O.; Łącki. T. The comparative analysis of the selected construction types of axial compressor stage, including the modal analysis. Journal of Machine Engineering 2017, 17, 91–97. [Google Scholar] [CrossRef]
  13. Kozakiewicz, A.; Grzejszczak, O. An influence of geometrical parameters of the lock of the blade-disc joint on stress in FEA and DIC methods. Advances in Science and Technology Research Journal 2021, 15, 209–217. [Google Scholar]
  14. Deshpande, A.S.; Keane, J.A.; Sobester, A.; Toal, J.J.D. Geometric parameterisation of firtree joints in gas turbine discs considering manufacturing variability. In Proceedings of the 3rd Aircraft Structural Design Conference, Delft, The Netherlands, 2012. [Google Scholar]
  15. Meguid, S.A.; Refaat, M.H.; Papanikos, P. Theoretical and experimental studies of structural integrity of dovetail joints in aeroengine discs. Journal of Materials Processing Technology 1996, 56, 668–677. [Google Scholar] [CrossRef]
  16. Amaresh, H.G.; et al. Design and Analysis on Dovetail Joint of an Aero Engine Compressor Disc and Blade with Different Skew Angle. International Journal for Ignited Minds. 2015, 2, 238–244. [Google Scholar]
  17. Beisheim, J.R.; Sinclair, G.B. On the three-dimensional finite element analysis of dovetail attachments. Journal of Turbomachinery 2003, 125, 372–379. [Google Scholar] [CrossRef]
  18. Nowotarski, I. Analysis of loads in trapezoidal roots of rotating machines. WAT Bulletin 1997, 6, 39–49. [Google Scholar]
  19. Tao, S.; Yi, W.; Rong, X. Application of FSI on Turbomachinery. IEEE 2011. [Google Scholar] [CrossRef]
  20. Krzesiński, G.; et al. Finite element method in structural mechanics. Solving selected issues using ANSYS; Warsaw University of Technology Publishing House: Warsaw, Poland, 2015. [Google Scholar]
  21. Bijak-Żochowski, M.; et al. Mechanics of materials and structures, volume 2; Warsaw University of Technology Publishing House: Warsaw, 2013. [Google Scholar]
  22. ANSYS Fluent 12.0 User’s Guide, 2009.
  23. ANSYS Fluent Fluid Structure Interaction with Ansys Mechanical. Training materials. ANSYS, 2020.
  24. ANSYS System Documentation, v. 21.
Preprints 80176 g001
Figure 1. Scheme of a perimeter-fixed trapezoidal root.
Figure 1. Scheme of a perimeter-fixed trapezoidal root.
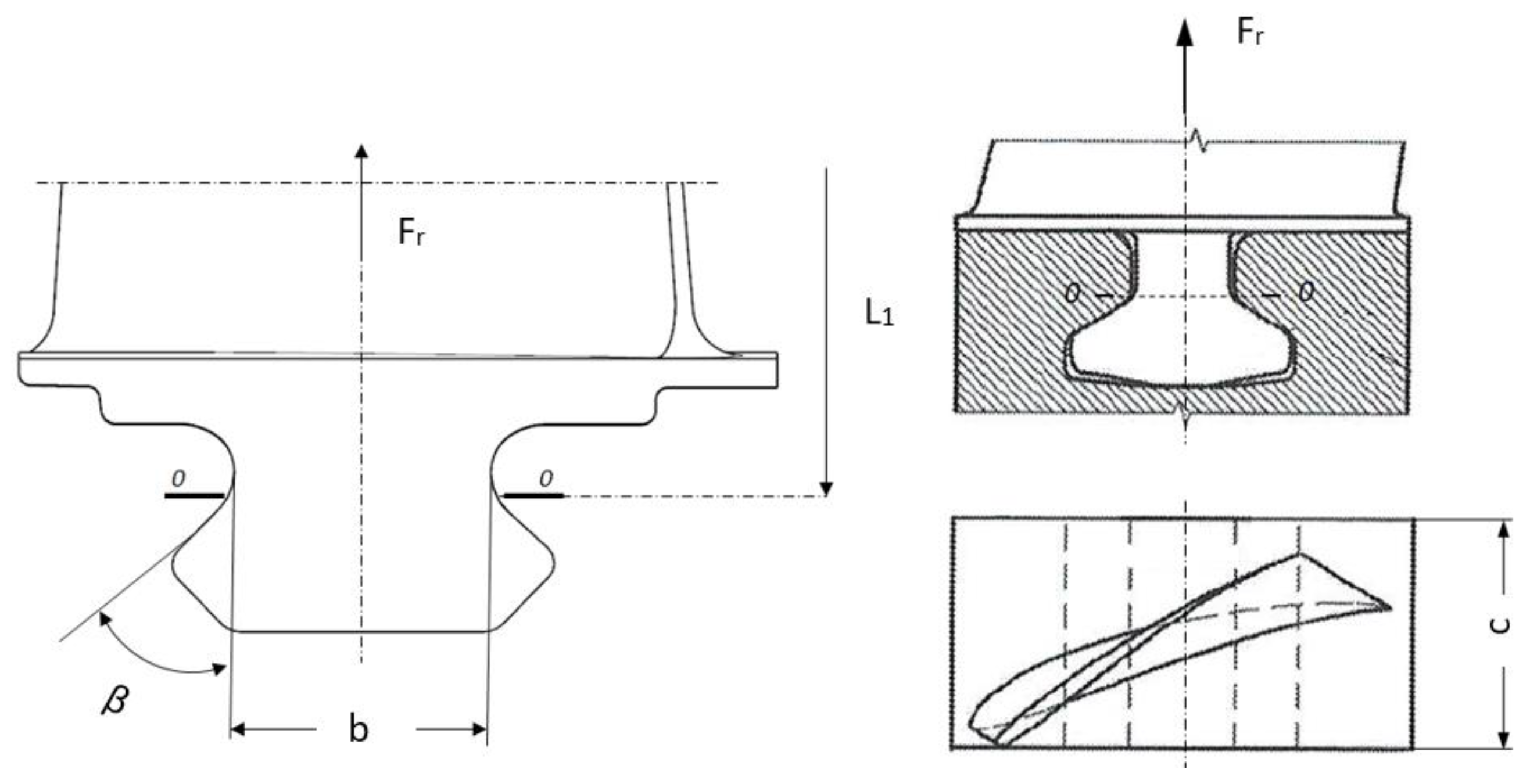
Preprints 80176 g001
Preprints 80176 g002
Figure 2. Parametric analysis algorithm with FSI.
Figure 2. Parametric analysis algorithm with FSI.
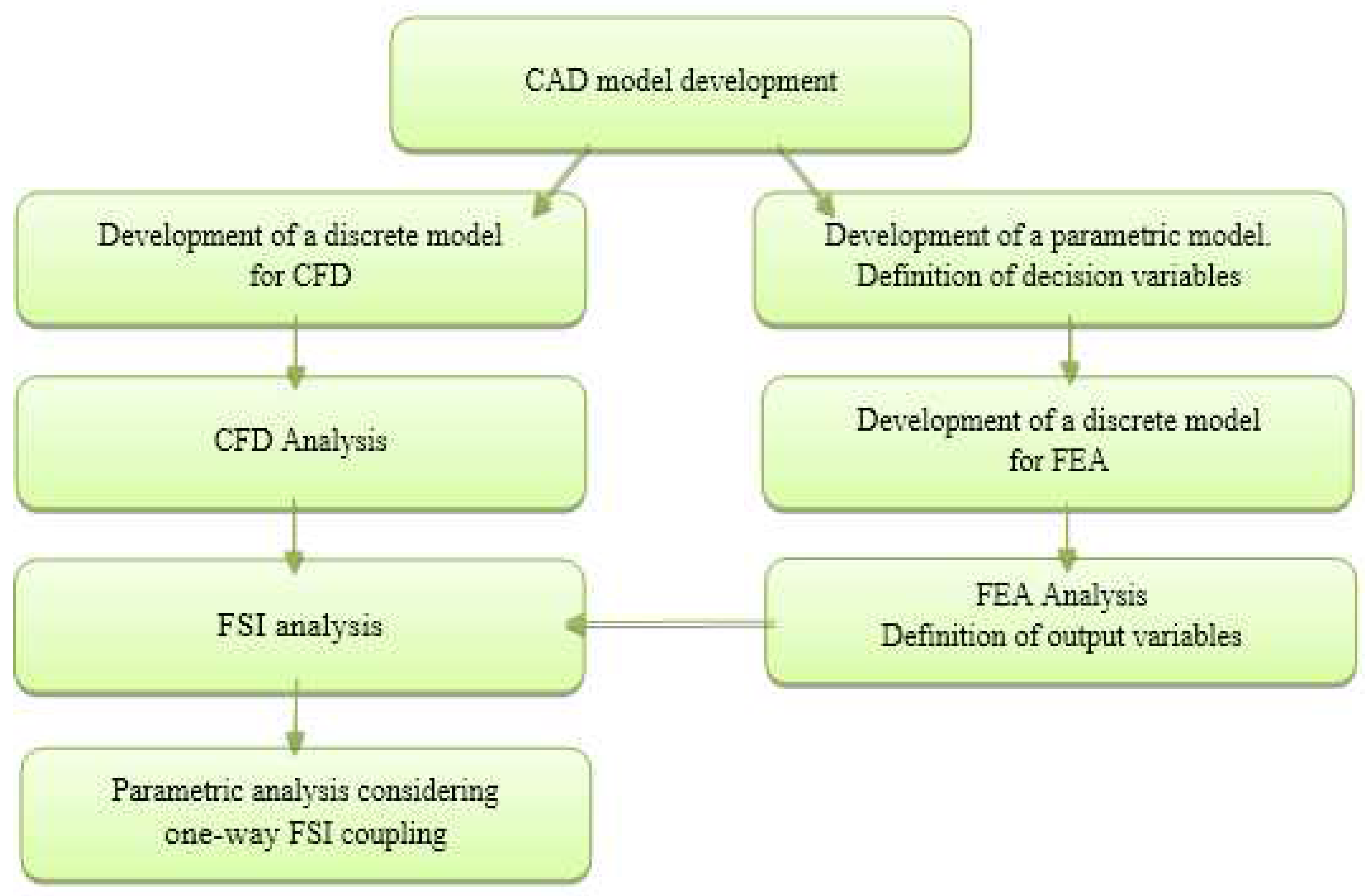
Preprints 80176 g002
Preprints 80176 g003
Figure 3. Geometric model of the rotor blade.
Figure 3. Geometric model of the rotor blade.
Preprints 80176 g003
Preprints 80176 g004
Figure 4. Geometric model of the rotor stage with the repeating slice (a) marked (in green), model of the calculation domain of a single rotor blade (b).
Figure 4. Geometric model of the rotor stage with the repeating slice (a) marked (in green), model of the calculation domain of a single rotor blade (b).
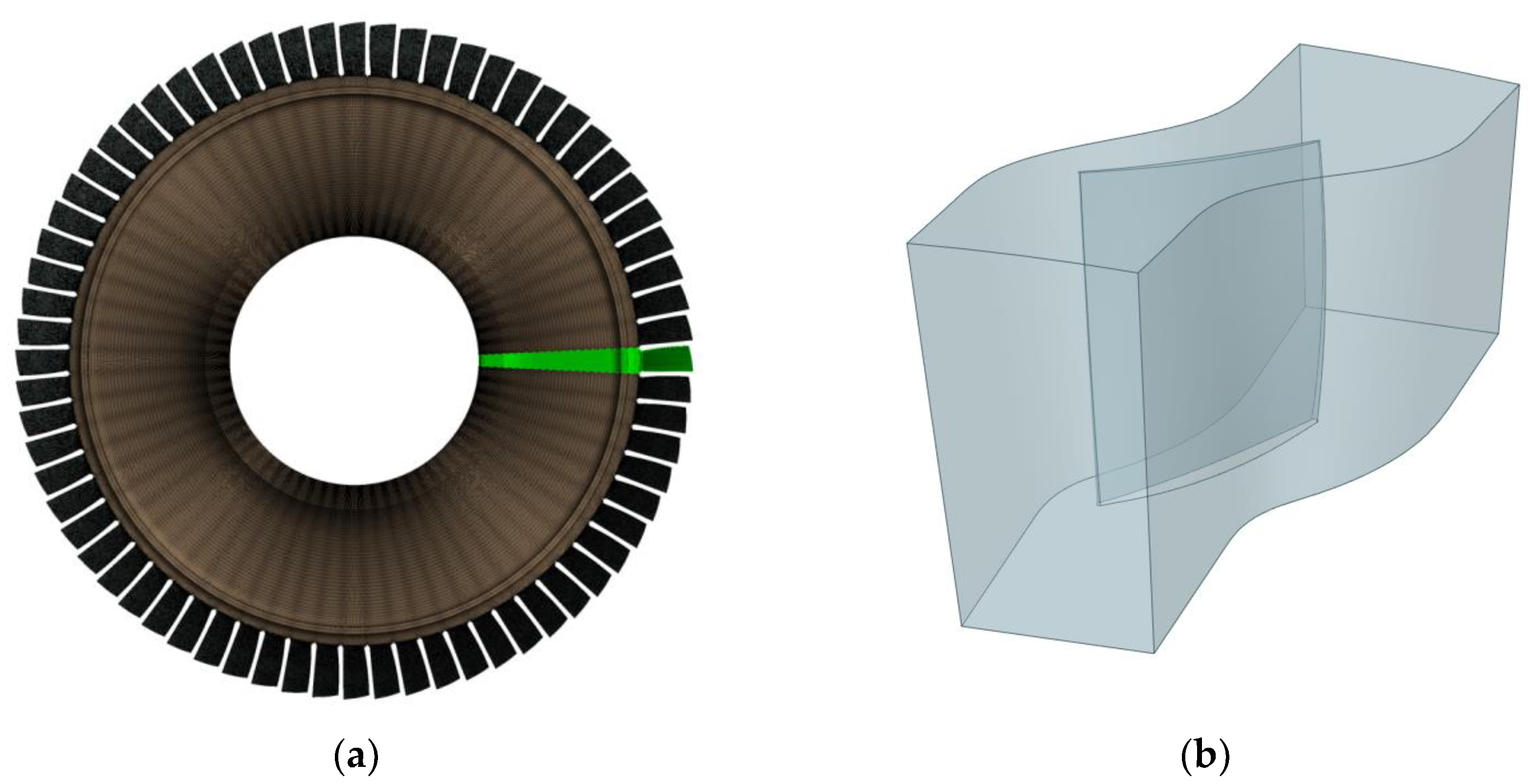
Preprints 80176 g004
Preprints 80176 g005
Figure 5. Discrete model of compressor rotor stage: the repeating slice of the rotor stage model (a), FEM model of blade (b), FEM model of disc (c).
Figure 5. Discrete model of compressor rotor stage: the repeating slice of the rotor stage model (a), FEM model of blade (b), FEM model of disc (c).
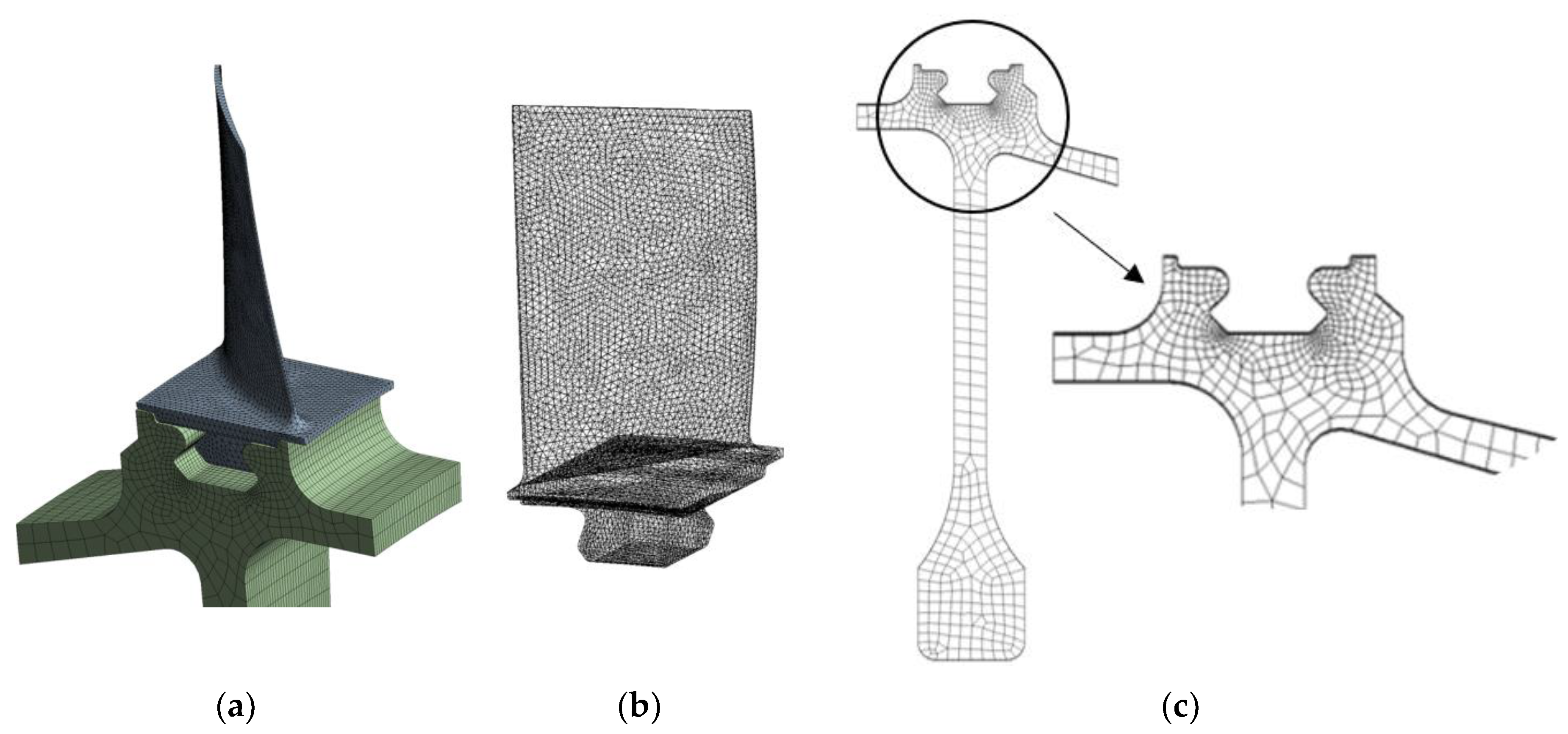
Preprints 80176 g005
Preprints 80176 g006
Figure 6. Discrete model for CFD analysis: (a) non-structural mesh, (b) non-structural mesh in cross-section.
Figure 6. Discrete model for CFD analysis: (a) non-structural mesh, (b) non-structural mesh in cross-section.
Preprints 80176 g006
Preprints 80176 g007
Figure 7. One-way FSI analysis scheme in ANSYS Workbench.
Figure 7. One-way FSI analysis scheme in ANSYS Workbench.
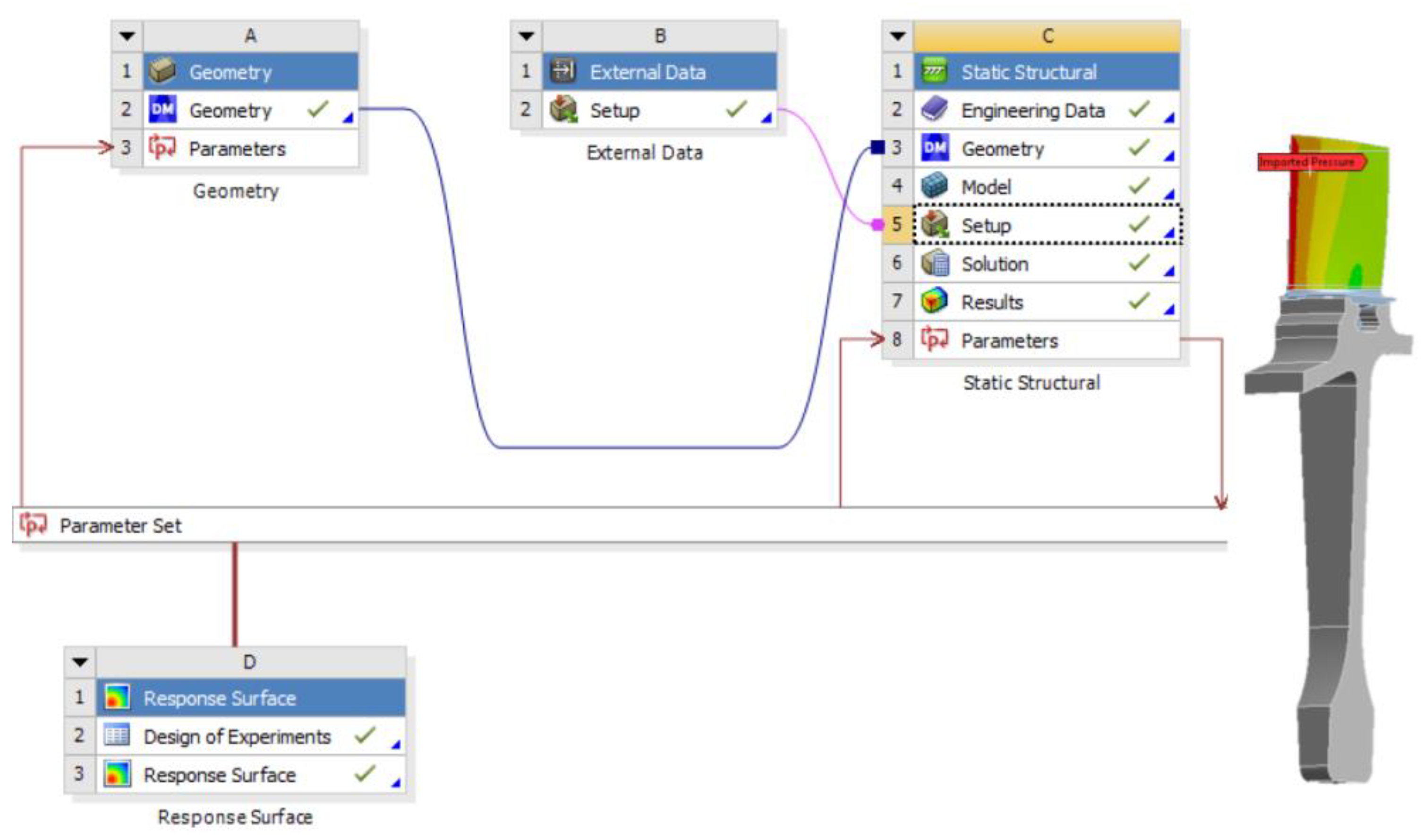
Preprints 80176 g007
Preprints 80176 g008
Figure 8. Geometrical parameters of the blade root.
Figure 8. Geometrical parameters of the blade root.
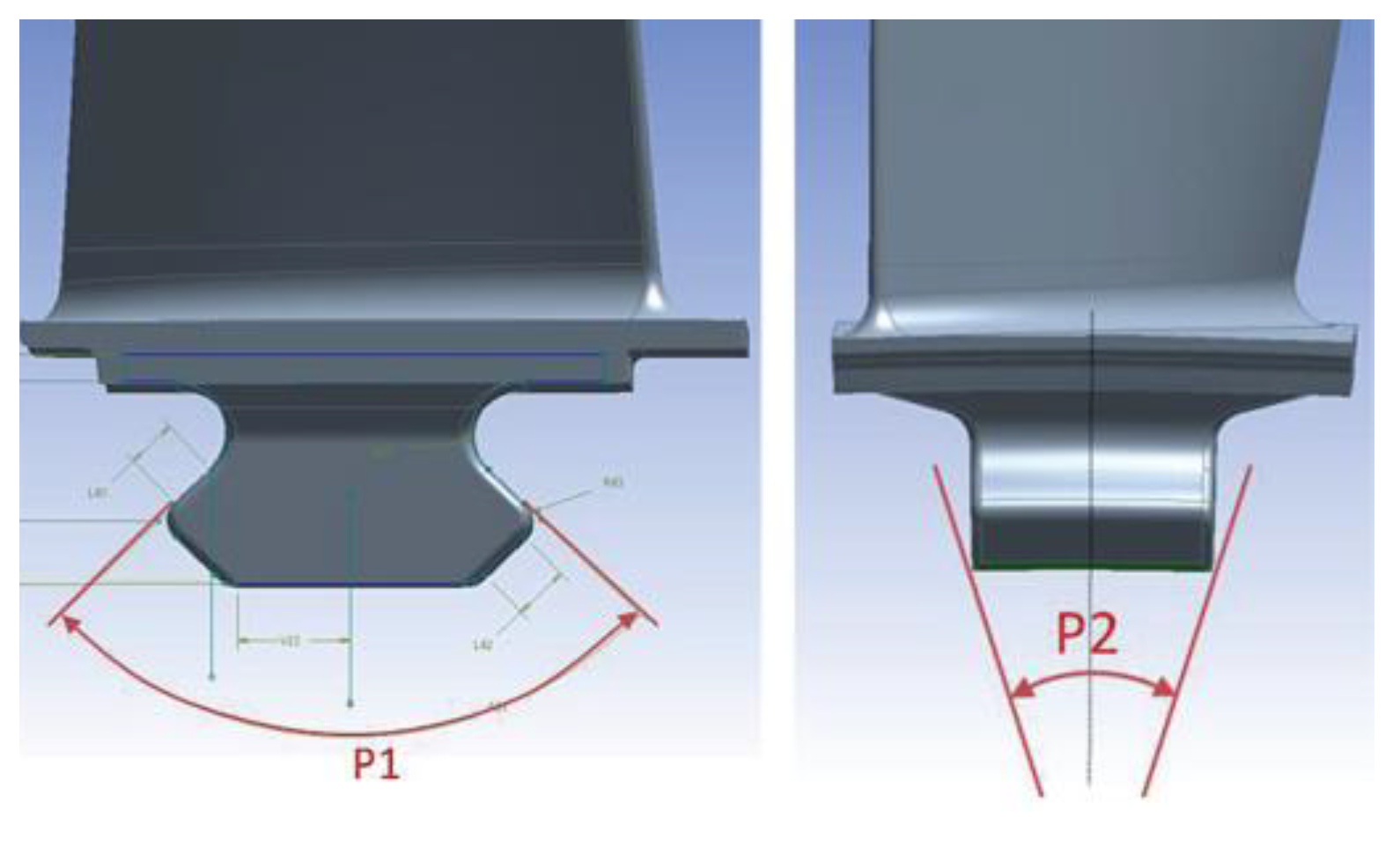
Preprints 80176 g008
Preprints 80176 g009
Figure 9. Influence of the coefficient of friction on the maximum reduced stresses at different speed ranges n [rpm].
Figure 9. Influence of the coefficient of friction on the maximum reduced stresses at different speed ranges n [rpm].
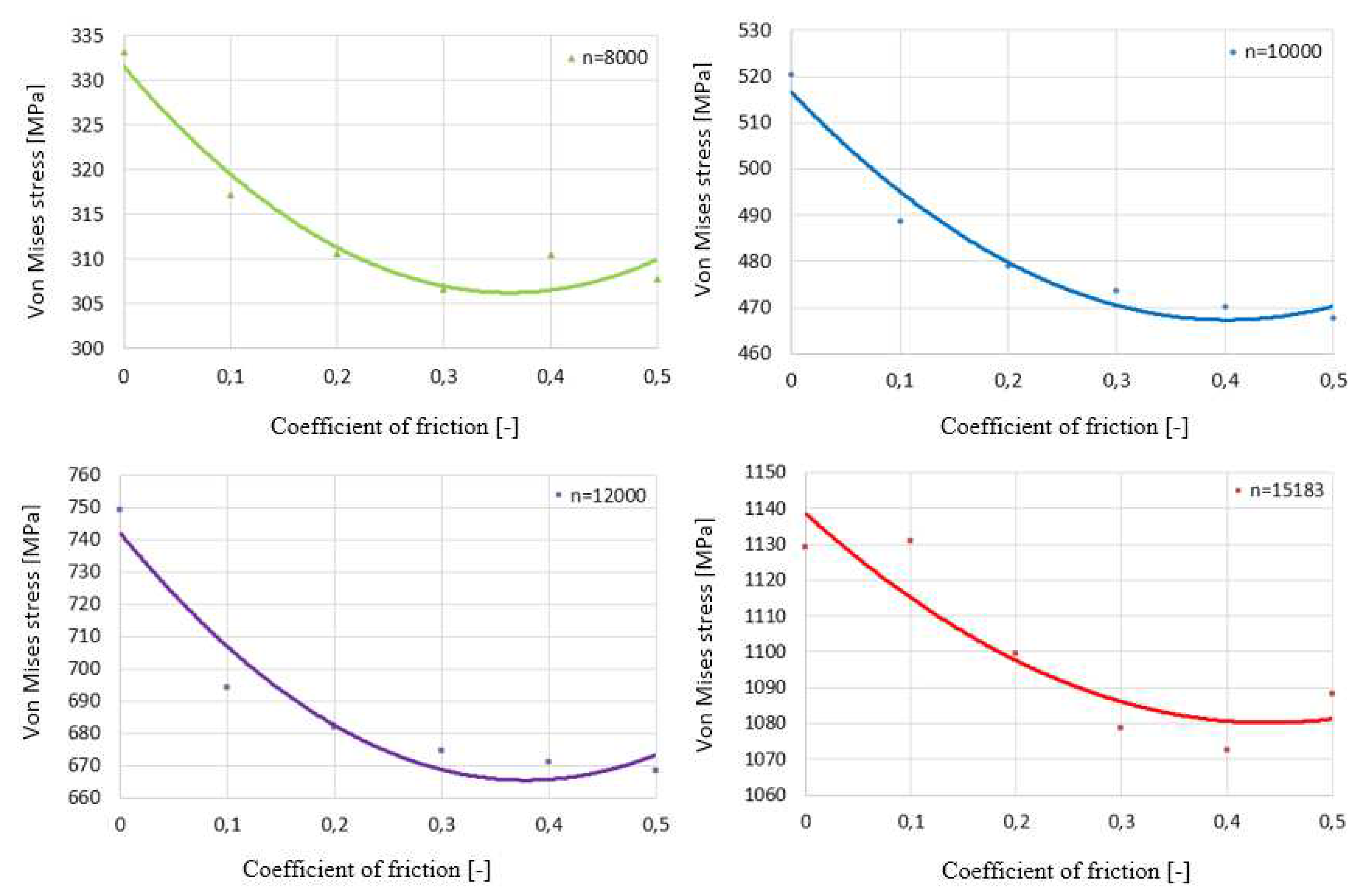
Preprints 80176 g009
Table 1. Effect of P1 change on reduced stresses.
Table 1. Effect of P1 change on reduced stresses.
Preprints 80176 i001
Table 2. Effect of P2 change on reduced stresses.
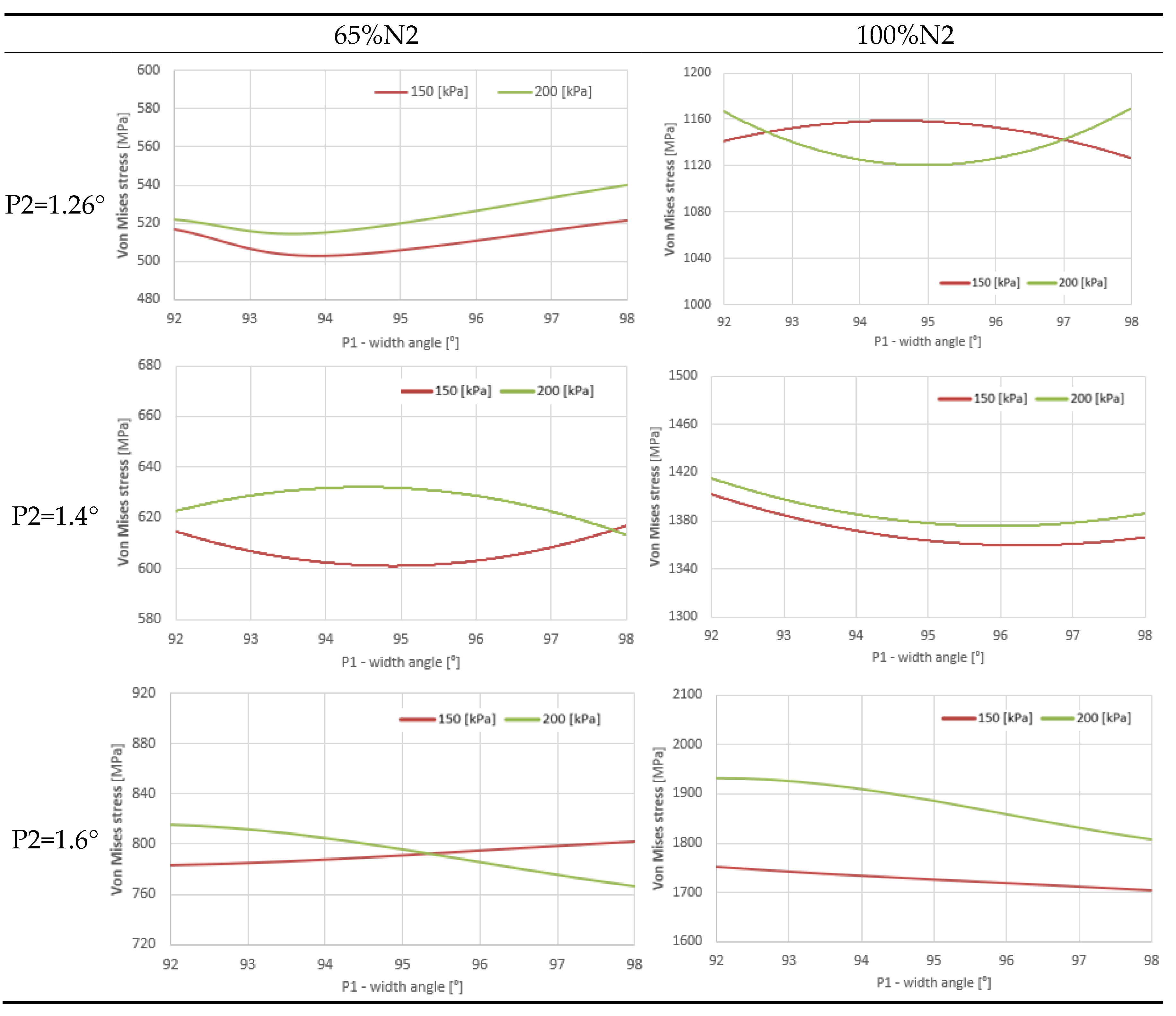Table 2. Effect of P2 change on reduced stresses.
Preprints 80176 i002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated