1. Introduction
Different types of phenomenon occurring chemically, biologically, economically and others are represented as a non-linear partial differential equations (NLPDEs). Many different methods are developed to gain the analytical wave solutions of these NLPDEs i.e optical soliton solutions of coupled nonlinear Schrödinger equation have been gained with the use of Kudryashov R function technique [
1], some new kind of optical soliton solutions of time-fractional perturbed nonlinear Schrödinger equation have been achieved by using the generalized Kudryashov scheme [
2], by applying the modified auxiliary equation technique, optical wave solutions of time-fractional resonant non-linear Schrödinger equation have been obtained [
3], new optical wave solutions for the time-fractional perturbed non-linear Schrödinger equation have been achieved by utilizing the improved
-expansion scheme [
4].
We utilize the Sardar sub-equation method for our research work. This method have so many applications in the literature. For example; some solitons solutions of perturbed Fokas-lenells model have been obtained with the use of Sardar sub-equation method [
5], new kind of soliton wave solutions of (2+1)-dimensional Sawada-Kotera model have been gained by this method [
6], the dark, bright and singular optical wave solutions of higher order non-linear Schrödinger have been gained by using Sardar sub-equation scheme [
7], The singular, bright, dark, periodic singular, combined dark-bright solitons and other wave solutions of strain wave equation have been achieved with the use of this model [
8].
Our study model is complex three coupled Maccari’s system along with truncated M-fractional derivative. Different types of exact wave solutions of this model have been obtained with the help of different methods in the literature. Instantly, the dark, bright and complex optical wave solutions have been achieved by using extended rational sine-cosine and rational sinh-cosh techniques [
9], trigonometric, rational and hyperbolic solutions have been attained with the use of unified solver technique [
10], the optical soliton solutions have been gained by utilizing the planar dynamic system scheme [
11], some new travelling wave solutions have been obtained by applying the modified trial equation technique [
12], the periodic, double periodic, dark, bright, combined soliton solutions etc have been obtained with the help of generalized auxiliary equation mapping technique [
13].
Main aim of this research is to discover the new exact wave solutions to the truncated M-fractional complex three coupled Maccari’s system with the help of Sardar sub-equation method.
Paper consists of different sections; In
Section 2: we describe the main steps of our concerned method Sardar sub-equation.. In
Section 3: we explain the our concerned model and it’s mathematical analysis. In
Section 4: we apply the method to gain the new exact wave solutions of our concerned model. In
Section 5: we explain the some obtained solutions through 2-D, 3-D and contour graphs. In
Section 6: we give the conclusion of our research work.
2. Description of Sardar Sub-Equation METHOD
Here, we explain the fundamental points of Sardar sub-equation method [
14]. Let’s consider the non-linear fractional partial differential equation:
here
represents a wave function.
Applying the wave transformations given as follow:
We obtain a non-linear ODE shown as:
Consider Equation (
3) posses the results in the given shape:
here
fulfill the ODE shown as:
here
and
are constants.
Using Equation (
4) into Equation (
3) with Equation (
5) and collecting the coefficients of each power of
. Putting co-efficient of each power equal to 0, we gain a sets of algebraic equations in the term
,
,
. By solving the obtained system of equation, we get the values of parameters..
Case 1: If
and
, then
where,
,
Case 2: If
and
, then
where,
,
Case 3: If
and
, then
where,
,
Case 4: If
and
, then
where,
,
3. The governing model and it’s mathematical treatment
Assume the M-fractional three coupled non-linear Maccari’s system shown in [
15]:
where
here
represents truncated Mittag-Leffler function of one parameter given in [
16,
17].
Let’s consider the following transformations:
here
,
,
,
and
are the unknowns and
is arbitrary constant.
Substituting Equation (
22) into Equation (
20), yields the real and imaginary parts:
By Equation (
24), implies
.
Integrating the fourth equation of system (
23), yields
Putting Equation (
25) into first three terms of Equation (
33), we get
Taking
U and Taking
U, we obtain
4. Solutions through Sardar Sub-Equation Method
Equation (
4) changes into given form for m=1.
Putting Equation (
28) into Equation (
27) with Equation (
5). By collecting co-efficients of every order of
and taking them equal to 0, we get a set of algebraic equations. By solving the obtained set of equations by Mathematica software, we gain the following sets.
Case 4:
where
5. Graphical Representation of Solutions
In this section we present the graphically behavior of solutions in the 3D, contour and 2D surfaces.
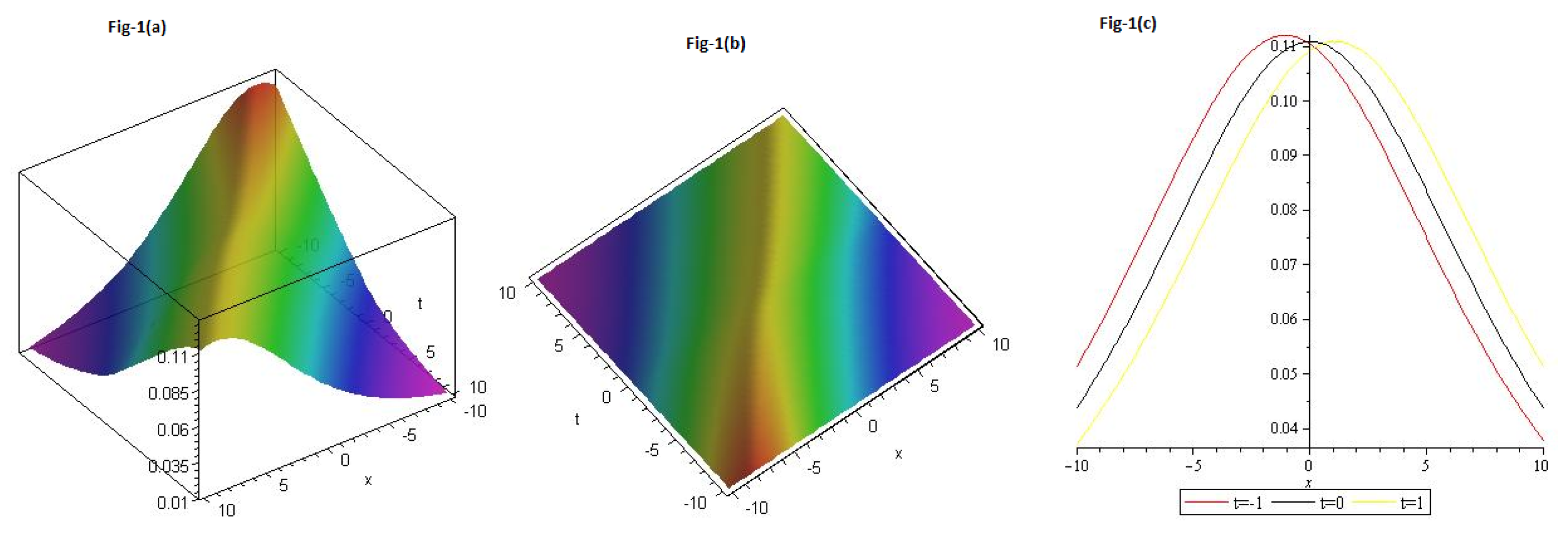
We gave graphs for solution (
30) in
Figure 1a,b in Contour and
Figure 1c 2D with different values of t=-1 is represent the red line, t=0 is represent the black line and t=1 is represent the yellow with
and
.
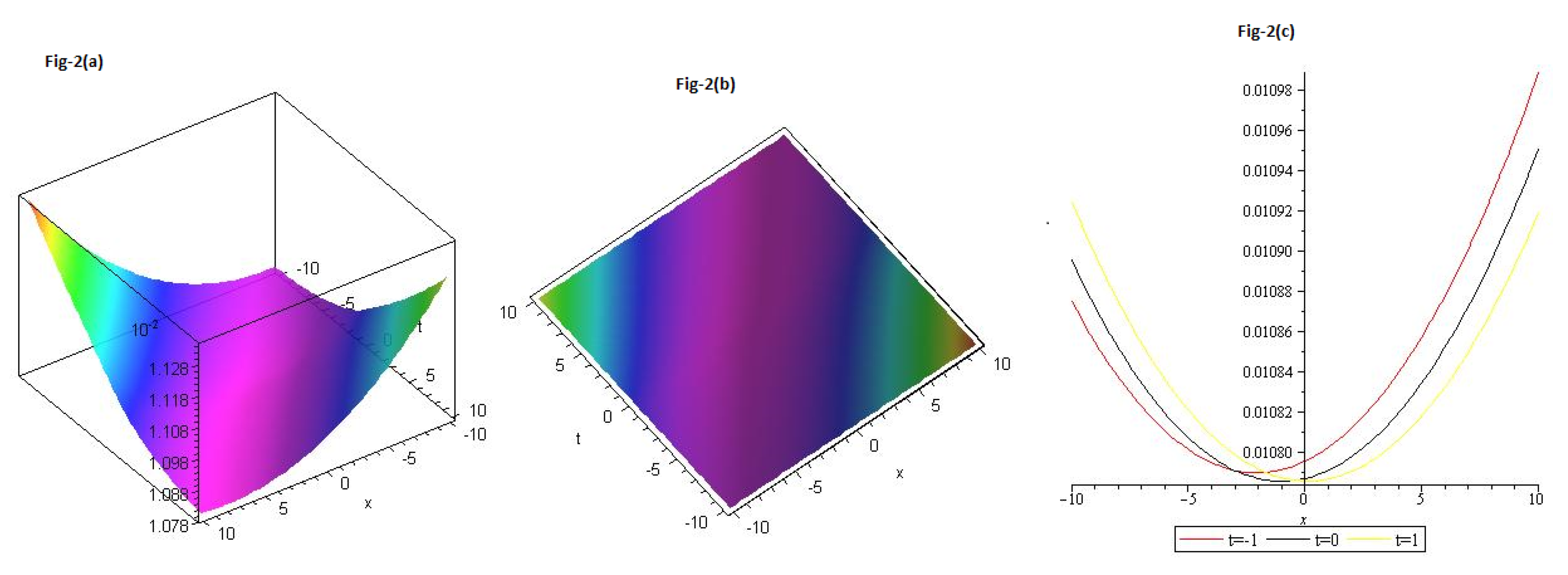
We gave graphs for solution (
38) in
Figure 2a,b in Contour and
Figure 2c 2D with different values of t=-1 is represent the red line, t=0 is represent the black line and t=1 is represent the yellow with
and
.
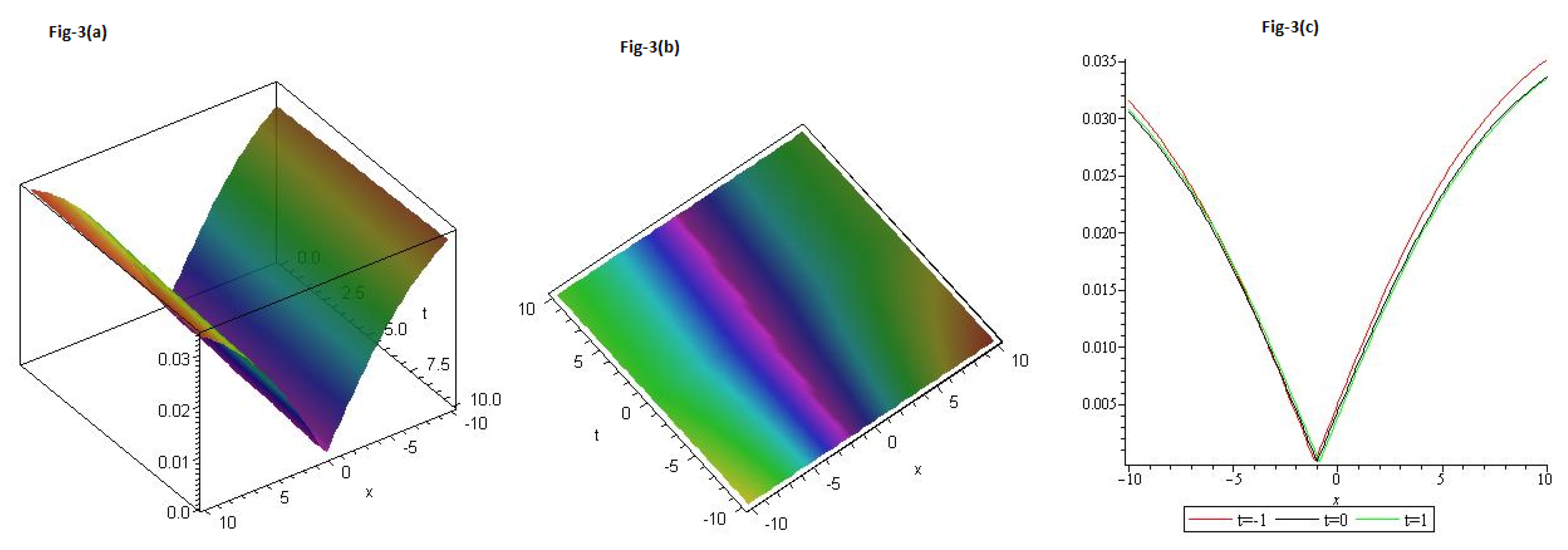
We gave graphs for solution (
46) in
Figure 3a,b in Contour and
Figure 3c 2D with different values of t=-1 is represent the red line, t=0 is represent the black line and t=1 is represent the green with
and
.
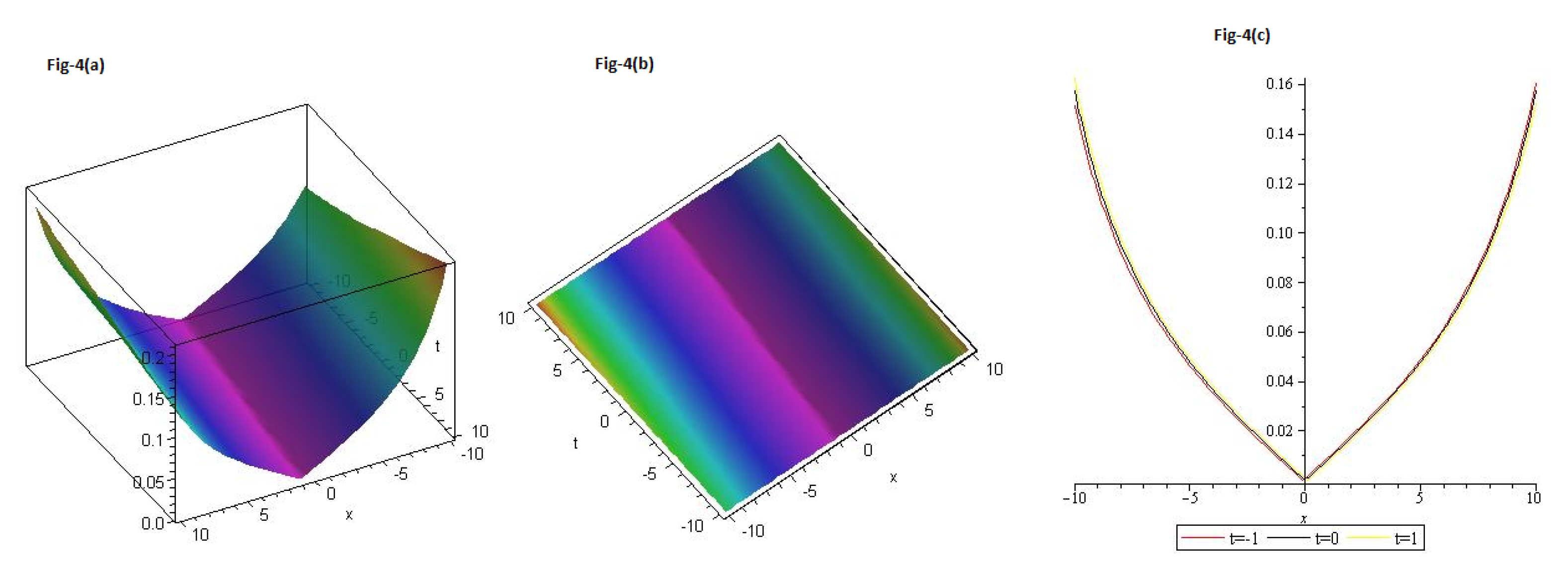
We gave graphs for solution (
66) in
Figure 4a,b in Contour and
Figure 4c 2D with different values of t=-1 is represent the red line, t=0 is represent the black line and t=1 is represent the green with
and
.
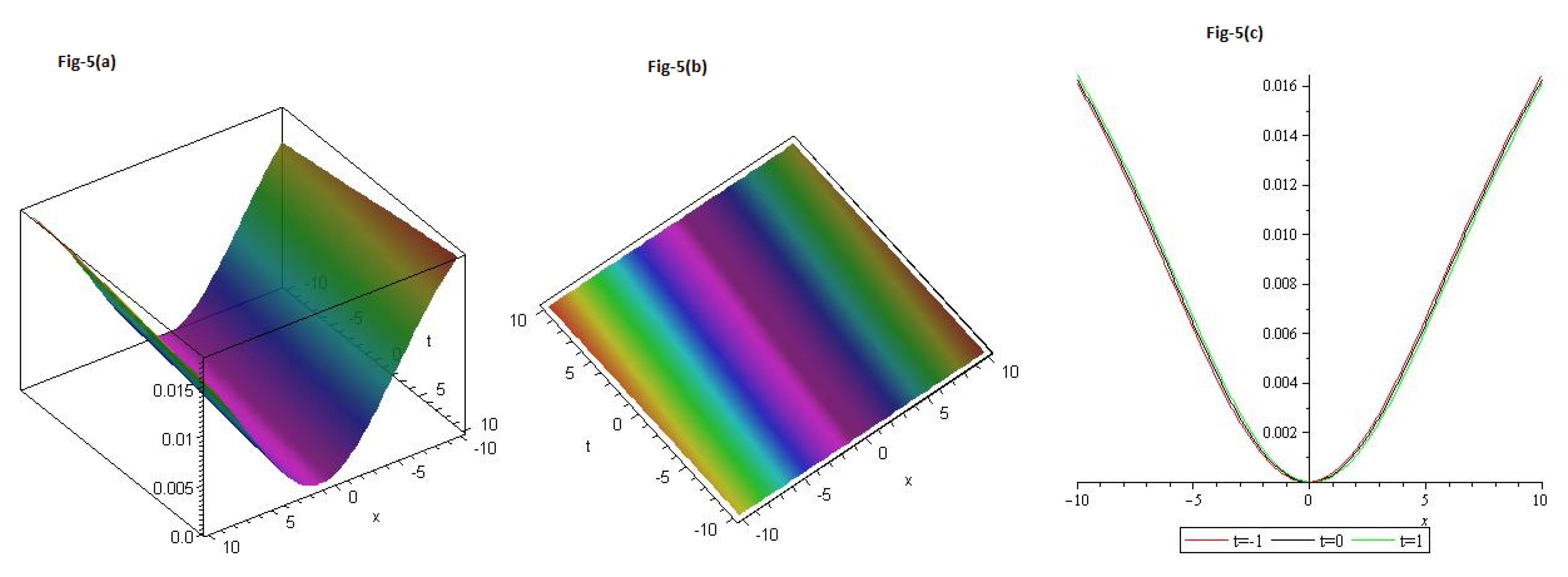
We gave graphs for solution (
106) in
Figure 5a,b in Contour and
Figure 5c 2D with different values of t=-1 is represent the red line, t=0 is represent the black line and t=1 is represent the green with
and
.
6. Conclusions
Overall, this paper contributes to our understanding of the truncated M-fractional complex three coupled Maccari’s system and provides a useful technique for handling nonlinear partial differential equations. This paper describes the successful application of the Sardar sub-equation method to obtain new optical wave solutions for the truncated M-fractional complex three coupled Maccari’s system. The obtained solutions are useful for future studies of the concerned model and provide insights into the behavior of optical waves in complex media. The Sardar sub-equation method is shown to be a simple, fruitful, and reliable technique for handling nonlinear partial differential equations. The solutions were verified using Mathematica software and were also described graphically using 2-dimensional, 3-dimensional, and contour plots through Maple software.
Acknowledgments
The authors acknowledge the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia, under project Grant No. 2213.
References
- Das, Nilkanta and Saha Ray, S; Dispersive optical soliton solutions of the (2+ 1)-dimensional cascaded system governing by coupled nonlinear Schrödinger equation with Kerr law nonlinearity in plasma, Optical and Quantum Electronics, 55, 4, 328, (2023). [CrossRef]
- Das, Nilkanta and Saha Ray, S; Dispersive optical soliton wave solutions for the time-fractional perturbed nonlinear Schrödinger equation with truncated M-fractional conformable derivative in the nonlinear optical fibers, Optical and Quantum Electronics, 54, 9, 544, (2022). [CrossRef]
- Das, N and Saha Ray, S; Novel optical soliton solutions for time-fractional resonant nonlinear Schrödinger equation in optical fiber, Optical and Quantum Electronics, 54, 2, 112, (2022). [CrossRef]
- Saha Ray, S and Das, N; New optical soliton solutions of fractional perturbed nonlinear Schrödinger equation in nanofibers, Modern Physics Letters B, 36, 02, 2150544, (2022). [CrossRef]
- Cinar, Melih and Secer, Aydin and Ozisik, Muslum and Bayram, Mustafa; Derivation of optical solitons of dimensionless Fokas-Lenells equation with perturbation term using Sardar sub-equation method, Optical and Quantum Electronics, 54, 7, 402, (2022). [CrossRef]
- Debin, Kong and Rezazadeh, Hadi and Ullah, Najib and Vahidi, Javad and Tariq, Kalim U and Akinyemi, Lanre; New soliton wave solutions of a (2+ 1)-dimensional Sawada-Kotera equation, Journal of Ocean Engineering and Science, (2022). [CrossRef]
- Faisal, Khalida and Abbagari, Souleymanou and Pashrashid, Arash and Houwe, Alphonse and Yao, Shao-Wen and Ahmad, Hijaz; Pure-cubic optical solitons to the Schrödinger equation with three forms of nonlinearities by Sardar subequation method, Results in Physics, 48, 106412, (2023). [CrossRef]
- Ur Rehman, Hamood and Awan, Aziz Ullah and Habib, Azka and Gamaoun, Fehmi and El Din, ElSayed M Tag and Galal, Ahmed M; Solitary wave solutions for a strain wave equation in a microstructured solid, Results in Physics, 39, 105755, (2022)
. [CrossRef]
- Vahidi, Javad and Zekavatmand, Sayyed Masood and Rezazadeh, Hadi and Inc, Mustafa and Akinlar, Mehmet Ali and Chu, Yu-Ming; New solitary wave solutions to the coupled Maccari’s system, Results in Physics, 21, 103801, (2021). [CrossRef]
- Alkhidhr, Hanan A and Abdelrahman, Mahmoud AE; Wave structures to the three coupled nonlinear Maccari’s systems in plasma physics, Results in Physics, 33, 105092, (2022). [CrossRef]
- Li, Zhao and Xie, Xinyu and Jin, Changjiang; Phase portraits and optical soliton solutions of coupled nonlinear Maccari systems describing the motion of solitary waves in fluid flow, Results in Physics, 41, 105932, (2022). [CrossRef]
- Bulut, Hasan and Yel, Gülnur and Baskonus, Haci Mehmet; Novel structure to the coupled nonlinear Maccari’s system by using modified trial equation method, Advanced Mathematical Models & Applications, 2, 1, 14–19, (2017).
- Akbar, Yasir and Afsar, Haleem and Abbas, Shahzad and Javed, Muhammad Waqas and Ullah, Najib; Dromions for the coupled Maccari’s system in fluid mechanics, Chaos, Solitons & Fractals, 150, 111114, (2021). [CrossRef]
- Ullah, Naeem and Asjad, Muhammad Imran and Awrejcewicz, Jan and Muhammad, Taseer and Baleanu, Dumitru; On soliton solutions of fractional-order nonlinear model appears in physical sciences, AIMS Mathematics, 7, 5, 7421–7440, (2022)
.
- Emad H., M. Zahran, Maha S. M. Shehata, S. M. Mirhosseini-Alizamini, Md Nur Alam, Lanre Akinyemi; Exact propagation of the isolated waves model described by the three coupled nonlinear Maccari’s system with complex structure; International Journal of Modern Physics B, 2150193, (15 pages), (2021). [CrossRef]
- Tukur Abdulkadir Sulaiman, Gulnur Yel and Hasan Bulut; M-fractional solitons and periodic wave solutions to the Hirota- Maccari system, Modern Physics Letters B, 1950052, (2019). [CrossRef]
- J. Vanterler D A C. Sousa, and E. Capelas D E Oliveira; A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties, International Journal of Analysis and Applications, 16, 1, 83-96, (2018). [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).