Prerpints.org logo
Preprint
Article

Electrochemical Degradation of Diuron by anodic oxidation on DSA in sulfate medium

Altmetrics

Downloads

120

Views

58

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

24 July 2023

Posted:

25 July 2023

You are already at the latest version

Alerts
Abstract
This work presents the electrochemical degradation of the herbicide Diuron by anodic oxidation on a Ti/Ru0.3Ti0.7O2 dimensionally stable anode (DSA) using sulfate as electrolyte. The study includes the influence of the Diuron concentration and the current density on the anodic oxidation. The results evidence a first-order degradation, with the highest degradation capacity achieved at 40 mA cm2 and an initial Diuron concentration of 38 mg L1. Nevertheless, in terms of efficiency and energy demand, the operation at 10 mA cm2 is favored due to the more efficient and less energy-consuming condition. To discern the optimum design and operation conditions, this work presents the results of a preliminary technical-economical analysis, demonstrating that, to minimize the total costs of the system, it is recommended to seek the most efficient conditions, i.e., the conditions demanding the lowest applied charges with the highest Diuron degradation. At the same time, attention must be given to the required cell voltage to not increase excessively the operating costs.
Keywords: 
Subject: Environmental and Earth Sciences  -   Sustainable Science and Technology

1. Introduction

Water contamination by manufactured organic chemicals such as herbicides, pesticides, dyes, and antibiotics demands attention for appropriate removal. Classical wastewater treatment plants (WWTP) are based on physical and biochemical processes, which cannot remove persistent pollutants [1]. In this sense, advanced oxidation processes (AOP) emerge as a suitable alternative based on the generation of the powerful hydroxyl radical (OH•) oxidant [2,3]. Among the different AOP, electro-oxidation presents some advantages, such as adding few or no chemicals to the medium, versatility, easy automation, high energy efficiency, and capacity to mineralize the pollutants completely [4].
Herbicides are a group of refractory chemicals that deserve attention due to their extensive worldwide application from intensive agriculture. Diuron ((3-(3,4-dichlorophenyl)-1,1-dimethyl urea)) is a systemic herbicide used to control the growth of one herbicide used to manage the growth of large and narrow-leaf weed plants. It belongs to the arylurea class, acting by inhibition of photosynthesis [5]. Diuron, present in drinking waters, is known to be potentially carcinogenic [6], mandatorily demanding adequate treatment. As Diuron is not readily biodegradable [7], physicochemical removal methods emerge as suitable for the Diuron treatment, particularly the anodic oxidation.
Anodic oxidation is based on applying an electrical current or potential difference to an electrolytic solution (it could be the residue to treat if it possesses enough conductivity) between an anode, where the pollutant degradation occurs, and a cathode, where hydrogen evolution evolves [8]. Two types of anodes are used, the non-active ones, in which the water discharge reaction produces hydroxyl radicals weakly adsorbed onto the anode surface, allowing an intense interaction between the pollutant and the powerful oxidant OH•, allowing a deep pollutant oxidation or even mineralization (boron-doped diamond (BDD) and PbO2); and the active anodes, represented by the mixed metal oxides (MMO), such as RuO2/TiO2, IrO2/TiO2, SnO2/TiO2, Sb2O5, among the most representative semiconductors, platinum and graphite. These materials strongly adsorb the OH• species and favor the oxygen evolution reaction [9]. In terms of oxidative power, BDD is recognized as the best material, given its capacity to produce large amounts of OH•, as well as high chemical resistance, long-time stability, low capacitive current, and a wide electrochemical window [10]. Nevertheless, BDD anodes possess two primary counterparts: (i) a significant initial investment [11]; (ii) the formation of perchlorate in the presence of chloride [12,13]. These BDD shortcomings have stimulated the development and application of MMO (also known as dimensionally stable anodes, DSA) to the degradation of refractory pollutants as an alternative anode [14,15,16,17]. In this sense, some works demonstrate the successful application of DSA to the degradation of herbicides/pesticides, especially in the presence of chloride with the consequent generation of active chlorine [18,19,20,21,22,23,24,25]. There are few studies dealing with Diuron electrodegradation. Zheng et al. [26] recently presented the results of some herbicides removal −Diuron included− by anodic oxidation on graphite at low voltages. The authors elucidated that the main oxidant present in the medium was the superoxide radical. Rahmani et al. [27] achieved the complete mineralization of Diuron by the treatment with the non-active PbO2 anode and suspended granular activated carbon acting as bipolar electrodes. Zheng et al. [28] applied a solar-driven electro-oxidation on three different anodes: titanium, graphite, and BDD, observing that the most efficient and stable performance, attaining 90% of Diuron elimination, was obtained when BDD was used as the anode. Pipi et al. [29] reported the Diuron degradation on DSA anodes, studying the influence of the composition (IrO2 vs. RuO2). RuO2 emerged as the most active material. Khongthom et al. [30] studied the Diuron degradation on a graphite anode in a microscale reactor with levels of degradation above 90% for residence times of 100 s. Zhu et al. [31] achieved a 100% Diuron degradation on a Co3O4/graphite composite anode at pH 2.0, 2 mA cm-2. Finally, Bumroongsakulsawat et al. [32] analyzed the influence of sulfate and nitrate interferences on the Diuron degradation mechanism and toxicity of the final effluent, observing that both anions reduced the efficacy of the Diuron oxidation by scavenging hydroxyl radicals. It is important to note that most of these studies used chloride salts as supporting electrolytes, which may give rise to the formation of organochlorines [33], an issue that deserves attention.
With these antecedents, this manuscript addresses the Diuron degradation on a commercial electrochemical reactor equipped with a Ru0.3Ti0.7O2 commercial DSA anode using sodium sulfate as the supporting electrolyte. Some critical operating parameters, such as the current density and the initial Diuron concentration, are studied in this work. The kinetics of the degradation under the different operating conditions and the energy demand are analyzed to establish the optimum operating conditions in terms of a large Diuron removal combined with the lowest possible energy consumption. Finally, a preliminary technical-economic assessment is presented to support selecting the most suitable conditions to design and operate such a system to reduce the total costs of the electrochemical reactors, considering the annualized capital costs (from the electrodes) and the operating costs (electricity consumption).

2. Materials and Methods

Sodium sulfate and Diuron were purchased from Sigma-Aldrich (Sigma-Aldrich Brasil Ltda., São Paulo, Brazil) and used as received. Ultrapure water was obtained from a Millipore Milli-Q system (resistivity = 18 MΩ cm, total organic carbon below 2 μg L−1). The synthetic wastewater polluted with Diuron was prepared by initially dissolving Na2SO4 in the ultrapure water to render a 0.17 mol L−1 Na2SO4 solution. Afterward, Diuron was dissolved in the different studied concentrations, 9.5, 19, and 38 mg L−1. Higher concentrations were unfeasible due to the low solubility of Diuron in water [34] (42 mg L−1).
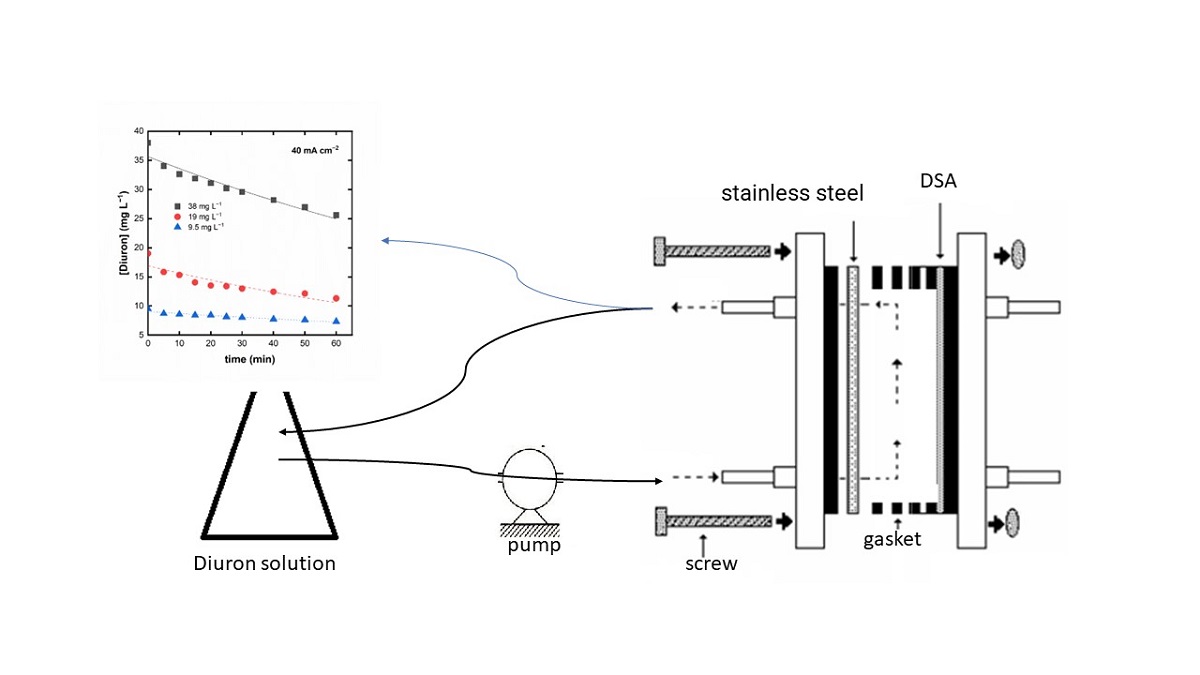
The electrochemical reactor consisted of two electrodes, a DSA-Cl anode (Ru0,3Ti0,7O2 supported on Ti), and a stainless-steel cathode, with a geometric area of 15 cm2. The interelectrode gap was 2 cm, and the reactor was tightened with a silicone gasket. A peristaltic pump (IntLLabTM) was used to apply a flow rate of 4 L h-1 operating in recirculation mode. The electrolysis experiments were carried out by connecting the reactor to a power supply EMG 18135 30 A(Orion-EMG Elektronikus, Budapest, Hungary). The current was measured by Minipa DT-930B multimeter (Minipa do Brasil Ltda., São Paulo, Brazil), and the cell voltage was measured by Minipa ET-1002 multimeter (Minipa do Brasil Ltda., São Paulo, Brazil). A scheme of the electrochemical reactor is shown in the Supplementary Material (Fig. S1).
The electrolysis studies were also performed at different current densities, 10, 20, and 40 mA cm−2, collecting aliquots at different degradation times. The sequence and label of the applied conditions are summarized in Table 1.
Diuron was quantified by UV-VIS spectroscopy. The herbicide presents an absorption peak at 250 nm, which allows monitoring the Diuron degradation. Finally, the energy demand was estimated according to Equation 1, where E is the volumetric energy consumption, Vcell is the cell voltage, I is the applied current, t is the degradation time, and υ is the volume of the electrochemical reactor.
E ( kWh   m - 3 ) = 0.001   V cell ( V )   I ( A ) t ( h ) υ ( m 3 )

3. Results and discussions

Figure 1 shows the Diuron removed for the different degradation times at the studied current densities and initial Diuron concentrations. As can be seen, the maximum Diuron removal is achieved for the operation at the highest current density and Diuron initial concentration, D40-38. These two combined conditions render the most oxidative degradation environment with the highest availability of the target molecule, resulting in the largest degraded Diuron at any time. The operation at lower current densities and/or smaller initial Diuron concentrations results in less effective Diuron degradation. This behavior is typical of mass-transfer-controlled processes, where the more limited access of the Diuron molecule to the electrode surface or the available electrogenerated oxidants (OH• radicals, peroxide, persulfate given the supporting electrolyte used, ozone…) favors the development of ineffective parasitic reactions (e.g., oxygen evolution). In fact, the operation at low current densities reduces the extension of parasitic secondary reactions, increasing the efficiency of the Diuron oxidation for the least Diuron concentrated condition (experiment D10-9.5) [35]. In general terms, the operation at higher Diuron initial concentrations for a fixed current density increases the Diuron removed due to a more efficient process. The effect of the initial Diuron concentration is more dependent on the applied current density. A higher initial concentration (DXX-38) allows operating effectively at higher current densities, whereas operating at DXX-9.5 degrades Diuron more rapidly at lower current densities, as abovementioned. It is also interesting to analyze the results in terms of the percentage of Diuron removed. The corresponding results are collected in the Supplementary Material (Fig. S1). Regarding the relative Diuron degradation, the operation in the condition D40-19 renders the highest percentage.
Figure 2 shows the evolution of the degraded Diuron with the applied volumetric charge (Equation 2, where Q is the applied volumetric charge). This figure allows us to visualize better the efficacy of the Diuron degradation, as it compares the applied charge with the actual degradation of Diuron.
Q ( Ah   L - 1 ) = I ( A ) t ( h ) υ ( L )
As can be observed, the most efficient degradation is reached for the D10-9.5 experiment, operated at the lowest current density and higher initial Diuron concentration, conditions that disfavor the evolution of ineffective reaction, along with the high concentration of the target pollutant. On the contrary, the operation D40-9.5 results in the least effective degradation due to the smallest target pollutant availability combined with the operation at high current density. Higher initial concentrations and lower current densities increase the efficiency of the Diuron degradation, it can be assigned to parallel reactions. Nevertheless, caution should be taken since this would lead to longer operation times and higher electrode areas, demanding a dedicated technoeconomic analysis.
Figure 3 displays the constant rate of the degradation process. The concentration profiles are shown in the Supplementary Material (Figure S2). The results fit well with a first-order kinetics, which is expected for a mass-transfer-controlled degradation [37].
The values of the constant rates reveal that the fastest degradation occurs for the D40-19, as observed in Fig. S1, with the highest use of the available oxidants. In contrast, the D40-9.5 results in the slowest degradation due to the significant evolution of parasitic reactions. Not as fast as operating at the optimum, operating at D10-9.5, D20-19, and D40-38 also render a fast Diuron degradation kinetics, where the oxidant conditions are also effectively utilized.
Another relevant parameter of the anodic oxidation is the energy consumption. Figure 4 depicts the energy consumption as a function of time and Diuron removed. In terms of energy demand, as expected, the operation at low current densities is favorable due to the smallest values of the cell voltage accompanied by the highest degree of Diuron removal at D10-38. Under this condition of high target pollutant availability and low current density, we can oxidize more effectively the Diuron molecule with a less energy-costly process. Note that for all experiments the final concentration of Diuron were close to 67% from inicial concentration (Figure S2) , thus the energy consumption can be assigned totally to Diuron degradation.
Nevertheless, caution needs to be taken when analyzing these results since, during the treatment at high initial concentrations, the Diuron concentration drop is expected to make the process less efficient, increasing the energy demand as the degradation proceeds. Such an effect could, in the end, make the process more onerous. In this sense, we present a preliminary and straightforward estimate of the electrodes cost based on the required area and the energy consumption, given that these two parameters account for most of the fixed capital and operation costs of the system [38]. The DSA cost can be estimated from the value provided by Wenderich et al. [11], estimated at US$ 3,500.00 per m2 of electrode. The cost of electricity (Celec is considered to be 0.0845 US$ kWh‒1 [39]. To design the system, it is necessary to know the required charge to degrade the target molecule. Let us consider a treatment plant whose capacity is equal to that presented by Cabral Coelho and Santos Brega [40], 1 m3 h‒1, with an effluent containing 38 mg L‒1 of Diuron. Based on the results of Kučić Grgić et al. [41] regarding the influence of the initial Diuron concentration in an effluent on its biodegradation, we can consider a treatment down to 9.5 mg L‒1 (Diuron could be effectively degraded below 10 mg L‒1). Thus, the design of the treatment plant will be executed based on the two initial concentrations in successive sequences, i.e., from 38 down to 19 mg L‒1 (Stage 1), and 19 down to 9.5 mg L‒1 (Stage 2), in which we will achieve the goal for the biological treatment. The required electrode area can be estimated from Equation 3, where j is the applied current density. In this case, the parameter υ is the volume to be treated. If we consider three operating cycles, including 1 h for the charge and 1 h for the discharge of the storage tank that contains the solution to be treated, each cycle would have an operating time of 6 h to treat 8 m3. Finally, the parameter j is the applied current density.
A ( m 2 ) = Q ( A   h   L - 1 ) υ ( L ) j ( A   m - 2 ) t   ( h )
To establish the required charge for Stage 1 and Stage 2, we have tentatively fitted the experimental data to an empirical power equation (y = a xb), whose fitting is shown in the SI (Fig. S3). Also, Table S1 collects the values of the required volumetric charges. Table 2 presents the required DSA electrode areas and their corresponding fixed capital costs (FCC) based on this latter parameter, the operation time, and the current density. In order to compare the FCC with the operating costs (OC), the FCC are divided by 3, according to Towler and Sinnott [42].
As can be observed, the increase in the applied current density reduces the required electrode area as the required charges do not increase at the same rate as the current density. This is beneficial from the point of view of the initial investment of the plant. Nevertheless, attention must be given to the operational costs, exclusively estimated from the electricity consumption. Equation 4 allows us to estimate the operating costs, where OF is the operating factor, considered to be 8000 h year‒1 corrected by the 6/8 factor corresponding to the 2 h devoted to charge/discharge stages. The cell voltage for the operation at 10 mA cm‒2 is 3.3 V, at 20 mA cm‒2 is 3.7 V, and at 40 mA cm‒2 is 4.3 V.
OC ( $   year - 1 ) = 0.001 V cell ( V ) j ( A   m - 2 ) A ( m 2 ) OF ( h   year - 1 ) C elec ( $   kWh - 1 )
Table 3 collects the OC for the different current densities, whereas Figure 5 displays the corresponding FCC and OC and the total annualized costs. As observed, the decay in the annualized CC as the current density rises is counterbalanced by the higher OC from the energy consumption. Thus, the optimum condition based on the system's total costs corresponds to the current density of 10 mA cm‒2.
One interesting feature of the applied charge versus Diuron removed is that at low Diuron removal, the operation at 40 mA cm‒2 is more efficient. Figure S4 shows in detail the mentioned regions from which we can infer the volumetric charges that could be applied at a current density of 40 mA cm‒2, whereas the remaining volumetric charge would be applied at 10 mA cm‒2 for each stage. To minimize the total annualized costs, we have optimized the time at which each current density is applied with the aid of the Solver tool of Microsoft Excel. Table 4 summarizes the main results. It is important to note that the electrode area would have a unique value calculated from the highest area obtained in the optimization of the four steps. In contrast, the OC would be different, as the required electrode area could be different, as well as the power. Figure 6 graphically compares the total annualized cost for the more economical option of Fig. 5 (10 mA cm‒2) and the combined current densities) to better visualize the positive effect of combining the operation at different current densities.
The results in Fig. 6 demonstrate the beneficial effect of operating at combined current densities. The main impact lies in the reduction of the annualized CC due to the reduction in the time operating at the lowest current density, which results in a drop in the required electrode area that still attends to the required area during the operation at 40 mA cm‒2. In contrast, the OC slightly increases due to the operation for a short period at 40 mA cm‒2, not to the point of counterbalancing the drop in the CC.
The results show the necessity of cautiously analyzing the results from the influence of the operating parameters in an electrochemical oxidation system. In addition to the technical-scientific studies, an economic assessment is very advisable to complement the results, discovering the optimum designing and operative conditions to minimize the costs of applying this technology.

4. Conclusions

As a general conclusion, this study has demonstrated that Diuron, an extensively used herbicide, can be removed by anodic oxidation on a Ti/Ru0,3Ti0,7O2 DSA in Sodium Sulfate media also. In addition to that, other important conclusions drawn from this study are as follows:
  • In terms of a rapid Diuron degradation, the condition D40-38 is the most favorable owing to the synergy of the most oxidative conditions with the highest pollutant availability, accelerating the degradation process.
  • Nevertheless, attention must be given to efficiency and energy consumption, in which case the operation at 10 mA cm−2, regardless of the initial Diuron concentration, becomes more attractive as it removes Diuron with the lowest applied charge and energy demand.
  • This information drawn from the analysis of the influence of the operating parameters is precious for establishing the design and operating conditions of an electrochemical treatment plant based on the minimization of the costs.
  • Operating in the most efficient conditions is beneficial for reducing the FCC, whose impact is more substantial than the OC, provided there is no significant increase in the cell voltage.
  • In this latter sense, as demonstrated in the work, it may be interesting to modulate the applied current density during the treatment, beginning with a higher current density and reducing it as the degradation proceeds to guarantee the operation at the highest possible efficiency and lowest electricity consumption, minimizing the total costs of the systems.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: Final percentages of Diuron removed for the different initial Diuron concentrations and current densities studied; Figure S2: Concentration profiles for the different current densities, along with the fitting parameter to a first-order kinetics (C = C0 exp (−kt)); Figure S3: Fitting of the applied charges versus the Diuron removed to estimate the required volumetric charges for designing the treatment system; Figure S4: Fitting of the applied charges versus the Diuron removed to estimate the required volumetric charges for designing the treatment system; Table S1: Required volumetric charges (AhL−1) for each stage of Diuron removal for each applied current density.

Author Contributions

Conceptualization, L.B.F. and F.C.; methodology, L.B.F., F.C., and A.J.M.; formal analysis, G.F.T., A.C.F.A.; investigation, L.B.F., G.F.T., A.C.F.A.; resources, F.C. and A.J.M.; Data curation, G.F.T.; A.J.M. and J.J.L.; writing—original draft preparation, J.J.L.; and S. B. O.; writing—review and editing, F.C. and A.J.M; visualization, S.B.O and A.J.M.; supervision, F.C.; project administration, F.C.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.

Acknowledgments

The authors thank Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), Fundação de Amparo à Pesquisa do Estado de Goiás (FAPEG) and Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) for financial support. LBF thanks CAPES also for the scholarship #88882.386519/2019-01.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kishor, R.; Purchase, D.; Saratale, G.D.; Saratale, R.G.; Ferreira, L.F.R.; Bilal, M.; Chandra, R.; Bharagava, R.N. Ecotoxicological and Health Concerns of Persistent Coloring Pollutants of Textile Industry Wastewater and Treatment Approaches for Environmental Safety. J. Environ. Chem. Eng. 2021, 9, 105012. [Google Scholar] [CrossRef]
  2. Yakamercan, E.; Bhatt, P.; Aygun, A.; Adesope, A.W.; Simsek, H. Comprehensive Understanding of Electrochemical Treatment Systems Combined with Biological Processes for Wastewater Remediation. Environ. Pollut. 2023, 330, 121680. [Google Scholar] [CrossRef]
  3. Najafinejad, M.S.; Chianese, S.; Fenti, A.; Iovino, P.; Musmarra, D. Application of Electrochemical Oxidation for Water and Wastewater Treatment: An Overview. Molecules 2023, 28, 4208. [Google Scholar] [CrossRef]
  4. Martínez-Sánchez, C.; Robles, I.; Godínez, L.A. Review of Recent Developments in Electrochemical Advanced Oxidation Processes: Application to Remove Dyes, Pharmaceuticals, and Pesticides. Int. J. Environ. Sci. Technol. 2022, 19, 12611–12678. [Google Scholar] [CrossRef]
  5. Bellas, J.; García-Pimentel, M.d.M.; León, V.M. Current-Use Pesticides in the Marine Environment. In Contaminants of Emerging Concern in the Marine Environment; León, V.M., Bellas, J., Eds.; Elsevier: Amsterdam, Netherlands, 2023; pp. 229–309. [Google Scholar]
  6. Panis, C.; Candiotto, L.Z.P.; Gaboardi, S.C.; Gurzenda, S.; Cruz, J.; Castro, M.; Lemos, B. Widespread Pesticide Contamination of Drinking Water and Impact on Cancer Risk in Brazil. Environ. Int. 2022, 165, 107321. [Google Scholar] [CrossRef]
  7. European Food Safety Authority Conclusion Regarding the Peer Review of the Pesticide Risk Assessment of the Active Substance Diuron. EFSA J. 2005, 3, 1–58. [CrossRef]
  8. Martínez-Huitle, C.A.; Rodrigo, M.A.; Sirés, I.; Scialdone, O. Single and Coupled Electrochemical Processes and Reactors for the Abatement of Organic Water Pollutants: A Critical Review. Chem. Rev. 2015, 115, 13362–13407. [Google Scholar] [CrossRef]
  9. Comninellis, C.; Kapalka, A.; Malato, S.; Parsons, S.A.; Poulios, I.; Mantzavinos, D. Advanced Oxidation Processes for Water Treatment: Advances and Trends for R&D. J. Chem. Technol. Biotechnol. 2008, 83, 769–776. [Google Scholar] [CrossRef]
  10. Freitas, J.M.; Oliveira, T. da C.; Munoz, R.A.A.; Richter, E.M. Boron Doped Diamond Electrodes in Flow-Based Systems. Front. Chem. 2019, 7, 190. [Google Scholar] [CrossRef]
  11. Wenderich, K.; Nieuweweme, B.A.M.; Mul, G.; Mei, B.T. Selective Electrochemical Oxidation of H2O to H2O2 Using Boron-Doped Diamond: An Experimental and Techno-Economic Evaluation. ACS Sustain. Chem. Eng. 2021, 9, 7803–7812. [Google Scholar] [CrossRef]
  12. Bergmann, M.E.H.; Rollin, J.; Iourtchouk, T. The Occurrence of Perchlorate during Drinking Water Electrolysis Using BDD Anodes. Electrochim. Acta 2009, 54, 2102–2107. [Google Scholar] [CrossRef]
  13. Radjenovic, J.; Sedlak, D.L. Challenges and Opportunities for Electrochemical Processes as Next-Generation Technologies for the Treatment of Contaminated Water. Environ. Sci. Technol. 2015, 49, 11292–11302. [Google Scholar] [CrossRef]
  14. Santos, G.O.S.; Dória, A.R.; Vasconcelos, V.M.; Sáez, C.; Rodrigo, M.A.; Eguiluz, K.I.B.; Salazar-Banda, G.R. Enhancement of Wastewater Treatment Using Novel Laser-Made Ti/SnO2–Sb Anodes with Improved Electrocatalytic Properties. Chemosphere 2020, 259, 127475. [Google Scholar] [CrossRef]
  15. Dória, A.R.; Gonzaga, I.M.D.; Santos, G.O.S.; Pupo, M.; Silva, D.C.; Silva, R.S.; Rodrigo, M.A.; Eguiluz, K.I.B.; Salazar-Banda, G.R. Ultra-Fast Synthesis of Ti/Ru0.3Ti0.7O2 Anodes with Superior Electrochemical Properties Using an Ionic Liquid and Laser Calcination. Chem. Eng. J. 2021, 416, 129011. [Google Scholar] [CrossRef]
  16. Gonzaga, I.M.D.; Moratalla, A.; Eguiluz, K.I.B.; Salazar-Banda, G.R.; Cañizares, P.; Rodrigo, M.A.; Saez, C. Outstanding Performance of the Microwave-Made MMO-Ti/RuO2IrO2 Anode on the Removal of Antimicrobial Activity of Penicillin G by Photoelectrolysis. Chem. Eng. J. 2021, 420, 129999. [Google Scholar] [CrossRef]
  17. Gonzaga, I.M.D.; Dória, A.R.; Castro, R.S.S.; Souza, M.R.R.; Rodrigo, M.A.; Eguiluz, K.I.B.; Salazar-Banda, G.R. Microwave-Prepared Ti/RuO2-IrO2 Anodes: Influence of IrO2 Content on Atrazine Removal. Electrochim. Acta 2022, 426, 140782. [Google Scholar] [CrossRef]
  18. Zhao, R.; Zhang, X.; Chen, F.; Man, X.; Jiang, W. Study on Electrochemical Degradation of Nicosulfuron by IrO2-Based DSA Electrodes: Performance, Kinetics, and Degradation Mechanism. Int. J. Environ. Res. Public Health 2019, 16, 343. [Google Scholar] [CrossRef]
  19. Moreno-Palacios, A. V.; Palma-Goyes, R.E.; Vazquez-Arenas, J.; Torres-Palma, R.A. Bench-Scale Reactor for Cefadroxil Oxidation and Elimination of Its Antibiotic Activity Using Electro-Generated Active Chlorine. J. Environ. Chem. Eng. 2019, 7, 103173. [Google Scholar] [CrossRef]
  20. Espinoza, L.C.; Sepúlveda, P.; García, A.; Martins de Godoi, D.; Salazar, R. Degradation of Oxamic Acid Using Dimensionally Stable Anodes (DSA) Based on a Mixture of RuO2 and IrO2 Nanoparticles. Chemosphere 2020, 251, 126674. [Google Scholar] [CrossRef]
  21. Santos, T.É.S.; Silva, R.S.; Eguiluz, K.I.B.; Salazar-Banda, G.R. Development of Ti/(RuO2)0.8(MO2)0.2 (M=Ce, Sn or Ir) Anodes for Atrazine Electro-Oxidation. Influence of the Synthesis Method. Mater. Lett. 2015, 146, 4–8. [Google Scholar] [CrossRef]
  22. Malpass, G.R.P.; Miwa, D.W.; Machado, S.A.S.; Olivi, P.; Motheo, A.J. Oxidation of the Pesticide Atrazine at DSA® Electrodes. J. Hazard. Mater. 2006, 137, 565–572. [Google Scholar] [CrossRef] [PubMed]
  23. Vlyssides, A.; Arapoglou, D.; Mai, S.; Barampouti, E.M. Electrochemical Detoxification of Four Phosphorothioate Obsolete Pesticides Stocks. Chemosphere 2005, 58, 439–447. [Google Scholar] [CrossRef] [PubMed]
  24. Arapoglou, D.; Vlyssides, A.; Israilides, C.; Zorpas, A.; Karlis, P. Detoxification of Methyl-Parathion Pesticide in Aqueous Solutions by Electrochemical Oxidation. J. Hazard. Mater. 2003, 98, 191–199. [Google Scholar] [CrossRef] [PubMed]
  25. Malpass, G.R.P.; Miwa, D.W.; Miwa, A.C.P.; Machado, S.A.S.; Motheo, A.J. Study of Photo-Assisted Electrochemical Degradation of Carbaryl at Dimensionally Stable Anodes (DSA®). J. Hazard. Mater. 2009, 167, 224–229. [Google Scholar] [CrossRef] [PubMed]
  26. Zheng, Z.; Deletic, A.; Toe, C.Y.; Amal, R.; Zhang, X.; Pickford, R.; Zhou, S.; Zhang, K. Photo-Electrochemical Oxidation Herbicides Removal in Stormwater: Degradation Mechanism and Pathway Investigation. J. Hazard. Mater. 2022, 436, 129239. [Google Scholar] [CrossRef]
  27. Rahmani, A.; Leili, M.; Seid-mohammadi, A.; Shabanloo, A.; Ansari, A.; Nematollahi, D.; Alizadeh, S. Improved Degradation of Diuron Herbicide and Pesticide Wastewater Treatment in a Three-Dimensional Electrochemical Reactor Equipped with PbO2 Anodes and Granular Activated Carbon Particle Electrodes. J. Clean. Prod. 2021, 322, 129094. [Google Scholar] [CrossRef]
  28. Zheng, Z.; Zhang, K.; Toe, C.Y.; Amal, R.; Zhang, X.; McCarthy, D.T.; Deletic, A. Stormwater Herbicides Removal with a Solar-Driven Advanced Oxidation Process: A Feasibility Investigation. Water Res. 2021, 190, 116783. [Google Scholar] [CrossRef]
  29. Pipi, A.R.F.; Aquino Neto, S.; Andrade, A.R. De Electrochemical Degradation of Diuron in Chloride Medium Using DSA® Based Anodes. J. Braz. Chem. Soc. 2013, 24, 1259–1266. [Google Scholar] [CrossRef]
  30. Khongthon, W.; Jovanovic, G.; Yokochi, A.; Sangvanich, P.; Pavarajarn, V. Degradation of Diuron via an Electrochemical Advanced Oxidation Process in a Microscale-Based Reactor. Chem. Eng. J. 2016, 292, 298–307. [Google Scholar] [CrossRef]
  31. Zhu, K.; Qi, H.; Sun, X.; Sun, Z. Anodic Oxidation of Diuron Using Co3O4/Graphite Composite Electrode at Low Applied Current. Electrochim. Acta 2019, 299, 853–862. [Google Scholar] [CrossRef]
  32. Bumroongsakulsawat, P.; Khongthon, W.; Pavarajarn, V. Degradation of Diuron in Water by Electrochemical Advanced Oxidation in a Microreactor: Effects of Anion Contamination on Degradation and Toxicity. J. Environ. Chem. Eng. 2020, 8, 103824. [Google Scholar] [CrossRef]
  33. Wu, W.; Huang, Z.-H.; Lim, T.-T. Recent Development of Mixed Metal Oxide Anodes for Electrochemical Oxidation of Organic Pollutants in Water. Appl. Catal. A Gen. 2014, 480, 58–78. [Google Scholar] [CrossRef]
  34. Liu, J. Phenylurea Herbicides. In Hayes' Handbook of Pesticide Toxicology; Krieger, R., Ed.; Elsevier: London, United Kingdom, 2010; pp. 1725–1731. [Google Scholar]
  35. Brillas, E.; Sirés, I.; Arias, C.; Cabot, P.L.; Centellas, F.; Rodríguez, R.M.; Garrido, J.A. Mineralization of Paracetamol in Aqueous Medium by Anodic Oxidation with a Boron-Doped Diamond Electrode. Chemosphere 2005, 58, 399–406. [Google Scholar] [CrossRef] [PubMed]
  36. Deng, J.; Shao, Y.; Gao, N.; Deng, Y.; Tan, C.; Zhou, S.; Hu, X. Multiwalled Carbon Nanotubes as Adsorbents for Removal of Herbicide Diuron from Aqueous Solution. Chem. Eng. J. 2012, 193–194, 339–347. [Google Scholar] [CrossRef]
  37. Panizza, M.; Michaud, P.A.; Cerisola, G.; Comninellis, C.H. Anodic Oxidation of 2-Naphthol at Boron-Doped Diamond Electrodes. J. Electroanal. Chem. 2001, 507, 206–214. [Google Scholar] [CrossRef]
  38. de Araújo, B.R.S.; Linares, J.J. Electrochemical Treatment of Cetrimonium Chloride with Boron-Doped Diamond Anodes. A Technical and Economical Approach. J. Environ. Manage. 2018, 214, 86–93. [Google Scholar] [CrossRef]
  39. Statista Average Retail Electricity Price for Industrial Consumers in the United States from 1970 to 2022. Available online: https://www.statista.com/statistics/190680/us-industrial-consumer-price-estimates-for-retail-electricity-since-1970/#:~:text=Industrial retail electricity price in the U.S. 1970-2022&text=Industrial consumers of electricity in,per kilowatt-hour in 2022.
  40. Coelho, E.R.C.; Brega, R.S. Evaluation of a Pilot System for Removal of the Herbicide 2,4-Dichlorophenoxyacetic Acid and Absorbance Determination after Clarification and Adsorption on Granular Activated Carbon. Eng. Sanit. e Ambient. 2023, 28, e20220170. [Google Scholar] [CrossRef]
  41. Kučić Grgić, D.; Ocelić Bulatović, V.; Cvetnić, M.; Dujmić Vučinić, Ž.; Vuković Domanovac, M.; Markić, M.; Bolanča, T. Biodegradation Kinetics of Diuron by Pseudomonas Aeruginosa FN and Optimization of Biodegradation Using Response Surface Methodology. Water Environ. J. 2020, 34, 61–73. [Google Scholar] [CrossRef]
  42. Towler, G.; Sinnott, R. Economic Evaluation of Projects. In Chemical Engineering Design; Towler, G., Sinnott, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 305–337. [Google Scholar]
Preprints 80341 g001
Figure 1. Evolution of the removed Diuron for the experiments carried out at different initial Diuron concentrations and current densities.
Figure 1. Evolution of the removed Diuron for the experiments carried out at different initial Diuron concentrations and current densities.
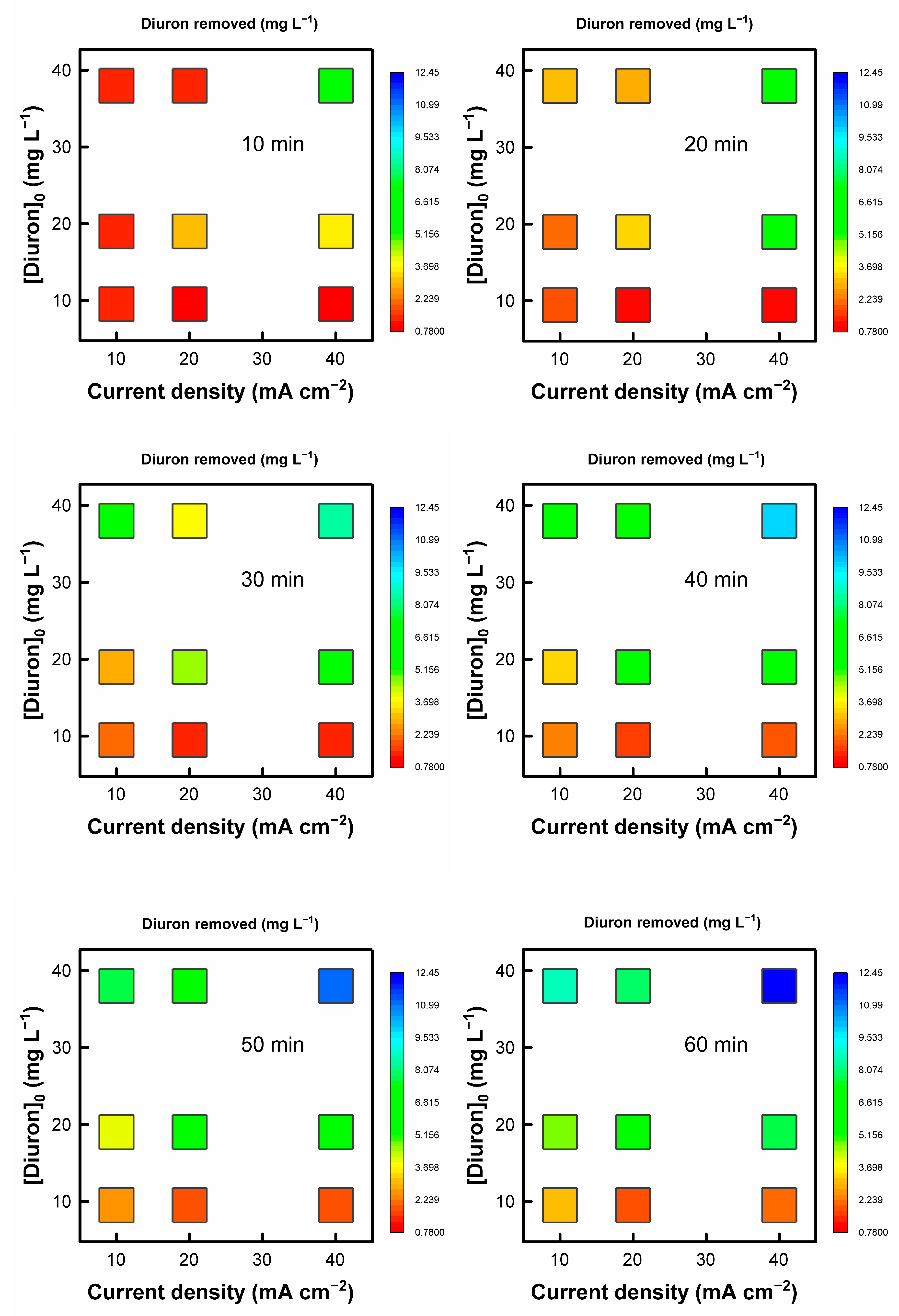
Preprints 80341 g001
Preprints 80341 g002
Figure 2. Diuron removal for the different applied charges in the experiments.
Figure 2. Diuron removal for the different applied charges in the experiments.
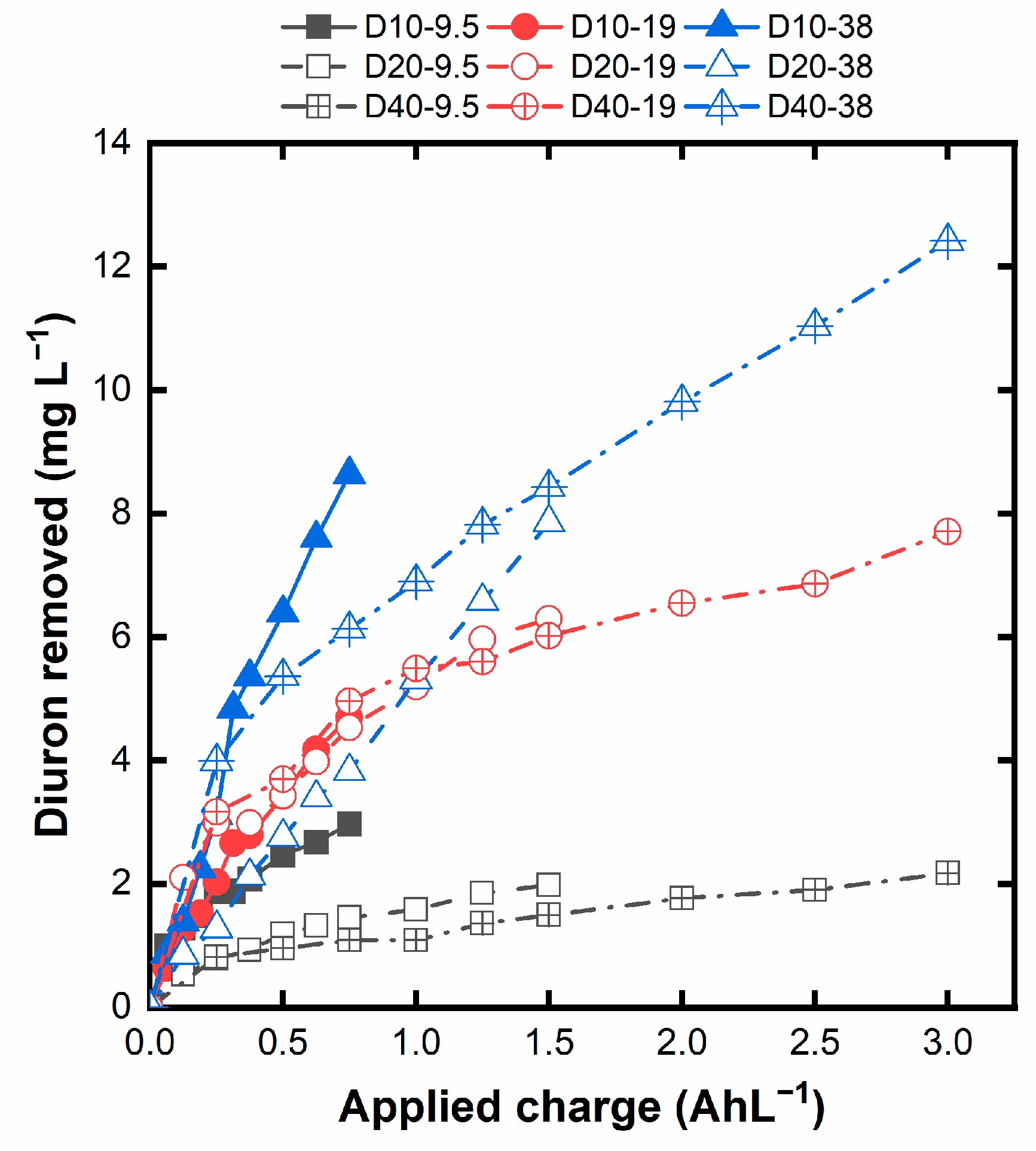
Preprints 80341 g002
Preprints 80341 g003
Figure 3. Kinetics constant rate for the degradation process.
Figure 3. Kinetics constant rate for the degradation process.
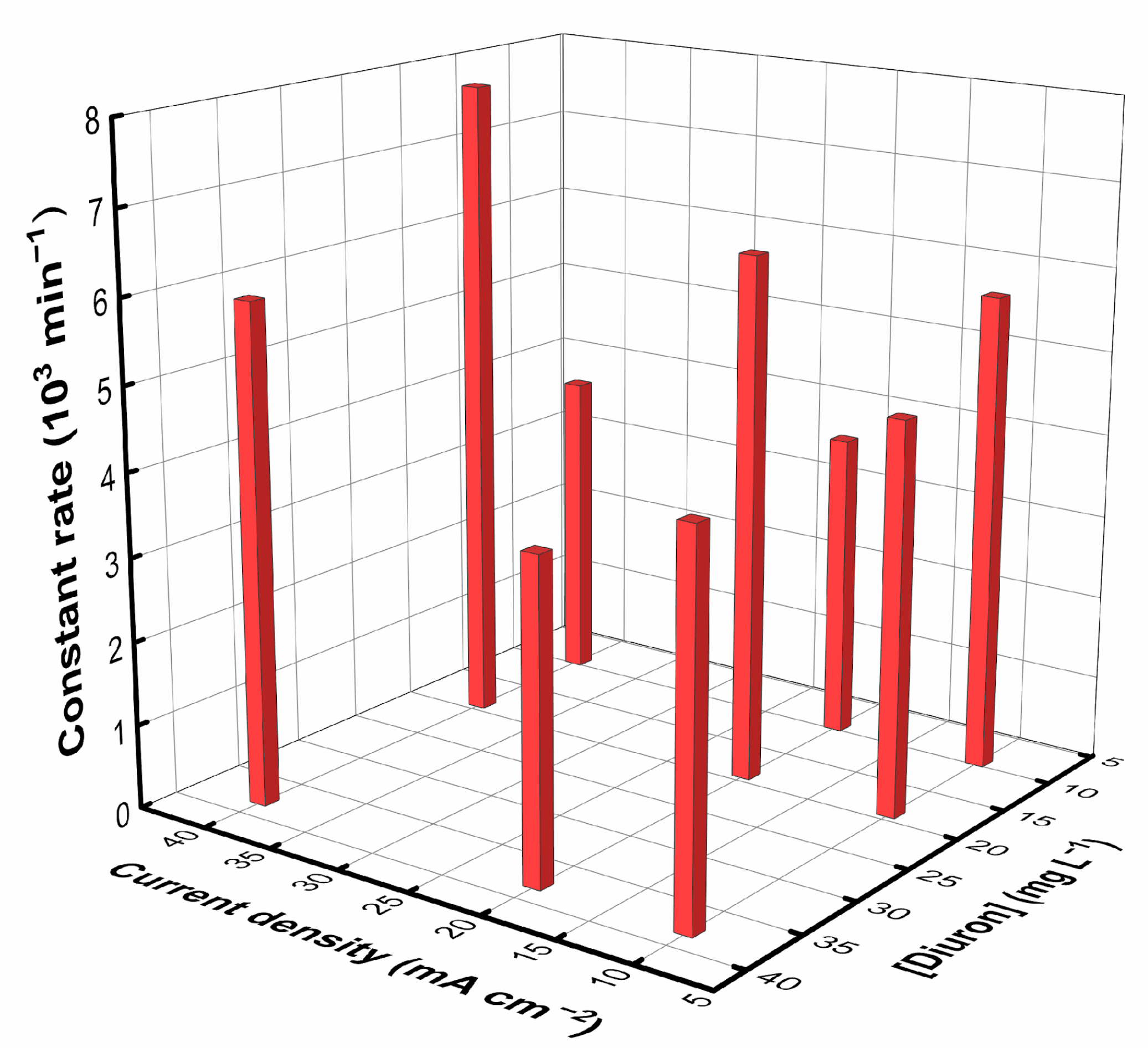
Preprints 80341 g003
Preprints 80341 g004
Figure 4. Energy consumption for the different degradation processes.
Figure 4. Energy consumption for the different degradation processes.
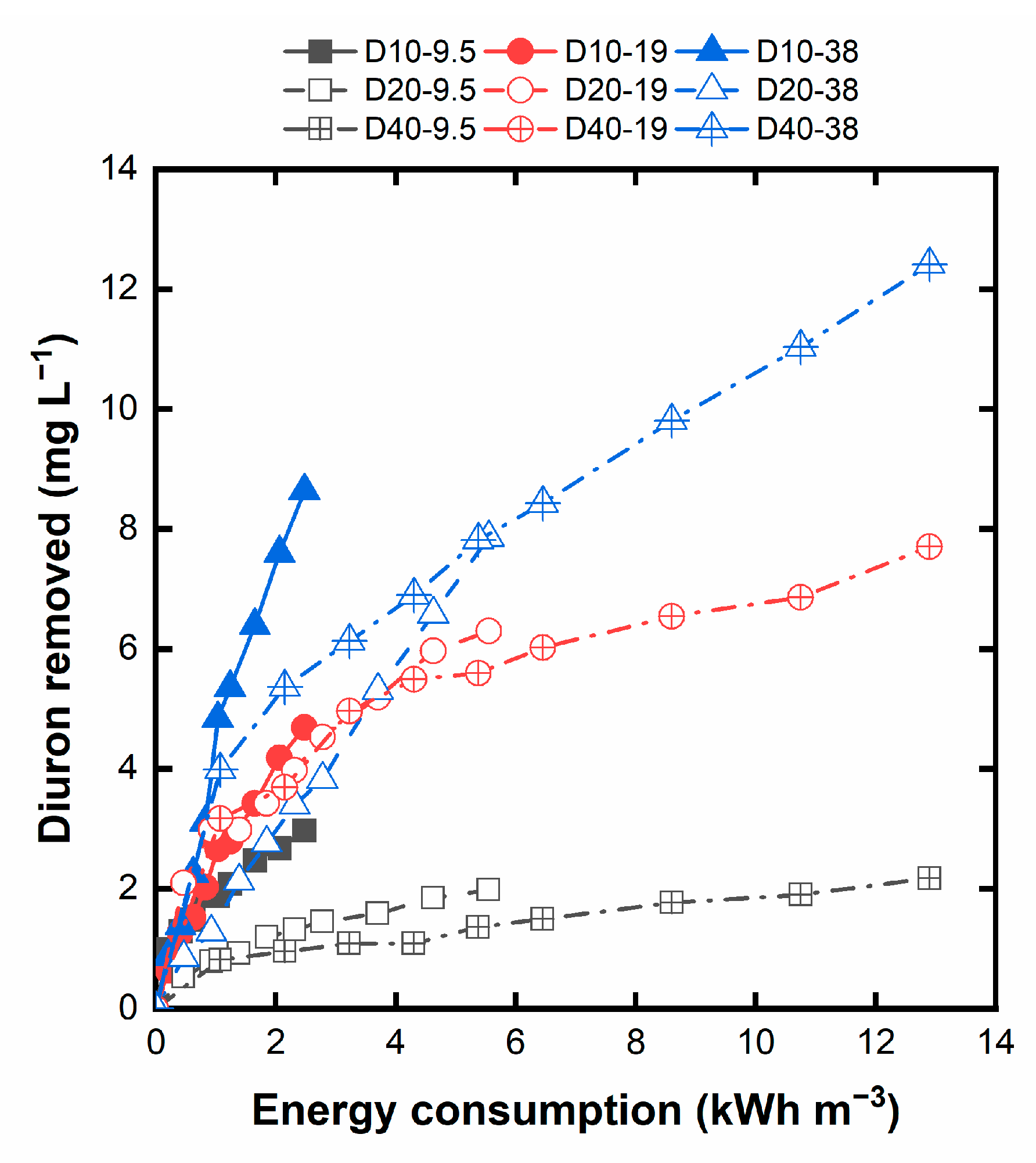
Preprints 80341 g004
Preprints 80341 g005
Figure 5. Estimation of the CC and OC for the different current densities. The height of each bar represents the total annualized cost.
Figure 5. Estimation of the CC and OC for the different current densities. The height of each bar represents the total annualized cost.
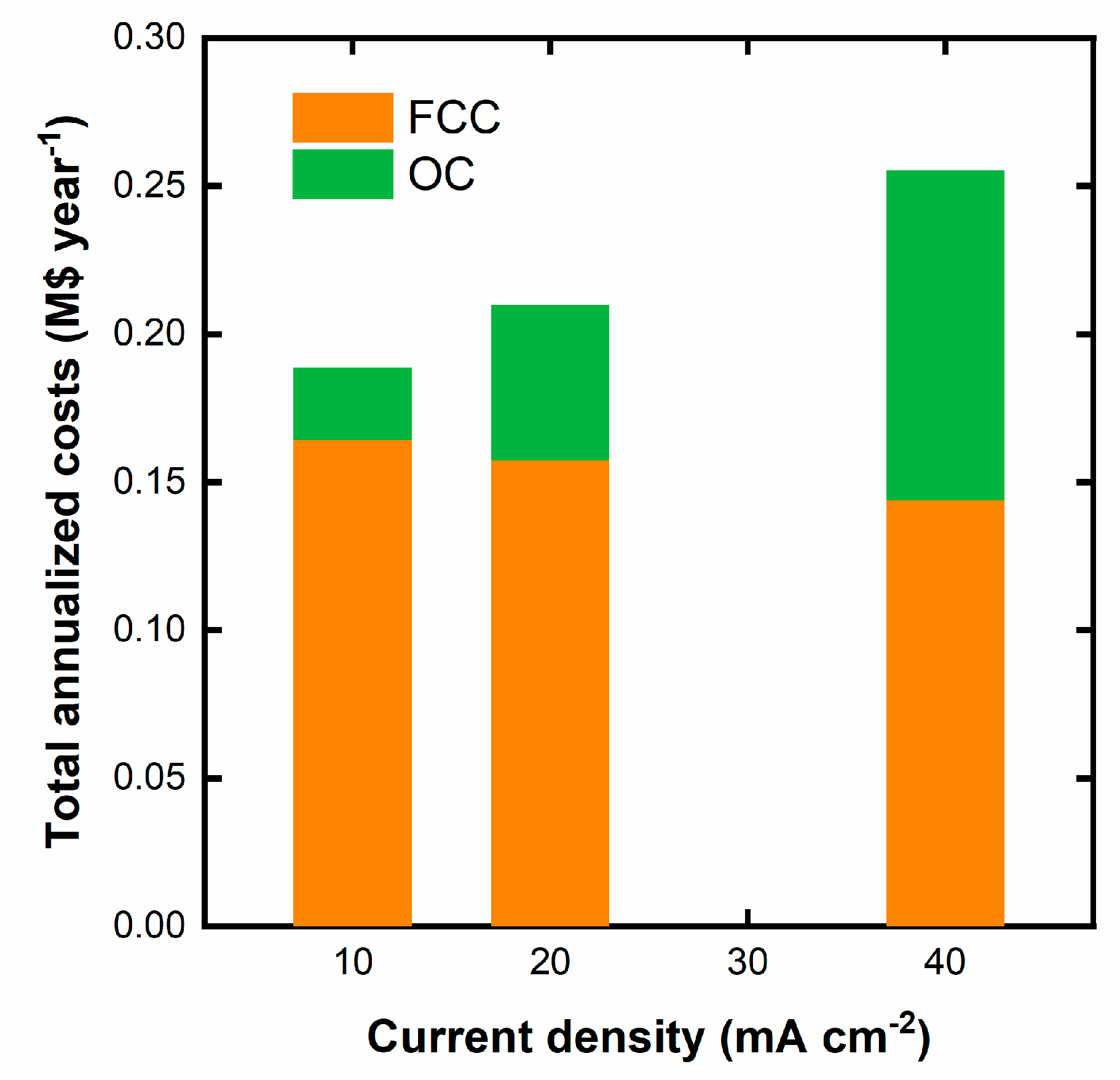
Preprints 80341 g005
Preprints 80341 g006
Figure 6. Comparison of the CC and OC for the operation at 10 mA cm−2 and for the operation with combined current densities.
Figure 6. Comparison of the CC and OC for the operation at 10 mA cm−2 and for the operation with combined current densities.
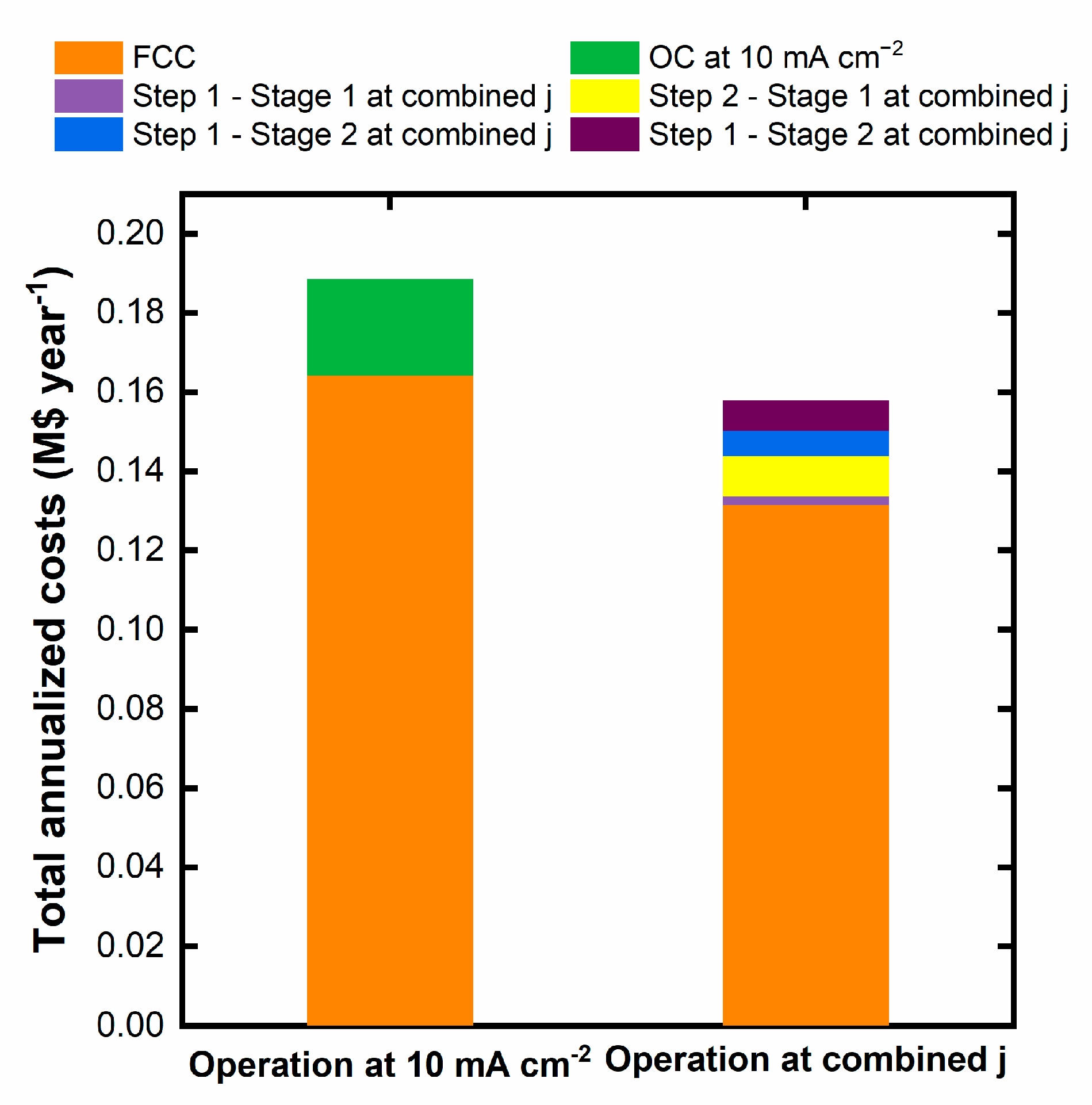
Preprints 80341 g006
Table 1. Experiments carried out in this study and their corresponding labels.
Table 1. Experiments carried out in this study and their corresponding labels.
Diuron concentration (mg L−1)
9.5 19 38
Current density (mA cm−2) 10 D10−9.5 D10−19 D10−38
20 D20−9.5 D20−19 D20−38
40 D40−9.5 D40−19 D40−38
Table 2. Required electrode area of the designed plant, corresponding total and annualized costs (M$ = 106 $).
Table 2. Required electrode area of the designed plant, corresponding total and annualized costs (M$ = 106 $).
A (m2) FCC (M$) = 10‒6 ⋅ A ⋅ 3500 $ m‒2 Annualized FCC (M$ year−1) = 0.33 ⋅ CC
Current density (mA cm−2) 10 146.6 0.513 0.164
20 140.4 0.492 0.157
40 128.4 0.449 0.144
Table 3. OC for the different applied current densities.
Table 3. OC for the different applied current densities.
Vcell (V) j (A m‒2) A (m2) OF (h year‒1) OC (M$ year−1)
Current density (mA cm−2) 10 3.3 100 146.6 6000 0.0244
20 3.7 200 140.4 6000 0.0525
40 4.3 400 128.4 0.449 0.112
Table 4. Optimized operation time for each cycle, required electrode area, annualized CC, OC, and total costs (addition of the annualized CC and the OC of the four steps).
Table 4. Optimized operation time for each cycle, required electrode area, annualized CC, OC, and total costs (addition of the annualized CC and the OC of the four steps).
j (mA cm−2) Q (ALh−1) t (h) Electrode area (m2) Annualized CC (M$ year−1) Operative electrode area (m2) OC (M$ year−1) Total annualized cost (M$ year−1)
Stage 1 (38 → 19 mg L−1) Step 1 → 40 0.250 0.148 117.4 0.131 102.0* 0.00218 (Total OC = 0.0164)

0.158
Step 2 → 10 1.524 3.12 117.4 0.0102
Stage 2 (19 → 9.5 mg L−1) Step 1 → 40 0.735 0.376 117.4 0.00639
Step 2 → 10 1.15 2.36 117.4 0.00769
*In this case, not all the cells would be operative
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated