The Kinetic and Energetic Pull of Chemical Entropy

Preprint

Hypothesis

The Kinetic and Energetic Pull of Chemical Entropy

Altmetrics

Downloads

111

Views

Comments

Josh Baker^*

This version is not peer-reviewed

Submitted:

24 July 2023

Posted:

25 July 2023

You are already at the latest version

Alerts

Abstract

Proteins in biological systems function at the interface of single molecule and bulk chemistry and thus provide novel insights into the basic physical chemistry of scaling and emergent phenomena. For example, a binary mechanical model based on the chemistry of muscle contraction unifies molecular mechanics and thermodynamics and provides an explicit solution to the Gibbs paradox. Using the same model system, here I show that chemical activities of molecular states have no effect on chemical kinetics or energetics. Specifically, while the concentration or number of molecules in a molecular state is widely thought to contribute to reaction free energies, here I show that it is not the physical presence of molecules that pushes a reaction forward but the number of microstates, , accessible in a chemical state that pulls a reaction toward equilibrium with an entropic force down an entropic funnel. With the derivation of an entropic contribution to chemical kinetics, I develop a novel chemical kinetic formulation that fully describes the chemical thermodynamics of both equilibrium and non-equilibrium reactions in terms of an a priori system reaction energy landscape.

Keywords:

Subject: Physical Sciences - Chemical Physics

Introduction

Technological advances over the past 70 years have fueled a molecular revolution in the biological sciences, providing remarkably detailed descriptions of the structure and function of a myriad of biomolecules. The question remains, however, to what extent is biological function the sum of these molecular parts versus an emergent property of systems of molecules? While this is fundamentally a physical chemical question, insights from small molecular ensembles in biological systems are informing new perspectives on this important chemical thermodynamic problem. For example, a model system based on the chemistry of muscle contraction offers a new perspective on entropic forces in enzyme-catalyzed reactions [1,2]. Using this model system, the mechanisms required to contain entropic forces have been clearly characterized, providing an explicit solution to the Gibbs paradox [3]. Here I show this entropic force, not some physical force exerted by molecules, balances chemical reactions.

Specifically, emergent properties of a system are broadly described by chemical activities, and the chemical activity, a_i, of a molecular state, i, in a reaction is typically described by the number, N_i, or concentration of molecules, [i], in that molecular state. However, while N molecules have chemical activity, here I show that this chemical activity does not in general change with a change in the molecular state of those N molecules. What is referred to as a concentration of a molecular state in fact describes the number of microstates accessible to a system within a given chemical state. It follows that the “concentration” of a molecular state describes an entropic reaction free energy, not a chemical potential, and the “concentration”-dependence of reaction rates are physically determined by the number of micropathways between microstates, not by the activity or active mass of a molecular state.

Reaction Free Energy

Chemical systems have properties that are described both by the state of the system (T, P, V) and by the state of molecules within the system (a system containing yellow molecules appears yellow). In a given system state, the standard free energy, ΔG°, for a reaction is a molecular property. For example, under standard conditions, ΔG° for the hydrolysis of ATP to ADP and P_i can be physically defined for one molecule as the change in free energy associated with breaking a single phosphoanhydride bond. The reaction free energy, Δ_rG, on the other hand, is a system property because it includes free energy changes that do not exist within individual molecules or molecular bonds.

Figure 1A describes the physical chemistry of a single molecule in a solution held at constant T,P, and V that reversibly switches between molecular states A and B with forward and reverse rate constants, k°₊ and k°_–, and a free energy difference between A and B of ΔG° = ΔH° – TΔS°, where ΔH° and ΔS° are the molecular enthalpic and entropic contributions to ΔG° [4]. The free energy landscape of the molecule (Figure 1A) describes changes in free energy along the reaction (or conformational) coordinate of that molecule [5]. The inverse times to diffuse in both forward, k°₊, and reverse, k°_–, directions over an activation energy barrier separating A and B (Figure 1A) are related to ΔG° as k°₊/k°_- = exp(–ΔG°/k_BT) [6]. For an isolated single molecule, the time-averaged occupancy of molecular states A and B is then

N_B/N_A = exp(-ΔG^o/kT).

(1)

For an ensemble of N such molecules contained in a solution held at constant T, P, and V, the reaction occurs along a system reaction coordinate that describes changes in free energy of the system, Δ_rG, with changes in the chemical (not molecular) state of the system [7,8]. In other words, in addition to ΔG^o, Δ_rG accounts for non-ΔG^o changes in the free energy of the system with a chemical step from{N_A,N_B} to {N_A–1,N_B+1}. These non-ΔG^o free energy changes include PΔV work performed with changes in solution volume, ΔV; non-PΔV work (F·d-work) performed with molecular displacements, d, against system forces, F [9]; and changes in system entropy, ΔS_sys [7]. In general [7],

Δ_rG = ΔG° + PΔV + F·d – TΔS_sys.

(2)

The terms on the right hand side of Equation (2) are the chemical forces that (when Δ_rG < 0) energetically drive a reaction from {N_A,N_B} to {N_A–1,N_B+1}, or that (when Δ_rG > 0) energetically drive a reaction from {N_A–1,N_B+1} to {N_A,N_B}, or that (when Δ_rG = 0) balance the reaction.

In 1864, Waage and Guldberg [10] proposed that the forces that balance chemical reactions are Newtonian, arguing that an active mass, N_A, of molecules in state A pushes against an equal and opposite reactive mass, N_B, of molecules in state B, such that N_A·k°₊ = N_B·k°_–. However, no term in Equation (2) is consistent with the concept of an active mass. It was subsequently shown that a change in the number of molecules, N, (the chemical activity) in a system affects the volume of a system, which through Equation (1) (PΔV) accounts for the partial pressure of a gas. In the early 1900’s, this approach was modified in an attempt to account for the forces that balance chemical reactions. Specifically, it was proposed that the chemical activity of N molecules fundamentally changes when the molecular state of those N molecules change. However, the state of a molecule is a property of that molecule and is in general fully defined by the molecular reaction energy landscape (Figure 1A) independent of system chemical activities. This is evident in the nonsensical description below that results from defining a molecular property as a chemical activity.

In most chemistry textbooks today, a term k_BT·ln(N_B/N_A) [or the molar equivalent RT·ln([B]/[A])] is derived from the envisaged chemical activities of molecular states A and B, and Equation (1) takes the form

Δ_rG = ΔG° + k_BT·ln(N_B/N_A),

which at equilibrium (Δ_rG = 0 and forces balance the chemical reaction) becomes

(N_B/N_A)_eq = exp(–ΔG^o/k_BT).

(3)

Equation (3) is equivalent to Equation (1), implying the following circular argument: if chemical activities assigned to molecular states, N_A and N_B, are defined by ΔG° (Equation (3)), then N_A and N_B are molecular (ΔG°) properties (Equation (1)), not non-ΔG° chemical activities. Chemical activities describe interactions between an individual molecule and the system of N molecules within which it is contained, which means chemical activities contribute to a system reaction energy landscape with reaction coordinates {N_A,N_B} not a molecular energy landscape with reaction coordinates A and B (Figure 1A). Equation (2) nonsensically describes N molecules diffusing within the reaction free energy landscape of a single molecule. Perhaps the intent is that each of N molecular energy landscapes has one molecule diffusing within it, in which case there is no chemical activity – the whole is the sum of its molecular ΔG° parts with no emergent non-ΔG° system behaviors – and if there is no chemical activity, the question remains what are the forces that balance chemical reactions?

Here, I develop a formulation that describes chemical entropy, TΔS_sys, as the force that balances chemical reactions. I show that while active masses and chemical activities purportedly push reactions forward, chemical entropy kinetically and energetically pulls chemical reactions down an entropic funnel.

System Entropy

For a system of N molecules (Figure 1A) contained in a solution held at constant T,P, and V, Equation (1) is

Δ_rG = ΔG° – TΔS_sys.

According to Boltzmann, S_sys = k_B·ln(Ω_NA,NB), where Ω_NA,NB is the number of microstates available to the system in chemical state {N_A,N_B}. Specifically, Ω_NA,NB = N!/(N_A!N_B!). The change in entropy with a single chemical step from {N_A,N_B} to {N_A–1,N_B+1} is then

ΔS_sys = –k_B·ln[((N_A – 1)!(N_B + 1)!)/(N_A!N_B!)] = –k_B·ln[(N_B + 1))/(N_A)], and so

Δ_rG = ΔG° + k_BT·ln[(N_B + 1))/(N_A)].

(4)

Equation (4) resembles Equation (3), only here N_B and N_A are reaction coordinates {N_A,N_B} in a system energy landscape that are defined independent from the physical occupancy of states A and B.

The change in system entropy associated with δN chemical steps from.

{N_A,N_B} to {N_A– δN,N_B+δN} is

ΔS_sys = –k_B·ln[((N_A – δN)!(N_B + δN)!)/(N_A!N_B!)] ≈ –δN·k_B·ln[(N_B + δN/2))/(N_A – δN/2)], and so

Δ_rG = δN·ΔG° + δN·k_BT·ln[(N_B + δN/2)/(N_A – δN/2)].

(5)

Here again the gradient established by δN is not a physical gradient that energetically drives the reaction. The reaction is driven by the average change in entropy per chemical step, k_BT·ln[(N_B + δN/2)/(N_A – δN/2)], summed over δN chemical steps, where the average change in entropy is defined by the system reaction coordinate {N_A,N_B} independent from the physical occupancy of states A and B.

A change in ΔS_sys relative to S_sys = 0 occurs from {N/2,N/2} to {N/2–δN, N/2+δN}, or

ΔS_sys = –δN·k_B·ln[(N/2 + δN/2))/(N_A – δN/2), or

ΔS_sys = –δN·k_B·ln[(1 + δN/N))/(1 – δN/N),

(6)

where δN/N is a fractional change in the extent of the reaction relative to unity. Assuming δN = 1 mol, Equation (6) can be written

ΔS_sys = –R·ln([B]/[A]), and

Δ_rG = ΔG° + RT·ln([B]/[A])

While this demonstrates consistency with the results of a chemical activity analysis, it does not demonstrate that physical concentration gradients drive chemical reactions. Again, here [B]/[A] is not a physical concentration gradient. At equilibrium [B]/[A] equals exp(–ΔG°/RT) not because [A] + [B] molecules physically equilibrate within the energy landscape of a single molecule, but because ΔG° a priori determines the approximate point along the system reaction coordinate, {N_A,N_B}, at which the system equilibrates. This is illustrated in Figure 1B and Figure 2 for small numbers of molecules.

System Reaction Coordinate

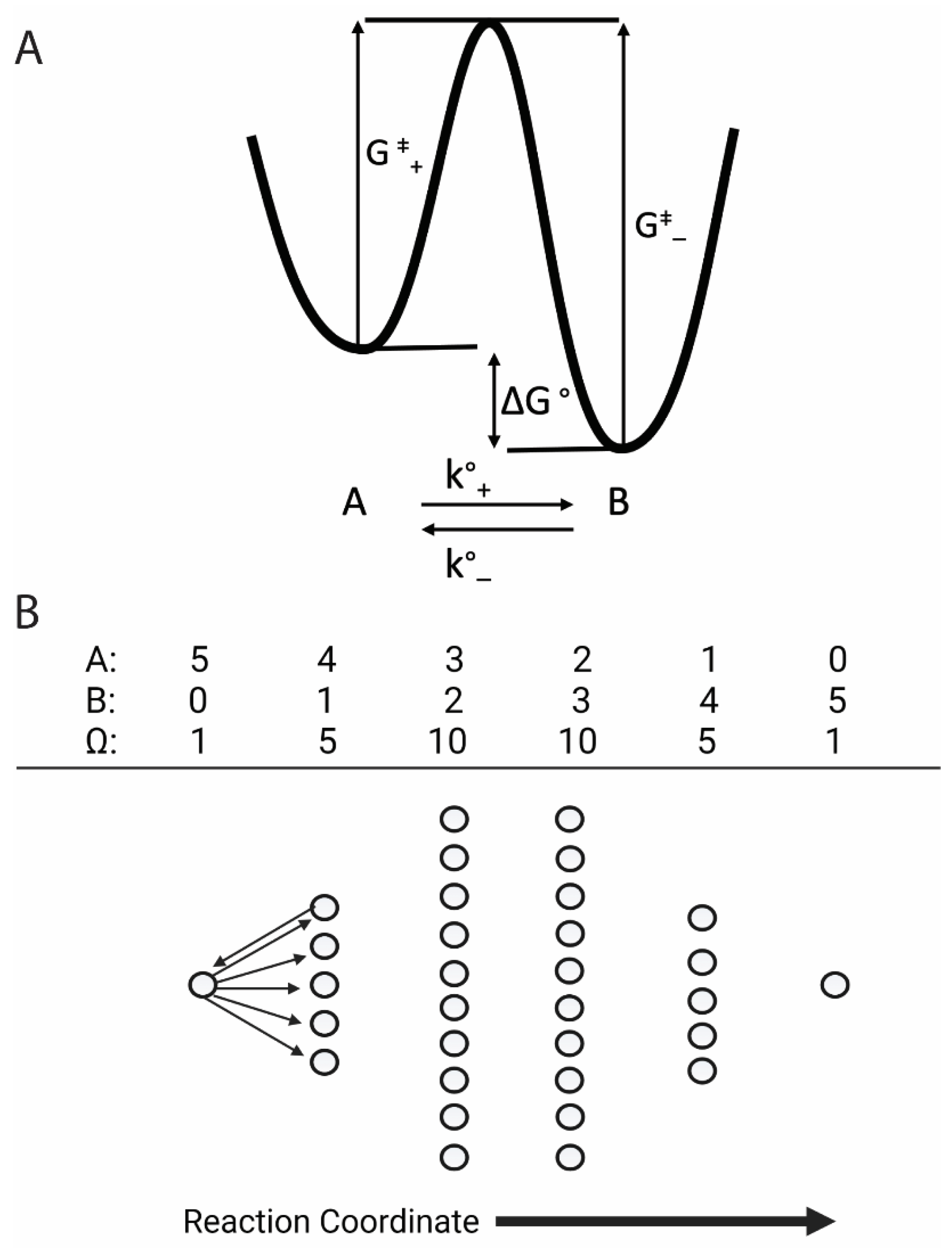
Figure 1B illustrates entropic changes along the reaction coordinate for a system of N = 5 molecules each occupying either molecular state A or B. When the system is in state {5,0}, Ω_5,0 = 1. Unlike in chemical activity models where k_B·ln(0/5) is undefined, here the system entropy, k_B·ln(1), is zero. After one net forward step, the system enters state {4,1}, increasing the number of microstates from 1 to 5 and increasing the system entropy from 0 to k_B·ln(5). This increase in the number of microstates physically pulls the reaction forward since there are five-times more micropathways in the forward direction than in the reverse direction. This contrasts with the chemical forces of molecules that purported push a reaction forward. When ΔG^o = 0, the reaction continues until a maximum system entropy is reached along the reaction coordinate, equilibrating in system state {3,2} when (N_B + 1)/N_A = exp(0) (Equation (3)).

Figure 2A is a plot of Equation (3), illustrating both the change in entropic energy, k_BT·ln[N_B+1,N_A], and the change in molecular free energy, ΔG^o, along the system reaction coordinate {N_A,N_B} for a system containing N = 10 molecules. Figure 2A illustrates that the change in system entropy increases logarithmically with each step whereas the change in molecular free energy, ΔG^o, is the same for each step (the effect of ΔG^o on Δ_rG is a constant offset). When ΔG^o decreases from 0 to –1.5 k_BT (Figure 2A, down arrow) the equilibrium state of the system changes from {5.5,4.5} to {2,8} (Figure 2, right arrow) corresponding to a change from (N_B + 1)/N_A = exp(0) to (N_B + 1)/N_A = exp(1.5).

Figure 2. Change in Free energy along a reaction coordinate. (A) For N = 10, Equation (3) is plotted for a ΔG° of 0 (green line) and –1.5 k_BT (blue line). For ΔG° = 0, the reaction equilibrates (Δ_rG = 0) at {5.5,4.5}. When ΔG° is decreased from 0 to –1.5 k_BT (down arrow) the system re-equilibrates (right arrow) at {2,8}. (B) The system free energy, G, (the integral of Δ_rG over the reaction coordinate) is calculated and plotted for ΔG° of 0 (green line) and –1.5 k_BT (blue line) values in panel A. The same trajectory in panel A describing re-equilibration following a decrease in ΔG° is illustrated in panel B (arrows).

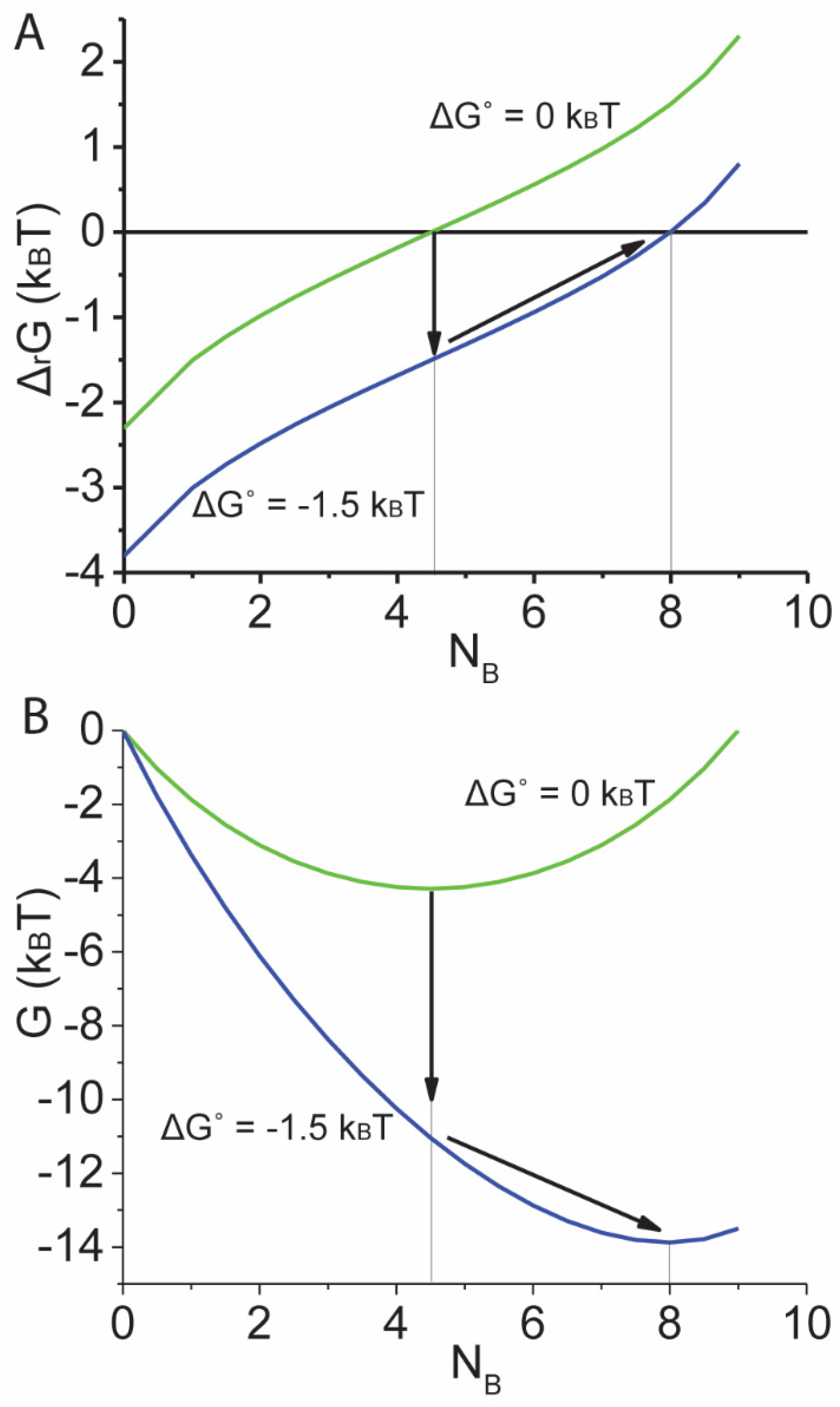
Because Δ_rG is the change in free energy, G, of the system with a chemical step, the integral of Equation (3) over the reaction coordinate is the free energy, G, of the system. The two graphs in Figure 2A are integrated and replotted in Figure 2B as free energy, G. These are the system free energy landscapes described by Gibbs within which the reaction equilibrates at a point along the reaction coordinate{N_A,N_B} where G is a minimum. According to Gibbs, the walls of the energy landscape represent the energy that balances a reaction at equilibrium, and here the walls of the energy landscape are TS_sys (the integral of TΔS_sys). In other words, entropic forces, TΔS_sys, (Figure 2A) drive a reaction toward equilibrium down an entropic funnel, TS_sys (Figure 2B).

Figure 2B illustrates how changes in ΔG° affect the energy landscape. Changes in non-ΔG° chemical activities have similar effects [2]. However, changes in N_A and N_B have no effect on the energy landscape because they are reaction coordinates, not chemical activities, and changes in reaction coordinates describe movement along the landscape, not changes to the landscape. Because reaction kinetics and energetics are defined by reaction energy landscapes, N_A and N_B have no effect on the kinetics or energetics of a reaction.

Equilibrium Energetics

At equilibrium (Δ_rG = 0), the probability of finding the system in state {N_A+1,N_B–1} relative to {N_A,N_B} is exp[–ΔG°/k_BT + ln(Ω_NA-1,NB+1/Ω_NA,NB)], where ln(Ω_NA-1,NB+1/Ω_NA,NB) = TΔS_sys/k_BT. Thus, when ΔG° = 0, Ω_NA,NB is the probability density function, P_NA,NB. For comparison, according to chemical activity models the probability of finding a molecule in state B relative to state A is exp[–ΔG°/k_BT], and when ΔG° = 0, P_NA,NB is a binomial distribution. The equilibrium constant, K = (Ω_NA,NB/Ω_NA-1,NB+1)_eq = exp[–ΔG°/k_BT] is K = (N_B(eq) + 1)/N_A(eq), and describes the reaction coordinate {N_A,N_B}_eq at equilibrium (Figure 2). For comparison, in chemical activity models the equilibrium constant K = N_B(eq)/N_A(eq) describes the physical distribution of N molecules within the energy landscape of a single molecule (Figure 1A).

Non-Equilibrium Energetics

When the system is perturbed from equilibrium by a change in the internal energy of the system, δE, [i.e., a change in ΔG° or k_BT·ln[(Ω_NA-1,NB+1/Ω_NA,NB) ], the free energy equation becomes

Δ_rG = [ΔG° – k_BT·ln(Ω_NA-1,NB+1/Ω_NA,NB)] _eq + δE = δE,

where δE is a non-equilibrium (ne) perturbation to any of the energy term on the right-hand side of Equation (1). Here,

δE = [ΔG° – k_BT·ln(Ω_NA-1,NB+1/Ω_NA,NB)]_ne.

As illustrated in Figure 2, if the system perturbation is a change in ΔG°, the system relaxes to a new equilibrium state, {N_A,N_B}_eq, as k_BT·ln(Ω_NA-1,NB+1/Ω_NA,NB) approaches the new ΔG°. Through this process, Δ_rG returns to zero and δE remains in the system in the form of a change in system entropy. If the system perturbation is a change in k_BT·ln(Ω_NA-1,NB+1/Ω_NA,NB) [an irreversible transfer of molecules between molecular states] the system relaxes back to the original equilibrium state, {N_A,N_B}_eq, as k_BT·ln(Ω_NA-1,NB+1/Ω_NA,NB)_ne approaches ΔG°. Through this process the entropic δE is lost from the system as heat. This analysis becomes more complex when non-PΔV work is performed, in which case upon a chemical relaxation, in addition to exchanges between k_BT·ln(Ω_NA-1,NB+1/Ω_NA,NB) and ΔG°, δE can be exchanged with internal mechanical potentials. And, in addition to being lost from the system as heat or stored in the system as entropy, δE can be lost from the system as work performed on the surroundings [2].

Equilibrium Kinetics

Chemical kinetics, like energetics, have both molecular and system components. The net rate at which the system transitions from chemical state {N_A,N_B} to chemical state {N_A–1,N_B+1} is

d{N_A,N_B}/dt = k₊ – k_–,

where k₊ and k_– are the forward and reverse transition rates between these states. At equilibrium, the probability of finding the system in state {N_A+1,N_B–1} relative to state {N_A,N_B} is

k_+(eq)/k_–(eq) = exp[(–ΔG° + k_BT·ln[Ω_NA-1,NB+1/Ω_NA,NB]_eq)/k_BT] or

k_+(eq)/k_–(eq) = (k°₊/k°_–)·exp[k_BT·ln(Ω_NA-1,NB+1/Ω_NA,NB)_eq/k_BT]

Here, k°₊ and k°_– are molecular contributions to k₊ and k_– and exp[–TΔS_sys/k_BT] is the system contribution to k₊ and k_–. The influence of –ΔS_sys/k_B on kinetics can be understood energetically as a tilt of the system landscape that adds to the tilt of the molecular landscape, ΔG°. It can also be understood kinetically as

k_+(eq)/k_–(eq) = (k°₊/k°_–)·(Ω_NA-1,NB+1/Ω_NA,NB)_eq

where the factor Ω_NA-1,NB+1/Ω_NA,NB describes the number of micropathways available for the forward reaction relative to the reverse reaction. For example, in Figure 1B there are five micropathways from {5,0} to {4,1} and one micropathway back from {4,1} to {5,0}, which means that the forward reaction is entropically five-fold more likely than the reverse reaction (Ω_NA-1,NB+1/Ω_NA,NB = 5). This implies forward and reverse rate constants of

k_+(eq) = k°₊·Ω_{NA-1,NB+1(eq)}

k_–(eq) = k°_–·Ω_NA,NB(eq).

At equilibrium, k_+(eq) = k_–(eq), or

k°₊·Ω_{NA-1,NB+1(eq)} = k°_–·Ω_NA,NB(eq).

To demonstrate consistency with the chemical activity approach,

k_+(eq) = k°₊·N_A_(eq)

k_–(eq) = k°_–·(N_B_(eq) + 1)

where here again N_A(eq) and N_B(eq) are not physical, active numbers of molecules, they are the system reaction coordinates {N_A,N_B}_eq at equilibrium.

Non-Equilibrium Kinetics

Chemical kinetics is fully determined from the molecular and system tilt of the system energy landscape. It follows that non-equilibrium kinetics is fully determined by the non-equilibrium tilt, δE, of these landscapes, where a non-equilibrium perturbation to ΔG° affects the molecular rates k°₊/k°_–, and an irreversible transfer of molecules between molecular states affects Ω_NA,NB/Ω_NA-1,NB+1. In general,

k₊(t)/k_–(t) = (k°₊/k°_–)(Ω_NA-1,NB+1(t)/Ω_NA,NB(t)) = exp[–δE(t)/k_BT].

(7)

According to Equation (7), for a negative δE(t), k₊(t) > k_–(t) which is consistent with the energetic requirement that a negative δE(t) drives the reaction forward. This forward reaction increases TΔS_sys (Figure 2) until δE(t) = 0, at which point k₊(t) = k_–(t). For a positive δE(t), k₊(t) > k_–(t) which is consistent with the energetic requirement that a positive δE(t) drives the reaction backward. This reaction decreases TΔS_sys (Figure 2) until δE(t) = 0, at which point k₊(t) = k_–(t). Not only do kinetics fully account for thermodynamics, they also describe the constraints placed on mechanisms through which δE is exchanged among ΔG°, TΔS_sys, and other energetic components (right side of Equation (2)) in minimizing the free energy of the system.

The non-equilibrium rate equation is the same as the equilibrium rate equation

d{N_A,N_B}/dt = k°₊·Ω_NA-1,NB+1 – k°_–·Ω_NA,NB(t).

For comparison with a chemical activity analysis, from above

dN_A/dt = k°₊·N_A(t) – k°_–·(N_B(t) + 1)

where one last time, N_A(t) and N_B(t) describe the time dependence of steps along the system reaction coordinate {N_A,N_B}, not the time-dependence of the physical numbers of molecules in different states. Changes in N_B(t) + 1 are equal and opposite changes in N_A(t) along the system reaction coordinate, and so

dN_A/dt = –N_A(t)·[k°_– + k°₊]

which means that N_A(t) decreases exponentially with time as

N_A(t) = N_Ao·exp(–(k°₊ + k°_–)t),

with a relaxation rate, k°₊ + k°_–, where N_Ao is the starting point on the reaction coordinate {N_A,N_B}_o.

Conclusion

In summary, a molecular energy landscape (Figure 1A) a priori defines ΔG° and rate constants, k°₊ and k°_–, for an isolated molecule (Figure 1A) independent of the physical existence of that molecule [5]. Similarly, an entropic energy landscape a priori defines system energetics and rates for N molecules (Figure 1B and Figure 2) independent of the existence of those molecules. Together ΔG° and entropy create a system energy landscape within which chemical entropy contains ΔG° and entropic forces balance a reaction against ΔG° by driving a reaction down an entropic funnel. The entropic contribution to chemical kinetics results in a new kinetic formalism that fully accounts for the chemical thermodynamics of a system both under equilibrium and non-equilibrium conditions.

Funding

JEB was funded by a grant from the National Institutes of Health 1R01HL090938.

Data and materials availability

All data are available in the main text.

Acknowledgments

I thank LEB, JWG, Julie, my students, colleagues, and mentors who have over many years inspired and guided this work. This was funded by a grant from the National Institutes of Health 1R01HL090938-01.

Competing interests

Author declares that they have no competing interest.

References

J.E. Baker and D.D. Thomas, A Thermodynamic Muscle Model and a Chemical Basis for A.V. Hill’s Muscle Equation. J Muscle Res Cell Motil. 2000, 21, 335. [CrossRef] [PubMed]
J.E. Baker, Thermodynamics and Kinetics of a Binary Mechanical System: Mechanisms of Muscle Contraction. Langmuir 2022, 38, 15905. [CrossRef] [PubMed]
J.E. Baker. Cells Solved the Gibbs Paradox by Learning How to Contain Entropic Forces. arxiv 2023.
L. Styer. Biochemistry; W.H. Freeman and Company: New York, NY, USA, 1995. [Google Scholar]
H. Frauenfelder, S.G. Sligar, P.G. Wolynes, H. Frauenfelder, S.G. Sligar, and P. G. Wolynes. The Energy Landscapes and Motions of Proteins. 1991, 254, 1598.
J. Howard, Mechanics of Motor Proteins and the Cytoskeleton, 1st ed. (Sinauer Associates, 2001).
C. Kittel and H. Kroemer, Thermal Physics (1980).
J. Gibbs, Elementary Principles in Statistical Mechanics Developed with Especial Reference to the Rational Foundation of Thermodynamics (1902).
J.E. Baker, L.E.W. LaConte, I. Brust-Mascher, and D. D. Thomas, Mechanochemical Coupling in Spin-Labeled, Active, Isometric Muscle. Biophys. J. 1999, 77, 2657. [CrossRef] [PubMed]
J. Quílez. On the Early Thermodynamic and Kinetic Deductions of the Equilibrium Constant Equation. Found. Chem. 2021, 23, 85. [CrossRef]

Figure 1. The molecular and system contributions to the reaction free energy. (A) The molecular contribution to the reaction free energy is described by a molecular energy landscape. The free energy difference between the two metastable states, A and B, is ΔG°. The rate, k°₊, at which a molecule transitions from molecular state A to B varies exponentially with –G^‡₊, where G^‡₊ is the height of the activation barrier in the forward direction. The rate, k°_–, at which a molecule transitions from B to A varies exponentially with –G^‡_–, where G^‡_– is the height of the activation energy barrier in the reverse direction. (B) The system contribution to the reaction free energy is entropic. For N = 5, there are 6 system states, {N_A,N_B}, along the reaction coordinate each with Ω_NA,NB = N!/(N_A!N_B!) microstates, illustrated with circles, and entropy k_B·ln(Ω_NA,NB). There are five micropathways (right arrows) by which a molecule in state {5,0} can transition to state {4,1}, and one micropathway (left arrow) by which a molecule in state {4,1} can transition to state {5,0}.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Kinetic and Energetic Pull of Chemical Entropy

Abstract

Introduction

Reaction Free Energy

System Entropy

System Reaction Coordinate

Equilibrium Energetics

Non-Equilibrium Energetics

Equilibrium Kinetics

Non-Equilibrium Kinetics

Conclusion

Funding

Data and materials availability

Acknowledgments

Competing interests

References

MDPI Initiatives

Important Links

Subscribe