Prerpints.org logo
Preprint
Article

Resource-Efficient Optimization for FPGA-Based Convolution Accelerator

Altmetrics

Downloads

165

Views

60

Comments

0

This version is not peer-reviewed

Submitted:

24 July 2023

Posted:

26 July 2023

You are already at the latest version

Alerts
Abstract
Convolution forms one of the most essential operations for the FPGA-based hardware accelerator. However, the existing designs often neglect the inherent architecture of FPGA, which puts forward an austere challenge on hardware resource requirements. Even though some previous works have proposed approximate multipliers or convolution acceleration algorithms to deal with this issue, the inevitable accuracy loss and resource occupation easily lead to performance degradation. Toward this, we first propose two kinds of resource-efficient optimized accurate multipliers based on LUTs or carry chains. Then targeting FPGA-based platforms, a generic multiply-accumulate structure is constructed by directly accumulating the partial products produced by our proposed optimized radix-4 Booth multipliers without intermediate multiplication and addition results. Experimental results demonstrate that our proposed multiplier achieves a maximum 51% look-up-table (LUT) reduction compared to the Vivado area optimized multiplier IP. Furthermore, the convolutional process unit using the proposed structure achieves a 36% LUT reduction compared to existing methods. As case studies, the proposed method is applied to DCT transformer and LeNet to achieves hardware resource saving without loss of accuracy.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

In recent years, with the development of neural networks and image processing, there brings out a substantial growth of the convolution operation featuring by large number of multiply-accumulate calculations. Generally, the field-programmable gate array (FPGA) has become a promising platform for hardware acceleration of CNN due to its flexibility and energy efficiency [1]. However, when the convolution processing units are directly implemented on FPGA, the corresponding multiplication and addition operations, which have been widely investigated for ASIC-based systems, are achieved based on the configurable logic blocks instead of logic gates. It may probably result in unnecessary waste of hardware resources due to inherent architectural differences between FPGA and ASIC. Therefore, optimization and acceleration of convolution processing units form one of the essential topics for FPGA-based accelerator.
When directly implementing the convolutional process units on FPGA, although the vendors, such as AMD and Intel, have provided DSPs to achieve fast multipliers, it may probably result in performance degradation due to their fixed locations and limited quantity for multiplier-intensive applications [2]. For the implementation of large-scale neural network, such as VGG-16, the quantity of DSPs is usually insufficient [3]. In addition, previous works have also reported that with exhaustive use of DSPs, performance degradation will appear because of their fixed locations when implementing applications like Nova and Viterbi decoder [4]. Furthermore, the fixed bit-width multiplier of DSP, usually 25×18, will easily lead to higher latency of convolutional process units, most of which employs only 8×8 or 16×16 multipliers. Therefore, it is necessary to adopt some other methods to achieve convolution processing units implemented on FPGA.
The existing literature on convolution processing units implemented on FPGA is extensive and focuses mainly on multiplier or adder optimization. That is, accurate intermediate computations are considered to be unnecessary, so approximate operations can be employed to improve performance and energy efficiency further. For example, G. Lentaris and Z. Ebrahimi use optimized approximate logarithmic multipliers in convolution processing units [5,6]. G. Csordas converts the similar weights into a canonical signed digit code, then a multiplier is employed for each code [7]. H. Zhang [8] and C. Lammie [9] employ the Karatsuba algorithm and random calculation to realize approximate multipliers. Besides, approximate adders are also proposed to optimize convolution processing units in [10,11,12]. While in fact, compared with accurate multipliers, despite saving hardware resources, the existing accuracy loss will inevitably reduce the performance of CNN.
Among the other available designs, S. Sarwar proposes an alphabet set multiplier and shares the alphabets with multiple multiplication units [13]. However, a strict requirement exists for the multiplication order, which must be one input multiplied by multiple weights. This special order results in more storage resources being occupied. S. Kala [14], Toan [15], and X. Wang [16] use Winograd to reduce the number of multiplications, but the number of additions is increased instead. Not to say that it has to fulfill the requirement of the order of input data, which may bring out additional latency. Moreover, the methods mentioned above also impose challenges on storage resources, additionally.
In particular, most of the state-of-art designs only considers ASIC-based system. Actually, resulting from the inherent architectural difference between FPGA and ASIC, the performance of the proposed optimization methods will be limited when directly synthesized and implemented on FPGA [17]. In addition, the bulks of the existing accelerators have to be operated according to a strict multiplication and addition order. Considering the possible discontinuous memory address existing in the input data, it may lead to significant latency and increased storage resources.
To address the above limitations, we present a general novel methodology of implementing convolutional process unit for FPGA-based accelerator. To the best of our knowledge, there has been no extensive research on convolution accelerators based on high performance single-cycle accurate multipliers for FPGA-based systems with comparable performance to those based on approximate multipliers.
The main contributions of this work are:
  • Utilizing the 6-input look-up-table (LUT) and associated carry chain of FPGA, two resource-efficient optimization methods of single-cycle radix-4 accurate Booth multiplier are proposed, further supporting the addition operation for the multiply-accumulate functionality.
  • Based on partial product accumulation, a multiply-accumulate structure is proposed without calculating intermediate multiplication and addition results for each input data, which further reduces the hardware utilization effectively and can be expanded to other multiply-accumulate operations.
  • Our proposed convolution accelerator based on optimized multiply-accumulate structure achieves comparable performance and resource utilization to those based on approximate multipliers without accuracy loss.
The rest of this paper is organized as follows. Section 2 presents the problem formulation. The FPGA-targeted optimization methods are described in Section 3. Section 4 provides the experimental results and discussion. Finally, Section 5 concludes the paper.

2. Problem Formulation

A convolution processing unit consists of multipliers and adders. Practically, for the FPGA-based convolutional process unit, multiplier occupies more than 96% of the LUT resources [18]. Therefore, multiplier optimization plays a critical role in high-performance FPGA-based accelerators. Even though state-of-the-art FPGAs provide DSPs for high-performance multiplication, owing to their fixed locations and bit-width, the exhaustive use of DSPs may result in performance degradation. Moreover, the quantity of DSPs is usually insufficient for large scale industrial application. Hence, previous designs have attempted to reduce the multipliers for resource saving by decreasing the partial products and dots [19]. However, when implemented on FPGAs, they may increase the LUT utilization due to the inherent architectural difference.
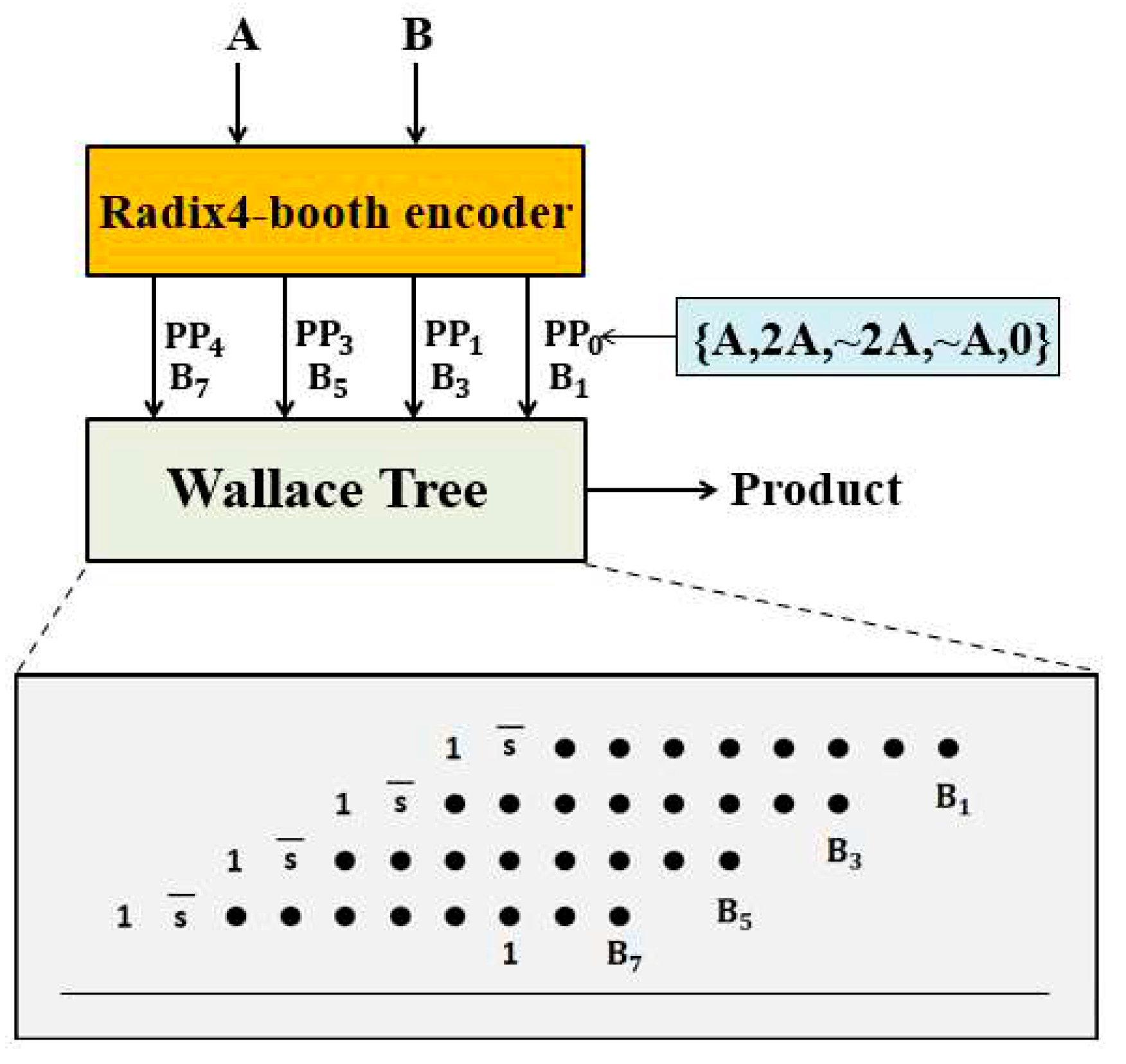
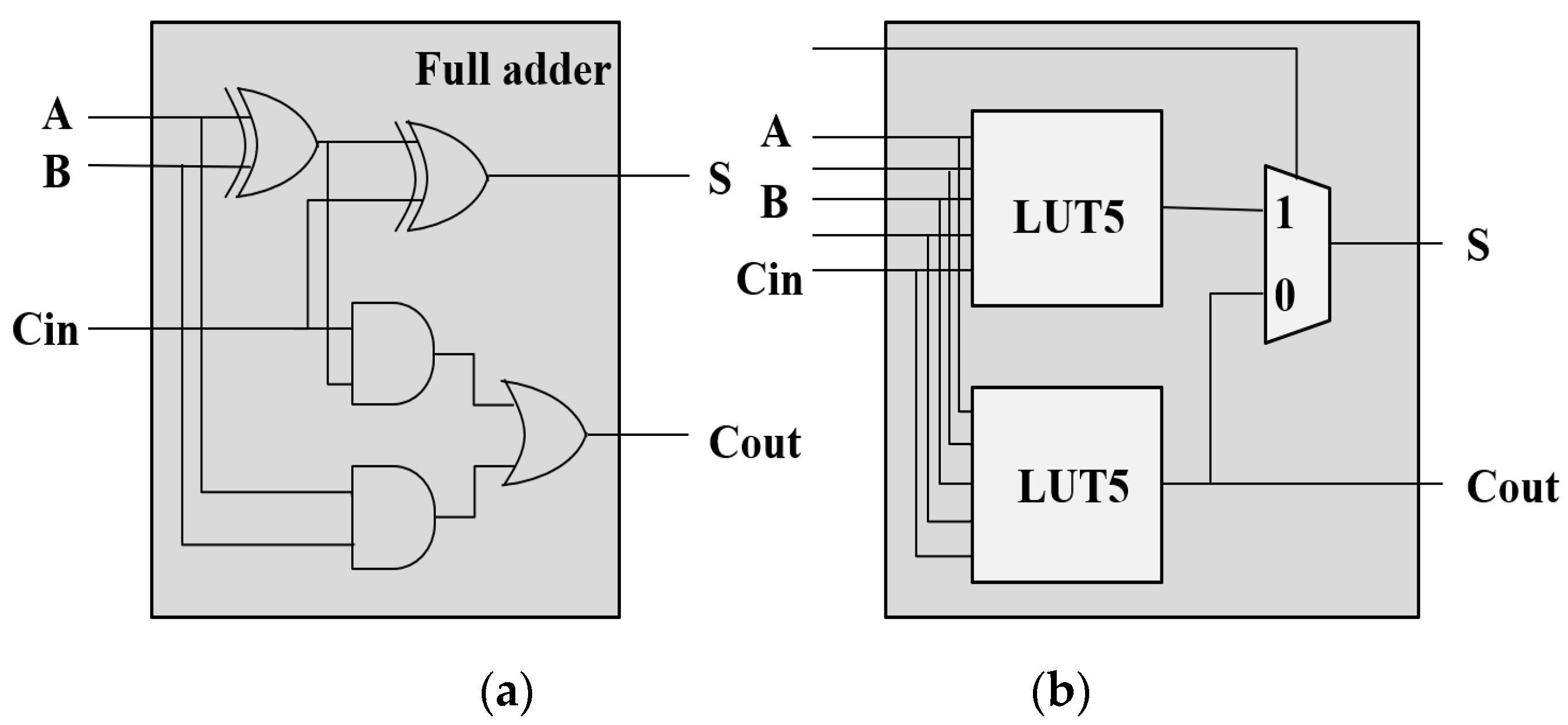
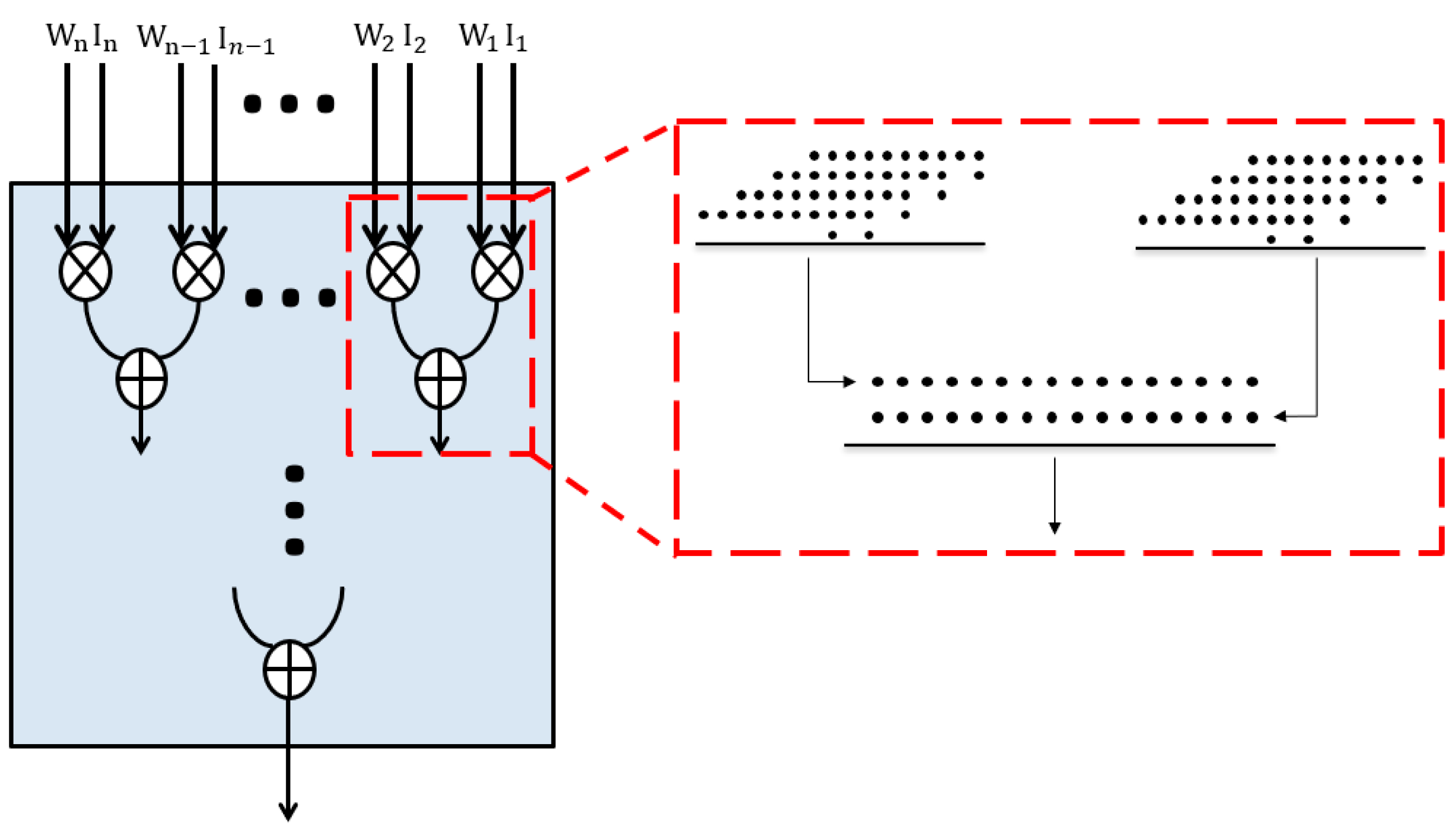
Taking 8×8 radix-4 Booth-Wallace tree multiplier as an example, the partial products can be compressed to 4 and the dots can be reduced to 44 by sign bit extension, which has become the most resource-efficient method [20]. Nevertheless, when synthesized for FPGAs, it actually takes more LUTs, as listed in Table 1. We consider the reason is due to the inherited architectural difference between FPGA and ASIC, together with the operation modes of LUT. That is, the multiplier above is designed for ASIC-based systems, which are at the logic gate level, whereas FPGA-based systems use configurable logic blocks, including LUTs and carry chains. In addition, LUT usually operates in the mode of either 6-input 1-output or 5-input 2-output. A LUT can calculate 5 dots, whereas a full adder calculates 3. When implemented on FPGAs, a full adder will be transformed into a LUT, which makes two ports of a LUT idle, as shown in Figure 1. Considering the dots generated by compression, the number of dots will increase from 44 to 83. Excluding bits with insufficient dots, every five dots will use one more LUT due to the accumulation of idle ports, resulting in a waste of hardware resources. In addition, plenty of carry chains are always idle in application. Therefore, it is available to make full use of carry chains to improve LUT utilization further.
Moreover, the existing methods operate multiplication and addition separately in hardware accelerators. That is, calculating the results of each multiplication and then performing accumulation. However, in each multiplier, the LUTs or carry chains will not be fully used during the final processing due to the fewer dots, which causes unnecessary waste of hardware resources in a multiply-accumulate structure. For further saving resources, the partial products should be accumulated without deriving the multiplication results first.
Therefore, in this paper, we try to investigate the optimization methods based on LUT and carry-chain for the radix-4 Booth multipliers in FPGA-based accelerators by making full use of LUT and idle carry chains. The proposed method makes full use of the ports of LUT and idle resources, thus, achieving a 55% maximum reduction of LUTs, as shown in Table 1. Then an optimized multiply-accumulate structure based on accumulating partial products is proposed, achieving a reduction of LUTs without accuracy loss.

3. Proposed Designs

3.1. Radix-4 Booth multiplier and its sign bit extension

Since the bit-width of the multiplication is the sum of the bit-width of multipliers, the symbol bits should be extended if using Wallace tree for partial product compression. The procedure of the sign bit extension method for Radix-4 Booth multiplier can be separated into the following steps.
Step1. Reverse the sign bit of each partial product.
Step2. Add 1 to the lowest sign bit.
Step3. Add 1 to the previous bit of the sign bit of all partial products.
The structure of the 8×8 radix-4 Booth multiplier using the sign bit expansion method is shown in Figure 2. However, when this multiplier is directly implemented on FPGA, it will cause unnecessary waste of resources due to inherent architectural differences.

3.2. LUT-based optimization of radix-4 Booth multiplier

The mentioned radix-4 Booth multiplier uses logic gates as basic units, while FPGA-based computational blocks are configurable logic blocks, mainly including LUTs and carry chains. LUT corresponds to inputs and outputs by storing a truth table, and carry chains are used to perform addition. Therefore, two optimization methods can be proposed for the FPGA-based convolution processing units.
When the radix-4 Booth multipliers are directly implemented on FPGA, lots of 3-input/4-input 1-output LUTs will be generated, whereas a fully utilized LUT is usually 5-input 2-output or 6-input 1-output. Therefore, using the 3-2 compression of the traditional Wallace tree will cause many idle ports. In radix-4 Booth multipliers, the demand for output ports is always higher than the input ones for the multi-input structure of LUT. Therefore, full utilization of the output ports should be primarily taken into consideration during implementation. Taking the 8×8 radix-4 Booth multiplier as an example, we treat all partial products as inputs, multiplication results as outputs, and middle carry as both inputs and outputs. The number of inputs and outputs are 126 and 57, respectively, which approximates 5:2 rather than 6:1. In this case, the demand for output ports is always higher than the input ones for the multi-input structure of LUT.
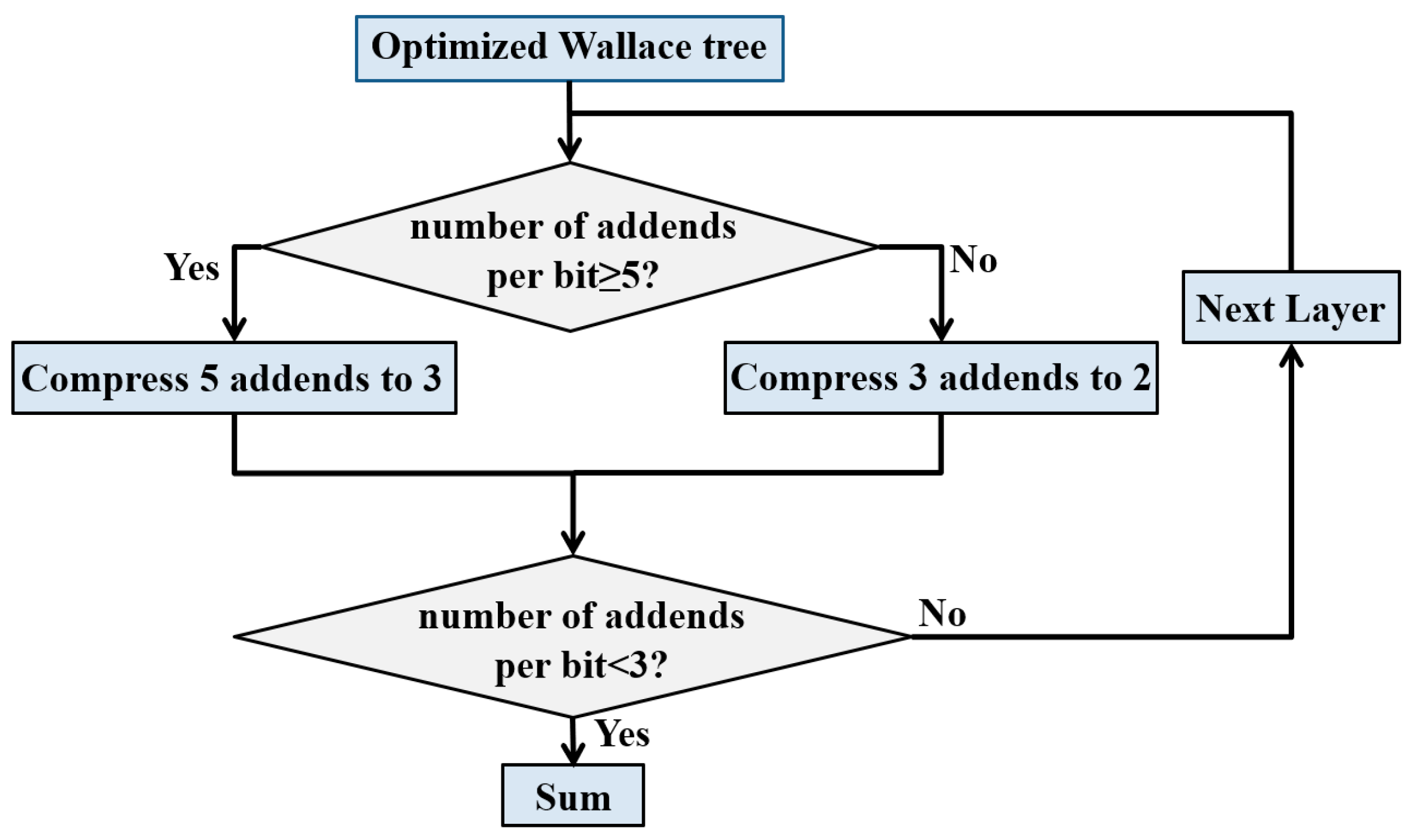
The following optimization method is proposed for Wallace tree, as shown in Figure 3. For each parallel bit, if the number of addends is less than 5, they are compressed according to the previous Wallace tree. Otherwise, every 5 addends are compressed to 3. Loop this operation until the addend of each bit is less than 3.

3.3. Carry-chain-based optimization of radix-4 Booth multiplier

For each configurable logic unit of FPGA, the ratio of 6-input LUT and 8-bit carry chain is 8:1. However, during the Vivado synthesis procedure, low-bit-width additions (less than 16 bits) are implemented using LUT resources prior to carry chains. Moreover, the resource requirement for carry chains is commonly very low. Consequently, it is possible to improve LUT utilization further by using surplus carry chain resources on FPGA.
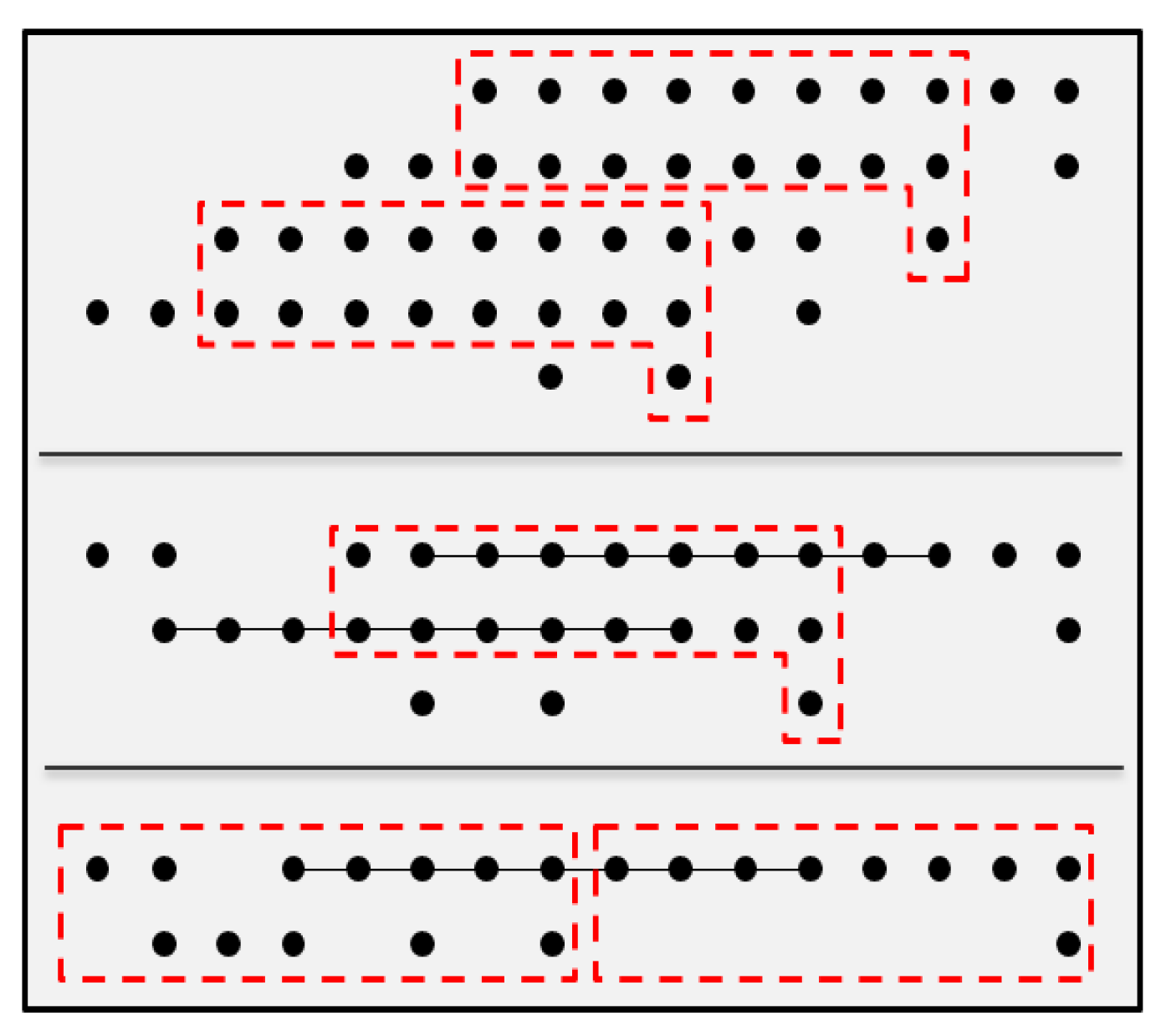
For the carry-chain-based optimization method, a partial product reduction tree is proposed, aiming to fully utilize the carry chains. Using an 8-bit carry chain, two 8-bit numbers and a carry bit will be compressed into a 9-bit number. This operation is repeated until the addends of each bit are less than 3. The result then can be obtained by adding the remaining addends. Different from other multipliers, a sign bit is left at the lowest bit of each partial product of the radix-4 Booth multiplier. It meets the requirement that there should be a carry bit in a low bit number so that the carry chain can be fully used. Figure 4 shows the optimization of the 8×8 radix-4 Booth multiplier. Compared with LUT compression using optimized Wallace tree, the carry chain compression has the same height, which means the latency is mainly related to the device itself.
To further study the latency, we implemented 10 LUTs and 8-bit carry chains on FPGA. The average delays of LUTs and 8-bit carry chains are 0.179ns and 0.209ns, respectively. In spite of an increase of 16% delay, using carry chains to compress partial products can effectively reduce the LUT cost.

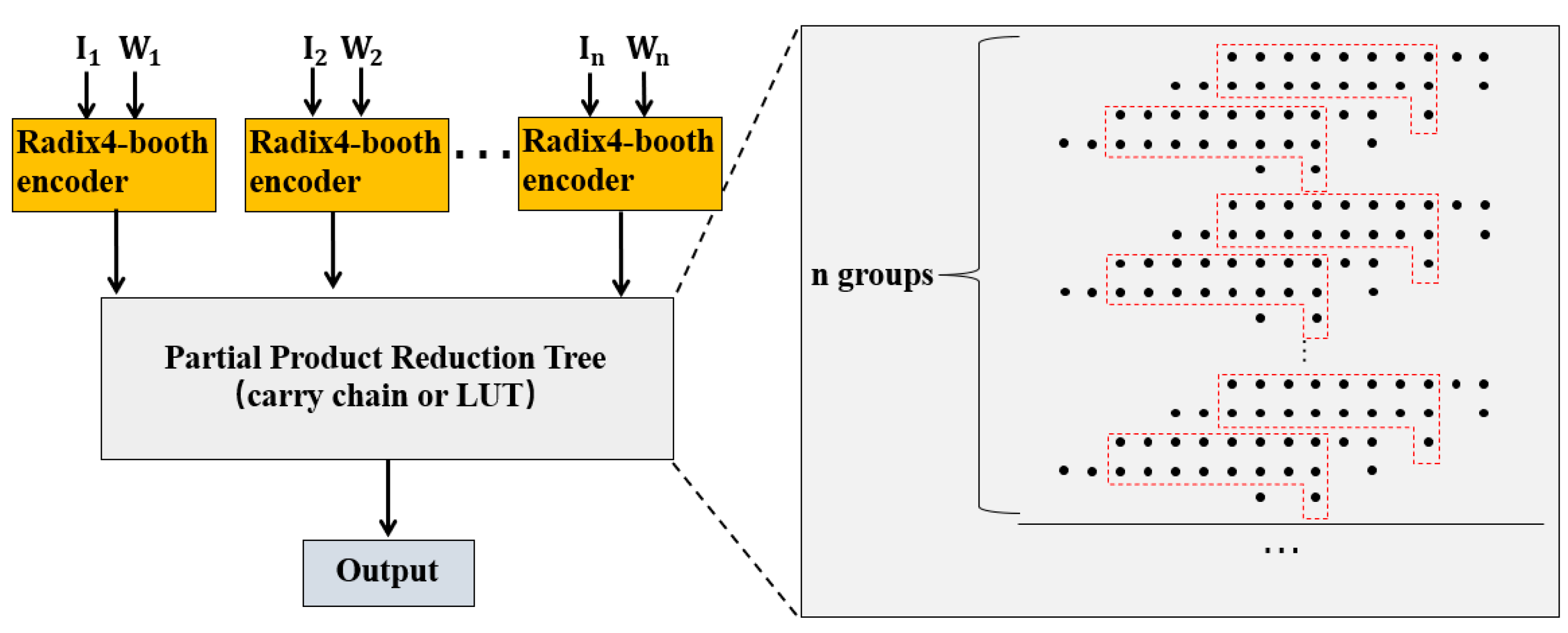
3.4. Partial product accumulation based optimization of convolutional process unit

The convolution calculation can be described as a large number of parallel multiply-accumulate operations. Due to the resource limitation of FPGA, most of the convolution process units have to execute the multiplication and addition of each channel and window individually in one clock cycle. As shown in Figure 5, in traditional convolution processing units, after computing each product of the characteristic graph and weight, the calculated results are accumulated by the adder. It means that assuming an n×n convolution kernel, we have to use n×n single-circle multipliers and n×n-1 adders in a convolutional process unit. To further save the resources, LUT utilization can be optimized by a direct partial product accumulation. That is, instead of calculating and adding the result of each multiplier successively, we can calculate all partial products and achieve accumulation by the same partial product reduction tree, as shown in Figure 6.
It is worthy of noticing that, different from the previous work of a general compressor tree [21], our proposed method first calculates the partial products through the radix-4 Booth encoder. Then, all partial products are accumulated in an optimized partial product reduction tree for compression and calculation. Moreover, the partial product reduction tree is more resource-efficient on accumulating partial products generated by radix-4 Booth encoder.
Besides, in our proposed method, there is no need to derive the intermediate results of each multiplication, the partial products in accumulation are directly sent to the adder, which occupies fewer hardware resources than all previous similar works because the 1s generated by the sign bit extension method in radix-4 booth encoders can be calculated ahead without resources occupation when multiple partial products are accumulated.
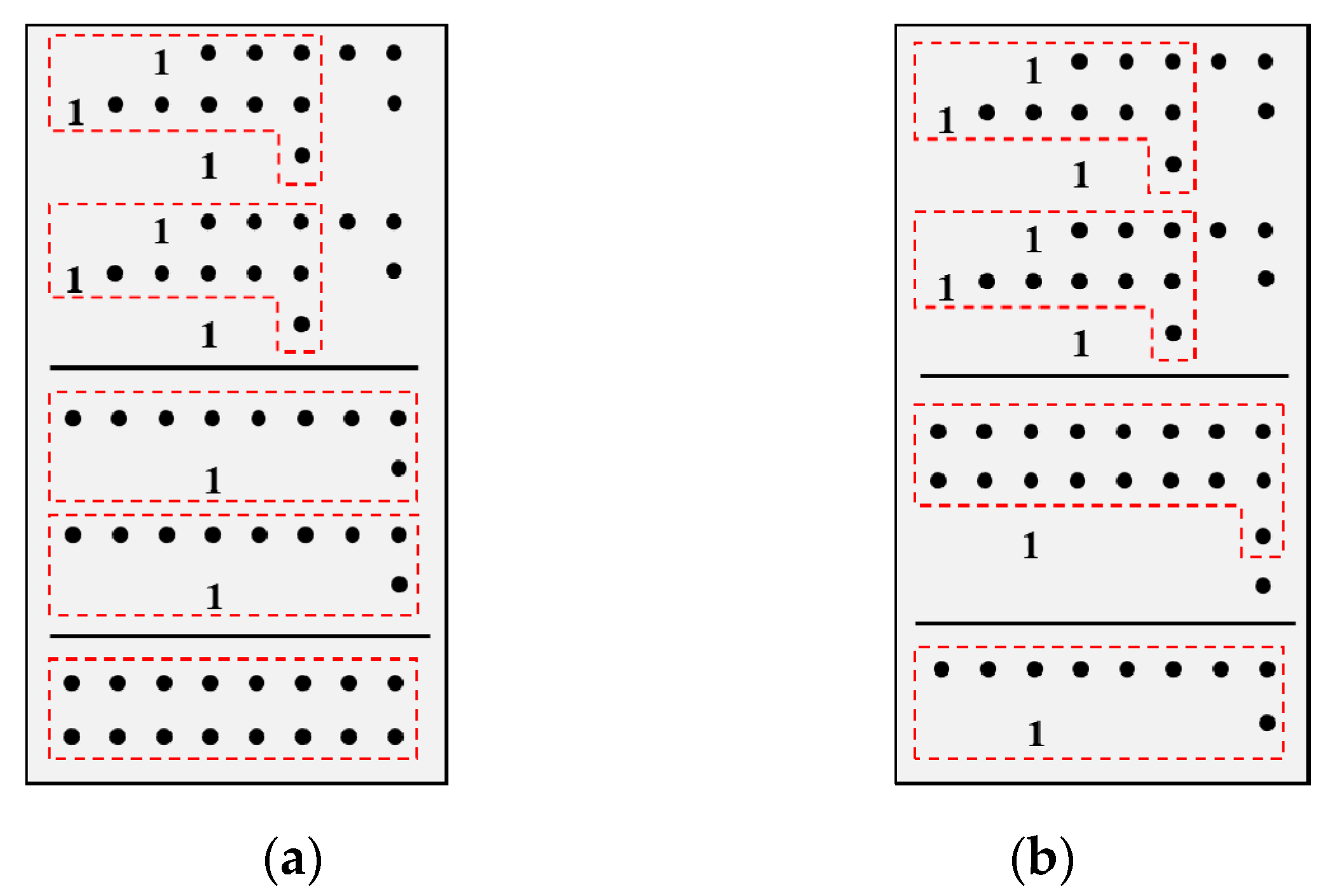
Specifically, suppose there are M multipliers in a convolutional process unit with the bit-width of 4. If calculating the result of each multiplier first, as shown in Figure 7(a), then 3×M-1 carry chains are needed, where 2×M are for each multiplier, and the others are for the final addition. However, if direct accumulating all partial products, there are only 2×M carry chains, as shown in Figure 7(b), which reduces M-1 carry chains. Moreover, the height of partial product reduction tree will not be increased due to its parallelism, neither be the delay. In fact, the proposed method can not only reduce the resource utilization but also be effective for all multiply-accumulate structures without requirement for the input data order, different from the Systolic Array Architecture and Winograd Algorithm.

4. Discussion

4.1. Experimental Setup

The proposed designs have been implemented in Verilog HDL and synthesized by Xilinx Vivado 2021.2 for the Virtex-7 xczu3cg-sfvc784-1-e FPGA. For calculating their critical path delay (CPD), power, and hardware resource usage, the Vivado simulator and power analyzer tools are employed. In order to evaluate the effectiveness of our proposed designs, we have implemented the present multipliers [17,22,23,24,25] on our FPGA. Further, our proposed multipliers have been implemented for our proposed multiply-accumulate structure, then applied to image processing and CNN for comparison.

4.2. Implementation results of optimized multiplier

Table 2 compares the resource utilization, CPD, and energy consumption of our proposed multipliers with other typical multipliers of different bit-width. It is demonstrated that our proposed multipliers are more resource-efficient than the others across different bit-width without obvious performance degradation on CPD and energy consumption. Taking 8×8 multipliers as an example, the LUT utilization is reduced by 18.18% and 46.75% with our proposed multipliers to the radix-4 Booth multiplier using sign-bit expansion, respectively. Even compared with the approximate multiplier [17], our proposed carry-chain-based optimized multiplier still exhibits fewer LUT utilization.
It is worth noting that although the proposed multipliers demonstrate an increase in CPD compared with the Vivado IP, it is still at an acceptable level with a significant reduction of LUT and 8-bit carry chain utilization. It is due to the Booth coding, which in spite of reducing the resource consumption, inevitably leads to the delay.
In addition, our proposed carry-chain-based optimized multipliers can further improve the LUT utilization and energy consumption for the reason that using carry chains can reduce logical flipping effectively. It delivers better PDP improvements of 38.67% to the previous best FPGA-targeted design [22]. Compared to the speed-optimized Vivado IP, the proposed multiplier is higher on PDP because of the latency. However, we think the increased latency is acceptable with a 43% reduction in LUT utilization. To highlight the efficiency of our proposed multipliers, Figure 8 illustrates the product of normalized values of total utilized LUTs and PDP for each design across different bit-width. All values have been normalized to the corresponding values of Vivado area optimized multiplier IP. A smaller value of the product (LUTs×PDP) presents an implementation with better performance. Although for simple applications, the proposed carry-chain-based optimized multiplier exhibits similar performance to Vivado speed optimized IP, it has significant advantages for larger scale designs. Even compared with the approximate multiplier [17,25], there exists a noticeable improvement of LUTs with our proposed carry-chain-based optimized multipliers without performance degradation.

4.3. Implementation results of multiply-accumulate structure

For hardware resource saving, the proposed carry-chain-based optimized multiplier is employed. For the 8-bit multiplication, the method of accumulating two partial products can reduce 10 LUTs and 2 8-bit carry chains.
To verify the effectiveness of our proposed method, we implement it to the convolutional process unit with the bit-width of 8 and convolution kernel size of 3×3. Table 3 lists the comparison results of our method with DSPs and approximate multipliers [17,25]. Compared with them, our proposed multiplier and multiply-accumulate structure reduce LUT by 43.9%. For further verifying, Table 4 lists the comparison results of our proposed convolution processing unit and the others with the bit-width of 16 and convolution kernel size of 4×4, which is not commonly used, implementing only for comparison. It should be noted that although the bit-width and multiplication times are the same, the implemented FPGAs are different, which means some important performances are not comparable, such as frequency and power. However, the architectures of the present mainstream Xilinx FPGAs are similar, so we directly compare the utilization of hardware resources. In fact, for most existing convolutional process units of the hardware accelerator, the realization of multipliers and multiply-accumulate structures are either ignored or just optimized by ASIC-based multipliers, which easily leads to performance degradation. Compared with them, our proposed multiplier and multiply-accumulate structure reduce LUT by 22.7%.
For the high-level application environment, we apply the multiply-accumulate structure to Discrete Cosine Transform (DCT) in JPEG compression. For each 8×8 block, the DCT is employed as two matrix multiplications of sizes 8×8 thus requires 1024 multiplications and 896 additions. As shown in Figure 9(a), the input image with bit-width of 16 is from MIT Adobe FiveK dataset. The peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) are used to evaluate the quality of the output images. Figure 9 and Table 5 indicate that even compared with the ones using approximate multipliers [17,25], our proposed structure can obviously reduce the LUT utilization without loss of accuracy.
We also implement LeNet shown in Table 6 with two convolutional layers on FPGA, to realize the target recognition of 10 types of common objects by Cifar-10 Dataset. For hardware resource reduction, the 8-bit fixed-point quantization is used, resulting in an accuracy of 69.32%. The implementation results of using our proposed multiply-accumulate structure and directly using DSPs are listed in Table 7. It shows that when dealing with multiplier-intensive applications, our proposed method can promote maximum clock frequency and save 58% of the DSP resources by only increasing 12% LUT.

5. Conclusion

In this paper, a design methodology for convolution accelerator has been presented. Based on LUTs and carry chains on FPGA, we first introduced two types of resource-efficient optimization of radix-4 Booth’s multiplier. Then a generic multiply-accumulate structure is proposed, which directly accumulates the partial products without intermediate multiplication and addition results. The proposed methods are implementable on the Xilinx FPGA Virtex-7 xczu3cg-sfvc784-1-e. Compared to Vivado area optimized multiplier IP, the optimized multipliers achieve a maximum 51% reduction in area (LUT). The proposed multiply-accumulate structure achieves a maximum of 22.7% LUT reduction compared to the existing methods. For verifying our proposed convolutional process unit, we finally presented high-level applications by implementing DCT transformer and LeNet on FPGA. In DCT transformer, our proposed method reduces LUT utilization by 12% without accuracy loss, while in LeNet on FPGA, our proposed convolution accelerator saves 58% of the DSP resources.

Author Contributions

Conceptualization, Y.M. and Q.X.; methodology, Q.X.; validation, Q.X. and Z.S.; formal analysis, Y.M. and Q.X.; investigation, Y.M. and Q.X.; resources, Q.X.; data curation, Z.S.; writing—original draft preparation, Q.X.; writing—review and editing, Y.M., Q.X. and Z.S.; visualization, Z.S.; supervision, Y.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded in part by the National Science and Technology Major Project under Grant J2019-I-0019-0018; in part by the Aeronautical Science Foundation of China under Grant 20200013063001; and in part by the Science and Technology Innovation Foundation of Dalian under Grant 2021JJ12GX012.

Data Availability Statement

The Cifar-10 dataset is available on http://www.cs.toronto.edu/~kriz/cifar.html (access on 21 July 2023) and the MIT Adobe FiveK dataset is available on https://data.csail.mit.edu/graphics/fivek (access on 21 July 2023).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Mittal, S. A survey of FPGA-based accelerators for convolutional neural networks, Neural Comput. Appl. 2020, 32, 1109–1139. [Google Scholar]
  2. Wang, D.; Xu, K.; Guo, J.; Ghiasi, S. DSP-efficient hardware acceleration of convolutional neural network inference on FPGAs. IEEE Trans. Comput-Aided Des. Integr. Circuits Syst. 2020, 39, 4867–4880. [Google Scholar]
  3. Ullah, S.; Sripadra, S.; Murthy, J.; Kumar, A. SMApproxLib: Library of FPGA-based approximate multipliers. In Proceedings of the IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 24-28 June 2018; pp. 1–6. [Google Scholar]
  4. Xilinx LogiCORE IP v12.0. Available online: https://www.xilinx.com/support/documentation/ip_documentation/mult_gen/v12_0/pg108- mult-gen.pdf. (accessed on 21 July 2023).
  5. Lentaris, G. Combining arithmetic approximation techniques for improved CNN circuit design. In Proceedings of the IEEE International Conference on Electronics, Circuits and Systems (ICECS), Glasgow, UK, 23-25 November 2020; p. 9294869. [Google Scholar]
  6. Ebrahimi, Z.; Ullah, S.; Kumar, A. LeAp: Leading-one detection-based softcore approximate multipliers with tunable accuracy. In Proceedings of the Asia and South Pacific Design Automation Conference (ASP-DAC), Beijing, China, 13-16 January 2020; pp. 605–610. [Google Scholar]
  7. Csordás, G.; Fehér, B.; Kovácsházy, T. Application of bit-serial arithmetic units for FPGA implementation of convolutional neural networks. In Proceedings of the International Carpathian Control Conference (ICCC), Szilvasvarad, Hungary, 28-31 May 2018; pp. 322–327. [Google Scholar]
  8. Zhang, H.; Xiao, H.; Qu, H.; Ko, S. FPGA-based approximate multiplier for efficient neural computation. In Proceedings of the IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia), Gangwon, South Korea, 1-3 November 2021; pp. 1–4. [Google Scholar]
  9. Lammie, C.; Azghadi, M. Stochastic computing for low-power and high-speed deep learning on FPGA. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26-29 May 2019; pp. 1–5. [Google Scholar]
  10. Thamizharasan, V.; Kasthuri, N. High-Speed Hybrid Multiplier Design Using a Hybrid Adder with FPGA Implementation. IETE J. Res. 2021, 69, 2301–2309. [Google Scholar]
  11. Balasubramanian, P.; Nayar, R.; Maskell, D. L. Digital Image Blending Using Inaccurate Addition. Electronics 2022, 11, 3095. [Google Scholar] [CrossRef]
  12. Kumar, S. R.; Balasubramanian, P.; Reddy, R. Optimized Fault-Tolerant Adder Design Using Error Analysis. J. Circuits Syst. Comput. 2023, 32, 6. [Google Scholar]
  13. Sarwar, S.; Venkataramani, S. A. Raghunathan and K. Roy, Multiplier-less artificial neurons exploiting error resiliency for energy-efficient neural computing, In Proceedings of Design, Automation and Test in Europe Conference and Exhibition (DATE), Dresden, Germany, 14-18 March 2016, pp. 145-150. Dresden, Germany, 14-18 March 2016, 145–150.
  14. Kala, S.; Jose, B.; Mathew, J.; Nalesh, S. High-performance CNN accelerator on FPGA using unified Winograd-GEMM architecture. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2019, 27, 2816–2828. [Google Scholar] [CrossRef]
  15. Toan, N. V.; Lee, J. G. FPGA-based multi-Level approximate multipliers for high-performance error-resilient applications. IEEE Access 2020, 8, 25481–25497. [Google Scholar] [CrossRef]
  16. Wang, X.; Wang, C.; Cao, J.; Gong, L,; WinoNN: Optimizing FPGA-Based Convolutional Neural Network Accelerators Using Sparse Winograd Algorithm, IEEE Trans. Comput-Aided Des. Integr. Circuits Syst., 2020, 39, 4290-4302.
  17. Ullah, S.; Rehman, S.; Shafique, M.; Kumar, A.; High-performance accurate and approximate multipliers for FPGA-based hardware accelerators, IEEE Trans. Comput.-Aided Design Integr. Circuits Syst., 2022, 41, 211-224.
  18. Farrukh, F. Power efficient tiny Yolo CNN using reduced hardware resources based on Booth multiplier and Wallace tree adders. IEEE Open J. Circuits Syst. 2020, 1, 76–87. [Google Scholar] [CrossRef]
  19. Rooban, S. Implementation of 128-bit radix-4 booth multiplier. In Proceedings of the International Conference of Computer Communication and Informatics (ICCCI), Coimbatore, India, 27-29 January 2021; pp. 1–7. [Google Scholar]
  20. Chang, Y.; Cheng, Y.; Liao, S.; Hsiao, C. A low power radix-4 booth multiplier with pre-encoded mechanism. IEEE Access 2020, 8, 114842–114853. [Google Scholar] [CrossRef]
  21. Kumm, M.; Kappauf, J. Advanced compressor tree synthesis for FPGAs. IEEE Trans. Comput. 2018, 67, 1078–1091. [Google Scholar] [CrossRef]
  22. Ullah, S.; Nguyen, T.; Kumar, A. Energy-efficient low-latency signed multiplier for FPGA-based hardware accelerators. IEEE Emded. Syst. Lett. 2021, 13, 41–44. [Google Scholar] [CrossRef]
  23. Ullah, S. Area-optimized low-latency approximate multipliers for FPGA-based hardware accelerators. In Proceedings of the IEEE Design Automation Conference (DAC), San Francisco, USA, 24-28 June 2018; pp. 1–6. [Google Scholar]
  24. Kumm, M.; Abbas, S.; Zipf, P. An efficient softcore multiplier architecture for Xilinx FPGAs. In Proceedings of the Symposium on Computer Arithmetic (ARITH), Lyon, France, 22-24 June 2015; pp. 18–25. [Google Scholar]
  25. Waris, H.; Wang, C.; Liu, W.; Lombardi, F. AxBMs: Approximate radix-8 booth multipliers for high-performance FPGA-based accelerators. IEEE Trans. Circuits Syst. Express Briefs 2021, 68, 1566–1570. [Google Scholar] [CrossRef]
  26. Yan, S. An FPGA-based MobileNet accelerator considering network structure characteristics. In Proceedings of the International Conference on Field-Programmable Logic and Applications (FPL), Virtual, Dresden, Germany, 30 August 2021; pp. 17–23. [Google Scholar]
Preprints 80402 g001
Figure 1. Full adder deployment (a) Logic gates; (b) LUT.
Figure 1. Full adder deployment (a) Logic gates; (b) LUT.
Preprints 80402 g001
Preprints 80402 g002
Figure 2. 8×8 Radix-4 Booth multiplier (S represents sign bit of partial products).
Figure 2. 8×8 Radix-4 Booth multiplier (S represents sign bit of partial products).
Preprints 80402 g002
Preprints 80402 g003
Figure 3. LUT-based optimization for Wallace tree.
Figure 3. LUT-based optimization for Wallace tree.
Preprints 80402 g003
Preprints 80402 g004
Figure 4. Optimization of 8×8 radix-4 Booth multiplier, a red box represents an 8-bit carry chain.
Figure 4. Optimization of 8×8 radix-4 Booth multiplier, a red box represents an 8-bit carry chain.
Preprints 80402 g004
Preprints 80402 g005
Figure 5. Traditional structure of convolutional process unit.
Figure 5. Traditional structure of convolutional process unit.
Preprints 80402 g005
Preprints 80402 g006
Figure 6. The optimized multiply-accumulate structure based on partial product accumulation.
Figure 6. The optimized multiply-accumulate structure based on partial product accumulation.
Preprints 80402 g006
Preprints 80402 g007
Figure 7. Strategy comparison, a red box represents an 8-bit carry chain: (a) Calculating the result of multipliers first; (b) Accumulating partial products.
Figure 7. Strategy comparison, a red box represents an 8-bit carry chain: (a) Calculating the result of multipliers first; (b) Accumulating partial products.
Preprints 80402 g007
Preprints 80402 g008
Figure 8. Comparison results of multipliers: (a) Normalized performance metrics (LUT×PDP); (b) Normalized LUT.
Figure 8. Comparison results of multipliers: (a) Normalized performance metrics (LUT×PDP); (b) Normalized LUT.
Preprints 80402 g008
Preprints 80402 g009
Figure 9. Image compression results: (a)Input image; (b)Our proposed method; (c)Approximate multiplier [17]; (d)Approximate multiplier [25].
Figure 9. Image compression results: (a)Input image; (b)Our proposed method; (c)Approximate multiplier [17]; (d)Approximate multiplier [25].
Preprints 80402 g009
Table 1. LUT utilization of Multipliers (8×8).
Table 1. LUT utilization of Multipliers (8×8).
Designs LUT
Unoptimized 92
Sign bit extension 77
Proposed (LUT) 63
Proposed (carry-chain) 41
Table 2. Implementation Results of Multipliers (Shaded Row: approximate design).
Table 2. Implementation Results of Multipliers (Shaded Row: approximate design).
Design 8×8 16×16
LUT Carry Chain Delay
(ns)		 Power
(mW)		 PDP
(pJ)		 LUT Carry Chain Delay
(ns)		 Power(mW) PDP
(pJ)
Sign expansion 77 0 3.011 15.8 47.5 279 0 3.583 56.8 203.5
Proposed(LUT) 63 0 2.774 16.3 45.1 256 0 3.296 55.1 181.6
Proposed(Carry chain) 41 5 2.530 7.2 18.1 167 18 2.782 29.2 81.3
Vivado IP area 85 7 1.967 10.8 21.2 324 26 2.177 47.0 102.3
Vivado IP speed 73 14 1.602 8.3 13.3 281 45 1.922 31.7 60.83
T. Nguyen [22] 69 2 2.927 10.1 29.5 263 4 3.323 41.8 139
S. Ullah [23] 81 0 2.954 13.8 40.7 296 0 3.738 48.3 180.7
S. Abbas [24] 73 2 3.037 15.1 45.9 270 4 3.642 67.6 246.2
S. Rehman[17] 56 2 1.980 8.9 17.7 240 4 2.380 42.4 101
H. Waris [25] 60 2 2.140 6.6 14.1 194 4 2.413 28.6 69.1
Table 3. Implementation Results of 3×3 convolutional process units (including approximate multipliers).
Table 3. Implementation Results of 3×3 convolutional process units (including approximate multipliers).
Designs LUT DSP Freq.(Mhz) Power(mW)
Proposed 362 0 395 71
DSP blocks 68 9 400 81
Rehman [17] 570 0 397 89
H. Waris [25] 604 0 383 69
Table 4. Implementation Results of 4×4 convolutional process units.
Table 4. Implementation Results of 4×4 convolutional process units.
Designs LUT DSP Freq.(Mhz) Power(mW)
Proposed 2792 0 342 154
R. Cai [26] 5342 0 330 293
DSP blocks 158 16 177 226
F. Farrukh [18] 3612 0 533 176
Table 5. Comparison Results of DCT Transformation.
Table 5. Comparison Results of DCT Transformation.
Design LUT DSP Freq.(Mhz) Power(W) PSNR SSIM
Proposed 9688 0 379 1.144 ∞ 1
DSP blocks 608 64 383 1.181 ∞ 1
Rehman [17] 11025 0 393 1.296 56.17 0.990
H. Waris [25] 10870 0 387 1.004 52.58 0.974
Table 6. LeNet architecture on FPGA.
Table 6. LeNet architecture on FPGA.
Layer Input Filter Size Stride Output
Conv1 32×32×3 16 3×3 1 30×30×16
Conv2 30×30×16 16 3×3 1 28×28×16
Max pooling1 28×28×16 N/A 2×2 2 14×14×16
Conv3 14×14×16 32 3×3 1 12×12×32
Conv4 12×12×32 32 3×3 1 10×10×32
Max pooling2 10×10×32 N/A 2×2 2 5×5×32
Full connect1 800 N/A N/A N/A 120
Full connect2 120 N/A N/A N/A 84
Table 7. Comparison Results of DCT Transformation.
Table 7. Comparison Results of DCT Transformation.
Design LUT utilization DSP utilization Freq.(Mhz)
Proposed 23887(34%) 0(0%) 175
DSP blocks 15695(22%) 211(58%) 173
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated