Prerpints.org logo
Preprint
Article

Recommended Separation Distances for 1.3 Ammunition and Explosives

Altmetrics

Downloads

191

Views

54

Comments

1

A peer-reviewed article of this preprint also exists.

supplementary.zip (3.64KB )

This version is not peer-reviewed

Submitted:

29 July 2023

Posted:

02 August 2023

You are already at the latest version

Alerts
Abstract
Separation Distances are used throughout the world to protect people and assets from the potential hazardous effects from propellants, explosives, and pyrotechnics. The current separation distances for Hazard Division (HD) 1.3 substances and articles used in the United States, in some cases, may not adequately protect against the effects from heat flux and debris when those substances and articles are ignited in a confined structure. Multiple tests in such a confined scenario with HD 1.3 substances have shown that the heat flux and debris hazards could result in injury at distances beyond the current specified explosives safety separation distance (ESSD). Herein are recommended ESSD’s for confined as well as unconfined HD 1.3 articles and substances based on the analysis of hundreds of tests. Recommended ESSD’s include a smaller value for unconfined quantities less than 145 kilograms and ESSD’s that are consistent with NATO distances for confined substances and articles.
Keywords: 
Subject: Engineering  -   Safety, Risk, Reliability and Quality

1. Introduction

Safe manufacturing and staging of energetic substances and articles requires stand-off distances to reduce the severity of the effects in an ignition scenario. The United States Department of Defense has specified those stand-off distances in the Defense Explosives Safety Regulation 6055.09 (DESR) [1] which is used as the standard throughout the United States. Within that document are stand-off guidelines for the different divisions of energetics such as hazard division (HD) 1.3 that are substances and articles that primarily burn or deflagrate. The stand-off distance is known as the Explosives Safety Separation Distance or ESSD. The ESSD to an inhabited building (i.e. Inhabited Building Distance, IBD) is the distance required to protect structures occupied by people both inside and outside Department of Defense property lines. Protection is for blast pressures and effects, debris or fragments, and thermal hazards.
Multiple scenarios including accidents and experimental test results (see for example References [2,3,4]) have shown that the current HD 1.3 ESSD in the DESR may not adequately protect against the hazards from burning propellants, explosives, or pyrotechnics when in a structure that does not provide adequate venting (i.e. a confined scenario). Boggs, et al. (Ref. [2]) details 80+ accidents; one of which is the Milan 2004 storage magazine event (primarily with HD 1.3 substances) that resulted in a hazardous fragment density beyond the IBD with a large portion of the magazine head wall thrown 1300 feet. Experimental testing of confined scenarios of HD 1.3 M1 propellant inside a small concrete structure result in hazardous fragment densities beyond the IBD for multiple test scenarios as reported with detailed mappings of debris fields and heat flux measurements in Reference [3]. Indeed, the DESR 6055.09 acknowledges significant hazards from confined burning of HD 1.3 substances and articles as called out in Section V1.E8.4.1.3:
Where there is minimal venting and structural containment (extreme confinement), an [explosion] of the HD 1.3 may occur with effects similar to those of an HD 1.1 explosion. For example, HD 1.3 AE is considered HD 1.1 (mass explosion) for QD purposes when stored in underground chambers.
Despite the above quoted language, the specification of "minimal venting" or "structural containment similar to an underground chamber" is insufficient to protect against significant injury from accidental ignition of HD 1.3 substances and articles. Or in other words, the HD 1.3 distances in the widely used DESR do not distinguish between confined or unconfined scenarios and assignment of the much larger HD 1.1 IBD distances as suggested in Section V1.E8.4.1.3 may be over conservative. Over conservative distances can significantly limit the efficient production and storage of explosives, pyrotechnics, and propellants. Herein are recommended explosives safety separation distances for unconfined and confined HD 1.3 ammunition and explosives (AE). The below analysis treats unconfined and confined scenarios of HD 1.3 or primarily burning reactions of energetic substances.
Unconfined burning allows the generated gases to freely exit the immediate area around the substance or article such that the pressure surrounding the substances or articles is not elevated significantly. Confined burning is when the gases generated are not able to freely escape due to insufficient venting. Insufficient venting results in an elevated pressure inside the structure. With elevated pressure, the burn rate increases substantially as the burn rate is a strong function of pressure. With increasing pressure, the hot gases escape through the spaces and vents in the structure with greater speed choking the gaseous flow leading to a likely violent structural failure. Prior to structure failure, effects of those hot gases exiting through the vent extend well beyond a distance for an unconfined of unpressurized burn. With violent structural failure, the hazardous debris generated can approach that from a HD 1.1 event.
Determining if a HD 1.3 burning scenario is unconfined or confined with choked or nearly choked flow requires knowledge of the gas generation rate of the burning HD 1.3 material as well as the size and behavior of the gaseous escape routes (vents). Fast running models such as the Integrated Violence Model can be used to obtain an estimate of the internal pressure during the burning event and subsequent violence (Reference [5]). Analysis of hundreds of scenarios of unconfined and confined HD 1.3 experiments and accidents are presented here with recommended ESSD’s as a function of the net explosive weight (NEW). Additionally, modeling results with the Integrated Violence Model are given. Validated modeling has augmented the experimental and accident data where the scale is very costly in obtaining experimental data.

2. Materials and Methods

An explosives safety separation distance, ESSD, from a substance, article, or structure with reacting material, specifically burning material, is one where an individual would not receive second degree burns and would not be exposed to hazardous debris (<79 Joules) at a density greater than one fragment per six-hundred square feet. These standards are from the Defense Explosive Safety Regulation (DESR) 6055.09 as outlined in Sections V1.E8.2.2.4 and V1.E8.2.2.5 [1].
Determining the safe distance from a HD 1.3 event requires quantifying the heat flux and debris hazards. The debris generated from an event can be quantified and the distance at which the fragment count per 600 square feet decreases below 1 can be found which is typically a calculated value. The heat flux allowed decreases with increasing exposure time per the equation in Section V1.E9.3.1.2 of the DESR 6055 where the allowable exposure time is per Equation 1:
t = 200 · q − 1 . 46
In all the analysis reported on here, the maximum exposure time was assumed to be 20 seconds which corresponds to a heat flux of 4.84 kW/m 2 or 0.116 cal/(cm 2 · sec). If the burn time was longer than 20 seconds, that 4.84 (or 0.116) value was the allowable heat flux to prevent a second degree burn. The 20 second exposure time maximum is a conservative estimate of the duration of time an individual would need to move away from the event. The distance at the allowable heat flux is the explosives safety separation distance (ESSD) for thermal hazards.
The radiative heat flux received from a high temperature substance decreases with increasing distance. The rate of decrease can depend on the receptor’s view factor of the emitting source and the atmospheric conditions between the receptor and the source. That rate of decrease is approximately proportional to the inverse square of the distance and is commonly referred to as the point source model:
q = α / d 2
where α is a constant and d is the distance from the heat source. The point source model is used by first determining the α value from experimental or model data based on the reported values of the heat flux at the given distance d or distances. With the calculated or regressed α value the distance at which the allowable heat flux from Equation 1 could be expected is found. Enumerated, the methodology used here to obtain the ESSD with each set of test data of burning bulk explosive material is as follows:
  • Obtain the max allowable heat flux from the burn time of the test and Equation 1,
  • Estimate the α factor in the point source model given the average heat flux data (assumed constant over the duration) at various distances by taking the 75th inclusive percentile of the q · d 2 values (the 75th percentile is used to better approximate the area of the curve where the allowable heat flux is expected),
  • Using the point source model with the estimated α factor and a view factor of 1, determine the ESSD that corresponds to the max allowable heat flux.
For example, 47.6 pounds of propellant was burned in the open with an average heat flux of 0.733, 0.467, 0.464, 0.212, and 0.166 cal/cm 2 /sec recorded at distances of 3.2, 4.0, 5.0, 6.4 and 8.0 m, respectively (Reference [6]). The burn time in this scenario was 15 seconds. Per equation 1, the allowable heat flux is 0.141 cal/cm 2 /sec. The α value is 10.6E4 cal/sec and the safe distance estimated to be 8.7 m.
Table 1 summarizes the collection of references with test or modeling data compiled for over 100 tests and over 600 data points where the ESSD was calculated. The majority of the test data is from open burning of barrels of propellant as described in References [6,7,8]. Fireworks were also tested in various configurations as reported by TNO in Reference [9]. The compilation of data together with the references and calculations are available in a public github repository (github.com/clint-bg/publicationdata/safeSeparation).
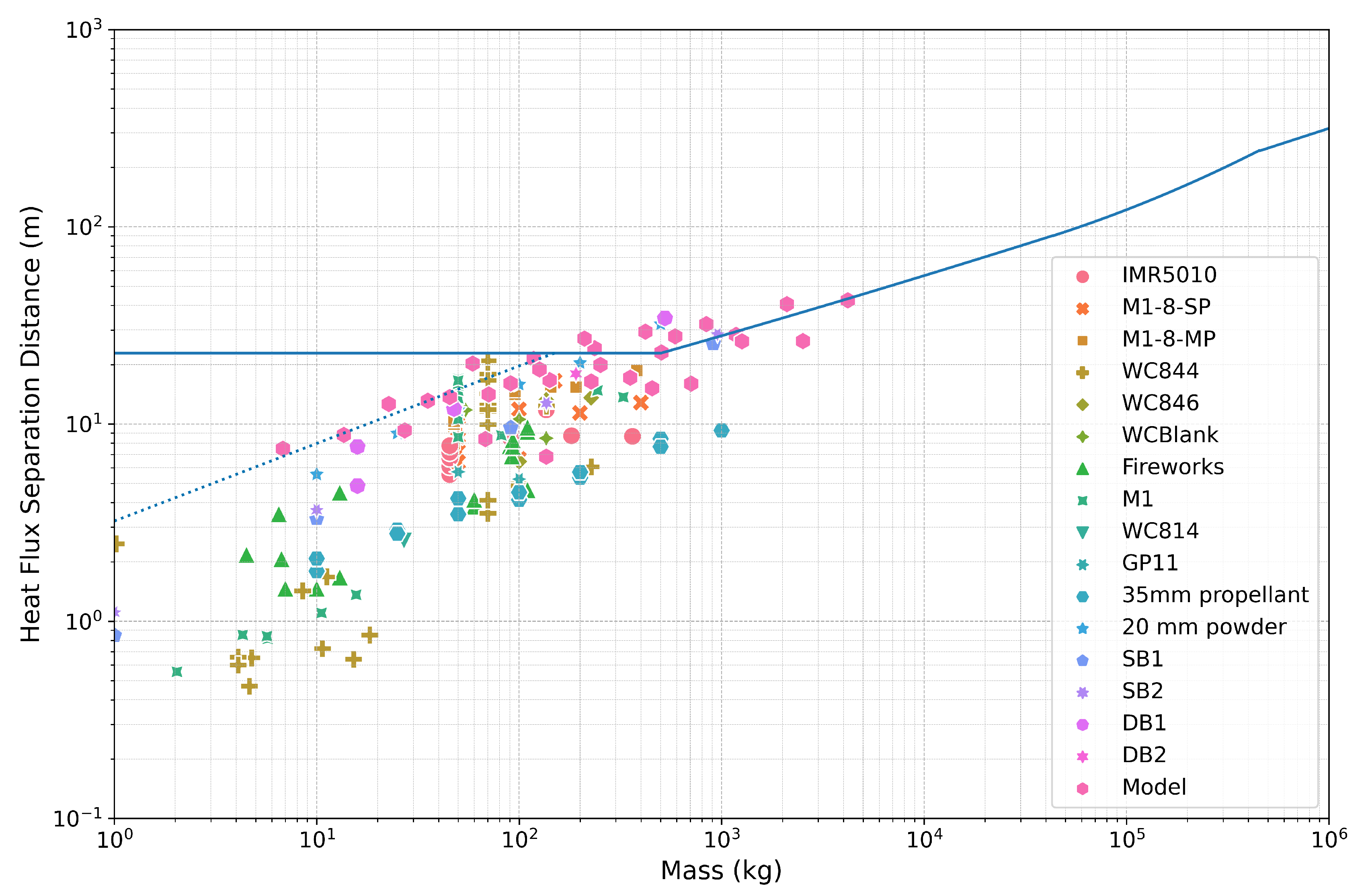
Each test scenario consists of a collection of propellant with a given mass. That mass is then ignited and the resulting heat flux is measured at one or more distances away from the event to quantify the amount of thermal radiation. The heat flux values together with burn times are used to calculate the safe distance that are summarized graphically in Figure 2 and Figure 3.

2.1. Example Unconfined Test Details

Previously unpublished testing of a top ignition of a single barrel of WC814 smokeless powder [8] provides a good example of the testing typical of that performed to determine the heat flux from unconfined scenarios.
A single metal barrel (diameter of 36 cm) with 27 kilograms of WC814 propellant with an open top was ignited at the top of the collection of propellant. Medtherm Schmidt-Boelter Series 64 heat flux gauges were used to measure the heat flux from the burning propellant at distances of 8, 15, 20, and 24 feet from the edge of the barrel oriented in a linear array with the gauges slightly offset so they aren’t shielded by a closer gauge. The height of the gauges coincided with the height of the barrel. The face of the gauges were oriented parallel to the barrel wall. Testing was completed at the Tooele Army Depot. The average heat flux of the 120 second burn was 3.51, 1.38, 0.84, 0.63 kW/m 2 for the above distances, respectively. Those average heat fluxes were then used according to the above method to estimate the safe separation distance to prevent a second degree burn. That distance is estimated to be approximately 8 feet or 2.5 meters. This is a satisfactory result as the allowable heat flux to prevent a second degree burn for that burn duration is 4.84 kW/m 2 which experimentally at 8 feet was less than that value.

2.2. Modeling Details

Modeling of heat flux and debris scenarios with confined and unconfined propellant is beneficial as the cost of completing the modeling study can be significantly less than the experimental scenarios, especially with larger masses of substances. There are many different model types but discussed and used here are empirically-based and theoretically-based fast-running models. Fast running models typically do not resolve the three dimensional or positional dependent result but estimate the average result as a function of time or distance.

2.2.1. Heat flux modeling details

COMSOL Multiphysics [13] is a commercial simulation package that was used to estimate the radiative heat flux from the burning of propellant inside barrels of different diameters. Burn rates modeled ranged from 0.5 to 70 kg/s with various barrel diameters from 36 to 160 cm. The gas flow rate from the top of the barrel was estimated from the burn rate and a gas generation rate for smokeless powder of 30 moles per kilogram. The modeled exit gas temperature from the barrel was 2800K. Other simulation parameters such as the emissivity of the gas were adjusted once to match experimental results for the single- and multi-barrel data in References [6,8]. Once those parameters were adjusted, all that was changed was the burn rate and barrel diameters for other conditions not experimentally tested. The separation distances to prevent 2nd degree burns were also found according to the above described method. 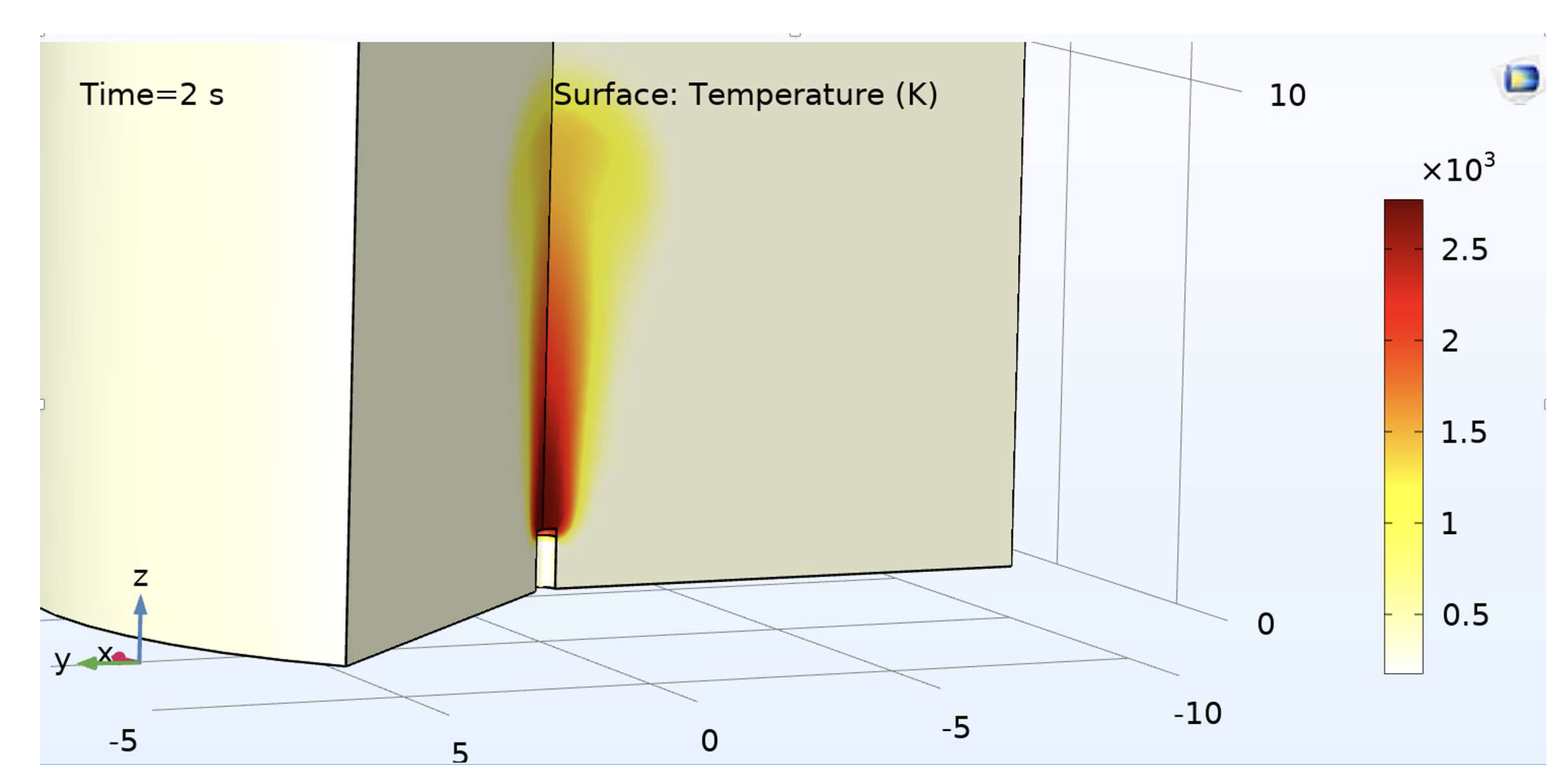Figure 1 shows an example image of one of the model simulations with the temperatures shown. The barrel is white in the image.

2.2.2. Pressure and debris modeling details

The Integrated Violence Model or IVM is a thermochemical based model that tracks the temperature, pressure, composition and enthalpy of gases inside a structure as a function of time as gases enter (from burning propellant) and exit the structure (through dynamic vents). Material and energy balances of the gases inside the structure are solved each explicit time-step with the following assumptions: reversible process, ideal gas, immediate thermal equilibrium in the gas volume, and uniform pressure throughout the control volume. Material and energy balances are specifically:
d n d t = n ˙ i n − n ˙ o u t
d n U d t = n ˙ H i n − n ˙ H + q g e n
where t is time, n is moles, U the internal energy, and H enthalpy. The dot represents a rate and the q g e n term accounts for the afterburning of reactive gases like carbon monoxide or hydrogen. Afterburning was assumed to be 1:1 in that for every mole of gases reacting with oxygen 1 mole of product gases is produced so that no change in the number of moles in the chamber results. This is conservative as usually 2 moles of CO or H2 (common combustion products that participate in afterburning) react with 1 mole of oxygen to form 2 moles of products. Thus 3 reactant moles typically result in 2 product moles. The q g e n term is thus:
q g e n = k a · P C O · P O 2 · H c o m b
where k a is the burn constant (units of mol per second per pressure squared) and P C O is the partial pressure of the reactant gases (like CO) and P O 2 is the partial pressure of the oxidizing gases (like oxygen) and H c o m b is the combustion heat of reacting gases (CO) afterburning with the O2 in the air inside the chamber. Four gases are modeled to represent the many different gases: inert gases (modeled as carbon dioxide), reactive gases (modeled as carbon monoxide), oxidizing gases (modeled as oxygen), and water vapor.
The amount of gas generated by the propellant depends on the burn rate and the gas pressure according to:
n ˙ i n = − g g e n · d m s d t = − k · P P r e f β
where g g e n is the gas generation rate, m s is the mass of the 1.3 substance, k the atmospheric burn rate, P the gas pressure, and β the pressure exponent. Other gas generation models can be used to simulate dust or vapor explosions or burn rates that depend on the mass of substance present.
Gases exit the space through vents of various sizes that can open as a door or as a panel with the exit mass flow rate depending on the Mach number as outlined in gaseous flow equations through orifices such as those outlined in Perry’s Chemical Engineering Handbook Seventh Edition, McGraw-Hill 1997, page 6-22 and 6-23 were used.
Once the derivative of temperature and moles are known (from the above equations) the gaseous temperature and number of moles in the structure can be found by solving those differential equations (solved here with an explicit fourth order Runge-Kutta approach). The pressure can also be found using the ideal gas relationship. Knowing the pressure as a function of time inside the structure can indicate if the venting is sufficient to prevent the pressure from exceeding the structural max pressure to prevent failure.
Inputs to the model include the atmospheric burn rate of the propellant, burn rate pressure exponent, the amount of gas generated, the temperature or enthalpy of the gas generated, the composition of the combustion gases, the total gas volume of the structure, and the vent sizes and associated vent dynamics (weight and opening type such as a door or panel). With these relatively few parameters, accurate pressure versus time results have been obtained for a number of scenarios with burning propellant including small pressure vessels, processing dryers, and concrete structures. Example simulations of the internal pressure and temperature in several different conditions with the Integrated Violence Model are published online here.
In addition to determining if there is sufficient venting to prevent extreme pressures inside the structure, IVM was used to predict the debris throw distances when the pressure does exceed the strength of the structure. The size distribution or number of fragments for each fragment size (normalized by the total mass) was used for concrete as obtained from the Kasun structure testing in Reference [3]. Those debris fragments were then randomly positioned with the masses for each structure quadrant maintained such that the concrete structure was roughly reproduced. The initial direction for each fragments was found from the geometric center of the structure to the initial fragment location. Then those fragments are accelerated with the venting pressurized gases with that acceleration decreasing as the fragments move away from their initial positions. The debris trajectories for each fragment are based on that acceleration and initial trajectory from their position relative to the center of the structure. Drag forces are included as is gravity. The max fragment energy total from all the debris is held to 5 percent of the product of the failure pressure and void volume of the structure. Once the debris fragment strikes the ground, it’s assumed to stay there. With this approach, the fragment distribution after the event was found with surprisingly good agreement with the experimental fragment distributions as reported in [5]. This same approach was used to predict the hazardous fragment ranges for larger, untested concrete structures with results shown in Figure 3, labeled "Debris:Modeling".

3. Results

Results of the literature and modeling analysis of confined and unconfined scenarios are summarized here. The existing HD 1.3 IBD distances are compared to the calculated separation distances to prevent 2nd degree burns and prevent exposure to hazardous fragment densities greater than 1 in 600 square feet. For both confined and unconfined scenarios a new curve is recommended for safe and efficient work with HD 1.3 ammunition and explosives.

3.1. Comparison of ESSD to IBD for Unconfined Scenarios

Table 1 lists literature values of more than 100 open burn tests with HD 1.3 substances and a total of over 600 heat flux measurements. From these data, ESSD’s have been estimated per the above method. The distances for each mass were then compared with the current HD 1.3 IBD separation distances. As can be seen in Figure 2, the current separation distances (blue line) for HD 1.3 substances in the DESR 6055.09 protects against second degree burns when those substances are unconfined as almost all of the points are under that blue line. In the cases where ESSD’s are above the IBD distance, the test data is likely overly conservative as the burn times from those events were not reported in the literature and so were estimated (see Reference [11,22] and the csv file at the github site). Also, for some of the literature values, the peak heat flux is reported but the average heat flux for the duration of the burn was not reported. In those cases the average was assumed to be half the peak value.
The model points shown in Figure 2 are from COMSOL modeling (Ref. [13]) of radiative heat transfer from a source with different diameters and propellant burn rates according to the modeling method described above. Some of the data from the model is slightly above the IBD line for scenarios with high burn rates. Those points are slightly above the line as the gas temperature is likely too high in the model (2800 K); more realistic temperatures are in the range of 1000 - 2100 K (see for example the fireball temperatures from MTV flares of 1700-1800 K as reported in Reference [23]).
The above results and comparison were for unconfined scenarios (open burning). Confined events of HD 1.3 substances and articles can have much more violent results as presented in the next section.

3.2. ESSD for HD 1.3 Confined Scenarios

Confined scenarios where rapidly produced hot gases are not allowed to sufficiently escape can result in a pressurization and violent bursting of the structure. Typically, that violence can scale with the product of the failure pressure and the internal gaseous volume, as is true for pressurized cylinders. Those pressure bursts can generate fragments or debris that can travel long distances in addition to generating a large fireball.
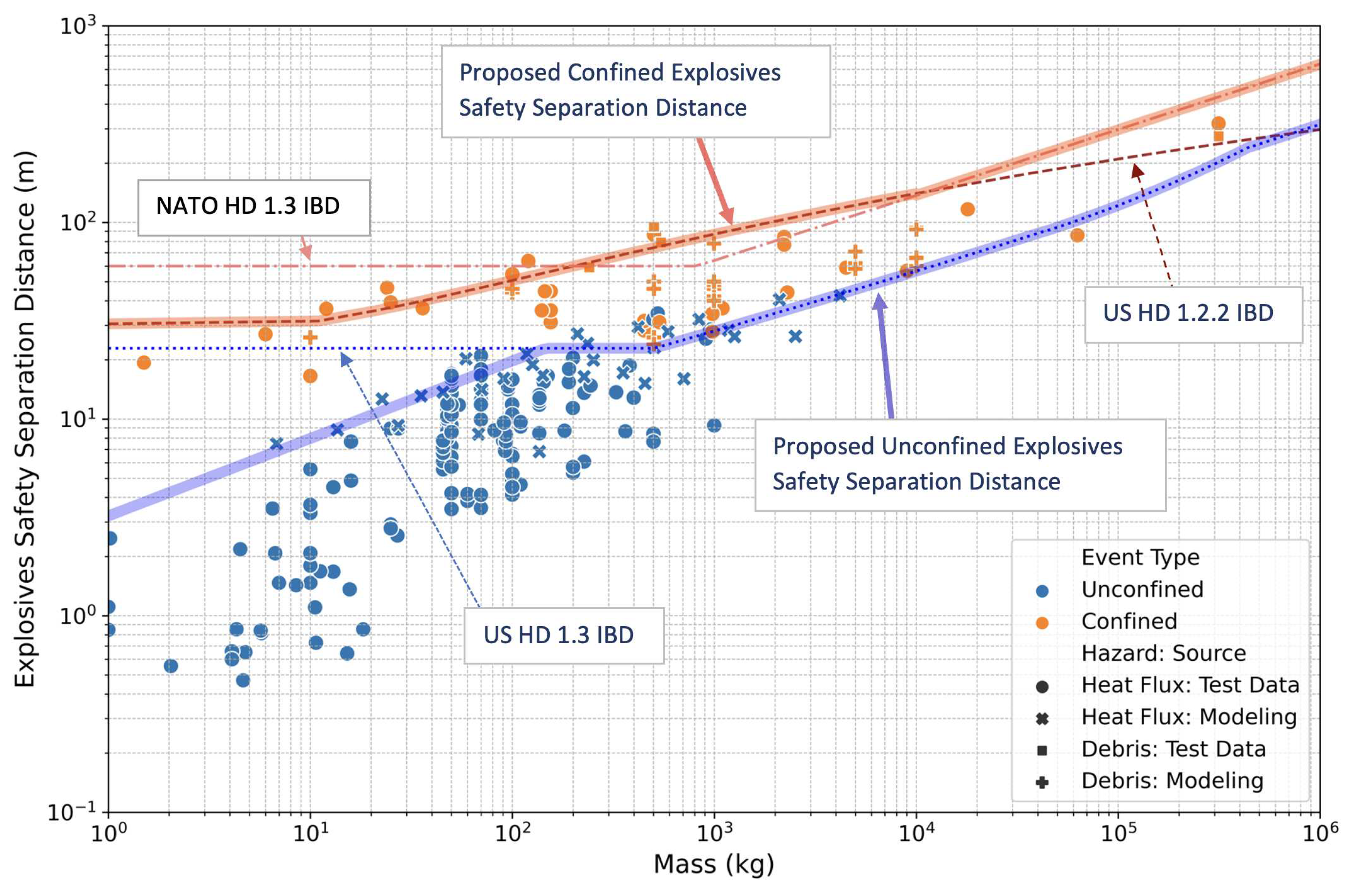
Literature values for multiple confined scenarios are summarized graphically in Figure 3. The confinement where the venting is limited is in concrete structures (References [3,21]), earth covered structures (References [18]), and a very large rocket motor (Reference [19,20]). Some of the test data for the confined scenarios did not have measured heat flux values, but the fireball size was reported or estimated from video. The explosives safety separation distance was then found per the above enumerated steps assuming an average heat flux of 80 kW/m 2 at the fireball distance. The value of 80 kW/m 2 is reported by Dorofeev at the surface of a fireball (Ref. [24]). That value is considered conservative as the predicted distance for the allowed heat flux is so far away from the fireball edge. The accuracy of the point source model is relied upon with a power law dependence on distance of 2. In reality it is likely to be greater than 2 due to the atmospheric absorbance of the radiated energy. For example, 2.09 is used in some NATO combustion models [25].
The debris estimates for the confined scenarios are primarily from the Kasun structure testing reported in References [3,21]. A significant amount of work was completed to catalog and mark all of the debris from multiple tests. The Hazardous Fragment Distance (HFD) of 1 hazardous fragment in 600 square feet was then determined. Integrated Violence Modeling was completed for multiple scenarios as outlined above where the fragment distances and densities were predicted from the test parameters given the concrete structure fragment size distribution as described above (Ref. [5]). For the Titan rocket motor event [20], the HFD was estimated as 0.6 times the maximum fragment distance (457 meters for a mass of more than 300,000 kg) estimated from video evidence.
The relations for the recommended separation distances that are intended to prevent 2nd degree burns and exposure to hazardous fragment densities greater than 1 in 600 square feet are given in Figure 3 for both unconfined and confined scenarios. The equations used to generate those lines are given in Table 2 in SI units and in Table 3 for English units.
The relationships given in Table 2 and Table 3 were not found from a fit to the max of the data but are based on relationships previously defined (such as the US HD 1.3, US HD 1.2.2 IBD, and NATO HD 1.3 IBD) that appear to match the upper values of the data and modeling results.

4. Discussion

We have recommended updated ESSD values for HD1.3 substances and articles based on a large amount of test data that would allow for more material at current separation distances when the unconfined quantity is less than 145 kg and which better protect people and property for confined scenarios and are consistent with the NATO distances used around the world. The difference between the confined and unconfined cases are currently subjective in that a required vent area limiting the internal gas pressure in the building or structure is not defined for all possible structures. Further work to readily define the difference between the two is needed.
The recommended ESSD’s use the average heat flux for the burn duration. Other methods could be used to estimate the separation distance such as using the peak heat flux and a burn duration that also conserves energy which could give slightly higher explosives safety separation distances. The average over the entire burn duration was chosen here due to the layers of conservatism: inverse squared law relating the radiation to distance (more likely a faster decline) and the heat flux and exposure time to prevent second degree burns in Eq. 1 is also conservative.
The recommended ESSD’s are not directional. In other words, for the test scenarios that were directional, the ESSD’s are reported at the direction where the largest heat flux would be experienced. Directional effects could be accounted for in a straight forward way, for example by including the location information of vents through which the hot gases exit and then afterburn. Similarly, instead of using the net explosive weight (NEW) as the key parameter, the ESSD could be related to a different set of key parameters such as the burn rate, loading density, vent area, vent area location, among others. The net explosive weight was used here as the current US and NATO ESSD’s are functions of the NEW.

5. Conclusions

Combined analysis of hundreds of HD 1.3 tests, accidents, and detailed modeling results show that there is a significant difference in the heat flux and debris hazards between confined and unconfined scenarios. Additionally, the data analysis shows that current explosives safety separation distances for HD 1.3 ammunition and explosives do adequately protect people from hazards for unconfined scenarios. However, hazards from confined scenarios are currently not adequately protected against. Those hazards to personnel include when the internal pressure rapidly rises from insufficient venting and the structure fails violently or when the gases from the structure are violently forced out resulting in much larger than expected directional heat fluxes. The recommended unconfined and confined explosives safety separation distances given here would protect people adequately for both scenarios.
Additionally, the recommended adjustment to the existing HD 1.3 curve for unconfined scenarios has efficiencies due to lower separation distances required with masses less than 145 kg, as the current HD 1.3 IBD relation appears to be overly conservative at low masses. Both modeling and experimental data have proved valuable in evaluating and recommending the explosive safety separation distances for unconfined and confined scenarios with HD 1.3 ammunition and explosives.

Author Contributions

Conceptualization, C.G., M.L. and J.C.; methodology, C.G.; formal analysis, C.G.; data curation, C.G.; writing—original draft preparation, C.G.; writing—review and editing, C.G. and J.C; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The compilation of data together with the reference and calculations are available in a public github repository (github.com/clint-bg/publicationdata/safeSeparation).

Acknowledgments

We acknowledge helpful discussions with Martijn van der Voort and Matt Ferran with the Munitions Safety Information Analysis Center (MSIAC) and for providing some of the referenced heat flux data points.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

m , M mass of energetic substance, kilograms
d distance from substance, article, or structure, meters
t time, seconds
q heat flux, kilowatts per square meter
α point source model parameter, kilowatts
n moles inside the structure
m s mass of substance, kg
g g e n gas generation rate, mol/kg
P pressure, Pa
k rate constant or atmospheric burn rate
H enthalpy, J/mol
U internal energy, J/mol
q g e n heat generation from afterburning, W

References

  1. DESR 6055.09_AFMAN 91-201. Defense Explosives Safety Regulation 2020.
  2. Boggs, T.L.; Ford, K.P.; Covino, J. Realistic Safe-Separation Distance Determination for Mass Fire Hazards. Defense Technical Information Center 2013, NAWCWD TM 8668.
  3. Farmer, A.; Ford, K.P.; Covino, J.; Boggs, T.L.; Atwood, A.I. Combustion of Hazard Division 1.3 M1 Gun Propellant in a Reinforced Concrete Structure. Defense Technical Information Center 2015, NAWCWD TM8742.
  4. Covino, J.; Romo, C.P.; Phillips, J.W.; Atwood, A.I.; Boggs, T.L. Combustion Behavior and Quantity Distance (QD) Siting. 2018 International Explosives Safety Symposium and Exposition; Defense Technical Information Center: San Diego, DC, 2018.
  5. Guymon, C.G. Integrated Violence Model (IVM) of 1.3 Events. 2018 NDIA Conference, 2018.
  6. Hay, J.E.; Watson, R.W. Scaling Studies of Thermal Radiation Flux From Burning Propellants. Defense Technical Information Center 1992, 1992-08-01, 233–268.
  7. Pape, R.; Waterman, T.E.; Takata, A.N. Fire Hazards from Combustible Ammunition, Methodology Development (Phase I). Defense Technical Information Center 1980, pp. 0–154.
  8. Guymon, C.G. Heat Flux from the Top Ignition of a Single Barrel of WC814. Safety Management Services, Inc. Unpublished Data 2020.
  9. Harmanny, A. Thermal Radiation Flux of Fireworks. OECD-IGUS Report: Prins Maurits Laboratorium, TNO 1992.
  10. Wyssen. Abbrandversuche mit Treibladungspulver in Mengen von 10 bis 1000 kg. Gruppe für Rüstungsdienste / Tecnische Abteilung 6 1982.
  11. Paquet, F.; Ng, H.D.; Paquet, M.; Cottin, F.; Groulx, D. Modeling propellant fires radiant heat flux. Journal of Energetic Materials 2019, 37, 110–124. [CrossRef]
  12. Wyssen. Thermische Wirkgrössen bei Pulverabbränden. Gruppe für Rüstungsdienste / Tecnische Abteilung 6 1983.
  13. Guymon, C.G. COMSOL Estimates of Radiative Heat Flux from Propellant Barrel. Safety Management Services, Inc. Unpublished Model Results 2020.
  14. Williams, M.R.; Dunne, J.L. Heat Flux Measurement from Bulk Magnesium/Teflon/Viton (MTV) Flare Composition Combustion. Propellants, Explosives, Pyrotechnics 2013, 38, 563–568. [CrossRef]
  15. Trinkler. Thermal Effects in Relation to Ammunition Storage 1958.
  16. Blankenhagel, P.; Wehrstedt, K.D.; Mishra, K.B.; Steinbach, J. Thermal radiation assessment of fireballs using infrared camera. Journal of Loss Prevention in the Process Industries 2018, 54, 246–253. [CrossRef]
  17. Joachim, C.E. M-1 Propellant Tests: Deflagration in Partial Confinement. US Army Corps of Engineers 1991, Technical Report SL-91-11.
  18. Allain, L. Combustion of Gun Propellant in Igloo, Thermal Flux Measurements. US Army Corps of Engineers 1991, SNPE.
  19. Internal Video Footage of Titan Rocket Motor Ignition after Crane Failure. Safety Management Services, Inc., 1990.
  20. Wilson, W.; Anderson, J.; Meyden, M., Titan IV SRMU PQM-1 Overview; 28th Joint Propulsion Conference and Exhibit, 2012. doi:10.2514/6.1992-3819.
  21. Farmer, A.; Ford, K.P.; Covino, J.; Boggs, T.L.; Atwood, A.I. Combustion of Hazard Division 1.3 M1 Gun Propellant in a Reinforced Concrete Structure. Part 2. Tests 5 Through 7. Defense Technical Information Center 2017, NAWCWD TM8764.
  22. Lucotte. Measurement and prediction of heat flux in gun propellant fires. Proceedings of the 20th DoD Safety Seminar 1982.
  23. Williams, M.R.; Dunne, J.L. Heat Flux Measurement from Bulk Magnesium/Teflon/Viton (MTV) Flare Composition Combustion. Propellants, Explosives, Pyrotechnics 2013, pp. 563–568.
  24. Dorofeev, S.B.; Sidorov, V.P.; Efimenko, A.A.; Kochurko, A.S.; Kuznetsov, M.S.; Chaivanov, B.B.; Matsukov, D.I.; Pereverzev, A.K.; Avenyan, V.A. Fireballs from deflagration and detonation of heterogeneous fuel-rich clouds. Fire Safety Journal 1995, 25, 323–336. doi:10.1016/0379-7112(96)00008-2.
  25. Lihou, D.A.; Maund, J.K. Thermal Radiation Hazard from Fireballs. Symposium on Assessment of Major Hazards, I. Chem. E. Symp. 1982.
Preprints 80921 g001
Figure 1. Image showing the COMSOL 3D modeling completed for this study. The thermal radiation away from the simulated barrel (white area) was estimated for multiple cases.
Figure 1. Image showing the COMSOL 3D modeling completed for this study. The thermal radiation away from the simulated barrel (white area) was estimated for multiple cases.
Preprints 80921 g001
Preprints 80921 g002
Figure 2. Plot of the unconfined explosives safety separation distances from testing and modeling as reported in References [6,7,8,9,13]. The solid blue line is the current HD 1.3 IBD per DESR 6055.09. Almost all of the estimated ESSD distances from the test data are within the current IBD indicating sufficient protection against potential injury for unconfined burning of energetic material. The dotted blue line is the proposed adjustment for smaller masses (<145 kg).
Figure 2. Plot of the unconfined explosives safety separation distances from testing and modeling as reported in References [6,7,8,9,13]. The solid blue line is the current HD 1.3 IBD per DESR 6055.09. Almost all of the estimated ESSD distances from the test data are within the current IBD indicating sufficient protection against potential injury for unconfined burning of energetic material. The dotted blue line is the proposed adjustment for smaller masses (<145 kg).
Preprints 80921 g002
Preprints 80921 g003
Figure 3. Plot of the data (as points) for the unconfined (blue) and confined (orange) scenarios. The unconfined data points are repeated from Figure 2. Also shown are the proposed ESSD’s (as lines). The recommended unconfined ESSD’s (thick blue line) and confined ESSD’s (thick orange line) are per Table 2.
Figure 3. Plot of the data (as points) for the unconfined (blue) and confined (orange) scenarios. The unconfined data points are repeated from Figure 2. Also shown are the proposed ESSD’s (as lines). The recommended unconfined ESSD’s (thick blue line) and confined ESSD’s (thick orange line) are per Table 2.
Preprints 80921 g003
Table 1. HD 1.3 Test and Modeling Measurements with References.
Table 1. HD 1.3 Test and Modeling Measurements with References.
Reference Propellant Types # of Tests # of Measurements Event Type
Hay J. E. et al. [6] IMR5010, M1-8-SP, M1-8-MP, WC844, WC846, WCBlank 49 206 Unconfined: Heat Flux
Pape R. et al. [7] M1, WC844 46 79 Unconfined: Heat Flux
Wyssen [10] GP11, 35mm prowder 17 176 Unconfined: Heat Flux
Paquet F. et al. [11] SB1, SB2, DB1, DB2 16 48 Unconfined: Heat Flux
Harmanny A. [9] Fireworks 16 16 Unconfined: Heat Flux
Wyssen [12] 20 mm powder 6 120 Unconfined: Heat Flux
Guymon C. G. [8] WC814 1 4 Unconfined: Heat Flux
Guymon C. G. [13] Model - 30 Unconfined: Heat Flux
Williams M. R. et al. [14] MTV 12 36 Confined: Heat Flux
Trinkler [15] Cordite 8 35 Confined: Heat Flux
Blankenhagel P. et al. [16] di-tert-butyl peroxide 3 9 Confined: Heat Flux
Farmer et al. [3] M1 3 3 Confined: Heat Flux
Joachim C E [17] M1 3 3 Confined: Heat Flux
Allain L. [18] LB 7 T 72 2 12 Confined: Heat Flux
Titan Crane Failure [19] Rocket Propellant 1 1 Confined: Heat Flux
Wilson et al. [20] Rocket Propellant 1 1 Confined: Heat Flux
Farmer et al. [3] M1 2 2 Confined: Debris
Farmer et al. [21] M1 1 2 Confined: Debris
Wilson et al. [20] Rocket Propellant 1 1 Confined: Debris
Guymon C. G. [5] Model - 25 Confined: Debris
Table 2. Proposed HD 1.3 Explosives Safety Separation Distances (SI Units).
Table 2. Proposed HD 1.3 Explosives Safety Separation Distances (SI Units).
Condition Mass, M (kg) Relation (m)
Unconfined M ≤ 453 min(3.216·M 0 . 3939 ,22.9)
453 < M ≤ 43,540 max(22.9,exp[1.4715 + 0.2429·ln(M) + 0.00384·(ln(M)) 2 ])
43,540 < M ≤ 453,590 exp[5.5938 – 0.5344·ln(M) + 0.04046·(ln(M)) 2 ]
453,590 < M 3.17·M 1 / 3
Confined M ≤ 10,000 max(30.5,28.127-2.364·ln(M)+1.577·ln(M) 2 )
10,000 < M 6.4·M 1 / 3
Table 3. Proposed HD 1.3 Explosives Safety Separation Distances (English Units).
Table 3. Proposed HD 1.3 Explosives Safety Separation Distances (English Units).
Condition Mass, M (lb) Relation (ft)
Unconfined M ≤ 1,000 min(7.73·M 0 . 3939 ,75)
1,000 < M ≤ 96,000 max(75,exp[2.463 + 0.238·ln(M) + 0.00378·(ln(M)) 2 ])
96,000 < M ≤ 1,000,000 exp[6.8633 – 0.5418·ln(M) + 0.03828·(ln(M)) 2 ]
1,000,000 < M 7.99·M 1 / 3
Confined M ≤ 22,050 max(100,101.61-15.926·ln(M)+5.173·ln(M) 2 )
22,050 < M 16.13·M 1 / 3
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated