Prerpints.org logo
Preprint
Article

Coastal Erosion Caused by River Mouth Migration on Cuspate Delta: An Example from Thanh Hoa, Vietnam

Altmetrics

Downloads

127

Views

63

Comments

0

Submitted:

24 July 2023

Posted:

26 July 2023

You are already at the latest version

Alerts
Abstract
Coastal erosion is threatening the infrastructures of coastal community at the Ma River mouth in Thanh Hoa province, Vietnam. When coastal erosion happens, people try to prevent it by emergency solutions like hard structures. However, this approach usually leads to more severe problem since the mechanism for coastal erosion is not investigated and understood properly. In this study the long-term configuration of Ma River mouth in Thanh Hoa Province, Central Vietnam has been investigated using Landsat imagery from 1987 to 2023. An analytical solution of one-line model for shoreline change was also employed to calculate the sand discharge from Ma River as well as the diffusion coefficient for sand transported along-shore by breaking waves. There was an asymmetric configuration of the Ma River mouth during the last 37 years. The sand supply from the Ma River is around 350,000 m3/year. This amount of sand is going mainly to the northern beach of the Ma River delta (from 55% to 75%). The asymmetric morphology of the Ma River mouth delta is the trigger for severe coastal erosion reported recently. This study provides a quick and easy method to investigate the morphological change of cuspate deltas where measured data is limited.
Keywords: 
Subject: Environmental and Earth Sciences  -   Oceanography

1. Introduction

Cuspate delta, which was first defined by Wright and Coleman [1] as an example of a slightly protruding delta into open water, has been the object of numerous studies by coastal scholars [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] because they are one of the three most popular delta shapes in the world classified by Galloway [3]. According to Galloway [3], this type of landform was designated as a wave-dominated delta because the morphologies of these deltas were formed mainly by the interaction between riverine (sediment supply) and ocean forces (waves).
Because of urbanization and the need for natural resources, 31% of Vietnam’s population is living on the coast [19]. However, this narrow belt is susceptible to the threads of waves, flooding, storm surge, and sea level rise [20]. Along the coastline of Vietnam, coastal erosion has become a natural hazard in the last decade and come with significant cost to communities and nature [21,22,23,24]. In the Ma River mouth delta, a similar disaster is happening on the cuspate of the delta. Coastal erosion has negatively affected infrastructures and livelihoods in recent years. The cuspate delta has experienced a significant loss of agricultural land and infrastructure to the sea. In this study, the long-term evolution of Ma River mouth in Thanh Hoa province, Vietnam will be investigated to find out the relationship between coastal morphological change and coastal erosion in this cuspate delta.
Ma River delta is a cuspate delta located in Thanh Hoa province, Vietnam as shown in Figure 1. The protruding part of this delta is formed by sediment supplied from Ma River and under effects of waves from the East Sea of Vietnam [12]. According to Quang et al. [25], Ma River delta is the third largest river delta in Vietnam which drains to the East Sea 5.17 million tons of sediment every year. Under action of the waves, sediment supplied from the river is transported along-shore to nourish the beaches on both sides of the Ma River mouth. It should be noticed that at the end of the southern coast, there is a mountainous region that acts as a boundary to block the longshore sediment transport (Figure 1c,d).

2. Materials and Methods

2.1. Landsat Image Analysis

Landsat imagery has been applied intensively for coastal studies especially in areas with significant temporal variation of the shorelines such as as river mouths, sand spits, and around coastal structures [26,27,28,29,30,31]. In this study, Landsat images from 1987 to 2023 were collected (Table 1) for mapping the changes of the shorelines around the Ma River mouth. Shoreline detection was performed based on the Normalized Difference Water Index (NDWI) [32]:
N D W I = X g r e e n − X n i r X g r e e n + X n i r
where Xgreen and Xnir are the GREEN and NIR wavelengths, respectively. Subsequently, the shorelines of several years from 1987 to 2023 are mapped together to observe the temporal variation of the delta’s cuspate.

2.2. Application of Analytical Solutions for Shoreline Change

In this section, an analytical solution of one-line model for shoreline changes in a wave-dominated delta will be utilized to quickly estimate the diffusion coefficient for longshore sand transport ( ε ). Currently, there are two types of analytical solutions for modelling wave-dominated river delta evolution. The first solution was introduced by Larson et al. [33] for infinite shorelines (Figure 2a). Later, Duy et al. [18], derived another closed-form solution for shorelines with definite lengths (L) (Figure 2b).
As can be seen in Figure 1, there is a headland at the end of the southern shoreline in Ma River delta. This headland can be considered as a rigid boundary as shown in Figure 2b. Hence, the southern shoreline of Ma River delta well fits the analytical solution proposed by Duy et al. [18] as follows:
y = q 0 2 ε D L [ x 2 2 − L | x | + L 2 3 + ε t − 2 L 2 π 2 ∑ n = 1 ∞ 1 n 2 e − n 2 π 2 ε t L 2 cos ( n π x L ) ]
where y is the shoreline position, q0 is the sand discharge from the river, ε is the diffusion coefficient, D is the sum of depth of closure (DC) and beach berm height (DB), x is the along-shore distance, and L is the length of the shoreline.
In order to make the comparison between the shoreline extracted from Landsat image and the shoreline calculated using the analytical solution, a Cartesian Coordinate system was used consistently in this study. In which, the abscissa is 1980 clockwise from the north and crossing the point O (595,288.00 m E; 2,188,386.00 m N) in the UTM system (Figure 3b). In the interest of expediency, a 1080 counterclockwise rotation is applied to the coordinate system to establish the configuration depicted in Figure 3a.
The shoreline position extracted from the Landsat image on 1991/02/14 will be used as the measured data to compare with the computed data. The shoreline position on 1991/02/14 was chosen since it has the most protruding part of the cuspate and a symmetric configuration concerning the y-axis. These conditions satisfy the shoreline configuration in Figure 2b.
To apply Equation (2) for modeling the shoreline position in 1991, all variables are collected and presented in Table 2.
Quang et al. [25], reported that the Ma River discharges a total of 5.17 tons of sediment annually into the Vietnamese East Sea. Among this amount, 20% constitutes bed load sediment [34]. Consequently, the annual contribution of bed load sediment from the Ma River to the river mouth beaches is estimated to be 1.03 tons. To determine the sand transport rate, considering a sand density of 2,065 kg/m3 [35], the calculated value is 390,000 m3/year. This value is utilized as the initial value for sand supply from the Ma River, as presented in Table 2.
The determination of the formation time (t) draws upon the research conducted by Yen et al. [36]. It is worth noting that while Yen et al.'s [36] investigation focuses on the Red River delta, it also includes a map encompassing the neighboring Ma River delta. This map provides distinct evidence that the historical shoreline positions in the Late Holocene originated between 500 to 200 years Before Present (BP). Consequently, the establishment time of the Ma River delta is considered to be 500 years.
The depth of closure is calculated based on the following equation of Hallermeier [37] as follows:
D C = 2.28 H s e − 68.5 ( H s e 2 g T s e 2 )
where DC is the depth of closure, Hse and Tse are the significant wave height and wave period of the extreme wave condition (extrememly high waves expected 12 hours per year), and g is the gravitational acceleration. According to Thomson & Harris [38], Tse should be taken to be the typical period of the measured wave height. The extreme high wave conditions were taken from the study of Hung et al. [39] with Hse = 3 m and Tse = 7 s, respectively. Substituting Hse and Tse to Equation (3) yields Dc = 5.6 m.
The beach berm height is calculated based on the expression proposed by Uda [40] as follows:
D B = 0.32 × D C
The value of Dc = 5.6 m yields DB = 1.8 m.
Finally, the length of the shoreline is measured from the Landsat image captured on 1991/02/14 as shown in Figure 4.
Table 2 contains the initial values employed for computing the shoreline position in 1991. A comparison between these calculated positions and the shoreline positions extracted from the Landsat image on 1991/02/14 will be performed. Given that the value of e is unknown, an iterative calculation process is adopted, considering a range of e values. The root mean square error (RMSE) of the shoreline positions is utilized to determine the optimal value of e that best fits the data. Consequently, the iterative process terminates once the minimum RMSE is achieved.

2.3. Geometrical Characteristics of the Cuspate Delta

2.3.1. Evolution of the Cuspate Delta

In this section, the along-shore and cross-shore coordinates of the cuspate tips on both sides of Ma River mouth will be measured and used for discussing the morphological behavior of the river mouth. The method of using the coordinates of special points such as sand spit’s tips or the central of gravity to discuss the evolution of a sand body has been applied widely in coastal engineering [26,28,29,31,41,42]. Figure 5 illustrates the schematic for measuring the coordinates of the cuspate tips, which are considered as the most prominent protrusions into the open water. The schematic elucidates the fundamental variables involved in the process, namely xS and xN, signifying the along-shore coordinates of the cuspates' tips on the southern and northern sectors, respectively. Additionally, the variables yS and yN are designated to represent the cross-shore extents of the cuspate tips on the southern and northern parts, respectively. It is imperative to note that all measurements of these variables are expressed in the metric unit of meters.

2.3.2. Shoreline Orientations at the River Mouth

Moreover, the investigation of the Ma River mouth encompasses not only the geometrical characteristics of the delta cuspate but also the determination of shoreline orientations. In the context of wave-dominated river deltas, the assessment of shoreline orientations on both sides of the river mouth assumes paramount significance for understanding the evolution of this geographical feature [2,23,43,44]. To facilitate the estimation of shoreline orientations, it is imperative to define shoreline angles. As elucidated in [43], shoreline angles correspond to the angles formed between the trendlines (red lines) and a horizontal reference line, as illustrated in Figure 6. Denoting the shoreline angles on the north and south of the Ma River mouth as θN and θS, respectively, the expressions for the shoreline orientations at the river mouth can be represented as follows:
β N = tan ( θ N )
and
β S = tan ( θ S )
where β N and β S are the shoreline orientations on the north and the south of the river mouth, respectively.
In Figure 6, we examine the angles of the delta cuspate formed on the northern (θN) and southern (θS) sections. To ascertain shoreline orientations, we employ the linear regression method, utilizing shoreline positions depicted as blue dots, extracted at regular 50 m intervals. For visual clarity, the figure displays shoreline positions at 300 m intervals. The measurement range for shoreline orientations encompasses -3000 m ≤ x ≤ -1200 m for the northern shoreline and 500 m ≤ x ≤ 2500 m for the southern shoreline
According to Hu et al. [45], on wave-dominated river deltas, the coastline shapes affect the distribution of sand supply from the river. This mechanism was also studied by Ashton et al. [46] and Ashton and Giosan [47]. Therefore, it would be useful to investigate the relationship between the shoreline orientations and the distribution rate of sand supply from the Ma River. If the distribution rate of sand supply from the Ma River to the north is α , it can be expressed as a function of the shoreline orientations as:
α = β N β N + β S

3. Results

3.1. Temporal Variation of Shorelines at the River Mouth

Shoreline positions extracted from Landsat imagery are plotted in Figure 7. Only shoreline positions in 1987, 2000, 2010 and 2023 are plotted to ensure legibility. As can be seen from the figure, the southern tip of the cuspate has retreated significantly by a distance of approximately 1000 m from 1987 to 2023. On the other hand, the shoreline position of the northern tip has moved to the north.
Moreover, a significant northward displacement of the shoreline at the erosion hot spot (indicated by the red rectangle in Figure 7a) has also been observed, measuring a distance of approximately 200 m. These shifting shoreline patterns are attributed to severe coastal erosion, which has prompted local communities to implement the use of hard structures as a protective measure, as illustrated in Figure 7b.

3.2. Diffusion Coefficient for Sand Transport Induced by Breaking Waves

Figure 8 displays the optimal alignment between the computed shoreline and the observed shoreline. In this context, the shoreline position in 1991, determined through Equation (2), is depicted by the red line, while the shoreline position obtained from the Landsat image taken on 1991/02/14 is represented by the blue dots. The minimum Root Mean Square Error (RMSE) between these shoreline positions amounts to 26.4 m. For reference, Table 3 presents the final values of the variables employed in the calculation procedure.

3.3. Geometrical Characteristics of the Cuspate Delta

3.3.1. Evolution of the Delta Cuspate

Figure 9 shows the long-term variation of the northern and southern tips' coordinates of the sand cuspates over time in the along-shore direction. The horizontal axis represents the timeline, ranging from 1987 to the present year (2023). The vertical axis represents the along-shore coordinates of the cuspates' tips, measured in meters. The blue circles on the graph represent the along-shore coordinate for the southern cuspate (xS), while the orange squares represent the along-shore coordinate for the northern cuspate (xN).
From the data presented in Figure 9, it is evident that both cuspates have been moving in opposite directions along the shoreline over time. The southern cuspate (xS) has shown an increasing trend, moving at a rate of 17.59 meters per year to the south. On the other hand, the northern cuspate (xN) has been decreasing in its along-shore coordinate, moving at a rate of approximately -21.28 meters per year to the north. These observations are in line with the changes observed in the shoreline of the Ma River mouth, as depicted in Figure 7a.
Figure 10 presents a temporal variation diagram of the cuspates' tips in the cross-shore direction from 1987 to the present. The diagram includes two sets of data points represented by different shapes and colors. The orange triangles represent the coordinates of the southern cuspate (yS), while the blue diamonds represent the northern cuspate (yN).
Concerning the southern cuspate, the cross-shore coordinate of the southern cuspate decreased steadily over the tracking time. This means that the position of the southern cuspate moved closer to the shoreline as time progressed.
On the other hand, the cross-shore coordinates of the northern cuspate showed fluctuations during the survey period. From 1987 to 2000, the northern cuspate's cross-shore coordinate decreased. This indicates that the position of the northern cuspate moved closer to the shoreline during this time period. Between 2001 and 2005, there was a sharp increase in the northern cuspate's cross-shore coordinate. It expanded from 2000 meters to 3600 meters, indicating that the northern cuspate moved further away from the shoreline during this period. Since 2006, the northern cuspate's cross-shore coordinate decreased significantly and reached 2500 meters again at the present time. This suggests that the position of the northern cuspate moved closer to the shoreline again in recent years.
In addition, the significant increase in the northern cuspate's cross-shore coordinates from 2001 to 2005 indicates a large sediment supply from the Ma River, but the protrusion towards the sea of only the northern cuspate implies an asymmetric distribution of this sand supply, favoring the northern cuspate.

3.3.2. Shoreline Orientations at the River Mouth

Figure 11 illustrates the temporal variation of the shoreline orientations at the Ma River mouth. The diagram displays two key values: bN, representing the shoreline orientation of the north, and bS, representing the shoreline orientation of the south.
The diagram indicates that there is a significant gap between the shoreline orientations of the north and the south. This disparity suggests that the cuspate in the Ma River delta possesses an asymmetric shape. In other words, the two sides of the river mouth, the northern and southern tips, have different angles at which they meet the water.
Furthermore, the higher values of bN compared to the values of bS indicate that the northern tip of the river mouth protrudes more prominently into the water than the southern one. This difference in protrusion further contributes to the overall asymmetry of the cuspate delta.
Figure 12 illustrates the calculated ratio of sand supply to the northern lobe of the Ma River delta from 1987 to 2023. The ratio is determined using Equation (7), and the results indicate that the amount of sand supplied to the northern lobe has consistently been larger than that supplied to the southern lobe during this period. The trend over time shows a continuous increase in the sand supply to the northern lobe, indicating a greater deposition of sand in that region compared to the south. This is evidenced by the entire data points consistently lying above the midpoint (a = 0.5), suggesting an asymmetric distribution of sand towards the north (from 55% to 75%). However, there was an exception in the year 1990 when the sand supply was equal to both sides of the Ma River mouth, resulting in a balanced ratio with a value of a equal to 0.5. This suggests that in 1990, the sediment distribution between the northern and southern lobes was approximately equal.

4. Discussion

Figure 13 shows a representation of a river mouth where sand is being supplied symmetrically to both sides of the river's opening. Additionally, the sketch includes illustrations of longshore sand transport along the coastlines. Arrows are drawn parallel to the shorelines, indicating the direction of sand movement along the coast.
According to the study of Duy et al. [18], longshore sand transport can be mathematically expressed as:
Q = − ε D ∂ y ∂ x
where Q is the longshore sand transport along the coastline, ∂ y ∂ x is the shoreline’s orientations at the river mouth, ∂ y ∂ x = tan θ = β .
By equating Q and q0/2, it yields:
∂ y ∂ x = − q 0 2 ε D
For the asymmetric condition at Ma River delta, the sand supply from the Ma River and the ratios of sand transported to the north and south at the Ma River mouth can be calculated as follows:
-
Sand supply from the Ma River:
q 0 = ( β N + β S ) ε D
-
Sand transported to the north:
q N = α q 0
-
Sand transported to the south:
q S = ( 1 − α ) q 0
Figure 14 shows the sand supply from Ma River (orange squares) and the amounts of sand distributed to the north (blue diamonds) and the south (black dots), repsectively. There is an asymmetric of sand distributed to the north and the south of the delta which indicates the waves approach the delta from a dominant direction more often at this study site. It is interesting from Figure 14 that the average amount of sand supply from the Ma River is around 380,000 m3/year. This value is very close to the sand supply estimated using the analytical solution shown in Table 3 (350,000 m3/year).

5. Conclusions

Coastal erosion at the Ma River mouth in Thanh Hoa province, Vietnam has been investigated using Landsat imagery from 1987 to 2023 and an analytical solution. The research findings reveal the following key points:
-
The northern part of the Ma River delta is experiencing northward movement, leading to severe coastal erosion at the river mouth.
-
In contrast, the southern part of the Ma River Delta is moving southward and landward.
-
The sand diffusion coefficient at the Ma River delta has been calculated to be 90 m2/day, indicating the rate at which sand particles are transported.
-
The present investigation provides an evaluation of the sand supply originating from the Ma River to the delta's lobes. According to the analytical solution, the estimated annual sand supply amounts to approximately 350,000 m3/year. Additionally, an alternative approach based on the shoreline orientations at the river mouth yields a slightly higher value, specifically 380,000 m3/year. This discrepancy underscores the reliability of the sand supply assessment derived through the current study's methodologies.
-
The research also highlights an asymmetric configuration of shoreline shapes at the Ma River mouth, as evidenced by the uneven distribution of sediment to the delta flanks. In which, the ratio of sand supply to the north ranges from 55% to 75%.
These findings provide valuable insights into the erosion mechanism at the Ma River mouth and can serve as a basis for further studies and potential coastal management strategies in the area.

Author Contributions

Conceptualization, H.T. and D.V.D; methodology, H.T. and D.V.D; formal analysis, D.V.D., C.T.N.T, C.N.T, H.T.C.H. and T.N.T; investigation, D.V.D., C.T.N.T, L.T.P., N.T.A. and T.N.T.; resources, D.V.D., L.T.P. and T.N.T.; data curation, H.T., D.V.D., T.N.T and N.T.A.; writing—original draft preparation, D.V.D., T.V.T. and L.T.P.; writing—review and editing, H.T., N.T.V., T.V.T and D.V.D.; visualization, H.T. and D.V.D.; supervision, H.T., N.T.V. and T.V.T; funding acquisition, H.T. and T.V.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

We encourage all authors of articles published in MDPI journals to share their research data. In this section, please provide details regarding where data supporting reported results can be found, including links to publicly archived datasets analyzed or generated during the study. Where no new data were created, or where data is unavailable due to privacy or ethical restrictions, a statement is still required. Suggested Data Availability Statements are available in section “MDPI Research Data Policies” at https://www.mdpi.com/ethics.

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wright, L.D.; Coleman, J.M. Variations in Morphology of Major River Deltas as Functions of Ocean Wave and River Discharge Regimes1. AAPG Bulletin 1973, 57, 370–398. [Google Scholar]
  2. Komar, P.D. Computer models of delta growth due to sediment input from rivers and longshore transport. Geological Society of America Bulletin 1973, 84, 2217–2226. [Google Scholar] [CrossRef]
  3. Galloway, W.E. Process Framework for Describing the Morphologic and Stratigraphic Evolution of Deltaic Depositional Systems. 1975.
  4. Pranzini, E. A model for cuspate delta erosion. in Waterfront Planning and Development. 1989. ASCE.
  5. REFAAT, H.E.-d.A. The formation and reduction processes of river deltas and their control. 1990.
  6. Mikhailova, M. Sediment balance in nontidal river mouths and method of calculation of protruding delta formation. WATER RESOUR.; VODNYE RESURSY 1995, 5.
  7. Pranzini, E. Updrift river mouth migration on cuspate deltas: two examples from the coast of Tuscany (Italy). Geomorphology 2001, 38, 125–132. [Google Scholar] [CrossRef]
  8. Bhattacharya, J.P.; Giosan, L. Wave-influenced deltas: geomorphological implications for facies reconstruction. Sedimentology 2003, 50, 187–210. [Google Scholar] [CrossRef]
  9. Mikhailova, M. Quantitative assessment of the role of deltas in the processes of deposition of river sediments. Water Resources 2007, 34, 644–656. [Google Scholar] [CrossRef]
  10. Seybold, H.; Andrade, J.S., Jr.; Herrmann, H.J. Modeling river delta formation. Proceedings of the National Academy of Sciences 2007, 104, 16804–16809. [Google Scholar] [CrossRef]
  11. Nienhuis, J.H. Plan-view evolution of wave-dominated deltas. 2016, Massachusetts Institute of Technology.
  12. Quan, N.C.; Hung, P.V. Characteristics of dynamic geomorphology of coastal-river mouth zones of Ma river, Thanh Hoa province. Vietnam Journal of Earth Sciences 2016, 38, 59–65. [Google Scholar]
  13. Besset, M.; Anthony, E.J.; Sabatier, F. River delta shoreline reworking and erosion in the Mediterranean and Black Seas: The potential roles of fluvial sediment starvation and other factors. Elementa: Science of the Anthropocene 2017, 5. [Google Scholar] [CrossRef]
  14. Quang Tuan, N.; Cong Tin, H.; Quang Doc, L.; Anh Tuan, T. Historical Monitoring of Shoreline Changes in the Cua Dai Estuary, Central Vietnam Using Multi-Temporal Remote Sensing Data. Geosciences 2017, 7, 72. [Google Scholar] [CrossRef]
  15. Anthony, E.J.; Besset, M.; Zainescu, F.; Sabatier, F. Multi-Decadal Deltaic Land-Surface Changes: Gauging the Vulnerability of a Selection of Mediterranean and Black Sea River Deltas. Journal of Marine Science and Engineering 2021, 9, 512. [Google Scholar] [CrossRef]
  16. Quang, D.N.; Ngan, V.H.; Tam, H.S.; Viet, N.T.; Tinh, N.X.; Tanaka, H. Long-Term Shoreline Evolution Using DSAS Technique: A Case Study of Quang Nam Province, Vietnam. Journal of Marine Science and Engineering 2021, 9, 1124. [Google Scholar] [CrossRef]
  17. Broaddus, C.M.; Vulis, L.M.; Nienhuis, J.H.; Tejedor, A.; Brown, J.; Foufoula-Georgiou, E.; Edmonds, D.A. First-Order River Delta Morphology Is Explained by the Sediment Flux Balance From Rivers, Waves, and Tides. Geophysical Research Letters 2022, 49, e2022GL100355. [Google Scholar] [CrossRef]
  18. Duy, D.V.; Tanaka, H.; Larson, M.; Viet, N.T. A Theory for Estuarine Delta Formation with Finite Beach Length under Sediment Supplied from the River. Journal of Marine Science and Engineering 2022, 10, 947. [Google Scholar] [CrossRef]
  19. Lappe, R.; Ullmann, T.; Bachofer, F. State of the Vietnamese Coast—Assessing Three Decades (1986 to 2021) of Coastline Dynamics Using the Landsat Archive. Remote Sensing 2022, 14, 2476. [Google Scholar]
  20. Ghiasian, M.; Carrick, J.; Rhode-Barbarigos, L.; Haus, B.; Baker, A.C.; Lirman, D. Dissipation of wave energy by a hybrid artificial reef in a wave simulator: implications for coastal resilience and shoreline protection. Limnology and Oceanography: Methods 2021, 19, 1–7. [Google Scholar] [CrossRef]
  21. Duc, D.M.; Nhuan, M.T.; Ngoi, C.V. An analysis of coastal erosion in the tropical rapid accretion delta of the Red River, Vietnam. Journal of Asian Earth Sciences 2012, 43, 98–109. [Google Scholar] [CrossRef]
  22. Anthony, E.J.; Brunier, G.; Besset, M.; Goichot, M.; Dussouillez, P.; Nguyen, V.L. Linking rapid erosion of the Mekong River delta to human activities. Scientific Reports 2015, 5, 14745. [Google Scholar] [CrossRef]
  23. Tanaka, H.; Viet, N.T.; Hoang, V.C.; Duy, D.V. Erosion mechanism of Cua Dai Beach, Central Vietnam. Journal of Japan Society of Civil Engineers, Ser. B3 (Ocean Engineering) 2015, 71, I_449–I_454. [Google Scholar] [CrossRef]
  24. Fan, D.; Nguyen, D.V.; Su, J.; Bui, V.V.; Tran, D.L. Coastal morphological changes in the Red River Delta under increasing natural and anthropic stresses. Anthropocene Coasts 2019, 2, 51–71. [Google Scholar] [CrossRef]
  25. Nguyen, M.Q.; Vu, V.H.; Mai, T.T.; To, X.B.; Tran, N.D.; Dang, M.T.; Dang, X.T.; Nguyen, T.M.; Hoang, V.T.; Giap, T.K.C. Geomorphological sedimentary characteristics in the coastal area of Ma river delta, Thanh Hoa province. Vietnam Journal of Marine Science and Technology 2021, 21, 283–298. [Google Scholar] [CrossRef]
  26. Tanaka, H.; Hoang, V.C.; Viet, N.T. Investigation of morphological change at the Cua Dai river mouth through satellite image analysis. Coastal Engineering 2016, 2016. [Google Scholar] [CrossRef]
  27. Hein, C.J.; Fallon, A.R.; Rosen, P.; Hoagland, P.; Georgiou, I.Y.; FitzGerald, D.M.; Morris, M.; Baker, S.; Marino, G.B.; Fitzsimons, G. Shoreline dynamics along a developed river mouth barrier island: Multi-decadal cycles of erosion and event-driven mitigation. Frontiers in Earth Science 2019, 7, 103. [Google Scholar] [CrossRef]
  28. Duc Anh, N.Q.; Tanaka, H.; Tam, H.S.; Tinh, N.X.; Tung, T.T.; Viet, N.T. Comprehensive Study of the Sand Spit Evolution at Tidal Inlets in the Central Coast of Vietnam. Journal of Marine Science and Engineering, 2020. 8. [CrossRef]
  29. Lawson, S.K.; Tanaka, H.; Udo, K.; Hiep, N.T.; Tinh, N.X. Morphodynamics and Evolution of Estuarine Sandspits along the Bight of Benin Coast, West Africa. Water 2021, 13, 2977. [Google Scholar] [CrossRef]
  30. Carvalho, B.C.; Gomes, C.L.D.S.; Guerra, J.V. , Spatio-temporal morphological variability of a tropical barrier island derived from the Landsat collection. Frontiers in Remote Sensing 2023, 4. [Google Scholar] [CrossRef]
  31. Duy, D.V.; Ty, T.V.; Thanh, T.N.; Minh, H.V.T.; De, C.V.; Duong, V.H.T.; Dan, T.C.; Viet, N.T.; Tanaka, H. Sand Spit Morphology at an Inlet on Phu Quoc Island, Vietnam. Water 2023, 15, 1941. [Google Scholar] [CrossRef]
  32. McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. International journal of remote sensing 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
  33. Larson, M.; Hanson, H.; Kraus, N.C. Analytical solutions of the one-line model of shoreline change. 1987, COASTAL ENGINEERING RESEARCH CENTER VICKSBURG MS.
  34. Vietnam - Trung Son Hydropower Project : environmental assessment (Vol. 7) : Supplementary environmental and social impact assessment (English). 2009: Washington, D.C. : World Bank Group.
  35. Rosati, J.D.; Walton, T.; Bodge, K. Longshore sediment transport, in Coastal Engineering Manual. 2002. p. 119.
  36. Yen, H.P.H.; Nhan, T.T.T.; Nghi, T.; Toan, N.Q.; Khien, H.A.; Lam, D.D.; Van Long, H.; Thanh, D.X.; Hung, N.T.; Trang, N.T.H.; Dien, T.N.; Tuyen, N.T.; Truong, T.X.; Dung, T.T.; Thao, N.T.P.; Lan, V.Q. Late Pleistocene-Holocene sedimentary evolution in the coastal zone of the Red River Delta. Heliyon 2021, 7, e05872. [Google Scholar] [CrossRef]
  37. Hallermeier, R.J. Uses for a calculated limit depth to beach erosion, in Coastal engineering 1978. 1978. p. 1493–1512.
  38. Thompson, E.F.; Harris, D.L. A Wave CI imatology for US Coastal Waters. in Offshore Technology Conference. 1972. OnePetro.
  39. Thanh, H.N.; Cuong, V.D.; Tajima, Y.; Cuong, T.V. Numerical modeling of Hydrodynamics and sediment transport processes in Ma rivier estuary, Vietnam. in Proceedings of the 19th IAHR-APD Congress. 2014. [Google Scholar]
  40. Uda, T. Japan’s beach erosion: reality and future measures. 2010: World Scientific.
  41. Duy, D.V.; Tanaka, H.; Mitobe, Y.; Anh, N.Q.D.; Viet, N.T. Sand Spit Elongation and Sediment Balance at Cua Lo Inlet in Central Vietnam. Journal of Coastal Research 2018, 81, 32–39. [Google Scholar]
  42. Paladio-Hernandez, A.; Salles, P.; Arriaga, J.; López-González, J. Characterization of the Morphological Behavior of a Sand Spit Using UAVs. Journal of Marine Science and Engineering 2022, 10, 600. [Google Scholar] [CrossRef]
  43. FURUIKE, K.; UDA, T.; SERIZAWA, M.; SAN-NAMI, T.; ISHIKAWA, T. Model for predicting long-term beach changes originating from accretive features of a natural delta coast, in Asian and Pacific Coasts 2009: (In 4 Volumes, with CD-ROM). 2010, World Scientific. p. 266-272.
  44. Uda, T.; Shiho, M.; Toshiro, S.-N.; Masumi, S. A Long-Term Prediction of Beach Changes around River Delta using Contour-Line-Change Model, in Sedimentary Processes, A. Gemma, Editor. 2019, IntechOpen: Rijeka. p. Ch. 5.
  45. Hu, N.; Murray, A.B.; Ratliff, K.M.; Little, Z.; Hutton, E.W.H. Wave-Climate Asymmetry Influence on Delta Evolution and River Dynamics. Geophysical Research Letters 2022, 49, e2021GL096315. [Google Scholar] [CrossRef]
  46. Ashton, A.; Murray, A.B.; Arnoult, O. Formation of coastline features by large-scale instabilities induced by high-angle waves. Nature 2001, 414, 296–300. [Google Scholar] [CrossRef] [PubMed]
  47. Ashton, A.D.; Giosan, L. Wave-angle control of delta evolution. Geophysical Research Letters 2011, 38. [Google Scholar] [CrossRef]
Preprints 80437 g001
Figure 1. Study area. (a) Vietnam map, (b) Thanh Hoa province, and (c) Ma River delta, and (d) Mountainous region which is considered as a no sand transport boundary.
Figure 1. Study area. (a) Vietnam map, (b) Thanh Hoa province, and (c) Ma River delta, and (d) Mountainous region which is considered as a no sand transport boundary.
Preprints 80437 g001
Preprints 80437 g002
Figure 2. Sketch for river delta with (a) infinite shorelines and (b) finite shorelines. The sketch is redrawn based on the idea of Duy et al. [18]. In this figure, q0 is the sand supply from the river and y0 is the maximum extents of the cuspate to the ocean.
Figure 2. Sketch for river delta with (a) infinite shorelines and (b) finite shorelines. The sketch is redrawn based on the idea of Duy et al. [18]. In this figure, q0 is the sand supply from the river and y0 is the maximum extents of the cuspate to the ocean.
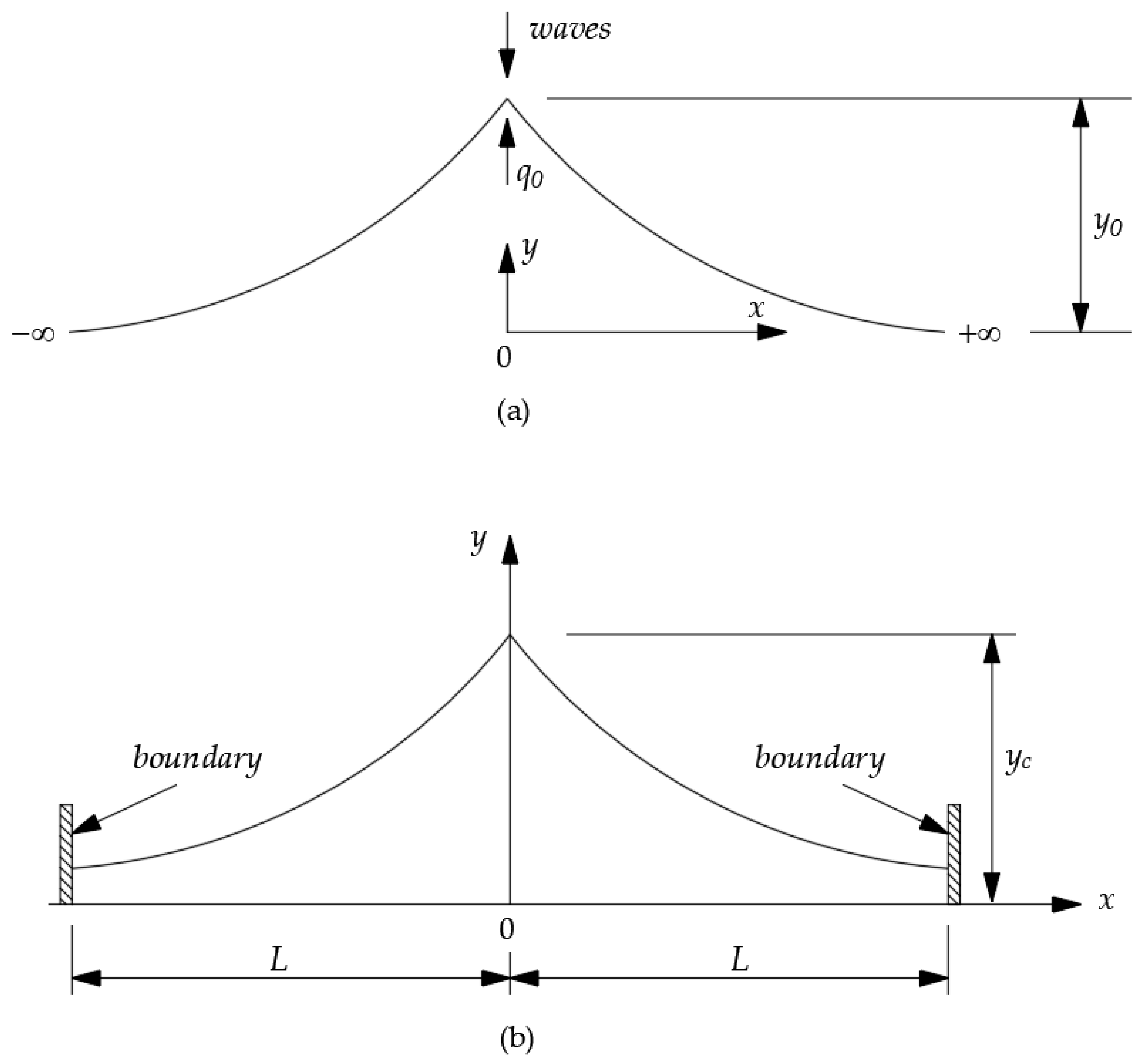
Preprints 80437 g002
Preprints 80437 g003
Figure 3. The Cartesian Coordinates used in this study by rotating the images 1080 and taking the Origin O (0;0) in the Cartesian Coordinates as the O (595,288.00 m E; 2,188,386.00 m N) in the UTM system.
Figure 3. The Cartesian Coordinates used in this study by rotating the images 1080 and taking the Origin O (0;0) in the Cartesian Coordinates as the O (595,288.00 m E; 2,188,386.00 m N) in the UTM system.
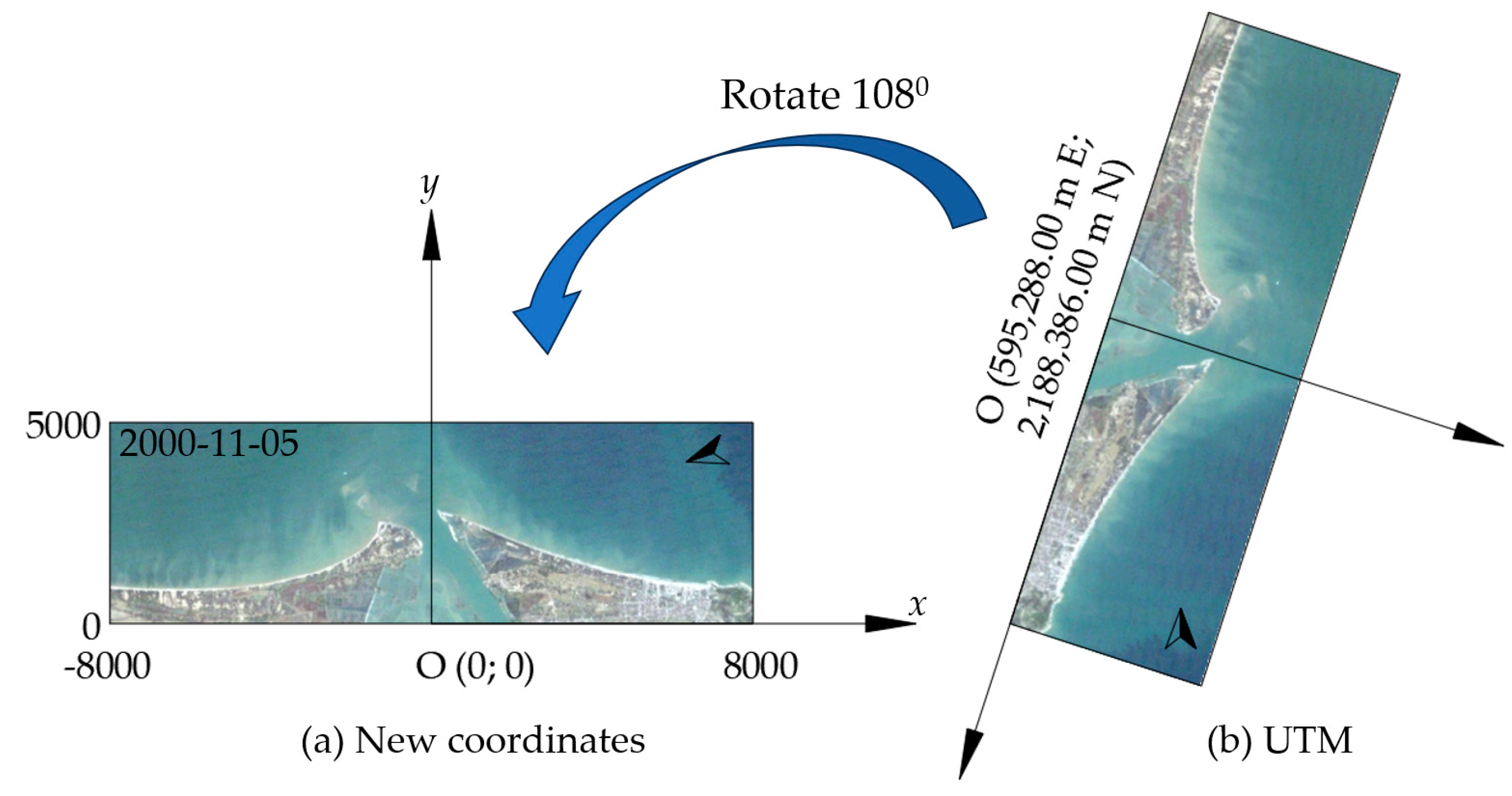
Preprints 80437 g003
Preprints 80437 g004
Figure 4. Shoreline configuration on 1991/02/14 is used to compare with the computed shoreline using the analytical solution.
Figure 4. Shoreline configuration on 1991/02/14 is used to compare with the computed shoreline using the analytical solution.
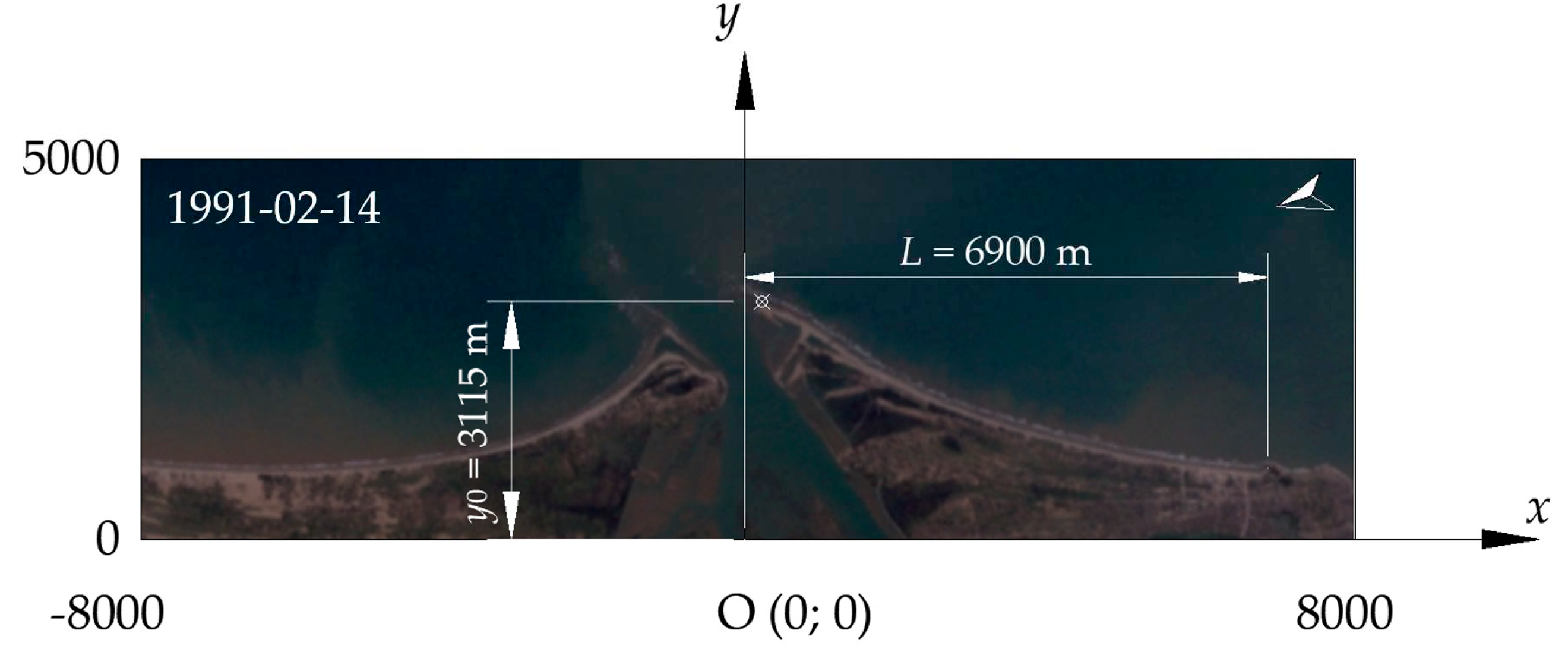
Preprints 80437 g004
Preprints 80437 g005
Figure 5. The sketch for measuring the tips’ coordinates on the north (xn, yn) and south (xs, ys) of the Ma River mouth.
Figure 5. The sketch for measuring the tips’ coordinates on the north (xn, yn) and south (xs, ys) of the Ma River mouth.
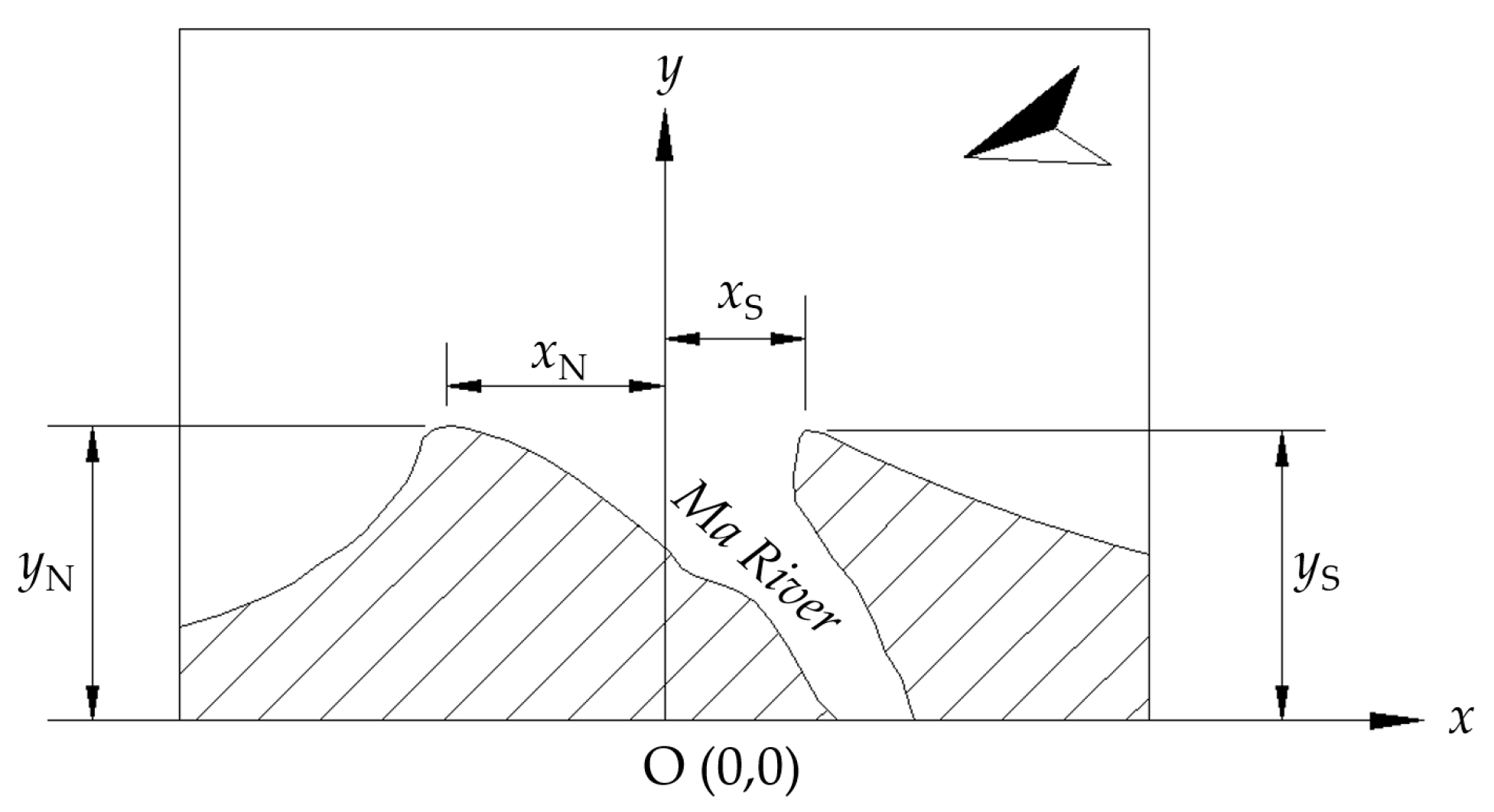
Preprints 80437 g005
Preprints 80437 g006
Figure 6. Angles of the delta cuspate on the north (qN) and the south (qS).
Figure 6. Angles of the delta cuspate on the north (qN) and the south (qS).
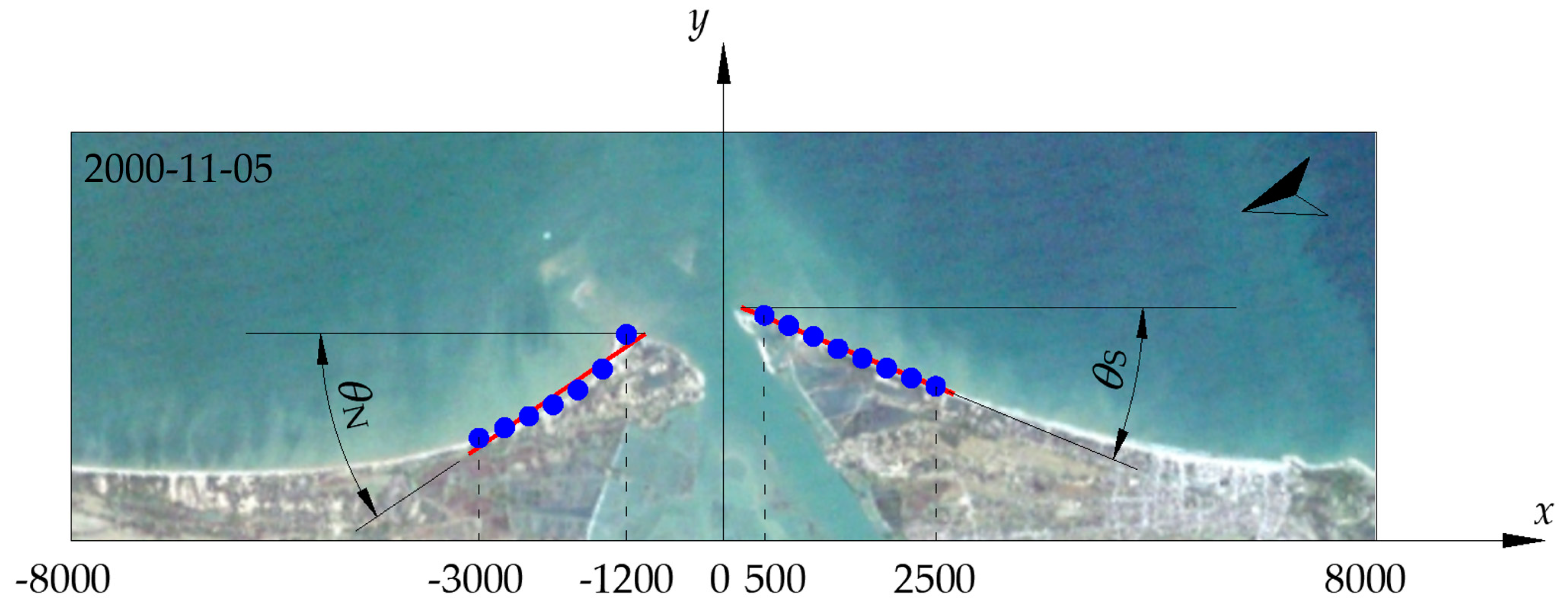
Preprints 80437 g006
Preprints 80437 g007
Figure 7. (a) Temporal variation of shorelines at the Ma River mouth, (b) Beach erosion due to northward shifting of the river mouth and a sea dike was built by the local government to reduce wave forces prior to the construction of an embankment to prevent coastal erosion (image downloaded from Google™ earth).
Figure 7. (a) Temporal variation of shorelines at the Ma River mouth, (b) Beach erosion due to northward shifting of the river mouth and a sea dike was built by the local government to reduce wave forces prior to the construction of an embankment to prevent coastal erosion (image downloaded from Google™ earth).
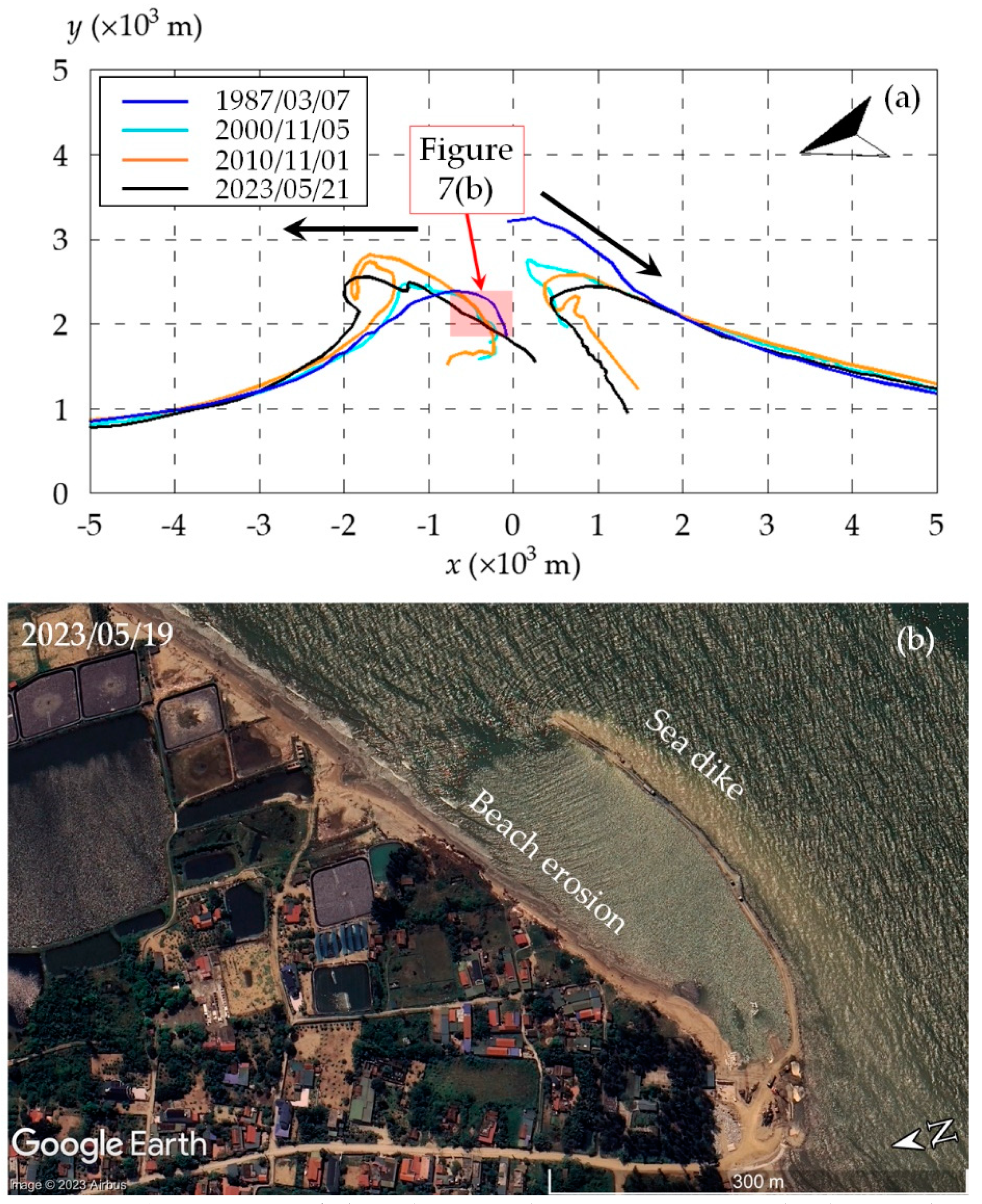
Preprints 80437 g007
Preprints 80437 g008
Figure 8. Comparison between computed shoreline and measured shoreline in 1991.
Figure 8. Comparison between computed shoreline and measured shoreline in 1991.
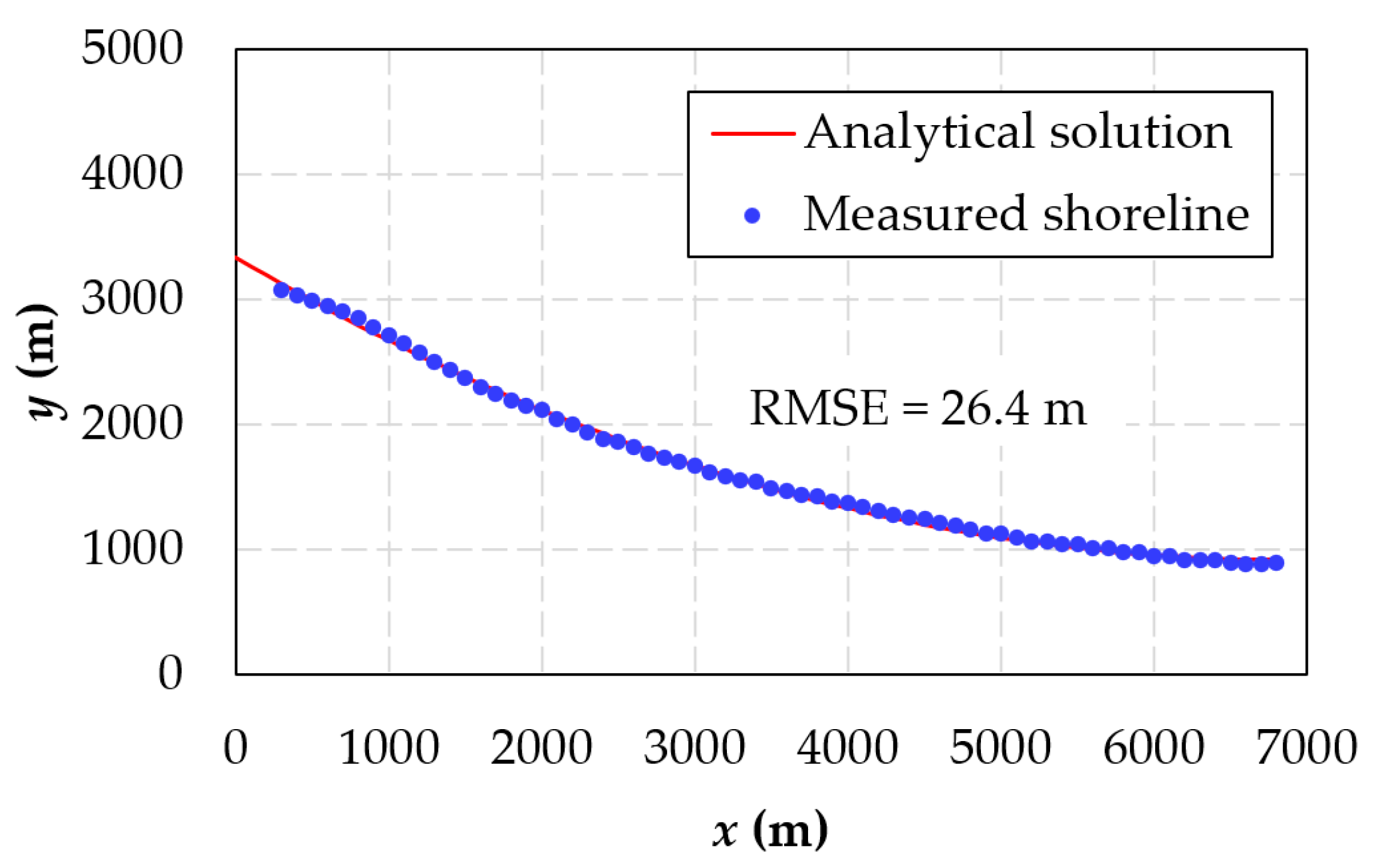
Preprints 80437 g008
Preprints 80437 g009
Figure 9. Temporal variation of the northern and southern cuspates’ tips coordinates in the along-shore direction.
Figure 9. Temporal variation of the northern and southern cuspates’ tips coordinates in the along-shore direction.
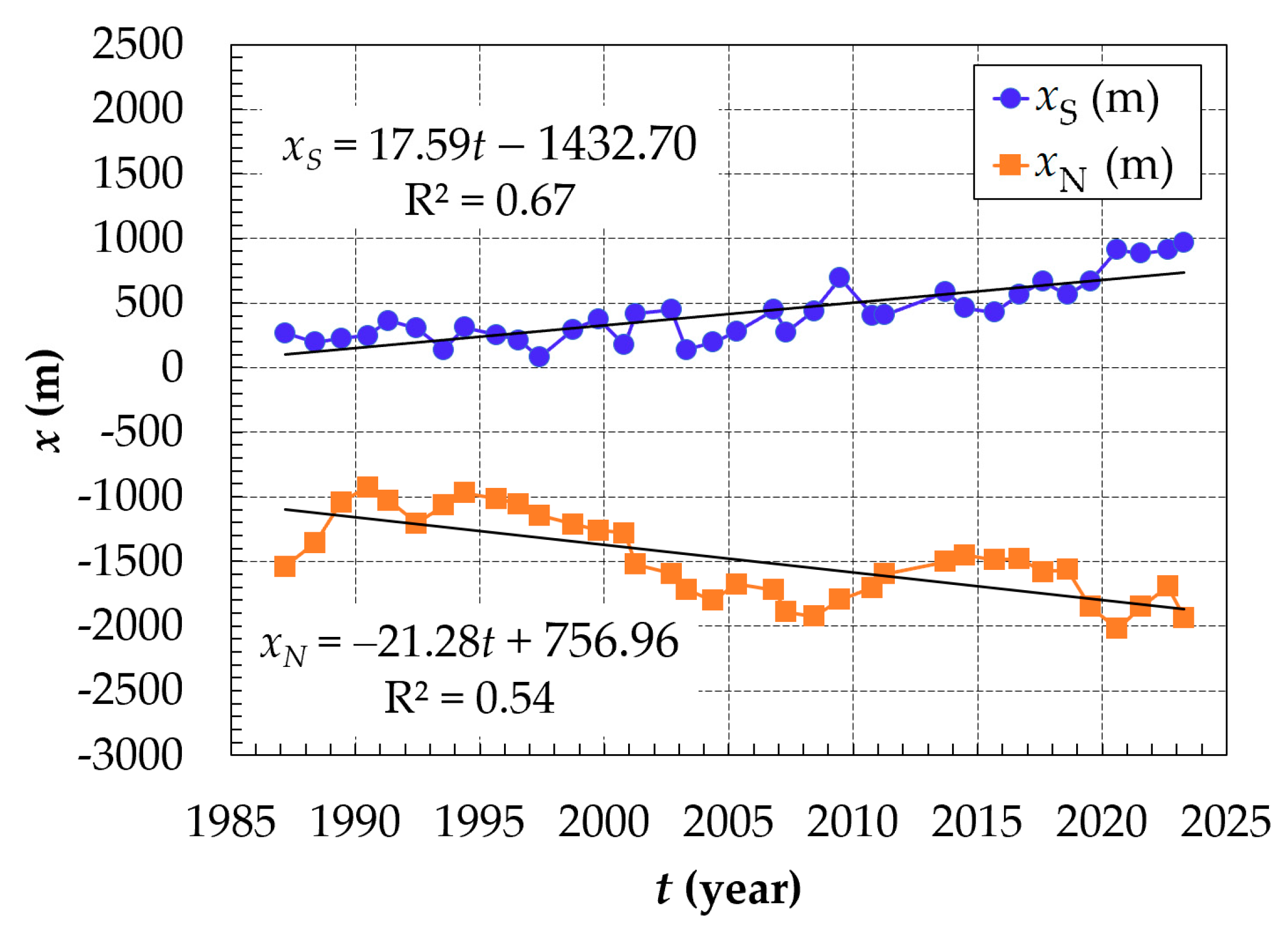
Preprints 80437 g009
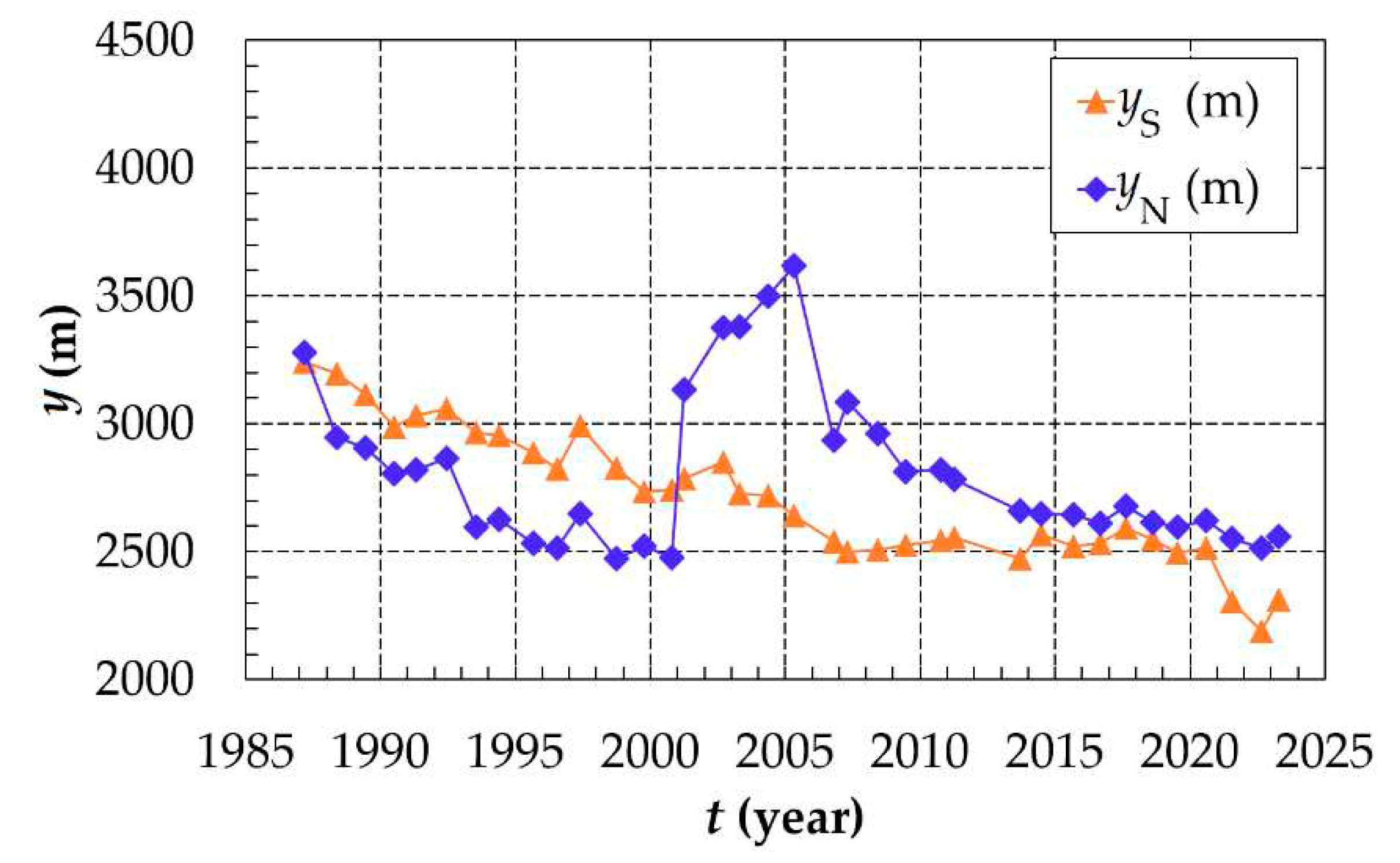
Preprints 80437 g010
Figure 10. Temporal variation of the northern and southern cuspates’ tips coordinates in the cross-shore direction.
Figure 10. Temporal variation of the northern and southern cuspates’ tips coordinates in the cross-shore direction.
Preprints 80437 g010
Preprints 80437 g011
Figure 11. Shoreline orientations on both sides of the river mouth.
Figure 11. Shoreline orientations on both sides of the river mouth.
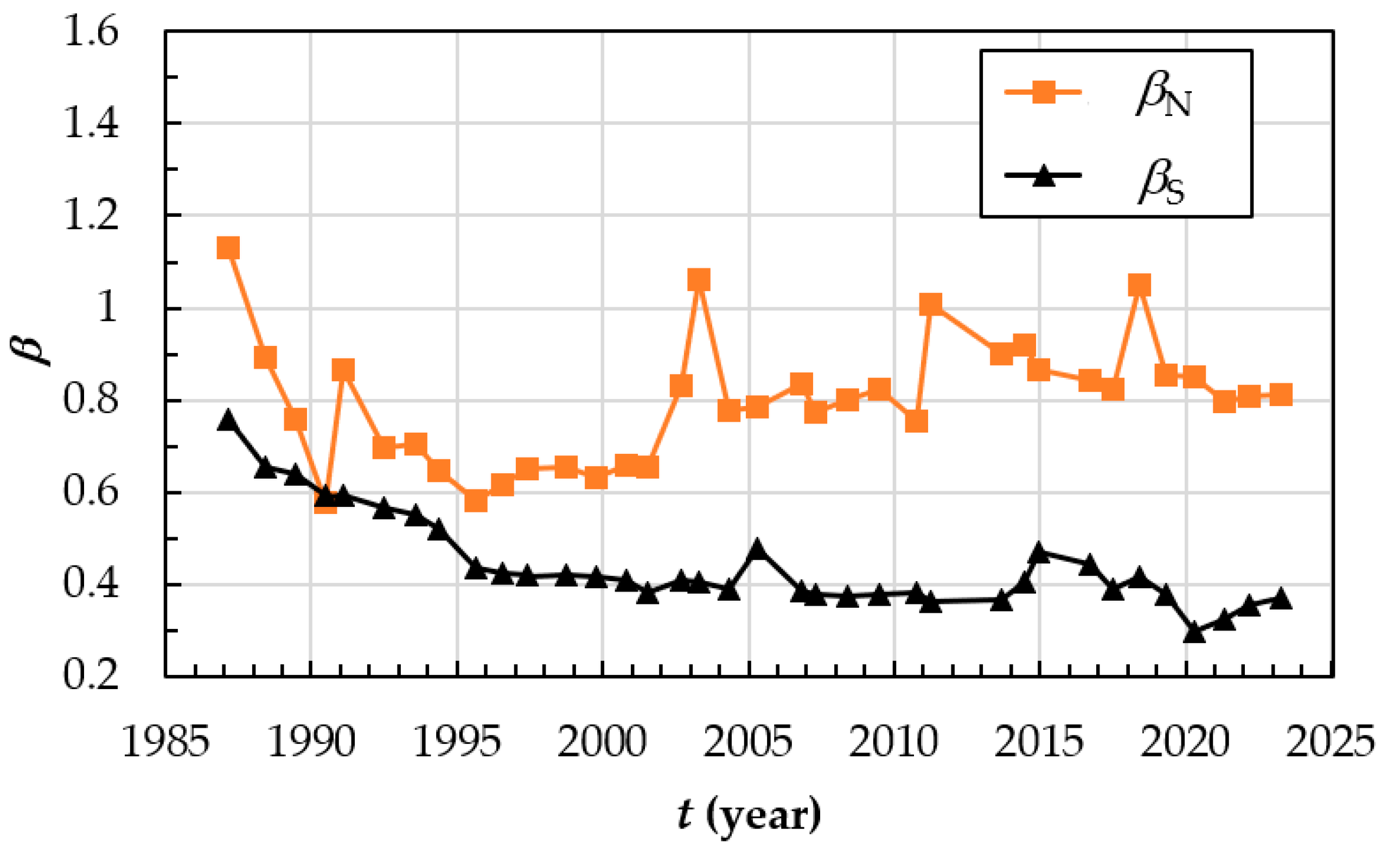
Preprints 80437 g011
Preprints 80437 g012
Figure 12. Ratio of sand supply to the north.
Figure 12. Ratio of sand supply to the north.
Preprints 80437 g012
Preprints 80437 g013
Figure 13. Symmetric sand distributed at the rivermouth and along-shore sand transport rate.
Figure 13. Symmetric sand distributed at the rivermouth and along-shore sand transport rate.
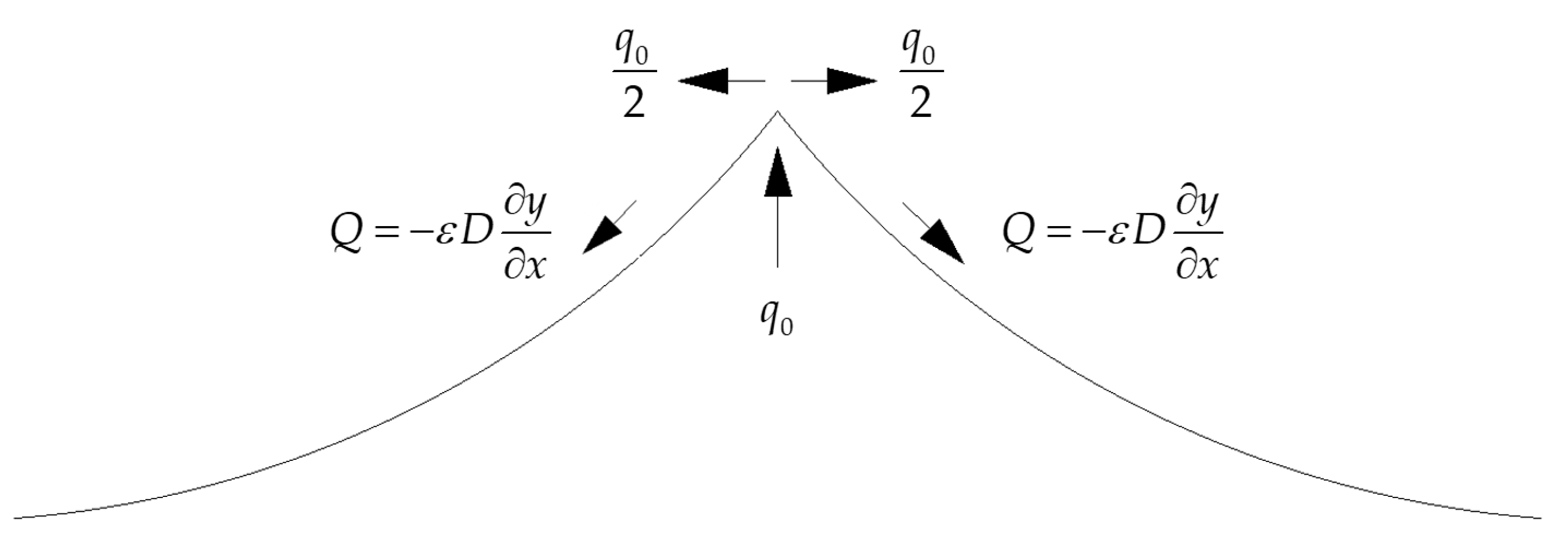
Preprints 80437 g013
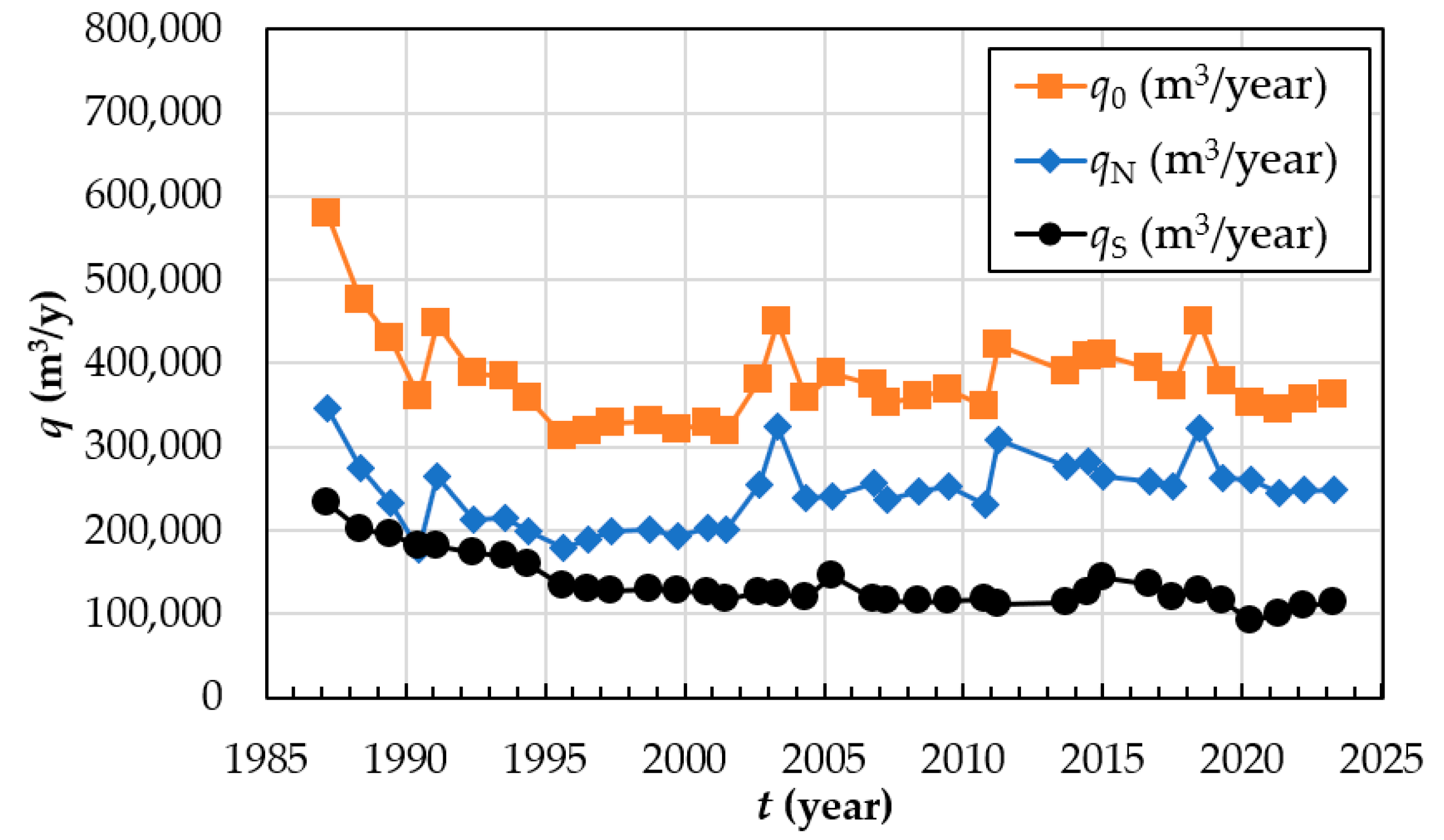
Preprints 80437 g014
Figure 14. Ratio of sand supply to the north.
Figure 14. Ratio of sand supply to the north.
Preprints 80437 g014
Table 1. Information of Landsat images.
Table 1. Information of Landsat images.
No. Date (yyyy/mm/dd) Sensor Resolution (m) Data Source
1 1987/03/07 TM 30 Landsat 5
2 1988/05/28 TM 30 Landsat 5
3 1989/06/16 TM 30 Landsat 5
4 1990/07/05 TM 30 Landsat 5
5 1991/02/14 TM 30 Landsat 5
6 1992/06/24 TM 30 Landsat 5
7 1993/07/29 TM 30 Landsat 5
8 1994/05/29 TM 30 Landsat 5
9 1995/09/05 TM 30 Landsat 5
10 1996/08/06 TM 30 Landsat 5
11 1997/06/06 TM 30 Landsat 5
12 1998/10/15 TM 30 Landsat 5
13 1999/10/18 TM 30 Landsat 5
14 2000/11/05 TM 30 Landsat 5
15 2001/07/19 TM 30 Landsat 5
16 2002/09/24 TM 30 Landsat 5
17 2003/05/06 TM 30 Landsat 5
18 2004/05/24 TM 30 Landsat 5
19 2005/05/11 TM 30 Landsat 5
20 2006/11/06 TM 30 Landsat 5
21 2007/05/01 TM 30 Landsat 5
22 2008/06/20 TM 30 Landsat 5
23 2009/07/09 TM 30 Landsat 5
24 2010/11/01 TM 30 Landsat 5
25 2011/04/26 TM 30 Landsat 5
26 2013/10/08 OLI/TIRS 30 Landsat 8
27 2014/07/23 OLI/TIRS 30 Landsat 8
28 2015/01/15 OLI/TIRS 30 Landsat 8
29 2016/10/07 OLI/TIRS 30 Landsat 8
30 2017/07/31 OLI/TIRS 30 Landsat 8
31 2018/07/02 OLI/TIRS 30 Landsat 8
32 2019/05/18 OLI/TIRS 30 Landsat 8
33 2020/05/20 OLI/TIRS 30 Landsat 8
34 2021/05/23 OLI/TIRS 30 Landsat 8
35 2022/04/08 OLI/TIRS 30 Landsat 8
36 2023/05/21 OLI/TIRS 30 Landsat 9
Table 2. Initial values of variables used for modeling the evolution of the Ma River delta using the analytical solution of Duy et al [18].
Table 2. Initial values of variables used for modeling the evolution of the Ma River delta using the analytical solution of Duy et al [18].
Diffusion coefficient, (m2/day) unknown
Sediment supply from the river, q0 (m3/y) 390,000
Formation time, t (yr) 500
Depth of closure, DC (m) 5.6
Berm height, DB (m) 1.8
Length of the shoreline, L (m) 6,900
Table 3. Final values of variables used for modeling the evolution of the Ma River delta using the analytical solution of Duy et al. [18].
Table 3. Final values of variables used for modeling the evolution of the Ma River delta using the analytical solution of Duy et al. [18].
Diffusion coefficient, ε (m2/day) 90
Sediment supply from the river, q0 (m3/y) 350,000
Formation time, t (yr) 500
Depth of closure, DC (m) 5.6
Berm height, DB (m) 1.8
Length of the shoreline, L (m) 6,900
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated