Prerpints.org logo
Preprint
Article

EvolveNet: Evolving Networks by Learning Scale of Depth and Width

Altmetrics

Downloads

100

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 July 2023

Posted:

26 July 2023

You are already at the latest version

Alerts
Abstract
Convolutional Neural Networks (CNNs) are largely hand-crafted, which leads to inefficiency in the constructed network. Various other algorithms have been proposed to address this issue, but the inefficiencies resulting from human intervention have not been addressed. Our proposed EvolveNet algorithm is a task-agnostic evolutionary search algorithm that can find optimal depth and width scales automatically in an efficient way. The optimal configurations are not found using grid search, instead evolved from an existing network. This eliminates inefficiencies that emanate from hand-crafting, thus reducing the drop in accuracy. The proposed algorithm is a framework to search through a large search space of subnetworks until a suitable configuration is found. Extensive experiments on the ImageNet dataset demonstrate the superiority of the proposed method by outperforming the state-of-the-art methods.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

Convolutional Neural Network (CNN) is one of the most significant networks in the field of deep learning, showing decent performance in various computer vision tasks including classification [1,2], semantic segmentation [3,4], and action recognition [5,6]. They were designed to extract two-dimensional features by taking structured data such as images as input and then processing them using convolutional operators [7,8]. Studies have shown that a larger number of layers results in increased receptive fields and therefore captures more detail of the image [9]. Recent networks have achieved higher accuracy by becoming deeper and more complex [10,11,12]. There have also been cases of improved block architecture that yielded higher accuracy without significantly increasing the size of the networks [13,14].
Scaling is a widely used technique to achieve better accuracy and numerous methods have been utilized to scale networks. Upscaling depth is the most prevalent method, although scaling models by image resolution is also becoming increasingly popular. Figure 1 represents the depth and width of a network. EfficientNet [15] was created by compound scaling MobileNets [14,16] and ResNet [9] networks, i.e., scaling the network width, depth, and resolution by fixed coefficients. Upscaling, however, could result in the configurations of the upscaled networks being ill-suited to their tasks because hand-crafting networks lead to human errors and consequent inaccuracies, resulting in an inefficient network. Filter pruning has long been considered a good alternative to accelerate deep neural networks, but this does not solve the core inefficiencies in the construction of the network. He et al. [9] observed that the accuracy of a network saturates quickly as its size increases. In other words, the accuracy gain diminishes as networks get larger because all parameters in a network have different sensitivity to its accuracy.
Identifying these superfluous parameters in a network is crucial to the optimization process. The Lottery Ticket Hypothesis [17] states that any trained dense neural network contains a subnetwork (called a winning ticket) which, when trained in isolation for at most the same number of epochs, can match the test accuracy of the original network. Automated Machine Learning (AutoML) [18] introduced the process of automating the steps in the machine learning pipeline, from hyperparameter optimization to parameter evaluation. This concept has been applied for Neural Architecture Search (NAS) [19,20,21] to optimize the search for winning tickets within large networks. However, applying AutoML concepts for NAS has wider consequences that can be aggravated during the search stage. The No Free Lunch Theorem [22] posits that no universal optimization algorithm consistently outperforms all other algorithms across every optimization problem. Therefore, it is necessary to optimize networks with respect to the tasks at hand.
Networks can be optimized by removing all channel connections in the depth-wise layer, instead increasing the number of channels to boost capacity [15]. This reduces the number of parameters, but significantly increases data movement, resulting in poor performance on hardware accelerators. The final scaling coefficients are determined by grid search [23]. However, the search cost of using grid search is very expensive when scaling larger networks. Therefore, scaling algorithms are primarily applied to small networks, and large networks are created by massively upscaling small networks. The proposed algorithm addresses this issue by downscaling large networks to generate slightly smaller networks. Larger networks downscaled from models designed with larger channel connections in mind would not increase the number of channels. Thus, the generated network is similar in both size and accuracy to the large networks but is much closer in size to its corresponding original network. Grid search can be used to search through various scaling coefficients until the ideal network size was found, but this is only possible with relatively smaller networks like MobileNets and ResNet-50 [24]. However, as the size of the networks increases, the search space also increases exponentially.
Evolutionary algorithms have been found to significantly outperform random and systemic search methods when searching in large search spaces [25]. Over the years, various multi-objective evolutionary algorithms have been proposed to varying degrees of success [26,27]. But they tend to suffer from a weak global search ability in low inter-task relevance problems [28] because the cross-over operator is unable to distinguish between information and noise. This problem can be addressed by introducing multiple search strategies into the fitness landscape. Incorporating multiple objectives into the fitness function is crucial to evolve an efficient network with high accuracy.
In this paper, we present a framework to automatically generate the optimal number of layers and channels for a network without manual interference. We use evolutionary algorithms to search through the large sample space of possible subnetworks to address this issue. The proposed method uses evolutionary search to find an optimized subnetwork that keeps the number of parameters low without compromising accuracy. Instead of upscaling networks, a collection of layers and channels are downscaled to find the optimal configuration. The evolved network is built to counteract the lack of expressiveness and effectiveness that is inherent to hand-crafted and grid-searched networks. Generated networks counteract these drawbacks by integrating pruning concepts into the creation of new networks, resulting in more efficient networks.
Our contribution lies in three folds:
  • We propose an algorithm to counter inefficiencies in subnetworks by evolving task-agnostic networks of ideal depth and width for a given architecture.
  • We created a framework to efficiently search through a large sample space of subnetworks to identify smaller networks without a major loss in accuracy.
  • We experimentally show the superiority of the network generated by the proposed method on publicly available pre-trained CNNs.
The remainder of this study is organized as follows: Section 3 briefly discusses the algorithm and its working concept, and Section 4 describes the result of experiments conducted on networks evolved using the EvolveNet algorithm. We also discuss the advantages and future work of this algorithm in Section 4.4 and conclude this study in Section 5.

2. Related Works

2.1. Convolutional Neural Networks

CNN is the popular design choice for visual recognition tasks and has gone through many upgrades over the years. VGG [29] used very small convolution filters and increased the depth of the model to achieve high accuracy. GoogLeNet [30] proposed the idea of an Inception module to find the optimal local sparse structure in a CNN that can be approximated by its dense components. ResNet [9] stacked layers to fit a residual mapping using skip connections, which further improved the accuracy. MobileNet [16] introduced depth-wise separable convolution layers which separated the filtering and combining operations of the convolution operation, which in turn reduced the computational complexity and model size. DenseNet [13] connected all layers to combine the feature maps together instead of just the feature summations, resulting in larger models with higher accuracy. ConvNeXt [1] improved a standard ResNet by gradually modernizing the architecture to construct a hierarchical vision transformer, Swin-T [31]. These models have one thing in common; beyond just the architecture or convolution layers, the depth of the networks and width of each layer were handcrafted by humans.

2.2. Neural Architecture Search

Searching for optimal network structures has been studied using reinforcement learning [11,32], gradient-based approaches [33], parameter sharing [34], weight prediction [35], and genetic algorithms [36,37]. Zoph et al. [11] uses reinforcement learning to optimize the networks generated from the model descriptions given by a recurrent network. MetaQNN [32] uses reinforcement learning with a greedy exploration strategy to generate high-performance CNN architectures. Gradient-based learning allows a network to efficiently optimize new instances of a task [38]. FBNets (Facebook-Berkeley-Nets) [33] uses a gradient-based method to optimize CNNs created by a differentiable neural architecture search framework. DARTS [39] formulate tasks in a differentiable manner to address the scalability of the architecture search. LEMONADE [40] penalizes excessive resource consumption by approximating the network morphism operators while generating subnetworks. ENAS [41] constructs a large computational graph, where each subgraph represents a neural network architecture. Thus all subgraphs share parameters, delivering strong empirical performances while using a lower amount of resources. TE-NAS [42] ranks the architectures by analyzing the spectrum of the neural tangent kernel and the number of linear regions in the input space, which imply the trainability and expressivity of the networks. RENAS [43] integrates reinforced mutation into the evolutionary search algorithm for architectural exploration, which efficiently evolves the model.
Evolutionary algorithms are widely used to deal with complex and non-linear optimization problems [44,45,46]. It is a common solution for difficult real-world problems where the sample space is large. Genetic algorithms are used to solve search and optimization problems using bio-inspired operators [36]. Real et al. [37] uses genetic algorithms to discover neural network architectures, minimizing the role of humans in the design.

2.3. Network Scaling

Network scaling is necessary to keep up with the growing datasets that have very large samples and large memory requirements. Network scaling is usually implemented on network architectures after they are constructed. Residual Networks [9] were scaled up to ResNet-200, and down to ResNet-18. WideResNet [47] is a width-scaled interpretation of the original Residual Network, with the number of channels in various layers increased to increase the resolution of feature maps. Modern CNNs have also been shown to use higher-resolution input images. Higher accuracies were obtained when using higher resolution images at 299 × 299 [48] and 331 × 331 [12]. Dryden et al. [49] exploits parallelism in convolutional layers beyond data parallelism to tackle scaling and memory issues. However, this does not focus on batch normalization, ReLUs, pooling, and fully-connected layers which are also present in conventional networks.

3. EvolveNet

EvolveNet algorithm attempts to build new networks from scratch by evolving an ideal configuration of layers for a pre-defined architecture. There are four major steps to EvolveNet: 1) Filter training to strengthen the individuality of layers, 2) Depth evolution to find the ideal number of layers, 3) Width evolution to compute the ideal width for each layer, and 4) Retraining to fine-tune the evolved network.
Pre-built networks used bottleneck blocks used by EfficientNet. The bottleneck blocks allow the network to reduce the number of parameters, and consequently, the number of floating-point operations. This makes the network more compact and efficient. The bottleneck operation consists of three operators: a linear transformation followed by a non-linear transformation, then another linear transformation. Each bottleneck first expands a low-dimensional feature map into a high-dimensional feature map using a point-wise convolution. A depth-wise convolution then performs spatial filtering on the high-dimensional tensor. Finally, another point-wise convolution projects the spatially-filtered map back down into a low-dimensional tensor.

3.1. Filter Training

An initial network N is constructed as a set of layers and filters whose configurations are ideal as found from existing network architectures as follows:
N = { L j : j ∈ ( 0 , N ) } ,
where L j represents each layer with channel and kernel sizes. N is the total number of layers, with each group of a layer consisting of N * layers. Using the weights θ , the new collection of layers is derived into a pseudo network N θ * , which is a parameterized subset of the layers in N , i.e., N θ * ⊆ θ ( N ) . During each epoch of the training stage, random layers and filters are chosen to be trained which omits certain layers and filters from N as shown in Figure 2. N θ * is trained and its cross-entropy loss is computed as follows:
L D t ( N θ * ) = − ∑ i = 1 n t i log p i ,
where L D t represents the cross entropy loss w.r.t. training data D t , and t i and p i are the truth label and softmax probability of class i w.r.t. N θ * . This loss is smoothed as a consequence of cross-entropy, then backpropagated through every layer of N including the omitted layers as follows:
θ ← θ − β ∂ L ( N θ ) ∂ θ ,
where β is the learning rate, adjusted by the Lambda scheduler [50] to converge quickly and optimally. This trains the larger network, which will have layers that can efficiently be recalibrated into smaller networks composed of only a few of its layers without impacting the overall accuracy. Each layer contributes to the feature map without taking away from the feature map of the larger network, which is made up of other layers trained in a similar fashion.

3.2. Evolving Depth

The network N θ , which is now a collection of layers that have been trained to work independently of the network, is used to evolve a recalibrated network with ideal depth configurations. Configurations of the architecture of each block, such as the number of out-channels, kernel sizes, and strides of each layer remain the same as before. The depth of the recalibrated network, i.e., the layers chosen to be trained, are chosen by Depth Encoding Vectors (DEVs). DEV is a vector that has the depths of each layer of the recalibrated network encoded into it as the presence or absence of a layer in the network. These DEVs generate networks of parameter sizes within preset constraints, and the computed reward is assigned as the reward of each DEV. Since N θ is only a collection of layers strung together to build a network, the recalibrated layer, the layers of which are chosen by the DEV, shows the various layers that will be present in the network to be built.
The reward function computes the pre-train accuracy of the generated network. The networks are then evolved as chromosomes under the same preset constraints to maximize their rewards, as seen in Algorithm 1. The best chromosomes are chosen, then mutated, and crossed over to be propagated through to the next chromosome pool. Mutation is the genetic operation of flipping arbitrary genes in a parent chromosome to generate offspring. Cross-over is the genetic operation of combining the genetic information of the two parent genes to generate offspring. In EvolveNet, the mutation is implemented by giving every gene on a random chromosome the 10% chance to be switched to a random new gene. Cross-over is implemented by choosing two random chromosomes and then selecting a gene from either chromosome with a 50% chance of being selected from either parent. We assume that every genetically modified offspring will not be better than every parent, hence the subsequent chromosome pools are selected from the overall pool and not just the genetically modified pool.
After multiple chromosome pools are generated, the best chromosome is chosen and the network generated from it has the ideal depth configuration for a network block architecture for the given task.
Algorithm 1 Algorithm for evolving Depth
Preprints 80505 i001

3.3. Evolving Width

The best DEV after depth evolution is used to build a recalibrated network for width evolution, as explained in Algorithm 1. The recalibrated network is then used to compute rewards for the networks derived from it, using the Width Encoding Vectors (WEVs). Unlike DEVs, each WEV is injectively mapped to a network of specific depth and layers of out-channels, i.e., the networks created by every WEV are unique to each element in it, and also to the DEV it is evolved from. As shown in Figure 3, 50 WEVs are built from the recalibrated network, and their rewards are computed. Each gene of a chromosome, represented by the WEV, is encoded with the ratio of channels of each layer compared to the original. The individual genes chosen do not matter, as this evolution is used to resolve the size of the final network, not the specific configuration. The size of each chromosome is dependent on the size of the recalibrated network. At every step before evolution, random chromosomes are used to generate sub-networks for the recalibrated network, and their reward is computed agnostic to the training dataset. The chromosomes with the highest rewards are mutated and crossed over, and the subsequent chromosome pool is created by selecting the best chromosomes from a pool of the parents and their offspring.
The chromosome with the highest reward from the final chromosome pool is used to derive the final network from the recalibrated network. The final derived network has had its depth and width evolved to be ideal for the given task and architecture.

3.4. Retraining

Once the final configurations of the network have been evolved, the derived network is retrained to achieve competitive accuracy with minimum parameters. The final network is a subnetwork, hence according to Frankle et al., it has to be trained to achieve similar accuracy. The number of retraining epochs is determined by the network whose architecture is used to build N θ , i.e., EfficientNet [15]. The number of layers and their configurations have been determined by the DEV, while the number of channels in each specific layer is determined by the WEV. Thus, unlike in EfficientNet, where the network configuration was found using grid search, the channel configurations of the final network here are selected by evolutionary computation without manual influence.

4. Experiments

In this section, we demonstrate the superiority of networks generated by EvolveNet. We compare the results obtained with other major state-of-the-art models. Lastly, we discuss the impact of various hyperparameters to understand their impact on the proposed method.

4.1. Experimental Settings

The networks generated were trained on ImageNet dataset [51] for image classification tasks. The kernel sizes were selected after conducting ablation studies and the best results were found for kernels of sizes 1 × 1 and 3 × 3 . In other words, the ideal resolution was hand-crafted. The images were randomly cropped to size 224 × 224 , after resizing to 256 × 256 , to augment the data. Experiments were conducted on four NVIDIA RTX A6000 GPUs with 40 workers and a batch size of 512.

4.2. Evaluation Protocol

We measured the Top-1 and Top-5 accuracies, as well as the number of parameters, to evaluate the evolved networks and compared them to existing state-of-the-art networks. The primary aim of this experiment is to showcase an improvement in the performance and efficiency of a network before and after the depth and width have evolved. Accuracy is the proportion of images that have been labeled correctly. For each image, the network computes the probability of them being classified into each label. Top-1 accuracy is the proportion of images in which the predicted label is the same as the actual label. Top-5 accuracy is the proportion of images where the actual label is present as at least one of the top five predictions. A fewer number of parameters result in a more streamlined and efficient network.

4.3. Experimental Results

We present the performance of different networks created using EvolveNet. The networks have been created by setting the parameter size as a constraint and generating networks with an ideal network configuration. The generated networks have been called EvolveNet-XS, EvolveNet-S, EvolveNet-M, and EvolveNet-L. These networks are then compared with state-of-the-art methods of similar size.

4.3.1. Performance against Very Small Networks

A set of very small state-of-the-art networks including DenseNet121 [13], HRFormer-T [52], EfficientNetB1 [15], and EfficientNetV2B1 [53] are selected for comparing to EvolveNet-XS. Table 1 presents the result of the comparison with those networks. EvolveNet-XS shows Top-1 and Top-5 accuracy of 80.4% and 95.1% respectively, with 7.8M parameters. Overall, it shows competitive performance compared to other methods with the least number of parameters. It outperforms DenseNet121 and HRFormer-T by 5.4% and 1.9% in Top-1 accuracy. Also, it has 0.3M fewer parameters compared to DenseNet121. EvolveNet-XS shows comparable performance to the EfficientNetB1 and EfficientNetV2B1. The difference in number of parameters between EfficientNetB1 and EvolveNet-XS is only 0.1M. However, EvolveNet-XS shows a gain of 1.3% and 0.7% in Top-1 and Top-5 accuracies respectively. It outperforms EfficientNetV2B1 by small margins of 0.6% and 0.1% in Top-1 and Top-5 accuracies respectively, in spite of having 0.4M fewer parameters.

4.3.2. Performance against Small Networks

Table 2 presents the results of the EvolveNet-S network compared to small networks including EfficientNetB2 [15], and EfficientNetV2B1 [53]. EvolveNet-S shows Top-1 and Top-5 accuracy of 81.1% and 95.6% respectively, with 8.6M parameters. It shows competitive performance against those networks with the least number of parameters, outperforming LeViT-128 and ConViT-Ti+ by 1.5% and 4.4% respectively in Top-1 accuracy while using 0.2M and 1.4M parameters lower. EfficientNetV2B1 has 10.2M parameters with Top-1 and Top-5 accuracy of 80.5% and 95.1% respectively. Although EvolveNet-S outperforms it by a small margin of 0.6% and 0.5% in Top-1 and Top-5 accuracy respectively, it has 1.6M fewer parameters than EfficientNetV2B1. Similarly, EvolveNet-S outperforms EfficientNetB2 by a small margin of 0.7% in Top-5 accuracy. It also shows a decent gain of 1.0% in Top-1 accuracy with 0.6M fewer parameters compared to EfficientNetB2.

4.3.3. Performance against Medium-sized Networks

A set of medium-sized networks including DenseNet169 [13], TinyNet [58], EfficientNetB3 [15], EfficientNetV2B3 [53] are selected for comparing EvolveNet-M network. Table 3 shows the results for EvolveNet-M compared to these networks. It shows top-1 and top-5 accuracy of 82. 8% and 96. 3%, respectively. Overall, it outperforms other networks by a decent margin, with fewer parameters. It outperforms SAMix ResNet-18, which has 0.4M more parameters, by 10.5%. DenseNet169, with 14.3M parameters, shows 76.2% and 93.2% of Top-1 and Top-5 accuracy, respectively. However, EvolveNet-M with 3M fewer parameters outperforms it by a significant margin of 6.6% and 3.1% in Top-1 and Top-5 accuracies. Similarly, it outperforms TinyNet by 3.4% and 1.8% in Top-1 and Top-5 accuracy, respectively, despite having 0.6M fewer parameters. EvolveNet-M shows comparable performance with EfficientNetB3 and EfficientNetV2B3 in Top-5 accuracy. It outperforms them by a small margin of 0.6% and 0.5%. However, EvolveNet-M has 1M and 3.2M fewer parameters, respectively. Also, the Top-1 accuracy of EvolveNet-M is 1.2% and 0.8% higher than EfficientNetB3 and EfficientNetV2B3, respectively.

4.3.4. Performance against Large Networks

For the comparison of EvolveNet-L, a collection of larger networks with a significantly large number of parameters is selected. These include Xception [59], ConNeXtTiny [1], ConvNeXtSmall [1], NASNETLarge [12] and EfficientNetB4 [15]. The results of EvolveNet-L compared to the above networks are presented in Table 4. EvolveNet-L outperforms other networks with a decent margin in Top-1 accuracy, with the least number of parameters. It shows Top-1 and Top-5 accuracy of 83.2% and 96.5% respectively, with 17.6M parameters. The performance of EfficientNetB4 with Top-1 and Top-5 accuracy of 82.9% and 96.4% respectively are comparable to EvolveNet-L. However, EvolveNet-L has significantly fewer parameters compared to EfficientNetB4. With 1.9M fewer parameters EvolveNet-L outperforms it by 0.3% and 0.1% in Top-1 and Top-5 accuracy respectively. EvolveNet-L has significantly fewer parameters than NASNETLarge. In spite of having 71.3M fewer parameters, it outperforms NASNETLarge by 0.7% and 0.5% in Top-1 and Top-5 accuracy respectively. Similarly, with 32.6M fewer parameters, it outperforms ConvNeXtSmall by 0.9% in Top-1 accuracy. EvolveNet-L outperforms ConvNeXtTiny by a decent margin of 1.9% in Top-1 accuracy despite having 11M fewer parameters. Xception has 22.9M parameters and shows Top-1 and Top-5 accuracy of 79.0% and 94.5% respectively. However, EvolveNet-L with 5.3M fewer parameters outperforms it by a decent margin of 4.2% and 2.0% in Top-1 and Top-5 accuracy respectively.

4.4. Discussion

We have experimentally shown that the networks generated by the Depth and Width Encoding Vectors evolved using the EvolveNet method consistently show better performance when compared to EfficientNet while maintaining their architecture. The improvement is significant, and the generated network can still be pruned using the same methods that are used on EfficientNet and other similar CNNs. Hence, it can be inferred that the architecture computed by evolution outperforms the architectures computed using the grid-search method. MobileNetV2 introduced inverted residuals, and bottlenecks and improved the accuracy of MobileNetV1 using the new architecture. EfficientNet was an improvement on the MobileNetV2 architecture, where the accuracy of the network was improved by scaling the width, depth, and resolution of MobileNetV2 using grid-search. By evolving networks with higher accuracy and efficiency, EvolveNet has experimentally proven that hand-crafting and grid search are not ideal methods to build networks. Pruning algorithms have shown that a randomly initialized dense network contains multiple sub-networks with fewer parameters and comparable accuracies. However, most pruning algorithms limit themselves by trying to reduce the number of parameters. Since the proposed algorithm evolves networks to emphasize ideal configurations while maximizing rewards, the focus is placed on accuracy, and efficiency is taken care of as a consequence of it. This allows for high accuracies on a relatively smaller network.
The generated network is also independent of the original network, but given the original network and the depth and width encoding vectors, the network can be regenerated. The generated network is injectively mapped to each DEV and WEV, and the number of layers in the larger network. Therefore, changing any of these encoding vectors will significantly change the final network. The number of randomly generated layers, from which recalibrated networks are generated, is a hyperparameter used to control the size of the final network, but it has no other bearing on the evolution of the final network. This can be seen in Table 5. Before evolving the width of the final network, the number of out-channels in each layer is equal to the number of out-channels in MobileNetV2. The structure is the same as that of each block in EfficientNet and MobileNetV2. There is one fixed-out channel for each block layer, but the number of additional blocks is determined by the network encoding vector.

5. Conclusions

In this study, we described a simple evolutionary algorithm to evolve ideal depths and widths that are task-agnostic for a given architecture. We also experimentally proved its superiority over networks where the architecture was hand-crafted or grid-searched. EvolveNet is dependent on the architectures of individual blocks in a network, but not the network as a whole. The architecture used can be replaced with better-performing architectures, but the hyperparameters that constrain the network should be adjusted appropriately. In the future, we intend to pursue this research and improve the algorithm for the selection of chromosomes. Some constraints are more important to the overall schema than others, so treating them as the same would cause inefficiencies in the recalibrated network. EvolveNet can be made more robust with more experiments to understand the importance of the various hyperparameters that make it function.

Author Contributions

This research was conceptualized and the methodology and software were written by Athul Shibu. It was then validated and formally analyzed by Dong-Gyu Lee. The writing was drafted, reviewed, and edited by Athul Shibu under the supervision of Dong-Gyu Lee. The project is administered and funding is secured by Dong-Gyu Lee.

Funding

This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean Government (MSIT) (No.2021R1C1C1012590), (No. 2022R1A4A1023248), Project BK21 FOUR and the Information Technology Research Center (ITRC) support program supervised by the Institute of Information Communications & Technology Planning & Evaluation (IITP) grant funded by the Korean Government (MSIT) (IITP-2023-2020-0-01808).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The Imagenet dataset can be found at https://www.image-net.org/download.php.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A convnet for the 2020s. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 11976–11986.
  2. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Communications of the ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
  3. Sultana, F.; Sufian, A.; Dutta, P. Evolution of image segmentation using deep convolutional neural network: A survey. Knowledge-Based Systems 2020, 201, 106062. [Google Scholar] [CrossRef]
  4. Kumar, S.; Kumar, A.; Lee, D.G. Semantic Segmentation of UAV Images Based on Transformer Framework with Context Information. Mathematics 2022, 10, 4735. [Google Scholar] [CrossRef]
  5. Duan, H.; Zhao, Y.; Chen, K.; Lin, D.; Dai, B. Revisiting skeleton-based action recognition. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 2969–2978.
  6. Lee, D.G.; Lee, S.W. Human activity prediction based on sub-volume relationship descriptor. 2016 23rd International Conference on Pattern Recognition (ICPR). IEEE, 2016, pp. 2060–2065.
  7. Zhang, Q.; Zhang, M.; Chen, T.; Sun, Z.; Ma, Y.; Yu, B. Recent advances in convolutional neural network acceleration. Neurocomputing 2019, 323, 37–51. [Google Scholar] [CrossRef]
  8. Liu, Y.; Pu, H.; Sun, D.W. Efficient extraction of deep image features using convolutional neural network (CNN) for applications in detecting and analysing complex food matrices. Trends in Food Science & Technology 2021, 113, 193–204. [Google Scholar] [CrossRef]
  9. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
  10. Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 1492–1500.
  11. Zoph, B.; Le, Q.V. Neural architecture search with reinforcement learning. arXiv 2016, arXiv:1611.01578. [Google Scholar]
  12. Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning transferable architectures for scalable image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition. CVPR, 2018, pp. 8697–8710.
  13. Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 4700–4708.
  14. Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 4510–4520.
  15. Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. International conference on machine learning. PMLR, 2019, pp. 6105–6114.
  16. Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
  17. Frankle, J.; Carbin, M. The lottery ticket hypothesis: Finding sparse, trainable neural networks. arXiv 2018, arXiv:1803.03635. [Google Scholar]
  18. Hutter, F.; Kotthoff, L.; Vanschoren, J. Automated machine learning: methods, systems, challenges; Springer Nature, 2019.
  19. Elsken, T.; Metzen, J.H.; Hutter, F. Neural architecture search: A survey. The Journal of Machine Learning Research 2019, 20, 1997–2017. [Google Scholar]
  20. Yu, K.; Sciuto, C.; Jaggi, M.; Musat, C.; Salzmann, M. Evaluating the search phase of neural architecture search. arXiv 2019, arXiv:1902.08142. [Google Scholar]
  21. Mellor, J.; Turner, J.; Storkey, A.; Crowley, E.J. Neural architecture search without training. International Conference on Machine Learning. PMLR, 2021, pp. 7588–7598.
  22. Ho, Y.C.; Pepyne, D.L. Simple explanation of the no free lunch theorem of optimization. Proceedings of the 40th IEEE Conference on Decision and Control (Cat. No. 01CH37228). IEEE, 2001, Vol. 5, pp. 4409–4414.
  23. Liashchynskyi, P.; Liashchynskyi, P. Grid search, random search, genetic algorithm: a big comparison for NAS. arXiv 2019, arXiv:1912.06059. [Google Scholar]
  24. Hesterman, J.Y.; Caucci, L.; Kupinski, M.A.; Barrett, H.H.; Furenlid, L.R. Maximum-likelihood estimation with a contracting-grid search algorithm. IEEE transactions on nuclear science 2010, 57, 1077–1084. [Google Scholar] [CrossRef] [PubMed]
  25. Godefroid, P.; Khurshid, S. Exploring very large state spaces using genetic algorithms. Tools and Algorithms for the Construction and Analysis of Systems: 8th International Conference, TACAS 2002 Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2002 Grenoble, France, April 8–12, 2002 Proceedings 8. Springer, 2002, pp. 266–280.
  26. Zhang, T.; Qi, W.; Zhao, X.; Yan, Y.; Cao, Y. A local dimming method based on improved multi-objective evolutionary algorithm. Expert Systems with Applications 2022, 117468. [Google Scholar] [CrossRef]
  27. Zheng, W.; Sun, J. Two-stage hybrid learning-based multi-objective evolutionary algorithm based on objective space decomposition. Information Sciences 2022, 610, 1163–1186. [Google Scholar] [CrossRef]
  28. Chen, Q.; Ma, X.; Yu, Y.; Sun, Y.; Zhu, Z. Multi-objective evolutionary multi-tasking algorithm using cross-dimensional and prediction-based knowledge transfer. Information Sciences 2022, 586, 540–562. [Google Scholar] [CrossRef]
  29. Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
  30. Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 1–9.
  31. Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. Proceedings of the IEEE/CVF international conference on computer vision, 2021, pp. 10012–10022.
  32. Baker, B.; Gupta, O.; Naik, N.; Raskar, R. Designing neural network architectures using reinforcement learning. arXiv 2016, arXiv:1611.02167. [Google Scholar]
  33. Wu, B.; Dai, X.; Zhang, P.; Wang, Y.; Sun, F.; Wu, Y.; Tian, Y.; Vajda, P.; Jia, Y.; Keutzer, K. Fbnet: Hardware-aware efficient convnet design via differentiable neural architecture search. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 10734–10742.
  34. Cai, H.; Zhu, L.; Han, S. Proxylessnas: Direct neural architecture search on target task and hardware. arXiv 2018, arXiv:1812.00332. [Google Scholar]
  35. Brock, A.; Lim, T.; Ritchie, J.M.; Weston, N. Smash: one-shot model architecture search through hypernetworks. arXiv 2017, arXiv:1708.05344. [Google Scholar]
  36. Xie, L.; Yuille, A. Genetic cnn. Proceedings of the IEEE international conference on computer vision, 2017, pp. 1379–1388.
  37. Real, E.; Moore, S.; Selle, A.; Saxena, S.; Suematsu, Y.L.; Tan, J.; Le, Q.V.; Kurakin, A. Large-scale evolution of image classifiers. International Conference on Machine Learning. PMLR, 2017, pp. 2902–2911.
  38. Tancik, M.; Mildenhall, B.; Wang, T.; Schmidt, D.; Srinivasan, P.P.; Barron, J.T.; Ng, R. Learned initializations for optimizing coordinate-based neural representations. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 2846–2855.
  39. Liu, H.; Simonyan, K.; Yang, Y. Darts: Differentiable architecture search. arXiv 2018, arXiv:1806.09055. [Google Scholar]
  40. Elsken, T.; Metzen, J.H.; Hutter, F. Efficient multi-objective neural architecture search via lamarckian evolution. arXiv 2018, arXiv:1804.09081. [Google Scholar]
  41. Pham, H.; Guan, M.; Zoph, B.; Le, Q.; Dean, J. Efficient neural architecture search via parameters sharing. International conference on machine learning. PMLR, 2018, pp. 4095–4104.
  42. Chen, W.; Gong, X.; Wang, Z. Neural architecture search on imagenet in four gpu hours: A theoretically inspired perspective. arXiv 2021, arXiv:2102.11535. [Google Scholar]
  43. Chen, Y.; Meng, G.; Zhang, Q.; Xiang, S.; Huang, C.; Mu, L.; Wang, X. Renas: Reinforced evolutionary neural architecture search. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 4787–4796.
  44. Mallipeddi, R.; Suganthan, P.N.; Pan, Q.K.; Tasgetiren, M.F. Differential evolution algorithm with ensemble of parameters and mutation strategies. Applied soft computing 2011, 11, 1679–1696. [Google Scholar] [CrossRef]
  45. Nguyen, B.M.; Thi Thanh Binh, H.; The Anh, T.; Bao Son, D. Evolutionary algorithms to optimize task scheduling problem for the IoT based bag-of-tasks application in cloud–fog computing environment. Applied Sciences 2019, 9, 1730. [Google Scholar] [CrossRef]
  46. Bäck, T.; Schwefel, H.P. An overview of evolutionary algorithms for parameter optimization. Evolutionary computation 1993, 1, 1–23. [Google Scholar] [CrossRef]
  47. Zagoruyko, S.; Komodakis, N. Wide residual networks. arXiv 2016, arXiv:1605.07146. [Google Scholar]
  48. Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. Proceedings of the IEEE conference on computer vision and pattern recognition. CVPR, 2016, pp. 2818–2826.
  49. Dryden, N.; Maruyama, N.; Benson, T.; Moon, T.; Snir, M.; Van Essen, B. Improving strong-scaling of CNN training by exploiting finer-grained parallelism. 2019 IEEE International Parallel and Distributed Processing Symposium (IPDPS). IEEE, 2019, pp. 210–220.
  50. Lewkowycz, A. How to decay your learning rate. arXiv 2021, arXiv:2103.12682. [Google Scholar]
  51. Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. 2009 IEEE conference on computer vision and pattern recognition. Ieee, 2009, pp. 248–255.
  52. Yuan, Y.; Fu, R.; Huang, L.; Lin, W.; Zhang, C.; Chen, X.; Wang, J. Hrformer: High-resolution transformer for dense prediction. arXiv 2021, arXiv:2110.09408. [Google Scholar]
  53. Tan, M.; Le, Q. Efficientnetv2: Smaller models and faster training. International conference on machine learning. PMLR, 2021, pp. 10096–10106.
  54. Graham, B.; El-Nouby, A.; Touvron, H.; Stock, P.; Joulin, A.; Jégou, H.; Douze, M. Levit: a vision transformer in convnet’s clothing for faster inference. Proceedings of the IEEE/CVF international conference on computer vision, 2021, pp. 12259–12269.
  55. d’Ascoli, S.; Touvron, H.; Leavitt, M.L.; Morcos, A.S.; Biroli, G.; Sagun, L. Convit: Improving vision transformers with soft convolutional inductive biases. International Conference on Machine Learning. PMLR, 2021, pp. 2286–2296.
  56. Chiley, V.; Thangarasa, V.; Gupta, A.; Samar, A.; Hestness, J.; DeCoste, D. RevBiFPN: The Fully Reversible Bidirectional Feature Pyramid Network. arXiv 2022, arXiv:2206.14098. [Google Scholar]
  57. Li, S.; Liu, Z.; Wu, D.; Liu, Z.; Li, S.Z. Boosting discriminative visual representation learning with scenario-agnostic mixup. arXiv 2021, arXiv:2111.15454. [Google Scholar]
  58. Han, K.; Wang, Y.; Zhang, Q.; Zhang, W.; Xu, C.; Zhang, T. Model rubik’s cube: Twisting resolution, depth and width for tinynets. Advances in Neural Information Processing Systems 2020, 33, 19353–19364. [Google Scholar]
  59. Chollet, F. Xception: Deep learning with depthwise separable convolutions. Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 1251–1258.
Preprints 80505 g001
Figure 1. Configuration of a network. The depth represents the number of layers in a network, while the width of a layer represents the number of filters present in it.
Figure 1. Configuration of a network. The depth represents the number of layers in a network, while the width of a layer represents the number of filters present in it.
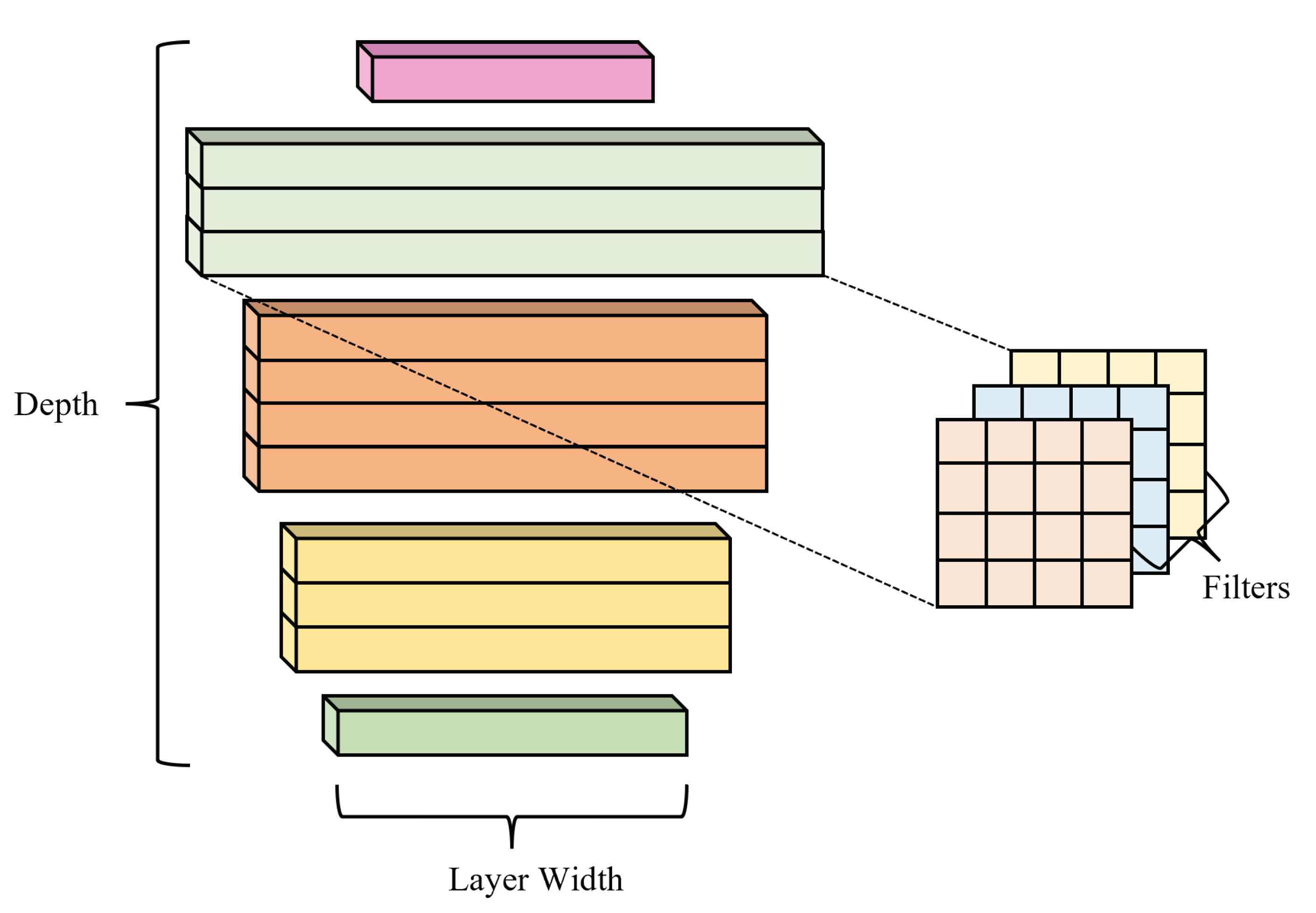
Preprints 80505 g001
Preprints 80505 g002
Figure 2. Overview of the filter training step. White and green layers represent the temporary and permanent layers of the network. During each of the m epochs, a random layer filter is generated, which filters out some temporary layers to create a network. This recalibrated network is trained and the loss is back-propagated through all the temporary and permanent layers.
Figure 2. Overview of the filter training step. White and green layers represent the temporary and permanent layers of the network. During each of the m epochs, a random layer filter is generated, which filters out some temporary layers to create a network. This recalibrated network is trained and the loss is back-propagated through all the temporary and permanent layers.
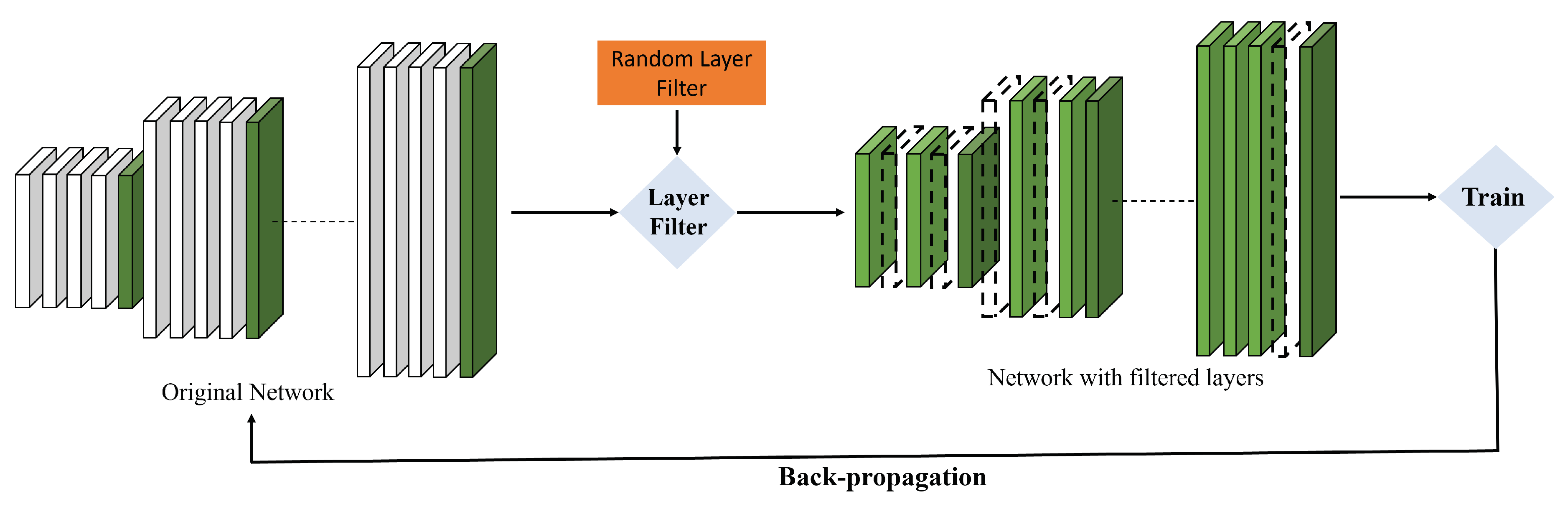
Preprints 80505 g002
Preprints 80505 g003
Figure 3. Overview of width evolution. White layers denote the layers omitted by DEVs while the width of red channels denotes the channels omitted by WEV. Each search epoch generates 50 chromosomes, and the rewards corresponding to the network generated from them are appended. The best chromosomes, after mutation and crossover, are selected and propagated to the subsequent epochs.
Figure 3. Overview of width evolution. White layers denote the layers omitted by DEVs while the width of red channels denotes the channels omitted by WEV. Each search epoch generates 50 chromosomes, and the rewards corresponding to the network generated from them are appended. The best chromosomes, after mutation and crossover, are selected and propagated to the subsequent epochs.
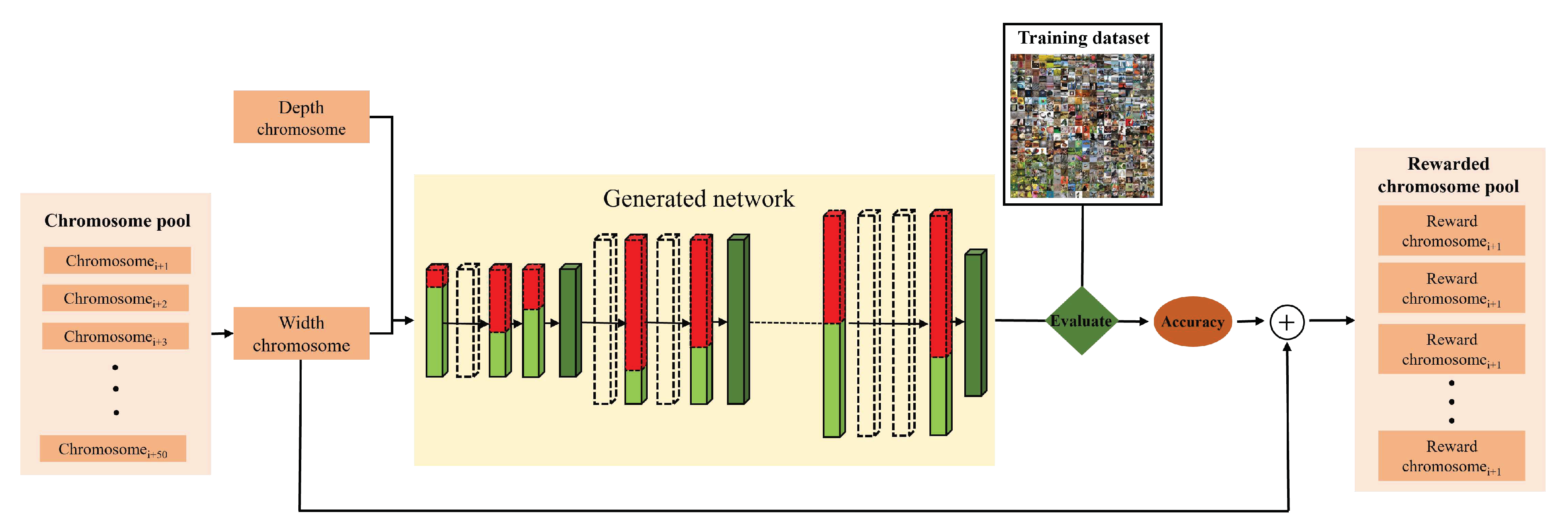
Preprints 80505 g003
Table 1. Performance against Very Small Networks on ImageNet Dataset
Table 1. Performance against Very Small Networks on ImageNet Dataset
Model Top-1 Accuracy Top-5 Accuracy #Parameters
EfficientNetB1 [15] 79.1% 94.4% 7.9M
HRFormer-T [52] 78.5% - 8.0M
DenseNet121 [13] 75.0% 92.3% 8.1M
EfficientNetV2B1 [53] 79.8% 95.0% 8.2M
EvolveNet-XS 80.4% 95.1% 7.8M
Table 2. Performance against Small Networks on ImageNet Dataset
Table 2. Performance against Small Networks on ImageNet Dataset
Model Top-1 Accuracy Top-5 Accuracy #Parameters
LeViT-128 [54] 79.6% - 8.8M
EfficientNetB2 [15] 80.1% 94.9% 9.2M
ConViT-Ti+ [55] 76.7% - 10.0M
EfficientNetV2B2 [53] 80.5% 95.1% 10.2M
RevBiFPN [56] 79.0% - 10.6M
EvolveNet-S 81.1% 95.6% 8.6M
Table 3. Performance against Medium-sized Networks on ImageNet Dataset
Table 3. Performance against Medium-sized Networks on ImageNet Dataset
Model Top-1 Accuracy Top-5 Accuracy #Parameters
SAMix ResNet-18 [57] 72.33% 91.8% 11.7M
Densenet169 [13] 76.2% 93.2% 14.3M
TinyNet [58] 79.4% 94.5% 11.9M
EfficientNetB3 [15] 81.6% 95.7% 12.3M
EfficientNetV2B3 [53] 82.0% 95.8% 14.5M
EvolveNet-M 82.8% 96.3% 11.3M
Table 4. Performance against Large Networks on ImageNet Dataset
Table 4. Performance against Large Networks on ImageNet Dataset
Model Top-1 Accuracy Top-5 Accuracy #Parameters
Xception [59] 79.0% 94.5% 22.9M
ConvNeXtTiny [1] 81.3% - 28.6M
ConvNeXtSmall [1] 82.3% - 50.2M
NasNetLarge [12] 82.5% 96.0% 88.9M
EfficientNetB4 [15] 82.9% 96.4% 19.5M
EvolveNet-L 83.2% 96.5% 17.6M
Table 5. Each layer used in the evolved model. DEV i represents the i-th element of the depth encoding vector, which indicates the number of layers, and n represents the number of classes.
Table 5. Each layer used in the evolved model. DEV i represents the i-th element of the depth encoding vector, which indicates the number of layers, and n represents the number of classes.
Input Operation out-channels #layers
224 2 × 3 Conv2D 32 1
112 2 × 16 Bottleneck 24 DEV 0
112 2 × 16 Bottleneck 24 1
56 2 × 24 Bottleneck 32 DEV 1
56 2 × 24 Bottleneck 32 1
28 2 × 32 Bottleneck 64 DEV 2
28 2 × 32 Bottleneck 64 1
14 2 × 64 Bottleneck 96 DEV 3
14 2 × 64 Bottleneck 96 1
14 2 × 96 Bottleneck 160 DEV 4
14 2 × 96 Bottleneck 160 1
7 2 × 160 Bottleneck 320 DEV 5
7 2 × 160 Bottleneck 320 1
7 2 × 320 Conv2D 1280 1
7 2 × 1280 AvgPool - 1
112 2 × 32 Conv2D n 1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated