Strengthening of Ancient Timber Beams in Restoration Operation: Effect of Wood Cutting on MOE

In ancient buildings, timber members could need specific on-site interventions, including reinforcement or repair, sometimes inserting of reinforcing material into grooves routed in the original sound wood. Grooves number, positions and dimensions, and strengthening materials may differ, according to the desired increase of bending stiffness and strength. The Modulus-of-Elasticity (MOE) of each beam is of key importance, but the incisions can affect it, net of the reduction of the removed wood. In this study 12 old beams were accurately measured and their static and dynamic MOEs calculated before and after the grooves processing, to simulate the operations of typical reinforcing interventions. One groove was routed along the length of each beam and deepened progressively by three steps. Tests have showed how the MOE is affected by the groove depth, decreasing up to one third. The paper proves how the weakening effect of grooves on-site can be assessed with dynamic MOE and roughly predicted by means of visual survey. Grooves need for strengthening beams, must be carefully evaluated because of the variation of the actual mechanical properties, net to lost wood.

Keywords:

Subject: Engineering - Architecture, Building and Construction

1. Introduction

Historical timber structures are an important part of the World Cultural Heritage; timber buildings materials and construction techniques are part of our history and their conservation is an essential contribution to cultural diversity and global cultural wealth. Indeed, the principles for historical timber structures conservation are universally accepted and mentioned in different documents and papers [1,2,3,4,5]. According to such principles, the primary aim of the conservation is to maintain the historical authenticity and integrity, to conserve the load-bearing function, to minimize any intervention and to preserve as much original materials as possible. In order to fulfill those principles, the residual mechanical properties of timber must be considered; strengthening interventions planned without taking into account this aspect are not in agreement with the mentioned principles and can be considered as the consequence of an obsolete approach.

Strengthening interventions of old timber elements is a complex field of research because the proposed solutions have to take into account not only the engineering aspects, but also some other critical principles: the intervention should be as much as possible reversible, low invasive, conservative of the original material and of proved efficiency [6,7].

Timber members of existing buildings could need specific on site interventions, including reinforcement or repair [8]. Upgrading wooden structures for higher working loads or restoring their original design strength and stiffness, is an engineering task. Nowadays, a common technique for the timber strengthening and repairing consists in embedding reinforcing materials (e.g. steel plates, pultruded fiberglass rod, CFRP etc., typically bonded in with epoxy resins) in grooves routed into the original sound wood [9,10,11,12,13,14] (Figure 1).

Many papers present the results of tests performed on specimens of various dimensions and different species [10,15,16,17,18]. The results of such papers are not always in agreement: for instance Duarte et al. [16] observed that the Modulus of Rupture (MOR) of the strengthened timber elements did not increase, Alam et al. [17] recorded MOR and Modulus of Elasticity (MOE) increasing only for some of the investigated techniques. Schober and Rautenstrauch [15] among diverse intervention proposals, testing four old timber beams reinforced with CFRP, bonded centrally to the tension zone in a vertical slot, observed a very little MOE increasing (+2.8%), to be considered negligible. In the same way Alhayek and Svecova [19] on 20 salvaged timber stringers, strengthened with glass fiber-reinforced polymer (GFRP) laminates, obtained a very low increment in stiffness (EI), equal to 3.3%, with a minimum of -0.36%. However, in general, the reinforced timber elements show an increasing of the load bearing capacity and ultimate strength, an augmentation in ductility, although the stiffness increment seems lower.

Limit States criteria design (both Ultimate and Serviceability) must be evaluated with great attention when strengthening interventions on old timber structures are planned. Design data on bending strength are important to avoid failures, while the stiffness of timber elements is fundamental to preserve the historical structures from excessive deformations which could become not reversible in the long period. Indeed a common problem for such structures is to meet the Serviceability Limit States criteria, since the elastic modulus is often the limiting factor in the design of wooden structures. Considering also that the principle of minimum intervention is universally recognized as fundamental for the conservation of historical timber structures integrity [1], the MOE of the residual beam is of great importance, especially when a strengthening intervention is planned on a wooden Cultural Heritage.

All the mentioned research works consider the MOE as a material property, unchangeable and unaffected by any operations, also after the grooves making. This concept could not always be applied to wood as a material, because it is affected by the presence of natural defects and anomalies, which effects depend on their dimension and position. Interruption of the grain continuity, along the span and around the knots and the interaction between grooves and other wood anomalies, as a consequence of the grooves making, could affect the mechanical properties of wood; such effect could be greater than the lack of the material caused by the removal of a portion of beam, as reported in [13,20]. Particularly Cavalli e Togni [20] found strict direct relationships between reduction of MOE and shrinkage fissures and an unexpected relationship between straightness of the grain and MOE decreasing.

If current requirements for the strengthening intervention is to respect the original construction and to preserve as much original material as possible, the reinforcing project must consider any effects of the grooves on the original mechanical properties of wood. For instance, when the strengthening intervention target is to increase the beam stiffness, the project is planned to add the necessary strengthening material; however, if the needed grooves to insert the additional material, reduce the original stiffness, the strengthening ratio must increase. So, in order to preserve the original material and to minimize the intervention, the described strengthening techniques must take into account any possible source of variation of the original mechanical properties, because a different approach may lead to ineffective results (e.g. in an experimental strengthening intervention in the cited paper [15]).

The aim of this research is to investigate how much the grooves routed along the length of old timber members affect the bending MOE and how to predict it. Such information is useful for the evaluations and the strengthening intervention plans, based on a modern approach which includes the concepts of “minimum repair” and “respect of the original structural member”. In order to facilitate the work of structural engineers, their evaluations and design, the results of this study were processed to work out two simplified methods for the assessment of the weakening effect on the timber MOE caused by the grooves.

2. Materials and Methods

2.1. Timber beams

Twelve old beams of Silver Fir (Abies alba Mill.) were dismantled and collected from some ancient buildings. According to historical information, all the beams were older than 70 years. Their cross sections were different, in the range 16x14 – 28x22 cm. All the defects that potentially affect the structural behavior of each timber member were recorded and measured, that is: slope of the grain, knots, wanes, position of the pith (11 beams with boxed heart and pith inside), fissures extension as the ratio between the fissures depth and the cross section width). Such defects have been considered for their position, dimensions and characteristics. Position of the piths and measurements of the fissures are reported in Table 1. More detailed information about the tested beams can be found in [20].

2.2. The grooves

In order to simulate the strengthening interventions, a single groove was routed along the intrados face for the entire length of each beam, by means of an electrical chainsaw controlling depth and position. The depth of the groove was progressively deepened in three steps, since in practice it could be: 25% of the beam depth (first step), 50% of the beam depth (second step) and the 75% (third step).

The executed grooves were narrow (around 9 mm), (Figure 2) and the second moment of area (J), on the centroid position was recalculated on the actual cross-section (its value changed after the realization of each groove). After each woodworking process, a little quantity of wood was removed and J decreased, in the worst case, of 3.7%.

2.3. Mechanical tests

Four point bending tests were performed according to the standard [21] in order to calculate the global MOE (Em,g) which was chosen because it is easy to measure (potentially also on-site by means of a proof-loading test) and useful to monitor the behavior of the full beam.

E_{m, g} = \frac{Δ P a}{6 J_{i} Δ η} (\frac{3}{4} l^{2} - a^{2})

(1)

where E_m,g is Global Modulus of Elasticity [MPa], ΔP is the load increase in the elastic range [N], a is the distance between the support and the load application point [mm], l is the testing span [mm], J is the second moment of area [mm⁴] recalculated after each groove, with index i for the 4 different testing condition, Δη is the intrados displacement measured at a given ΔP [mm].

Timber elements were tested within the elastic range, before and after cutting the first groove as well as after each groove deepening, the same stress was applied without altering the testing geometry.

2.4. Dynamic tests

Various dynamic tests were used in order to both predict the MOE and develop specific techniques for the on-site assessment of the MOE reduction due to the grooves. We did not use an automatic timber grading system (e.g. a strength grading machine - SGM) to assess the MOE and its variation, because many SGMs are not usable on site for their dimensions and all them are not calibrated to test old beams with a groove on the extrados. In order to reduce the influence of boundary conditions for all the dynamic tests, the beams were suspended at their theoretical nodal points for fundamental vibration mode in flexural vibration (0.224 of the length). All the dynamic tests were carried out using coaxial piezoelectric accelerometers connected to a notebook and to a digital storage oscilloscope. Piezoelectric accelerometers are quite affordable, easy to be used on-site, thanks to their compact dimensions and to their self-powering system; they offer very accurate measurement for low vibration with very low noise level.

The dynamic MOEs were calculated for the following conditions: no grooves, grooves at 25% of the cross section depth, grooves at 50% of the depth, grooves at 75%.

In flexural vibration test, vibration was induced by a hammer impact and collected by an accelerometer connected to a notebook pc. Resonance frequency was determined by FFT analysis using “GS Spectrum Analyser” software. Dynamic flexural MOE (E_f) was calculated using Equation 2 [22].

E_{f} = \frac{4 π^{2} f_{1}^{2} l^{3}}{k^{4} J} m

(2)

where E_f is the dynamic flexural MOE [MPa], f₁ is the fundamental vibration frequency [kHz], l is the beam length [m], J is the second moment of area [m⁴] calculated for each testing conditions, m is beam weight [kg] and k is a constant corresponding to the fundamental mode of free-free flexural vibration.

In longitudinal vibration test an accelerometer was fixed at one end and the opposite end was hit by a hammer. Vibration frequency was recorded and dynamic MOE was determined according to equation 3 [23].

E_{l} = 4 ρ l^{2} f_{1}^{2}

(3)

where E_l is the dynamic longitudinal MOE [MPa], ρ is the density [kg/m³], f₁ is the fundamental vibration frequency [kHz] and l is the beam length [m].

With stress wave transmission time test each beam was excited by hammer impact, while two accelerometers were fixed on the beams ends. The accelerometers were connected to a digital storage oscilloscope and the one nearer the hit end starts up a microsecond counter, while the second one stops it, thus providing the time for the impact stress wave between the two ends. The velocity of stress waves was calculated by dividing the beam length by the flight time of stress waves [24] and the dynamic MOE was calculated as reported in the equation 4:

E_{s w} = ρ v^{2}

(4)

where E_sw is the dynamic stress wave MOE [MPa], ρ is the wood density [kg/m³] and v is the stress wave velocity [km/s].

3. Results

3.1. MOE reduction

The average value of the MOE is quite low, if compared with new sound wood, as could be expected for beams with several defects as knots, slope of grain and unknown load history. In general, all the beams showed a MOE value reduction, higher than the J reduction (Figure 3), which is a consequence of the interaction between groove and beam characteristics. Such interaction reduces the original timber quality, causing a general worsening of their mechanical behavior in various ways:

-: interrupting the grain continuity [25,26],
-: cutting the fiber around the knots and increasing the stress in their proximity [27],
-: interaction between shrinkage fissures and grooves depth [20].

Cavalli and Togni [20] observed that the distance between this kind of fissure and groove, influences particularly the MOE reduction.

Since the pith is the reference point for the position of the shrinkage fissures, which deepen in its direction in the beam, lower is the distance between groove and pith, more sensible is the MOE reduction. This outcome is well explained by the relationship between the maximum MOE decreasing (M∆E_m,g), the combination of the fissure extension (with the section width ratio) and the fissure distance from the pith (equation 5):

M Δ E_{m, g} = 3.88 \times p i t h_p o s i t i o n + 66.0 \times f i s s u r e - 28.7

(5)

where M∆E_m,g is the maximum decreasing of the MOE, pith_position is the ratio between h (pith to intrados distance) and d (cross section depth), as reported in Table 1. The regression chart is shown in Figure 4.

3.1.1. Practical consequences

The results show that the described strengthening intervention, designed without take into account the potential MOE reduction, may lead to ineffective results, even if they are designed respecting the principles of minimum intervention.

The design of such intervention must take into account the characteristics of each beam, because each beam shows a specific MOE reduction for each grooves depth.

Moreover, the above discussed data are originated from one small groove, but strengthening intervention based on grooves comparable for depth, and different for number and dimensions, may produce higher weakening effect. Therefore, the on-site assessment of the potential MOE reduction is of key importance for the strengthening intervention design, concerning the enhancement of the stiffness.

4. Assessment of the MOE reduction

Two different ways are here proposed for the on-site assessment of the MOE reduction, which is a consequence of the grooves making. The first one is based on dynamic tests and it can be used on timber members after the grooves making, and before the insertion of the strengthening materials. The second one can be used ante-grooves to firstly estimate the possible MOE reduction and it is based on the recording of the visual features of the beams.

4.1. Dynamic tests

The relation between the dynamic and static MOEs for different tests are reported in the Table 2. The capacity of the tested techniques to predict the MOE on ancient timber beams has been investigated and presented in some previous works by [20,28]. While all the techniques are capable to assess the E_m,g with high or medium correlation (correlation level defined according to [29]), the capacity to predict the maximum E_m,g reduction is different for each dynamic test. For the stress wave test and longitudinal vibration test, the average maximum MOE reduction is small (4% and 7% respectively after the third deepening of the grooves), when compared to the static tests results (average maximum static MOE reduction 17%). This phenomenon is a consequence of the characteristics of the dynamic tests itself [30,31] and results in an unsatisfactory capability to predict higher weakening effects. Therefore, for practical purposes, these two techniques have low reliability in the assessment of the MOE reduction.

Flexural vibration test shows better capacity to predict the E_m,g and its variation (Figure 5), however it requires specific boundary conditions to be arranged on-site and it underestimates the E_m,g reduction (average maximum E_m,g reduction 17%, average maximum E_f reduction 11%). Since the flexural vibration test can be used on-site only after the grooves realization (whit respect to the boundary conditions), the assessment of the MOE reduction in those conditions may help structural engineers to design the intervention, correcting the strengthening ratio.

4.2. Visual survey

In many cases it would be more important to know in advance the potential effect of the grooves on the MOE, in order to plan the strengthening interventions. In this case the MOE reduction can be roughly assessed indirectly, surveying the features of the timber beams which are related to the MOE reduction.

The diagram in Figure 6, based on the outcomes of the presented work, is referred to the E_m,g decrease calculated after each groove deepening realized at the intrados face. For each case the scheme reports the expected potential E_m,g reduction for each groove depth (respectively 25%, 50% and 75% of the cross section depth). The starting point in Figure 6 consists in the identification of the presence of shrinkage fissures. If the pith is not included, there are not fissures in the beam and in the bottom part of the figure, the estimated decrease of the MOE is reported for each groove depth. If the pith is included and the fissures are present, the position of the pith must be identified: if the pith is above the neutral axis, go straight to the potential decrease of the MOE; otherwise, if the pith is below the neutral axis, the fissures depth must be considered in relation to the width of the beam. Due to the large variability in the response of each beam, and to the limited number of beams tested, the range values must be considered as an approximation to provide an order of magnitude about the MOE reduction for various grooves depth. The same diagram can be applied with grooves on the extrados, considering the drawn sections upside down.

The diagram takes into account the presence and extension of the shrinkage fissures and the position of the pith which are the most important factors affecting the MOE reduction. In practice this method must be adopted by experts, because other timber features, not presented in the studied sample, could have additional influence on the MOE and on its decrease (e.g. dimension and position of ring-shakes, presence of localized decay, etc.). The potential effects of grooves for strengthening intervention, variable for number, dimensions and positions, must be carefully considered.

5. Conclusions

The MOE reduction of old timber beams after grooves making is mainly due to the interaction between grooves and grain course, and between fissures (depth and position) and grooves, so that it is particularly important in beams with boxed heart and pith inside.

The higher MOE reduction observed (up to 30%), net of J reduction, suggests to evaluate alternative strengthening techniques for specific timber elements, because reducing stiffness of an element that requires to be strengthened, could be considered as a senseless intervention.

The large variability of the MOE reduction observed after the grooves making, suggests a general caution in planning the strengthening interventions using the described techniques, and it demonstrates that the reinforcing design must consider carefully the relevant characteristics of each beam.

Two methodologies for the on-site assessment of the potential MOE reduction were discussed. The one based on dynamic test, can be used after the realization of the grooves. The other one based on specific features of the beam (presence of shrinkage fissures, their position and extension, pith position) is useful for the MOE reduction assessment before the realization of the grooves. Both of them, to be used with caution because based on the outcome of a small sample, can be of service to design correctly the strengthening operation conducted on ancient timber beams.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

IWC - ICOMOS Principles for the preservation of historic timber structures, 2017 https://www.icomos.org/images/DOCUMENTS/General_Assemblies/19th_Delhi_2017/Working_Documents-First_Batch-August_2017/GA2017_6-3-4_WoodPrinciples_EN_final20170730.pdf (accessed on 17/07/23).
Kasal, B.; Anthony, R.W. Advances in situ evaluation of timber structures. Prog. Struct. Eng. Mater. 2004, Vol. 6, 94–103. [CrossRef]
Tampone, G. (2007) Mechanical failures of the timber structural systems. In From Material to Structure - Mechanical Behaviour and Failures of the Timber Structures, I. IWC, ed. (Florence, Venice and Vicenza), p. 21. http://iiwc.icomos.org/assets/tampone.pdf (accessed 16 April 2022).
Palaia, L.; López, V.; Tormo, S.; Pérez, C.; Navarro, P. Assessment of timber structures in service, by using combined methods of non-destructive testing together with traditional ones. In 9th International Conference on NDT of Art, Jerusalem, Israel, 2008: pp. 25–30. http://www.ndt.net/article/art2008/papers/060Palaia.pdf (accessed 17/07/23).
Pinto, L. Inventory of repair and strengthening methods timber. Master Thesis. University of Minho; 2009; http://upcommons.upc.edu/pfc/bitstream/2099.1/7903/1/01.pdf (accessed 17/07/23).
Stumes, P. Testing the Efficiency of Wood Epoxy Reinforcement Systems. Bull. Assoc. Preserv. Technol. 1975 Vol. 7, 2–35. doi.org/10.2307/1493504.
Piazza, M.; Riggio, M. Typological and Structural Authenticity in Reconstruction: The Timber Roofs of Church of the Pieve in Cavalese, Italy. Int. J. Archit. Herit. 2007 Vol. 1, 60–81. [CrossRef]
Cavalli, A.; Cibecchini, D.; Togni, M.; Sousa, H.S. A review on the mechanical properties of aged wood and salvaged timber. Constr. Build. Mater., 2016, vol. 114, 681-687, ISSN:0950-0618. [CrossRef]
Tampone, G. Il restauro delle strutture di legno. Hoepli, Milano, 1996; pp. 305-325.
Gentile, C.; Svecova, D.; Rizkalla, S.H. (2002) Timber beams strengthened with GFRP bars: Development and applications. J. Compos. Constr., 2002, Vol.6:1, 11-20. [CrossRef]
Rotafix, Timber Resin Splice; 2018 http://rotafix.co.uk/wp-content/uploads/2016/09/TRS-Brochure.pdf (accessed 17/07/23).
Hanan, A.; Dagmar, S. Flexural Stiffness and Strength of GFRP-Reinforced Timber Beams J. Compos. Constr., 2012, Vol. 16(3), 245-252. [CrossRef]
Arriaga, F. Iñiguez-Gonzalez, G.; Esteban, M.; Fernandez-Cabo, J.L. Simplified model for strength assessment of timber beams joined by bonded plates. J. Mater. Civ. Eng., 2013, Vol.25, 980–990. [CrossRef]
Salčin, M., Džubur, Ž., Ćatović, F., Džiho, E. (2022). Strengthening Timber Structure with Fiber Reinforced Polymer – An Overview. In: Karabegović, I., Kovačević, A., Mandžuka, S. (eds) New Technologies, Development and Application V. NT 2022. Lecture Notes in Networks and Systems, vol 472. Springer, Cham. [CrossRef]
Schober, K.U.; Rautenstrauch, K. Post-strengthening of timber structures with CFRP’s. Mater. Struct., 2007, Vol. 40 (1), 27–35. [CrossRef]
Duarte, A.; de Oliveira Negrão, J.; Cruz, H.; Balseiro, A. Bending strength of timber beams rehabilitated with reinforced epoxy mortar plates. J. Struct. Eng., 2008, Vol. 34, 792–800. [CrossRef]
Alam, P.; Ansell, M. Smedley D. Mechanical repair of timber beams fractured in flexure using bonded-in reinforcements. Compos. 2009, Part B: Eng. 40, 95–106. [CrossRef]
Jankowski, L.J.; Jasieńko, J.; Nowak, T.P. Experimental assessment of CFRP reinforced wooden beams by 4-point bending tests and photoelastic coating technique. Mater. Struct., 2010, Vol 43, 141–150. [CrossRef]
19. Alhayek, H; Svecova, D. Flexural Stiffness and Strength of GFRP-Reinforced Timber Beams. J. Compos. Constr., 2012, Vol. 16, No. 3, June 1st. [CrossRef]
Cavalli, A.; Togni, M. The influence of routed grooves on the bending behaviour of old timber beams. Adv. Mater. Res. 2013(a), Vol. 778, 393–401. [CrossRef]
EN 408 Timber structures. Structural timber and glued laminated timber. Determination of some physical and mechanical properties. European Committee for Standardization, 2012.
Giordano, G. Tecnologia del Legno. 2nd ed., UTET, Torino, Italy, 1981, pp. 314-315.
Kollman, F.; Krech, H. Dynamische Messung der elastischen Holzeigenschaften und der Dampfung. Holz Roh- Werkst., 1960, Vol. 18, 41–54.
Kolsky, H. (1963) Stress Waves in Solids. Dover Publication, New York, 1963; pp 74, 141.
Arriaga, F.; Herrero, M.; Álvarez, R.; Maldonado, I. Efecto de las gemas en la resistencia a flexión de piezas enterizas de madera. The effect of wanes on the bending strength of solid timber beams. Mater. Construcc., 2007, Vol. 57, 61–76. arXiv:10.3989/mc.2007.v57.i288.65.
Togni, M.; Cavalli, A.; Mannozzi, D. Chestnut: from coppice to structural timber. The case study of “Uso Fiume” beams sampled in Liguria. J. Agric. Eng., 2013, Vol. XLIV.; 1-9. [CrossRef]
27. Ranta-Maunus, A. Round small-diameter timber for construction. Final report of project; 1999 https://www.vttresearch.com/sites/default/files/pdf/publications/1999/P383.pdf (accessed 17/07/23).
Cavalli, A.; Togni, M. How to improve the on-site MOE assessment of old timber beams combining NDT and visual strength grading. J. Nondestruct. Test. Eval., 2013(b), Vol. 28, 252-262. [CrossRef]
JCSS (2006) Probabilistic model code Part 3: Resistance models. 3.5.3.3, pag. 7. https://www.jcss-lc.org/publications/jcsspmc/timber.pdf (accessed on 17/07/23).
Bodig, J.; Jayne, B.A. Mechanics of wood and wood composites. Van Nostrand Reinhold Ed., New York, 1982; pp. 103-104.
Andrews, M. Which acoustic speed? In Proceedings 13th International Symposium on Non-Destructive Testing of Wood, University of California Ed., Berkeley, CA, USA, 2002; pp. 159-165.

Figure 1. Above: ancient structures with some old timber beam strengthened at the intrados face by inserting steel plates into the grooves routed along the longitudinal axis. Below: schematization of some types of grooving which involve insertion for internal glued reinforcement arrangement.

Figure 2. Beam n. 3 after the third groove to 75% of the depth.

Figure 3. Load – Deformation chart of the beam n. 4. Comparison between natural beam and the beam after the second cut (50% of height). The difference between the expected and the actual stiffness reduction is shown.

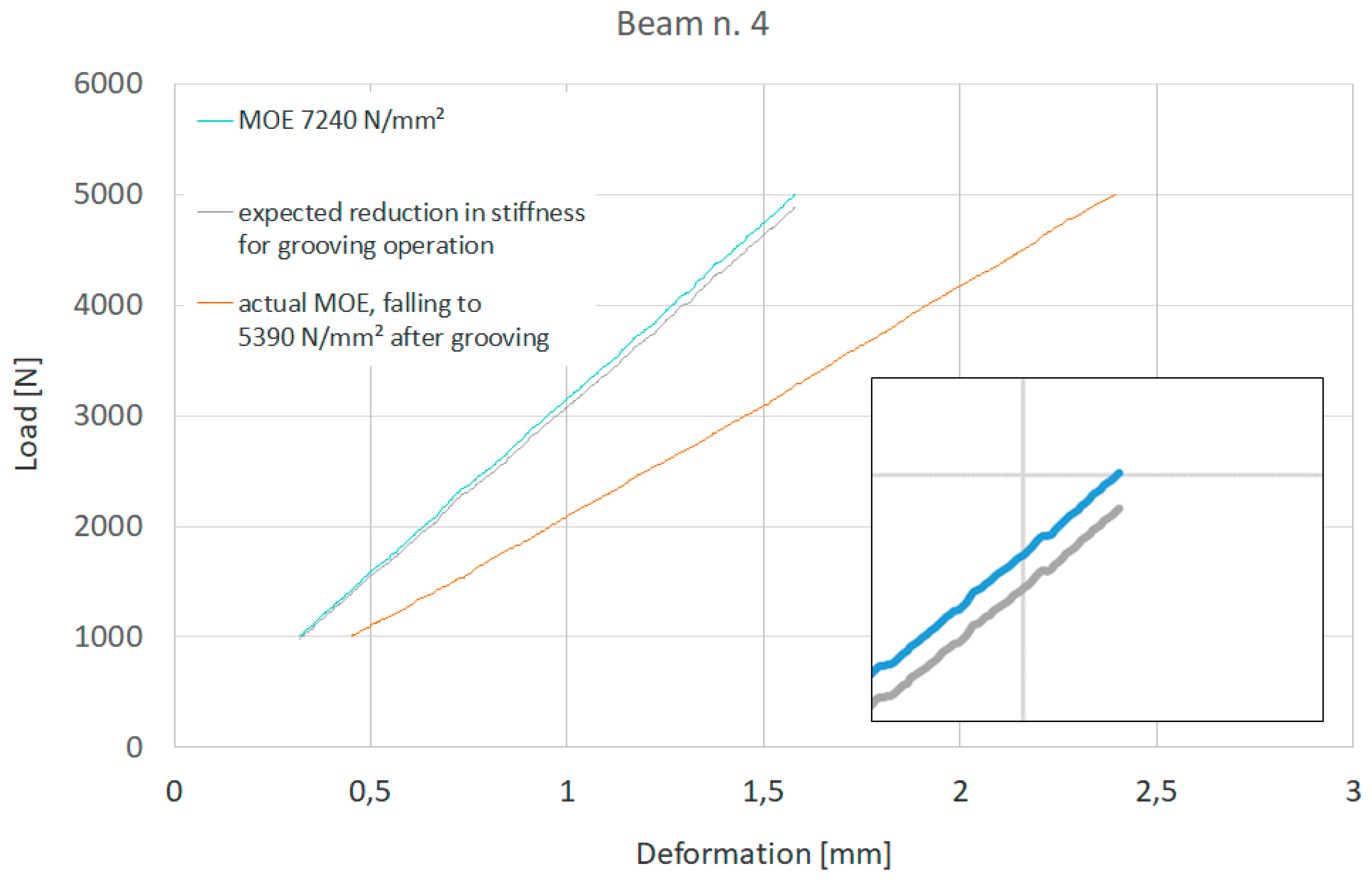
Figure 4. Multiple regression: MΔE_m,g= -28.7 + 38.8·pith_position + 66.0·fissure; R²_adj=54.2%, p-value= 0.018; MAE value (Mean Absolute Error)= 4.90, MAPE value (Mean Absolute Percentage Error)= 0.33.

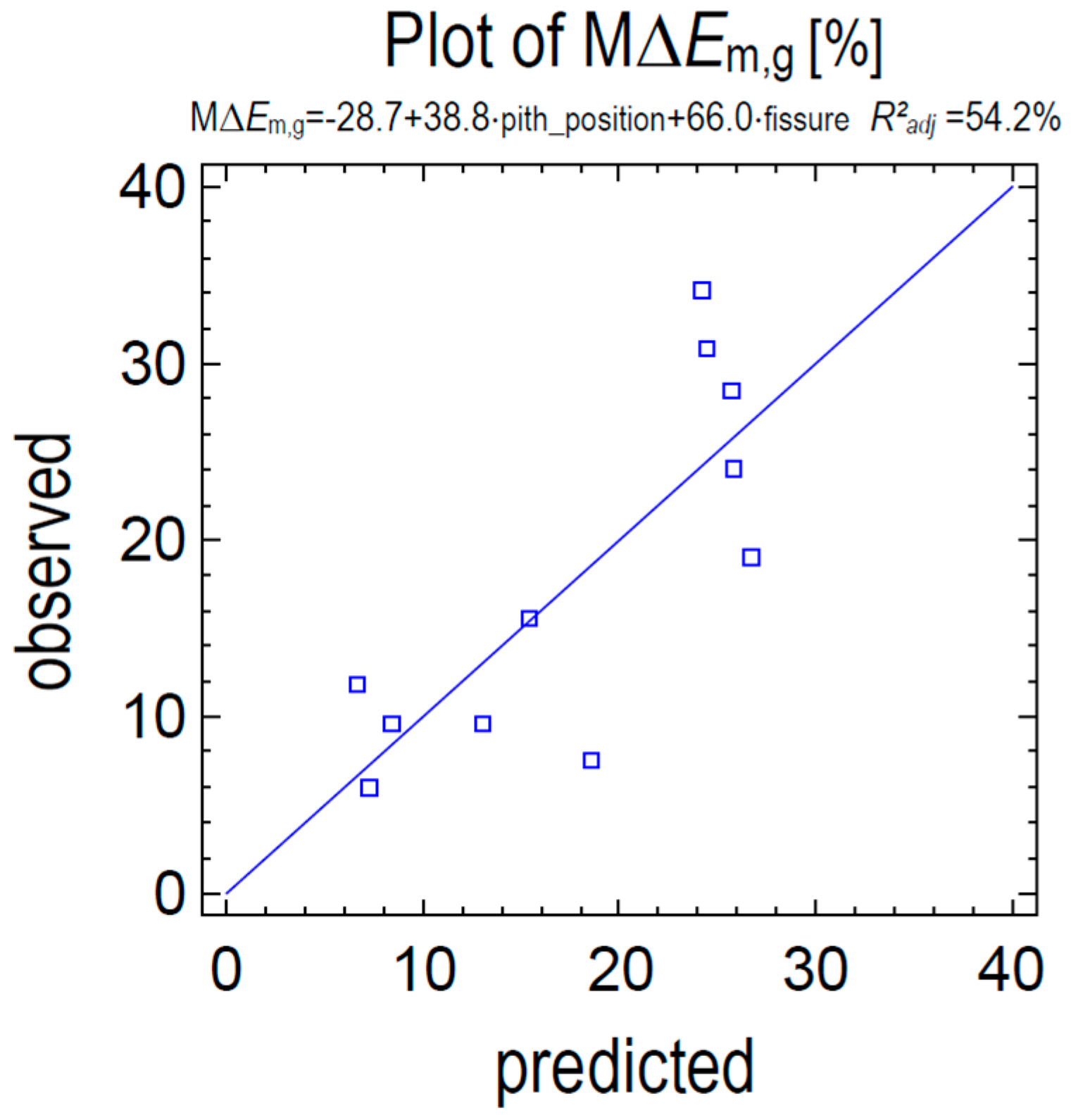
Figure 5. Relationship between the maximum decrease of E_f (MΔE_f) and the corresponding maximum decrease of E_m,g. Simple regression: MΔE_m,g = 0.157 + 1.34 x MΔE_f; R²_adj=69.8%, p-value=0.0004; MAE=4.29, MAPE=0.35.

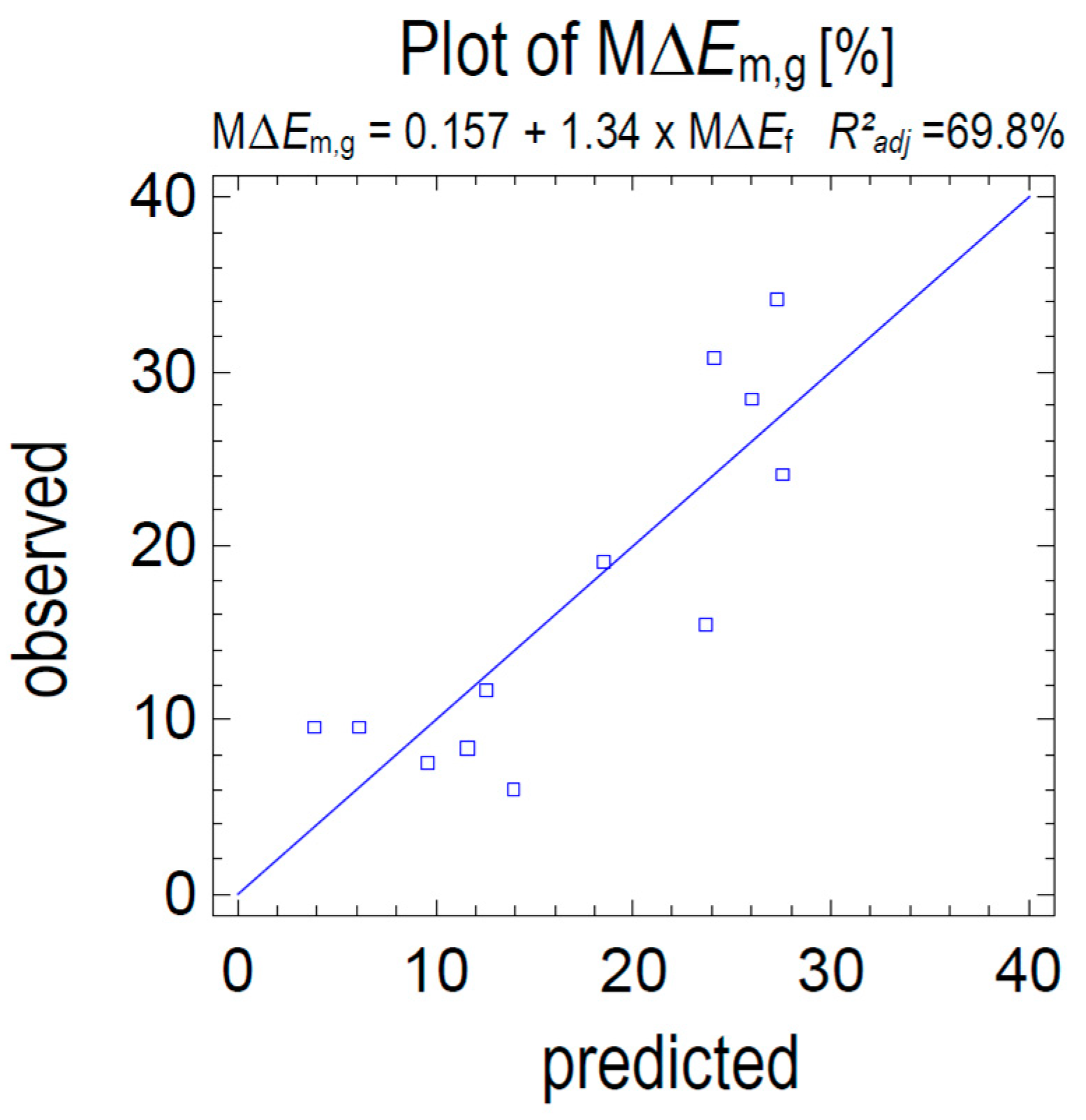
Figure 6. Assessment of MOE reduction by visual survey. For each groove depth (25%, 50% and 75% of the cross section depth) the weakening effect (WE) is expected on MOE as the percentage decreasing of the elastic modulus. Symbols: a,b=depths of shrinkage fissures, d=cross section depth, w=cross section width.

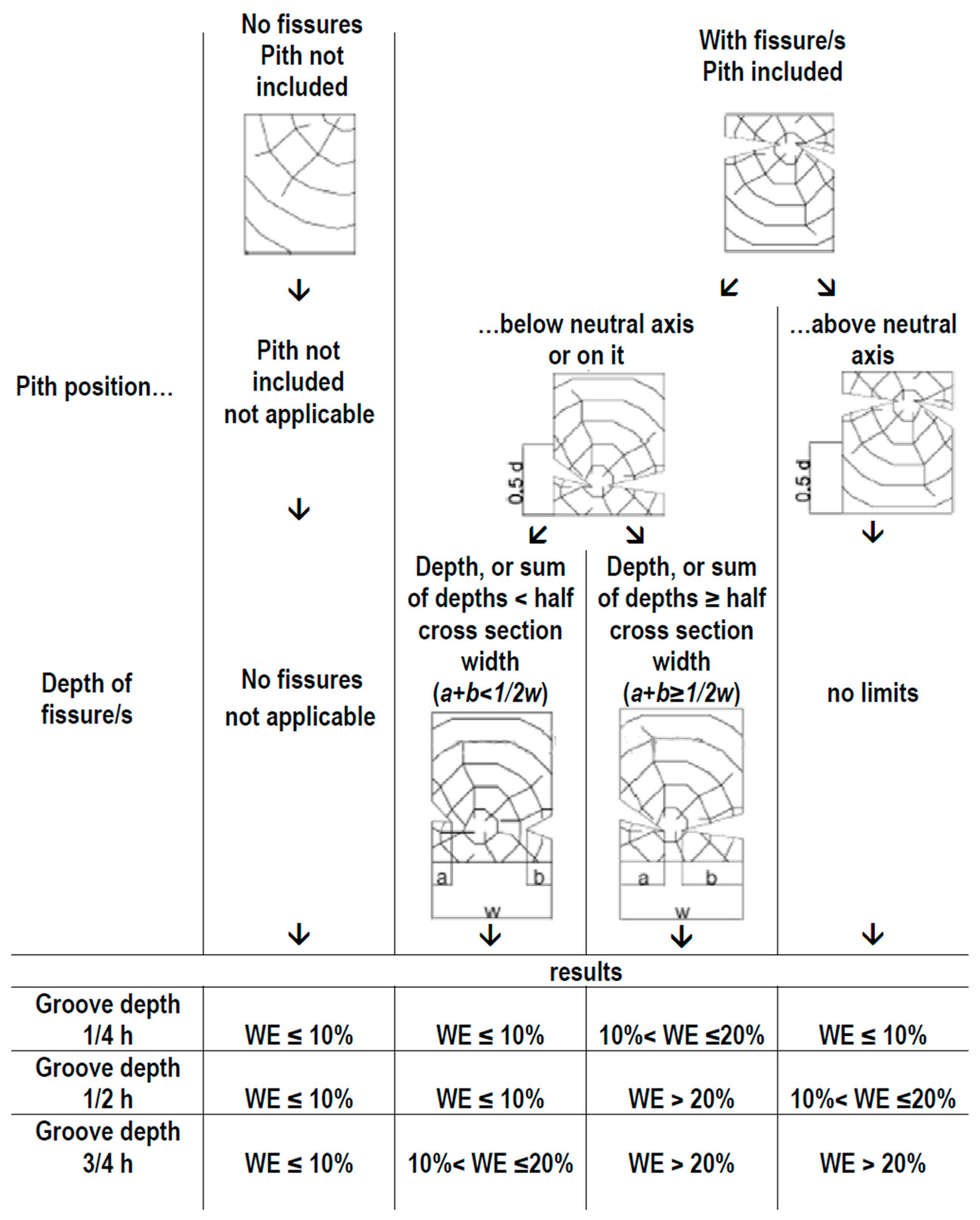
Table 1. Data of timber beams sampled and effect of the groove routed on J and E.

Beam n°	Height d [cm]	Width w [cm]	Fissures	Pith position h/d	J_y,25/ J_y [%]	J_y,50/J_y [%]	J_y,75/J_y [%]	E_m,g25/E_m,g0 [%]	E_m,g50/E_m,g0 [%]	E_m,g75/E_m,g0 [%]	M E_m,g [%]
1	15.0	13.6	0.58	0.44	96.9	96.6	96.3	85.3	81.0	82.9	19.0
2	18.3	16.3	0.28	0.48	97.6	97.1	97.0	101.5	91.9	90.5	9.51
3	22.3	16.5	0.22	0.70	97.1	96.7	96.5	95.9	91.2	90.4	9.60
4	23.8	21.0	0.49	0.53	98.1	97.7	96.8	96.1	74.4	65.9	34.1
5	23.0	20.0	0.28	0.45	98.0	97.6	96.6	94.9	94.0	94.2	6.00
6	21.0	18.6	0.00	no pith	97.4	97.1	96.8	95.5	92.3	91.7	8.35
7	21.8	17.6	0.57	0.43	97.6	97.3	97.3	75.0	72.4	71.5	28.5
8	26.8	21.8	0.44	0.47	98.2	97.9	97.0	92.5	95.2	93.0	7.51
9	27.6	22.0	0.23	0.52	98.2	97.9	97.7	99.7	88.2	89.0	11.8
10	26.4	20.2	0.52	0.52	98.0	97.7	97.5	92.7	88.6	75.9	24.1
11	24.9	17.6	0.54	0.45	99.0	98.5	98.3	82.8	75.9	69.2	30.8
12	25.8	18.6	0.38	0.49	97.8	97.3	97.0	102.4	98.7	84.5	15.5
average	231	187	0.38	0.50	97.8	97.4	97.1	92.9	87.0	83.2	17.1
minimum	160	136	0	0.43	96.9	96.6	96.3	75.0	72.4	65.9	6.00
maximum	276	220	0.58	0.70	99.0	98.5	98.3	102.4	98.7	94.2	34.1
stand. dev.	3.52	2.50	0.18	0.08	0.56	0.54	0.56	8.10	8.84	10.07	9.98

Note: s=ratio between the fissures depth and cross section width; h=pith to intrados distance; d=cross section depth; J=second moment of area; J_y=J before the groove making; J_y;25 =J after the first groove; J_y;50=J after the second groove; J_y;75=J after the third groove; E=Modulus of Elasticity; E_m,g0=E before the groove making; E_m,g25=E after the first groove;E_m,g50=E after the second groove; E_m,g75=E after the third groove; M E_m,g maximum decrease of E_m,g.

Table 2. Correlation between dynamic and static MOEs.

	E_f0	E_f25	E_f50	E_f75	E_l0	E_l25	E_l50	E_l75	E_sw0	E_sw25	E_sw50	E_sw75
E_m.g0	0.83(11.8)				0.70 (14.8)				0.60 (18)
E_m.g25		0.84 (11.2)				0.70 (17.2)				0.63 (18.9)
E_m.g50			0.85 (10.5)				0.66 (16.5)				0.55 (18.7)
E_m.g75				0.81 (11.9)				0.68 (15.8)				0.50 (19.4)

Note: E_f=dynamic flexural MOE, E_l=dynamic longitudinal MOE; E_sw=dynamic stress wave MOE; E_m,g MOEs are listed in the caption of Table 2. In brackets ()=MAPE values - Mean Absolute Percentage Error (in %). All the values reported have high significance level (p-values < 0.01).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer