Prerpints.org logo
Preprint
Article

Theoretical Prediction of the Anti-Icing Activity of Two-Dimensional Ice I

Altmetrics

Downloads

113

Views

100

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 July 2023

Posted:

27 July 2023

You are already at the latest version

Alerts
Abstract
Two-dimensional (2D) ice I is an atomic-level ice that is composed of two interlocked atom-ic layers saturated with hydrogen bonds. It has recently been experimentally observed but its properties have yet to be clarified. Accordingly, we theoretically studied the hydrophobic properties of 2D ice I. On the contrary, simulation of a hydrogen fluoride molecule on a 2D ice surface manifested that it destroyed the 2d ice structure and connected new hydrogen bonds with water molecules. Investigations of the interfacial effect between 2D and three-dimensional (3D) ice films indicated that the network structure of 2D ice was not de-stroyed by a 3D ice surface, as the former was saturated with hydrogen bonds. However, the surface of 3D ice reorganized to form as many hydrogen bonds as possible. Thus, the 2D ice film was hydrophobic and inhibited the growth of 3D ice. This shows that if 2D ice can be produced on an industrial scale, it could be used as an anti-3D-icing agent under low tem-perature.
Keywords: 
Subject: Physical Sciences  -   Chemical Physics

1. Introduction

Water ice is a ubiquitous substance. More than 19 three-dimensional (3D) ice phases have been observed under extreme temperature and pressure conditions at the laboratory scale [1,2]. In addition, two-dimensional (2D) ice has recently attracted considerable research interest. In 1997, Koga proposed a double-layer ice structure based on molecular dynamics simulations [3]. In 2015, Molinero et al. reported the discovery of a tetragonal 2D ice phase in bilayer graphene [4]. In 2020, Jiang and co-workers described their use of high-resolution qPlus atomic microscopy to observe an interlocked 2D ice structure based on Au (111) that they named 2D ice I [5,6]. They found that 2D ice I is stably saturated with hydrogen bonds. So far, many methods have been used to detect the properties of ice, such as X-ray method. These methods will have important applications in the detection of 2D ice properties [7,8,9,10]. Most of the research on the properties of 2D ice has been focused on its structural characteristics and electronic, dielectric, and optical properties [11,12]. This has revealed that 2D ice phase I has an indirect band-gap lattice and thus exhibits anisotropic optical properties.
As an atomic-level material, 2D ice is likely to be of significance in the fields of material science, atmospheric science, and biology, among others [13,14,15,16,17,18]. However, laboratory characterization of 2D ice is highly challenging, owing to the complexity of the experimental conditions involved. As such, we used density functional theory (DFT), a quantum mechanical method, to simulate the interaction between a water monomer and 2D ice, and thus determined the adsorption properties of 2D ice. The results indicated that 2D ice was hydrophobic and inhibited the growth of 3D ice. Thus, if 2D ice can be produced on an industrial scale, it would be a useful anti-icing agent and a valuable lubricant.

2. Simulation Strategy

The DFT code CASTEP [19] was used to identify the geometries of water adsorption on 2D ice. Given the large fluctuations in the electron densities, we used the generalized gradient approximation method for geometry optimization. According to our work on 3D ice phases, the revised Perdew–Burke–Ernzerhof functional is the optimal exchange–correlation functional for phonon calculation [20,21,22,23,24,25]. The self-consistent field tolerance was set as 1 × 10 − 6 eV/atom. Using an ultrasoft pseudopotential, the energy cut-off was set to 340 eV, and the k-point mesh was 3 × 3 × 1 .
With reference to the work of Jiang [5], we constructed a primitive cell of the 2D ice I structure, as shown in Figure 1. The lattice constants were a = b = 5   Å , c = 22.74   Å , α =   γ = 90 ° , a n d   γ = 120 ° . To represent the 2D film, a large vacuum interval was set on the surface. Thus, the c -axis appeared to be rather long. In general, CASTEP simulations are based on periodic structures. To avoid the influence of the neighbouring cells, we extended the 2D ice plane to a 4 × 4 supercell, i.e., a = b = 20   Å . Then, we built a water monomer and copied it to the ice surface. Finally, three conformations were obtained, as shown in Figure 2. To compare the adsorption effect, a model of hydrogen fluoride monomer placed on the 2D ice surface was constructed too.
In the interfacial effect simulations, to match the coordinates of 2D ice, we selected ice Ic as the 3D ice sample. The lattice constants of ice Ic were set as follows: a = b = c = 6.38     Å , c = 22.7473   Å , a n d   α =   γ = γ = 90 ° . To match the lattice constants of the 2D ice, a film along the Ic (111) plane was cleaved with a thickness of four layers. Therefore, the parameters of the Ic film were adjusted as follows: a = b = 15.6   Å ,   a n d   γ = 120 ° . Subsequently, we expanded the 2D ice to a 3 × 3 supercell with lattice constants of a = b = 15   Å . Finally, we combined the 2D ice (001) film with the 3D ice Ic (111) film. In addition, we cleaved a bulk Ic sample into two samples placed approximately 3 Å apart and then performed geometry optimization, as a comparative study.

3. Results and Discussion

To demonstrate the hydrophobicity of 2D ice, we simulated the adsorption behaviour of a water molecule on the 2D ice (001) surface to determine whether this monomer could break the 2D ice structure and construct new hydrogen bonds with the 2D ice film. As the length of a hydrogen bond is approximately 1.8 Å, the monomer was placed at approximately 1.9–2.5 Å above the 2D ice surface. We constructed three kinds of configurations by adjusting the monomer orientations, namely two horizontal configurations (Figure 2a,b) and one upright configuration (Figure 2c). Figure 2a shows the horizontal configuration in which a hydrogen atom of the monomer was placed on top of an oxygen atom on the ice surface. Figure 2b shows the horizontal configuration in which an O-H bond of the monomer was placed on top of an H-O bond on the ice surface. Figure 2c shows the upright configuration. After geometry optimization (bottom row of Figure 2), in each configuration, the monomer was repelled by the 2D ice and thus moved farther from the surface. Supplementary Movie S1 demonstrates how the monomer disturbed the surface molecules and was ultimately repelled. The distances between the nearest hydrogen atom of the monomer and an oxygen atom on the ice surface changed from 1.995 Å to 2.728 Å (Figure 2a); from 1.995 Å to 3.299 Å (Figure 2b); and from 1.914 Å to 2.355 Å (Figure 2c), respectively. Clearly, the oxygen atom of the monomer exhibited more repulsive behaviour than its two hydrogen atoms.
After optimization, the total energies of the three systems depicted in Figure 2a–c were -30,545.874 eV, -30,545.872 eV, and -30,545.882 eV, respectively. The upright configuration (Figure 2c) exhibited the lowest potential, and the system energy was -30,544.857 eV before optimization. Thus, the energy of the system is reduced by 1 eV. This shows that the monomer could not break the 2D ice structure to form new hydrogen bonds. Supplementary Movie S1 shows the process of water molecules being repelled by 2D ice.
Two comparative models of HF and H2O monomers in parallel with one O-H bond of H2O at the 2D ice surface were optimized. The distance of fluorine and hydrogen atoms was set as 1.927 Å. After geometry optimization, the HF molecule clearly broke the film structure and reformed two hydrogen bonds with two water molecules at the 2D ice surface (Figure 3b). On the contrary, the H2O monomer in the same position was repelled away from 1.927 Å to 2.904Å (Figure 3c). This is because the electronegativity of F is stronger than that of O, so F could break the hydrogen bond of 2D ice and reformed hydrogen bond with it. This illustrated that HF is a good solvent to melt 2D ice. Supplementary Movie S2 shows the process of 2D ice film being destroyed by HF molecule.
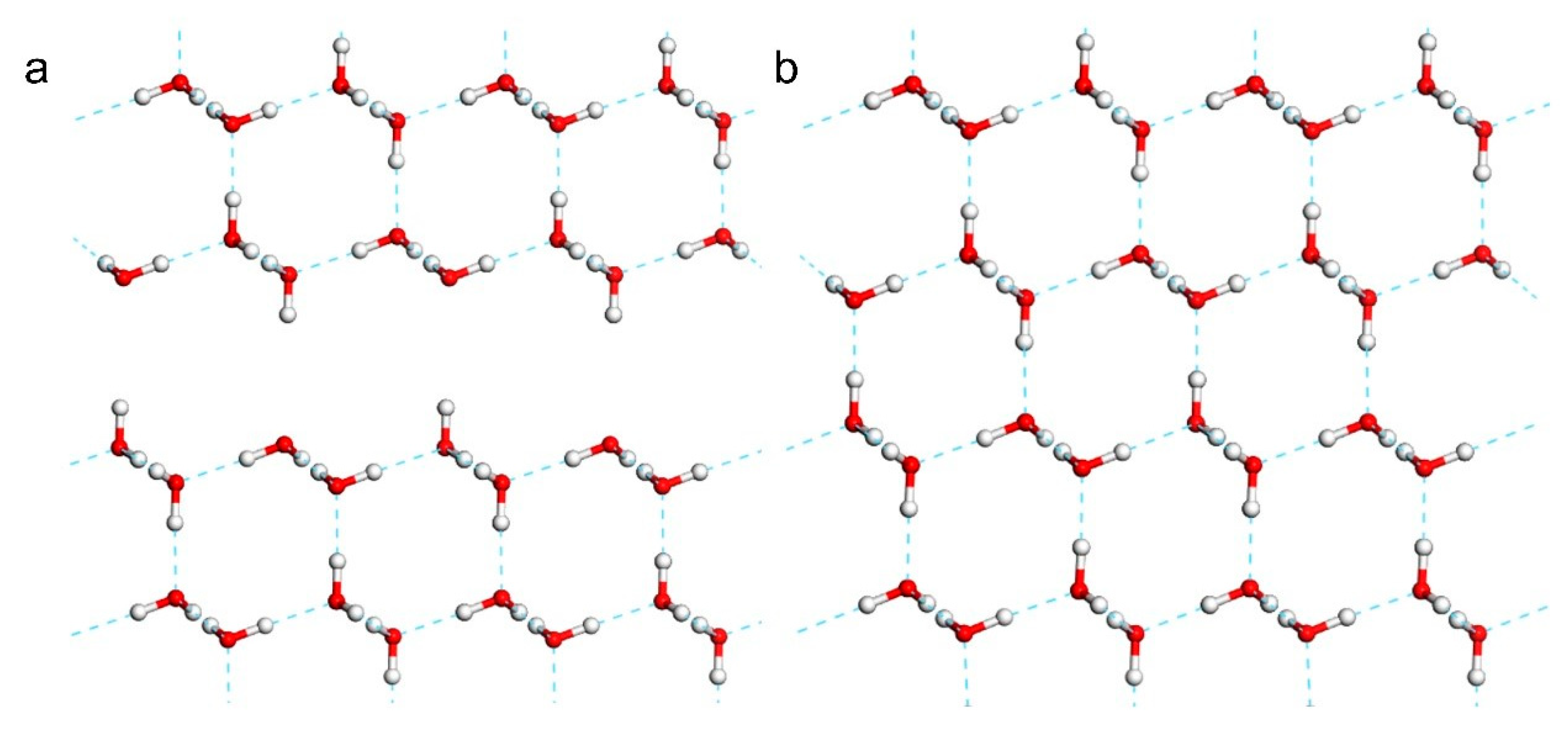
Subsequently, we studied the interfacial effect between 3D and 2D ice. To integrate the two types of films into one periodic cell, hydrogen-ordered ice Ic was used as the 3D ice because its lattice constant is well matched with that of 2D ice. The 3D ice film was superimposed onto the 2D ice (Figure 4a), and the geometry of the resulting system was optimized. Simulations were performed to explore whether 3D ice could destroy the stable hydrogen bond structure of the 2D ice and recombine to form a new 3D ice film. The result is shown in Figure 4b. There were no hydrogen bonds connecting the two layers. Because 2D ice was saturated with hydrogen bonds, the atomic-level film was highly stable. In contrast, because the 3D ice surface was not saturated with hydrogen bonds, the surface atoms encountered repulsive forces from 2D ice and reorganized to form as many hydrogen bonds as possible. That is, 2D ice inhibited the growth of 3D ice on its surface. Supplementary Movie S3 shows the dynamic process of this interfacial effect.
The results of the simulation of the interfacial effect between two 3D ice films are shown in Figure 5. Although the two 3D ice films were placed in parallel at a large distance, they easily integrated through the formation of hydrogen bonds. This result was expected because 3D ice is hydrophilic and thus did not inhibit the growth of a new ice film on its surface (Supplementary Movie S4 shows the effect). Comparing these two cases reveals that the 2D ice was hydrophobic. Because the 2D ice was saturated with hydrogen bonds, the interlocking hexagonal double-layer 2D ice film could not be destroyed by water molecules in the ambient environment. This demonstrates that 2D ice is a potential anti-icing agent. Furthermore, a multilayer framework composed of 2D ice is expected to be a promising lubricant, similar to graphite [26], for use in cold environments.

4. Conclusions

Owing to the challenges in experimentally observing atomic-level 2D ice films [5], research on this material has been limited because it is difficult to prepare in laboratory environments. In this study, we used DFT to examine the hydrophobic properties of 2D ice. The dynamic analysis of adsorption of a water monomer onto a 2D ice surface showed that the monomer could not break the 2D structure to form new hydrogen bonds. This hydrophobicity of the 2D ice was due to its being saturated with hydrogen bonds. On the contrary, the HF molecule may destroy the 2D ice film easily to show that HF is a good solvent to melt 2D ice.
An analysis of the interfacial effect between a 2D ice film and 3D ice showed that the surface of 3D ice reorganized to form more hydrogen bonds when it was placed close to the 2D ice film. In contrast, two 3D ice films placed in parallel at a large distance from each other were easily connected by hydrogen bonds. These results suggest that 2D ice inhibits the growth of 3D ice. Therefore, 2D ice is a promising anti-icing material. In addition, a multilayer framework of 2D ice may exhibit excellent lubricating properties, similar to those of graphite. Experimental observations are expected to be made in the future.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

Si-Cheng Liu is mainly responsible for model construction and article writing; Xiao-Yan Liu helped to build the model; Yi-Ning Li, Qing Guo, and Xiang-Ting Yu helped to analyze the data and discuss the results; Yi Yin and Hao-Ze Jing participated in the discussion. All authors have read and agreed to the published version of the manuscript.

Funding

We are grateful to the project ZR2022MA017 supported by Shandong Provincial Natural Science for financial support.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgement

The numerical calculations were performed on the supercomputing system at the Supercomputing Center, Shandong University, Weihai. Professional English-language editing support provided by AsiaEdit.

Conflicts of Interest

The Authors declare no Competing Financial or Non-Financial Interest.

Sample Availability

Samples of the compounds are available from the authors.

References

  1. Millot, M.; Coppari, F.; Rygg, J. R.; Correa Barrios, A.; Hamel, S.; Swift, D. C.; Eggert, J. H. , Nanosecond X-ray diffraction of shock-compressed superionic water ice. Nature 2019, 569, 251–255. [Google Scholar] [CrossRef]
  2. Gasser, T. M.; Thoeny, A. V.; Fortes, A. D.; Loerting, T. , Structural characterization of ice XIX as the second polymorph related to ice VI. Nat. Commun. 2021, 12, 1128. [Google Scholar] [CrossRef]
  3. Koga, K.; Zeng, X. C.; Tanaka, H. , Freezing of confined water: A bilayer ice phase in hydrophobic nanopores. Phys. Rev. Lett. 1997, 79, 5262. [Google Scholar] [CrossRef]
  4. Moore, E. B.; Molinero, V. , Is it cubic? Ice crystallization from deeply supercooled water. Phys. Chem. Chem. Phys. 2011, 13, 20008–20016. [Google Scholar] [CrossRef]
  5. Ma, R.; Cao, D.; Zhu, C.; Tian, Y.; Peng, J.; Guo, J.; Chen, J.; Li, X.-Z.; Francisco, J. S.; Zeng, X. C. , Atomic imaging of the edge structure and growth of a two-dimensional hexagonal ice. Nature 2020, 577, 60–63. [Google Scholar] [CrossRef] [PubMed]
  6. Guo, J.; Meng, X.; Chen, J.; Peng, J.; Sheng, J.; Li, X.-Z.; Xu, L.; Shi, J.-R.; Wang, E.; Jiang, Y. , Real-space imaging of interfacial water with submolecular resolution. Nat. Mater. 2014, 13, 184–189. [Google Scholar] [CrossRef] [PubMed]
  7. Zhu, Y.; Wang, F.; Bai, J.; Zeng, X. C.; Wu, H. , Compression limit of two-dimensional water constrained in graphene nanocapillaries. ACS Nano 2015, 9, 12197–12204. [Google Scholar] [CrossRef]
  8. Bragg, W. , The crystal structure of ice. Proc. Phys. Soc. Lond. 1921, 34, 98. [Google Scholar] [CrossRef]
  9. Whalley, E. , A detailed assignment of the O–H stretching bands of ice I. Can. J. Chem. 1977, 55, 3429–3441. [Google Scholar] [CrossRef]
  10. Perakis, F.; Hamm, P. , Two-dimensional infrared spectroscopy of neat ice Ih. Phys. Chem. Chem. Phys. 2012, 14, 6250–6256. [Google Scholar] [CrossRef] [PubMed]
  11. Ghasemi, S.; Alihosseini, M.; Peymanirad, F.; Jalali, H.; Ketabi, S.; Khoeini, F.; Neek-Amal, M. , Electronic, dielectric, and optical properties of two-dimensional and bulk ice: A multiscale simulation study. Phys. Rev. B 2020, 101, 184202. [Google Scholar] [CrossRef]
  12. Chen, J.; Schusteritsch, G.; Pickard, C. J.; Salzmann, C. G.; Michaelides, A. , Two dimensional ice from first principles: Structures and phase transitions. Phys. Rev. Lett. 2016, 116, 025501. [Google Scholar] [CrossRef] [PubMed]
  13. Kiselev, A.; Bachmann, F.; Pedevilla, P.; Cox, S. J.; Michaelides, A.; Gerthsen, D.; Leisner, T. , Active sites in heterogeneous ice nucleation—the example of K-rich feldspars. Science 2017, 355, 367–371. [Google Scholar] [CrossRef]
  14. Zheng, S.; Li, C.; Fu, Q.; Hu, W.; Xiang, T.; Wang, Q.; Du, M.; Liu, X.; Chen, Z. , Development of stable superhydrophobic coatings on aluminum surface for corrosion-resistant, self-cleaning, and anti-icing applications. Mater. Des. 2016, 93, 261–270. [Google Scholar] [CrossRef]
  15. Murray, B. J.; Knopf, D. A.; Bertram, A. K. , The formation of cubic ice under conditions relevant to Earth's atmosphere. Nature 2005, 434, 202–205. [Google Scholar] [CrossRef]
  16. Atkinson, J. D.; Murray, B. J.; Woodhouse, M. T.; Whale, T. F.; Baustian, K. J.; Carslaw, K. S.; Dobbie, S.; O’Sullivan, D.; Malkin, T. L. , The importance of feldspar for ice nucleation by mineral dust in mixed-phase clouds. Nature 2013, 498, 355–358. [Google Scholar] [CrossRef] [PubMed]
  17. Liou, Y.-C.; Tocilj, A.; Davies, P. L.; Jia, Z. , Mimicry of ice structure by surface hydroxyls and water of a β-helix antifreeze protein. Nature 2000, 406, 322–324. [Google Scholar] [CrossRef]
  18. Hetzel, R.; Hampel, A. , Slip rate variations on normal faults during glacial–interglacial changes in surface loads. Nature 2005, 435, 81–84. [Google Scholar] [CrossRef]
  19. Clark, S. J.; Segall, M. D.; Pickard, C. J.; Hasnip, P. J.; Probert, M. I.; Refson, K.; Payne, M. C. , First principles methods using CASTEP. Z. Für Krist. -Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
  20. Yuan, X.-Q.; Yu, X.-H.; Zhu, X.-L.; Wang, X.-C.; Liu, X.-Y.; Cao, J.-W.; Qin, X.-L.; Zhang, P. , Comparative analysis of the hydrogen bond vibrations of ice XII. ACS Omega 2022, 7, 2970–2974. [Google Scholar] [CrossRef]
  21. Ning, S.-Y.; Cao, J.-W.; Liu, X.-Y.; Wu, H.-J.; Yuan, X.-Q.; Dong, X.-T.; Li, Y.-N.; Jiang, Y.; Zhang, P. , Computational Analysis of Hydrogen Bond Vibrations of Ice III in the Far-Infrared Band. Crystals 2022, 12, 910. [Google Scholar] [CrossRef]
  22. Liu, X.-Y.; Cao, J.-W.; Qin, X.-L.; Zhu, X.-L.; Yu, X.-H.; Wang, X.-C.; Yuan, X.-Q.; Liu, Y.-H.; Wang, Y.; Zhang, P. , A Computational Validation of water Molecules Adsorption on an NaCl surface. Crystals 2021, 11, 610. [Google Scholar] [CrossRef]
  23. Dong, X.-T.; Qin, X.-L.; Wang, X.-C.; Cao, J.-W.; Liu, X.-Y.; Yu, X.-H.; Yuan, X.-Q.; Guo, Q.; Sun, Y.; Zhang, P. , Computer simulation of hypothetical hydrogen ordered structure of ice XIX. Phys. Chem. Chem. Phys. 2022, 24, 11023–11029. [Google Scholar] [CrossRef] [PubMed]
  24. Xiao-Ling, Q.; Xu-Liang, Z.; Jing-Wen, C.; Hao-Cheng, W.; Peng, Z. Investigation of hydrogen bond vibrations of ice. ACTA PHYSICA SINICA 2021, 70, (14). [Google Scholar]
  25. Zhu, X.-L.; Cao, J.-W.; Qin, X.-L.; Jiang, L.; Gu, Y.; Wang, H.-C.; Liu, Y.; Kolesnikov, A. I.; Zhang, P. , Origin of two distinct peaks of ice in the THz region and its application for natural gas hydrate dissociation. J. Phys. Chem. C 2019, 124, 1165–1170. [Google Scholar] [CrossRef]
  26. Geim, A. K. , Graphene: status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef]
Preprints 80509 g001
Figure 1. Primitive cell of 2D ice I. The left and right images show the top and side views, respectively.
Figure 1. Primitive cell of 2D ice I. The left and right images show the top and side views, respectively.
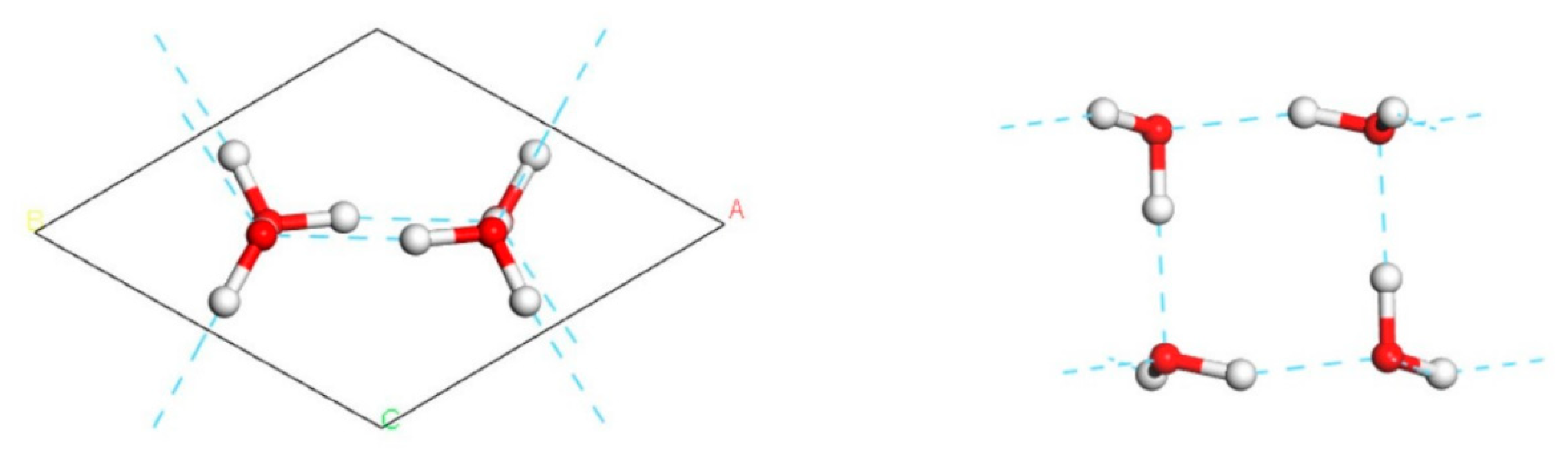
Preprints 80509 g001
Preprints 80509 g002
Figure 2. Side view of three models involving a water molecule on the 2D ice surface. The top row shows the constructed conformations, and the bottom row shows the corresponding optimized geometries. Red and grey balls represent oxygen and hydrogen atoms, respectively.
Figure 2. Side view of three models involving a water molecule on the 2D ice surface. The top row shows the constructed conformations, and the bottom row shows the corresponding optimized geometries. Red and grey balls represent oxygen and hydrogen atoms, respectively.
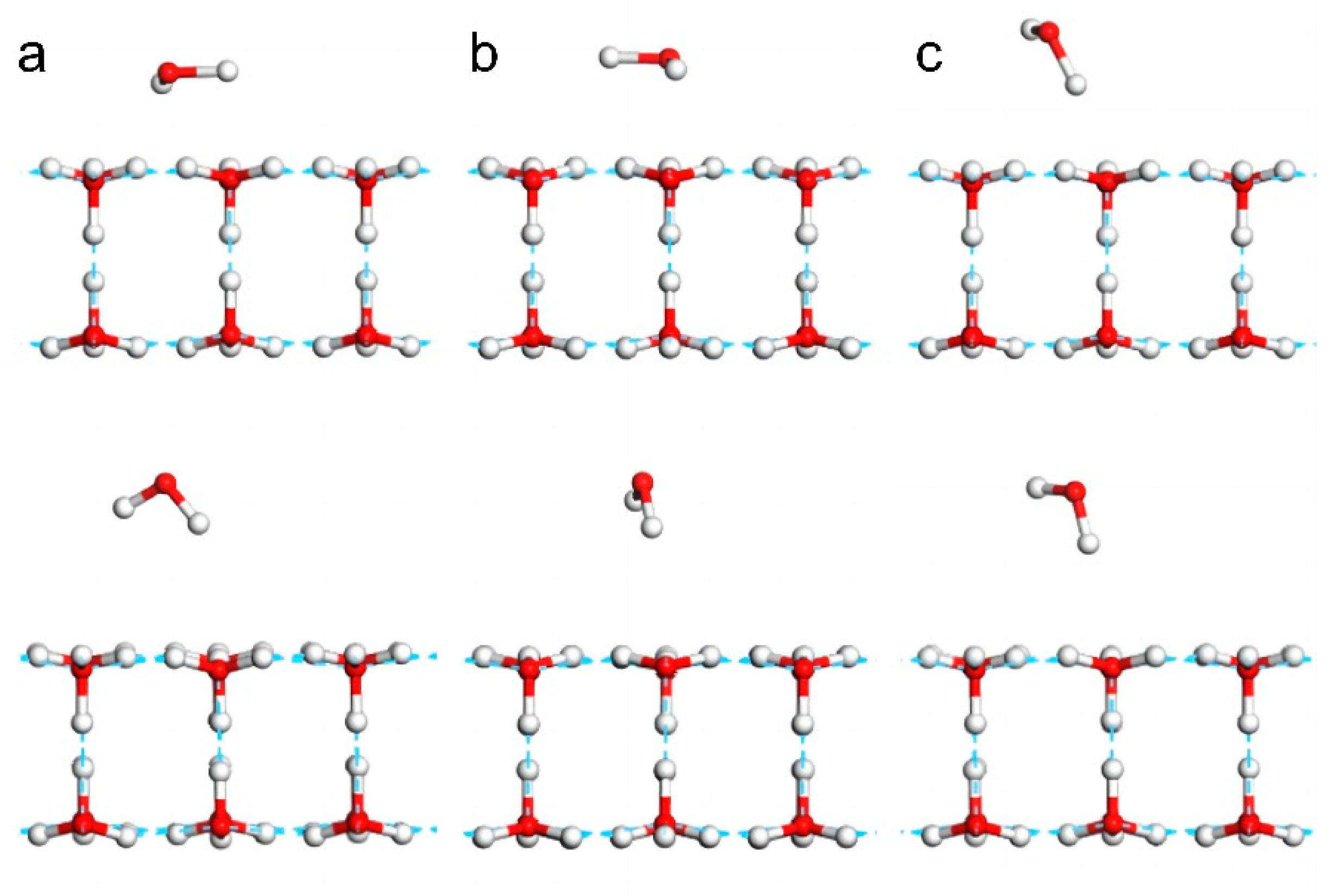
Preprints 80509 g002
Preprints 80509 g003
Figure 3. Comparisons of adsorption effect of HF and H2O on 2D ice surface. (a) The initial position of a HF molecule on the 2D ice surface and (b) The optimized result of HF model. (c) The optimized result of a H2O molecule placed in the same position.
Figure 3. Comparisons of adsorption effect of HF and H2O on 2D ice surface. (a) The initial position of a HF molecule on the 2D ice surface and (b) The optimized result of HF model. (c) The optimized result of a H2O molecule placed in the same position.
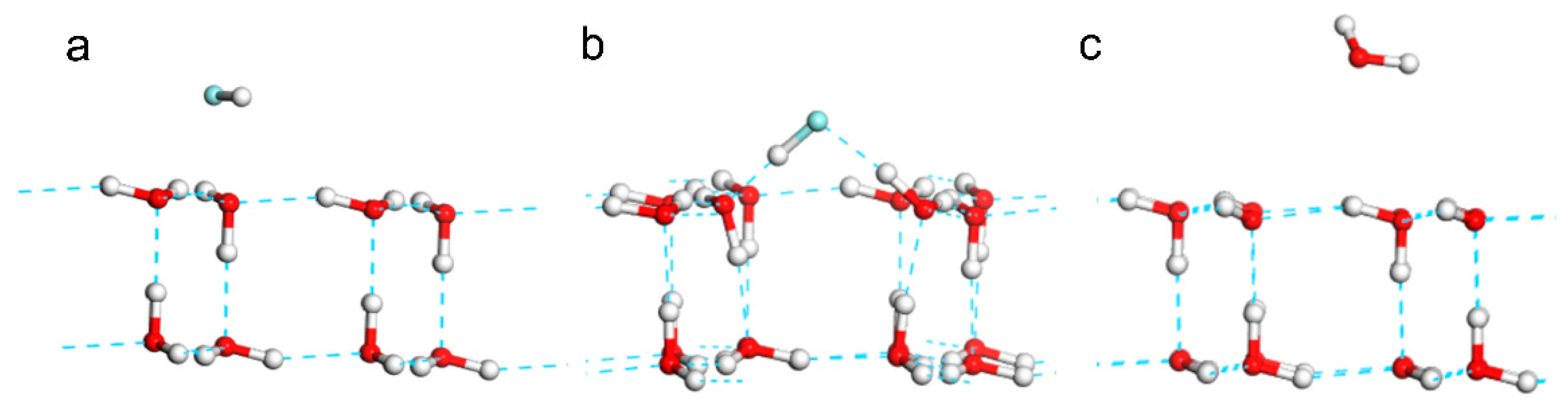
Preprints 80509 g003
Preprints 80509 g004
Figure 4. Interfacial effect between ice Ic (111) surface and 2D ice (001) surface. (a) Constructed model of 2D and 3D ice films; and (b) geometry optimization results. The surface of 3D ice reorganized to form more hydrogen bonds while the 2D ice keep stable.
Figure 4. Interfacial effect between ice Ic (111) surface and 2D ice (001) surface. (a) Constructed model of 2D and 3D ice films; and (b) geometry optimization results. The surface of 3D ice reorganized to form more hydrogen bonds while the 2D ice keep stable.
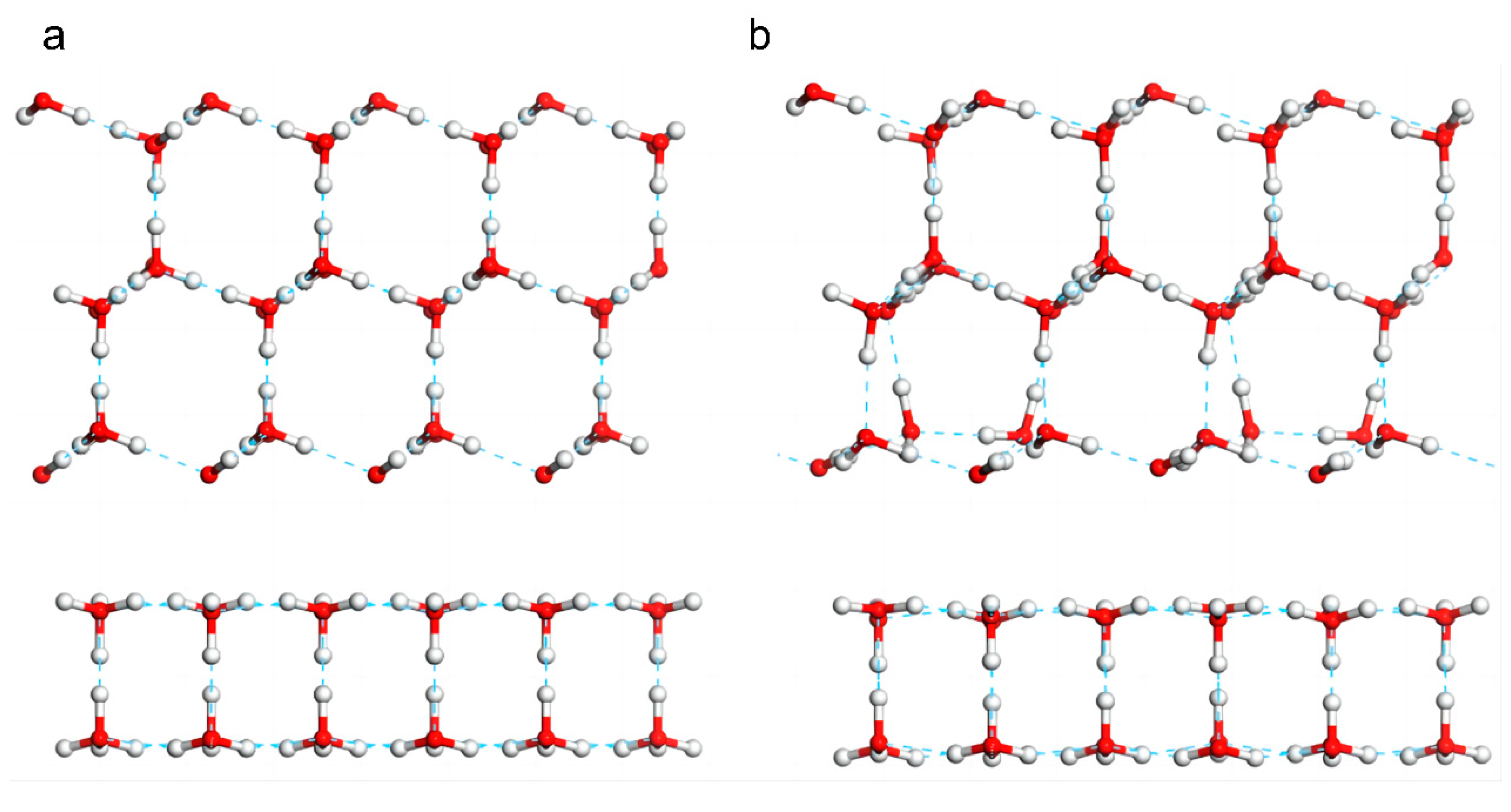
Preprints 80509 g004
Preprints 80509 g005
Figure 5. Interfacial effect between two 3D ice films. (a) Constructed model of two 3D ice films; and (b) geometry optimization results.
Figure 5. Interfacial effect between two 3D ice films. (a) Constructed model of two 3D ice films; and (b) geometry optimization results.
Preprints 80509 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated