Preprint
Article
First Quantization Approach Under the Extreme Conditions of Ultra-High Gravity
Altmetrics
Downloads
122
Views
71
Comments
0
This version is not peer-reviewed
Submitted:
22 July 2023
Posted:
27 July 2023
You are already at the latest version
Alerts
Abstract
Novel approaches under the extreme conditions of ultra-high gravity of a super massive black hole allow us to assume that the spacetime degrades into the single dimension of time. A unique interpretation of the non-relativistic Schrödinger equation together with the relativistic Klein-Gordon and Dirac equations is presented by swapping the three dimensional space derivatives with the singular time derivative in the D’Alembertian operator. This apparatus reveals a unique time dependent wave equation that results in some implications such as possible time quantization with the intervals of around 3.36 × 10−21 ? which is in the order of uncertainty in time, ∆? = 1.3 × 10−21 ?, calculated from the energy-time version of the Heisenberg uncertainty principle for electrons. As a result of this, an antisymmetric wave function around the edge of the event-horizon zone appears and indicates that the virtual particle-antiparticle pairs of the electron field split into two real components with the spin-up and down states, reconfirming the Hawking radiation. Energy eigenvalues calculated from the application of the Dirac equation satisfies the preservation of energy and charge. The wave equation invoked in this study reduces into the time dependent Dirac equation within the neighborhood of zero-point, ? = 0, insuring the relevance of the evaluations.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. Introduction
It is considered by ‘t Hooft [1] that black holes should be subject to the same rules of quantum mechanics as ordinary elementary particles or composite systems. On the other hand, parallel evaluations of quantum mechanics and general relativity revived an important problem so-called the black hole information paradox, predicting that physical information could permanently disappear in a black hole, because the calculations show the degeneration of many physical states unified into the same state. This contradicts with the fundamental postulate of quantum physics which predicts in principle that “the value of a wave function of a physical system at a time should determine its value at any other time”. This was in fact invoked by Hawking’s explanation on the issue [2,3]. However later calculations of him using elementary quantum gravity interactions resolved the problem, and showed that the information is preserved inside black holes, proposing a quantum mechanical model for black holes and resulting in a black body radiation named after him [4].
Physical implications of the quantum mechanical process of the black hole emission can be understood by imagining that a particle or its antiparticle radiation is emitted from just on the edge of the event horizon [3,5]. This radiation does not apparently come from the black hole itself, but it is rather created by the virtual particles of the quantum fluctuations inserted by ultra-high gravitational field of black holes. One of the partners of these virtual particles is eventually released as a real particle just off the event horizon zone. As a result of this process, the escape of one of the particles lowers the mass of the black hole [6]. Another explanation to this event is that one of the partners of virtual particle-antiparticle pairs, produced by the vacuum fluctuations near the event horizon, is captured by the black hole while the other survives [7]. The fact that the masses of the virtual particles are not counted as real masses, the particle that fell into the black hole must have had a negative energy in order to preserve the total energy. This is in fact observed as the loss of mass with respect to an observer far away from the black hole. In another alternative model which is much closer to the predictions in this study, the process is considered as a quantum tunneling effect just off the event horizon where one partner of the virtual pairs of vacuum fluctuations would tunnel outside the event horizon [8,9].
As well-known, time has been introduced as another dimension in addition to 3D-(x,y,z) space dimensions, after the recognition of relativity theories of Einstein, establishing the space-time structure of the universe. However, quantization of time has not yet been demonstrated by any powerful fundamental theory or experiment, according to the author’s and others’ knowledge [10]. Some suggest that the upper limit for the possible quantization of time should be 10-33 s due to the upper limit for the period of the universal oscillator is in this order [11]. On the other hand, this quantum of time can be extended up to the orders of 10-43 s which is the lowest possible time duration of the universe—the Planck time [12].
Most of the times, experimental and theoretical evaluations at extreme or reverse conditions would result in extraordinary theories and applications such as special and general relativities, superconductivity and lasers. In this paper, it is therefore demonstrated that the quantization of time is possible by considering an extreme situation of time dimension near the singularity of a black hole and that this kind of time quantization reconfirm the quantum mechanical models [1,2,3] of black holes that resolved the black hole information paradox [4,5,8].
2. Results and discussions
We exemplify the extreme situation by considering that what happens when time dimension becomes flat like the 3D-(xyz) is as in the case of the Galilean relativity—the relativity in daily life. In other words, let us consider the situation of quantum mechanics on the extreme end of general relativity when the gravity becomes infinite or extremely high. In this case, space is so sharply curved that we cannot comprehend the relativeness of space but only time. Reverse is true in the case of daily life (Galilean relativity) so that we always feel the relativity of space and we think that time is an absolute and positive variable, and simultaneous for all frames of references. General relativity accepts both space and time as dimensions which is in between the two situations explained above [13].
The results evaluated at the extreme conditions where time dimension becomes flat are extraordinary as might be expected, demonstrating a possible quantization of time by considering wave mechanics of a particle under the effect of ultra-high gravity. It is possible to have extremely high or infinite gravity close to the singularity of a black hole where even the light cannot escape due to the fact that it is so sharply curved and swallowed by it, as described after Schwarzschild [14,15,16]. Therefore, we will experience an unusual quantum mechanical exercise for a particle just outside the event-horizon of a Schwarzschild black hole.
2.1. Application of the Klein-Gordon equation
As you know that a non-relativistic quantum mechanical system is described by Schrödinger equation involving a Hamiltonian with second derivatives of 3D-space i.e. the Laplace operator. Klein [17] and Gordon [18] have extended the equation for a relativistic context by the inclusion of time as the 4th dimension in non-Euclidian Minkovski space where the Laplace operator is replaced by a 4D-operator so called the D’Alembartian operator given as
where is the Laplace operator and the speed of light. The first ever relativistic version of Schrödinger equation is called the Klein-Gordon equation which has opened a new gateway in sorting out the quantum fields in particle physics especially after the advancement of it by the Dirac equation [19] with the involvement of electromagnetic interaction and fermions.
Now, let us think that we are neither living in Schrödinger’s non-relativistic quantum world nor in Klein, Gordon and Dirac’s relativistic one, we are living in one dimensional space of time approximated from the case of the conditions at the singularity of a Schwarzschild black hole where general relativity and Galilean relativity collapse. In other words, we assume the conditions at which the 3D-space swaps with the 1D-time. Then the question arises; how would Schrödinger write his equation for a free particle with a mass of m in the 1D-time world? Using only the time derivative term of the D’Alembartian operator in Eq.1, one can probably write it as
where ℏ is the reduced Planck constant and the particle wave function in dimension. One should notice the fact that partial differentiation is not used here, because time is considered to be the only dimension. We ignore the presence of the other spatial dimensions at all, as we ignore the presence of the time dimension in conventional Schrödinger equations. This is neither a non-relativistic ordinary Schrödinger equation nor Klein-Gordon’s relativistic one. This is a unique equation adopted from the Schrödinger equation for a particle at a point in time, , considering space is simultaneous for all frames of references but only time is relativistic. We can probably call this situation as singularity of time. This is a kind of reverse conjuncture to the situation in Galilean space where time is simultaneous but normal 3D-space differs. The overall layout of the circumstances is summarized and tabulated in Table 1.
Table 1.
The summary of circumstances predicted in, respectively, Galilean relativity, general relativity and this study. .
Table 1.
The summary of circumstances predicted in, respectively, Galilean relativity, general relativity and this study. .
| Circumstance | Galilean relativity | General relativity | Present work |
| Relativity | Non-relativistic | relativistic | ? |
| Dimensions | |||
| Wave equation | Schrödinger equation | Klein-Gordon and Dirac Equations | Eq.2 |
| Wave operator | Laplace Operator, | D’Alembartian operator, |
We now focus on the situation of a particle with a rest mass of under the effect of ultra-high gravity of a Schwarzschild black hole with a mass of . We can rewrite Eq.2 with the inclusion of the potential term [20].
where is the gravitational constant and the Schwarzschild radius, considering the particle near the edge of the event-horizon. Form the definition of the Schwarzschild radius as
we can rearrange Eq.3 as
or in much simplified notation, using the natural units where
This is entirely time dependent wave equation of a particle with a mass of and can be considered stationary in terms of ordinary (xyz) positions, just as normal Schrödinger equation of an atom is considered to be stationary in terms of time. A solution of Eq.6 gives rise to
where is a probability constant smaller than unity applied in both positive and negative -directions since we consider that the situation is rather symmetrical around the edge of the event horizon. It can be calculated from the normalization condition over time. The angular frequency, can simply be calculated from the equivalent mass energy of the particle, provided . appears as a dimensionless factor bigger than unity in the wave function solution, acting like an emerging factor which is going to be discussed later on. Time, represents all the points in time dimension, ranging from to . However, there is a limit of time range within which the described wave equations given by Eqs.5 and 6, and corresponding wave function given by Eq.7 is valid. Out of this limited time range, the effect of ultra-high gravity eventually weakens and normal relativistic quantum mechanical wave equations become applicable where the particle is considered to be in 4D-spacetime.
The conceptual descriptions of black holes given by scientists such as Hawking and Penrose [21] and Schwarzschild [22] brought about some important issues, such as the fact that noting (even light) can escape from a black hole, which contradicts with fundamental observations and principles of quantum mechanics. Some other scientists such as Zeldovich and Starobinsky [23] raised the question that it is impossible due to the fact that the black hole has a certain absolute temperature, even though it is too small, and this should have caused a black body radiation at long wavelength range. As a result of these discussions, Hawking came up with a quantum mechanical model [3] of black holes, describing a kind of black hole evaporation named after him—the Hawking radiation.
It is considered in Hawking’s quantum mechanical model that there always exists a possibility of virtual particles (virtual positron-electron pairs) of the quantum fluctuations becoming a real particle by separation at the edge of the event horizon zone. One of the partners of the particle pair goes out traveling forward in time, and the other stay in traveling backward in time, at the boundary between the event horizon and infinity. Ingoing partner is called the Hawking partner, and outgoing the Hawking particle, released to the infinity according to Hawking’s quantum mechanical approach [3]. It is described by Hawking [3] that the first has to move in negative and the latter in positive t-direction. Eq.7 shows the possibility of the particle moving in both directions which is in agreement with the predictions of Hawking.
In order to briefly understand time can change in both directions near the event horizon, let us draw attention to the following discussion. According to general relativity time flows slower on a planet then it does in free space. The time, on a planet measured from a reference time is behind the time in free space. Therefore, we can apparently assume that time flows normally in free space while it is stopped at the edge of the event-horizon of the black hole. It is consequently right to assume that time originates from the edge of the event-horizon being positive towards free space and so, being negative towards the singularity.
Figure 1 and Figure 2 respectively show the distribution of wave function given by Eq.7 and its absolute square i.e. the probability function. They are drawn for an electron or positron for which rad/s, calculated from the equivalent mass energy of an electron or a positron. As can be seen, wave function and corresponding probability distributions are respectively antisymmetric and symmetric for the particles moving in and out. It has been quantum mechanically shown by the wave function in Eq.7 and by these corresponding figures that there exist real particles on the edge of the event-horizon moving either reverse or forward in time with the same possibility. It is to show that there is a possibility of particle escaping the infinite gravity of black hole which is impossible to accept in classical theory. This is the reconfirmation of Hawking radiation theory, once again quantum mechanically proved in this study. The wave function of the particle in Figure 1 is antisymmetric, meaning that particle spin changes sign in both sides of the event horizon; that is, ψ(t) = −ψ(-t), where the variables t and -t respectively correspond to the particle moving forward and backward in time as described by the Hawking quantum model of black holes, preserving the angular momenta. Since the absolute value is not changed by a sign swap, this corresponds to equal probabilities. It is true of the fact that once the virtual pairs of the quantum fluctuations are separated into real particles at the boundary of the event horizon, they only have one of the choices of being inside or outside.
As seen in Figure 1 and Figure 2, the first peak appears at , which is comparable with the uncertainty in time, , calculated from the energy-time version of the Heisenberg Uncertainty Principle (HUP). can be considered to be the average lifetime until the virtual electron-positron pairs of an electron field annihilate in accordance with the standard model of particle physics [24,25,26]. This is to say that escape of one of the partners of the virtual electron-positron pairs is only possible, if they live about twice as much longer than the average lifetime of the virtual electron-positron pairs. This reduces the amplitude of the cumulative distribution function (CDF) as time increases in positive direction, which will be discussed in the next section 2.2.
The second peak is illustrated in Figure 3. As the Hawking particle move away from the event horizon, it is more likely to survive from the event-horizon as the second and third peaks appear at respectively and s. This is because of the fact that the probability function exponentially increase as can be seen from the logarithmic version of the probability function shown in Figure 4. However, number of virtual particles that live longer than the average lifetime rather exponentially reduces, resulting in low probability current densities discussed later. Dimensionless coefficient appears to be 1.73 in Eq.7, and somehow act as an emerging factor that helps increase the probability of particle emission and backdate the peaks, without which particle emission seems to be impossible, since the first peak would have appeared as late as at , if was unity for instance.
On the other hand, the peaks appearing by certain intervals are the possible indication for the quantization of time. The time intervals between the subsequent peaks increase as the time goes on, meaning that the gaps between the peaks enlarge and the uncertainty in time becomes low in comparison to the gaps. Analogical analyses between the uncertainty in time () and uncertainty in space ( mean that should be similar to the quantum steps of the particle along t-dimension, as likens to be the quantum steps corresponding to the de Broglie wavelength of a certain quantum mechanical particle in normal ordinary space. The fact that time intervals increase as the time increases further away from the event-horizon, the possibility of the particle jumping from one peak to the other so weakens that the theory presented here become invalid, after which the relativistic 4D Klein-Gordon or Dirac equations should be applied. Exact value of the time at which particle appears to have an escape possibility will be given after the calculations of the probability current density (PCD) along time dimension.
Before we move on these calculations, let us have a look at the shapes of wave and corresponding probability functions. As can be seen in Figure 1, Figure 2, Figure 3 and Figure 4 the peaks are broader when they emerge and steeper when they descent. This is a kind of similarity that appears in the Franck-Hertz experiment which is one of the first demonstrations of energy quantization of atoms. This similarity shows that the predicted time quantization probably occurs in a similar manner. In t-dimension, transition from an upper peak to the lower would probably result in the emission of a particle just as in the case of the transition of an electron from higher energy states, resulting in photon emission due to atomic quantization of energy levels. In the case of possible time quantization, transition from one peak to the other will probably result in either an absorption or emission of gravitation particle, hypothetically introduced as gravitons. The time intervals between the peaks along time dimension would be an important measure in absorption or dissipation of gravitational energy, hypothesizing that time also has energy.
2.2. Probability current density and cumulative distribution functions in time dimension
Let us now calculate the PCD, in -dimension. Taking the account that in time dimension appears in a similar way as it does in spatial dimensions, it can be written as
and substituting Eq.7 in Eq.8, we find that
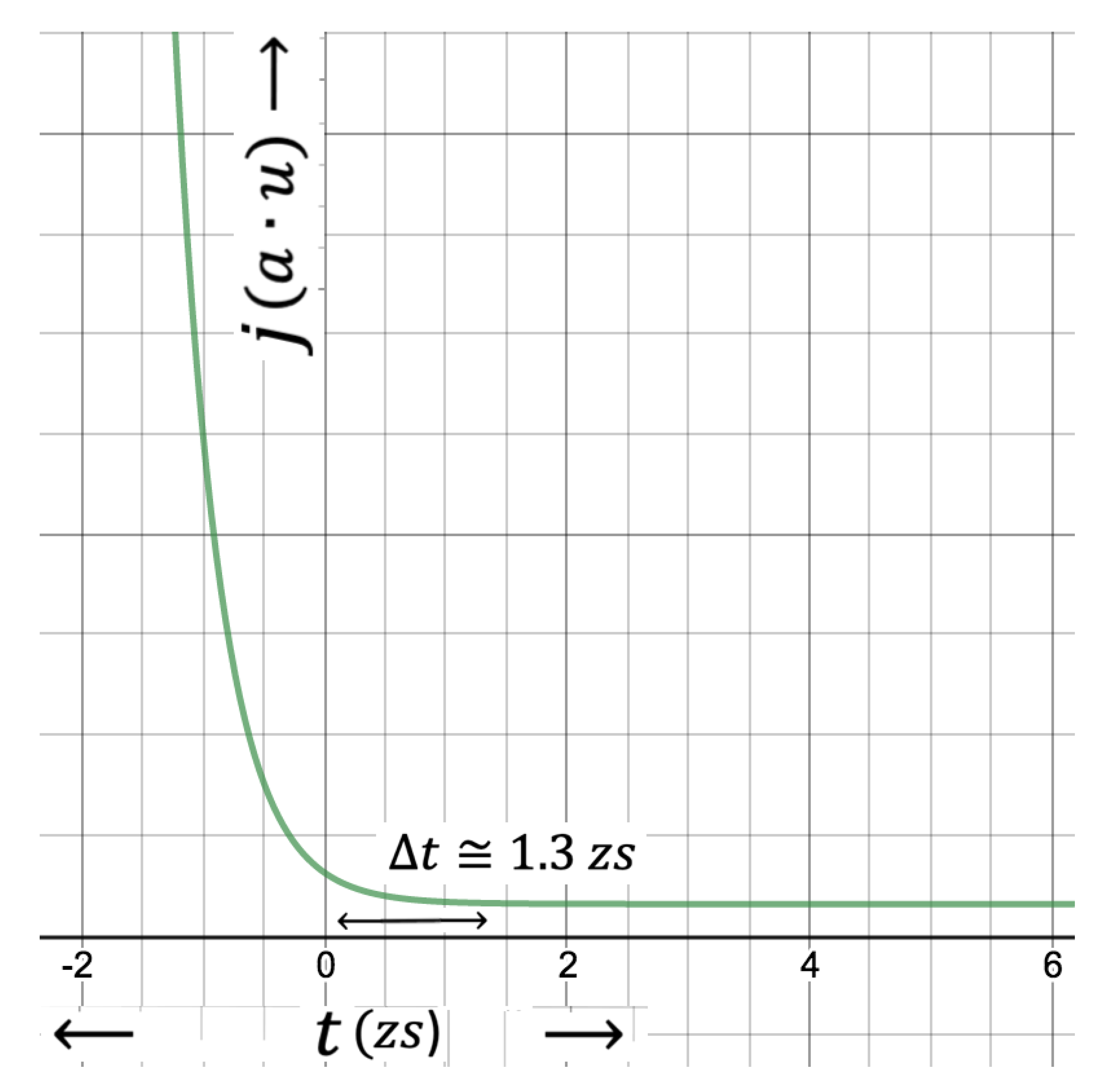
The distribution of the PCD is shown in Figure 5 and Figure 6 around the edge of the event horizon. As can be seen, , exhibiting the distribution of particles, exponentially increases in backward in time towards the singularity, and reduces forward in time towards the infinity. This is quite expected that number of particles leaving the event horizon will be extremely low in comparison to particles captured by the black hole. On the other hand, reduces rapidly just outside the event horizon and settles down to a background value at around , which corresponds to uncertainty in time according to the energy-time version of the HUP.
We also calculated the CDF,
for certain time ranges. One meaningful calculation is in between and , within which period of time, the first peaks in both sides emerge and vanish as seen in Figure 1 and Figure 2. The ratio between the CDFs for the particles moving forward in time and for those moving backwards work out to be
i.e. around ten-thousandth of 2.4 which is comparably small as a matter of fact. This is in fact the overall cumulative ratio of the number of particles released from the off-shell surface area () of the event horizon and it is independent from the mass of the black hole. This means that the surface area of the event horizon of the black hole should be constant no matter how much material it merges. This is in away correct in terms of the third law of thermodynamics, since it is indicated that there ought to be a constant entropy at temperatures as low as the temperature of a super-massive black hole, which is virtually absolute zero according to the temperature of black holes given, in Kelvins, as
where is the Boltzmann constant and the solar mass [27]. It follows that the constant entropy, of black holes should be proportional to the constant area of the event-horizon, i.e. . This is exactly what is proposed by Bekenstein [28], and that the entropy of black holes is called the Bekenstein-Hawking entropy. Therefore, this work also confirms the proposition of Bekenstein, from a different perspective.
Returning the possible quantization of time, we have simply demonstrated the time quantization around the edge of the event horizon where . Time intervals () between the peaks increase as we go further away from the edge in both directions. Near the event horizon is comparable with the uncertainty in time, calculated from the energy-time version of the HUP. For this reason, we can assume that the time quantization is prominent near the event horizon. The quantization lose its significance as the particle goes further away from the event horizon to free space because time intervals become so big that in comparison to which is in the order of zepto-seconds (zs) for an electron or positron. It is like the uncertainty in space ( is very small in macroscopic scale while it is comparable or occasionally even bigger than the microscopic quantum mechanical entities. Just as this is the limit of classical mechanics that thereafter quantum mechanical predictions come into play, there is a limit of the predictions invoked in this study where time is possibly quantized, out of which the time quantization is not that distinct. Further to this, we are in normal space and feeling the time passing smoothly and irreversibly at very low or nearly zero gravities in comparison to those near the event horizon.
2.3. Application of the Dirac equation
In the evaluations of Eqs.6 and 7, antisymmetric wave function proves that the particles’ spins have opposite signs for particles mowing forward and backward in time. This also ensures the conservation of angular momentum. However, these predictions don’t give a clue about the particle character whether it is electron or positron. Now we shall try and understand the particle types by the application of the Dirac equation squeezed in t-dimension.
Dirac equation in natural units for free electron in the 4D space-time is given as
where , , and are the Dirac matrixes and the column matrix, indicating that it is four component spinor given by
representing electron-positron pairs of the electron field corresponding to spin up and down states of them. Since the final Dirac matrix, in Eq.13 is given by
and represent the positive energy states while and represent the negative ones. Although Dirac tried to explain the negative energy states by the Dirac sea model, after the discovery of positron by Anderson [29], these states are interpreted as positrons in QFT.
Rearranging Eq.13 for 1D-time dimension, we can write
Substituting Eqs.14 and 15 in Eq.16, we find
representing electron and positron in spin up and down characters. Now let us apply the Schwarzschild potential energy [28] in Eq.16, we find
where is supposed to be a unit matrix given as
in order not to perturb potential term in Eq.18. Applying and matrixes in the final Dirac equation, we write
where
using the and matrixes given respectively in Eqs.15 and 19. The eigenvalues of the energy are given by
corresponding to wave functions given in Eq.14, representing particles and antiparticles with spin up and down states. Energy matrix in Eq.22 shows the situations both no emission of particle or emission of either spin up () or down () particle, since respectively the diagonal values of the energy matrix and . However, this seems to come up with a confusion, supposing a loss of energy of the black hole twice as much more than it is expected. This is actually required in terms of the fact that there ought to be inclusion of a partner particle accompanying with each emission. Before the emission the particle-antiparticle pairs are virtual and their masses are counted to be zero. However, by the emission, the virtual pairs are transferred to real particles each having masses of . Therefore, the total energy of the black hole after emission is given as
resulting in a loss of energy equivalent to the mass energy of one particle per each instance of emission, ensuring the conservation of energy. If there was only in the E matrix in Eq.22, there would be no energy difference of the black hole before and after emission which is against the conservation of energy and, the Hawking radiation theory predicting a loss of matter from the black hole. So this is one of the strengths of the squeezed Dirac equation given by Eq.20. We can probably better understand the equivalency conditions of Eq.20 with the followings:
where represents the eigenvalues in the diagonal of the energy matrix in Eq.22, which is in the case of particle emission from the event horizon. On the other hand, considering the energy matrix of the eigenvalues in Eq.22 and its trace, we can calculate the expectation value of the energy as , which is not necessarily be equal to the eigenvalues of the energy in the diagonal of the energy matrix. However, this expectation value is quite expected, indicating the overall loss of the mass or energy of the black hole is one particular mass of the emitted particle.
Another strength of Eq.20 is as follows; let us draw the attention to the fact that, provided the second derivative of the wave function with respect to time in Eq.6 is zero, Eq.6 reduces to Eq.20 found from the Dirac equation, since the overall expectation value of is 1 for all possible events. In fact, the second derivatives mean the curvature as
where is the radius of the curvature . This is compatible with Figure 1 which shows that wave function is fairly flat just around the event horizon within the neighborhood of where the virtual particles become real. Flatness means that and consequently at times close to the event horizon.
On the other hand, in order to resolve the time quantization, the distributions of the wave function and, consequently, the probabilities as a function of time, we use Eq.7 involving the second derivative of with respect to time, using the approximation of the curvature is different than zero just a bit beyond the neighborhood of . Yet, we already find out the energy and spin states with the Dirac equation expressed by Eq.20, involving the first derivatives, only.
Finally, one might argue that the apparatus employed in the paper is that of a first quantized Klein-Gordon and Dirac equations, squeezed to a single time dimension and thus the first quantized approach is not sufficient to describe such particle production processes. However the approach is presently adequate for real particle emission in this stage. The second quantized evaluations will be given in further studies.
3. Conclusions
Possible quantization of time is introduced by a unique first quantized approximation under the effect of infinite gravity conditions. Novel quantum mechanical wave equations involving only the time derivative reveal an antisymmetric wave function around the edge of the event horizon zone, indicating that virtual particle-antiparticle pairs of the electron field splits into two real components with spin-up and down states which is in agreement with the quantum mechanical models of massive black holes. Time intervals around the edge of the event horizon are comparable with the uncertainties in time, calculated from the energy-time version of the Heisenberg uncertainty principle. Energy eigenvalues calculated from the time dependent Dirac equation preserve the energy and charge, and show a clear energy dissipation from the event horizon zone resulting in one electron or positron mass evaporation per each instance. Evaluations of probability current density and cumulative distribution functions for the particles traveling forward and backward in time is compatible with the thermodynamic models of ultra-massive black holes, sustaining the Bekenstein-Hawking entropy. The wave equation invoked in this study reduces the time dependent Dirac equation within the neighborhood of zero-point, ensuring substantiality of the evaluations.
Acknowledgement:
I acknowledge the assistance of Cemal Mert Tüzemen in preparation of the figures.
Data Availability Statement
The data that supports the findings of this study are available within the article.
Conflict of Interst
The author has no conflicts to disclose.
References
- G. ‘t Hooft, On the quantum structure of a black hole, Nuclear Physics B. 256, 727 (1985). [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220,. [CrossRef]
- Hawking, S.W. The Quantum Mechanics of Black Holes. Sci. Am. 1977, 236, 34–41,. [CrossRef]
- Hawking, S.W. Information loss in black holes. Phys. Rev. D 2005, 72, 084013,. [CrossRef]
- S. B. Giddings, Black holes, quantum information and the foundations of physics, Physics Today, 30 (2013). [CrossRef]
- Carroll, B.W.; Ostlie, D.A.; Friedlander, M. An Introduction to Modern Astrophysics. Phys. Today 1997, 50, 66–67,. [CrossRef]
- M. Wittemer, F. Hakelberg, P. Kiefer, J.-P. Schröder, C. Fey, R. Schützhold, U. Warring and T. Schaetz, Particle pair creation by inflation of quantum vacuum fluctuations in an ion trap, arXiv:1903.05523v1 [quant-ph] (2019). [CrossRef]
- Q.-Q. Jiang, S.-Q. Wu, X. Cai, Hawking radiation as tunneling from the Kerr and Kerr-Newman black holes, Phys. Rev. D. 73, 069902 (2006). [CrossRef]
- Hotta, M.; Schützhold, R.; Unruh, W.G. Partner particles for moving mirror radiation and black hole evaporation. Phys. Rev. D 2015, 91, 124060,. [CrossRef]
- W. G. Tifft, A Brief History of Quantized Time, Mercury 25, 12, (1995).
- G. Wendel, L. Martinez and M. Bojowald, Phys. Rev. Lett. 124, 241301 (2020). [CrossRef]
- Khrennikov, A. Quantum Randomness as a Result of Random Fluctuations at the Planck Time Scale?. Int. J. Theor. Phys. 2007, 47, 114–124,. [CrossRef]
- D. Finkelstein, Space-Time Code, Phys. Rev. 184, 1261 (1969). [CrossRef]
- Janis, A.I.; Newman, E.T.; Winicour, J. Reality of the Schwarzschild Singularity. Phys. Rev. Lett. 1968, 20, 878–880,. [CrossRef]
- Regge, T.; Wheeler, J.A. Stability of a Schwarzschild Singularity. Phys. Rev. 1957, 108, 1063–1069,. [CrossRef]
- Virbhadra, K.S.; Ellis, G.F.R. Schwarzschild black hole lensing. Phys. Rev. D 2000, 62, 084003,. [CrossRef]
- O. Klein, Quantentheorie und fünfdimensionale Relativitätstheorie, Z. Phys 37(12), 895 (1926). [CrossRef]
- Von W. Gordon, Der comptoneffekt nach der schrödingerschen theorie, Z. Phys 40(1-2), 117 (1926). [CrossRef]
- P. A. M. Dirac, Proc. of Royal Society A. 117(778), 610 (1928).
- Dolan, S.; Doran, C.; Lasenby, A. Fermion scattering by a Schwarzschild black hole. Phys. Rev. D 2006, 74, 064005,. [CrossRef]
- S. W. Hawking, R. Penrose, Singularities of gravitational collapse and cosmology, Proceedings of the Royal Society of London Series A-Mathematical and Physical Sciences. 314(1519), 529 (1970). [CrossRef]
- K. Schwarzschild, Original: Uber das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, Phys.-Math. Klasse, 189 (1916), Translation: On the gravitational field of a mass point according to Einstein's theory, General Relativity and Gravitation. 35(5), 951 (2003).
- Y. B. Zeldovich and A. A. Starobinsky, Particle production and vacuum polarization in an anisotropic gravitational-field, Soviet Physics Jetp-USSR 34(6), 1159 (1972). [CrossRef]
- Tüzemen, S. A Possible Microscopic Model for Gravitational Interaction. Phys. Sci. Int. J. 2016, 9, 1–6,. [CrossRef]
- S. Tüzemen, Approaching to Gravity? Journal of Physics: Conference Series 707, 012003 (2016). [CrossRef]
- S. Tüzemen, The Quantum and Cosmic Codes of the Universe, Cambridge Scholars Publishing, 124 (2020).
- R. M. Wald, The Thermodynamics of Black Holes, Living Reviews in Relativity. 4, 6 (2001). ttps://doi.org/10.12942/lrr-2001-6.
- J. D. Bekenstein, Black Holes and Entropy, Phys. Rev. D. 7, 2333 (1973). [CrossRef]
- C. D. Anderson, The Positive Electron, Phys. Rev. 43, 491 (1933). [CrossRef]
Figure 1.
The wave function of an electron under the effect of ultra-high gravity near the event horizon. Antisymmetric behavior of ψ(t) = −ψ(-t) show the fact that the particle traveling forward in time has opposite spin with respect to the particle traveling backward in time.
Figure 1.
The wave function of an electron under the effect of ultra-high gravity near the event horizon. Antisymmetric behavior of ψ(t) = −ψ(-t) show the fact that the particle traveling forward in time has opposite spin with respect to the particle traveling backward in time.
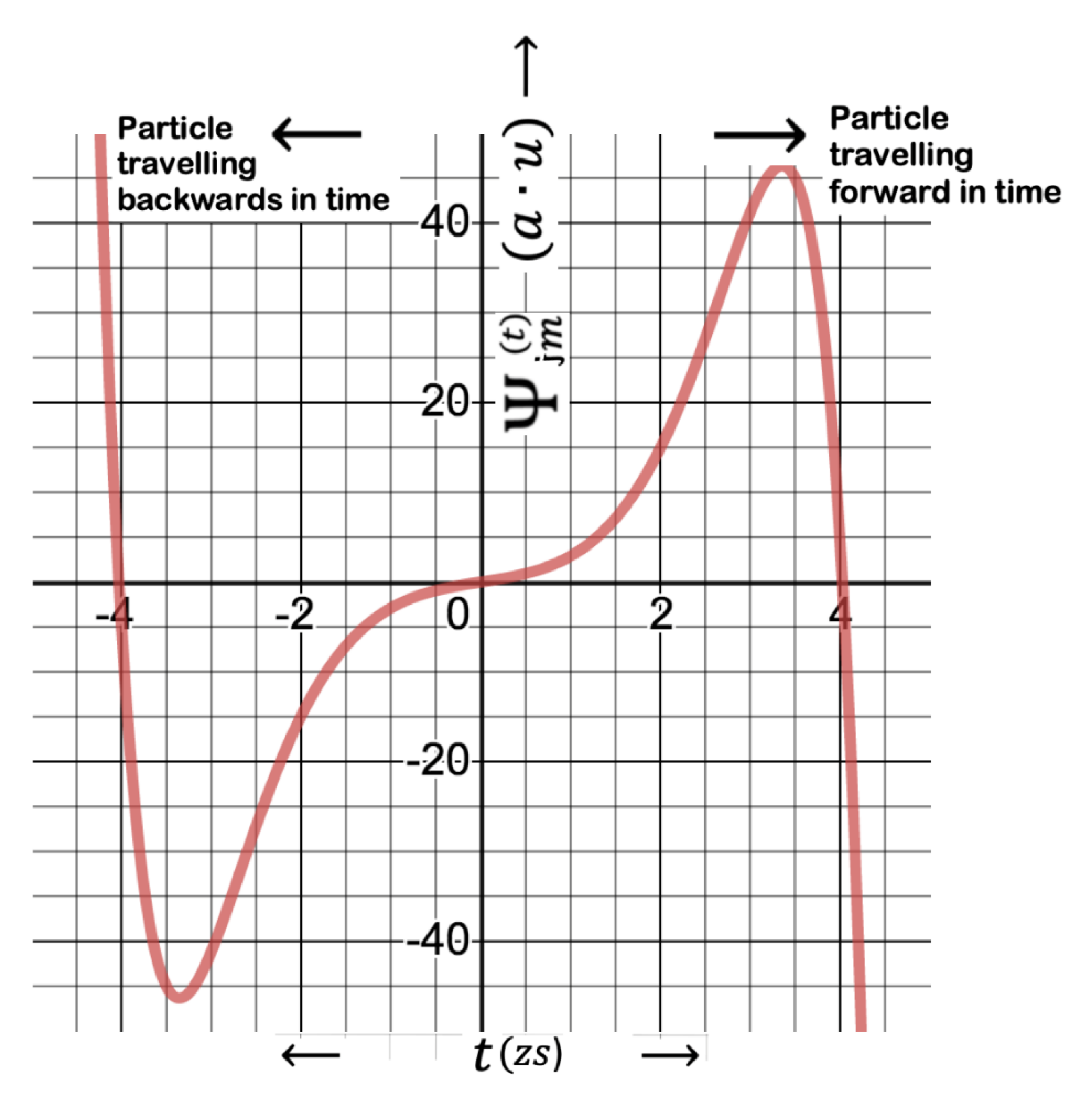
Figure 2.
Probability distribution function of an electron under the effect of ultra-high gravity near the event horizon, illustrating the first peak at , which is comparable with the uncertainty in time calculated from the energy-time version of the Heisenberg uncertainty principle. It is remarkable to see that the peak start to emerge at a time just off to . The shapes of the peaks exhibit a kind of formation similar to the ones appear in the Frank-Hertz experiments illustrating the energy quantization of atoms.
Figure 2.
Probability distribution function of an electron under the effect of ultra-high gravity near the event horizon, illustrating the first peak at , which is comparable with the uncertainty in time calculated from the energy-time version of the Heisenberg uncertainty principle. It is remarkable to see that the peak start to emerge at a time just off to . The shapes of the peaks exhibit a kind of formation similar to the ones appear in the Frank-Hertz experiments illustrating the energy quantization of atoms.
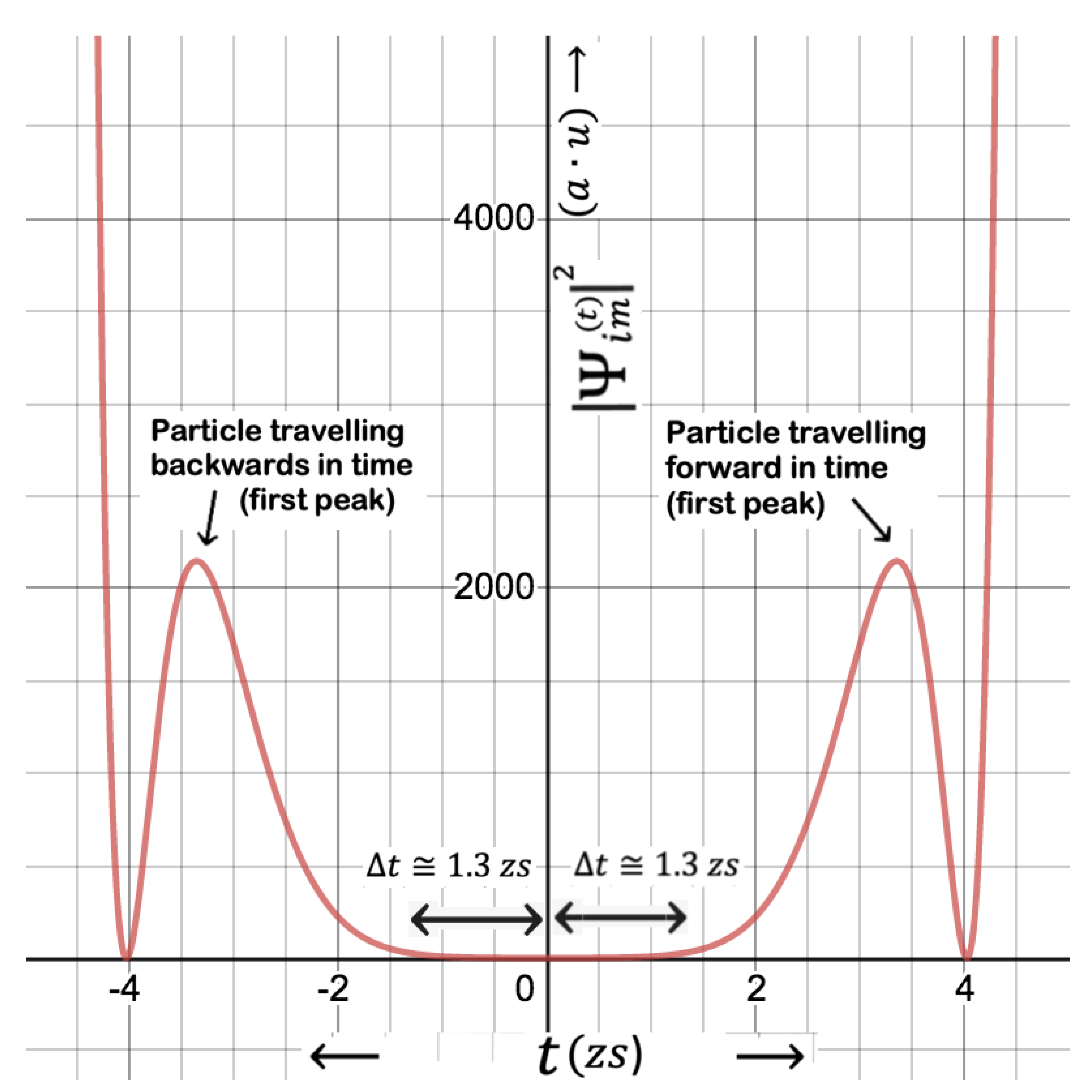
Figure 3.
Probability distribution function of an electron under the effect of ultra-high gravity near the event horizon, illustrating the second peak at . The third peak appears at 11.4 zs in the larger scales, exhibiting that the time intervals of between the subsequent peaks increase over the continuation of time.
Figure 3.
Probability distribution function of an electron under the effect of ultra-high gravity near the event horizon, illustrating the second peak at . The third peak appears at 11.4 zs in the larger scales, exhibiting that the time intervals of between the subsequent peaks increase over the continuation of time.
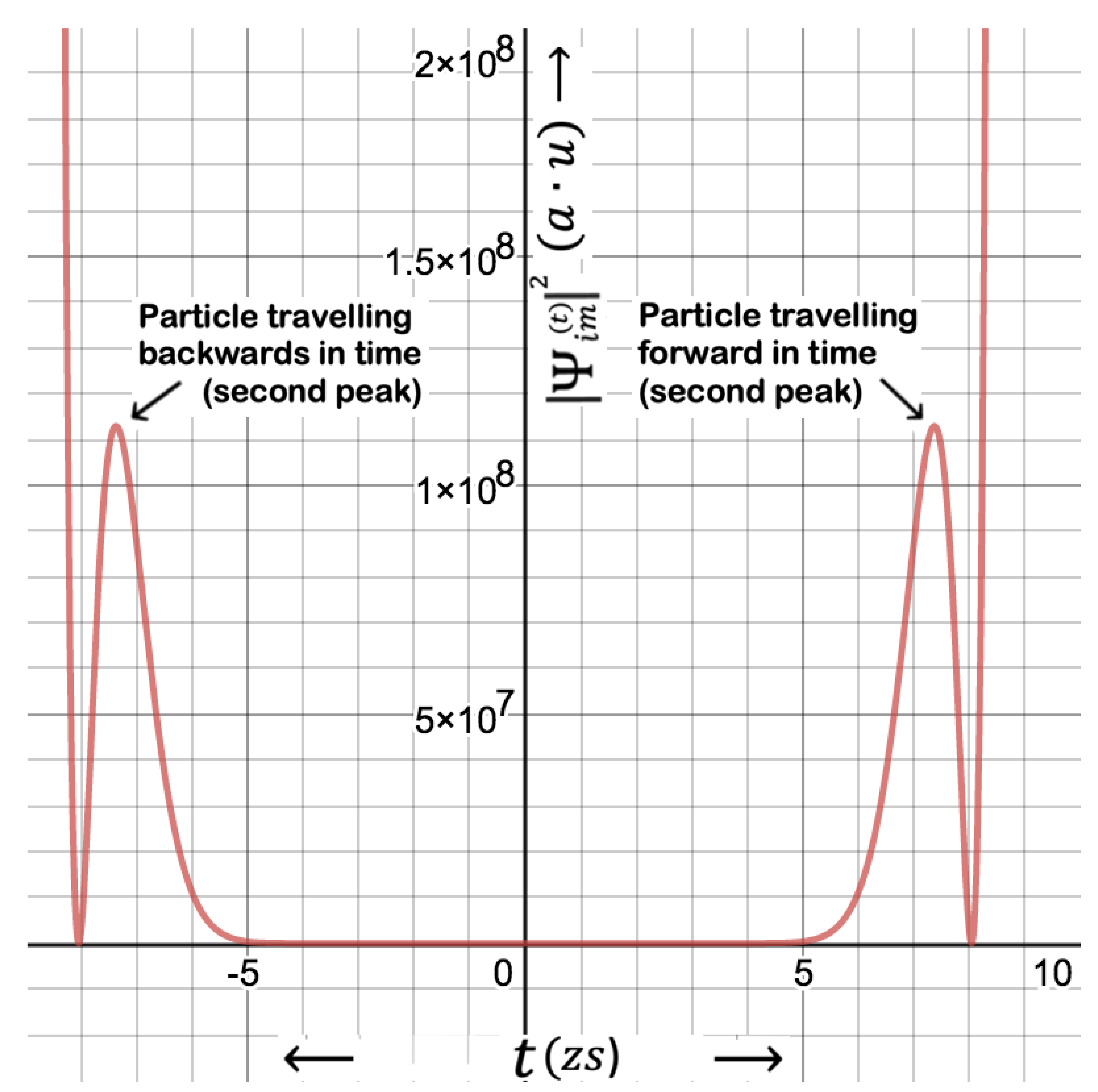
Figure 4.
Logarithmic illustration of probability distribution function of an electron under the effect of ultra-high gravity near the event horizon, illustrating five peaks together. The time intervals of between the subsequent peaks increase over the continuation of time.
Figure 4.
Logarithmic illustration of probability distribution function of an electron under the effect of ultra-high gravity near the event horizon, illustrating five peaks together. The time intervals of between the subsequent peaks increase over the continuation of time.
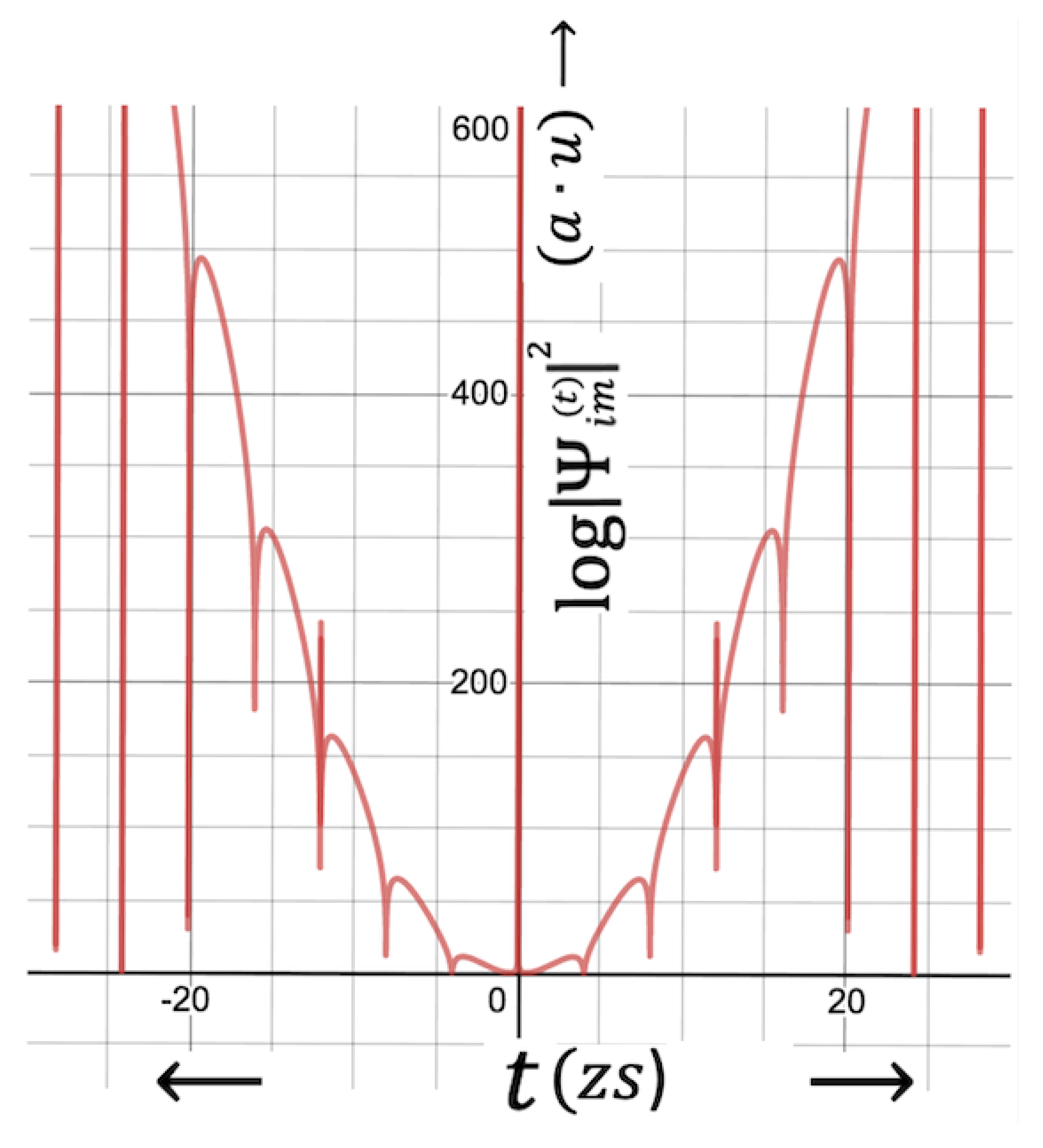
Figure 5.
Probability current density, along time dimension illustrated in a dilute scale of time. Notice the fact that vast amount of ingoing particles exists with respect to outgoing particles at the edge of the event horizon.
Figure 5.
Probability current density, along time dimension illustrated in a dilute scale of time. Notice the fact that vast amount of ingoing particles exists with respect to outgoing particles at the edge of the event horizon.
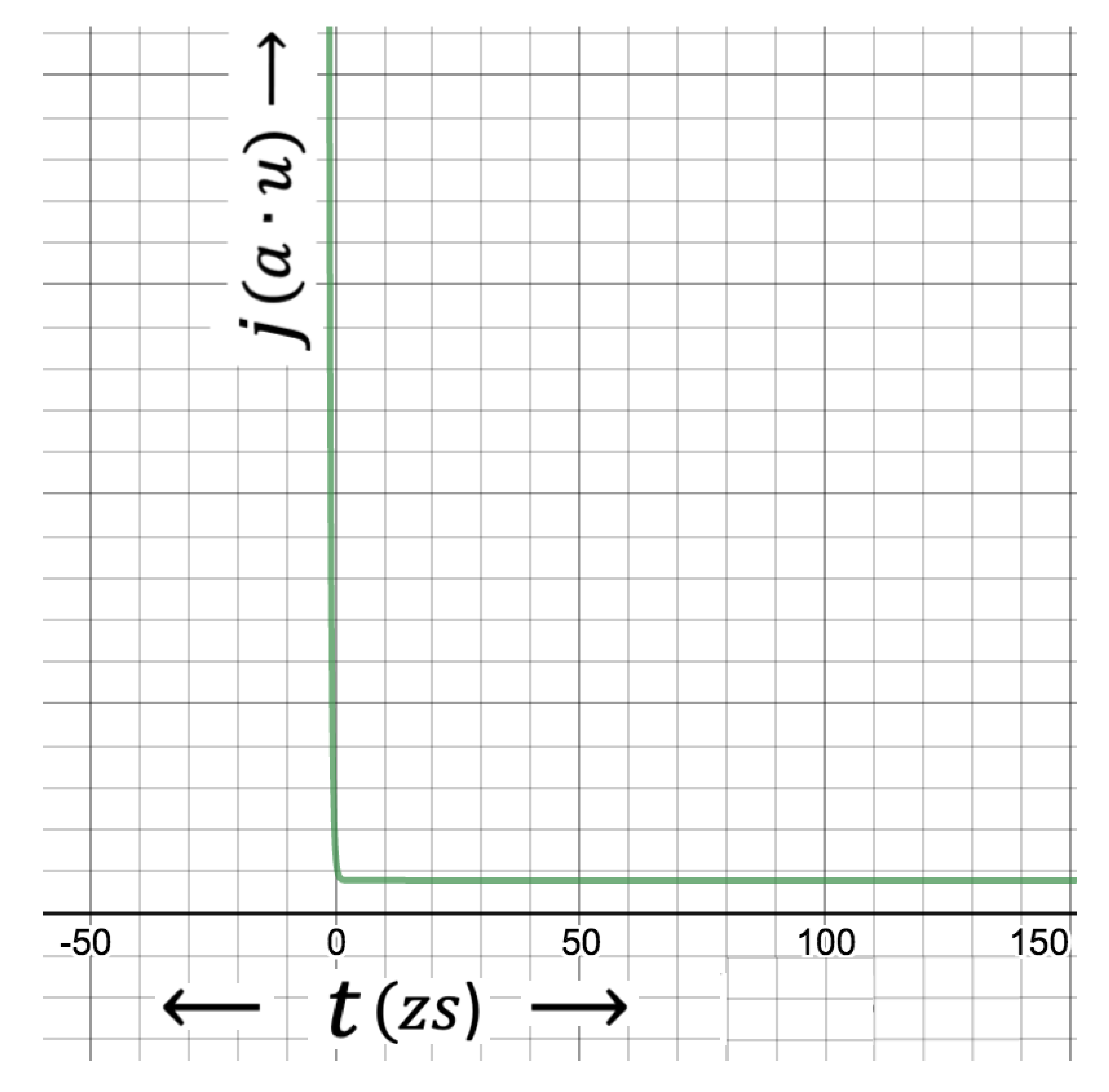
Figure 6.
Probability current density, along time dimension illustrated in a compact scale. Notice the settle of the graph just after the uncertainty in time from which the first peak of the wave function starts to emerge, illustrating the rareness of particle current density outside of this point towards the infinity.
Figure 6.
Probability current density, along time dimension illustrated in a compact scale. Notice the settle of the graph just after the uncertainty in time from which the first peak of the wave function starts to emerge, illustrating the rareness of particle current density outside of this point towards the infinity.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





