Submitted:
27 July 2023
Posted:
27 July 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Background And System Modelling
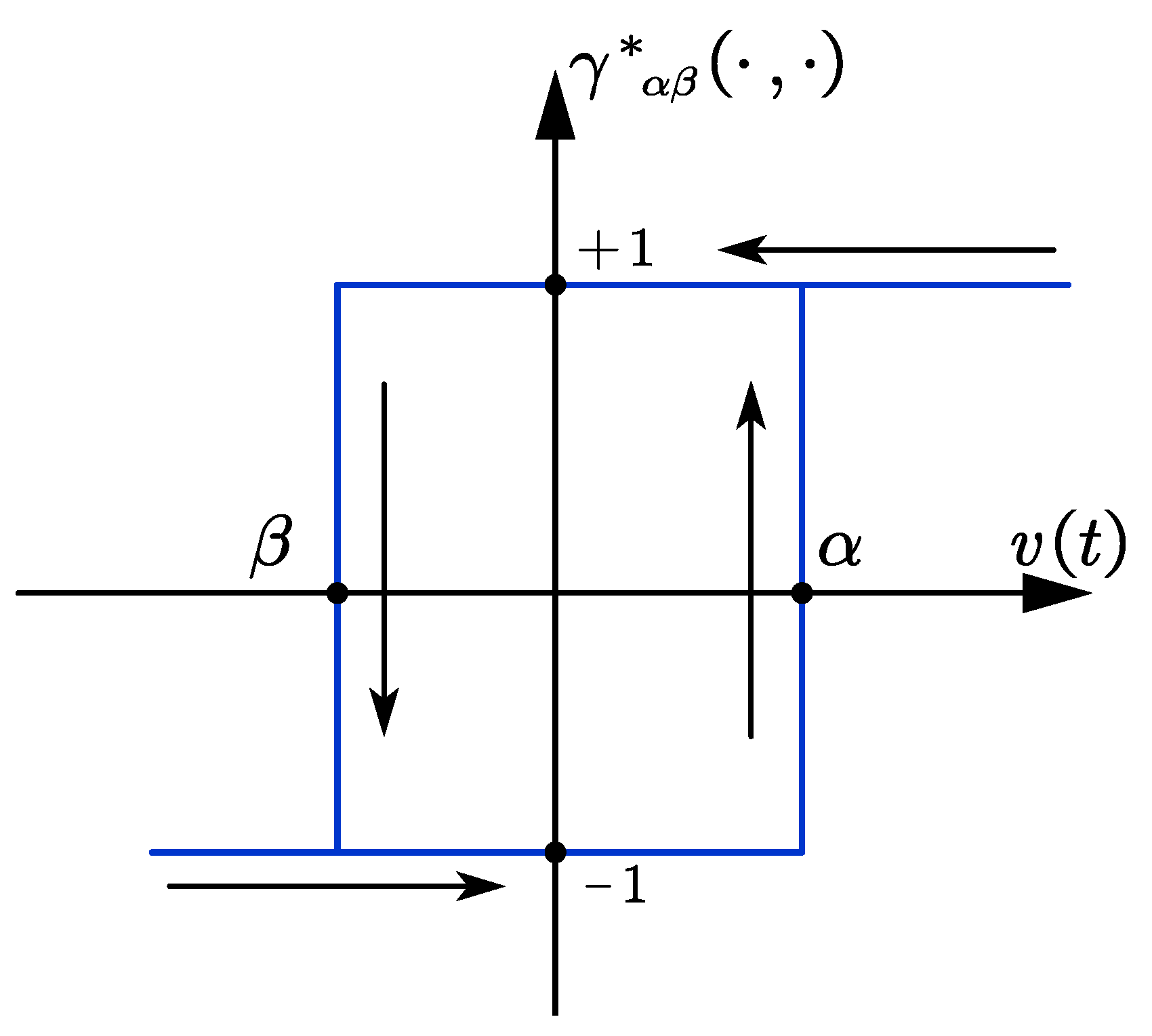
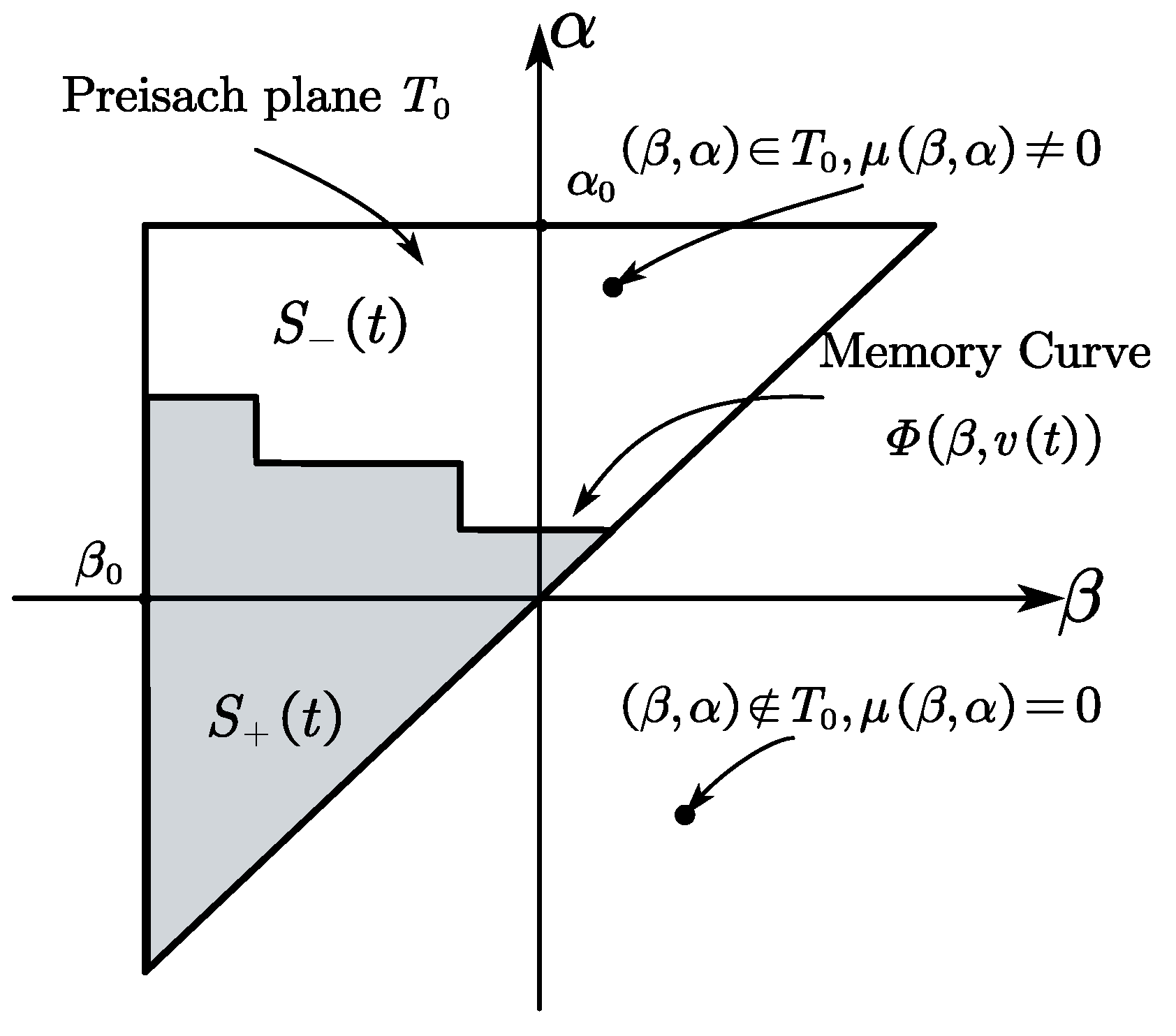
2.1. The Hysteresis Model
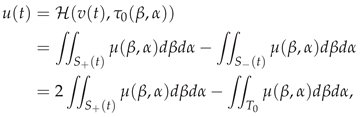
2.2. System Modeling
3. Relative Degree Conditions and Stability of Zero Dynamics Subsystem
4. Adaptive Inverse Control Scheme For Relative-Degree-One Case with Preisach Hysteresis
4.1. System Parameterization
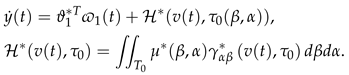
4.2. Implicit Controller Equation
4.3. Performance Analysis
5. Simulation Study
5.1. Experimental Equipment
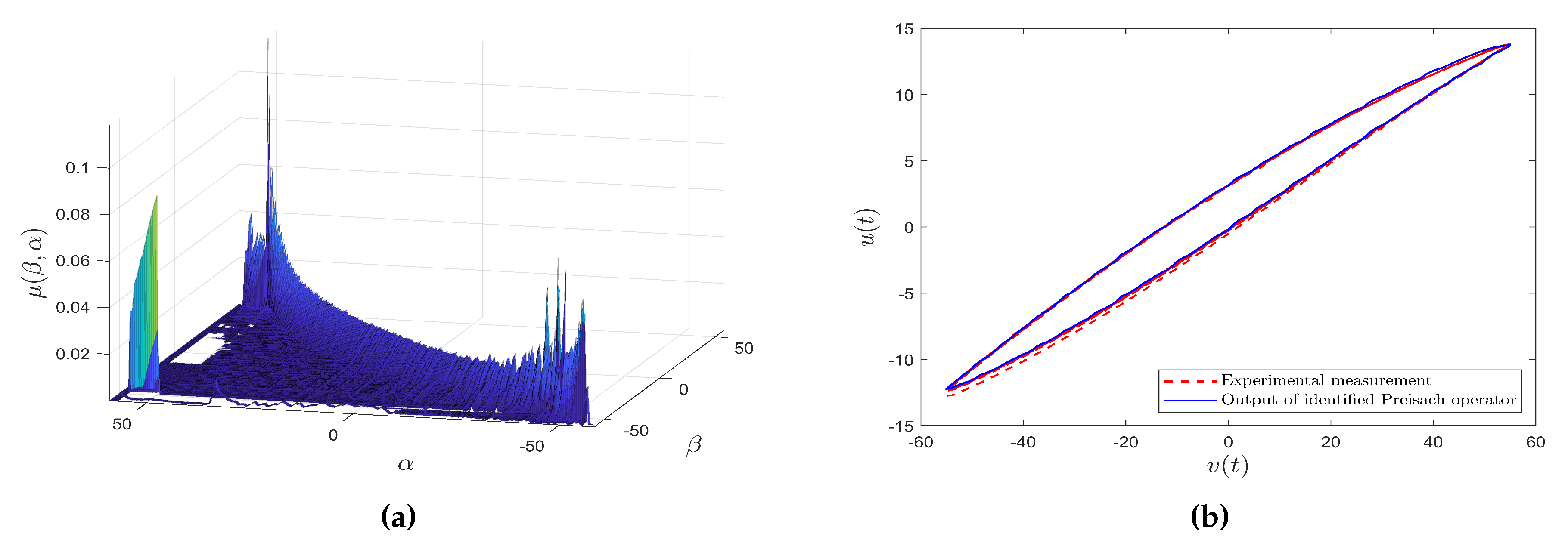
5.2. Hysteresis Identification
5.3. Simulation System Modeling
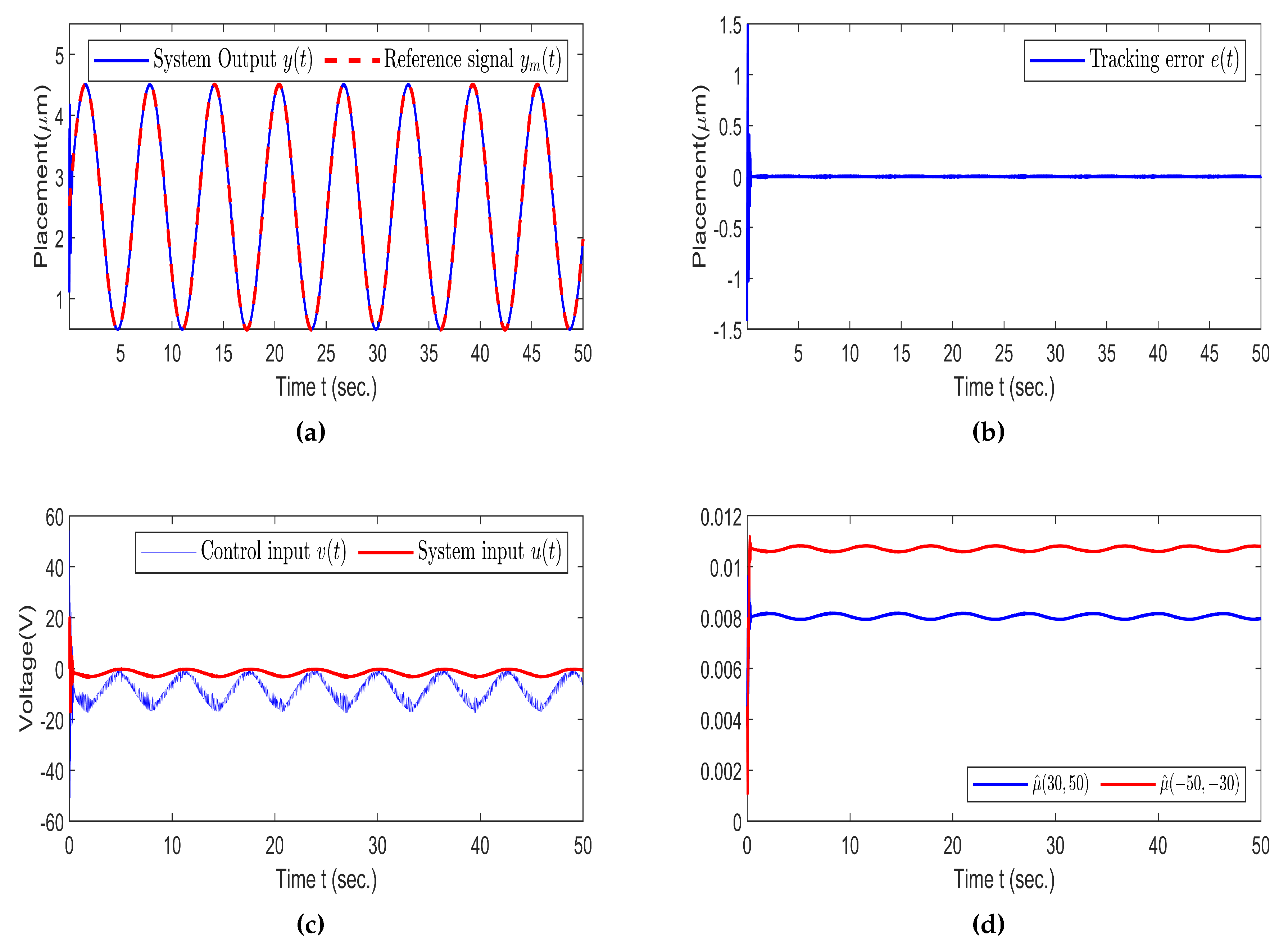
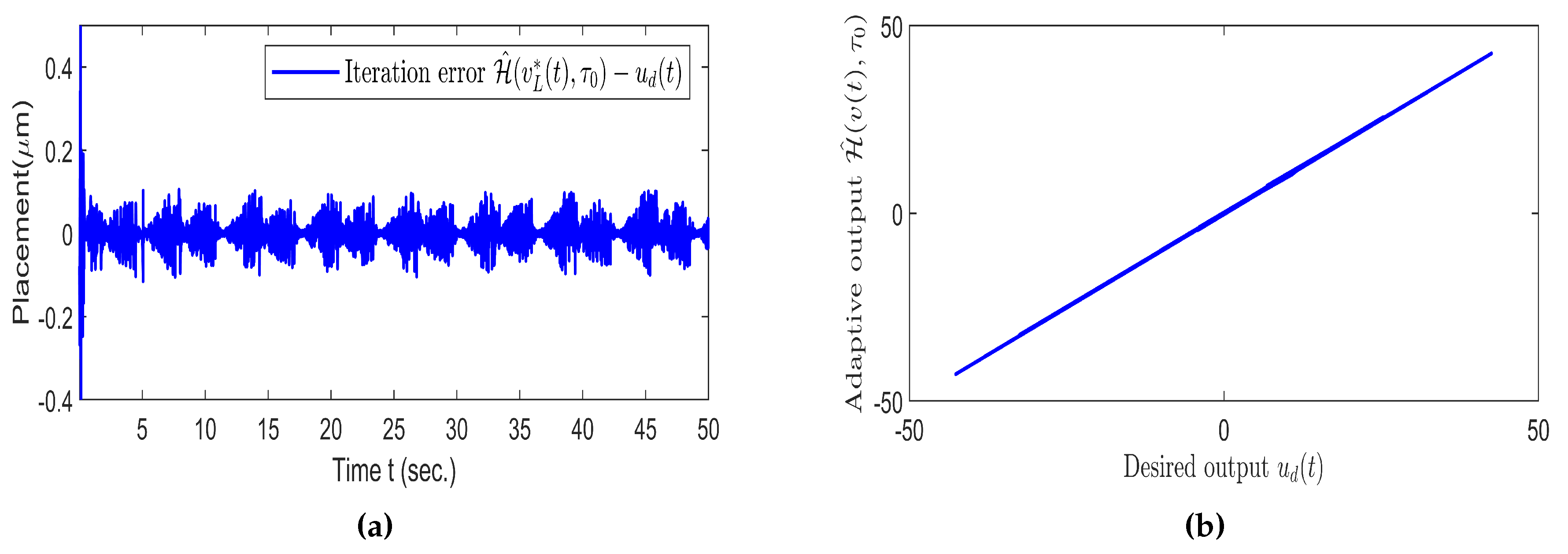
5.4. Simulation Results
6. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zaman, S.; Leyva, A.; Hassan, M.S.; Valladolid, A.; Herrera, N.E.; Gomez, S.G.; Mahmud, M.S.; Tucker, D.; Haynes, C.; Lin, Y. Implementation of Smart Materials for Actuation of Traditional Valve Technology for Hybrid Energy Systems. Actuators 2023, 12. [Google Scholar] [CrossRef]
- Frolova, L.; Ryba, T.; Diko, P.; Kavecansky, V.; Milkovic, O.; Dzubinska, A.; Reiffers, M.; Vargova, Z.; Varga, R. Smart Shape Memory Actuator Based on Monocrystalline Ni2FeGa Glass-Coated Microwire. IEEE Transactions on Magnetics 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Bocchetta, G.; Fiori, G.; Sciuto, S.A.; Scorza, A. Performance of Smart Materials-Based Instrumentation for Force Measurements in Biomedical Applications: A Methodological Review. Actuators 2023, 12. [Google Scholar] [CrossRef]
- Chen, L.; Niu, Y.; Yang, X.; Zhu, W.L.; Zhu, L.M.; Zhu, Z. A Novel Compliant Nanopositioning Stage Driven by a Normal-Stressed Electromagnetic Actuator. IEEE Transactions on Automation Science and Engineering 2022, 19, 3039–3048. [Google Scholar] [CrossRef]
- Baziyad, A.G.; Ahmad, I.; Salamah, Y.B.; Alkuhayli, A. Robust Tracking Control of Piezo-Actuated Nanopositioning Stage Using Improved Inverse LSSVM Hysteresis Model and RST Controller. Actuators 2022, 11. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, Y.; Ling, J.; Zhang, M. Development and Characteristic Investigation of a Multidimensional Discrete Magnetostrictive Actuator. IEEE/ASME Transactions on Mechatronics 2022, 27, 2071–2079. [Google Scholar] [CrossRef]
- Adly, A.; Mayergoyz, I.; Bergqvist, A. Preisach modeling of magnetostrictive hysteresis. Journal of Applied Physics 1991, 69, 5777–5779. [Google Scholar] [CrossRef]
- Preisach, F. Über die magnetische Nachwirkung. Zeitschrift für physik 1935, 94, 277–302. [Google Scholar] [CrossRef]
- Li, R.; Feng, Y.; Hu, Z. Dynamic Surface Control of Shape Memory Alloy Actuating Systems with Inverse Duhem Hysteresis Compensation. 2018 IEEE International Conference on Mechatronics and Automation (ICMA). IEEE, 2018, pp. 1305–1310.
- Brokate, M.; Sprekels, J. Hysteresis and Phase Transitions. Springer New York eBooks 1996. [Google Scholar]
- Rehman, O.U.; Petersen, I.R. Using inverse nonlinearities in robust output feedback guaranteed cost control of nonlinear systems. IEEE Transactions on Automatic Control 2014, 60, 1139–1144. [Google Scholar] [CrossRef]
- Köhler, J.; Soloperto, R.; Müller, M.A.; Allgöwer, F. A computationally efficient robust model predictive control framework for uncertain nonlinear systems. IEEE Transactions on Automatic Control 2020, 66, 794–801. [Google Scholar] [CrossRef]
- Wang, A.; Liu, L.; Qiu, J.; Feng, G. Event-triggered robust adaptive fuzzy control for a class of nonlinear systems. IEEE Transactions on Fuzzy Systems 2018, 27, 1648–1658. [Google Scholar] [CrossRef]
- Li, Z.; Shan, J.; Gabbert, U. Inverse compensation of hysteresis using Krasnoselskii-Pokrovskii model. IEEE/ASME Transactions on Mechatronics 2018, 23, 966–971. [Google Scholar] [CrossRef]
- Li, Z.; Shan, J.; Gabbert, U. A direct inverse model for hysteresis compensation. IEEE Transactions on Industrial Electronics 2020, 68, 4173–4181. [Google Scholar] [CrossRef]
- Li, Z.; Su, C.Y.; Chai, T. Compensation of hysteresis nonlinearity in magnetostrictive actuators with inverse multiplicative structure for Preisach model. IEEE Transactions on Automation Science and engineering 2013, 11, 613–619. [Google Scholar] [CrossRef]
- Zhang, J.; Iyer, K.; Simeonov, A.; Yip, M.C. Modeling and inverse compensation of hysteresis in supercoiled polymer artificial muscles. IEEE Robotics and Automation Letters 2017, 2, 773–780. [Google Scholar] [CrossRef]
- Li, Z.; Shan, J.; Gabbert, U. Inverse compensator for a simplified discrete Preisach model using model-order reduction approach. IEEE Transactions on Industrial Electronics 2018, 66, 6170–6178. [Google Scholar] [CrossRef]
- Visone, C. Hysteresis modelling and compensation for smart sensors and actuators. Journal of Physics: Conference Series. IOP Publishing, 2008, Vol. 138 1, p. 012028.
- Tan, X.; Venkataraman, R.; Krishnaprasad, P.S. Control of hysteresis: Theory and experimental results. Smart Structures and Materials 2001: Modeling, Signal Processing, and Control in Smart Structures. SPIE, 2001, Vol. 4326, pp. 101–112.
- Iyer, R.V.; Tan, X. Control of hysteretic systems through inverse compensation. IEEE Control Systems Magazine 2009, 29, 83–99. [Google Scholar] [CrossRef]
- Iyer, R.V.; Tan, X.; Krishnaprasad, P. Approximate inversion of the Preisach hysteresis operator with application to control of smart actuators. IEEE Transactions on automatic control 2005, 50, 798–810. [Google Scholar] [CrossRef]
- Tan, X.; Baras, J.S. Adaptive identification and control of hysteresis in smart materials. IEEE Transactions on automatic control 2005, 50, 827–839. [Google Scholar]
- Tan, X.; Baras, J.S. Modeling and control of hysteresis in magnetostrictive actuators. Automatica 2004, 40, 1469–1480. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.; Su, C.Y.; Chai, T. Nonlinear Control of Systems Preceded by Preisach Hysteresis Description: A Prescribed Adaptive Control Approach. IEEE Transactions on Control Systems Technology 2016, 24, 451–460. [Google Scholar] [CrossRef]
- Zhang.; Yanjun.; Tao.; Gang.; Chen.; Mou.. Adaptive Neural Network Based Control of Noncanonical Nonlinear Systems. IEEE Transactions on Neural Networks & Learning Systems 2016.
- Isidori, A. Nonlinear Control Systems; Springer Science & Business Media, 1995.
- Ma, X.; Tao, G. Adaptive actuator compensation control with feedback linearization. IEEE Transactions on Automatic Control 2000, 45, 1705–1710. [Google Scholar] [CrossRef]
- Sastry, S.; Bodson, M.; Bartram, J.F. Adaptive control: stability, convergence, and robustness, 1990.
- Ioannou, P.A.; Sun, J. Robust adaptive control; Vol. 1, PTR Prentice-Hall Upper Saddle River, NJ, 1996.
- Lai, G.; Tao, G.; Zhang, Y.; Liu, Z. Adaptive control of noncanonical neural-network nonlinear systems with unknown input dead-zone characteristics. IEEE Transactions on Neural Networks and Learning Systems 2019, 31, 3346–3360. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




