Prerpints.org logo
Preprint
Article

Evaluation of Selected Empirical Models for Asphalt Pavement Temperature Prediction in Tropical Climate: The Case of Ghana

Altmetrics

Downloads

122

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 July 2023

Posted:

28 July 2023

You are already at the latest version

Alerts
Abstract
Asphalt pavement temperature has several applications, including pavement structural design and evaluation, asphalt mixture design, asphalt binder grade determination and material aging characterization. However, available asphalt pavement temperature prediction models were mostly developed for temperate climatic conditions, outside of the tropics. Before such models are adopted for use in a tropical climate, their applicability must be evaluated. This study evaluated five empirical asphalt pavement temperature prediction models developed by Lukanen et al. [1], Park et al. [2], Diefenderfer et al. [3], Taamneh [4] all in the United States and Asefzadeh et al. [5] in Canada to ascertain their prediction accuracy in tropical climate, using Ghana as a case study. In-situ asphalt pavement temperature data were measured at two sites for eight months: Kumasi and Tamale in the Forest and Savannah climatic zones, respectively. The measured pavement temperature data were statistically compared with predicted temperatures, and it was found that the Park et al. [2] model provided a more accurate pavement temperature prediction in both climatic zones. The other models either over-predicted or under-predicted asphalt pavement temperature with significant error margins. However, there is a need to improve the prediction accuracy of the Park et al. [2] model or a local model developed.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Asphalt pavement temperature is useful for pavement analysis and design, asphalt mixture design, aging characterization and asphalt binder grade selection. For instance, in using a falling weight deflectometer (FWD) for structural evaluation of asphalt pavements, in-situ pavement temperature data is useful for adjusting the backcalculated asphalt layer modulus to a reference temperature [6], since asphalt layer deflection is significantly influenced by pavement temperature [7]. The long-term aging of asphalt material affects the durability and performance of asphalt pavements [8]. The aging process is a function of ambient temperature; hence, determination of asphalt pavement temperature is useful in characterizing the aging process to improve pavement structural analysis and design. Also, in-situ pavement temperature data are necessary for selecting appropriate binder grade, such as the Superior Performing Asphalt Pavements (Superpave) binder grade [9].
Over the years, in-situ asphalt pavement temperature has been determined by direct, manual measurements. While in-situ temperature measurement may provide accurate data, the process is slow, and may pose safety risks [7]. Also, the temperature data are applicable to single-drilled holes [6,7]. Comparatively, asphalt pavement temperature prediction models provide quicker, safer and efficient means of obtaining temperature data over a broader range of conditions [6,7,10]. Hence, several asphalt pavement temperature prediction models have been developed for pavement engineering applications. For instance, Walia et al. [11] developed an asphalt pavement temperature prediction model based on air temperature, time, and pavement depth. Viljoen [12] also developed asphalt pavement temperature prediction models that required input of air temperature, cloud cover, asphalt layer depth, and zenith angle. As may be expected, the prediction capability of such models may be limited to the geographical location of the model development. Extrapolation will require an assessment to ascertain the prediction accuracy of the models.
Ghana, a sub-Saharan African country, like many others, does not have an asphalt pavement temperature prediction model. There is a trend toward Superpave binder grade utilization in Ghana, but the binder grade determination appears to be ad hoc, owing to the non-existence of a locally-developed pavement temperature prediction model. A survey conducted in Ghana by the authors of this paper has shown that pavement engineering practitioners desire validated asphalt pavement temperature prediction models for various uses. Koranteng-Yorke [13], as part of a broader scope of developing pavement design framework for Ghana, formulated relationships between ambient temperature and asphalt layer temperature using data from two roads. The relationships were not validated and no goodness-of-fit parameters were reported.
The challenge with using asphalt pavement temperature prediction models developed elsewhere is that their accuracy is generally constrained within the scope of the original model development data and their prediction accuracy will require evaluation before their application in significantly different environments [6].
This study evaluated the prediction accuracy of the BELLS 3 [1], Park et al. [2], Diefenderfer et al. [3], Taamneh [4], and Asefzadeh et al. [5] models for asphalt pavement temperature prediction under the climatic conditions of Ghana, a West African country. Asphalt pavement temperature data were collected for eight months from Kumasi, in the Forest climatic zone and Tamale, in the Savannah climatic zone, to ascertain which of the models had better prediction accuracy. Climate data were sourced from Ghana Meteorological Agency (GMet) weather stations located near the study roads. R-studio and SPSS statistics, were used for the statistical analysis.

2. Asphalt Pavement Temperature Prediction

Asphalt pavement temperature prediction models may be empirical, numerical, or analytical, based on their theoretical underpinnings and method of analysis [14,15,16]. Numerical and analytical models, jointly referred to as theoretical models, are based on heat flow theories and require solving partial differential equations for a defined boundary conditions. On the other hand, empirical models are regression-based equations that show a relationship between pavement temperature and prediction factors such as climate variables, geolocation information, and pavement surface temperature [15,16].
Theoretical models are generally perceived to be cumbersome for practical purposes due to the complexities associated with boundary conditions definition, as well as the numerous input data requirements [10,14,15]. Such models are developed using both climatic data (e.g., air temperature, solar radiation) and pavement properties (e.g., surface albedo, emissivity, surface heat capacity, thermal conductivity); the last set of data is difficult to obtain. Chen et al. [15] noted that most of these pavement properties are sourced from literature, which makes them prone to approximation errors. In contrast, regression-based empirical models are developed from climatic, geographic, and pavement surface temperature data which are easier to obtain, and the models are easily applicable. For example, climatic data are available either from meteorological databases or weather stations located near project sites. Difficult-to-measure climatic parameters like solar radiation can be easily estimated. Notwithstanding, neural-based empirical models (e.g., [14,17,18]), by their nature, do not provide explicit mathematical equations for estimating pavement temperature, making their application very difficult.

2.1. Models Selected for Evaluation

Several asphalt pavement temperature prediction models were considered for evaluation based on ease of model application and availability of input data. By these criteria, theoretical and neural-based empirical models were excluded from evaluation. The selected models are briefly described below.

The BELLS 3 [1] Model

Lukanen et al. [1] developed the original version of the BELLS asphalt pavement temperature prediction model using data from the Long-Term Pavement Performance (LTPP) program. Data collected between 1994 and 1996 from 41 sites, in the U.S. were used to develop and validate the model. The asphalt layer thicknesses of the study pavements ranged from 46mm to 305mm. The BELLS 3 [1] model, the second version of the original BELLS model, accounts for shading on the pavement surface to allow for a wider range of applications of the model [1]. The BELLS 3 [1] model predicts asphalt pavement temperature at a specified depth using inputs of infrared-measured pavement surface temperature, time of day, previous day’s mean air temperature, and depth below the pavement surface, as illustrated in Equation (1). The adjusted coefficient of determination (R2) and the standard error (S.E) of the BELLS 3 [1] model were reported as 0.975 and 1.9 °C, respectively.
T d = 0.95 + 0.892 ( I R ) + [ log ( d ) − 1.25 ] [ 1.83 sin ( h r 18 − 15.5 ) − 0.448 ( I R ) + 0.621 T a v g ] + 0.042 ( I R ) sin ( h r 18 − 13.5 )  
where;
T d = Pavement temperature at desired depth (°C)
IR = Infrared-measured pavement surface temperature (°C)
d = Depth at which pavement temperature is required (mm)
T a v g = Mean of maximum and minimum air temperature on the day before FWD testing (°C)
sin = Sine function on an 18-hour clock system (one 18-hour cycle equals to 2π radians)
h r 18 = Time of day in 24-hr (converted to 18-hr asphalt concrete rise and fall cycle).

The Diefenderfer et al. [3] Model

The Diefenderfer et al. [3] models predict daily maximum and minimum pavement temperatures. The models were developed with data collected from the Virginia Smart Road test facility, while data from the LTPP sites were used for their validation [3]. Pavement temperatures were measured at depths ranging from 38 mm to 188 mm using thermocouples. The daily maximum pavement temperature prediction model had an adjusted R2 of 0.78 and a root mean square error (RMSE) of 5.8 °C. The model for predicting the daily minimum pavement temperature was not considered in this study. The daily maximum pavement temperature prediction model, as provided by [3], is shown in Equation (2).
T p ,   m a x = 2.78752 + 0.686 T a   m a x + 5.6736 × 10 − 4 R s − 27.8739 P d  
where;
T p ,   m a x = Predicted maximum pavement temperature (ºC)
T a   m a x = Daily maximum air temperature (ºC)
R s = Daily solar radiation (kJ/m2 day)
P d = Depth from pavement surface (m)

The Taamneh [4] Model

Taamneh [4] developed models for predicting daily maximum and minimum asphalt pavement temperatures using data collected on Interstate 90 in the U.S. state of Ohio. The daily maximum pavement temperature model had an adjusted R2 of 0.83 and RMSE of 5.1 °C and is shown in Equation (3).
T P − m a x = 9.720 + 0.947 T A − m a x − 24.179 D − 1.231 W S + ( 4.01 × 10 − 4 R S )
where;
T P − m a x = Predicted maximum pavement temperature (ºC)
T A − m a x = Daily maximum air temperature (ºC)
D = Depth below pavement surface (m)
WS = Daily wind speed (m/s)
RS = Daily Solar Radiation (kJ/m2day)

The Park et al. [2] Model

The Park et al. [2] model predicts asphalt pavement temperature based on pavement surface temperature, depth below the asphalt layer surface, and the time at surface temperature measurement. The model does not require the use of climatic variables and was developed from three test roads in the U.S. state of Michigan. Shown in equation (4), the Park et al. [2] model had an adjusted R2 of 0.90.
T z = T s u r f + { ( − 0.3451 z − 0.0432 z 2 + 0.00196 z 3 ) * s i n ( − 6.3252 t + 5.0967 ) }
where;
T z = Asphalt pavement temperature at depth, z (°C)
T s u r f = Asphalt pavement surface temperature (°C)
Z = Depth where pavement temperature is required (cm)
t = Time at surface temperature measurement (days).

The Asefzadeh et al. [5] Model

The set of Asefzadeh et al. [5] models predict the daily average asphalt pavement temperature for warm season, daily average pavement temperature for cold season, daily minimum pavement temperature, and daily maximum asphalt pavement temperature. The model for daily maximum pavement temperature prediction, evaluated in this study, is provided in Equation (5) [5]. Two years’ worth of data collected from an instrumented road test section at the Integrated Road Research Facility in Edmonton, Canada, were used to develop the model, while another two-month volume of data from the same facility were used for the model validation. The temperature data were collected at these depths ranging from 20 mm to 250 mm. The Asefzadeh et al. [5] daily maximum pavement temperature model was reported to have an adjusted R2 of 0.913.
T m a x = 2.0237 + 0.8709 ( T a i r − m a x ) + ( 7.6 × 10 − 4 S R ) − 16.1886 D
where;
T m a x = Predicted daily maximum pavement temperature (ºC)
T a i r − m a x = Daily maximum air temperature (ºC)
SR = Daily solar radiation (kJ/m2day)
D = Depth from pavement surface (m)

3. Materials and Methods

3.1. Study Area

The study was conducted in the two Ghanaian cities of Kumasi and Tamale, respectively representing the Forest and Savannah zones, two of the three climatic zones of Ghana [19]. The Savannah zone stretches between latitudes 7°46’48´´N to 11°0´0´´N and has the hottest and driest conditions, with a uni-modal rainfall pattern [19]. The Forest zone spans from about 30 km north of the Gulf of Guinea to latitude 7°46´48´´N [19] and is characterized by bi-modal rainfall patterns and is relatively cool and wet. The Savannah and Forest zones record average annual rainfall of 900 – 1200 mm and 1300 – 1800 mm, respectively [20]. The average monthly relative humidity ranges from 20% – 70% for the Savannah zone and 30% to 80% for the Forest zone [13,19]. The Savannah and Forest climatic zones constitute the largest portion of the country, as seen in Figure 1.

3.2. Data Collection

A study road was selected in the Kumasi (Forest zone) and Tamale (Savannah zone) for asphalt pavement temperature and climatic data collection. The characteristics of the study roads are described below:
(a)
The roads were within 3 km of a Ghana Meteorological Agency (GMet) synoptic weather station.
(b)
The roads were overlaid with asphalt concrete in 2021.
(c)
The data collection points had no tree cover and were on a generally flat terrain.
Table 1 provides additional details of the study roads. In-situ pavement temperatures were measured using Impact Model LH44T digital thermometer manufactured by Impact Test Equipment Limited. The pavement surface temperatures were measured using the RayTemp38 infrared thermometer manufactured by Electronic Temperature Instruments Limited (ETI). A digital thermometer was installed in drilled holes at a depth of 38 mm and 35 mm, representing asphalt concrete (AC) layer mid-depth of the study roads in Kumasi and Tamale, respectively. The drilled holes were 8 mm in diameter and were located near the pavement edge. Glycerine was used to fill the bottom 12mm of the holes to prevent heat loss.
The installation of the digital thermometers was done 20 minutes before taking the first reading at 6:00 GMT, and the thermometer was left in place until after the last reading of the day at 18:00 GMT. Pavement surface and AC mid-depth temperatures were recorded concurrently at 30-minute intervals for 12 hours. This data collection scheme was repeated for seven consecutive days per month, from May to December 2022.
The data collection week was selected based on stratified random sampling. Each calendar month (May to December) was subdivided into four weeks of sampling units. A simple random sampling technique was then used to select a specific week number per stratum (calendar month) for data collection. The week numbers in Table 2 were obtained and used for data collection in the respective months.
Climatic data – such as daily minimum air temperature, daily maximum air temperature, and daily wind speed – were obtained from the GMet weather stations during the data collection period. Daily solar radiation was computed using an approach utilized by Diefenderfer et al. [3], which required input of the latitude of the weather station and the concerned day of the year. The field pavement data collection setup is shown in Figure 2.

3.3. Data Analysis

Four criteria – statistical significance, coefficient of determination (R2), Line of Equality (LOE), and error statistics – were used for evaluation of the models. The error statistics included Root Mean Square Error (RMSE), Mean Percentage Error (MPE), and Mean Bias Error (MBE), which are given in Eqs. (6), (7), and (8), respectively.
R M S E = 1 n ∑ i = 1 n ( T c a l − T m e a ) 2
M P E = 1 n ∑ i = 1 n ( T m e a − T c a l T m e a × 100 )
M B E = 1 n ∑ i = 1 n ( T c a l − T m e a )
Where T c a l and T m e a are the predicted and measured pavement temperatures (ºC), respectively, for n number of observations. RMSE, MPE and MBE are as defined above.
RMSE measures the level of dispersion of the model predictions in absolute values, while MPE indicates the percentage deviation of the model predictions from measured values. MBE, on the other hand, quantifies the variation of the measured pavement temperature from the predicted. The closer RMSE, MPE, and MBE are to zero, the better the accuracy of the model predictions. Negative MPE and MBE values indicate over-prediction and under-prediction, respectively.
In testing the statistical significance of the difference between the means of the predicted and measured asphalt pavement temperatures, the two-independent sample t-test was conducted at 5% level of significance.
R2 measures the goodness-of-fit of a model. It denotes the proportion of variation in the dependent variable explained by the linear combination of the independent variables. The LOE is a 45-degree line drawn on a scatter plot of predicted versus measured values. A well-fitted model has predicted and measured values balanced along the LOE [21,22]. Microsoft Excel was used to compute the error statistics (RMSE, MPE, and MBE); SPSS statistics (version 23) was employed to produce the charts, while R-studio was used for the statistical analysis.

4. Results and Discussions

4.1. Model Evaluation Based on Statistical Significance Testing

From the statistical significance test results in Table 3, the following inferences are made:
  • For Kumasi, the means of the predicted asphalt pavement temperature by the Park et al. [2] and the Diefenderfer et al. [3] models were statistically equal to the mean of the measured asphalt pavement temperatures (p > 0.05).
  • For Tamale, the asphalt pavement temperatures predicted by the Park et al. [2] model had an equal mean as the measured asphalt pavement temperature (p > 0.05).
  • The rest of the model-predicted asphalt pavement temperatures had means that were statistically different from the means of their corresponding measured asphalt pavement temperatures (p < 0.05).
The statistical testing has shown that, only the Park et al. [2] model has potential to predict asphalt pavement temperature in the Savannah zone with acceptable accuracy, while the Park et al. [2] and Diefenderfer et al. [3] models exhibited similar potential for the Forest zone.

4.2. Model Evaluation Based on Error Statistics

Table 4 shows the error statistics for the model predictions. Both the MPE and MBE suggested that the BELLS 3 [1] and Diefenderfer et al. [3] models under-predicted asphalt pavement temperatures for both Kumasi and Tamale. The MPE and MBE also indicated that the Taamneh [4] and the Asefzadeh et al. [5] models over-predicted temperature for both locations. In the case of the Park et al. [2] model, there was over-prediction for Kumasi based on the MPE and MBE, while the MPE for Tamale indicated under-prediction.
In the Savannah zone, the Park et al. [2] model recorded the lowest RMSE, MPE, and MBE, making it a plausible model for asphalt pavement temperature prediction. The Park et al. [2] model also produced the smallest MPE and MBE in the Forest zone, but its RMSE of 3.6 ºC was only second lowest to BELLS 3 [1]. Hence, it could be said that the Park et al. [2] model predictions in both climatic zones were associated with the lowest errors. This could possibly be explained by the exclusion of climatic variables in the Park et al. [2] model.
The magnitude of MPE and MBE produced by the Diefenderfer et al. [3] model for both zones were second lowest to the Park et al. [2] model. These results corroborate earlier findings from the statistical significance testing that these two models have potential to predict asphalt pavement temperature for the Forest zone. Table 4 also revealed that the BELLS 3 [1] and the Diefenderfer et al. [3] models yielded lower prediction errors for the Forest zone than for the Savannah zone. The Park et al. [2], Taamneh [4], and Asefzadeh et al. [5] models rather exhibited lower prediction errors for the Savannah zone. The error analysis results has complemented the statistical significance testing results in determining the best-performing models for the study zones.

4.3. Model Evaluation Based on Line of Equality and Coefficient of Determination

Figure 3 shows a graph of BELLS 3 [1] model-predicted versus measured asphalt pavement temperature for Kumasi. The predicted temperatures did not fully match the measured values, especially at low and high pavement temperatures; there was some amount of under-prediction at the extreme temperatures. The relatively high R2 of 0.866 is notable, but this be viewed in the light of the other evaluation criteria.
The Park et al. [2] model-predicted and the measured temperature for Kumasi were sufficiently balanced along the LOE, indicating a good match. However, there were some appreciable over-prediction after temperatures of about 47 °C (Figure 4). The R2 of 0.825 shows a well-fitted model but its relevance must be established after a careful consideration of the other evaluation criteria.
Figure 5 shows a weak correlation between the predicted pavement temperature by the Diefenderfer et al. [3] model and the measured temperature for Kumasi, with a low R2 of 0.309 and no clustering along the LOE. This finding indicated a mismatch between the predicted and measured pavement temperature. Thus, the Diefenderfer et al. [3] model is inappropriate for asphalt pavement temperature prediction in Ghana.
Figure 6 and Figure 7, respectively, show the Taamneh [4] and Asefzadeh et al. [5] model-predicted asphalt pavement temperature against measured temperature for Kumasi. Though the Taamneh [4] model prediction shows some moderately positive relationship with measured temperature (R2 of 0.594), almost all the pavement temperatures lied above the LOE, indicating over-prediction. The Asefzadeh et al. [5] model prediction (Figure 7) produced a weak correlation with the measured pavement temperature (R2 of 0.305), and all the temperatures were above the LOE, an indication of over-prediction.
The LOE plots have highlighted the disparity between the predicted and measured asphalt pavement temperatures, an important factor in assessing model performance. For example, Diefenderfer et al.’s [3] model error levels for the Forest zone were moderate, but the distribution about the LOE was unsatisfactory. Singh et al. [21] classified R2 values in the range of 0.70 – 0.89 as good; hence, the BELLS 3 [1] and Park et al. [2] models may be described as good on the basis of R2. However, an overall assessment is necessary to reach a practical decision about model acceptability.
Figure 8 through 12 present similar results for the Savannah zone. Figure 8 shows under-prediction by the BELLS 3 [1] model. Notwithstanding, a high R2 of 0.930 was recorded.
However, the Park et al. [2] model prediction for Tamale (Figure 9) produced a good clustering along the LOE, indicating a good match between the measured and predicted pavement temperature, which was corroborated by the high R2 value of 0.905.
The Diefenderfer et al. [3] model-predicted daily maximum versus measured pavement temperature is shown in Figure 10. The Diefenderfer et al. [3] model did not correctly predict pavement temperature, as there was no balance between the predicted and measured pavement temperatures around the LOE. Considerable errors were associated with the use of this model for asphalt pavement temperature prediction in the Savannah zone. The model prediction yielded a moderate R2 value of 0.599.
As seen in Figure 11, the Taamneh [4] model-predicted pavement temperature versus measured pavement temperature is scattered above from the LOE, indicating significant errors between the predicted and measured temperatures. The data point distribution shows significant over-prediction of pavement temperatures for Tamale. As expected, a relatively low R2 value of 0.443 was recorded.
The Asefzadeh et al. [5] model-predicted and measured pavement temperature for Tamale lied above the LOE (Figure 12), indicating significant over-prediction. The Asefzadeh et al. [5] model also yielded a moderate R2 value of 0.570.

4.4. Summary of Model Evaluation Results

For the Forest zone, the Park et al. [2] and Diefenderfer et al. [3] models were the only models which asphalt pavement temperature predictions did not differ significantly from measured temperatures. However, the Park et al. [2] model displayed a better distribution of pavement temperatures around the LOE, registered the smallest error levels, and had the highest R2. Hence, the Park et al. [2] model maybe considered to have outperformed Diefenderfer et al.’s [3].
For the Savannah zone, all the assessment criteria were in favor of the Park et al. [2] model, making it the most feasible model. It should be noted that the Park et al. [2] model registered lower error statistics and higher R2 value for the Savannah zone compared with the Forest zone. Overall, the Park et al. [2] model’s performance was better in the Savannah zone.
The failure of the BELLS 3 [1] model to predict pavement temperature with high accuracy in both cities could have resulted from the fact that the model was calibrated for a maximum pavement temperature of 40 °C ([1,11]), which is smaller than the highest pavement temperatures in Ghana. Also, the non-use of climatic data by the Park et al. [2] model could have accounted for its high prediction accuracy. The R2 and RMSE values produced for Kumasi by the Diefenderfer et al. [3] model compared well with Lekea and Steyn [23] findings, where an evaluation of the Diefenderfer et al. [3] model in Pretoria yielded R2 of 0.378 and RMSE of 4.6 ºC. However, higher R2 and RMSE values were recorded by the Diefenderfer et al. [3] model for Tamale than Pretoria [23].

5. Conclusions

This study evaluated the applicability of the BELLS 3 [1], Park et al. [2], Diefenderfer et al. [3], Taamneh [4], and Asefzadeh et al. [5] models for asphalt pavement temperature prediction in Ghana’s Forest and Savannah climate zones. Based on the results of this study, the following conclusions and recommendations are provided:
  • The Park et al. [2] model showed the highest accuracy in predicting asphalt pavement temperature for both the Forest and Savannah zones.
  • Asphalt pavement temperature predicted by the BELLS 3 [1], Taamneh [4], and Asefzadeh et al. [5] models were significantly different from the measured pavement temperatures in both climatic zones. The BELLS 3 [1] model under-predicted, whiles the Taamneh [4] and Asefzadeh et al. [5] models over-predicted asphalt pavement temperatures, in both climatic zones.
  • The Diefenderfer et al. [3] model significantly under-predicted asphalt pavement temperature for the Savannah zone and was poorly fitted for prediction in the Forest zone.
  • The Park et al. [2] model is recommended for asphalt pavement temperature prediction in both the Forest and Savannah zones of Ghana pending locally developed models.

Author Contributions

Conceptualization, K.A.T., S.N. and Y.A.T.; methodology, S.N., K.A.T., Y.A.T. and C.A.A.; validation, S.N., K.A.T and Y.A.T.; formal analysis, S.N. and E.K.A.; investigation, S.N.; resources, K.A.T., Y.A.T. and C.A.A.; data curation, S.N. and E.K.A.; writing—original draft preparation, S.N.; writing—review and editing, S.N., K.A.T., E.K.A., Y.A.T. and C.A.A.; supervision, K.A.T., Y.A.T. and C.A.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data is available upon request.

Acknowledgments

The authors acknowledge all enumerators who helped with the field data collection and TRECK for supporting financially.

Conflicts of Interest

The authors declare that they have no conflicting interest.

References

  1. E. O. Lukanen, R. Stubstad, and R. Briggs, “Temperature Predictions and Adjustment Factors for Asphalt Pavement. Publication no. FHWA-RD-98-085.,” McLean, VA, 2000.
  2. D. Park, N. Buch, and K. Chatti, “Effective Layer Temperature Prediction Model and Temperature Correction via Falling Weight Deflectometer Deflections,” Transp. Res. Rec., vol. 1764, pp. 97–111, 2001.
  3. B. K. Diefenderfer, I. L. Al-Qadi, and S. D. Diefenderfer, “Model to predict pavement temperature profile: Development and validation,” J. Transp. Eng., vol. 132, no. 2, pp. 2006. [CrossRef]
  4. M. Taamneh, “Temperature profile prediction for flexible pavement structures,” HKIE Trans. Hong Kong Inst. Eng., vol. 23, no. 3, pp. 150–156, 2016. [CrossRef]
  5. Asefzadeh, L. Hashemian, and A. Bayat, “Development of statistical temperature prediction models for a test road in Edmonton, Alberta, Canada,” Int. J. Pavement Res. Technol., vol. 10, no. 5, pp. 369–382, 2017. [CrossRef]
  6. M. Z. Alavi, M. R. Pouranian, and E. Y. Hajj, “Prediction of asphalt pavement temperature profile with finite control volume method,” Transp. Res. Rec., vol. 2456, no. 2456, pp. 96–106, 2014. [CrossRef]
  7. E. Kassem, F. M. S. Bayomy, C. Williams, E. Saasita, S. Lamichane, and D. D. Permadi, “Development of Pavement Temperature Prediction Model, Report No. FHWA-ID-20-279,” Moscow, Idaho, 2020.
  8. Y. Liang, R. Wu, J. T. Harvey, D. Jones, and M. Z. Alavi, “Investigation into the Oxidative Aging of Asphalt Binders,” Transp. Res. Rec., vol. 2673, no. 6, pp. 368–378, 2019. [CrossRef]
  9. T. W. Kennedy, G. A. Huber, E. T. Harrigan, R.J. Cominsky, C. S. Hughes, H. V. Quintus, and J. S. Moulthrop, “Superior Performing Asphalt Pavements (Superpave): The Product of the SHRP Asphalt Research Program. Report SHRP-A-410,” Washington, D.C., 1994.
  10. D. S. Gedafa, M. Hossain, and S. A. Romanoschi, “Perpetual pavement temperature prediction model,” Road Mater. Pavement Des., vol. 15, no. 1, pp. 55–65, 2014. [CrossRef]
  11. Walia, R. Rastogi, P. Kumar, and S. S. Jain, “Development of a temperature prediction model for asphalt pavements considering air temperature data of preceding hours,” Int. J. Pavement Eng., pp. 1–17, 2022. [CrossRef]
  12. Viljoen, “Estimating Asphalt Temperatures from Air Temperatures and Basic Sky Parameters,” Pretoria, South Africa, 2001.
  13. J. B. Koranteng-Yorke, “Proposed Framework for Asphaltic Concrete Pavement Design for Tropical Soils - Case Study of Ghana. A thesis submitted to the University of Birmingham for the degree of Doctor of Philosophy.,” University of Birmingham, Birmingham, UK, 2012.
  14. Rigabadi, M. Rezaei Zadeh Herozi, and A. Rezagholilou, “An attempt for development of pavements temperature prediction models based on remote sensing data and artificial neural network,”. Int. J. Pavement Eng. 2021, 23, 2912–2921. [CrossRef]
  15. J. Chen, H. Wang, and P. Xie, “Pavement temperature prediction: Theoretical models and critical affecting factors,” Appl. Therm. Eng., vol. 158, no. December 2018, 2019. [CrossRef]
  16. D. Wang, J. R. Roesler, and D.-Z. Guo, “Analytical Approach to Predicting Temperature Fields in Multilayered Pavement Systems,” J. Eng. Mech., vol. 135, no. 4, pp. 334–344, 2009. [CrossRef]
  17. Xu, H. C. Dan, and L. Li, “Temperature prediction model of asphalt pavement in cold regions based on an improved BP neural network,” Appl. Therm. Eng., vol. 120, pp. 568–580, 2017. [CrossRef]
  18. Milad, I. Adwan, S. A. Majeed, N. I. M. Yusoff, N. Al-Ansari, and Z. M. Yaseen, “Emerging Technologies of Deep Learning Models Development for Pavement Temperature Prediction,” IEEE Access, vol. 9, pp. 23840–23849, 2021. [CrossRef]
  19. E. Bessah, W. Amponsah, S. O. Ansah, A. Afrifa, B. Yahaya, C. S. Wemegah, M. Tanu, L. K. Amekudzi, and W. A. Agyare, “Climatic zoning of Ghana using selected meteorological variables for the period 1976–2018,” Meteorol. Appl., vol. 29, no. 1, pp. 0–15, 2022. [CrossRef]
  20. E. I. Yamba, J. N. A. Aryee, E. Quansah, P. Davies, C. S. Wemegah, M. A. Osei, M. A. Ahiataku, and L. K. Amekudzi, “Revisiting the agro-climatic zones of Ghana: A re-classification in conformity with climate change and variability,” PLOS Clim., vol. 2, no. 1, p. e0000023, 2023. [CrossRef]
  21. Singh, M. Zaman, and S. Commuri, “Evaluation of predictive models for estimating dynamic modulus of hot-mix asphalt in Oklahoma,” Transp. Res. Rec., no. 2210, pp. 57–72, 2011. [CrossRef]
  22. N. Solatifar, M. Abbasghorbani, A. Kavussi, and H. Sivilevičius, “Prediction of depth temperature of asphalt layers in hot climate areas,” J. Civ. Eng. Manag., vol. 24, no. 7, pp. 516–525, 2018. [CrossRef]
  23. Lekea and W. J. Steyn, “Performance of Pavement Temperature Prediction Models,” Appl. Sci., vol. 13, no. 4164, pp. 1–12, 2023. [CrossRef]
Preprints 80769 g001
Figure 1. Climatic zones of Ghana [19].
Figure 1. Climatic zones of Ghana [19].
Preprints 80769 g001
Preprints 80769 g002
Figure 2. Installed digital thermometer for in-situ temperature measurement on Mango Road (Kumasi).
Figure 2. Installed digital thermometer for in-situ temperature measurement on Mango Road (Kumasi).
Preprints 80769 g002
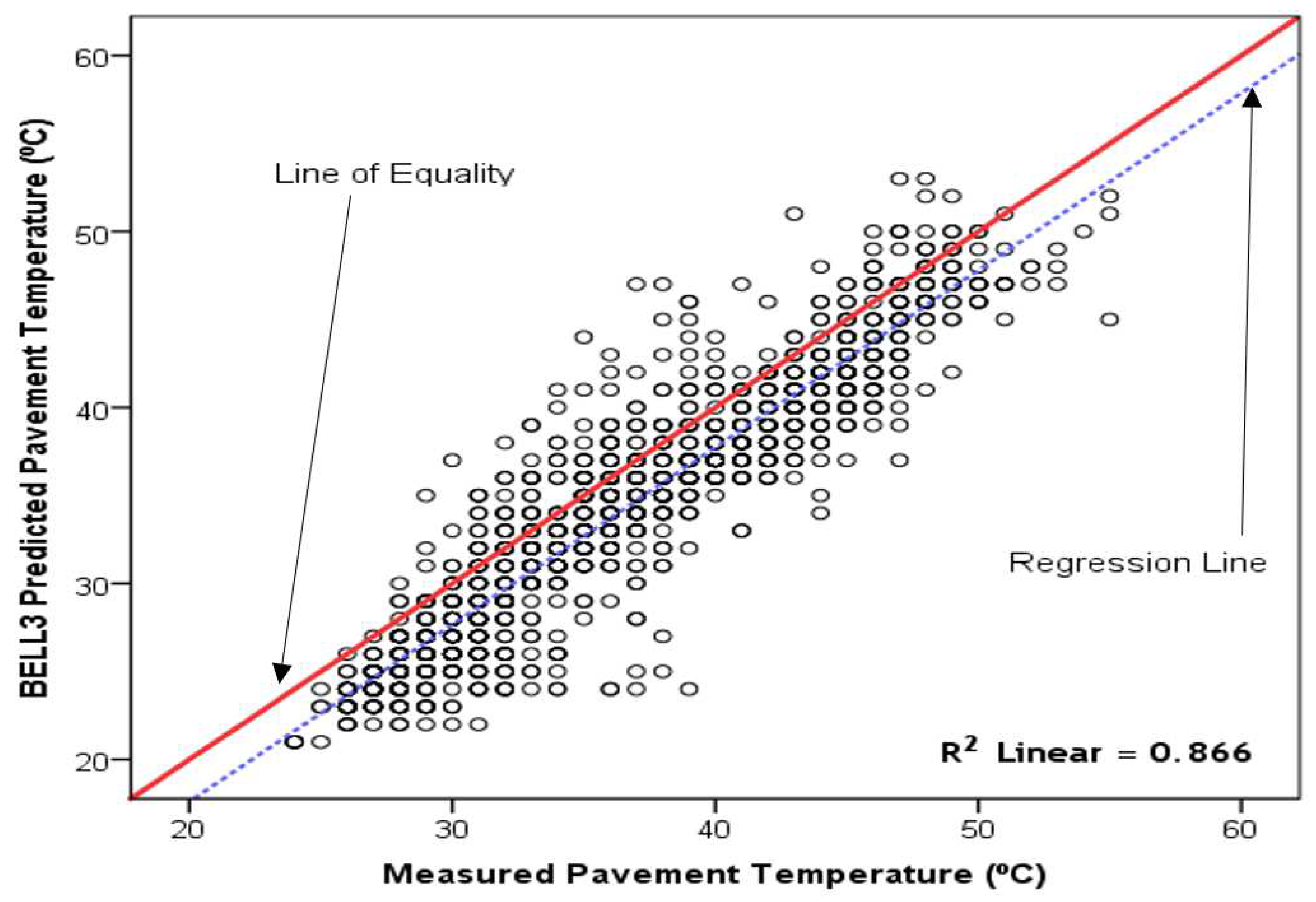
Preprints 80769 g003
Figure 3. BELLS 3 [1] model-predicted versus measured pavement temperature on Mango Road (Kumasi).
Figure 3. BELLS 3 [1] model-predicted versus measured pavement temperature on Mango Road (Kumasi).
Preprints 80769 g003
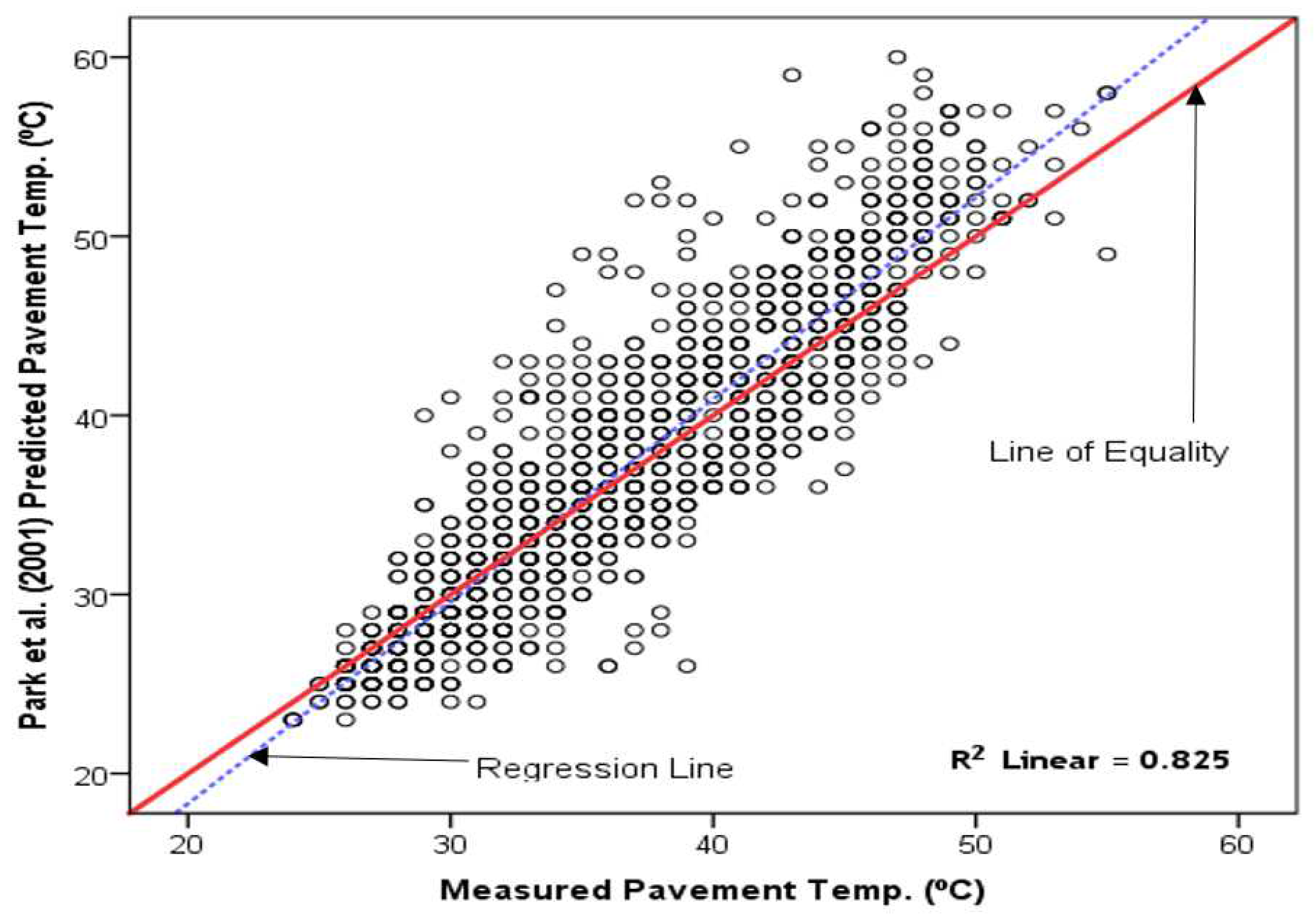
Preprints 80769 g004
Figure 4. The Park et al. [2] model-predicted versus measured pavement temperature on Mango Road (Kumasi).
Figure 4. The Park et al. [2] model-predicted versus measured pavement temperature on Mango Road (Kumasi).
Preprints 80769 g004
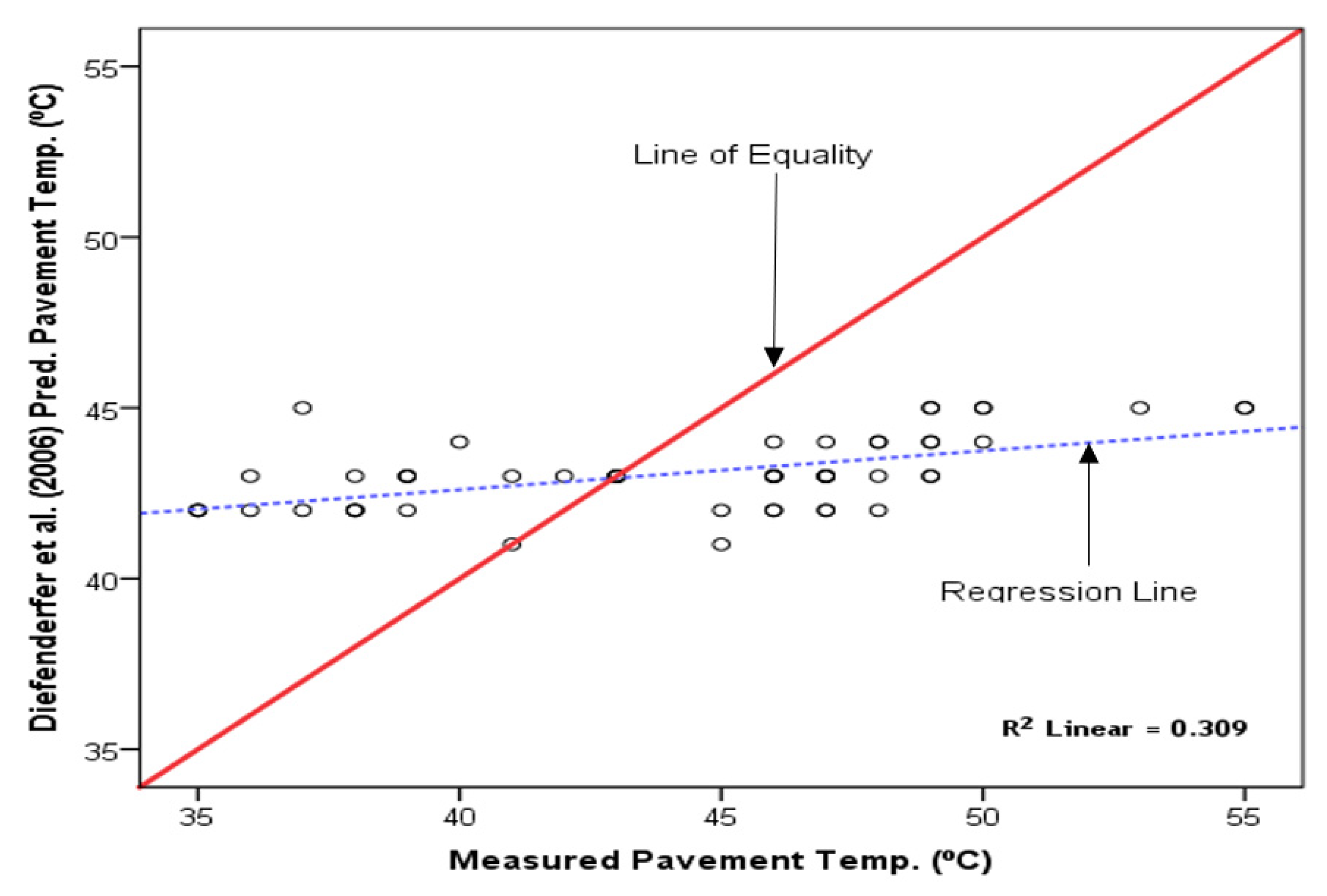
Preprints 80769 g005
Figure 5. The Diefenderfer et al. [3] model-predicted daily maximum versus measured daily maximum pavement temperature on Mango Road (Kumasi).
Figure 5. The Diefenderfer et al. [3] model-predicted daily maximum versus measured daily maximum pavement temperature on Mango Road (Kumasi).
Preprints 80769 g005
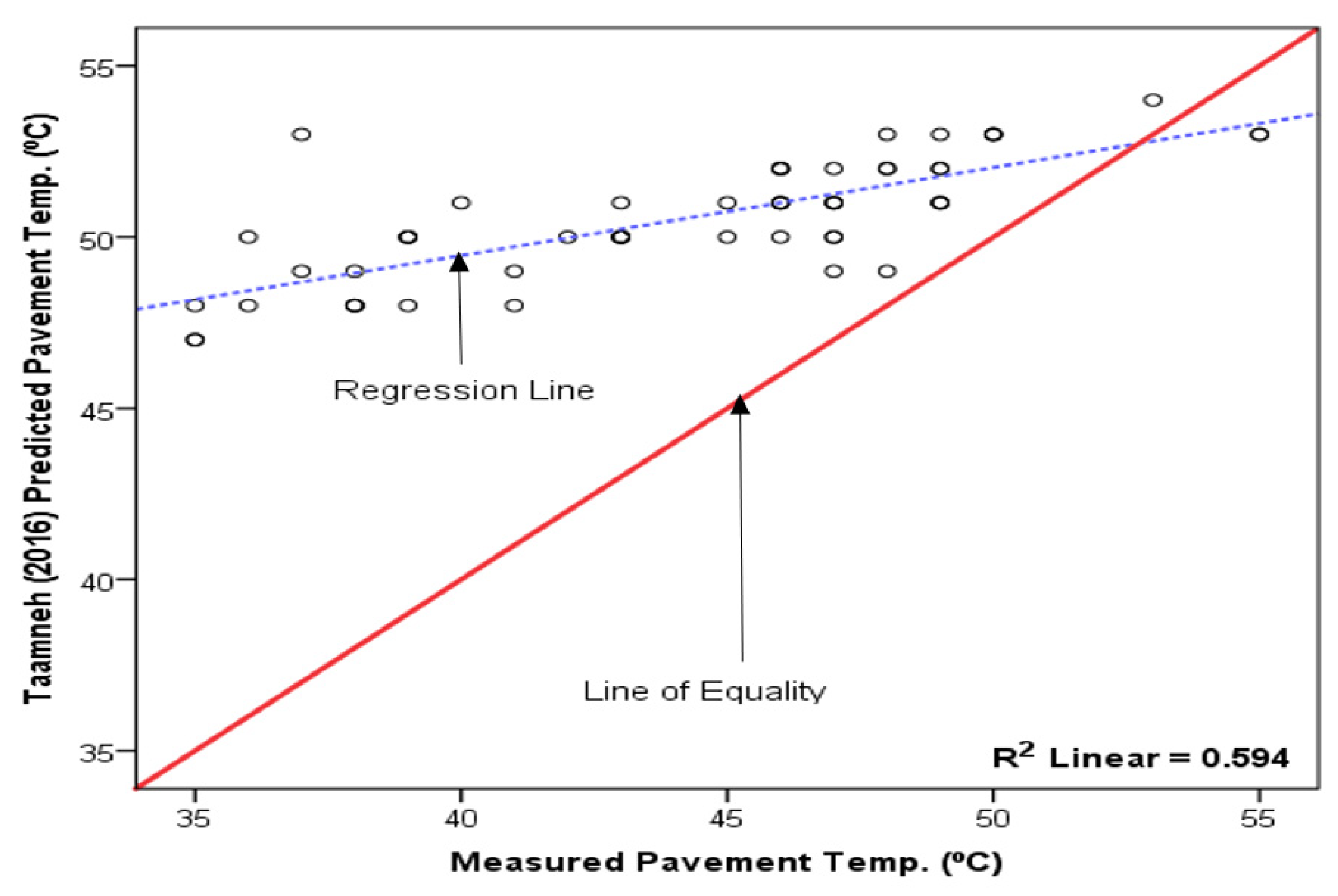
Preprints 80769 g006
Figure 6. The Taamneh [4] model-predicted daily maximum versus measured daily maximum pavement temperature on Mango Road (Kumasi).
Figure 6. The Taamneh [4] model-predicted daily maximum versus measured daily maximum pavement temperature on Mango Road (Kumasi).
Preprints 80769 g006
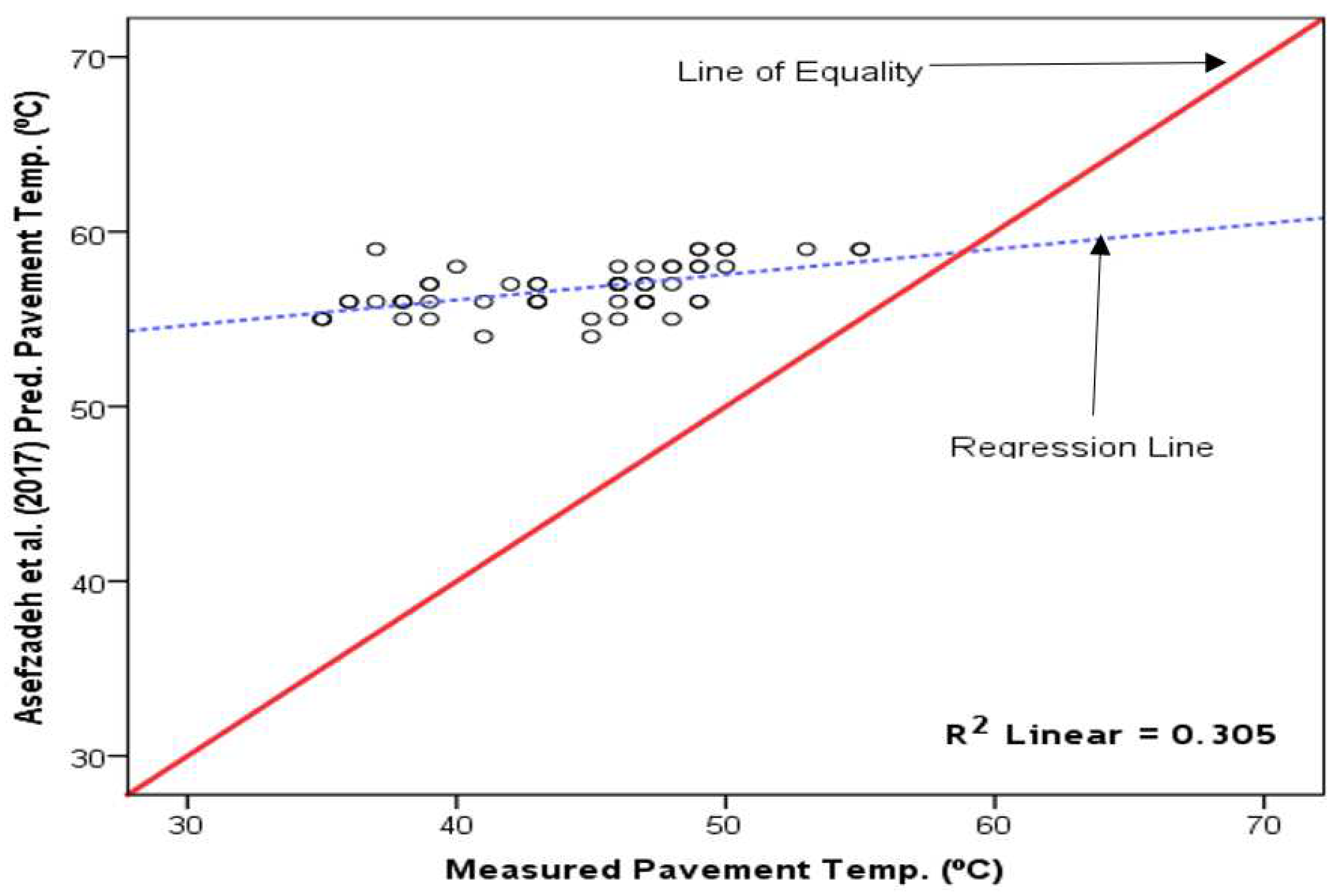
Preprints 80769 g007
Figure 7. The Asefzadeh et al. [5] model-predicted daily maximum versus measured daily maximum pavement temperature on Mango Road (Kumasi).
Figure 7. The Asefzadeh et al. [5] model-predicted daily maximum versus measured daily maximum pavement temperature on Mango Road (Kumasi).
Preprints 80769 g007
Preprints 80769 g008
Figure 8. BELLS 3 [1] model-predicted versus measured pavement temperature on RSM Road (Tamale).
Figure 8. BELLS 3 [1] model-predicted versus measured pavement temperature on RSM Road (Tamale).
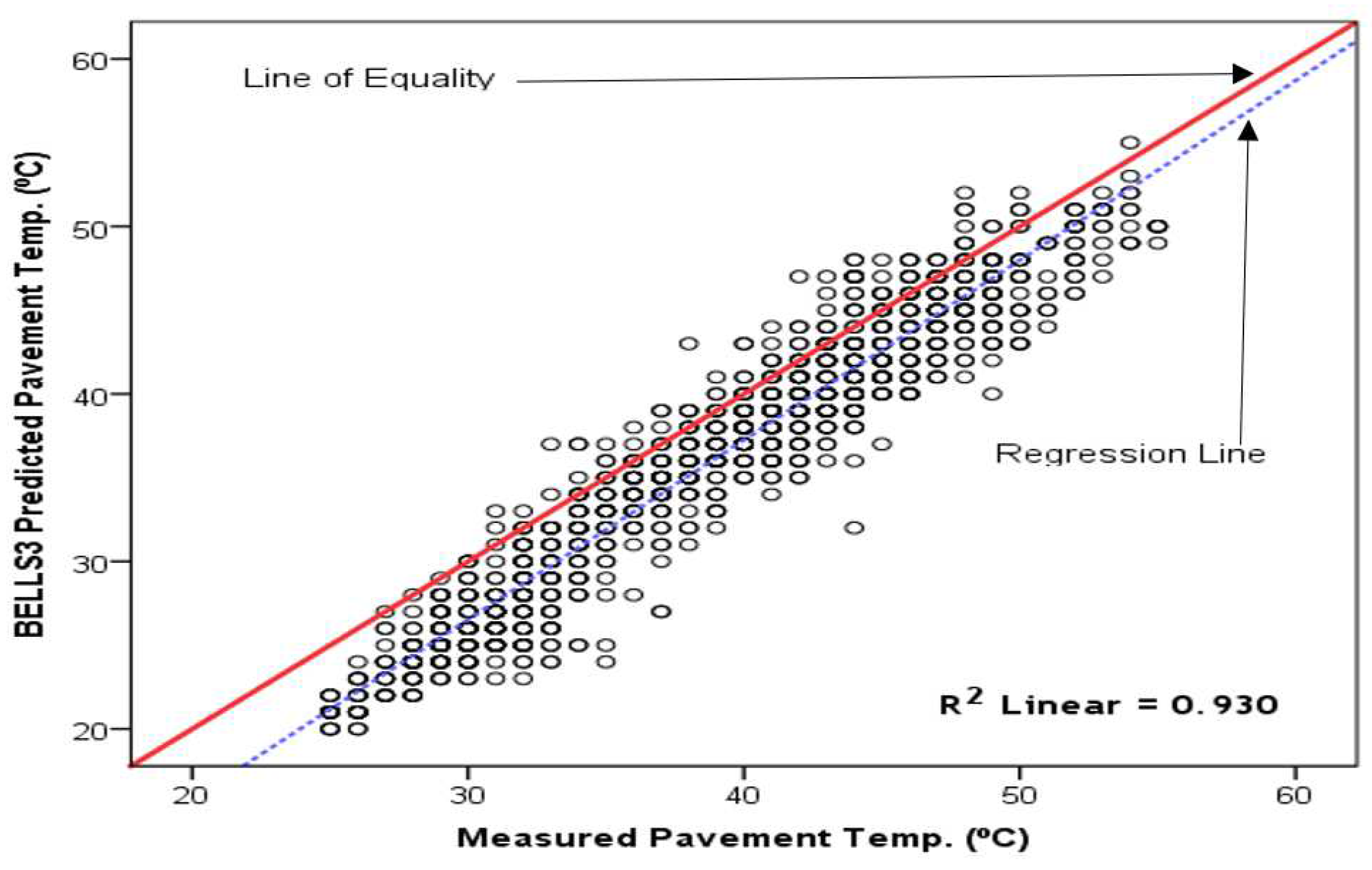
Preprints 80769 g008
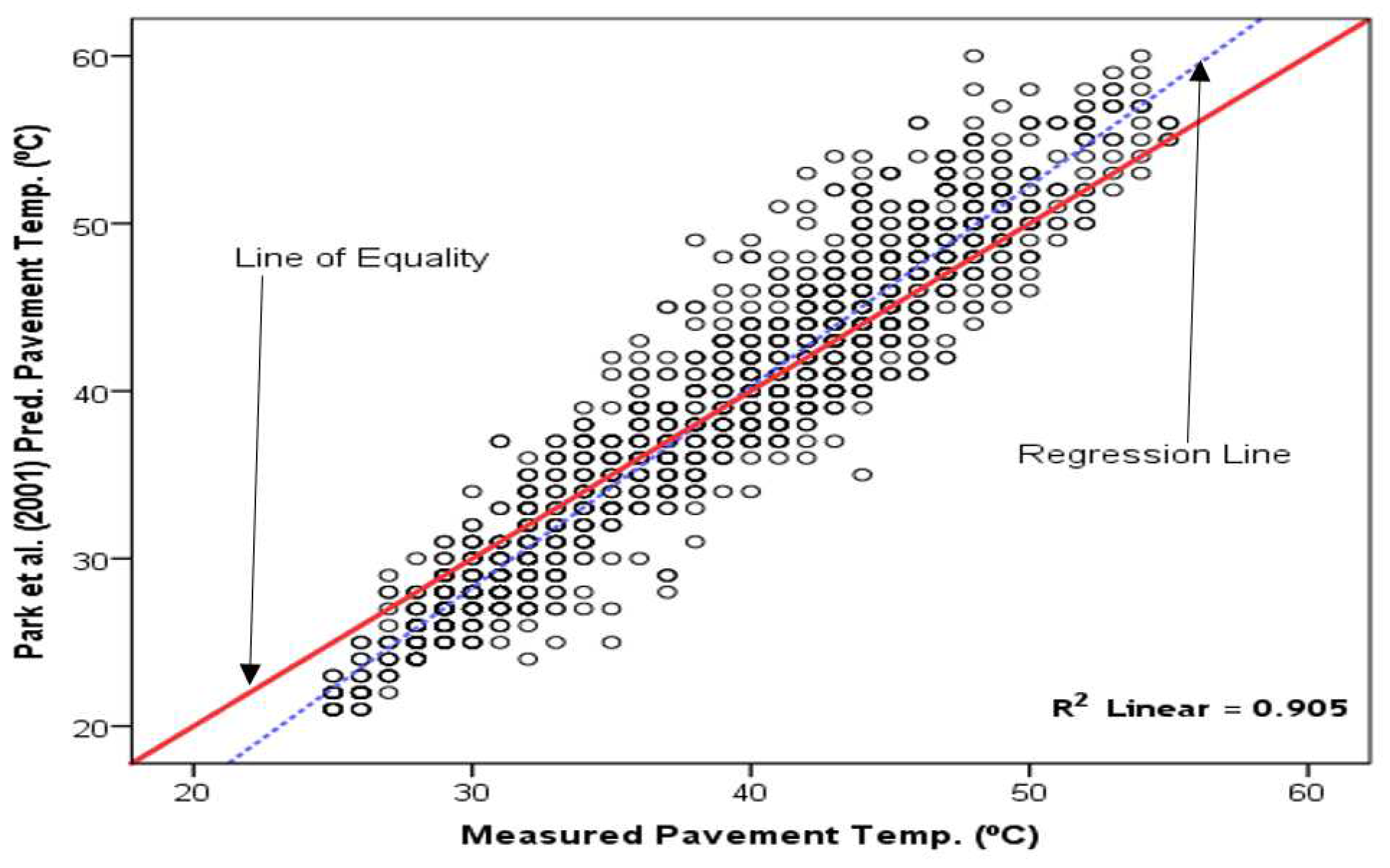
Preprints 80769 g009
Figure 9. The Park et al. [2] model-predicted versus measured daily maximum pavement temperature on RSM Road (Tamale).
Figure 9. The Park et al. [2] model-predicted versus measured daily maximum pavement temperature on RSM Road (Tamale).
Preprints 80769 g009
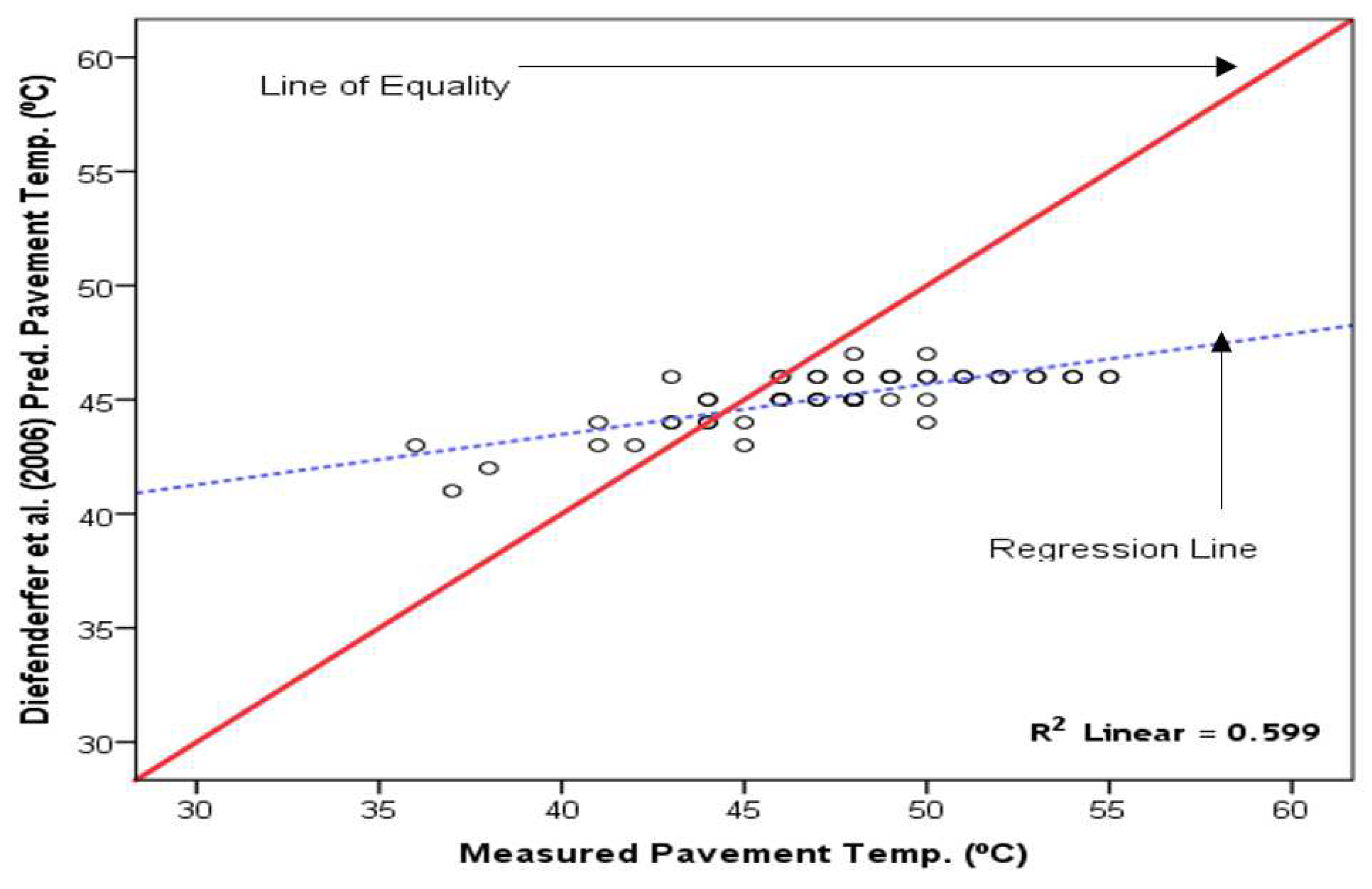
Preprints 80769 g010
Figure 10. The Diefenderfer et al. [3] model-predicted daily maximum versus measured daily maximum pavement temperature on RSM Road (Tamale).
Figure 10. The Diefenderfer et al. [3] model-predicted daily maximum versus measured daily maximum pavement temperature on RSM Road (Tamale).
Preprints 80769 g010
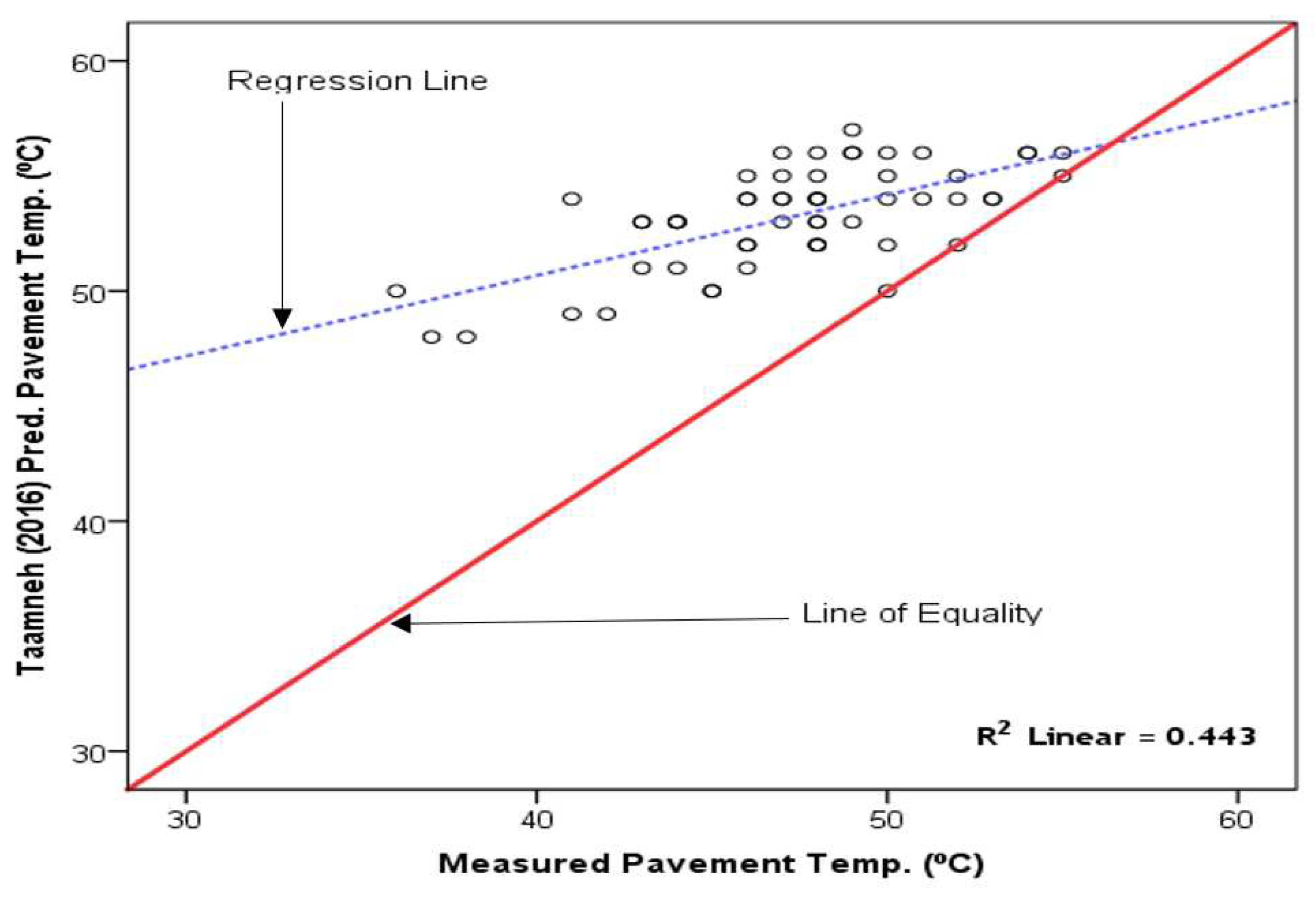
Preprints 80769 g011
Figure 11. The Taamneh [4] model-predicted daily maximum versus measured daily maximum pavement temperature on RSM Road (Tamale).
Figure 11. The Taamneh [4] model-predicted daily maximum versus measured daily maximum pavement temperature on RSM Road (Tamale).
Preprints 80769 g011
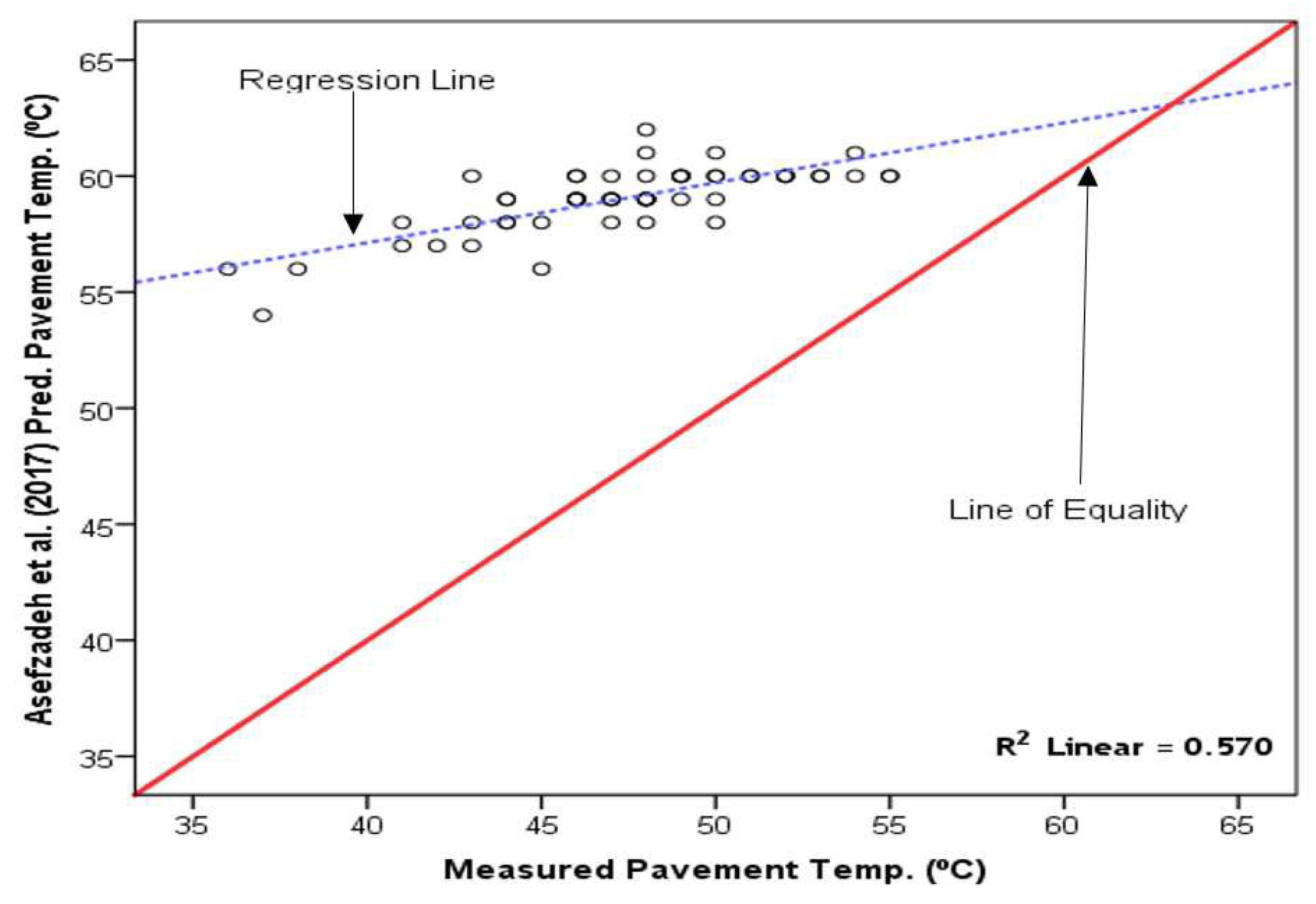
Preprints 80769 g012
Figure 12. The Asefzadeh et al. [5] model-predicted daily maximum versus measured daily maximum pavement temperature on RSM Road (Tamale).
Figure 12. The Asefzadeh et al. [5] model-predicted daily maximum versus measured daily maximum pavement temperature on RSM Road (Tamale).
Preprints 80769 g012
Table 1. Details of Study Roads.
Table 1. Details of Study Roads.
Road City AC Layer Thickness (mm) Distance from GMet Station (km) Latitude of GMet Station (°)
Mango Road Kumasi 76 0.8 6.68
RSM Road Tamale 70 1.9 9.58
Table 2. Pavement Temperature Data Collection Schedule.
Table 2. Pavement Temperature Data Collection Schedule.
Month May 2022 June 2022 July 2022 Aug 2022 Sept 2022 Oct 2022 Nov 2022 Dec 2022
Week No. 4 4 1 2 1 4 4 3
Data Collection Period 23rd – 29th 22nd – 28th 4th – 10th 8th – 14th 1st - 7th 24th – 30th 22nd – 28th 15th -21st
Table 3. T-test results of predicted versus measured asphalt pavement temperatures.
Table 3. T-test results of predicted versus measured asphalt pavement temperatures.
Location Model df t P-value
Kumasi BELLS3 [1] 2780.9 -8.704 <0.0001
Park et al. [2] 2676.1 1.602 0.1092
Diefenderfer et al. [3] 59.6 -1.635 0.1074
Taamneh [4] 67.1 8.596 <0.0001
Asefzadeh et al. [5] 62.6 17.326 <0.0001
Tamale BELLS3 [1] 2766.9 -9.762 <0.0001
Park et al. [2] 2660.9 0.014 0.989
Diefenderfer et al. [3] 63.9 -3.799 0.0003
Taamneh [4] 83.3 9.359 <0.0001
Asefzadeh et al. [5] 67.668 19.775 <0.0001
Table 4. Comparison of Error Statistics.
Table 4. Comparison of Error Statistics.
Models Kumasi (Forest Zone) Tamale (Savannah Zone)
RMSE (°C) MPE (%) MBE (°C) RMSE (°C) MPE (%) MBE (°C)
BELLS3 [1] 3.5 6.5 -2.3 3.6 7.9 -2.8
Park et al. [2] 3.6 -0.9 0.5 3.2 0.8 0.0
Diefenderfer et al. [3] 4.8 1.2 -1.1 4.0 4.0 -2.2
Taamneh [4] 7.5 -15.6 6.4 6.7 -13.2 5.9
Asefzadeh et al. [5] 13.2 -29.6 12.4 12.1 -25.4 11.7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated